On Fast Jerk-Continuous Motion Functions with Higher-Order Kinematic Restrictions for Online Trajectory Generation

Abstract

In robotics and automated manufacturing, motion functions for parts of machines need to be designed. Many proposals for the shape of such functions can be found in the literature. Very often, time efficiency is a major criterion for evaluating the suitability for a given task. If there are higher precision requirements, the reduction in vibration also plays a major role. In this case, motion functions should have a continuous jerk function but still be as fast as possible within the limits of kinematic restrictions. The currently available motion designs all include assumptions that facilitate the computation but are unnecessary and lead to slower functions. In this contribution, we drop these assumptions and provide an algorithm for computing a jerk-continuous fifteen segment profile with arbitrary initial and final velocities where given kinematic restrictions are met. We proceed by going systematically through the design space using the concept of a varying intermediate velocity and identify critical velocities and jerks where one has to switch models. The systematic approach guarantees that all possible situations are covered. We implemented and validated the model using a huge number of random configurations in Matlab, and we show that the algorithm is fast enough for online trajectory generation. Examples illustrate the improvement in time efficiency compared to existing approaches for a wide range of configurations where the maximum velocity is not held over a period of time. We conclude that faster motion functions are possible at the price of an increase in complexity, yet which is still manageable.

1. Introduction

Moving quickly from one motion state (position, velocity, acceleration, …) to another one is essential for efficiency and quick reactions to unforeseen events in robotics as well as in other areas such as automated manufacturing machines [1,2,3]. This has led to numerous suggestions of motion functions that take into account restrictions on velocity, acceleration and even higher-order derivatives [1]. The meanwhile classical approach using a “bang-zero-bang” discontinuous acceleration profile, which switches from maximum to zero to minimum constant values, turned out to be unsuitable in many cases, since it cannot be realized by controllers and induces unwanted vibrations. Therefore, very often, motion functions are required to have at least a continuous acceleration. An algorithm for computing such a function with piecewise constant jerk (”seven segment profile”) was presented by the author in [4], where restrictions on velocity, acceleration, and jerk and boundary conditions regarding velocity and acceleration can be prescribed. If there are stronger requirements on vibration reduction (e.g., for restricting position errors), higher-order continuity of the motion function has proven to be effective in experimental settings [5,6,7,8,9,10,11,12]. In this contribution, we present an algorithm for computing a jerk-continuous motion function (as opposed to the piecewise-constant, discontinuous jerk function designed in [4]) in one dimension, such that symmetric restrictions regarding velocity, acceleration, jerk, and snap (the derivative of the jerk, abbreviated as sn in the sequel) are fulfilled and boundary conditions for position and velocity can be arbitrarily prescribed. We term this function as “fast” because, at any time, for at least one of the kinematic restrictions, the maximum or minimum is reached. Moreover, we show that the algorithm for computing this function is fast enough for online trajectory generation where a computation should be performed within a controller cycle [13,14].

Since the task of designing a fast motion function is so elementary, a considerable number of research articles have appeared, particularly in the last two decades. This work can roughly be organized into two classes: in the first one, the task has been formulated as a restricted optimization problem, and algorithms from this field have been applied (e.g., [15,16,17,18,19,20,21,22,23,24,25]). This approach has the advantage that other aspects such as position errors regarding a given path or energy consumption can be easily included, and even a multi-objective optimization can be performed [22]. Moreover, optimization approaches often employ quintic spline functions, which guarantees continuity up to the snap function (fourth derivative). Yet, for online trajectory generation, the optimization algorithms are too slow. Only the contribution by Valente et al. [18] reports a sufficiently fast optimization procedure, but their three-segment profile could also be computed directly and leaves much space for improving on time efficiency. This leads to a second kind of approach, which construct the motion function directly based on the given restrictions and boundary conditions. For the subsequent literature overview, we restrict ourselves to those approaches which design a jerk-continuous motion function where restrictions at least regarding velocity, acceleration and jerk can be prescribed [11,12,26,27,28,29,30,31,32,33,34].

In order to provide a well-structured overview, we apply the following criteria in our description: we first consider the kind of task regarding the boundary conditions of the motion. In many tasks, point-to-point motions are to be designed (e.g., in pick-and-place tasks) where initial and final velocities and accelerations are zero. These are also called rest-to-rest motions and are abbreviated as RR in

Table 1. Jerk-Continuous Motion Functions with Restrictions.

Author/Year	Boundary Conditions	Type of Jerk Function	Continuity Level	Kinematic Restrictions	Constant Phases	Additional Assumptions
Lambrechts et al. 2005 [26]	RR	Piecewise linear, 15 segments	3	v, a, j, sn	v, a, j	j = 0 at max./min. velocity
Nguyen et al. 2008 a [27]	RR	Piecewise linear, 15 segments or higher order	3+	v, a, j, sn +	v, a, j, sn +	j = 0 at max./min. velocity +
Nguyen et al. 2008 b [27]	RR	Piecewise trigon. and zero, 7 segments	4	v, a, j	v, a	j = 0 at max./min. velocity
Lee/Choi 2015 [29]	RR	Piecewise trigon. and zero, 7 segments	4	v, a, j	v, a	j = 0 at max./min. velocity; sn = 0 at max./min. acceleration
Fang et al. 2019 [30]	RR	Piecewise sigmoid and constant, 15 segments	$\infty$	v, a, j, sn	v, a, j, sn	j = 0 at max./min. velocity; sn = 0 at max./min. acceleration
Wang et al. 2019 [31]	RR	3rd degree poly., constant, 3rd degree poly.	3	v, a, j	v	$v_{max}$ is reached
Fang et al. 2020 [12]	RR	Piecewise trigon. and constant, 15 segments	3	v, a, j	v, a, j	j = 0 at max./min. velocity
Wu et al. 2022 [32]	RR	Piecewise trigon. and constant, 15 segments	3	v, a, j	v, a, j	j = 0 at max./min. velocity; $j_{max}$ is reached
Biagiotti/Melchiorri 2019 [11]	RR	Piecewise linear, 15 segments or higher order	3+	v, a, j, sn +	v, a, j, sn +	algorithms are based on assumptions
Biagiotti /Melchiorri 2020 [33]	RR	Piecewise trigon. and zero, 7 segments	3+	v, a, j +	v, a +	j = 0 at max./min. velocity
Biagiotti et al. 2008 [1]	GG	Piecewise linear, 15 segments	3	v, a, j, sn	v, a, j, sn	all maximal/minimal values are reached
Fan et al. 2012 [28]	GG	Piecewise linear, 15 segments	3	v, a, j, sn	v, a, j, sn	j = 0 at max./min. velocity
Own 2022	GG	Piecewise linear, 15 segments	3	v, a, j, sn	v, a, j, sn	none
Ezair et al. 2015 [34]	BB+	Piecewise linear, 15 segments or higher order	3+	v, a, j, sn +	v, a, j, sn +	j = 0 at max./min. velocity +

. In automated manufacturing, one often has a situation where initial and final velocities are given and higher-order derivatives are zero (cf. [17,35,36]), e.g., when a tool moves with constant velocity for performing a certain task and then has to quickly move to another place to again perform a task with constant velocity. Using an abbreviation from a guideline of the German Association of Engineers [37], we term this task GG in Table 1 (for more information on the tasks, see [4]). Note that the task GG comprises the task RR, since the velocities are allowed to be zero. In robotics, there are also situations where the initial and final velocities and accelerations are arbitrary, e.g., when one has to react to unforeseen events (see [13]). This kind of task is abbreviated as BB in Table 1, where BB+ denotes that higher-order derivatives greater than 2 can also be prescribed. Again, the task BB contains the task GG. As can be seen in Table 1, most of the recent articles are restricted to RR, since this task can become already quite complicated when a fast motion function using the limitations as far as possible is required. The second criterion consists of the type of jerk function. Many of the designed functions in Table 1 work with a fifteen-segment approach, which is the natural extension of the seven-segment profile for motion functions with continuous acceleration. Some authors [11,27,34] also allow more generally for $2^n-1$ segments when restrictions up to the n-th derivative are to be taken into account. Other approaches achieve smoother jerk functions using trigonometric and zero pieces (having less discontinuities in the snap), but this restricts the possibilities to stay at the maximum value for some period of time. The next criterion is the continuity level of the motion function, i.e., up to which derivative continuity is guaranteed. All functions considered in this summary are required to be at least jerk-continuous, i.e., the continuity level must be at least 3. As can be seen from Table 1, most of the reviewed articles guarantee just the minimum order of 3. In the functions proposed by Lee and Choi [29] and Nguyen et al. [27] (part b), the snap is also continuous, which, on the other hand, has the disadvantage of a slower motion. In the approach by Ezair et al. [34], Nguyen et al. [27] (part a) and Biagiotti and Melchiorri [11,33], the continuity order can be freely chosen (we denote this by adding a “+” in Table 1), but orders higher than 3 lead to an increase in computational effort, which can make the suitability for online trajectory generation questionable. Fang et al. [30] propose the sigmoid function for going from one constant segment to another one, where all derivatives are continuous. Again, this leads to slower motion functions, as there is always a tradeoff between smoothness and time efficiency. The next criterion is concerned with the kind of kinematic restrictions that can be taken into account. As stated above, we only consider proposals where restrictions on velocity, acceleration and jerk can be guaranteed. Only the designs that work with fifteen segments using linear pieces (or the sigmoid function) also allow us to prescribe a restriction on the snap. This way, it is possible to avoid jerk functions that are “theoretically” continuous but have such a steep increase in jerk that the intended property of vibration reduction is not achieved. In the proposals by Ezair et al. [34], Nguyen et al. [27] (part a) and Biagiotti and Melchiorri [11], one can choose up to which derivative restrictions can be described (denoted by a “+” in Table 1).

The final two criteria deal with the question of whether the proposed shape or algorithm affects the time optimality of the motion function. The first one states for which kinematic functions periods of constant maximum or minimum value are possible. If this is not the case, the resulting functions are often sub-optimal because they do not take full advantage of the given restrictions. Only the designs working with a piecewise linear function with fifteen segments (or more) provide the possibility of having constant phases for maximum/minimum velocity, acceleration, jerk and snap. If there are only three segments as in Wang et al. [31], only the velocity can be held at a constant extremal value. Secondly, there are assumptions in nearly all proposals that are often implicit in the jerk functions and are only seldom stated explicitly. Biagiotti and Melchiorri [1] point out that the provided formulae are only valid when all extremal values (for v, a, j) are taken (this requires a minimum distance to be travelled). In the function proposed by Fang et al. [29], the extremal jerk must occur, which, again, is not necessary for small distances. All but one of the approaches include an assumption that is recognized as making the function potentially sub-optimal by Ezair et al. [34] and Biagiotti and Melchiorri [11]: they assume that when the velocity reaches its extremum in the middle piece (in functions with fifteen segments, this is segment eight), the jerk goes back to zero. This is only necessary when the extremum is the maximum/minimum possible velocity, and this is held for a time period of length greater than zero. If the distances to be travelled are not so large that this is the case, then the assumption leads to an avoidable loss in time efficiency. In the approaches by Fang et al. [30], Nguyen et al. [27] (part b) and Lee and Choi [29], additionally, the shape of the function requires the snap to be zero when the extremum of the acceleration is reached, which is also unnecessary. Moreover, this applies to higher-order derivatives in Ezair et al. [34] and Nguyen et al. 2008 a [27]. The reason for making this assumption is quite obvious: it leads to a mathematically better tractable problem with manageable complexity. Only in the approach by Biagiotti and Melchiorri [19] (in the task RR) is a way to remedy this problem suggested by staying at the maximum/minimum jerk level, but we will give an example showing that, still, their algorithm includes assumptions that prevent them from finding a time-optimal solution in several configurations.

The design presented in this contribution improves what can be found in the literature in the following ways:

• We design a jerk-continuous motion function with better time efficiency by avoiding any additional assumption, particularly that the jerk must go down to zero at the intermediate extremal velocity. This improves the currently available approaches relating to the rest-to-rest (RR) task as well as the work on the GG task (arbitrary initial and final velocities). Using randomly generated input data (restrictions, distance, initial and final velocities), we demonstrate that there are a variety of different possible configurations, and hence we show that the task has an inherent level of complexity that cannot be sidestepped without staying sub-optimal in some situations. Therefore, one cannot expect that simple algorithms will optimally cover all situations.
• The algorithm presented in this contribution is also computationally efficient and hence suitable for Online Trajectory Generation (OLG), which is needed to quickly react to unforeseen events in human–robot interactions.

We do not term our approach “optimal” because we do not have mathematical proof for this (for such kinds of proof see [28,34] where, for example, in [28] the proof is performed by assuming that there is a motion function needing less time, which leads to a contradiction based on a theorem from the field of differential equations; the proof depends on the additional assumption that the jerk is zero at an intermediate velocity). Since, at any time, at least one restriction is adopted, we term our function “fast”.

Our approach has two main areas of real-world application: first, to improve on time efficiency and hence throughput in automated production and, at the same time, to control vibrations and positioning errors by guaranteeing jerk continuity and restriction; secondly, to allow for quick reaction in case of unforeseen events in robotics, particularly when human interaction is involved and computing a new motion function must be performed within a controller cycle (cf. [13,25]).

The paper is structured as follows: Section 2 provides some basic concepts and visualizations that guide our work, and we split the task into two major cases depending on whether or not the maximum jerk can be reached before the maximum acceleration (the distinction is already made in Fan et al. [28]). In Section 3 and Section 4, the motion models that can occur in cases I and II are stated, and criteria for switching between models are investigated depending on the intermediate critical velocities and jerk values being reached. In Section 5, we outline our algorithm for setting up the fifteen-segment profile by finding the suitable model. We present our implementation in Matlab^®, which we validated using a huge number of randomly chosen tasks. Stability and time efficiency aspects important for online trajectory generation are discussed. In Section 6, we compare our results with those of Fan et al. [28], Ezair et al. [34] and Biagiotti and Melchiorri [11] by presenting some numerical experiments in example configurations. Section 7 summarizes the results, highlights the improvements and outlines directions of future work. All formulae and algorithms needed to reproduce our work have been placed in the appendices.

2. Basic Concepts and Situations

This contribution is concerned with finding a fast jerk-continuous motion function when the following six values are given: $s{n}_{max}$, $j_{max}$, $a_{max}$, $v_{max}$ (each >0) such that $-s{n}_{max}\le sn\left(t\right)\le s{n}_{max}$,$-j_{max}\le j\left(t\right)\le j_{max}$,$-a_{max}\le a\left(t\right)\le a_{max}$,$-v_{max}\le v\left(t\right)\le v_{max}$; initial velocity: $v_A$; final velocity: $v_E$; distance: Δs (arbitrary real numbers). Initial and final accelerations and jerks are assumed to be zero. 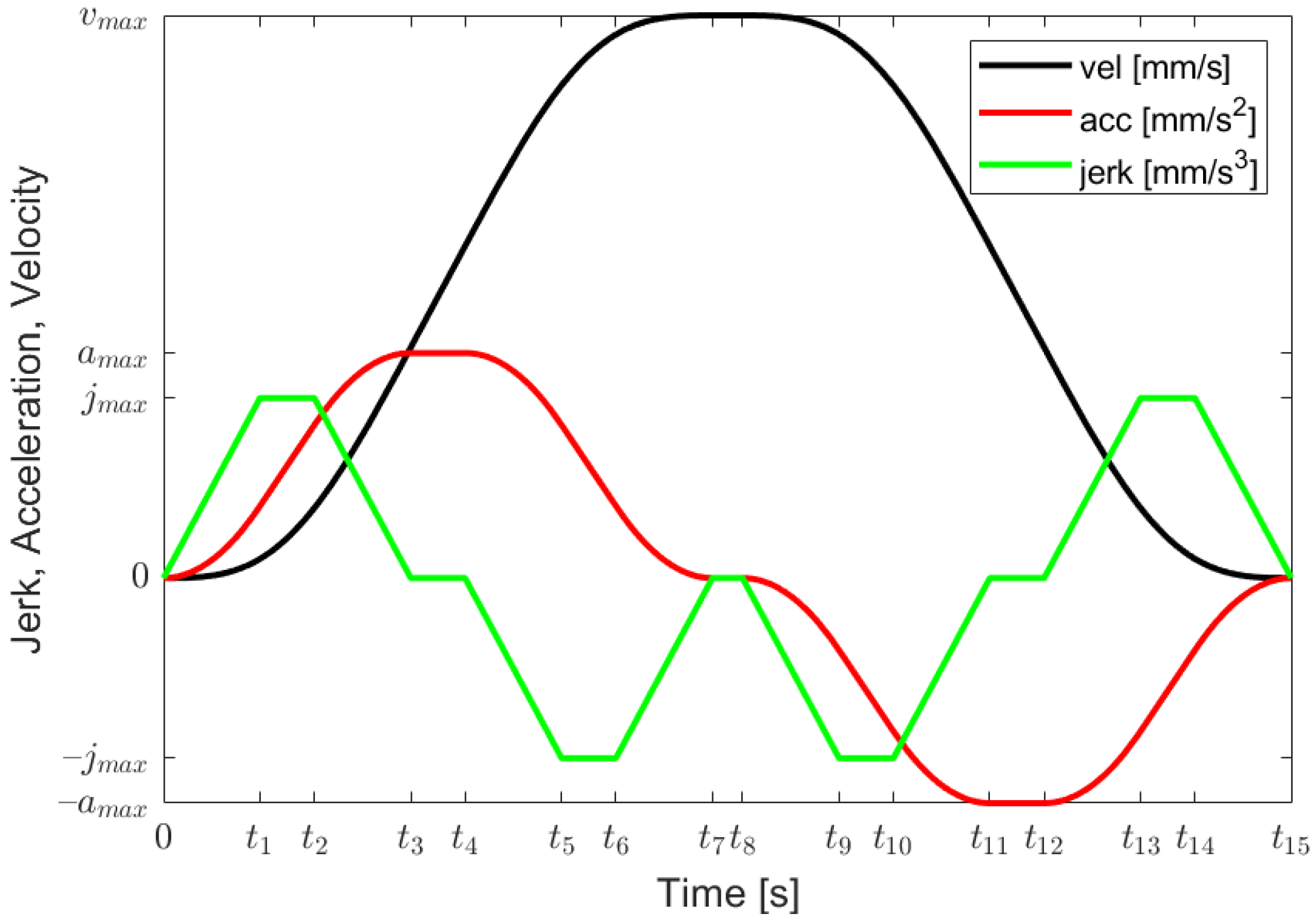Without loss of generality, we only consider the case $v_A\le v_E$, since otherwise, we can simply change the positive direction of the distance. We solved this task using a fifteen-segment profile, as shown in Figure 1, for the rest-to-rest (RR) situation. Note that all fifteen segments are only needed when the maximum and minimum jerk, acceleration and velocity values are taken for a time period of length larger than zero.

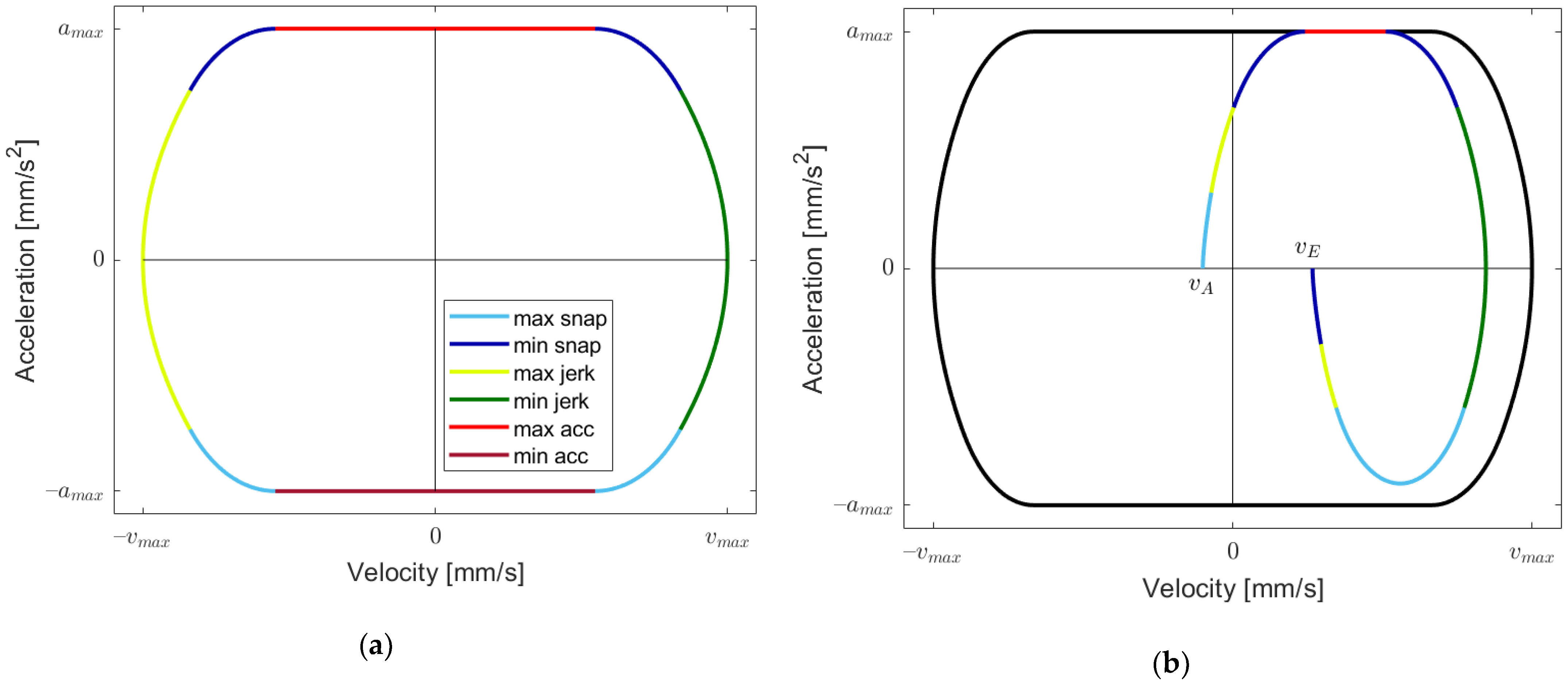
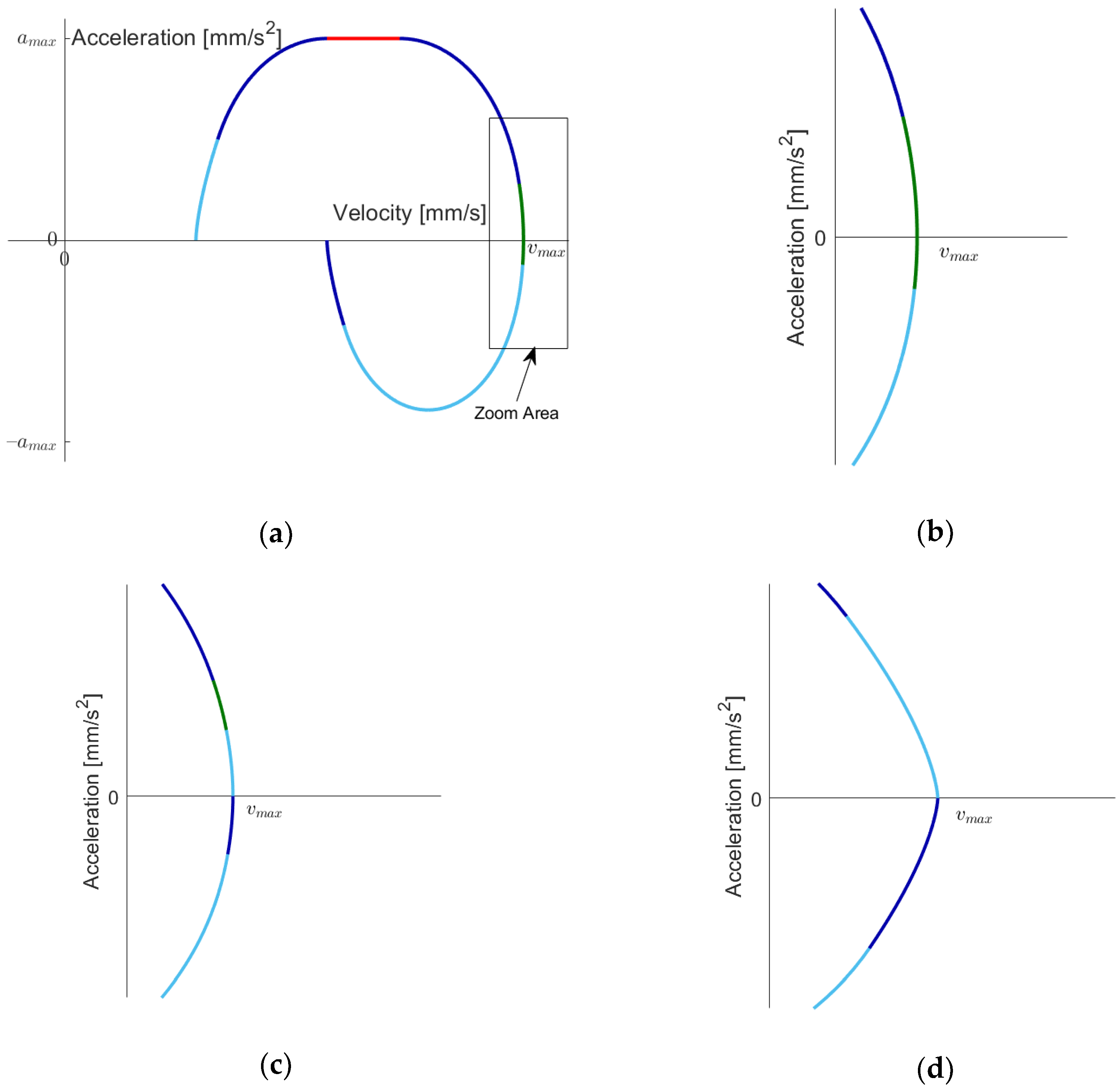
Broquere et al. [38] introduced the so-called velocity-acceleration plane to visualize seven-segment motion functions. This visualization has proved to be very helpful in [4] in order to systematically go through the space of all possible situations. In this contribution, we proceed analogously, but the plane has more structure to it. Figure 2a depicts the area of the plane within which a motion can be placed as a parametric curve $\left(v\left(t\right),a\left(t\right),t=0\dots t_{end}\right)$. The boundary curve consists of pieces where the extremal values of snap, jerk and acceleration, respectively, are taken. We apply the following color coding: light blue, light green and light red denote the maximum values of snap, jerk and acceleration, respectively. The “dark” versions of the colors denote the minimum values. In order to avoid over-coloring, we draw the boundary curve in black and only apply the color coding for the parametric motion curves. This can be seen in Figure 2b, where an example curve is displayed, which has only nine segments. Such a curve must run from left to right through the upper half-plane and from right to left through the lower one. Note that the parametric curves do not have any kinks, as is the case for only acceleration–continuous motion functions with piecewise constant jerk, as considered in [4,38].

As is conducted in [28], we distinguish between two major cases depending on whether or not the maximum jerk is reached when applying the maximum and minimum snap in order to get from acceleration zero to maximal acceleration. For the convenience of the reader, we briefly summarize some of the results developed in [28]. The maximum jerk is not reached (Case I) if and only if $j_{max}>\sqrt{a_{max}·s{n}_{max}}$ holds. We term the other case as Case II in the sequel. We describe a point in the velocity–acceleration plane by a triple $\left(v,a, j\right)$, where the third “coordinate” provides the jerk value of the point $\left(v,a\right)$. A straightforward computation (cf. [28]) yields the time needed for going from $\left(v_A,0, 0\right)$ to $(v_E,0, 0)$ in the velocity–acceleration plane by accelerating and decelerating as much as possible (see Figure 3a), abbreviated as $T\left(v_A,v_E\right)$. The results need further sub-cases and are given in

Table 2. Results by Fan et al. [28].

Cases	Additional Conditions	Durations
$\mathrm{Case} \mathrm{I} (j_{max}$ not reached)
$\mathrm{Sub}-\mathrm{Case}: a_{max}$ is not reached	$v_E-v_A<2s{n}_{max}{\left(\frac{a_{max}}{s{n}_{max}}\right)}^{3/2}$	$T\left(v_A,v_E\right)=4·\sqrt[3]{\frac{v_E-v_A}{2s{n}_{max}}}$
$\mathrm{Sub}-\mathrm{Case}: a_{max}$ is reached	$v_E-v_A\ge 2s{n}_{max}{\left(\frac{a_{max}}{s{n}_{max}}\right)}^{3/2}$	$T\left(v_A,v_E\right)=4·\sqrt{\frac{a_{max}}{s{n}_{max}}}+\frac{v_E-v_A-2s{n}_{max}{\left(\frac{a_{max}}{s{n}_{max}}\right)}^{3/2}}{a_{max}}$
$\mathrm{Case} \mathrm{II} (j_{max}$ reached)
$\mathrm{Sub}-\mathrm{Case}: a_{max}$$\mathrm{and} j_{max}$ not reached	$v_E-v_A<2s{n}_{max}{\left(\frac{j_{max}}{s{n}_{max}}\right)}^3$	$T\left(v_A,v_E\right)=4·\sqrt[3]{\frac{v_E-v_A}{2s{n}_{max}}}$
$\mathrm{Sub}-\mathrm{Case}: a_{max}$$\mathrm{not} \mathrm{reached}, j_{max}$ reached	$v_E-v_A\ge 2s{n}_{max}{\left(\frac{j_{max}}{s{n}_{max}}\right)}^3$ and $v_E-v_A<a_{max}\left(\frac{j_{max}}{s{n}_{max}}+\frac{a_{max}}{j_{max}}\right)$	$T\left(v_A,v_E\right)=\frac{j_{max}}{s{n}_{max}}+\frac{\sqrt{4\left(v_E-v_A\right)·j_{max}·s{n}_{max}{}^2+j_{max}^4}}{j_{max}·s{n}_{max}}$
$\mathrm{Sub}-\mathrm{Case}: a_{max}$$\mathrm{reached} (\mathrm{hence} j_{max}$)	$v_E-v_A\ge a_{max}\left(\frac{j_{max}}{s{n}_{max}}+\frac{a_{max}}{j_{max}}\right)$	$T\left(v_A,v_E\right)=\frac{j_{max}}{s{n}_{max}}+\frac{a_{max}}{j_{max}}+\frac{v_E-v_A}{a_{max}}$

.

Using the durations stated in Table 2, the distance for going directly from $\left(v_A,0, 0\right)$ to $(v_E,0, 0)$ can simply be computed as:

$$S\left(v_A,v_E\right)=\frac{v_A+v_E}{2}·T\left(v_A,v_E\right)$$

(1)

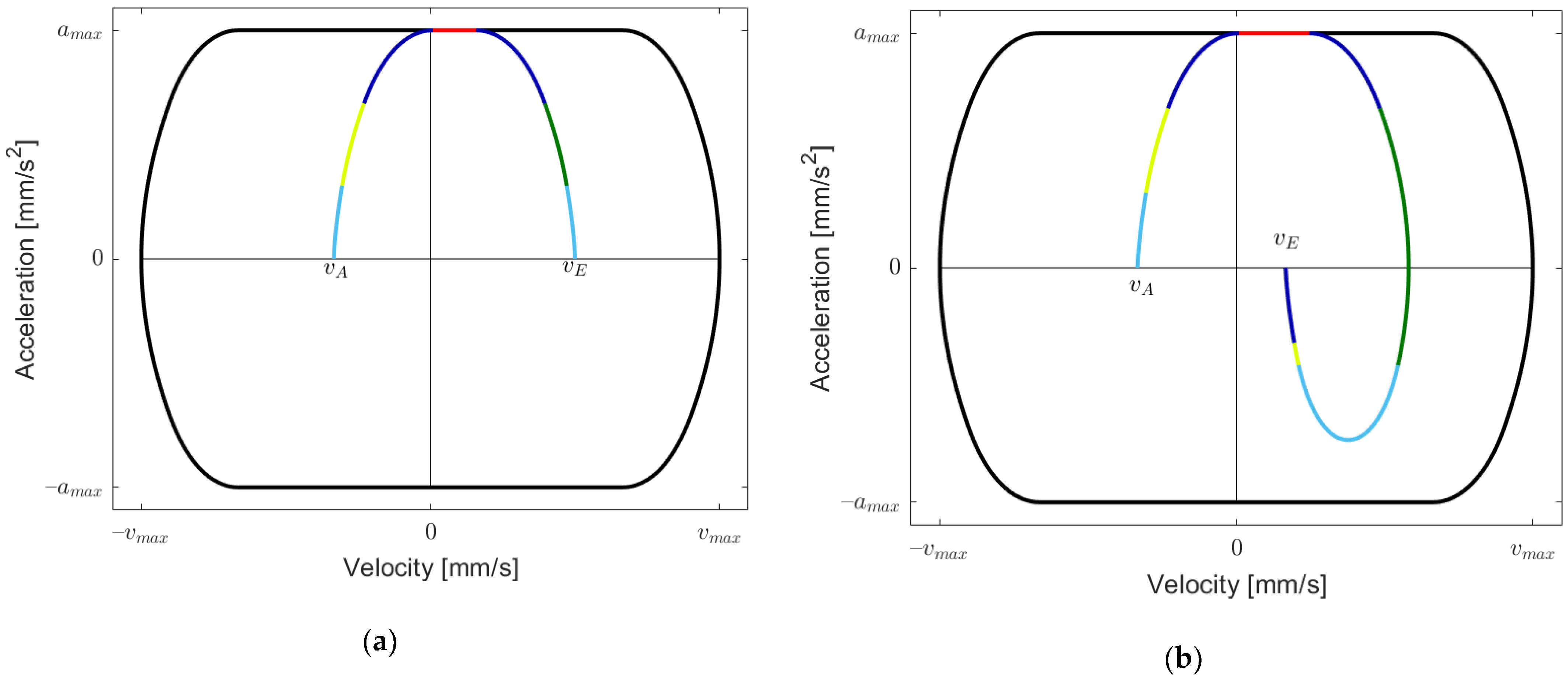
In [28], this consideration is actually sufficient, since it is assumed that when the velocity reaches its extremal value $v_m$, then the jerk goes back to zero, such that the overall motion can be split up into two parts, from $\left(v_A,0, 0\right)$ to $(v_m,0, 0)$ and from $\left(v_m,0, 0\right)$ to $(v_E,0, 0)$. This is depicted in Figure 3b.

Our basic idea is also to work with an intermediate extremal velocity $v_m$, but we obtain a shorter time (in cases where the maximum velocity is not taken for a non-zero period) by allowing the jerk to be non-zero. We will provide an example in Section 6. We first restrict ourselves to the situation where the required distance Δs is greater than or equal to $S\left(v_A,v_E\right)$. For finding a suitable intermediate velocity, we let $v_m$ move from $v_E$ to $v_{max}$. We choose the corresponding jerk value by finding the lowest (negative) value $j_m$ such that it is possible to get back from $\left(v_m, 0,j_m\right)$ to $\left(v_E,0, 0\right)$ using extremal snap. 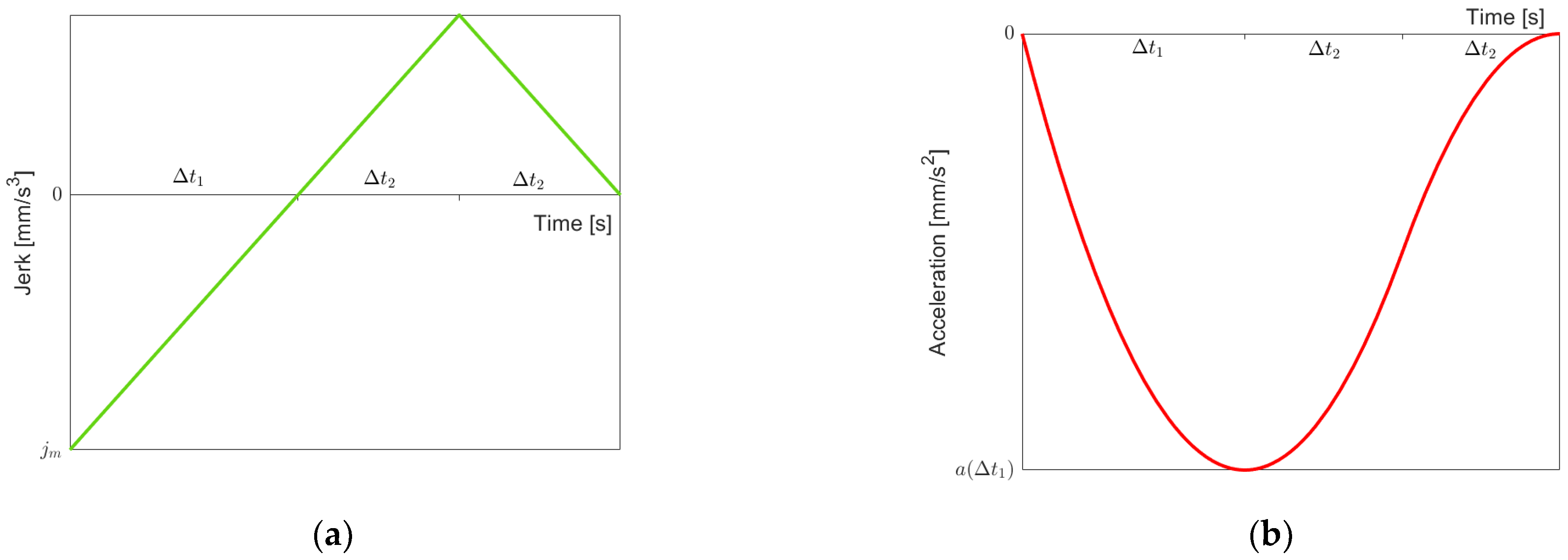Figure 4a shows the jerk function $j\left(t\right)$ with three time intervals of lengths $\Delta t_1$, $\Delta t_2$ and $\Delta t_3=\Delta t_2$. This function must fulfill the two requirements: $a\left(\Delta t_1+2\Delta t_2\right)=0$ and $v\left(\Delta t_1+2\Delta t_2\right)=v_E$. Since the snap is maximal on the first interval, we obtain

$$\Delta t_1=-\frac{j_m}{s{n}_{max}}.$$

(2)

From the first requirement, it follows that $-\frac{1}{2}{j}_m·\Delta t_1=s{n}_{max}{\left(\Delta t_2\right)}^2$, and hence

$$\Delta t_2=-\sqrt{\frac{1}{2}}·\frac{j_m}{s{n}_{max}}.$$

(3)

Now, we consider $a\left(t\right)$, as shown in Figure 4b. Since for $t\le \Delta t_1$, we have $a\left(t\right)=j_{m}t+\frac{1}{2}s{n}_{max}{t}^2$, we obtain

$$a\left(\Delta t_1\right)=-\frac{1}{2}·\frac{j_m^2}{s{n}_{max}}.$$

(4)

Now, we consider $v\left(t\right)$. For $t\le \Delta t_1$, we have $v\left(t\right)=v_m+\frac{1}{2}{j}_m{t}^2+\frac{1}{6}s{n}_{max}{t}^3$, and hence

$$v\left(\Delta t_1\right)=v_m+\frac{1}{2}{j}_m\Delta t_1{}^2+\frac{1}{6}s{n}_{max}\Delta t_1{}^3.$$

(5)

From the second requirement, we obtain $v_E=v\left(\Delta t_1+2\Delta t_2\right)=v\left(\Delta t_1\right)+\frac{1}{2}a\left(\Delta t_1\right)·2\Delta t_2$. By substituting according to Equations (2)–(5), we finally obtain

$$v_E=v_m+\left(\frac{1}{3}+\frac{\sqrt{2}}{4}\right)·\frac{j_m^3}{s{n}_{max}^2}$$

(6)

$$j_m=-\sqrt[3]{\frac{12s{n}_{max}{}^2·\left(v_m-v_E\right)}{4+3\sqrt{2}}}$$

(7)

From Equation (6), we can also easily compute the intermediate velocity $v_m$ for which $j_m$ reaches $j_{min}=-j_{max}$, which is $v_E-\left(\frac{1}{3}+\frac{\sqrt{2}}{4}\right)·\frac{j_{max}^3}{s{n}_{max}^2}$. Note that this might be larger than $v_{max}$, but we neglect this for the moment. We now define the function vm2jm, which maps $v_m$ to the corresponding jerk value $j_m$:

$$vm2jm\left(v_m\right)=\{\begin{array}{c}-\sqrt[3]{\frac{12s{n}_{max}{}^2·\left(v_m-v_E\right)}{4+3\sqrt{2}}} for v_E\le v_m\le v_E-\left(\frac{1}{3}+\frac{\sqrt{2}}{4}\right)·\frac{j_{max}^3}{s{n}_{max}^2}\\ -j_{max} for v_m>v_E-\left(\frac{1}{3}+\frac{\sqrt{2}}{4}\right)·\frac{j_{max}^3}{s{n}_{max}^2}\end{array}.$$

(8)

The main reasoning behind our method can be summarized as follows:

• In order to cover all possible distances larger than or equal to $S\left(v_A,v_E\right)$, we let the intermediate velocity and corresponding jerk $\left(v_m, 0,j_m\right)$ “flow” from $\left(v_E,0, 0\right)$ via $\left(v_m,0, vm2jm\left(v_m\right)\right)$ to $\left(v_{max},0, vm2jm\left(v_{max}\right)\right)$ where $vm2jm\left(v_m\right)$ might become constantly $j_{min}$ at some intermediate velocity. Then, we proceed further by going from $\left(v_{max},0, vm2jm\left(v_{max}\right)\right)$ to $\left(v_{max},0, 0\right)$. From there, one can achieve arbitrarily large distances by moving constantly with $v_{max}$. Since in this “flow”, we make continuous changes in $v_m$ and $j_m$, the covered distances also change continuously, and thus we have full coverage of all distances $\ge S\left(v_A,v_E\right)$. One can proceed in a similar way by letting $\left(v_m,0,j_m\right)$ run from $\left(v_A,0, 0\right)$ to $\left(-v_{max},0,0\right)$, covering all distances $\le S\left(v_A,v_E\right)$.
• In this “flow”, we identify the occurring jerk models and the switching points when there is a model change. For this, we compute the so-called “critical” velocities and jerks where extremal values of acceleration or jerk are reached.
• For all velocity-jerk combinations where there is a model change, we compute the distances reached such that we can determine which model must be applied for the given distance. In that model, we then can compute the time periods of the segments it consists of.

The subsequent Section 3 and Section 4 describe the occurring models, the computation of “critical” velocities and jerks as well as model sequences when traversing the velocity-acceleration plane. In Section 5, we describe how to compute the time periods in the applicable model using a simple bisection method.

3. Models and Critical Velocities and Jerks in Case I

In Case I, $j_{max}$ is not reached when going from $\left(v_A,0, 0\right)$ to the maximal acceleration where the jerk must be zero. The maximal possible jerk value occurs when starting at a point with $a=a_{min}$ and applying maximal snap until one reaches $a=0$. A simple computation yields the value $\sqrt{2a_{max}s{n}_{max}}$. If $j_{max}$ is larger than this value, we simply set $j_{max}=\sqrt{2a_{max}s{n}_{max}}$.

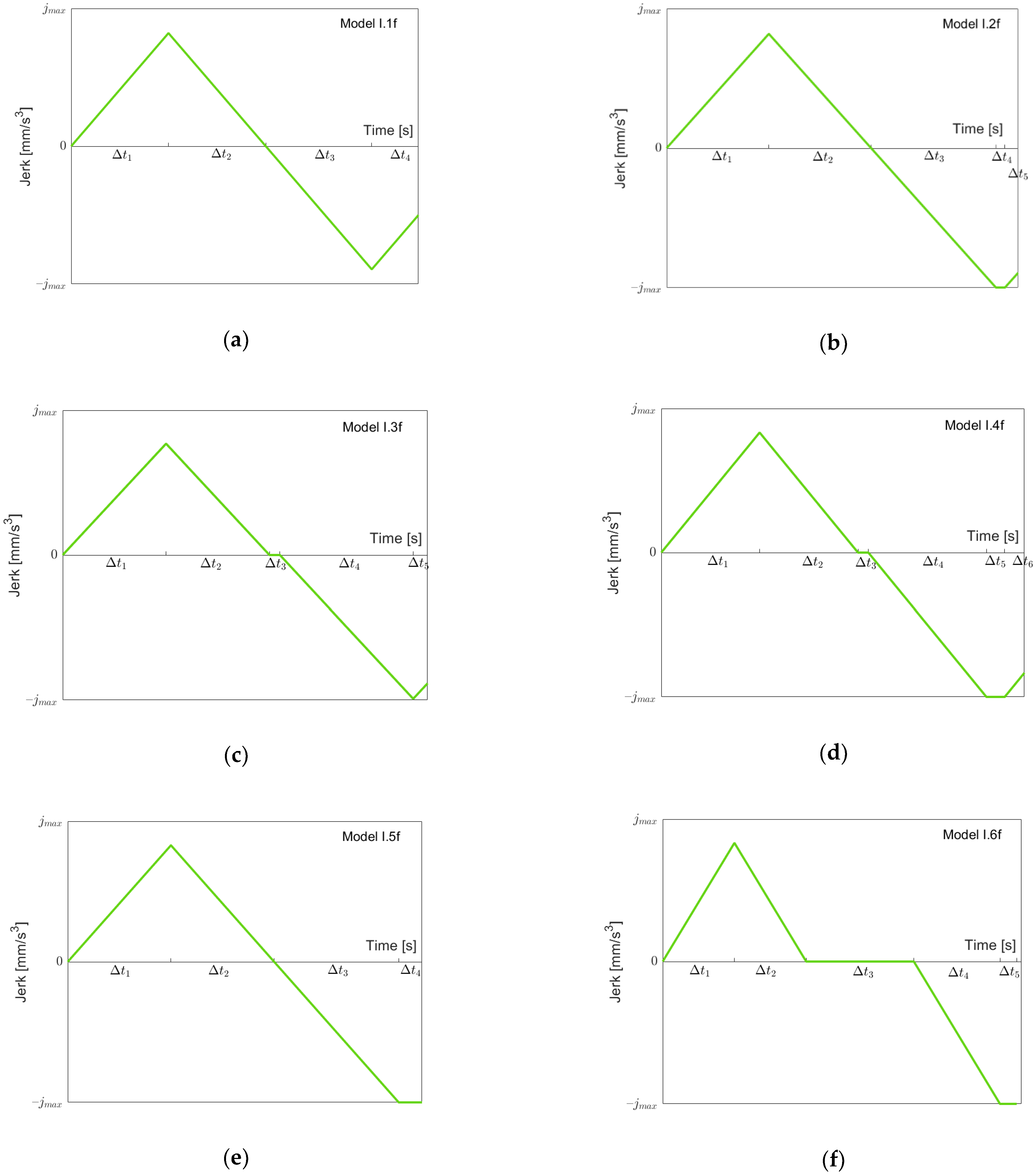
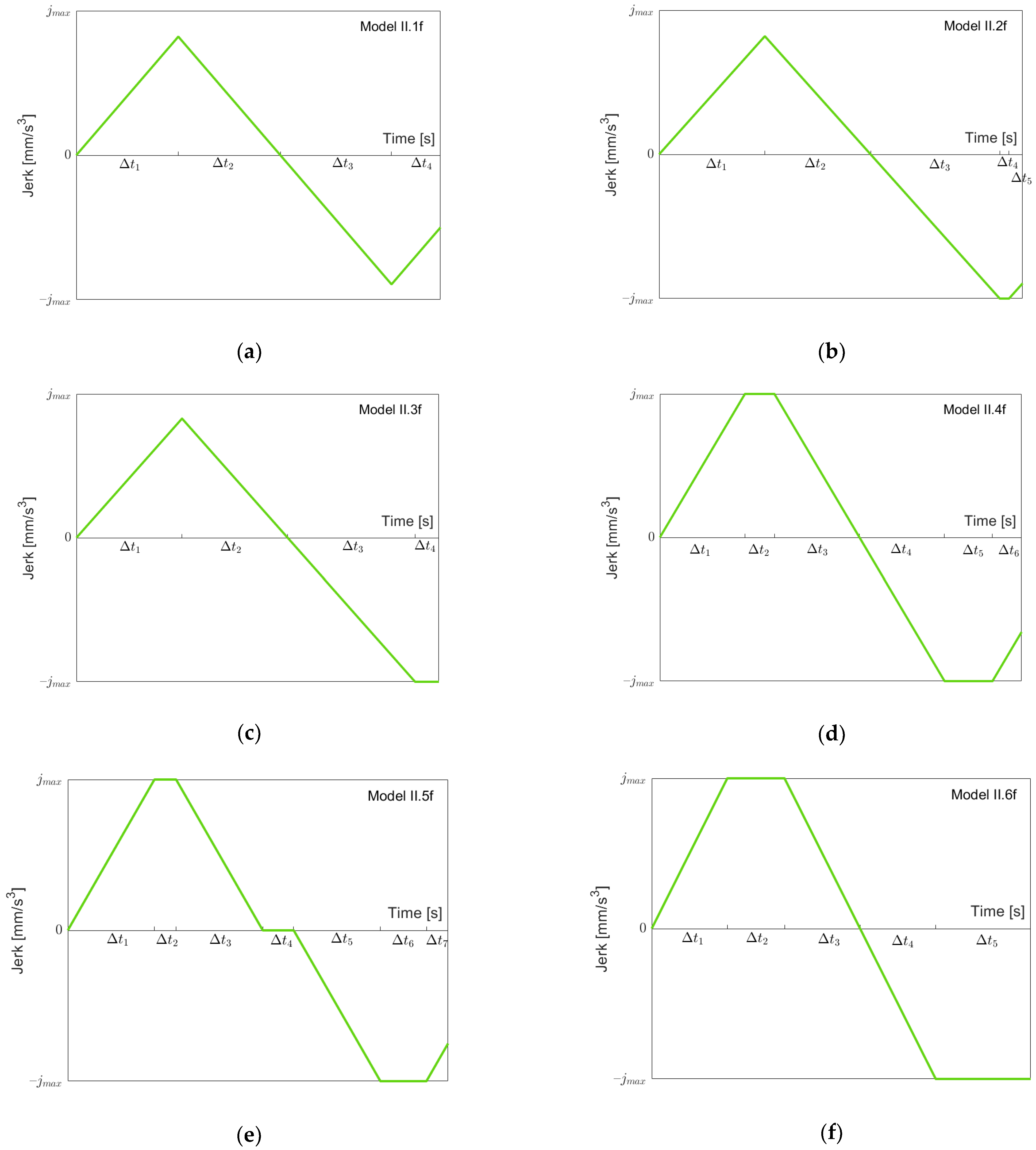
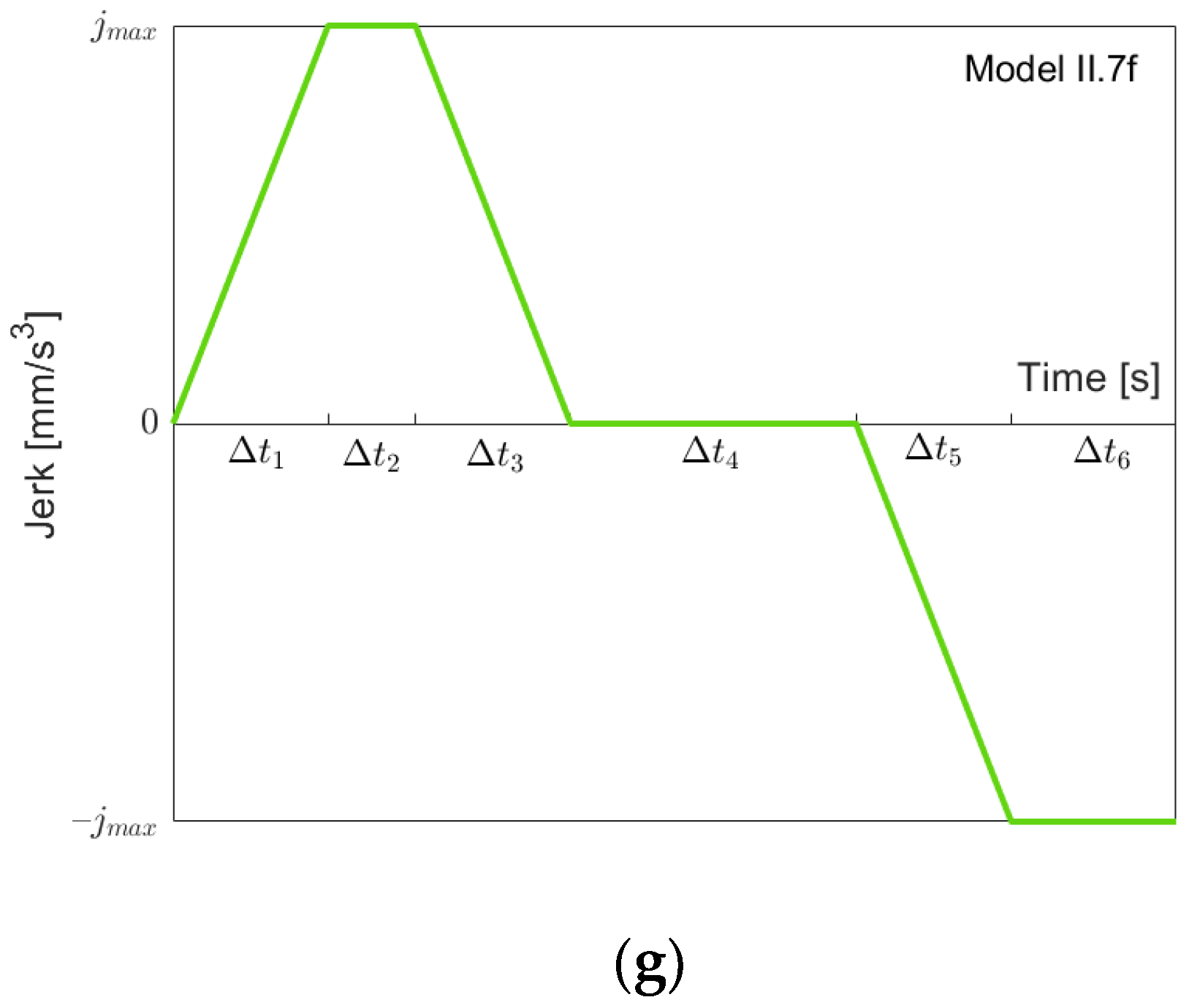
We first assume $\Delta s\ge S\left(v_A,v_E\right)$, and we neglect the restriction on maximal velocity. In order to manage complexity, we split the task of finding suitable models into two parts: going “forth” from $\left(v_A,0, 0\right)$ to $\left(v_m,0,j_m\right)$ and going “back” from $\left(v_m,0, j_m\right)$ to $\left(v_E,0, 0\right)$. Figure 5 shows possible jerk models for going “forth” using maximal, minimal or zero snap (the notation “I.xf” refers to these models in Case I). The first four models are built using the criteria of whether $j_{min}$ is or is not reached when going from the maximal acceleration (of this function) down to acceleration zero, and $a_{max}$ is or is not reached. Model I.1f depicts the situation where $j_{min}$ and $a_{max}$ are both not reached. Model I.2f shows the motion going “forth” when $j_{min}$ is reached but $a_{max}$ is not reached, whereas Model I.3f is vice versa. In Model I.4f, both $j_{min}$ and $a_{max}$ are reached. In both models I.2f and I.4f where $j_{min}$ is reached, $j_m>j_{min}$ still holds, which need not be the case. As in Model I.2f, in Model I.5f $j_{min}$ is reached and $a_{max}$ is still not reached, but now, $j_m=j_{min}$. Finally, in Model I.6f, both $j_{min}$ and $a_{max}$ are reached (as in Model I.4f), and $j_m=j_{min}$. Note that Models I.5f and I.6f could also be treated as special cases of Models I.2f resp. I.4f with $\Delta t_5=0$ resp. $\Delta t_6=0$. We decided to set up separate models for two reasons: reaching certain limits (here $j_m=j_{min}$) is more recognizable by having a model change, and the models can then be simpler (see the formulae in

Table A1. Formulae and polynomials for computing time intervals in Case I going forth.

Model	$\mathbf{\Delta }{\mathit{t}}_{\mathit{i}}$	Formulae and Polynomials
I.1f	$\Delta t_1$	$\sqrt{\frac{2\Delta t_3^2\Delta s{n}_{max}^2-j_m^2}{2s{n}_{max}^2}}$
	$\Delta t_3$	$$\begin{gathered} \frac{1}{s{n}_{max}}·roots\left(\left[36j_m^2,48j_m^3-144s{n}_{max}^2{v}_A+144s{n}_{max}^2{v}_m,-18j_m^4,-48j_m^5+144j_m^{2}s{n}_{max}^2{v}_A \\ -144j_m^{2}s{n}_{max}^2{v}_m,-17j_m^6+48j_m^{3}s{n}_{max}^2{v}_A-48j_m^{3}s{n}_{max}^2{v}_m-72s{n}_{max}^4{v}_A{}^2+144s{n}_{max}^4{v}_A{v}_m \\ -72s{n}_{max}^4{v}_m{}^2\right]\right) \end{gathered}$$
	$\Delta t_4$	$\Delta t_3+\frac{j_m}{s{n}_{max}}$
I.2f	$\Delta t_1$	$-\frac{j_{max}}{2s{n}_{max}}+\frac{\sqrt{9j_{max}^2+6\sqrt{9j_m^4+24j_m^3{j}_{max}+18j_m^2{j}_{max}^2-72j_{max}s{n}_{max}^2{v}_A+72j_{max}s{n}_{max}^2{v}_m}}}{6s{n}_{max}}$
	$\Delta t_3$	$\frac{j_{max}}{s{n}_{max}}$
	$\Delta t_4$	$\frac{2\Delta t_1^{2}s{n}_{max}^2+j_m^2-2j_{max}^2}{2s{n}_{max}{j}_{max}}$
	$\Delta t_5$	$\frac{j_m+j_{max}}{s{n}_{max}}$
I.3f	$\Delta t_1$	$\sqrt{\frac{a_{max}}{s{n}_{max}}}$
	$\Delta t_3$	$\frac{\left(-6a_{max}s{n}_{max}+3j_m^2\right)\sqrt{4a_{max}s{n}_{max}+2j_m^2}-12s{n}_{max}^2{a}_{max}\sqrt{\frac{a_{max}}{s{n}_{max}}}+12s{n}_{max}^2\left(-v_A+v_m\right)+4j_m^3}{12s{n}_{max}^2{a}_{max}}$
	$\Delta t_4$	$\Delta t_5-\frac{j_m}{s{n}_{max}}$
	$\Delta t_5$	$\frac{j_m+\raisebox{1ex}{$\sqrt{4a_{max}s{n}_{max}+2j_m^2}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{s{n}_{max}}$
I.4f	$\Delta t_1$	$\sqrt{\frac{a_{max}}{s{n}_{max}}}$
	$\Delta t_3$	$\frac{\left(\left(-24\sqrt{\frac{a_{max}}{s{n}_{max}}}{a}_{max}-24v_A+24v_m\right)j_{max}-12a_{max}^2\right)s{n}_{max}^2-12a_{max}{j}_{max}^{2}s{n}_{max}+3j_m^4+8j_m^3{j}_{max}+6j_m^2{j}_{max}^2}{24s{n}_{max}^2{j}_{max}{a}_{max}}$
	$\Delta t_4$	$\frac{j_{max}}{s{n}_{max}}$
	$\Delta t_5$	$\frac{2a_{max}s{n}_{max}+j_m^2-2j_{max}^2}{2s{n}_{max}{j}_{max}}$
	$\Delta t_6$	$\frac{j_m+j_{max}}{s{n}_{max}}$
I.5f	$\Delta t_1$	$-\frac{j_{max}}{2s{n}_{max}}+\frac{\sqrt{9j_{max}^2+6\sqrt{3j_{max}^4-72j_{max}s{n}_{max}^2{v}_A+72j_{max}s{n}_{max}^2{v}_m}}}{6s{n}_{max}}$
	$\Delta t_3$	$\frac{j_{max}}{s{n}_{max}}$
	$\Delta t_4$	$\frac{2\Delta t_1^{2}s{n}_{max}^2-j_{max}^2}{2s{n}_{max}{j}_{max}}$
I.6f	$\Delta t_1$	$\sqrt{\frac{a_{max}}{s{n}_{max}}}$
	$\Delta t_3$	$\frac{\left(\left(-24\sqrt{\frac{a_{max}}{s{n}_{max}}}{a}_{max}-24v_A+24v_m\right)j_{max}-12a_{max}^2\right)s{n}_{max}^2-12a_{max}{j}_{max}^{2}s{n}_{max}+j_{max}^4}{24s{n}_{max}^2{j}_{max}{a}_{max}}$
	$\Delta t_4$	$\frac{j_{max}}{s{n}_{max}}$
	$\Delta t_5$	$\frac{2a_{max}s{n}_{max}-j_{max}^2}{2s{n}_{max}{j}_{max}}$

In all models $\Delta t_2=\Delta t_1$ holds.

).

If one of these models is suitable for going from $\left(v_A,0, 0\right)$ to $\left(v_m,0,j_m\right)$ (conditions for this are investigated below), one has to compute the length of the time intervals $\Delta t_i$ (I = 1…4 or 5 or 6). In order to have a simple notation in the subsequent computations, we define the point in time $t_i$ ($i=1\dots \#intervals$) as $t_i={\displaystyle \sum }_{k=1}^i\Delta t_k$. From the jerk models, one can easily produce acceleration and velocity models using the initial values 0 and $v_A$, respectively. We have three conditions that must be fulfilled ($t_{end}$ denotes the sum of the time intervals):

$$j\left(t_{end}\right)=j_m, a\left(t_{end}\right)=0, v\left(t_{end}\right)=v_m$$

(9)

Further conditions originate from the special shape of the model functions: In all models we have $\Delta t_1=\Delta t_2$; additional equations can be set up when $j_{min}$ or $a_{max}$ are reached. It is easy to check that this results in a sufficient number of equations for computing the time intervals. These equations lead either directly to formulae for the time intervals or to a polynomial equation that has a time interval as one of its roots. We demonstrate this for Model I.1f, where the equations to be fulfilled are the following:

$$\Delta t_1=\Delta t_2, v\left(t_4\right)=v_m, a\left(t_4\right)=0, j\left(t_4\right)=j_m$$

(10)

From $a\left(t_4\right)=0$, we obtain ${\left(\Delta t_1\right)}^{2}s{n}_{max}={\left(\Delta t_3\right)}^{2}s{n}_{max}-\frac{1}{2}{\left(\Delta t_3-\Delta t_4\right)}^{2}s{n}_{max}$, and hence

$$\Delta t_1=\sqrt{\frac{1}{2}{\left(\Delta t_3\right)}^2+\Delta t_3\Delta t_4-\frac{1}{2}{\left(\Delta t_4\right)}^2}.$$

(11)

From $j\left(t_4\right)=j_m$, it follows that

$$\Delta t_4=\Delta t_3+\frac{j_m}{s{n}_{max}}.$$

(12)

By integrating the jerk function twice and using $v\left(t_4\right)=v_m$, one obtains:

$$\begin{gathered} v_m=v_A+s{n}_{max}{\left(\Delta t_1\right)}^3+s{n}_{max}{\left(\Delta t_1\right)}^2\Delta t_3-\frac{1}{6}s{n}_{max}{\left(\Delta t_1\right)}^3+\left(s{n}_{max}{\left(\Delta t_1\right)}^2-\frac{1}{2}s{n}_{max}{\left(\Delta t_3\right)}^3\right)\Delta t_4- \\ \frac{1}{2}s{n}_{max}\Delta t_3{\left(\Delta t_4\right)}^2+\frac{1}{6}s{n}_{max}{\left(\Delta t_4\right)}^3. \end{gathered}$$

(13)

By substituting $\Delta t_1$ and $\Delta t_4$ in Equation (13) using Equations (11) and (12), we obtain an equation where only $\Delta t_3$ is unknown. This equation cannot be solved analytically, and because of the square root in Equation (11), it is not a polynomial equation. Yet, using algebraic transformations, it can be turned into a polynomial equation of degree 6, the solutions of which have to be multiplied with $s{n}_{max}{}^{-1}$. We used the Computer Algebra System (CAS) Maple^® for doing this. The coefficients of the polynomial are given in Appendix A (Table A1, Model I.1f). Note that all solutions to the original Equation (13) are also solutions to the transformed polynomial problem but not the other way around, such that it must be checked which of the solutions solve the original problem. Nonetheless, by transforming the problem into a polynomial one, stable polynomial solvers can be employed, which find all roots such that one can avoid the problem of depending on suitable initial values in order to find feasible solutions. This strategy has been pursued at several places in our algorithms, and all resulting polynomials can be found in the appendices.

In all other models in Case I “going forth”, we similarly get the respective equations but those can be solved directly where again a CAS is helpful. Sometimes, one obtains more than one solution, but it is always possible to find among those the only one that provides a real positive value. The results are shown in Table A1 (Appendix A).

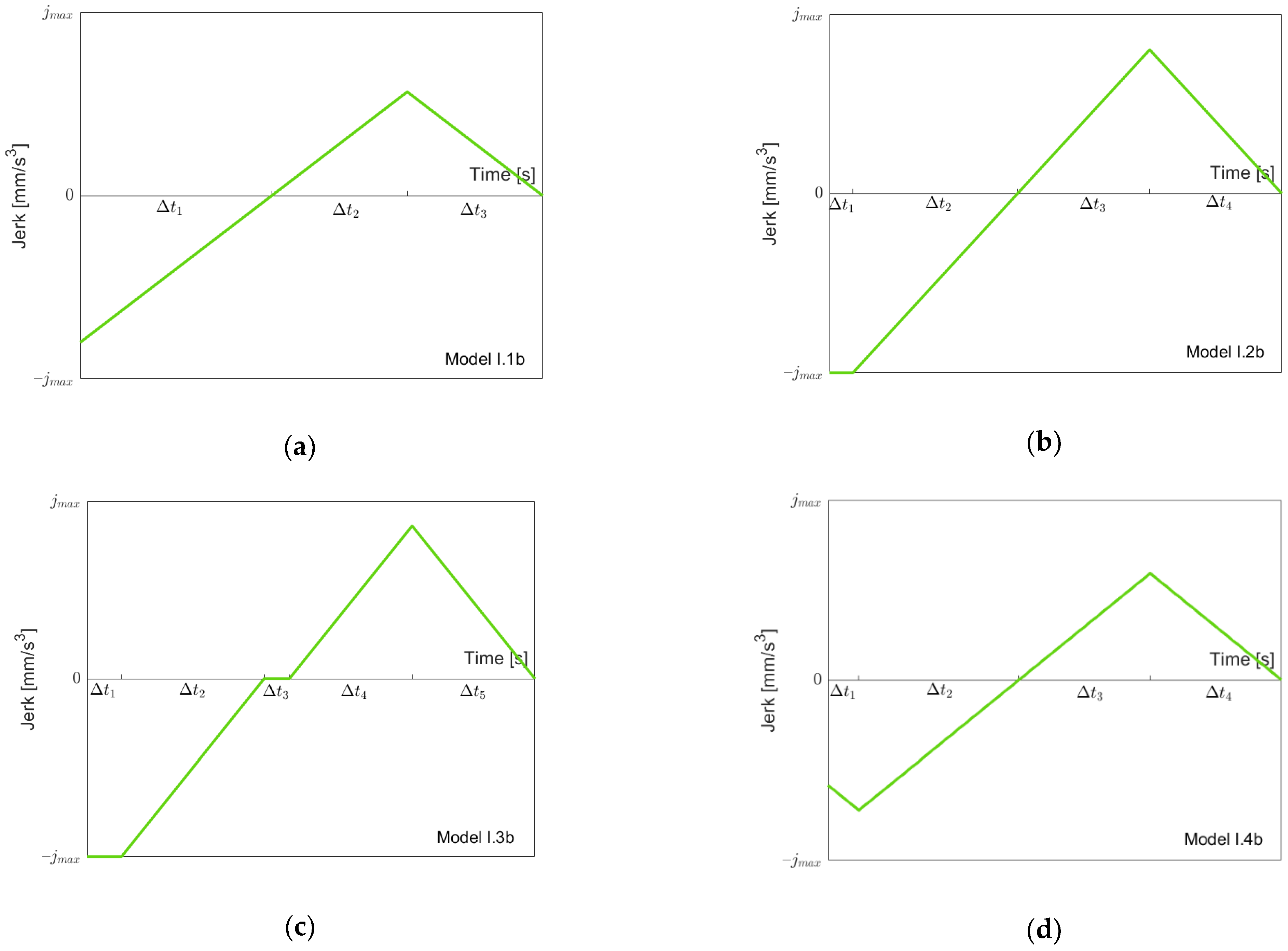
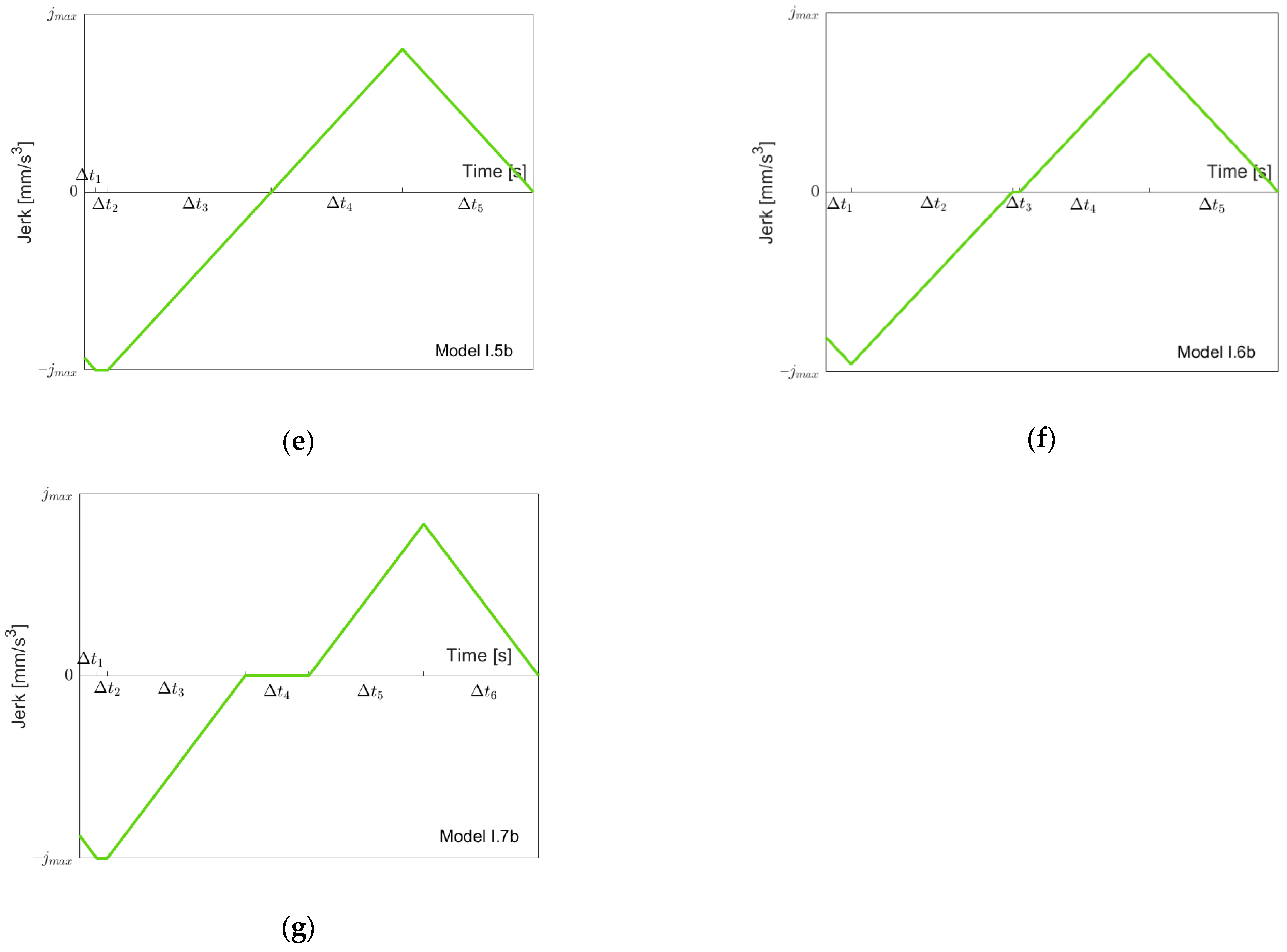
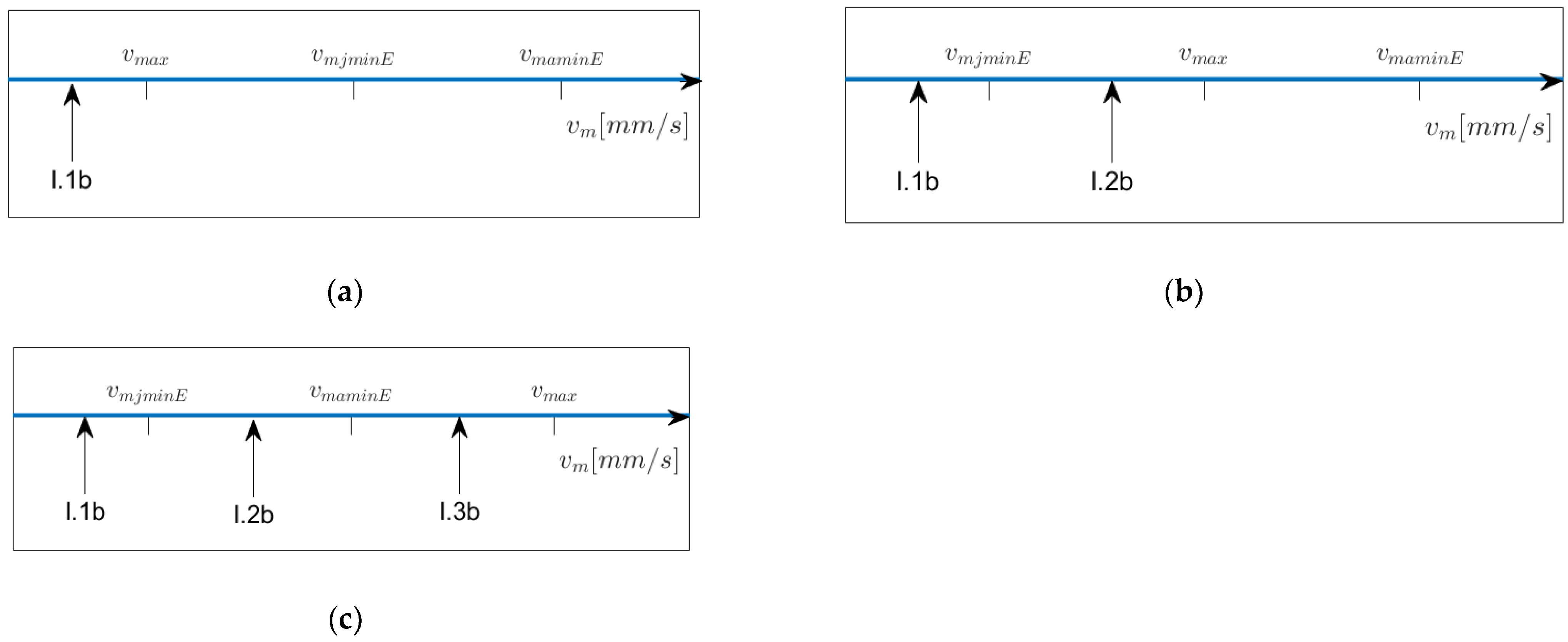
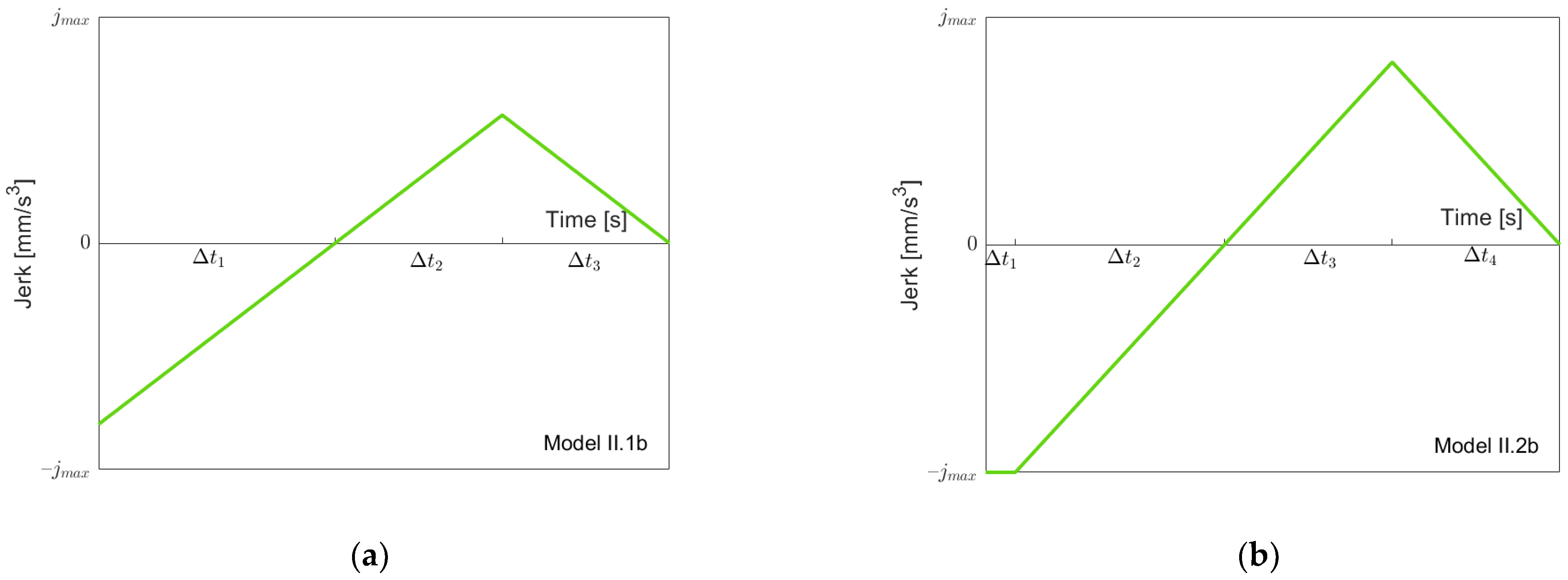
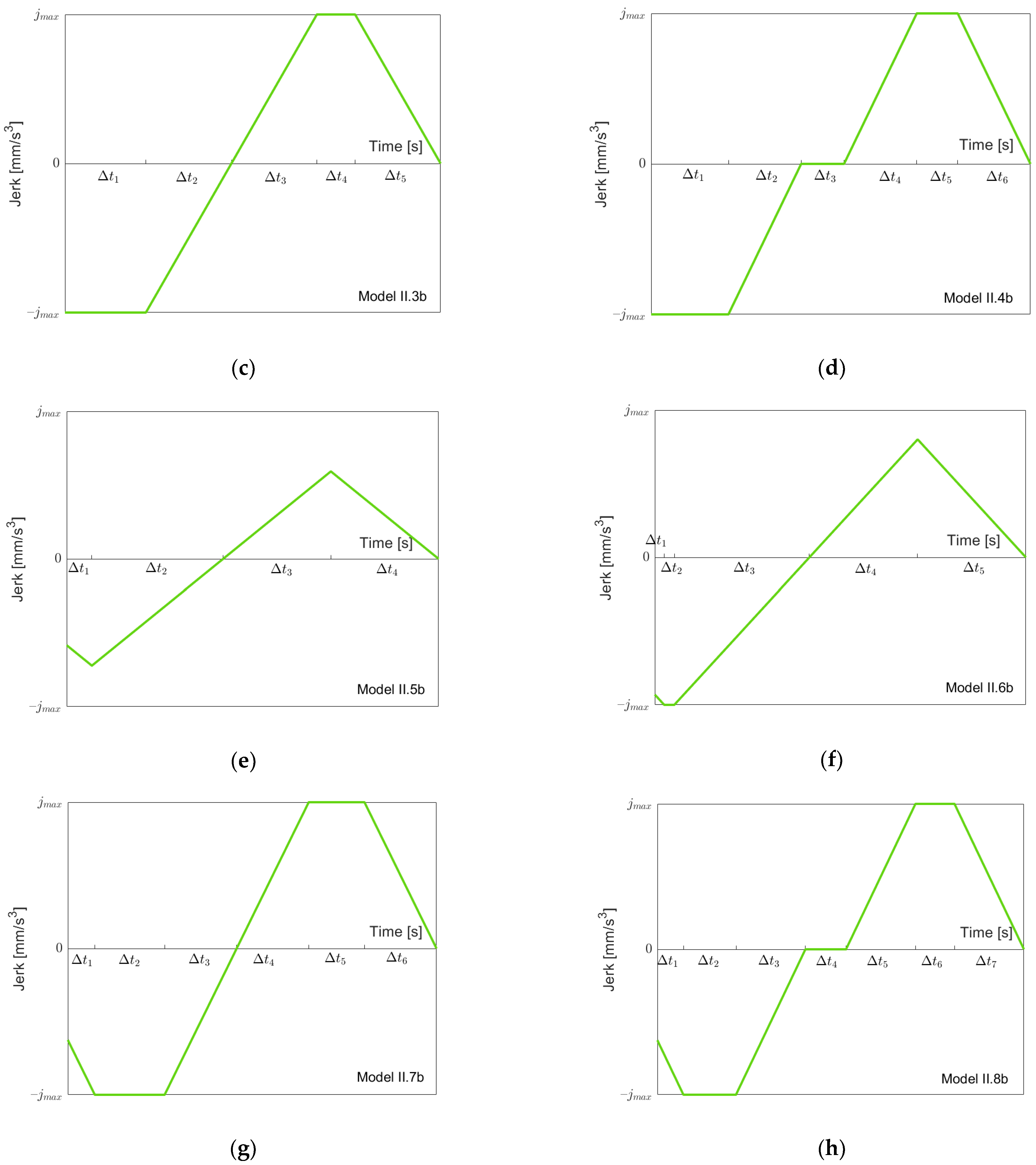
Figure 6 depicts the possible models for going “back” from $\left(v_m,0,j_m\right)$ to $\left(v_E,0, 0\right)$. Clearly, before (or at the same moment as) the acceleration goes down to $a_{min}$, the jerk $j_m$ reaches its minimal value $j_{min}$. Therefore, we have a simple sequence of the three models I.1b, I.2b and I.3b, as shown in Figure 6a–c when we proceed from $\left(v_E,0, 0\right)$ to $\left(v_{max},0, vm2jm\left(v_{max}\right)\right)$. Note that not all models must be present depending on the value of $v_{max}$. When we then proceed from $\left(v_{max},0,vm2jm\left(v_{max}\right)\right)$ to $\left(v_{max},0, 0\right)$, as described in the previous section, one of the Models I.4b to I.7b might occur (Figure 6d–g). Models I.4b, I.5b and I.7b simply add a “front piece” starting at $j_m$, which goes up to zero. Model I.6b is needed, since when starting with Model I.7b and reducing $j_m$, it is possible that first, the minimal jerk becomes larger than $j_{min}$ before the minimal acceleration becomes larger than $a_{min}$. Note that when reaching $\left(v_{max},0, 0\right)$, the model must be symmetric, since one starts and ends with acceleration zero. Again, one could treat Models I.1b, I.2b and I.3b as special cases of Models I.4b, I.5b and I.7b with $\Delta t_1=0$, but, for the same reasons as stated above, for going forth, we treat them separately. From the jerk models, one can easily produce acceleration and velocity models using the initial values 0 and $v_m$, respectively. We have three conditions that must be fulfilled ($t_{end}$ denotes the sum of the time intervals):

$$j\left(0\right)=j_m, a\left(t_{end}\right)=0, v\left(t_{end}\right)=v_E$$

(14)

Further conditions originate from the special shape of the model functions: in all models, the final two time intervals must have equal length. Moreover, in Models I.2b, I.3b, I.5b and I.7b, there is an interval where the jerk goes from its minimum to zero. In Models I.3b, I.6b and I.7b, the minimal acceleration is reached. Finally, there is a relation between the start jerk $j_m$ and the first two resp. three time intervals in Models I.4b, I.6b resp. I.5b, I.7b (note that in Model I.1b, $v_m$ and $j_m$ are related via Equation (8), upper part, so the system of equations is not overdetermined). It is easy to check that this leads to a sufficient number of conditions to determine the time intervals in all models going “back”. The corresponding equations lead either directly to formulae for the time intervals or to a polynomial equation of a degree of at most four, which has a time interval as one of its roots (cf. the exemplary computation of time intervals for the “going forth” model I.1f above). We provide the respective expressions in Appendix A,

Table A2. Formulae and polynomials for computing time intervals in Case I going back.

Model	$\mathbf{\Delta }{\mathit{t}}_{\mathit{i}}$	Formulae and Polynomials
I.1b	$\Delta t_1$	$-\frac{j_m}{s{n}_{max}}$
	$\Delta t_2$	$-\sqrt{2}\frac{j_m}{2s{n}_{max}}$
	$\Delta t_3$	$\Delta t_2$
I.2b	$\Delta t_1$	$\frac{2\Delta t_3^{2}s{n}_{max}^2-j_{max}^2}{2s{n}_{max}{j}_{max}}$
	$\Delta t_2$	$\frac{j_{max}}{s{n}_{max}}$
	$\Delta t_3$	$-\frac{j_{max}}{2s{n}_{max}}+\frac{\sqrt{9j_{max}^2+6\sqrt{3j_{max}^4-72j_{max}s{n}_{max}^2{v}_E+72j_{max}s{n}_{max}^2{v}_m}}}{6s{n}_{max}}$
	$\Delta t_4$	$\Delta t_3$
I.3b	$\Delta t_1$	$\frac{2a_{max}s{n}_{max}-j_{max}^2}{2s{n}_{max}{j}_{max}}$
	$\Delta t_2$	$\frac{j_{max}}{s{n}_{max}}$
	$\Delta t_3$	$\frac{\left(\left(-24\sqrt{\frac{a_{max}}{s{n}_{max}}}{a}_{max}-24v_E+24v_m\right)j_{max}-12a_{max}^2\right)s{n}_{max}^2-12a_{max}{j}_{max}^{2}s{n}_{max}+j_{max}^4}{24s{n}_{max}^2{j}_{max}{a}_{max}}$
	$\Delta t_4$	$\sqrt{\frac{a_{max}}{s{n}_{max}}}$
	$\Delta t_5$	$\Delta t_4$
I.4b	$\Delta t_1$	$\frac{j_m+\raisebox{1ex}{$\sqrt{4\Delta t_3^{2}s{n}_{max}^2+2j_m^2}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{s{n}_{max}}$
	$\Delta t_2$	$\Delta t_1-\frac{j_m}{s{n}_{max}}$
	$\Delta t_3$	$$\begin{gathered} \frac{1}{s{n}_{max}}·roots\left(\left[36j_m^2,-48j_m^3+144s{n}_{max}^2{v}_E-144s{n}_{max}^2{v}_m,18j_m^4,0,-j_m^6-48j_m^{3}s{n}_{max}^2{v}_E+48j_m^{3}s{n}_{max}^2{v}_m \\ +72s{n}_{max}^4{v}_E{}^2-144s{n}_{max}^4{v}_E{v}_m+72s{n}_{max}^4{v}_m{}^2\right]\right) \end{gathered}$$
	$\Delta t_4$	$\Delta t_3$
I.5b	$\Delta t_1$	$\frac{j_m+j_{max}}{s{n}_{max}}$
	$\Delta t_2$	$\frac{2\Delta t_4^{2}s{n}_{max}^2+j_m^2-2j_{max}^2}{2s{n}_{max}{j}_{max}}$
	$\Delta t_3$	$\frac{j_{max}}{s{n}_{max}}$
	$\Delta t_4$	$-\frac{j_{max}}{2s{n}_{max}}+\frac{\sqrt{9j_{max}^2+6\sqrt{9j_m^4+24j_m^3{j}_{max}+18j_m^2{j}_{max}^2-72j_{max}s{n}_{max}^2{v}_E+72j_{max}s{n}_{max}^2{v}_m}}}{6s{n}_{max}}$
	$\Delta t_5$	$\Delta t_4$
I.6b	$\Delta t_1$	$\frac{j_m+\raisebox{1ex}{$\sqrt{4a_{max}s{n}_{max}+2j_m^2}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{s{n}_{max}}$
	$\Delta t_2$	$\Delta t_1-\frac{j_m}{s{n}_{max}}$
	$\Delta t_3$	$\frac{\left(6a_{max}s{n}_{max}-3j_m^2\right)\sqrt{4a_{max}s{n}_{max}+2j_m^2}-12s{n}_{max}^2{a}_{max}\sqrt{\frac{a_{max}}{s{n}_{max}}}+12s{n}_{max}^2\left(-v_E+v_m\right)+4j_m^3}{12s{n}_{max}^2{a}_{max}}$
	$\Delta t_4$	$\sqrt{\frac{a_{max}}{s{n}_{max}}}$
	$\Delta t_5$	$\Delta t_4$
I.7b	$\Delta t_1$	$\frac{j_m+j_{max}}{s{n}_{max}}$
	$\Delta t_2$	$\frac{2a_{max}s{n}_{max}+j_m^2-2j_{max}^2}{2s{n}_{max}{j}_{max}}$
	$\Delta t_3$	$\frac{j_{max}}{s{n}_{max}}$
	$\Delta t_4$	$\frac{\left(\left(-24\sqrt{\frac{a_{max}}{s{n}_{max}}}{a}_{max}-24v_E+24v_m\right)j_{max}-12a_{max}^2\right)s{n}_{max}^2-12a_{max}{j}_{max}^{2}s{n}_{max}+3j_m^4+8j_m^3{j}_{max}+6j_m^2{j}_{max}^2}{24s{n}_{max}^2{j}_{max}{a}_{max}}$
	$\Delta t_5$	$\sqrt{\frac{a_{max}}{s{n}_{max}}}$
	$\Delta t_6$	$\Delta t_5$

.

Next, we address the question in which possible sequences the models occur when $\left(v_m,0,j_m\right)$ runs from $\left(v_E,0, 0\right)$ to $\left(v_{max},0,vm2jm\left(v_{max}\right)\right)$, as stated in the previous section. For this, we investigate the values of $v_m$ for which, in the going forth situation, the minimal jerk reaches the value $j_{min}=-j_{max}$ (denoted by $v_{mjminA}$), and the maximal acceleration reaches the value $a_{max}$ (denoted by $v_{mamaxA}$). In the sequel, we present the procedure for which the algorithm can be found in Appendix B, Algorithm A1.

• If the inequality $v_E-v_A\ge 2s{n}_{max}{\left(\frac{a_{max}}{s{n}_{max}}\right)}^{3/2}$ holds (cf. Table 1), then $a_{max}$ is already reached for $v_m=v_E$, so we have $v_{mamaxA}=v_E$. In order to find $v_{mjminA}$, we set $j\left(t_4\right)=j_{min}$ in Model I.3f. In the equations given for the time intervals in Appendix A, Table A1, for this model, now, $j_m$ is unknown, but the additional equation $j\left(t_4\right)=j_{min}$ allows us to compute this quantity: since $\Delta t_4=\frac{j_{max}}{s{n}_{max}}$, $\Delta t_5=\frac{j_{max}+j_m}{s{n}_{max}}$, and $a_{max}=\frac{1}{2}{j}_{max}\Delta t_4+\frac{j_{max}-j_m}{2}\Delta t_5$, we obtain the formula presented in line 3 for $j_m$. The corresponding value for $v_m$ can be determined using Equation (6). This gives $v_{mjminA}$, and we are done.
• Otherwise, we consider Model I.1f and investigate the condition $j\left(t_3\right)=j_{min}$, i.e., $\Delta t_3=\frac{j_{max}}{s{n}_{max}}$. Again, $j_m$ is an additional unknown. If $v_A=v_E$, we have $j_m=j_{min}$ because of symmetry. Otherwise, by substituting $\Delta t_1$ and $\Delta t_4$ in Equation (13) using Equations (11) and (12), we obtain an equation where, now, only $j_m$ is unknown. This equation can be transformed into a polynomial one of degree 6, the coefficients of which are given in line 8 of algorithm A1. We pick the real root for which $j_{min}\le j_m\le 0$ holds.
• Next, we have to check whether $j_{min}$ is really reached before $a_{max}$. For this, we compute $a\left(t_2\right)$ in Model I.1f, which gives $\frac{2j_{max}^2-j_m^2}{2s{n}_{max}}$, and we check whether $a\left(t_2\right)\le a_{max}$ holds. If that is the case, then $j_{min}$ is reached first, and we compute $v_{mjminA}$ according to Equation (6) (cf. line 14). Then, we set $a\left(t_2\right)=a_{max}$ in Model I.2f. This leads to the formula for $j_m$ presented in line 15. If $j_m\ge j_{min}$, then Model I.2f was applicable, and we obtain $v_{mamaxA}$ according to Equation (6), as presented in line 17. Otherwise, we have to apply Model I.5f (i.e., $j_m$ has already reached $j_{min}$), and we obtain $v_{mamaxA}$ according to line 18.
• Otherwise (i.e., $a\left(t_2\right)>a_{max}$), $a_{max}$ is reached first, and we have to set $a\left(t_2\right)=a_{max}$ in Model I.1f. This additional equation allows us to compute $j_m$ as the real root of the polynomial of degree 4 presented in line 21, for which $0\ge j_m\ge j_{min}$ holds. Then, again, we obtain $v_{mamaxA}$ according to Equation (6), as given in line 23. By setting $j\left(t_4\right)=j_{min}$ in Model I.3f, we obtain the value for $j_m$ when $j_{min}$ is reached, and line 25 computes the corresponding value for $v_{mjminA}$.

The algorithm illustrates a strategy often pursued in this work: By going stepwise through the available models one ends up with an applicable model in which one can compute the desired value either directly or by computing roots of a polynomial.

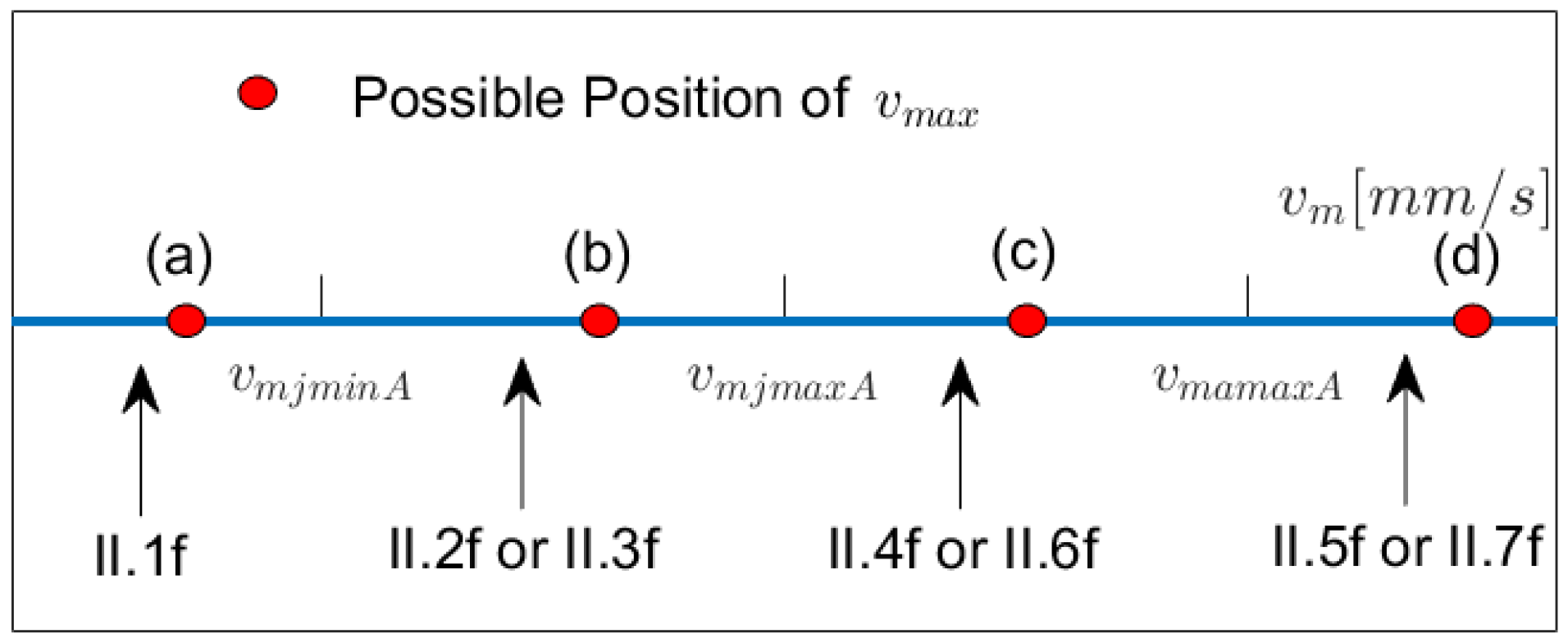
Note that “critical” velocities $v_{mjminA}, v_{mamaxA}$ might be larger than $v_{max}$. We will look at the possible configurations below. Next, we investigate at which value of $v_m$ in the going “back” part the minimal jerk and the minimal acceleration are reached (denoted by $v_{mjminE}$ and by $v_{maminE}$, resp.). In the “going back” situation, we always have $v_{mjminE}\le v_{maminE}$, and we obtain $v_{mjminE}$ using Equation (6) with $j_m=j_{min}$ and $v_{maminE}$ by setting $a\left(t_2\right)=a_{min}$ in Model I.2b (see

Table A5. Formulae for computing critical velocities in Case I going back.

$v_{mjminE}=v_E+\frac{j_{max}^3}{12s{n}_{max}^2}\left(3\sqrt{2}+4\right)$

$v_{maminE}=v_E+a_{max}\sqrt{\frac{a_{max}}{s{n}_{max}}}+\frac{a_{max}^2}{2j_{max}}+\frac{a_{max}{j}_{max}}{2s{n}_{max}}-\frac{j_{max}^3}{24s{n}_{max}^2}$

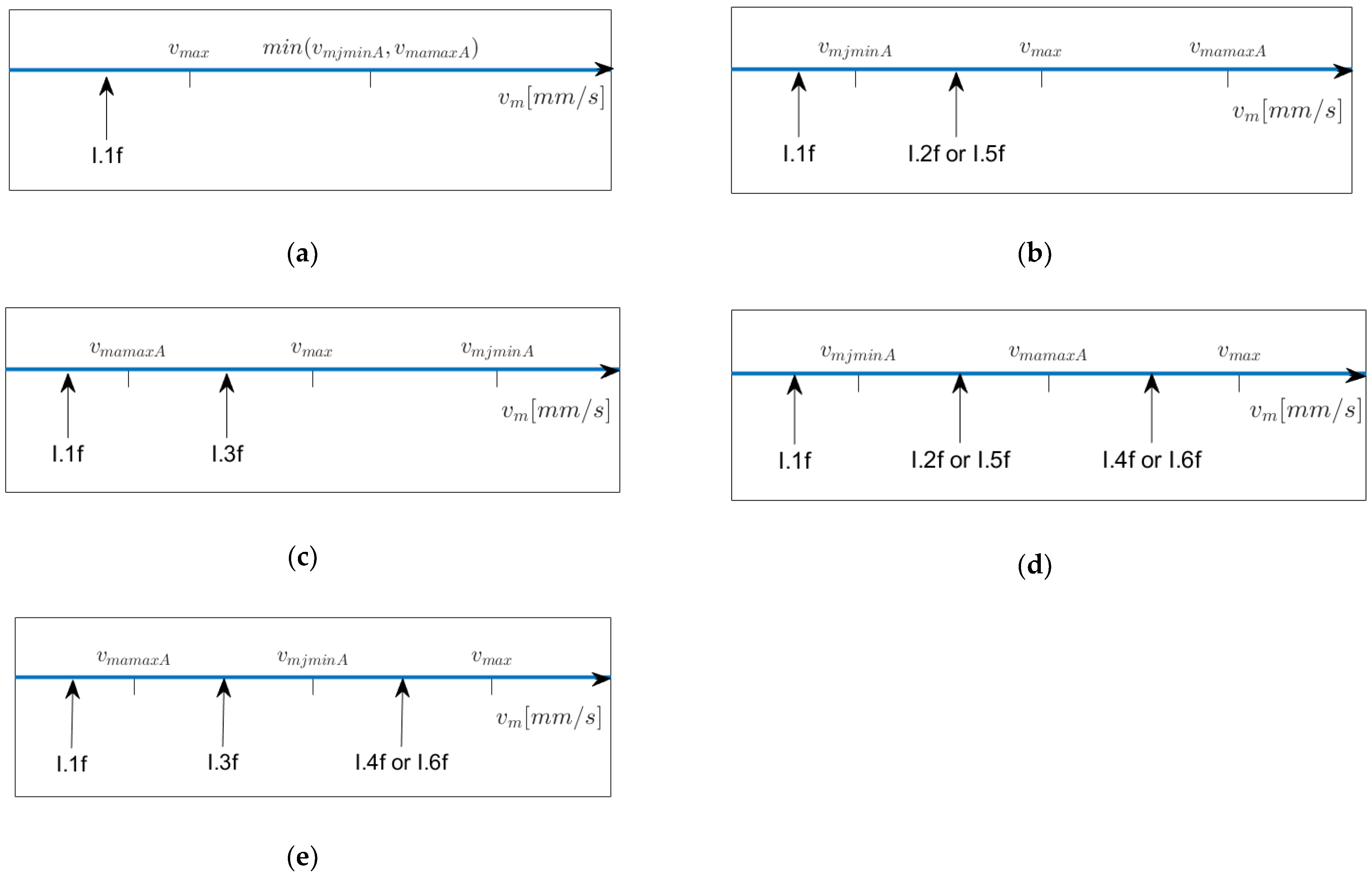
).) Figure 7 depicts the possible relative positionings of $v_{max}$, $v_{mjminA}$ and $v_{mamaxA}$ on the $v_m$-scale and provides information on which model to apply when $v_m$ lies within a certain interval left of $v_{max}$. In Figure 7b,d,e, Models I5.f resp. I.6f have to be chosen once $v_{mjminE}$ is reached. Note that the interval of possible values for $v_m$ starts at $v_E$ and ends at $v_{max}$, so if, for example, $v_E=v_{mamaxA}$ in Figure 7c or e, then Model I.1f does not occur.

Figure 8 depicts the possible relative positionings of $v_{max}$, $v_{mjminE}$ and $v_{maminE}$ on the $v_m$ scale and provides information on which model to apply when $v_m$ lies within a certain interval left of $v_{max}$.

So, we are able to specify the applicable model when $v_m$ runs from from $\left(v_E,0, 0\right)$ to $\left(v_{max},0,vm2jm\left(v_{max}\right)\right)$ in Case I. The remaining task consists of finding the correct model when we go from $\left(v_{max},0,vm2jm\left(v_{max}\right)\right)$ to $\left(v_{max}, 0, 0\right)$, i.e., we keep $v_m=v_{max}$ constant and let $j_m$ run from $vm2jm\left(v_{max}\right)$ to 0. The additional challenge here originates from the possibility that already-reached extremal values $j_{min}$, $a_{max}$ (for going forth) resp. $j_{min}$, $a_{min}$ (for going back) might be no longer reached. For example, when $j_{min}$ was reached (going forth) and $j_m$ moves to zero again then, at some value of $j_m$, the minimal jerk has to be above $j_{min}$ since we are in Case I. Figure 9 demonstrates this in the velocity acceleration plane where we omit the boundary curve for better visibility of interesting curve sections: we have $v_{max}=35, a_{max}=10,j_{max}=12,s{n}_{max}=10$ for the restrictions, $v_A=10,v_E=20$, $v_m=v_{max}$ and $j_m=vm2jm\left(vmax\right)=j_{min}$, resulting in a distance $\Delta s=166.45$ (in our examples, the units are always $\mathrm{mm}$, $\raisebox{1ex}{$\mathrm{mm}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{s}$}\right.$, $\raisebox{1ex}{$\mathrm{mm}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{s}}^2$}\right.$, $\raisebox{1ex}{$\mathrm{mm}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{s}}^3$}\right.$ and $\raisebox{1ex}{$\mathrm{mm}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{s}}^4$}\right.$, respectively, and we omit these in the sequel for brevity). We recognize Model I.6f for going forth and I.2b for going back in Figure 9a,b. When we now enlarge $j_m$ to $-10.58$, we obtain a distance of 167, and we see in Figure 9c that the models switched to I.4f and I.4b, respectively. When we now consider the final jerk value zero, we obtain as distance 201.19, and Figure 9d shows that the going forth model again switched to I.3f, whereas the going back model does not change. The three curves in Figure 9b–d are close to each other, but by zooming, we see that we obtain higher curvature when moving to $j_m=0$. In this case, the maximal acceleration is still reached, but when one moves $v_A$ closer to $v_E$ such that the part with constant acceleration $a_{max}$ is very short, another model switch might occur. This illustrates the inherent complexity, which cannot simply be sidestepped.

Next, we find out at which values for $j_m$ certain model switches occur. We set $v_m=v_{max}$ and proceed similarly as when determining the critical velocities: in the models, we add an additional equation depending on which extremal acceleration or jerk has been reached, and we determine $j_m$ as an additional unknown; the latter can be computed directly or via solving a polynomial equation. If the solution leads to non-admissible values for $j_m$ or to negative values for time intervals, then there is no feasible solution. Since the computations are straightforward and can be easily performed using a CAS, we just give the results that are needed for implementation. The procedure is described in more detail in Algorithm A3. We first consider the going forth part and refer to Figure 7 regarding the possible positionings of $v_{max}$. If we have situation (a), Model I.1f will be applied for all jerk values. If situation (b) applies, we proceed as follows:

• In Model I.1f, set $v_m=v_{max}$ and $j\left(t_3\right)=j_{min}$ and compute $j_m$ by proceeding as stated in Algorithm A3, line 2, denoted by $j_{mswitch}$. There must be a solution, since we must end up with a symmetric model, and Model I.2f is not symmetric.
• For $vm2jm\left(v_{max}\right)\le j_m<j_{mswitch}$, apply Model I.2f, for $j_{mswitch}\le j_m\le 0$ Model I.1f.

If situation (c) applies, the procedure is as follows:

• In Model I.1f, set $v_m=v_{max}$ and $a\left(t_2\right)=a_{max}$ and compute $j_m$ by proceeding as stated in Algorithm A3, line 5, denoted by $j_{mswitch}$ in case of existence. If there is no such solution, the suitable model is always Model I.3f. This is also the case when $v_E=v_{mamaxA}$ holds (cf. the explanation for Figure 5).
• Otherwise, for $vm2jm\left(v_{max}\right)\le j_m<j_{mswitch}$, apply Model I.3f, for $j_{mswitch}\le j_m\le 0$ Model I.1f.

If situation (d) applies, perform the following:

• In Model I.4f, set $v_m=v_{max}$ and $\Delta t_5=0$ (i.e., the phase of constant minimal jerk has duration zero). Compute $j_m$ and substitute the value into the expression given for $\Delta t_3$ in Table A1, Model I.4f. If $\Delta t_3\ge 0$ holds (i.e., the solution is admissible), set $j_{mswitch1}=j_m$, and the next model is I.3f. Otherwise, set $\Delta t_3=0$ in Model I.4f (i.e., the phase of constant maximal acceleration has duration zero) and compute $j_m$ by proceeding as stated in Algorithm A3, lines 12/13, also denoted by $j_{mswitch1}$. If there is a real solution with $vm2jm\left(v_{max}\right)\le j_{mswitch1}\le 0$, the next model is I.2f. Since Model I.4f is not symmetric, a valid $j_{mswitch1}$ must exist.
• If Model I.3f is next, set $v_m=v_{max}$ and $a\left(t_2\right)=a_{max}$ in Model I.1f and compute $j_m$ as in situation (c), denoted by $j_{mswitch2}$. This need not exist.
• If Model I.2f is next, set $v_m=v_{max}$ and $j\left(t_3\right)=j_{min}$ in Model I.1f and compute $j_m$ as in situation (b), denoted by $j_{mswitch2}$. This, then, must exist, since I.2f is not symmetric.
• Now, for $j_{min}\le j_m<j_{mswitch1}$, take Model I.4f. For $j_{mswitch1}\le j_m<j_{mswitch2}$, apply Model I.3f or I.2f, resp. If no valid $j_{mswitch2}$ exists, apply Model I.3f for $j_{mswitch1}\le j_m\le 0$. Otherwise, for $j_{mswitch2}\le j_m\le 0$, Model I.1f is suitable.

Finally, if situation (e) applies, we have the same procedure as for situation (d). If $v_E=v_{mamaxA}$, there is no $j_{mswitch2}$ and we switch directly from Model I.4f to I.3f.

Next, we consider the going back situation and refer to Figure 8. If we have situation (a), Model I.4b will be used for all jerk values. If situation (b) applies, we proceed as follows:

• In Model I.5b, set $v_m=v_{max}$ and $\Delta t_2=0$ and compute $j_m$, denoted by $j_{mswitch}$ by proceeding as stated in Algorithm A4, line 2. There must be a solution, since we must end up with a symmetric model, and Model I.5b is not symmetric.
• For $j_{min}\le j_m<j_{mswitch}$, apply Model I.5b; for $j_{mswitch}\le j_m\le 0$, Model I.4b.

If situation (c) applies, perform the following:

• In Model I.7b, set $v_m=v_{max}$ and $\Delta t_2=0$ (i.e., the phase of constant minimal jerk has duration zero), and compute $j_m$ according to Table A2. Substitute the value in the formula given for $\Delta t_4$ (Model I.7b), and check if $\Delta t_4\ge 0$. If this is the case, set $j_{mswitch1}=j_m$, and the next model is I.6b. Otherwise, set $\Delta t_4=0$ in Model I.7b (i.e., the phase of constant maximal acceleration has duration zero), and compute $j_m$ according to Algorithm A4, line 10, also denoted by $j_{mswitch1}$. If there is a real solution, the next model is I.5b. Since Model I.7b is not symmetric, a valid $j_{mswitch1}$ must exist.
• If Model I.6b is next, set $v_m=v_{max}$ and $\Delta t_3=0$, and compute $j_m$ according to Algorithm A4, line 15, denoted by $j_{mswitch2}$. This need not exist.
• If Model I.5b is next, set $v_m=v_{max}$ and $\Delta t_2=0$, and compute $j_m$ according to Algorithm A4, line 2, denoted by $j_{mswitch2}$. This, then, must exist, since I.5b is not symmetric.
• Now, for $j_{min}\le j_m<j_{mswitch1}$, take Model I.7b. For $j_{mswitch1}\le j_m<j_{mswitch2}$, apply Model I.6b or I.5b, resp. If no valid $j_{mswitch2}$ exists, apply Model I.6b for $j_{mswitch1}\le j_m\le 0$. Otherwise, for $j_{mswitch2}\le j_m\le 0$, Model I.4b is suitable.

Now, for all triples $(v_m,0, j_m)$, we can determine the model to be applied in Case I when $S\left(v_A,v_E\right)\le \Delta s\le S\left(v_A,v_{max}\right)+S\left(v_{max},v_E\right)$ holds. Moreover, one can stay at $(v_{max},0, 0)$ for a period of arbitrary length, which can easily be included between the going back and the going forth part.

When $\Delta s<S\left(v_A,v_E\right)$, we can take intermediate velocities that lie left of $v_A$, and by reflection and reversion, we can rewrite the problem as one where $\Delta s\ge S\left(v_A,v_E\right)$: Assume, $v_A, v_E$ (still with $v_A\le v_E$), and $\Delta s$ are given where $\Delta s<S\left(v_A,v_E\right)$ holds. Then, consider the reflected configuration (denoted by a bar): ${\overline{v}}_A=-v_E$, ${\overline{v}}_E=-v_A$, and $\Delta \overline{s}=-\Delta s$. Since $\Delta \overline{s}\ge S\left({\overline{v}}_A,{\overline{v}}_E\right)$, we can perform the procedure explained above. Then, we reverse the solution by reflecting it again, i.e., we consider

$$\begin{gathered} j\left(t\right)=-\overline{j}\left(t_{end}-t\right), a\left(t\right)=\overline{a}\left(t_{end}-t\right), v\left(t\right)=-\overline{v}\left(t_{end}-t\right), s\left(t\right) \\ =\overline{s}\left(t_{end}-t\right)-s\left(t_{end}\right) \end{gathered}$$

(15)

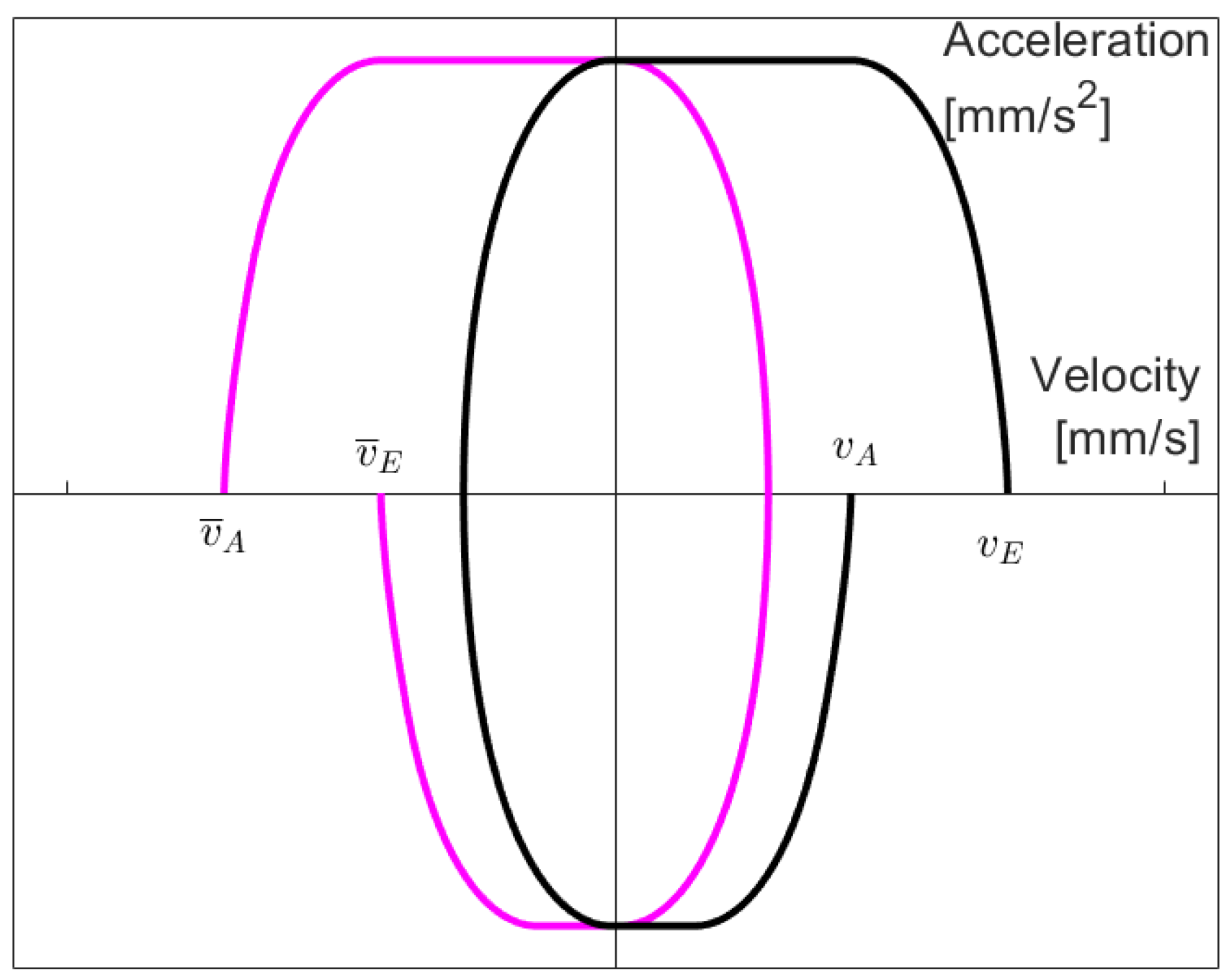
Figure 10 illustrates this (we omit the boundary and color coding for simplicity reasons). The left magenta part shows the solution to the reflected problem, and then by reflection (and thus reversion), we obtain the solution to the original problem in black. Thus, we cover all possible distances.

4. Models and Critical Velocities and Jerks in Case II

In Case II, we proceed analogously to Case I. Again, we take an intermediate velocity $v_m$ and a corresponding jerk $j_m$ and go “forth” from $\left(v_A, 0, 0\right)$ to $\left(v_m, 0,j_m\right)$ and “back” from $\left(v_m,0,j_m\right)$ to $\left(v_E,0, 0\right)$. Figure 11 shows possible jerk models for going “forth” (the notation “II.xf” describes these models in Case II) using maximal, minimal or zero snap. In Case II, there are three interesting switching points: $j_{min}$ is reached when going down from the maximal acceleration; $j_{max}$ resp. $a_{max}$ is reached when going up from $\left(v_A,0, 0\right)$. Note that Models II.1f, II.2f and II.3f are identical to Models I.1f, I.2f and I.5f. In the other models, the maximum jerk $j_{max}$ is reached, which is not possible in Case I.

If one of these models is suitable for going from $\left(v_A,0, 0\right)$ to $\left(v_m,0,j_m\right)$, one has to compute the length of the time intervals $\Delta t_i$ (I = 1…4, 5, 6 or 7). Again, the conditions stated in Equation (9) for Case I carry over to Case II. Further conditions can be identified by looking at the special shape of a jerk model. If an interval starts or ends at $j_{max}$ or $j_{min}$, it has to have a length $\frac{j_{max}}{s{n}_{max}}$. In Models II.1f, II.2f and II.3f, the first two intervals have the same length. Moreover, in Models II.5f and II.7f, $a\left(t_3\right)=a_{max}$. It is easy to check that these conditions provide the required number of equations for determining the $\Delta t_i$ in the respective model. The results are given in Appendix A,

Table A3. Formulae and polynomials for computing time intervals in Case II going forth.

Model	$\mathbf{\Delta }{\mathit{t}}_{\mathit{i}}$	Formulae and Polynomials
II.1f		Same as Model I.1f
II.2f		Same as Model I.2f
II.3f		Same as Model I.5f
II.4f	$\Delta t_1$	$\frac{j_{max}}{s{n}_{max}}$
	$\Delta t_2$	$\frac{-3j_{max}^2+\raisebox{1ex}{$\sqrt{18j_m^4+48j_m^3{j}_{max}+36j_m^2{j}_{max}^2+36j_{max}^4-144j_{max}s{n}_{max}^2{v}_A+144j_{max}s{n}_{max}^2{v}_m}$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}{2s{n}_{max}{j}_{max}}$
	$\Delta t_3$	$\Delta t_1$
	$\Delta t_4$	$\Delta t_1$
	$\Delta t_5$	$\Delta t_2+\frac{j_m^2}{2s{n}_{max}{j}_{max}}$
	$\Delta t_6$	$\frac{j_m+j_{max}}{s{n}_{max}}$
II.5f	$\Delta t_1$	$\frac{j_{max}}{s{n}_{max}}$
	$\Delta t_2$	$\frac{a_{max}s{n}_{max}-j_{max}^2}{s{n}_{max}{j}_{max}}$
	$\Delta t_3$	$\Delta t_1$
	$\Delta t_4$	$\frac{\left(\left(-24v_A+24v_m\right)j_{max}-24a_{max}^2\right)s{n}_{max}^2-24a_{max}{j}_{max}^{2}s{n}_{max}+3j_m^4+8j_m^3{j}_{max}+6j_m^2{j}_{max}^2}{24s{n}_{max}^2{j}_{max}{a}_{max}}$
	$\Delta t_5$	$\Delta t_1$
	$\Delta t_6$	$\frac{2a_{max}s{n}_{max}+j_m^2-2j_{max}^2}{2s{n}_{max}{j}_{max}}$
	$\Delta t_7$	$\frac{j_m+j_{max}}{s{n}_{max}}$
II.6f	$\Delta t_1$	$\frac{j_{max}}{s{n}_{max}}$
	$\Delta t_2$	$\frac{-{18}_{max}^2+\sqrt{42j_{max}^4-144j_{max}s{n}_{max}^2{v}_A+144j_{max}s{n}_{max}^2{v}_m}}{12s{n}_{max}{j}_{max}}$
	$\Delta t_3$	$\Delta t_1$
	$\Delta t_4$	$\Delta t_1$
	$\Delta t_5$	$\Delta t_2+\frac{j_{max}}{2s{n}_{max}}$
II.7f	$\Delta t_1$	$\frac{j_{max}}{s{n}_{max}}$
	$\Delta t_2$	$\frac{a_{max}s{n}_{max}-j_{max}^2}{s{n}_{max}{j}_{max}}$
	$\Delta t_3$	$\Delta t_1$
	$\Delta t_4$	$\frac{\left(\left(-24v_A+24v_m\right)j_{max}-24a_{max}^2\right)s{n}_{max}^2-24a_{max}{j}_{max}^{2}s{n}_{max}+j_{max}^4}{24s{n}_{max}^2{j}_{max}{a}_{max}}$
	$\Delta t_5$	$\Delta t_1$
	$\Delta t_6$	$\frac{2a_{max}s{n}_{max}-j_{max}^2}{2s{n}_{max}{j}_{max}}$

.

Figure 12 depicts the possible models for going “back” from $\left(v_m,0,j_m\right)$ to $\left(v_E,0, 0\right)$ in Case II. Models II.1b and II.2b are identical to I.1b resp. I.2b. In Model II.3b, $j_{max}$ is reached, and finally, $a_{min}$ is reached in Model II.4b. We have a simple sequence of the four models, as shown in Figure 12a–d, when we proceed from $\left(v_E,0, 0\right)$ to $\left(v_{max},0,vm2jm\left(v_{max}\right)\right)$. Note that not all models must be present depending on the value of $v_{max}$. When we then go further from $\left(v_{max},0,vm2jm\left(v_{max}\right)\right)$ to $\left(v_{max},0, 0\right)$, one of the Models II.5b to II.8b might occur (Figure 6e–h). These models simply add a “front piece” starting at $j_m$. When reaching $\left(v_{max},0, 0\right)$, the model must be symmetric.

For computing the length of the time intervals, as in Case I, Equation (14) provides some conditions. Further necessary conditions can be derived similarly, as stated for the going forth part in a straightforward manner, so we omit this. The results are given in Appendix A,

Table A4. Formulae and polynomials for computing time intervals in Case II going back.

Model	$\mathbf{\Delta }{\mathit{t}}_{\mathit{i}}$	Formulae and Polynomials
II.1b		Same as Model I.1b
II.2b		Same as Model I.2b
II.3b	$\Delta t_1$	$\frac{-12j_{max}^2+\sqrt{42j_{max}^4-144j_{max}s{n}_{max}^2{v}_E+144j_{max}s{n}_{max}^2{v}_m}}{12s{n}_{max}{j}_{max}}$
	$\Delta t_2$	$\frac{j_{max}}{s{n}_{max}}$
	$\Delta t_3$	$\Delta t_2$
	$\Delta t_4$	$\Delta t_1-\frac{j_{max}}{2s{n}_{max}}$
	$\Delta t_5$	$\Delta t_2$
II.4b	$\Delta t_1$	$\frac{2a_{max}s{n}_{max}-j_{max}^2}{2s{n}_{max}{j}_{max}}$
	$\Delta t_2$	$\frac{j_{max}}{s{n}_{max}}$
	$\Delta t_3$	$\frac{\left(\left(-24v_E+24v_m\right)j_{max}-24a_{max}^2\right)s{n}_{max}^2-24a_{max}{j}_{max}^{2}s{n}_{max}+j_{max}^4}{24s{n}_{max}^2{j}_{max}{a}_{max}}$
	$\Delta t_4$	$\Delta t_2$
	$\Delta t_5$	$\frac{a_{max}s{n}_{max}-j_{max}^2}{s{n}_{max}{j}_{max}}$
	$\Delta t_6$	$\Delta t_2$
II.5b		Same as Model I.4b
II.6b		Same as Model I.5b
II.7b	$\Delta t_1$	$\Delta t_3+\frac{j_m}{s{n}_{max}}$
	$\Delta t_2$	$\Delta t_5+\frac{j_m^2}{2s{n}_{max}{j}_{max}}$
	$\Delta t_3$	$\frac{j_{max}}{s{n}_{max}}$
	$\Delta t_4$	$\Delta t_3$
	$\Delta t_5$	$\frac{-3j_{max}^2+\raisebox{1ex}{$\sqrt{18j_m^4+48j_m^3{j}_{max}+36j_m^2{j}_{max}^2+36j_{max}^4-144j_{max}s{n}_{max}^2{v}_E+144j_{max}s{n}_{max}^2{v}_m}$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}{2s{n}_{max}{j}_{max}}$
	$\Delta t_6$	$\Delta t_3$
II.8b	$\Delta t_1$	$\frac{j_m+j_{max}}{s{n}_{max}}$
	$\Delta t_2$	$\frac{2a_{max}s{n}_{max}+j_m^2-2j_{max}^2}{2s{n}_{max}{j}_{max}}$
	$\Delta t_3$	$\frac{j_{max}}{s{n}_{max}}$
	$\Delta t_4$	$\frac{\left(\left(-24v_E+24v_m\right)j_{max}-24a_{max}^2\right)s{n}_{max}^2-24a_{max}{j}_{max}^{2}s{n}_{max}+3j_m^4+8j_m^3{j}_{max}+6j_m^2{j}_{max}^2}{24s{n}_{max}^2{j}_{max}{a}_{max}}$
	$\Delta t_5$	$\Delta t_3$
	$\Delta t_6$	$\frac{a_{max}s{n}_{max}-j_{max}^2}{s{n}_{max}{j}_{max}}$
	$\Delta t_7$	$\Delta t_3$

.

Next, we address the question of in which possible sequences these models occur when $\left(v_m,0,j_m\right)$ runs from $\left(v_E,0, 0\right)$ to $\left(v_{max},0,vm2jm\left(v_{max}\right)\right)$. For this, we consider the critical velocities starting with the going forth situation. The value of $v_m$ for which the minimal jerk reaches the value $j_{min}=-j_{max}$ is denoted by $v_{mjminA}$; the value for which the maximal jerk reaches $j_{max}$ is denoted by $v_{mjmaxA}$. Moreover, the intermediate velocity at which $a_{max}$ is reached is called $v_{mamaxA}$. Case II is simpler than Case I in that we always have the following inequality:

$$v_{mjminA}\le v_{mjmaxA}\le v_{mamaxA}$$

(16)

Using an analogous notation, we obtain the following for the going back situation:

$$v_{mjminE}\le v_{mjmaxE}\le v_{maminE}.$$

(17)

The algorithm and formulae for finding these velocities are given in Appendix B, Algorithm A2 and

Table A6. Formulae for computing critical velocities in Case II going back.

$v_{mjminE}=v_E+\frac{j_{max}^3}{12s{n}_{max}^2}\left(3\sqrt{2}+4\right)$

$v_{mjmaxE}=v_E+\frac{47j_{max}^3}{24s{n}_{max}^2}$

$v_{maminE}=v_E+\frac{a_{max}^2}{j_{max}}+\frac{a_{max}{j}_{max}}{s{n}_{max}}-\frac{j_{max}^3}{24s{n}_{max}^2}$

. In Case II, the line of argumentation is similar to that in Case I. Equations (16) and (17) make the model sequencing very simple depending on where $v_{max}$ lies. Figure 13 shows, for the going forth part, the possible positions of $v_{max}$ and the corresponding models that hold up to $v_{max}$. As in Case I, within the second, third and forth interval, the model changes (to II.3f, II.6f, II.7f, resp.) if $v_{mjminE}$ is reached. Additionally, as in Case I, the first model to be applied when going from $\left(v_E,0, 0\right)$ to $\left(v_{max},0,vm2jm\left(v_{max}\right)\right)$ need not be II.1f, since $v_E$ might, for example, already be identical to $v_{mamaxA}$ if the difference between $v_E$ and $v_A$ is large enough. Figure 14 shows the same for the going back part.

Finally, we determine the applicable model when we go from $\left(v_{max},0, vm2jm\left(v_{max}\right)\right)$ to $\left(v_{max},0, 0\right)$. First, we consider the going forth situation. As in Case I, we have to identify the critical jerk values $j_m$ where a model switch takes place. Our procedure is similar to that conducted in Case I. We refer to Figure 13. If the position of $v_{max}$ is as marked as (a) there is no switch, i.e., the model is still II.1f. If we have position (b), we proceed as follows:

• In Model II.1f, set $v_m=v_{max}$ and $j\left(t_3\right)=-j_{max}$, and compute $j_m$ by proceeding as stated in Algorithm A5, line 2, denoted by $j_{mswitch}$. There must be a solution, since we must end up with a symmetric model, and Model II.2f is not symmetric.
• For $vm2jm\left(v_{max}\right)\le j_m<j_{mswitch}$, apply Model II.2f; for $j_{mswitch}\le j_m\le 0$, Model II.1f.

If situation (c) applies, the procedure is as follows:

• In Model II.4f, set $v_m=v_{max}$ and $\Delta t_2=0$ (i.e., the phase of constant maximal jerk has duration zero), and compute $j_m$ by proceeding as stated in Algorithm A5, line 5, denoted by $j_{mswitch1}$ in case of existence. If there is such a solution, the next model is II.2f. If not, Model II.4f is suitable for all jerk values.
• If Model II.2f is next, set in this model $v_m=v_{max}$ and $\Delta t_4=0$, and compute $j_m$ by proceeding as stated in Algorithm A5, line 2, denoted by $j_{mswitch2}$. This, then, must exist, since Model II.2f is not symmetric. The next model is II.1f. So, for $vm2jm\left(v_{max}\right)\le j_m<j_{mswitch1}$, take Model II.4f; for $j_{mswitch1}\le j_m<j_{mswitch2}$, apply Model II.2f; and for $j_{mswitch2}\le -j_m\le 0$, Model I.1f.

If situation (d) applies, perform the following:

• In Model II.5f, set $v_m=v_{max}$ and $\Delta t_4=0$ (i.e., the phase of constant maximal acceleration has duration zero). Compute $j_m$ by proceeding as stated in Algorithm A5, line 13, denoted by $j_{mswitch1}$. If there is such a solution, the next model is II.4f. Otherwise, Model II.5f is suitable for all jerk values.
• If Model II.4f is next, set $v_m=v_{max}$ and $\Delta t_2=0$ in this model, and compute $j_m$ by proceeding as stated in Algorithm A5, line 5, denoted by $j_{mswitch2}$, in case of existence. If there is such a solution with $j_{mswitch1}\le j_{mswitch2}\le 0$, the next model is II.2f. If not, apply Model II.5f for $vm2jm\left(v_{max}\right)\le j_m<j_{mswitch1}$ and Model II.4f for $j_{mswitch1}\le j_m\le 0$.
• If Model II.2f is next, set $v_m=v_{max}$ and $\Delta t_4=0$ in this model, and compute $j_m$ by proceeding as stated in Algorithm A5, line 2, denoted by $j_{mswitch3}$. This, then, must exist, since II.2f is not symmetric. Now, for $vm2jm\left(v_{max}\right)\le j_m<j_{mswitch1}$, apply Model II.5f; for $j_{mswitch1}\le j_m<j_{mswitch2}$, Model II.4f; for $j_{mswitch2}\le j_m<j_{mswitch3}$, Model II.2f; and for $j_{mswitch3}\le j_m\le 0$, Model II.1f.

Next, we consider the going back situation and refer to Figure 14. If we have situation (a), Model II.5b is suitable for all jerk values. Note that, in situation (b–d), we have $vm2jm\left(v_{max}\right)=j_{min}$, which makes the inequalities a bit more compact. If situation (b) applies, we proceed as follows:

• In Model II.6b, set $v_m=v_{max}$ and $\Delta t_2=0$, and compute $j_m$ by proceeding as stated in Algorithm A6, line 2, denoted by $j_{mswitch}$. There must be a solution, since we must end up with a symmetric model, and Model II.6b is not symmetric.
• For $j_{min}\le j_m<j_{mswitch}$, apply Model II.6b; for $j_{mswitch}\le j_m\le 0$, Model II.5b.

If situation (c) applies, perform the following:

• In Model II.7b, set $v_m=v_{max}$ and $\Delta t_5=0$ (i.e., the phase of constant maximal jerk has duration zero). Compute $j_m$ by proceeding as stated in Algorithm A6, line 5, denoted by $j_{mswitch1}$, in case of existence. If there is such a solution, the next model is II.6b. Otherwise, Model II.7b is suitable for all jerk values.
• If Model II.6b is next, set $v_m=v_{max}$ and $\Delta t_2=0$, and compute $j_m$ by proceeding as stated in Algorithm A6, line 2, denoted by $j_{mswitch2}$. This, then, must exist, since Model II.6b is not symmetric. The next model then is II.5b. For $j_{min}\le j_m<j_{mswitch1}$, apply Model II.7b; for $j_{mswitch1}\le j_m<j_{mswitch2}$, Model II.6b; and for $j_{mswitch1}\le j_m\le 0$, Model II.5b.

In situation (d), we can perform the procedure of situation (c):

• In Model II.8b, set $v_m=v_{max}$ and $\Delta t_4=0$, and compute $j_m$ by proceeding as stated in Algorithm A6, line 13, denoted by $j_{mswitch1}$. If this does not exist, Model II.8b is suitable for all jerk values.
• If it does exist, the next model is II.7b, and we proceed as in (c), obtaining a total of up to three critical jerk values.

The remarks concerning the situation $\Delta s<S\left(v_A,v_E\right)$ given for Case I also apply to Case II.

5. Implementation and Validation

We assume that the following data are given:

• The kinematic restrictions $v_{max}, a_{max}, j_{max}, s{n}_{max}$.
• The initial and final velocities $v_A, v_E$, where $v_A\le v_E$.
• The distance $\Delta s\ge S\left(v_A,v_E\right)$.

The main task now consists of finding the intermediate velocity and corresponding jerk $\left(v_m, 0,j_m\right)$, such that the covered distance equals $\Delta s$ where $\left(v_m, 0,j_m\right)$ “flows” from $\left(v_E,0, 0\right)$ via $\left(v_{max},0, vm2jm\left(v_{max}\right)\right)$ to $\left(v_{max},0, 0\right)$ and stays there for an arbitrary period of time. Algorithm 1 sketches how this task can be achieved. Briefly explained, the algorithm determines all critical velocities and computes for each of them the distance $w$ covered using the appropriate models. If the given distance $\Delta s$ is exceeded, one knows the interval of critical velocities (including $v_E$ or $v_{max}$) within which $v_m$ must lie. A simple bisection method can then be applied to obtain a guaranteed solution. If $\Delta s$ even exceeds the distance one obtains for $\left(v_{max},0, vm2jm\left(v_{max}\right)\right)$, then the critical jerks are determined. These might be differently sequenced, e.g., if we have $j_{mswitch\_f}$ going forth and $j_{mswitch\_b}$ going back, the ordering might be $j_{mswitch\_f}\le j_{mswitch\_b}$ or the other way around. For each possible ordering, and for each critical jerk from $vm2jm\left(v_{max}\right)$ to 0, the covered distance is computed using the appropriate models. If the given distance $\Delta s$ is exceeded, one knows the interval of critical jerks (including 0 and $vm2jm\left(v_{max}\right)$) within which $j_m$ must lie. Again, a simple bisection method can then be applied to obtain a guaranteed solution. If $\Delta s$ even exceeds the distance one obtains for $\left(v_{max}, 0,0\right)$ as intermediate velocity and jerk, one takes the models to be applied for $\left(v_{max}, 0,0\right)$ and inserts a segment with constant maximal velocity, such that $\Delta s=w$.

Algorithm 1. Main Algorithm.
Input$: v_A, v_E,v_{max}, a_{max}, j_{max}, s{n}_{max}$$,\Delta s$
Output$: \left(v_m, 0,j_m\right)$$, \mathrm{models} \mathrm{going} \mathrm{forth} \mathrm{and} \mathrm{going} \mathrm{back}, \mathrm{corresponding} \Delta t_i$
1:	Determine the critical velocities using the algorithms/formulae presented in Appendix B
2:	$\mathrm{Determine} \mathrm{the} \mathrm{situation} \mathrm{regarding} \mathrm{the} \mathrm{positioning} \mathrm{of} v_{max}$
3:	$\mathrm{Determine} S\left(v_A,v_E\right)$ according to Equation (1) and Table 1
4:	If$\Delta s=S\left(v_A,v_E\right)$ Then
5:	$\left(v_m, 0,j_m\right)=\left(v_E, 0,0\right)$
6:	Determine the going forth model according to Table 1$\mathrm{and} \mathrm{the} \Delta t_i$ according to Table A1 resp. A3
7:	Else
8:	For Each $\mathrm{critical} \mathrm{velocity} \mathrm{from} \left(v_E, 0,0\right)$$\mathrm{to} \left(v_{max},0, vm2jm\left(v_{max}\right)\right)$$(\mathrm{including} v_{max}$)
9:	$\mathrm{Compute} \mathrm{the} \mathrm{distance} w$$\mathrm{reached} \mathrm{when} \mathrm{going} \mathrm{via} \mathrm{this} \mathrm{intermediate} \mathrm{velocity} \mathrm{from} \left(v_A, 0,0\right)$$\mathrm{to} \left(v_E, 0,0\right)$
10:	If $\Delta s>w$ Then
11:	$\mathrm{Pick} \mathrm{next} \mathrm{critical} \mathrm{velocity} (\mathrm{or} v_{max}$)
12:	Else
13:	$v_m$$\mathrm{must} \mathrm{lie} \mathrm{between} \mathrm{the} \mathrm{critical} \mathrm{velocity} \mathrm{reached} \mathrm{before} (\mathrm{or} v_E$) and the actual critical velocity.
14:	Determine the models going forth and going back according to Figure 7 and Figure 8 resp. 13, 14.
15:	$\mathrm{Apply} \mathrm{a} \mathrm{bisection} \mathrm{method} \mathrm{for} \mathrm{determining} v_m$$\mathrm{and} \mathrm{compute} \Delta t_i$ according to Appendix A.
16:	Return
17:	End If
18:	End For Each   % End to line 8
19:	Determine the critical jerks using the algorithms presented in Appendix C
20:	For Each possible sequence of critical jerks
21:	For Each $\mathrm{critical} \mathrm{jerk} \mathrm{from} vm2jm\left(v_{max}\right)$ to 0 (including 0)
22:	$\mathrm{Compute} \mathrm{the} \mathrm{distance} w$$\mathrm{reached} \mathrm{when} \mathrm{going} \mathrm{from} \left(v_A, 0,0\right)$ to $\left(v_E, 0,0\right)$$\mathrm{via} \left(v_{max}, 0,j_{mswitch}\right)$
23:	If $\Delta s>w$ Then
24:	Pick next critical jerk (or 0)
25:	Else
26:	$j_m$$\mathrm{must} \mathrm{lie} \mathrm{between} \mathrm{the} \mathrm{critical} \mathrm{jerk} \mathrm{reached} \mathrm{before} (\mathrm{or} vm2jm\left(v_{max}\right)$) and the actual critical jerk, and the models to be applied are known according to the algorithms in Appendix C.
27:	$\mathrm{Apply} \mathrm{a} \mathrm{bisection} \mathrm{method} \mathrm{for} \mathrm{determining} j_m$$\mathrm{and} \mathrm{compute} \Delta t_i$ according to Appendix A.
28:	Return
29:	End If
30:	End For Each % End to line 21
31:	End For Each % End to line 20
32:	$\% \mathrm{now} \Delta s>S\left(v_A,v_{max}\right)+S\left(v_{max},v_E\right)$ must hold
33:	$\mathrm{Return} \left(v_{max}, 0,0\right)$$\mathrm{and} \mathrm{the} \mathrm{models} \mathrm{to} \mathrm{be} \mathrm{applied} \mathrm{for} \left(v_{max}, 0,0\right)$$, \mathrm{compute} \Delta t_i$ according to Appendix A, $\mathrm{and} \mathrm{insert} \mathrm{a} \mathrm{segment} \mathrm{with} \mathrm{constant} \mathrm{maximal} \mathrm{velocity} \mathrm{such} \mathrm{that} \Delta s=w$.
34:	End If % End to line 4
35:	Return

We implemented the main algorithm and the auxiliary algorithms given in Appendix B and Appendix C as Matlab ^® functions using the Matlab ^® programming language. In these functions, the only calls to genuine mathematical facilities offered by Matlab ^® are the ones to Matlab’s polynomial solver called “roots”. Therefore, when implementing the algorithms in another environment, only a polynomial solver needs to be programmed or imported from a mathematics library.

We set up the following test scenario in order to check whether viable results are provided:

• $v_{max}, a_{max}, j_{max}, s{n}_{max}$ are chosen randomly between 5 and 100 ($\raisebox{1ex}{$\mathrm{mm}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{s}$}\right.$, $\raisebox{1ex}{$\mathrm{mm}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{s}}^2$}\right.$, $\raisebox{1ex}{$\mathrm{mm}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{s}}^3$}\right.$ and $\raisebox{1ex}{$\mathrm{mm}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{s}}^4$}\right.$, respectively; in the sequel, we will omit the units).
• $v_A$ is chosen randomly between $v_{min}$ and $v_{max}$, $v_E$ between $v_A$ and $v_{max}$.
• $\Delta s$ is chosen randomly between $S\left(v_A,v_E\right)$ and $S\left(v_A,v_{max}\right)+S\left(v_{max},v_E\right)$.

We generated ${10}^8$ test configurations and checked and stopped the bisection iteration when the resulting distance was reached with a maximal error of ${10}^{-3}$ (i.e., $1 \mathsf{\mu }\mathrm{m}$). We also checked the error regarding $v_E$ and $a(t_{end})=0$. In addition, we counted whether all possible combinations for positioning $v_{max}$ depicted in Figure 7 and Figure 8 for Case I and in Figure 13 and Figure 14 for Case II are covered, as well as all feasible combinations of numbers of $j_{mswitch}$ values.

Table 3. Coverage of situations in Case I.

	I.b (a)	I.b (b)	I.b(c)
I.f (a)	68,162,974	*	*
I.f (b)	2,565,497	3,135,975	*
I.f (c)	4,472,190	*	*
I.f (d)	689,239	2,251,849	4,733,898
I.f (e)	2,564,185	2,123,533	9,246,440

The left column contains the different situations for positioning $v_{max}$ for going forth; the upper row contains the different situations for positioning $v_{max}$ when going back. An asterisk * denotes that the combination is not possible.

and

Table 4. Coverage of combinations of $j_{mswitch}$ values for $v_m=v_{max}$ in Case I.

# ${\mathit{j}}_{\mathit{m}\mathit{s}\mathit{w}\mathit{i}\mathit{t}\mathit{c}\mathit{h}}$	0	1	2
0	2,044,3058	*	*
1	1,598,261	4,048,933	77,431
2	39,112	54,537	3063

The left column contains the number of $j_{mswitch}$ values for going forth; the upper row contains the number of $j_{mswitch}$ values for going back (# stands for number). An asterisk * denotes that the combination is not possible.

provide the values for Case I;

Table 5. Coverage of situations in Case II.

	II.b (a)	II.b (b)	II.b (c)	II.b (d)
II.f (a)	21,589,590	*	*	*
II.f (b)	4,578,466	6,321,463	*	*
II.f (c)	4,569,027	8,493,669	33,378,435	*
II.f (d)	1,156,690	2,154,669	6,511,882	11,191,542

The left column contains the different situations for positioning $v_{max}$ for going forth; the upper row contains the different situations for positioning $v_{max}$ when going back. An asterisk * denotes that the combination is not possible.

and

Table 6. Coverage of combinations of $j_{mswitch}$ values for $v_m=v_{max}$ in Case II.

# ${\mathit{j}}_{\mathit{m}\mathit{s}\mathit{w}\mathit{i}\mathit{t}\mathit{c}\mathit{h}}$	0	1	2	3
0	13,516,719	2,448,930	72,459	236
1	1,291,857	1,620,708	346	3
2	33,538	57,046	1202	*
3	145	291	3	2

The left column contains the number of $j_{mswitch}$ values for going forth; the upper row contains the number of $j_{mswitch}$ values for going back (# stands for number). An asterisk * denotes that the combination is not possible.

those for Case II. Those entries that are marked with a star are not feasible. We will demonstrate the reasoning behind this by giving two examples:

• When, in Case I, “going forth”, we have situation (c) (see Figure 7), then, because of $v_{mjminA}\le v_{mjminE}$ (see Section 3), only situation (a) is possible for “going back”.
• Assume, in Case II, that we have two $j_{mswitch}$ values when “going forth”, so we must have situation (c). Then, three $j_{mswitch}$ values for going back are only possible when we have situation (d) for “going back”, but then, because of $v_{mamaxA}\le v_{maminE}$, we must also have situation (d) for “going forth”, which is a contradiction. Note that not all values in the upper triangle of Table 6 need to be zero: for example, we can have the combination 0–1 in case of situation (c) “going forth” and situation (b) “going back”.

The data presented in Table 3, Table 4, Table 5 and Table 6 demonstrate a satisfactorily coverage of all possible combinations of situations and numbers of $j_{mswitch}$ values.

Table 7. Maximum error and number of iterations in Cases I and II.

	Case I	Case II
Error Δs (mm)	$\le {10}^{-3}$	$\le {10}^{-3}$
$\mathrm{Error} v_E$ (mm/s)	$\le 1.62\times {10}^{-5}$	$\le 1.5\times {10}^{-5}$
$\mathrm{Error} a\left(t_{end}\right)$ (mm/s²)	$\le {10}^{-12}$	$\le {10}^{-12}$
Mean number of iterations	13.97	13.75
Standard deviation	2.67	2.72
Maximum number of iterations	48	48

shows the maximum error regarding distance, final velocity and final acceleration, as well as the mean and maximum number of iterations performed by the bisection method in Cases I and II. The maximum error regarding distance is due to our stopping criterion for the bisection method. All errors regarding the final velocity above ${10}^{-5}$ were recorded. The number of occurrences was below 10, and the maximum value is given in the table. No errors for $a\left(t_{end}\right)=0$ larger than ${10}^{-12}$ were recorded. It is clear that the boundary set for the maximum admissible error in Δs has a considerable influence on the number of iterations performed by the bisection method, but one cannot relate the values directly, since the bisection is not performed for distance intervals but for velocity or jerk intervals.

All runs were completed successfully. In initial trials, occasionally, a run did not succeed because of numerical problems. The latter were removed by applying the following measures:

• If certain velocity values are very close to each other (i.e., $<{10}^{-5}$), they are set as equal, e.g., if $v_E\approx v_A$, set $v_E=v_A$; if $v_E\approx v_{max}$, set $v_E=v_{max}$; if $v_m\approx v_E$, set $v_m=v_E$.
• If in the bisection method, the middle of the considered interval coincides with a boundary because of rounding, bisection is stopped, and the middle is taken.
• If $v_E=v_A$, models I.1f and II.1f are simplified by removing the fourth time interval, which must be zero.
• When finding and checking the zeros of polynomials, small imaginary parts are neglected, and inequalities and equations of solutions are checked using an admissible error margin.

To be suitable for online trajectory generation, it should be possible to complete the computation within one controller cycle. As in [4] (cf. the discussion presented there), we use 1ms as length of such a cycle. Time data were generated using the respective “tic” and “toc” facilities offered by Matlab^®, which start and stop a timer and provide information on the time spent between the calls. Since the time needed by Matlab ^® varies considerably when one makes several computations using the same data set, we apply the same approach as in [4]: for each random configuration, we make 1000 runs and take the minimum time. We randomly generated 100.000 configurations. The time data are given in

Table 8. Computational effort in Cases I and II.

	Case I	Case II
Mean time per run	276 µs	154 µs
Standard deviation	144 µs	140 µs
Maximum time	831 µs	732 µs

for Cases I and II; the underlying hardware consisted of a desktop PC running Windows 10 with a Xeon E5-1630v4 processor working at 3.7 GHz and 32GB RAM. Although the mean values and standard deviations suggest that, in general, a boundary of 1ms can be achieved, the maximum values show that, occasionally, computation might take longer. Using the profiling tool in Matlab©, one can see that finding the roots of polynomials takes about 50% of the overall computation time. In the bisection iterations, only polynomials of degree 4 occur. Whereas Matlab© implements a general polynomial solver, there are special ones for degree four that are very efficient, needing only 0.5 μs per run (cf. the discussion and references in [4]). Even for 50 bisection iterations in models I.1f and I.4f resp. II.1f and II.5f, with two polynomials per iteration, this would reduce the time needed considerably, such that completion within 1 ms can be achieved (see also the discussion on code optimization in [4]).

6. Numerical Comparison with Related Work

In this section, we compare our results with two approaches from the literature that also apply a fifteen-segment profile with piecewise constant snap and claim to provide a time-optimal solution. For the point-to-point motion (abbreviated as RR, “rest-to-rest”) with initial and final velocity equal to zero, we consider the algorithm by Biagiotti and Melchiorri [11], and for the constant-velocity-to-constant-velocity situation (abbreviated as GG) with arbitrary initial and final velocities and zero acceleration and jerk, we consider the algorithm by Fan et al. [28], who assume zero jerk at the intermediate velocity $v_m$. Ezair et al. [34] make the same assumption and hence should provide identical results, but they explicitly recognize the sub-optimality.

The algorithm presented by Biagiotti/Melchiorri (“CheckConstraintsT1” in [11]) is based upon rectangular filter functions and has four time parameters $T_1,\dots ,T_4$ in case of piecewise constant snap functions. It is strikingly simple and hence seems to contradict the complexity of the situation as presented in this contribution. We first compare the results of a configuration of Case I: $v_A=v_E=0, v_{max}=30, a_{max}=10, j_{max}=12, s{n}_{max}=10$. We let $\Delta s$ run from $S\left(v_A,v_E\right)$ to $S\left(v_A,v_{max}\right)+S\left(v_{max},v_E\right)$, compute $T_1,\dots ,T_4$ according to [11] and sum up to obtain the overall time $t_{sum}$. Then, we compute the time intervals $\Delta t_i$ as specified in this article and sum up to obtain the overall time $t_{sum}$ for our approach. 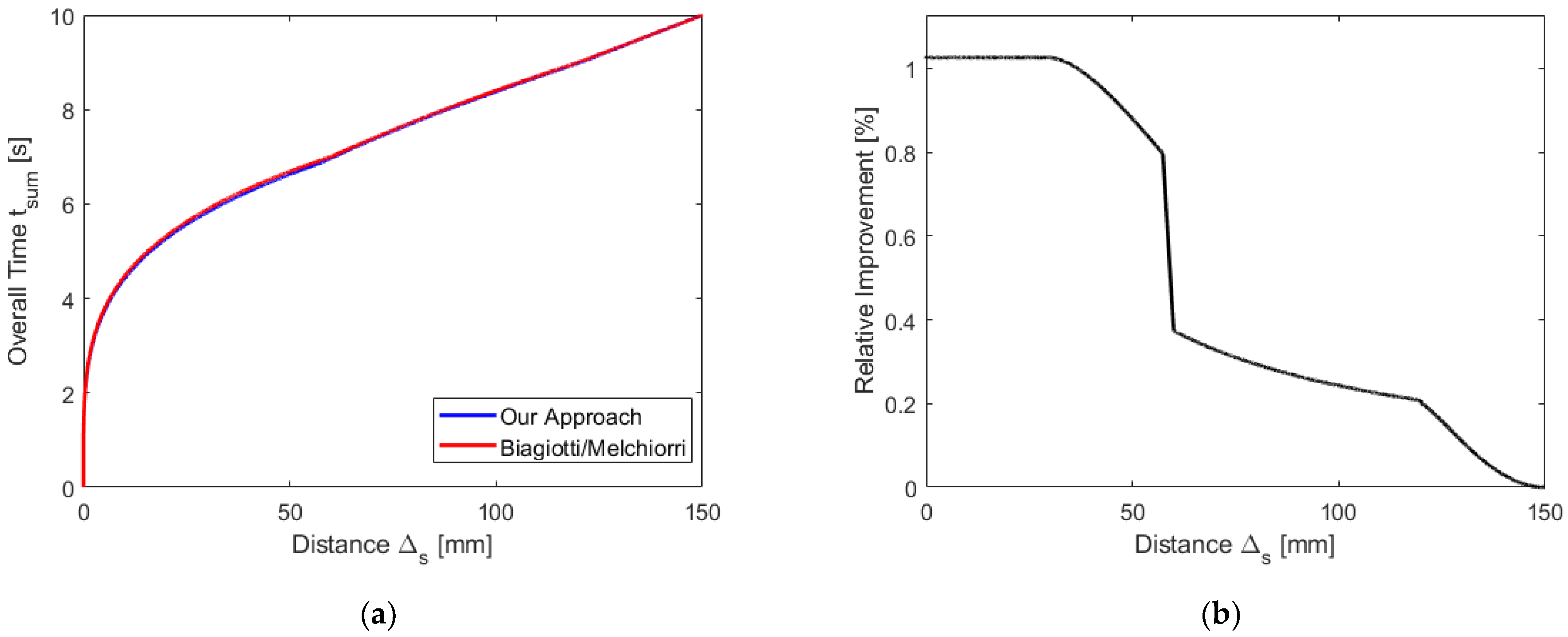Figure 15a depicts the two quite similar curves, but the plot of the improvement of our approach compared to [11] in Figure 15b (in %) reveals that, over the whole range of distances, there is a reduction in time, which goes up to about 1%.

In order to better understand this difference, we picked one specific distance $\Delta s=25$, with which we obtained the following results: the algorithm in [11] results in $T_1=2.4103,T_2=1.6069, T_3=T_4=0.80343$, summing up to $t_{sum}=5.624s$; our algorithm gives as models to be applied I.1f and I.1b with symmetric time interval lists. For model I.1f, we have $\Delta t_1=\Delta t_2=0.8152, \Delta t_3=1.1528, \Delta t_4=0$, resulting in $t_{sum}=5.566s$. 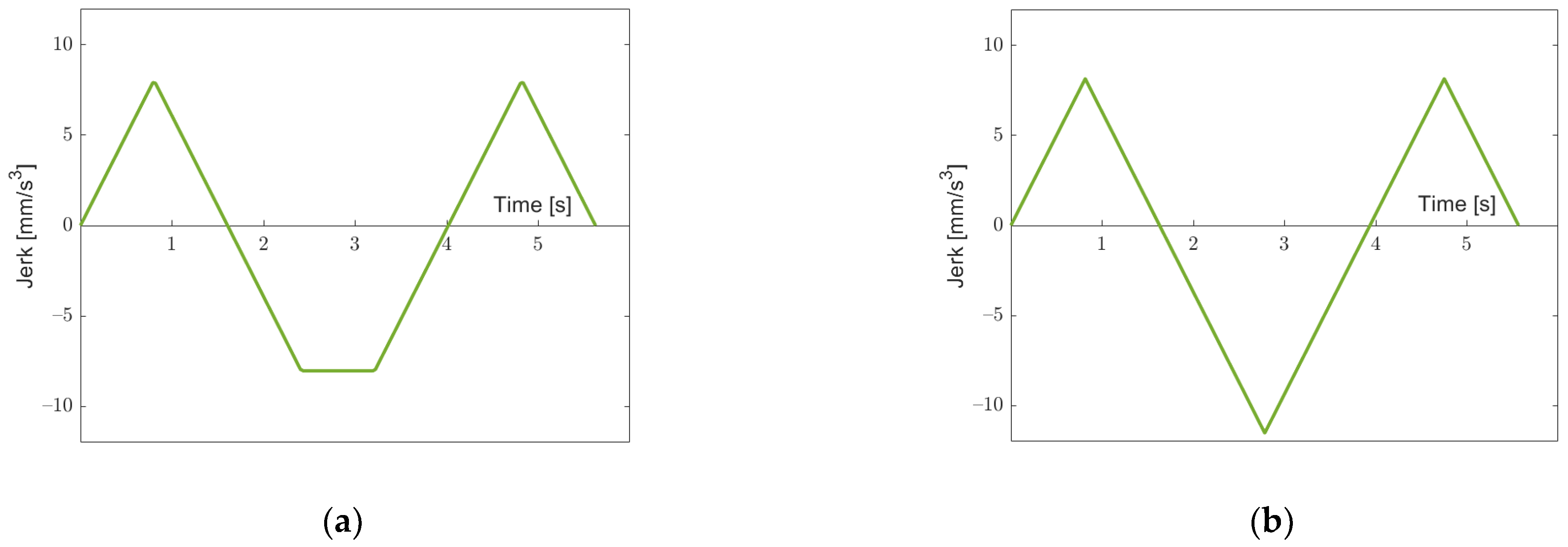We compare the jerk functions provided by both approaches in Figure 16. This shows that our approach takes full advantage of the lower jerk limit $j_{min}=-j_{max}$, whereas the algorithm of Biagiotti and Melchiorri [11] seems to enforce that the maximum and minimum value of the resulting jerk function have the same absolute value. This additional assumption might lead to a sub-optimal result. Actually, in the given configuration, we have Case I, so the maximum and minimum values of the resulting jerk function in our approach will have different absolute values over the full range of considered distances. Hence, our approach always results in a shorter time, as long as $\left(v_m, 0,j_m\right)$ has not reached $(v_{max},0,0)$. This shows that the complexity of the situation demonstrated in this article cannot simply be sidestepped. Yet, it is fair to state that the approach by [11] can be extended to also include frequency restrictions, which makes it particularly interesting for vibration reduction.

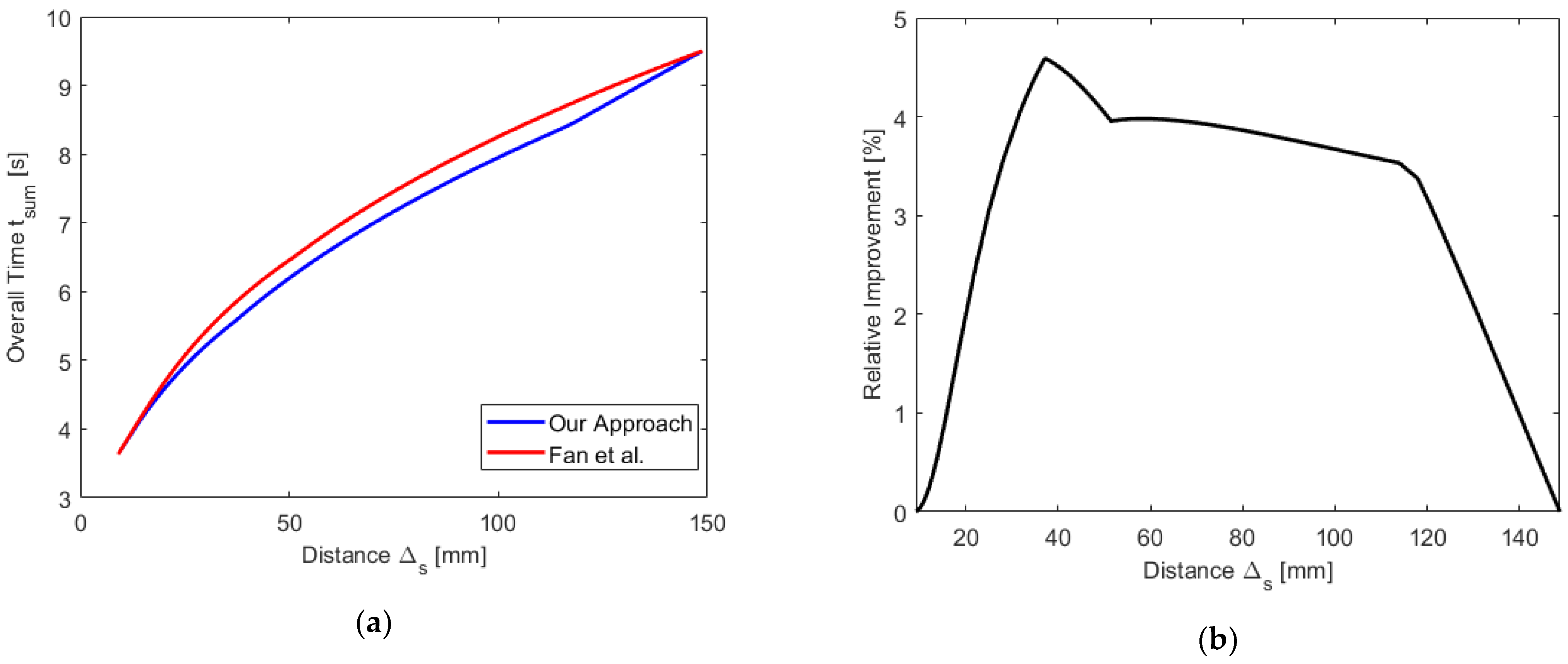
The following configuration serves to compare our approach with the one by Fan et al. [28]: $v_A=-5,v_E=10, v_{max}=30, a_{max}=10, j_{max}=13, s{n}_{max}=10$ (Case I). Again, we let $\Delta s$ run from $S\left(v_A,v_E\right)$ to $S\left(v_A,v_{max}\right)+S\left(v_{max},v_E\right)$ and compute the overall time provided by our approach and by Fan et al., which is shown in Figure 17a. Here, the difference is well-recognizable. Figure 17b shows the relative improvement realized by our approach (in %), which goes up to 4.6%. If $v_A=v_E$ holds, we even found examples with a relative gain of up to 7%, which is due to the fact that the “base time” for going from $v_A$ directly to $v_E$ is zero. Numerical experiments also show that if $s{n}_{max}$ is higher, the gain is reduced, since one can quickly get back from $j_{max}$ to zero.

Again, it is fair to state that the algorithm by Ezair et al. [34] providing the same results as Fan et al. [28] has a wider range of applicability, since arbitrary boundary values for acceleration and jerk can also be prescribed, and it can be applied to higher orders.

7. Conclusions

In this contribution, we describe how a fast jerk–continuous motion function can be found when restrictions on velocity, acceleration, jerk and snap as well as initial and final values for velocity are given. We apply a fifteen-segment motion function with piecewise constant snap and ensure that, at each point in time, at least one restriction is reached, because of which we call the function fast. Note that, as shown in [4], this does not guarantee optimality. The research literature published so far has mainly dealt with point-to-point motions, where initial and final velocities are assumed to be zero, and the jerk becomes zero when the velocity takes its extremal value. We drop this assumption, which makes the situation much more complex, as was shown in the previous sections. Yet, the additional complexity is manageable by suitably structuring the problem in the following way:

• We distinguished two major cases depending on whether the maximum /minimum jerk value can be reached when going from acceleration zero to maximum/minimum acceleration.
• We picked an intermediate velocity $v_m$ with a corresponding jerk value and split up the motion in the velocity–acceleration plane into a going forth and a going back part.
• We identified all possible jerk models for going forth and back
• We identified the switching points for models by computing critical velocities and (at $v=v_{max}$) jerks.

By providing the corresponding algorithms, formulae and polynomials, a re-implementation is possible. Our own implementation in Matlab^© showed that, in large test runs, a solution could always be found, and the complexity is necessary. Moreover, the investigation of time efficiency revealed that the computation should be achievable within a control cycle of 1 ms, where there is still considerable potential for improvement using dedicated quartic solvers.

We compared our approach with other motion functions suggested in the literature that apply the same fifteen-segment profile, since only those approaches allow us to stay at each restriction over a time interval of non-zero length. Numerical experiments revealed that a time improvement of up to 7% could be achieved compared to the algorithm by Fan et al., which also includes the case where initial and final velocities are non-zero. The algorithm by [11] is restricted to the point-to-point motion, and it is the only one that drops the additional assumption that the jerk must be zero when reaching the extremal velocity value. Yet, here, our algorithm showed an improvement of up to 1%, since the algorithm in [11] includes other assumptions, which, for certain configurations, make the algorithm sub-optimal.

The main progress compared to approaches that can be found in the literature can be summarized as follows:

• We take full advantage of restrictions on velocity, acceleration, jerk, and snap, and by dropping any additional assumption reducing optimality we provide the fastest currently available jerk-continuous motion function for rest-to-rest tasks and for tasks where initial and final velocities are given.
• In spite of the complexity caused by dropping any additional assumption our algorithm is still computationally efficient and hence suitable for Online Trajectory Generation.

Our improvement in time efficiency has its price, because it leads to a considerable extension of complexity. It certainly depends on the application whether the shorter processing time is worth this effort. Moreover, our approach has all the limitations that come with the application of fifteen-segment motion functions: the restrictions on jerk and snap are usually not provided in specifications of electronic drives but must be determined experimentally or taken from former experience. Another limitation of our approach consists of not taking into account the dynamics of manipulators, whereas in approaches working with optimization procedures, these can be easily included in the form of restrictions.

Given that the complexity our approach already has for the point-to-point and constant velocity-to-constant velocity task (termed RR and GG above), it might be worth investigating whether a general solution with arbitrary initial and final velocity, acceleration and jerk can be achieved. Further investigation is required to determine whether a reduction in the general case to the situation treated in this contribution is possible, as in [4].