Performance Index for Dimensional Synthesis of Robots for Specific Tasks

Abstract

This study proposes a performance index for the dimensional optimization of parallel manipulators with specific tasks. In particular, the index evaluates the dexterity of the mechanism to be designed and compares it with that of the required specific task, e.g., rehabilitation tasks. The proposed index is implemented to design a 3UPS + RPU parallel manipulator for performing physical rehabilitation treatments on lower limbs. First, the condition numbers of both the mechanism and the lower limb are determined. Subsequently, the indexes are compared such that both systems exhibit similar dexterity. As a case study, the approach is implemented in the dimensional synthesis of the 3UPS + RPU parallel manipulator. The optimization approach enables obtaining a dexterity space of the mechanism that best matches that of the lower limb. The results are graphically presented, showing the matching areas of both workspaces, verifying the effectiveness of the proposed index.

1. Introduction

A performance index for a robotic manipulator is a scalar quantity measuring its performance based on a particular criterion [1]. These indices are valuables to guide the design of a mechanism, as well as the trajectory planning. In particular, they can be used as the objective function to optimize the manipulator operation with respect to the design parameters of the manipulator. In general, measures inherent to the robot’s configuration or post are optimized, such as the condition number of the transpose of the Jacobian matrix [2], manipulability [3], dynamic behavior [4], number of singular configuration [5], and stiffness [6]. These measures can be used for single-objective function optimization or in a multiobjective approach [7].

Yoshikawa, in 1985, introduced one of the first indexes, called the manipulability index [3]. Subsequently, most extensively proposed indexes rely on evaluating the Jacobian matrix of the manipulator [8]. Nevertheless, particular attention should be paid because the Jacobian matrix sometimes has entries with different units, e.g., to represent the link lengths and joint angles, making the index physically inconsistent [9]. Thus, Patel and Sobh [10] recommend implementing a performance index independent of the scale, dimensions, or coordinates.

Most of the measures mentioned above apply to a single configuration of the robots. However, global indexes have been proposed to expand the study of manipulability and dexterity to measure the ability of robotic arms in positioning and orienting end-effectors within the entire workspace. For instance, the Global Conditioning Index (GCI) [11] considers the distribution of the conditioning number of the Jacobian matrix over the entire workspace, regardless of its position. Numerous studies have widely implemented the indices mentioned above, e.g., [12].

In sum, some indices found in the literature can improve the performance of the mechanism globally, such as a better GCI [11]. However, global indexes do not necessarily imply that all points within the workspace of the mechanism are dexterous, as some configurations in the workspace could present low dexterity. Nevertheless, most of the manipulator tasks do not require high dexterity throughout the workspace. Instead, they require dexterity on those configurations for the specific task. In this regard, few indices have focused on improving the design of a mechanism according to a particular task. These indexes are regarded as extrinsic indices [13]. Among them, the compatibility of the manipulator posture with the task requirements based on force and speed was proposed as a performance index [14]. Moreover, the power manipulability index was proposed in [15]. The index is a completely homogeneous index suitable for manipulators combining both translational and rotational movements. Another extrinsic index is the task-dependent performance index, defined as the weighted sum of the squares of the deviation between the actual and desired force transmission ratios, that is, the difference between the speed of the mechanism and the task ellipsoid [16]. Note that very few studies have considered the element manipulated by the mechanism, even though most of the mechanisms in the literature have been designed to perform a particular task. One of the few attempts in this regard is the direction-selective index (DSI) [17], specifically developed for parallel manipulators. The DSI provides decoupled evaluations of the robot translation capabilities along with relevant directions. However, DSI is limited to translational parallel robots. Robotic rehabilitation requires the design of a mechanism that could follow the trajectories of rehabilitation tasks that include rotational and translational motion. Therefore, developing an index to evaluate the performance of a parallel robot for a particular task remains open.

For example, the rehabilitation mechanism that motivated this study [18] was designed for lower limb rehabilitation. We have noted that when the condition number of the Jacobian matrix related to the human leg is determined, there are points where its value is high, implying that the limb at that point does not present good mobility. Thus, the mechanism does not necessarily have to provide good dexterity at that particular point. However, at another point in the workspace, the condition number of the leg may be low, which implies that the limb has very good dexterity at that particular point. A practical design of a mechanism should consider that a low condition number of the Jacobian matrix is required at this point. Therefore, this study proposes an index comparing the dexterity of a mechanism with that of the lower limb. This difference is minimized throughout the entire workspace so that both workspaces exhibit similar dexterity. The proposed index is implemented for the dimensional synthesis of a parallel manipulator.

The organization of the paper is as follows: Section 2 presents the geometry of the mechanism and a simplified geometry of the human lower limbs. In Section 3, the equations to solve the inverse kinematics of both systems are determined. Subsequently, the equation to calculate the condition number of the Jacobian matrix is presented. Section 5 introduces the concept of the proposed performance index. Then, the proposed index is implemented in Section 6 to show the results from an initial test. Finally, conclusions are presented in Section 7.

2. Geometry of the Mechanism and the Lower Limb

2.1. Geometry of the 3UPS + RPU Parallel Robot

Figure 1 shows the schematic representation of the 3UPS + RPU parallel robot [18]. The mechanism comprises four limbs, each with an active prismatic joint (P). The limbs are located as follows: (a) a central RPU limb with a passive revolute joint connecting the fixed platform to the limb and a universal passive joint connecting the limb to the mobile platform; (b) three identical 3-UPS external limbs with a universal joint connecting the fixed platform to the limb, and a spherical passive joint connecting the limb to the mobile platform. The external limbs are equally spaced around the central limb at a radius r. The first axis of the U-joints points parallel to the axis of the revolution joint.

Figure 2 shows the reference frame (O_f-x_f,y_f,z_f) defining the global coordinate frame, and it is located at the center of the fixed base where the x_f axis points perpendicular to the axis of the revolution joint, and the z_f axis points upward vertically to the fixed base. The (O_m-x_m,y_m,z_m) system defines the local coordinate frame attached to the moving platform.

In addition, the mobile (X-Y-Z), (ψ,γ,ϕ) Euler angles represent the orientation of the moving frame system (O_m-x_m,y_m,z_m) with respect to the global coordinate system (O_f-x_f,y_f,z_f).

Regarding the orientation of the union of each lateral arm to the fixed and mobile platforms, angles β_ij are defined, being i = 2 for the second lateral arm and i = 3 for the third lateral arm, j = f for the fixed platform and j = m for the mobile platform. Finally, r_f represents the radius of the fixed platform, and r_m represents the radius of the mobile platform.

The term q_ij represents the parameters of the passive and active joints of each arm. In particular, i = 0, 1, 2 y 3, refers to each arm, where i = 0 applies to the central arm, and j refers to the joints in the arm, starting from the fixed platform. That is, for the central arm, q₀₂ is the displacement of the prismatic joint. Moreover, for each lateral arm, q_i3 represents the displacement of the prismatic joint of each arm. The terms q₁₃, q_23, and q₃₃ are determined from the displacement of the prismatic joints.

2.2. Geometry of the Lower Limb

The geometry of a human lower limb has been extensively studied. Various models have been proposed to analyze the most prominent joints involved in the movement of this limb, e.g., the hip, knee, and ankle joints, knowing that during the movement of the leg, other joints contribute to the motion, such as intertarsal, tarsometatarsal, metatarsophalangeal and interphalangeal ones.

Additionally, as stated in the literature, the knee joint is one of the most complex in the human body, and it has been the subject of numerous studies in which several kinematic models have been proposed to model it [19]. Regarding the ankle joint, various kinematic models have also been developed to simulate this joint. For instance, Carrillo et al. [20] proposed and validated a kinematic model of the ankle joint.

Kinematic models related to the knee sometimes have six degrees of freedom, while for the ankle, at least three rotations are required. For the sake of simplicity, in this study, the geometry of the leg has been simplified to a model considering them as revolute joints. The reason is that the interest of this article is not to develop an extensive biomechanics model of the human lower limb. Instead, we focused on using a kinematic model of the limb to compare its mobility with the mobility of the rehabilitation manipulator.

The proposed model is as follows: (a) a revolution joint is located in the hip; allowing the extension and flexion of the thigh with respect to the body, (b) a second revolution joint in the knee, allowing the extension and flexion of the leg respect to the thigh, (c) two more revolutions joints, located at the ankle, as a universal joint. The first joint allows the extension and flexion of the foot with respect to the leg, while the second one allows the abduction and adduction of the foot with respect to the leg.

Figure 3 shows the simplified model of the lower limb, including the coordinate systems to perform the kinematic analysis using the Denavit-Hartenberg (D-H) notation [21].

3. Kinematic Equations

3.1. Kinematic Analysis of the 3UPS + RPU Parallel Robot

The kinematics of the 3UPS + RPU parallel robot were fully developed [22]. For the sake of completeness, we summarized the basis equation below. The equations are used to develop the mechanism workspace and evaluate the condition number of the Jacobian matrix.

The fundamental equations defining the magnitude of each limb of the mechanism to achieve a specific position and orientation in the end effector can be written as follows:

$${\mathrm{q}}_{02} = {\left({{\mathrm{x}}_{\mathrm{m}}}^2 + {{\mathrm{z}}_{\mathrm{m}}}^2\right)}^{1/2},$$

(1)

q₁₃ = [(x_m + c_γ c_ϕ r_m − r_f)² + s_ϕ² r_m² + (z_m − s_γ c_ϕ r_m)²]^1⁄2,

(2)

q₂₃ = [(x_m − c_γ c_ϕ c_β2m r_m − c_γ s_ϕ s_β2m r_m + c_β2f r_f)² + (−s_ϕ c_β2m r_m + c_ϕ s_β2m r_m − s_β2f r_f)²
+ (z_m + s_γ c_ϕ c_β2m r_m + s_γ s_ϕ s_β2m r_m)²]^1⁄2,

(3)

q₃₃ = [(x_m − c_γ c_ϕ c_β3m r_m + c_γ s_ϕ s_β3m r_m + c_β2f r_f)² + (−s_ϕ c_β3m r_m − c_ϕ s_β3m r_m − s_β3f r_f)²
+ (z_m + s_γ c_ϕ c_β3m r_m − s_γ s_ϕ s_β3m r_m)²]^1⁄2.

(4)

In the equation, c* = cos(*) and s* = sin(*).

In this case, q₀₂, q₁₃, q_23, and q₃₃, represent the generalized coordinates of the mechanism actuators, while x_m and z_m indicate the position of the central point of the mobile platform, γ and ϕ indicate the orientation of the mobile platform, which represents the end effector coordinates.

After deriving these equations, the velocity equations for the actuators can be obtained as follows:

$${\stackrel{.}{\mathrm{q}}}_{02}=-{\mathrm{s}}_{\mathsf{\theta }01} {\stackrel{.}{x}}_{\mathrm{m}} + {\mathrm{c}}_{\mathsf{\theta }01} {\stackrel{.}{z}}_{\mathrm{m}},$$

(5)

$$\begin{gathered} {\stackrel{.}{\mathrm{q}}}_{13} =-{\mathrm{c}}_{\mathsf{\theta }11} {\mathrm{s}}_{\mathsf{\theta }12} {\stackrel{.}{x}}_{\mathrm{m}} + {\mathrm{s}}_{\mathsf{\theta }11} {\mathrm{s}}_{\mathsf{\theta }12} {\stackrel{.}{z}}_{\mathrm{m}} + \left({\mathrm{c}}_{\mathsf{\theta }11} {\mathrm{s}}_{\gamma } - {\mathrm{s}}_{\mathsf{\theta }11} {\mathrm{c}}_{\gamma }\right){\mathrm{s}}_{\mathsf{\theta }12} {\mathrm{c}}_{\mathsf{\varphi }} {\mathrm{r}}_{\mathrm{m}} \stackrel{.}{\gamma } + \\ + \left[\left({\mathrm{c}}_{\mathsf{\theta }11} {\mathrm{c}}_{\gamma } + {\mathrm{s}}_{\mathsf{\theta }11} \right.\right.\left.\left.{\mathrm{s}}_{\gamma }\right) {\mathrm{s}}_{\mathsf{\theta }12} {\mathrm{s}}_{\mathsf{\varphi }} - {\mathrm{c}}_{\mathsf{\theta }12} {\mathrm{c}}_{\mathsf{\varphi }} \right] {\mathrm{r}}_{\mathrm{m}} \stackrel{.}{\mathsf{\varphi }}, \end{gathered}$$

(6)

$$\begin{gathered} {\stackrel{.}{\mathrm{q}}}_{23} = -{\mathrm{c}}_{\mathsf{\theta }12} {\mathrm{s}}_{\mathsf{\theta }22} {\stackrel{.}{x}}_{\mathrm{m}} + {\mathrm{s}}_{\mathsf{\theta }21} {\mathrm{s}}_{\mathsf{\theta }22} {\stackrel{.}{z}}_{\mathrm{m}} + \\ + \left[\left({\mathrm{c}}_{\mathsf{\theta }21} {\mathrm{s}}_{\gamma } (-{\mathrm{c}}_{\mathsf{\varphi }} {\mathrm{c}}_{\mathsf{\beta }22} - {\mathrm{s}}_{\mathsf{\varphi }} {\mathrm{s}}_{\mathsf{\beta }22}) + {\mathrm{s}}_{\mathsf{\theta }21} {\mathrm{c}}_{\gamma }({\mathrm{c}}_{\mathsf{\varphi }} {\mathrm{c}}_{\mathsf{\beta }22} + {\mathrm{s}}_{\mathsf{\varphi }} {\mathrm{s}}_{\mathsf{\beta }22} )\right)\right.{\mathrm{s}}_{\mathsf{\theta }22} {\mathrm{r}}_{\mathrm{m}}] \stackrel{.}{\gamma } + \\ + \left[\left( {\mathrm{s}}_{\mathsf{\theta }22} \left({\mathrm{c}}_{\mathsf{\theta }21} {\mathrm{c}}_{\gamma } + {\mathrm{s}}_{\mathsf{\theta }21} {\mathrm{s}}_{\gamma }\right)(-{\mathrm{s}}_{\mathsf{\varphi }} {\mathrm{c}}_{\mathsf{\beta }22} + {\mathrm{c}}_{\mathsf{\varphi }} {\mathrm{s}}_{\mathsf{\beta }22}) + {\mathrm{c}}_{\mathsf{\theta }22} ({\mathrm{c}}_{\mathsf{\varphi }} {\mathrm{c}}_{\mathsf{\beta }22} + {\mathrm{s}}_{\mathsf{\varphi }} {\mathrm{s}}_{\mathsf{\beta }22}) {\mathrm{r}}_{\mathrm{m}}\right] \stackrel{.}{\mathsf{\varphi }},\right. \end{gathered}$$

(7)

$$\begin{gathered} {\stackrel{.}{\mathrm{q}}}_{33} = -{\mathrm{c}}_{\mathsf{\theta }31} {\mathrm{s}}_{\mathsf{\theta }32} {\stackrel{.}{x}}_{\mathrm{m}} + {\mathrm{s}}_{\mathsf{\theta }31} {\mathrm{s}}_{\mathsf{\theta }32} {\stackrel{.}{z}}_{\mathrm{m}} + \\ + \left[\left(-{\mathrm{c}}_{\mathsf{\theta }31} {\mathrm{s}}_{\gamma } ({\mathrm{c}}_{\mathsf{\varphi }} {\mathrm{c}}_{\mathsf{\beta }32} - {\mathrm{s}}_{\mathsf{\varphi }} {\mathrm{s}}_{\mathsf{\beta }32}) + {\mathrm{s}}_{\mathsf{\theta }31} {\mathrm{c}}_{\gamma }({\mathrm{c}}_{\mathsf{\varphi }} {\mathrm{c}}_{\mathsf{\beta }32} - {\mathrm{s}}_{\mathsf{\varphi }} {\mathrm{s}}_{\mathsf{\beta }32} )\right)\right.{\mathrm{s}}_{\mathsf{\theta }32} {\mathrm{r}}_{\mathrm{m}}] \stackrel{.}{\gamma } + \\ + \left[\left( {\mathrm{s}}_{\mathsf{\theta }32} \left({\mathrm{s}}_{\mathsf{\theta }31} {\mathrm{s}}_{\gamma } + {\mathrm{c}}_{\mathsf{\theta }31} {\mathrm{c}}_{\gamma }\right)(-{\mathrm{s}}_{\mathsf{\varphi }} {\mathrm{c}}_{\mathsf{\beta }32} + {\mathrm{c}}_{\mathsf{\varphi }} {\mathrm{s}}_{\mathsf{\beta }32}) + {\mathrm{c}}_{\mathsf{\theta }32} ({\mathrm{c}}_{\mathsf{\varphi }} {\mathrm{c}}_{\mathsf{\beta }32} + {\mathrm{s}}_{\mathsf{\varphi }} {\mathrm{s}}_{\mathsf{\beta }32}) {\mathrm{r}}_{\mathrm{m}}\right] \stackrel{.}{\mathsf{\varphi }}.\right. \end{gathered}$$

(8)

The angle θ₀₁ is the rotation of the revolution joint of the central arm, while the angles θ_i1 and θ_i2 for i = 1, 2 and 3, are the rotations of the universal joint of each lateral limb.

From the velocity equations, the Jacobian of the mechanism can be defined as follows:

$$\overrightarrow{\dot{\mathrm{q}}}={\mathbf{J}}_{\mathbf{PR}}\overrightarrow{\dot{\mathrm{X}}}.$$

(9)

In Equation (9), $\overrightarrow{\dot{\mathrm{q}}}$ ₌ [$\dot{q}$₀₂, $\dot{q}$₁₃, $\dot{q}$₂₃, $\dot{q}$₃₃ ]^T, $\overrightarrow{\dot{X}}$ ₌ [$\dot{x}$_m, $\dot{z}$_m, $\dot{\mathsf{\gamma }}$, $\dot{\mathsf{\varphi }}$]^T. and J_PR is the Jacobian matrix related to the parallel robot, i.e., the robot being designed.

3.2. Kinematic Analysis of the Lower Limb with 4DOF

According to the geometry presented in the previous section, the kinematics of the leg are defined. Firstly, a fixed coordinate system located at the hip joint (O₀ − x₀, y₀, z₀) is defined, where z₀ axis points upward in the vertical direction. Then, using the D-H notation, the parameters of the rest of the system are defined.

Table 1. D-H parameters for the lower limb.

j-1,j	αlj	alj	dlj	θlj
01	π/2	0	0	θl1
12	0	l1	0	θl2
23	0	l2	0	θl3
34	π/2	0	0	θl4

lists the D-H parameters for the lower limb.

Subsequently, the rotation matrices between each of the local systems can be determined as follows:

$${}_{ }{}^{0}R{}_{01}=\left[\begin{array}{ccc}{c}_{\theta l1}& -s_{\theta l1}& 0\\ 0& 0& -1\\ s_{\theta l1}& c_{\theta l1}& 0\end{array}\right], {}_{ }{}^{1}R{}_{12}=\left[\begin{array}{ccc}{c}_{\theta l2}& -s_{\theta l2}& 0\\ s_{\theta l2}& c_{\theta l2}& 0\\ 0& 0& 1\end{array}\right]$$

$${}_{ }{}^{2}R{}_{23}=\left[\begin{array}{ccc}{c}_{\theta l3}& -s_{\theta l3}& 0\\ s_{\theta l3}& c_{\theta l3}& 0\\ 0& 0& 1\end{array}\right],{}_{ }{}^{3}R{}_{34}=\left[\begin{array}{ccc}{c}_{\theta l4}& -s_{\theta l4}& 0\\ 0& 0& -1\\ s_{\theta l4}& c_{\theta l4}& 0\end{array}\right].$$

(10)

Point F is considered the end effector of the lower limb, and its position can be defined from the following vectorial equation:

$${}^0{\overrightarrow{\mathrm{r}}}_{0\mathrm{F}} = 0{\mathbf{R}}_{01}.{}^1{\overrightarrow{\mathrm{r}}}_{12} + {}^0{\mathbf{R}}_{02}.{ }^2{\overrightarrow{\mathrm{r}}}_{23} + {}^0{\mathbf{R}}_{04}. {}^4{\overrightarrow{\mathrm{r}}}_{4\mathrm{F}},$$

(11)

where ${}^0{\overrightarrow{\mathrm{r}}}_{0\mathrm{F}}$ represents the position vector of point F with respect to point 0. In Equation (11),

$${}^1{\overrightarrow{\mathrm{r}}}_{12} = {\left[{\mathrm{l}}_1;0;0\right]}^{\mathrm{T}};{}^2{\overrightarrow{\mathrm{r}}}_{23} = {\left[{\mathrm{l}}_2; 0; 0\right]}^{\mathrm{T}};{}^4{\overrightarrow{\mathrm{r}}}_{4\mathrm{F}} = {\left[{\mathrm{l}}_3;0;0\right]}^{\mathrm{T}},$$

(12)

The position of point F can also be defined as the position of the end effector according to $\overrightarrow{r}$_EE = [x_m, y_m, z_m]^T. Therefore, considering that $\overrightarrow{r}$_{EE =} ⁰$\overrightarrow{r}$_0F, the following equation is obtained:

$$\begin{gathered} {}_{ }{}^0\overrightarrow{\mathrm{r}}{}_{0\mathrm{F}}=\left[\begin{array}{c}{c}_{\theta l1}\\ 0\\ s_{\theta l1}\end{array}\begin{array}{c}-s_{\theta l1}\\ 0\\ c_{\theta l1}\end{array}\begin{array}{c}0\\ -1\\ 0\end{array}\right].\left[\begin{array}{c}{l}_1\\ 0\\ 0\end{array}\right]+\left[\begin{array}{c}{c}_{\theta l12}\\ 0\\ s_{\theta l12}\end{array}\begin{array}{c}-s_{\theta l12}\\ 0\\ c_{\theta l12}\end{array}\begin{array}{c}0\\ -1\\ 0\end{array}\right].\left[\begin{array}{c}{\mathrm{l}}_2\\ 0\\ 0\end{array}\right]+ \\ +\left[\begin{array}{c}{c}_{\theta l123}{c}_{\theta l4}\\ -s_{\theta l4}\\ s_{\theta l123}{c}_{\theta l4}\end{array} \begin{array}{c}-c_{\theta l123}{s}_{\theta l4}\\ -c_{\theta l4}\\ -s_{\theta l123}{s}_{\theta l4}\end{array} \begin{array}{c}{s}_{\theta l123}\\ 0\\ -c_{\theta l123}\end{array}\right].\left[\begin{array}{c}{\mathrm{l}}_3\\ 0\\ 0\end{array}\right], \end{gathered}$$

$${}_{ }{}^0\overrightarrow{\mathrm{r}}{}_{0\mathrm{F}}=\left[\begin{array}{c}{c}_{\theta l1}{\mathrm{l}}_1+c_{\theta l12}{\mathrm{l}}_2+c_{\theta l123}{c}_{\theta l4}{\mathrm{l}}_3\\ -s_{\theta l4}{\mathrm{l}}_3\\ s_{\theta l1}{\mathrm{l}}_1+s_{\theta l12}{\mathrm{l}}_2+s_{\theta l123}{c}_{\theta l4}{\mathrm{l}}_3\end{array}\right]=\left[\begin{array}{c}{x}_m\\ y_m\\ z_m\end{array}\right],$$

(13)

where θ_l12 = θ_l1 + θ_l2 and θ_l123 = θ_l1 + θ_l2 + θ_l3.

Three equations are defined for x_m, y_m, and z_m from which the kinematic of the leg is determined:

x_m = c_θl1 l₁ + c_θl12 l₂ + c_θl123 c_θl4 l₃,

(14)

$${\mathrm{y}}_{\mathrm{m}}=-\mathrm{s}{\mathsf{\theta }\mathrm{l}}_4 {\mathrm{l}}_3,$$

(15)

$${\mathrm{z}}_{\mathrm{m}}=\mathrm{s}{\mathsf{\theta }\mathrm{l}}_1 {\mathrm{l}}_1+\mathrm{s}{\mathsf{\theta }\mathrm{l}}_{12} {\mathrm{l}}_2+\mathrm{s}{\mathsf{\theta }\mathrm{l}}_{123} \mathrm{c}{\mathsf{\theta }\mathrm{l}}_4 {\mathrm{l}}_3.$$

(16)

Moreover, the rotation of the reference frame determined using the D-H notation is defined by the following rotational matrix:

$${}_{ }{}^{0}R{}_{04}={}_{ }{}^{0}R{}_{01}.{}_{ }{}^{1}R{}_{12}.{}_{ }{}^{2}R{}_{23}.{}_{ }{}^{3}R{}_{34}=\left[\begin{array}{ccc}{c}_{\theta l123}{c}_{\theta l4}& -c_{\theta l123}{s}_{\theta l4}& s_{\theta l123}\\ s_{\theta l4}& c_{\theta l4}& 0\\ s_{\theta l123}{c}_{\theta l4}& -s_{\theta l123}{s}_{\theta l4}& -c_{\theta l123}\end{array}\right].$$

(17)

Considering the Euler angles for the lower limb, (X-Y-Z), the transformation matrix of the end effector, R_T = R_X.R_Y·R_Z, can be defined as follows:

$$R_T=\left[\begin{array}{c}{c}_{\gamma }{c}_{\varphi }\\ s_{\psi }{s}_{\gamma }{c}_{\varphi }+c_{\psi }{s}_{\varphi }\\ -c_{\psi }{s}_{\gamma }{c}_{\varphi }+s_{\psi }{s}_{\varphi }\end{array} \begin{array}{c}-c_{\gamma }{c}_{\varphi }\\ -s_{\psi }{s}_{\gamma }{s}_{\varphi }+c_{\psi }{c}_{\varphi }\\ -c_{\psi }{s}_{\gamma }{s}_{\varphi }+s_{\psi }{c}_{\varphi }\end{array} \right],$$

(18)

Making the elements (1,3) of the rotation matrices expressed in Equations (17) and (18) equal, the value of the angle γ can be determined as the sum of the angles of the first three actuators. Equalizing the element (1,1) of both matrices the value of the angle ϕ is equal to the rotation of the fourth actuator. Finally, the element (2,3) allows for determining that the angle ψ = 0.

$$\mathsf{\gamma }={\mathrm{q}}_{\mathrm{l}1}+{\mathrm{q}}_{\mathrm{l}2}+{\mathrm{q}}_{\mathrm{l}3},$$

(19)

ϕ = q_l4,

(20)

ψ = 0,

(21)

where q_l1 represents the rotation of the first link located at the hip joint, q_l2 the rotation of the knee joint, q_l3 the first rotation of the ankle joint, and q_l4 the second rotation of the ankle joint.

The position of the end effector in the direction of the y axis can be determined as a function of the rotation around the z axis by substituting Equation (20) in Equation (15).

y_m = −s_ϕ l₃,

(22)

The direct kinematic problem can be solved from Equations (14), (16), (19) and (20), while the inverse kinematic problem can be solved from the following equations:

q_l2 = arcos[((x_m − c_γc_ϕl₃)² + (z_m − s_γc_ϕl₃)²-l₁² − l₂²)/(2 l₁ l₂)].

(23)

Equation (23) is obtained by squaring Equations (14) and (16), and then computing the sum of them. In the equation, the angles γ and ϕ are defined as in Equations (19) and (20) as a function of the actuator angle.

To determine q_l1, Equation (14) is multiplied by c_θl1 and Equation (16) by s_θl1. Then, adding the obtained equations, the following equation that relates q_l1 with q_l2 is obtained:

c_θl1 (x_m − c_γc_ϕl₃) + s_θl1 (z_m − s_γc_ϕl₃) = l₁ + c_θl2l₂.

The solution of q_l1 is obtained according to the procedure presented in Tsai [23] where the result is expressed as follows:

q_l1 = atan[(z_m − s_γc_ϕl₃ ± ((z_m − s_γc_ϕl₃)² + (x_m − c_γc_ϕl₃)² − (l₁ + c_θl2l₂)²)^1/2)/(x_{m +} l₁ +
c_θl2l₂ − c_γc_ϕl₃)].

(24)

Finally, q_l3 and q_l4 are determined from Equations (19) and (20).

q_l3 = γ − q_l1 − q_l2,

(25)

q_l4 = ϕ.

(26)

The velocity kinematic problem and the Jacobian matrix are solved simultaneously, applying the method of Whitney et al. [24]. For serial mechanisms the Jacobian that relates the velocity of the end effector with the velocity of the actuator is as follows:

$$\overrightarrow{\dot{X}}={\mathbf{J}}_{\mathbf{L}}\overrightarrow{\dot{q}},$$

(27)

where J_L is the Jacobian matrix related to the task, i.e., the connecting point betwwen the leg and the robot.

For revolute joints, the vector that goes from the actuator pointing to the end effector expressed in the fixed coordinate system is determined for each of the actuators as follows:

$${}^0{\overrightarrow{r}}_{4E}={}_{ }{}^{0}R{}_{04}.{}^4{\overrightarrow{r}}_{4E}=\left[\begin{array}{c}{c}_{\theta l123}{c}_{\theta l4}{\mathrm{l}}_3\\ -s_{\theta l4}{\mathrm{l}}_3\\ s_{\theta l123}{c}_{\theta l4}{\mathrm{l}}_3\end{array}\right], {}^0{\overrightarrow{r}}_{3E}={}_{ }{}^{0}R{}_{03}.{}^3{\overrightarrow{r}}_{3E}=\left[\begin{array}{c}{c}_{\theta l123}{c}_{\theta l4}{\mathrm{l}}_3\\ -s_{\theta l4}{\mathrm{l}}_3\\ s_{\theta l123}{c}_{\theta l4}{\mathrm{l}}_3\end{array}\right],$$

$${}^0{\overrightarrow{r}}_{2E}={}_{ }{}^{0}R{}_{02}.\left({}^2{\overrightarrow{r}}_{23}+{}_{ }{}^{2}R{}_4{}^4{\overrightarrow{r}}_{4E}\right)=\left[\begin{array}{c}{c}_{\theta l12}{\mathrm{l}}_2+c_{\theta l123}{c}_{\theta l4}{\mathrm{l}}_3\\ -s_{\theta l4}{l}_3\\ s_{\theta l12}{\mathrm{l}}_2+s_{\theta l123}{c}_{\theta l4}{\mathrm{l}}_3\end{array}\right],$$

$$\begin{gathered} {}^0{\overrightarrow{r}}_{1E}={}_{ }{}^{0}R{}_{01}.\left({}^1{\overrightarrow{r}}_{12}+{}_{ }{}^{1}R{}_2{}^2{\overrightarrow{r}}_{23}+{}_{ }{}^{1}R{}_4{}^4{\overrightarrow{r}}_{4E}\right)= \\ \left[\begin{array}{c}{c}_{\theta l1}{\mathrm{l}}_1+c_{\theta l12}{\mathrm{l}}_2+c_{\theta l123}{c}_{\theta l4}{\mathrm{l}}_3\\ -s_{\theta l4}{l}_3\\ s_{\theta l1}{\mathrm{l}}_1+s_{\theta l12}{\mathrm{l}}_2+s_{\theta l123}{c}_{\theta l4}{\mathrm{l}}_3\end{array}\right], \end{gathered}$$

(28)

The direction of the axes of the actuators expressed in the fixed system is also determined as follows:

$$\begin{gathered} {}^0{\overrightarrow{z}}_4 = {}^0{\mathbf{R}}_{04}.\overrightarrow{z} = [\mathrm{s}\mathsf{\theta }1123; 0; -\mathrm{c}\mathsf{\theta }1123{]}^{\mathrm{T}}, {}^0{\overrightarrow{z}}_3 = {}^0{\mathbf{R}}_{03}.\overrightarrow{z} = [0;-1; 0{]}^{\mathrm{T}}, \\ {}^0{\overrightarrow{z}}_2 = {}^0{\mathbf{R}}_{02}.\overrightarrow{z} = [0; -1; 0{]}^{\mathrm{T}}, {}^0{\overrightarrow{z}}_1 ={}^0{\mathbf{R}}_{01.}\overrightarrow{z} = [ 0;-1;0{]}^{\mathrm{T}}, \end{gathered}$$

(29)

$$J_q=\left[\begin{array}{c}{J}_{11}\\ 0\\ J_{31}\\ 0\\ -1\\ 0\end{array} \begin{array}{c}{J}_{12}\\ 0\\ J_{32}\\ 0\\ -1\\ 0\end{array} \begin{array}{c}{J}_{13}\\ 0\\ J_{33}\\ 0\\ -1\\ 0\end{array} \begin{array}{c}{J}_{14}\\ J_{24}\\ J_{34}\\ J_{44}\\ 0\\ J_{64}\end{array}\right],$$

(30)

where

J_{11 =} −s_θl1l₁ − s_θl12l₂ −s_θl123c_θl4l₃, J₃₁ = c_θl1l₁ + c_θl12l₂ + c_θl123c_θl4l₃,
J₁₂ = −s_θl2l₂ −s_θl123c_θl4l₃, J₃₂ = c_θl12l₂ + c_θl123c_θl4l₃,
J₁₃ = −s_θl123c_θl4l₃, J₃₃ = c_θl123c_θl4l₃,
J₁₄ = −c_θl123s_θl4l₃, J₂₄ = −c_θl4l₃, J₃₄ = −s_θl123s_θl4l₃, J₄₄ = s_θl123, J₆₄ = −c_θl123,

(31)

4. Condition Number

The condition number was proposed in [2] for designing the limbs of a robotic manipulator. It is defined as the condition number of its Jacobian. A computationally simpler form for calculating the condition number k for a homogeneous Jacobian matrix J is given as follows:

k = ‖J‖.‖J^⁻¹‖,

(32)

A condition number close to unity indicates a well-conditioned Jacobian at that point. The manipulator configurations for which the condition number is unity are known as isotropic configurations. In contrast, when the Jacobian does not have a full rank, the condition number becomes infinity.

This condition number can be calculated for the mechanism and the leg models. For the norm of the Jacobian matrix, any particular norm can be used, according to Moreno et al. (2012), the Frobenius norm can be used [1].

The condition number can measure the precision of the manipulator. Furthermore, it measures the distribution uniformity for the velocity and the operational forces of the mechanism [8]. To define the performance index proposed in this article, the condition number of the mechanism is determined within all the points of the workspace. Moreover, the condition number of the lower limb model is determined within a space equivalent to the workspace of the rehabilitation mechanism.

5. Proposed Performance Index

The index proposed in this study is as follows: First, a device performing a specific task is required. In this case, the mechanism is designed to perform rehabilitation treatments for the lower limbs. This implies that the element interacting with the robot is a human leg, which has limited mobility due to its physiognomy.

Some points in the workspace of the human limb have good mobility. Consequently, the condition number is low. Therefore, at these points, the mechanism should provide good mobility. That is, the condition number of the mechanism must be low. Therefore, it is convenient for a similar dexterity between the mechanism and that of the limb at all workspace points. This indicates that the mechanism must present good mobility where the leg also has good mobility, while at the points where the limb has low mobility, the mechanism must not provide good dexterity.

In this way, the index proposed in this article seeks to compare the condition number of the mechanism and the leg at each point of the workspace. Then, based on this index, the difference between the two condition numbers is kept as small as possible. Moreover, by following the aforementioned approach, the mechanism might have the dexterity required for the rehabilitation motion without requiring an outstanding performance in the places where it is not necessary since the limb does not require it.

To reach this goal, several facts must be considered. First, the workspace where the mechanism is evaluated must be delimited in such a way that both the mechanism and the limb are evaluated in the same physical space. In the case study, the limb and the mechanism do not have the same working space. According to previous analyzes, the leg presents greater mobility than the mechanism in certain directions. Thus, a rehabilitation task with a trajectory similar to that of the preliminary workspace of the mechanism should be considered.

To illustrate the difference in the workspace of both elements, the rotations of the mechanism and the limb are fixed. It implies that the workspace of both elements is evaluated, keeping the rotations null, with the possibility of displacement in the x and z directions.

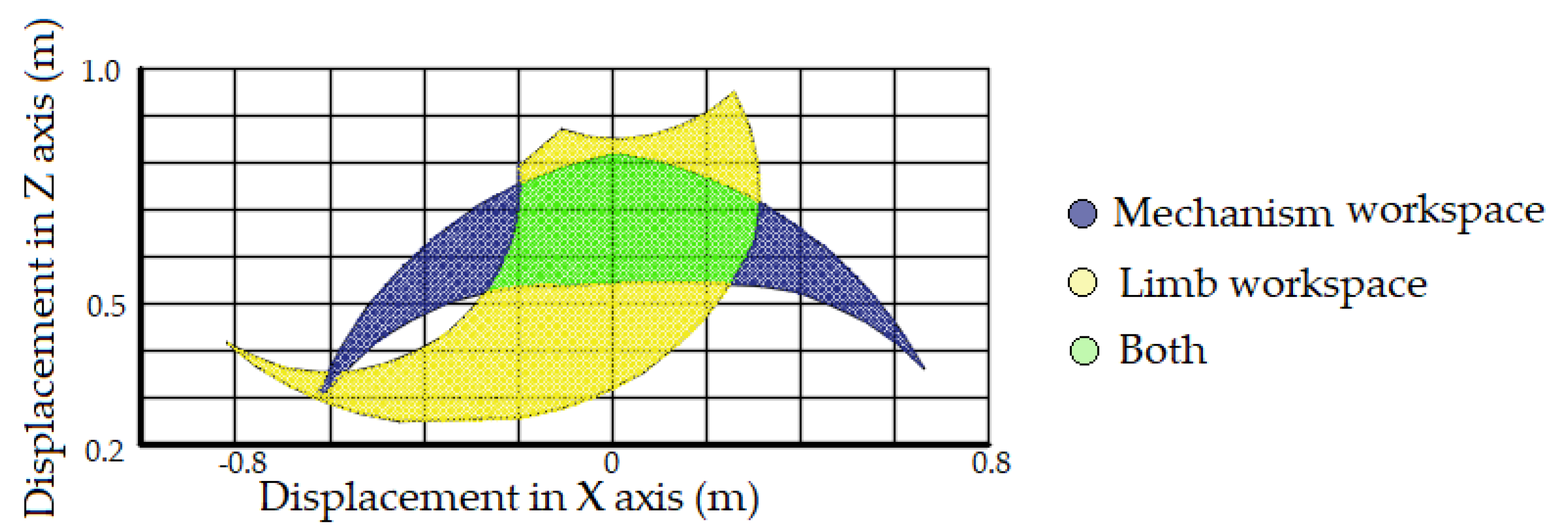
Figure 4 shows the workspace of the mechanism (blue), the mobility space of the lower limb (yellow), and finally, both elements (green) in such a way that they achieve the greatest number of coincident points since both spaces are different in shape and size. In this way, the common workspace for both elements is highlighted in green. This intersecting workspace represents the space where the novel performance index will be evaluated.

The second aspect of configuring the proposed performance index is related to the condition number. The condition number of a mechanism has a highly variable range, 1–infinity. For this reason, if there are points where the condition number is much higher than other ones, the proposed index could be altered. In this way, a relative comparison between both condition number leg and mechanism is proposed, avoiding the points where the condition numbers are high. Therefore, the difference as well these values may affect the novel index.

In other words, if instead of calculating the absolute difference in all the points of the evaluated workspace, the relative difference is calculated, the average of the differences would not be affected by the points where the condition number of both leg and mechanism is high.

Finally, the third aspect to consider is when the condition numbers are close; it implies that the mechanism can handle the limb well, regardless of which of the two is greater. Therefore, the differences to be determined are absolute and their sign is not relevant.

The desirable situation is when the mechanism has a condition number lower than the condition number of the limb, which implies more dexterity in the mechanism than the leg. In this case, the percentage difference becomes positive. When the condition number in a limb is higher than in the mechanism, the percentage difference is negative. In both cases, the percentage difference is the value required for optimization. Therefore, it is proposed to determine the magnitude of this difference regardless of the sign. That is, the absolute value of the percentage difference of the condition numbers between the mechanism and the element to be manipulated is determined.

Equation (33) presents the proposed performance index.

$$GCCI=\frac{1}{n}{\sum }_{i=1}^n\left|\frac{K_m-K_l}{K_m}\right|,$$

(33)

where GCCI is the novel global comparative index of the condition number, K_m is the condition number of the robotic manipulator, K_l is the condition number of the human limb, and n represents all the points of the workspace that will be evaluated.

In Equation (33), the difference between K_m and K_l represents the difference between the two determined indices; the ratio between the previous difference and Km generates the relative evaluation of the index. Finally, the sum of all the differences and their subsequent product with 1/n convert the index into a global index.

In the next section, the evaluation of the proposed index for the rehabilitation device is presented.

6. Results

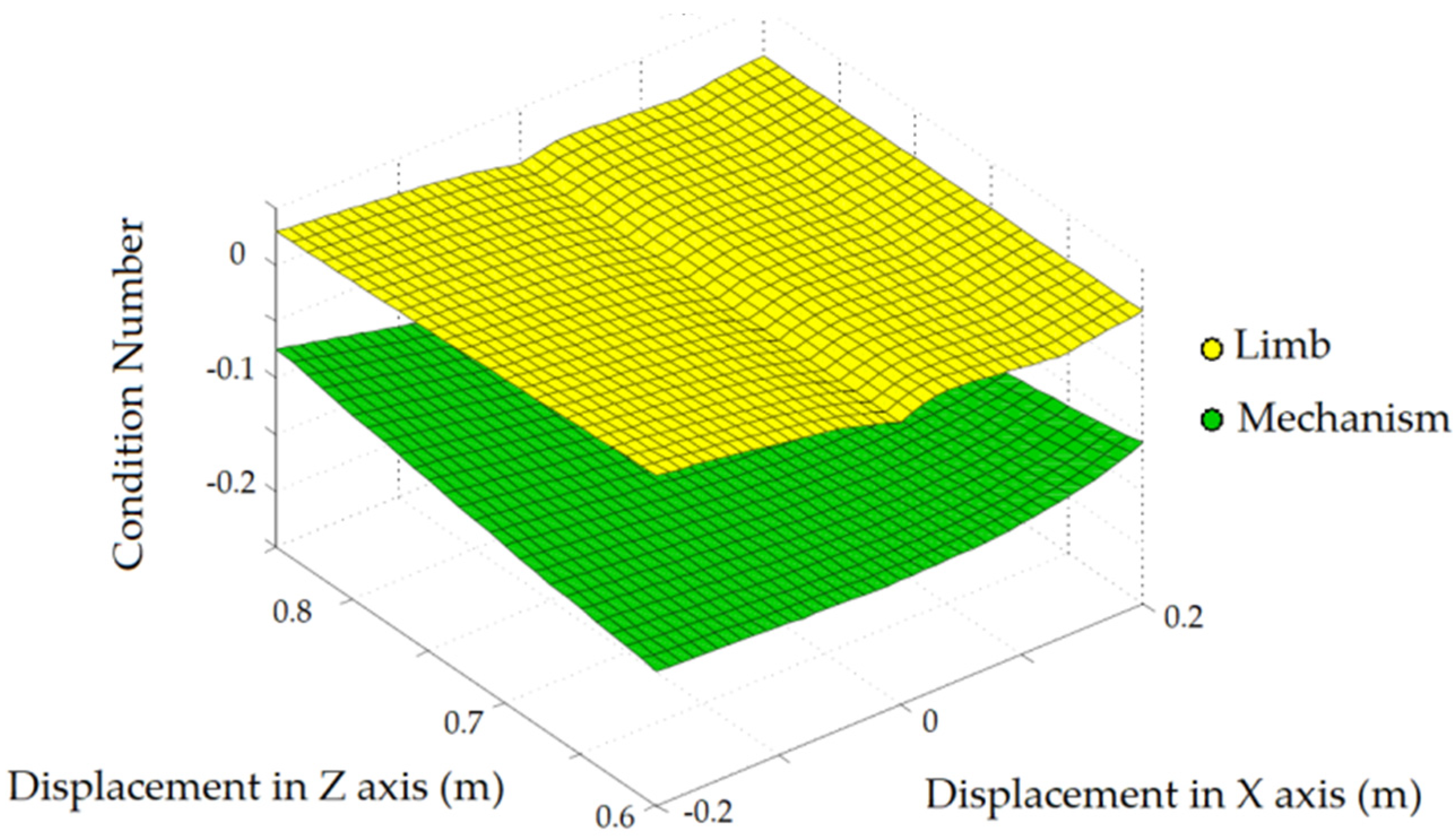
To evaluate the proposed index for the rehabilitation mechanism, the first step should be the determination of the condition number of the mechanism and of the lower limb. Figure 5 shows the inverse of the condition number of both elements within the delimited workspace.

For the sake of simplicity, the inverse of the condition number has been represented, because precisely in this area, the mechanism approaches a singularity and consequently the condition numbers become very high.

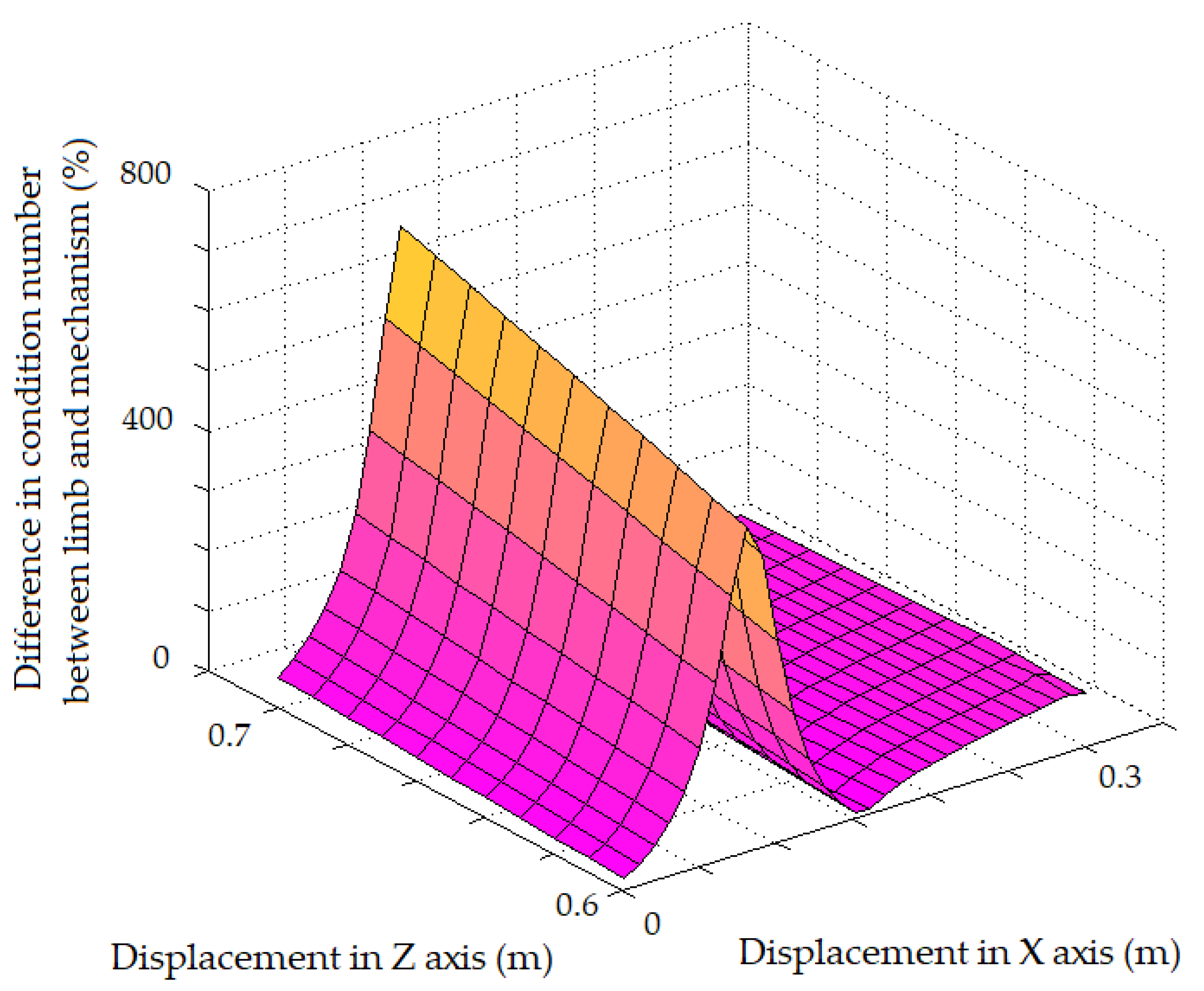
The percentage difference between the condition numbers of both elements, for all the evaluated points, is shown in Figure 6.

By averaging the differences and finding the global comparative index of the condition number, the result is 149.98%. It can be interpreted that in the evaluated points, the mechanism has a mobility capacity that is very far from the mobility capacity of the leg in that space, indicating that this is one of the aspects that should be improved in the proposal presented.

However, it should be remembered that this index is a percentage value, and additionally, as it is a new index, further simulations should be performed to get insights into expressing an adequate value.

To test the performance of the proposed index for the dimensional synthesis of robots, in the following, the results for the optimal design of the studied robot are presented.

Optimal Dimensional Design of the 3UPS + RPU Parallel Robot

The proposed index includes the computation of two Jacobian matrixes: the mechanism and the extremity. This implies that the computational burden of the optimization process is high, and many parameters can affect it. Thus, prior to optimization, (1) the relative position between the limb and the robot must be defined, (2) the size of the workspace to be optimized, (3) the dimensions of the robot’s limb and extremity. Consequently, these three aspects must be determined before performing the robot dimensional synthesis process.

Starting from the original design dimensions of the mechanism [25], we proceeded to perform the dimensional optimization using the IGCC as the objective function.

First, the dimensions of the human limb were determined. For this, measurements of the human extremity reported in [26] were considered. In particular, the study measured the anthropometric measurements of the Latin American population. In particular, the measurements between the joints of the leg for the average Latin American adult were considered. From there, the distance between the hip and knee joints is approximately 0.40 m, and the distance between the knee and ankle is 0.35 m. Subsequently, a relative position between the human limb and the mechanism was defined and adapted such that the workspace between both was the largest possible area, see Figure 4. Finally, this workspace was limited to the shared region between the leg and the robot.

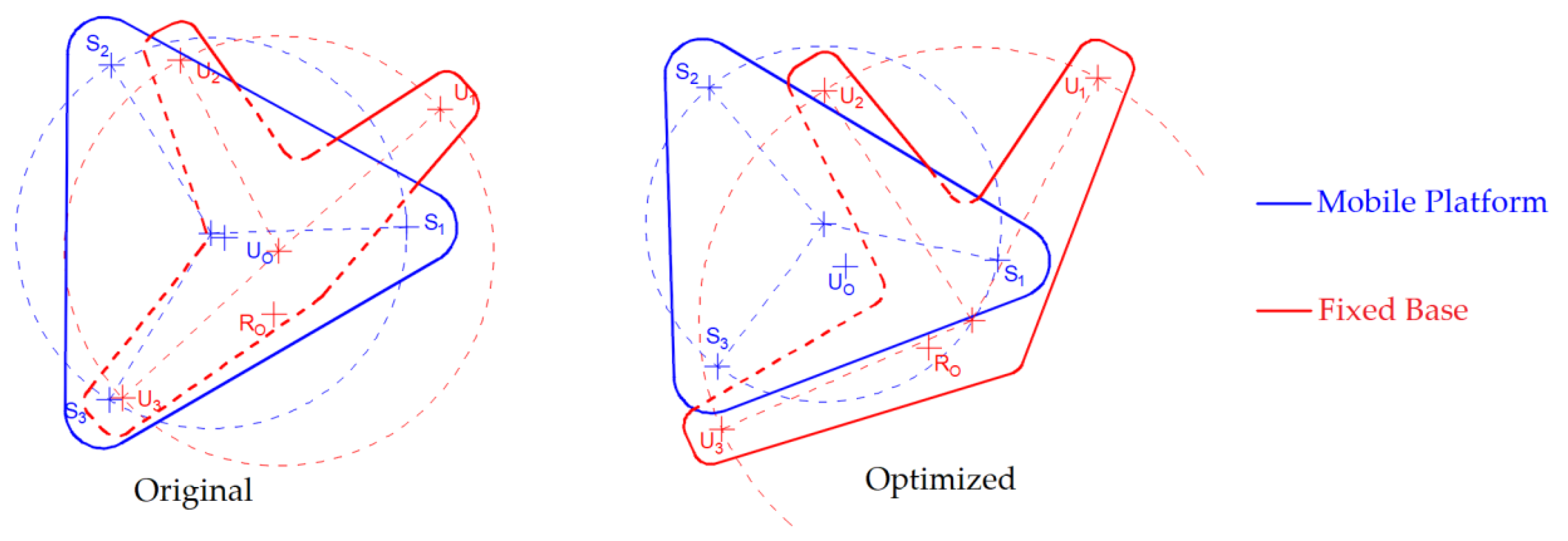
Subsequently, the optimization of the mechanism was executed. The set of variables for the optimization process of the robot referred to the anchor point of each limb in each platform, a total of 16 variables (Points Ui and Si in the upper and lower platform, respectively, i = 1 … 3). We considered two coordinates in each anchor point and a total of 8 anchor points.

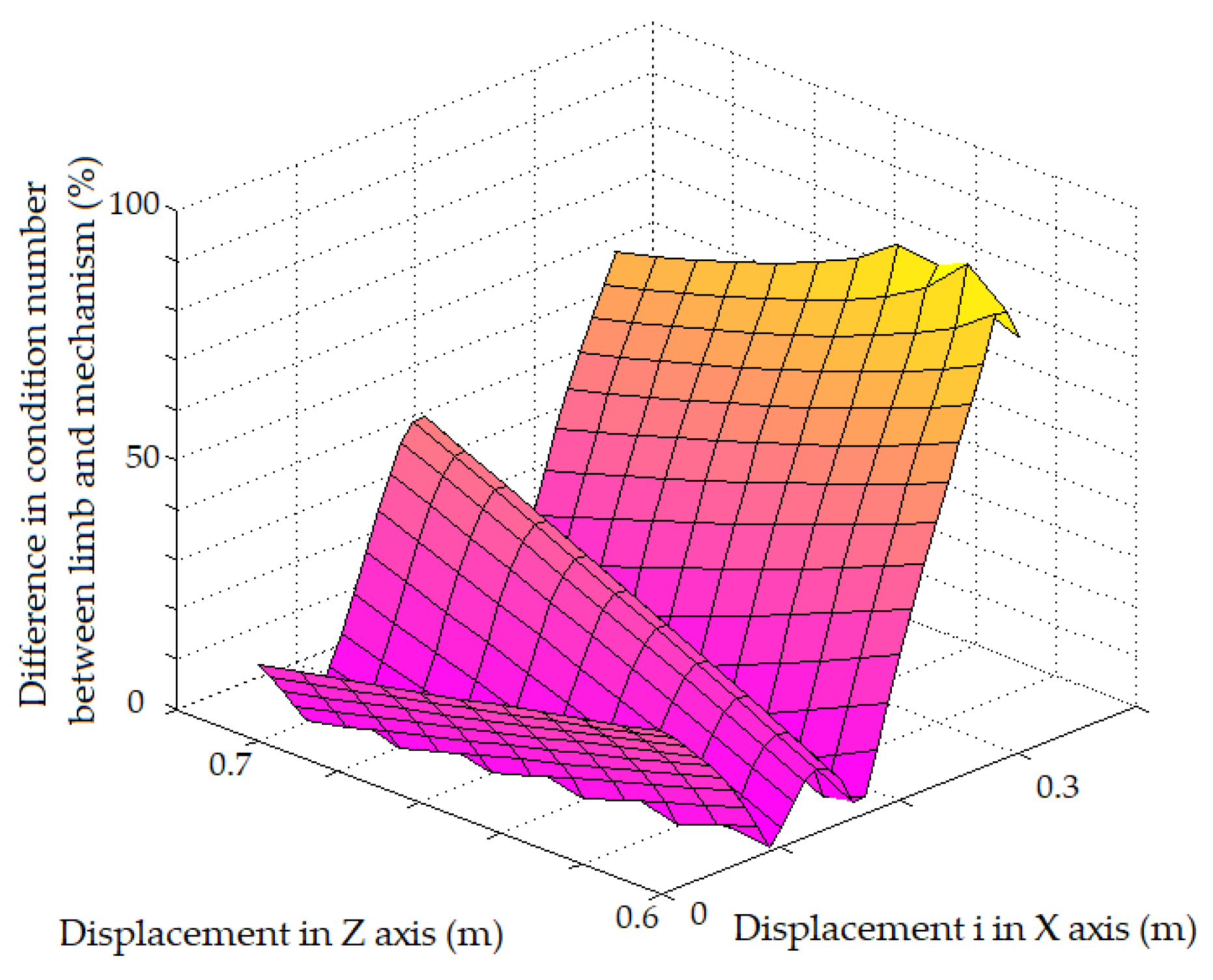
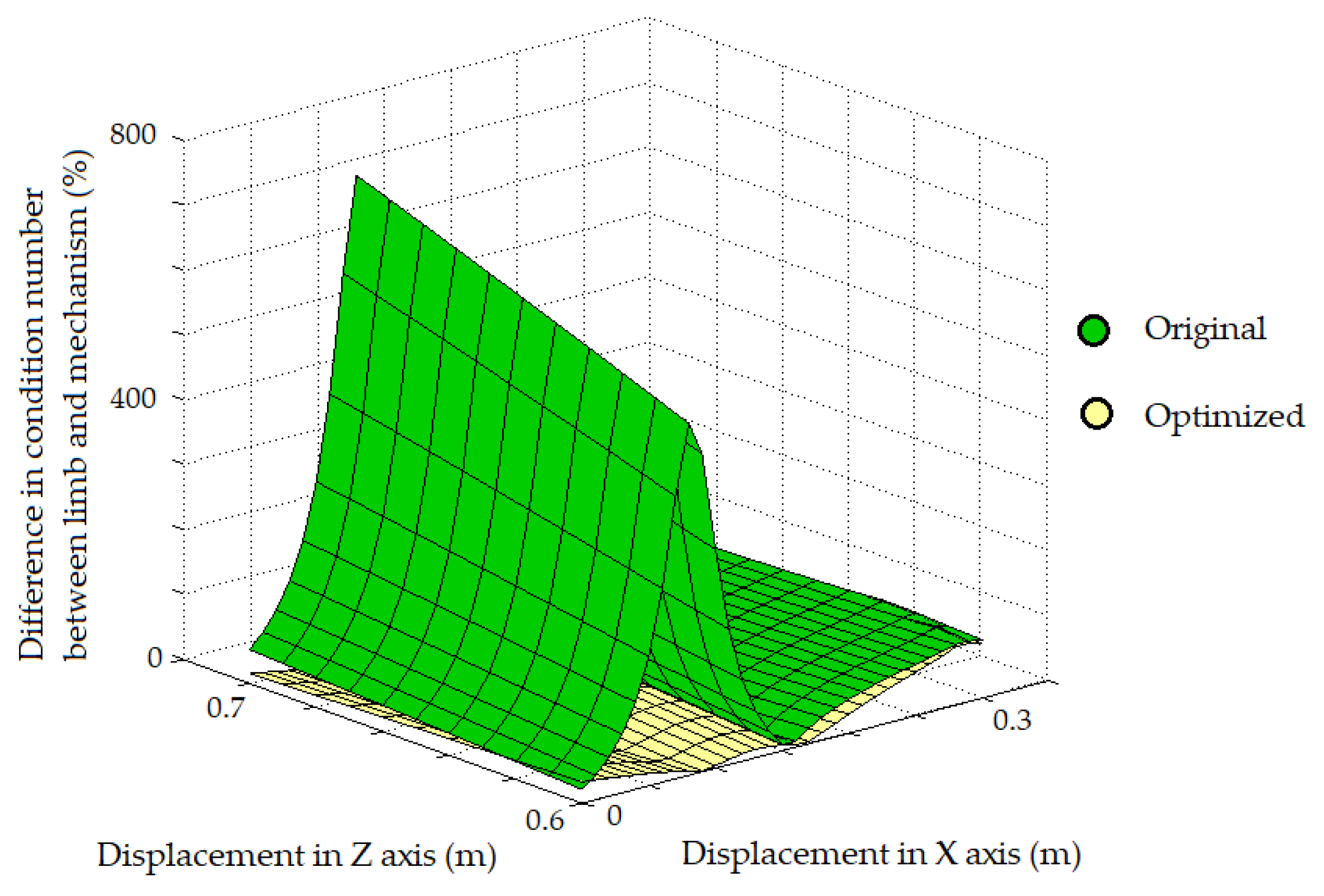
Figure 7 shows the obtained values of the difference between the condition number of mechanism and the limb along all the points of the workspace. Note that all the points within the evaluated workspace have a different of less than 100%. Before the optimization most points exceeded this value. In particular, the optimization decreased the differences from the initial value of 149.98% to the value of 29.75%. This results implies that the mechanism is better suited to the dexterity of the lower limb in the workspace studied.

Figure 8 shows the decrease in the difference between the condition numbers of the mechanism and the limb before and after optimization.

Figure 9 shows the location of the anchoring points before and after optimization. Some of the location of the anchor points do not change substantially; however, the index improved significantly.

Finally, several aspects can be improved, such as positioning the mechanism with respect to the lower limb end-effector location on the platform. For example, the position of the limb in the platform might be the change of the end-effector location can avoid spaces where the mechanism does not approach singular points. In addition, the proposed index compared the dexterity of both systems regardless of the motion direction. That is, the dexterity in a particular direction, i.e., a similar translation dexterity in the x-direction of both systems, cannot be guaranteed. A future work to overcome this limitation is to consider the index proposed in [17]. In this case, the optimization approach could consider optimizing movements along with specific directions for the specific task.

7. Conclusions

A performance index for the kinematic optimization of robotic manipulators was proposed. The index represents the global behavior of the relative difference between the condition number of the mechanism and the condition number of the element to be manipulated. The proposed index was verified through a case study considering the design of a 3UPS + RPU parallel robot for rehabilitation tasks. The optimization decreased the differences between the condition number of the mechanism and the condition number of the element to be manipulated, from the initial value of 149.98% to the value of 29.75%. The example presented here showed a procedure with and straightforward implementation. The index was evaluated in a parallel manipulator; however, its application could be extended to serial mechanisms or cobots, for instance, in an industrial task with the robot interacting with the human upper extremity. The dexterity of the robot can be designed to match that of the upper limb. Further studies will consider implementing and strategy based on matching the DSI of both the task and the manipulator.