Evaluation Criteria for Trajectories of Robotic Arms
Abstract
:1. Introduction
2. Criteria
3. Validation of Criteria
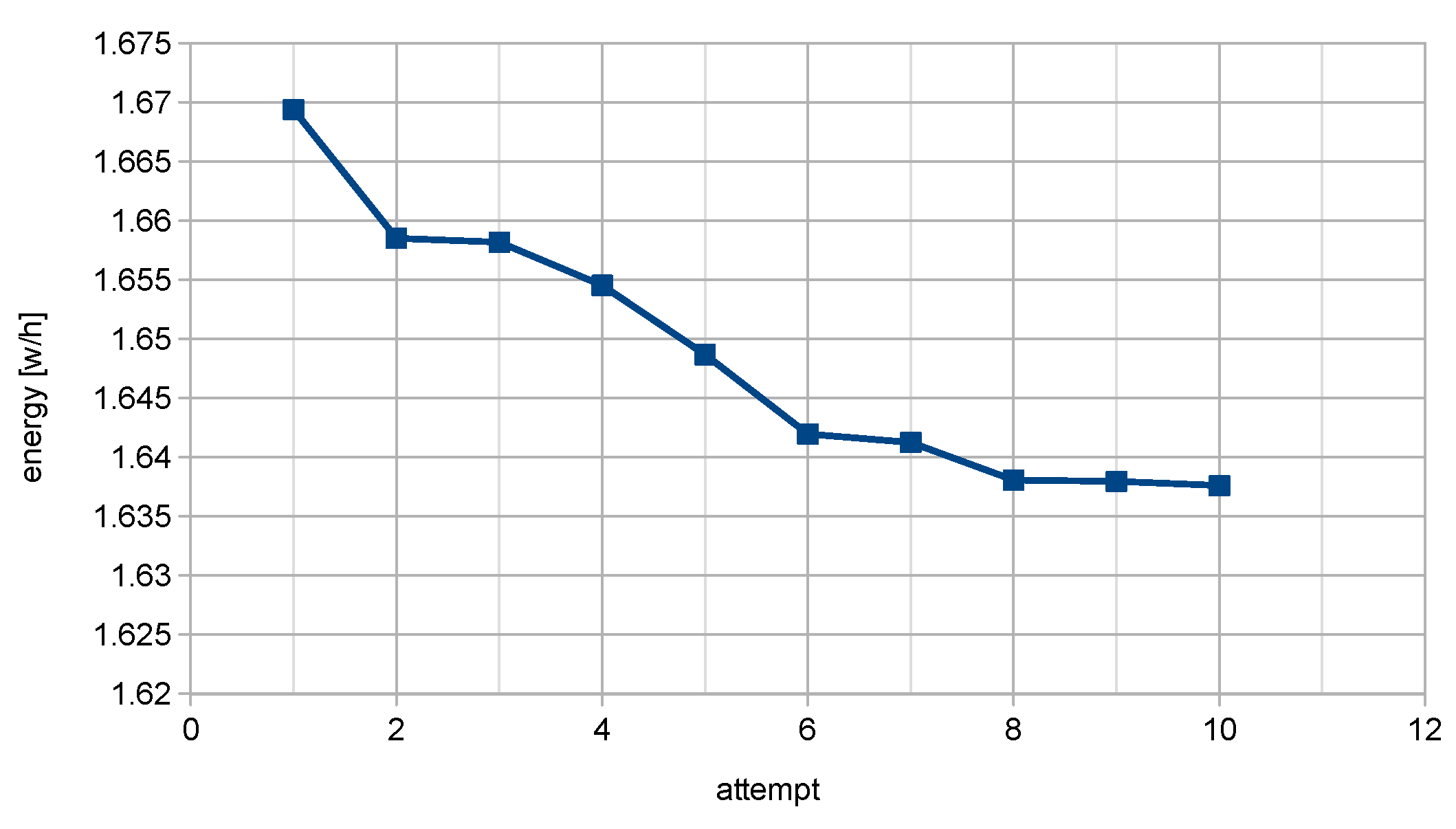
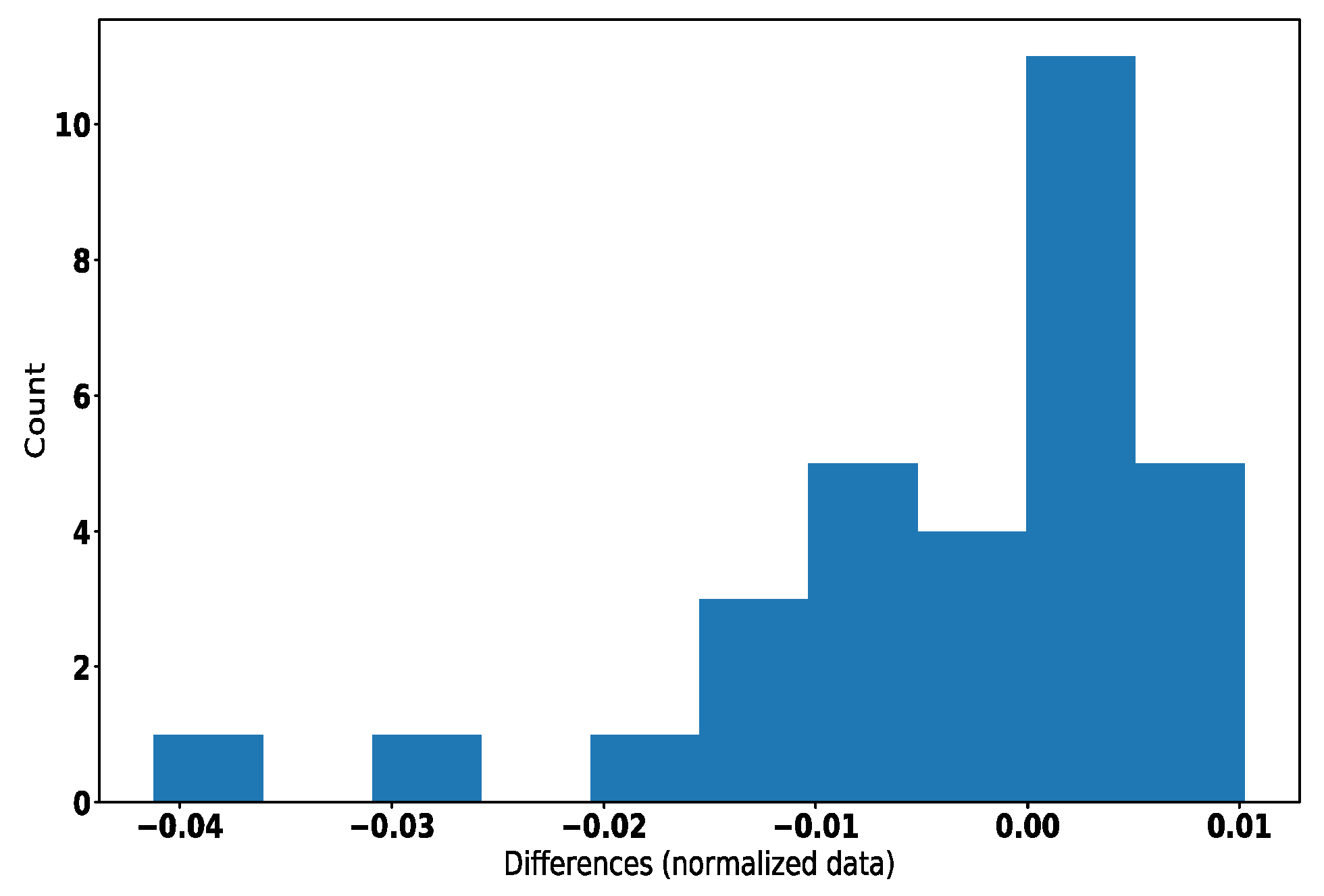
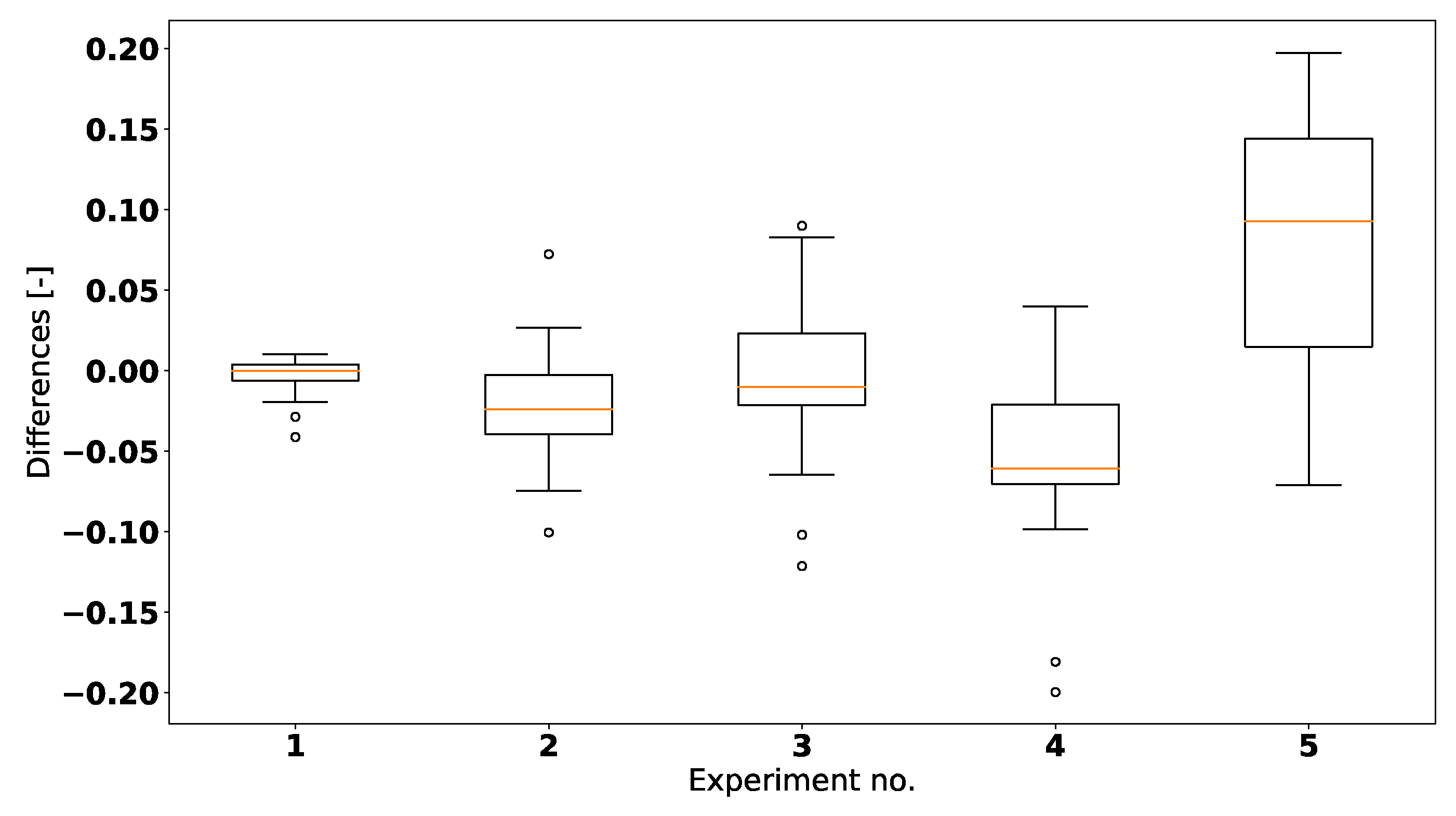
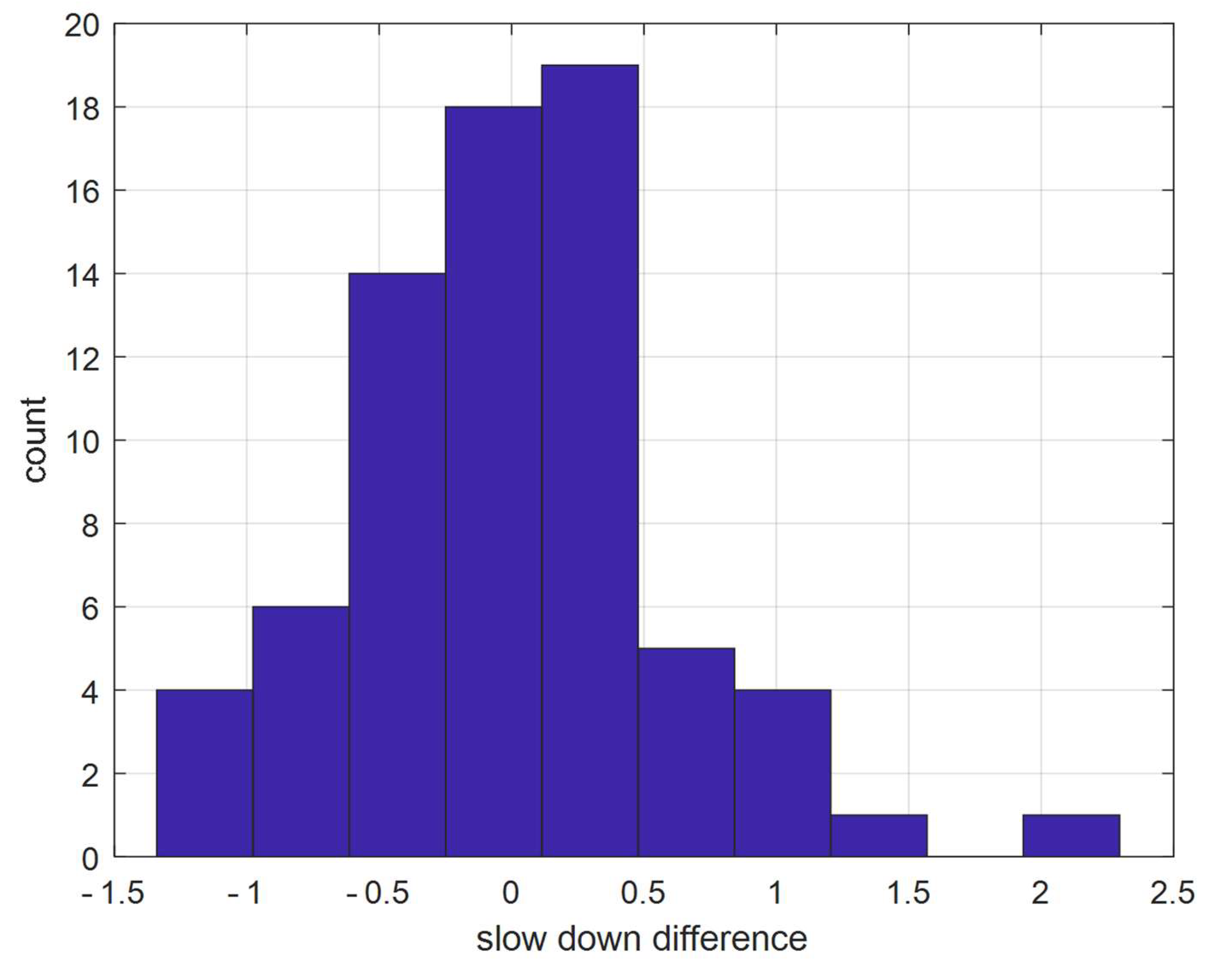
3.1. Control Pseudo-Cost
- Warm-up of the robot;
- Generate paths between the same start and the same goal using a path planner;
- Execute the generated trajectories on a real robot and measure energy consumption;
- Make cycles through the whole constant space, in which constants are gradually changed:
- Compute the criterion score using current constants for each path;
- Normalize the measured energy with the criterion score;
- If the summary of differences between measured energy and criterion score on each trajectory is lower than the minimum (from previous cycles), store this value as a new minimum.
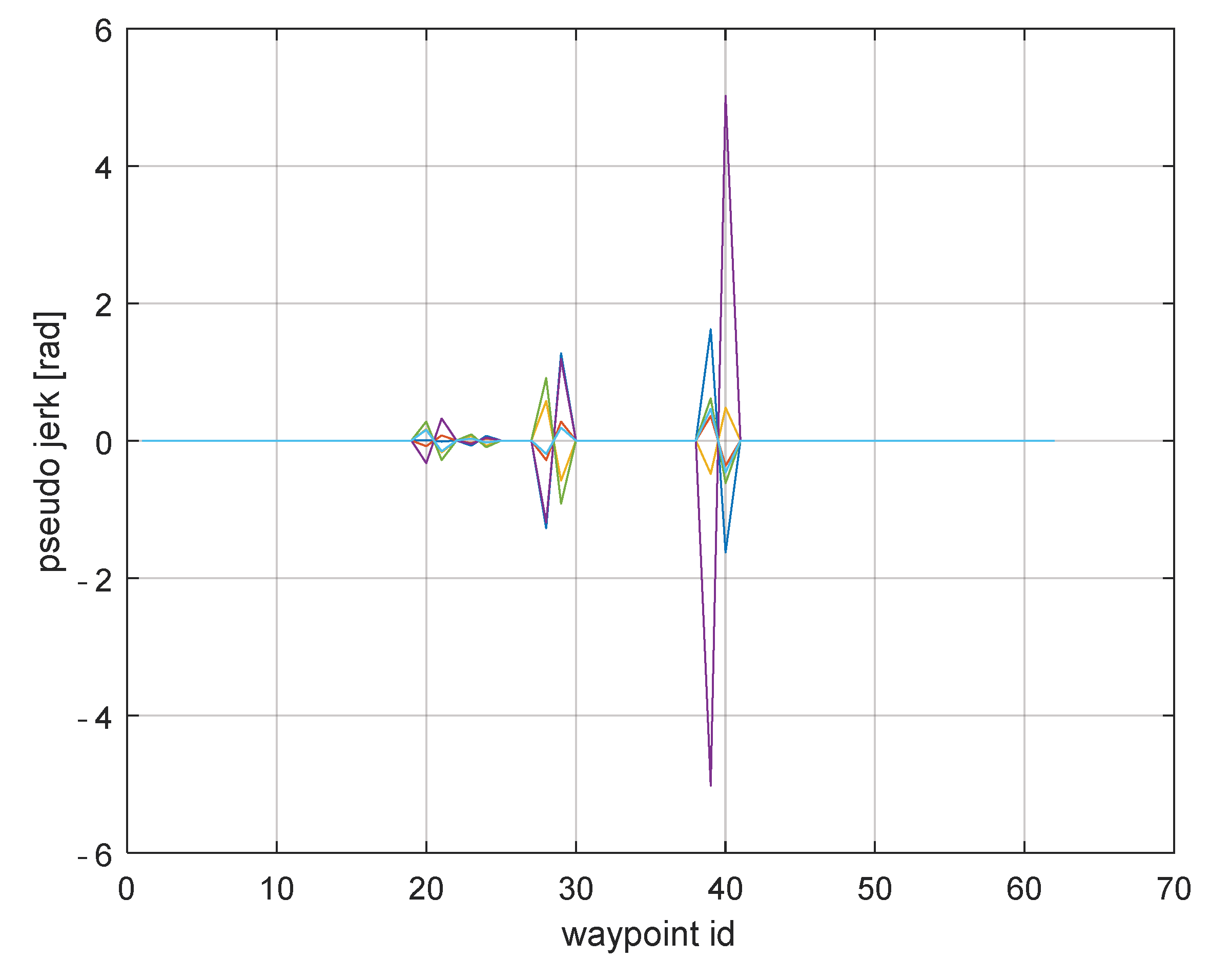
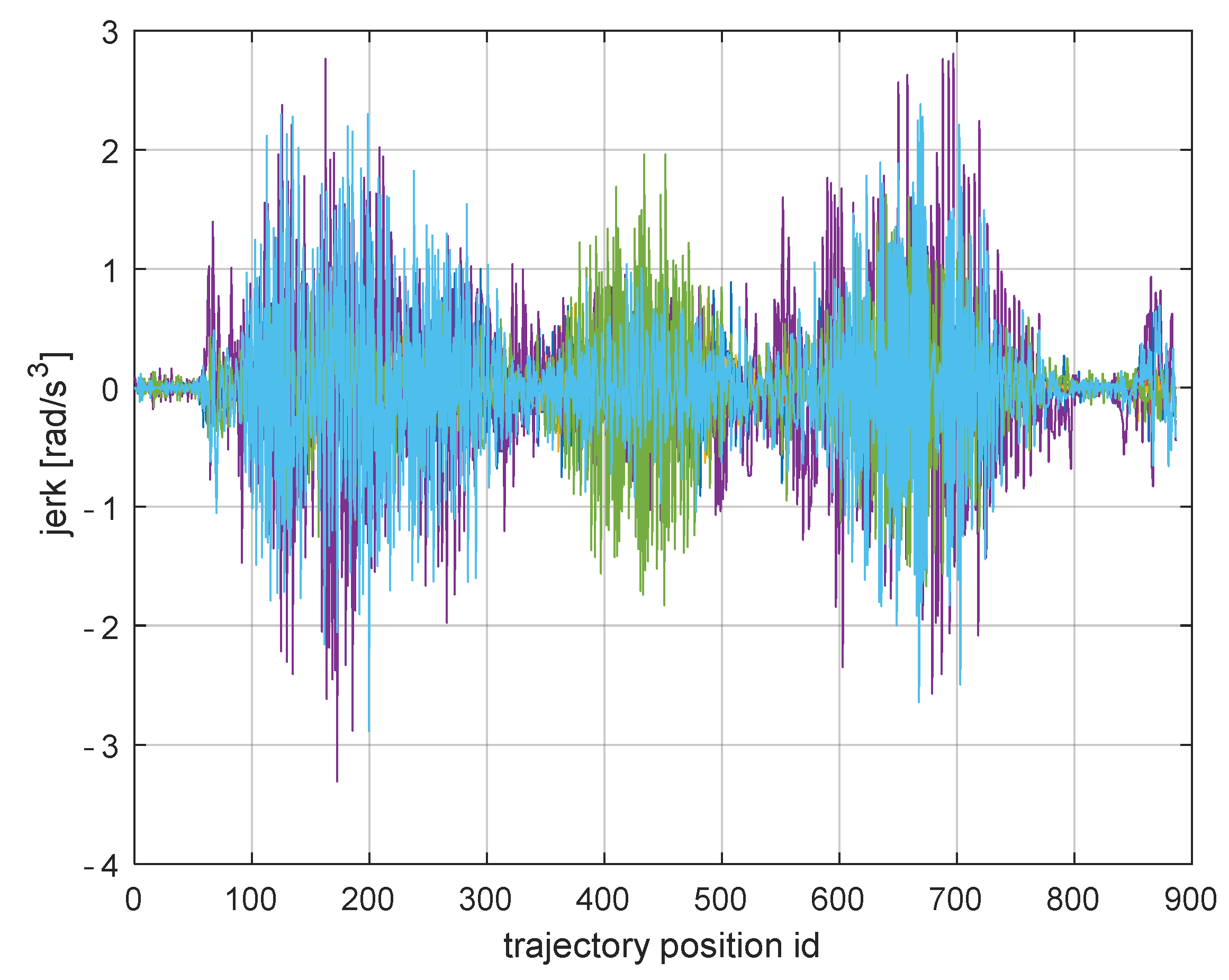
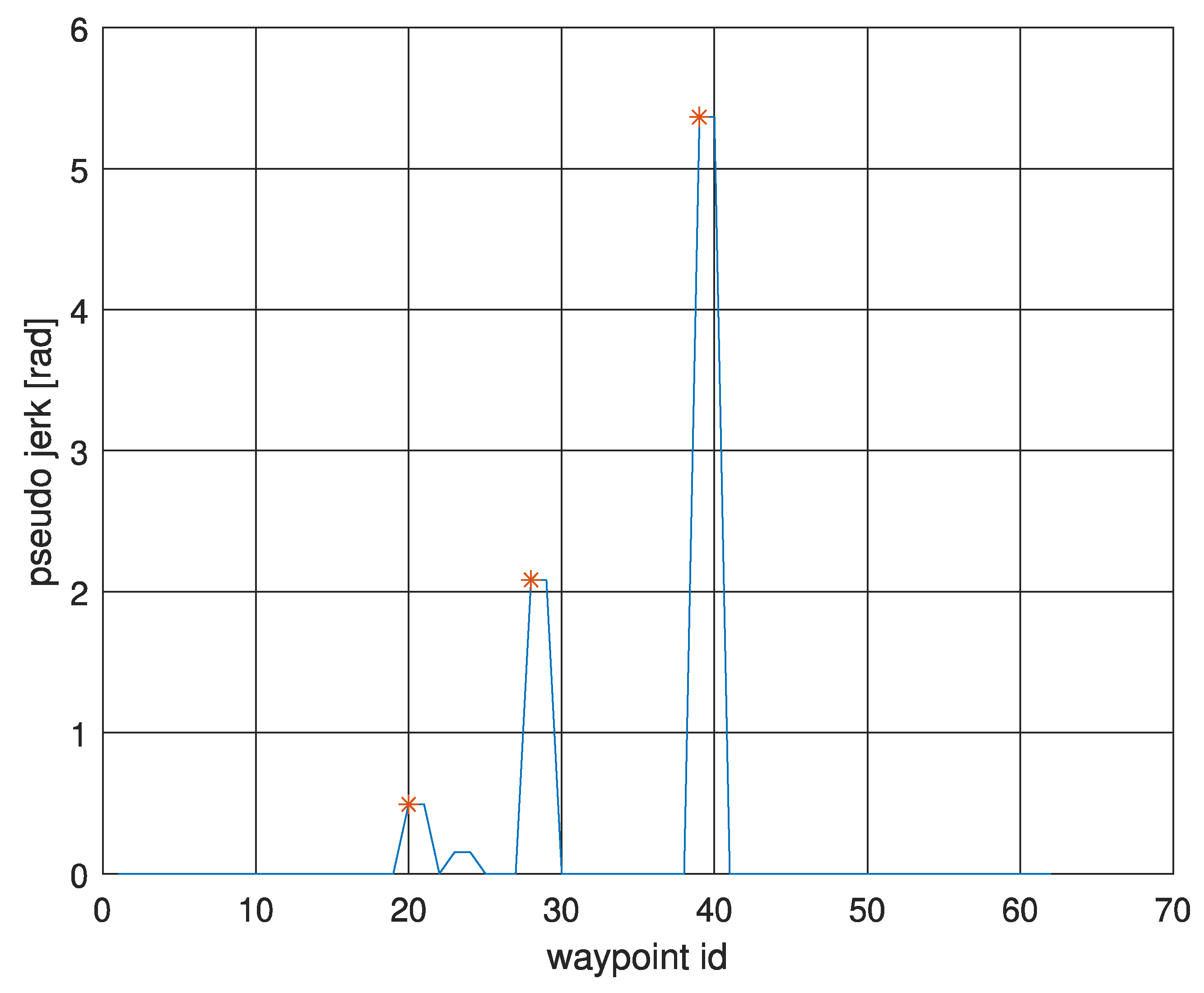
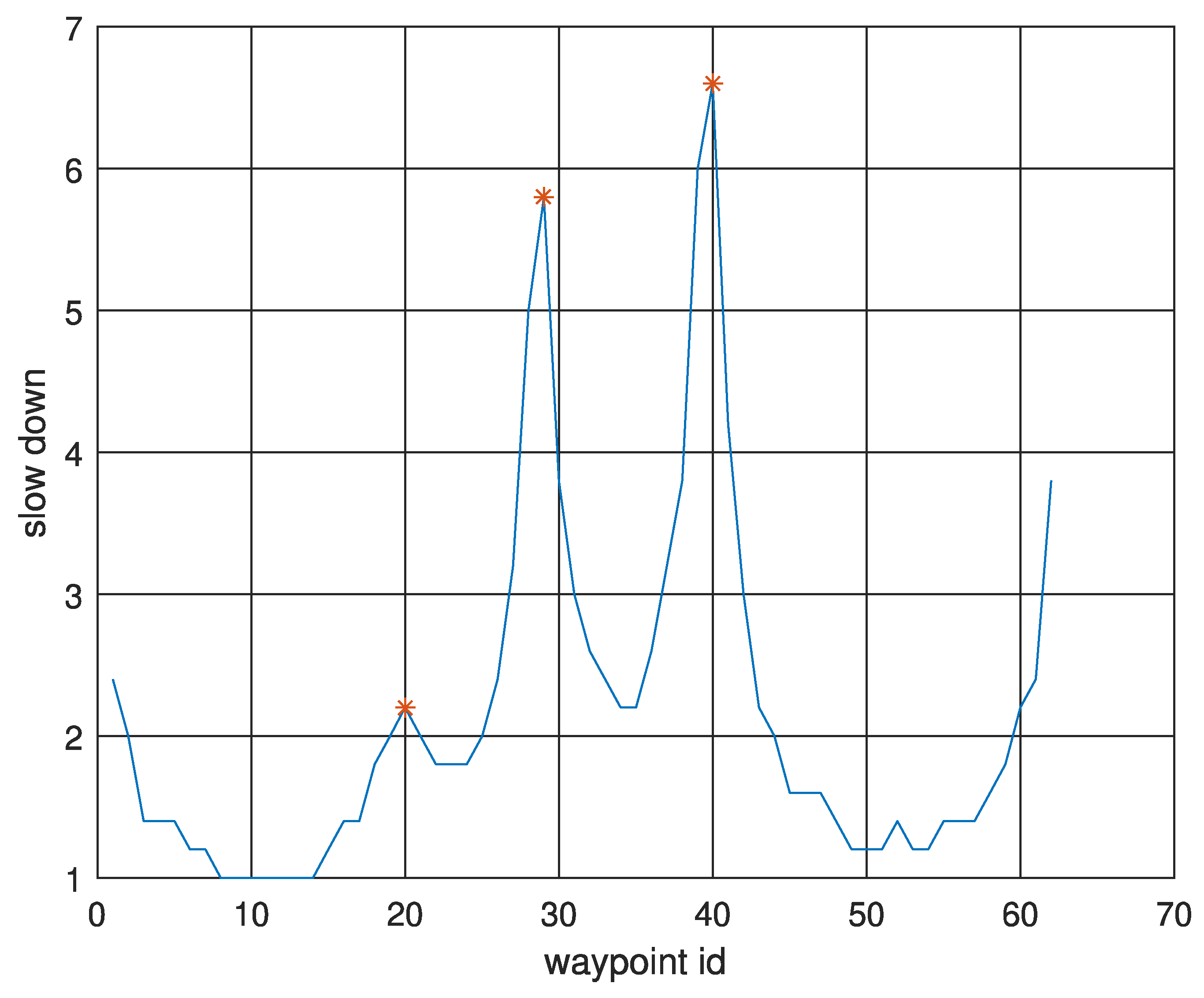
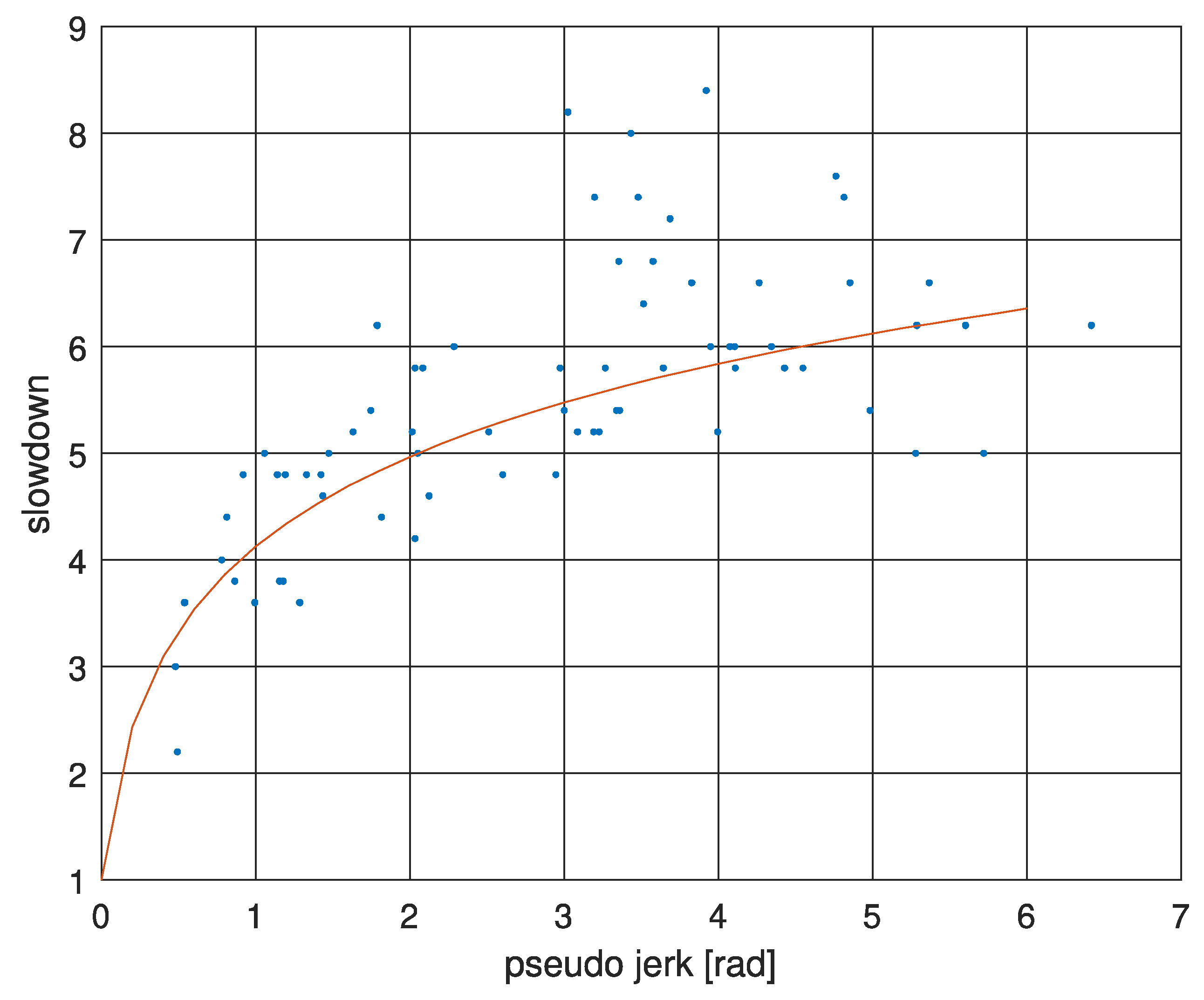
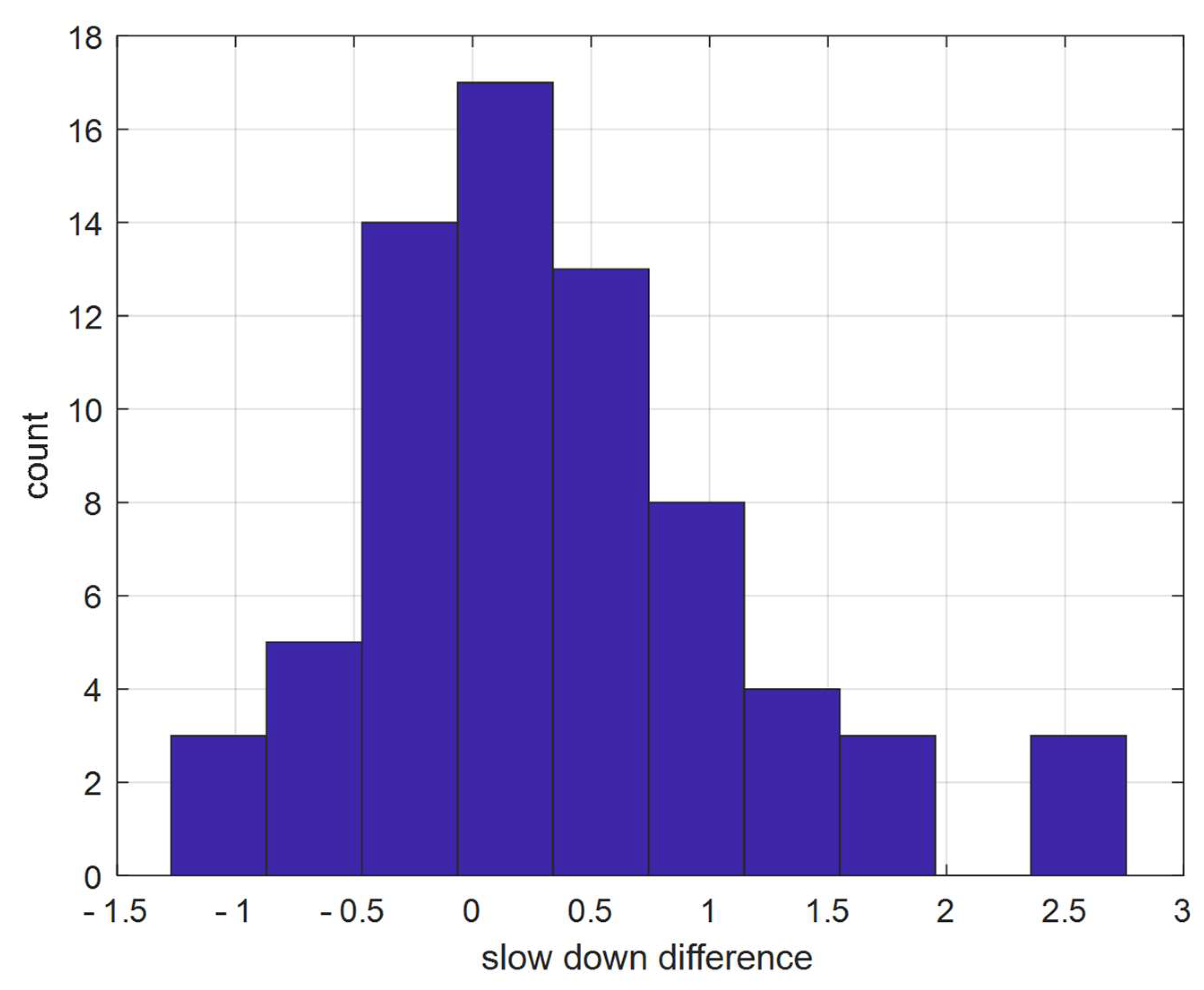
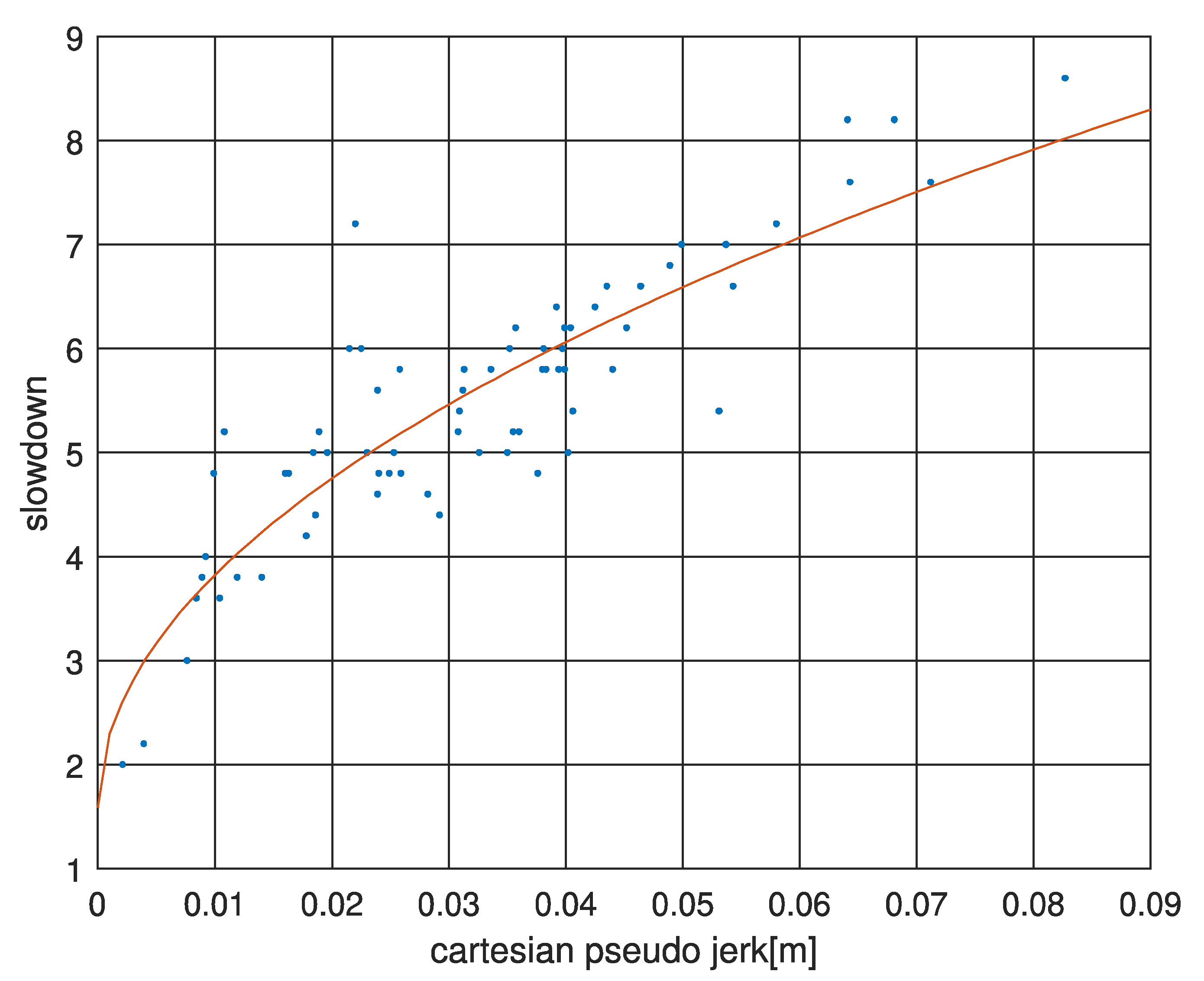
3.2. Jerk-Based Criteria
4. Criteria Usage
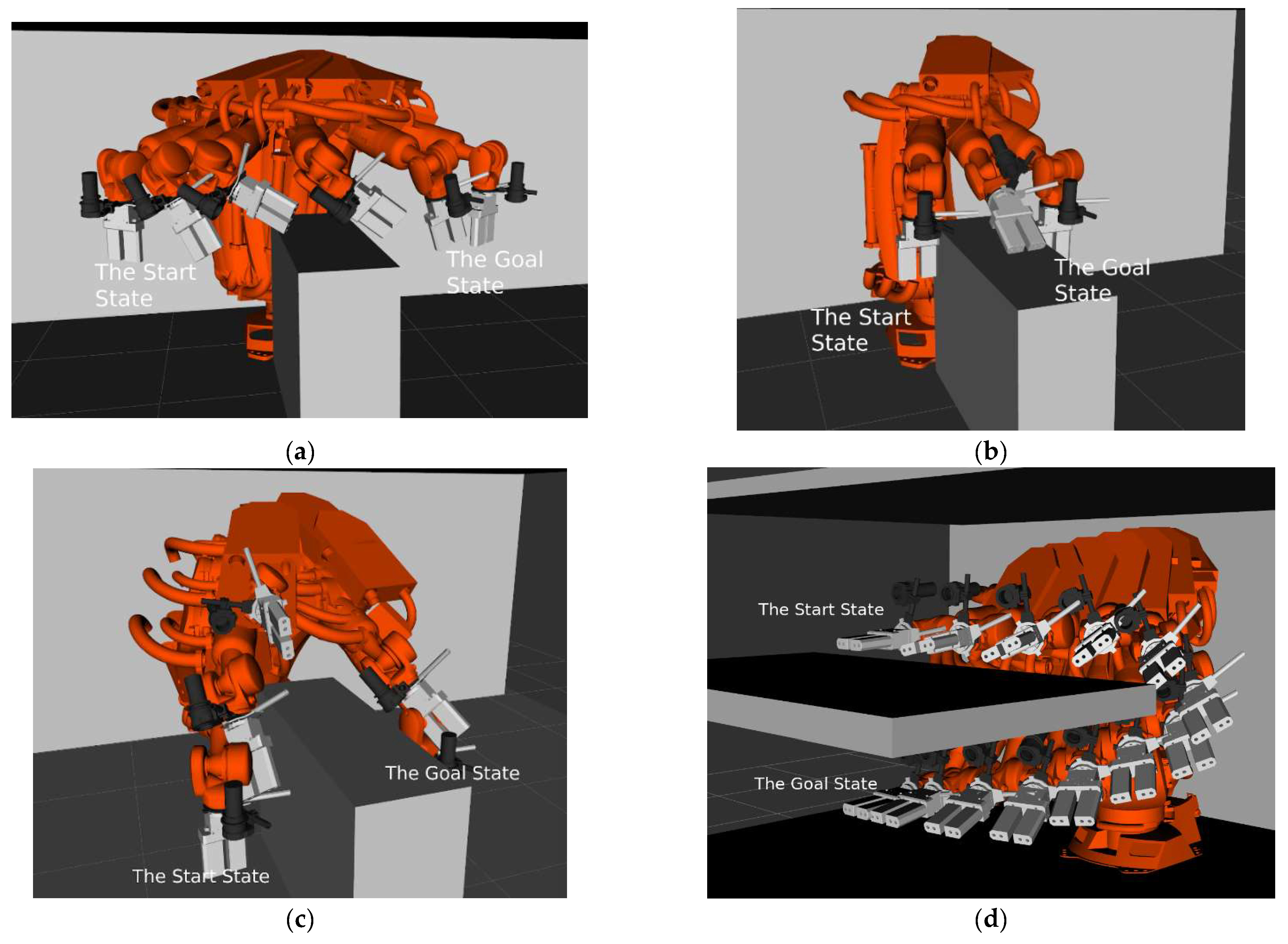
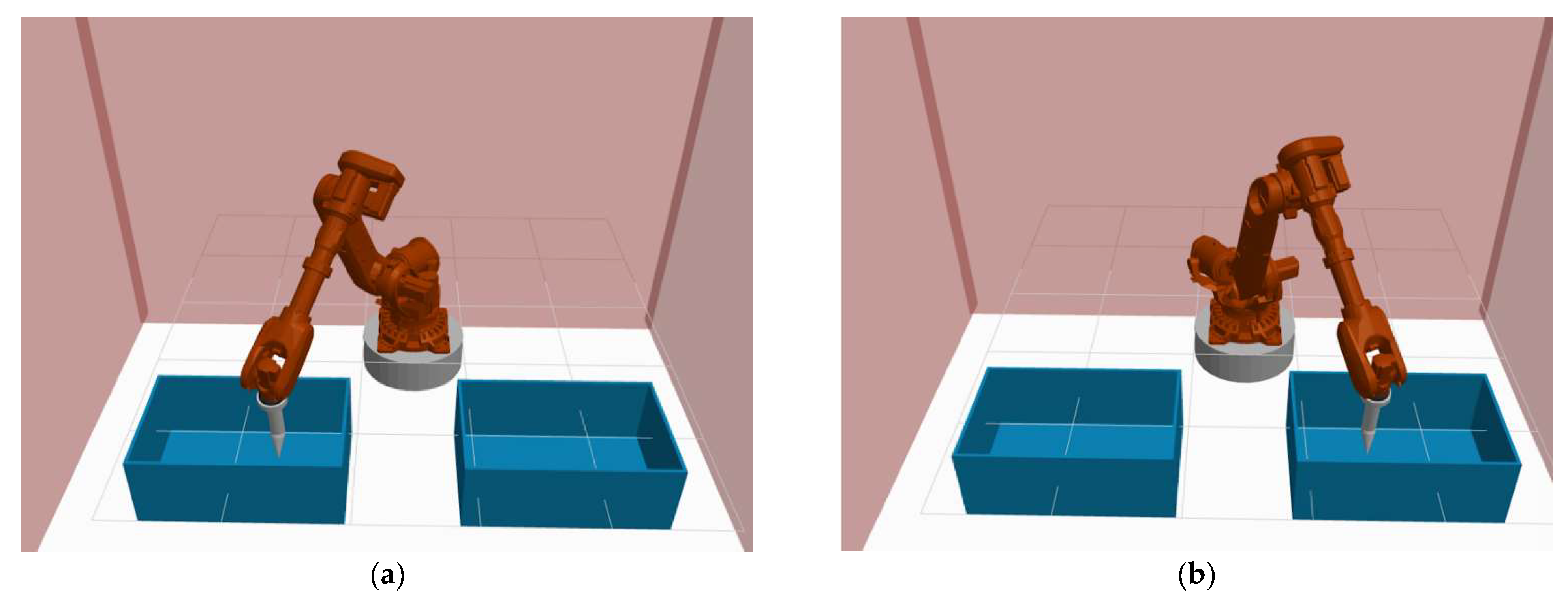
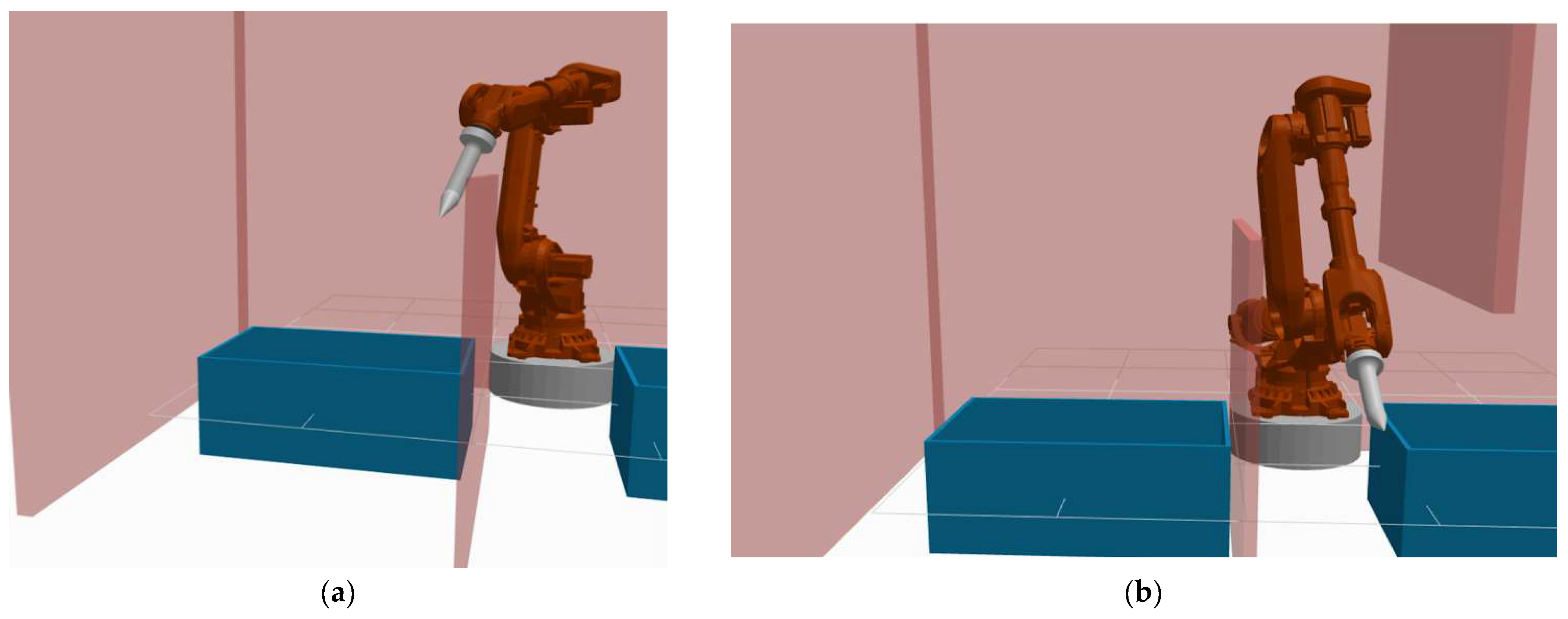
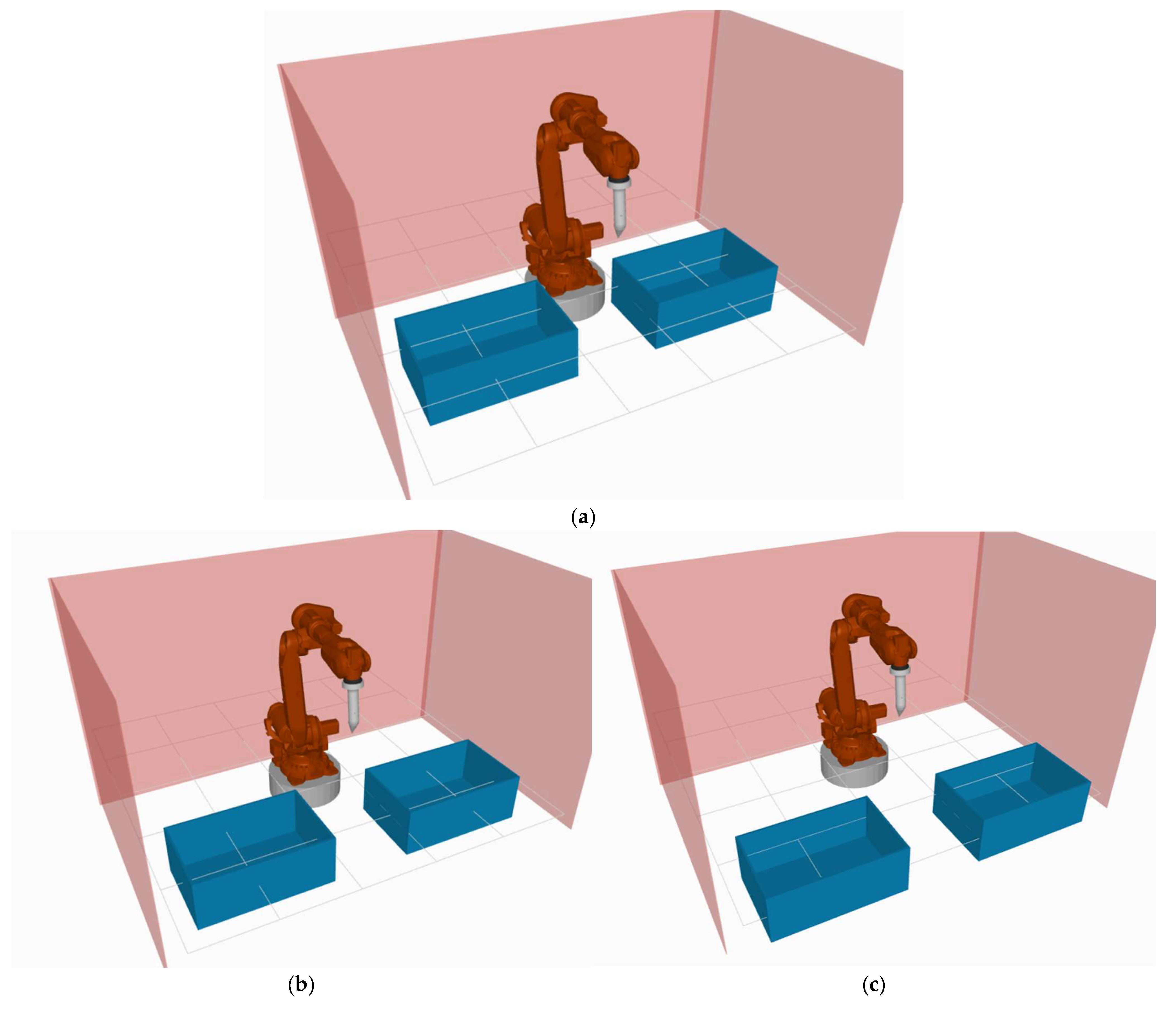
4.1. The Impact of the Environment’s Complexity on the Path Planner
4.2. The Impact on the Path Planner of the Bin’s Position
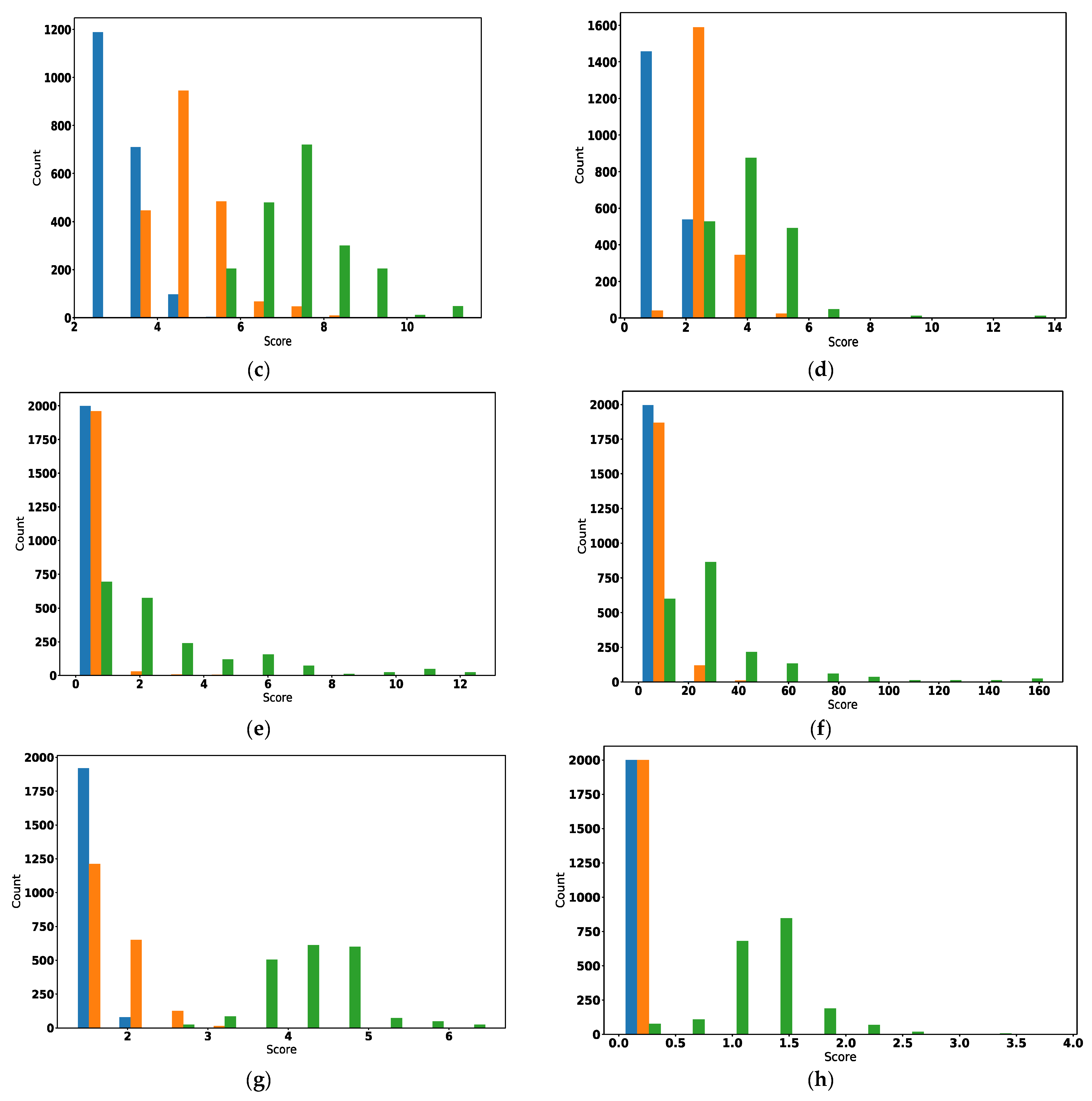
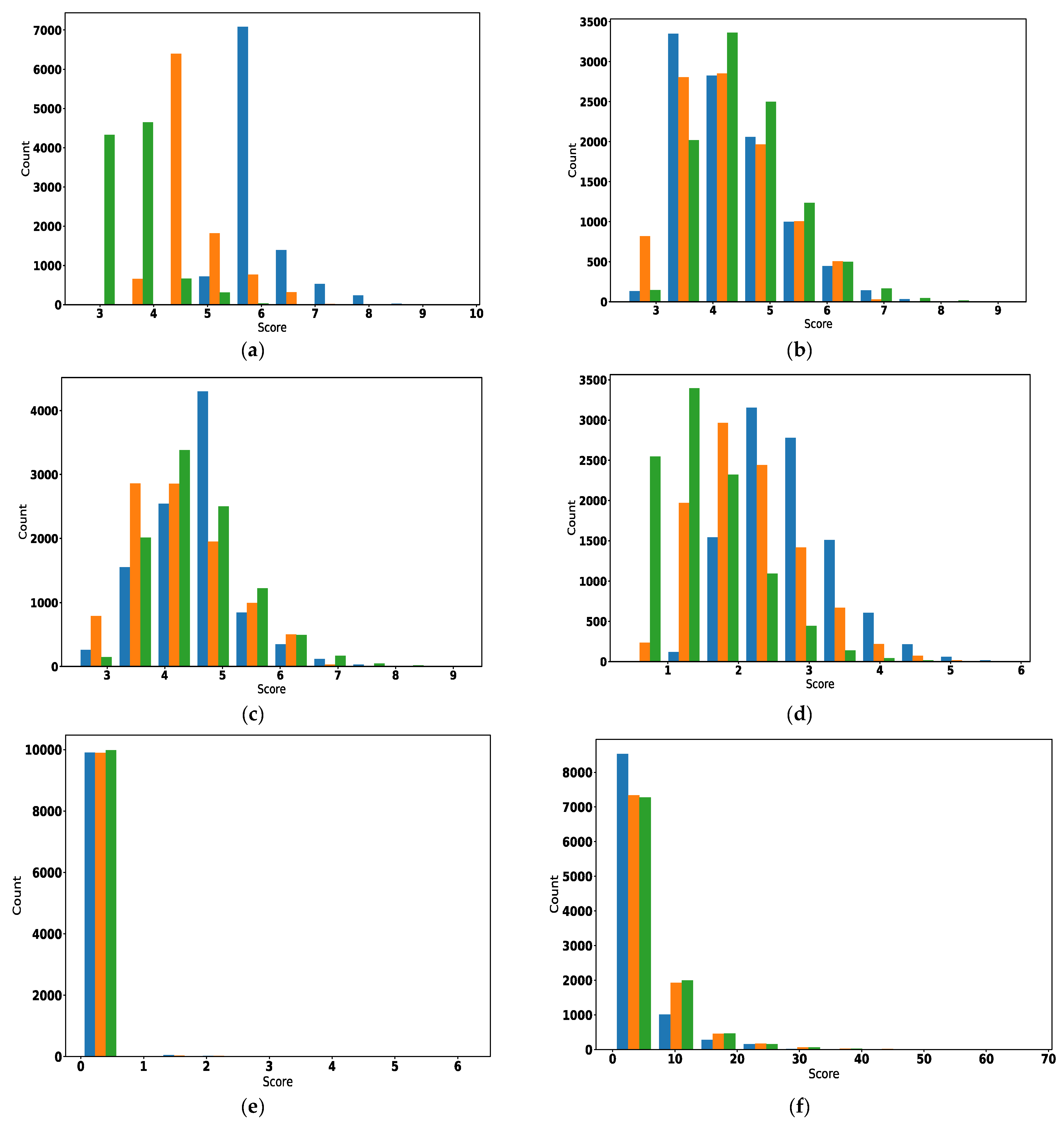
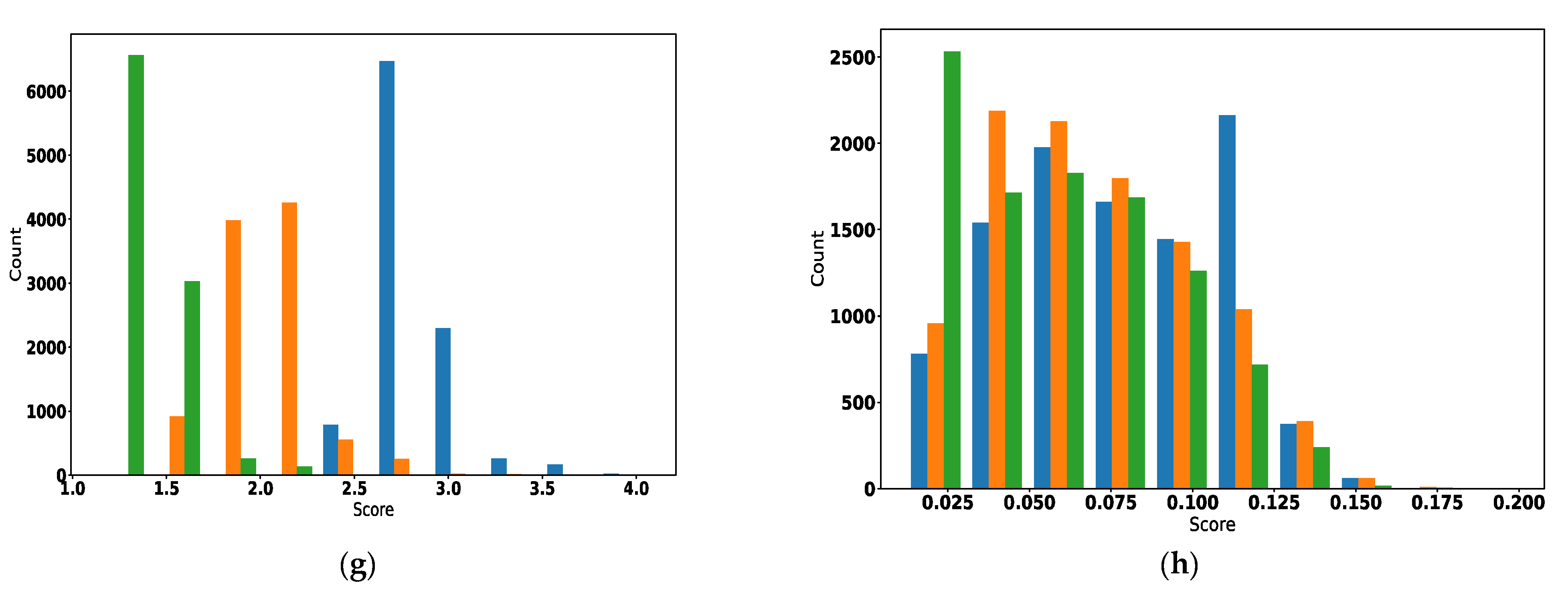
5. Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kavraki, L.E.; Svestka, P.; Latombe, J.-C.; Overmars, M.H. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef] [Green Version]
- Lavalle, S.M. Rapidly-Exploring Random Trees: A New Tool for Path Planning. 1998. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.35.1853 (accessed on 14 February 2022).
- Zucker, M.; Ratliff, N.; Dragan, A.D.; Pivtoraiko, M.; Klingensmith, M.; Dellin, C.M.; Bagnell, J.A.; Srinivasa, S.S. CHOMP: Covariant Hamiltonian optimization for motion planning. Int. J. Robot. Res. 2013, 32, 1164–1193. [Google Scholar] [CrossRef] [Green Version]
- Kalakrishnan, M.; Chitta, S.; Theodorou, E.; Pastor, P.; Schaal, S. STOMP: Stochastic trajectory optimization for motion planning. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011. [Google Scholar]
- Rodriguez, C.; Suárez, R. Comparison of motion planners in an environment with removable obstacles. In Proceedings of the 2015 IEEE 20th Conference on Emerging Technologies & Factory Automation (ETFA), Luxembourg, 08–11 September 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Paulin, S.; Botterill, T.; Lin, J.; Chen, X.; Green, R. A comparison of sampling-based path planners for a grape vine pruning robot arm. In Proceedings of the 2015 6th International Conference on Automation, Robotics and Applications (ICARA), Queenstown, New Zealand, 17–19 February 2015; pp. 98–103. [Google Scholar]
- Magyar, B.; Tsiogkas, N.; Brito, B.; Patel, M.; Lane, D.; Wang, S. Guided Stochastic Optimization for Motion Planning. Front. Robot. AI 2019, 6, 6. [Google Scholar] [CrossRef] [Green Version]
- De Maeyer, J.; Demeester, E. Benchmarking framework for robotic arc welding motion planning. Procedia CIRP 2021, 97, 247–252. [Google Scholar] [CrossRef]
- Larsen, L.; Kim, J.; Kupke, M.; Schuster, A. Automatic Path Planning of Industrial Robots Comparing Sampling-based and Computational Intelligence Methods. Procedia Manuf. 2017, 11, 241–248. [Google Scholar] [CrossRef]
- Dobiš, M.; Dekan, M.; Beňo, P.; František, D.; Miroslav, K. The Comparison of Motion Planners for Robotic Arms. J. Control. Eng. Appl. Inform. 2021, 23, 87–94. [Google Scholar]
- Chettibi, T.; Lehtihet, H.E.; Haddad, M.; Hanchi, S. Minimum cost trajectory planning for industrial robots. Eur. J. Mech. A/Solids 2004, 23, 703–715. [Google Scholar] [CrossRef]
- Gandhi, P.; Jain, A.K. Optimization Performance of a Robot to Reduce Cycle Time Estimate. Int. J. Sci. Res. (IJSR) 2013, 2, 357–363. [Google Scholar]
- Trnka, K.; Božek, P. Optimal Motion Planning of Spot Welding Robot Applications. Appl. Mech. Mater. 2012, 248, 589–593. [Google Scholar]
- Mumm, J.; Mutlu, B. Human-robot proxemics: Physical and psychological distancing in human-robot interaction. In Proceedings of the 6th International Conference on Human-Robot Interaction—HRI’11, Lausanne, Switzerland, 6–9 March 2011. [Google Scholar] [CrossRef]
- Farouki, R.T.; Li, S. Optimal tool orientation control for 5-axis CNC milling with ball-end cutters. Comput. Aided Geom. Des. 2013, 30, 226–239. [Google Scholar] [CrossRef]
- Toh, C.A. study of the effects of cutter path strategies and orientations in milling. J. Mater. Process. Technol. 2004, 152, 346–356. [Google Scholar] [CrossRef]
- Su, H.; Yang, C.; Ferrigno, G.; De Momi, E. Improved Human–Robot Collaborative Control of Redundant Robot for Teleoperated Minimally Invasive Surgery. IEEE Robot. Autom. Lett. 2019, 4, 1447–1453. [Google Scholar] [CrossRef] [Green Version]
- Tölgyessy, M.; Dekan, M.; Duchoň, F.; Rodina, J.; Hubinský, P.; Chovanec, L. Foundations of Visual Linear Human–Robot Interaction via Pointing Gesture Navigation. Int. J. Soc. Robot. 2017, 9, 509–523. [Google Scholar] [CrossRef]
- Cohen, B.; Chitta, S.; Likhachev, M. Search-based planning for dual-arm manipulation with upright orientation constraints. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 24–27 May 2012; pp. 3784–3790. [Google Scholar] [CrossRef] [Green Version]
- Lavalle, S.M. Planning Algorithms; Cambridge University Press: New York, NY, USA, 2014; pp. 153–206. [Google Scholar]
- Gregory, J.; Olivares, A.; Staffetti, E. Energy-optimal trajectory planning for robot manipulators with holonomic constraints. Syst. Control. Lett. 2012, 61, 279–291. [Google Scholar] [CrossRef]
- Mohammed, A.; Schmidt, B.; Wang, L.; Gao, L. Minimizing Energy Consumption for Robot Arm Movement. Procedia CIRP 2014, 25, 400–405. [Google Scholar] [CrossRef] [Green Version]
- Prado, J.; Marques, L. Energy Efficient Area Coverage for an Autonomous Demining Robot. In Proceedings of the ROBOT2013: First Iberian Robotics Conference, Madrid, Spain, 28–29 November 2013; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2014; pp. 459–471. [Google Scholar] [CrossRef]
- Carabin, G.; Scalera, L. On the Trajectory Planning for Energy Efficiency in Industrial Robotic Systems. Robotics 2020, 9, 89. [Google Scholar] [CrossRef]
- Vidussi, F.; Boscariol, P.; Scalera, L.; Gasparetto, A. Local and Trajectory-Based Indexes for Task-Related Energetic Performance Optimization of Robotic Manipulators. J. Mech. Robot. 2021, 13, 1–12. [Google Scholar] [CrossRef]
- Huang, J.; Hu, P.; Wu, K.; Zeng, M. Optimal time-jerk trajectory planning for industrial robots. Mech. Mach. Theory 2018, 121, 530–544. [Google Scholar] [CrossRef]
- Galloway, K.C.; Becker, K.P.; Phillips, B.; Kirby, J.; Licht, S.; Tchernov, D.; Wood, R.J.; Gruber, D.F. Soft Robotic Grippers for Biological Sampling on Deep Reefs. Soft Robot. 2016, 3, 23–33. [Google Scholar] [CrossRef]
- Pettersson, A.; Davis, S.; Gray, J.O.; Dodd, T.J.; Ohlsson, T. Design of a magnetorheological robot gripper for handling of delicate food products with varying shapes. J. Food Eng. 2010, 98, 332–338. [Google Scholar] [CrossRef]
- Rubio, F.; Llopis-Albert, C.; Valero, F.; Suñer, J.L. Industrial robot efficient trajectory generation without collision through the evolution of the optimal trajectory. Robot. Auton. Syst. 2016, 86, 106–112. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Lai, X.; Wu, W. Time-optimal and jerk-continuous trajectory planning for robot manipulators with kinematic constraints. Robot. Comput. Manuf. 2013, 29, 309–317. [Google Scholar] [CrossRef]
- Pan, J.; Chitta, S.; Manocha, D. FCL: A general purpose library for collision and proximity queries. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 24–27 May 2012; pp. 3859–3866. [Google Scholar]
- KUKA. System Software KUKA System Software 8.3 Operating and Programming Instructions for System Integrators. 2015. Available online: http://www.wtech.com.tw/public/download/manual/kuka/krc4/KUKA%20KSS-8.3-Programming-Manual-for-SI.pdf (accessed on 14 February 2022).

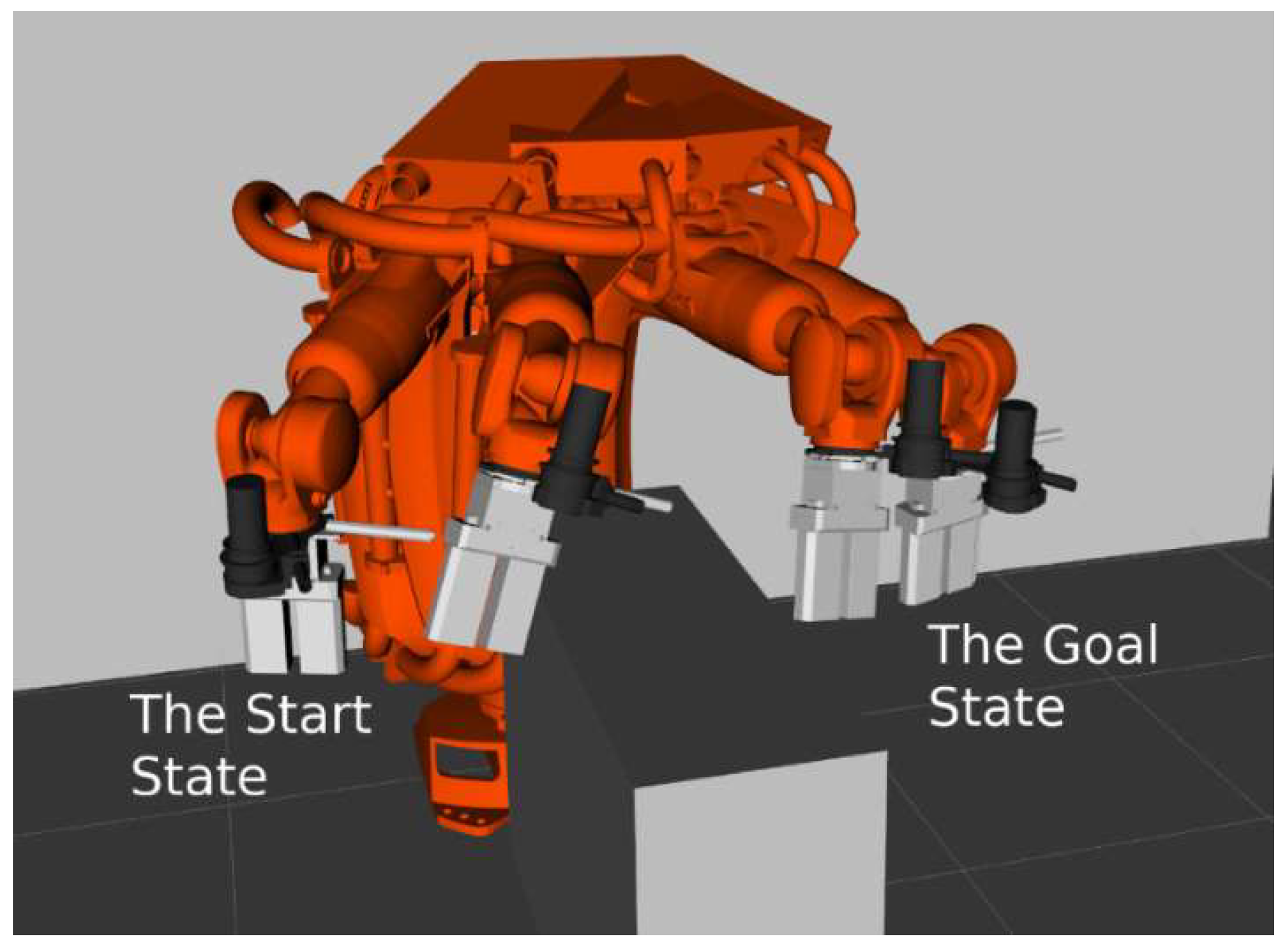
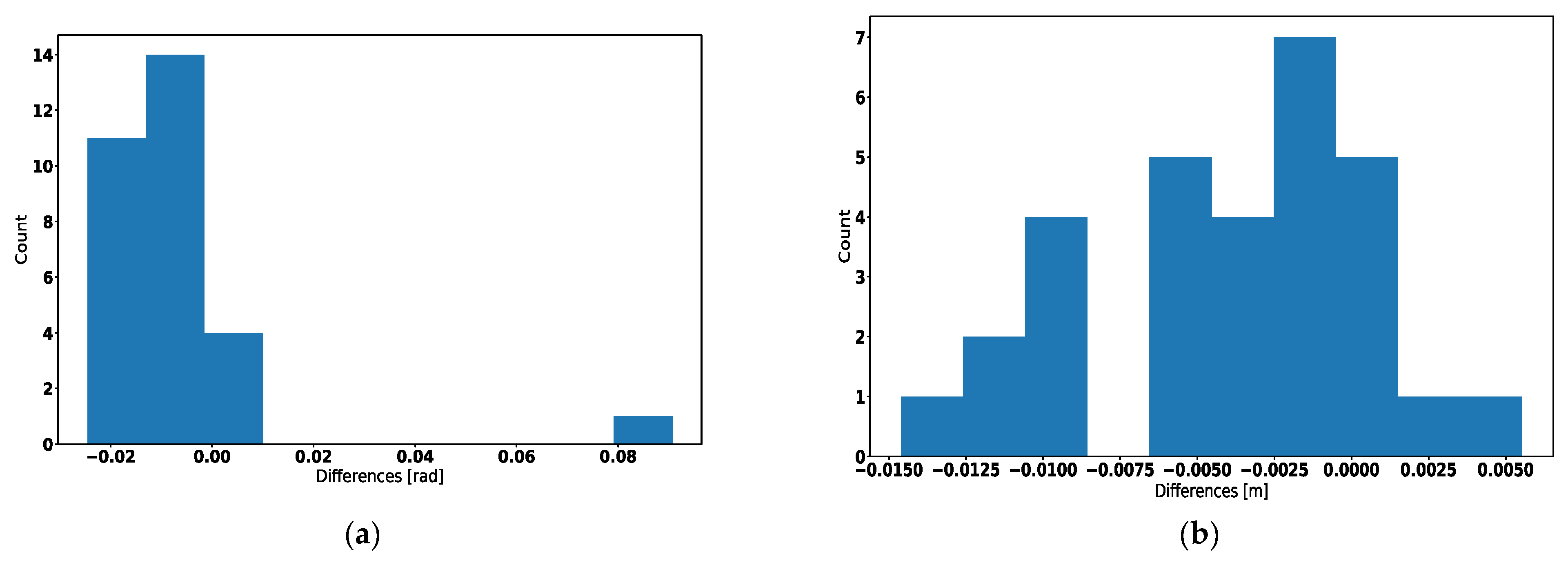
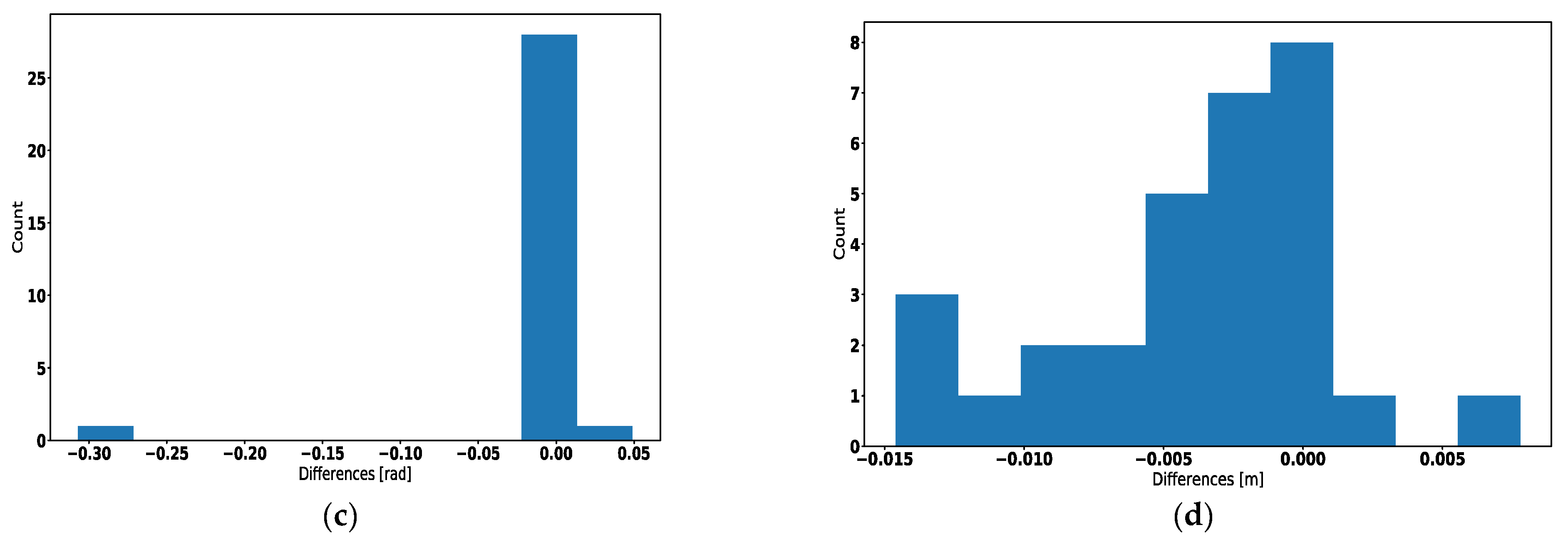
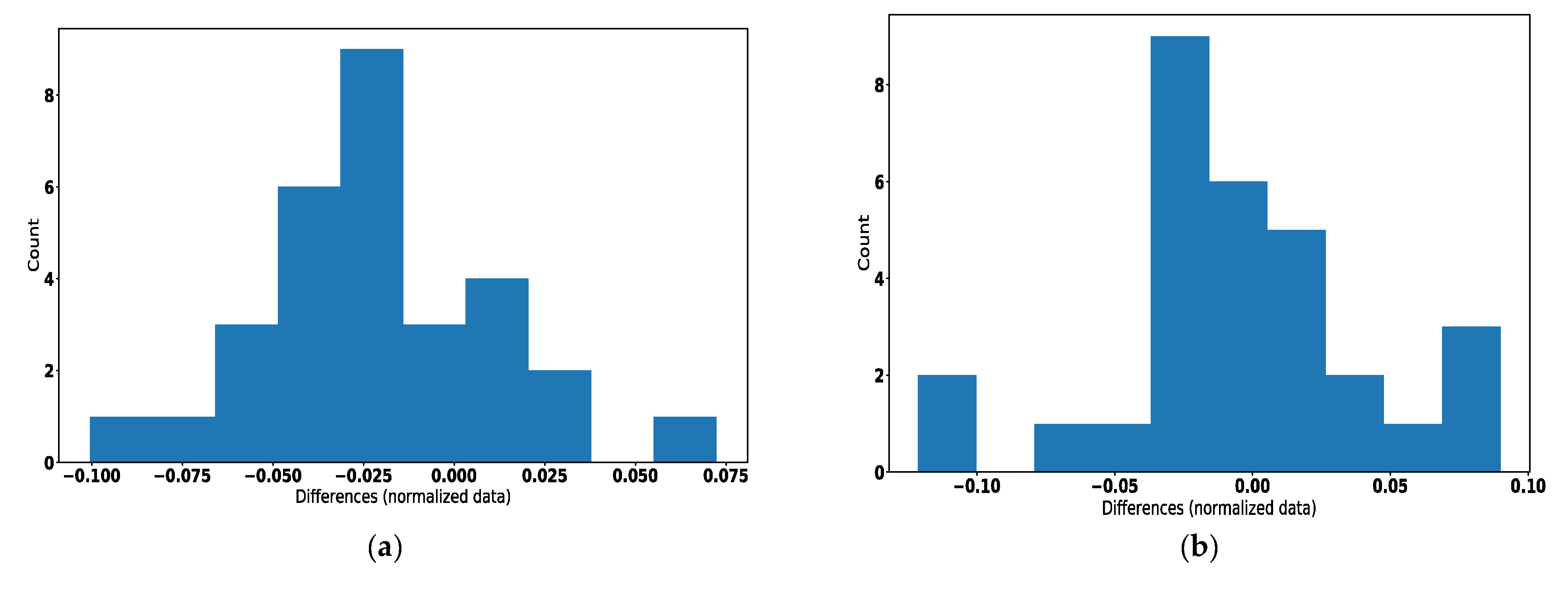
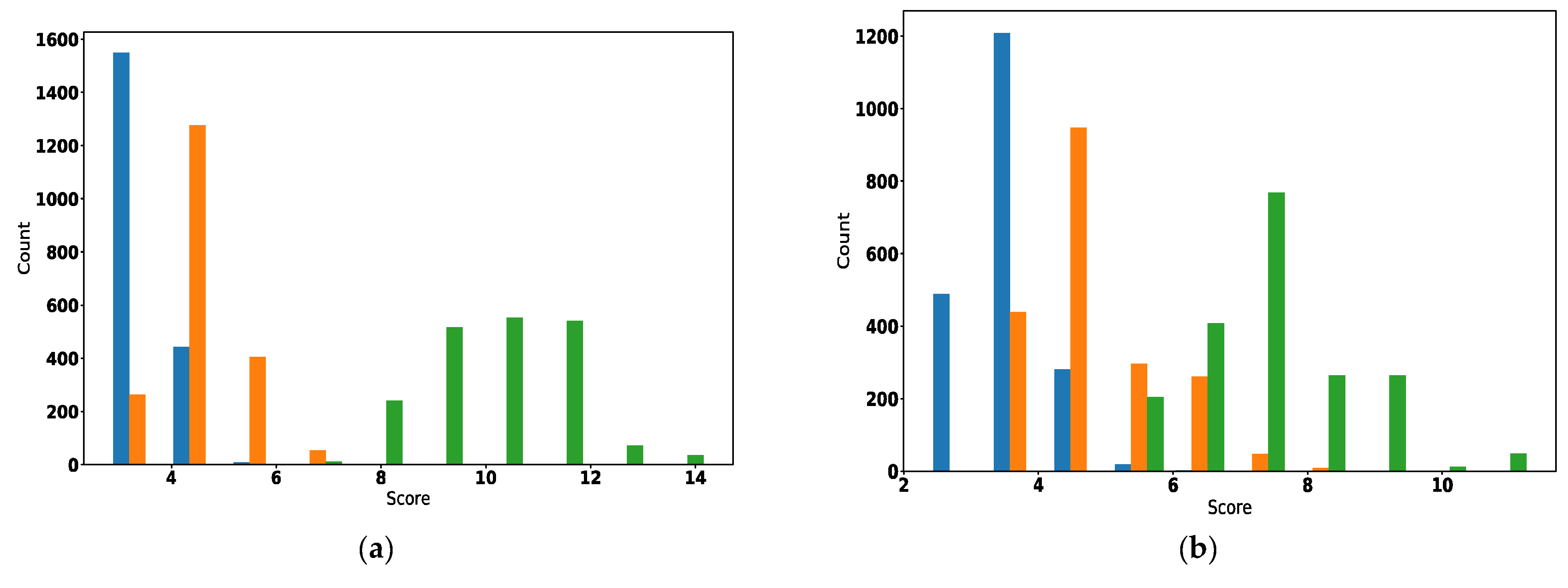
| Criterions | Average | Variance |
|---|---|---|
| Joint Distance [rad] | −5.75 × 10−3 | 3.76 × 10−4 |
| Cartesian Distance [m] | −4.09 × 10−3 | 2.22 × 10−5 |
| Orientation Change [rad] | −1.24 ×10−2 | 3.09 × 10−3 |
| Robot Displacement [m] | −3.75 × 10−3 | 2.52 × 10−5 |
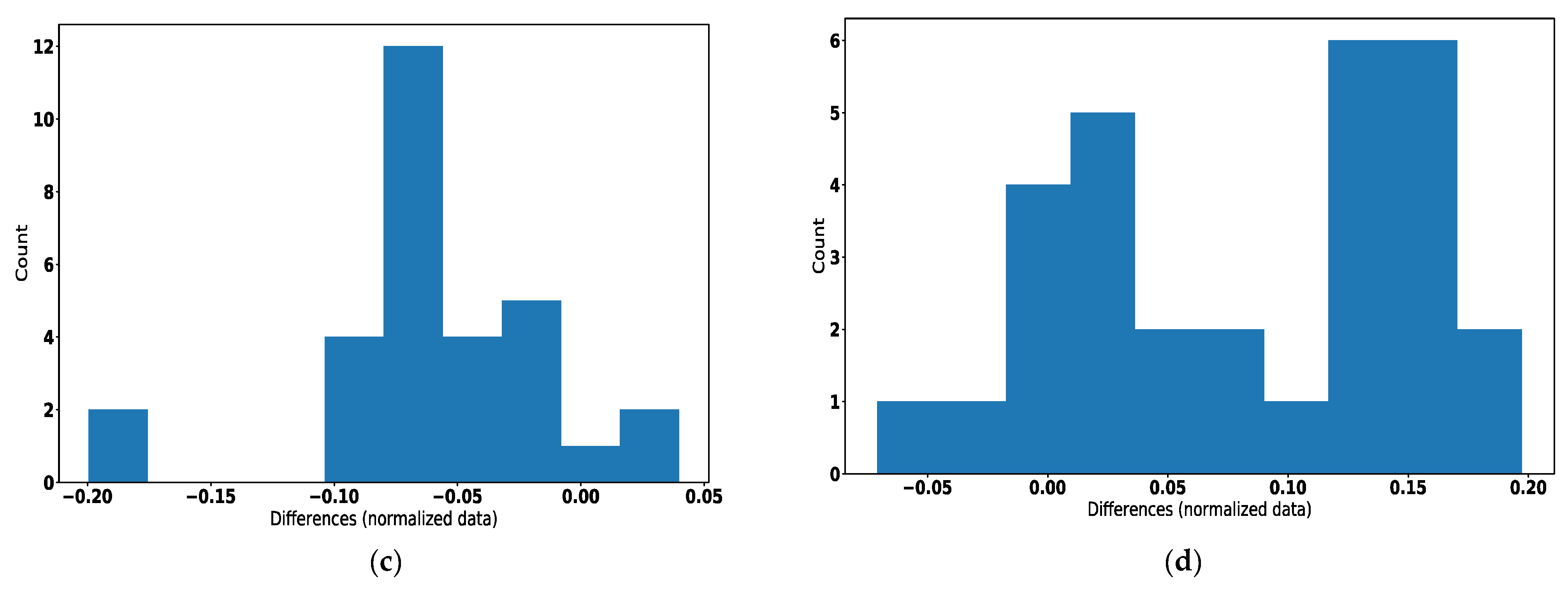
| Experiment No. | Average | Variance |
| 1 | −3.38 × 10−3 | 1.25 × 10−4 |
| 2 | −2.20 × 10−2 | 1.14 × 10−3 |
| 3 | −3.58 × 10−3 | 2.28 × 10−3 |
| 4 | −5.67 × 10−2 | 2.42 × 10−3 |
| 5 | 8.08 × 10−2 | 5.25 × 10−3 |
| Criterions | Average | Variance |
| Joint Distance [rad] | −5.75 × 10−3 | 3.76 × 10−4 |
| Cartesian Distance [m] | −4.09 × 10−3 | 2.22 × 10−5 |
| Orientation Change [rad] | −1.24 × 10−2 | 3.09 × 10−3 |
| Robot Displacement [m] | −3.75 × 10−3 | 2.52 × 10−5 |
| Control Pseudo Cost 1 | −2.20 × 10−2 | 1.14 × 10−3 |
| Control Pseudo Cost 2 | 8.08 × 10−2 | 5.6 × 10−3 |
| Joint Jerk Peaks [rad] | 0.3344 | 0.8290 |
| Cartesian Jerk Peaks [m] | 5.1 × 10−3 | 0.6036 |
| Criterion | Experiment No.1 | Experiment No.2 | Experiment No.3 | ||||
|---|---|---|---|---|---|---|---|
| Average | Variance | Average | Variance | Average | Variance | ||
| 1 | Joint Distance [rad] | 3.699 | 0.1511 | 4.9824 | 0.51754 | 10.456 | 1.544 |
| 2 | Cartesian Distance [m] | 3.6277 | 0.2882 | 5.107 | 0.7206 | 7.6689 | 1.3505 |
| 3 | Orientation Change [rad] | 1.6659 | 0.199 | 2.8288 | 0.3863 | 4.6727 | 1.64228 |
| 4 | Robot Displacement [m] | 3.6315 | 0.2800 | 5.1134 | 0.7182 | 7.753 | 1.307 |
| 5 | Control Pseudo Cost | 1.6349 | 0.0208 | 2.0629 | 0.0870 | 4.3652 | 0.3606 |
| 6 | Joint Jerk Peaks [rad] | 0.0022 | 0.0103 | 0.0575 | 0.1551 | 2.824 | 9.454 |
| 7 | Cartesian Jerk Peaks [m] | 2.42 | 10.5699 | 6.7953 | 60.34 | 31.2399 | 943.78 |
| 8 | Duration [s] | 8.02 × 10−2 | 4.5 × 10−4 | 8.6 × 10−2 | 9.2 × 10−4 | 1.44 | 0.2 |
| Criterion | Experiment No.1 | Experiment No.2 | Experiment No.3 | ||||
|---|---|---|---|---|---|---|---|
| Average | Variance | Average | Variance | Average | Variance | ||
| 1 | Joint Distance [rad] | 6.2858 | 0.3452 | 4.9181 | 0.4432 | 3.729 | 0.3086 |
| 2 | Cartesian Distance [m] | 4.797 | 0.730 | 4.328 | 0.7535 | 4.737 | 0.897 |
| 3 | Orientation Change [rad] | 2.974 | 0.4137 | 2.2203 | 0.518 | 1.804 | 0.368 |
| 4 | Robot Displacement [m] | 4.810 | 0.707 | 4.337 | 0.7435 | 4.7405 | 0.894 |
| 5 | Control Pseudo-Cost | 2.9122 | 0.0518 | 2.0887 | 0.0584 | 1.4711 | 0.0431 |
| 6 | Joint Jerk Peaks [rad] | 0.049 | 0.1156 | 0.0651 | 0.1909 | 0.0148 | 0.0347 |
| 7 | Cartesian Jerk Peaks [m] | 5.2656 | 30.308 | 5.43026 | 47.276 | 4.8859 | 38.443 |
| 8 | Duration [s] | 0.082 | 0.0011 | 0.078 | 0.0011 | 0.0719 | 0.0010 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dobiš, M.; Dekan, M.; Beňo, P.; Duchoň, F.; Babinec, A. Evaluation Criteria for Trajectories of Robotic Arms. Robotics 2022, 11, 29. https://doi.org/10.3390/robotics11010029
Dobiš M, Dekan M, Beňo P, Duchoň F, Babinec A. Evaluation Criteria for Trajectories of Robotic Arms. Robotics. 2022; 11(1):29. https://doi.org/10.3390/robotics11010029
Chicago/Turabian StyleDobiš, Michal, Martin Dekan, Peter Beňo, František Duchoň, and Andrej Babinec. 2022. "Evaluation Criteria for Trajectories of Robotic Arms" Robotics 11, no. 1: 29. https://doi.org/10.3390/robotics11010029
APA StyleDobiš, M., Dekan, M., Beňo, P., Duchoň, F., & Babinec, A. (2022). Evaluation Criteria for Trajectories of Robotic Arms. Robotics, 11(1), 29. https://doi.org/10.3390/robotics11010029








