Abstract
There is a need for semi-autonomous systems capable of performing both automated tasks and supervised maneuvers. When dealing with multiple robots or robots with high complexity (such as humanoids), we face the issue of effectively coordinating operators across robots. We build on our previous work to present a methodology for designing trajectories and policies for robots such that a few operators can supervise multiple robots. Specifically, we: (1) Analyze the complexity of the problem, (2) Design a procedure for generating policies allowing operators to oversee many robots, (3) Present a method for designing policies and robot trajectories to allow operators to oversee multiple robots, and (4) Include both simulation and hardware experiments demonstrating our methodologies.
1. Introduction
Multi-robot systems are making a significant impact on fundamental societal areas. From oceanic exploration to border surveillance, from robotic warehousing to precision agriculture, and from automated construction to environmental monitoring, collaborating groups of robots will play a central role in the coming years [1]. In some of these scenarios, however, due to technical, ethical, regulatory or safety issues [2], one or more humans should monitor or help the robot during the execution of its tasks in certain critical parts. These critical segments of the robot trajectory can be kinematically or dynamically complex maneuvers, locations near obstacles, or regions where sensing is poor.
Most teleoperated systems assume more than one human operator per robot. More than one human may be required for each subsystem in more complex scenarios, such as humanoids or mobile manipulator teleoperation (e.g., manipulation, locomotion, head positioning). For instance, in control rooms in Unmanned Aerial Vehicles missions, several operators are needed to operate a single drone. While it may remain infeasible to remove altogether the portion of a task which cannot be automated, we can efficiently allocate human attention in these portions. As an application of our ideas, we envision scenarios where a single operator can coordinate a group of automated construction machinery, several agricultural pieces of equipment or even a production line of industrial robots. Indeed, the recent pandemic has demonstrated teleoperation control paradigms are favoured in situations where remote presence is desirable and where complexity precludes the use of fully autonomous systems [3]. Effectively combining the cognitive capabilities of a human operator with robot physical capacities [4] has provided great benefits in industrial applications [5,6] and more general methodologies are needed.
Another motivation behind our ideas is robot-assisted search and rescue. In traditional mobile robot search and rescue operations using unmanned vehicles, operators’ ratio to robots is commonly 2 to 1 [7]. More recently, motivated by disasters such as the Fukushima nuclear plant, there has been a need for robots with larger degrees of freedom that can operate in environments designed for humans. Concretely, lessons learned analyzing human-robot interfaces used by different teams in the DARPA Robotics Challenge (DRC) [8], gave two important reasons motivating our ideas to reduce the number of operators: (1) fewer operators reduces confusion and coordination overhead, and (2) the number of human errors (one of the main sources of problems in the DRC [9]) is reduced.
This work addresses the question of operator attention at critical moments of a teleoperation task. In most situations, an operator is only required in specific parts of a robot’s operation. Knowing this, we can schedule these operator interactions so that a single operator can perform multiple tasks. Thus, our objective is to develop a planning strategy for the remote task involving multiple robots such that the operator can pay sufficient attention to each robot during critical operations. This work’s contributions are: extending our preliminary ideas from [10,11] in the following directions: First, we analyze the complexity of this problem. Secondly, we present a sampling-based approach that allows us to design policies for many teleoperators instead of a complete algorithm that only works for a small set of operators. Thirdly, we allow re-planning of the robot’s task alongside the operator. Finally, we present the results of both simulated and physical experiments using mobile robots and a humanoid.
Our work deals with planning for robots using a small set of operators that can help the robot when needed. As a convention, we will use the term “robot” throughout this paper; however, the method is formulated within the robots’ configuration space and is agnostic to the robot type. It can model multiple robots and a single robot with multiple degrees of freedom such as a humanoid robot. To the best of our knowledge, our contribution is one of the few that attempts to formalize operator scheduling problem using a geometric approach.
The rest of the paper is organized as follows: Section 2 discusses relevant related literature. Section 3 describes the preliminaries and formulates the problems of interest. Section 4 describes algorithms to solve the formulated problems in the previous section. In Section 5, we present an extension of the solution in Section 4 which can also re-plan robot trajectories. Section 6 presents both software and hardware experimental results, and a case study is provided in Section 7. Conclusions and future directions are presented in Section 8.
2. Related Work
Teleoperation is an established robot control paradigm with particular widespread use in surgical and medical operations [12]. While teleoperation is classically defined using 1:1 operator to robot ratio [13,14], there is a growing need for systems that facilitate operator oversight of multiple robots [15]. This work focuses on reducing operator supervision to only temporally critical passages. Previous work took a different approach, aiming to reduce the cognitive burden on the operator by, for instance, using virtual fixtures [16,17]. Virtual fixtures create zones where the robot can operate and thus reduce the operators’ supervision load. These zones can be obtained using point cloud data [18], shape primitives, [19], manually created [20], selected interactively [21] or generated on-line based on obstacle proximity and manipulator capabilities [22]. For the teleoperation of multiple agents, Farkhatdinov et al. [23] proposed a discrete switching control algorithm where an operator can trigger a switch to control different robots or different inputs, i.e., position, velocity of the same agent. In [24], the authors propose modeling operator behavior in a multi-robot control task and hypothesize that these models can be used to improve the teleoperation control strategies. Alternatively, for more complex systems, the introduction of a degree of autonomy in the robots’ behavior, often denoted as shared control, can enable operators to control multi-agent or complex systems [25]. Using operators alongside partially autonomous robots yields systems that are less brittle and more effective than either one working alone [26]. A study case of a foraging task is presented in [27] where queuing techniques were used to schedule the operator’s attention. In [28], Dardona et al. have shown that the output side sensor configuration of a teleoperated system is altered to reduce the workload of a remote surgeon.
While the above techniques enhance the operators’ control of a robot system, we focus on complex autonomous systems that require supervision and analyse how this supervising burden may be reduced. Using one operator to control multiple robots has benefits in terms of cost and control coherency but leads to a higher workload and decrease in situation awareness [29]. The human operator is often overlooked when supervising robots [30], despite their workload influencing task performance [31] and in fact having long-term negative effects on well-being [32]. Indeed, J. M. Riley et al. [33] have demonstrated that an increase in the number of robots per human significantly degrades performance and situation awareness. An increase in supervision burden has been shown to increase accidents during multi-robot control trials [34]. While this may be mitigated by smart alert systems [35,36], it has been shown in [37] that too many robot systems will eventually saturate operator capabilities and, in turn, lead the operators to neglect some robots. Neglect is mainly due to the robots competing for operator attention [38]. In [39], the authors propose real-time measurements of neurophysiological parameters to estimate workload as a potential input to new forms of adaptive automation.
Our work focuses on eliminating this failure mode by judicious scheduling events that are likely to require concentrated operator attention.
We build upon our recent work [10,11], to perform multi-robot planning [40,41]. We also find complementary goals in [42] where a robot attempts to move from one location in its environment to another by calculating which obstacles can be minimally displaced to generate a feasible trajectory. In our work, we will similarly generate a coordination space, where operator “collision obstacles” must be avoided, and seek to find the minimal displacement needed to avoid them. In work by LaValle and Hutchinson [43,44], as well as by Wang et al. [45], the complexity of coordinating both many robots and operators is handled by separating the planning and scheduling aspects into two separate steps. This division greatly assists in devising a feasible solution and is echoed here as well. Our work develops techniques for planning multi-robot missions that can assist in outlining mission requirements and robot policies. There are relevant approaches such as Crandall et al. [46] which investigates the effects of allocating operator attention to robots, and [47,48,49] which investigate additional methods of distributing operators across robots and the effects this has. Particularly relevant to our research ideas are [50,51] where the expected behaviors of humans in an environment are incorporated into the planning phase of robots, allowing them to perform more elaborate plans than without this prediction. This argument also extends into more industrial settings, where it is often repeated, scheduled interaction between robots and operators [5]. Our work also relates to motion planning approaches that generate joint plans for humans and robots [52,53,54].
3. Preliminaries
We start with a set of m of bodies, which can be kinematic chains or mobile robots, . Each robot has a configuration space representing the set of all possible transformations, where the set of valid configurations is called the free space . Robots also have initial and goal configurations, where the trajectory takes the robot from -corresponding to -through to the final configuration -corresponding to , where is the total runtime for to execute given a dedicated operator.
When executing , may enter critical configurations during which it will require one of the p operator’s supervision. A conflict occurs when more than p robots require supervision at the same time. Given a range of time where the mission is executing, we will attempt to minimize when all robots have finished, while also providing operator attention when required.
Problem 1.
Scheduling for Multiple Operators:Given p the number of operators, a set of robots —each with their trajectories , and a set of critical configurations —determine a policy for each robot such that (1) all robots are only in critical configurations when an operator can supervise them, (2) the number of operators requested at any time does not exceed p, and (3) attempt to reduce the total runtime of the mission .
Building on this problem, we can add the following condition: Is it possible to yield a shorter mission runtime by generating alternative trajectories for bodies such that they do not require supervision simultaneously as other robots in the first place, thus avoiding operator attention “collisions” altogether? This question leads us to a concrete extension of Problem 1.
Instead of a pre-determined trajectory, we use a sequence of waypoints —where each waypoint is a specific configuration the robot must achieve, and the application-specific function yields a trajectory that visits while avoiding during operator-denied times —an example of which can be found in Section 6.
Problem 2.
Scheduling with Re-Planning:Given p operators, a set of robots each with a sequence of sub-goals , and a set of critical configurations . Determine a trajectory and policy for each robot satisfying the waypoints such that (1) robots are in critical configurations only when an operator can supervise them, (2) the number of operators requested at any time is less than or equal to p, and (3) an effort is made to minimize the ending time of the mission .
4. Scheduling Operator Attention
This section will propose solutions to Problem 1 defined in Section 3. A schematic representation of the steps of our approach is outlined in Figure 1. Details of the method will be explained below.

Figure 1.
Overall steps involved in the proposed scheduling approach.
4.1. Computational Complexity of Scheduling for Multiple Operators
In our previous work [11], we described the operator scheduling problem and presented a geometric approach for its solution. There were several issues with the proposed methodology related to the computational complexity of creating the entire set of obstacles with the coordination space. To solve this problem, we give a proof sketch proving the complexity of this problem.
We prove that Problem 1 is NP-Hard by using the technique or restriction ([55], p. 63). An NP-Hardness proof by restriction consists of showing that a problem (in our case, Problem 1) contains a known NP-Hard as a special case.
In our proof, is the Multiprocessor Scheduling problem ([55], p. 238), which consists of a set of J jobs, each job has a corresponding length . Given p processors, we must schedule this set of jobs so that they (1) do not overlap and (2) execute in the minimum amount of time.
Starting from problem 1 (our operator scheduling problem), assume that all possible configurations for the robot will require operator attention, meaning that the entire execution of will need an operator. This plan’s runtime is , and is analogous to the length of a job in the original Multiprocessor Scheduling problem. These jobs are scheduled and allocated to p operators, which would be the processors in the original formulation. This problem then reduces to the Multiprocessor Scheduling problem where we schedule j jobs across p processors and indicates that the problem we are trying to solve is NP-hard.
4.2. A Sampling-Based Solution
Knowing that the problem is NP-hard we ask, we will propose heuristics to find feasible solutions.
We start by by creating a Coordination Space (following a procedure similar to [56]) representing all possible configurations of the robots along their trajectories. Each of the m axes corresponds to the normalized execution time of robot , given by , with the position along the axis corresponding to progress along the trajectory. Let be the set of invalid configurations where the number of robots requesting supervision exceeds p, and be the set of all valid configurations where the number of requests does not exceed p. At all robots are in their initial configurations, and at all robots are in their final configuration.
We define auxiliary functions, borrowing the notation from [57]: is the Euclidean distance between two points, and is the cost of a path corresponding to the sum of the pairwise Euclidean lengths of the pairwise linear points within it.
The above formulation serves to create a coordination space where the position along axes represents robot configurations and invalid configurations where multiple robots request obstacles represent an operator. This process allows us to convert the coordination problem into a path-planning problem. We must find a path from to . Following h will give us an implicit representation of time with each robot’s positions along their trajectory, such that each robot will move from its initial state to its goal state, with at most p robots requiring operator attention. We performed this calculation by mapping h to the trajectory corresponding to a particular robot. Define , which indicates the position of the robot along its trajectory at the corresponding point of path h through . We then perform the composition , which yields , mapping from the path h to . This allows us to determine the configuration of a robot at any point q in h via . We can now obtain the series of configurations for each robot that will guarantee that at most p robots require operator attention at any given time and reduces the total run-time of the mission.
Our preliminary solution [11] required generating the entire set of obstacles within the coordination space. Here, we instead use a lazy approach which only checks sampled locations. This is combined with a modified version of the Bidirectional originally described in [57,58,59], and shown in Algorithm 1 for reference. Define graphs , , where and . The objective will be to derive an obstacle-free path such that . Given a user-defined function that can estimate when robots will enter a critical section we can check if a point is obstacle-free as in Algorithm 2, where for the point being evaluated, we iterate over each robot’s critical segments (lines 3, 4) and check if the corresponding axis of x lies within the segment (line 5). If the number of collisions is greater than the number of operators (line 7), then the location is not obstacle-free. With some abuse of notation, we also use this to refer to checking if an edge is obstacle-free by sampling along the edge and checking if the samples are all within .
The modified is presented in Algorithm 1. In lines 1, 2, we initialize the final path as currently being none, and the corresponding cost to be infinite. Subsequently, we perform the following procedure over N samples: Beginning with —the graph starting at the origin—in lines 4, 5 we draw a randomly selected point from . Checking if the point lies within is done using Algorithm 2, and select the nearest point in the graph (we use an r-tree to accomplish this efficiently). In line 6, create a point that is closer to than . Then in lines 7–9, select the r points in that are nearest to and sort them in order of increasing distance from , where the sorted list consists of tuples of the form , where , is an edge from to , and is the cost of that path, and select the closest one with an obstacle-free path to as in [60]. If there is a valid “best parent” —defined as the vertex with the lowest combined cost-to-come and cost-to-go—we insert it into the graph and rewire as in [60] (lines 10–13). We then attempt to connect both trees. In lines 14–17, we select the nearest vertex in the opposite graph and attempt to draw a straight path from the newly added vertex to , if possible. We then check if the resulting path is better than our current best-path and update if necessary.
| Algorithm 1:B- |
 |
At this point in the algorithm, we may have a valid path through . We then perform as in [60] to attempt reducing the length of . The user may assign a probability , corresponding to the likelihood of checking for an early-exit solution; this is to balance between the run-time of B- and yielding a better path. We evaluate this in lines 20–23, returning a valid solution if one exists. Otherwise, we swap and and continue until all N samples have been drawn and return .
We then proceed, in Algorithm 3, by mapping h to the sequence of configurations that correspond to robot . Movement parallel to an axis corresponds to that robot moving at full speed, perpendicular segments indicate the robot is paused, and diagonal segments to velocity-tuning depending on the slope.
To the best of our knowledge, our approach is one of the first to use geometric and motion planning techniques to schedule operators’ attention. Since most previous methods are based on human factor techniques or combinatorial scheduling algorithms, head-to-head comparison is difficult. Furthermore, our study cases (multi-robot control and humanoid manipulation) are different from the ones presented in related work (e.g., foraging [27]). In the near term, one direction for comparison would be applying our techniques to previously used study cases and benchmark the approach.
We believe that our proposed method has a good scaling behavior. An additional robot and its constraints represent an additional variable in our coordination space. Since we are using sampling-based methods for finding a feasible solution (which have been used in large dimensions [61]), we believe that our method can scale to larger groups. Furthermore, in sampling-based motion planning, a significant part of the computational cost is collision checking, and since this is simple in our formulation (obstacles are hypercubes), there is good potential for scaling.
5. Scheduling with Re-Planning
The previous solution provides us with a coordination space and corresponding path that yields a velocity-tuning approach preventing operator collisions. We now look for a solution that yields a shorter mission runtime by also altering the robot trajectories. This solution is found by comparing the current path through the coordination space h and the desired shortest-path path which would be a straight line. Given the example in Figure 2a,b, where we see the robots and environment, and the resulting coordination space, we indicate an “ideal” path as in Figure 2c. When searching for a path through the coordination space, we may find a point such that , representing an obstacle. In the example shown in Figure 2c, this is indicated by the blue region, meaning that the ideal path is not valid as it intersects the obstacle. In these situations, the solution is to either plan around the obstacle, corresponding to tuning the velocity of the robots involved—as in the solution for Problem 1—or creating alternative plans for the robots. In the latter case, the number of operators requested during the original set of times corresponding to the obstacle can now be fulfilled, potentially reducing the overall mission runtime if the resulting plans are shorter than the wait times.
| Algorithm 2: CollisionCheck |
 |
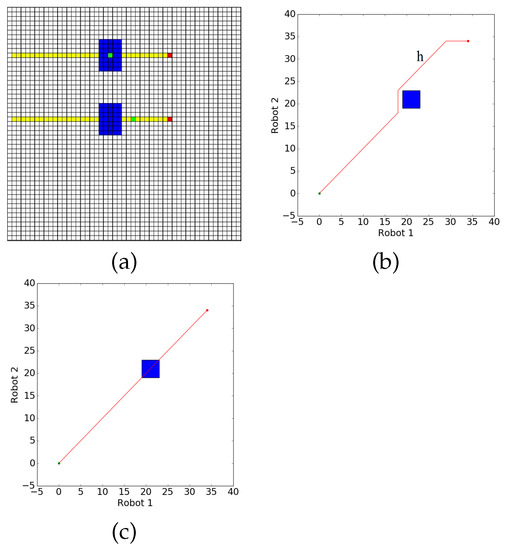
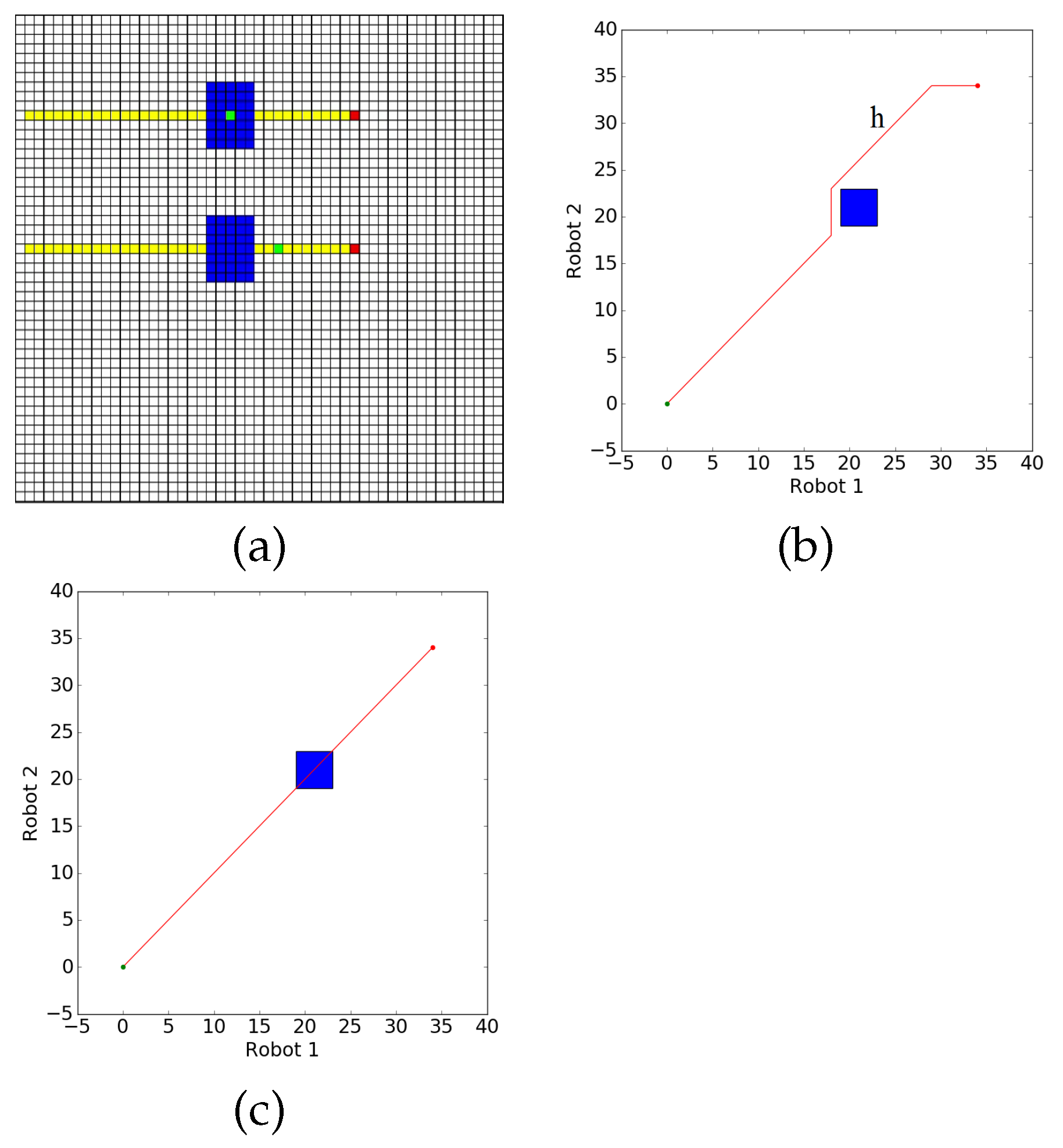
Figure 2.
Example Environment and resulting Coordination Space (a) A planar environment with dangerous regions requiring operator supervision to traverse shown in blue, and robot trajectories in yellow. (b) The two-dimensional Coordination Space resulting from (a). Each axis corresponds to the positions of robots along with their trajectories. The red line indicates an attention-conflict-free path through the coordination space. (c) Coordination space from (b), with the desired (optimal) policy shown as the red line.
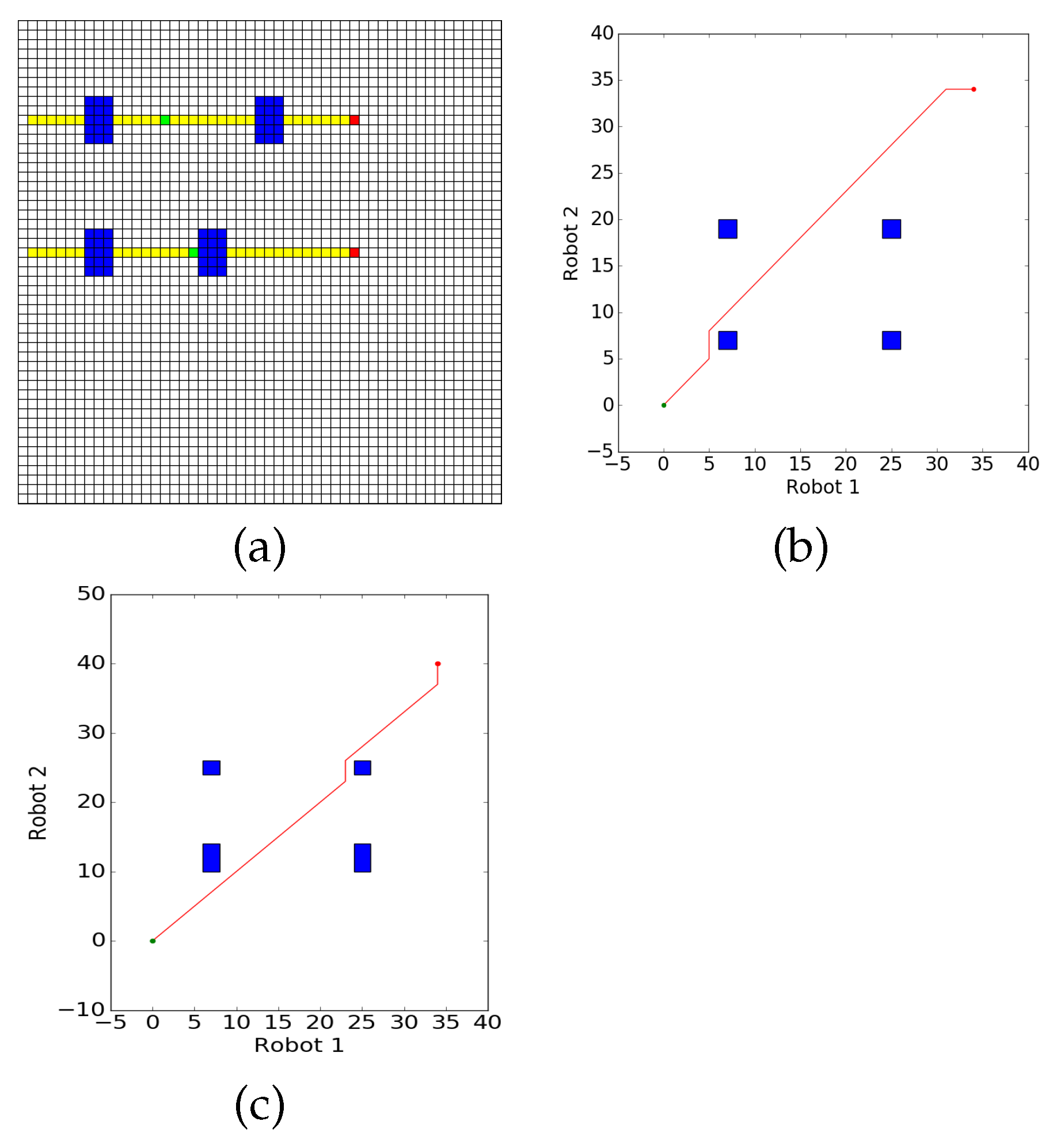
A critical side-effect to keep in mind is that by modifying robots’ trajectories when avoiding collisions caused by conflicting operator attention requests, we are also potentially changing later parts of their trajectory. This change will lead to a different coordination space and the possibility of shifting, creating, or removing subsequent obstacles. As an illustrative example, Figure 3a shows two robots, which enter regions requiring supervision at the same time and produce the coordination space in Figure 3b. The vertical segment of the path h shown in red corresponds to the collision being resolved by pausing robot 1 until robot 2 has finished its operator request before continuing. This scenario could also be solved by re-planning robot 2 so that it avoids operator requests during the original times. However, robot 1 will then require more time to travel around the dangerous region, causing it to encounter its second critical section at a later time—precisely when robot 1 is entering its second request as well (Figure 3c)—creating another conflict that must be solved.
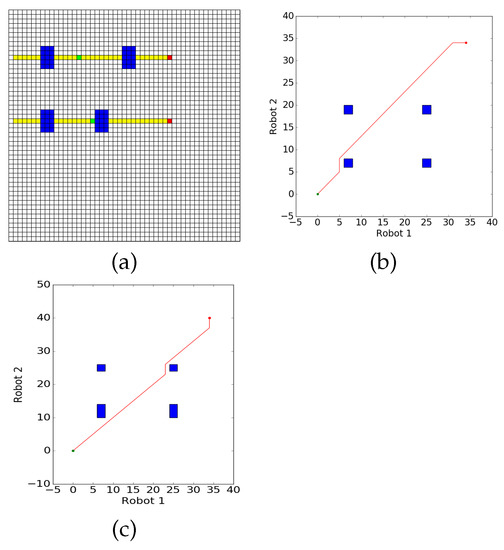
Figure 3.
Example Environment, resulting Coordination Space, and Shifting Conflict Regions (a) Robots in their environment, and their expected trajectories; (b) Original Coordination Space resulting from (a); (c) Final Coordination Space after re-planning around the first attention obstacle.
This setup yields our initial solution via velocity-tuning. Then create an ideal path , given by a straight line that assumes no robots require supervision (line 3). Next, we verify if the optimal solution is valid by checking for collisions between and obstacles in the coordination space and return the first obstacle encountered—if any in line 4. returns the robots involved in the “collision” , along with the corresponding configurations and times that each robot has in conflict . If the ideal path is invalid (line 5), we can resolve this in two ways:
- Alter the involved robots policies (as in the previous solution).
- Re-plan the involved robots trajectories to eliminate the obstacle.
We now describe how to re-plan the robot’s trajectories. Given the robots involved in the collision, , we sort them in order of ascending length of execution time and select the shortest —the minimum number of robots to re-plan to remove the attention collision (lines 6, 7). This procedure is performed on the robots with the shortest current plans so that extensions to their plans due to re-planning should have a minimal effect on the mission’s overall length. Then generate alternative trajectories for the robots, provided operator-denied times , and create an alternative goal location to account for any shifts in the ending times of the robot plans (lines 8–11).
Suppose the distance between and the alternative is longer than the current solution. In that case, velocity-tuning will yield a better solution, and we incorporate the obstacle into the “desired” set of obstacles (lines 12, 22). Otherwise, we test if the alternative, a re-planned solution is better (lines 13, 14). If it is, then update the robots with their re-planned trajectories, and replace the current coordination space and goal to account for any changes in execution times (lines 15–17); else we incorporate the obstacle into the “desired” set of obstacles as before (line 19).
We repeat this process of generating desired solutions (line 24) and testing them until the desired path no longer intersects any obstacles. At this point, we return the final that will have no operator conflicts.
6. Experimental Results
In this section, we cover the design and of both simulated and physical experiments, and the results obtained.
6.1. Software Simulation for Scheduling with Re-Planning
Here we describe our simulation and provide an example algorithm that re-plans a robot’s trajectory around unsafe areas in the environment—which would require operator supervision—given operator-denied times.
The simulated environment consisted of a discretized 2-dimensional grid-world where robots can only move either horizontally or vertically. The environment also contains hazardous regions (shown in blue) which require operator supervision to traverse, corresponding to configurations in .
Example Re-plan Algorithm: The algorithm used in this example attempts to find the shortest path between and within the robot’s environment, which can be easily attained via the algorithm [62,63]. However, this path may intersect with regions requiring supervision. First, denote the starting time of the mission as . Given times when an operator will not be available for the robot, , we modify as follows: Augment ’s nodes with an additional parameter. When visiting a node, update its neighbor’s attributes to where is the current time, and is the time required to move from the current node to the neighbor. If the neighbor physically resides within and the neighbors is inside , then we treat it as an obstacle. This modification of provides paths that circumvent obstacles during operator-denied times, with an example shown in Figure 4.
| Algorithm 3: Scheduler |
 |
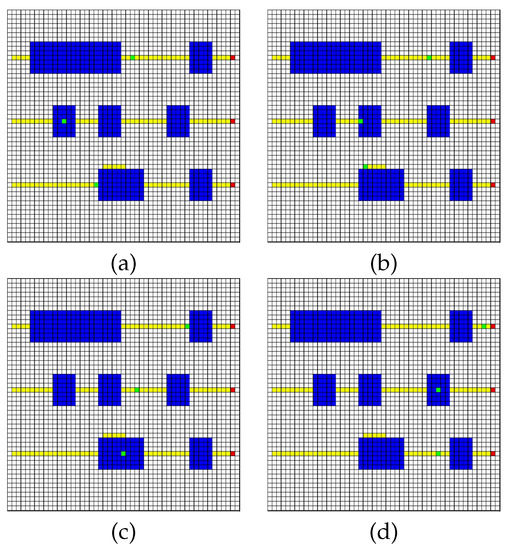
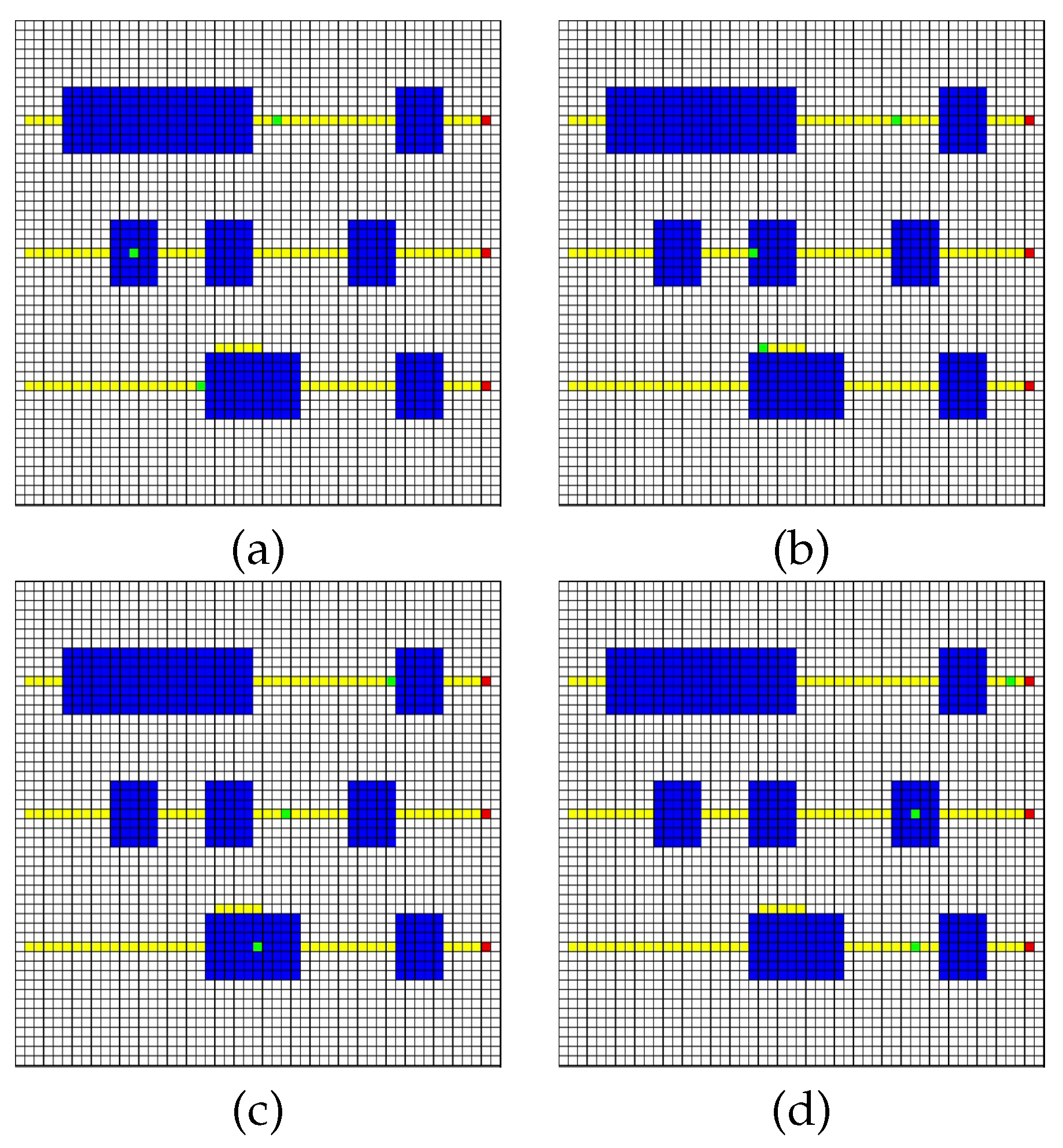
Figure 4.
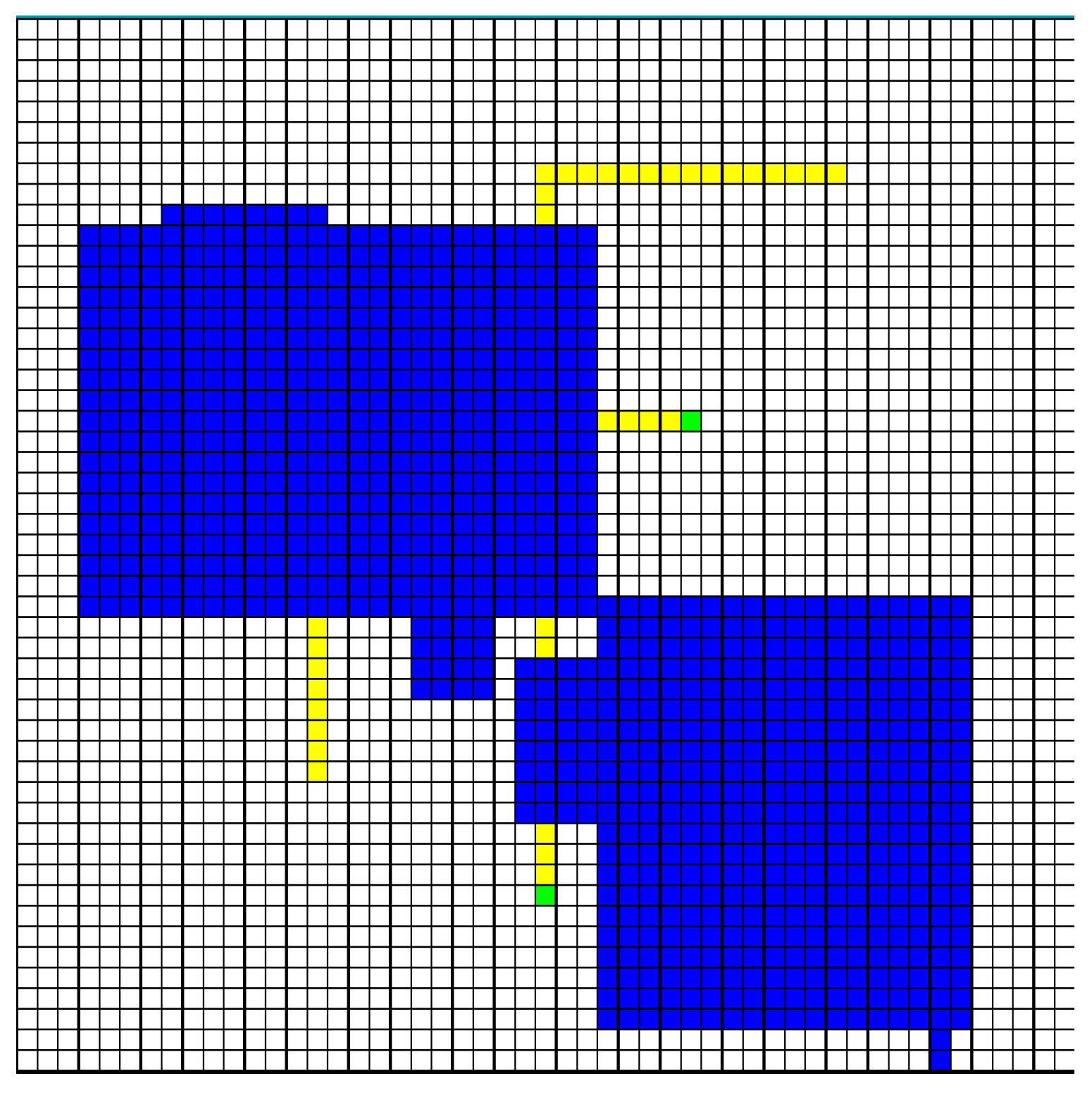
Example Simulation Environment Example simulation. The robots are numbered 1, 2, 3 from top to bottom. (a) Robot 3 stops while Robot 2 passes through its dangerous region. (b) Robot 3 has re-planned its trajectory and is going around the dangerous area, allowing Robot 2 to be supervised. (c) Robot 1 stops to allow Robot 3 enter its dangerous area with supervision. (d) All robots continue to their final goal locations.
In Figure 4, we show a simulated example given an environment with three robots. The blue areas in the environment are dangerous, and require operator supervision to prevent an accident. The example was designed to show several operator attention “collision” scenarios. As the robots move from left to right, the following operator requests might arise:
- requiring an operator
- and require an operator at the same time
- require an operator at the same time
- requiring an operator while and leave their critical regions
- requiring an operator
- and require an operator at the same time
The resulting coordination space is shown in Figure 5, where (a, b) is only velocity-tuning, and (c, d) is with re-planning the robot trajectories, which yields a slightly shorter mission ending time than strictly velocity-tuning.
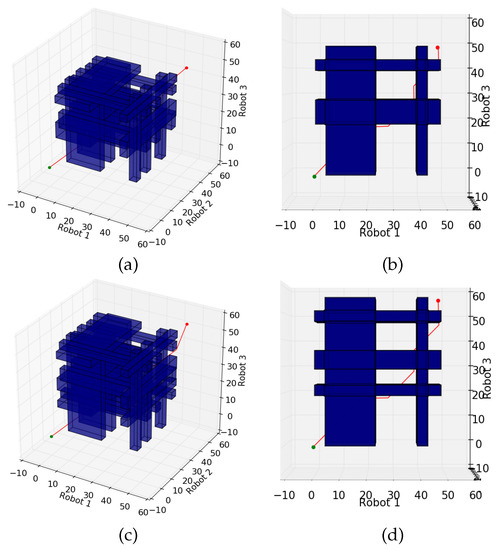
For further validation, simulations were run using a two-dimensional environment populated with a set of randomly sized, randomly placed dangerous regions, and robots placed in randomized obstacle-free starting and goal locations along with a corresponding path between them as shown in Figure 6. Across each iteration of the simulations, environments and the starting and goal positions for the robots were randomly generated. In each generated environment, trials were run using 2, 4, or 8 robots, moving at 1 cell/second. These trials were then solved using the solutions for Problem 1 (Scheduling) and Problem 2 (Scheduling with Re-Planning), with 1, 2, 4, or 8 operators. The results can be found in Table 1.
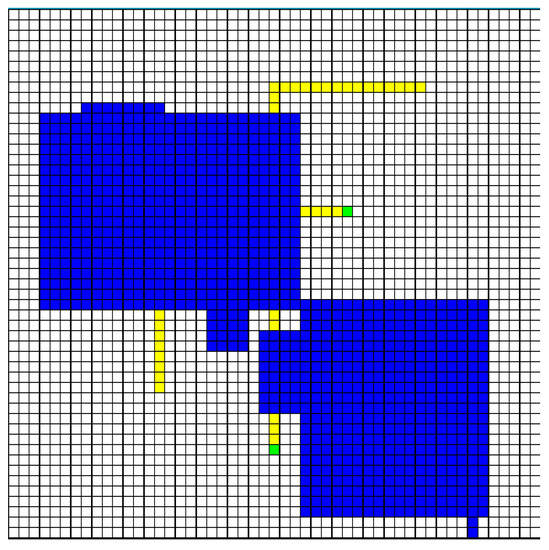
Figure 6.
Example Random Environment Example of a randomly generated environment and trajectories intersecting critical regions.

Table 1.
Average time savings via re-planning vs velocity-tuning.
There is an increase in the average time saved when dealing with larger numbers of robots, as re-scheduling can simultaneously resolve multiple robots at once. We purposefully ran the simulations with equal numbers of robots and operators to ensure that there would be no time saved—as there would be no obstacles generated in the first place—and this performed as expected. All tests with two and four robots completed successfully. In trials with eight robots and a single operator, a solution was not found with the parameters that were used. Given 2 operators, ∼30% completed, and ∼60% for four operators. This result was due to the low sample count used when running Attention , and the large length, which prevented it from exploring paths in narrow gaps between obstacles. The tuning of the sample count, steer length and rewire count lie outside the scope of this work, but is nonetheless an interesting problem we expect to incorporate in future work.
6.2. Hardware Experiment for Scheduling with Re-Planning
Here, we further illustrate the problem and solution via a hardware example. This example consisted of a single operator that had to be allocated across three line-following robots in a discrete grid environment.
The robots use a deterministic finite state machine to keep track of the position and orientation, and a transition function given by a second transition-state machine that ensures the robots inter-state path does not deviate from a grid line.
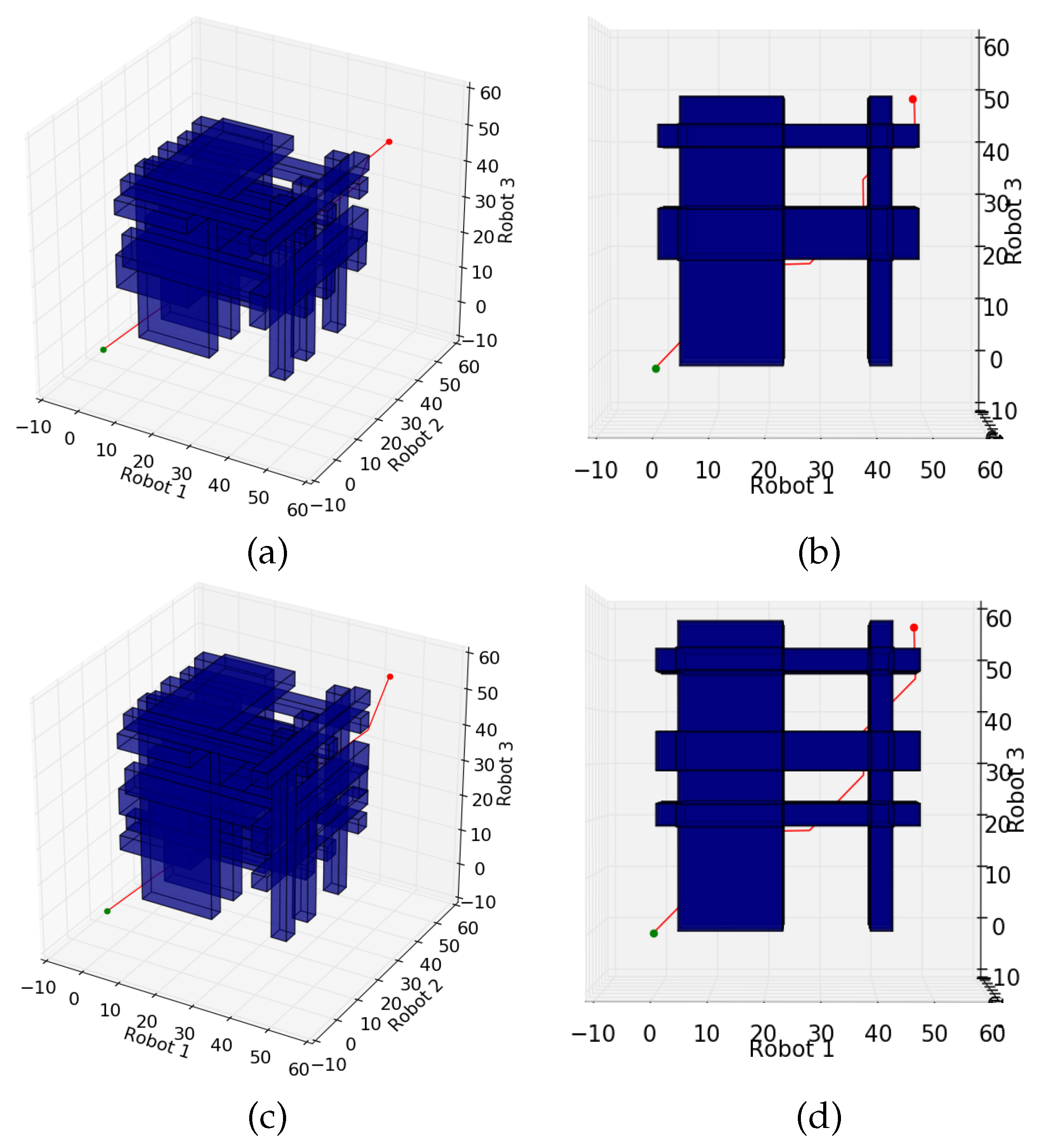
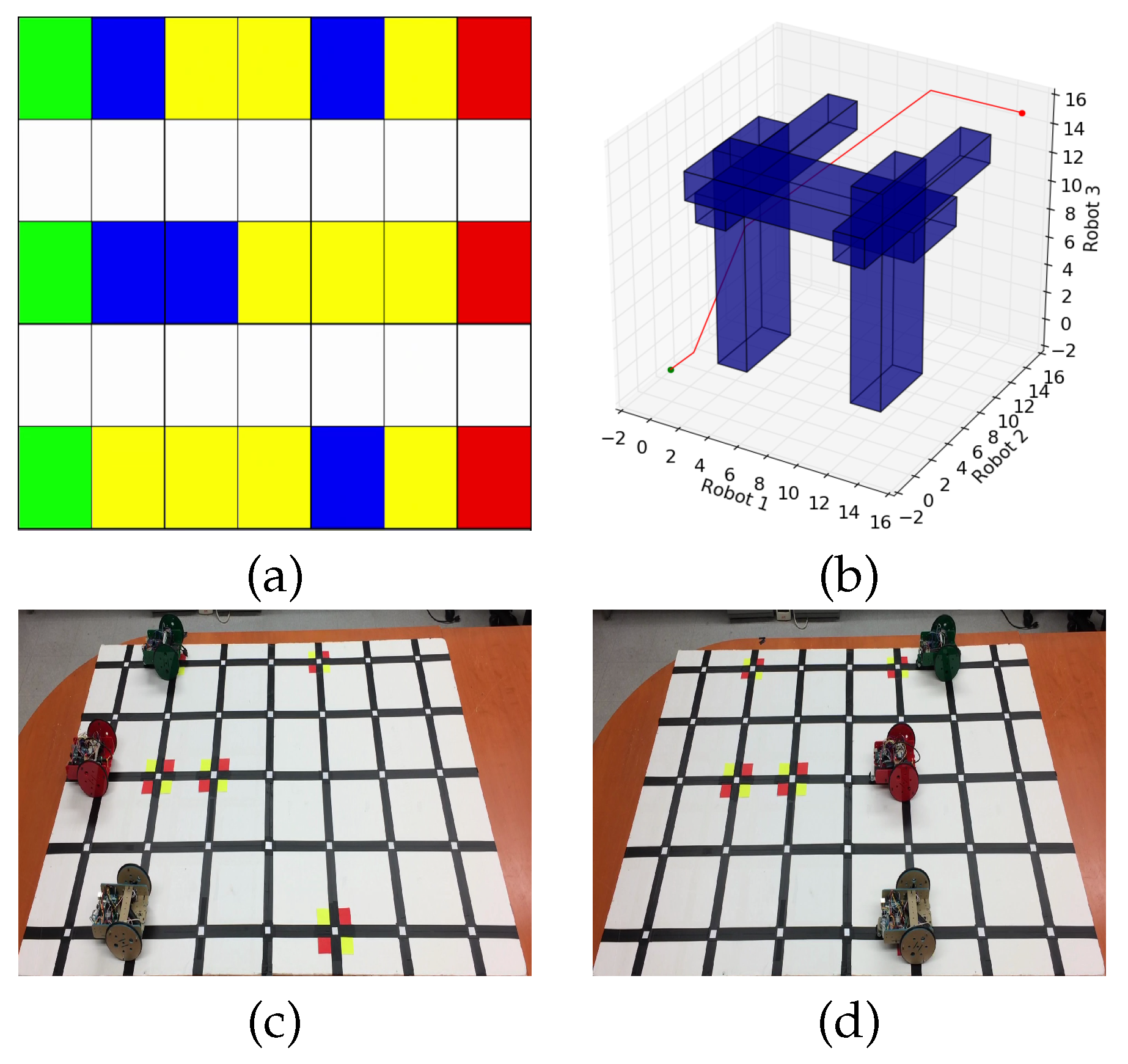
The hardware experiment in Figure 7 has an equivalent simulated environment shown in Figure 7a. The robots have initial trajectories shown in yellow, which pass through dangerous areas of the environment (blue) requiring operator supervision. The physical implementation represents the dangerous areas using red/yellow squares, in the same locations as in the virtual simulation. The resulting coordination space in Figure 7b provides a set of policies enabling the robots to execute their trajectories while ensuring that the operator is not split among multiple robots at the same time. The robots then executed their corresponding policies, moving and pausing when appropriate, with at most one robot entering a dangerous region at a time. Additional experiments and videos can be found at: http://users.cis.fiu.edu/~jabobadi/oa/ (accessed on 4 April 2021).
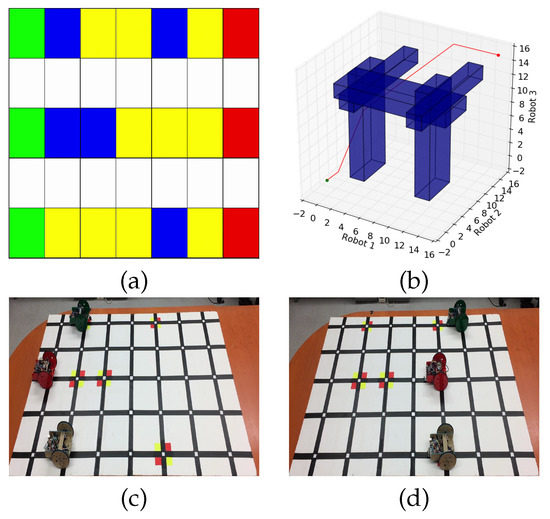
Figure 7.
Hardware Experiment Example (a) Simulated Environment; (b) Coordination Space resulting from (a); (c) Analogous hardware simulation at ; (d) Hardware simulation at .
The hardware experiments that were run and shown in the above link show successful runs using the above procedures to design trajectories and policies for three different robots under the supervision of a single operator. The mission ended in the shortest time possible, and the operator did not receive multiple concurrent requests.
7. Study Case: Humanoid Robots
In this section, an application of the proposed method to NASA’s humanoid robot Valkyrie [64] as shown Figure 8, is presented. Humanoid robots are high degree of freedom complex systems that have been proposed for diverse applications including nuclear-decommissioning tasks [65,66], disaster response assistance [67], and vehicles of space exploration [64]. For many of these tasks, it is desirable to have a human-in-the-loop controller to ensure critical and hazardous sub-tasks are completed. The supervised autonomy frameworks to make humanoid robots applicable in performing complex tasks require an effective design for a shared operator control interface which remains an open question. As seen during the DRC, completion of complex tasks in simulated environments with humanoids requires large teams of operators and shared control is indispensable [67]. Indeed even a simple manipulation task requires coherent operator collaboration or inter-operator communication problems can have detrimental effects [9]. Thus, it is preferable to enforce a 1:1 ratio between humanoids and operator [8].

Figure 8.
(Left) NASA’s humanoid robot Valkyrie. (Middle, Right) Experimental setup showing coordination space obstacles and kinematic chains that are treated as independent robots.
7.1. Methodology
We propose partitioning the humanoid robot into two serial kinematic chains, the left and right arm, which are denoted as and respectively. The desired task is modeled as a typical pick and place operation where the robots must visit designated picking and placing zones defined by the bounding boxes . For example, picks an object from and places it in . Next, collects the object from and places it in a final location . The picking and placing actions are executed by the end effectors of the right and left arms whose positions are respectively given by and . When an end effector (robot’s hand) is within a bounding box , it requires operator attention, i.e., the action is considered sensitive and require operator supervision. Thus, constitute configuration space constraints that must be transformed into critical regions in the coordination space. Thus, the constraints are represented in the configuration space as follows:
Additionally, the re-planning algorithm is modified as follows: Given a set of waypoints and operator-denied times , will re-plan sections of that reside within during times if possible. If re-planning is not possible, or if there are critical waypoints that should not be altered (such as waypoints denoting pick and place actions) the waypoints and relevant sections of will be untouched and returned to the scheduler as is.
7.2. Results
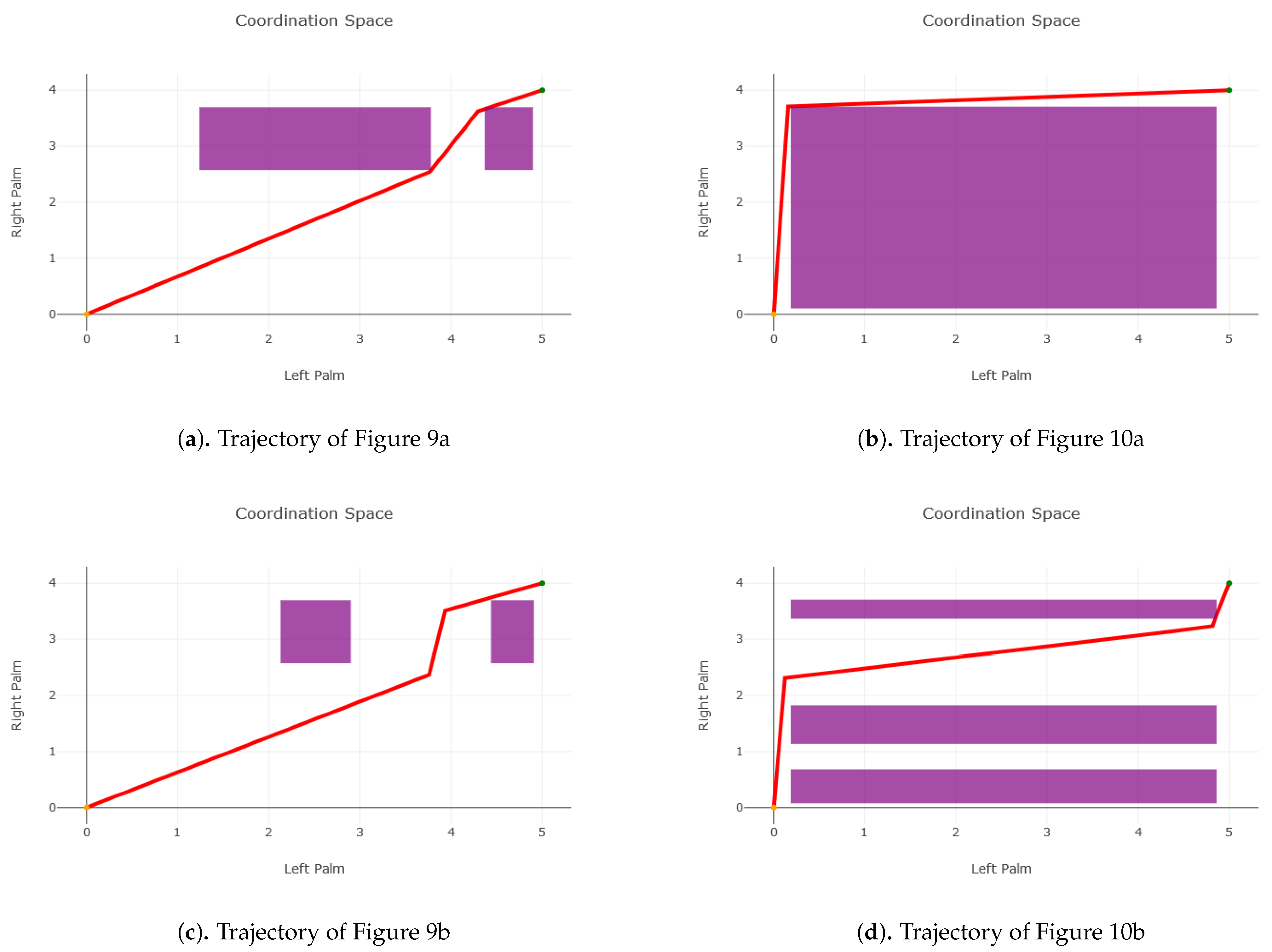
The simulation experiments are executed using the dynamic simulator Gazebo. An initial set of waypoints are defined for and . These waypoints consist of a set of Cartesian positions and velocities for the kinematic chains such that and satisfy the pick and place task constraints. The initial waypoints are passed to the scheduling algorithm which generates a new set of waypoints that—when separated by a monotonic time step—satisfy both the configuration and coordination space constraints. A cubic interpolation of the waypoints is used to generate a continuous trajectory for execution on the robot. A comparison between the executions before and after the scheduling algorithm is shown in Figure 9 and Figure 10. The coordination space of these trajectories is shown in Figure 11.
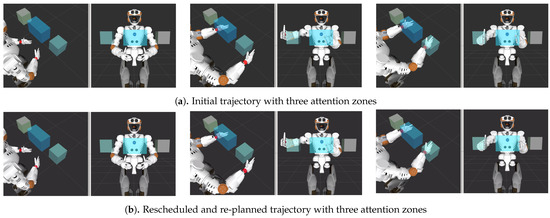
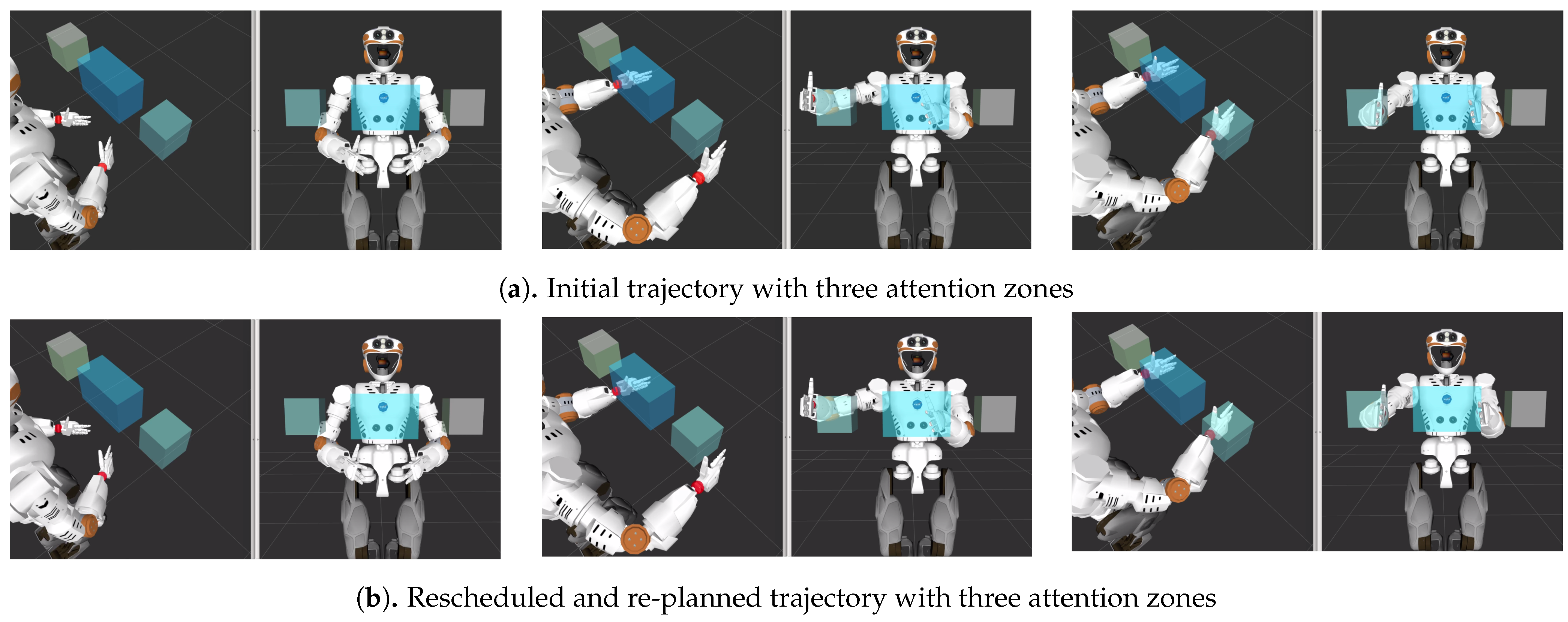
Figure 9.
Pick and place task with three attention obstacles. The planning reference frame is located at the wrist of the respective arms and is highlight by a red square. (Left): Both plans start in a valid position. Middle: Both plans approach the bounding in the same manner, but in the rescheduled case, the right arm execution is slowed down to ensure that before entering the bounding box the left hand has already left the attention zone (Right).
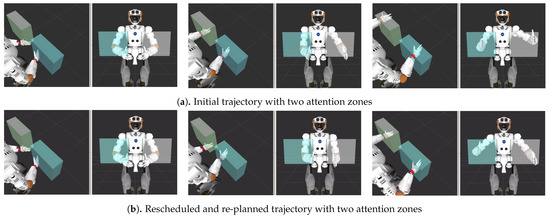
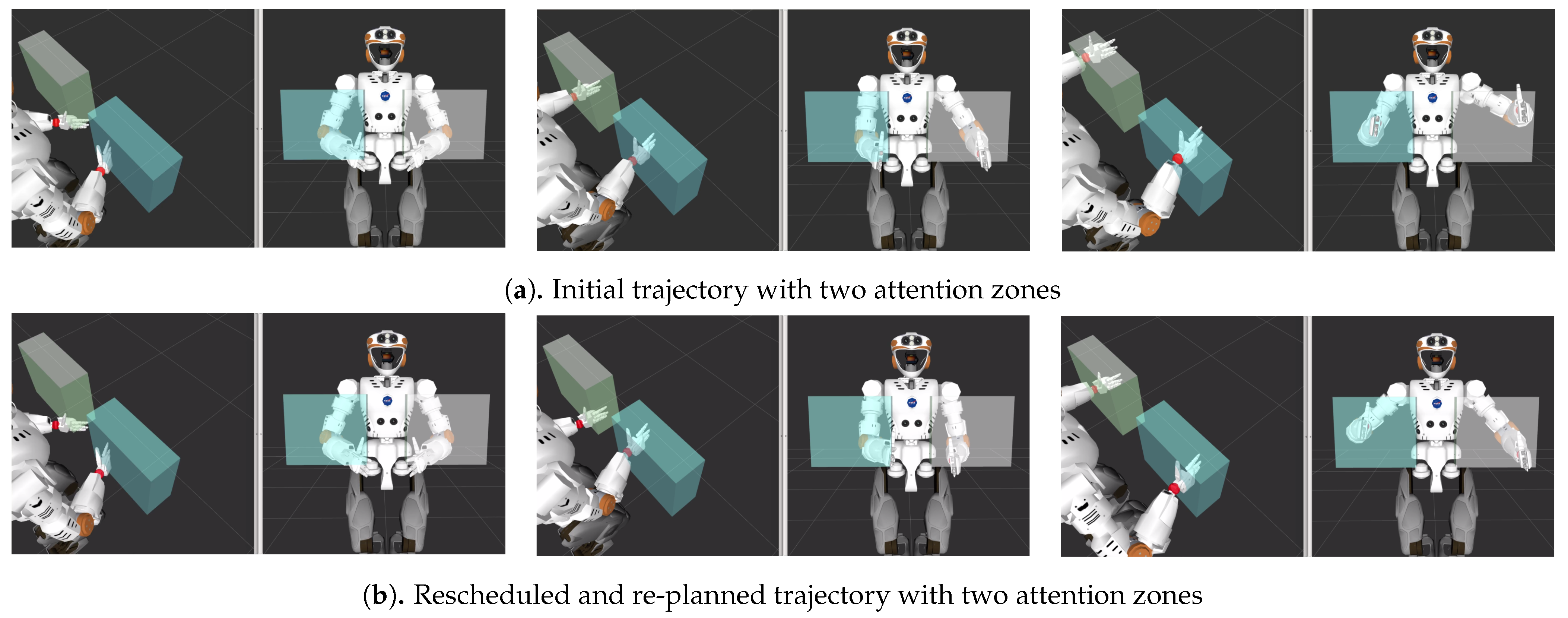
Figure 10.
Pick and place task with two attention obstacles. The planning reference frame is located at the wrist of the respective arms and is highlight by a red square. (Left): Both plans start in a valid position. Middle: The initial trajectory immediately violates attention constraints while the rescheduled trajectory slows the left arm to prevent entry into the area. (Right): The right arm is slightly withdrawn (re-planning) to ensure target frame is outside the bounding box before the left has to enter.
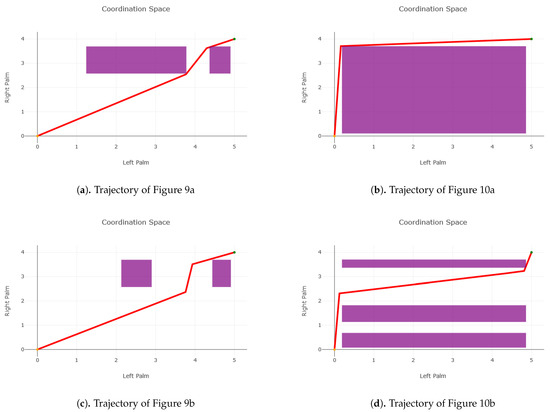
Figure 11.
Purple areas represent times when both palms will be in a critical zone while the red line is the scheduled times to reach a point for each palm.
The two original trajectories shown in Figure 11a,b have conflicts in critical areas as illustrated by the line passing through purple areas. The reduced purple areas in Figure 11c,d demonstrate the re-planning of waypoints, and the altered slope of the line through space indicates a change in time through the waypoints. Both trajectories use a combination of re-planning and rescheduling to generate a collision-free path through the coordination space.
8. Conclusions and Future Work
This work provides a geometric approach for converting robot trajectories and supervision requests into a set of policies for the robots that permit operators to oversee critical sections of robot plans without being over-allocated. The provided solution is also capable of determining when re-planning robots would yield a better solution than velocity-tuning. There are exciting avenues for future work.
In the short term, we would like to look at the effects that robot movement has on an operator’s effectiveness in overseeing them [68], and incorporate this effect into our solution. As an example, operators require time to switch their attention from one robot to another. This context switching time might be represented by extending obstacles in the coordination space towards the origin. Similarly, a robot’s path may have some element of uncertainty, especially when outside of a factory setting. In this case, we can “inflate” the obstacles within the coordination space, which would provide a more cautious solution.
We are also interested in improving our modeling of context switching times by using constructions from Human-Robot Interaction research. Potential sources of information that can be incorporated are mental states (MS) modeling and physiological factors [30]. We believe that the combination of realistic human cognition models and algorithmic, scalable methodologies such as the one we proposed in this paper can lead to fundamental insights.
Searching through the coordination space might be modified to use a receding horizon approach to allow for more rapidly changing robot plans if presented with a dynamic environment. We would like to include the stability constraints and interdependence between kinematic chains when working with robots with large degree of freedom.
We studied the complexity of problem 1 and argued that it is NP-Hard by using the technique or restriction, and we proceeded to propose feasible heuristics to solve it. A natural direction will be to carefully study approximation algorithms [69] for scheduling problems [70] that can be translated into our framework. This can help us calculate approximation ratios and performance guarantees for our approach.
In our paper, we presented two study cases to show our approach’s practical feasibility and range of applications. The first scenario is on a set of mobile robots, and the second is on a robot with several degrees of freedom. We want to continue exploring applications and extend this work to human studies to investigate the framework’s effectiveness for complex teleoperation tasks. A domain of interest where our ideas can apply are one-to-many (OTM) scenarios where a human operator needs to monitor and coordinate multiple multiple autonomous vehicles [39].
Author Contributions
Conceptualization, S.A.Z., P.L., L.B. and T.P.; Methodology, S.A.Z., P.L. and L.B.; Software, P.D., S.A.Z., P.L. and L.B.; Validation, S.A.Z. and P.D.; Writing—original draft preparation, S.A.Z., P.L., L.B.; Writing—review and editing, P.L., L.B. and T.P.; Supervision, P.L., L.B. and T.P.; Project administration L.B. and T.P.; Funding acquisition, L.B. and T.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the Department of Energy under Award Number DE-EM0004482, by the National Aeronautics and Space Administration under Grant No. NNX16AC48A issued through the Science and Technology Mission Directorate and by the National Science Foundation under Award No. 1451427. This research is also supported in part by the National Science Foundation through awards IIS-2034123 and IIS-2024733 and by the U.S. Department of Homeland Security under Grant Award Numbers 2017-ST-062000002.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviation is used in this manuscript:
| RRT | Rapidly Exploring Random Tree |
References
- Alam, T.; Bobadilla, L. Multi-Robot Coverage and Persistent Monitoring in Sensing-Constrained Environments. Robotics 2020, 9, 47. [Google Scholar] [CrossRef]
- Bandala, M.; West, C.; Monk, S.; Montazeri, A.; Taylor, C.J. Vision-based assisted tele-operation of a dual-arm hydraulically actuated robot for pipe cutting and grasping in nuclear environments. Robotics 2019, 8, 42. [Google Scholar] [CrossRef]
- Murphy, R.R.; Gandudi, V.B.M.; Adams, J. Applications of robots for Covid-19 response. arXiv 2020, arXiv:2008.06976. [Google Scholar]
- Shah, J.; Wiken, J.; Williams, B.; Breazeal, C. Improved human-robot team performance using chaski, a human-inspired plan execution system. In Proceedings of the 6th International Conference on Human-Robot Interaction, Lausanne, Switzerland, 6–9 March 2011; ACM: New York, NY, USA, 2011; pp. 29–36. [Google Scholar]
- Wilcox, R.; Nikolaidis, S.; Shah, J. Optimization of temporal dynamics for adaptive human-robot interaction in assembly manufacturing. Robot. Sci. Syst. VIII 2012, 441–448. [Google Scholar] [CrossRef]
- Helms, E.; Schraft, R.D.; Hagele, M. rob@ work: Robot assistant in industrial environments. In Proceedings of the IEEE International Workshop on Robot and Human Interactive Communication, Berlin, Germany, 27–27 September 2002; IEEE: Piscataway, NJ, USA, 2002; pp. 399–404. [Google Scholar]
- Murphy, R.R. Human-robot interaction in rescue robotics. IEEE Trans. Syst. Man Cybern. Part Appl. Rev. 2004, 34, 138–153. [Google Scholar] [CrossRef]
- Yanco, H.A.; Norton, A.; Ober, W.; Shane, D.; Skinner, A.; Vice, J. Analysis of human-robot interaction at the darpa robotics challenge trials. J. Field Robot. 2015, 32, 420–444. [Google Scholar] [CrossRef]
- Atkeson, C.G.; Benzun, P.B.; Banerjee, N.; Berenson, D.; Bove, C.P.; Cui, X.; De Donato, M.; Du, R.; Feng, S.; Franklin, P.; et al. What happened at the DARPA robotics challenge finals. In The DARPA Robotics Challenge Finals: Humanoid Robots to the Rescue; Springer: Berlin/Heidelberg, Germany, 2018; pp. 667–684. [Google Scholar]
- Zanlongo, S.A.; Rahman, M.; Abodo, F.; Bobadilla, L. Multi-robot Planning for Non-overlapping Operator Attention Allocation. In Proceedings of the IEEE International Conference on Robotic Computing, Taichung, Taiwan, 10–12 April 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 109–112. [Google Scholar]
- Zanlongo, S.; Abodo, F.; Long, P.; Padir, T.; Bobadilla, L. Multi-Robot Scheduling and Path-Planning for Non-Overlapping Operator Attention. In Proceedings of the 2018 Second IEEE International Conference on Robotic Computing (IRC), Laguna Hills, CA, USA, 31 January–2 February 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 87–94. [Google Scholar]
- Sandoval Arévalo, J.S.; Laribi, M.A.; Zeghloul, S.; Arsicault, M. On the design of a safe human-friendly teleoperated system for doppler sonography. Robotics 2019, 8, 29. [Google Scholar] [CrossRef]
- Lasota, P.A.; Fong, T.; Shah, J.A. A Survey of Methods for Safe Human-Robot Interaction; Now Publishers: Delft, The Netherlands, 2017. [Google Scholar]
- Sun, D.; Liao, Q.; Loutfi, A. Single master bimanual teleoperation system with efficient regulation. IEEE Trans. Robot. 2020, 36, 1022–1037. [Google Scholar] [CrossRef]
- Li, Y.; Liu, K.; He, W.; Yin, Y.; Johansson, R.; Zhang, K. Bilateral teleoperation of multiple robots under scheduling communication. IEEE Trans. Control Syst. Technol. 2019, 28, 1770–1784. [Google Scholar] [CrossRef]
- Rosenberg, L.B. The Use of Virtual Fixtures as Perceptual Overlays to Enhance Operator Performance in Remote Environments; Technical Report; Stanford University Center for Design Research: Stanford, CA, USA, 1992. [Google Scholar]
- Bowyer, S.A.; Davies, B.L.; y Baena, F.R. Active constraints/virtual fixtures: A survey. IEEE Trans. Robot. 2014, 30, 138–157. [Google Scholar] [CrossRef]
- Yamamoto, T.; Abolhassani, N.; Jung, S.; Okamura, A.M.; Judkins, T.N. Augmented reality and haptic interfaces for robot-assisted surgery. Int. J. Med. Robot. Comput. Assist. Surg. 2012, 8, 45–56. [Google Scholar] [CrossRef] [PubMed]
- Bettini, A.; Marayong, P.; Lang, S.; Okamura, A.M.; Hager, G.D. Vision-assisted control for manipulation using virtual fixtures. IEEE Trans. Robot. 2004, 20, 953–966. [Google Scholar] [CrossRef]
- Quintero, C.P.; Dehghan, M.; Ramirez, O.; Ang, M.H.; Jagersand, M. Flexible virtual fixture interface for path specification in tele-manipulation. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 5363–5368. [Google Scholar]
- Pruks, V.; Farkhatdinov, I.; Ryu, J.H. Preliminary study on real-time interactive virtual fixture generation method for shared teleoperation in unstructured environments. In Proceedings of the International Conference on Human Haptic Sensing and Touch Enabled Computer Applications, Pisa, Italy, 13–16 June 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 648–659. [Google Scholar]
- Long, P.; Keleştemur, T.; Önol, A.Ö.; Padir, T. Optimization-Based Human-in-the-Loop Manipulation Using Joint Space Polytopes. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 204–210. [Google Scholar]
- Farkhatdinov, I.; Ryu, J.H. Teleoperation of multi-robot and multi-property systems. In Proceedings of the 2008 6th IEEE International Conference on Industrial Informatics, Daejeon, Korea, 13–16 July 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1453–1458. [Google Scholar]
- Roldán, J.J.; Díaz-Maroto, V.; Real, J.; Palafox, P.R.; Valente, J.; Garzón, M.; Barrientos, A. Press start to play: Classifying multi-robot operators and predicting their strategies through a videogame. Robotics 2019, 8, 53. [Google Scholar] [CrossRef]
- Luo, J.; Lin, Z.; Li, Y.; Yang, C. A teleoperation framework for mobile robots based on shared control. IEEE Robot. Autom. Lett. 2019, 5, 377–384. [Google Scholar] [CrossRef]
- Hughes, T. Human-Automation Coordination in Multi-UAV Control. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; p. 6315. [Google Scholar]
- Chien, S.Y.; Lewis, M.; Mehrotra, S.; Brooks, N.; Sycara, K. Scheduling operator attention for multi-robot control. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Algarve, 7–12 October 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 473–479. [Google Scholar]
- Dardona, T.; Eslamian, S.; Reisner, L.A.; Pandya, A. Remote presence: Development and usability evaluation of a head-mounted display for camera control on the da Vinci Surgical System. Robotics 2019, 8, 31. [Google Scholar] [CrossRef]
- Wong, C.Y.; Seet, G. Workload, awareness and automation in multiple-robot supervision. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417710463. [Google Scholar] [CrossRef]
- Roy, R.N.; Drougard, N.; Gateau, T.; Dehais, F.; Chanel, C.P. How Can Physiological Computing Benefit Human-Robot Interaction? Robotics 2020, 9, 100. [Google Scholar] [CrossRef]
- Dybvik, H.; Løland, M.; Gerstenberg, A.; Slåttsveen, K.B.; Steinert, M. A low-cost predictive display for teleoperation: Investigating effects on human performance and workload. Int. J. Hum. Comput. Stud. 2021, 145, 102536. [Google Scholar] [CrossRef]
- Lu, S.; Zhang, M.Y.; Ersal, T.; Yang, X.J. Workload management in teleoperation of unmanned ground vehicles: Effects of a delay compensation aid on human operators’ workload and teleoperation performance. Int. J. Hum. Comput. Interact. 2019, 35, 1820–1830. [Google Scholar] [CrossRef]
- Riley, J.M.; Endsley, M.R. Situation awareness in HRI with collaborating remotely piloted vehicles. In Proceedings of the Human Factors and Ergonomics Society Annual Meeting, Orlando, FL, USA, 26–30 September 2005; SAGE Publications: Los Angeles, CA, USA, 2005; Volume 49, pp. 407–411. [Google Scholar]
- Adams, J.A. Multiple robot/single human interaction: Effects on perceived workload. Behav. Inf. Technol. 2009, 28, 183–198. [Google Scholar] [CrossRef]
- Al-Hussaini, S.; Gregory, J.M.; Guan, Y.; Gupta, S.K. Generating Alerts to Assist With Task Assignments in Human-Supervised Multi-Robot Teams Operating in Challenging Environments. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 24–30 October 2020. [Google Scholar]
- Al-Hussaini, S.; Gregory, J.M.; Shriyam, S.; Gupta, S.K. An Alert-Generation Framework for Improving Resiliency in Human-Supervised, Multi-Agent Teams. arXiv 2019, arXiv:1909.06480. [Google Scholar]
- Velagapudi, P.; Scerri, P.; Sycara, K.; Wang, H.; Lewis, M.; Wang, J. Scaling effects in multi-robot control. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 2121–2126. [Google Scholar]
- Prewett, M.S.; Johnson, R.C.; Saboe, K.N.; Elliott, L.R.; Coovert, M.D. Managing workload in human–robot interaction: A review of empirical studies. Comput. Hum. Behav. 2010, 26, 840–856. [Google Scholar] [CrossRef]
- Lim, Y.; Pongsarkornsathien, N.; Gardi, A.; Sabatini, R.; Kistan, T.; Ezer, N.; Bursch, D.J. Adaptive Human-Robot Interactions for Multiple Unmanned Aerial Vehicles. Robotics 2021, 10, 12. [Google Scholar] [CrossRef]
- Parker, L. Multiple mobile robot systems. In Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2008; pp. 921–941. [Google Scholar]
- Ponda, S.; Johnson, L.; Geramifard, A.; How, J. Cooperative mission planning for Multi-UAV teams. In Handbook of Unmanned Aerial Vehicles; Springer: Berlin/Heidelberg, Germany, 2015; pp. 1447–1490. [Google Scholar]
- Hauser, K. Minimum Constraint Displacement Motion Planning. Robot. Sci. Syst. 2013, 6, 2. [Google Scholar]
- LaValle, S.; Hutchinson, S. Optimal Motion Planning for Multiple Robots Having Independent Goals. In Proceedings of the IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 22–28 April 1996; pp. 2847–2852. [Google Scholar]
- LaValle, S.; Hutchinson, S. Optimal Motion Planning for Multiple Robots Having Independent Goals. IEEE Trans. Robot. Autom. 1998, 14, 912–925. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y.; Geng, L.; Fuh, J.; Teo, S. Mission planning for heterogeneous tasks with heterogeneous UAVs. In Proceedings of the International Conference on Control Automation Robotics & Vision (ICARCV), Singapore, 10–12 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1484–1489. [Google Scholar]
- Crandall, J.; Cummings, M.; Della Penna, M.; de Jong, P.M. Computing the effects of operator attention allocation in human control of multiple robots. IEEE Trans. Syst. Man Cybern. Part Syst. Hum. 2011, 41, 385–397. [Google Scholar] [CrossRef]
- Cummings, M.; Mitchell, P. Operator scheduling strategies in supervisory control of multiple UAVs. Aerosp. Sci. Technol. 2007, 11, 339–348. [Google Scholar] [CrossRef][Green Version]
- Murphy, R.; Shields, J. The Role of Autonomy in DoD Systems; Technical Report; Department of Defense, Defense Science Board Task Force Report: Washington, DC, USA, 2012. [Google Scholar]
- Ramchurn, S.; Fischer, J.; Ikuno, Y.; Wu, F.; Flann, J.; Waldock, A. A study of human-agent collaboration for multi-UAV task allocation in dynamic environments. In Proceedings of the 24th International Joint Conference on Artificial Intelligence (IJCAI), Buenos Aires, Argentina, 25–31 July 2015. [Google Scholar]
- Trautman, P. Probabilistic tools for human-robot cooperation. In Proceedings of the Human Agent Robot Teamwork Workshop HRI, Boston, MA, USA, 5–8 March 2012. [Google Scholar]
- Trautman, P.; Ma, J.; Murray, R.M.; Krause, A. Robot navigation in dense human crowds: Statistical models and experimental studies of human—Robot cooperation. Int. J. Robot. Res. 2015, 34, 335–356. [Google Scholar] [CrossRef]
- Rahman, M.M.; Bobadilla, L.; Mostafavi, A.; Carmenate, T.; Zanlongo, S.A. An Automated Methodology for Worker Path Generation and Safety Assessment in Construction Projects. IEEE Trans. Autom. Sci. Eng. 2018, 15, 479–491. [Google Scholar] [CrossRef]
- Rahman, M.M.; Carmenate, T.; Bobadilla, L.; Zanlongo, S.; Mostafavi, A. A coupled discrete-event and motion planning methodology for automated safety assessment in construction projects. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 3849–3855. [Google Scholar]
- Rahman, M.M.; Carmenate, T.; Bobadilla, L.; Mostafavi, A. Ex-ante assessment of struck-by safety hazards in construction projects: A motion-planning approach. In Proceedings of the 2014 IEEE International Conference on Automation Science and Engineering (CASE), Taipei, Taiwan, 18–22 August 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 277–282. [Google Scholar]
- Gary, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-completeness. J. Symb. Log. 1979, 48, 498–500. [Google Scholar]
- LaValle, S. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Karaman, S.; Frazzoli, E. Incremental sampling-based algorithms for optimal motion planning. Robot. Sci. Syst. VI 2010, 104. [Google Scholar] [CrossRef]
- Jordan, M.; Perez, A. Optimal Bidirectional Rapidly-Exploring Random Trees; Technical Report; Computer Science and Artificial Intelligence Laboratory: Cambridge, MA, USA, 2003. [Google Scholar]
- Qureshi, A.H.; Ayaz, Y. Intelligent bidirectional rapidly-exploring random trees for optimal motion planning in complex cluttered environments. Robot. Auton. Syst. 2015, 68, 1–11. [Google Scholar] [CrossRef]
- Shkolnik, A.; Tedrake, R. Path planning in 1000+ dimensions using a task-space Voronoi bias. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 2061–2067. [Google Scholar]
- Beardwood, J.; Halton, J.; Hammersley, J. The shortest path through many points. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1959; Volume 55, pp. 299–327. [Google Scholar]
- Matthews, J. Basic A* pathfinding made simple. AI Game Programming Wisdom, Section 3; Charles River Media: Hingham, MA, USA, 2002; pp. 105–113. [Google Scholar]
- Radford, N.A.; Strawser, P.; Hambuchen, K.; Mehling, J.S.; Verdeyen, W.K.; Donnan, A.S.; Holley, J.; Sanchez, J.; Nguyen, V.; Bridgwater, L.; et al. Valkyrie: Nasa’s first bipedal humanoid robot. J. Field Robot. 2015, 32, 397–419. [Google Scholar] [CrossRef]
- Long, P.; Padir, T. Constrained Manipulability for Humanoid Robots Using Velocity Polytopes. Int. J. Humanoid Robot. 2020, 17, 1950037. [Google Scholar] [CrossRef]
- Long, P.; Padir, T. Evaluating robot manipulability in constrained environments by velocity polytope reduction. In Proceedings of the 2018 IEEE-RAS 18th International Conference on Humanoid Robots (Humanoids), Beijing, China, 6–9 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–9. [Google Scholar]
- DeDonato, M.; Dimitrov, V.; Du, R.; Giovacchini, R.; Knoedler, K.; Long, X.; Polido, F.; Gennert, M.A.; Padır, T.; Feng, S.; et al. Human-in-the-loop Control of a Humanoid Robot for Disaster Response: A Report from the DARPA Robotics Challenge Trials. J. Field Robot. 2015, 32, 275–292. [Google Scholar] [CrossRef]
- Koppenborg, M.; Nickel, P.; Naber, B.; Lungfiel, A.; Huelke, M. Effects of movement speed and predictability in human–robot collaboration. Hum. Factors Ergon. Manuf. Serv. Ind. 2017, 27, 197–209. [Google Scholar] [CrossRef]
- Vazirani, V.V. Approximation Algorithms; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Pinedo, M. Scheduling; Springer: Berlin/Heidelberg, Germany, 2012; Volume 29. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).