Balancing of the Orthoglide Taking into Account Its Varying Payload †
Abstract
1. Introduction
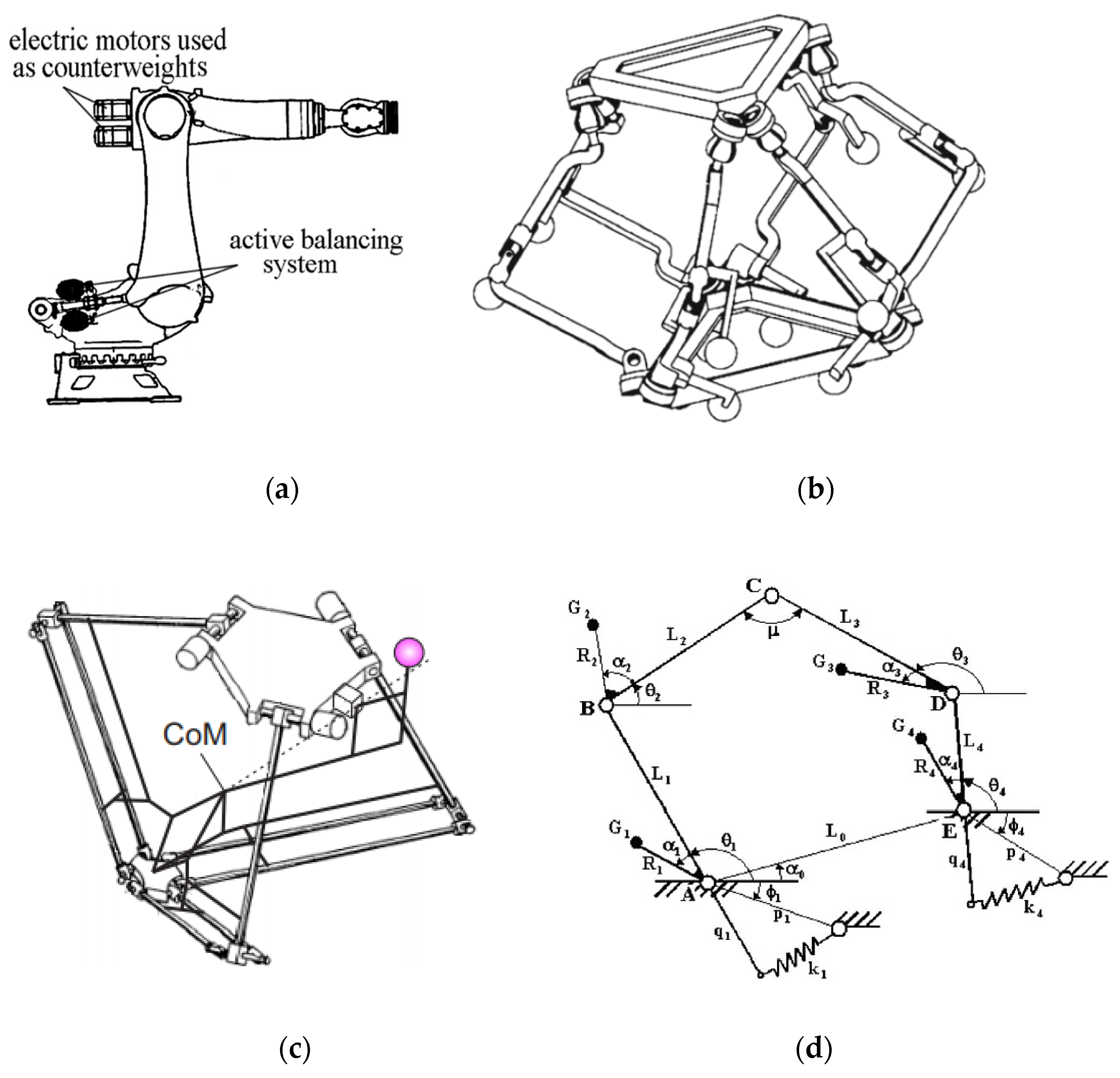
- By adding counterweight in order to keep the total mass center of moving links stationary [1]. It is obvious that the adding of the counterweights is not desirable because it leads to the increase of the total mass, of the overall size and of the efforts in joints. To avoid these drawbacks, the masses of the motors can be used as counterweights [2] (Figure 1a). Taking into account the complexity of the parallel manipulators, adding counterweights became not interesting, especially in spatial ones [3] (Figure 1b);
- By adding auxiliary structures. In [4,5,6], the parallelograms were used as auxiliary structures in order to create the balanced manipulators. In [7], the pantograph (Figure 1c) has been added in order to balance the shaking force of the Delta robot. Such a solution leads to a decrease in the added masses of counterweights, but the practical application remains a challenge;
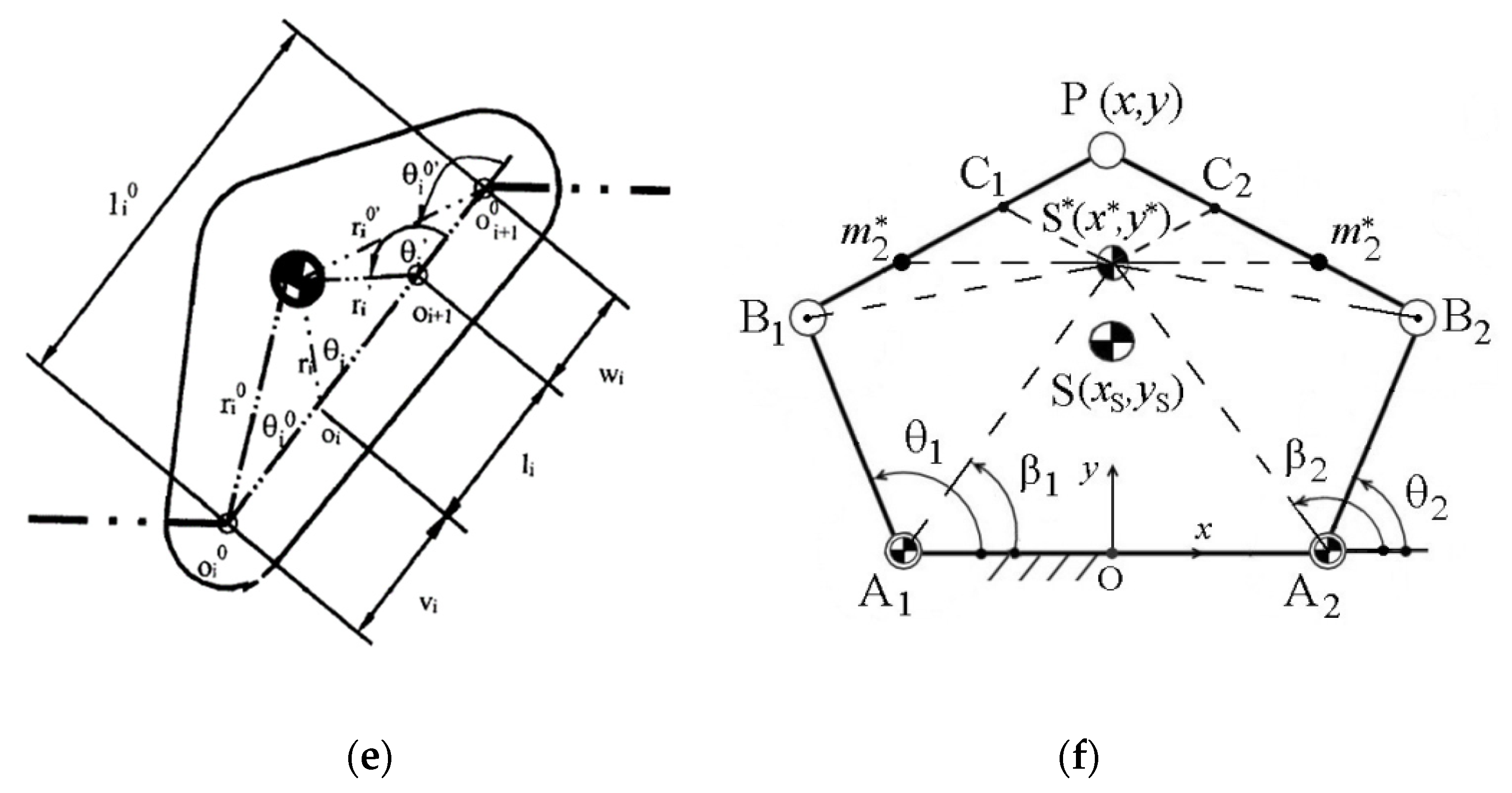
- Via center of mass acceleration control [11,12,13,14,15,16,17]. This approach is based on the optimal control of the acceleration of the manipulator center of masses. For this purpose, the “bang–bang” profile was used. The aim of the suggested method consists in the fact that the manipulator is controlled not by applying end-effector trajectories but by planning the displacements of the total mass center of moving links. Such a solution does not allow for complete balancing, but it leads to a significant decrease in shaking forces. In [17], a substituted point mass (Figure 1f) was found to replace the common center of mass of the 5R parallel manipulators as a virtual point. In this case, the motion planning of the substituted point mass can ensure a reduction of the shaking force.
2. Shaking Force Balancing of the Orthoglide
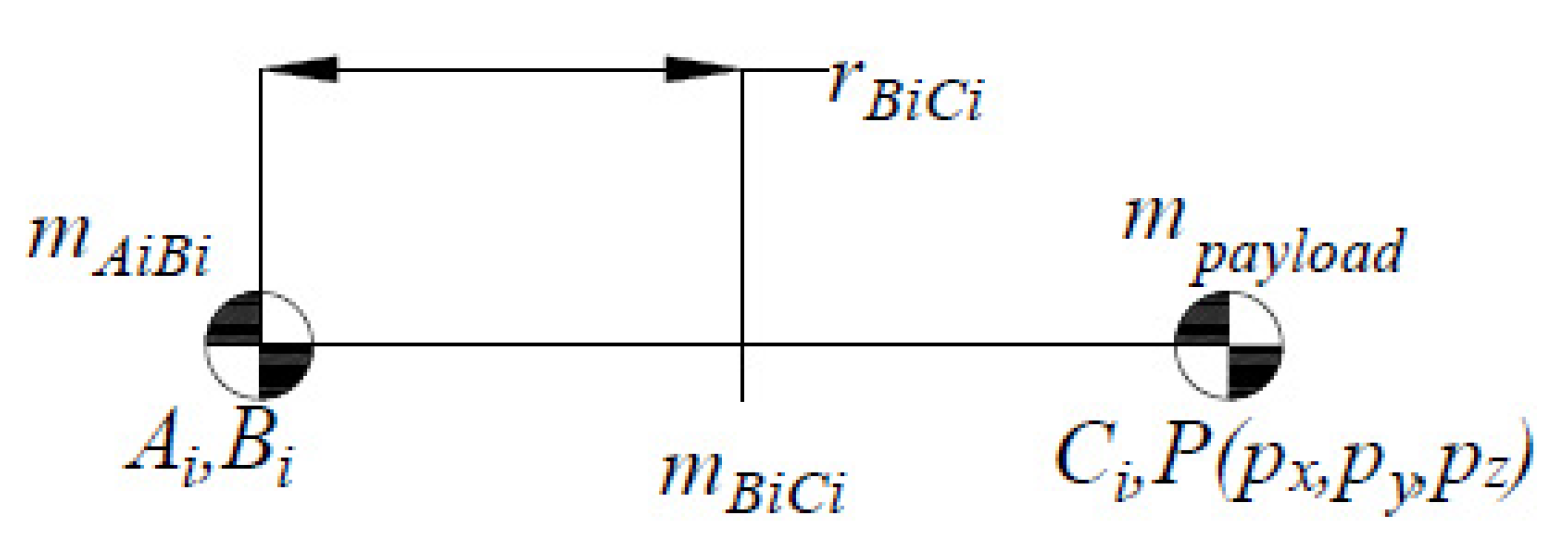
2.1. Problem Formulation
2.2. The Relationship between the Total Center of Mass and the Input Parameters of the Robot
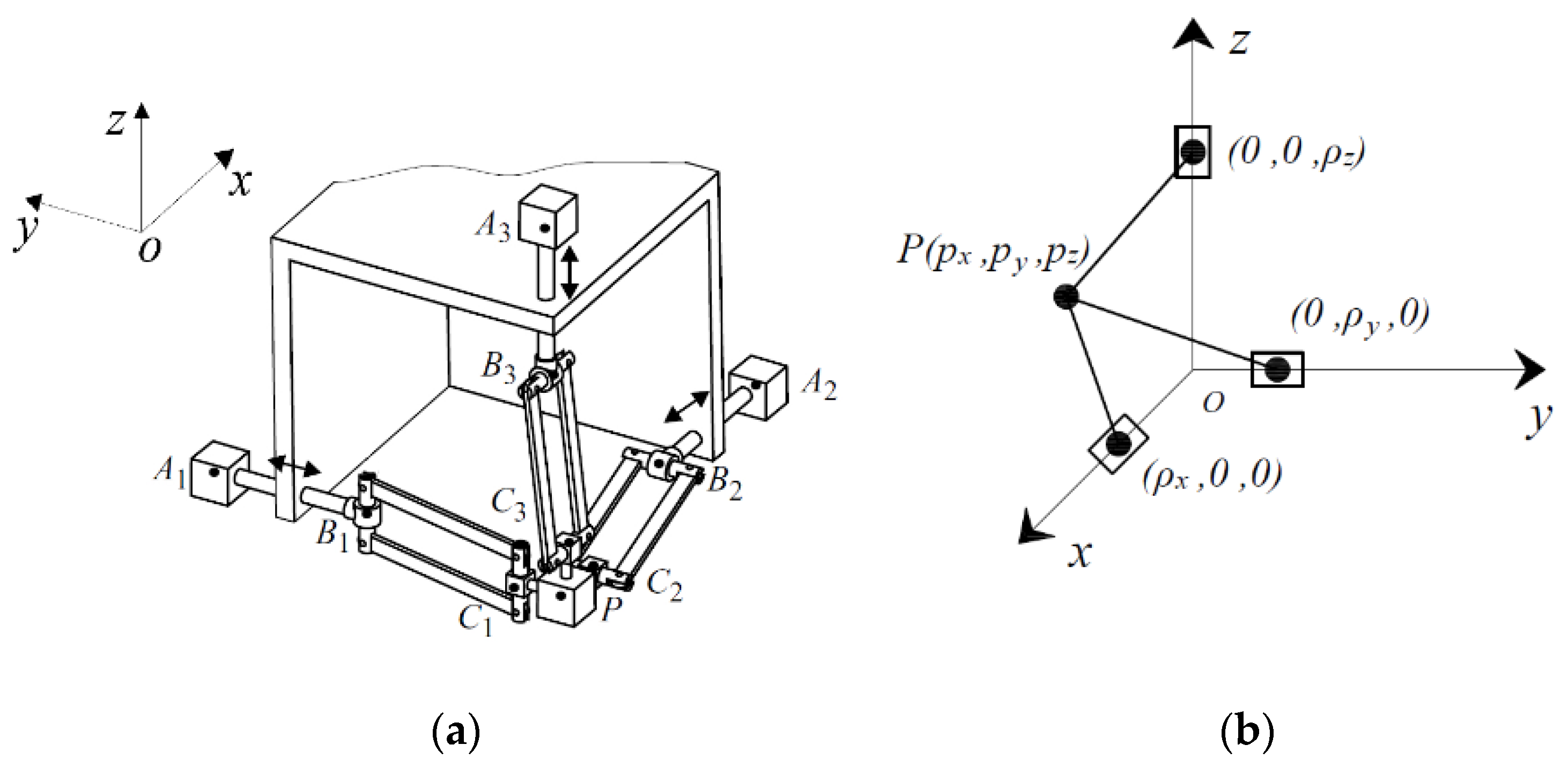
3. Illustrative Example via CAD Model
3.1. Balancing of the Orthoglide without Taking into Account the Payload
- Case 1: defining the displacement of the end-effector of the unbalanced manipulator as a straight line and parameterized with “fifth-order polynomial” profile;
- Case 2: defining the displacement of the end-effector of the unbalanced manipulator as a straight line and parameterized with “bang–bang” profile;
- Case 3: the generation of the displacement of the manipulator center of mass as a straight line and parameterized with the “bang–bang” profile.
3.2. Balancing of the Orthoglide While Taking into Account the Payload
3.3. Sensitivity Analysis of the Shaking Force and Shaking Moment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Filaretov, V.F.; Vukobratovic, M.K. Static balancing and dynamic decoupling of the motion of manipulation robots. Mechatronics 1993, 3, 767–783. [Google Scholar] [CrossRef]
- Bayer, A.; Merk, G. Industrial Robot with a Weight Balancing System. Patent EP 2011, 301, 727. [Google Scholar]
- Gosselin, C.M. Gravity compensation, static balancing and dynamic balancing of parallel mechanisms. In Smart Devices and Machines for Advanced Manufacturing; Springer: London, UK, 2008; pp. 27–48. [Google Scholar]
- Agrawal, S.K.; Fattah, A. Reactionless space and ground robots: Novel design and concept studies. Mech. Mach. Theory 2004, 39, 25–40. [Google Scholar] [CrossRef]
- Fattah, A.; Agrawal, S.K. Design and modeling of classes of spatial reactionless manipulators. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation (ICRA), Taipei, Taiwan, 14–19 September 2003; pp. 3225–3230. [Google Scholar]
- Fattah, A.; Agrawal, S.K. Design arm simulation of a class of spatial reactionless manipulators. Robotica 2005, 23, 75–81. [Google Scholar] [CrossRef]
- Wijk, V.; van der Herder, J.L. Dynamic Balancing of Clavel’s Delta Robot. In Computational Kinematics; Kecskeméthy, A., Müller, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 315–322. [Google Scholar]
- Alici, G.; Shirinzadeh, B. Optimum force balancing with mass distribution and a single elastic element for a five-bar parallel manipulator. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation (ICRA), Taipei, Taiwan, 14–19 September 2003; pp. 3666–3671. [Google Scholar]
- Alici, G.; Shirinzadeh, B. Optimum force balancing of a planar parallel manipulator. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2003, 217, 515–524. [Google Scholar] [CrossRef]
- Ouyang, P.R.; Zhang, W.J. A Novel Force Balancing Method for Real-Time Controllable Mechanisms. In Proceedings of the ASME 2002 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Montreal, QC, Canada, 29 September–2 October 2002; pp. 183–190. [Google Scholar]
- Briot, S.; Arakelian, V.; Le Baron, J.-P. Shaking Force Minimization of High-Speed Robots via Center of Mass Acceleration Control. Mech. Mach. Theory 2012, 57, 1–12. [Google Scholar] [CrossRef]
- Briot, S.; Arakelian, V.; Sauvestre, N.; Baron, J.-P.L. Shaking Forces Minimization of High-Speed Robots via an Optimal Motion Planning. In ROMANSY 18 Robot Design, Dynamics and Control; Springer: Vienna, Austria, 2010; pp. 307–314. [Google Scholar]
- Arakelian, V. Design of Partially Balanced 5R Planar Manipulators with Reduced Center of Mass Acceleration (RCMA). In ROMANSY 21—Robot Design, Dynamics and Control; Parenti-Castelli, V., Schiehlen, W., Eds.; Springer: Udine, Italy, 2016; Volume 569, pp. 113–122. [Google Scholar]
- Arakelian, V.; Geng, J.; Fomin, A.S. Minimization of Shaking Loads in Planar Parallel Structure Manipulators by Means of Optimal Control. J. Mach. Manuf. Reliab. 2018, 47, 303–309. [Google Scholar] [CrossRef]
- Geng, J.; Arakelian, V. Design of Partially Balanced Planar 5R Symmetrical Parallel Manipulators via an Optimal Motion Planning. In Advances in Mechanism and Machine Science. IFToMM 2019; Uhl, T., Ed.; Springer: Krakow, Poland, 2019; Volume 73, pp. 2211–2220. [Google Scholar]
- Geng, J.; Arakelian, V. Partial Shaking Force Balancing of 3-RRR Parallel Manipulators by Optimal Acceleration Control of the Total Center of Mass. In Multibody Dynamics 2019, ECCOMAS 2019, Computational Methods in Applied Sciences; Kecskeméthy, A., Flores, F.G., Eds.; Springer: Cham, Germany, 2019; Volume 53, pp. 375–382. [Google Scholar]
- Geng, J.; Arakelian, V. Balancing of Planar 5R Symmetrical Parallel Manipulators Taking into Account the Varying Payload. In ROMANSY 23—Robot Design, Dynamics and Control, ROMANSY 2020, CISM International Center for Mechanical Sciences (Courses and Lectures); Venture, G., Solis, J., Takeda, Y., Konno, A., Eds.; Springer: Cham, Germany, 2020; Volume 601, pp. 372–379. [Google Scholar]
- Wenger, P.; Chablat, D. Kinematic Analysis of a New Parallel Machine Tool: The Orthoglide. In Advances in Robot Kinematics; Lenarčič, J., Stanišić, M.M., Eds.; Springer: Dordrecht, The Netherlands, 2000; pp. 305–314. [Google Scholar]
- Chablat, D.; Wenger, P. Architecture Optimization of a 3-DOF Translational Parallel Mechanism for Machining Applications, the Orthoglide. IEEE Trans. Robot. Autom. 2003, 19, 403–410. [Google Scholar] [CrossRef]
- Geng, J.; Arakelian, V.; Chablat, D.; Lemoine, P. Shaking Force Balancing of the Orthoglide. In Advances in Service and Industrial Robotics. RAAD 2020. Mechanisms and Machine Science; Zeghloul, S., Laribi, M., Arevalo, J.S., Eds.; Springer: Cham, Germany, 2020; Volume 84, pp. 227–234. [Google Scholar]
- Pashkevich, A.; Chablat, D.; Wenger, P. Kinematics and Workspace Analysis of a Three-Axis Parallel Manipulator: The Orthoglide. Robotica 2006, 24, 39–49. [Google Scholar] [CrossRef][Green Version]
- Arakelian, V.; Briot, S. Balancing of Linkages and Robot Manipulators: Advanced Methods with Illustrative Examples; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Khalil, W.; Dombre, E. Modeling, Identification and Control of Robots; Butterworth-Heinemann: Oxford, UK, 2003. [Google Scholar]
- Guegan, S.; Khalil, W.; Lemoine, P. Identification of the dynamic parameters of the Orthoglide. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation(ICRA), Taipei, Taiwan, 14–19 September 2003; pp. 3666–3671. [Google Scholar]

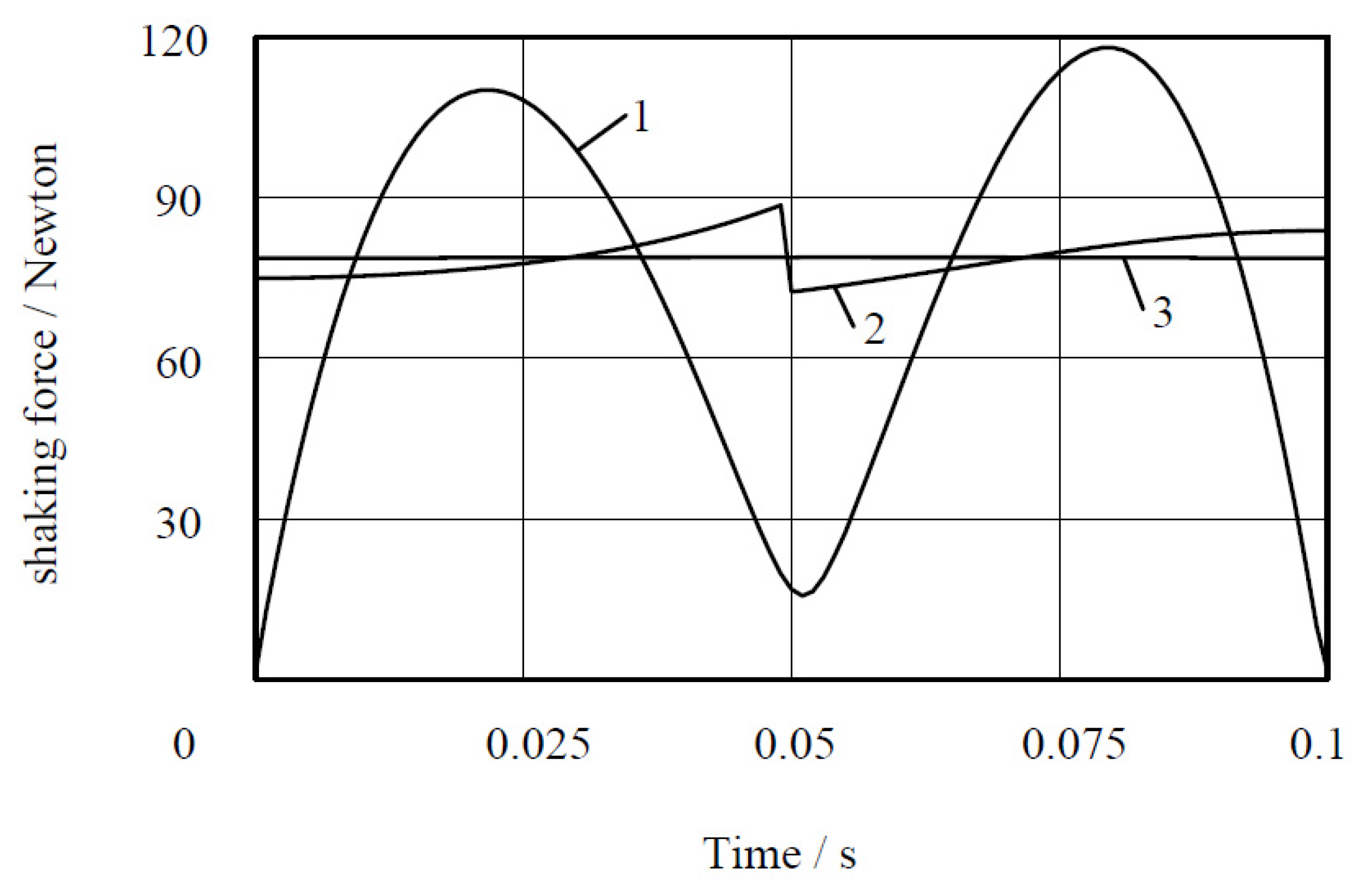

| Mass of Payload/kg | Shaking Force 1/Newton · m | Reduction 2/% | |||
|---|---|---|---|---|---|
| Case 1 | Case 2 | Case 3 | Case 2 | Case 3 | |
| 0 | 117.99 | 88.56 | 78.86 | 24.9 | 33.2 |
| 1 | 212.08 | 152.82 | 144.57 | 27.9 | 31.8 |
| 2 | 306.73 | 218.08 | 210.55 | 28.9 | 31.3 |
| 3 | 401.55 | 283.65 | 276.31 | 29.3 | 31.2 |
| 4 | 496.43 | 349.36 | 342.22 | 29.6 | 31.1 |
| 5 | 591.35 | 415.14 | 408.14 | 29.8 | 30.9 |
| Mass of Payload/kg | Shaking Moment 1/Newton · m | Reduction 2/% | |||
|---|---|---|---|---|---|
| Case 1 | Case 2 | Case 3 | Case 2 | Case 3 | |
| 0 | 38.19 | 29.11 | 25.35 | 23.8 | 33.6 |
| 1 | 64.11 | 47.18 | 43.66 | 26.4 | 31.9 |
| 2 | 90.08 | 65.25 | 61.82 | 27.6 | 31.4 |
| 3 | 116.06 | 83.33 | 79.93 | 28.2 | 31.1 |
| 4 | 142.03 | 101.40 | 98.02 | 28.6 | 31.0 |
| 5 | 168.01 | 119.47 | 116.09 | 28.9 | 30.9 |
| Input Errors | Output Errors | |||||||
|---|---|---|---|---|---|---|---|---|
| 0.04 | 0 | 0 | 0 | 0 | 0.077 | 0 | 0 | 0 |
| 0 | 0.1 | 0 | 0 | 0 | 0.187 | 0 | 0 | 0 |
| 0 | 0 | 31 | 0 | 0 | 2.887 | 37.296 | 6.048 | 11.824 |
| 0 | 0 | 0 | 16 | 0 | 0.025 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0.02 | 0.202 | 0 | 0 | 0 |
| 10.105 | 1.930 | 1.874 | 1.581 |
| 0.093 | 1.203 | 0.195 | 0.381 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, J.; Arakelian, V.; Chablat, D.; Lemoine, P. Balancing of the Orthoglide Taking into Account Its Varying Payload . Robotics 2021, 10, 30. https://doi.org/10.3390/robotics10010030
Geng J, Arakelian V, Chablat D, Lemoine P. Balancing of the Orthoglide Taking into Account Its Varying Payload . Robotics. 2021; 10(1):30. https://doi.org/10.3390/robotics10010030
Chicago/Turabian StyleGeng, Jing, Vigen Arakelian, Damien Chablat, and Philippe Lemoine. 2021. "Balancing of the Orthoglide Taking into Account Its Varying Payload " Robotics 10, no. 1: 30. https://doi.org/10.3390/robotics10010030
APA StyleGeng, J., Arakelian, V., Chablat, D., & Lemoine, P. (2021). Balancing of the Orthoglide Taking into Account Its Varying Payload . Robotics, 10(1), 30. https://doi.org/10.3390/robotics10010030





