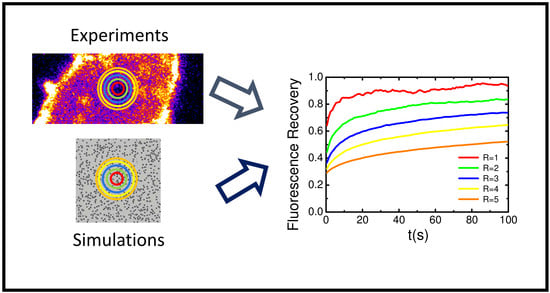
Numerical Simulation and FRAP Experiments Show That the Plasma Membrane Binding Protein PH-EFA6 Does Not Exhibit Anomalous Subdiffusion in Cells
Abstract
1. Introduction
- “Rafts” model where lipid/lipid phase separation drives the lateral partitioning of transmembrane proteins [7].
2. Results
2.1. Anomalous Subdiffusion Modeling
2.2. Validating Numerical Simulation and Analytical Models
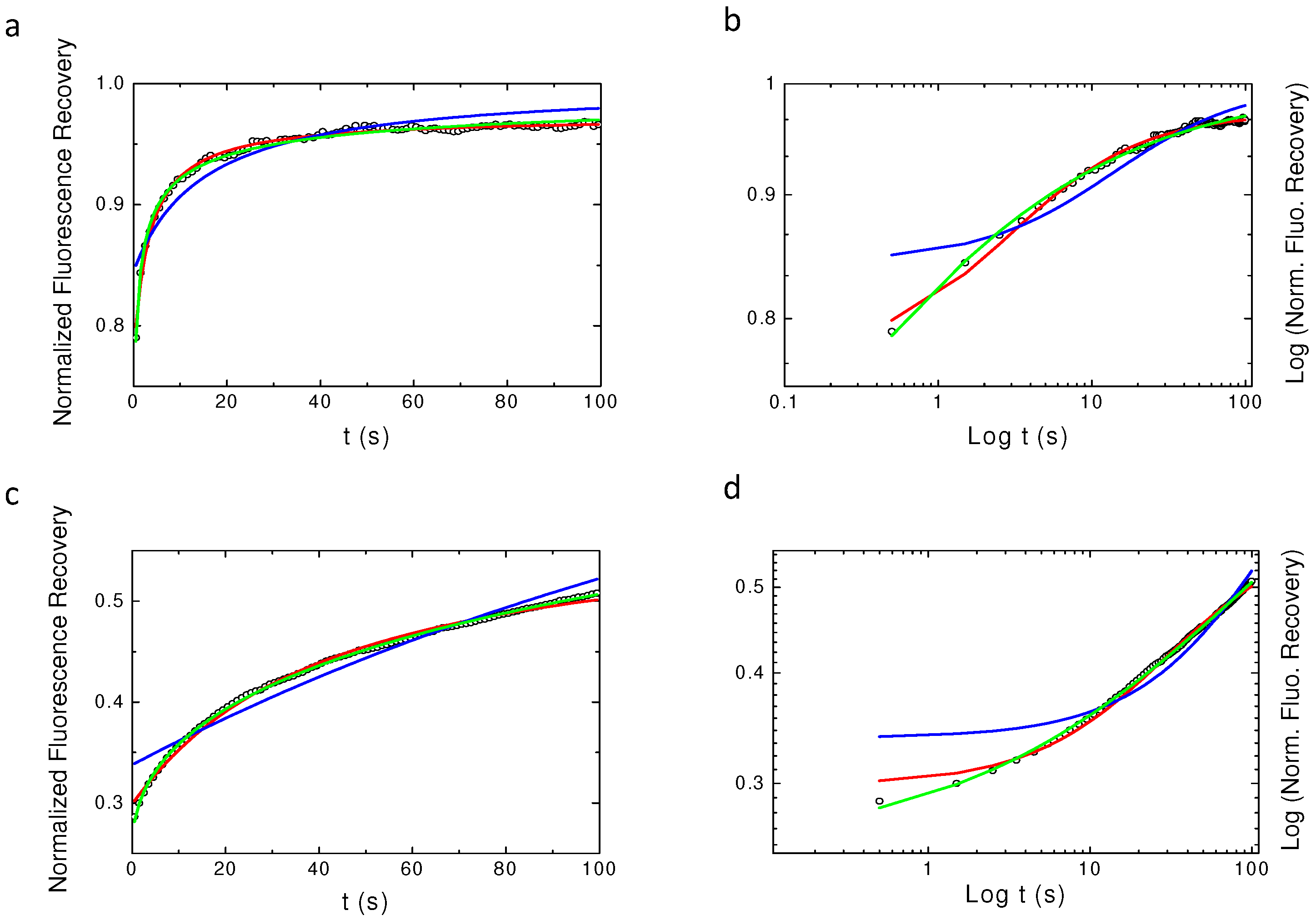
2.3. Challenging Analytical Models to Identify Numerically Simulated Anomalous Diffusion Fluorescence Recoveries
- Anomalous diffusion motion (aDm): see Equation (8) in Section 2.1,
- Free Brownian motion (Bm):
- Restricted Brownian motion (rBm):where M accounts for the mobile fraction.
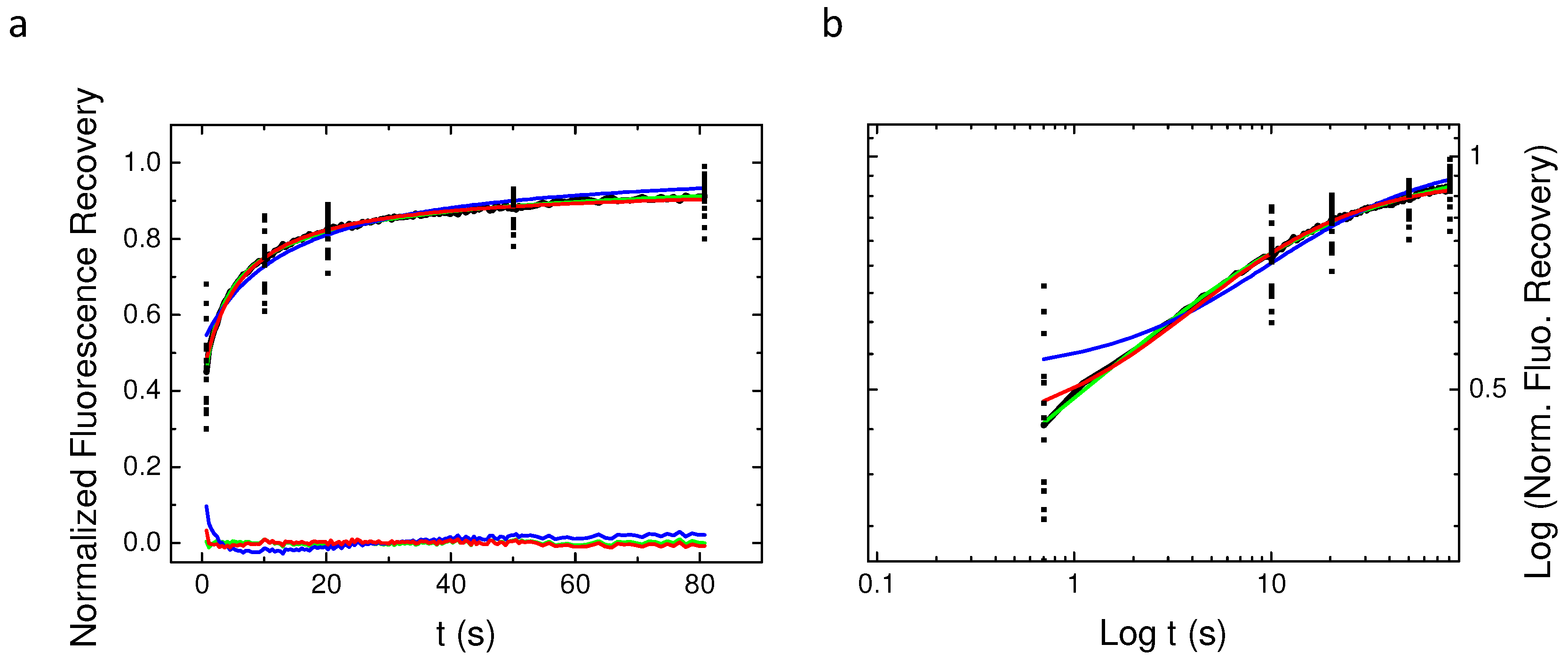
2.4. Single Spot Fluorescence Recovery After Photobleaching Does Not Allow for Identifying the Nature of PH-EFA6 Diffusion in Cells
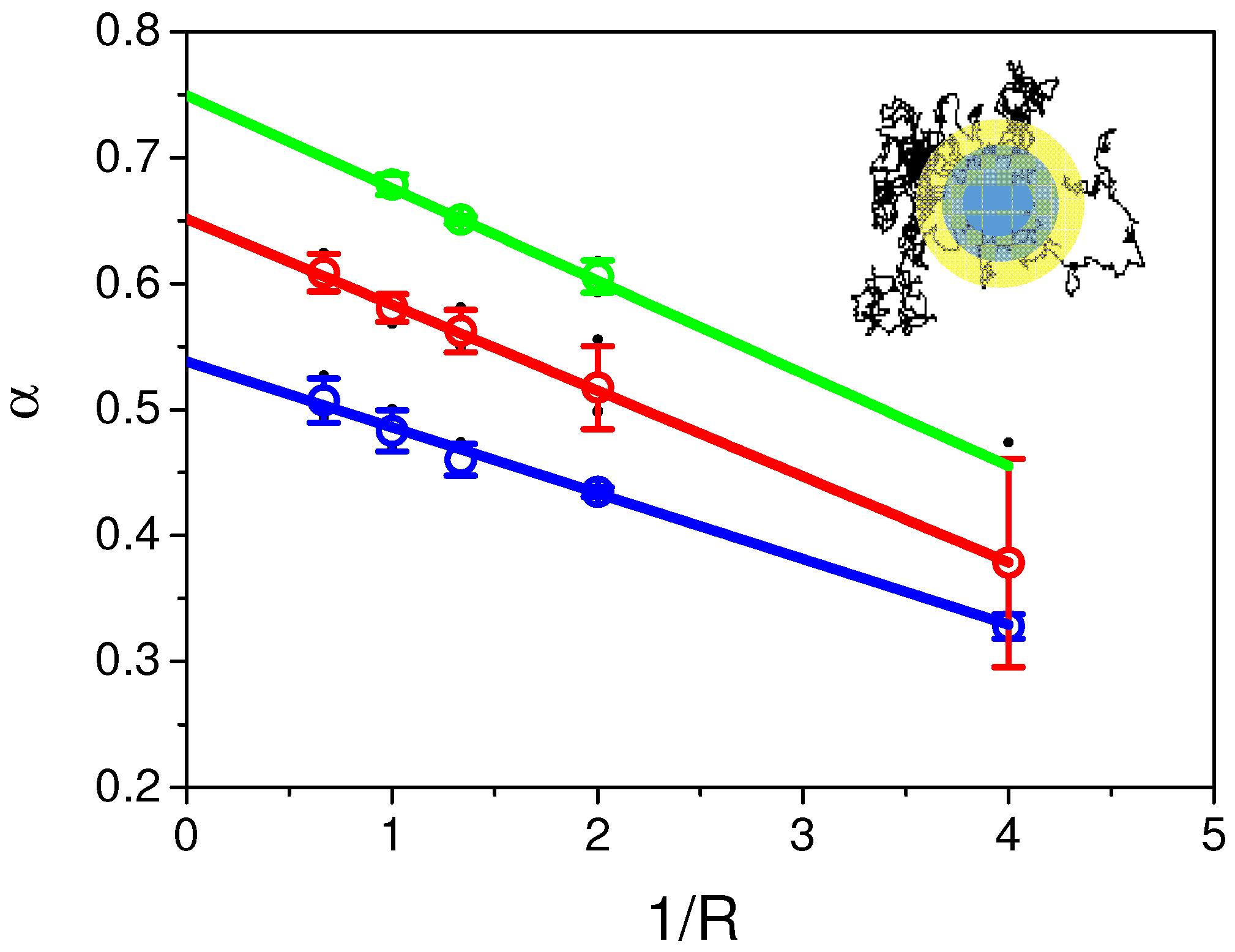
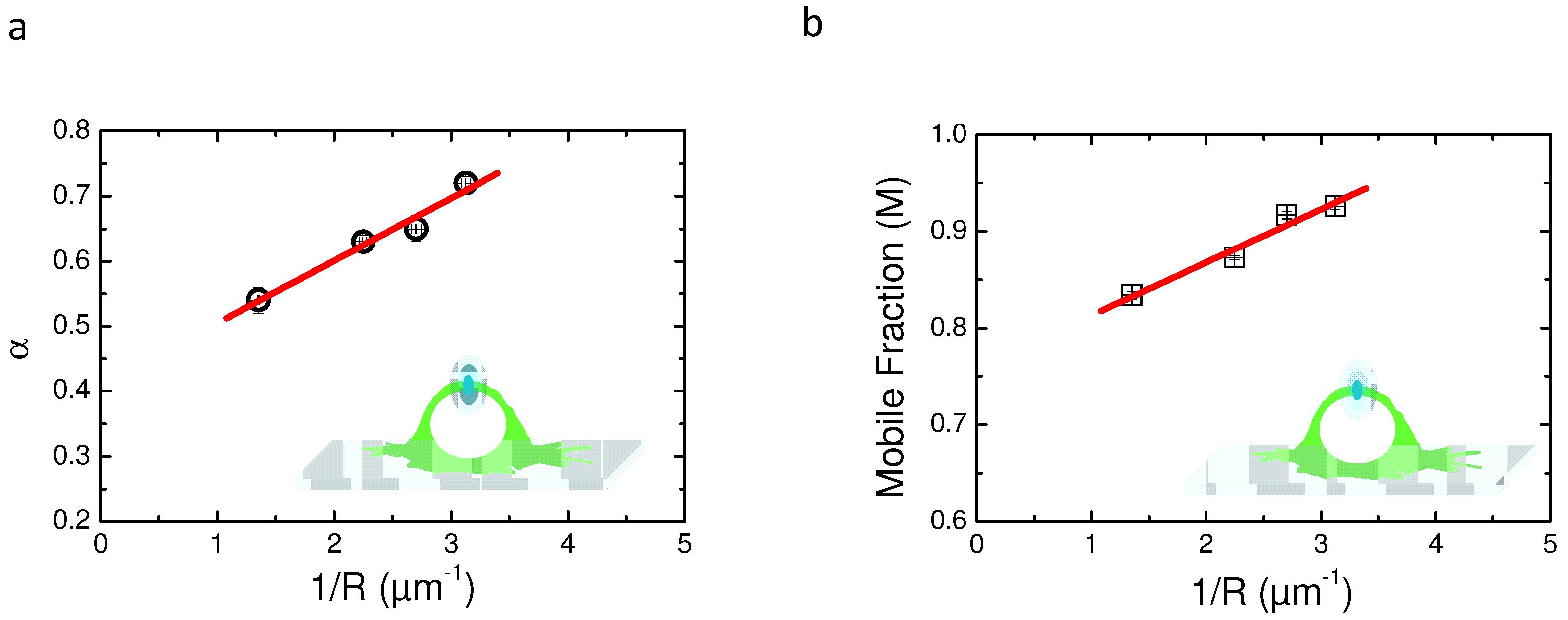
2.5. Variable Radii Fluorescence Recovery After Photobleaching Allows Correct Estimation of the Anomalous Sub-Diffusion Exponent
2.6. Continuous Time Random Walk Anomalous Subdiffusion Does Not Explain PH-EFA6 Motions in the Plasma Membrane of BHK Cells
3. Discussion
4. Materials and Methods
4.1. Monte Carlo Simulation
4.2. Cell Culture and Transfection
4.3. Fluorescence Recovery After Photobleaching Experiments
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
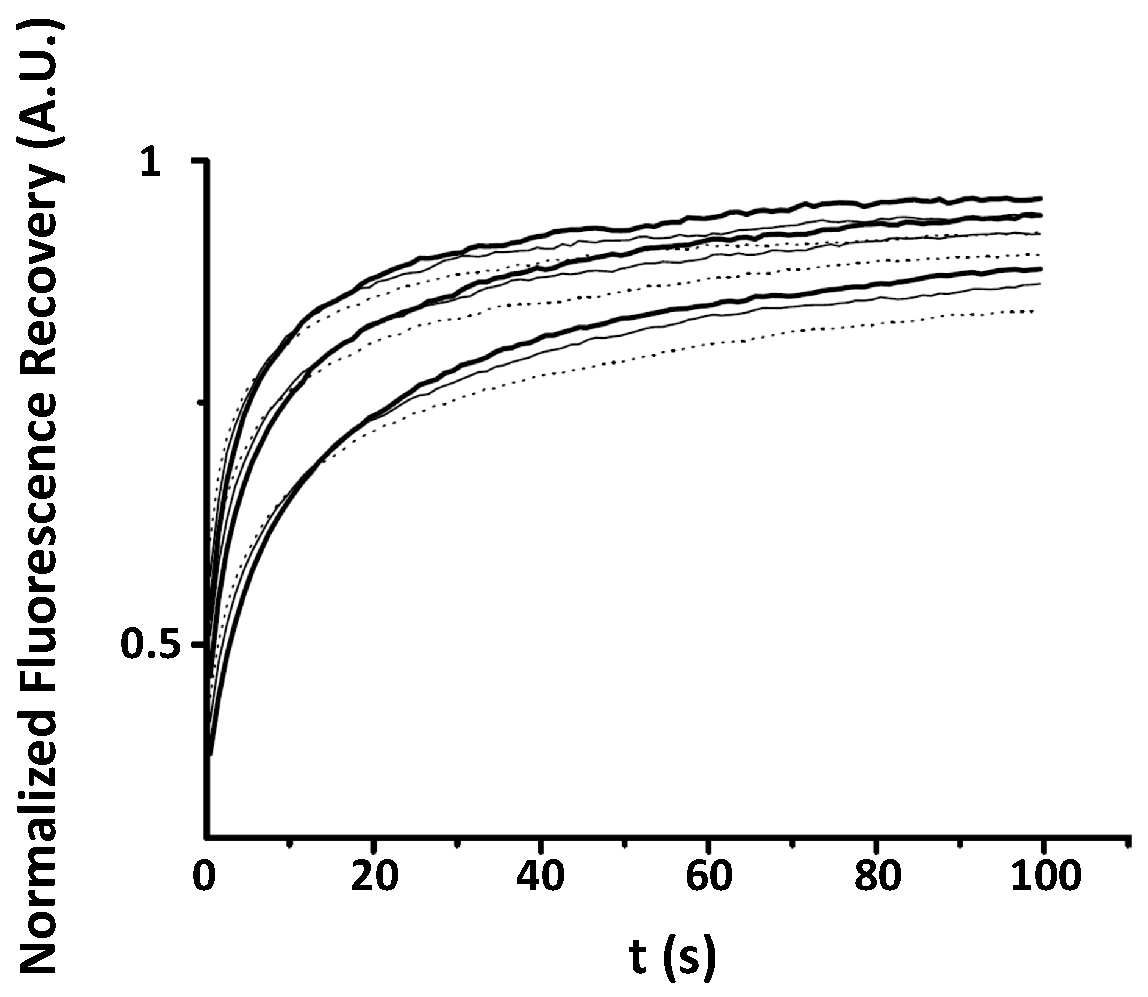
Appendix A. Examples of Numerically Generated Fluorescence Recovery Curves
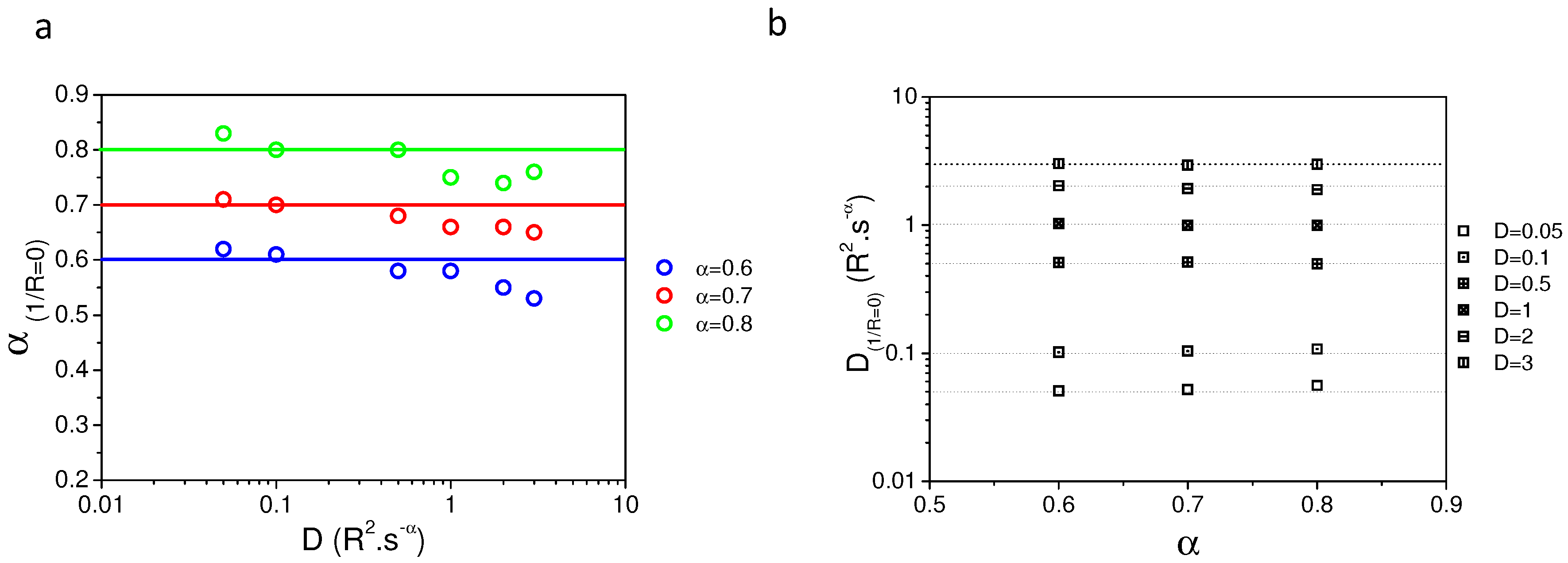
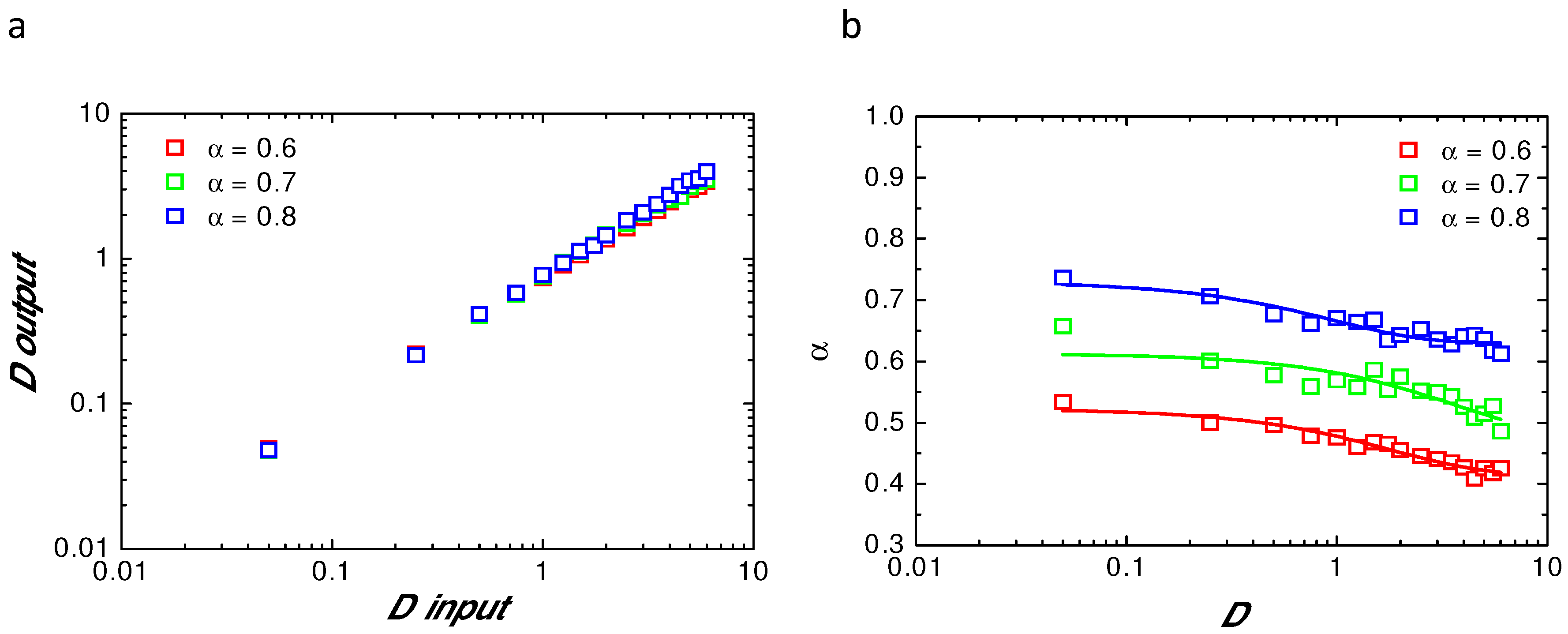
Appendix B. Comparison of Input and Fitted D and α at Variable Radii
References
- Singer, S.J.; Nicolson, G.L. The Fluid Mosaic Model of the Structure of Cell Membranes. Science 1972, 175, 720–731. [Google Scholar] [CrossRef] [PubMed]
- Favard, C.; Wenger, J.; Lenne, P.F.; Rigneault, H. FCS diffusion laws in two-phase lipid membranes: Determination of domain mean size by experiments and Monte Carlo simulations. Biophys. J. 2011, 100, 1242–1251. [Google Scholar] [CrossRef] [PubMed]
- Hac, A.E.; Seeger, H.M.; Fidorra, M.; Heimburg, T. Diffusion in two-component lipid membranes—A fluorescence correlation spectroscopy and monte carlo simulation study. Biophys. J. 2005, 88, 317–333. [Google Scholar] [CrossRef] [PubMed]
- Edidin, M.; Kuo, S.C.; Sheetz, M.P. Lateral movements of membrane glycoproteins restricted by dynamic cytoplasmic barriers. Science 1991, 254, 1379–1382. [Google Scholar] [CrossRef] [PubMed]
- Salomé, L.; Cazeils, J.L.; Lopez, A.; Tocanne, J.F. Characterization of membrane domains by frap experiments at variable observation areas. Eur. Biophys. J. 1998, 27, 391–402. [Google Scholar] [CrossRef] [PubMed]
- Yechiel, E.; Edidin, M. Micrometer-scale domains in fibroblast plasma membranes. J. Cell Biol. 1987, 105, 755–760. [Google Scholar] [CrossRef] [PubMed]
- Lingwood, D.; Simons, K. Lipid rafts as a membrane-organizing principle. Science 2010, 327, 46–50. [Google Scholar] [CrossRef] [PubMed]
- Kusumi, A.; Sako, Y.; Yamamoto, M. Confined lateral diffusion of membrane receptors as studied by single particle tracking (nanovid microscopy). Effects of calcium-induced differentiation in cultured epithelial cells. Biophys. J. 1993, 65, 2021–2040. [Google Scholar] [CrossRef]
- Sako, Y.; Kusumi, A. Compartmentalized structure of the plasma membrane for receptor movements as revealed by a nanometer-level motion analysis. J. Cell Biol. 1994, 125, 1251–1264. [Google Scholar] [CrossRef] [PubMed]
- Wawrezinieck, L.; Rigneault, H.; Marguet, D.; Lenne, P.F. Fluorescence correlation spectroscopy diffusion laws to probe the submicron cell membrane organization. Biophys. J. 2005, 89, 4029–4042. [Google Scholar] [CrossRef] [PubMed]
- Lenne, P.F.; Wawrezinieck, L.; Conchonaud, F.; Wurtz, O.; Boned, A.; Guo, X.J.; Rigneault, H.; He, H.T.; Marguet, D. Dynamic molecular confinement in the plasma membrane by microdomains and the cytoskeleton meshwork. EMBO J. 2006, 25, 3245–3256. [Google Scholar] [CrossRef] [PubMed]
- Eggeling, C.; Ringemann, C.; Medda, R.; Schwarzmann, G.; Sandhoff, K.; Polyakova, S.; Belov, V.N.; Hein, B.; von Middendorff, C.; Schönle, A.; et al. Direct observation of the nanoscale dynamics of membrane lipids in a living cell. Nature 2009, 457, 1159–1162. [Google Scholar] [CrossRef] [PubMed]
- Axelrod, D.; Koppel, D.E.; Schlessinger, J.; Elson, E.; Webb, W.W. Mobility measurement by analysis of fluorescence photobleaching recovery kinetics. Biophys. J. 1976, 16, 1055–1069. [Google Scholar] [CrossRef]
- Soumpasis, D.M. Theoretical analysis of fluorescence photobleaching recovery experiments. Biophys. J. 1983, 41, 95–97. [Google Scholar] [CrossRef]
- Feder, T.J.; Brust-Mascher, I.; Slattery, J.P.; Baird, B.; Webb, W.W. Constrained diffusion or immobile fraction on cell surfaces: A new interpretation. Biophys. J. 1996, 70, 2767–2773. [Google Scholar] [CrossRef]
- Bouchaud, J.P.; Georges, A. Anomalous diffusion in disordered media: Statistical mechanisms, models and physical applications. Phys. Rep. 1990, 195, 127–293. [Google Scholar] [CrossRef]
- Hoefling, F.; Franosch, T. Anomalous transport in the crowded world of biological cells. Rep. Prog. Phys. 2013, 76, 046602. [Google Scholar] [CrossRef] [PubMed]
- Saxton, M.J. Anomalous diffusion due to obstacles: A Monte Carlo study. Biophys. J. 1994, 66, 394–401. [Google Scholar] [CrossRef]
- Saxton, M.J. Anomalous diffusion due to binding: A Monte Carlo study. Biophys. J. 1996, 70, 1250–1262. [Google Scholar] [CrossRef]
- Saxton, M.J. Anomalous Subdiffusion in Fluorescence Photobleaching Recovery: A Monte Carlo Study. Biophys. J. 2001, 81, 2226–2240. [Google Scholar] [CrossRef]
- Hyvönen, M.; Macias, M.J.; Nilges, M.; Oschkinat, H.; Saraste, M.; Wilmanns, M. Structure of the binding site for inositol phosphates in a PH domain. EMBO J. 1995, 14, 4676–4685. [Google Scholar] [CrossRef] [PubMed]
- Franco, M.; Peters, P.J.; Boretto, J.; van Donselaar, E.; Neri, A.; D’Souza-Schorey, C.; Chavrier, P. EFA6, a sec7 domain-containing exchange factor for ARF6, coordinates membrane recycling and actin cytoskeleton organization. EMBO J. 1999, 18, 1480–1491. [Google Scholar] [CrossRef] [PubMed]
- Macia, E.; Partisani, M.; Favard, C.; Mortier, E.; Zimmermann, P.; Carlier, M.F.; Gounon, P.; Luton, F.; Franco, M. The pleckstrin homology domain of the Arf6-specific exchange factor EFA6 localizes to the plasma membrane by interacting with phosphatidylinositol 4,5-bisphosphate and F-actin. J. Biol. Chem. 2008, 283, 19836–19844. [Google Scholar] [CrossRef] [PubMed]
- Nagle, J.F. Long tail kinetics in biophysics? Biophys. J. 1992, 63, 366–370. [Google Scholar] [CrossRef]
- Schram, V.; Tocanne, J.F.; Lopez, A. Influence of obstacles on lipid lateral diffusion: computer simulation of FRAP experiments and application to proteoliposomes and biomembranes. Eur. Biophys. J. 1994, 23, 337–348. [Google Scholar] [CrossRef] [PubMed]
- Waharte, F.; Brown, C.M.; Coscoy, S.; Coudrier, E.; Amblard, F. A two-photon FRAP analysis of the cytoskeleton dynamics in the microvilli of intestinal cells. Biophys. J. 2005, 88, 1467–1478. [Google Scholar] [CrossRef] [PubMed]
- Smith, P.R.; Morrison, I.E.; Wilson, K.M.; Fernández, N.; Cherry, R.J. Anomalous diffusion of major histocompatibility complex class I molecules on HeLa cells determined by single particle tracking. Biophys. J. 1999, 76, 3331–3344. [Google Scholar] [CrossRef]
- Weigel, A.V.; Simon, B.; Tamkun, M.M.; Krapf, D. Ergodic and nonergodic processes coexist in the plasma membrane as observed by single-molecule tracking. Proc. Natl. Acad. Sci. USA 2011, 108, 6438–6443. [Google Scholar] [CrossRef] [PubMed]
- Vrljic, M.; Nishimura, S.Y.; Brasselet, S.; Moerner, W.E.; McConnell, H.M. Translational diffusion of individual class II MHC membrane proteins in cells. Biophys. J. 2002, 83, 2681–2692. [Google Scholar] [CrossRef]
- Crane, J.M.; Verkman, A.S. Long-range nonanomalous diffusion of quantum dot-labeled aquaporin-1 water channels in the cell plasma membrane. Biophys. J. 2008, 94, 702–713. [Google Scholar] [CrossRef] [PubMed]
- Baker, A.M.; Saulière, A.; Gaibelet, G.; Lagane, B.; Mazères, S.; Fourage, M.; Bachelerie, F.; Salomé, L.; Lopez, A.; Dumas, F. CD4 interacts constitutively with multiple CCR5 at the plasma membrane of living cells. A fluorescence recovery after photobleaching at variable radii approach. J. Biol. Chem. 2007, 282, 35163–35168. [Google Scholar] [CrossRef] [PubMed]
- Morone, N.; Fujiwara, T.; Murase, K.; Kasai, R.S.; Ike, H.; Yuasa, S.; Usukura, J.; Kusumi, A. Three-dimensional reconstruction of the membrane skeleton at the plasma membrane interface by electron tomography. J. Cell Biol. 2006, 174, 851–862. [Google Scholar] [CrossRef] [PubMed]
- Andrade, D.M.; Clausen, M.P.; Keller, J.; Mueller, V.; Wu, C.; Bear, J.E.; Hell, S.W.; Lagerholm, B.C.; Eggeling, C. Cortical actin networks induce spatio-temporal confinement of phospholipids in the plasma membrane—A minimally invasive investigation by STED-FCS. Sci. Rep. 2015, 5, 11454. [Google Scholar] [CrossRef] [PubMed]
- Sadegh, S.; Higgins, J.L.; Mannion, P.C.; Tamkun, M.M.; Krapf, D. Plasma Membrane is Compartmentalized by a Self-Similar Cortical Actin Meshwork. Phys. Rev. X 2017, 7, 011031. [Google Scholar] [CrossRef] [PubMed]
- Schneider, M.B.; Webb, W.W. Measurement of submicron laser beam radii. Appl. Opt. 1981, 20, 1382–1388. [Google Scholar] [CrossRef] [PubMed]
| Model | D () | M | () | ||
|---|---|---|---|---|---|
| Bm | 0.12 ± 0.06 | 1 | - | - | 5.7 ± 0.5 |
| rBm | 0.22 ± 0.01 | 0.92 ± 0.01 | - | - | 3.8 ± 1.6 |
| aDm | - | - | 0.65 ± 0.02 | 1.48 ± 0.05 | 2.9 ± 1.6 |
| Objective | R () | ΔR () | Laser Waist (nm) |
|---|---|---|---|
| 16× (NA = 1.0) | 0.74 | 0.04 | 370 |
| 40× (NA = 1.3) | 0.44 | 0.03 | 222 |
| 63× (NA = 1.4) | 0.37 | 0.01 | 185 |
| 100× (NA = 1.4) | 0.32 | 0.01 | 160 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Favard, C. Numerical Simulation and FRAP Experiments Show That the Plasma Membrane Binding Protein PH-EFA6 Does Not Exhibit Anomalous Subdiffusion in Cells. Biomolecules 2018, 8, 90. https://doi.org/10.3390/biom8030090
Favard C. Numerical Simulation and FRAP Experiments Show That the Plasma Membrane Binding Protein PH-EFA6 Does Not Exhibit Anomalous Subdiffusion in Cells. Biomolecules. 2018; 8(3):90. https://doi.org/10.3390/biom8030090
Chicago/Turabian StyleFavard, Cyril. 2018. "Numerical Simulation and FRAP Experiments Show That the Plasma Membrane Binding Protein PH-EFA6 Does Not Exhibit Anomalous Subdiffusion in Cells" Biomolecules 8, no. 3: 90. https://doi.org/10.3390/biom8030090
APA StyleFavard, C. (2018). Numerical Simulation and FRAP Experiments Show That the Plasma Membrane Binding Protein PH-EFA6 Does Not Exhibit Anomalous Subdiffusion in Cells. Biomolecules, 8(3), 90. https://doi.org/10.3390/biom8030090