Understand the Specific Regio- and Enantioselectivity of Fluostatin Conjugation in the Post-Biosynthesis
Abstract
1. Introduction
2. Computation Details
3. Results and Discussion
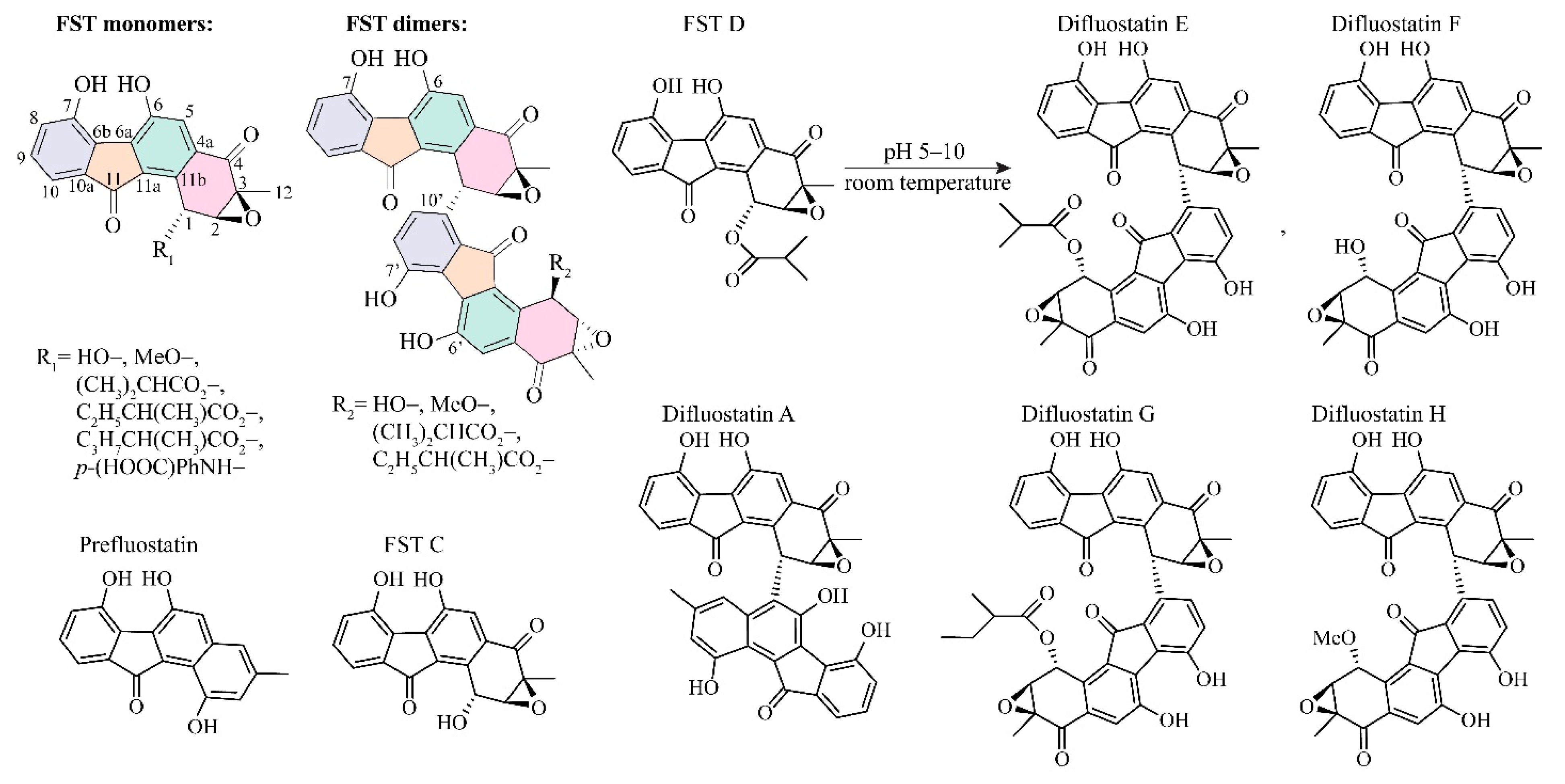
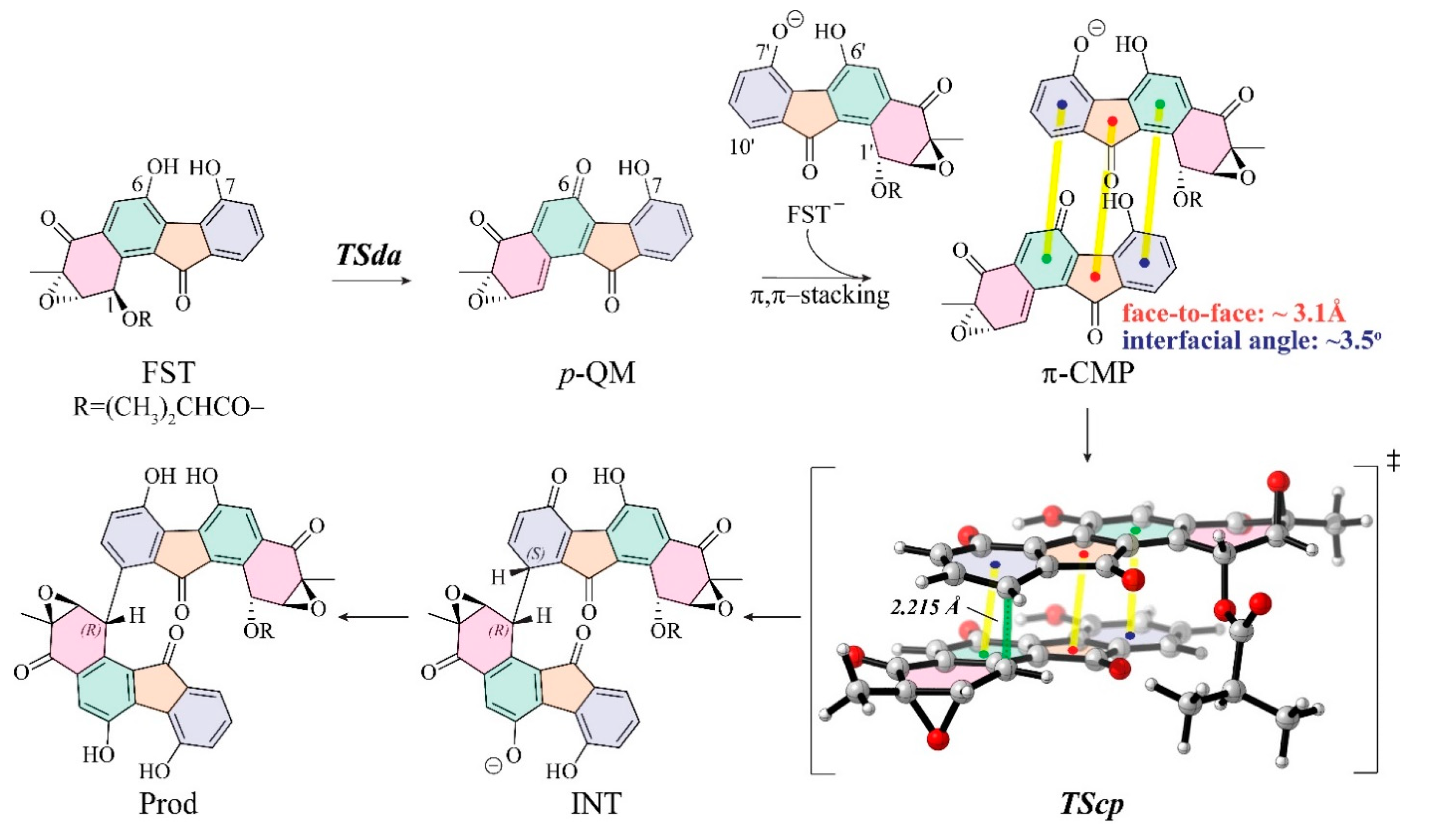
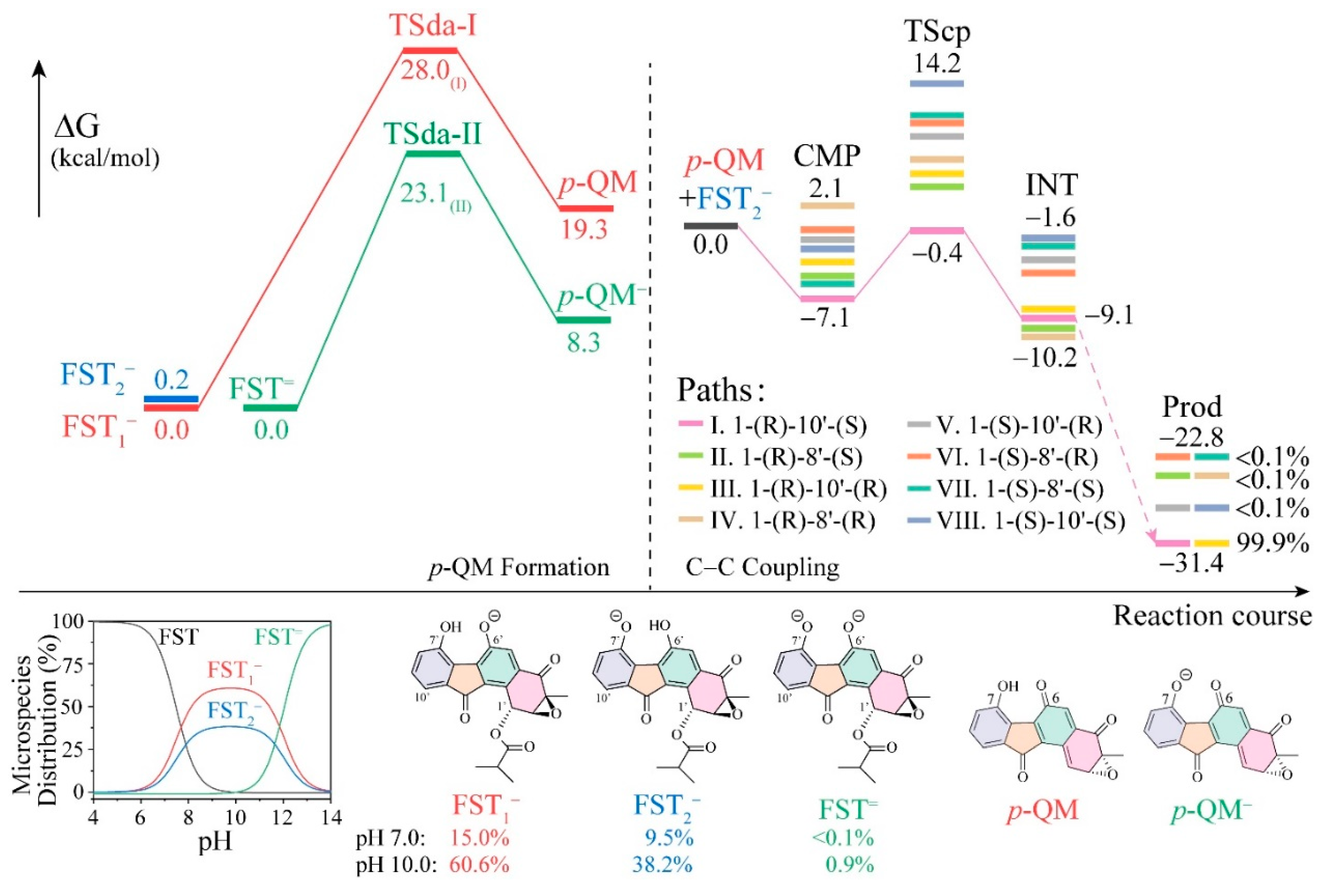
3.1. The Reaction Energy Profile of Fluostatin Dimerization
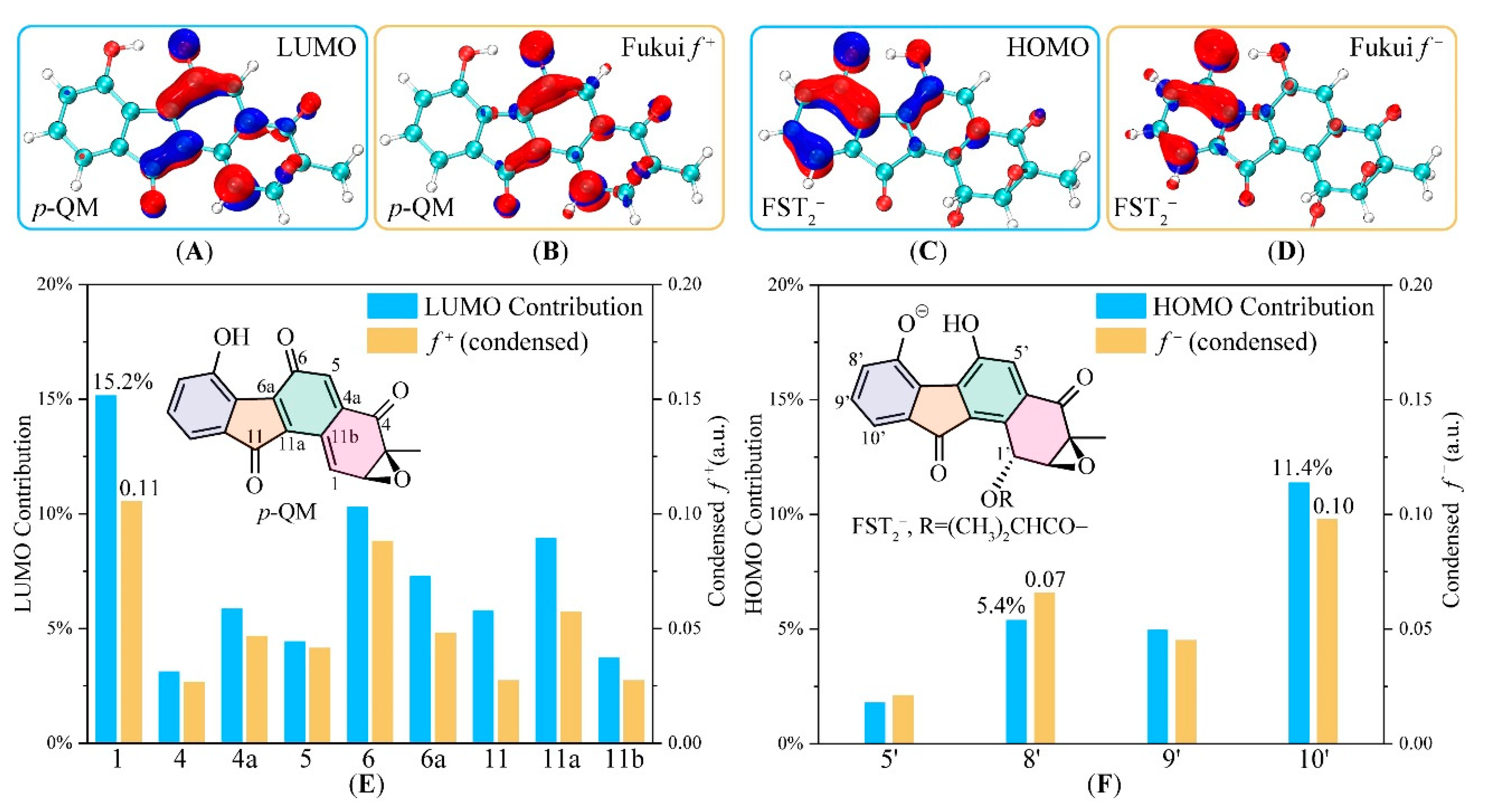
3.2. Electronic Structure Analysis for Regioselectivity of the Conjugate Addition
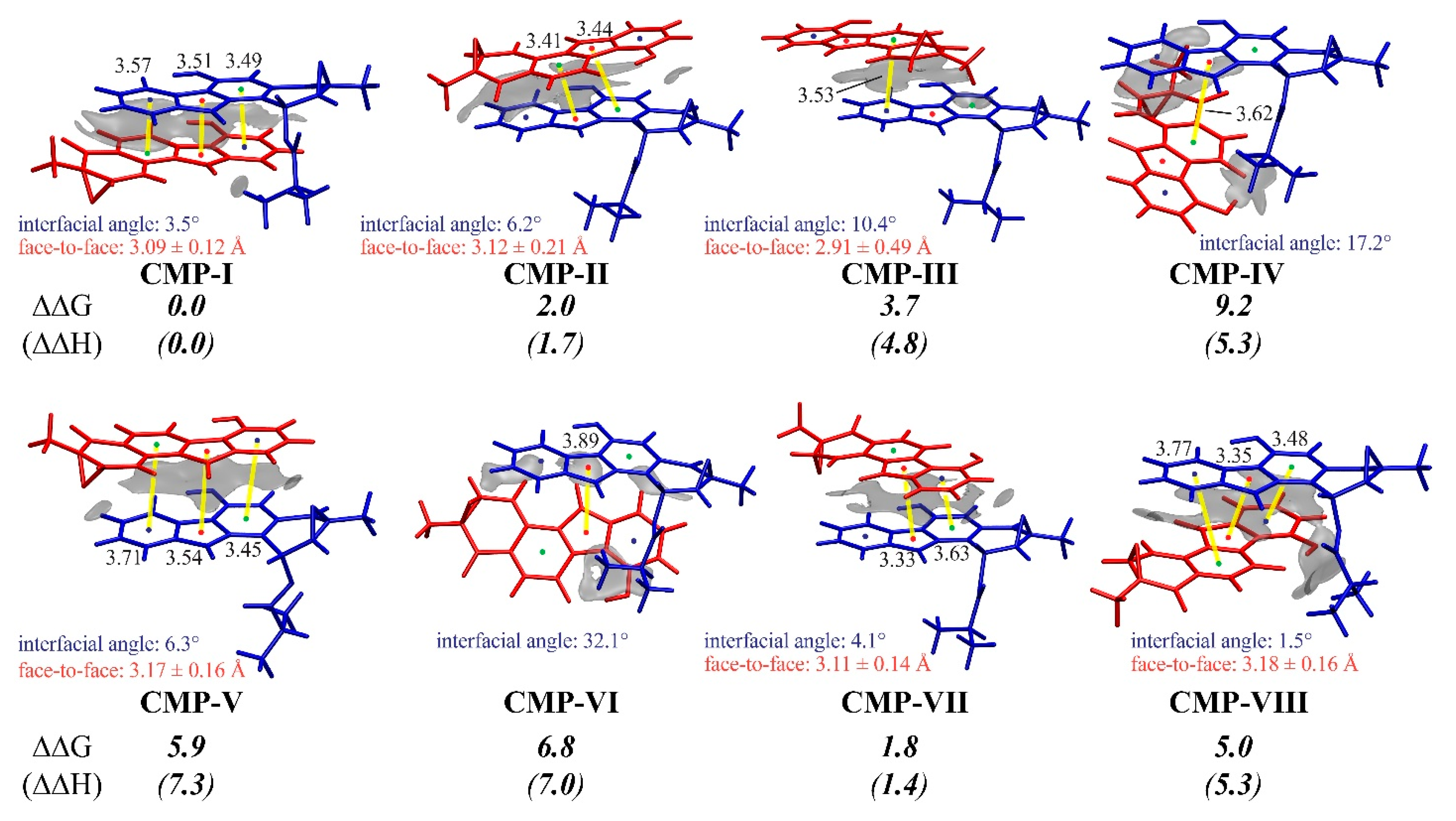
3.3. Insight into π–π Stacking’s Influence on Regio- and Stereoselectivity
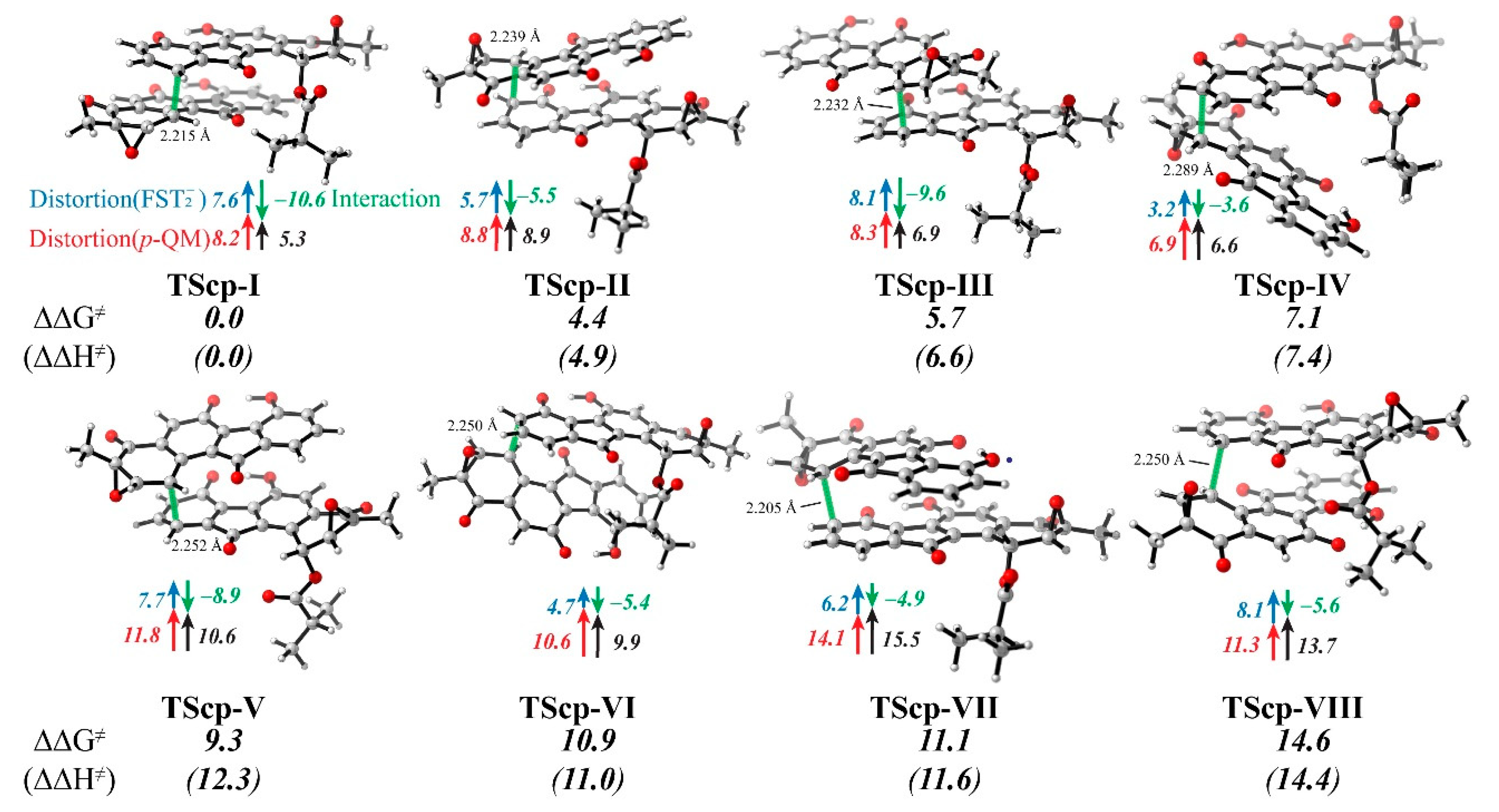
3.4. Distortion/Interaction-Activation Strain Analysis of Transition States (TScp)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Huang, C.; Yang, C.; Zhang, W.; Zhang, L.; De, B.C.; Zhu, Y.; Jiang, X.; Fang, C.; Zhang, Q.; Yuan, C.S.; et al. Molecular basis of dimer formation during the biosynthesis of benzofluorene-containing atypical angucyclines. Nat. Commun. 2018, 9, 2088. [Google Scholar] [CrossRef] [PubMed]
- Gould, S.J.; Tamayo, N.; Melville, C.R.; Cone, M.C. Revised structures for the kinamycin antibiotics: 5-diazobenzo[b]fluorenes rather than benzo[b]carbazole cyanamides. J. Am. Chem. Soc. 1994, 116, 2207–2208. [Google Scholar] [CrossRef]
- Proteau, P.J.; Li, Y.; Chen, J.; Williamson, R.T.; Gould, S.J.; Laufer, R.S.; Dmitrienko, G.I. Isoprekinamycin is a diazobenzo[a]fluorene rather than a diazobenzo[b]fluorene. J. Am. Chem. Soc. 2000, 122, 8325–8326. [Google Scholar] [CrossRef]
- Wang, B.; Guo, F.; Ren, J.; Ai, G.; Aigle, B.; Fan, K.; Yang, K. Identification of Alp1U and Lom6 as epoxy hydrolases and implications for kinamycin and lomaiviticin biosynthesis. Nat. Commun. 2015, 6, 7674. [Google Scholar] [CrossRef]
- He, H.; Ding, W.-D.; Bernan, V.S.; Richardson, A.D.; Ireland, C.M.; Greenstein, M.; Ellestad, G.A.; Carter, G.T. Lomaiviticins A and B, Potent Antitumor Antibiotics from Micromonospora lomaivitiensis. J. Am. Chem. Soc. 2001, 123, 5362–5363. [Google Scholar] [CrossRef]
- Woo, C.M.; Beizer, N.E.; Janso, J.E.; Herzon, S.B. Isolation of lomaiviticins C–E, transformation of lomaiviticin C to lomaiviticin A, complete structure elucidation of lomaiviticin A, and structure–activity analyses. J. Am. Chem. Soc. 2012, 134, 15285–15288. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, Q.; Zhu, Y.; Nie, F.; Wu, Z.; Yang, C.; Zhang, L.; Tian, X.; Zhang, C. Isolation, structure elucidation and biosynthesis of benzo[b]fluorene nenestatin A from deep-sea derived Micromonospora echinospora SCSIO 04089. Tetrahedron 2017, 73, 3585–3590. [Google Scholar] [CrossRef]
- Baur, S.; Niehaus, J.; Karagouni, A.D.; Katsifas, E.A.; Chalkou, K.; Meintanis, C.; Jones, A.L.; Goodfellow, M.; Ward, A.C.; Beil, W. Fluostatins C∼E, Novel Members of the Fluostatin Family Produced by Streptomyces Strain Acta 1383. J. Antibiot. 2006, 59, 293–297. [Google Scholar] [CrossRef][Green Version]
- Akiyama, T.; Harada, S.; Kojima, F.; Takahashi, Y.; Imada, C.; Okami, Y.; Muraoka, Y.; Aoyagi, T.; Takeuchi, T. Fluostatins A and B, New Inhibitors of Dipeptidyl Peptidase III, Produced by Streptomyces sp. TA-3391. J. Antibiot. 1998, 51, 553–559. [Google Scholar] [CrossRef]
- Feng, Z.; Kim, J.H.; Brady, S.F. Fluostatins Produced by the Heterologous Expression of a TAR Reassembled Environmental DNA Derived Type II PKS Gene Cluster. J. Am. Chem. Soc. 2010, 132, 11902–11903. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, Z.; Li, S.; Lu, Y.; Chen, Y.; Zhang, H.; Zhang, G.; Zhu, Y.; Zhang, G.; Zhang, W.; et al. Fluostatins I–K from the South China Sea-Derived Micromonospora rosaria SCSIO N160. J. Nat. Prod. 2012, 75, 1937–1943. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Huang, C.; Zhang, W.; Zhu, Y.; Zhang, C. Heterologous Expression of Fluostatin Gene Cluster Leads to a Bioactive Heterodimer. Org. Lett. 2015, 17, 5324–5327. [Google Scholar] [CrossRef] [PubMed]
- Jin, J.; Yang, X.; Liu, T.; Xiao, H.; Wang, G.; Zhou, M.; Liu, F.; Zhang, Y.; Liu, D.; Chen, M.; et al. Fluostatins M–Q Featuring a 6-5-6-6 Ring Skeleton and High Oxidized A-Rings from Marine Streptomyces sp. PKU-MA00045. Mar. Drugs 2018, 16, 87. [Google Scholar] [CrossRef] [PubMed]
- Shee, P.K.; Ratnayake, N.D.; Walter, T.; Goethe, O.; Onyeozili, E.N.; Walker, K.D. Exploring the Scope of an α/β-Aminomutase for the Amination of Cinnamate Epoxides to Arylserines and Arylisoserines. ACS Catal. 2019, 9, 7418–7430. [Google Scholar] [CrossRef]
- Desmons, S.; Fauré, R.; Bontemps, S. Formaldehyde as a Promising C1 Source: The Instrumental Role of Biocatalysis for Stereocontrolled Reactions. ACS Catal. 2019, 9, 9575–9588. [Google Scholar] [CrossRef]
- Müller, M. Recent Developments in Enzymatic Asymmetric C–C Bond Formation. Adv. Synth. Catal. 2012, 354, 3161–3174. [Google Scholar] [CrossRef]
- Voigt, B.; Scheffler, U.; Mahrwald, R. Stereoselective amine-catalyzed carbohydrate chain elongation. Chem. Commun. 2012, 48, 5304–5306. [Google Scholar] [CrossRef]
- Luo, Y.; Li, B.-Z.; Liu, D.; Zhang, L.; Chen, Y.; Jia, B.; Zeng, B.-X.; Zhao, H.; Yuan, Y.-J. Engineered biosynthesis of natural products in heterologous hosts. Chem. Soc. Rev. 2015, 44, 5265–5290. [Google Scholar] [CrossRef]
- Siegel, J.B.; Zanghellini, A.; Lovick, H.M.; Kiss, G.; Lambert, A.R.; St.Clair, J.L.; Gallaher, J.L.; Hilvert, D.; Gelb, M.H.; Stoddard, B.L.; et al. Computational Design of an Enzyme Catalyst for a Stereoselective Bimolecular Diels-Alder Reaction. Science 2010, 329, 309–313. [Google Scholar] [CrossRef]
- Zhang, Z.; Jamieson, C.S.; Zhao, Y.-L.; Li, D.; Ohashi, M.; Houk, K.N.; Tang, Y. Enzyme-Catalyzed Inverse-Electron Demand Diels–Alder Reaction in the Biosynthesis of Antifungal Ilicicolin H. J. Am. Chem. Soc. 2019, 141, 5659–5663. [Google Scholar] [CrossRef]
- Ghattas, W.; Dubosclard, V.; Tachon, S.; Beaumet, M.; Guillot, R.; Réglier, M.; Simaan, A.J.; Mahy, J.-P. CuII-Containing 1-Aminocyclopropane Carboxylic Acid Oxidase Is an Efficient Stereospecific Diels–Alderase. Angew. Chem. Int. Ed. 2019, 58, 14605–14609. [Google Scholar] [CrossRef] [PubMed]
- Dan, Q.; Newmister, S.A.; Klas, K.R.; Fraley, A.E.; McAfoos, T.J.; Somoza, A.D.; Sunderhaus, J.D.; Ye, Y.; Shende, V.V.; Yu, F.; et al. Fungal indole alkaloid biogenesis through evolution of a bifunctional reductase/Diels–Alderase. Nat. Chem. 2019, 11, 972–980. [Google Scholar] [CrossRef] [PubMed]
- Little, R.; Paiva, F.C.R.; Jenkins, R.; Hong, H.; Sun, Y.; Demydchuk, Y.; Samborskyy, M.; Tosin, M.; Leeper, F.J.; Dias, M.V.B.; et al. Unexpected enzyme-catalysed [4+2] cycloaddition and rearrangement in polyether antibiotic biosynthesis. Nat. Catal. 2019, 2, 1045–1054. [Google Scholar] [CrossRef]
- Gal, J.; Cintas, P. Early History of the Recognition of Molecular Biochirality. In Biochirality: Origins, Evolution and Molecular Recognition; Cintas, P., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–40. ISBN 978-3-642-37626-9. [Google Scholar]
- Okamoto, S.; Taguchi, T.; Ochi, K.; Ichinose, K. Biosynthesis of Actinorhodin and Related Antibiotics: Discovery of Alternative Routes for Quinone Formation Encoded in the act Gene Cluster. Chem. Biol. 2009, 16, 226–236. [Google Scholar] [CrossRef]
- Taguchi, T.; Ebihara, T.; Furukawa, A.; Hidaka, Y.; Ariga, R.; Okamoto, S.; Ichinose, K. Identification of the actinorhodin monomer and its related compound from a deletion mutant of the actVA-ORF4 gene of Streptomyces coelicolor A3(2). Bioorg. Med. Chem. Lett. 2012, 22, 5041–5045. [Google Scholar] [CrossRef]
- Wheeler, S.E.; Houk, K.N. Substituent effects in the benzene dimer are due to direct interactions of the substituents with the unsubstituted Benzene. J. Am. Chem. Soc. 2008, 130, 10854–10855. [Google Scholar] [CrossRef]
- Catak, S.; D’hooghe, M.; De Kimpe, N.; Waroquier, M.; Van Speybroeck, V. Intramolecular π−π stacking interactions in 2-substituted N,N-dibenzylaziridinium ions and their regioselectivity in nucleophilic ring-opening reactions. J. Org. Chem. 2010, 75, 885–896. [Google Scholar] [CrossRef]
- Sarotti, A.M.; Fernández, I.; Spanevello, R.A.; Sierra, M.Á.; Suárez, A.G. π-Stacking effect on levoglucosenone derived internal chiral auxiliaries. A case of complete enantioselectivity inversion on the Diels−Alder reaction. Org. Lett. 2008, 10, 3389–3392. [Google Scholar] [CrossRef]
- Huffman, B.J.; Chen, S.; Schwarz, J.L.; Plata, R.E.; Chin, E.N.; Lairson, L.L.; Houk, K.N.; Shenvi, R.A. Electronic complementarity permits hindered butenolide heterodimerization and discovery of novel cGAS/STING pathway antagonists. Nat. Chem. 2020, 12, 310–317. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Accounts 2008, 120, 215–241. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian09 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Maeda, S.; Harabuchi, Y.; Ono, Y.; Taketsugu, T.; Morokuma, K. Intrinsic reaction coordinate: Calculation, bifurcation, and automated search. Int. J. Quantum Chem. 2015, 115, 258–269. [Google Scholar] [CrossRef]
- Tian, L.; Feiwu, C. Calculation of molecular orbital composition. Acta Chim. Sinica 2011, 69, 2393–2406. [Google Scholar]
- Tsuneda, T. Chemical reaction analyses based on orbitals and orbital energies. Int. J. Quantum Chem. 2015, 115, 270–282. [Google Scholar] [CrossRef]
- Domingo, L.R. A new C–C bond formation model based on the quantum chemical topology of electron density. RSC Adv. 2014, 4, 32415–32428. [Google Scholar] [CrossRef]
- Parr, R.G.; Yang, W. Density functional approach to the frontier-electron theory of chemical reactivity. J. Am. Chem. Soc. 1984, 106, 4049–4050. [Google Scholar] [CrossRef]
- Fukui, K.; Yonezawa, T.; Shingu, H. A molecular orbital theory of reactivity in aromatic hydrocarbons. J. Chem. Phys. 1952, 20, 722–725. [Google Scholar] [CrossRef]
- Bultinck, P.; Fias, S.; Van Alsenoy, C.; Ayers, P.W.; Carbó-Dorca, R. Critical thoughts on computing atom condensed Fukui functions. J. Chem. Phys. 2007, 127, 034102. [Google Scholar] [CrossRef]
- Geerlings, P.; Fias, S.; Boisdenghien, Z.; De Proft, F. Conceptual DFT: Chemistry from the linear response function. Chem. Soc. Rev. 2014, 43, 4989–5008. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Hirshfeld, F.L. Bonded-atom fragments for describing molecular charge densities. Theor. Chem. Accounts 1977, 44, 129–138. [Google Scholar] [CrossRef]
- Heidar-Zadeh, F.; Ayers, P.W.; Verstraelen, T.; Vinogradov, I.; Vöhringer-Martinez, E.; Bultinck, P. Information-Theoretic Approaches to Atoms-in-Molecules: Hirshfeld Family of Partitioning Schemes. J. Phys. Chem. A 2018, 122, 4219–4245. [Google Scholar] [CrossRef] [PubMed]
- Macchi, P. Modern charge density studies: The entanglement of experiment and theory. Crystallogr. Rev. 2013, 19, 58–101. [Google Scholar] [CrossRef]
- Bickelhaupt, F.M.; Houk, K.N. Analyzing reaction rates with the distortion/interaction-activation strain model. Angew. Chem. Int. Ed. 2017, 56, 10070–10086. [Google Scholar] [CrossRef] [PubMed]
- Ess, D.H.; Houk, K.N. Theory of 1,3-Dipolar Cycloadditions: Distortion/Interaction and Frontier Molecular Orbital Models. J. Am. Chem. Soc. 2008, 130, 10187–10198. [Google Scholar] [CrossRef] [PubMed]
- Lefebvre, C.; Rubez, G.; Khartabil, H.; Boisson, J.-C.; Contreras-García, J.; Hénon, E. Accurately extracting the signature of intermolecular interactions present in the NCI plot of the reduced density gradient versus electron density. Phys. Chem. Chem. Phys. 2017, 19, 17928–17936. [Google Scholar] [CrossRef] [PubMed]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- van Duijneveldt, F.B.; van Duijneveldt-van de Rijdt, J.G.C.M.; van Lenthe, J.H. State of the Art in Counterpoise Theory. Chem. Rev. 1994, 94, 1873–1885. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD–Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Bukharov, S.V.; Syakaev, V.V.; Pod’’yachev, S.N.; Nugumanova, G.N.; Mukmeneva, N.A. Solvolysis of 3,5-di-tert-butyl-4-hydroxybenzyl acetate in alcohol solutions. Russ. J. Gen. Chem. 2002, 72, 924–927. [Google Scholar] [CrossRef]
- Wang, Z.; Wong, Y.F.; Sun, J. Catalytic asymmetric 1,6-conjugate addition of para-quinone methides: Formation of all-Carbon quaternary stereocenters. Angew. Chem. Int. Ed. 2015, 54, 13711–13714. [Google Scholar] [CrossRef]
- Csizmadia, F.; Tsantili-Kakoulidou, A.; Panderi, I.; Darvas, F. Prediction of distribution coefficient from structure. 1. Estimation method. J. Pharm. Sci. 1997, 86, 865–871. [Google Scholar] [CrossRef]
- Marvin Software; ChemAxon, VAT: HU12333369, Hungary, 2019. Available online: http://chemaxon.com (accessed on 9 May 2019).
- Online pKa Prediction Platform, Beijing, China, 2019. Available online: http://pka.luo-group.com (accessed on 12 March 2020).
- Internet Bond-Energy Databank (pKa and BDE), Beijing, China, 2019. Available online: http://ibond.chem.tsinghua.edu.cn (accessed on 12 March 2020).
- Romero, R.; Salgado, P.R.; Soto, C.; Contreras, D.; Melin, V. An Experimental Validated Computational Method for pKa Determination of Substituted 1,2-Dihydroxybenzenes. Front. Chem. 2018, 6, 208. [Google Scholar] [CrossRef] [PubMed]
- Dufrasne, F.; Gelbcke, M.; Neve, J.; Kiss, R.; Kraus, J.-L. Quinone Methides and their Prodrugs: A Subtle Equilibrium Between Cancer Promotion, Prevention, and Cure. Curr. Med. Chem. 2011, 18, 3995–4011. [Google Scholar] [CrossRef] [PubMed]
- Thompson, D.C.; Thompson, J.A.; Sugumaran, M.; Moldéus, P. Biological and toxicological consequences of quinone methide formation. Chem.-Biol. Interact. 1993, 86, 129–162. [Google Scholar] [CrossRef]
- Qi, Y.-B.; Wang, X.-L.; Shi, T.; Liu, S.; Xu, Z.-H.; Li, X.; Shi, X.; Xu, P.; Zhao, Y.-L. Multicomponent kinetic analysis and theoretical studies on the phenolic intermediates in the oxidation of eugenol and isoeugenol catalyzed by laccase. Phys. Chem. Chem. Phys. 2015, 17, 29597–29607. [Google Scholar] [CrossRef]
- Caruana, L.; Fochi, M.; Bernardi, L. The Emergence of Quinone Methides in Asymmetric Organocatalysis. Molecules 2015, 20, 11733–11764. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, K.; Cao, W.; Liu, X.; Feng, X. Diastereo- and Enantioselective 1,6-Conjugate Addition of 2-Azaarylacetamides to para-Quinone Methides. Org. Lett. 2019, 21, 6063–6067. [Google Scholar] [CrossRef]
- Fukui, K. Role of Frontier Orbitals in Chemical Reactions. Science 1982, 218, 747–754. [Google Scholar] [CrossRef]
- Hirao, H.; Ohwada, T. Theoretical Study of Reactivities in Electrophilic Aromatic Substitution Reactions: Reactive Hybrid Orbital Analysis. J. Phys. Chem. A 2003, 107, 2875–2881. [Google Scholar] [CrossRef]
- La Porta, F.A.; Ramalho, T.C.; Santiago, R.T.; Rocha, M.V.J.; da Cunha, E.F.F. Orbital Signatures as a Descriptor of Regioselectivity and Chemical Reactivity: The Role of the Frontier Orbitals on 1,3-Dipolar Cycloadditions. J. Phys. Chem. A 2011. [Google Scholar] [CrossRef]
- Rong, F.; Tian, L.; Fei-Wu, C. Comparing Methods for Predicting the Reactive Site of Electrophilic Substitution. Acta Phys.-Chim. Sin. 2014, 30, 628–639. [Google Scholar]
- Townsend, P.A.; Grayson, M.N. Density Functional Theory Transition-State Modeling for the Prediction of Ames Mutagenicity in 1,4 Michael Acceptors. J. Chem. Inf. Model. 2019, 59, 5099–5103. [Google Scholar] [CrossRef] [PubMed]
- Oláh, J.; Van Alsenoy, C.; Sannigrahi, A.B. Condensed Fukui Functions Derived from Stockholder Charges: Assessment of Their Performance as Local Reactivity Descriptors. J. Phys. Chem. A 2002, 106, 3885–3890. [Google Scholar] [CrossRef]
- Rai, V.; Namboothiri, I.N.N. A Theoretical Evaluation of the Michael-Acceptor Ability of Conjugated Nitroalkenes. Eur. J. Org. Chem. 2006, 2006, 4693–4703. [Google Scholar] [CrossRef]
- Ponce-Vargas, M.; Lefebvre, C.; Boission, J.-C.; Henon, E. Atomic decomposition scheme of noncovalent interaction applied to host-guest assemblies. J. Chem. Inf. Model. 2020, 60, 268–278. [Google Scholar] [CrossRef] [PubMed]
- Šponer, J.; Gabb, H.A.; Leszczynski, J.; Hobza, P. Base-base and deoxyribose-base stacking interactions in B-DNA and Z-DNA: A quantum-chemical study. Biophys. J. 1997, 73, 76–87. [Google Scholar] [CrossRef]
- Šponer, J.; Jurečka, P.; Marchan, I.; Luque, F.J.; Orozco, M.; Hobza, P. Nature of Base Stacking: Reference Quantum-Chemical Stacking Energies in Ten Unique B-DNA Base-Pair Steps. Chem. Eur. J. 2006, 12, 2854–2865. [Google Scholar] [CrossRef]
- Šponer, J.; Leszczyński, J.; Hobza, P. Nature of Nucleic Acid−Base Stacking: Nonempirical ab Initio and Empirical Potential Characterization of 10 Stacked Base Dimers. Comparison of Stacked and H-Bonded Base Pairs. J. Phys. Chem. 1996, 100, 5590–5596. [Google Scholar] [CrossRef]
- De Andres, P.L.; Ramírez, R.; Vergés, J.A. Strong covalent bonding between two graphene layers. Phys. Rev. B 2008, 77, 045403. [Google Scholar] [CrossRef]
- Antony, J.; Grimme, S. Structures and interaction energies of stacked graphene–nucleobase complexes. Phys. Chem. Chem. Phys. 2008, 10, 2722–2729. [Google Scholar] [CrossRef]
- Feng, C.; Lin, C.S.; Fan, W.; Zhang, R.Q.; Van Hove, M.A. Stacking of polycyclic aromatic hydrocarbons as prototype for graphene multilayers, studied using density functional theory augmented with a dispersion term. J. Chem. Phys. 2009, 131, 194702. [Google Scholar] [CrossRef] [PubMed]
- Butz, B.; Dolle, C.; Niekiel, F.; Weber, K.; Waldmann, D.; Weber, H.B.; Meyer, B.; Spiecker, E. Dislocations in bilayer graphene. Nature 2014, 505, 533–537. [Google Scholar] [CrossRef] [PubMed]
- Bootsma, A.N.; Doney, A.C.; Wheeler, S.E. Predicting the Strength of Stacking Interactions between Heterocycles and Aromatic Amino Acid Side Chains. J. Am. Chem. Soc. 2019, 141, 11027–11035. [Google Scholar] [CrossRef] [PubMed]
- Martinez, C.R.; Iverson, B.L. Rethinking the term “pi-stacking”. Chem. Sci. 2012, 3, 2191–2201. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhang, C.; Zhao, Y.-L.; Zhao, R.; Houk, K.N. Understand the Specific Regio- and Enantioselectivity of Fluostatin Conjugation in the Post-Biosynthesis. Biomolecules 2020, 10, 815. https://doi.org/10.3390/biom10060815
Wang Y, Zhang C, Zhao Y-L, Zhao R, Houk KN. Understand the Specific Regio- and Enantioselectivity of Fluostatin Conjugation in the Post-Biosynthesis. Biomolecules. 2020; 10(6):815. https://doi.org/10.3390/biom10060815
Chicago/Turabian StyleWang, Yuanqi, Changsheng Zhang, Yi-Lei Zhao, Rosalinda Zhao, and Kendall N. Houk. 2020. "Understand the Specific Regio- and Enantioselectivity of Fluostatin Conjugation in the Post-Biosynthesis" Biomolecules 10, no. 6: 815. https://doi.org/10.3390/biom10060815
APA StyleWang, Y., Zhang, C., Zhao, Y.-L., Zhao, R., & Houk, K. N. (2020). Understand the Specific Regio- and Enantioselectivity of Fluostatin Conjugation in the Post-Biosynthesis. Biomolecules, 10(6), 815. https://doi.org/10.3390/biom10060815





