A Comparison between Several Response Surface Methodology Designs and a Neural Network Model to Optimise the Oxidation Conditions of a Lignocellulosic Blend
Abstract
1. Introduction
2. Materials and Methods
2.1. Samples
2.2. Empirical Models: Factorial Design and the Desirability Function
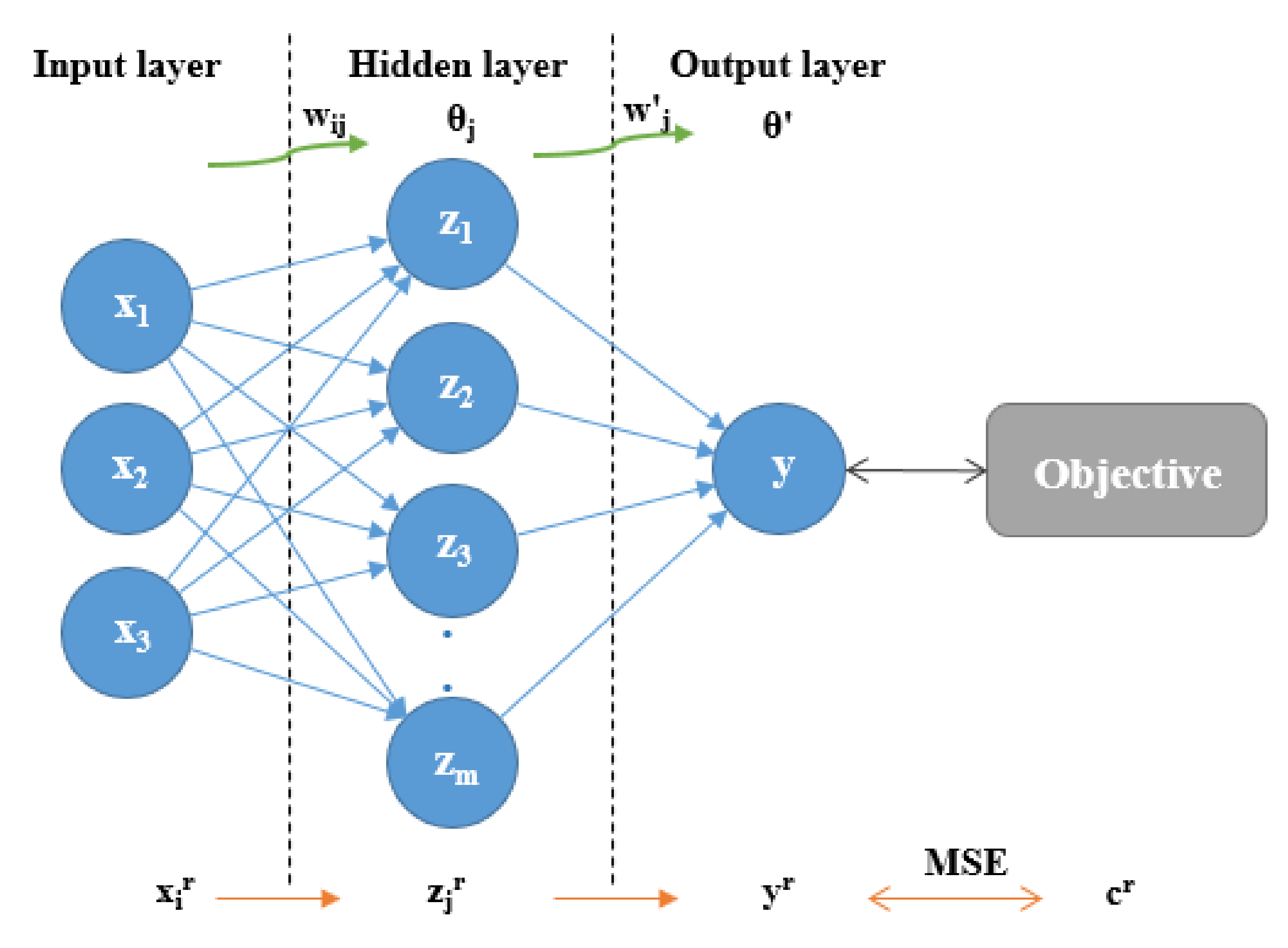
2.3. Artificial Intelligence Model: the Artificial Neural Network
2.3.1. Fundamentals
- The input variables, xj, and their synaptic weights wij, (j = 1, …, n).
- A propagation rule, hi, which is based on the input variables and their synaptic weights. This can be expressed by an additional parameter, θi, also called the bias. If we let the i and j indices begin at zero, and set wi0 = θi and x0 = −1, the propagation rule can be expressed as
- An activation function, pi, which represents the output of a neuron and its activation state at the same time. The activation function can be obtained as
2.3.2. Training and Validation Data Sets
2.4. Data Collection
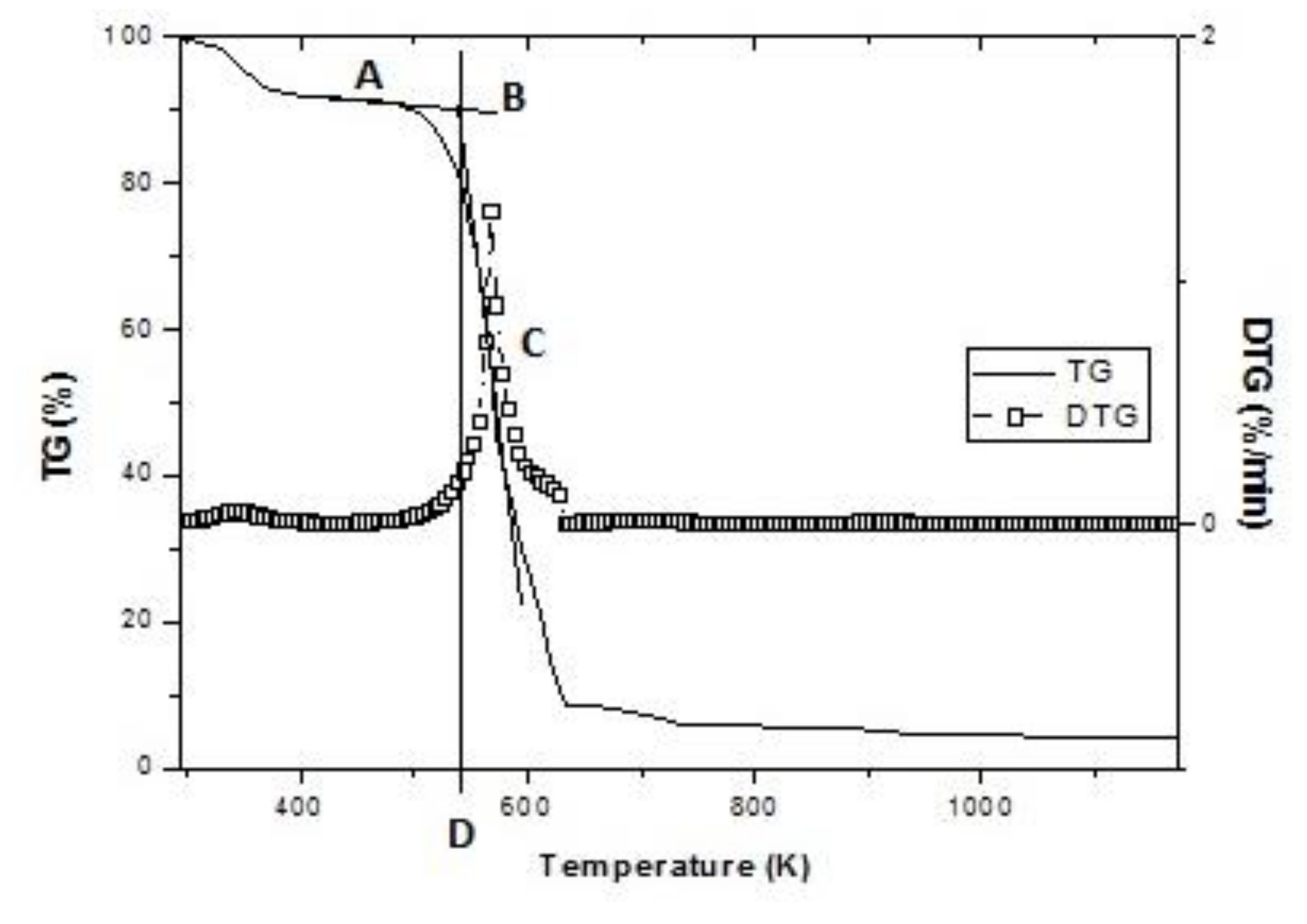
2.5. Determination of the Oxy-Combustion Indexes
2.5.1. Ignition Temperature (Te)
2.5.2. Burnout Index (Df)
3. Results and Discussion
3.1. General Comments and Section Organisation
- The RSM results (Section 3.2, Section 3.3, Section 3.4, Section 3.5, Section 3.6), which were used to understand the effect of each factor and the effect of the interactions of the factors on each response. These results include the mathematical model obtained for each RSM applied.
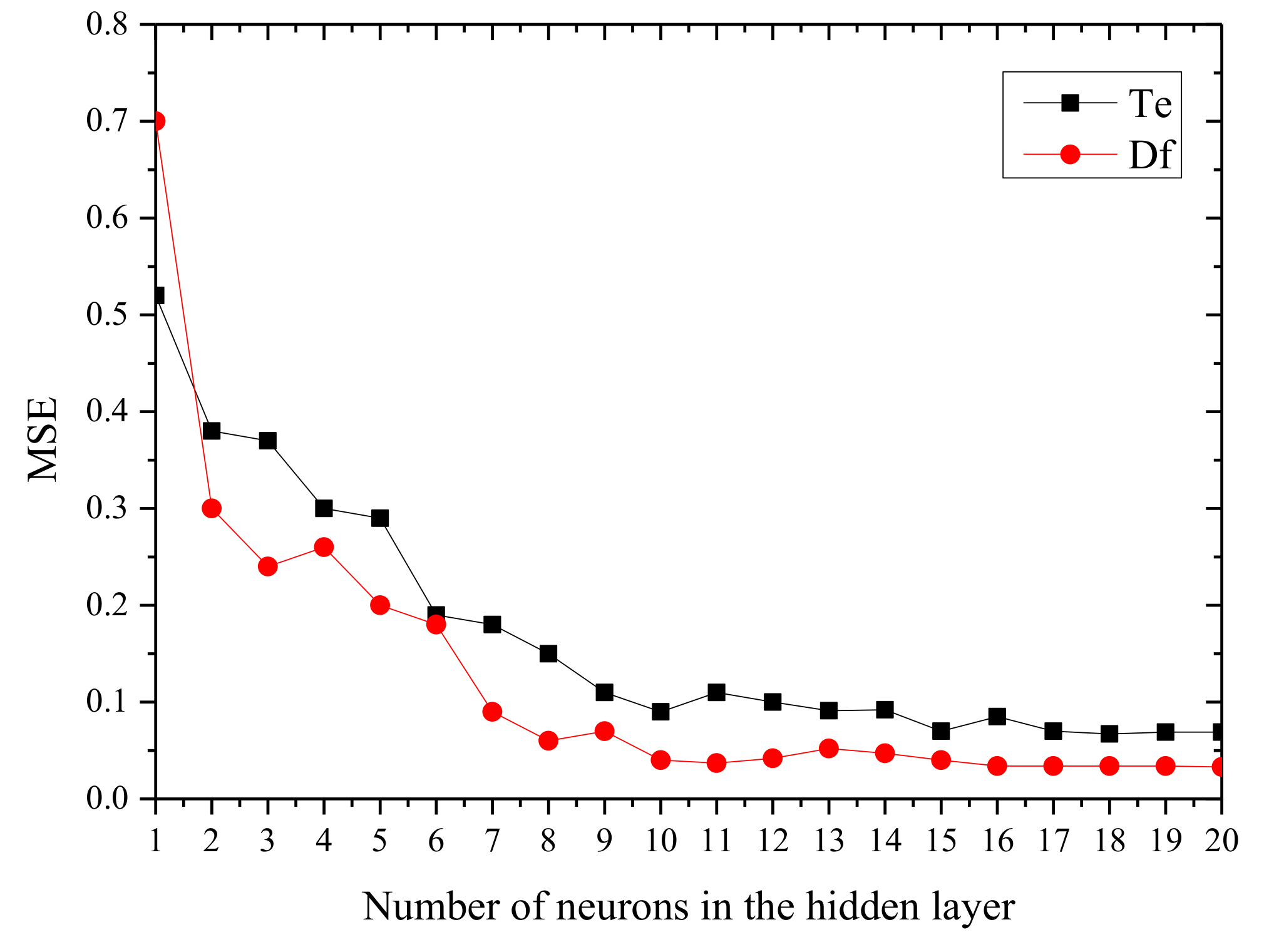
- The ANN results (Section 3.7), including the optimisation of the number of hidden layers, the number of neurons of each hidden layer, and the parametrisation of the ANN model. The validation of the model is included in this section.
- Comparison between all of the optimisation methods tested (Section 3.8).
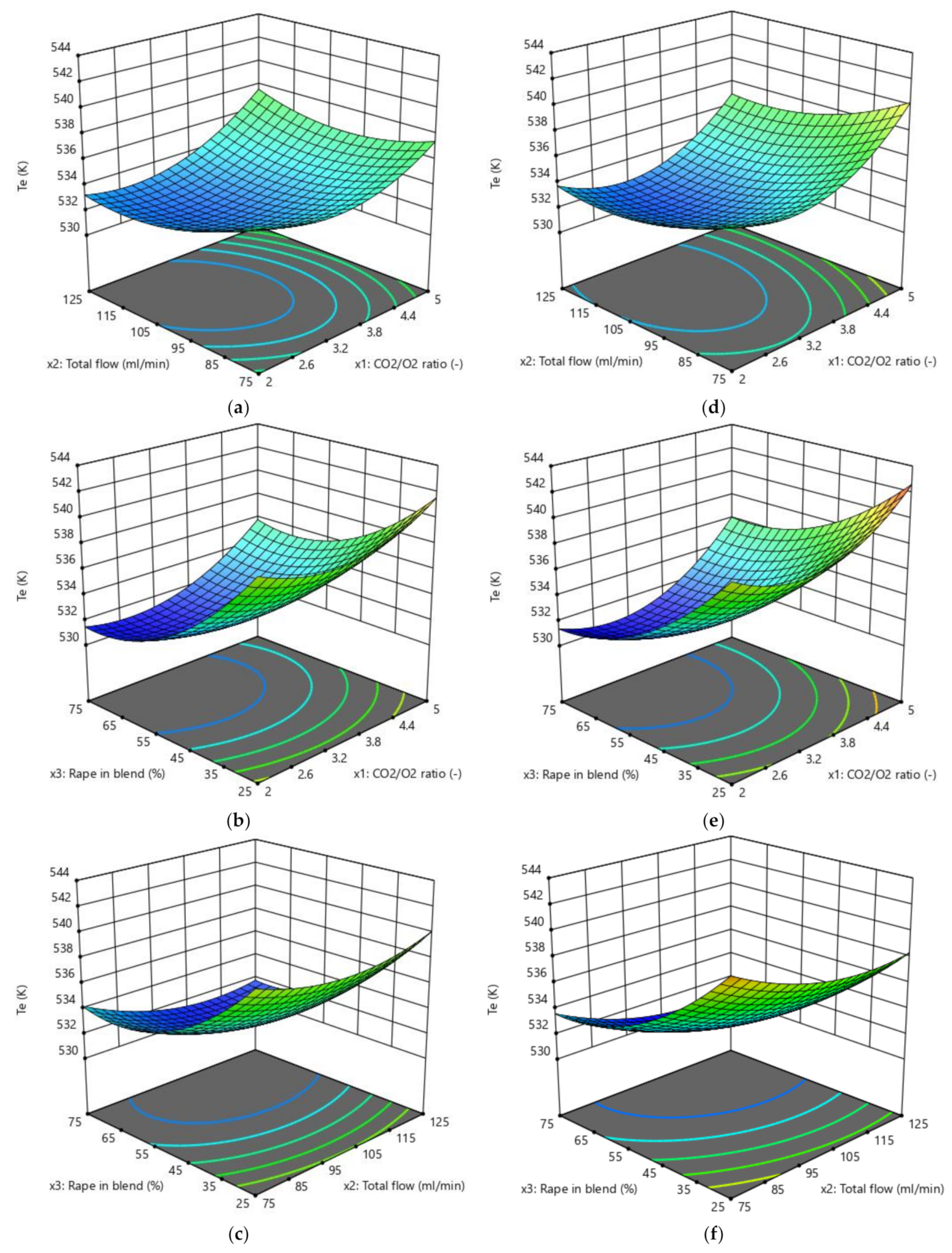
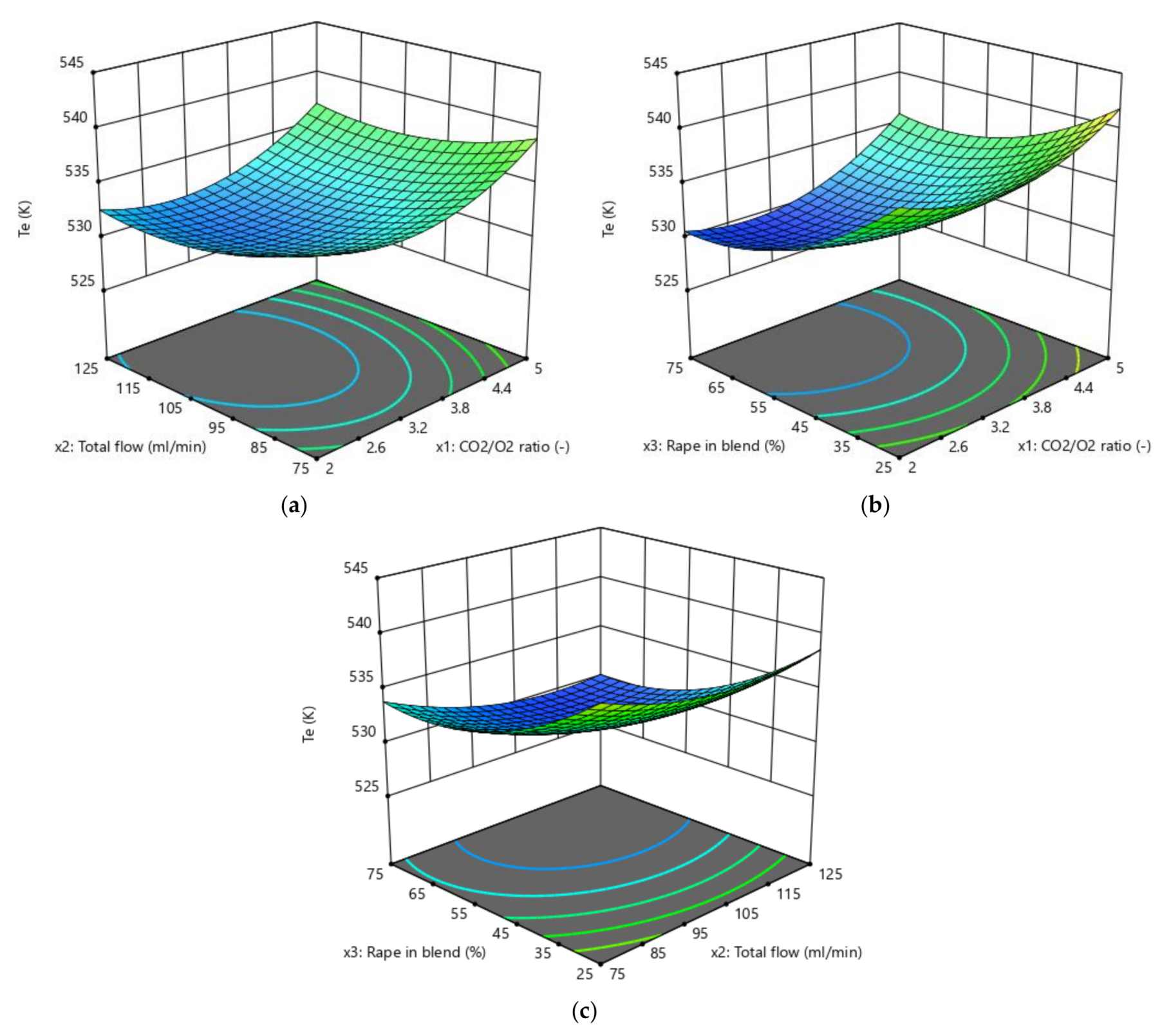
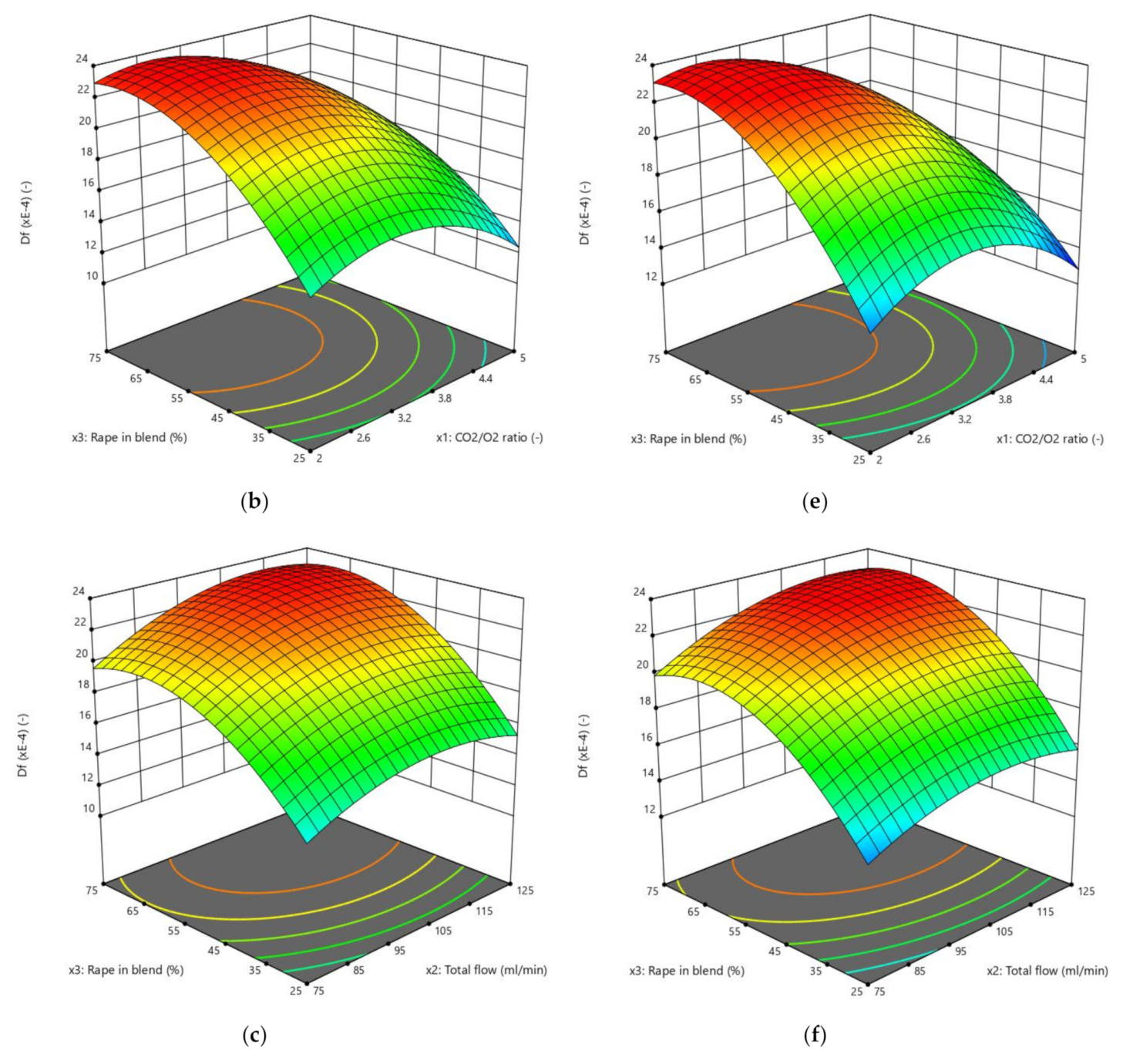
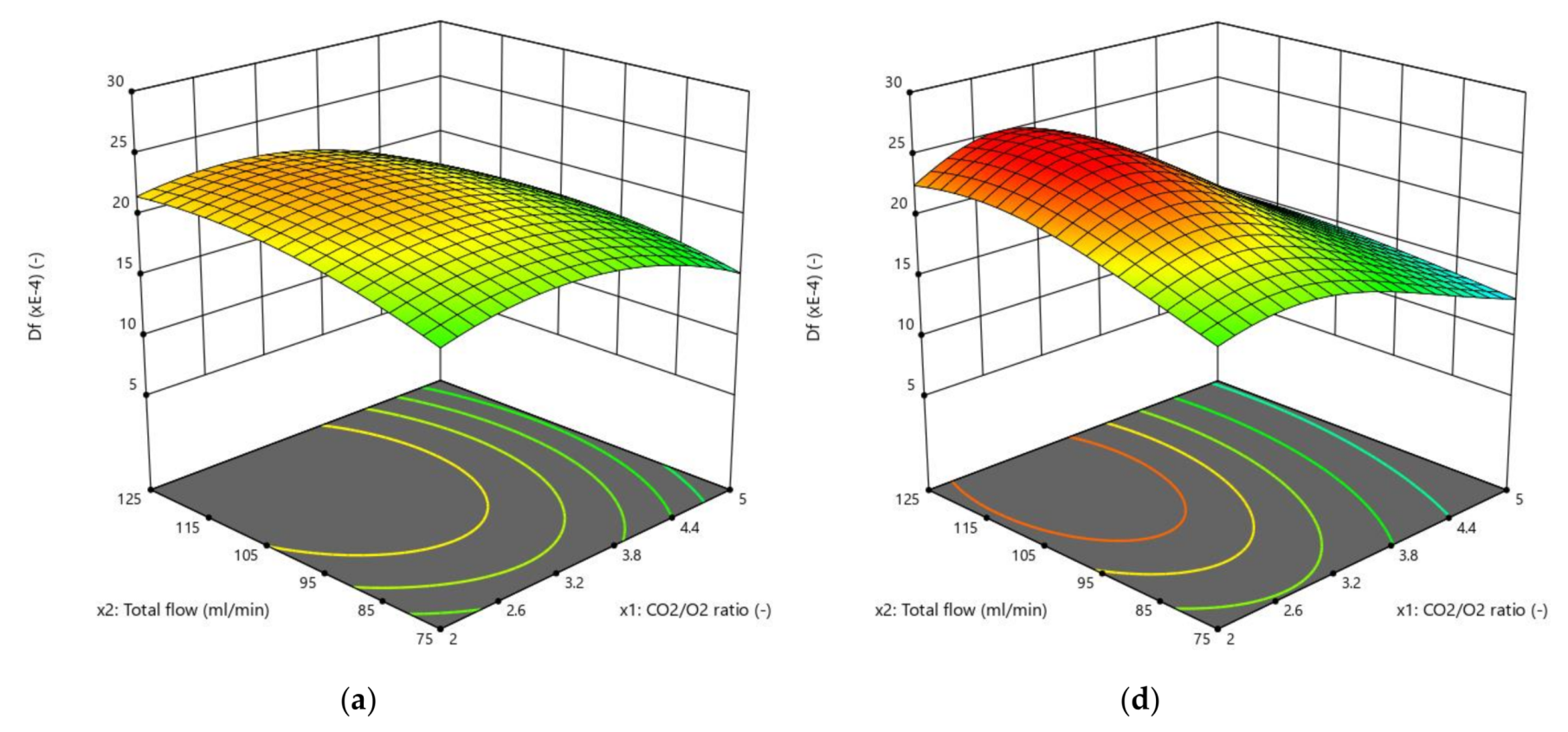
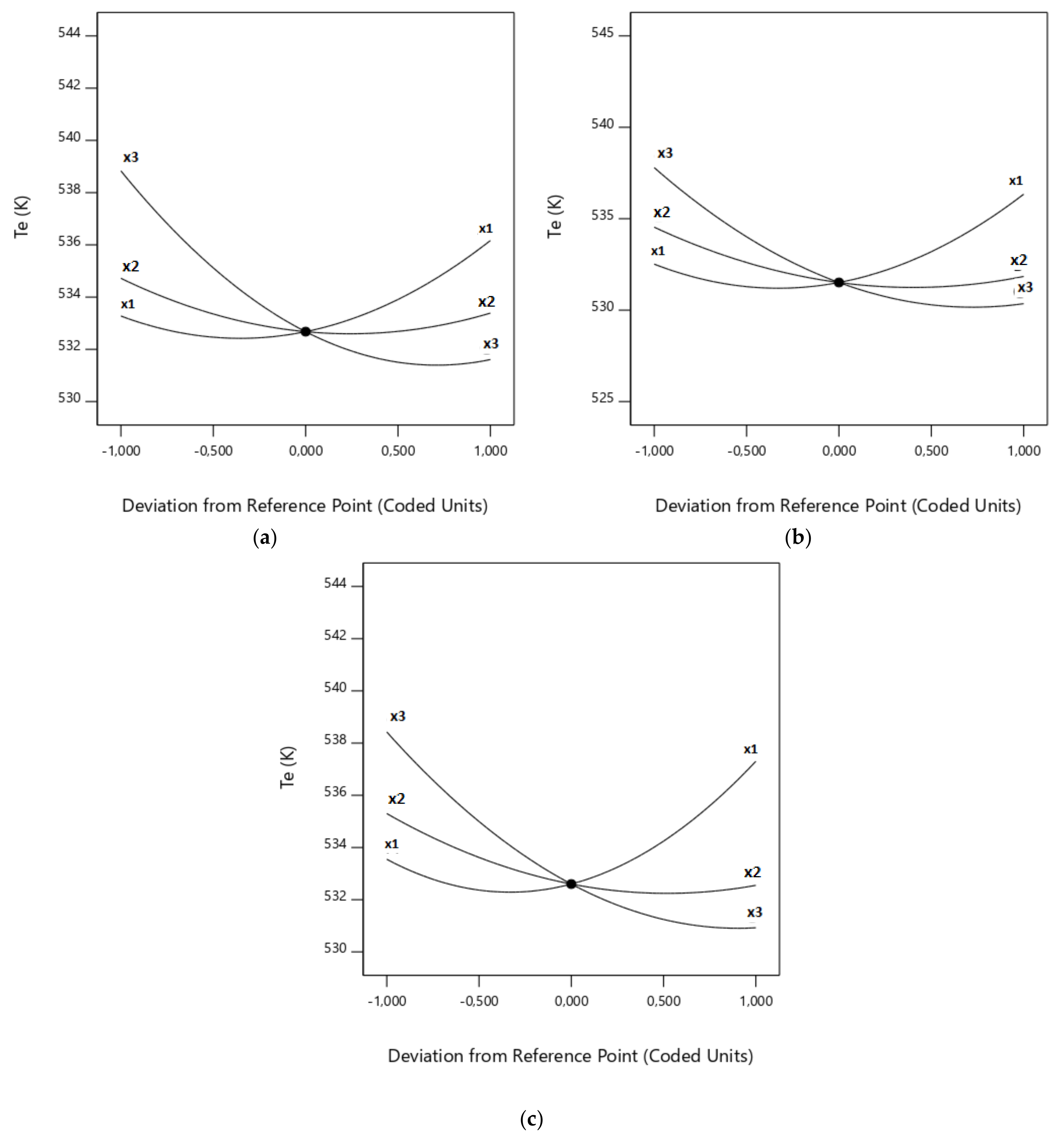
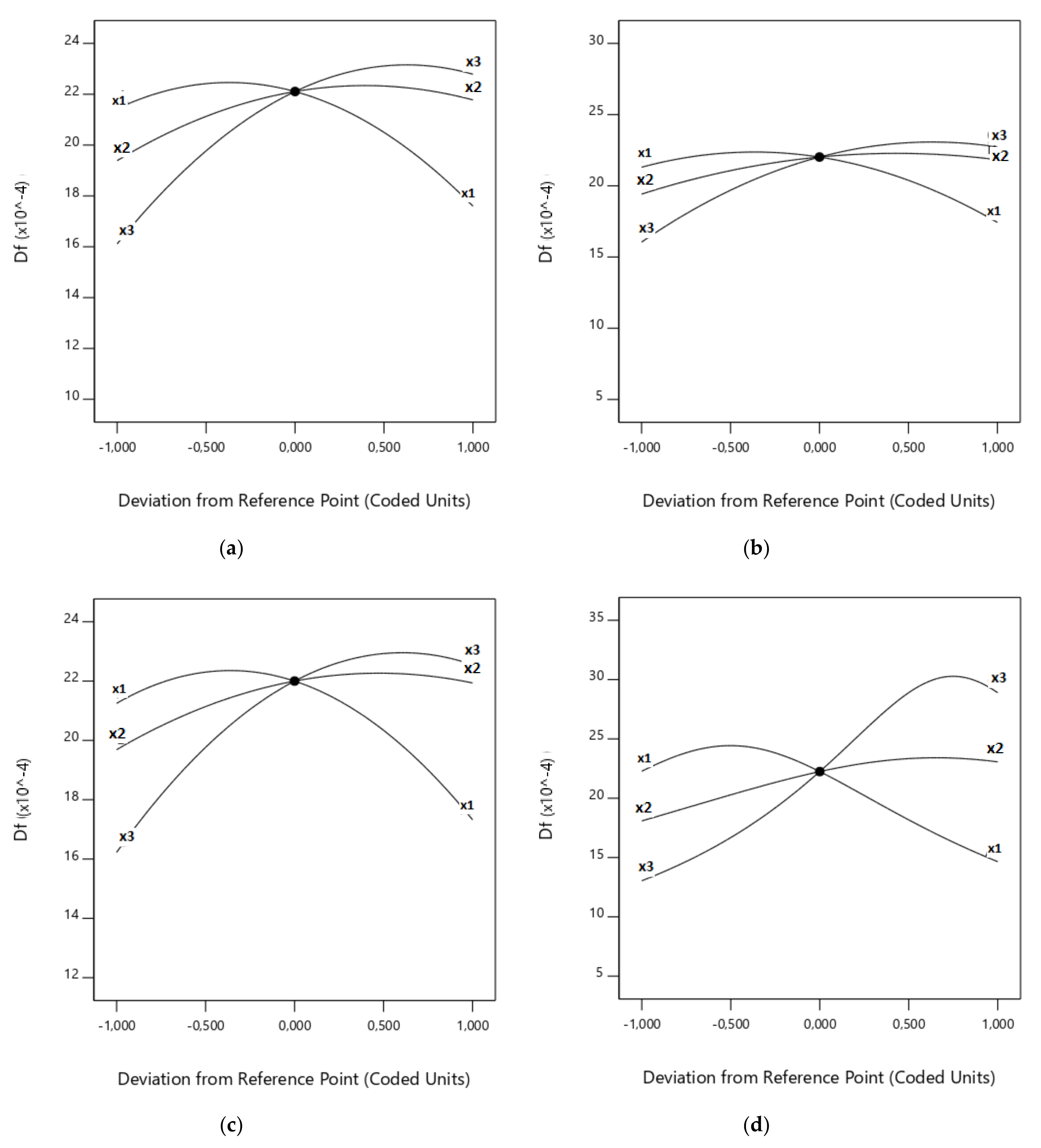
3.2. Effects of CO2/O2 Molar Ratio on the Responses
3.3. Effects of the Total Flow on the Responses
3.4. Effects of the Proportion of Rape in the Corn–Rape Blend on the Responses
3.5. Effects of the Interactions of the Factors on the Responses
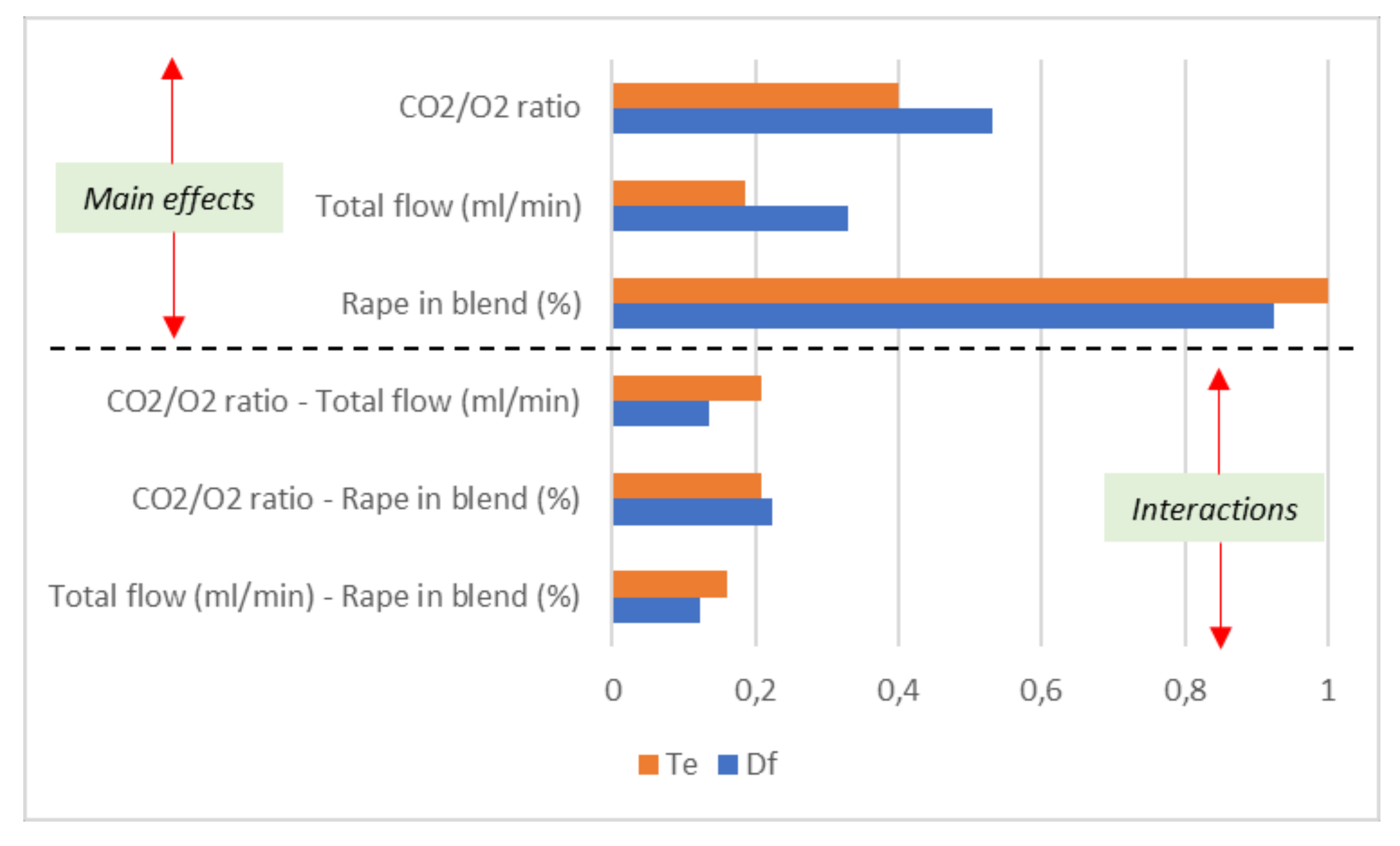
3.6. Comparison of the Relative Impact of the Effects of Factors and Their Interactions on the Responses
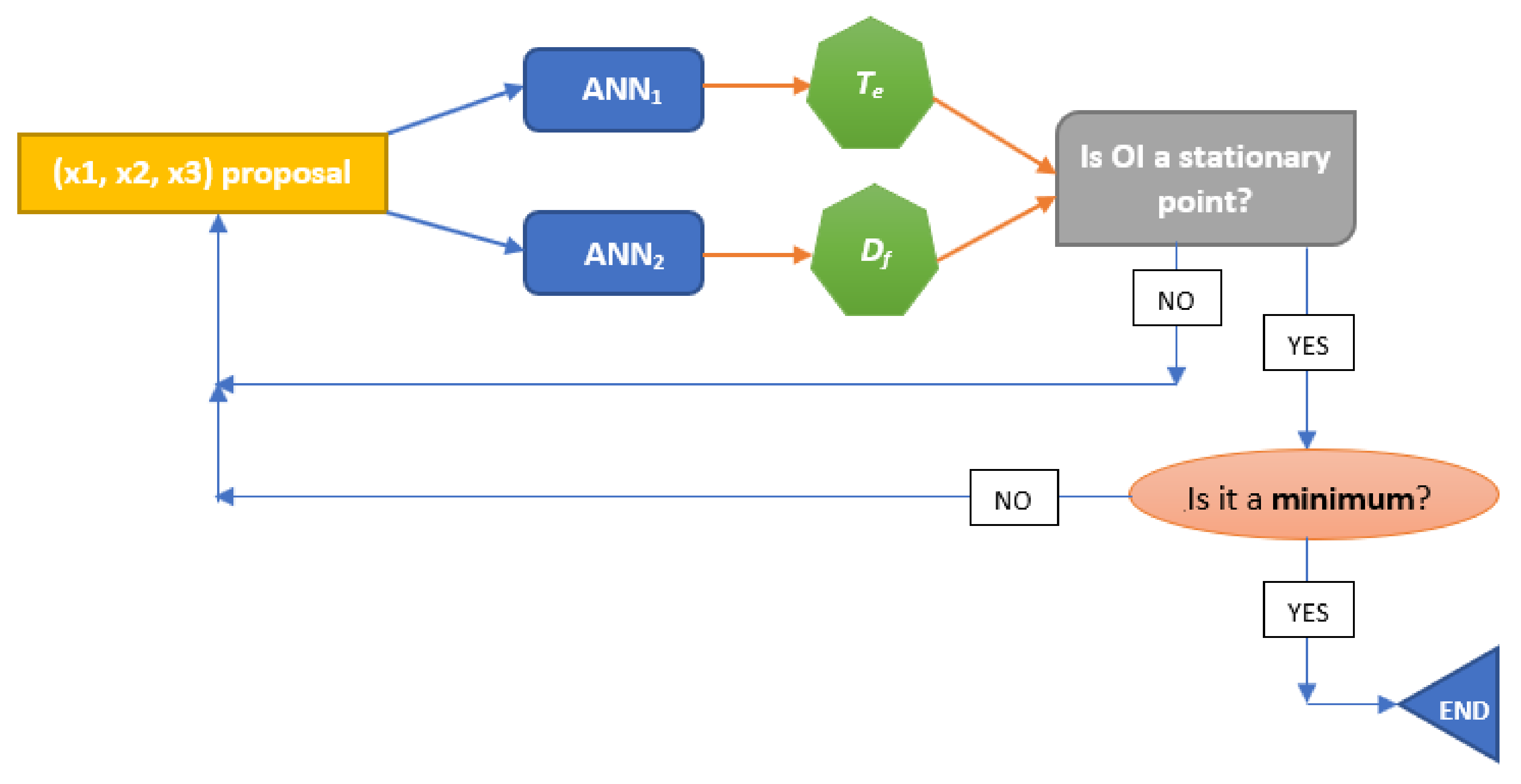
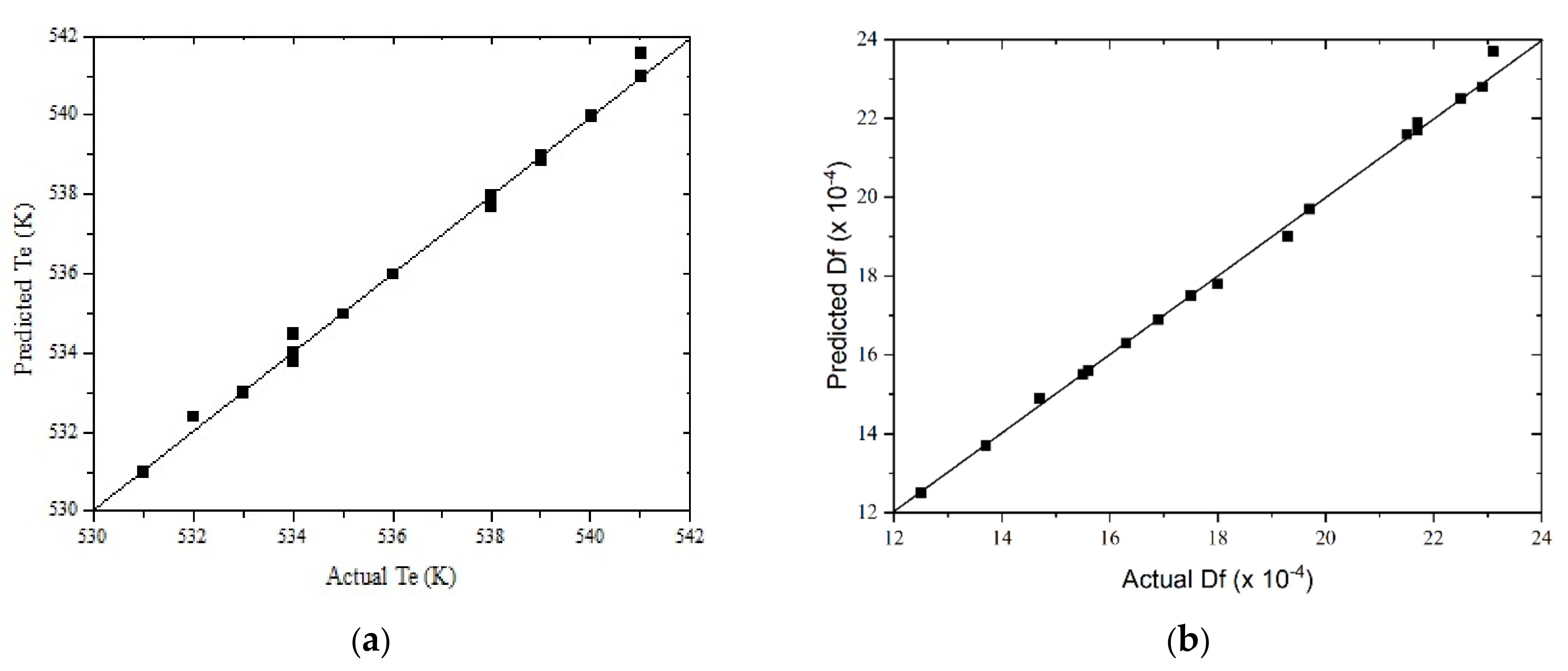
3.7. Application of the ANN as an Optimisation Method
3.8. Comparison of the Oxy-Combustion Optimisation between RSM and ANN Models
4. Conclusions
- Main new findings:
- The ANN method with two hidden layers is a better optimising method than RSM for oxy-combustion of lignocellulosic biomass. In addition, the ANN needed only 20 experiments to reach the best predictions. For the RSM methods, the most similar model was the complete design model, which required 32 experiments in the training stage. Hence, the ANN was found to be the most efficient model, in terms of good predictions and lower resource needs. The optimum point was found to be a CO2/O2 molar ratio of 3.3, total flow of 108 mL/min, and 61% of rape in the biomass blend.
- The complete design model allowed us to successfully discuss the factor behaviours (including all factors interactions) with good accuracy. However, the Box–Behnken and central composite designs only allowed us to discuss the single-factor effects, but not their interactions (even when a power data transformation was used). However, the optimisation of the process was successful for both reduced methods.
- Of the RSM models, only the complete design should be chosen to 1) study the effects of the CO2/O2 molar ratio, the total flow, and the proportion of rape in the corn–rape blend on the ignition temperature and the burnout index; 2) study the interactions between the previous factors; and 3) optimise the process in terms of the ignition temperature and the burnout index.
- Findings complementary to other studies:
- The most important factor to control in the oxy-fuel combustion of the feedstock is the proportion of rape in the blend, where the influence of the factors on the responses can be listed as proportion of rape in blend > CO2/O2 molar ratio > total flow.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- World Energy Highlights|Energy Storytelling|Enerdata. Available online: https://yearbook.enerdata.net/highlights/#total-energy-2 (accessed on 1 April 2020).
- The World Databank The Energy Consumption. Available online: https://data.worldbank.org/indicator/EG.USE.PCAP.KG.OE?most_recent_value_desc=true (accessed on 10 May 2020).
- International Energy Agency World Energy Outlook. 2018. Available online: https://www.iea.org/weo2018/ (accessed on 19 November 2019).
- Hall, S. King College of London No Deal Brexit Uncertainties in the UK’s Financial Services Sector Extend beyond London—UK in a Changing EuropeUK in a Changing Europe. Available online: https://ukandeu.ac.uk/no-deal-brexit-uncertainties-in-the-uks-financial-services-sector-extend-beyond-london/# (accessed on 20 November 2019).
- UNFCCC. UNFCCC United Nations Climate Change Annual Report 2018; UNFCCC: Bonn, Germany, 2018. [Google Scholar]
- Toftegaard, M.B.; Brix, J.; Jensen, P.A.; Glarborg, P.; Jensen, A.D. Oxy-fuel combustion of solid fuels. Prog. Energy Combust. Sci. 2010, 36, 581–625. [Google Scholar] [CrossRef]
- Liu, H.; Yao, H.; Yuan, X.; Xu, X.; Fan, Y.; Ando, T.; Okazaki, K. Efficient desulfurization in O2/CO2 combustion: Dependence on combustion conditions and sorbent properties. Chem. Eng. Commun. 2012, 199, 991–1011. [Google Scholar] [CrossRef]
- Sanchez-Silva, L.; López-González, D.; Villaseñor, J.; Sánchez, P.; Valverde, J.L. Thermogravimetric-mass spectrometric analysis of lignocellulosic and marine biomass pyrolysis. Bioresour. Technol. 2012, 109, 163–172. [Google Scholar] [CrossRef] [PubMed]
- European Comission Emissions Cap and Allowances|Climate Action. Available online: https://ec.europa.eu/clima/policies/ets/cap_en#tab-0-0 (accessed on 19 November 2019).
- Irfan, M.F.; Usman, M.R.; Kusakabe, K. Coal gasification in CO2 atmosphere and its kinetics since 1948: A brief review. Energy 2011, 36, 12–40. [Google Scholar] [CrossRef]
- Li, Q.; Zhao, C.; Chen, X.; Wu, W.; Li, Y. Comparison of pulverized coal combustion in air and in O2/CO2 mixtures by thermo-gravimetric analysis. J. Anal. Appl. Pyrolysis 2009, 85, 521–528. [Google Scholar] [CrossRef]
- Jenkins, B.; Baxter, L.; Miles, T.; Miles, T. Combustion properties of biomass. Fuel Process. Technol. 1998, 54, 17–46. [Google Scholar] [CrossRef]
- Shaddix, C.R.; Molina, A. Fundamental investigation of NOxformation during oxy-fuel combustion of pulverized coal. Proc. Combust. Inst. 2011, 33, 1723–1730. [Google Scholar] [CrossRef]
- López, R.; Menéndez, M.; Fernández, C.; Bernardo-Sánchez, A. The effects of scale-up and coal-biomass blending on supercritical coal oxy-combustion power plants. Energy 2018, 148, 571–584. [Google Scholar] [CrossRef]
- Liu, Q.; Shi, Y.; Zhong, W.; Yu, A. Co-firing of coal and biomass in oxy-fuel fluidized bed for CO2 capture: A review of recent advances. Chin. J. Chem. Eng. 2019, 27, 2261–2272. [Google Scholar] [CrossRef]
- Acciona, S.A. Cubillos del Sil Biomass Plant. Available online: https://www.acciona-industrial.com/projects/thermal-power-generation/cubillos-del-sil-biomass-plant/ (accessed on 19 November 2019).
- Gestamp Biomass Garray Biomass Plant. Available online: http://www.gestampbiomass.com/en/business/innovating-projects/garray (accessed on 19 November 2019).
- Cui, Y.; Geng, Z.; Zhu, Q.; Han, Y. Review: Multi-objective optimization methods and application in energy saving. Energy 2017, 125, 681–704. [Google Scholar] [CrossRef]
- Kheiri, F. A review on optimization methods applied in energy-efficient building geometry and envelope design. Renew. Sustain. Energy Rev. 2018, 92, 897–920. [Google Scholar] [CrossRef]
- Riaza, J.; Khatami, R.; Levendis, Y.A.; Álvarez, L.; Gil, M.V.; Pevida, C.; Rubiera, F.; Pis, J.J. Single particle ignition and combustion of anthracite, semi-anthracite and bituminous coals in air and simulated oxy-fuel conditions. Combust. Flame 2014, 161, 1096–1108. [Google Scholar] [CrossRef]
- Giménez-López, J.; Martínez, M.; Millera, A.; Bilbao, R.; Alzueta, M.U. SO2effects on CO oxidation in a CO2atmosphere, characteristic of oxy-fuel conditions. Combust. Flame 2011, 158, 48–56. [Google Scholar] [CrossRef]
- Abanades, J.C.; Arias, B.; Lyngfelt, A.; Mattisson, T.; Wiley, D.E.; Li, H.; Ho, M.T.; Mangano, E.; Brandani, S. Emerging CO2 capture systems. Int. J. Greenh. Gas Control 2015, 40, 126–166. [Google Scholar] [CrossRef]
- Salakij, S.; Yu, N.; Paolucci, S.; Antsaklis, P. Model-Based Predictive Control for building energy management. I: Energy modeling and optimal control. Energy Build. 2016, 133, 345–358. [Google Scholar] [CrossRef]
- Reynolds, J.; Rezgui, Y.; Kwan, A.; Piriou, S. A zone-level, building energy optimisation combining an artificial neural network, a genetic algorithm, and model predictive control. Energy 2018, 151, 729–739. [Google Scholar] [CrossRef]
- Shankar, T.J.; Sokhansanj, S.; Bandyopadhyay, S.; Bawa, A.S. A case study on optimization of biomass flow during single-screw extrusion cooking using genetic algorithm (GA) and response surface method (RSM). Food Bioprocess Technol. 2010, 3, 498–510. [Google Scholar] [CrossRef]
- McCall, J. Genetic algorithms for modelling and optimisation. J. Comput. Appl. Math. 2005, 184, 205–222. [Google Scholar] [CrossRef]
- Krzywanski, J.; Fan, H.; Feng, Y.; Shaikh, A.R.; Fang, M.; Wang, Q. Genetic algorithms and neural networks in optimization of sorbent enhanced H2 production in FB and CFB gasifiers. Energy Convers. Manag. 2018, 171, 1651–1661. [Google Scholar] [CrossRef]
- Luo, K.; Xing, J.; Bai, Y.; Fan, J. Prediction of product distributions in coal devolatilization by an artificial neural network model. Combust. Flame 2018, 193, 283–294. [Google Scholar] [CrossRef]
- Xing, J.; Wang, H.; Luo, K.; Wang, S.; Bai, Y.; Fan, J. Predictive single-step kinetic model of biomass devolatilization for CFD applications: A comparison study of empirical correlations (EC), artificial neural networks (ANN) and random forest (RF). Renew. Energy 2019, 136, 104–114. [Google Scholar] [CrossRef]
- Khuri, A.I.; Mukhopadhyay, S. Response surface methodology. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 128–149. [Google Scholar] [CrossRef]
- Danmaliki, G.I.; Saleh, T.A.; Shamsuddeen, A.A. Response surface methodology optimization of adsorptive desulfurization on nickel/activated carbon. Chem. Eng. J. 2017, 313, 993–1003. [Google Scholar] [CrossRef]
- Lewis, G.; Mathieu, R.; Phan-Tan-Luu, R. Pharmaceutical Experiment Design; Wiley, D.E., Ed.; Taylor & Francis Group: New York, NY, USA, 1999. [Google Scholar]
- Braatz, A.L.; Hisken, H. Response surfaces for advanced consequence models: Two approaches. J. Loss Prev. Process Ind. 2017, 49, 683–699. [Google Scholar] [CrossRef]
- Xie, Y.; Guo, X.; Ma, Z.; Gong, J.; Wang, H.; Lv, Y. Efficient Extraction and Structural Characterization of Hemicellulose from Sugarcane Bagasse Pith. Polymers 2020, 12, 608. [Google Scholar] [CrossRef]
- Paterakis, P.; Korakianiti, E.; Dallas, P.; Rekkas, D. Evaluation and simultaneous optimization of some pellets characteristics using a 33 factorial design and the desirability function. Int. J. Pharm. 2002, 248, 51–60. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, F.; Dong, L.; Li, Z.; Chen, L.; He, X.; Gong, J.; Zhang, J.; Li, Q. Design and Optimization of Flexible Polypyrrole/Bacterial Cellulose Conductive Nanocomposites Using Response Surface Methodology. Polymers 2019, 11, 960. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments; Wiley, D.E., Ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- López, R.; Fernández, C.; Gómez, X.; Martínez, O.; Sánchez, M.E. Thermogravimetric analysis of lignocellulosic and microalgae biomasses and their blends during combustion. J. Therm. Anal. Calorim. 2013, 114, 295–305. [Google Scholar] [CrossRef]
- Van Soest, P.J.; Robertson, J.B.; Lewis, B.A. Methods for Dietary Fiber, Neutral Detergent Fiber, and Nonstarch Polysaccharides in Relation to Animal Nutrition. J. Dairy Sci. 1991, 74, 3583–3597. [Google Scholar] [CrossRef]
- Cuetos, M.J.; Gómez, X.; Escapa, A.; Morán, A. Evaluation and simultaneous optimization of bio-hydrogen production using 32factorial design and the desirability function. J. Power Sources 2007, 169, 131–139. [Google Scholar] [CrossRef]
- Villasante, J.; Pérez-Carrillo, E.; Heredia-Olea, E.; Metón, I.; Almajano, M.P. In Vitro Antioxidant Activity Optimization of Nut Shell (Carya illinoinensis) by Extrusion Using Response Surface Methods. Biomolecules 2019, 9, 883. [Google Scholar] [CrossRef] [PubMed]
- Domínguez-Robles, J.; Stewart, S.A.; Rendl, A.; González, Z.; Donnelly, R.F.; Larrañeta, E. Lignin and Cellulose Blends as Pharmaceutical Excipient for Tablet Manufacturing via Direct Compression. Biomolecules 2019, 9, 423. [Google Scholar] [CrossRef] [PubMed]
- Stat-Ease Design-Expert, version 11; Stat-Ease: Minneapolis, MN, USA, 2019.
- NIST/SEMATECH e-Handbook of Statistical Methods. Available online: http://www.itl.nist.gov/div898/handbook/ (accessed on 21 July 2019).
- López, R.; Fernández, C.; Fierro, J.; Cara, J.; Martínez, O.; Sánchez, M.E. Oxy-combustion of corn, sunflower, rape and microalgae bioresidues and their blends from the perspective of thermogravimetric analysis. Energy 2014, 74, 845–854. [Google Scholar] [CrossRef]
- López, R.; Fernández, C.; Cara, J.; Martínez, O.; Sánchez, M.E. Differences between combustion and oxy-combustion of corn and corn-rape blend using thermogravimetric analysis. Fuel Process. Technol. 2014, 128, 376–387. [Google Scholar] [CrossRef]
- López, R.; Fernández, C.; Martínez, O.; Sánchez, M.E. Modelling and kinetics studies of a corn-rape blend combustion in an oxy-fuel atmosphere. Bioresour. Technol. 2015, 183, 153–162. [Google Scholar] [CrossRef]
- López, R.; Fernández, C.; Martínez, O.; Sánchez, M. Techno-economic analysis of a 15MW corn-rape oxy-combustion power plant. Fuel Process. Technol. 2016, 142, 296–304. [Google Scholar] [CrossRef]
- Ramón y Cajal, S. Textura del Sistema Nervioso del Hombre y de los Vertebrados; Moya, N., Ed.; Moya: Madrid, Spain, 1899. [Google Scholar]
- Rumelhart, D.; McClelland, J. Parallel Distributed Processing: Explorations in the Microstructure of Cognition; MIT, Ed.; MIT: New York, NY, USA, 1986; ISBN 978-0262181235. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Lee, T.L. Back-propagation neural network for long-term tidal predictions. Ocean Eng. 2004, 31, 225–238. [Google Scholar] [CrossRef]
- Lai, Z.; Ma, X.; Tang, Y.; Lin, H. A study on municipal solid waste (MSW) combustion in N2/O2 and CO2/O2 atmosphere from the perspective of TGA. Energy 2011, 36, 819–824. [Google Scholar] [CrossRef]
- Nie, Q.; Sun, S.; Li, Z.; Zhang, X.; Wu, S.; Qin, Y. Thermogravimetric analysis on the combustion characteristics of brown coal blends. J. Combust. Sci. Technol. 2001, 7, 72–76. [Google Scholar]
- Dhaneswar, S.R.; Pisupati, S.V. Oxy-fuel combustion: The effect of coal rank and the role of char-CO2reaction. Fuel Process. Technol. 2012, 102, 156–165. [Google Scholar] [CrossRef]
- U.S. National Library of Medicine Carbon Dioxide|CO2—PubChem. Available online: https://pubchem.ncbi.nlm.nih.gov/compound/280 (accessed on 23 November 2019).
- Benedetti, A.; Modesti, M.; Strumendo, M. CFD analysis of the CaO-CO2reaction in a thermo-gravimetric apparatus. Chem. Eng. Trans. 2015, 43, 1039–1044. [Google Scholar]
- Buczyński, R.; Czerski, G.; Zubek, K.; Weber, R.; Grzywacz, P. Evaluation of carbon dioxide gasification kinetics on the basis of non-isothermal measurements and CFD modelling of the thermogravimetric analyser. Fuel 2018, 228, 50–61. [Google Scholar] [CrossRef]
- Janković, B.; Manić, N.; Radović, I.; Janković, M.; Rajačić, M. Model-free and model-based kinetics of the combustion process of low rank coals with high ash contents using TGA-DTG-DTA-MS and FTIR techniques. Thermochim. Acta 2019, 679, 178337. [Google Scholar] [CrossRef]
- Dhahak, A.; Bounaceur, R.; Le Dreff-Lorimier, C.; Schmidt, G.; Trouve, G.; Battin-Leclerc, F. Development of a detailed kinetic model for the combustion of biomass. Fuel 2019, 756–774. [Google Scholar] [CrossRef]
- Žajdlík, R.; Jelemenský, L.; Remiarová, B.; Markoš, J. Experimental and modelling investigations of single coal particle combustion. Chem. Eng. Sci. 2001, 56, 1355–1361. [Google Scholar] [CrossRef]
- Adomeit, G.; Hocks, W.; Henriksen, K. Combustion of a carbon surface in a stagnation point flow field. Combust. Flame 1985, 59, 273–288. [Google Scholar] [CrossRef]

| Material | Corn | Rape |
|---|---|---|
| Proximate analysis | ||
| Moisture (%) | 8.0 | 9.2 |
| Volatile matter a (%) | 76.8 | 80.4 |
| Ash a (%) | 5.7 | 2.6 |
| Fixed carbon a,c (%) | 17.5 | 17.0 |
| Ultimate analysis | ||
| C b (%) | 48.8 | 49.7 |
| H b (%) | 6.2 | 6.3 |
| N b (%) | 0.5 | 0.2 |
| S b (%) | 0.1 | 0.2 |
| O b,c (%) | 44.4 | 43.6 |
| Calorific value | ||
| HHV (MJ/kg) | 18.45 | 19.49 |
| Composition | ||
| Cellulose (%) | 18.6 | 25.7 |
| Hemicellulose (%) | 29.7 | 21.6 |
| Lignin (%) | 12.0 | 7.4 |
| RSM Method | Characteristics | Symbol |
|---|---|---|
| Complete design |
| 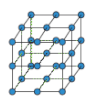 |
| Central composite design |
| 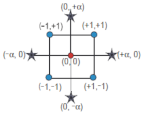 |
| Box–Behnken design |
| 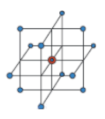 |
| Factors | y1: Te (K) | y2: Df (× 10−4) | ||||
|---|---|---|---|---|---|---|
| Uncoded Factors Coefficient | Coded Factors Coefficient | p-Values | Uncoded Factors Coefficient | Coded Factors Coefficient | p-Values | |
| Model 1: Complete design | ||||||
| Constant | +588.35 | +532.68 | <0.0001 a | −38.83 | +22.11 | <0.0001 a |
| x1 | −8.39 | +1.44 | <0.0001 a | +9.17 | −1.92 | <0.0001 a |
| x2 | −0.49 | −0.67 | 0.0002 a | +0.55 | +1.19 | <0.0001 a |
| x3 | −0.53 | −3.61 | <0.0001 a | +0.56 | +3.34 | <0.0001 a |
| x1x2 | +0.02 | +0.75 | 0.0006 a | −0.01 | −0.49 | <0.0001 a |
| x1x3 | +0.02 | +0.75 | 0.0006 a | −0.02 | −0.81 | <0.0001 a |
| x2x3 | −9 × 10−4 | −0.58 | 0.0050 a | +7 × 10−4 | +0.44 | <0.0001 a |
| x12 | +0.91 | +2.04 | <0.0001 a | −1.15 | −2.59 | <0.0001 a |
| x22 | +2.2 × 10−3 | +1.38 | <0.0001 a | −2.4× 10−3 | −1.52 | <0.0001 a |
| x32 | +4.1 × 10−3 | +2.54 | <0.0001 a | −4.3 × 10−3 | −2.66 | <0.0001 a |
| Model 2: Box–Behnken design | ||||||
| Constant | +586.11 | +532.60 | <0.0001 a | −37.21 | +22.00 | <0.0001 a |
| x1 | −7.54 | +1.88 | 0.0007 a | +10.43 | −1.96 | <0.0001 a |
| x2 | −0.46 | −1.37 | 0.0039 a | +0.45 | +1.13 | <0.0001 a |
| x3 | −0.53 | −3.75 | <0.0001 a | +0.61 | +3.16 | <0.0001 a |
| x1x2 | −6.7 × 10−3 | −0.25 | 0.6044 | −0.02 | −0.60 | 0.0005 a |
| x1x3 | +0.01 | +0.50 | 0.3140 | −0.03 | −1.28 | <0.0001 a |
| x2x3 | +3 × 10−18 | +0.0 | 1.0000 | +6 × 10−4 | +0.35 | 0.0090 a |
| x12 | +1.26 | +2.82 | 0.0004 a | −1.21 | −2.71 | <0.0001 a |
| x22 | +2.1 × 10−3 | +1.32 | 0.0214 a | −1.9 × 10−3 | −1.19 | <0.0001 a |
| x32 | +3.3 × 10−3 | +2.08 | 0.0024 a | −4.2 × 10−3 | −2.61 | <0.0001 a |
| Model 3: Central composite design | ||||||
| Constant | +594.70 | +531.51 | <0.0001 a | −36.68 | +22.02 | <0.0001 a |
| x1 | −9.46 | +1.91 | <0.0001 a | +9.34 | −1.94 | 0.0001 a |
| x2 | −0.57 | −1.35 | 0.0005 a | +0.50 | +1.21 | 0.0043 a |
| x3 | −0.55 | −3.72 | <0.0001 a | +0.55 | +3.34 | <0.0001 a |
| x1x2 | +6.7 × 10−3 | +0.25 | 0.4918 | −0.01 | −0.49 | 0.2818 |
| x1x3 | +0.02 | +0.75 | 0.0580 | −0.02 | −0.81 | 0.0872 |
| x2x3 | −8 × 10−4 | −0.50 | 0.1840 | +8 × 10−4 | +0.49 | 0.2818 |
| x12 | +1.30 | +2.92 | <0.0001 a | −1.18 | −2.65 | <0.0001 a |
| x22 | +2.7 × 10−3 | +1.68 | <0.0001 a | −2.2 × 10−3 | −1.40 | 0.0014 a |
| x32 | +4.1 × 10−3 | +2.56 | <0.0001 a | −4.2 × 10−3 | −2.63 | <0.0001 a |
| Model 4: Central composite design with power transformation | ||||||
| Constant | Not necessary for Te response | +0.02 | +1.6 × 10−3 | <0.0001 a | ||
| x1 | −1.9 × 10−3 | +1.1 × 10−3 | <0.0001 a | |||
| x2 | −1 × 10−4 | −5 × 10−4 | <0.0001 a | |||
| x3 | −3 × 10−4 | −1.9 × 10−3 | <0.0001 a | |||
| x1x2 | −2 × 10−6 | −1 × 10−4 | 0.4873 | |||
| x1x3 | −1 × 10−5 | −4 × 10−4 | 0.0020 a | |||
| x2x3 | +3 × 10−7 | +2 × 10−4 | 0.0541 | |||
| x12 | +5 × 10−4 | +1.1 × 10−3 | <0.0001 a | |||
| x22 | +6 × 10−7 | +4 × 10−4 | 0.0006 a | |||
| x32 | +2 × 10−6 | +1.2 × 10−3 | <0.0001 a | |||
| Model | Te | Df | ||
|---|---|---|---|---|
| R2 | R2 Predicted | R2 | R2 Predicted | |
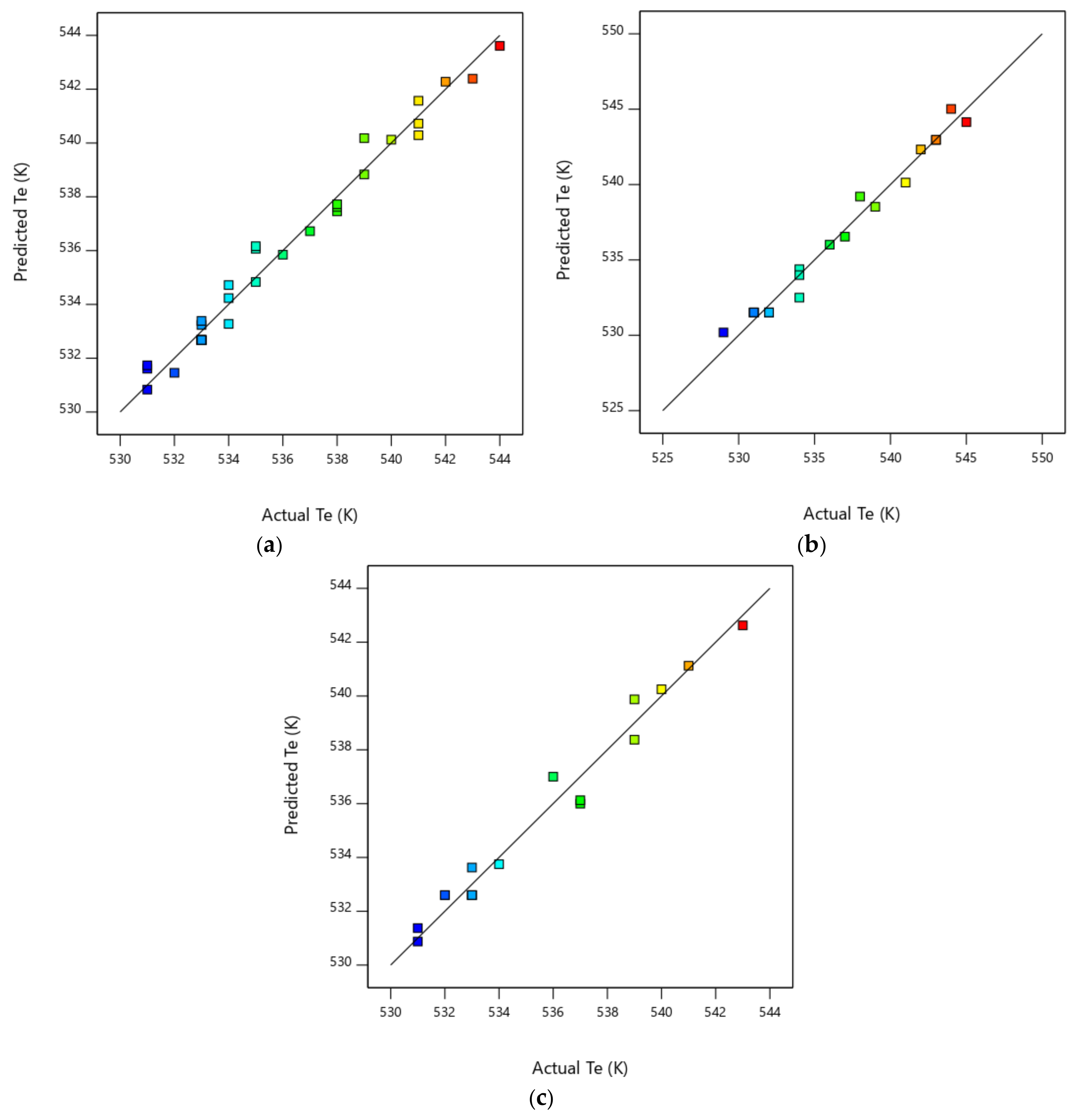
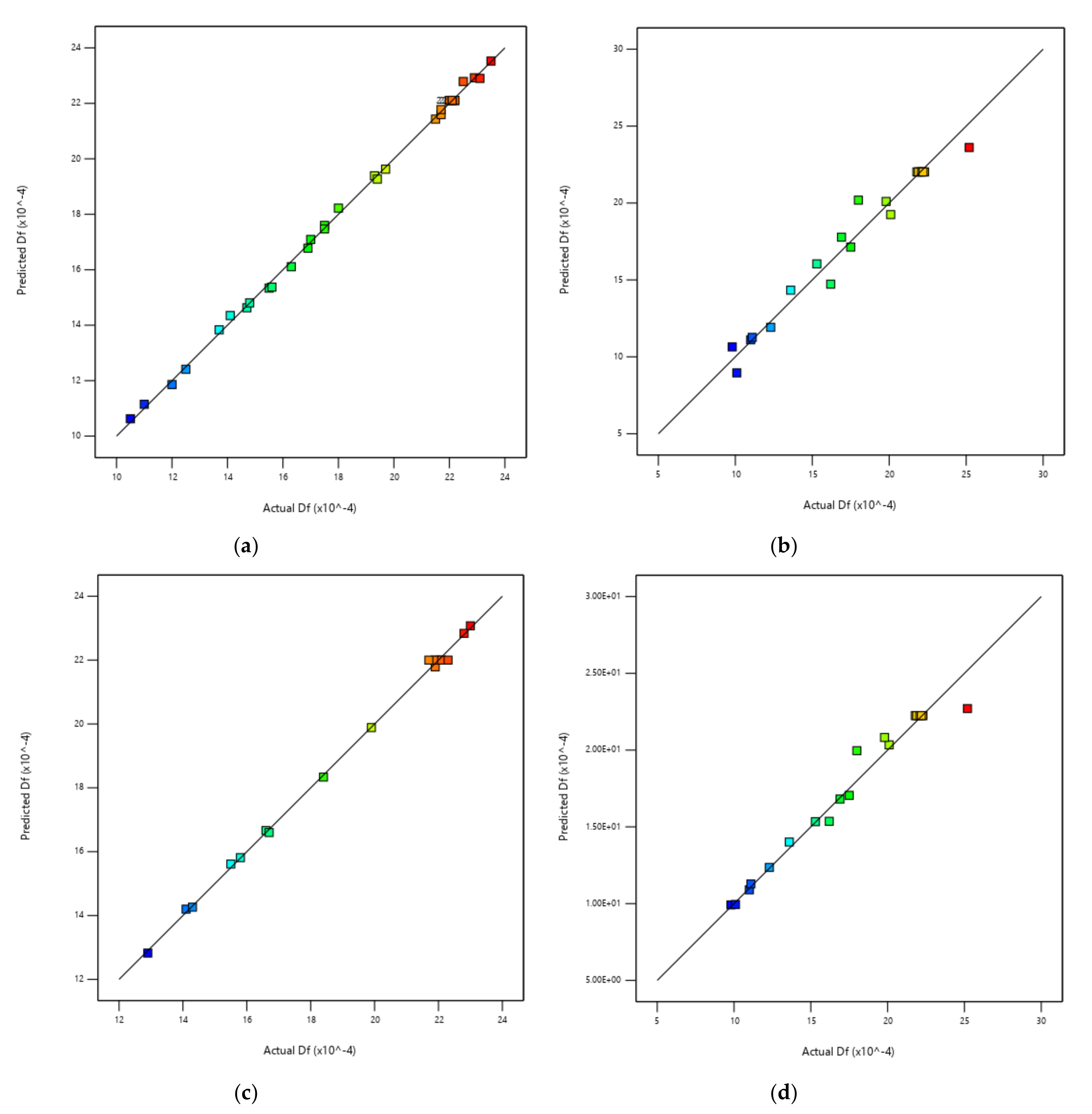
| Complete design | 0.979 | 0.955 | 0.999 | 0.997 |
| Box–Behnken design | 0.974 | 0.659 | 0.999 | 0.993 |
| Central composite design | 0.980 | 0.863 | 0.967 | 0.744 |
| Central composite design with power transformation | N/A * | N/A * | 0.993 | 0.944 |
| Model | Te | Df | ||
|---|---|---|---|---|
| R2 | R2 Predicted | R2 | R2 Predicted | |
| Artificial neural network | 0.999 | 0.996 | 0.999 | 0.997 |
| Model | x1: CO2/O2 Ratio | x2: Total Flow (mL/min) | x3: % Rape in Blend | Optimal Values | Differences with ANN |
|---|---|---|---|---|---|
| Artificial neural network | 3.3 | 108 | 61 | Te (K): 533 | - |
| Df (× 10−4): 23.8 | |||||
| Complete design | 3.1 | 111 | 65 | Te (K): 531 | −0.37% |
| Df (× 10−4): 24.0 | −0.84% | ||||
| Box–Behnken design | 2.6 | 118 | 63 | Te (K): 531 | −0.37% |
| Df (× 10−4): 24.1 | 1.26% | ||||
| Central composite design | 2.7 | 115 | 70 | Te (K): 529 | −0.75% |
| Df (× 10−4): 24.2 | 1.68% | ||||
| Central composite design with power transformation | 2.8 | 114 | 71 | Te (K): N/A * | N/A * |
| Df (× 10−4): 31.6 | 32.77% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
López, R.; Fernández, C.; Pereira, F.J.; Díez, A.; Cara, J.; Martínez, O.; Sánchez, M.E. A Comparison between Several Response Surface Methodology Designs and a Neural Network Model to Optimise the Oxidation Conditions of a Lignocellulosic Blend. Biomolecules 2020, 10, 787. https://doi.org/10.3390/biom10050787
López R, Fernández C, Pereira FJ, Díez A, Cara J, Martínez O, Sánchez ME. A Comparison between Several Response Surface Methodology Designs and a Neural Network Model to Optimise the Oxidation Conditions of a Lignocellulosic Blend. Biomolecules. 2020; 10(5):787. https://doi.org/10.3390/biom10050787
Chicago/Turabian StyleLópez, Roberto, Camino Fernández, Fernando J. Pereira, Ana Díez, Jorge Cara, Olegario Martínez, and Marta E. Sánchez. 2020. "A Comparison between Several Response Surface Methodology Designs and a Neural Network Model to Optimise the Oxidation Conditions of a Lignocellulosic Blend" Biomolecules 10, no. 5: 787. https://doi.org/10.3390/biom10050787
APA StyleLópez, R., Fernández, C., Pereira, F. J., Díez, A., Cara, J., Martínez, O., & Sánchez, M. E. (2020). A Comparison between Several Response Surface Methodology Designs and a Neural Network Model to Optimise the Oxidation Conditions of a Lignocellulosic Blend. Biomolecules, 10(5), 787. https://doi.org/10.3390/biom10050787







