Relativistic B-Spline R-Matrix Calculations for Electron Scattering from Thallium Atoms
Abstract
:1. Introduction
2. Computational Method
3. Results and Discussion
3.1. Energy Levels and Oscillator Strengths
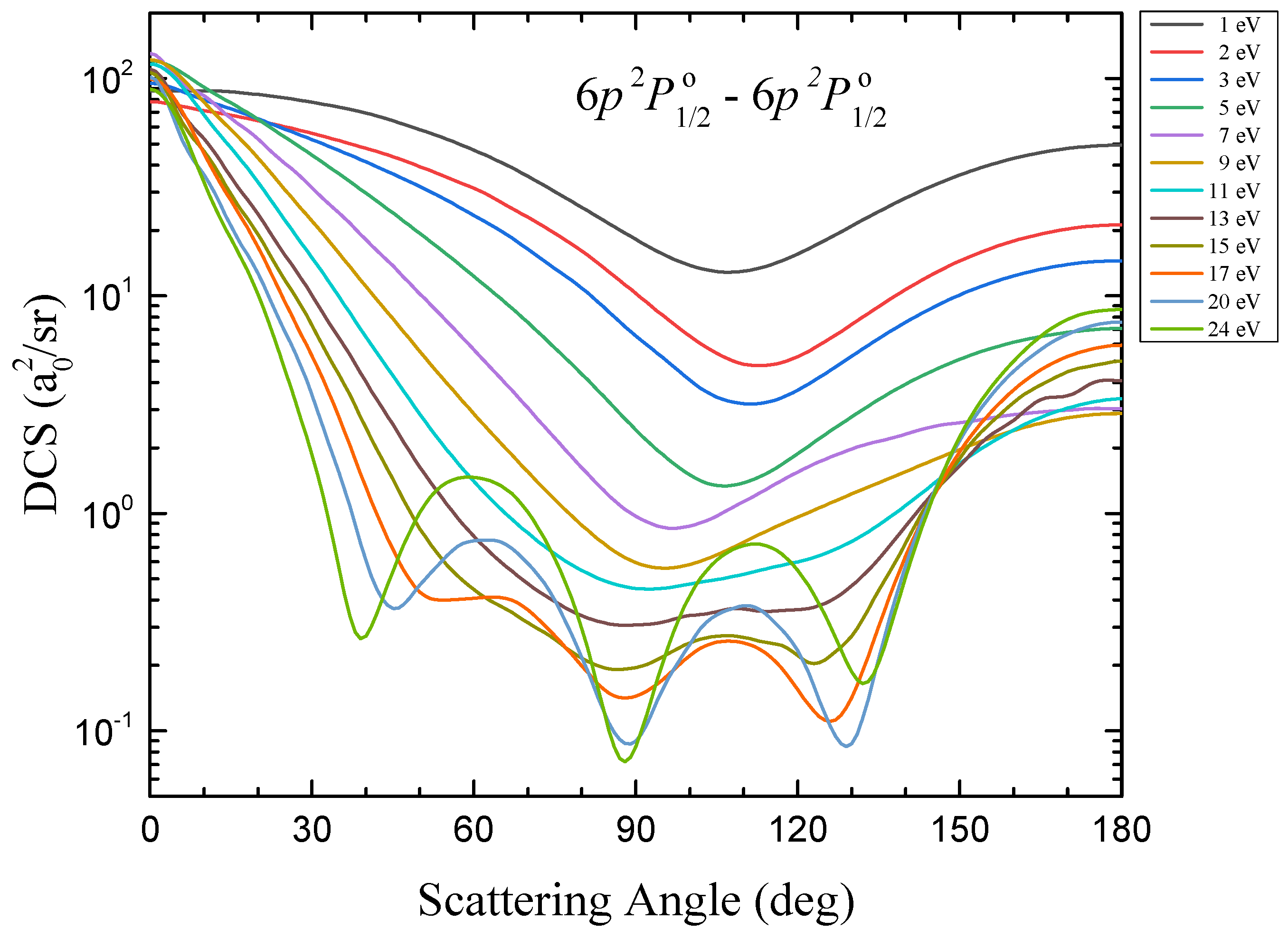
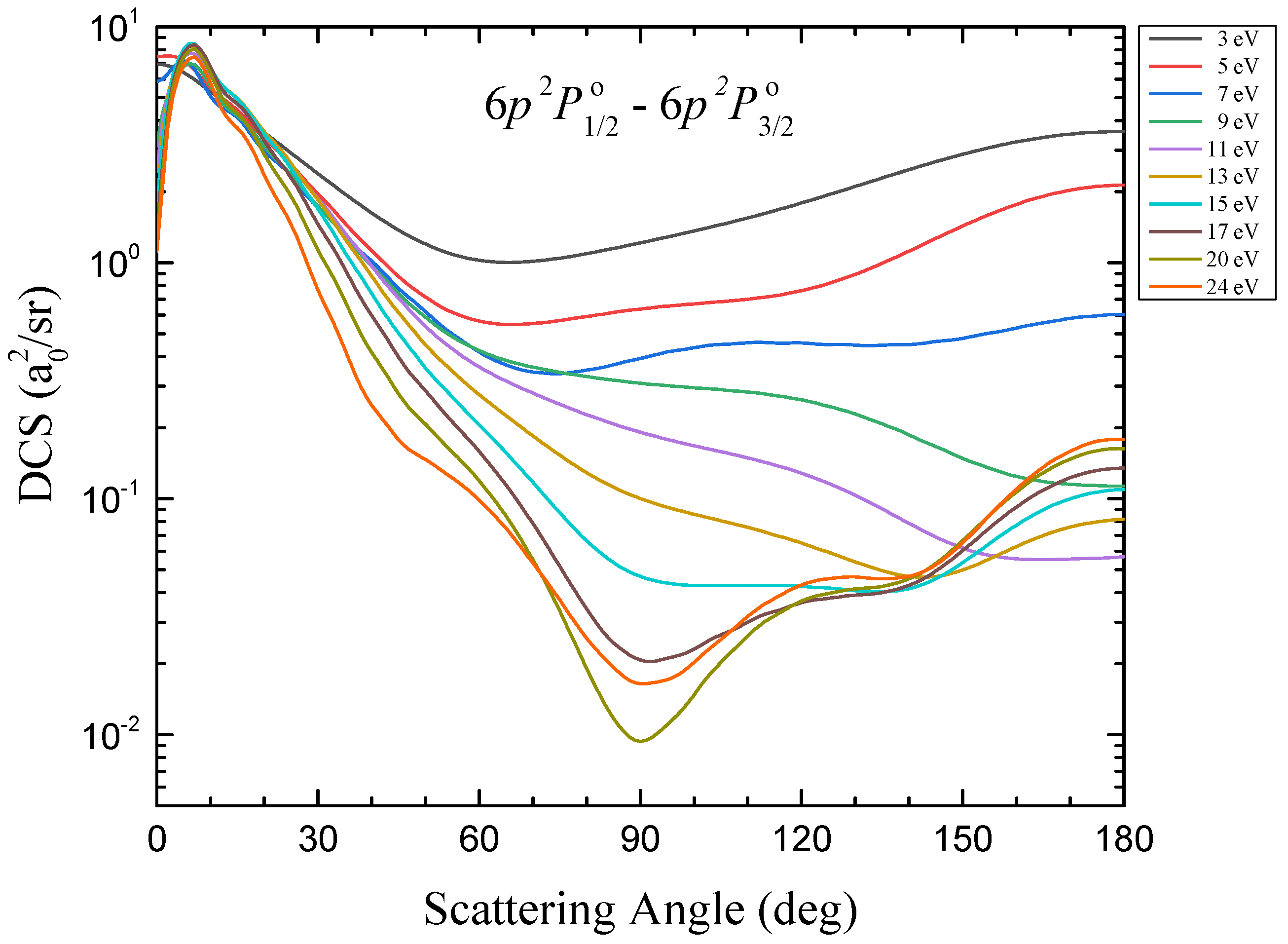
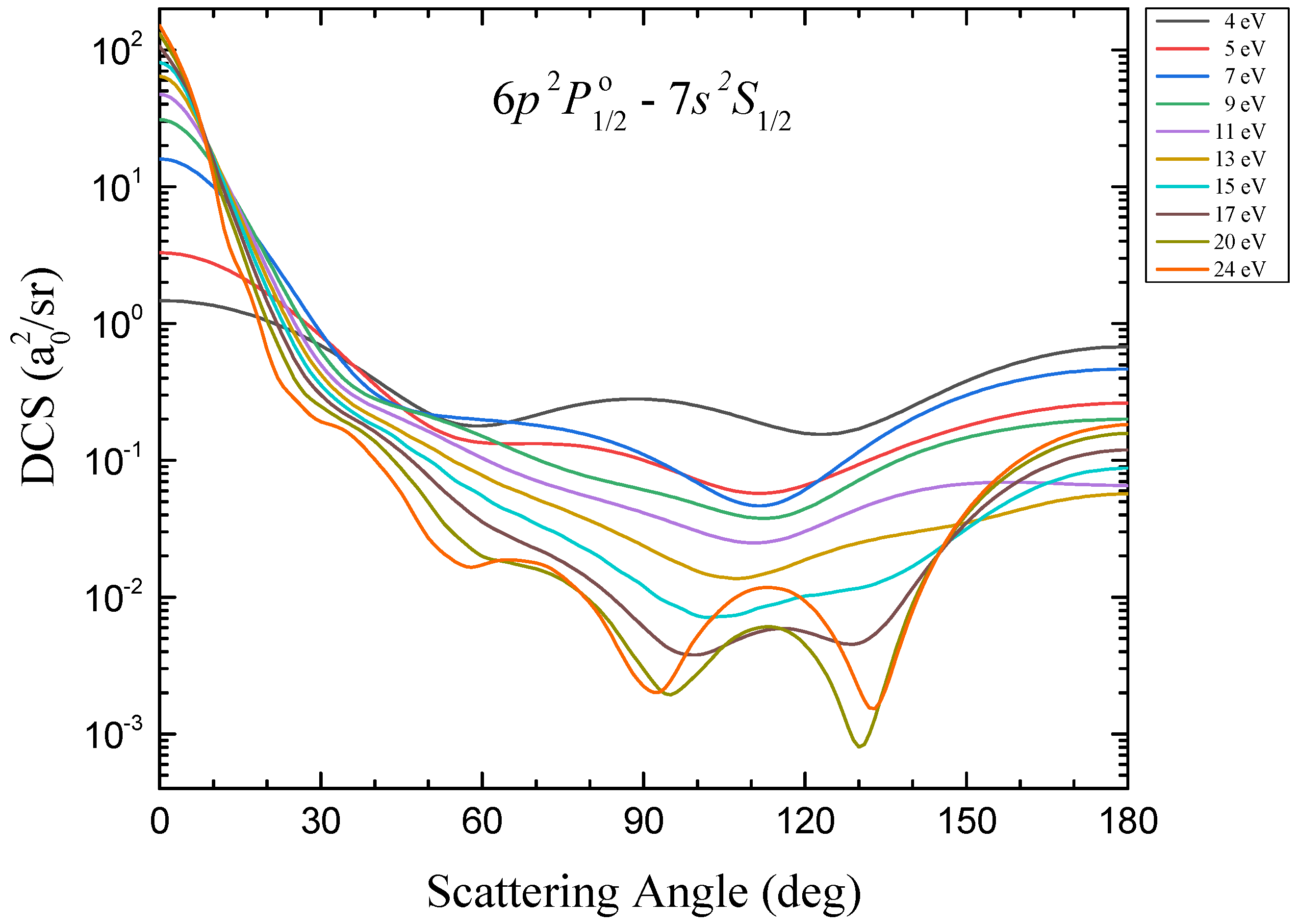
3.2. Differentical Cross-Sections
| No. | State | Term | J | NIST [25] | This Work | Difference |
|---|---|---|---|---|---|---|
| 1 | 6s26p | 2P° | 1/2 | 0.00000 | 0.00000 | 0.00000 |
| 2 | 6s26p | 2P° | 3/2 | 0.96617 | 0.93535 | −0.03082 |
| 3 | 6s27s | 2S | 1/2 | 3.28279 | 3.35298 | 0.07019 |
| 4 | 6s27p | 2P° | 1/2 | 4.23529 | 4.26149 | 0.02620 |
| 5 | 6s27p | 2P° | 3/2 | 4.35942 | 4.30594 | −0.05348 |
| 6 | 6s26d | 2D | 3/2 | 4.47805 | 4.47796 | −0.00009 |
| 7 | 6s26d | 2D | 5/2 | 4.48822 | 4.48293 | −0.00529 |
| 8 | 6s28s | 2S | 1/2 | 4.80388 | 4.81059 | 0.00671 |
| 9 | 6s28p | 2P° | 1/2 | 5.12899 | 5.12293 | −0.00606 |
| 10 | 6s28p | 2P° | 3/2 | 5.1752 | 5.15013 | −0.02507 |
| 11 | 6s27d | 2D | 3/2 | 5.20875 | 5.18402 | −0.02473 |
| 12 | 6s27d | 2D | 5/2 | 5.21341 | 5.17956 | −0.03385 |
| 13 | 6s25f | 2F° | 5/2 | 5.24681 | 5.22070 | −0.02611 |
| 14 | 6s25f | 2F° | 7/2 | 5.24681 | 5.22151 | −0.02530 |
| 15 | 6s29s | 2S | 1/2 | 5.35193 | 5.34096 | −0.01097 |
| 16 | 6s29p | 2P° | 1/2 | 5.50253 | 5.48915 | −0.01338 |
| 17 | 6s29p | 2P° | 3/2 | 5.52505 | 5.50476 | −0.02029 |
| 18 | 6s28d | 2D | 3/2 | 5.5387 | 5.51819 | −0.02051 |
| 19 | 6s28d | 2D | 5/2 | 5.54119 | 5.51857 | −0.02262 |
| 20 | 6s26f | 2F° | 5/2 | 5.55741 | 5.53341 | −0.02400 |
| 21 | 6s26f | 2F° | 7/2 | 5.55741 | 5.53366 | −0.02375 |
| 22 | 6s6p2 | 4P | 1/2 | 5.607 | 5.32811 | −0.27889 |
| 23 | 6s210s | 2S | 1/2 | 5.61609 | 5.61945 | 0.00336 |
| 24 | 6s210p | 2P° | 1/2 | 5.69575 | 5.74420 | 0.04845 |
| 25 | 6s210p | 2P° | 3/2 | 5.70868 | 5.76181 | 0.05313 |
| 26 | 6s29d | 2D | 3/2 | 5.71549 | 5.75791 | 0.04242 |
| 27 | 6s29d | 2D | 5/2 | 5.71695 | 5.75781 | 0.04086 |
| 28 | 6s27f | 2F° | 5/2 | 5.72625 | 5.75303 | 0.02678 |
| 29 | 6s27f | 2F° | 7/2 | 5.72625 | 5.75313 | 0.02688 |
| 30 | 6s210d | 2D | 3/2 | 5.82105 | 6.05811 | 0.23706 |
| 31 | 6s210d | 2D | 5/2 | 5.82205 | 6.06582 | 0.24377 |
| 32 | 6s28f | 2F° | 5/2 | 5.82783 | 6.03291 | 0.20508 |
| 33 | 6s28f | 2F° | 7/2 | 5.82783 | 6.03290 | 0.20507 |
| Lower | Upper | This Work | ||||
|---|---|---|---|---|---|---|
| Level | Level | NIST [25] | ODRT [26] | BFT [27] | V | L |
| 6s26p1/2 | 6s26d3/2 | 0.29 | 0.29 ± 0.022 | 0.34 | 0.2271 | 0.3307 |
| 6s27s1/2 | 0.134 | 0.133 ± 0.007 | 0.13 | 0.1276 | 0.1399 | |
| 6s27d3/2 | 0.075 | 0.074 ± 0.009 | 0.09 | 0.0555 | 0.0814 | |
| 6s28s1/2 | 0.018 | 0.0176 ± 0.0016 | 0.0169 | 0.0199 | ||
| 6s28d3/2 | 0.028 ± 0.004 | 0.0237 | 0.0331 | |||
| 6s29s1/2 | 0.0062 ± 0.0008 | 0.0050 | 0.0050 | |||
| 6s26p3/2 | 6s26d3/2 | 0.0411 | 0.04 ± 0.004 | 0.0349 | 0.0499 | |
| 6s26d5/2 | 0.346 | 0.346 ± 0.035 | 0.37 | 0.3100 | 0.4273 | |
| 6s27s1/2 | 0.151 | 0.151 ± 0.007 | 0.14 | 0.1295 | 0.1870 | |
| 6s27d3/2 | 0.0091 ± 0.0009 | 0.0079 | 0.0109 | |||
| 6s27d5/2 | 0.08 | 0.081 ± 0.009 | 0.08 | 0.0619 | 0.0858 | |
| 6s28s1/2 | 0.0135 | 0.0136 ± 0.0014 | 0.0118 | 0.0172 | ||
| 6s28d3/2 | 0.004 ± 0.0004 | 0.0031 | 0.0043 | |||
| 6s28d5/2 | 0.028 ± 0.003 | 0.03 | 0.0233 | 0.0316 | ||
| 6s29s1/2 | 0.0048 ± 0.0005 | 0.0027 | 0.0043 | |||
| 6s29d3/2 | 0.002 ± 0.0002 | 0.0025 | 0.0035 | |||
| 6s210s1/2 | 0.003 ± 0.0003 | 0.0023 | 0.0035 | |||
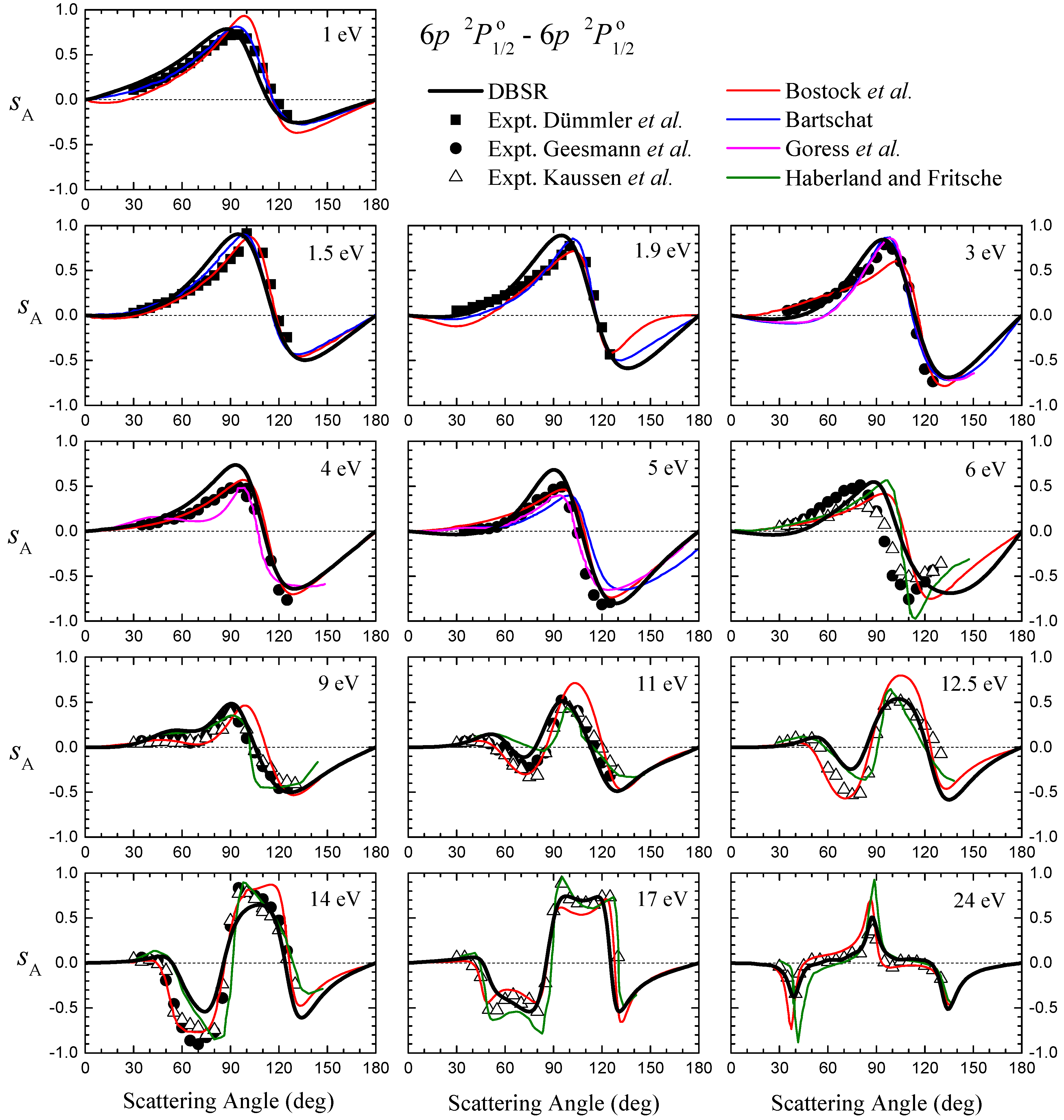
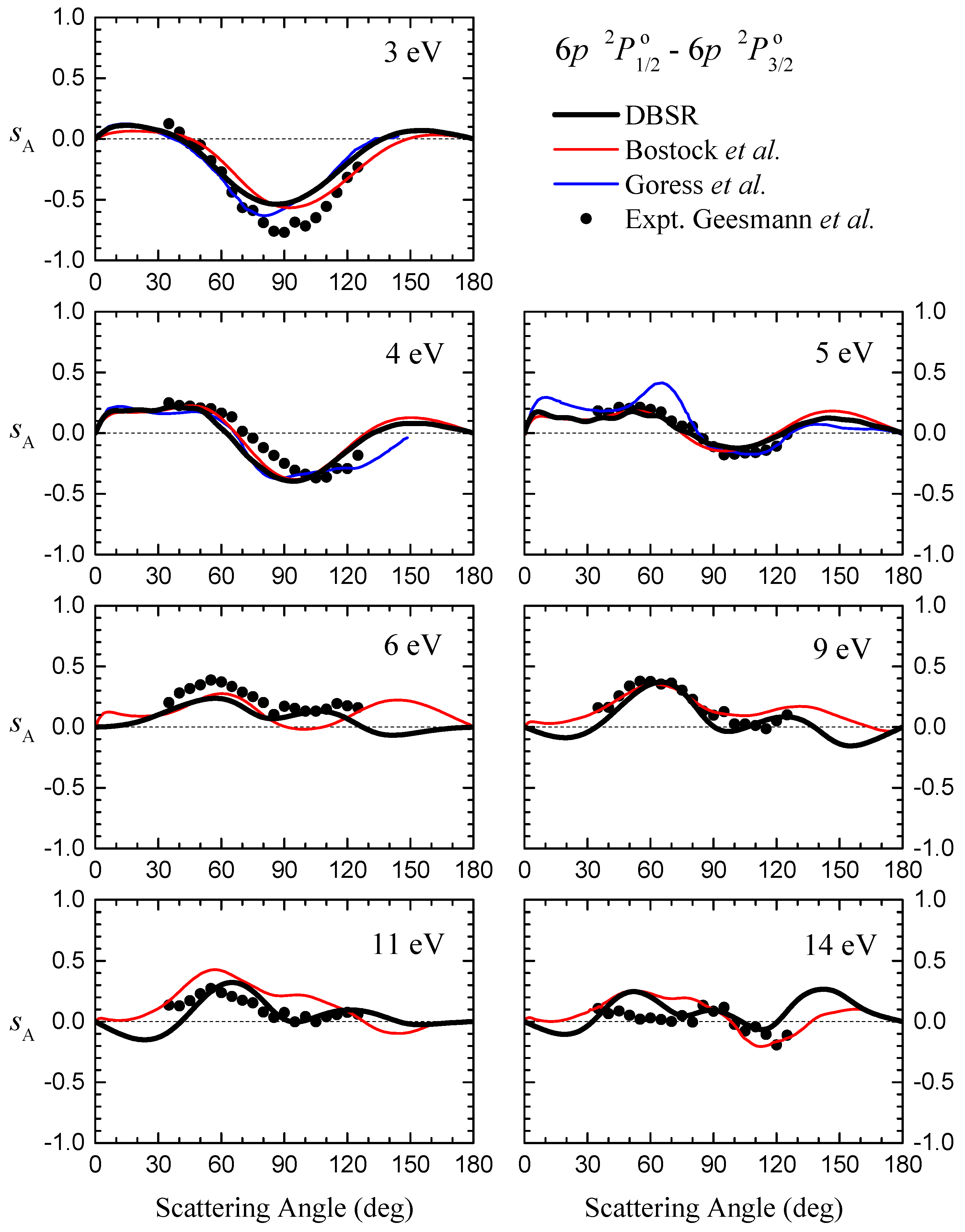
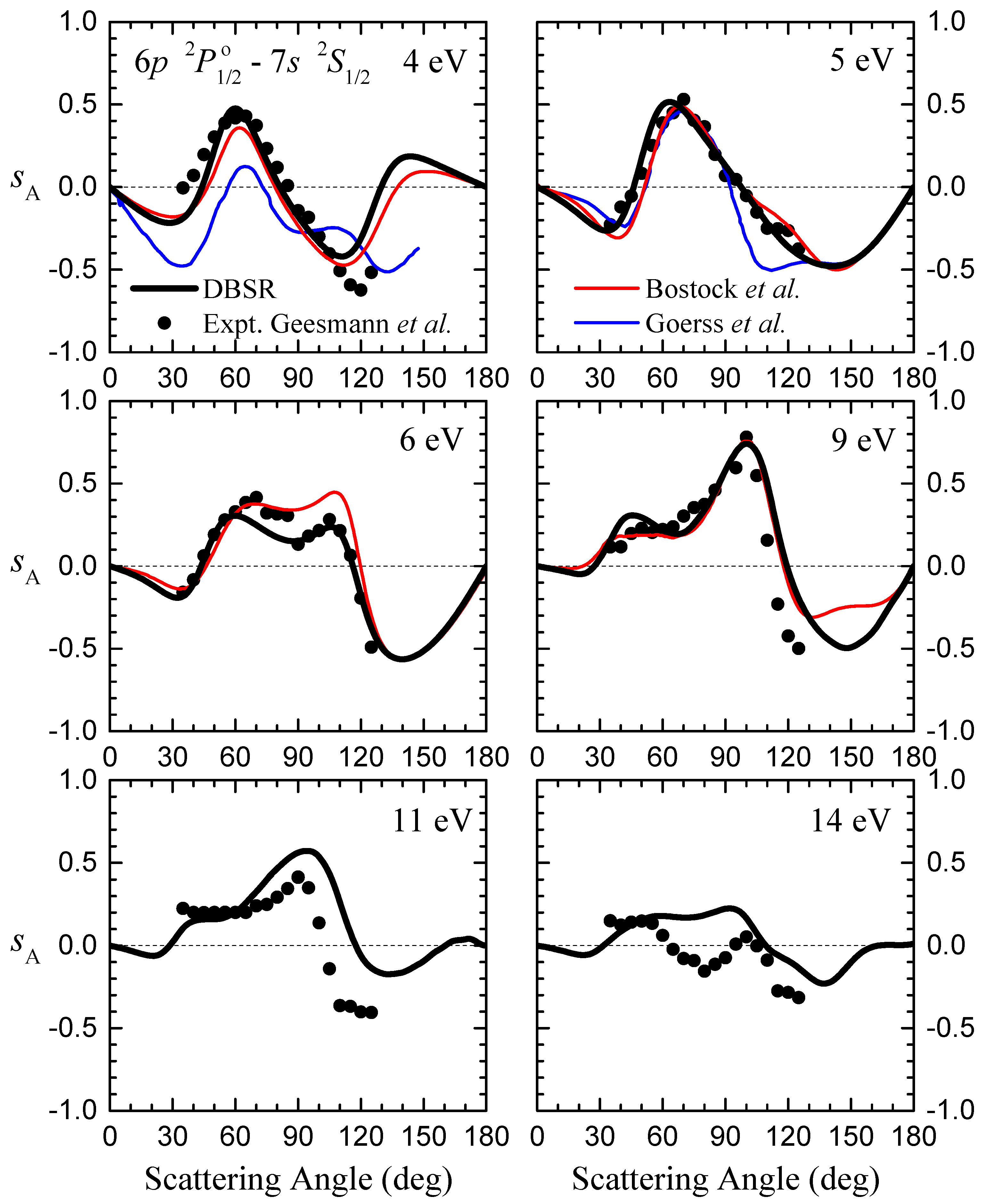
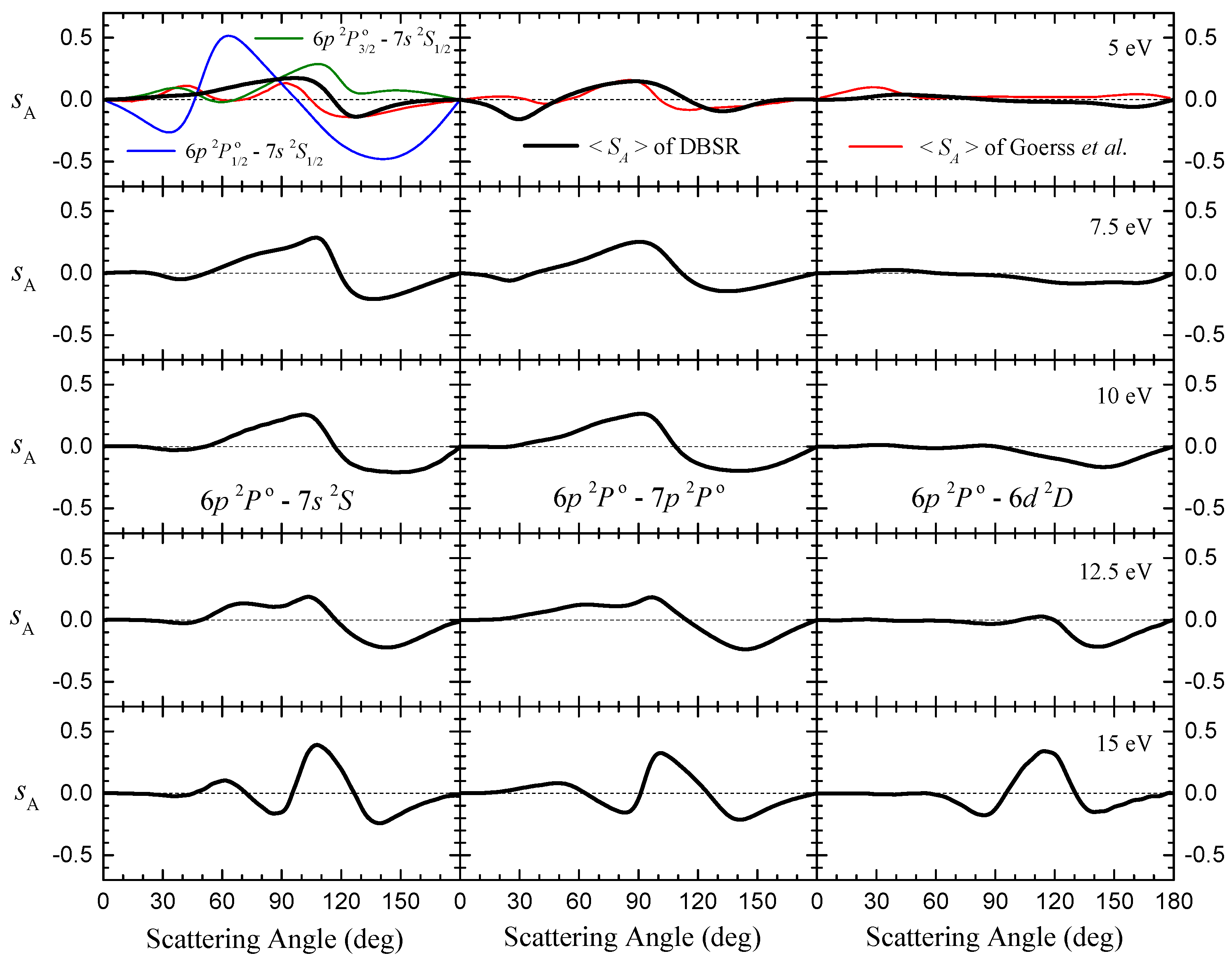
3.3. Spin Asymmetries
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kessler, J. Polarized Electrons, 2nd ed.; Springer: New York, NY, USA, 1985. [Google Scholar]
- Andersen, N.; Bartschat, K.; Broad, J.T.; Hertel, I.V. Collisional alignment and orientation of atomic outer shells: III. Spin-resolved excitation. Phys. Rep. 1997, 279, 251–396. [Google Scholar] [CrossRef]
- Andersen, N.; Bartschat, K. Polarization, Alignment, and Orientation in Atomic Collisions; Springer: New York, NY, USA, 2001. [Google Scholar]
- Hanne, G.F. Spin effects in inelastic electron–atom collisions. Phys. Rep. 1983, 95, 95–165. [Google Scholar] [CrossRef]
- Kaussen, F.; Geesmann, H.; Hanne, G.F.; Kessler, J. Study of spin polarisation in elastic scattering of electrons from Hg, Tl, Pb and Bi atoms. J. Phys. B At. Mol. Phys. 1987, 20, 151. [Google Scholar] [CrossRef]
- Geesmann, H.; Bartsch, M.; Hanne, G.F.; Kessler, J. Left–right asymmetry for scattering of polarized electrons from thallium and lead atoms. J. Phys. B At. Mol. Opt. Phys. 1991, 24, 2817. [Google Scholar] [CrossRef]
- Dummler, M.; Bartsch, M.; Geesmann, H.; Hanne, G.F.; Kessler, J. Low-energy data of the Sherman function of Hg, Tl and Pb. J. Phys. B At. Mol. Opt. Phys. 1992, 25, 4281. [Google Scholar] [CrossRef]
- Bartschat, K.; Scott, N.S. Resonances in the low-energy scattering of electrons by atomic thallium. J. Phys. B At. Mol. Phys. 1984, 17, 3787. [Google Scholar] [CrossRef]
- Bartschat, K.; Blum, K.; Burke, P.G.; Hanne, G.F.; Scott, N.S. The fine-structure effect in the low-energy scattering of electrons on Hg and Tl atoms. J. Phys. B At. Mol. Phys. 1984, 17, 3797. [Google Scholar] [CrossRef]
- Bartschat, K.; Goerss, H.-J.; Nordbeck, R.-P. Generalized STU-parameters for elastic electron scattering from thallium and lead atoms. Z. Phys. D-At. Mol. Clust. 1990, 17, 25–31. [Google Scholar] [CrossRef]
- Bartschat, K. Close-coupling calculations for low-energy elastic from thallium atoms. Z. Phys. D-At. Mol. Clust. 1994, 30, 85–90. [Google Scholar] [CrossRef]
- Goerss, H.-J.; Nordbeck, R.-P.; Bartschat, K. Generalized STU parameters for elastic and inelastic low-energy scattering of electrons from thallium atoms. J. Phys. B At. Mol. Opt. Phys. 1991, 24, 2833. [Google Scholar] [CrossRef]
- Haberland, R.; Fritsche, L. On the elastic scattering of low-energy electrons by Hg, Tl, Pb and Bi atoms. J Phys. B At. Mol. Phys. 1987, 20, 121. [Google Scholar] [CrossRef]
- Fritsche, L.; Kroner, C.; Reinert, T. A consistent relativistic theory of electron scattering by atoms. J. Phys. B At. Mol. Opt. Phys. 1992, 25, 4287. [Google Scholar] [CrossRef]
- Bostock, C.J.; Fursa, D.V.; Bray, I. Relativistic convergent close-coupling calculation of spin asymmetries for electron-thallium scattering. Phys. Rev. A 2012, 86, 062701. [Google Scholar] [CrossRef]
- Zatsarinny, O. BSR: B-spline atomic R-matrix codes. Comput. Phys. Commun. 2006, 174, 273–356. [Google Scholar] [CrossRef]
- Zatsarinny, O.; Bartschat, K. Relativistic B-spline R-matrix method for electron collisions with atoms and ions: Application to low-energy electron scattering from Cs. Phys. Rev. A 2008, 77, 062701. [Google Scholar] [CrossRef]
- Zatsarinny, O.; Bartschat, K. The B-spline R-matrix method for atomic processes: Application to atomic structure, electron collisions, and photoionization. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 112001. [Google Scholar] [CrossRef]
- Jönsson, P.; He, X.; Fischer, C.F.; Grant, I.P. The grasp2K relativistic atomic structure package. Comput. Phys. Commun. 2007, 177, 597–622. [Google Scholar] [CrossRef]
- Zatsarinny, O.; Fischer, C.F. DBSR_HF: A B-spline Dirac–Hartree–Fock program. Comput. Phys. Commun. 2016, 202, 287–303. [Google Scholar] [CrossRef] [Green Version]
- Fischer, C.F.; Zatsarinny, O. A B-spline Galerkin method for the Dirac equation. Comput. Phys. Commun. 2009, 180, 879–886. [Google Scholar] [CrossRef] [Green Version]
- Burke, V.M.; Noble, C.J. Farm—A flexible asymptotic R-matrix package. Comput. Phys. Commun. 1995, 85, 471–500. [Google Scholar] [CrossRef]
- Bartschat, K. Excitation and ionization of atoms by interaction with electrons, positrons, protons and photons. Phys. Rep. 1989, 180, 1–81. [Google Scholar] [CrossRef]
- Grum-Grzhimailo, A.N. MJK: A program to calculate observable quantities in electron–atom collisions. Comput. Phys. Commun. 2003, 152, 101–119. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (Ver. 5.8). 2020. Available online: https://physics.nist.gov/asd (accessed on 29 September 2021).
- Gallagher, A.; Lurio, A. Thallium Oscillator Strengths and 6d2D3/2 State hfs. Phys. Rev. A 1964, 136, 87. [Google Scholar] [CrossRef]
- Andersen, T.; Sørensen, G. Systematic study of atomic lifetimes in gallium, indium, and thallium measured by the beam-foil technique. Phys. Rev. A 1972, 5, 2447. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Du, H.-L.; Zhu, X.-M.; Zatsarinny, O.; Bartschat, K. Relativistic B-Spline R-Matrix Calculations for Electron Scattering from Thallium Atoms. Atoms 2021, 9, 94. https://doi.org/10.3390/atoms9040094
Wang Y, Du H-L, Zhu X-M, Zatsarinny O, Bartschat K. Relativistic B-Spline R-Matrix Calculations for Electron Scattering from Thallium Atoms. Atoms. 2021; 9(4):94. https://doi.org/10.3390/atoms9040094
Chicago/Turabian StyleWang, Yang, Hai-Liang Du, Xi-Ming Zhu, Oleg Zatsarinny, and Klaus Bartschat. 2021. "Relativistic B-Spline R-Matrix Calculations for Electron Scattering from Thallium Atoms" Atoms 9, no. 4: 94. https://doi.org/10.3390/atoms9040094
APA StyleWang, Y., Du, H.-L., Zhu, X.-M., Zatsarinny, O., & Bartschat, K. (2021). Relativistic B-Spline R-Matrix Calculations for Electron Scattering from Thallium Atoms. Atoms, 9(4), 94. https://doi.org/10.3390/atoms9040094








