Electron-Impact Ionization of Heavy Atoms Using the Time-Dependent Close-Coupling Method
Abstract
1. Introduction
2. Theory
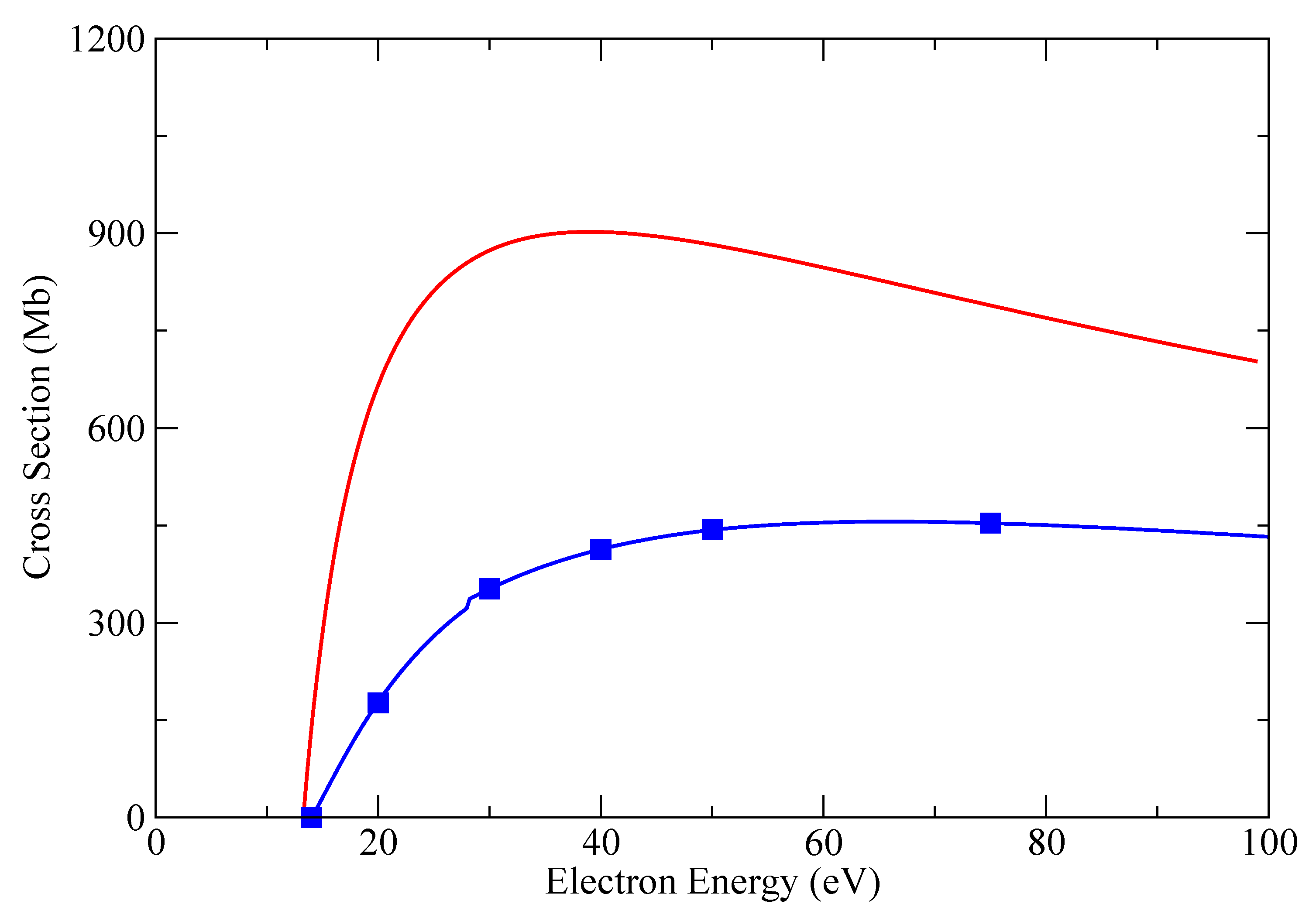
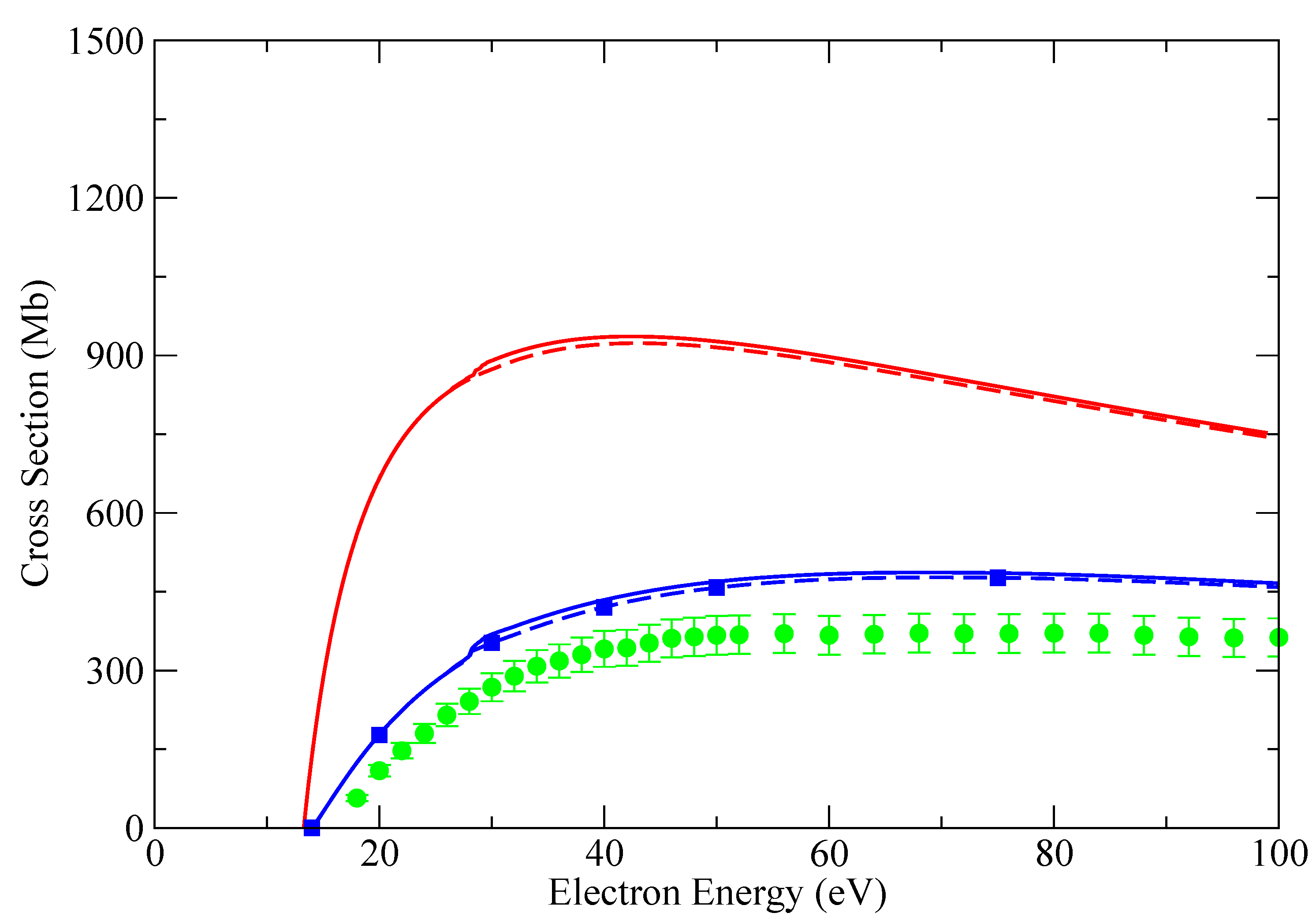
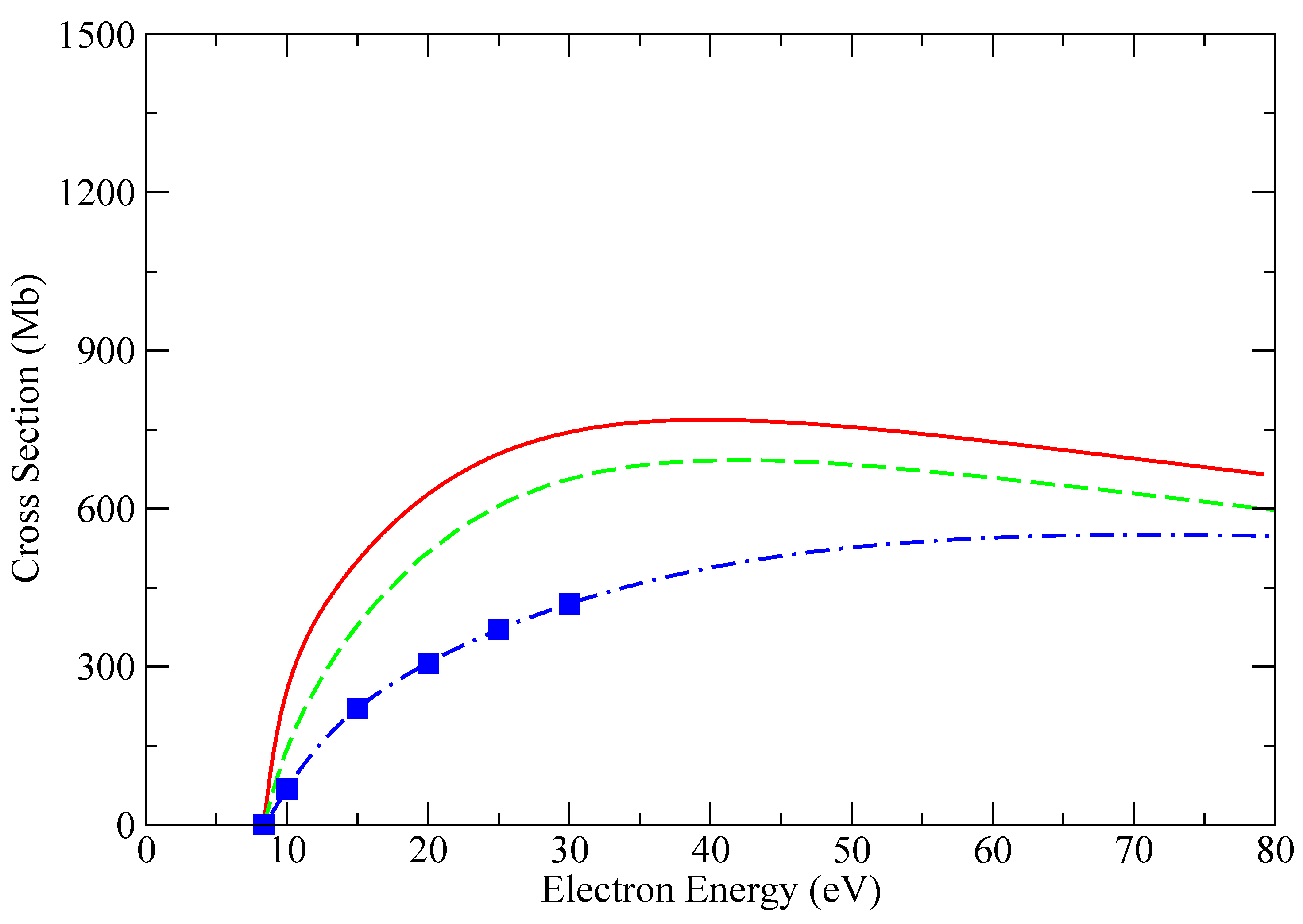
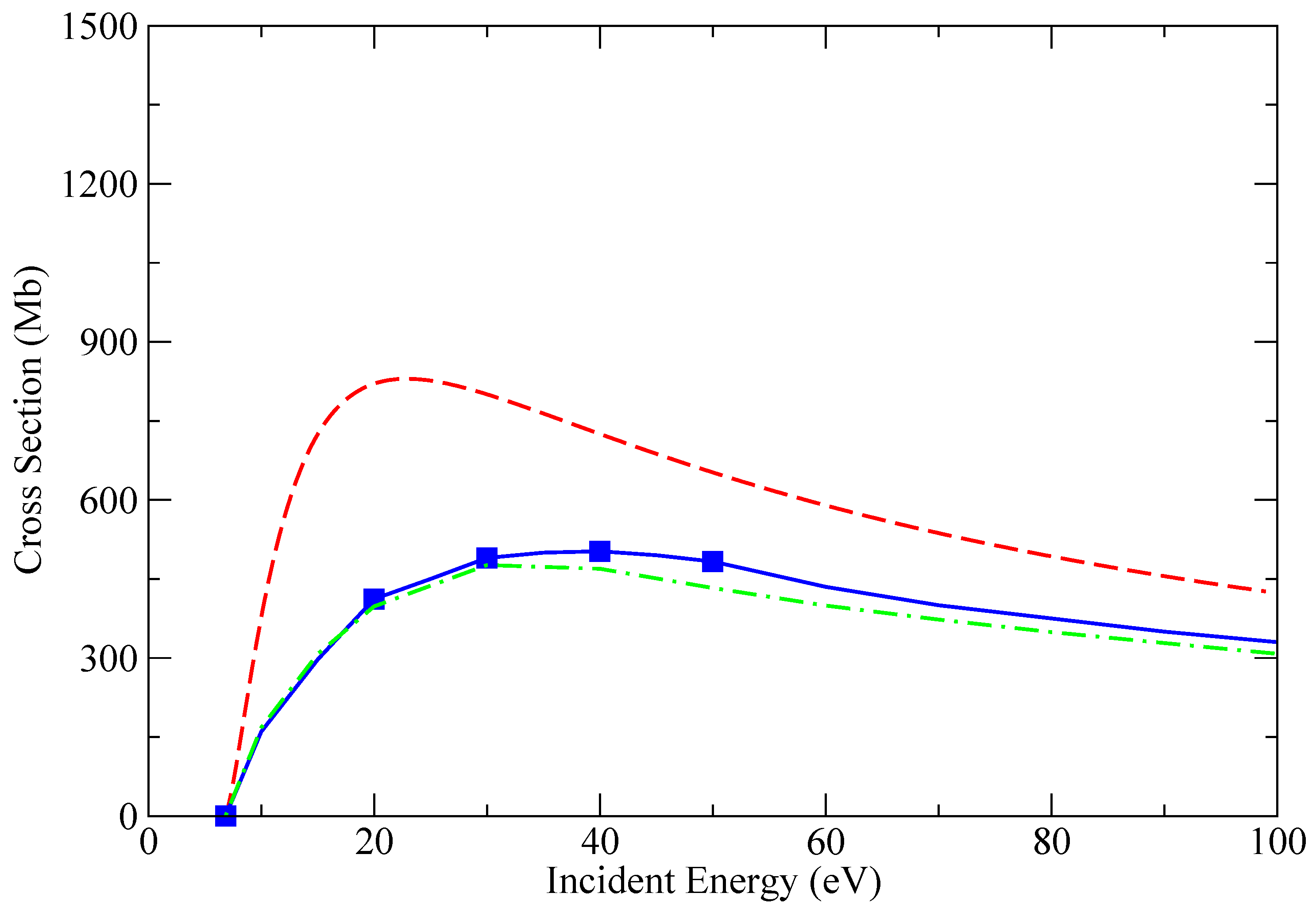
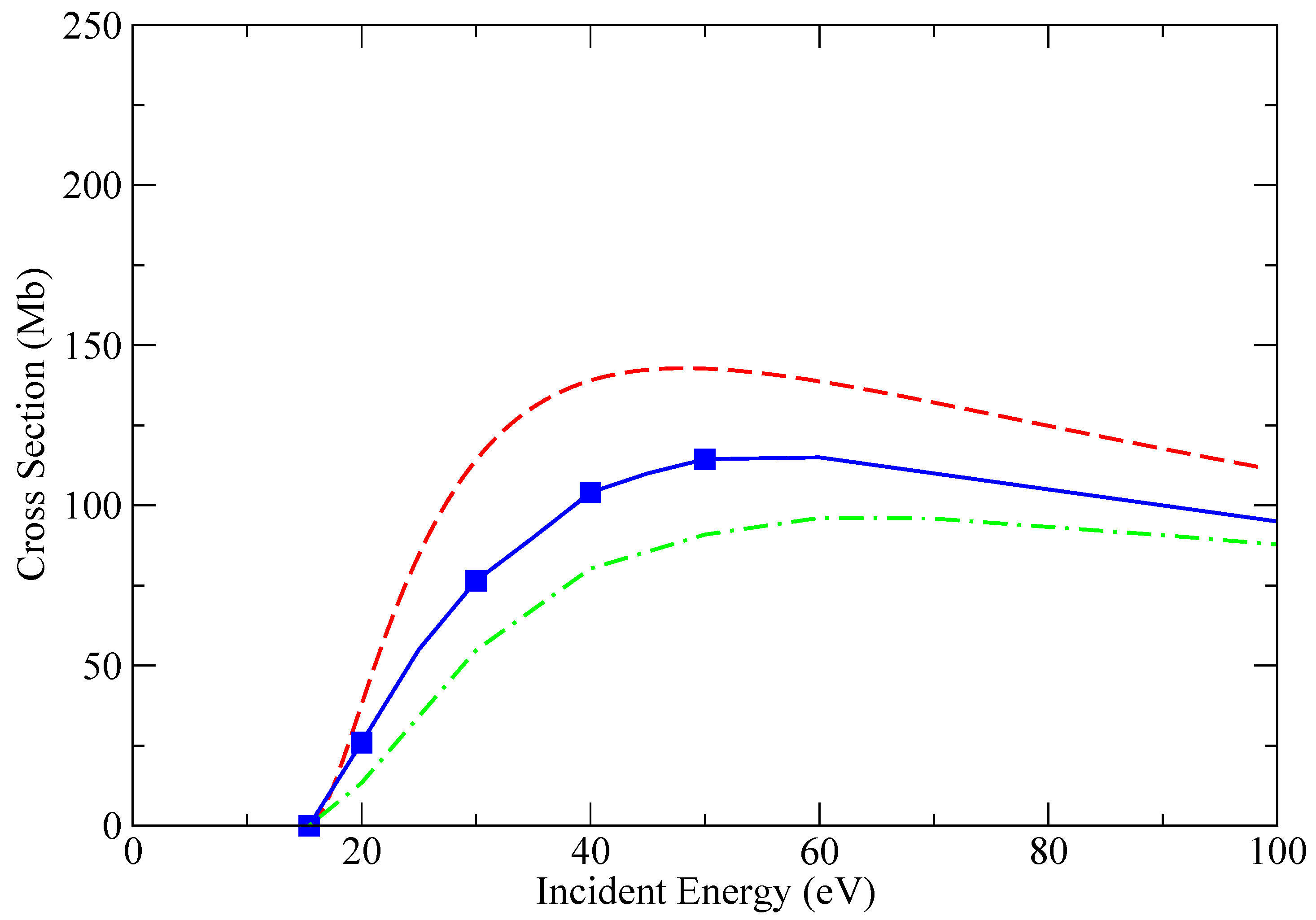
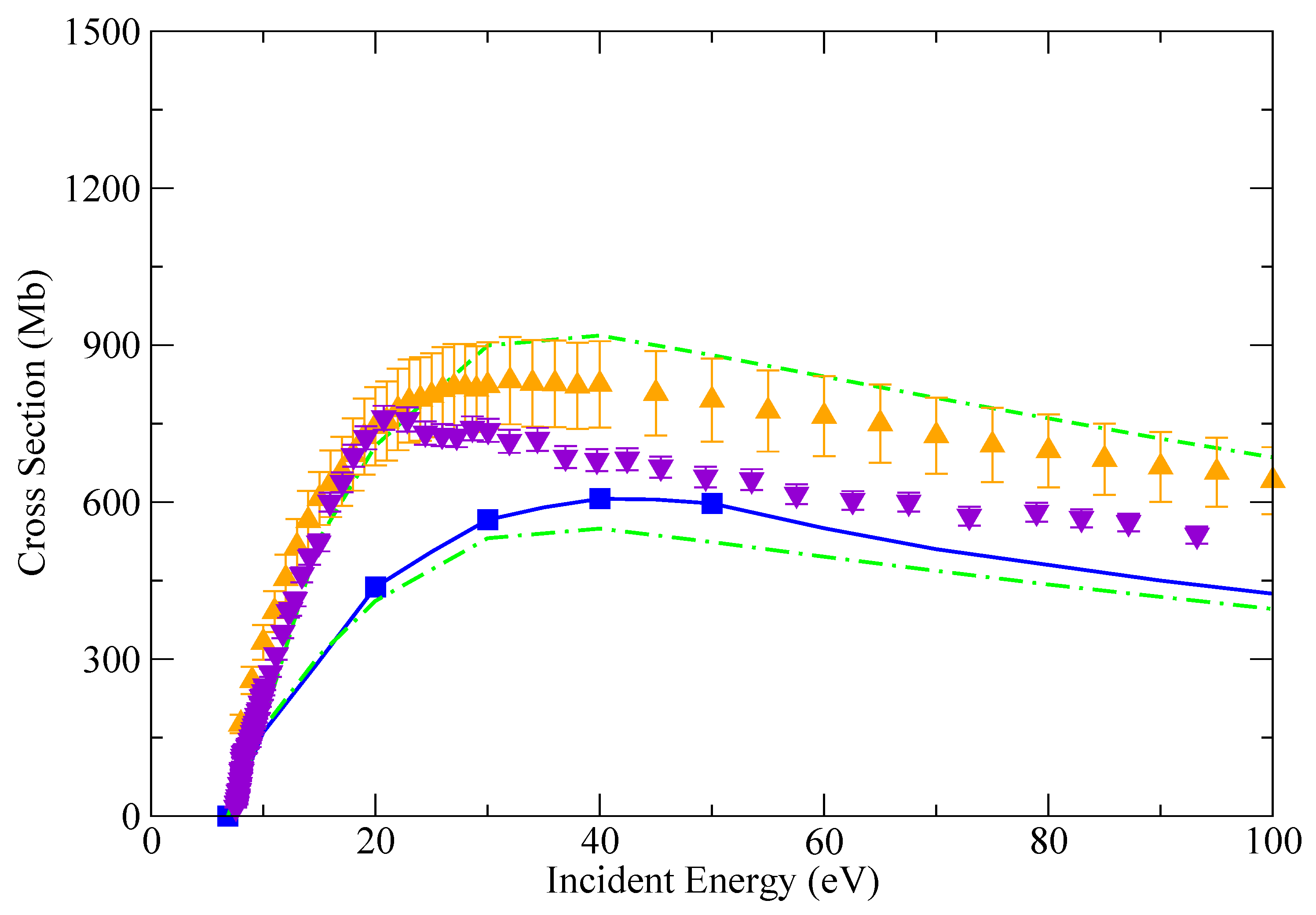
3. Results
4. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pindzola, M.S.; Loch, S.D. Electron-impact ionization of the Kr atom. J. Phys. B 2019, 52, 245205. [Google Scholar] [CrossRef]
- Pindzola, M.S.; Loch, S.D.; Foster, A.R. Electron-impact single and double ionization of W. J. Phys. B 2017, 50, 095201. [Google Scholar] [CrossRef]
- Pindzola, M.S.; Loch, S.D.; Colgan, J.P. Electron-impact ionization of the Pb atom. Eur. Phys. J. D 2021, 75, 45. [Google Scholar]
- Matthews, G.F.; Su, M.-G.; Sun, D.-X.; Fu, Y.-B.; Dong, C.-Z. Theoretical Analysis of 4f and 5p Inner-Shell Excitations of W-W3+ Ions. Phys. Scr. 2007, 128, 137. [Google Scholar] [CrossRef]
- Alonso-Medina, A. Experimental determination of the Stark widths of Pb I spectral lines in a laser-induced plasma. Spectrochim Acta Port B 2008, 63, 598–602. [Google Scholar] [CrossRef]
- Kallenbach, A.; Bernert, M.; Dux, R.; Casali, L.; Eich, T.; Giannone, L.; Herrmann, A.; McDermott, R.; Mlynek, A.; Müller, H.W. Impurity seeding for tokamak power exhaust: From present devices via ITER to DEMO. Plasma Phys. Control. Fusion 2013, 55, 124041. [Google Scholar] [CrossRef]
- Linnell, J.A.; Gillimore, A.D. Internal plasma potential measurements of a Hall thruster using plasma lens focusing. Phys. Plasmas 2006, 13, 103504. [Google Scholar] [CrossRef]
- Syage, J.A. Electron-impact cross sections for multiple ionization of Kr and Xe. Phys. Rev. A 1992, 46, 5666. [Google Scholar] [CrossRef] [PubMed]
- van Eck, M.P.; Fursa, D.V.; Bray, I.; Zatsarinny, O.; Bartschat, K. Cross sections for electronscattering from atomic lead. J. Phys. B 2020, 53, 015204. [Google Scholar] [CrossRef]
- Freund, R.S.; Wetzel, R.C.; Shul, R.J.; Hayes, T.R. Cross-section measurements for electron-impact ionization of atoms. Phys. Rev. A 1990, 41, 3575. [Google Scholar] [CrossRef]
- McCartney, P.C.E.; Shah, M.B.; Geddes, J.; Gilbody, H.B. Cross-section measurements for electron-impact ionization of atoms. J. Phys. B 1998, 31, 4821. [Google Scholar] [CrossRef]
- Goswarni, B.; Naghma, R.; Antony, B. Calculation of electron impact total ionization cross sections for tungsten, uranium and their oxide radicals. Int. J. Mass Spectrom. 2014, 372, 8. [Google Scholar]
- Pindzola, M.S. Electron-impact ionization of the inner subshells of Au. J. Phys. B 2015, 48, 015201. [Google Scholar] [CrossRef]
- Pindzola, M.S. Electron-impact ionization of the inner subshells of uranium. Phys. Rev. A 2014, 90, 022708. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pindzola, M.S.; Loch, S.D.; Colgan, J.P. Electron-Impact Ionization of Heavy Atoms Using the Time-Dependent Close-Coupling Method. Atoms 2021, 9, 32. https://doi.org/10.3390/atoms9020032
Pindzola MS, Loch SD, Colgan JP. Electron-Impact Ionization of Heavy Atoms Using the Time-Dependent Close-Coupling Method. Atoms. 2021; 9(2):32. https://doi.org/10.3390/atoms9020032
Chicago/Turabian StylePindzola, Michael S., Stuart D. Loch, and James P. Colgan. 2021. "Electron-Impact Ionization of Heavy Atoms Using the Time-Dependent Close-Coupling Method" Atoms 9, no. 2: 32. https://doi.org/10.3390/atoms9020032
APA StylePindzola, M. S., Loch, S. D., & Colgan, J. P. (2021). Electron-Impact Ionization of Heavy Atoms Using the Time-Dependent Close-Coupling Method. Atoms, 9(2), 32. https://doi.org/10.3390/atoms9020032




