Low-Energy Electron Elastic Total Cross Sections for Ho, Er, Tm, Yb, Lu, and Hf Atoms
Abstract
1. Introduction
2. Method of Calculation
3. Results
4. Summary and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Kasdan, K.; Lineberger, W.C. Alkali-metal negative ions. II. Laser photoelectron spectrometry. Phys. Rev. A 1974, 10, 1658. [Google Scholar] [CrossRef]
- Msezane, A.Z.; Felfli, Z.; Sokolovski, D. Novel mechanism for nanoscale catalysis. J. Phys. B 2010, 43, 201001. [Google Scholar] [CrossRef]
- Msezane, A.Z.; Felfli, Z.; Sokolovski, D. Cold fusion mechanism in nanoscale catalysis. Eur. News 2010, 41, 11. [Google Scholar]
- Cheng, S.-B.; Castleman, A.W. Direct experimental observation of weakly-bound character of the attached electron in europium anion. Sci. Rep. 2015, 5, 12414. [Google Scholar] [CrossRef] [PubMed]
- Felfli, Z.; Msezane, A.Z. Conundrum in Measured Electron Affinities of Complex Heavy Atoms. JAMCNP 2018, 5, 73–80. [Google Scholar] [CrossRef][Green Version]
- Msezane, A.Z. Negative Ion Binding Energies in Complex Heavy Systems. JAMCNP 2018, 5, 195–204. [Google Scholar] [CrossRef][Green Version]
- Hotop, H.; Lineberger, W.C. Dye-laser photodetachment studies of Au−, Pt−, PtN−, and Ag−. J. Chem. Phys. 2003, 58, 2379. [Google Scholar] [CrossRef]
- Andersen, T.; Haugen, H.K.; Hotop, H. Binding Energies in Atomic Negative Ions: III. J. Phys. Chem. Ref. Data 1999, 28, 1511. [Google Scholar] [CrossRef]
- Zheng, W.; Li, X.; Eustis, S.; Grubisic, A.; Thomas, O.; De Clercq, H.; Bowen, K. Anion photoelectron spectroscopy of Au−(H2O) 1, 2, Au2-(D2O) 1–4, and AuOH−. Chem. Phys. Lett. 2007, 444, 232–236. [Google Scholar] [CrossRef]
- Gibson, D.; Davies, B.J.; Larson, D.J. The electron affinity of platinum. J. Chem. Phys. 1993, 98, 5104. [Google Scholar] [CrossRef]
- Bilodeau, R.C.; Scheer, M.; Haugen, H.K.; Brooks, R.L. Near-threshold laser spectroscopy of iridium and platinum negative ions: Electron affinities and the threshold law. Phys. Rev. A 1999, 61, 012505. [Google Scholar] [CrossRef]
- Leimbach, D.; Sundberg, J.; Guo, Y.; Ahmed, R.; Ballof, J.; Bengtsson, L.; Pamies, F.B.; Borschevsky, A.; Chrysalidis, K.; Eliav, E.; et al. The electron affinity of astatine. arXiv 2002, arXiv:2002.11418. [Google Scholar]
- Huang, D.-L.; Dau, P.D.; Liu, H.T.; Wang, L.-S. High-resolution photoelectron imaging of cold C60- anions and accurate determination of the electron affinity of C60 . J. Chem. Phys. 2014, 140, 224315. [Google Scholar] [CrossRef] [PubMed]
- Brink, C.; Andersen, L.H.; Hvelplund, P.; Mathur, D.; Voldstad, J.D. Laser photodetachment of C60− and C70− ions cooled in a storage ring. Chem. Phys. Lett. 1995, 233, 52–56. [Google Scholar] [CrossRef]
- Msezane, A.Z.; Felfli, Z. New insights in low-energy electron-fullerene interactions. Chem. Phys. 2018, 503, 50–55. [Google Scholar] [CrossRef]
- Felfli, Z.; Msezane, A.Z. Simple method for determining fullerene negative ion formation. Eur. Phys. J. D 2018, 72, 78. [Google Scholar] [CrossRef]
- Andersen, H.H.; Andersen, T.; Pedersen, U.V. Search for stable or metastable negative Yb ions. J. Phys. B 1998, 31, 2239. [Google Scholar] [CrossRef]
- Davis, V.T.; Thompson, J.S. Measurement of the electron affinity of thulium. Phys. Rev. A 2001, 65, 010501. [Google Scholar] [CrossRef]
- Felfli, Z.; Msezane, A.Z.; Sokolovski, D. Resonances in low-energy electron elastic cross sections for lanthanide atoms. Phys. Rev. A 2009, 79, 012714. [Google Scholar] [CrossRef]
- O’Malley, S.M.; Beck, D.R. Valence calculations of lanthanide anion binding energies: 6p attachments to 4fn6s2 thresholds. Phys. Rev. A 2008, 78, 012510. [Google Scholar] [CrossRef]
- Davis, V.T.; Thompson, J.S. An experimental investigation of the atomic europium anion. Phys. B 2004, 37, 1961. [Google Scholar] [CrossRef]
- Msezane, A.Z.; Felfli, Z. Atomic Negative Ions Creation: Application in Nanocatalysis. In Advances in Nanotechnology; Bartul, Z., Trenor, J., Eds.; Nova Science Publishers Inc.: New York, NY, USA, 2017; Volume 17, pp. 1–41. ISBN 978-1-53611-004-3. [Google Scholar]
- Felfli, Z.; Msezane, A.Z.; Sokolovski, D. Strong resonances in low-energy electron elastic total and differential cross sections for Hf and Lu atoms. Phys. Rev. A 2008, 78, 030703. [Google Scholar] [CrossRef]
- Davis, V.T.; Thompson, J.S. Measurement of the electron affinity of lutetium. J. Phys. B 2001, 34, L433. [Google Scholar] [CrossRef]
- Vosko, S.H.; Chevary, J.A. Prediction of a further irregularity in the electron filling of subshell: Lu-(Xe)4f145d16s26p1 and its relation to the group IIIB anions. J. Phys. B 1993, 26, 873. [Google Scholar] [CrossRef]
- Eliav, E.; Kaldor, U.; Ishikawa, Y. Transition energies of ytterbium, lutetium, and lawrencium by the relativistic coupled-cluster method. Phys. Rev. A 1995, 52, 291. [Google Scholar] [CrossRef]
- Felfli, Z.; Msezane, A.Z. Negative Ion Formation in Low-Energy Electron Collisions with the Actinide Atoms Th, Pa, U, Np and Pu. Appl. Phys. Res. 2019, 11, 52. [Google Scholar] [CrossRef][Green Version]
- Luo, Z.; Chen, X.; Li, J.; Ning, C. Precision measurement of the electron affinity of niobium. Phys. Rev. A 2016, 93, 020501. [Google Scholar] [CrossRef]
- Cole, L.A.; Perdew, J.P. Calculated electron affinities of the elements. Phys. Rev. A 1982, 25, 1265. [Google Scholar] [CrossRef]
- Calaminici, P.; Mejia-Olvera, R. Structures, Frequencies, and Energy Properties of Small Neutral, Cationic, and Anionic Niobium Clusters. J. Phys. Chem. C 2011, 115, 11891–11897. [Google Scholar] [CrossRef]
- Feigerle, C.S.; Corderman, R.R.; Bobashev, S.V.; Lineberger, W.C. Binding energies and structure of transition metal negative ions. J. Chem. Phys. 1981, 74, 1580. [Google Scholar] [CrossRef]
- Pan, L.; Beck, D.R. Calculations of Hf-electron affinity and photodetachment partial cross sections. J. Phys. B 2010, 43, 025002. [Google Scholar] [CrossRef][Green Version]
- Felfli, Z.; Msezane, A.Z.; Sokolovski, D. Low-energy electron elastic collision cross sections for ground and excited Tm, Lu and Hf atoms. NIMB 2011, 269, 1046–1052. [Google Scholar] [CrossRef][Green Version]
- Hiscox, A.; Brown, B.M.; Marletta, M. On the low energy behavior of Regge poles. J. Math. Phys. 2010, 51, 102104. [Google Scholar] [CrossRef]
- Frautschi, S.C. Regge Poles and S-matrix Theory; Benjamin: New York, NY, USA, 1963; Chapter X. [Google Scholar] [CrossRef]
- D’Alfaro, V.; Regge, T.E. Potential Scattering; North-Holland Pub. Co.: Amsterdam, The Netherlands, 1965. [Google Scholar]
- Thylwe, K.W. On relativistic shifts of negative-ion resonances. Eur. Phys. J. D 2012, 66, 7. [Google Scholar] [CrossRef]
- Mulholland, H.P. An asymptotic expansion for Σ(2n+1)exp (Àσ(n+1/2)2). Proc. Camb. Phil. Soc. 1928, 24, 280–289. [Google Scholar] [CrossRef]
- Macek, J.H.; Krstic, P.S.; Ovchinnikov, S.Y. Regge Oscillations in Integral Cross Sections for Proton Impact on Atomic Hydrogen. Phys. Rev. Lett. 2004, 93, 183203. [Google Scholar] [CrossRef]
- Sokolovski, D.; Felfli, Z.; Ovchinnikov, S.Y.; Macek, J.H.; Msezane, A.Z. Regge oscillations in electron-atom elastic cross sections. Phys. Rev. A 2007, 76, 012705. [Google Scholar] [CrossRef]
- Dolmatov, V.K.; Amusia, M.Y.; Chernysheva, L.V. Electron elastic scattering off A@C60: The role of atomic polarization under confinement. Phys. Rev. A 2017, 95, 012709. [Google Scholar] [CrossRef]
- Felfli, Z.; Belov, S.; Avdonina, N.B.; Marletta, M.; Msezane, A.Z.; Naboko, S.N. Regge Poles Trajectories for Nonsingular Potentials: The Thomas-Fermi Potentials. In Proceedings of the Third International Workshop on Contemporary Problems in Mathematical Physics; Govaerts, J., Hounkonnou, M.N., Msezane, A.Z., Eds.; World Scientific: Singapore, 2004; pp. 217–232. ISBN 981-256-030-0. [Google Scholar]
- Belov, S.; Thylwe, K.-E.; Marletta, M.; Msezane, A.Z.; Naboko, S.N. On Regge pole trajectories for a rational function approximation of Thomas–Fermi potentials. J. Phys. A 2010, 43, 365301. [Google Scholar] [CrossRef]
- Burke, P.G.; Tate, C. A PROGRAM FOR CALCULATING REGGE TRAJECTORIES IN POTENTIAL SCATTERING. Comp. Phys. Commun. 1969, 1, 97. [Google Scholar] [CrossRef]
- Connor, J.N.L. New theoretical methods for molecular collisions: The complex angular-momentum approach. J. Chem. Soc. Faraday Trans. 1990, 86, 1627. [Google Scholar] [CrossRef]
- Regge, T. Bound states, shadow states and Mandelstam representation. Nuovo Cim. 1960, 18, 947–956. [Google Scholar] [CrossRef]
- Fabrikant, I.I.; Lebedev, V.S. Quenching of Rydberg states by atoms with small electron affinities. J. Phys. B 2000, 33, 1521. [Google Scholar] [CrossRef]
- Reicherts, M.; Roth, T.; Gopalan, A.; Ruf, M.W.; Hotop, H.; Desfrancois, C.; Fabrikant, I.I. Controlled formation of weakly bound atomic negative ions by electron transfer from state-selected Rydberg atoms. Eur. Phys. Lett. 1997, 40, 129. [Google Scholar] [CrossRef]
- Bahrim, C.; Thumm, U. Low-lying 3Po and 3Se states of Rb−, Cs−, and Fr−. Phys. Rev. A 2000, 61, 022722. [Google Scholar] [CrossRef]
- Johnson, W.R.; Guet, C. Elastic scattering of electrons from Xe, Cs+, and Ba2+. Phys. Rev. A 1994, 49, 1041. [Google Scholar] [CrossRef]
- Felfli, Z.; Msezane, A.Z. Resonances in low-energy electron elastic scattering from Fullerenes. J. Phys. Conf. Series 2017, 875, 052014. [Google Scholar] [CrossRef]
- Burrow, P.D.; Michejda, J.A.; Comer, J. Low-energy electron scattering from Mg, Zn, Cd and Hg: Shape resonances and electron affinities. J. Phys. B 1976, 9, 3225. [Google Scholar] [CrossRef]
- Davis, V.T.; Thompson, J.; Covington, A. Laser photodetachment electron spectroscopy studies of heavy atomic anions. Nucl. Instrum. Meth. Phys. Res. B 2005, 241, 118–124. [Google Scholar] [CrossRef][Green Version]
- Tang, R.; Chen, X.; Fu, X.; Wang, H.; Ning, C. Electron affinity of the hafnium atom. Phys. Rev. A 2018, 98, 020501. [Google Scholar] [CrossRef]
- Nadeau, M.J.; Litherland, A.E.; Garwan, M.A.; Zhao, X.L. Electric dissociation of negative ions—II. Nucl. Instrum. Meth. Phys. Res. B 1994, 92, 265–269. [Google Scholar] [CrossRef]
- Chevary, J.A.; Vosko, S.H. More theoretical evidence for binding of a 6p electron in the lanthanide anions: Tm-[Xe]4f136s26p1. J. Phys. B 1994, 27, 657. [Google Scholar] [CrossRef]
- Dzuba, V.A.; Gribakin, G.F. Correlation-potential method for negative ions and electron scattering. Phys. Rev. A 1994, 49, 2483. [Google Scholar] [CrossRef] [PubMed]
- Vosko, S.H.; Chevary, J.A.; Mayer, I.L. Predictions of stable Yb-in the Po1/2 state: The importance of spin-orbit coupling. J. Phys. B 1991, 24, L225. [Google Scholar] [CrossRef]
- Tang, R.; Si, R.; Fei, Z.; Fu, X.; Lu, Y.; Brage, T.; Liu, H.; Chen, C.; Ning, C. Candidate for Laser Cooling of a Negative Ion: High-Resolution Photoelectron Imaging of Th−. Phys. Rev. Lett. 2019, 123, 203002. [Google Scholar] [CrossRef]
- Si, R.; Froese Fischer, C. Electron affinities of At and its homologous elements Cl, Br, I. Phys. Rev. A 2018, 98, 052504. [Google Scholar] [CrossRef]
- Li, J.; Zhao, Z.; Andersson, M.; Zhang, X.; Chen, C. Theoretical Study for the Electron Affinities of Negative Ions with the MCDHF Method. J. Phys. B 2012, 45, 165004. [Google Scholar] [CrossRef]
- Zollweg, R.J. Electron Affinities of the Heavy Elements. J. Chem. Phys. 1969, 50, 4251. [Google Scholar] [CrossRef]
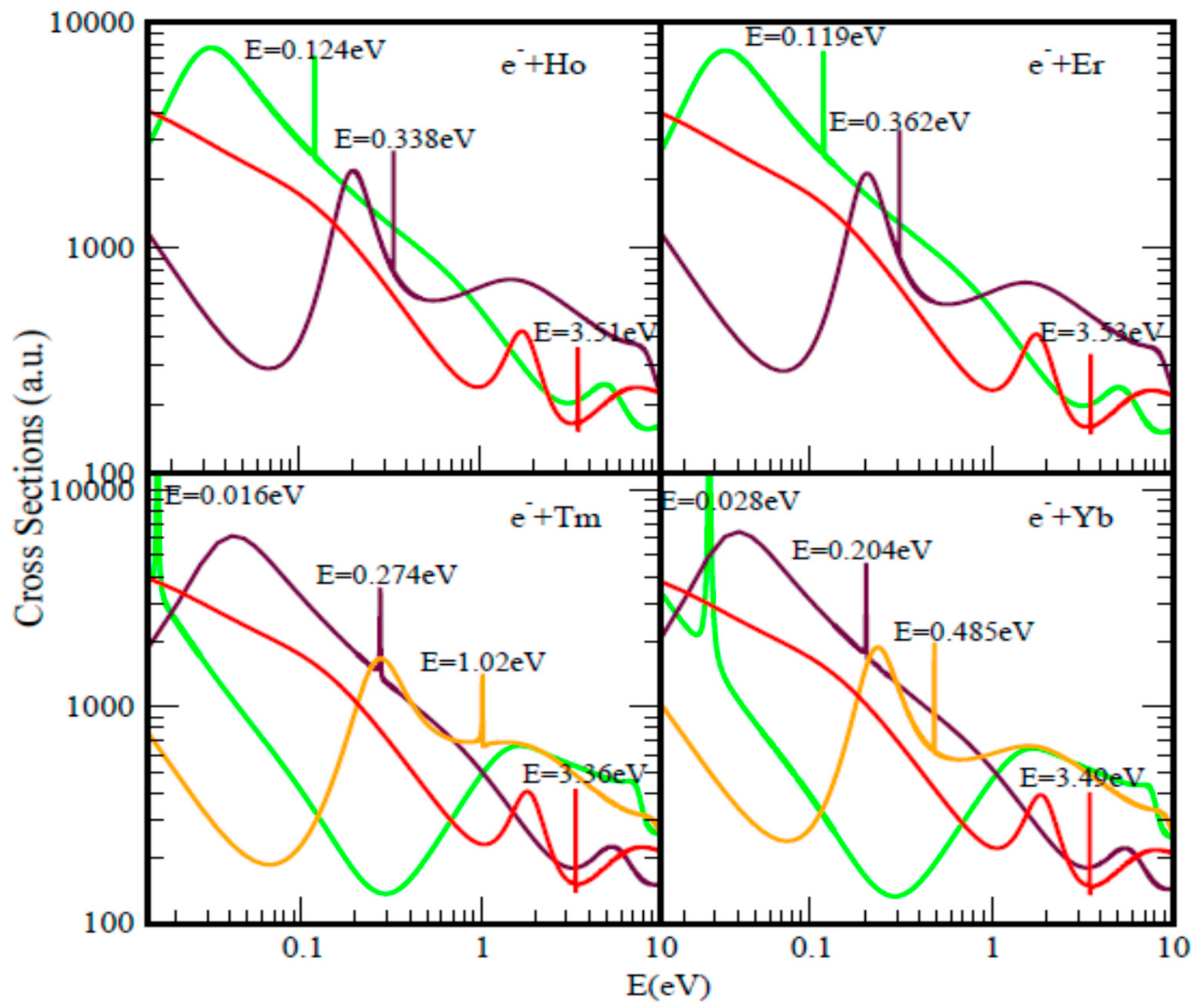
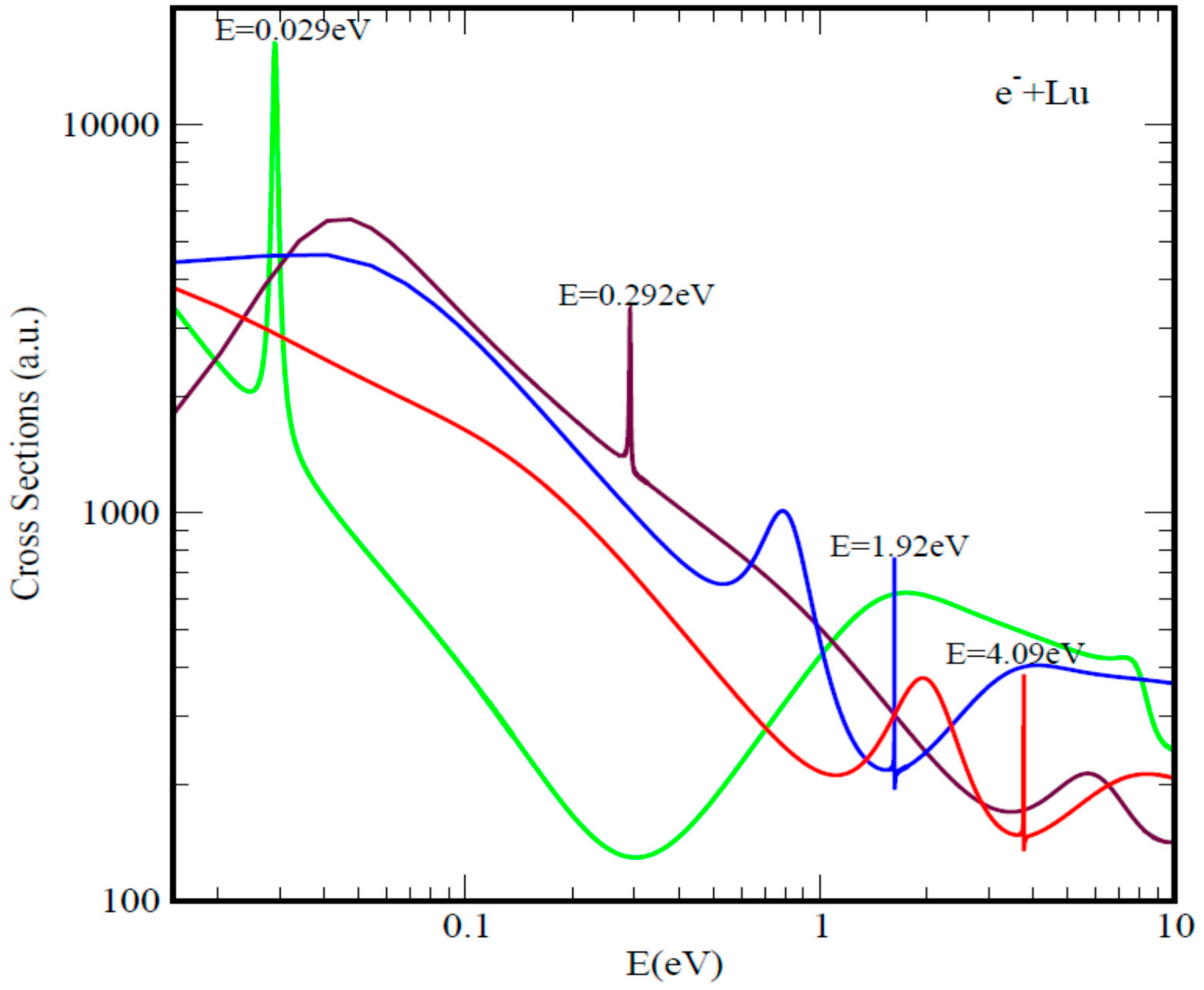
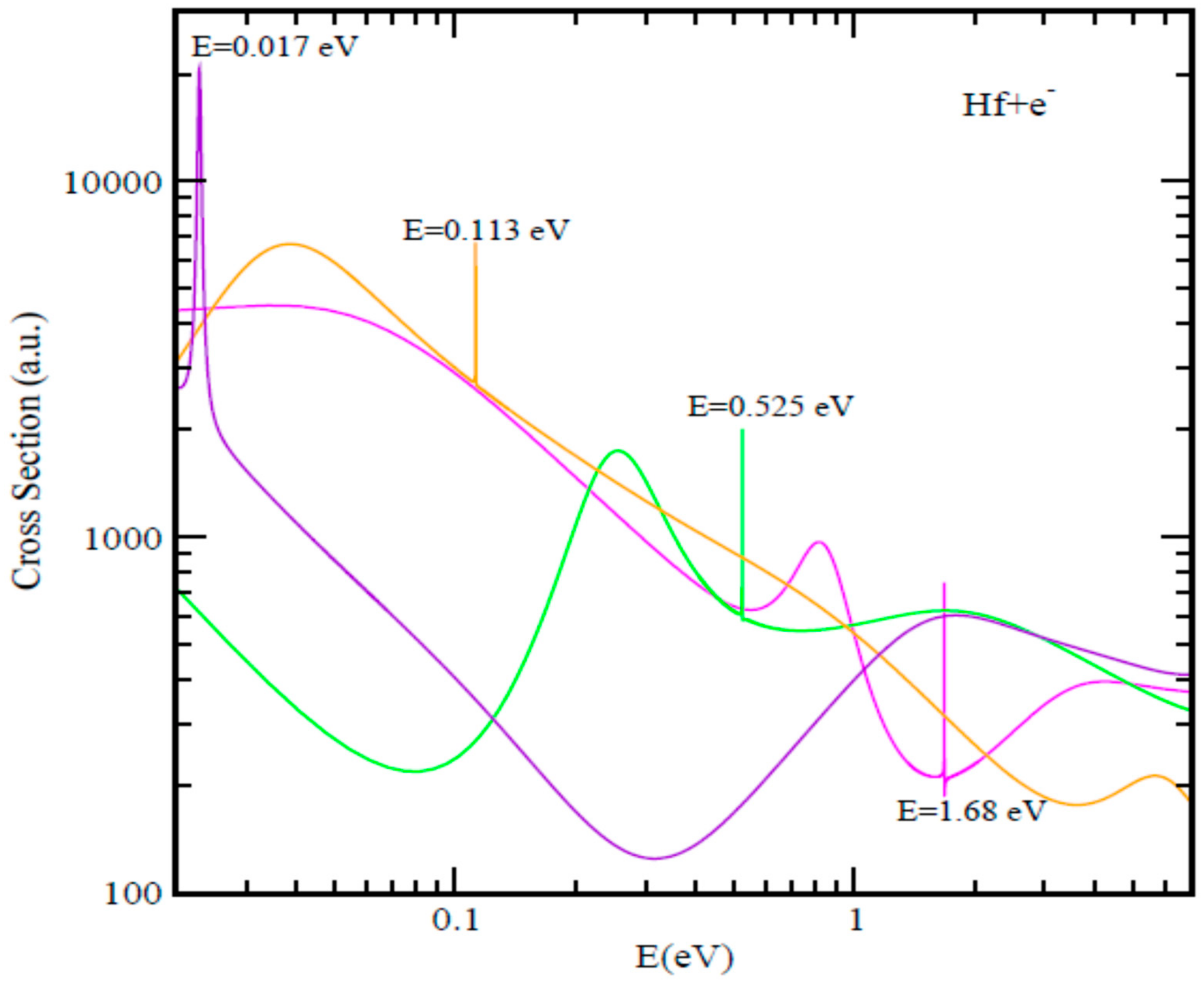
| Atom. | BEs | EAs | BEs | BEs | BEs | EAs | SR-1 | SR-2 | SR-3 | R-T Min |
|---|---|---|---|---|---|---|---|---|---|---|
| GRS | EXPT | MS-1 | EX-1 | EX-2 | Theory | GRS | ||||
| Ho | 3.51 | N/A | 0.338 | 0.124 | - | 0.338 [19] | 1.73 | 0.205 | 0.0331 | 3.43 |
| Er | 3.53 | N/A | 0.362 | 0.119 | - | 0.362 [19] | 1.8 | 0.191 | 0.0343 | 3.49 |
| Tm | 3.36 | 1.029 [18] | 1.02 | 0.274 | 0.016 | 0.032 [55] | 1.81 | 0.273 | 0.042 | 3.38 |
| 0.027–0.136 [56] | ||||||||||
| 1.02 [5] | ||||||||||
| Yb | 3.49 | <0.003 [17] | 0.485 | 0.204 | 0.028 | 0.036 [57] | 1.76 | 0.231 | 0.039 | 3.51 |
| 0.054 [58] | ||||||||||
| Lu | 4.09 | 0.346 [24,53] | 1.92 | 0.292 | 0.029 | 0.257 [26] | 2.01 | 0.801 | 0.046 | 4.07 |
| 0.190 [25] | ||||||||||
| Hf | 1.68 | 0.178 [54] | 0.525 | 0.113 | 0.017 | 0.114 [32] | 0.821 | 0.252 | 0.021 | 1.67 |
| 0.113 [33] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Felfli, Z.; Msezane, A.Z. Low-Energy Electron Elastic Total Cross Sections for Ho, Er, Tm, Yb, Lu, and Hf Atoms. Atoms 2020, 8, 17. https://doi.org/10.3390/atoms8020017
Felfli Z, Msezane AZ. Low-Energy Electron Elastic Total Cross Sections for Ho, Er, Tm, Yb, Lu, and Hf Atoms. Atoms. 2020; 8(2):17. https://doi.org/10.3390/atoms8020017
Chicago/Turabian StyleFelfli, Zineb, and Alfred Z. Msezane. 2020. "Low-Energy Electron Elastic Total Cross Sections for Ho, Er, Tm, Yb, Lu, and Hf Atoms" Atoms 8, no. 2: 17. https://doi.org/10.3390/atoms8020017
APA StyleFelfli, Z., & Msezane, A. Z. (2020). Low-Energy Electron Elastic Total Cross Sections for Ho, Er, Tm, Yb, Lu, and Hf Atoms. Atoms, 8(2), 17. https://doi.org/10.3390/atoms8020017





