Electron Broadening Operator Including Penetrating Collisions for Hydrogen
Abstract
1. Introduction
2. The Collision Operator
2.1. General Form
2.2. Collision Integral
- The duration of a collision is small compared to the mean time between collisions. In that case, radiation can be neglected during the collision, which can be considered as instantaneous.
- The duration of a collision is much smaller than the inverse HWHM (half width at half maximum) of the profile .
- The collisions are complete, which means that they can be considered as instantaneous in comparison with . Therefore, the radiation process of the emitter can be decoupled from the interaction process with perturbers.
2.3. Collision Integral and Factor Accounting for Penetration
2.4. Consequences of Penetration
3. Approximate Form of the Collision Operator
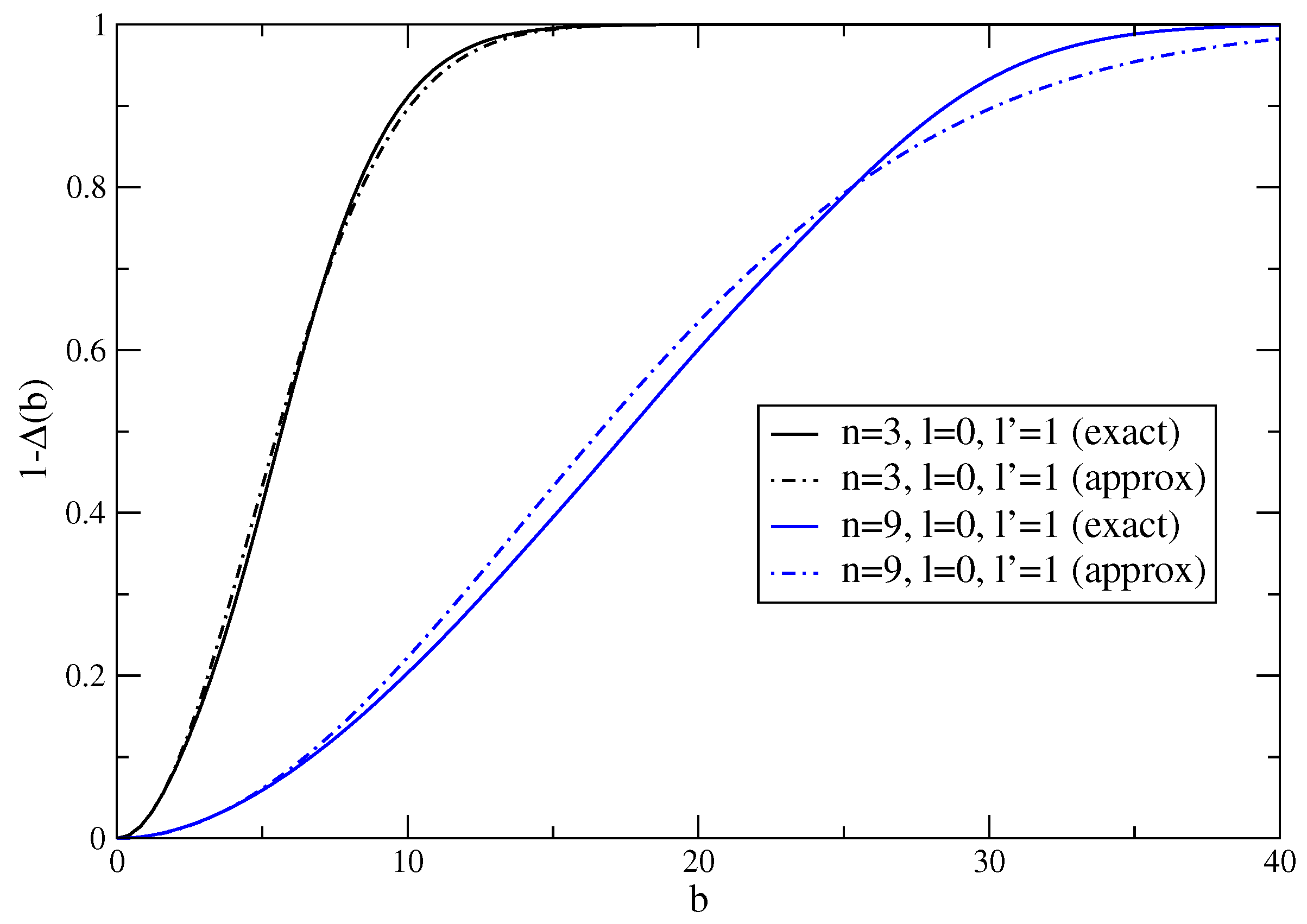
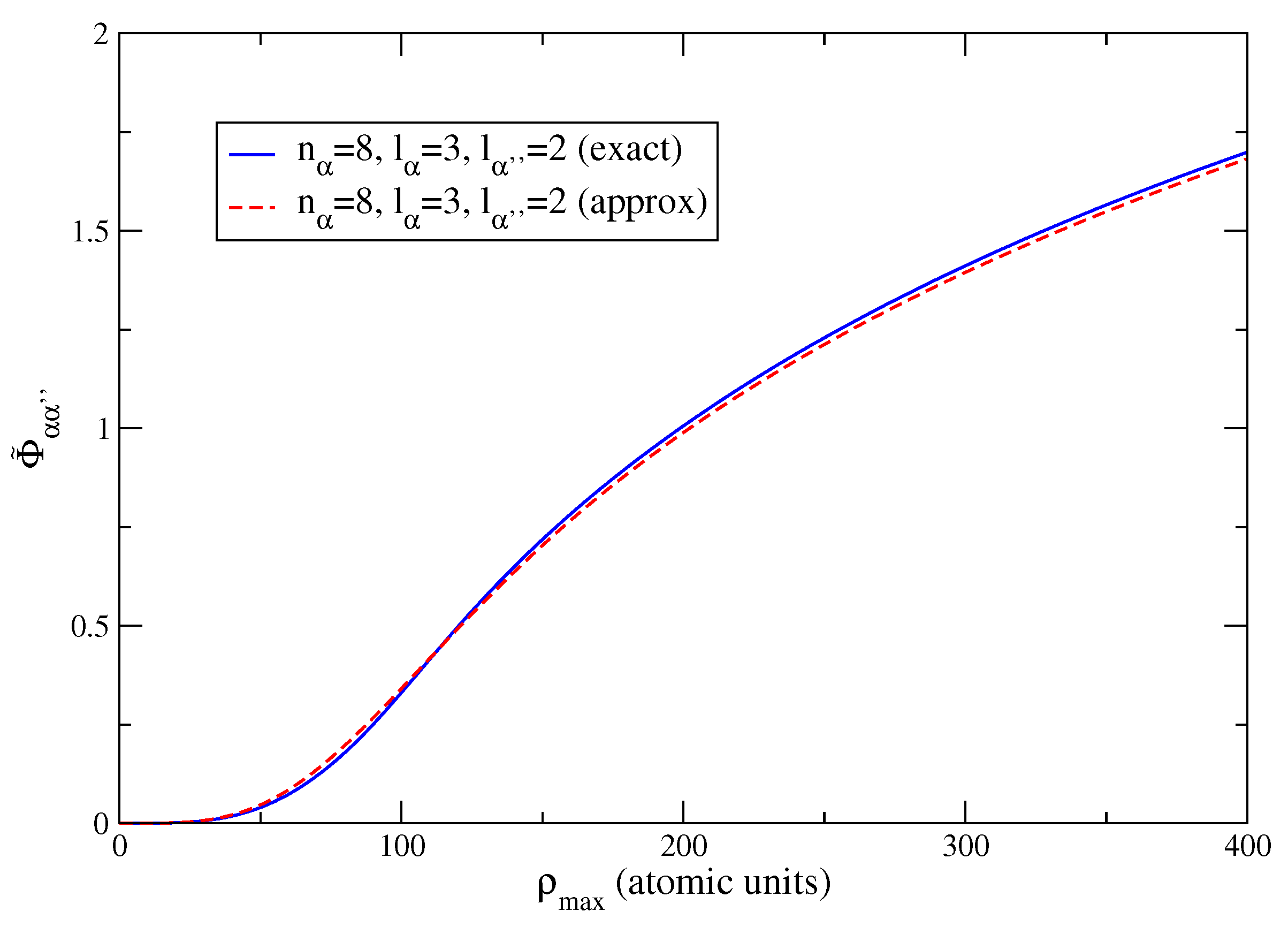
3.1. Collision Integral and Function
3.2. Analytical Representation of the Collision Operator
4. Strong Collisions
4.1. Case of Standard Theory
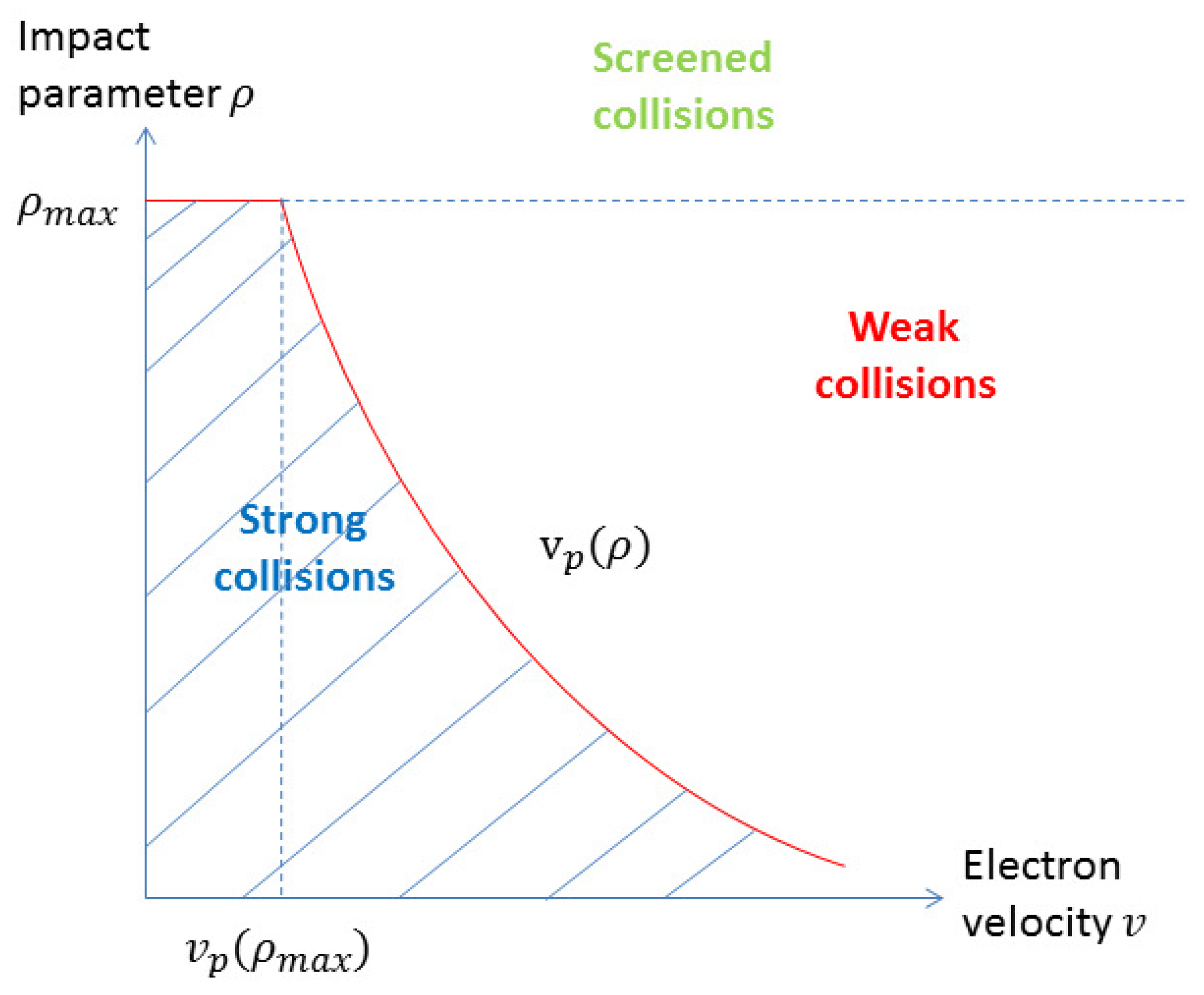
- Weak collisions: or . Unitarity ensured, in the integrand.
- Strong collisions: or . Unitarity violated, in the integrand (Lorentz–Weisskopf approach).
- Screened collisions: or . No contribution to .
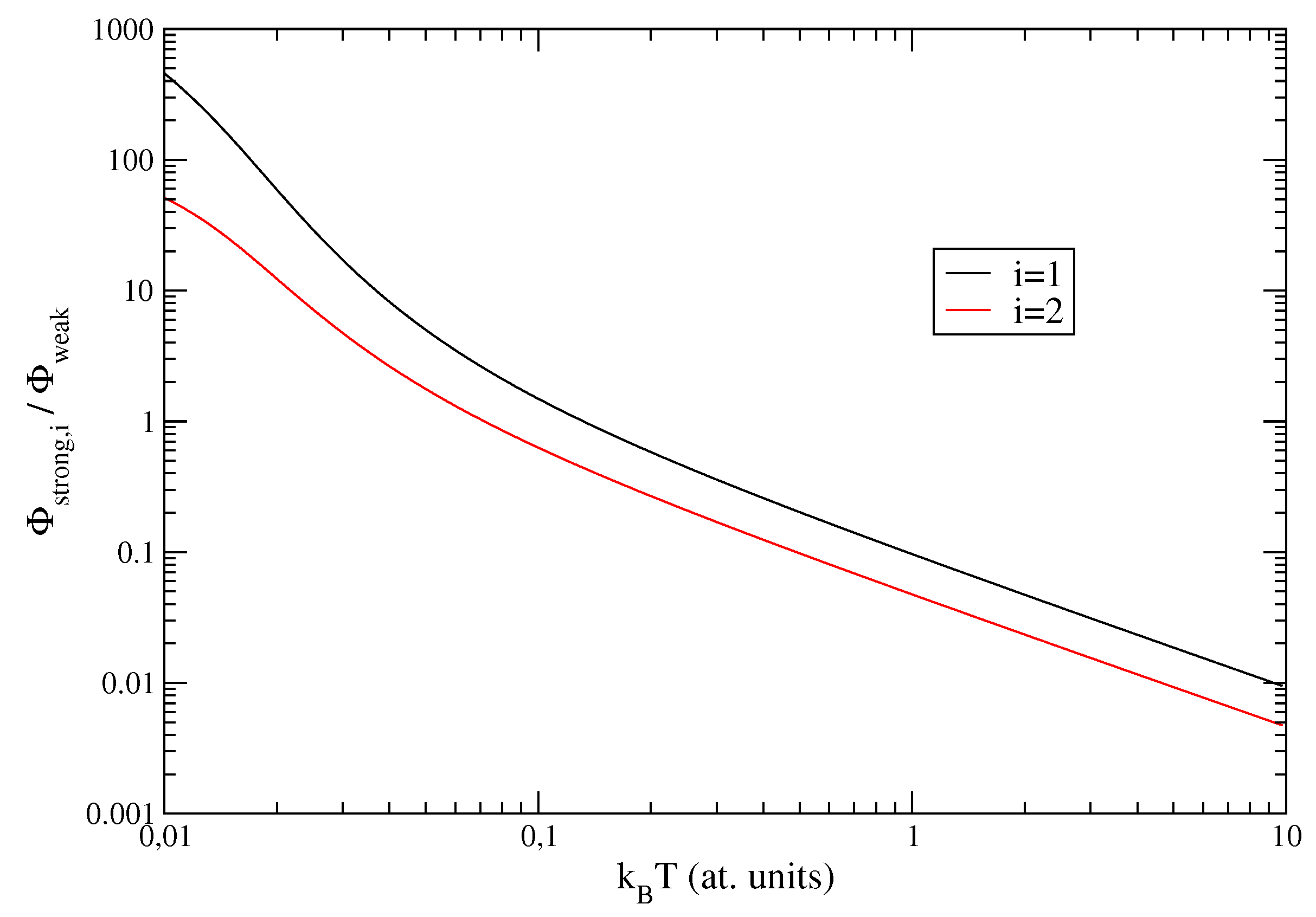
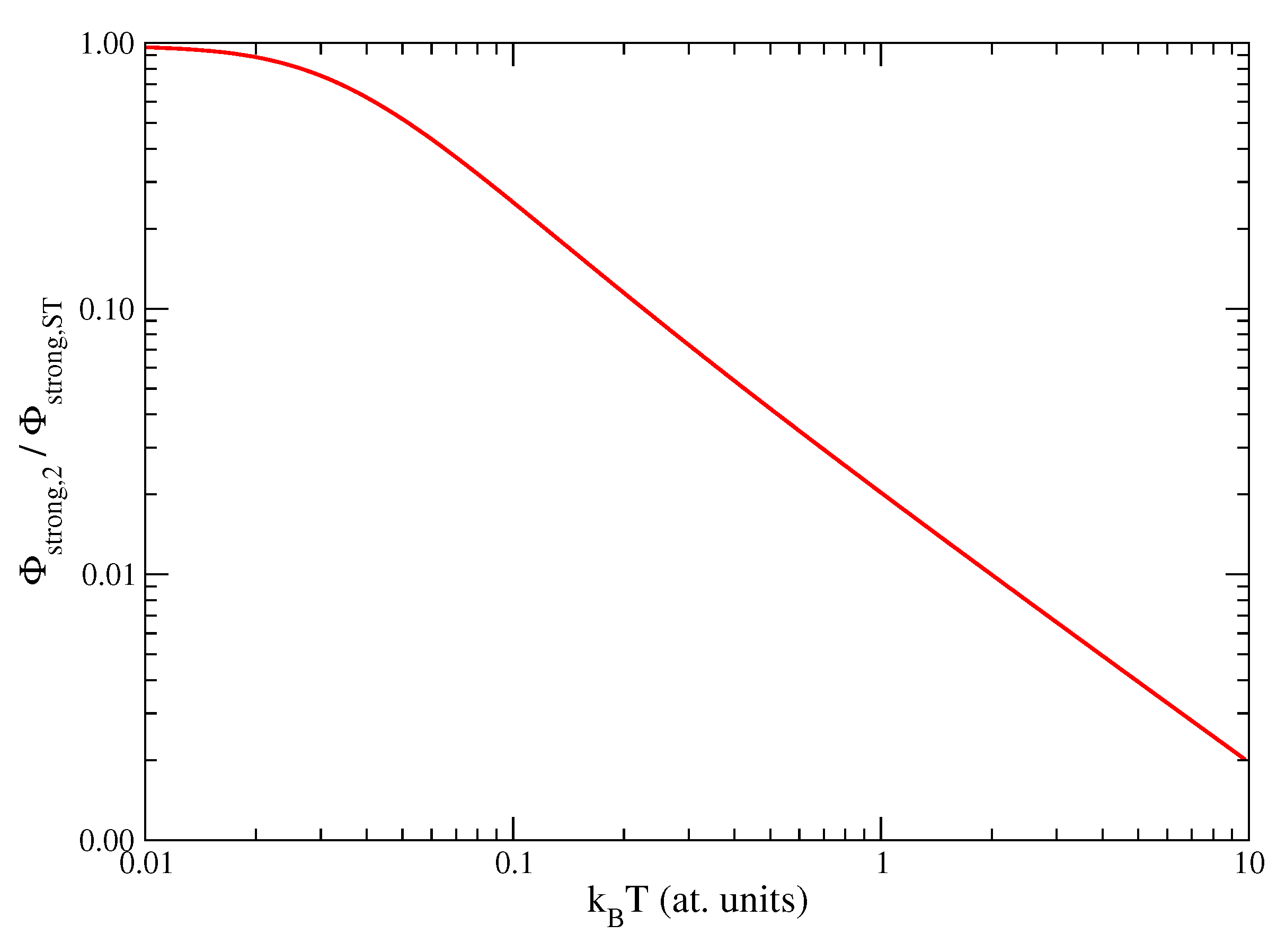
4.2. Case of Penetrating Collisions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The Interaction Picture: From the General Case to Hydrogen in the Standard Theory
Appendix A.1. Collision Operator in the Interaction Picture for Neutral Emitter
Appendix A.2. Case of Hydrogen
Appendix B. Strong Collisions in the Standard Theory: Integrating First on Velocity and Then on Impact Parameter
Appendix C. Checking the Matrix Elements Using Sum Rules
References
- Banaz, O. Spectral Line Broadening of He I and He-like Ions in Dense Plasmas. Ph.D. Thesis, Rostock University, Rostock, Germany, 2007. [Google Scholar]
- Baranger, M. Problem of Overlapping Lines in the Theory of Pressure Broadening. Phys. Rev. 1958, 111, 494–504. [Google Scholar] [CrossRef]
- Kolb, A.C.; Griem, H.R. Theory of Line Broadening in Multiplet Spectra. Phys. Rev. 1958, 111, 514–521. [Google Scholar] [CrossRef]
- Anderson, P.W. Pressure Broadening in the Microwave and Infra-Red Regions. Phys. Rev. 1949, 76, 647–661. [Google Scholar] [CrossRef]
- Hitzschke, L.; Röpke, G.; Seifert, T.; Zimmermann, R. Diagnostics of a laser-induced dense plasma by hydrogen-like carbon spectra. J. Phys. B At. Mol. Opt. Phys. 1986, 19, 2443–3000. [Google Scholar]
- Günter, S. Optische Eigenschaften dichter Plasmen. Habilitation Thesis, Rostock University, Rostock, Germany, 1995. [Google Scholar]
- Iglesias, C.A. Reformulation of plasma spectral line broadening with computer. High Energy Density Phys. 2019, 33, 1–6. [Google Scholar] [CrossRef]
- Stamm, R.; Voslamber, D. On the role of ion dynamics in the stark broadening of hydrogen lines. J. Quant. Spectros. Radiat. Transfer. 1979, 22, 599–609. [Google Scholar] [CrossRef]
- Bedida, N.; Meftah, M.T.; Difallah, M. Path Integral Formalism for Line Broadening in Plasmas: Lyman-α case. Contrib. Plasma Phys. 2014, 54, 783–790. [Google Scholar] [CrossRef]
- Feynman, R.H.; Hibbs, A.R. Quantum Mechanics and Path Integrals; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Sahal-Bréchot, S. Impact Theory of the Broadening and Shift of Spectral Lines due to Electrons and Ions in a Plasma. Astron. Astrophys. 1969, 1, 91–123. [Google Scholar]
- Sahal-Bréchot, S. Impact Theory of the Broadening and Shift of Spectral Lines due to Electrons and Ions in a Plasma (Continued). Astron. Astrophys. 1969, 2, 322–354. [Google Scholar]
- Deutsch, C.; Herman, L.; Drawin, H.W. Electron-impact broadening of overlapping He I lines in plasmas. Phys. Rev. 1969, 178, 261–270. [Google Scholar] [CrossRef]
- Deutsch, C.; Herman, L.; Drawin, H.W. Asymptotic behavior of the generalized width and shift functions in the electron-impact broadening theory of neutral spectral lines in plasmas. Phys. Rev. 1969, 186, 204–209. [Google Scholar] [CrossRef]
- Alexiou, S. Implementation of the Frequency Separation Technique. High Energy Density Phys. 2013, 9, 375–384. [Google Scholar] [CrossRef]
- Griem, H.R. Principles of Plasma Spectroscopy; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Alexiou, S.; Lee, R.W. Electron line broadening in plasmas: Resolution of the quantum vs. semiclassical calculations puzzle. In Spectral Line Shapes, Proceedings of the AIP Conference, Melville, NY, USA, 11–14 July 2001; Seidel, J., Ed.; AIP: College Park, MD, USA, 2001; Volume 599, p. 135. [Google Scholar]
- Alexiou, S.; Poquérusse, A. Standard line broadening impact theory for hydrogen including penetrating collisions. Phys. Rev. E 2005, 72, 046404. [Google Scholar] [CrossRef] [PubMed]
- Alexiou, S.; Lee, R.W. Semiclassical calculations of line broadening in plasmas: Comparison with quantal results. J. Quant. Spectrosc. Radiat. Transf. 2006, 99, 10–20. [Google Scholar] [CrossRef]
- Poquérusse, A.; Alexiou, S. Penetrating standard line broadening impact theory for hydrogen-like ions. J. Quant. Spectrosc. Radiat. Transf. 2006, 99, 493–498. [Google Scholar] [CrossRef]
- Alexiou, S. H-like ions with penetrating collision. J. Phys. Conf. Ser. 2017, 810, 012022. [Google Scholar] [CrossRef]
- Alexiou, S. Enhancement of line broadening in plasmas by penetrating collisions for hydrogenlike lines. High Energy Density Phys. 2017, 23, 188–194. [Google Scholar] [CrossRef]
- Pain, J.-C.; Gilleron, F. Modeling penetrating collisions in the standard line broadening impact theory for hydrogen. High Energy Density Phys. 2019, 30, 52–59. [Google Scholar] [CrossRef]
- Griem, H.R.; Ralchenko, Y.V. Stark broadening of the B III 2s-2p lines. Phys. Rev. E 1997, 56, 7186–7192. [Google Scholar] [CrossRef]
- Griem, H.R.; Ralchenko, Y.V. Electron collisional broadening of isolated lines from multiply ionized atoms. J. Quant. Spectrosc. Radiat. Transfer 2000, 65, 287–296. [Google Scholar] [CrossRef]
- Hey, J.D.; Griem, H.R. Central structure of low-n Balmer lines in dense plasmas. Phys. Rev. A 1975, 12, 169–185. [Google Scholar] [CrossRef]
- Voslamber, D. Upper-lower state interference term in Stark-broadening theory: Comment on a paper by J. D. Hey and H. R. Griem. Phys. Rev. A 1976, 14, 1903–1905. [Google Scholar] [CrossRef]
- Griem, H.R.; Hey, J.D. Reply to “Upper-lower state interference term in Stark broadening”. Phys. Rev. A 1976, 14, 1906. [Google Scholar] [CrossRef]
- Gigosos, M.A.; González, M.Á.; Talin, B.; Calisti, A. Exact expression of the impact broadening operator for hydrogen Stark broadening. Astron. Astrophys. 2007, 466, 1189–1196. [Google Scholar] [CrossRef][Green Version]
- Galtier, E.; Rosmej, F.B.; Calisti, A.; Talin, B.; Mossé, C.; Ferri, S.; Lisitsa, V.S. Interference effects and Stark broadening in XUV intrashell transitions in aluminum under conditions of intense XUV free-electron-laser irradiation. Phys. Rev. A 2013, 87, 033424. [Google Scholar] [CrossRef]
- Gordon, W. Zur Berechnung der Matrizen beim Wasserstoffatom. Ann. Phys. 1929, 2, 1031–1056. [Google Scholar] [CrossRef]
- Bethe, H.A.; Salpeter, E.E. Quantum Mechanics of One- and Two-Electron Atoms; Springer: Berlin/Heidelberg, Germany, 1957. [Google Scholar]
- Tarasov, V.F.W. Gordons integral (1929) and its representations by means of Appells functions F2, F1 and F3. J. Math. Phys. 2003, 44, 1449–1452. [Google Scholar] [CrossRef]
- Lewis, M. Stark broadening of spectral lines by high-velocity charged particles. Phys. Rev. 1960, 121, 501–505. [Google Scholar] [CrossRef]
- Smith, E.W. Electron Correlations in Plasma Line Broadening. Phys. Rev. 1968, 166, 102–113. [Google Scholar] [CrossRef]
- Griem, H.R.; Kolb, A.C.; Chen, K.Y. Stark Broadening of Hydrogen Lines in a Plasma. Phys. Rev. 1959, 116, 4–16. [Google Scholar] [CrossRef]
- Griem, H.R.; Baranger, M.; Kolb, A.C.; Oertel, G. Stark Broadening of Neutral Helium Lines in a Plasma. Phys. Rev. 1962, 125, 177–195. [Google Scholar] [CrossRef]
- Griem, H.R.; Shen, K.Y. Stark Broadening of Hydrogenic Ion Lines in a Plasma. Phys. Rev. 1961, 122, 1490–1496. [Google Scholar] [CrossRef]
- Kepple, P.C. Improved Stark-Profile Calculations for the He II Lines at 256, 304, 1085, 1216, 1640, 3203, and 4686 Å. Phys. Rev. A 1972, 6, 1–9. [Google Scholar] [CrossRef]
- Baranger, M. Simplified Quantum-Mechanical Theory of Pressure Broadening. Phys. Rev. 1958, 111, 481–493. [Google Scholar] [CrossRef]
- Nguyen-Hoe, H.; Drawin, W.; Herman, L. Asymetrie du profil de la raie Lyα de l’atome hydrogène. J. Quant. Spectrosc. Radiat. Transf. 1964, 4, 847–856. [Google Scholar] [CrossRef]
- Deutsch, C.; Klarsfeld, S. Quadrupole contributions to the electron broadening of overlapping neutral-atom lines in a plasma. Phys. Rev. A 1973, 7, 2081–2086. [Google Scholar] [CrossRef]
- Gomez, T.A.; Nagayama, T.; Kilcrease, M.H.; Winget, D.E. Effect of higher multipole moments on the Stark line shape. Phys. Rev. A 2016, 94, 022501. [Google Scholar] [CrossRef]
- Inglis, D.R.; Teller, E. Ionic depression of series limit in one-electron spectra. Astrophys. J. 1939, 90, 439–448. [Google Scholar] [CrossRef]
- Chappell, W.R.; Cooper, J.; Smith, E.W. Electron correlations in stark broadening. J. Quant. Spectrosc. Radiat. Transfer 1969, 9, 149–151. [Google Scholar] [CrossRef]
- Bacon, M.E.; Edwards, D.F. Effect of Strong Collisions on the Hα profile. Phys. Rev. 1968, 170, 125–127. [Google Scholar] [CrossRef]
- Griem, H.R.; Blaha, M.; Kepple, P.C. Stark-profile calculations for Lyman-series lines of one-electron ions in dense plasmas. Phys. Rev. A 1979, 19, 2421–2432. [Google Scholar] [CrossRef]
- Alexiou, S. Scaling of hydrogen electron Stark widths at high densities and the Inglis-Teller limit. High Energy Density Phys. 2009, 5, 68–73. [Google Scholar] [CrossRef]
- Günter, S. Contributions of strong collisions in the theory of spectral lines. Phys. Rev. E 1993, 48, 500–505. [Google Scholar] [CrossRef]
- Günter, S. Computational Investigation of Radiation from Dense Plasmas. Ph.D. Thesis, Universität Rostock, Rostock, Germany, 1990. [Google Scholar]
- Günter, S.; Röpke, G.; Hitzschke, L. Hydrogen spectral lines with the inclusion of dense-plasma effects. Phys. Rev. A 1991, 44, 6834–6844. [Google Scholar] [CrossRef]
- Griem, H.R. Spectral Line Broadening by Plasmas; Academic: New York, NY, USA, 1974. [Google Scholar]
- Griem, H.R. Shifts of hydrogen lines from electron collisions in dense plasmas. Phys. Rev. A 1983, 28, 1596–1601. [Google Scholar] [CrossRef]
- Iglesias, C.A.; Boercker, D.B.; Lee, R.W. Comment on “Shifts of hydrogen lines from electron collisions in dense plasmas. Phys. Rev. A 1985, 32, 1906–1907. [Google Scholar] [CrossRef]
- Griem, H.R. Shifts of hydrogen and ionized-helium lines from Δn = 0 interactions with electrons in dense plasmas. Phys. Rev. A 1988, 38, 2943–2952. [Google Scholar] [CrossRef]
- Voslamber, D. Unified Model for Stark Broadening. Z. Naturforschung A 1969, 24, 1458–1472. [Google Scholar]
- Vidal, R.; Cooper, J.; Smith, E.W. Hydrogen Stark broadening calculations with the unified classical path theory. J. Quant. Spectrosc. Radiat. Transf. 1970, 10, 1011–1063. [Google Scholar] [CrossRef]
- Baranger, M. General Impact Theory of Pressure Broadening. Phys. Rev. 1959, 112, 855–865. [Google Scholar] [CrossRef]
- Unnikrishnan, K.; Callaway, J. Shift and width of the Lyman-α line of neutral hydrogen due to electron collisions. Phys. Rev. A 1991, 43, 3619–3623. [Google Scholar] [CrossRef] [PubMed]
- Griem, H.R. Plasma Spectroscopy; McGraw-Hill: New York, NY, USA, 1964. [Google Scholar]
- Greene, R.L. Inclusion of ion dynamics in the unified classical path theory of Stark broadening. Phys. Rev. A 1979, 19, 2002–2008. [Google Scholar] [CrossRef]
- Böddeker, S.; Günter, S.; Könies, A.; Hitzschke, L.; Kunze, H.J. Shift and width of the Hα line of hydrogen in dense plasmas. Phys. Rev. 1993, 47, 2785–2791. [Google Scholar]
- Büscher, S.; Wrubel, T.H.; Ferri, S.; Kunze, H.-J. The Stark width and shift of the hydrogen Hα line. J. Phys. B At. Mol. Opt. Phys. 2002, 35, 2889–2897. [Google Scholar] [CrossRef]
- Kepple, P.; Griem, H.R. Improved Stark profiles calculations for the hydrogen lines Hα, Hβ, Hγ and Hδ. Phys. Rev. 1968, 173, 317–325. [Google Scholar] [CrossRef]
- Oks, E. Refinement of the semiclassical theory of the Stark broadening of hydrogen spectral lines in plasmas. J. Quant. Spectrosc. Radiat. Transfer 2015, 152, 74–83. [Google Scholar] [CrossRef]
- Varshalovich, D.A.; Moskalev, A.N.; Khersonskii, V.K. Quantum Theory of Angular Momentum; World Scientific: Singapore, 1988. [Google Scholar]
- Sobel’Man, I.I. Introduction to the Theory of Atomic Spectra, 1st ed.; International Series of Monographs in Natural Philosophy; Pergamon Press: New York, NY, USA, 1972. [Google Scholar]
- Sobel’Man, I.I.; Vainshtein, L.A.; Yukov, E.A. Excitation of Atoms and Broadening of Spectral Lines, 2nd ed.; Springer Series on Atoms and Plasmas; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Applied Mathematics Series 55; U. S. Government Printing Office: Washington, DC, USA, 1964.
- Cooper, J.; Oertel, G.K. Electron-Impact Broadening of Isolated Lines of Neutral Atoms in a Plasma. I. Phys. Rev. 1969, 180, 286–298. [Google Scholar] [CrossRef]
- McLean, L. General expression for the intensity of hydrogen lines. Phil. Mag. 1934, 18, 845–874. [Google Scholar] [CrossRef]
- Watson, J.K. A formula for line strengths of hydrogenic atoms. J. Phys. B At. Mol. Opt. Phys. 2006, 39, L291–L297. [Google Scholar] [CrossRef]
- Hey, J.D. The McLean-Watson line strength formula and its implementation. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 125701. [Google Scholar] [CrossRef]
- Casini, R.; Landi Degl’Innocenti, E.L. Algebraic proof of a sum rule occurring in Stark broadening of hydrogen lines. J. Math. Phys. 1995, 38, 3435–3445. [Google Scholar] [CrossRef][Green Version]
- Gilleron, F.; Pain, J.-C. Statistical modeling of line shapes of a hydrogenic atom broadened by the Stark effect. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 245001. [Google Scholar] [CrossRef]
| 1. | the formula has been symmetrized to account for . |
| 2. |
| Plasma | Electron Density (m) | Electron Temperature | Debye Length (m) | Approximate Value of n Such That (Case of Hydrogen) |
|---|---|---|---|---|
| Gas discharge | 10 | 10 | 7 × 10 | 1000 |
| Tokamak | 10 | 10 | 7 × 10 | 1000 |
| Ionosphere | 10 | 10 | 2 × 10 | 6000 |
| Solar center | 10 | 10 | 2 × 10 | 1 |
| Half-radius of the Sun | 4 × 10 | 3 × 10 | 2 × 10 | 2 |
| Base of the convective | 10 | 2 × 10 | 10 | 4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pain, J.-C.; Gilleron, F. Electron Broadening Operator Including Penetrating Collisions for Hydrogen. Atoms 2020, 8, 2. https://doi.org/10.3390/atoms8010002
Pain J-C, Gilleron F. Electron Broadening Operator Including Penetrating Collisions for Hydrogen. Atoms. 2020; 8(1):2. https://doi.org/10.3390/atoms8010002
Chicago/Turabian StylePain, Jean-Christophe, and Franck Gilleron. 2020. "Electron Broadening Operator Including Penetrating Collisions for Hydrogen" Atoms 8, no. 1: 2. https://doi.org/10.3390/atoms8010002
APA StylePain, J.-C., & Gilleron, F. (2020). Electron Broadening Operator Including Penetrating Collisions for Hydrogen. Atoms, 8(1), 2. https://doi.org/10.3390/atoms8010002






