Abstract
Cross sections for rotational excitation and de-excitation of the HeH+ ion by an electron impact are computed using a theoretical approach that combines the UK R-matrix code and the multi-channel quantum defect theory. The thermally-averaged rate coefficients derived from the obtained cross sections are fitted to an analytical formula valid for a wide range of temperatures.
1. Introduction
Cross sections for the electronic, rotational, and vibrational excitation of molecules in collisions with electrons are important for understanding and modeling various plasma environments, such as the interstellar medium (ISM), planetary ionospheres and exospheres, in plasma processing and de-pollution technologies, and others. Measuring cross sections experimentally for such processes is usually difficult and expensive. However, theoretical methods for electron–molecule scattering together with abundant computational resources have made it possible to obtain reliable cross sections numerically, at least for diatomic and small polyatomic molecules.
The excitation of rotational and vibrational states of molecular ions has been studied theoretically for several decades. In particular, in one of the earliest studies of this kind, Boikova and Ob’edkov [1] considered the process using the Coulomb–Born approximation for the low-energy region. The first-order perturbation theory was applied, and a general analytical formula was derived in which dipole and quadrupole moments of the target ion determine the cross section for rotational excitation, while derivatives of the moments with respect to nuclear distances determine the cross section for vibrational excitation. The direct non-resonant excitation mechanism of the molecules was assumed to maintain the validity of the Born–Oppenheimer approximation for such processes. Later, Chu and Dalgarno [2] applied the same Coulomb–Born approximation to compute rate coefficients for the rotational excitation of the CH+ ion.
Flower [3] applied the semi-classical approximation and the time-dependent perturbation theory to the transition for CH+ and HeH+. The rotation of the target molecule was quantised, while the motion of the incident electron was treated classically. The applicability of method is restricted to incident electron energies , where and are the energies of the rotational states of the target ion.
In a series of publications, Rabadan et al. [4,5,6] modified the method developed by Chu and Dalgarno [2] for diatomic molecules. In their approach, the scattering matrix is obtained from first principles using the R-matrix approach [7], rather than from the Coulomb–Born approximation. Similarly to Flower [3], cross sections for rotational excitation of CH+ and HeH+, as well as for NO+ [4,5] are computed. However, as in the other studies mentioned above, the method does not account for near-threshold effects and assumes that different rotational levels are degenerate. In particular, it does not account for Rydberg resonances associated with closed rotational states of the neutral molecule, such as rotational Rydberg resonances of the HeH molecule in the case of -HeH+ collisions. As it was shown later [8,9], this assumption is not appropriate if the incident electron couples strongly different rotational states of the target ion. In such a situation, the near-threshold effects should be accounted for to produce accurate rate coefficients at temperatures below 150 K. To address this problem, in Reference [10] the authors extrapolated the numerically-obtained cross sections down to the threshold using Wigner’s threshold law, producing more accurate results compared to those obtained from a kinetic scaling of the previous -matrix study [6] on HeH+ and CH+. However, closed-channel effects associated with rotational resonances were still neglected in this study [10].
The theoretical method accounts for near-threshold effects, including rovibrational Rydberg resonances, and makes use of first-principle calculations (or experimental spectroscopic data if necessary), and is based on (1) the electron–molecule scattering matrix computed for fixed positions of nuclei (molecular-frame scattering matrix), (2) the idea of the rotational frame transformation [11], and (3) the molecular quantum defect theory (QDT) [12,13], which makes it possible to evaluate the scattering matrix in the laboratory frame (with respect to which the molecule rotates) and excitation cross sections. This method will be referred to below as the QDT method. It has been used in slightly different implementations in theoretical studies of rotational excitation for several molecular ions: [14,15], [16], HeH+ [17], and CH+ [18].
The molecular-frame scattering matrix in the QDT method can be evaluated in different ways. For example, in Reference [16], in calculations of the rotational excitation of , the matrix was obtained by extrapolating quantum defects extracted from ab initio calculations of excited electronic states of for several internuclear geometries of the molecule. A similar method for the evaluation of the scattering matrix was used by Takagi et al. [19,20,21,22] in the study of the dissociative recombination of HeH+. Another way to obtain the molecular-frame scattering matrix is to perform electron scattering calculations directly, using first principles. In a recent study [10], Čurík and Greene employed the molecular scattering matrix computed directly using the UK R-matrix method [7] in the calculation of the rotational excitation cross sections in -HeH+ collisions.
In the present study, we discuss a general theoretical approach for the determination of rotational excitation cross sections for collisions of electrons with molecular ions at low scattering energies. A detailed derivation of the theory is presented for symmetric-top and linear target ions. A generalization to asymmetric top polyatomic targets is straightforward. We apply the method to the benchmark -HeH+ system and compute cross sections and rate coefficients for excitation and de-excitation of the ion from the five lowest rotational states. The HeH+ ion is one of the simplest molecular ions. It is present in helium-containing plasma, such as in fusion devices. It is thought to be the first molecule formed in the early Universe. It has also been suggested [23,24,25,26,27] that HeH+ could be detected in planetary atmospheres, white dwarfs, and the interstellar medium. At low energies, -HeH+ collisions can lead to dissociative recombination, rotational excitation, or dissociation recombination. The dissociative recombination of HeH+ has been extensively studied both experimentally and theoretically [19,20,21,22,28]. There are no experimental measurements of cross sections for the rotational excitation of HeH+, but there are a few previous theoretical studies [1,3,10,17]. Therefore, the present results can be compared with the previous calculations.
In the present study, essentially the same theoretical method as in Reference [17] is used to represent the rotational excitation of HeH+, but the results for a larger number of rotational transitions in HeH+ are obtained and an analytical fit of the thermally-averaged rate coefficients is performed, allowing the use of the data in plasma modeling.
The next section of the article presents the theoretical approach. In Section 3 we discuss the cross sections and rate coefficients obtained for the -HeH+ collisions. Section 4 summarizes the obtained results. Finally, in Appendix A, details of the theoretical derivation of the main formulas of Section 2 are provided.
2. Theoretical Approach
A detailed derivation of the present theory is given in Appendix A. Here, we discuss only the main steps in the implementation of the approach.
As the first step in the calculation, the body-frame -HeH+ reactance matrix is determined. For rotational-excitation transitions without changing the vibrational state of the target, the reactance matrix can be evaluated using just one internuclear distance corresponding to the equilibrium position of the target ion, 1.445 bohr for HeH+. The ground electronic state of the HeH+ ion is with the Hartree–Fock electronic configuration of . The matrix is obtained numerically using the UK R-matrix code [7,29]. Performing the scattering calculations, the R-matrix sphere of radius 10 bohr is used. Initially, several basis sets, including 6-311G*, DZP, and cc-pVTZ, were tested to investigate the stability of target properties such as dipole moment and ground state energy. Finally, the cc-pVTZ basis set was selected to perform the final calculations. A multicentered configuration interaction wave function expansion was used in the inner region, including two target states. The -HeH+ reactance matrix is smooth at low electron energies, and the lowest electronic resonance appears at about 4 eV at geometries near the equilibrium.
At electron energies below the first excited electronic state of the target ion, different channels of the body-frame reactance matrix are labeled with partial wave labels, including the angular momentum quantum number l and its projection of the molecular axis. The matrix is block-diagonal, where each block corresponds to a given projection of the total angular momentum (ion+electron) of the system. Thus, in practice, the body-frame reactance matrix is calculated separately for each . At low scattering energies, below 10 eV, the target ion can only be in the ground electronic state 1Σ+. Therefore, in the present calculations, the projection of the electronic angular momentum in a given channel is equal to .
The reactance matrix is used to compute the body-frame scattering matrix
where is the identity matrix. The laboratory-frame scattering matrix is then obtained by the transformation [30]
where J is the total angular momentum of the -HeH+ system, and are the angular momenta with their projections on the molecular axis of the target before and after the rotational excitation of HeH+, and and are Clebsch–Gordan coefficients.
The total energy E of the system is the sum of the relative kinetic energy and the energy of the initial state of the target. At a given energy E, the size of the scattering matrix should be equal to the number of open channels with energies below E. Therefore, varies with the energy depending on how many rotational states are open for a given E. However, the scattering matrix in Equation (2) does not contain information about which channels are open or closed. The actual scattering matrix with the correct energy dependence is obtained from using the procedure of the closed-channel elimination [31,32] according to Equation (A15) of Appendix A. The resulting “physical” scattering matrix represents properly rotational resonances associated with the closed rotational levels of the target.
Having the “physical” scattering matrix , the cross section for the rotational excitation or de-excitation of the linear molecule by an electron impact is given as
assuming that the initial and final rotational states are different (an inelastic process) and that the vibrational state is not changed during the process. In the above formula, is the Coulomb phase shift (see Equation (A5) in Appendix A).
3. Cross Sections and Rate Coefficients
Cross sections for electron impact transitions between the lowest five 0–4 rotational states of HeH+ were computed. Note that the only allowed projection in Equation (3) for HeH+ in its ground electronic state is zero. Therefore, for scattering energies below the first excited ionization threshold of HeH+, in Equation (3). Some examples are given in Figure 1. Solid lines in the figure represent the results obtained using the complete theoretical approach described in the previous section. The cross sections exhibit a strong resonant character. The resonances are produced by closed rotational states of the target. These resonances are washed out when thermally-averaged rate coefficients are computed. Therefore, in the calculation of the rate coefficients, one can use cross sections averaged over the resonances. Such averaged cross sections can be computed directly from the energy-independent scattering matrix , replacing in Equation (3) the matrix elements of the physical scattering matrix with the corresponding elements of the energy-independent matrix. The cross sections calculated using the energy-independent scattering matrix are shown by dotted lines in Figure 1. Due to the overall dependence of the cross sections as a function of the collision energy, it is convenient to see the products , which could be viewed as excitation probabilities. They are shown in Figure 2. It is evident that the excitation probabilities obtained in the full treatment, including the closed-channel elimination, oscillate near the averaged value obtained in the treatment without considering the closed channels (i.e., from the energy-independent scattering matrix ).
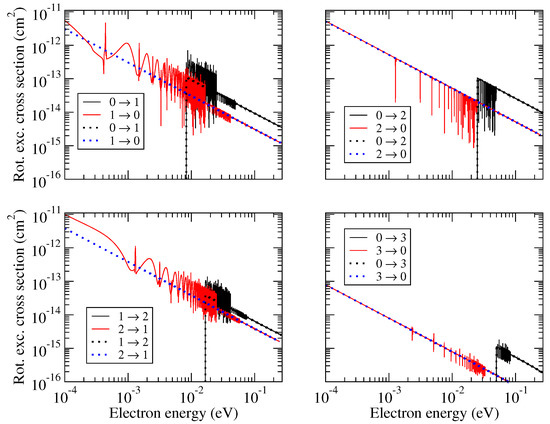
Figure 1.
Rotational (de-)excitation cross sections for transitions between the four lowest rotational states of HeH+. Solid lines represent the results obtained with the applied closed-channel elimination procedure of Equation (A14), while the dotted lines show the results for which the procedure was not applied.
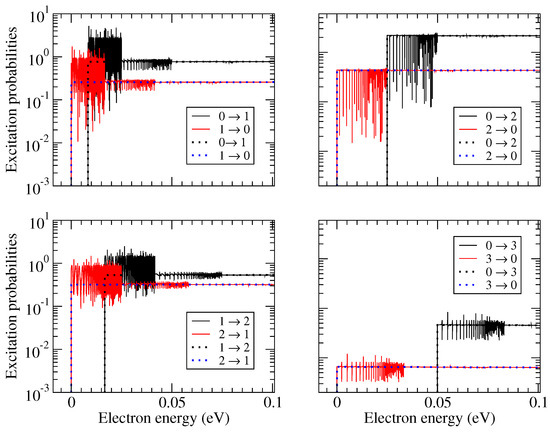
Figure 2.
Rotational (de-)excitation probabilities for transitions between the four lowest rotational states of HeH+. Solid lines represent the results obtained with the applied closed-channel elimination procedure, while the dotted lines show the results for which the procedure was not applied.
The obtained averaged rate coefficients are shown in Figure 3. They are compared with recently published data for the transitions: dotted lines are the calculations by Hamilton et al. [10] and the dashed lines are those of Čurík and Greene [17]. The agreement between the three sets of calculations are perfect to the transitions, while for the transitions the rate coefficients of Reference [10] are somewhat larger than the present result and the one from Reference [17]. For the transitions, the coefficients of Reference [17] are somewhat larger than the present result and the one from Reference [10]. For the transitions, the coefficients from the two other calculations agree with each other and are slightly larger than the present result.
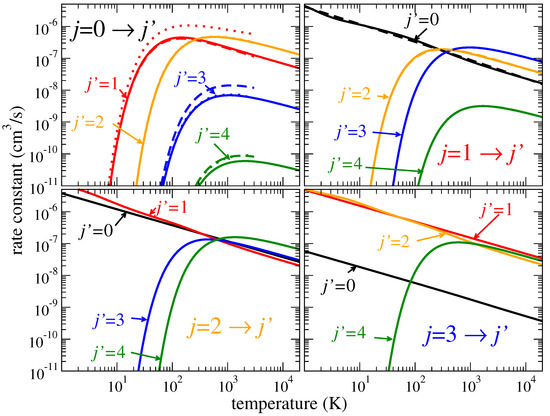
Figure 3.
Rate coefficients (solid lines) for transitions from the four lowest rotational states of HeH+, rotational states. Dotted lines in the upper left panel are the calculations by Hamilton et al. [10], and the dashed lines are those of Čurík and Greene [17]. For the transition, the dashed and solid lines overlap. For the transition, the curves for all three calculations overlap. For the transitions, the dotted and solid lines overlap. For the transitions, the dotted and dashed lines overlap.
The thermally averaged coefficients at low temperatures are sensitive to exact positions and widths of the lowest resonances, because the averaging integral over thermal velocities at low temperatures T is determined only by the small collision energies, . For example, the actual value of the cross sections for the and transitions in Figure 1 depends strongly on the position and the widths of the lowest resonances: at very low energies (below 2 meV), the cross sections are very different from the averaged ones shown with blue dotted lines. Therefore, the closed-channel elimination procedure is essential at low temperatures. Computationally, the procedure is not expensive if the number of channels is not very large (e.g., less than a thousand), and therefore, one can use the cross sections with all resonances in calculation of the rate coefficients for all temperatures.
Due to the general -dependence of cross sections , the calculated rate coefficients behave as for de-excitation and for excitation transitions, where (with for the present case) is the excitation energy. Therefore, similarly to References [16,33], for convenience of use, the rate coefficients are fitted to the formula
where are smooth functions of temperature and represented by the quadratic polynomial
where is the threshold energy defined as
The numerical parameters given in Table 1 are such that when used in Equations (4) and (5) along with the temperature T expressed in kelvin, the obtained numerical value of the rate coefficient in Equation (4) will be in units of cm3/s.

Table 1.
Parameters , , and of the polynomial of Equations (4) and (5) for several pairs of initial and final rotational states for de-excitation of HeH+, with . The probabilities for the opposite (excitation) process, , are obtained from multiplying them with the factor (see Equation (7)). For convenience, we also specify (the second column) the threshold energy in units of temperature (K) for the excitation process of the corresponding pair. For the de-excitation processes, .
Due to the detailed balance principle, the probabilities for the direct () and the inverse () processes are related to each other by the relative degeneracy factor
The coefficients () are obtained numerically for each pair of transitions and are given in Table 1.
4. Conclusions
In this study, cross sections and thermally-averaged rate coefficients for electron impact rotational transitions in HeH+ are computed for the five lowest rotational levels of HeH+ using the UK R-matrix method combined with the multichannel quantum defect theory (MQDT). Our improved channel elimination procedure removes this ambiguity to evaluate accurate results at low energy (<0.01 eV). This and our previous study [33] make us believe that once the collisional excitation cross section data is available, the analysis of the intensities of infra-red and microwave regions can provide information for the diagnostics of tokamak, as well as the study of planetary atmospheres and of the interstellar medium.
With certain modifications accounting for a different threshold behavior of the cross section at low collision energies, the present theoretical approach can be extended for collisions between an electron and a neutral molecule. These developments will be published later.
Author Contributions
Methodology, M.A., M.K. and V.K.; Software, M.A., M.K. and J.S.; Validation, M.A., M.K., J.S. and V.K.; Investigation, M.A., M.K. and V.K.; Resources, V.K.; Writing-Original Draft Preparation, M.K., J.S. and V.K.; Writing-Review & Editing, M.A. and V.K.; Supervision, V.K.
Funding
This work was supported by the National Science Foundation, Grant No. PHY-15-06391 and the University Grant Commission (UGC), Government of India under Raman Post Doctoral Fellowship No. 5-159/2016 (IC).
Acknowledgments
V.K. acknowledges a support from the Austrian–American Educational Commission.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
This section provides details on the formulas used for the cross section calculations.
First, rotational and electronic states of the target ion are introduced as:
where j, , and are the angular momentum of HeH+ and its projections in the laboratory frame (LF) and the molecular frame (MF), respectively. The function specifies the two-electron wave function of HeH+, which depends on . is the Wigner function depending on three Euler angles, which are called collectively by symbol . The vibrational state of the target ion is not specified (i.e., pure rotational transitions are considered). We assume that the incident electron plane wave propagates along the z-axis in the LF with a wave vector of magnitude . The complete scattering wave function of the system in the asymptotic region is given by the sum of the contributions due to the pure Coulomb field and the short-range potential , representing the difference between the actual +HeH+ interaction and the Coulomb potential, as follows [34]:
where is the Sommerfeld parameter. In the above expression, energetically open channels are labeled by the quantum numbers and ; denotes the differential amplitude for scattering from state to . The amplitude includes only the contributions due to . We assume that the incident wave in is a plane wave for large r, such that the incident current density is . Similar to Reference [30], channel functions with a definite total angular momentum and its projection in the LF are introduced:
where l and are the incident electron angular momentum and its projection in the LF. The scattering state of Equation (A1) takes the form
The pure Coulomb scattering wave function can be written in a similar form:
Moving the exponent factor to the right-hand side, we obtain
Multiplying both sides of the above equation with , integrating over electronic coordinates of the target and the angles , we obtain the scattering amplitude for the transition :
To make notations slightly more uniform, in the equations below, we use symbol instead of . The cross section for rotational excitation averaged over initial projections and summed over final projections is obtained as follows:
where is the energy of the incident electron, and and are spherical angles of the wave vector of the scattered electron in the LF.
Below, we assume that the incident plane wave propagates along the z-axis of the LF (i.e., in Equation (A9)). Therefore, the number of summation indexes in Equation (A9) is reduced from six to five, over and . The square of the amplitude in Equation (A10) doubles the number of summation indexes. We will refer to the additional indexes as and . With the sums over and in Equation (A10), the number of summation indexes becomes twelve. Due to the orthogonality of and , the integral over and reduces the number of summation indexes to ten with and . In the remaining ten-fold sum, the double sum over and is
which reduces the number of indexes to , and . Again, in the remaining sum (because ):
With the above simplifications, the cross section of Equation (A10) becomes:
assuming that the initial and final states are different (i.e., an inelastic process).
For a given total energy of the -HeH+ system, the size of the matrix in the formula above is equal to the number of open scattering channels with energies . However, the closed channels with , which are not included explicitly in Equation (A13), usually significantly influence the S-matrix and the cross section. Such closed channels are taken into account using the “closed channel elimination” procedure [31,32]. The S-matrix in Equation (A13) is obtained from another matrix, having a larger number of channels, including the channels that are closed at given E. Namely, in Equation (A13) is given by:
where is a [32] diagonal matrix with diagonal elements equal to the Coulomb phase shift in the corresponding channel, . The matrices , , , and are submatrices of the larger S-matrix, which includes open and closed channels (). The larger S-matrix, partitioned as:
where the partition of the matrix elements in the “o”- and “c”-parts is made on the basis whether the corresponding channel, or , is open or closed for ionization at the total energy E. The quantity is a diagonal matrix:
and is the number of closed channels.
We assume that the initial and final vibrational states of the target ion are the same. In this situation, it is a good approximation to consider that the averaged internuclear distance in the target ion is unchanged during the rotational excitation process and is equal to the equilibrium distance . The scattering matrix in Equation (A15) is therefore obtained for a fixed geometry in the basis of channel functions of Equation (A3). In the R-matrix calculation, the reactance matrix K is obtained in a different basis of functions [30], in which the molecule is fixed in space (i.e., the body-fixed (BF) basis). The channel functions transform into in the following way:
where is the projection of the orbital momentum l of the incident electron on the molecular axis, and is the projection of the total orbital momentum of all electrons on the molecular axis. For the HeH+ ion in the ground electronic state, and . The S-matrix obtained in the BF is diagonal over quantum numbers J and . Therefore, the transformation between the S-matrices obtained in the two bases is given by:
where is an element of the the BF S-matrix obtained from the reactance matrix K as:
with being the identity matrix and is the reactance matrix obtained numerically using the UK R-matrix code.
References
- Boikova, R.F.; Ob’edkov, V.D. Rotational and vibrational excitation of molecular ions by electrons. Sov. Phys. JETP 1968, 27, 772. [Google Scholar]
- Chu, S.I.; Dalgarno, A. Rotational excitation of CH+ by electron impact. Phys. Rev. A 1974, 10, 788. [Google Scholar] [CrossRef]
- Flower, D. Electron collisional excitation of rotational transitions in CH+ and HeH+. Astron. Astrophys. 1979, 73, 237–239. [Google Scholar]
- Rabadán, I.; Sarpal, B.K.; Tennyson, J. On the calculation of electron-impact rotational excitation cross sections for molecular ions. J. Phys. B At. Mol. Opt. Phys. 1998, 31, 2077. [Google Scholar] [CrossRef]
- Rabadán, I.; Sarpal, B.K.; Tennyson, J. Calculated rotational and vibrational excitation rates for electron-HeH+ collisions. Mon. Not. R. Astron. Soc. 1998, 299, 171–175. [Google Scholar] [CrossRef]
- Rabadán, I.; Tennyson, J. ROTIONS: A program for the calculation of rotational excitation cross sections in electron—Molecular ion collisions. Comput. Phys. Commun. 1998, 114, 129–141. [Google Scholar] [CrossRef]
- Tennyson, J. Electron—Molecule collision calculations using the R-matrix method. Phys. Rep. 2010, 491, 29–76. [Google Scholar] [CrossRef]
- Faure, A.; Kokoouline, V.; Greene, C.H.; Tennyson, J. Near-threshold rotational excitation of molecular ions by electron impact. J. Phys. B At. Mol. Opt. Phys. 2006, 39, 4261. [Google Scholar] [CrossRef]
- Faure, A.; Tennyson, J.; Kokoouline, V.; Greene, C.H. Rotational excitation of interstellar molecular ions by electrons. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2009; Volume 192. [Google Scholar]
- Hamilton, J.R.; Faure, A.; Tennyson, J. Electron-impact excitation of diatomic hydride cations—I. HeH+, CH+, ArH+. Mon. Not. R. Astron. Soc. 2016, 455, 3281–3287. [Google Scholar] [CrossRef]
- Chang, E.S.; Fano, U. Theory of electron-molecule collisions by frame transformations. Phys. Rev. A 1972, 6, 173. [Google Scholar] [CrossRef]
- Greene, C.H.; Jungen, C. Molecular applications ofquantum defect theory. Adv. At. Mol. Phys. 1985, 21, 51–121. [Google Scholar]
- Jungen, C. Molecular Applications of Quantum Defect Theory; Institute of Physics Publishing: Bristol, UK, 1996. [Google Scholar]
- Motapon, O.; Pop, N.; Argoubi, F.; Mezei, J.Z.; Epée Epée, M.D.; Faure, A.; Telmini, M.; Tennyson, J.; Schneider, I.F. Rotational transitions induced by collisions of HD+ ions with low-energy electrons. Phys. Rev. A 2014, 90, 012706. [Google Scholar] [CrossRef]
- Epée Epée, M.D.; Mezei, J.Z.; Motapon, O.; Pop, N.; Schneider, I.F. Reactive collisions of very low-energy electrons with rotational transitions and dissociative recombination. Mon. Not. R. Astron. Soc. 2015, 455, 276–281. [Google Scholar] [CrossRef]
- Kokoouline, V.; Faure, A.; Tennyson, J.; Greene, C.H. Calculation of rate constants for vibrational and rotational excitation of the ion by electron impact. Mon. Not. R. Astron. Soc. 2010, 405, 1195–1202. [Google Scholar]
- Čurík, R.; Greene, C.H. Inelastic low-energy collisions of electrons with HeH+: Rovibrational excitation and dissociative recombination. J. Chem. Phys. 2017, 147, 054307. [Google Scholar] [CrossRef] [PubMed]
- Faure, A.; Halvick, P.; Stoecklin, T.; Honvault, P.; Epée Epée, M.; Mezei, J.; Motapon, O.; Schneider, I.; Tennyson, J.; Roncero, O.; et al. State-to-state chemistry and rotational excitation of CH+ in photon-dominated regions. Mon. Not. R. Astron. Soc. 2017, 469, 612–620. [Google Scholar] [CrossRef] [PubMed]
- Tanabe, T.; Katayama, I.; Ono, S.; Chida, K.; Watanabe, T.; Arakaki, Y.; Haruyama, Y.; Saito, M.; Odagiri, T.; Hosono, K.; et al. Dissociative recombination of HeH+ isotopes with an ultra-cold electron beam from a superconducting electron cooler in a storage ring. J. Phys. B At. Mol. Opt. Phys. 1998, 31, L297. [Google Scholar] [CrossRef]
- Takagi, H. Theoretical study of the dissociative recombination of HeH+. Phys. Rev. A 2004, 70, 022709. [Google Scholar] [CrossRef]
- Takagi, H. Cross sections of the processes induced by electron collisions with , HeH+, and their isotopes. Fusion Sci. Technol. 2013, 63, 406–412. [Google Scholar] [CrossRef]
- Takagi, H.; Tashiro, M. Study on the dissociative recombination of HeH+ by multi-channel quantum defect theory. In EPJ Web of Conferences; EDP Sciences: Les Ulis, France, 2015; Volume 84. [Google Scholar]
- Dabrowski, I.; Herzberg, G. The predicted infrared spectrum of HeH+ and its possible astrophysical importance. Trans. N. Y. Acad. Sci. 1977, 38, 14–25. [Google Scholar] [CrossRef]
- Black, J. Molecules in planetary nebulae. Astrophys. J. 1978, 222, 125–131. [Google Scholar] [CrossRef]
- Flower, D.; Roueff, E. On the formation and destruction of HeH+ in gaseous nebulae and the associated infra-red emission line spectrum. Astron. Astrophys. 1979, 72, 361–366. [Google Scholar]
- Roberge, W.; Dalgarno, A. The formation and destruction of HeH+ in astrophysical plasmas. Astrophys. J. 1982, 255, 489–496. [Google Scholar] [CrossRef]
- Harris, G.; Lynas-Gray, A.; Miller, S.; Tennyson, J. The role of HeH+ in cool helium-rich white dwarfs. Astrophys. J. Lett. 2004, 617, L143. [Google Scholar] [CrossRef]
- Guberman, S.L. Dissociative recombination without a curve crossing. Phys. Rev. A 1994, 49, R4277. [Google Scholar] [CrossRef] [PubMed]
- Tennyson, J.; Brown, D.B.; Munro, J.J.; Rozum, I.; Varambhia, H.N.; Vinci, N. Quantemol-N: An expert system for performing electron molecule collision calculations using the R-matrix method. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2007; Volume 86. [Google Scholar]
- Douguet, N.; Fonseca dos Santos, S.; Raoult, M.; Dulieu, O.; Orel, A.E.; Kokoouline, V. Theory of radiative electron attachment to molecules: Benchmark study of CN−. Phys. Rev. A 2013, 88, 052710. [Google Scholar] [CrossRef]
- Seaton, M.J. Quantum defect theory. Rep. Prog. Phys. 1983, 46, 167. [Google Scholar] [CrossRef]
- Aymar, M.; Greene, C.H.; Luc-Koenig, E. Multichannel Rydberg spectroscopy of complex atoms. Rev. Mod. Phys. 1996, 68, 1015. [Google Scholar] [CrossRef]
- Ayouz, M.; Kokoouline, V. Cross Sections and Rate Coefficients for Vibrational Excitation of HeH+ Molecule by Electron Impactukrm. Atoms 2016, 4, 30. [Google Scholar] [CrossRef]
- Friedrich, H. Scattering Theory; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).