Influence of the p ¯ -p Nuclear Interaction on the Rate of the Low-Energy p ¯ + H μ → ( p ¯ p ) α + μ − Reaction
Abstract
1. Introduction
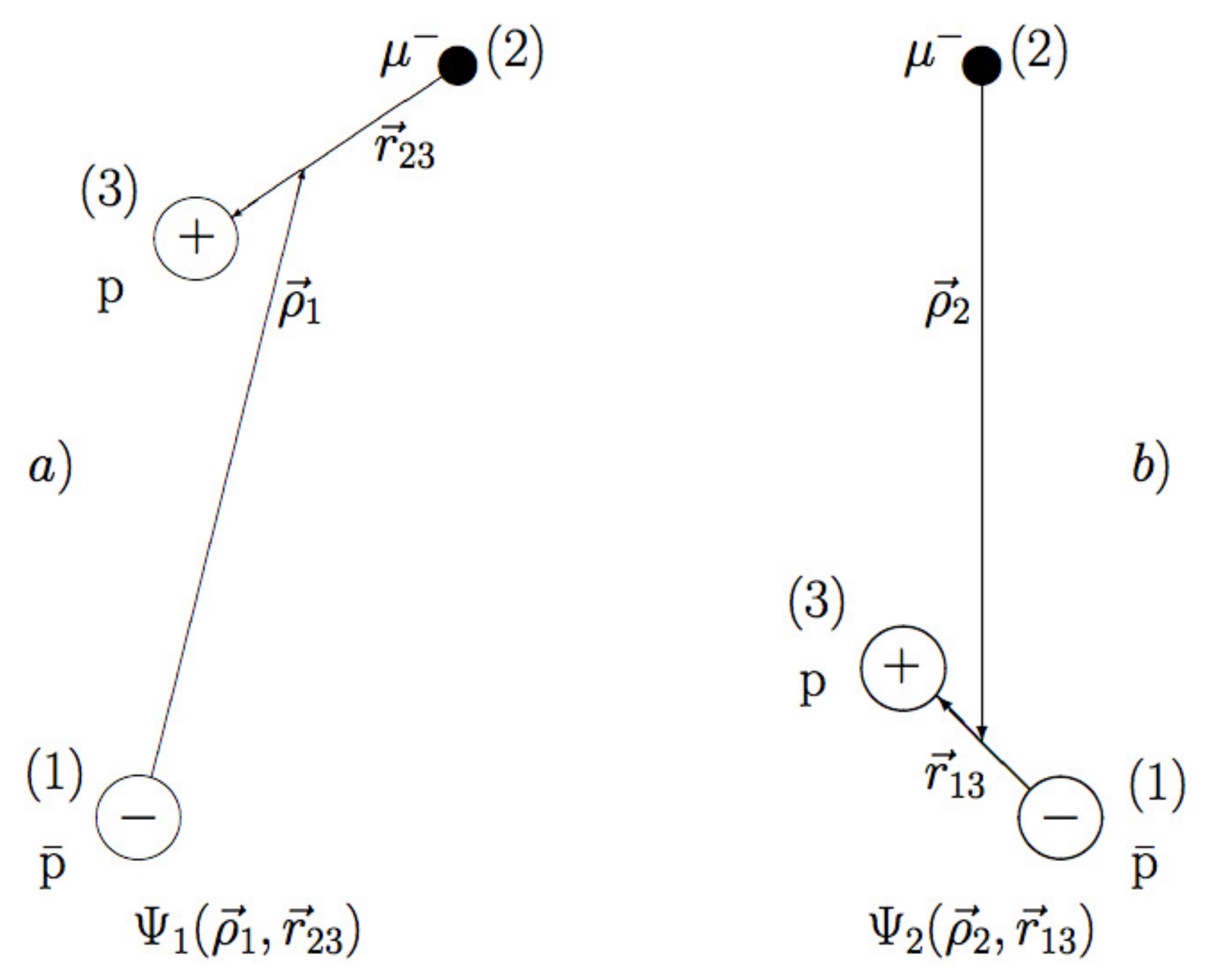
2. A Few-Body Approach
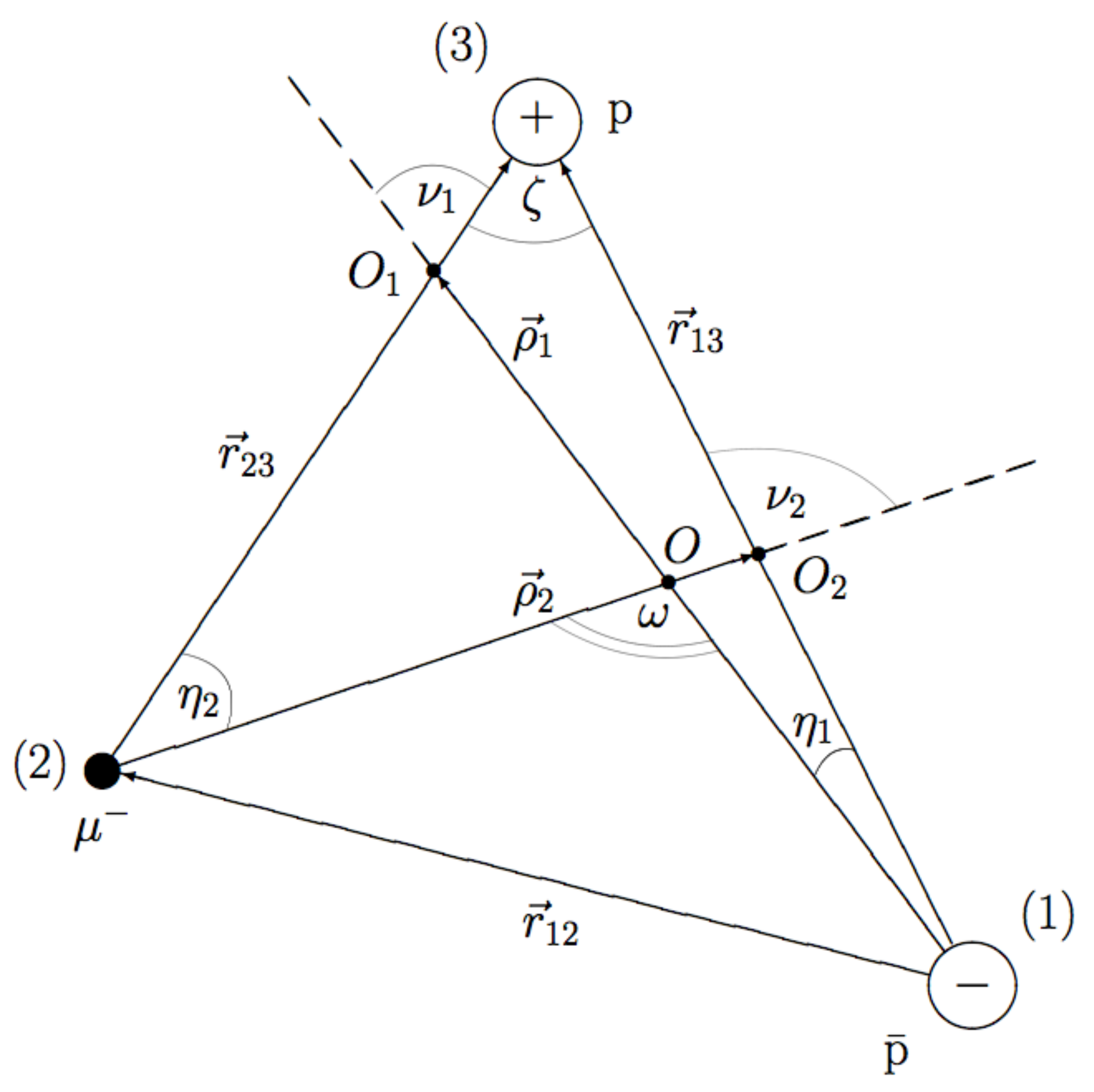
2.1. Coupled Integral-Differential Equations
2.2. Boundary Conditions and Reaction cross Section
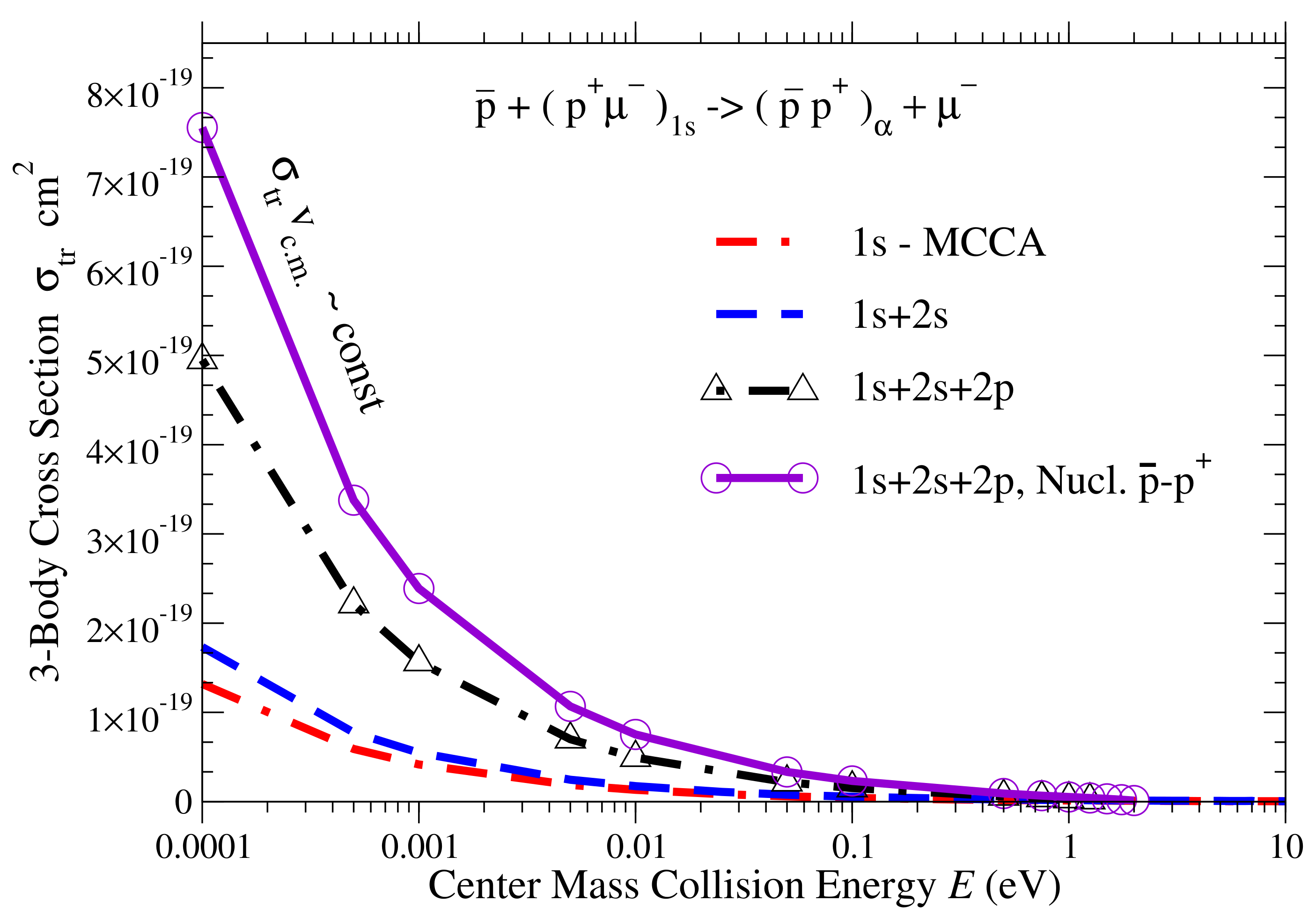
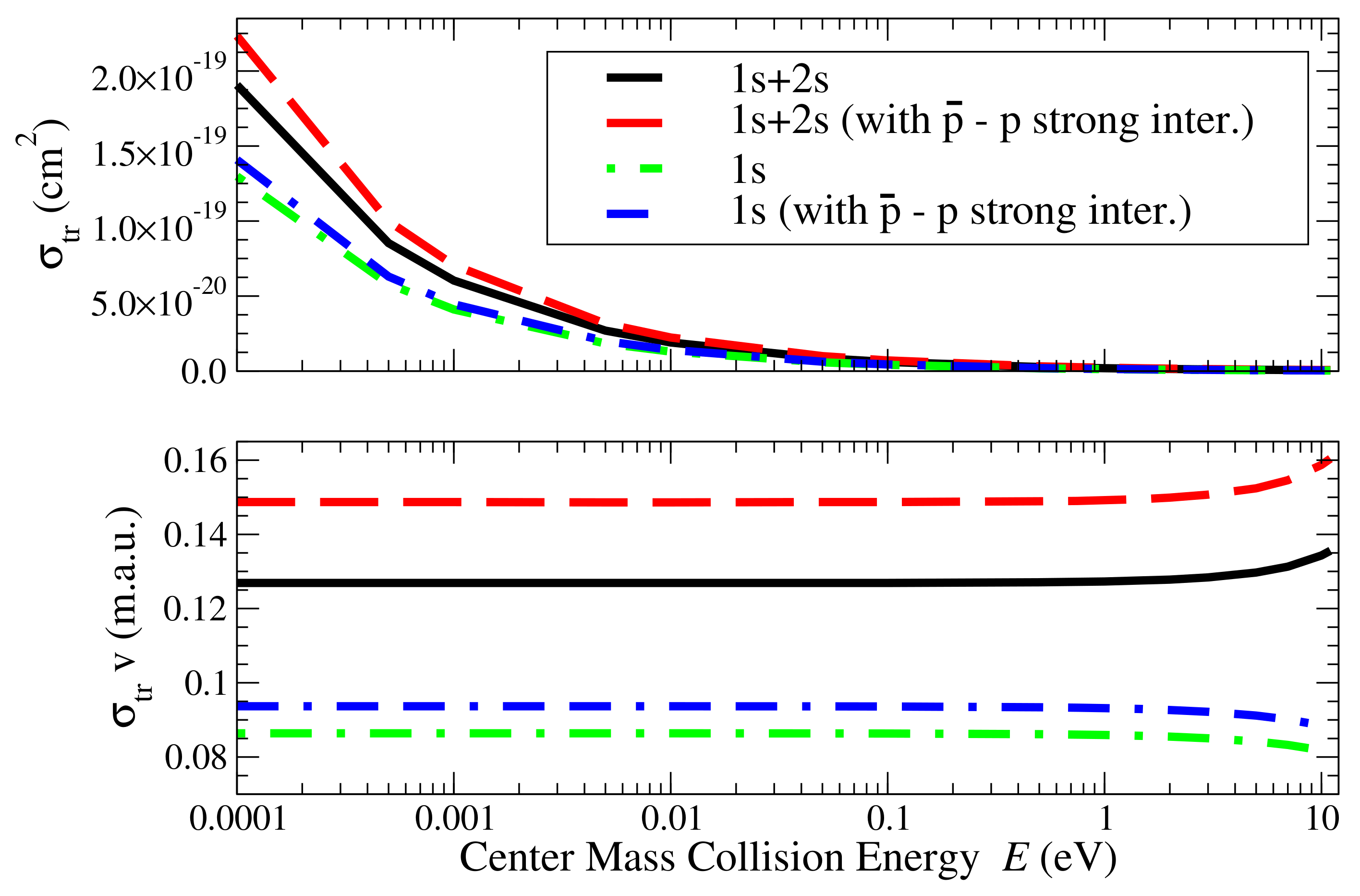
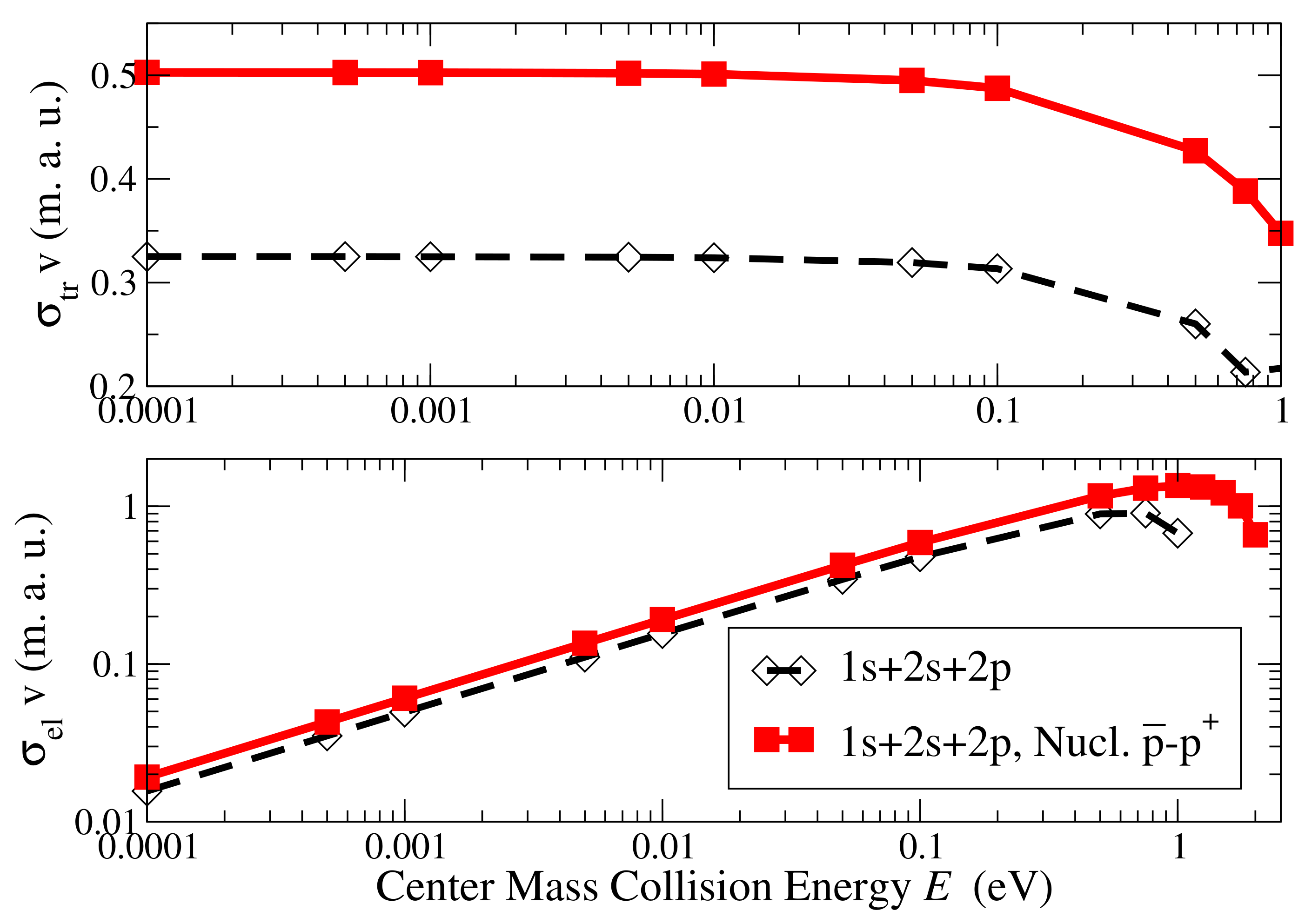
3. Results and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chamberlain, O.; Segré, E.; Wiegand, C.; Ypsilantis, T. Observation of Antiprotons. Phys. Rev. 1955, 100, 947. [Google Scholar] [CrossRef]
- Ahmadi, M.; Alves, B.X.; Baker, C.J.; Bertsche, W.; Butler, E.; Capra, A.; Carruth, C.; Cesar, C.L.; Charlton, M.; Cohen, S.; et al. Observation of the 1S–2S transition in trapped antihydrogen. Nature 2017, 541, 506–510. [Google Scholar] [CrossRef] [PubMed]
- Gabrielse, G.; Kalra, R.; Kolthammer, W.S.; McConnell, R.; Richerme, P.; Grzonka, D.; Oelert, W.; Sefzick, T.; Zielinski, M.; Fitzakerley, D.W.; (ATRAP Collaboration). Trapped Antihydrogen in Its Ground State. Phys. Rev. Lett. 2012, 108, 113002. [Google Scholar] [CrossRef] [PubMed]
- Hori, M.; Hossein, A.-K.; Anna, S.; Daniel, B.; Andreas, D.; Ryugo, H. Takumi Kobayashi Buffer-gas cooling of antiprotonic helium to 1.5 to 1.7 K, and antiproton-to-electron mass ratio. Science 2016, 354, 610–614. [Google Scholar] [CrossRef] [PubMed]
- Kuroda, N.; Ulmer, S.; Murtagh, D.J.; Van, G.S.; Nagata, Y.; Diermaier, M.; Federmann, S.; Leali, M.; Malbrunot, C.; Mascagna, V.; et al. A source of antihydrogen for in-flight hyperfine spectroscopy. Nat. Commun. 2014, 5, 3089. [Google Scholar] [CrossRef] [PubMed]
- Amoretti, M.; Amsler, C.; Bonomi, G.; Bouchta, A.; Bowe, P.; Carraro, C.; Cesar, C.L.; Charlton, M.; Collier, M.J.T.; Doser, M.; et al. Production and detection of cold antihydrogen atoms. Nature 2002, 419, 456–459. [Google Scholar] [CrossRef] [PubMed]
- Zurlo, N.; ATHENA Collaboration. Evidence for the production of slow antiprotonic hydrogen in vacuum. Phys. Rev. Lett. 2006, 97, 153401. [Google Scholar] [CrossRef] [PubMed]
- Venturelli, L.; Amoretti, M.; Amsler, C.; Bonomi, G.; Carraroc, C.; Cesar, C.L.; Charlton, M.; Doser, M.; Fontana, A.; Funakosh, R.; et al. Protonium production in ATHENA. Nucl. Instrum. Methods Phys. Res. Sect. B 2007, 261, 40–43. [Google Scholar] [CrossRef]
- Rizzini, E.; Venturelli, L.; Zurlo, N.; Charlton, M.; Amsler, C.; Bonomi, G.; Canali, C.; Carraro, C.; Fontana, A.; Genova, P.; et al. Further evidence for low-energy protonium production in vacuum. Eur. Phys. J. Plus 2012, 127, 124. [Google Scholar] [CrossRef][Green Version]
- Shapiro, I.S. The physics of nucleon-antinucleon systems. Phys. Rep. 1978, 35, 129–185. [Google Scholar] [CrossRef]
- Hrtánková, J.; Mareš, J. Interaction of antiprotons with nuclei. Nucl. Phys. A 2016, 945, 197–215. [Google Scholar]
- Carbonell, J.; Richard, J.-M.; Wycech, S. On the relation between protonium level shifts and nucleon-antinucleon scattering amplitudes. Z. Phys. A 1992, 343, 325–329. [Google Scholar] [CrossRef]
- Dover, C.B.; Richard, J.M. Spin observables in low energy nucleon-antinucleon scattering. Phys. Rev. C 1982, 25, 1952. [Google Scholar] [CrossRef]
- Richard, J.M.; Sainio, M.E. Nuclear effects in protonium. Phys. Lett. B 1982, 110, 349–352. [Google Scholar] [CrossRef][Green Version]
- Desai, B.R. Proton-Antiproton Annihilation in Protonium. Phys. Rev. 1960, 119, 1385. [Google Scholar] [CrossRef]
- Klempt, E.; Bradamante, F.; Martin, A.; Richard, J.M. Antinucleon nucleon interaction at low energy: Scattering and protonium. Phys. Rep. 2002, 368, 119–316. [Google Scholar] [CrossRef]
- Klempt, E.; Batty, C.; Richard, J.M. The antinucleon-nucleon interaction at low energy: Annihilation dynamics. Phys. Rep. 2005, 413, 197–317. [Google Scholar] [CrossRef]
- Bogdanova, L.N.; Dalkarov, O.D.; Shapiro, I.S. Quasinuclear systems of nucleons and antinucleons. Ann. Phys. 1974, 84, 261–284. [Google Scholar] [CrossRef]
- Esry, B.D.; Sadeghpour, H.R. Ultraslow anti-p - H collisions in hyperspherical coordinates: Hydrogen and protonium channels. Phys. Rev. A 2003, 67, 012704. [Google Scholar] [CrossRef]
- Cohen, J.S. Reactive collisions of atomic antihydrogen with the H2 and H2+ molecules. J. Phys. B At. Mol. Opt. Phys. 2006, 39, 3561. [Google Scholar] [CrossRef]
- Tong, X.M.; Hino, K.; Toshima, N. State-Specified Protonium Formation in Low-Energy Antiproton-Hydrogen-Atom Collisions. Phys. Rev. Lett. 2006, 97, 243202. [Google Scholar] [CrossRef] [PubMed]
- Sakimoto, K. Unified treatment of hadronic annihilation and protonium formation in slow collisions of antiprotons with hydrogen atoms. Phys. Rev. A 2013, 88, 012507. [Google Scholar] [CrossRef]
- Born, M.; Oppenheimer, R. Zur Quantentheorie der Molekeln. Ann. Phys. Liepzig 1927, 84, 457–484. [Google Scholar] [CrossRef]
- Lauss, B. Fundamental measurements with muons—View from PSI. Nucl. Phys. A 2009, 827, 401c–407c. [Google Scholar] [CrossRef]
- Faddeev, L.D. Scattering theory for a three-particle system. Zh. Eksp. Teor. Fiz. 1960, 39, 1459–1467, (Transl. Sov. Phys. JETP 1961, 12, 1014–1019). [Google Scholar]
- Igarashi, A.; Toshima, N. Application of hyperspherical close-coupling method to antiproton collisions with muonic hydrogen. Eur. Phys. J. D 2008, 46, 425–430. [Google Scholar] [CrossRef][Green Version]
- Hahn, Y.; Watson, K. Reduction Method and Distortion Potentials for Many-Particle Scattering Equations. Phys. Rev. A 1972, 5, 1718. [Google Scholar] [CrossRef]
- Sultanov, R.A.; Adhikari, S.K. Coordinate-space Faddeev-Hahn-type approach to three-body charge-transfer reactions involving exotic particles. Phys. Rev. A 2000, 61, 022711. [Google Scholar] [CrossRef]
- Sultanov, R.A.; Guster, D.; Adhikari, S.K. Three-body protonium formation in a collision between a slow antiproton () and muonic hydrogen: Hμ− Low energy + (pμ)1s → (p)1s + μ− reaction. Few-Body Syst. 2015, 56, 793–800. [Google Scholar] [CrossRef]
- Sultanov, R.A.; Guster, D. Integral-Differential Equations Approach to Atomic Three-Body Systems. J. Comp. Phys. 2003, 192, 231. [Google Scholar] [CrossRef]
- Sultanov, R.A.; Guster, D. Antihydrogen () and muonic antihydrogen () formation in low energy three-charge-particle collisions. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 215204. [Google Scholar] [CrossRef][Green Version]
- Sultanov, R.A.; Guster, D. Nuclear effects in protonium formation low-energy three-body reaction: + (pμ)1s → (p)1s + μ−. EPJ Web of Conf. 2016, 122, 09004. [Google Scholar] [CrossRef]
- Yakovlev, S.L.; Filikhin, I.N. Low-energy scattering in four nucleon systems. Method of Cluster Reduction. Few-Body Syst. Suppl. 1999, 10, 37–40. [Google Scholar]
- Sultanov, R.A. A few-body treatment of low energy atomic collisions involving exotic particles. Few-Body Syst. Suppl. 1999, 10, 281–284. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics, Non-Relativistic Theory, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 2003. [Google Scholar]
- Deser, S.; Goldberger, M.L.; Baumann, K.; Thirring, W. Energy Level Displacements in Pi-Mesonic Atoms. Phys. Rev. 1954, 96, 774. [Google Scholar] [CrossRef]
- Armour, E.A.G.; Liu, Y.; Vigier, A. Inclusion of the strong interaction in low-energy hydrogen-antihydrogen scattering using a complex potential. Phys. B At. Mol. Opt. Phys. 2005, 38, L47. [Google Scholar] [CrossRef]
- Trueman, T.L. Energy level shifts in atomic states of strongly-interacting particles. Nucl. Phys. 1961, 26, 57–67. [Google Scholar] [CrossRef]
- Popov, V.S.; Kudryavtsev, A.E.; Mur, V.D. Model-independent description of the dt and (d3He) systems near low-energy resonances. Sov. Phys. JETP 1979, 50, 865. [Google Scholar] [CrossRef]
- Thaler, J. Coulomb-nuclear interference in hadronic atoms. J. Phys. G Nucl. Phys. 1983, 9, 1009. [Google Scholar] [CrossRef]
- Cohen, J.S.; Struensee, M.C. Improved adiabatic calculation of muonic-hydrogen-atom cross sections. I. Isotopic exchange and elastic scattering in asymmetric collisions. Phys. Rev. A 1991, 43, 3460. [Google Scholar] [CrossRef] [PubMed]
- Kvitsinsky, A.A.; Hu, C.Y.; Cohen, J.S. Faddeev calculations of muonic-atom collisions: Scattering and fusion in flight. Phys. Rev. A 1996, 53, 255. [Google Scholar] [CrossRef] [PubMed]
- Kvitsinsky, A.A.; Carbonell, J.; Gignoux, C. s-wave positron-hydrogen scattering via Faddeev equations: Elastic scattering and positronium formation. Phys. Rev. A 1995, 51, 2997. [Google Scholar] [CrossRef] [PubMed]
- Kohno, M.; Weise, W. Proton-antiproton scattering and annihilation into two mesons. Nucl. Phys. A 1986, 454, 429–452. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sultanov, R.A.; Guster, D.; Adhikari, S.K. Influence of the p ¯ -p Nuclear Interaction on the Rate of the Low-Energy p ¯ + H μ → ( p ¯ p ) α + μ − Reaction. Atoms 2018, 6, 18. https://doi.org/10.3390/atoms6020018
Sultanov RA, Guster D, Adhikari SK. Influence of the p ¯ -p Nuclear Interaction on the Rate of the Low-Energy p ¯ + H μ → ( p ¯ p ) α + μ − Reaction. Atoms. 2018; 6(2):18. https://doi.org/10.3390/atoms6020018
Chicago/Turabian StyleSultanov, Renat A., Dennis Guster, and Sadhan K. Adhikari. 2018. "Influence of the p ¯ -p Nuclear Interaction on the Rate of the Low-Energy p ¯ + H μ → ( p ¯ p ) α + μ − Reaction" Atoms 6, no. 2: 18. https://doi.org/10.3390/atoms6020018
APA StyleSultanov, R. A., Guster, D., & Adhikari, S. K. (2018). Influence of the p ¯ -p Nuclear Interaction on the Rate of the Low-Energy p ¯ + H μ → ( p ¯ p ) α + μ − Reaction. Atoms, 6(2), 18. https://doi.org/10.3390/atoms6020018



