Influence of Helical Trajectories of Perturbers on Stark Line Shapes in Magnetized Plasmas
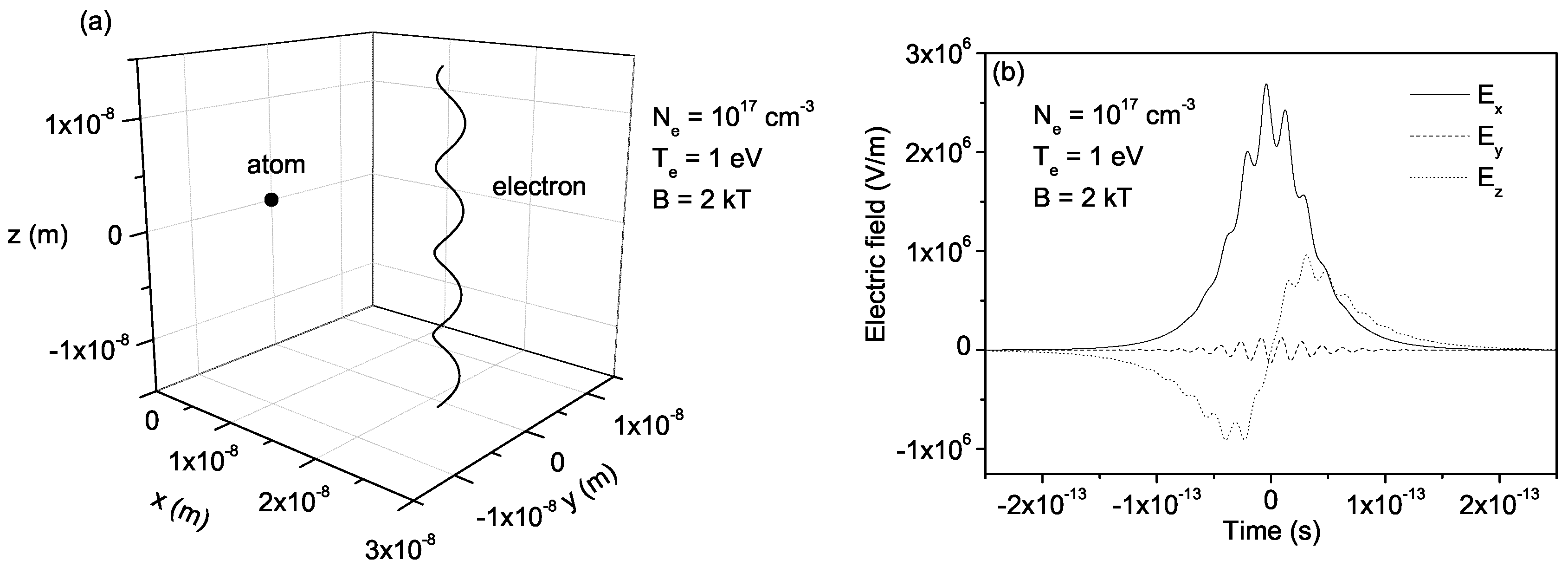
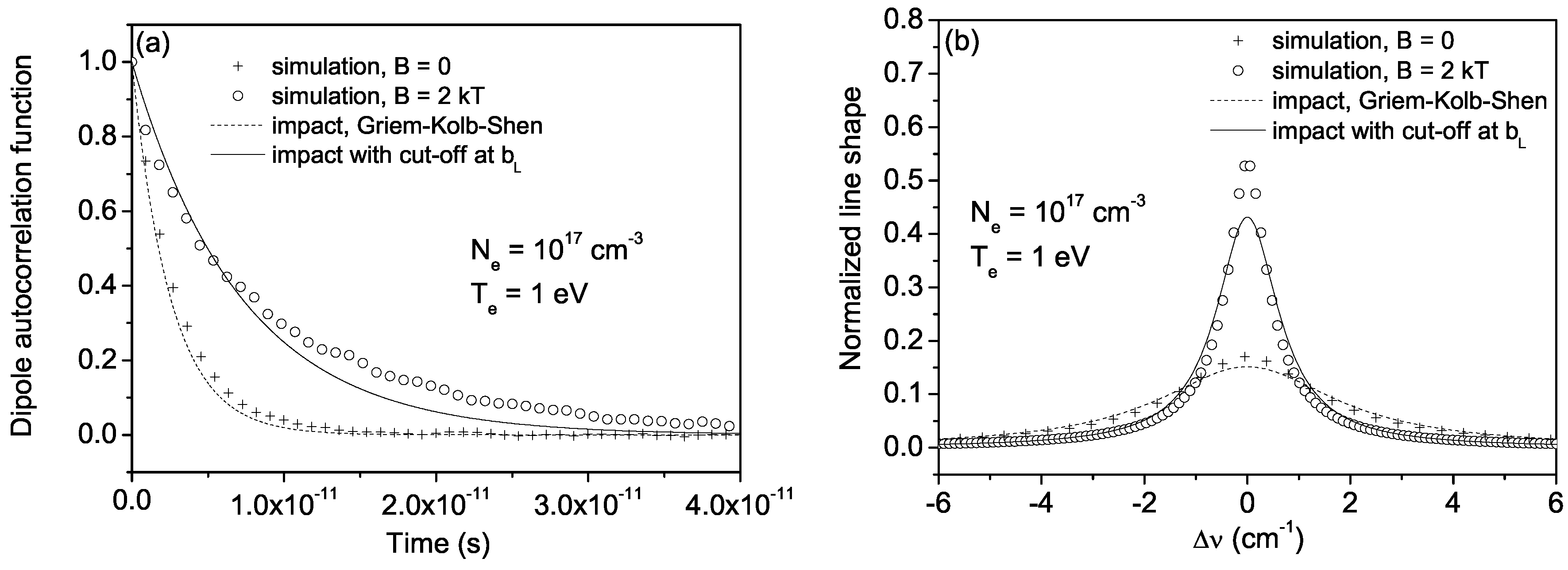
Abstract
:Acknowledgments
Author Contributions
Conflicts of Interest
References
- Külebi, B.; Jordan, S.; Euchner, F.; Gänsicke, B.T.; Hirsch, H. Analysis of hydrogen-rich magnetic white dwarfs detected in the Sloan Digital Sky Survey. Astron. Astrophys. 2009, 506, 1341–1350. [Google Scholar] [CrossRef]
- Kepler, S.O.; Pelisoli, I.; Jordan, S.; Kleinman, S.J.; Koester, D.; Külebi, B.; Peçanha, V.; Castanheira, B.G.; Nitta, A.; da Silveira Costa, J.E.; et al. Magnetic white dwarf stars in the Sloan Digital Sky Survey. Mon. Not. R. Astron. Soc. 2013, 429, 2934–2944. [Google Scholar] [CrossRef]
- Maschke, E.K.; Voslamber, D. Stark-Broadening of Hydrogen Lines in Strong Magnetic Fields; Report EUR-CEA-FC-354; The European Insurance and Reinsurance Federation (CEA): Fontenay-aux-Roses, France, 1966. [Google Scholar]
- Nguyen-Hoe; Drawin, H.-W.; Herman, L. Effet d’un champ magnétique uniforme sur les profils des raies de l’hydrogène. J. Quant. Spectrosc. Radiat. Transf. 1967, 7, 429–474. [Google Scholar] [CrossRef]
- Drawin, H.-W.; Henning, H.; Herman, L. Nguyen-Hoe Stark-broadening of hydrogen Balmer lines in the presence of strong magnetic fields in plasmas. J. Quant. Spectrosc. Radiat. Transf. 1969, 9, 317–331. [Google Scholar] [CrossRef]
- Oks, E. Influence of magnetic-field-caused modifications of trajectories of plasma electrons on spectral line shapes: Applications to magnetic fusion and white dwarfs. J. Quant. Spectrosc. Radiat. Transf. 2016, 171, 15–27. [Google Scholar] [CrossRef]
- Stambulchik, E. Review of the 1st Spectral Line Shapes in Plasmas code comparison workshop. High Energy Density Phys. 2013, 9, 528–534. [Google Scholar] [CrossRef]
- Rosato, J. Report on the third SLSP code comparison workshop. High Energy Density Phys. 2017, 22, 60–63. [Google Scholar] [CrossRef]
- Derevianko, A.; Oks, E. Generalized theory of ion impact broadening in magnetized plasmas and its applications for tokamaks. Phys. Rev. Lett. 1994, 73, 2059–2062. [Google Scholar] [CrossRef] [PubMed]
- Rosato, J.; Marandet, Y.; Capes, H.; Ferri, S.; Mossé, C.; Godbert-Mouret, L.; Koubiti, M.; Stamm, R. Stark broadening of hydrogen lines in low-density magnetized plasmas. Phys. Rev. E 2009, 79, 046408. [Google Scholar] [CrossRef] [PubMed]
- Rosato, J.; Capes, H.; Godbert-Mouret, L.; Koubiti, M.; Marandet, Y.; Stamm, R. Accuracy of impact broadening models in low-density magnetized hydrogen plasmas. J. Phys. B Atomic Mol. Opt. Phys. 2012, 45, 165701. [Google Scholar] [CrossRef]
- Griem, H.R.; Kolb, A.C.; Shen, K.Y. Stark broadening of hydrogen lines in a plasma. Phys. Rev. 1959, 116, 4–16. [Google Scholar] [CrossRef]
- Hegerfeldt, G.C.; Kesting, V. Collision time simulation technique for pressure-broadened spectral lines with applications to Ly-α. Phys. Rev. A 1988, 37, 1488–1496. [Google Scholar] [CrossRef]
- Alexiou, S. Implementation of the Frequency Separation Technique in general lineshape codes. High Energy Density Phys. 2013, 9, 375–384. [Google Scholar] [CrossRef]
- Kieu, N.; Rosato, J.; Stamm, R.; Kovačević-Dojcinović, J.; Dimitrijević, M.S.; Popović, L.C.; Simić, Z.S. A New analysis of Stark and Zeeman effects on hydrogen lines in magnetized DA white dwarfs. Atoms 2017, 5, 44. [Google Scholar] [CrossRef]
- Rosato, J.; Marandet, Y.; Stamm, R. Stark broadening by Lorentz fields in magnetically confined plasmas. J. Phys. B Atomic Mol. Opt. Phys. 2014, 47, 105702. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosato, J.; Ferri, S.; Stamm, R. Influence of Helical Trajectories of Perturbers on Stark Line Shapes in Magnetized Plasmas. Atoms 2018, 6, 12. https://doi.org/10.3390/atoms6010012
Rosato J, Ferri S, Stamm R. Influence of Helical Trajectories of Perturbers on Stark Line Shapes in Magnetized Plasmas. Atoms. 2018; 6(1):12. https://doi.org/10.3390/atoms6010012
Chicago/Turabian StyleRosato, J., S. Ferri, and R. Stamm. 2018. "Influence of Helical Trajectories of Perturbers on Stark Line Shapes in Magnetized Plasmas" Atoms 6, no. 1: 12. https://doi.org/10.3390/atoms6010012
APA StyleRosato, J., Ferri, S., & Stamm, R. (2018). Influence of Helical Trajectories of Perturbers on Stark Line Shapes in Magnetized Plasmas. Atoms, 6(1), 12. https://doi.org/10.3390/atoms6010012




