Stark-Zeeman Line Shape Modeling for Magnetic White Dwarf and Tokamak Edge Plasmas: Common Challenges
Abstract
:1. Introduction
2. Stark Broadening Formalism
3. Ion Broadening at the Impact Limit
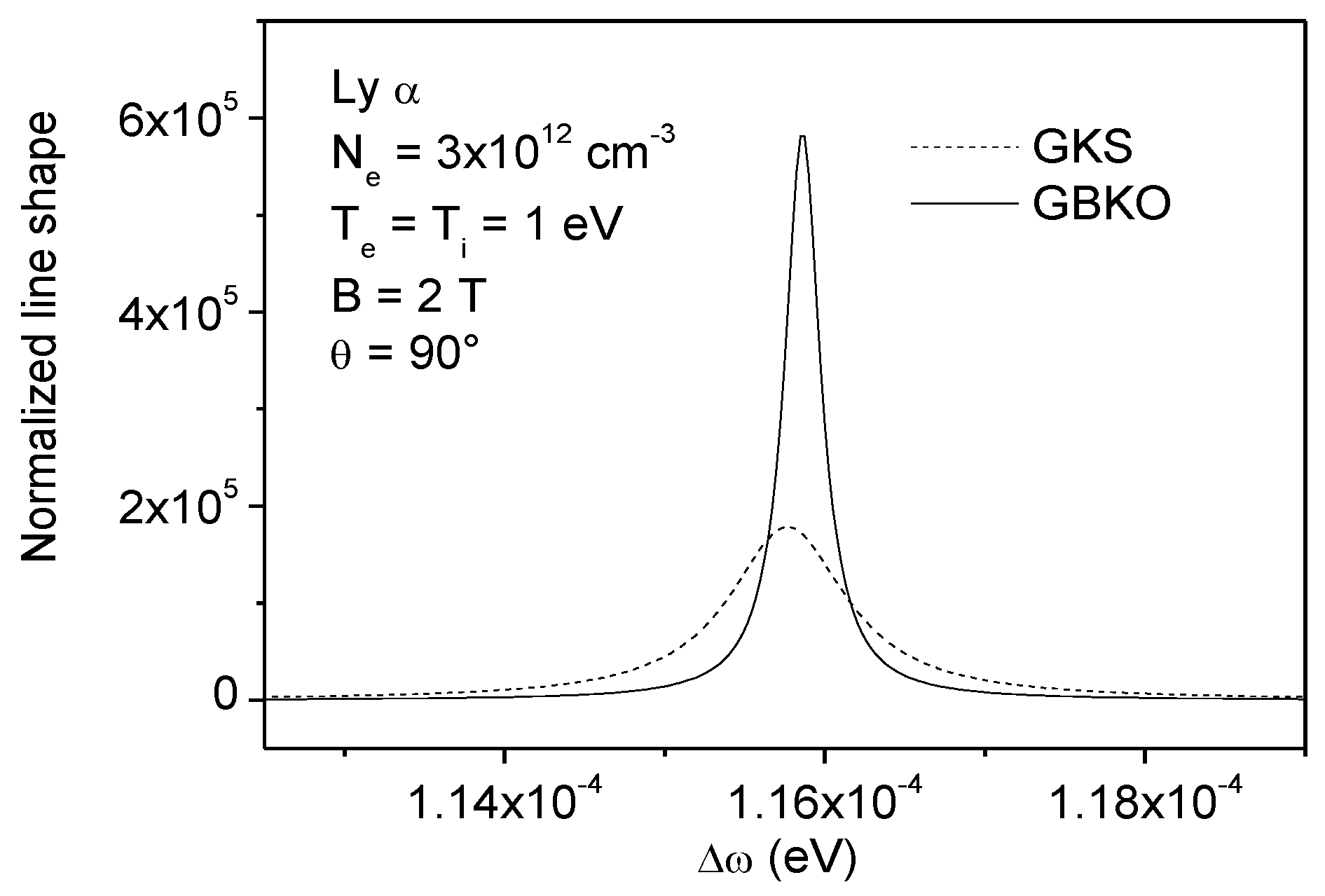
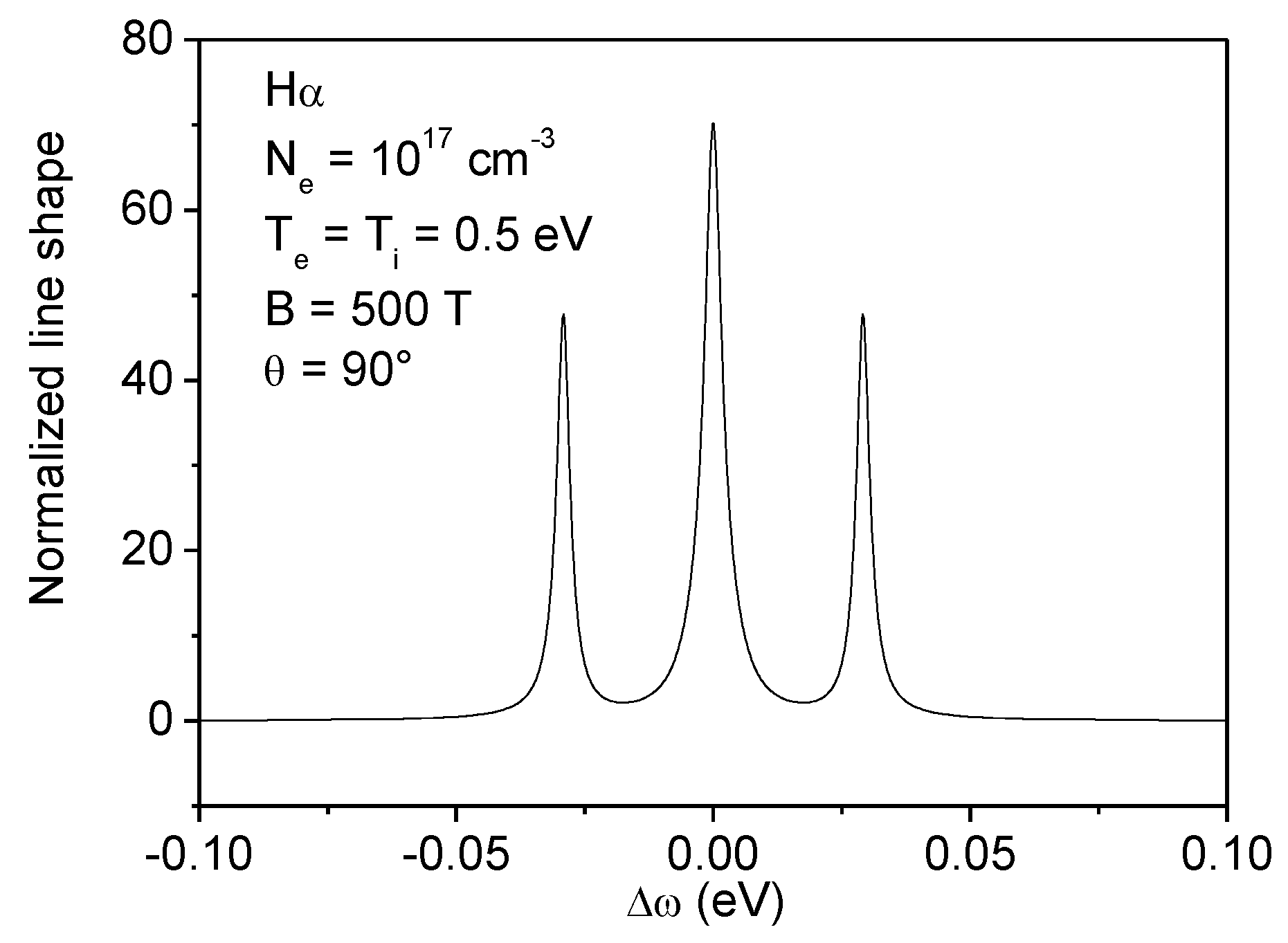
4. Influence of Zeeman Effect on Line Broadening
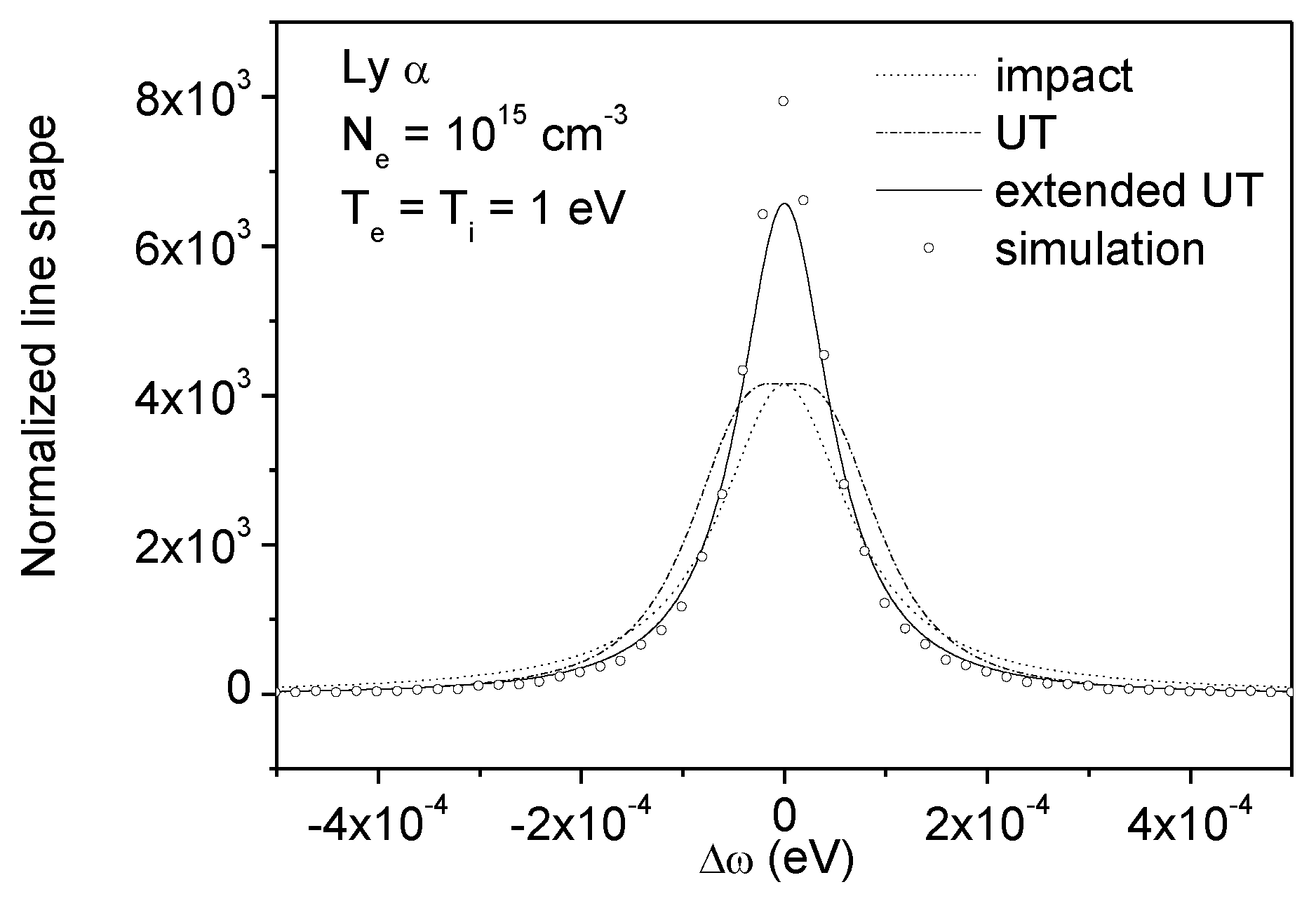
5. An Extension of the Impact theory to Non-Binary Interactions
6. Stark-Zeeman Line Shapes in Magnetic White Dwarfs
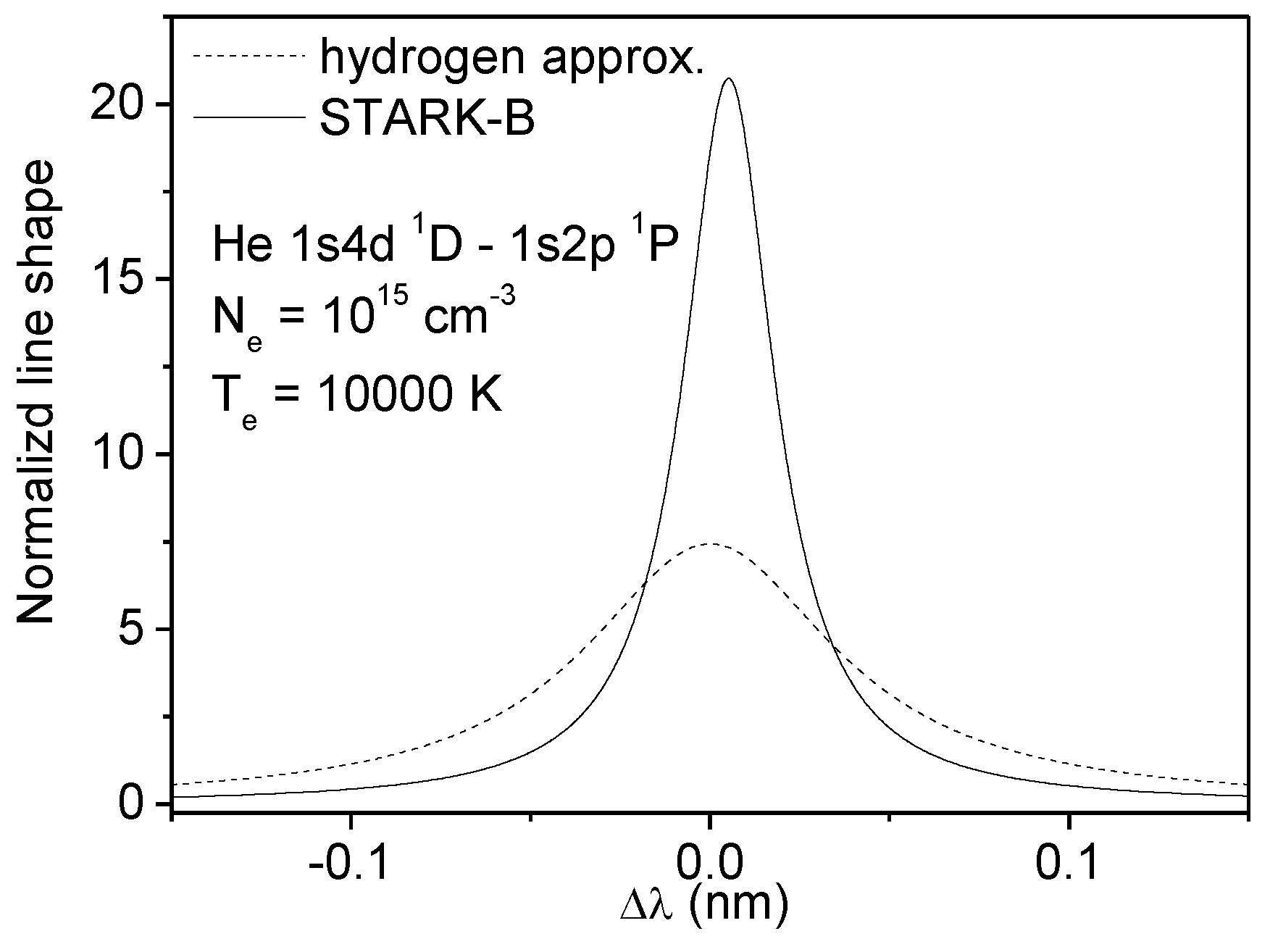
7. Non-Hydrogen Species
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- ITER Press Release. 16 June 2016. Available online: https://www.iter.org/news/pressreleases (accessed on 3 July 2017).
- Donne, A.J.H.; Costley, A.E.; Barnsley, R.; Bindslev, H.; Boivin, R.; Conway, G.; Fisher, R.; Giannella, R.; Hartfuss, H.; von Hellermann, M.G.; et al. Progress in the ITER Physics Basis, Chapter 7: Diagnostics. Nucl. Fusion 2007, 47, S337–S384. [Google Scholar] [CrossRef]
- Sugie, T.; Costley, A.; Malaquias, A.; Walker, C. Spectroscopic Diagnostics for ITER. J. Plasma Fusion Res. 2003, 79, 1051–1061. [Google Scholar] [CrossRef]
- Potzel, S.; Dux, R.; Müller, H.W.; Scarabosio, A.; Wischmeier, M.; ASDEX Upgrade Team. Electron density determination in the divertor volume of ASDEX Upgrade via Stark broadening of the Balmer lines. Plasma Phys. Control. Fusion 2014, 56, 025010. [Google Scholar] [CrossRef]
- Rosato, J.; Kotov, V.; Reiter, D. Modelling of passive spectroscopy in the ITER divertor: The first hydrogen Balmer lines. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 144024. [Google Scholar] [CrossRef]
- Rosato, J.; Marandet, Y.; Capes, H.; Ferri, S.; Mossé, C.; Godbert-Mouret, L.; Koubiti, M.; Stamm, R. Stark broadening of hydrogen lines in low-density magnetized plasmas. Phys. Rev. E 2009, 79, 046408. [Google Scholar] [CrossRef] [PubMed]
- Rosato, J.; Marandet, Y.; Stamm, R. A new table of Balmer line shapes for the diagnostic of magnetic fusion plasmas. J. Quant. Spectrosc. Radiat. Transf. 2017, 187, 333–337. [Google Scholar] [CrossRef]
- Sahal-Bréchot, S.; Dimitrijević, M.S.; Moreau, N.; Ben Nessib, N. The STARK-B database VAMDC node: A repository for spectral line broadening and shifts due to collisions with charged particles. Phys. Scr. 2015, 90, 054008. [Google Scholar] [CrossRef]
- Kepler, S.O.; Pelisoli, I.; Jordan, S.; Kleinman, S.J.; Kulebi, B.; Koester, D.; Peçanha, V.; Castanheira, B.G.; Nitta, A.; da Silveira Costa, J.E.; et al. Magnetic white dwarf stars in the Sloan Digital Sky Survey. Mon. Not. R. Astron. Soc. 2013, 429, 2934–2944. [Google Scholar] [CrossRef]
- Külebi, B.; Jordan, S.; Euchner, F.; Gänsicke, B.T.; Hirsch, H. Analysis of hydrogen-rich magnetic white dwarfs detected in the Sloan Digital Sky Survey. Astron. Astrophys. 2009, 506, 1341–1350. [Google Scholar] [CrossRef]
- Wickramasinghe, D.T. Model atmospheres for DA and DB white dwarfs. Mon. Not. R. Astron. Soc. 1972, 76, 129–179. [Google Scholar]
- Griem, H.R. Spectral Line Broadening by Plasmas; Academic Press: London, UK, 1974. [Google Scholar]
- Stamm, R.; Smith, E.W.; Talin, B. Study of hydrogen Stark profiles by means of computer simulation. Phys. Rev. A 1984, 30, 2039–2046. [Google Scholar] [CrossRef]
- Stambulchik, E.; Maron, Y. Plasma line broadening and computer simulations: A mini-review. High Energy Density Phys. 2010, 6, 9–14. [Google Scholar] [CrossRef]
- Rosato, J.; Reiter, D.; Kotov, V.; Marandet, Y.; Capes, H.; Godbert-Mouret, L.; Koubiti, M.; Stamm, R. Progress on Radiative Transfer Modelling in Optically Thick Divertor Plasmas. Contrib. Plasma Phys. 2010, 50, 398–403. [Google Scholar] [CrossRef]
- Kotov, V.; Reiter, D.; Kukushkin, A.S.; Pacher, H.D.; Börner, P.; Wiesen, S. Radiation Absorption Effects in B2-EIRENE Divertor Modelling. Contrib. Plasma Phys. 2006, 46, 635–642. [Google Scholar] [CrossRef]
- Griem, H.R.; Kolb, A.C.; Shen, K.Y. Stark Broadening of Hydrogen Lines in a Plasma. Phys. Rev. 1959, 116, 4–16. [Google Scholar] [CrossRef]
- Griem, H.R.; Baranger, M.; Kolb, A.C.; Oertel, G. Stark Broadening of Neutral Helium Lines in a Plasma. Phys. Rev. 1962, 125, 177–195. [Google Scholar] [CrossRef]
- Rosato, J.; Capes, H.; Godbert-Mouret, L.; Koubiti, M.; Marandet, Y.; Stamm, R. Accuracy of impact broadening models in low-density magnetized hydrogen plasmas. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 1–7. [Google Scholar] [CrossRef]
- Rosato, J.; Capes, H.; Stamm, R. Influence of correlated collisions on Stark-broadened lines in plasmas. Phys. Rev. E 2012, 86, 046407. [Google Scholar] [CrossRef] [PubMed]
- Voslamber, D. Unified Model for Stark Broadening. Z. Naturforsch. 1969, 24, 1458–1472. [Google Scholar]
- Smith, E.W.; Cooper, J.; Vidal, C.R. Unified Classical-Path Treatment of Stark Broadening in Plasmas. Phys. Rev. 1969, 185, 140–151. [Google Scholar] [CrossRef]
- Capes, H.; Voslamber, D. Electron Correlations in the Unified Model for Stark Broadening. Phys. Rev. A 1972, 5, 2528–2536. [Google Scholar] [CrossRef]
- Capes, H.; Voslamber, D. Spectral-line profiles in weakly turbulent plasmas. Phys. Rev. A 1977, 15, 1751–1766. [Google Scholar] [CrossRef]
- Dupree, T.H. A Perturbation Theory for Strong Plasma Turbulence. Phys. Fluids 1966, 9, 1773–1782. [Google Scholar] [CrossRef]
- Weinstock, J. Formulation of a Statistical Theory of Strong Plasma Turbulence. Phys. Fluids 1969, 12, 1045–1058. [Google Scholar] [CrossRef]
- Landstreet, J.D.; Bagnulo, S.; Valyavin, G.G.; Fossati, L.; Jordan, S.; Monin, D.; Wade, G.A. On the incidence of weak magnetic fields in DA white dwarfs. Astron. Astrophys. 2012, 545, A30. [Google Scholar] [CrossRef]
- Gomez, T.A.; Nagayama, T.; Kilcrease, D.P.; Montgomery, M.H.; Winget, D.E. Effect of higher-order multipole moments on the Stark line shape. Phys. Rev. A 2016, 94, 022501. [Google Scholar] [CrossRef]
- Maschke, E.K.; Voslamber, D. Stark broadening of hydrogen lines in strong magnetic fields. In Proceedings of the Seventh International Conference, Beograd, Yugoslavia, 22–27 August 1965; Gradevinska Knjiga Publishing House : Beograd, Yugoslavia, 1966; Volume II, p. 568. [Google Scholar]
- Rosato, J. Cases 10–11: B-induced trajectory effects. In Proceedings of the 4th Spectral Line Shapes in Plasmas (SLSP) Code Comparison Workshop, Vienna, Austria, 20–24 March 2017. [Google Scholar]
- Kieu, N.; Rosato, J.; Stamm, R.; Kovacević-Dojcinović, J.; Dimitrijević, M.S.; Popović, L.C.; Simić, Z. A New Analysis of Stark and Zeeman Effects on Hydrogen Lines in Magnetized DA White Dwarfs. Atoms 2017. submitted. [Google Scholar]
- Koubiti, M.; Nakano, T.; Capes, H.; Marandet, M.; Mekkaoui, A.; Mouret, L.; Rosato, J.; Stamm, R. Characterization of the JT-60U Divertor Plasma Region During the Formation of a Strong Radiation. Contrib. Plasma Phys. 2012, 52, 455–459. [Google Scholar] [CrossRef]
- Pütterich, T.; Neu, R.; Dux, R.; Whiteford, A.D.; O’Mullane, M.G. The ASDEX Upgrade Team. Modelling of measured tungsten spectra from ASDEX Upgrade and predictions for ITER. Plasma Phys. Control. Fusion 2008, 50, 085016. [Google Scholar] [CrossRef]
- Calisti, A.; Mossé, C.; Ferri, S.; Talin, B.; Rosmej, F.; Bureyeva, L.A.; Lisitsa, V.S. Dynamic Stark broadening as the Dicke narrowing effect. Phys. Rev. E 2010, 81, 016406. [Google Scholar] [CrossRef] [PubMed]
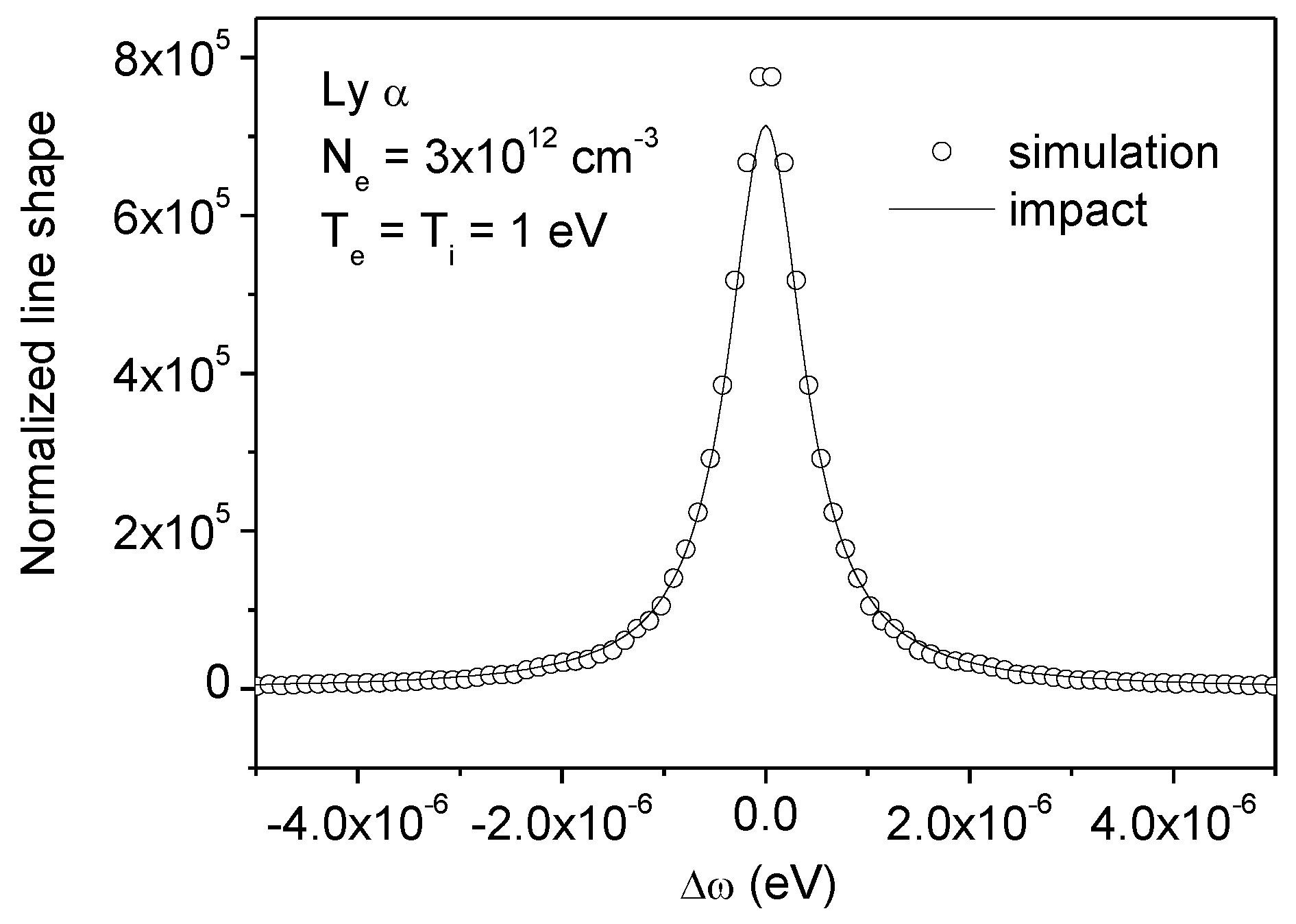
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosato, J.; Kieu, N.; Hannachi, I.; Koubiti, M.; Marandet, Y.; Stamm, R.; Dimitrijević, M.S.; Simić, Z. Stark-Zeeman Line Shape Modeling for Magnetic White Dwarf and Tokamak Edge Plasmas: Common Challenges. Atoms 2017, 5, 36. https://doi.org/10.3390/atoms5040036
Rosato J, Kieu N, Hannachi I, Koubiti M, Marandet Y, Stamm R, Dimitrijević MS, Simić Z. Stark-Zeeman Line Shape Modeling for Magnetic White Dwarf and Tokamak Edge Plasmas: Common Challenges. Atoms. 2017; 5(4):36. https://doi.org/10.3390/atoms5040036
Chicago/Turabian StyleRosato, Joël, Ny Kieu, Ibtissem Hannachi, Mohammed Koubiti, Yannick Marandet, Roland Stamm, Milan S. Dimitrijević, and Zoran Simić. 2017. "Stark-Zeeman Line Shape Modeling for Magnetic White Dwarf and Tokamak Edge Plasmas: Common Challenges" Atoms 5, no. 4: 36. https://doi.org/10.3390/atoms5040036
APA StyleRosato, J., Kieu, N., Hannachi, I., Koubiti, M., Marandet, Y., Stamm, R., Dimitrijević, M. S., & Simić, Z. (2017). Stark-Zeeman Line Shape Modeling for Magnetic White Dwarf and Tokamak Edge Plasmas: Common Challenges. Atoms, 5(4), 36. https://doi.org/10.3390/atoms5040036






