Inter-Series Interactions on the Atomic Photoionization Spectra Studied by the Phase-Shifted Multichannel-Quantum Defect Theory
Abstract
:1. Introduction
2. Resonance Structures in Phase-Shifted MQDT
3. Nondegenerate System
3.1. Autoionizing Rydberg Series Perturbed by an Interloper Series in Nondegenerate Systems
3.1.1. Two-Closed-Channel System Involving One Open Channel
3.1.2. A Two-Closed-Channel System Involving More than One Open Channel
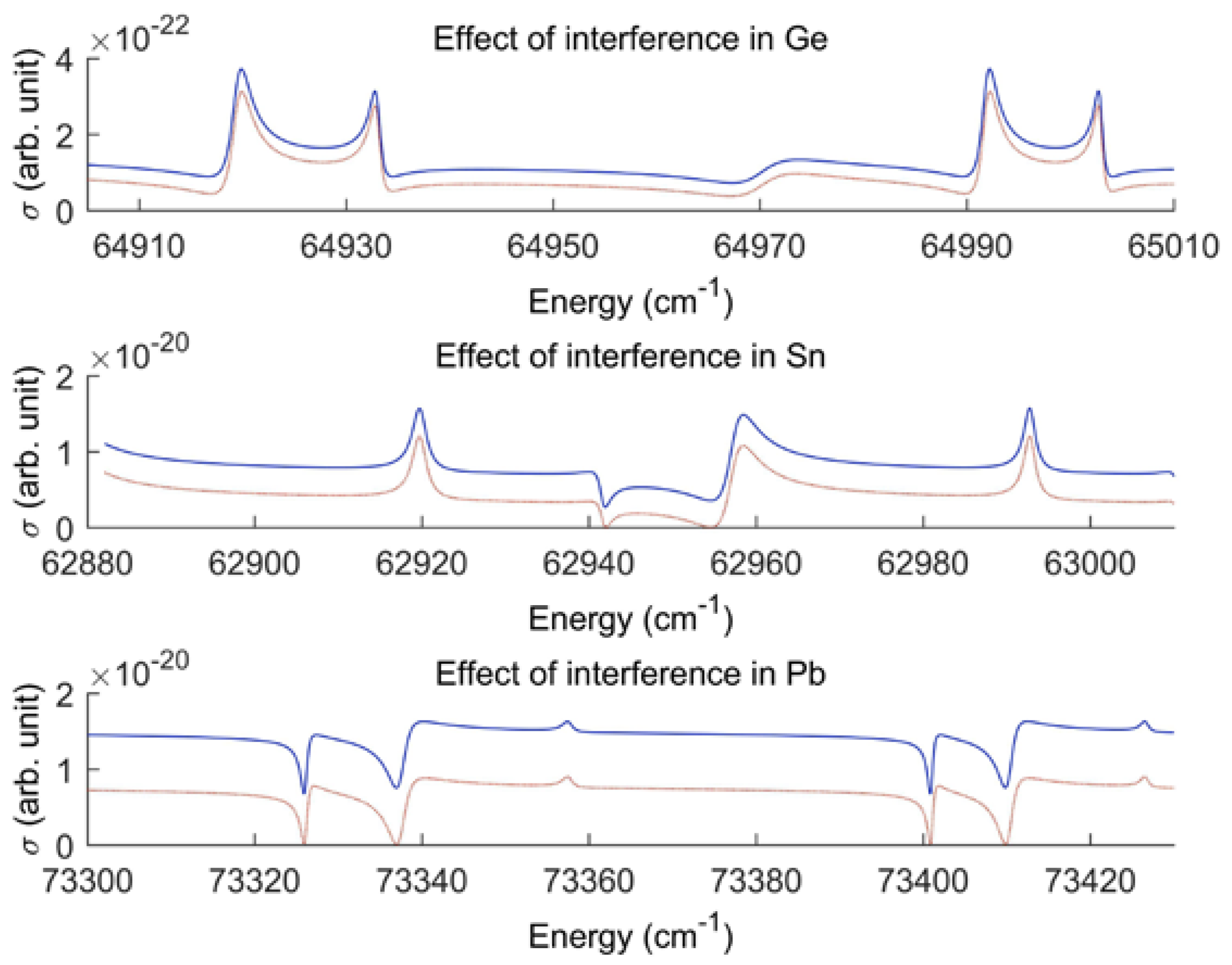
3.2. Inter-Series Interactions between Two Autoionizing Principal Series Perturbed by an Interloper
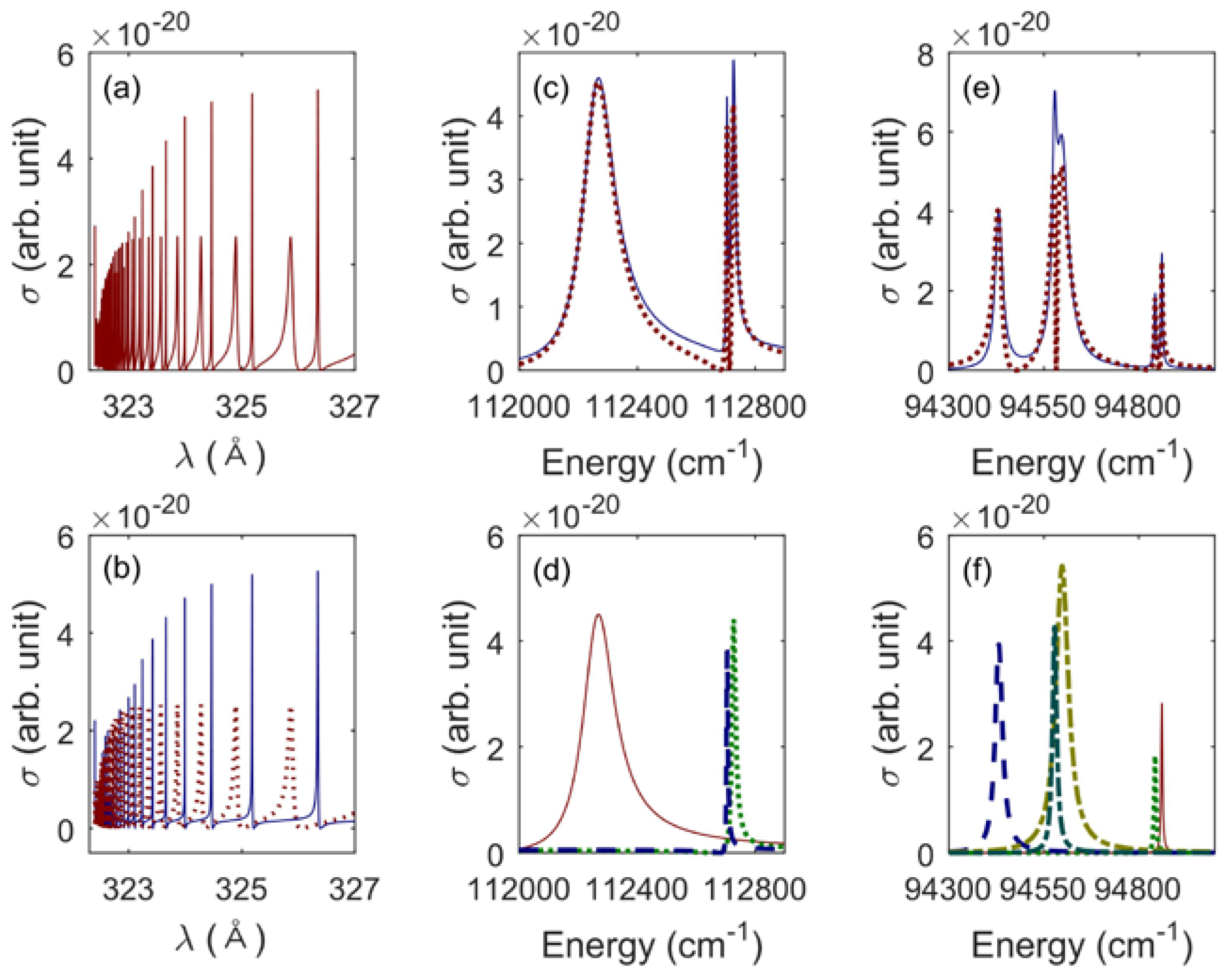
4. Degenerate System
4.1. Resonance Structures in Degenerate Autoionizing RYDBERG Series
4.2. Degenerate Autoionizing Rydberg Series Involving One Open Channel
4.3. Degenerate Autoionizing Rydberg Series Involving Many Open Channels
5. Conclusions
Conflicts of Interest
References
- Fano, U. Effects of Configuration Interaction on Intensities and Phase Shifts. Phys. Rev. 1961, 124, 1866–1878. [Google Scholar] [CrossRef]
- Fano, U. Unified treatment of perturbed series, continuous spectra and collisions. J. Opt. Soc. Am. 1975, 65, 979–987. [Google Scholar] [CrossRef]
- Fano, U. Quantum Defect Theory of l Uncoupling in H2 as an Example of Channel Interaction Treatment. Phys. Rev. A 1970, 2, 353–365. [Google Scholar] [CrossRef]
- Giusti-Suzor, A.; Fano, U. Alternative parameters of channel interactions. I. Symmetry analysis of the two-channel coupling. J. Phys. B 1984, 17, 215–229. [Google Scholar] [CrossRef]
- Cooke, W.E.; Cromer, C.L. Multichannel quantum-defect theory and an equivalent N-level system. Phys. Rev. A 1985, 32, 2725–2738. [Google Scholar] [CrossRef]
- Fano, U.; Rau, A.R.P. Atomic Collisions and Spectra; Academic: Orlando, FL, USA, 1986. [Google Scholar]
- Lecomte, J.M. Parametrisation of resonance structures in the multichannel quantum defect theory. J. Phys. B 1987, 20, 3645–3662. [Google Scholar] [CrossRef]
- Ueda, K. Spectral line shapes of autoionizing Rydberg series. Phys. Rev. A 1987, 35, 2484–2492. [Google Scholar] [CrossRef]
- Giusti-suzor, A.; Lefebvre-Brion, H. A multichannel quantum defect approach to molecular autoionization. Chem. Phys. Lett. 1980, 76, 132–135. [Google Scholar] [CrossRef]
- Wintgen, D.; Friedrich, H. Perturbed Rydberg series of autoionizing resonances. Phys. Rev. A 1987, 35, 1628–1633. [Google Scholar] [CrossRef]
- Cohen, S. Resonant widths, line intensities and lineshapes for MQDT models with two or more open channels. Eur. Phys. J. D 1998, 4, 31–38. [Google Scholar] [CrossRef]
- Giusti-Suzor, A.; Lefebvre-Brion, H. Theoretical study of complex resonances near ionization thresholds: Application to the N2 photoionization spectrum. Phys. Rev. A 1984, 30, 3057–3065. [Google Scholar] [CrossRef]
- Cho, B.; Lee, C.W. Multichannel quantum-defect study of q reversals in overlapping resonances in systems involving 1 open and 2 closed channels. Bull. Korean Chem. Soc. 2010, 31, 315–326. [Google Scholar] [CrossRef]
- Fano, U.; Cooper, J.W. Line profiles in the far-uv absorption spectra of the rare gases. Phys. Rev. 1965, 137, A1364–A1379. [Google Scholar] [CrossRef]
- Mies, F.H. Configuration interaction theory. Effects of overlapping resonances. Phys. Rev. 1968, 175, 164–175. [Google Scholar] [CrossRef]
- Cooke, W.E.; Gallagher, T.F. Observation of pair splittings in the autoionization spectrum of Ba. Phys. Rev. Lett. 1978, 41, 1648–1652. [Google Scholar] [CrossRef]
- Bhatti, S.A.; Cromer, C.L.; Cooke, W.E. Analysis of the Rydberg character of the 5d7d1D2 state of barium. Phys. Rev. A 1981, 24, 161–165. [Google Scholar] [CrossRef]
- Lee, C.W. Decoupling of background and resonance scatterings in multichannel quantum defect theory and extraction of dynamic parameters from Lu-Fano plot. Bull. Korean Chem. Soc. 2009, 30, 891–896. [Google Scholar]
- Fyodorov, Y.V.; Sommers, H.J. Statistics of resonance poles, phase shifts and time delays in quantum chaotic scattering: Random matrix approach for systems with broken time-reversal invariance. J. Math. Phys. 1997, 38, 1918–1981. [Google Scholar] [CrossRef]
- Seaton, M.J. Quantum defect theory. Rep. Prog. Phys. 1983, 46, 167–257. [Google Scholar] [CrossRef]
- Lee, C.W. Geometrical construction of the S matrix and multichannel quantum defect theory for the two open and one closed channel system. Bull. Korean Chem. Soc. 2002, 23, 971–984. [Google Scholar]
- Lee, C.W. Resonance structures in the multichannel quantum-defect theory for the photofragmentation processes involving one closed and many open channels. Phys. Rev. A 2002, 66, 052704:1–052704:7. [Google Scholar] [CrossRef]
- Lee, C.W. Identification of the Beutler-Fano formula in eigenphase shifts and eigentime delays near a resonance. Phys. Rev. A 1998, 58, 4581–4592. [Google Scholar] [CrossRef]
- Lee, C.W. Geometrical construction of the coupling between background and resonance scattering in the S matrix. Phys. Essays 2000, 13, 206–214. [Google Scholar] [CrossRef]
- Lee, C.-W. Decoupling of Background and Resonance Scatterings in Mulichannel Quantum Defect Theory and Extraction of Dynamic Parameters from Lu-Fano plot. Bull. Korean Chem. Soc. 2009, 30, 891–896. [Google Scholar]
- Simonius, M. Overlapping resonances and unitarity of the scattering matrix. Nucl. Phys. A 1974, 218, 53–60. [Google Scholar] [CrossRef]
- Lee, C.-W.; Kim, J. Effect of open channels on the isolation of overlapping resonances in the uniformly perturbed rydberg systems studied by multichannel quantum defect theory. Bull. Korean Chem. Soc. 2011, 32, 1519–1526. [Google Scholar] [CrossRef]
- Lee, C.W. Isolation of overlapping resonances by multichannel quantum defect theory in the uniformly perturbed Rydberg systems involving one open and many degenerate closed channels. J. Phys. B 2010, 43, 175002. [Google Scholar] [CrossRef]
- Lee, C.-W. Role of open channels in overlapping resonances studied by multichannel quantum defect theory in systems involving 2 nondegenerate closed and many open channels. Bull. Korean Chem. Soc. 2010, 31, 3201–3211. [Google Scholar] [CrossRef]
- Lane, A.M. Variation in cross section fluctuations arising from a Rydberg series interacting with a broad level. J. Phys. B 1985, 18, 2339–2356. [Google Scholar] [CrossRef]
- Bethe, H.A.; Salpeter, E.E. Quantum Mechanics of One- and Two-Electron Atoms; Springer: New York, NY, USA, 1957; p. 368. [Google Scholar]
- Lee, C.-W. Multichannel quantum defect study of the perturber’s effect on the overlapping resonances in rydberg series for the systems involving 2 closed and many open channels. Bull. Korean Chem. Soc. 2010, 31, 1669–1680. [Google Scholar] [CrossRef]
- Martins, M.; Zimmermann, P. Analysis of autoionizing Rydberg series Cu I 3d9 4snl with the multichannel quantum defect theory. Z. Phys. D 1993, 27, 115–121. [Google Scholar] [CrossRef]
- De Graaff, R.J.; Ubachs, W.; Hogervorst, W.; Abutaleb, M. Narrow 6p1/2,3/2np J = 1 autoionizing Rydberg series in barium and their interaction with 6p3/2nf states. Phys. Rev. A 1990, 42, 5473–5480. [Google Scholar] [CrossRef] [PubMed]
- Kalyar, M.A.; Rafiq, M.; Baig, M.A. Interaction of the 6p2 1S0 broad resonance with 5dnd J = 0 autoionizing resonances in barium. Phys. Rev. A 2009, 80, 052505. [Google Scholar] [CrossRef]
- Lee, C.-W. Study of the resonance structures of the interacting degenerate autoionizing Rydberg series perturbed by an interloper by multichannel quantum defect theory. J. Phys. B 2011, 44, 195005. [Google Scholar] [CrossRef]
- Lee, C.-W.; Kim, J.; Gim, Y.; Lee, W.-J. Channel coupling between perturbed autoionizing Rydberg series in the presence of an interloper by multichannel quantum defect theory in the systems involving one open and three closed channels. J. Phys. B 2011, 44, 065002. [Google Scholar] [CrossRef]
- Ueda, K. Spectral line shapes of autoionizing Rydberg series of xenon. J. Opt. Soc. Am. B 1987, 4, 424–427. [Google Scholar]
- Maeda, K.; Ueda, K.; Aymar, M.; Matsui, T.; Chiba, H.; Ito, K. Absolute photoionization cross sections of the Ba ground state in the autoionization region: II. 221–209 nm. J. Phys. B 2000, 33, 1943–1966. [Google Scholar] [CrossRef]
- Klar, D.; Aslam, M.; Baig, M.A.; Ueda, K.; Ruff, M.W.; Hotop, H. High-resolution measurements and multichannel quantum defect analysis of the Kr(4p5(2P1/2)nd’, J = 2, 3) autoionizing resonances. J. Phys. B 2001, 34, 1549. [Google Scholar] [CrossRef]
- Shore, B.W. Parametrization of absorption-line profiles. Phys. Rev. 1968, 171, 43–54. [Google Scholar] [CrossRef]
- Feshbach, H. Theoretical Nuclear Physics; John Wiley & Sons: New York, NY, USA, 1992. [Google Scholar]
- Wright, J.D.; Morgan, T.J.; Li, L.; Gu, Q.; Knee, J.L.; Petrov, I.D.; Sukhorukov, V.L.; Hotop, H. Photoionization spectroscopy of even-parity autoionizing Rydberg states of argon: Experimental and theoretical investigation of Fano profiles and resonance widths. Phys. Rev. A 2008, 77, 062512. [Google Scholar] [CrossRef]
- Petrov, I.D.; Sukhorukov, V.L.; Ruf, M.W.; Hotop, H. Odd autoionizing 2p1/25n(s’/d’) resonances of Ne excited from the 2p53p[K]J states. Eur. Phys. J. D 2009, 53, 289–302. [Google Scholar] [CrossRef]
- Lee, C.W.; Kong, J.H. Multichannel quantum defect theory analysis of overlapping resonance structures in Lu-Fano plots of rare gas spectra. Bull. Korean Chem. Soc. 2009, 30, 1783–1792. [Google Scholar]
- Baig, M.A.; Bhatti, S.A. High-resolution photoabsorption measurement and multichannel quantum-defect-theory analysis of the 2p53s(1P1) ns,nd autoionizing series of sodium. Phys. Rev. A 1994, 50, 2750–2753. [Google Scholar] [CrossRef] [PubMed]
- Baig, M.A. High resolution measurement and MQDT analysis of the 5d9 6s2np, nf (J = 1) autoionizing resonances of mercury. Eur. Phys. J. D 2008, 46, 437–442. [Google Scholar] [CrossRef]
- Baig, M.A. Photoabsorption spectra of silver in the 4d -subshell excitation region. Phys. Rev. A 2009, 79, 012509. [Google Scholar] [CrossRef]
- Ueda, K. Spectral line shapes of autoionizing Rydberg series of Sn and Pb. J. Opt. Soc. Am. B 1987, 4, 1136–1137. [Google Scholar] [CrossRef]
- Ueda, K. Analysis of the J = 1 odd-parity spectrum of germanium by the use of multichannel quantum-defect theory. J. Opt. Soc. Am. B 1987, 4, 648–651. [Google Scholar] [CrossRef]

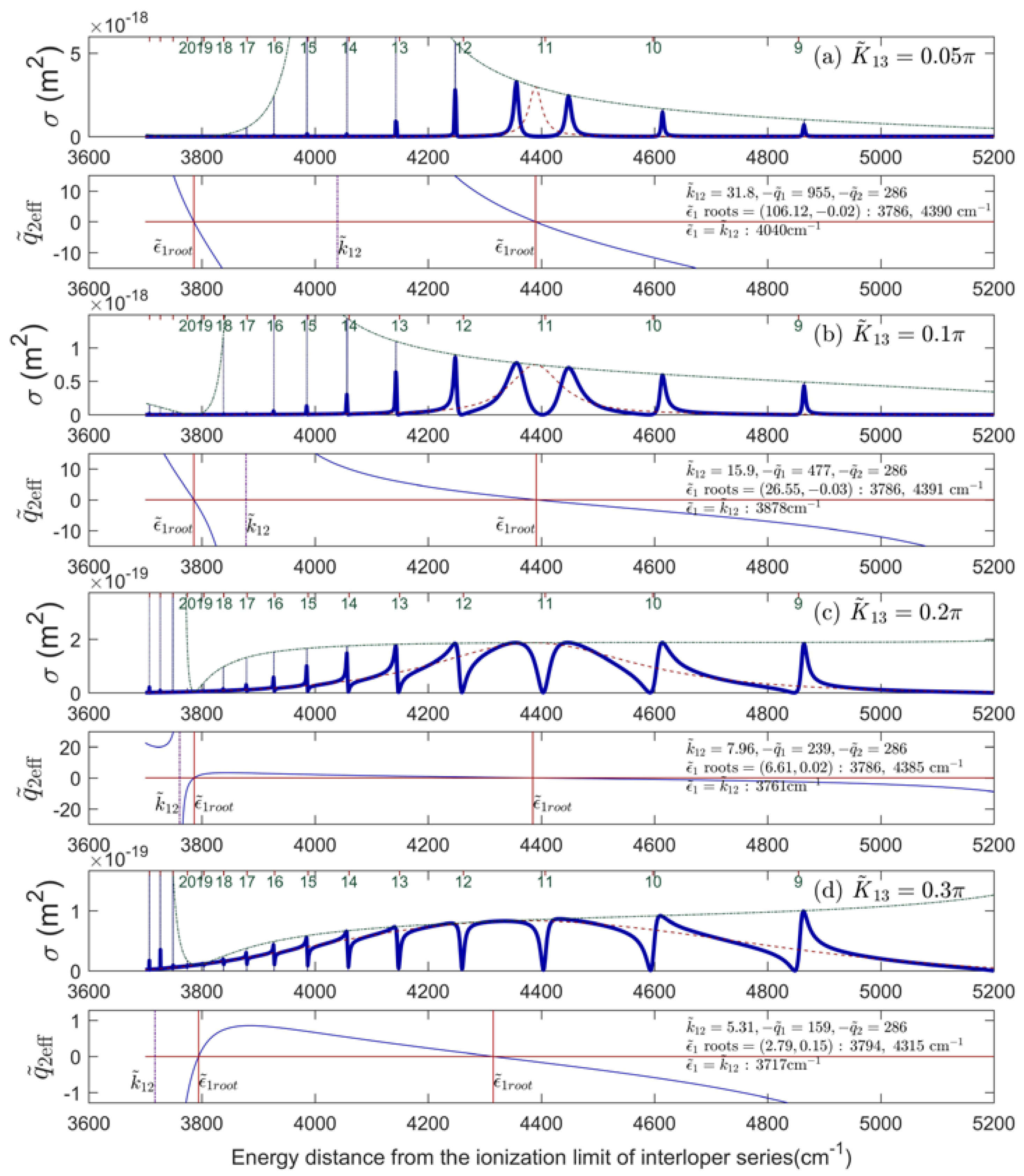
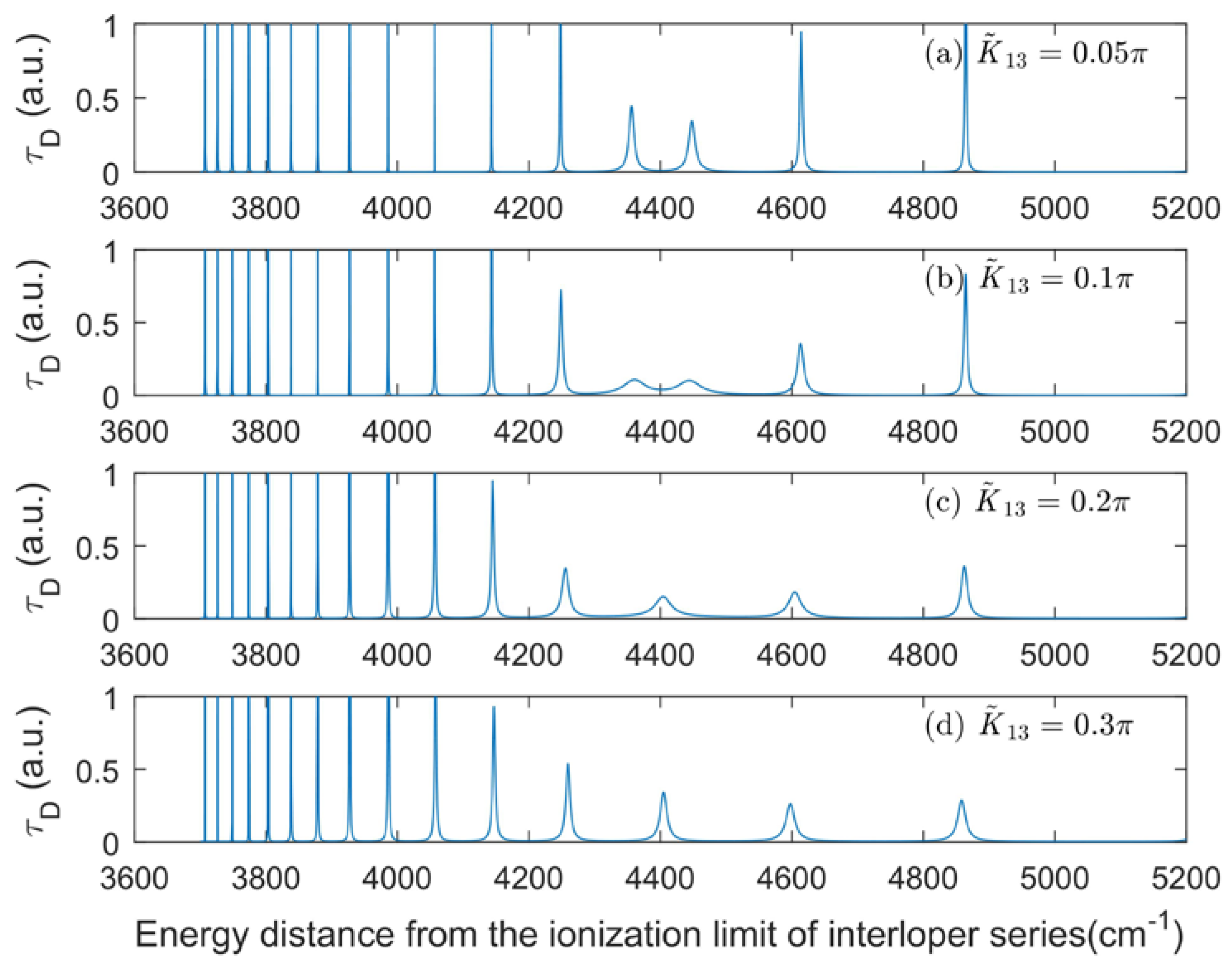



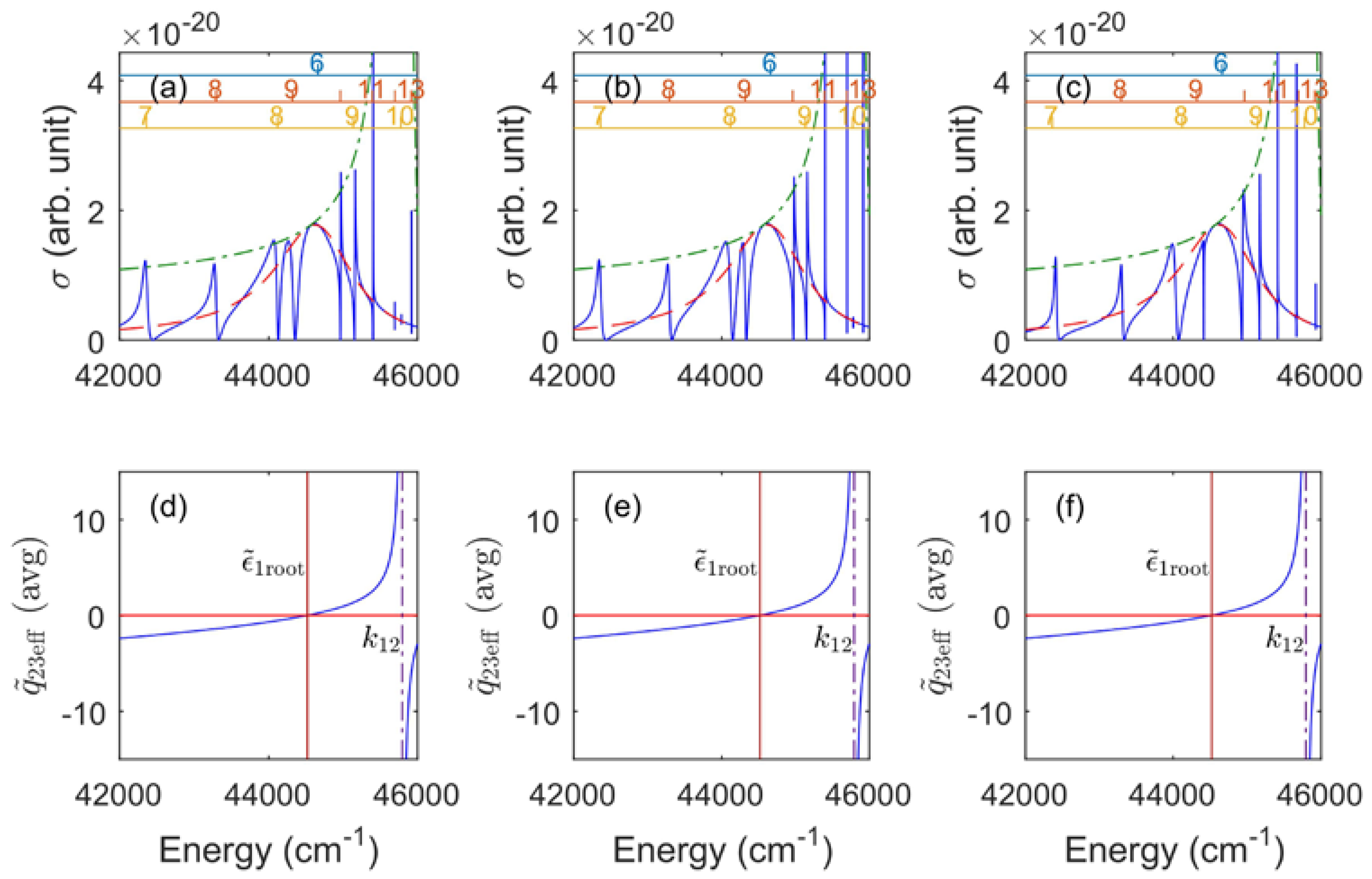
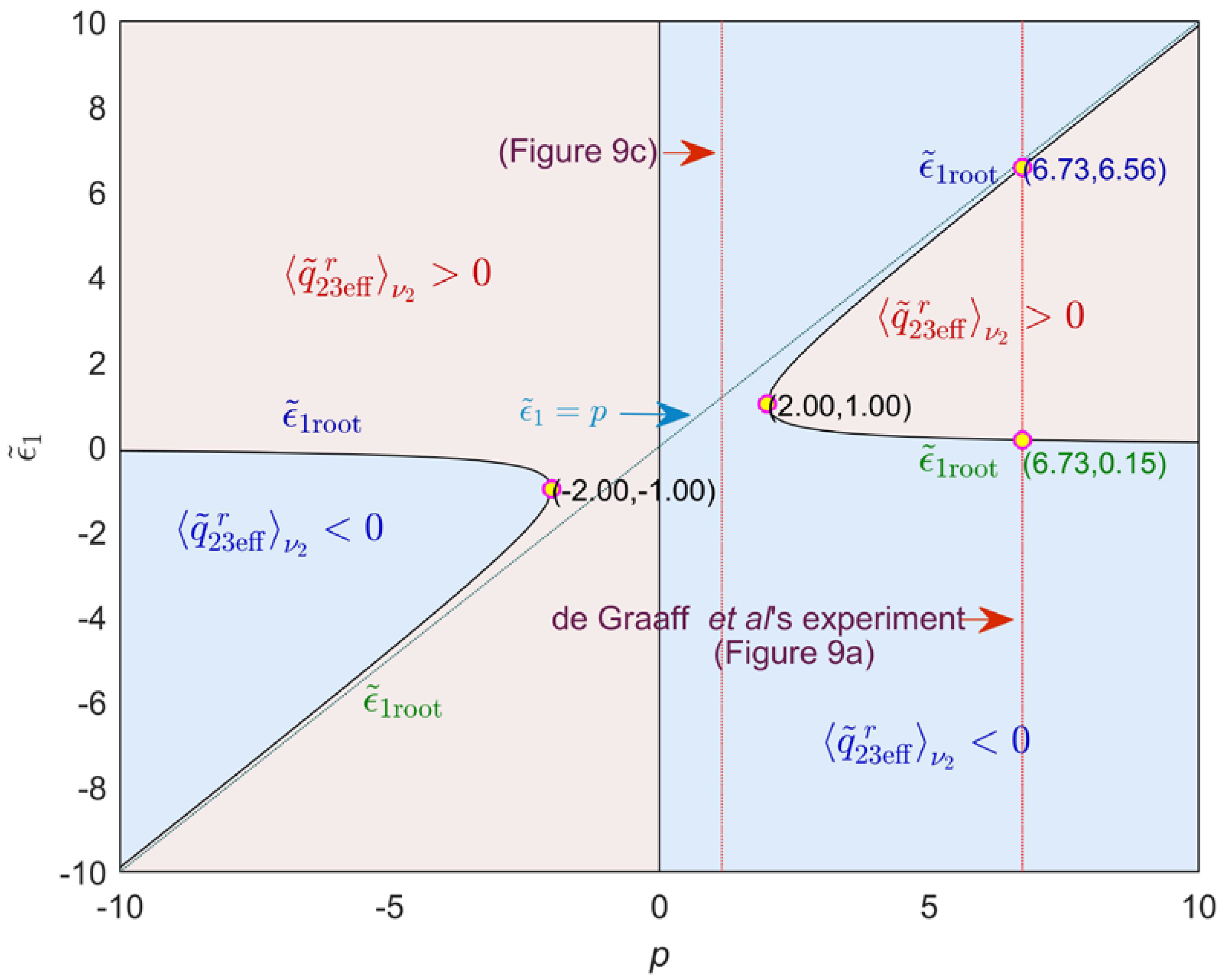




© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.-W. Inter-Series Interactions on the Atomic Photoionization Spectra Studied by the Phase-Shifted Multichannel-Quantum Defect Theory. Atoms 2017, 5, 21. https://doi.org/10.3390/atoms5020021
Lee C-W. Inter-Series Interactions on the Atomic Photoionization Spectra Studied by the Phase-Shifted Multichannel-Quantum Defect Theory. Atoms. 2017; 5(2):21. https://doi.org/10.3390/atoms5020021
Chicago/Turabian StyleLee, Chun-Woo. 2017. "Inter-Series Interactions on the Atomic Photoionization Spectra Studied by the Phase-Shifted Multichannel-Quantum Defect Theory" Atoms 5, no. 2: 21. https://doi.org/10.3390/atoms5020021
APA StyleLee, C.-W. (2017). Inter-Series Interactions on the Atomic Photoionization Spectra Studied by the Phase-Shifted Multichannel-Quantum Defect Theory. Atoms, 5(2), 21. https://doi.org/10.3390/atoms5020021





