Hyperfine Structure and Isotope Shifts in Dy II
Abstract
:1. Introduction
2. Experimental Setup
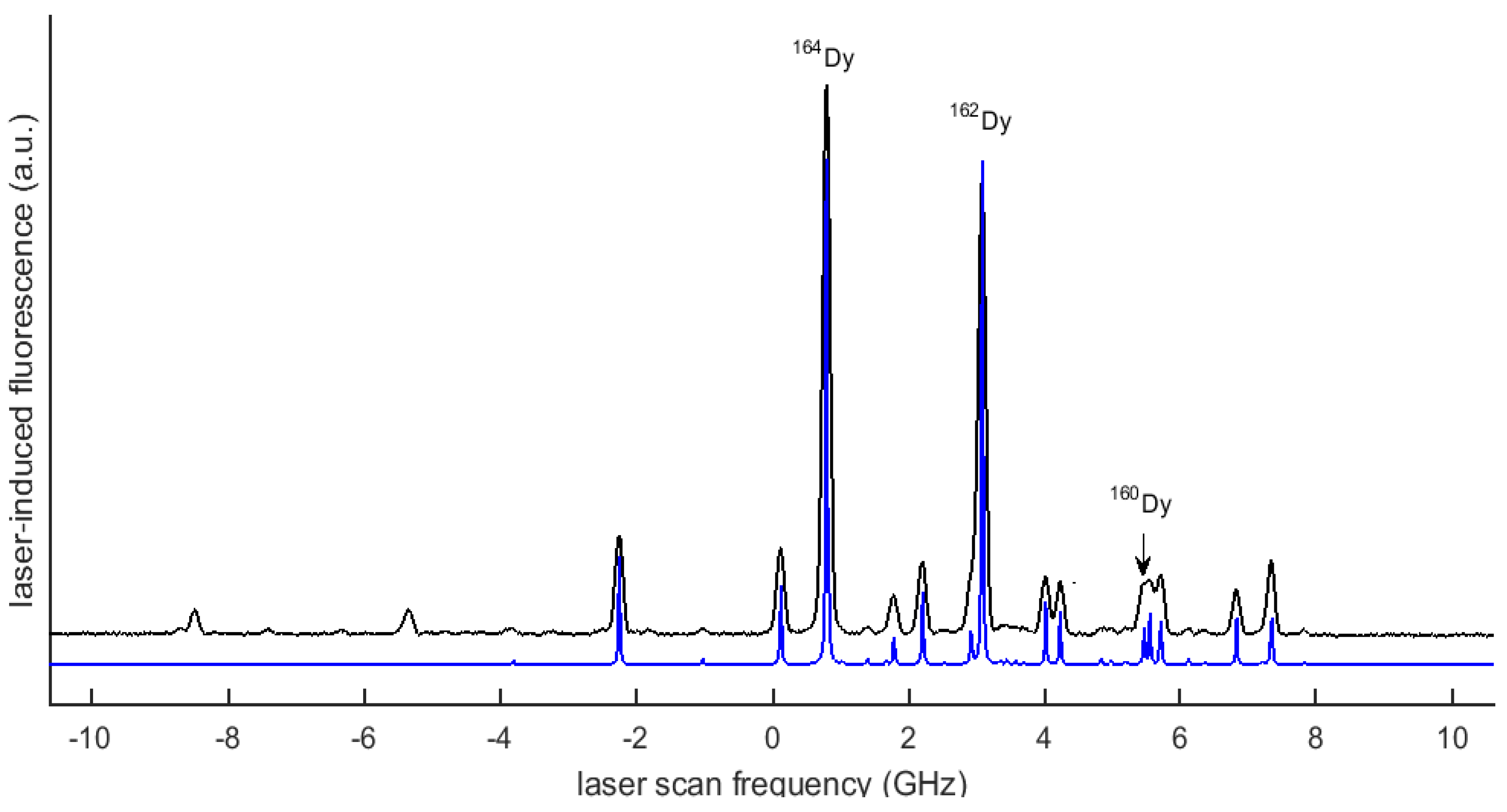
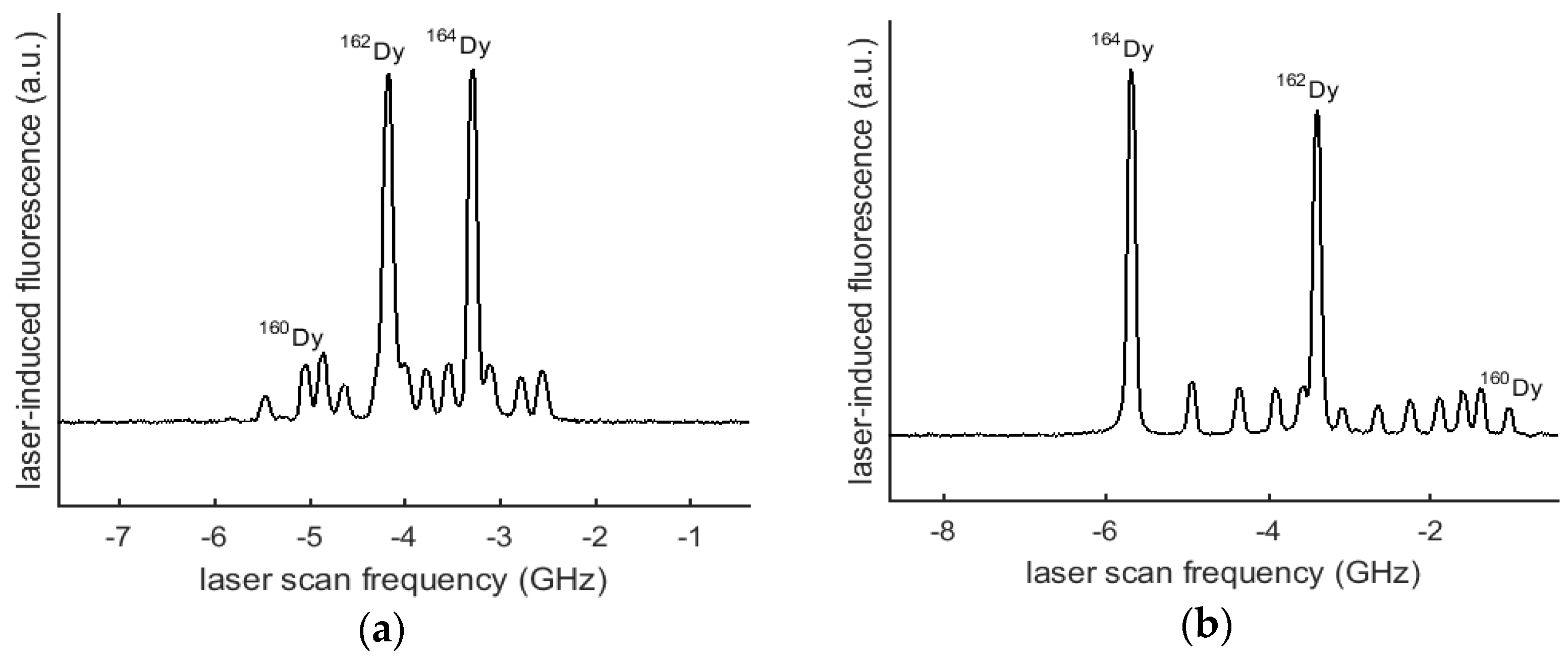
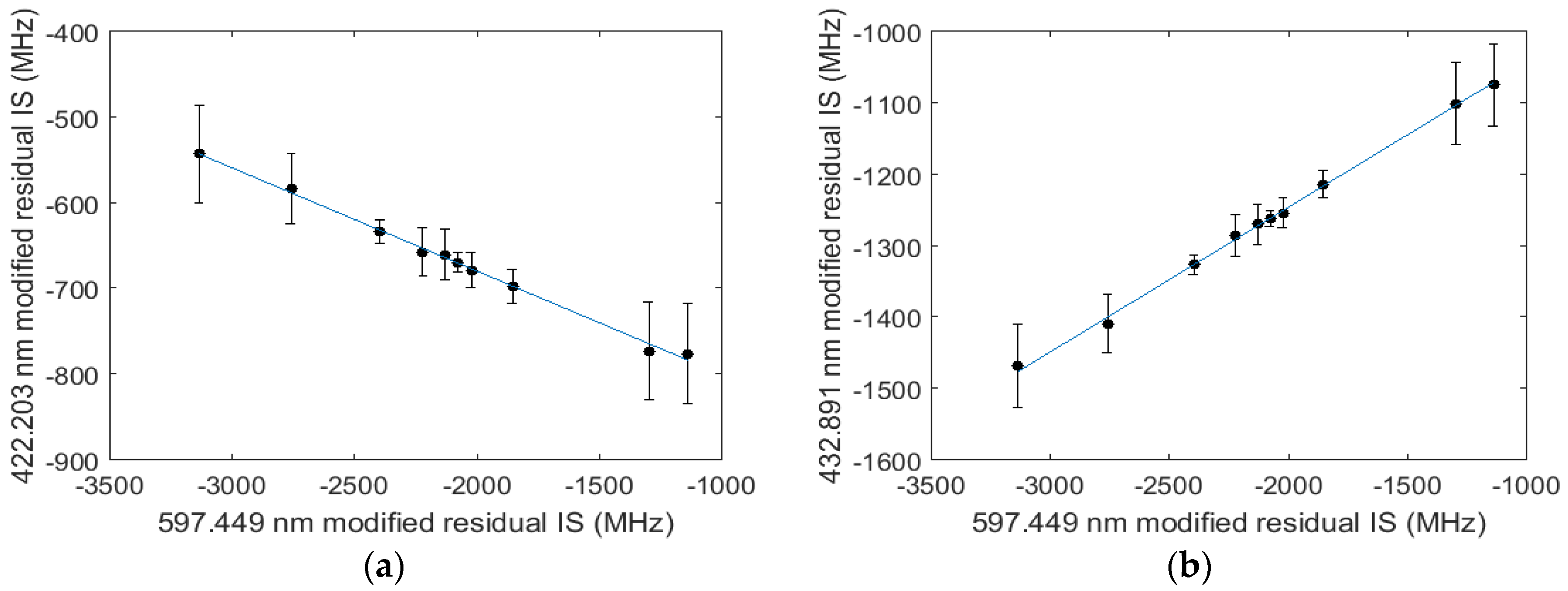
3. Data and Analysis
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Abt, A. Hyperfine structure in the solar spectrum. Astrophys. J. 1952, 115, 199–205. [Google Scholar] [CrossRef]
- Jomaron, C.M.; Dworetsky, M.M.; Allen, C.S. Manganese abundances in mercury-manganese stars. Mon. Not. R. Astron. Soc. 1999, 303, 555–564. [Google Scholar] [CrossRef]
- Kurucz, R.L. Atomic data for interpreting stellar spectra: Isotopic and hyperfine data. Phys. Scr. 1993, T47, 110–117. [Google Scholar] [CrossRef]
- Cowley, C.R. Lanthanide rare earths in stellar spectra with emphasis on chemically peculiar stars. Phys. Scr. 1984, T8, 28–38. [Google Scholar] [CrossRef]
- Sneden, C.; Cowan, J.J.; Gallino, R. Neutron-capture elements in the early Galaxy. Ann. Rev. Astron. Astrophys. 2008, 46, 241–288. [Google Scholar] [CrossRef]
- Aoki, W.; Ryan, S.G.; Norris, J.E.; Beers, T.C.; Ando, H.; Iwamoto, N.; Kajino, T.; Mathews, G.J.; Fujimoto, M.Y. Neutron Capture Elements in s-Process-Rich, Very Metal-Poor Stars. Astrophys. J. 2001, 561, 346–363. [Google Scholar] [CrossRef]
- Christlieb, N.; Beers, T.C.; Barklem, P.S.; Bessell, M.; Hill, V.; Holmberg, J.; Horn, A.J.; Marsteller, B.; Mashonkina, L.; Qian, Y.-Z.; et al. The Hamburg/ESO R-process Enhanced Star survey (HERES). I. Project description, and discovery of two stars with strong enhancements of neutron-capture elements. Astron. Astrophys. 2004, 428, 1027–1037. [Google Scholar] [CrossRef]
- François, P.; Depagne, E.; Hill, V.; Spite, M.; Spite, F.; Plez, B.; Beers, T.C.; Andersen, J.; James, G.; Barbuy, B.; et al. First stars. VIII. Enrichment of the neutron-capture elements in the early Galaxy. Astron. Astrophys. 2007, 476, 935–950. [Google Scholar] [CrossRef]
- Burris, D.L.; Pilachowski, C.A.; Armandroff, T.E.; Sneden, C.; Cowan, J.; Roe, H. Neutron-capture elements in the early Galaxy: Insights from a large sample of metal-poor giants. Astrophys. J. 2000, 544, 302–319. [Google Scholar] [CrossRef]
- Karinkuzhi, D.; Goswami, A. Chemical analysis of CH stars—II. Atmospheric parameters and elemental abundances. Mon. Not. R. Astron. Soc. 2015, 446, 2348–2362. [Google Scholar] [CrossRef]
- Chaplin, W.J.; Miglio, A. Asteroseismology of Solar-Type and Red-Giant stars. Ann. Rev. Astron. Astrophys. 2013, 51, 353–392. [Google Scholar] [CrossRef]
- Conway, J.G.; Worden, E.F. Preliminary level analysis of the first and second spectra of dysprosium, Dy I and Dy II. J. Opt. Soc. Am. 1971, 61, 704–726. [Google Scholar] [CrossRef]
- Wyart, J.F. Interpretation du spectre de Dy II. I. Etude des configurations impaires. Physica 1972, 61, 182–190. [Google Scholar] [CrossRef]
- Wyart, J.F. Interpretation du spectre de Dy II. II. Etude des configurations 4f 96s6p ET 4f 95d6p. Physica 1972, 61, 191–199. [Google Scholar] [CrossRef]
- Wyart, J.F. Interprétation du spectre de Dy II. III. Etude des configurations 4f 106s ET 4f 105d. Physica B+C 1976, 83, 361–366. [Google Scholar] [CrossRef]
- Nave, G.; Griesmann, U. New energy levels and classifications of spectral lines from neutral and singly-ionized dysprosium (Dy I and Dy II). Phys. Scr. 2000, 62, 463–473. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database; version 5.4; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2016. Available online: http://physics.nist.gov/asd (accessed on 9 January 2017).
- Pacheva, Y.; Abadjieva, L. ИЗОТОПНО ОТМЕСТВАНЕ В СПЕКТЪРА НА ДИСПРОЗИЯ. Bull. de l'Institut de Physique et de Recherche Atomique (Bulgaria) 1968, 17, 87–93. (In Bulgarian) [Google Scholar]
- Aufmuth, P. Isotope shift and configuration mixing in dysprosium II. Z. Phys. A 1978, 286, 235–241. [Google Scholar] [CrossRef]
- Ahmad, S.A.; Venugopalan, A.; Saksena, G.D. Electronic configuration mixing and isotope shifts in singly ionized dysprosium. Spectrochim. Acta 1983, 38B, 1115–1124. [Google Scholar] [CrossRef]
- Murakawa, K.; Kamei, T. Hyperfine structure of the spectra of dysprosium, cobalt, vanadium, manganese, and lanthanum. Phys. Rev. 1953, 92, 325–327. [Google Scholar] [CrossRef]
- Demtröder, W. Laser Spectroscopy, 5th ed.; Springer: Berlin, Germany, 2015; Volume 2, pp. 208–211. [Google Scholar]
- Kaufman, S.L. High-resolution laser spectroscopy in fast beams. Opt. Commun. 1976, 17, 309–312. [Google Scholar] [CrossRef]
- Nouri, Z.; Li, R.; Holt, R.A.; Rosner, S.D. A Penning sputter ion source with very low energy spread. Nucl. Instrum. Methods Phys. Res. A 2010, 614, 174–178. [Google Scholar] [CrossRef]
- Nouri, Z.; Li, R.; Holt, R.A.; Rosner, S.D. Corrigendum to “A Penning sputter ion source with very low energy spread” [Nuclear Instr. and Meth. A 614 (2010) 174–178]. Nucl. Instrum. Methods Phys. Res. A 2010, 621, 717. [Google Scholar] [CrossRef]
- Audi, G.; Wapstra, A.H.; Thibault, C. The AME2003 atomic mass evaluation. (II). Tables, graphs and references. Nucl. Phys. A 2003, 729, 337–676. [Google Scholar] [CrossRef]
- De Bièvre, P.; Taylor, P.D.P. Table of the isotopic compositions of the elements. Int. J. Mass Spectrom. Ion Proc. 1993, 123, 149–166. [Google Scholar] [CrossRef]
- Holden, N.E. Table of the isotopes. In CRC Handbook of Chemistry and Physics, 97th ed.; CRC Press: Boca Raton, FL, USA, 2016; p. 263. Available online: http://hbcponline.com/faces/documents/11_02/11_02_0263.xhtml (accessed on 17 January 2017).
- Hall, J.L.; Lee, S.A. Interferometric real-time display of CW dye laser wavelength with sub-Doppler accuracy. Appl. Phys. Lett. 1976, 29, 367–369. [Google Scholar] [CrossRef]
- Woodgate, G.K. Elementary Atomic Structure, 2nd ed.; Clarendon: Oxford, UK, 1980; p. 184. [Google Scholar]
- Kurucz, R.L.; Bell, B. Atomic Line Data; Kurucz CD-ROM No. 23; Cambridge, Mass: Smithsonian Astrophysical Observatory: Cambridge, MA, USA, 1995. [Google Scholar]
- Childs, W.J.; Crosswhite, H.; Goodman, L.S.; Pfeufer, V. Hyperfine structure of 4fN 6s2 configurations in 159Tb, 161,163Dy, and 169Tm. J. Opt. Soc. Am. B 1984, 1, 22–29. [Google Scholar] [CrossRef]
- Childs, W.J. Hyperfine Structure of Many Atomic Levels of Tb159 and the Tb159 Nuclear Electric-Quadrupole Moment. Phys. Rev. A 1970, 2, 316–336. [Google Scholar] [CrossRef]
- Dekker, J.W.M.; Klinkenberg, P.F.A.; Langkemper, J.F. Optical isotope shifts and nuclear deformation in dysprosium. Physica 1968, 39, 393–412. [Google Scholar] [CrossRef]
- Wakasugi, M.; Horiguchi, T.; Jin, W.G.; Sakata, H.; Yoshizawa, Y. Changes of the Nuclear Charge Distribution of Nd, Sm, Gd and Dy from Optical Isotope Shifts. J. Phys. Soc. Jpn. 1990, 59, 2700–2713. [Google Scholar] [CrossRef]
| Isotope | Mass (u) a | Abundance (%) b | I c | μ (nm) c | Q (b) c |
|---|---|---|---|---|---|
| 156Dy | 155.924278 | 0.06 | 0 | ||
| 158Dy | 157.924405 | 0.10 | 0 | ||
| 16°Dy | 159.925194 | 2.34 | 0 | ||
| 161Dy | 160.926930 | 18.91 | 5/2 | –0.480 (3) | +2.51 (2) |
| 162Dy | 161.926795 | 25.51 | 0 | ||
| 163Dy | 162.928728 | 24.90 | 5/2 | +0.673 (4) | +2.318 (6) |
| 164Dy | 163.929171 | 28.18 | 0 |
| Configuration a | Term a | J a | Energy a | A (161Dy) | B (161Dy) | A (163Dy) | B (163Dy) |
|---|---|---|---|---|---|---|---|
| (cm−1) | (MHz) | (MHz) | (MHz) | (MHz) | |||
| 4f10(5I7)6s1/2 | (7, ½) | 15/2 | 4341.104 | −251.89 (94) | 1045 (48) | 352.6 (1.3) | 1104 (46) |
| 4f10(5I6)6s1/2 | (6, ½) | 13/2 | 7485.117 | 93.22 (16) | −883.4 (7.1) | −130.48 (22) | −933.1 (7.5) |
| 4f10(5F5)6s1/2 | (5, ½) | 11/2 | 13,338.27 | −272.49 (23) | −818 (10) | 381.44 (32) | −864 (11) |
| 4f9(6H°)5d(7K°)6s | 8K° | 19/2 | 17,606.65 | −144.40 (30) | 4081 (17) | 202.13 (41) | 4310 (18) |
| 4f9(6H°)5d(7K°)6s | 6K° | 19/2 | 19,571.75 | −69.51 (35) | 3861 (24) | 97.29 (49) | 4078 (25) |
| 4f9(6H°)5d2(3F) | ° | 11/2 | 20,517.39 | −96.98 (37) | 2076 (17) | 135.76 (52) | 2193 (18) |
| 4f9(6H°)5d2(3P) | ° | 15/2 | 27,435.132 | −97.23 (12) | 252.8 (7.1) | 136.10 (17) | 267.1 (7.5) |
| 4f9(6H°)5d2(3F) | ° | 13/2 | 28,019.70 | −114.76 (56) | 1104 (37) | 159.67 (78) | 1166 (39) |
| 4f1°(5I)6p | ° | 13/2 | 30,287.36 | 278.44 (18) | −973.9 (7.3) | −389.76 (25) | −1028.6 (7.7) |
| ° | 9/2 | 36,466.34 | −110.97 (24) | 801 (14) | 155.34 (33) | 846 (15) | |
| 4f9(6H°)6s6p(3P°) | 17/2 | 40,455.73 | −165.08 (32) | 3851 (17) | 231.08 (44) | 4067 (18) | |
| 4f9(6H°)5d(7H°)6p | 17/2 | 41,583.90 | −102.69 (31) | 1826 (18) | 143.75 (43) | 1929 (19) | |
| 4f9(6H°)5d(7H°)6p | 13/2 | 42,289.33 | −96.92 (45) | 2773 (38) | 135.67 (63) | 2929 (40) | |
| 4f9(6H°)5d(7H°)6p | 19/2 | 42,478.98 | −113.16 (42) | 3099 (24) | 158.40 (59) | 3273 (26) |
| λair a | Configuration b | Term b | J b | Energy b | A (161Dy) | B (161Dy) | A (163Dy) | B (163Dy) |
|---|---|---|---|---|---|---|---|---|
| (nm) | (cm−1) | (MHz) | (MHz) | (MHz) | (MHz) | |||
| 424.846 | 4f9(6H°)5d(7H°)6s | 8H° | 11/2 | 14,347.205 | −63.33 (91) | 1905 (37) | 88.7 (1.3) | 2012 (39) |
| 4f9(6H°)6s6p(3P°) | 13/2 | 37,878.55 | −26.0 (1.4) | 1552 (31) | 36.4 (2.0) | 1639 (32) | ||
| 436.135 | 4f9(6H°)5d(7I°)6s | 8I° | 17/2 | 14,895.06 | −94.86 (79) | 2106 (60) | 132.8 (1.1) | 2224 (64) |
| 4f9(6H°)5d(7H°)6p | 15/2 | 37,817.31 | −65.15 (91) | 1598 (59) | 91.2 (1.3) | 1688 (62) | ||
| 451.851 | 4f9(6H°)5d2(3F) | 8K° | 21/2 | 22,031.98 | 11.69 (73) | −1613 (50) | −16.4 (1.0) | −1704 (53) |
| 4f9(6H°)5d(7I°)6p | 8K | 21/2 | 44,156.98 | −7.72 (73) | −503 (50) | 10.8 (1.0) | −531 (53) | |
| 457.385 | 4f9(6H°)5d2(3F) | ° | 17/2 | 20,884.42 | 68.32 (87) | −1358 (63) | −95.6 (1.2) | −1434 (66) |
| 4f9(6H°)5d(7H°)6p | 17/2 | 42,741.69 | 44.11 (88) | −1206 (63) | −61.7 (1.2) | −1274 (66) |
| λair a | Jlo a | Elo a | Jup a | Eup a | (160, 164) | (161, 164) | (162, 164) | (163, 164) |
|---|---|---|---|---|---|---|---|---|
| (nm) | (cm−1) | (cm−1) | (MHz) | (MHz) | (MHz) | (MHz) | ||
| 422.203 * | 15/2 | 4341.10 | 13/2 | 28,019.70 | −610 (11) | −427 (10) | −306 (10) | −129 (10) |
| 424.846 * | 11/2 | 14,347.21 | 13/2 | 37,878.55 | −960 (11) | −842 (11) | −456 (11) | −326 (10) |
| 432.253 * | 11/2 | 13,338.27 | 9/2 | 36,466.34 | −1760 (11) | −1453 (10) | −857 (10) | −533 (10) |
| 432.891 | 15/2 | 4341.10 | 15/2 | 27,435.12 | −1204 (10) | −945 (10) | −591 (10) | −331 (10) |
| 436.135 * | 17/2 | 14,895.06 | 15/2 | 37,817.31 | −1429 (10) | −1237 (11) | −694 (10) | −463 (11) |
| 436.421 | 19/2 | 19,571.75 | 19/2 | 42,478.98 | −1812 (10) | −1550 (10) | −870 (10) | −581 (10) |
| 437.531 | 19/2 | 17,606.65 | 17/2 | 40,455.73 | −108 (10) | −74 (10) | −52 (10) | −23 (10) |
| 438.430 * | 13/2 | 7485.12 | 13/2 | 30,287.36 | −1457 (11) | −1175 (10) | −707 (10) | −408 (10) |
| 451.851 * | 21/2 | 22,031.98 | 21/2 | 44,156.98 | −363 (10) | −334 (11) | −173 (10) | −133 (10) |
| 454.167 | 19/2 | 19,571.75 | 17/2 | 41,583.90 | −1759 (10) | −1506 (11) | −847 (10) | −565 (10) |
| 457.385 | 17/2 | 20,884.42 | 17/2 | 42,741.69 | −790 (11) | −700 (11) | −378 (10) | −272 (10) |
| 459.178 | 11/2 | 20,517.39 | 13/2 | 42,289.33 | −709 (11) | −628 (10) | −339 (10) | −244 (10) |
| λair (nm) | Mass Pair | IS (MHz) | |
|---|---|---|---|
| This Work | Ahmad [20] | ||
| 432.891 | (160, 164) | −1204 (10) | −1268 (90) |
| 436.421 | (160, 164) | −1812 (10) | −1820 (90) |
| 437.531 | (160, 164) | −108 (10) | ~0 (90) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Del Papa, D.F.; Holt, R.A.; Rosner, S.D. Hyperfine Structure and Isotope Shifts in Dy II. Atoms 2017, 5, 5. https://doi.org/10.3390/atoms5010005
Del Papa DF, Holt RA, Rosner SD. Hyperfine Structure and Isotope Shifts in Dy II. Atoms. 2017; 5(1):5. https://doi.org/10.3390/atoms5010005
Chicago/Turabian StyleDel Papa, Dylan F., Richard A. Holt, and S. David Rosner. 2017. "Hyperfine Structure and Isotope Shifts in Dy II" Atoms 5, no. 1: 5. https://doi.org/10.3390/atoms5010005
APA StyleDel Papa, D. F., Holt, R. A., & Rosner, S. D. (2017). Hyperfine Structure and Isotope Shifts in Dy II. Atoms, 5(1), 5. https://doi.org/10.3390/atoms5010005





