1. Introduction
Reactive scattering in three-body Coulomb systems is one of the most important problems for many fields of quantum physics. In particular, positron scattering on atoms and ions is fundamentally important for understanding annihilation processes as well as for imaging applications in medicine and material science. For these studies, precise calculations of electrons and positrons scattering on simple targets like atomic Hydrogen, Helium ion and molecular Hydrogen play an important role. This is due to the fact that existing methods for solving scattering problem in few-body systems allow one to obtain reliable results that can later be used to test methods and models for calculating positron scattering on complex targets [
1]. Although high energy scattering can be successfully treated with semiclassical models, the low energy scattering is computationally more difficult. Non-variational approaches, that are critical for studying annihilation, are reduced to two basic types: Merkuriev-Faddeev equations formalism [
2] and hyperspherical close coupling equations [
3] or adiabatic hyperspherical close coupling equations formalism [
4,
5,
6]. Being very suitable for bound state calculations, the adiabatic hyperspherical approach has certain technical difficulties when applied to Coulomb particle scattering. The Merkuriev-Faddeev equations have demonstrated their efficiency as a tool for Coulomb bound state, elastic and reactive scattering calculations. Although these equations are strictly equivalent to the Schrodinger equation, they contain an artificial functional parameter-the Merkuriev cut-off function-which is used for splitting of the Coulomb potentials into the short-range and the long-rage parts. Even though the Merkuriev formalism implies considerable freedom in an actual choice of this splitting function, deeper understanding of this splitting can help to produce more accurate results with smaller computational efforts.
In this article we discuss practical choices for the Merkuriev cut-off function and stability of the results using positron-hydrogen multichannel scattering above the Ps formation threshold as a testground. Even though this system has been studied previously, it still provides a good example of a computationally challenging problem.
2. Faddeev-Merkuriev Equations in Configuration Space
In this section we will bring a very short and qualitative introduction to the formalism of Faddeev-Merkuriev equations. Interested readers can find more information and mathematically sound statements in the original paper of Merkuriev [
2] and articles of other authors who used this approach to solving the Schrödinger equation for three Coulomb particles [
7,
8,
9,
10,
11,
12,
13]. In our discussion we shall assume that the energy of the three-body system is sufficiently low, so that the three-body break-up channel (“ionization”) is closed, and only the elastic scattering and a finite number of excitation/relaxation and charge-exchange channels contribute to the system asymptotic state. In this case the virtual ionization channel only contributes to the short-range dynamic of the system in the region of three-body collisions and its contribution to the long-range dynamics of the system is exponentially small.
Let us first remind our readers the Faddeev scheme for solving quantum three-body problems for particles with short-range interactions. Assume that the three-body Hamiltonian has the form
where
T is the kinetic energy operator of the three particles and
are the pairwise short-range interaction potentials. The index
α enumerates the possible pairings of the particles. The solution Ψ of the Schrödinger equation
can be represented as a sum of three components according to the clusterings of the particles in the initial and final states
Each of the components
corresponds to the particular pairing
α. It is natural to represent each component in the corresponding set of Jacobi coordinates (
Figure 1). The components satisfy a set of three equations - the Faddeev equations
It is easy to see that the sum of the components satisfies the Schrödinger equation. Indeed, if we sum up the three equations over
α we obtain the equivalent Schrödinger equation
The asymptotic behavior of these components is given by the following equations, assuming that the index
α corresponds to the initial state of the system
where
is the momentum of the incident particle,
is the momentum of the outgoing particle,
is the 2-body bound state wave function of the pair
β,
n and
ℓ are the corresponding main and orbital quantum numbers and
stands for the unit vector collinear with the vector
.
From a theorist’s point of view, the Faddeev equations have a very simple physically meaningful structure. Assume that the solution
is known. Than we can treat the right-hand sides of the equations as the “source” term which is a square integrable function, as for different
α and
β the product
is well localized in the region of three-body collisions [
14]. Then the asymptote of the components is determined by the Green’s function
, which is the inverse of the channel Hamiltonian written at the left-hand side of the Faddeev equations. It results in the asymptotic uncoupling of the components, so that the asymptotic channels corresponding to the clustering
α are present only in the component
. From a computational scientist’s point of view, the advantage of solving the Faddeev equations for the components
over solving the Schrödinger equation for the wave function Ψ directly is the simplicity of the component asymptotic behavior, which makes it easier to impose the appropriate boundary conditions. Moreover, the discretized channel Hamiltonians admit a simple and efficient way of inversion [
15,
16,
17], which leads to a natural way of preconditioning the equations and, therefore, very efficient iterative schemes.
In the case of Coulomb interactions, however, the simple Faddeev decomposition is not sufficient to produce a rigorous and stable base for scattering calculations even for binary collisions. Indeed, in this case the right-hand side of an Equation (
1) with Coulomb potential does not produce a square-integrable source. As a result, the channels corresponding to alternative pairings remain coupled in the component
at all distances. So, the equations need further modification. Such a modification was proposed by Merkuriev in [
2]. He had suggested to split the potential
into short-range and long-range parts
and
, so that
. In this notation the Merkuriev-Faddeev equations read
The short-range part in the “source” term should ensure asymptotic uncoupling of the components corresponding to different pairings. On the other hand, the long range parts, which are included into all channel Hamiltonians in order to reproduce the interaction between the charged fragments (also including polarization interaction) must satisfy an important condition: they should not hold any asymptotic bound states that correspond to the improper pairings in any channel Hamiltonian. This way Merkuriev-Faddeev equations have as simple asymptotic properties of the solutions for Coulomb interactions as the original Faddeev equations had for short-range potentials. For instance, for the components that describe a neutral cluster in the final state the same simple asymptote as for short-range interaction holds. For charged particle states the plane waves and the spherical waves should be replaced by their Coulomb counterparts.
Merkuriev had demonstrated that the compromise between the two requirements—minimizing the interchannel coupling and reproducing the physically correct asymptotic behavior of the solution—can be achieved by splitting the Coulomb potential into short-range and long-range parts in the three-body space by making the splitting dependent on the distance between the third particle and the selected pair center of mass
. Namely, one can introduce a cutoff function
such that
where
and
is some fall-off distance such that
with some
satisfying
. Assuming now that the potentials
are Coulomb potentials
, we introduce the corresponding short-range and long-range parts
Asymptotically, as
, the potentials
do not support pair bound states, and therefore do not contribute to the asymptotic behavior of the components.
Although, in principle, the particular choice of the cut-off function
is not important and the Equation (
3) are equivalent to the Schrödinger equation while having better structure of the asymptotic solutions, in practical calculations the cut-off function should satisfy several simple conditions. When constructing a numerical solution of the equation the finite size of the region where we solve the corresponding boundary value problem should be taken into account. For instance, consider the case of a simple two-body cut-off, which corresponds to
. The potential
changes from
to zero in the small vicinity of some point
. If the point
R is very close to the origin, the potential
can support a pair bound state within the energy range of interest. Thus, the lower bound on the
R values arises. On the other hand, the point
R should be separated from the border of the region where we solve the problem to make the potential
localized enough to ensure asymptotic uncoupling of the components. The bigger the value of
R is, the larger region is to be taken, and the latter is not preferable from the computational point of view. In the case of a three-body cut-off function the picture is a little more complicated since the both coordinates
x and
y are involved. We shall discuss the practical choice of the cut-off function in more detail in the next section while presenting the numerical results.
3. Results and Discussion
We solve the Faddeev-Merkuriev equations in total angular momentum representation for
. Our numerical approach is in line with the one of rare gas atom scattering calculations [
18]. Here we, however, use a more elaborated scheme of imposing boundary conditions for multichannel scattering. We introduce the internal coordinates
,
,
and solve the equations in a box
for each component.
In our calculations we use the following cut-off function
This function has 5 parameters. We use
and
which is slightly above the critical value
.
shifts the cut-off function along the
x axis,
regulates the fall-off rate along the axis
x, and
allows us to vary the shape of the cut-off function in three-body configuration space. For
(or
) the cutting function becomes
y-independent and turns into a simple two-body cut-off because in this limit it depends only on the distance between the particles in the interacting pair
. For smaller
the cutting function defines the three-body configuration space cut-off, when the cut-off radius increases with the distance between the free particle and the bound state
(
Figure 2). Our cut-off function differs from the original function that was introduced by Merkuriev. The difference is that the width of the region where it falls off from unity to zero is constant, that is
. We have found that this choice works good in our calculations.
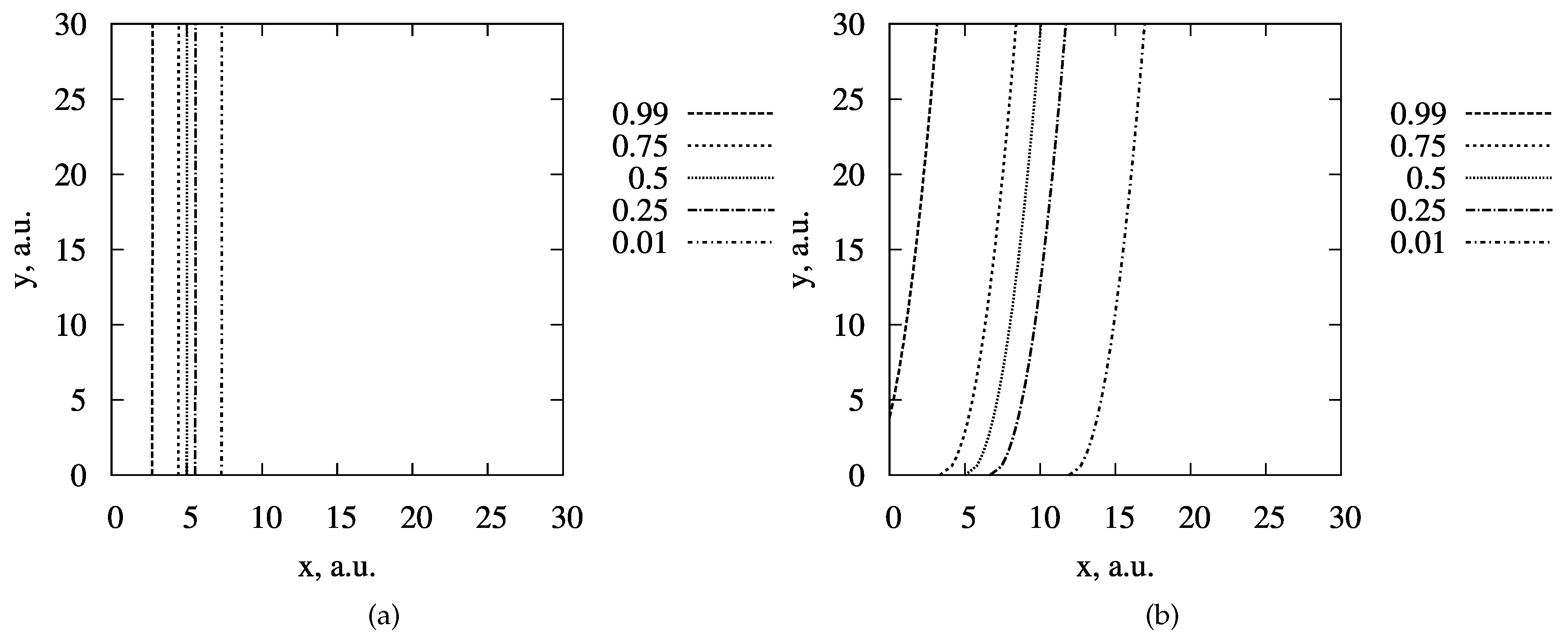
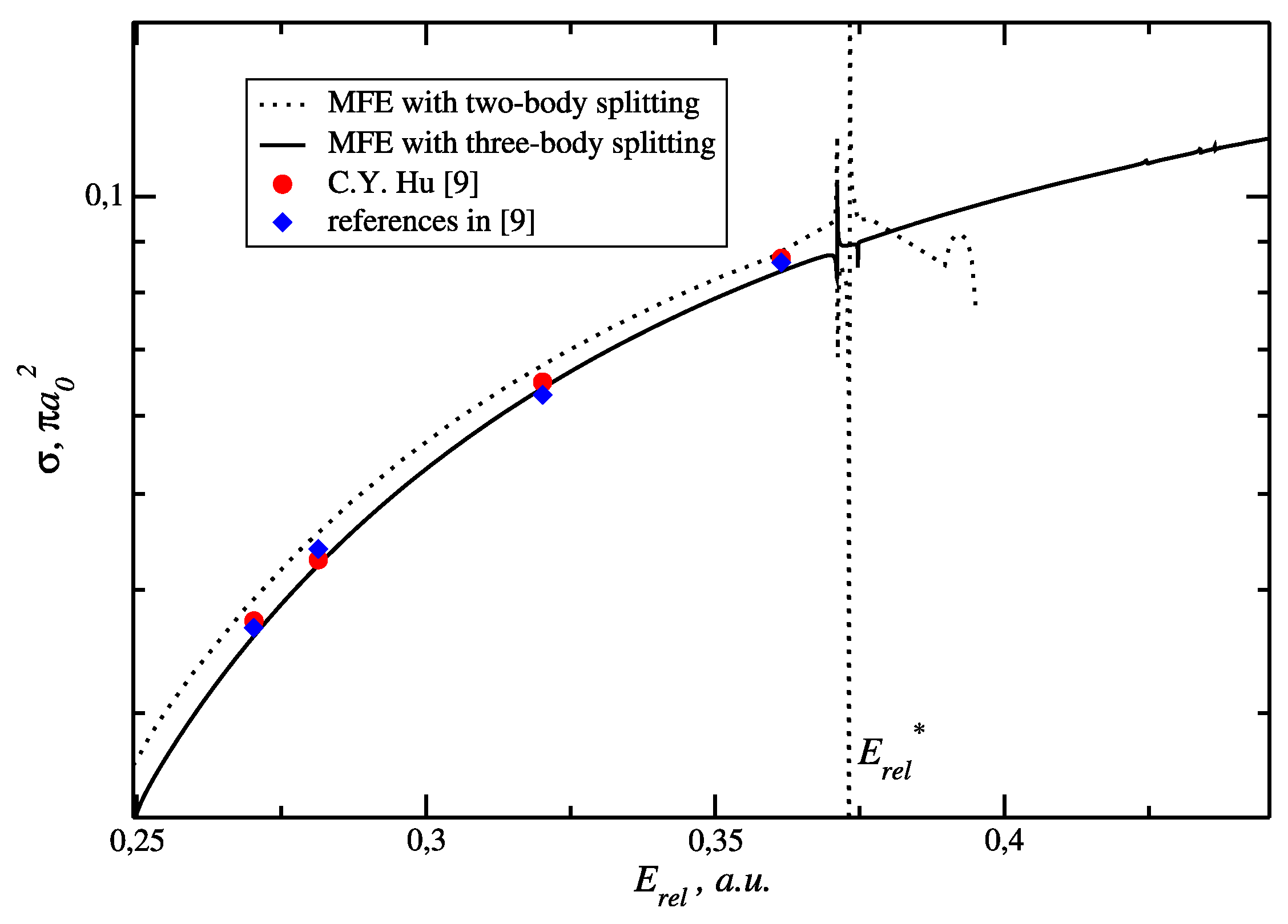
We shall compare the results of positron-hydrogen scattering calculations performed with the cut-off functions that we show in
Figure 2. First, consider the simple
y-independent (“two-body”) cut-off. Let us take a look at the results of the elastic cross section calculations for the energy range between the Ps formation threshold and the Hydrogen first excitation threshold. In
Figure 3 we show the elastic cross section as a function of
where
a.u. is the Hydrogen ground state energy. The most obvious feature that we observe is a strong instability of the calculated cross section above certain energy
. What happens when we reach this energy? Why the calculations become unstable?
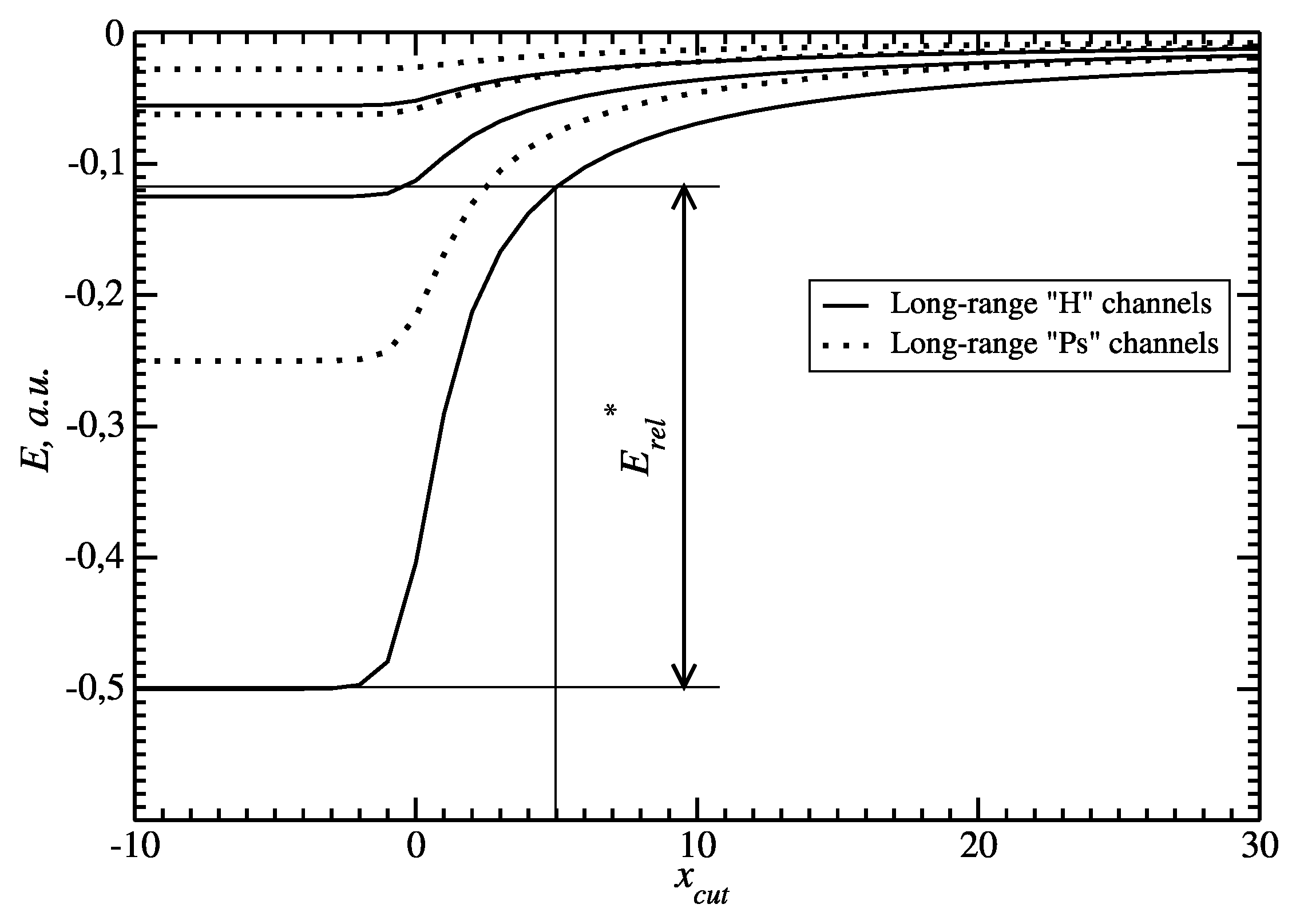
Consider the properties of the long-range part of the Coulomb potential. In
Figure 4 we show several lowest bound state energies supported by the long-range part of the Coulomb potential as a function of the cut-off parameter
. For a fixed
, as in the case of splitting the Coulomb potential in two-body configuration space, these long-range parts of the potential generate some unphysical channels that start opening above some critical energy of the system. This critical energy is determined by the lowest bound state supported by the long-range parts of the potentials (see
Figure 4 for the case
a.u.). In our case it is the long-range part of the electron-proton interaction. For the energies above this threshold, the behavior of the Faddeev component changes: besides the two-body wave corresponding to the physical binary scattering process for the appropriate particle pairing, a second wave in the direction corresponding to the alternative pairings shows up.
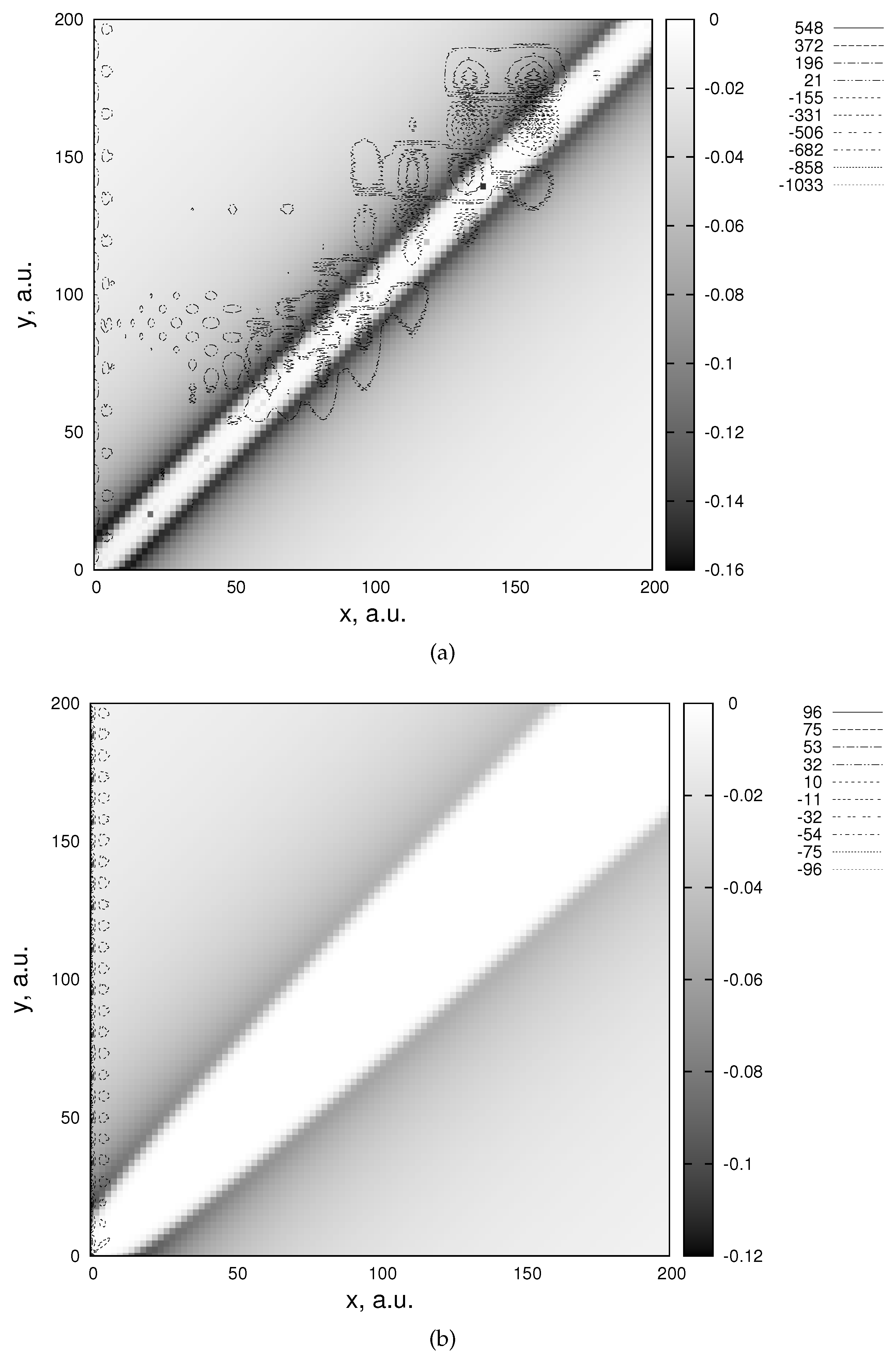
We can identify two major effects of this “unphysical” wave on the numerical solution. It influences the asymptotic properties of the wave function component and, consequently, inscreases the coupling between the components. We illustrate this in
Figure 5a, where a cut of the Faddeev components corresponding to aligned particles is shown. In addition to the physical outgoing channel (the outgoing wave along the
y axis), the long-range part of the potential supports an unphysical outgoing channel (the outgoing wave along the rotated Jacobi coordinate
going from bottom left to top right). In order to overcome this unpleasant effect we can increase the cut-off distance and, thus, extend the energy range where the calculations are stable. This extension, however, comes at a price: in order to obtain results with an acceptable numerical precision we also have to increase
and the number of grid points quite substantially.
The threshold energy can be moved to the region of higher energies in a more efficient way without increasing
by using the Merkuriev cut-off in three-body space which is scaled according to the distances between different clusters. As a result, the unphysical energy threshold created by the long-range part of the potential moves up with the distance between the bounded pair and the scattered particle, and the asymptotic structure of the Faddeev component is secured, as all the unphysical channels (
Figure 4) are closed in the asymptotic region. This can be seen explicitly in
Figure 5b. We see that for an appropriately chosen three-body splitting of the Coulomb potential the wave function component asymptotically behaves as the appropriate two-body wave.
The question remains: to what extent the cut-off parameters influence the numerical results? We shall see, on the one hand, that practically the converged results do not depend on the parameters of the cut-off function. On the other hand, a careful choice of the cut-off parameters may improve the convergence so that accurate results can be obtained faster on sparser grids. To illustrate that, we include several plots of the elastic positron hydrogen cross section computed with different angular basis sets and varying parameters of the cut-off function
and
. These parameters govern the shape of the parabola which splits the Coulomb potential in three-body configuration space. The bigger the
parameter is, the more the parabola reshapes to a straight line parallel to the
y axis, thus making the cut-off function
y-independent and the area where the short-range part is nonzero decreases accordingly. Conversely, increasing
parameter shifts the parabola along the
x axis and extends the area of nonzero short range part.
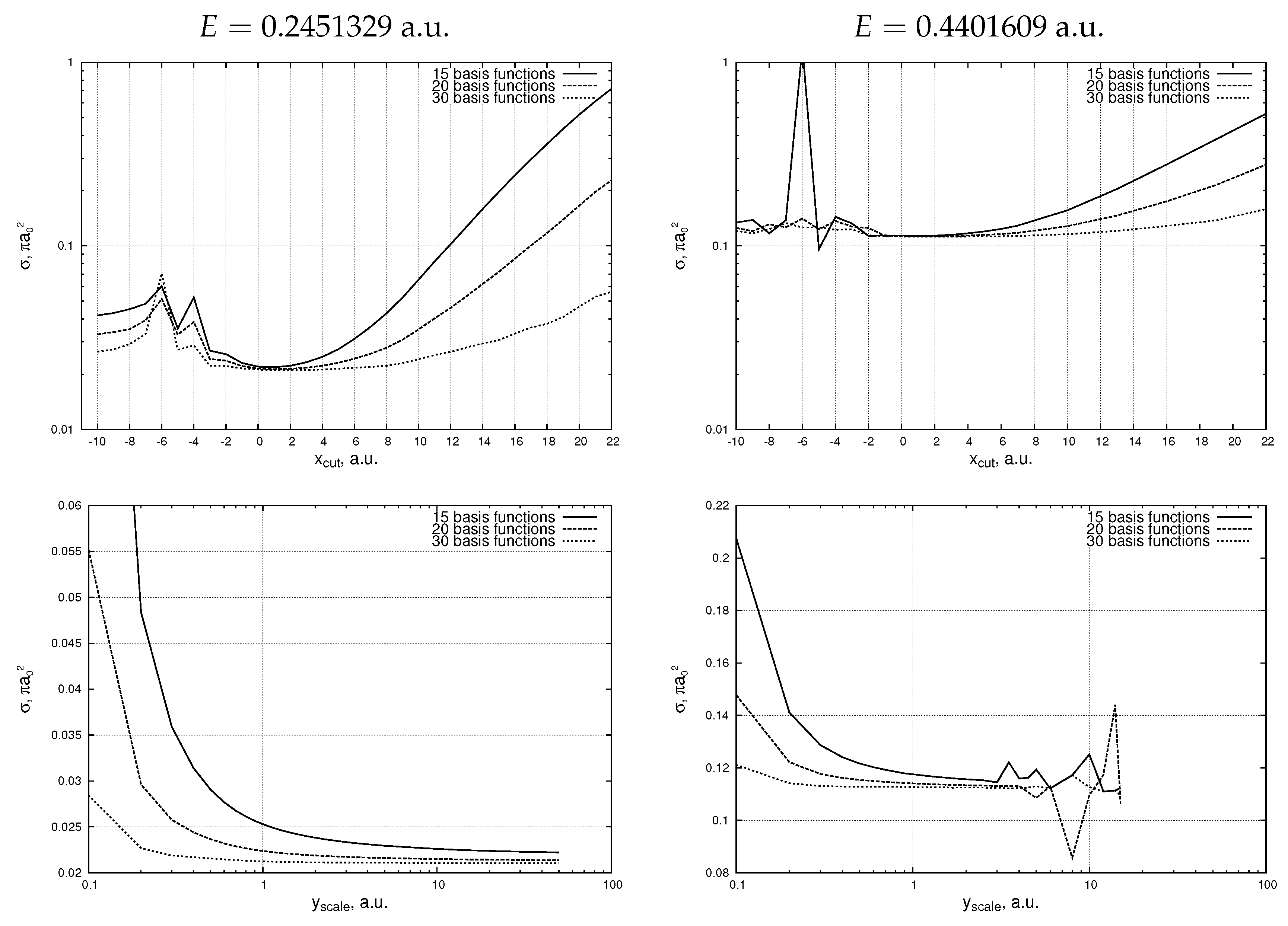
Figure 6 show the dependences for two values of the total energy
a.u. and
a.u., corresponding to the cases when only elastic channel is open and when six channels are open. All plots show that adding more functions to the angular basis extends the area of stability for the cross section suggesting that the converged result does not depend on the splitting function parameters as far as the proper asymptotic behavior of the wave function component is ensured. We see, however, that some choices of the cut-off parameters lead to faster numerical convergence than others, and, therefore, an appropriate choice of the Merkuriev cut-off can simplify numerical calculations considerably.
Finally, in
Figure 7 we report the results of our multichannel scattering calculations performed with an optimized set of splitting parameters
,
,
. There we show the cross sections for all the open channels. We have left several channels unmarked in order to facilitate the figure comprehension. The results are converged within 1% and all the known resonances are well reproduced.