Abstract
The validity of quantum-mechanical predictions has been confirmed with a high degree of accuracy in a wide range of experiments. Although the statistics of the outcomes of a measuring apparatus have been studied intensively, little has been explored and is known regarding the accessibility of quantum dynamics. For these sorts of fundamental studies of quantum mechanics, interferometry using neutron matter-waves in particular, provides almost ideal experimental circumstances. In this device quantum interference between spatially separated beams occurs on a macroscopic scale. Recently, the full determination of weak-values of neutrons - spin adds a new aspect to the study of quantum dynamics. Moreover, a new counter-intuitive phenomenon, called quantum Cheshire Cat, is observed in an interference experiment. In this article, we present an overview of these experiments.
Keywords:
quantum; neutron; interferometry; spin; weak-values; 03.65.Ta; 03.75.Dg; 42.50.Xa; 07.60.Ly PACS:
03.65.Ta; 03.75.Dg; 42.50.Xa; 07.60.Ly
1. Introduction
Double-slit experiments, in particular with massive particles, demonstrate a major peculiarity of quantum mechanics. Interference fringes, typical consequences of the wave-nature of quantum mechanics, appear when a screen is placed after the slits in an appropriate distance. However, at the same time, only one of the two detectors, which are put just behind the slits, clicks and not both simultaneously, because of the particle-nature of quantum mechanics. This remarkable duality is known as wave-particle duality in quantum mechanics. If one takes a look at the interference fringes in more detail, one notices a significant difference between interference outcomes due to classical and quantum consequences. That is, in the former, interference fringes are immediately visible. In contrast to that, in the latter, only statistically distributed detection-spots appear at the first stage, and interference fringes can be recognized only after an accumulation of enough particles or rather detection-signals [1]. These are the reasons why the double-slit experiment has been one of the best examples demonstrating the central mystery in quantum mechanics from the early stage of the development of quantum theory [2].
In classical physics, since each particle can go through only either one of the slits, the distribution at the screen behind the two opening slits is given by the sum of two single-slit distributions, which can be obtained separately. In contrast to that, in quantum physics when particles like neutrons, electrons, molecules and so forth are sent through a double-slit setup, one obtains a final distribution at the screen, which has dark and bright areas due to constructive and destructive interference. It differs from the distribution one would get by simply taking the sum of the single-slit distributions mentioned above [3,4]. This may be counter-intuitively understood if one accepts a situation in which the particle (which cannot be divided into pieces, in principle) hits both slits simultaneously and influences from both opening slits arrive at the screen, causing the final interference fringes to build up. It is worth noting that the non-local effect mentioned here, results from quantum dynamics and is described by quantum mechanically equations of motion [5]. It is another sort of non-locality, which originates in quantum kinematics and emerges in the correlation measurement [6].
Optical experiments with massive particles such as neutrons, electrons, atoms and molecules play a significant role while testing peculiar phenomena predicted by quantum theory. In interferometer experiments, separated coherent beams are produced typically by a wave-front division, e.g., in the Young type, or by an amplitude division, e.g., in the Mach–Zehnder type. These beams are recombined and superposed coherently after propagating through a region of space, where phase as well as amplitude can be manipulated by various interactions. In neutron optics, different kinds of interferometer configurations have been tested [7,8,9]. Among them, the advent of the Mach–Zehnder type interferometer in 1974 made of Si perfect-crystal with a monolithic structure opened up a new era of fundamental studies of quantum mechanics with matter-waves [10]. The coherent beam splitting obtained by amplitude division due to dynamical diffraction at the perfect crystal slabs makes a large beam separation possible. It is typically on the order of several centimeters and offers a large work area where optical elements such as a phase shifter, a spin rotator, and a beam attenuator can be inserted. The monolithic structure allows an alignment-free construction and provides a highly stable apparatus.The typical beam separation of several centimeters makes quantum mechanical studies on a macroscopic scale possible. It has to be stressed that all perfect-crystal neutron interferometer experiments up to now are self-interference experiments. Only one neutron traveling through the split beam paths, is inside the interferometer at a given time. The next neutron that will pass through the interferometer is still part of the nuclear fuel or spallation target inside the neutron source. Consequently, interference fringes can only be observed after an entire ensemble of neutrons has been detected.
The purpose of the present article is to give an overview of neutron interferometer experiments. Among many, two were selected, which will be presented in detail: one is the determination of spin weak-values by the use of neutron interferometry and the other is the demonstration of the so called quantum Cheshire Cat effect. Before those two experiments are described in detail, historically important neutron interferometer experiments are explained. This paper is organized as follows: Section 2 illustrates noteworthy neutron interferometer experiments in the past. Section 3 is dedicated to the full determination of spin weak-values of neutrons. Section 4 deals with an experiment concerning the separation of a neutron and its spin (quantum Cheshire Cat phenomenon). Conclusions and an outlook are offered in Section 5.
2. Neutron Interferometer Experiments in History
Neutron interferometry is one of the most fruitful approaches to study the foundations of quantum mechanics. One of the experiments on this topic was performed to study the -symmetry of spinor wave function Although the -symmetry of this kind was derived and known already at the early stage of the development of quantum theory, the phase factor was regarded as a theoretical convenience and considered as somehow artificial and inaccessible: in an intensity measurement, this phase factor is irrelevant. Only an interference experiment with a reference beam can reveal it. Neutron interferometry made it possible to create exactly such an experiment, and the obtained results agree well with theoretical predictions [11,12]. There are other approaches to access the -symmetry with neutrons using Fresnel diffraction at ferromagnetic domains [13] or RF flippers [14]. Another notable experiment that was performed in the early stage of neutron interferometry, is the measurement of an gravitationally-induced phase shift [15]. In this experiment, the neutron’s mass plays a crucial role. The gravitationally induced phase is a purely quantum mechanical consequence since interference fringes disappear as [16]. In 1975, the first experimental demonstration of a gravitationally induced phase was reported. The experimentally obtained phase shift deviated by about 10% from theoretical predictions. A deformation of the interferometer crystal caused by bending during its rotation around the beam axis was responsible for the large deviation from the theoretically predicted value. The discrepancy is minimized by taking the deformation of the crystal into account in the data analysis. The results of the most recent experiment differ by about from the theoretical prediction [17]. Another approach to precisely measure the gravitation-induced quantum phase with neutrons is realized by the use of a grating interferometer for very cold neutrons (VCN). The advantage of this approach is larger phase shifts due to a longer wavelength of the beam and lower sensitivity of the setup due to the thin almost weightless gratings [18]. The results of this measurement still have about inaccuracy due to broad spectrum of the incident beam. A completely different approach is offered by the concept of neutron polarimetry [19]. This makes gravitational phase measurements with the spin-echo spectrometer possible, where much longer path lengths and a white beam with a high intensity are available [20].
In the past decade, lots of attempts were made to develop a new technology known as quantum computation and information technology [21]. This technology makes use of quantum superposition and quantum state entanglement, where non-local correlation are utilized (e.g., quantum key distribution). In parallel to the derivation of the Bell’s inequality [22], where a statistical violation with several expectation values due to local assumption is presented, Kochen and Specker derived another powerful argument, which shows that logical contradictions occur if non-contextual assumption are made [23]. In this theorem, predictions of quantum mechanics are shown to be incompatible with the assumptions including: (i) a definite value of the measurements, i.e., observables A and B have predefined values v(A) and v(B); and (ii) non-contextuality, i.e., properties of the system exist independently of any measurement context. Studies of quantum contextuality were carried out with perfect-crystal neutron interferometers by entangling the neutron’s different degrees of freedom (DOF), instead of using entangled pairs of neutrons. The first experiment of this kind is the demonstration of the violation of a Bell-like inequality [24]. An entanglement between the spin and path DOF allows for generating a so-called Bell-like state and the appropriate combination of observables of spin-path joint measurements are performed. The obtained results of the measurements clearly show a violation of the Bell-like inequality. Afterwards, newly developed spin-rotators made it possible to obtain data with higher accuracy, which, in turn, offered a larger violation of the inequality [25]. In addition to that, a test of the Kochen–Specker theorem is carried out [26]. In this experiment, a combination of six observables is evaluated [27,28]. To be precise, three products of observables are measured and if the six measurement-observables, of which these products are built, had predetermined values independent of their combinations, one would immediately obtain contradicting results for three joint measurements. The contradiction due to quantum contextuality predicted by the Kochen–Specker theorem is clearly demonstrated. Not only two DOF but also three DOF of neutrons can be entangled: the (total) energy degree of freedom, in addition to the spin and path DOF, was used to generate tri-partite entangled states like the so-called GHZ state [29,30] which was generated in the neutron interferometer as well. With a radio-frequency spin-flipper in one path of the interferometer one can manipulate the neutrons’ total energy, thereby realizing a triple entanglement between the path, spin, and energy DOF [31]. The experimental results displayed once again the inconsistency between the quantum mechanical predictions and a non-contextual model. Beside the GHZ-state, generation of so-called tri-partite W-states is achieved [32].
It is worth emphasizing here that neutrons are sensitive to all four fundamental interactions, i.e., gravitational, weak, electromagnetic, and strong. Therefore any dynamical effects caused by those interactions during the evolution of the neutron’s wavefunction can be investigated in our experiments. Although they are not mentioned in detail here, there are many other neutron interferometric studies, e.g., on time-independent/dependent spin-superposition, stochastic/deterministic absorption of the beam, topological phases, the Aharonov–Casher (AC) effect, scalar Aharonov–Bohm (AB) effects, geometric/dynamical phases and so on. An overview of these neutron optical experiments is given in a textbook [10] and another review article [19].
3. Spin Weak Measurements
What can be said about the value of an observable during the time interval between two (successive) measurements ? A possible answer to this question has been given by Aharonov, Albert and Vaidman (AAV) in [33]. In their seminal paper “a new kind of value for a quantum variable” the so-called weak value is introduced, again demonstrating that quantum mechanics predicts striking and astonishing counter-intuitive phenomena. The weak value is obtain via a procedure, referred to as weak measurement [33,34,35], where the probed quantum system is left minimally disturbed and pursues its evolution from an initial state towards its final state. The weak value of a variable may differ significantly from the eigenvalues of an associated operator in that sense, that weak values may lie far outside the eigenvalue range of the operator.
3.1. Theoretical Framework
The weak value of an observable depends on both a pre- and a post-selected state vector denoted as and , respectively [36]. The former represents the state in which the quantum system was initially prepared, whereas the latter insures that the detector only clicks if the system is measured to be in a chosen final state. The weak measurement procedure involves three steps: (i) quantum state preparation of the initial state (pre-selection); (ii) a weak perturbation, i.e., a measurement of an observable that disturbs the system only minimally. This is achieved by weakly coupling the quantum system to a measuring device, acting as a probe system, via a Hamiltonian containing operators from both the measured quantum system and the probe system; (iii) post-selection of an eigenstates of an observable of the final quantum state . Finally the difference of the probe system’s initial and final state is evaluated, from which the value of the observable is inferred (pointer read out). Then, the eigenvalue of the measured observable is no longer the relevant quantity, since the measuring device consistently indicates the weak value given by
where , and are the operators to be measured, the initial (pre-selected) state, and the final (post-selected) state, respectively. A peculiarity of the weak values is that it is in general a complex number. The real part corresponds to a shift of the device system’s pointer value, i.e., a shift of the center of a Gaussian in p-space and is not bounded. On the other hand, the imaginary part contains information on back-action of the measuring device on the system and is obtained from the shift of the center of the probe system’s Gaussian in q-space (since q occurs in the coupling Hamiltonian).
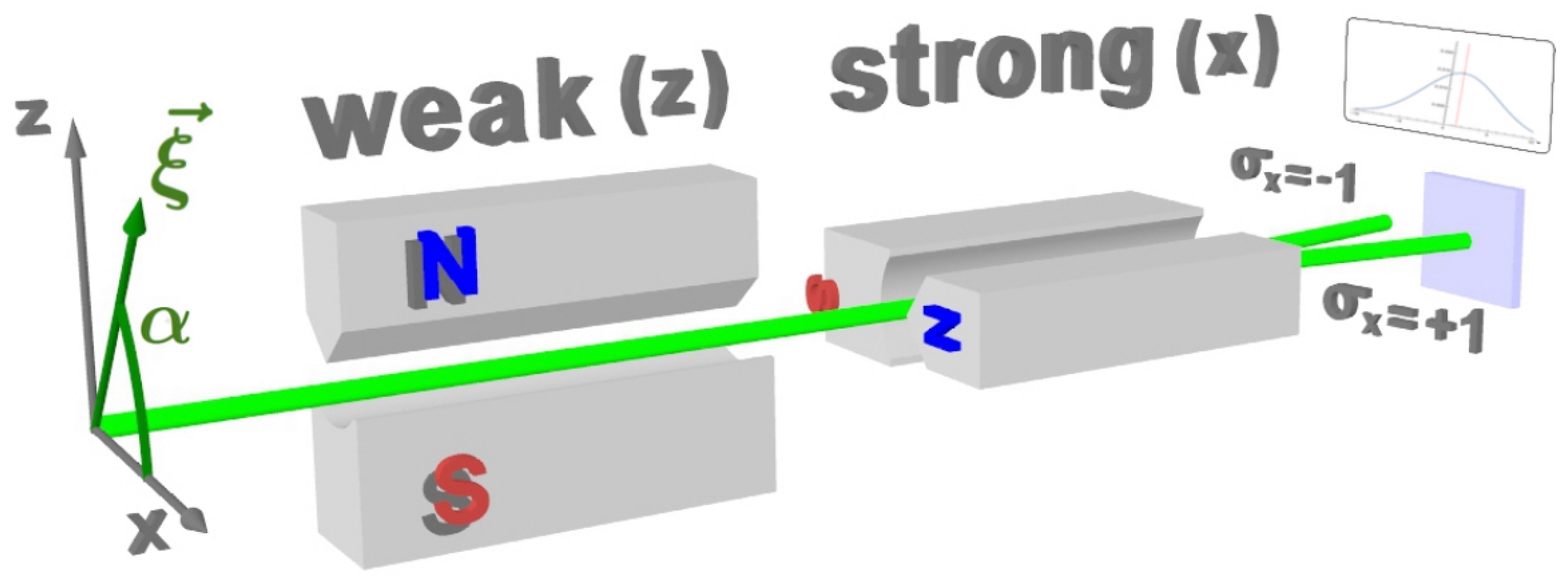
The original experiment proposed by AAV in [33] involves a beam of massive spin -particles. Here, the observed quantum system is represented by the spin of a particle, while the probe system is formed by the particle’s spatial wavefunction, A schematic illustration of the measurement apparatus from the AAV gedanken experiments is given in Figure 1. A beam of particles, initially polarized in -direction, where is chosen to lie in the -plane with an angle α in respect to the x-axis. Consistent with terminology used before the “quantum system”, corresponding to the particle’s spin state is denoted as state , while the probe system, provided by the particle’s spatial wave function and assumed to be of gaussian form, is given by . The prepared beam, with spin pointing in direction , passes through a weak magnetic field gradient, with the field pointing pointing in z-direction (non-ideal Stern–Gerlach apparatus). Here, “weakly” means that the beams are still overlapping, hence one cannot get complete information of the spin direction. In contrast, for a strong measurement, they are clearly separated. The weak interaction causes a coupling of the spin with the two slightly shifted partial spatial wave functions correlated to the two values of and creates a spin-momentum entanglement. Next, the beam passes another (standard) Stern-Gerlach apparatus, splitting it into two spatially separated sub-beams corresponding to . The weak value of is determined from the postselected spin component, via the deflection of the spot on the screen in z-direction. The z-distribution of the spatial wave function is detected via counts observed on the distant screen and directly reflects the distribution of p’s (momentum distribution) in the final beam.
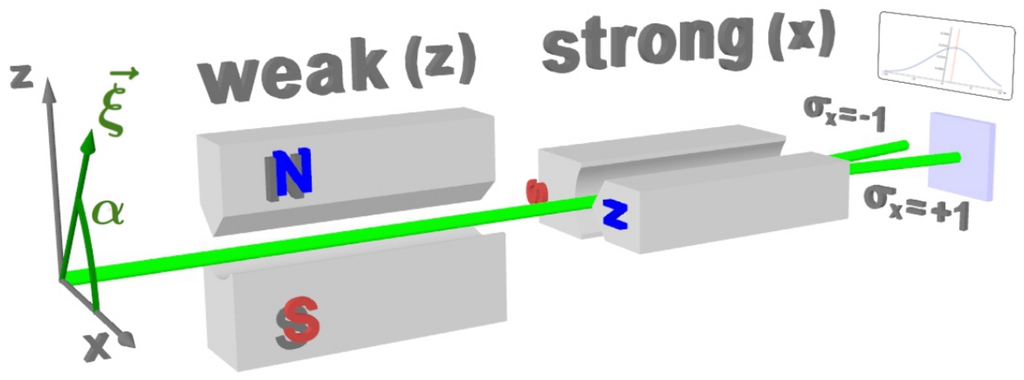
Figure 1.
Original setup for weak spin measurement of spin -particles, proposed by AAV. After the weak interaction, the sub beams belonging to are still overlapping by a large extent.
The first experimental realization of the procedure proposed by AAV was performed using an optical setup [37], following a proposed scheme given in [38]. The fact that the weak value may lie far outside the range of an observable’s eigenvalues has been found to be useful as a technique aimed at amplifying weak signal [39,40,41,42,43,44,45]. A review focusing on significant amplification of the pointer deflection is given in [46], where in addition a non-perturbative theory of weak pre- and post-selected measurements is presented. The weak value’s property of allowing information to be extracted from a quantum system with minimal disturbance is applied as a new method for estimation of quantum states [47,48,49,50] (see [51] for a recent review). This particular property of the weak value is also utilized in experimental tests of a reformulation of Heisenberg’s uncertainty principle [52,53,54,55] (an overview of different viewpoints of that topic can be found in [56]). In addition, the weak value and weak measurements have been successfully applied to quantum paradoxes such as the three-box problem [57] and Hardy’s paradox [58,59,60].
Though considered a quantum mechanical property, classical models of the weak value can explain quite well results of photonic measurement of weak values. For instance, measurements of average trajectories of single photons in a two-slit interferometer [47], are interpreted as measurements of the Poynting vector in an optical field [61] or a classical field approach of quantum weak measurements, in terms of an effective classical background field being probed [62].
3.2. Neutron Optical Approach
Our experiment [63] makes use of a beam of neutrons—-massive spin- particles—as originally proposed by AAV in [33]. A direct implementation of the setup from Figure 1 is not a trivial issue due to the fact that the coherence length of the matter-wave beam is of the same order, or even less, than the resolution of available position sensitive detectors. This circumstances call for a different approach. The idea is to couple the spin (system S) that shall be measured weakly to another two-level system as a probe system rather than using a probe system which is gaussian distributed in the canonical variables, which has already been discussed in [64]. Our two-level probe system P (measurement device) is formed by the two paths of a triple Laue neutron interferometer, denoted as path I and II, to which the z-component of the neutron’s spin is weakly coupled, which is schematically illustrated in Figure 2. The experiment was carried out at the neutron interferometer instrument S18 at the high-flux reactor of the Institute Laue-Langevin (ILL) in Grenoble, France.
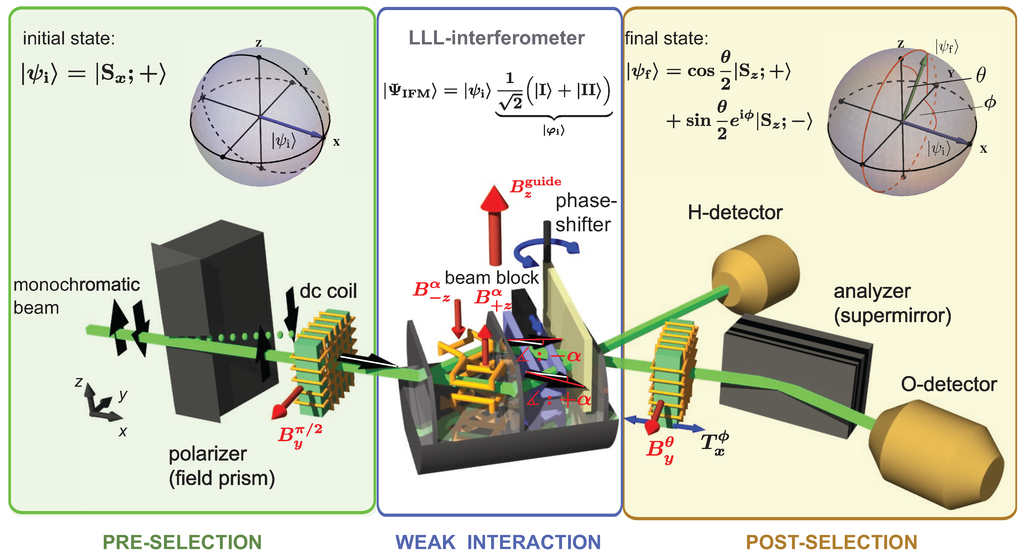
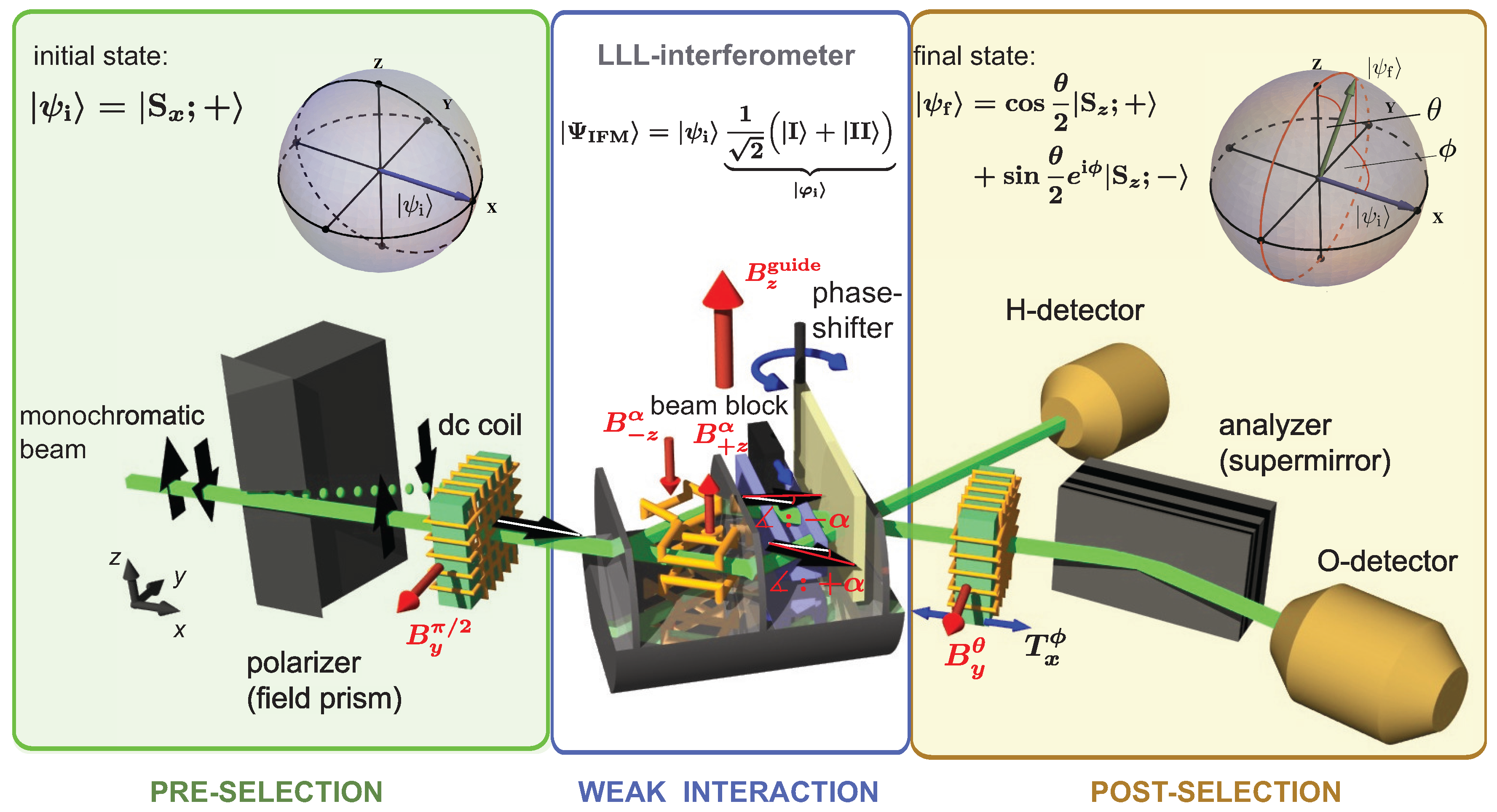
Figure 2.
Schematic illustration of a triple Laue (LLL) neutron interferometer experiment for a weak measurement of the spin operator . The setup consists of three stages: (i) pre-selection (green) using a magnetic field prism for polarisation and a -spinrotator the initial state is prepared; (ii) weak interaction (blue) in the interferometer a weak spin rotation by is applied in arm I and II, respectively; (iii) post-selection (brown) a combination of a spin-rotator and analysing supermirrow is used to post-select on the final state , before count rate detection.
(i) Pre-selection: A monochromatic beam with mean wavelength Å ( Å) and beam cross section crosses a birefringent magnetic prism, which produces a field in -direction. Due to the spin-dependent birefringence (a few seconds of arc between the parallel and anti-parallel spin state), only the spin-up component fulfils the Bragg condition at the first interferometer plate (beam splitter), resulting in an initial polarization in -direction. Next, the beam enters a static magnetic guide field (also pointing in the -direction), which covers the entire setup and prevents depolarization. Before the neutron beam enters the interferometer, the neutron’s spin is rotated into the x-direction by a spin-turner, which is a DC coil producing a magnetic field pointing in y-direction. Inside the coil, the spin precesses about the y-axis, due to Larmor precession. The magnetic field is adjusted such that it induces a spin rotation, thereby preparing the initial spin state denoted as . Behind the first plate of the interferometer (IFM), the neutron’s spatial wavefunction is found in a coherent superposition of the two sub-beams belonging to path and path . Inside the IFM, the total wavefunction, consisting of spin and spatial part of the neutron, is denoted as : the spatial wavefunctions is spanned by the path I and path II eigenstate basis and given by . After the first plate of the interferometer, the total wavefunction, composed of the system (spin) state and the pointer (path) state, is prepared in
where the initial pointer state of the probe system P, is given by .
(ii) Weak interaction: Small spin rotations of are introduced by local modification of the static guide field. This is achieved by small coils aligned in a Helmholtz configuration and placed in boxes which are completely flooded with temperature controlled water [25]. As a result, the Larmor frequency is increased in path and decreased in path , leading to the different spin rotations of in path and in path , respectively. The coupling of spin and path DOF is expressed by the interaction Hamiltonian
where μ is the neutron’s magnetic moment and and are projection operators to paths I and II, given by , with , restricting the interaction to the arm of the interferometer. Before the two sub-beams are recombined at the third plate, an adjustable relative phase factor is induced by a phase shifter plate. The phase shift is given by with atom density in the phase shifter plate of thickness D, the coherent scattering length and the neutron wavelength λ. By rotating the phase shifter plate, χ can be tuned systematically due to the change of the relative optical path length in path and path .
(iii) Post-selection: The spin is rotated by a polar angle θ inside a dc spin turner coil, which is mounted on a translation stage. The polar angle θ can be set by adjusting the coil’s static magnetic field . Depending on the position of the translation stage, the azimuthal angle is tuned due to Larmor precession in the static magnetic guide field. The spin is finally selected by a spin-dependent reflection from a bent Co-Ti supermirror array. These apparatuses make it possible to post-select an arbitrary final spin state
The outgoing beam is measured using a -detector, with an efficiency over 99 %.
The real component and modulus of the weak value can be determined from the intensities and , with phase shifts and . At this point, the remaining step is to extract the weak value from the probe system P. This can be done by evaluating the probe signals (observed intensities) in the O-beam, at appropriate phase shifter positions. Thus, the purpose of the phase shifter is to tune the final pointer state of the probe-system, before a read-out via a count rate detection. Using intensities with phase shift , denoted as , the real part of the weak value is given by
Similarly, using the modulus of the weak value of yields
In order to determine the imaginary part of the intensities have to be measured. These are the intensities of the individual beams in path I and path II, which have to be measured separately without interference effects. This is achieved by inserting a beam stopper between the second plate of the IFM and the phase-shifter (see Figure 2) in one of the paths of the interferometer which consequently blocks the respective sub-beam. This yields the intensities , from which the imaginary part of is determined as
A detailed derivation for the intensities , and is given in [63].
3.3. Experimental Results
The final results of the weak value determination of the Pauli spin operator are plotted in Figure 3, together with the theoretical predictions of the weak value of the spin operator given by
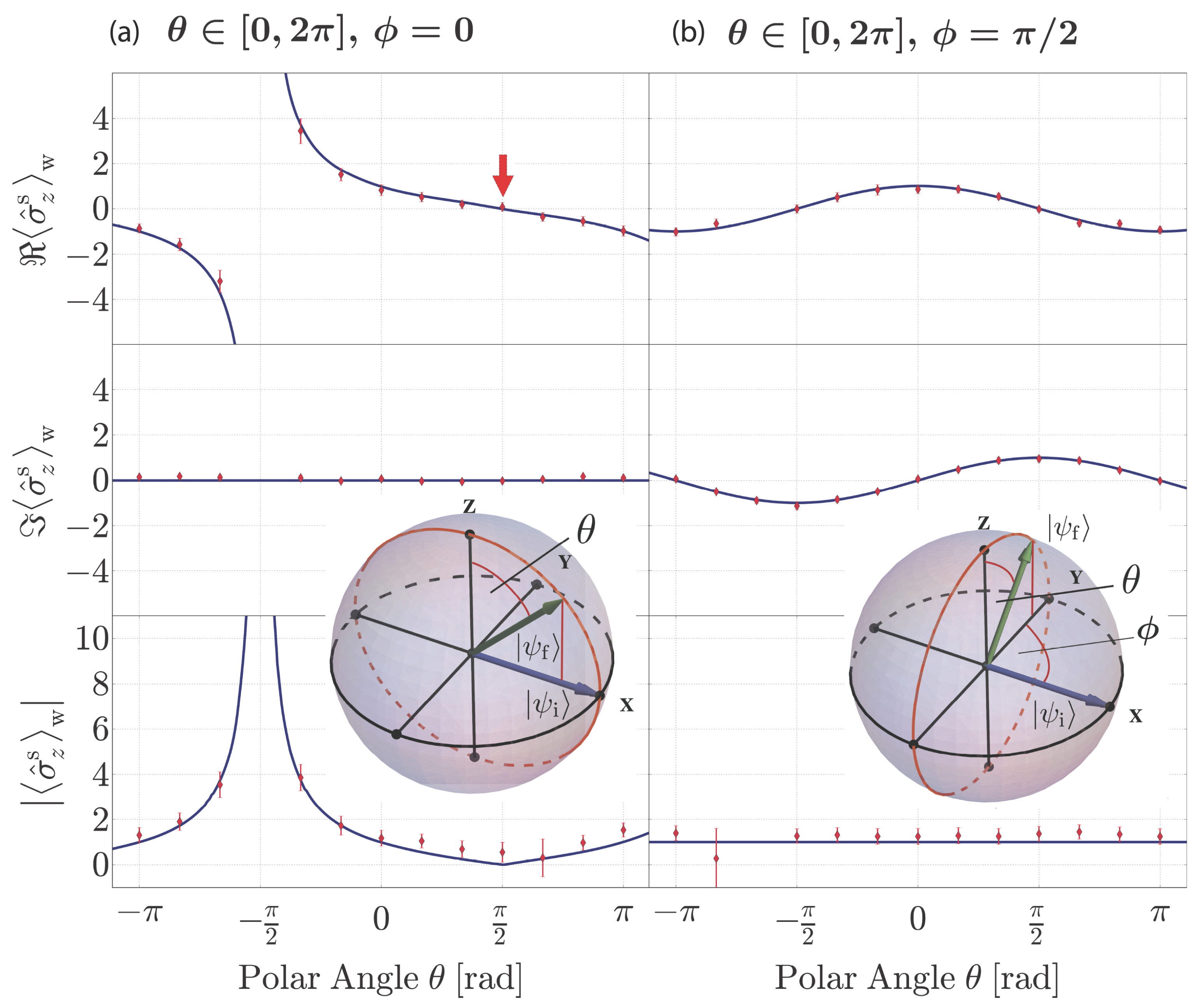
for initial state and an arbitrary final state , as defined in Equation (4). For , plotted in Figure 3a, no imaginary contributions of the weak value of are expected: the real part of exhibits values lying outside the usual range of spin eigenvalues, i.e., ±1, ranging from −3.2 to 3.4, while the imaginary parts remains zero. For and the initial and final state coincide. Thus, the weak value reduces to the expectation value , which yields zero and is marked by the red arrow in Figure 3a top panel. For in Figure 3b, real and imaginary component of oscillate in quadrature yielding a constant value of irrespective of the polar angle θ of the post-selected state . A good agreement of the measured data with the theoretical prediction is obtained.
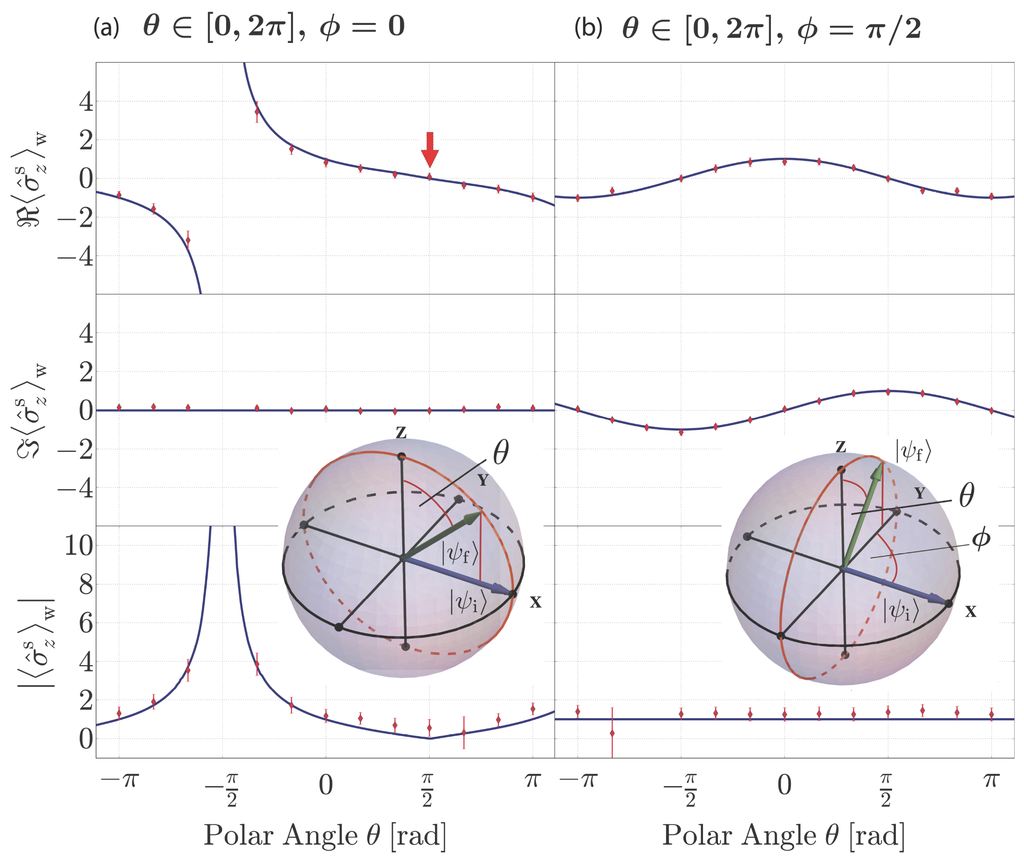
Figure 3.
Experimentally determined real (top panel) and modulus (bottom panel) and a direct measurement of the imaginary component (central panel), of the weak value of , together with the theoretical predictions (blue line). Bloch-sphere representations are given for pre- and post-selected spin state (a) ; and (b) . For and the weak value of equals the expectation value of (red arrow).
We want to emphasize that the presented weak measurements are realized in a purely quantum mechanical system of massive particles, since the spin of the neutron is a genuine quantum property and has no correspondence in terms of a classical variable, unlike the polarization of light.
4. The Quantum Cheshire-Cat
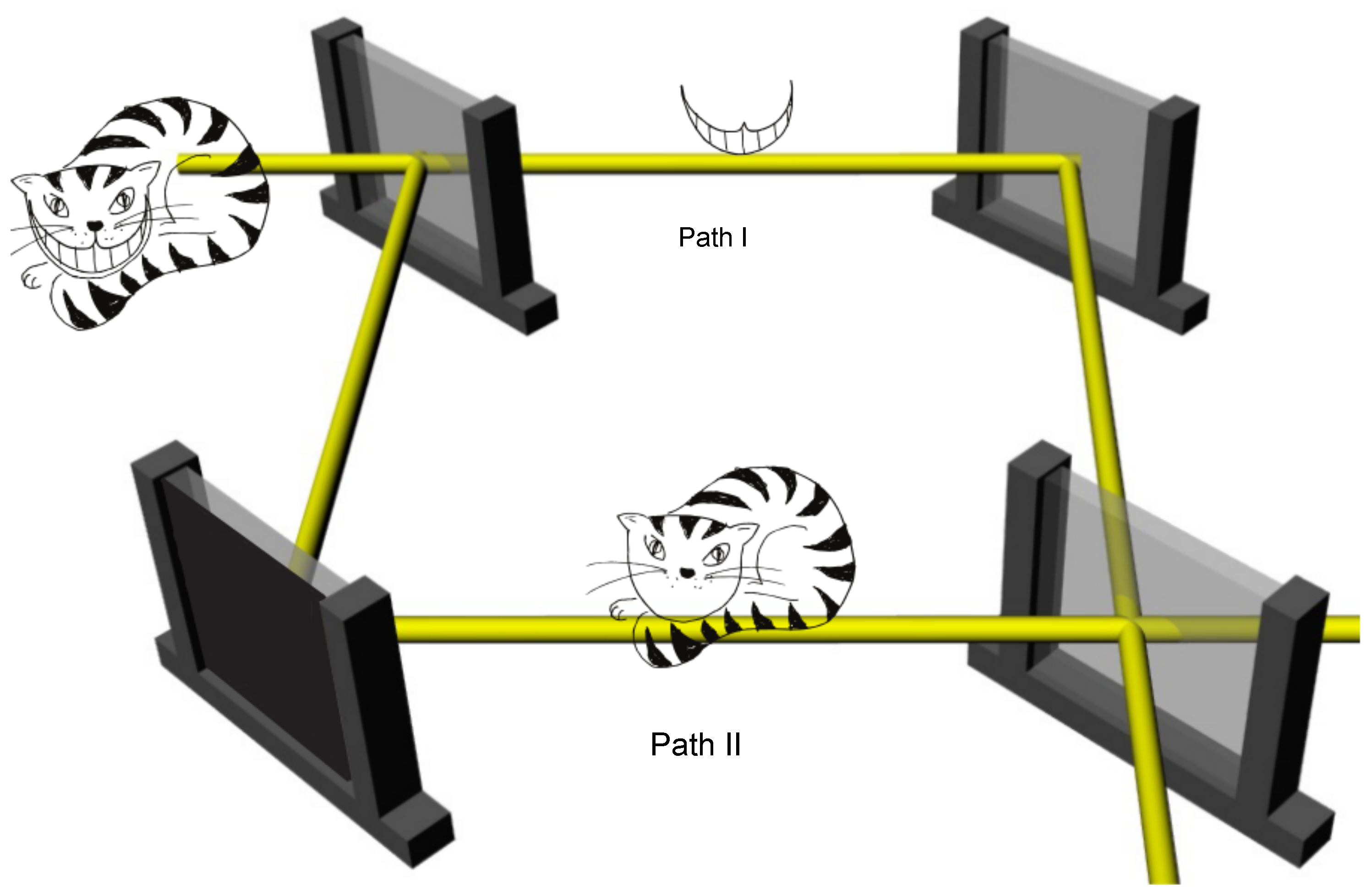
“Well! I’ve often seen a cat without a grin,” thought Alice; “but a grin without a cat! It’s the most curious thing I ever saw in all my life!”, these are Alice’s famous words after finding a passage to a surreal world in a rabbit hole, where she meets a cat that leaves her wondering. Such a phenomenon, which at first seems absurd, is actually possible in a quantum mechanical sense for the quantum Cheshire Cat in a Mach–Zehnder interferometer, where the cat itself is located in one beam path, while its grin is located in the other [65]. An artistic depiction of this behavior can be seen in Figure 4.
Figure 4.
Artistic depiction of the quantum Cheshire Cat. Inside the interferometer, the Cat goes through the upper beam path, while its grin travels along the lower beam path. Figure courtesy of Leon Filter.
4.1. Theory
In our realization of the quantum Cheshire Cat, the neutron plays the role of the cat and the cat’s grin is represented by the neutron’s spin component along the z-direction, applying the setup depicted in Figure 4. The system is initially prepared in such a way that after entering the beam splitter its quantum state is given by
where I (II) represents the spatial part of the neutron’s wavefunction in path I (path II) of the interferometer, and denotes the spin state along -direction. For an observation of the quantum Cheshire Cat, after pre-selection of an ensemble, a weak measurement of the neutrons’ population in a given path on the one hand and of the value of the spin in a given path on the other is performed. Subsequently, the ensemble is post-selected in the final state given by
Using the definition of the weak value given in Equation (1) together with initial and final state from Equations (9) and (10), the weak values of the projection operators on the neutron path eigenstates , with and yield and . The first expression indicates that a weak interaction coupling the spatial wavefunction to a probe localized on path I, has no effect on the probe on average—the system behaves as if there was no neutron travelling on path I. The weak value of the spin component along each path j suggests the location of the neutrons’ spin component. The appropriate observable of neutrons’ spin component on path j is given by , which yields and , for path I and II, respectively.
4.2. Experiment
The experiment was carried out at the S18 interferometer beam line at the research reactor of the ILL in Grenoble, France. Apart from small modification, the same setup and same beam parameters as in Section 3 were applied. Here, the small spin rotators are used to prepare the initial state given in Equation (9).
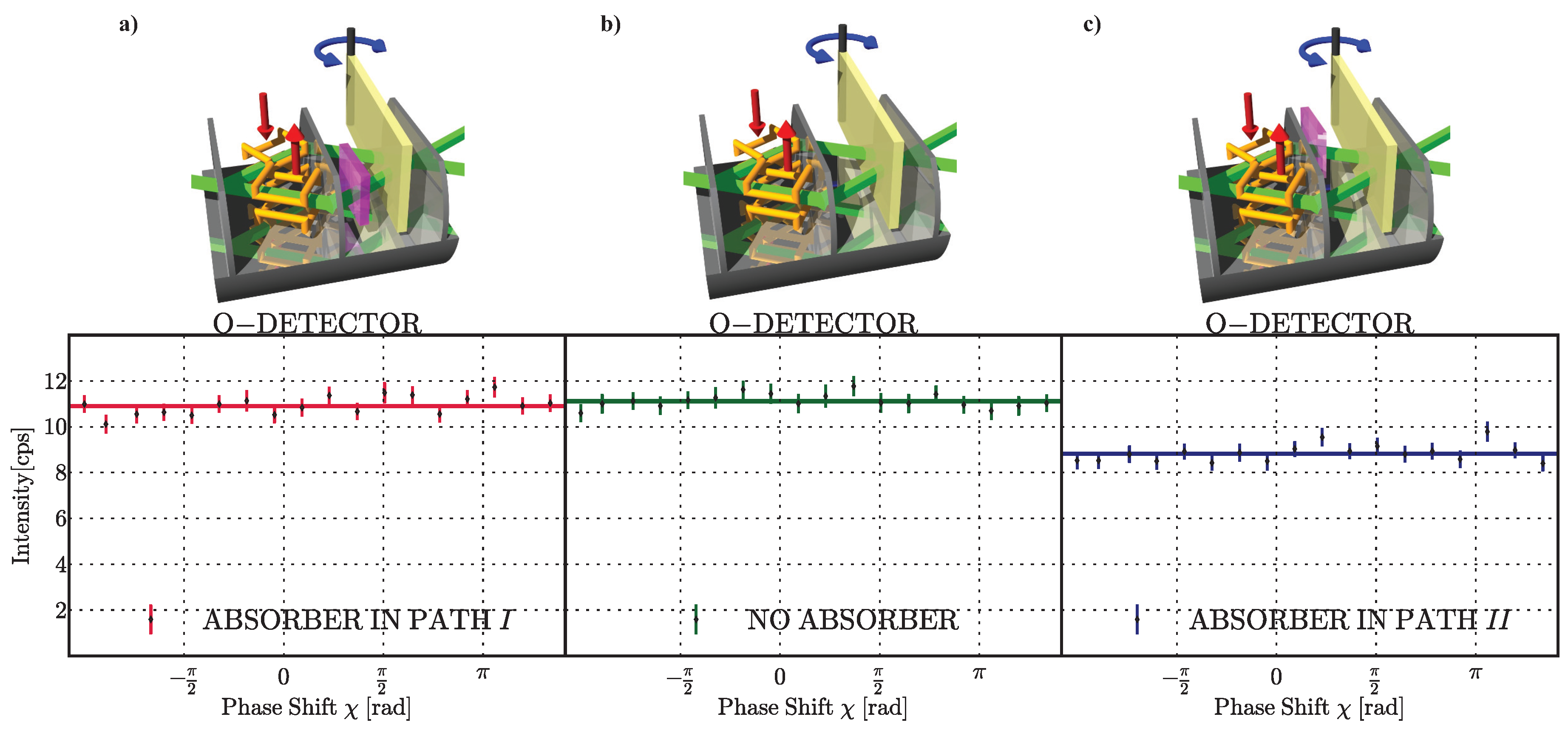
To determine the neutrons’ population in the interferometer’s paths, are measured by inserting an absorber, with transmissivity , into the respective path j of the interferometer. First, a reference measurement is performed, where the orthogonal spin states show no interference when rotating the phase shifter, as expected. Next, the absorber is inserted into path I and the phase shifter scan is repeated, where again no effect is observed. However, if the very same absorber were put in path II, the intensity decreases, suggesting that the neutrons’ population in the interferometer is obviously higher in path II than in path I. The observed intensities for measurements with absorber in path I and II as well as the reference measurement are depicted in Figure 5.
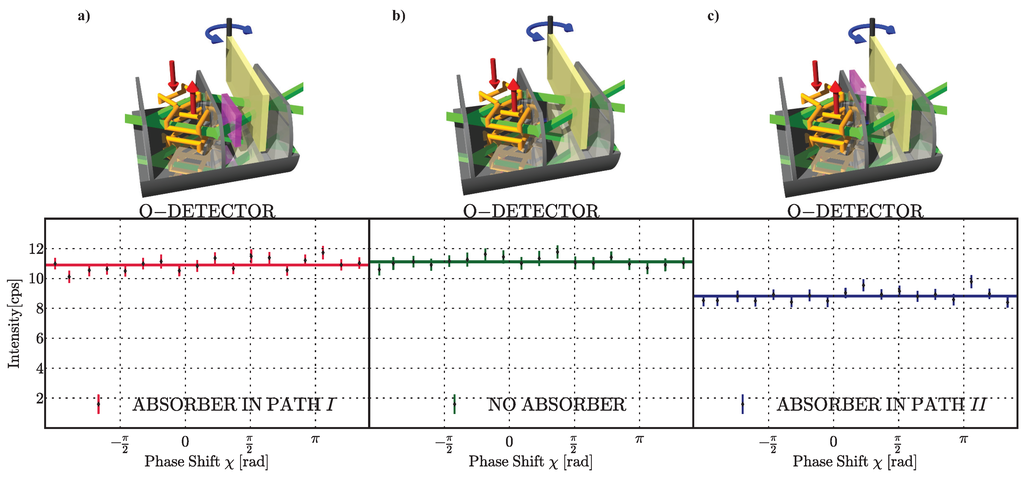
Figure 5.
Measurement of and using an absorber. The intensity is plotted as a function of the relative phase χ. The solid lines represent least-square fits to the data and the error bars represent one standard deviation (a) an absorber in path I; no significant loss in intensity is recorded; (b) a reference measurement without any absorber; (c) an absorber in path II: the intensity decreases. These results suggest that for the successfully post-selected ensemble, the neutrons behave as going through path II.
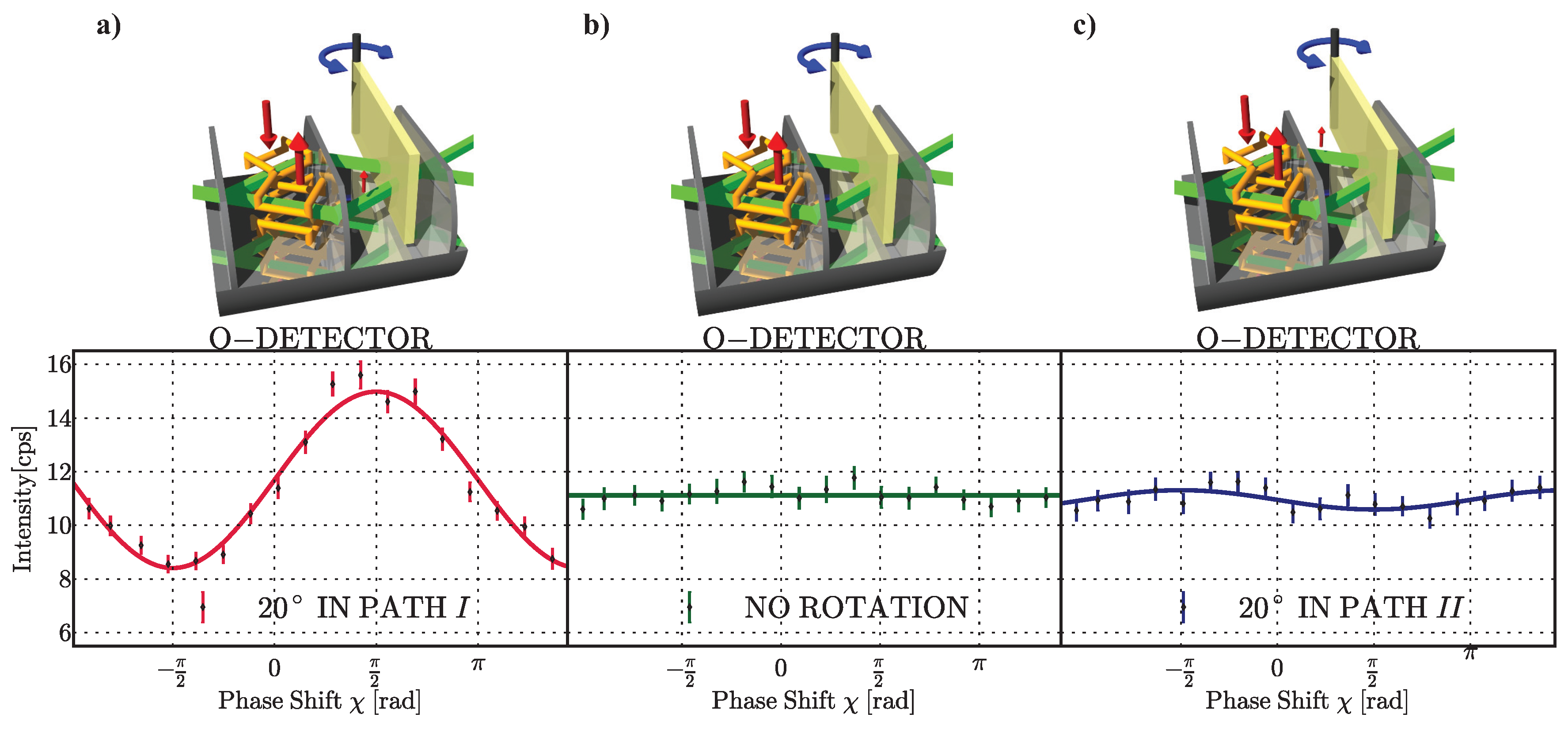
The weak measurements of the neutrons’ spin component in each path are achieved by applying an additional weak magnetic field in one or the other beam path, causing small spin rotations, which allows to probe the presence of the neutrons’ magnetic moment in the respective path. The condition of a weak measurement is fulfilled by tuning the magnetic field small enough. In this experiment, spin rotations of 20 deg were used, which corresponds to a wavefunction overlap of 98.5 %. An additional magnetic field in path I leads to emergence of interference fringes showing a contrast of 28.1 %, indicating the presence of a magnetic moment. On the other hand, the same field applied in path II causes no significant change in the intensity modulation. The measured intensities can be seen in Figure 6. This behavior can be quantified by calculating the weak values using the recorded intensities. Details of this calculation are presented in detail in the Methods of [66]. The final results for the weak values of the populations and magnetic moment are summarized in Table 1.
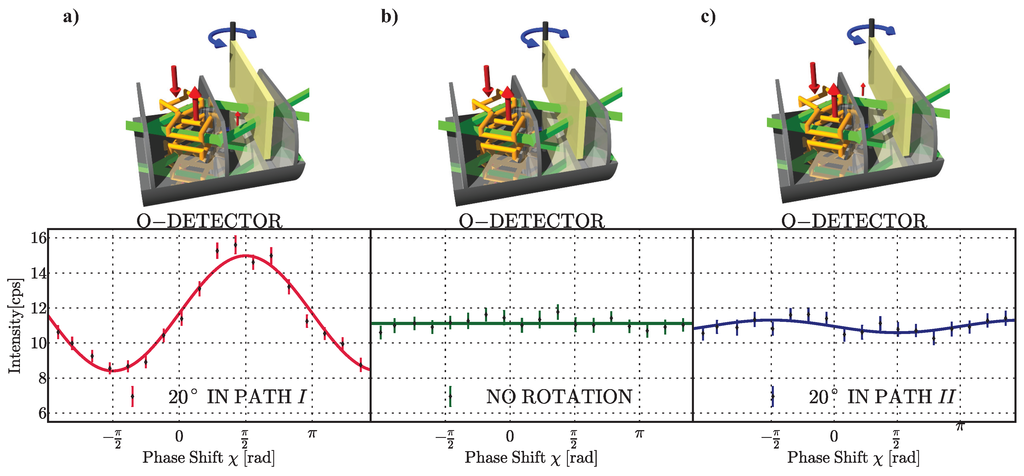
Figure 6.
Measurement of and applying small additional magnetic fields. The intensity is plotted as a function of the relative phase χ. The solid lines represent least-square fits to the data and the error bars represent one s.d. (a) a magnetic field in path I; interference fringes appear; (b) a reference measurement without any additional magnetic fields, where due to the orthogonal spin states no interference fringes are observed; (c) a magnetic field in path II; interference pattens do not differ significantly from reference measurement, suggesting the neutrons’ spin component travels along path I.

Table 1.
Final results of weak values.
Our results show that weak measurements combined with neutron interferometry allows to demonstrate the quantum Cheshire Cat, where (for pre- and post-elected ensembles) a property of a quantum system can behave as being spatially separated from the place of the particle’s presence. It has to be noted here, that quantum mechanics can give definite answers only for ensembles, no definite assertions about a single particle can be made. We want to emphasize that the Cheshire Cat phenomenon can be applied to any quantum system, opening doors for future applications in high-precision metrology and quantum information technology [39,51].
5. Conclusions
One cannot emphasize the importance of studies of quantum dynamics enough. The evolution of a quantum system cannot simply be described by classical trajectories given by equations of motion. In our neutron interferometer experiment, phase shifts caused by various interactions are directly accessible. Two recent experiments are described in this article, where fundamental features of quantum dynamics are made evident. The theoretical framework of our experiments is based on weak values, a new kind of quantum variable introduced by Aharonov and his co-workers [33]. In the first experiment, a neutron interferometric measurement is realized, making it possible to determine all aspects of the weak value of the neutron’s Pauli spin operator , i.e., its real component and the modulus, as well as the imaginary component. Our results clearly show that the determined weak values are of quantum-mechanical origin, no classical (wave) theory can describe the weak values observed in our experiment. A full determination of the weak value can be used to characterize the evolution of the neutron’s wave-function inside an interferometer, just like in a report of a photonic double-slit experiment [53]. Moreover, our measurement scheme with a neutron interferometer is applied to demonstrate a fundamental phenomenon of quantum mechanics, namely the quantum Cheshire Cat. At the level of a pre- and post-selected ensemble, a property of a quantum system, in our case the neutron’s spin, can behave as being spatially separated from the site where one is certain to probe the particle’s presence. This behavior could be utilized in high-precision metrology and quantum information technology, for example in situations where the magnetic moment of a particle overshadows another of the particle’s properties, which shall be measured very precisely. We are planning to perform neutron interferometer experiments to demonstrate the non-classical nature of the correlations in the quantum pigeonhole effect [67] and a multi-path measurement reported in a nested interferometer configuration [68].
Acknowledgments
For helpful discussions, we thank Alexandre Matzkin from the Laboratoire de Physique Thorique et Modlisation, Cergy-Pontoise (France), Dipankar Home from the Bose Institute, Kolkata (India) and Jeff Tollaksen from the Institute for Quantum Studies at Chapman University, Orange, CA, (USA). We would like to express our gratitude for the kind hospitality at the ILL in Grenoble and the ongoing support of the science division at ILL. This work was financed by the Austrian Science Fund (FWF): Projects No. P25795-N20 and No. P24973-N20 as well as from the Austrian-French binational Amadeus Project No. FR 06/2012.
Author Contributions
Stephan Sponar and Yuji Hasegawa wrote the paper. Tobias Denkmayr and Yuji Hasegawa conceived the experiments. Tobias Denkmayr, Hermann Geppert and Stephan Sponar performed the experiments.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AAV | Aharonov, Albert and Vaidman |
| AB | Aharonov-Bohm |
| AC | Aharonov-Casher |
| DC | direct current |
| DOF | degrees of freedom |
| GHZ | Greenberger-Horne-Zeilinger |
| ILL | Institute Laue-Langevin |
| IFM | interferometer |
| LLL | triple Laue |
| RF | radio frequency |
| VCN | very cold neutrons |
References
- Tonomura, A. Applications of electron holography. Rev. Mod. Phys. 1987, 59, 639–669. [Google Scholar] [CrossRef]
- Feynman, R.; Leighton, R.; Sands, M. The Feynman Lectures on Physics, 2nd ed.; Addison-Wesley: Boston, MA, USA, 1963; Volume 1. [Google Scholar]
- Arndt, M.; Ekers, A.; von Klitzing, W.; Ulbricht, H. Focus on modern frontiers of matter wave optics and interferometry. New J. Phys. 2012, 14, 125006. [Google Scholar] [CrossRef]
- Cronin, A.D.; Schmiedmayer, J.; Pritchard, D.E. Optics and interferometry with atoms and molecules. Rev. Mod. Phys. 2009, 81, 1051–1129. [Google Scholar] [CrossRef]
- Popescu, S. Dynamical quantum non-locality. Nat. Phys. 2010, 6, 151–153. [Google Scholar] [CrossRef]
- Bertlmann, R.A.; Zeilinger, A. Quantum [Un]speakables, from Bell to Quantum Information; Springer Verlag: Heidelberg, Germany, 2002. [Google Scholar]
- Maier-Leibnitz, H.; Springer, T. Ein Interferometer für langsame Neutronen. Z. Phys. 1962, 167, 386. [Google Scholar] [CrossRef]
- Mezei, F. Neutron spin echo: A new concept in polarized thermal neutron techniques. Z. Phys. 1972, 25, 146. [Google Scholar] [CrossRef]
- Rauch, H.; Treimer, W.; Bonse, U. Test of a single crystal neutron interferometer. Phys. Lett. A 1974, 47, 369–371. [Google Scholar] [CrossRef]
- Rauch, H.; Werner, S.A. Neutron Interferometry; Clarendon Press: Oxford, UK, 2000. [Google Scholar]
- Rauch, H.; Zeilinger, A.; Badurek, G.; Wilfing, A.; Bauspiess, W.; Bonse, U. Verification of Coherent Spinor Rotation of Fermions. Phys. Lett. A 1975, 54, 425–427. [Google Scholar] [CrossRef]
- Werner, S.A.; Colella, R.; Overhauser, A.W.; Eagen, C.F. Observation of the Phase Shift of a Neutron Due to Precession in a Magnetic Field. Phys. Rev. Lett. 1975, 35, 1053–1055. [Google Scholar] [CrossRef]
- Klein, A.G.; Opat, G.I. Observation of 2π Rotations by Fresnel Diffraction of Neutrons. Phys. Rev. Lett. 1976, 37, 238–240. [Google Scholar] [CrossRef]
- Grigoriev, S.; Kraan, W.; Rekveldt, M.Th. Observation of 4-pi periodicity of the spinor using neutron resonance interferometry. Europhys. Lett. 2004, 66, 164–170. [Google Scholar]
- Colella, R.; Overhauser, A.W.; Werner, S.A. Observation of Gravitationally Induced Quantum Interference. Phys. Rev. Lett. 1975, 34, 1472–1474. [Google Scholar] [CrossRef]
- Sakurai, J.J. Modern Quantum Mechanics; Addison-Wesley: New York, NY, USA, 1994. [Google Scholar]
- Littrell, K.C.; Allman, B.E.; Werner, S.A. Two-wavelength-difference measurement of gravitationally induced quantum interference phases. Phys. Rev. A 1997, 56, 1767–1780. [Google Scholar] [CrossRef]
- Van der Zouw, G.; Weber, M.; Felber, J.; Gähler, R.; Geltenbort, P.; Zeilinger, A. Aharonov-Bohm and gravity experiments with the very-cold-neutron interferometer. Nucl. Instrum. Meth. A 2000, 440, 568–574. [Google Scholar] [CrossRef]
- Klepp, J.; Sponar, S.; Hasegawa, Y. Fundamental phenomena of quantum mechanics explored with neutron interferometers. Prog. Theor. Exp. Phys. 2014, 2014. [Google Scholar] [CrossRef]
- De Haan, V.O.; Plomp, J.; van Well, A.A.; Rekveldt, M.T.; Hasegawa, Y.H.; Dalgliesh, R.M.; Steinke, N.J. Measurement of gravitation-induced quantum interference for neutrons in a spin-echo spectrometer. Phys. Rev. A 2014, 89, 063611. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I. Quantum Computation and Quantum Information; Cambridge Unviversity Press: Cambridge, UK, 2000. [Google Scholar]
- Bell, J.S. On the Einstein-Podolsky-Rosen paradox. Physics 1964, 1, 195–200. [Google Scholar]
- Kochen, S.; Specker, E.P. The problem of hidden variables in quantum mechanics. J. Math. Mech. 1967, 17, 59–87. [Google Scholar] [CrossRef]
- Hasegawa, Y.; Loidl, R.; Badurek, G.; Baron, M.; Rauch, H. Violation of a Bell-like inequality in single-neutron interferometry. Nature 2003, 425, 45–48. [Google Scholar] [CrossRef] [PubMed]
- Geppert, H.; Denkmayr, T.; Sponar, S.; Lemmel, H.; Hasegawa, Y. Improvement of the polarized neutron interferometer setup demonstrating violation of a Bell-like inequality. Nucl. Instrum. Methods Phys. Res. Sect. A 2014, 763, 417–423. [Google Scholar] [CrossRef] [PubMed]
- Hasegawa, Y.; Loidl, R.; Badurek, G.; Baron, M.; Rauch, H. Quantum Contextuality in a Single-Neutron Optical Experiment. Phys. Rev. Lett. 2006, 97, 230401. [Google Scholar] [CrossRef] [PubMed]
- Cabello, A.; Filipp, S.; Rauch, H.; Hasegawa, Y. Proposed Experiment for Testing Quantum Contextuality with Neutrons. Phys. Rev. Lett. 2008, 100, 130404. [Google Scholar] [CrossRef] [PubMed]
- Bartosik, H.; Klepp, J.; Schmitzer, C.; Sponar, S.; Cabello, A.; Rauch, H.; Hasegawa, Y. Experimental Test of Quantum Contextuality in Neutron Interferometry. Phys. Rev. Lett. 2009, 103, 040403. [Google Scholar] [CrossRef] [PubMed]
- Greenberger, D.M.; Horne, M.A.; Zeilinger, A. Bell’s Theorem, Quantum Theory, and Concepts of the Universe; Kafatos, M., Ed.; Kluwer Academics: Dordrecht, The Netherlands, 1989; pp. 73–76. [Google Scholar]
- Greenberger, D.M.; Shimony, A.; Horne, M.A.; Zeilinger, A. Bell’s theorem without inequalities. Am. J. Phys. 1990, 58, 1131–1143. [Google Scholar] [CrossRef]
- Hasegawa, Y.; Loidl, R.; Badurek, G.; Durstberger-Rennhofer, K.; Sponar, S.; Rauch, H. Engineering of triply entangled states in a single-neutron system. Phys. Rev. A 2010, 81, 032121. [Google Scholar] [CrossRef]
- Erdösi, D.; Huber, M.; Hiesmayr, B.C.; Hasegawa, Y. Proving the generation of genuine multipartite entanglement in a single-neutron interferometer experiment. New J. Phys. 2013, 15, 023033. [Google Scholar] [CrossRef]
- Aharonov, Y.; Albert, D.Z.; Vaidman, L. How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100. Phys. Rev. Lett. 1988, 60, 1351–1354. [Google Scholar] [CrossRef] [PubMed]
- Aharonov, Y.; Vaidman, L. Properties of a quantum system during the time interval between two measurements. Phys. Rev. A 1990, 41, 11–20. [Google Scholar] [CrossRef] [PubMed]
- Aharonov, Y.; Vaidman, L. The two-state vector formalism: an updated review. Lect. Nots. Phys. 2007, 734, 399–447. [Google Scholar]
- Aharonov, Y.; Bergmann, P.G.; Lebowitz, J.L. Time Symmetry in the Quantum Process of Measurement. Phys. Rev. 1964, 134, 1410–1416. [Google Scholar] [CrossRef]
- Ritchie, N.W.M.; Story, J.G.; Hulet, R.G. Realization of a measurement of a “weak value”. Phys. Rev. Lett. 1991, 66, 1107–1110. [Google Scholar] [CrossRef] [PubMed]
- Duck, I.M.; Stevenson, P.M.; Sudarshan, E.C.G. The sense in which a “weak measurement” of a spin-1/2 particle’s spin component yields a value 100. Phys. Rev. D 1989, 40, 2112–2117. [Google Scholar] [CrossRef]
- Hosten, O.; Kwiat, P. Observation of the Spin Hall Effect of Light via Weak Measurements. Science 2008, 319, 787–790. [Google Scholar] [CrossRef] [PubMed]
- Dixon, P.B.; Starling, D.J.; Jordan, A.N.; Howell, J.C. Ultrasensitive Beam Deflection Measurement via Interferometric Weak Value Amplification. Phys. Rev. Lett. 2009, 102, 173601. [Google Scholar] [CrossRef] [PubMed]
- Starling, D.J.; Dixon, P.B.; Jordan, A.N.; Howell, J.C. Precision frequency measurements with interferometric weak values. Phys. Rev. A 2010, 82, 063822. [Google Scholar] [CrossRef]
- Starling, D.J.; Dixon, P.B.; Williams, N.S.; Jordan, A.N.; Howell, J.C. Continuous phase amplification with a Sagnac interferometer. Phys. Rev. A 2010, 82, 011802. [Google Scholar] [CrossRef]
- Feizpour, A.; Xing, X.; Steinberg, A.M. Amplifying Single-Photon Nonlinearity Using Weak Measurements. Phys. Rev. Lett. 2011, 107, 133603. [Google Scholar] [CrossRef] [PubMed]
- Ota, Y.; Ashhab, A.; Nori, F. Entanglement amplification via local weak measurements. J. Phys. A 2012, 45, 415303. [Google Scholar] [CrossRef]
- Zhou, L.; Turek, Y.; Sun, C.P.; Nori, F. Weak-value amplification of light deflection by a dark atomic ensemble. Phys. Rev. A 2013, 88, 053815. [Google Scholar] [CrossRef]
- Kofman, A.G.; Ashhab, S.; Nori, F. Nonperturbative theory of weak pre- and post-selected measurements. Phys. Rep. 2012, 520, 43–133. [Google Scholar] [CrossRef]
- Kocsis, S.; Braverman, B.; Ravets, S.; Stevens, M.J.; Mirin, R.P.; Shalm, L.K.; Steinberg, A.M. Observing the Average Trajectories of Single Photons in a Two-Slit Interferometer. Science 2011, 332, 1170–1173. [Google Scholar] [CrossRef] [PubMed]
- Lundeen, J.S.; Sutherland, B.; Patel, A.; Stewart, C.; Bamber, C. Direct measurement of the quantum wavefunction. Nature 2011, 474, 188–191. [Google Scholar] [CrossRef] [PubMed]
- Goggin, M.E.; Almeida, M.P.; Barbieri, M.; Lanyon, B.P.; O’Brien, J.L.; White, A.G.; Pryde, G.J. Violation of the Leggett-Garg inequality with weak measurements of photons. Proc. Natl. Acad. Sci. USA 2011, 108, 1256–1261. [Google Scholar] [CrossRef] [PubMed]
- Salvail, J.Z.; Agnew, M.; Johnson, A.S.; Bolduc, E.; Leach, J.; Boyd, R.W. Full characterization of polarization states of light via direct measurement. Nat. Photonics 2013, 7, 316–321. [Google Scholar] [CrossRef]
- Dressel, J.; Malik, M.; Miatto, F.M.; Jordan, A.N.; Boyd, R.W. Colloquium: Understanding quantum weak values: Basics and applications. Rev. Mod. Phys. 2014, 86, 307–316. [Google Scholar] [CrossRef]
- Ozawa, M. Universally valid reformulation of the Heisenberg uncertainty principle on noise and disturbance in measurement. Phys. Rev. A 2003, 67, 042105. [Google Scholar] [CrossRef]
- Rozema, L.A.; Darabi, A.; Mahler, D.H.; Hayat, A.; Soudagar, Y.; Steinberg, A.M. Violation of Heisenberg’s Measurement-Disturbance Relationship by Weak Measurements. Phys. Rev. Lett. 2012, 109, 100404. [Google Scholar] [CrossRef] [PubMed]
- Ringbauer, M.; Biggerstaff, D.N.; Broome, M.A.; Fedrizzi, A.; Branciard, C.; White, A.G. Experimental Joint Quantum Measurements with Minimum Uncertainty. Phys. Rev. Lett. 2014, 112, 020401. [Google Scholar] [CrossRef] [PubMed]
- Kaneda, F.; Baek, S.Y.; Ozawa, M.; Edamatsu, K. Experimental Test of Error-Disturbance Uncertainty Relations by Weak Measurement. Phys. Rev. Lett. 2014, 112, 020402. [Google Scholar] [CrossRef] [PubMed]
- Dressel, J.; Nori, F. Certainty in Heisenberg’s uncertainty principle: Revisiting definitions for estimation errors and disturbance. Phys. Rev. A 2014, 89, 022106. [Google Scholar] [CrossRef]
- Resch, J.; Lundeen, J.; Steinberg, A. Experimental realization of the quantum box problem. Phys. Lett. A 2004, 324, 125–131. [Google Scholar] [CrossRef]
- Lundeen, J.S.; Steinberg, A.M. Experimental Joint Weak Measurement on a Photon Pair as a Probe of Hardy’s Paradox. Phys. Rev. Lett. 2009, 102, 020404. [Google Scholar] [CrossRef] [PubMed]
- Yokota, K.; Yamamoto, T.; Koashi, M.; Imoto, N. Direct observation of Hardy’s paradox by joint weak measurement with an entangled photon pair. New J. Phys. 2009, 11, 033011. [Google Scholar] [CrossRef]
- Aharonov, Y.; Botero, A.; Popescu, S.; Reznik, B.; Tollaksen, J. Revisiting Hardy’s paradox: counterfactual statements, real measurements, entanglement and weak values. Phys. Lett. A 2002, 301, 130–138. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Bekshaev, A.Y.; Kofman, A.G.; Nori, F. Photon trajectories, anomalous velocities and weak measurements: a classical interpretation. New J. Phys. 2013, 15, 073022. [Google Scholar] [CrossRef]
- Dressel, J.; Bliokh, K.Y.; Nori, F. Classical Field Approach to Quantum Weak measurements. Phys. Rev. Lett. 2014, 112, 110407. [Google Scholar] [CrossRef] [PubMed]
- Sponar, S.; Denkmayr, T.; Geppert, H.; Lemmel, H.; Matzkin, A.; Tollaksen, J.; Hasegawa, Y. Weak values obtained in matter-wave interferometry. Phys. Rev. A 2015, 92, 062121. [Google Scholar] [CrossRef]
- Wu, S.; Mølmer, K. Weak measurements with a qubit meter. Phys. Lett. A 2009, 374, 34–39. [Google Scholar] [CrossRef]
- Aharonov, Y.; Popescu, S.; Rohrlich, D.; Skrzypczyk, P. Quantum Cheshire Cats. New J. Phys. 2013, 15, 113015. [Google Scholar] [CrossRef]
- Denkmayr, T.; Geppert, H.; Sponar, S.; Lemmel, H.; Matzkin, A.; Tollaksen, J.; Hasegawa, Y. Experimental observation of a quantum cheshire cat in matter wave interferometry. Nat. Commun. 2014, 5, 4492. [Google Scholar] [CrossRef] [PubMed]
- Aharonov, Y.; Cohen, E. Weak Values and Quantum Nonlocality. 2015; arXiv:1504.03797. [Google Scholar]
- Danan, A.; Danan, D.; Bar-Ad, S.; Vaidman, L. Asking Photons Where They Have Been. Phys. Rev. Lett. 2013, 111, 240402. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).