1. Introduction
Highly-ionized atoms are of interest in various disciplines, including astronomy [
1,
2], spectroscopy [
3,
4,
5], ion-surface physics [
4,
6], plasma diagnostics [
7,
8] and laboratory astrophysics [
9,
10]. Recently, theoretical studies have revealed special features that could make highly-ionized atoms ideal for novel applications. Proposals include certain electronic configurations with greatly reduced sensitivity to external field perturbations [
11] and forbidden optical transitions that may be suitable candidates for the next generation of atomic clocks at the sub-
level of precision [
12,
13]. Some highly-ionized atoms have forbidden transitions near configuration crossings that are among the most sensitive to possible variation of the fine-structure constant [
14], a possibility suggested by grand unification theories. Others have several metastable states forming a low-lying manifold that allows quantum information processing in ways not possible with a neutral atom or an ion in a low charge state [
13].
Precise tests of fundamental physics have employed few-electron highly-charged ions in spectroscopic measurements of low-lying atomic levels to probe quantum electrodynamics (QED) in the high field regime (see, for example, [
4,
15,
16] and the references therein). An illustration of the role of highly-ionized atoms in metrology is the determination of the most precise value of the electron mass, which comes from measuring the spin flip of one electron tightly bound to a carbon nucleus that is confined in a triple Penning trap apparatus [
17]. In addition, theoretical studies show that the energy levels for one-electron ions in high angular momentum states can be calculated with high accuracy, comparable to the precision of state-of-the-art frequency metrology [
18]. This simplicity of Rydberg atoms is potentially useful for measurements of fundamental constants. One goal is to realize such Rydberg states in one-electron ions for laser spectroscopy to test the theory in a regime free of nuclear effects, which would be valuable in shedding light on the puzzling discrepancy in the value of the proton radius inferred from various measurements [
19]. We present here recent developments at NIST, including the use of a unitary Penning trap [
20] to isolate highly-ionized atoms at low energy [
21], experiments with electron capture [
22] and a different technique for measuring the radiative decay lifetime of a metastable state [
23].
2. Unitary Penning Traps
The Penning trap [
24] is frequently used to confine charged particles in an evacuated region of space through the use of static electric and magnetic fields, enabling the manipulation of trapped particles in a well-controlled environment. It finds applications in various disciplines, including physics of non-neutral plasmas, mass spectrometry, biomolecular chemistry, precision spectroscopy, antimatter science, quantum information and fundamental metrology (see [
20] and the references therein).
Penning trap stability and precision are optimal in a strong, uniform magnetic field. This is attainable to a high degree using a superconductive solenoid; persistent currents in superconductive coils can generate magnetic fields higher than five tesla (T). The electrode structure of the ion trap is housed in a vacuum envelope that is inserted into the bore of the superconductive magnet. This classic architecture is versatile and has been used in some of the most precise measurements in atomic physics and metrology. Past experiments to extract and recapture highly-ionized atoms have also generally utilized solenoidal magnets. In an early experiment at the Lawrence Livermore National Laboratory (LLNL), a cryogenic Penning trap (named RETRAP) with a high-field superconductive magnet [
25] was used to recapture highly-charged ions (HCI) extracted from an electron beam ion trap (EBIT). A recent room-temperature experiment [
26] (SMILETRAP II) demonstrated the capture and cooling of Ar
in a Penning trap with a 1.1-T magnet.
However, a superconductive solenoidal magnet with its cryostat occupies considerable volume, and the fringing field extends over many times more volume. Space constraints in some applications or existing setups (as in the case of the EBIT at NIST) may not be compatible with the operation of a superconductive magnet. These limitations have led us to explore certain architectures for making extremely compact Penning traps (
cm
) using rare-earth magnets with a permanent magnetization of about 1.3 T [
20]; they are “unitary” because the electric and magnetic fields come from one integral structure, rather than from the superposition of separable electric and magnetic structures. Unitary Penning traps have been demonstrated to be useful for capturing and isolating highly-ionized atoms extracted from an EBIT at NIST. In this section, we discuss the basic features of this method, with emphasis on a two-magnet, unitary Penning trap designed to provide access for atomic or laser beams.
2.1. Motions in a Penning Trap
A simple Penning trap consists of a stack of three cylindrically-symmetric electrodes that is electrically biased with a potential
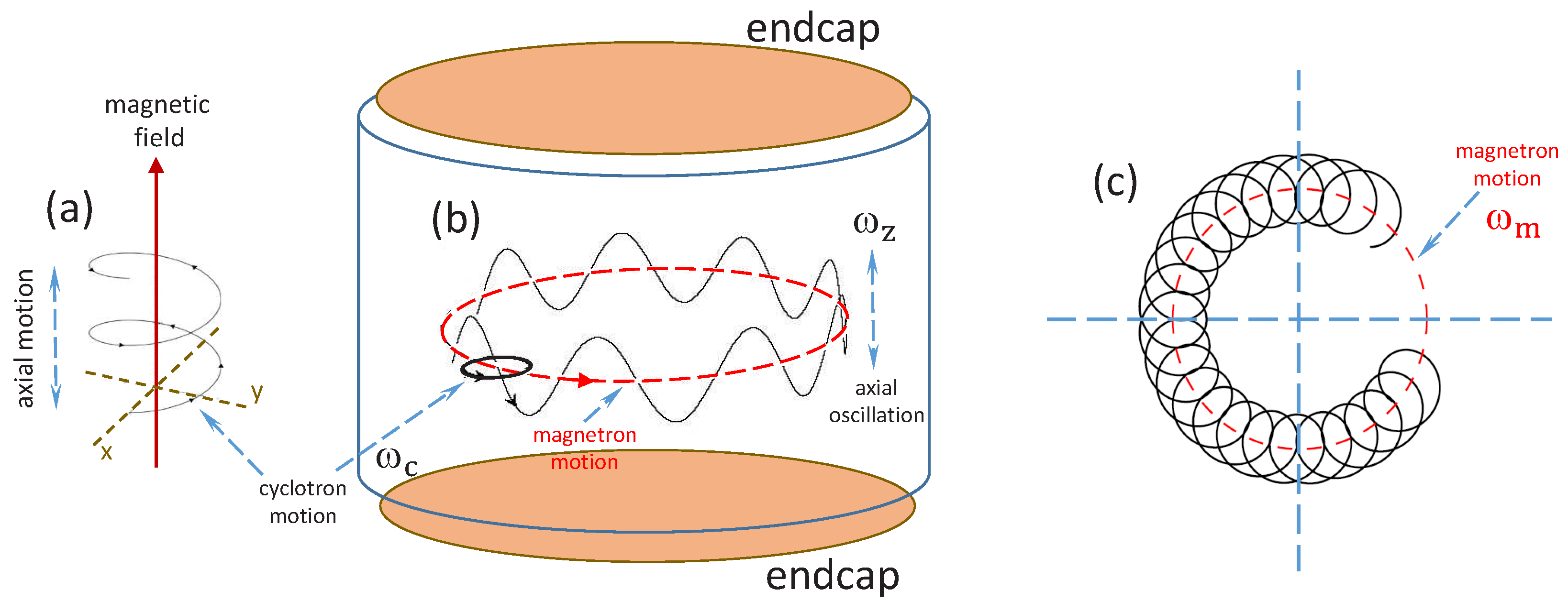
to generate a linear restoring force along the trap axis (symmetry axis) aligned parallel to a strong, uniform magnetic field. As illustrated in
Figure 1, an ion stored in a Penning trap undergoes harmonic motions [
27]. The cyclotron motion perpendicular to the magnetic field has a frequency given by:
where
q is the charge of the particle,
is the magnitude of the magnetic field and
m is the mass of the ion. A helical trajectory results since the ion drifts along the magnetic field, as shown in
Figure 1a. Confinement along the trap axis comes from the linear restoring force associated with the electric field of a quadrupole potential:
where
z and
r are cylindrical coordinates defined from the center of the trap,
λ is a dimensionless parameter of order unity,
is the applied electric potential and
d is the characteristic dimension of the trap [
20]. The simple harmonic oscillation along the trap axis has an angular frequency given by:
According to the theorem first proven by Earnshaw (1842), stable equilibrium is not possible for an ion (or collection of ions) confined using static electric and/or magnetic fields only. In this case, although the axial oscillation in a Penning trap is stable, the dynamical equilibrium for motions in a plane perpendicular to the axis is not assured. In fact, the axial restoring force derived from the quadrupole electric field in Equation (
2) incurs an outward radial force on the ion, pushing it towards the ring electrode. Unless the Lorentz force due to the magnetic field is sufficiently strong to counteract the radial part of the electric field, the ion would leave the trap. If dynamical equilibrium prevails, the center of the cyclotron motion drifts slowly around the center of the trap, defining a magnetron orbit with a frequency given by:
The combination of cyclotron, magnetron and axial oscillations gives rise to an epicyclic trajectory, such as shown in
Figure 1b. In
Figure 1c, the circular motions of an ion stored in a two-magnet Penning trap are projected onto the midplane, with the initial condition chosen to highlight the fast cyclotron motion drifting counter-clockwise in a magnetron orbit. Since steady-state motion requires this magnetron frequency to be real, system parameters are constrained for trapping [
27]. The goal is to select a set of trap characteristics that is compatible with planned operating conditions.
Figure 1.
Motions of an ion in a Penning trap. (a) Cyclotron motion around a magnetic field line; (b) illustration of the axial oscillation and magnetron motion around the center of the trap; (c) circular motions of an ion confined in a Penning trap, projected onto the trap mid-plane.
Figure 1.
Motions of an ion in a Penning trap. (a) Cyclotron motion around a magnetic field line; (b) illustration of the axial oscillation and magnetron motion around the center of the trap; (c) circular motions of an ion confined in a Penning trap, projected onto the trap mid-plane.
2.2. Unitary Penning Trap
Rare-earth magnets are made of alloys containing a lanthanide element. The most commonly used are neodymium and samarium. Elements in the lanthanide series have large magnetic moments due to the partial filling of the electron orbitals in the f-shell. In fact, as many as seven f-shell electrons can align in a lanthanide atom, shielded within highly-localized orbitals from inter-atomic interactions. However, the Curie temperatures of pure rare-earth magnets are too low to be useful at room temperature. Over two decades beginning in the 1970s, compounds containing transition elements (such as Fe) were developed that have Curie points above room temperature, as well as very high magnetic anisotropy, making them practical and economical room-temperature sources of strong magnetic fields. In fact, rare-earth magnets generate stronger fields than any other type of permanent magnet.
Rare-earth magnets are used in various technologies, such as mass data storage devices for computers, high-quality audio headphones, wind-turbine power generators, high-speed trains using magnetic levitation,
etc. The exploration of their use in creating special tools for research in physics and engineering overlapped closely with the early development of rare-earth magnets. A notable example is the wiggler magnets used in free electron lasers and accelerators [
28]. In some applications, large solenoidal magnets can be replaced with a more compact system of rare-earth multi-pole magnets, as has been done in constructing compact Penning traps [
29,
30]. A unitary Penning trap represents the limit of compactness attainable by changing the architecture in such a way that the rare-earth magnets become components of the electrode structure that generates the trapping fields; moreover, the entire electrode structure participates in the optimization of the magnetic field for ion storage.
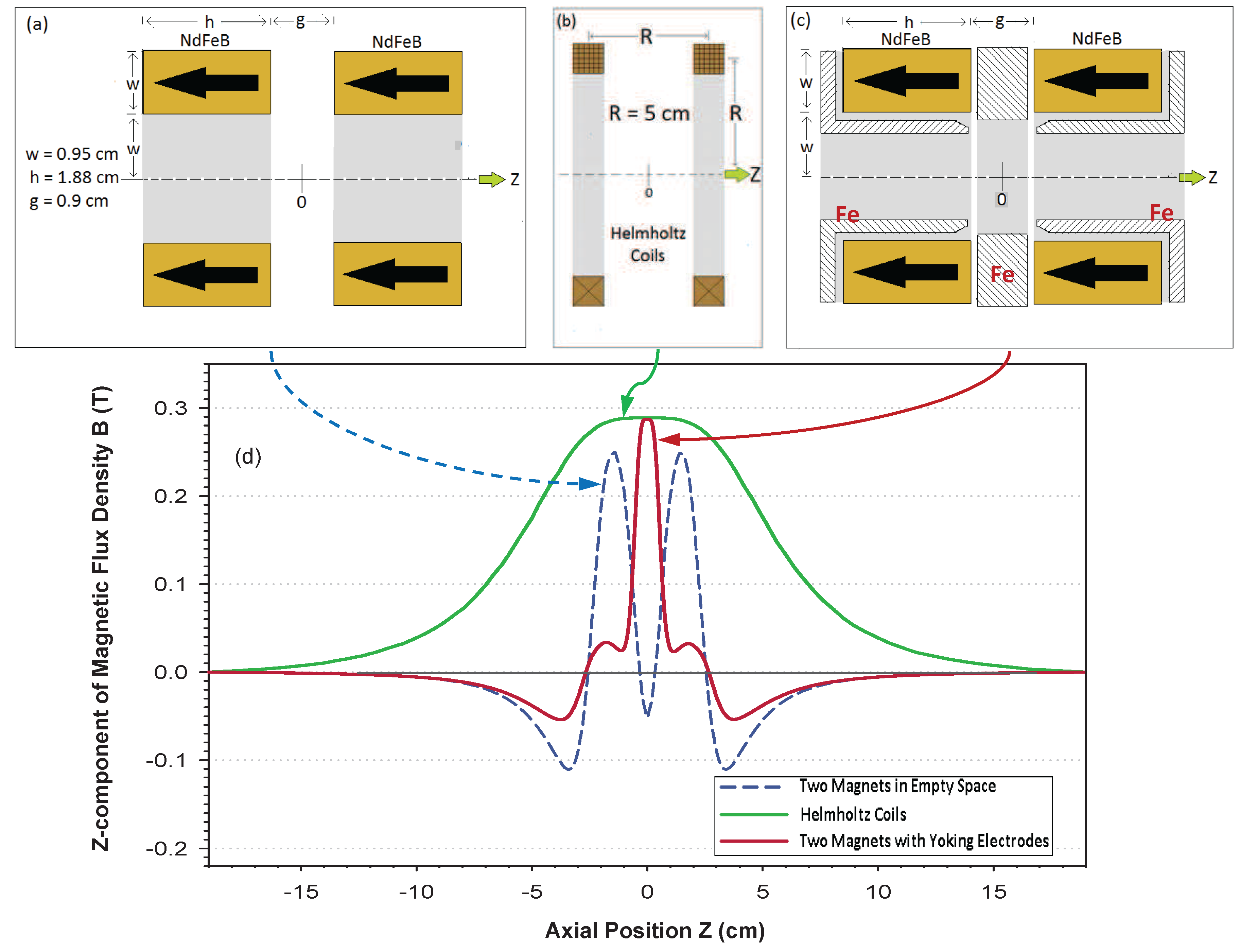
Choosing such a compact architecture does involve a trade-off between improved field homogeneity and smaller size. As an illustration of this,
Figure 2 compares the magnetic field generated by a pair of identical NdFeB annular magnets (axially magnetized), a yoked structure containing the same two NdFeB annular magnets (which produces the field of a unitary Penning trap) and a compact Helmholtz coil system giving the same central field value. To generate the
-T field at the trap center, a pair of Helmholtz coils with a 5-cm radius would require 1650 turns in each coil and would have to carry 10 A of current. Although it gives a more homogeneous field region, such a coil is near the limit of what would be possible to construct and is still over twice the diameter of the unitary Penning trap. For many experiments with highly-charged ions, the uniformity of the magnetic field in the two-magnet, unitary Penning trap is adequate; this is the simplest and most compact architecture involving two permanent magnets. However, with more working space, more sophisticated designs involving additional magnets and electrodes are possible to increase the uniformity and strength of the magnet field.
Designing a Penning trap with embedded rare-earth magnets is computationally intensive, but still feasible with a desktop computer and commercial software packages to implement finite element methods (FEM) for calculating electric and magnetic fields, as well as to solve the equations of motion of charged particles. A useful description of the magnetic structures, for example, can be obtained by FEM simulations using QuickField [
31], with a precision that depends on the mesh coarseness and accuracy of the material data. While there are various ways to produce a strong, uniform magnetic field given no constraints (see, e.g., [
20]), the architecture of a two-magnet unitary Penning trap emphasizes certain features that are useful for atomic physics experiments: (1) a trap sufficiently compact that it can entirely fit into typical commercial vacuum chambers (with the entire system of traps, ion-optic elements and detectors within one meter of the available user space at NIST); (2) on-axis loading and dumping of highly-charged ions; (3) midplane access to allow the interaction of stored ions with laser or atomic beams; and (4) line-of-sight collection of light emitted by the stored ions. Its implementation employs two identical annular magnets made of NdFeB that are coaxial, but separated by a spacing of 9 mm (
g in
Figure 2). These annular magnets are axially magnetized, along their common symmetry axis. To maximize the magnetic field near the midplane (
), the Penning trap ring and endcap electrodes surrounding the magnets are made of soft iron, as shown in
Figure 3a. With the optimal shape and position, these soft iron electrodes absorb the magnetic field lines from each magnet (dashed curve in
Figure 2d) and redirect/concentrate the flux near the midplane (red curve in
Figure 2d and red region in
Figure 3b), thus creating the 0.32-T magnetic field maximum in the central trapping region. Moreover, the design of the electrodes has been carefully chosen such that the trapping potential is well approximated by a quadrupole potential and reasonably harmonic near the center of the trap (without requiring compensation electrodes), although the deviation from a quadrupole potential is considerable for larger
z (see
Figure 3 in [
21]). The anharmonicity of the trap can be specified by estimating the coefficient
from the expansion of the Penning trap potential in the usual fashion [
27,
32]. For this uncompensated trap, using the trap parameters given in [
21], we calculate
. More details of the unitary Penning trap design and construction can be found in [
20,
21]. Typical voltages applied to the trap electrodes can be found in
Table 1 of [
21].
Figure 2.
Comparison of magnetic field sources. (a) Two annular NdFeB magnets with their axial magnetization aligned coaxially; (b) Helmholtz coils of radius cm (the scale is different), each wound with 1650 turns of wire carrying 10 A of current to produce the same central field as a unitary Penning trap; (c) two annular NdFeB magnets yoked by soft iron electrodes to form a unitary Penning trap; and (d) axial component of the magnetic field for these three sources as a function of axial position.
Figure 2.
Comparison of magnetic field sources. (a) Two annular NdFeB magnets with their axial magnetization aligned coaxially; (b) Helmholtz coils of radius cm (the scale is different), each wound with 1650 turns of wire carrying 10 A of current to produce the same central field as a unitary Penning trap; (c) two annular NdFeB magnets yoked by soft iron electrodes to form a unitary Penning trap; and (d) axial component of the magnetic field for these three sources as a function of axial position.
We have demonstrated that a variety of highly-ionized atoms can be stored in the unitary Penning trap illustrated in
Figure 3a, including Ne
, Ne
, Ne
, as well as Ar
, Ar
, Ar
, Ar
and Kr
[
20,
23]. The fully-assembled system shown in
Figure 3a occupies as little as 125
of space. The base pressure of our room-temperature apparatus can be as low as
Pa. Observed decay rates of the number of stored ions indicate that the ion storage lifetime is of order 1 s at base pressure and room temperature, sufficiently long for a variety of spectroscopic experiments. Improvement in the storage lifetime is expected at lower pressures, e.g., in a cryo-cooled apparatus.
Figure 3.
(a) A quarter-cut three-dimensional representation of a two-magnet unitary Penning trap. Ions are injected in pulses along the symmetry axis, with laser and photomultiplier (PMT) access perpendicular; (b) magnetic flux density for the unitary Penning trap illustrated on the left. The magnetic field is produced by two axially-magnetized NdFeB magnets with an internal flux density as high as T. Colors indicate equal magnetic flux density contours (full scale is arbitrarily set at 0.5 T to highlight the trapping region).
Figure 3.
(a) A quarter-cut three-dimensional representation of a two-magnet unitary Penning trap. Ions are injected in pulses along the symmetry axis, with laser and photomultiplier (PMT) access perpendicular; (b) magnetic flux density for the unitary Penning trap illustrated on the left. The magnetic field is produced by two axially-magnetized NdFeB magnets with an internal flux density as high as T. Colors indicate equal magnetic flux density contours (full scale is arbitrarily set at 0.5 T to highlight the trapping region).
3. Capture and Isolation of Highly-Ionized Atoms
Research with highly-ionized atoms, also known as highly-charged ions (HCI), has become more widespread with the development of laboratory facilities, like heavy-ion storage rings [
33], and more compact devices, like the electron-cyclotron resonance (ECR) ion source [
34] and the electron beam ion trap/source (EBIT/EBIS) [
35,
36]. For decades, the pursuit of more precise measurement and control to characterize and explore atomic/subatomic systems has motivated the isolation of ions at low energy in a variety of trap types [
37,
38]. Some of the techniques were honed by generations of experiments studying trapped antiprotons [
39], positrons [
40] and antihydrogen (see [
41] and the references therein). A high-field Penning trap at the TRIUMF TITAN (TRIUMF’s Ion Trap for Atomic and Nuclear science) facility in Canada has been used recently to capture short-lived nuclides [
42]; examples include experiments at the Max-Planck-Institut für Kernphysik (MPI-K) to capture highly-charged ions using Penning traps built with meter-long electrode structures and multi-tesla solenoid magnets [
43,
44].
Capturing ions in a unitary Penning trap has its own challenges as a consequence of the extremely compact geometry: the ion-confinement volume is small for a trap such as that shown in
Figure 3a, and it is made even smaller if the magnetic field is weaker in the outer regions. We are investigating the possibility that other configurations of rare-earth magnets could be useful for constructing unitary Penning traps with larger trapping volumes and higher magnetic field strengths. An important consideration imposed by the ion stability condition is that the trapping well depth of a unitary Penning trap tends to be shallower than the energy distribution of ions coming out of the source. Notwithstanding these constraints, our experiments show that even the simplest unitary Penning trap has sufficient trapping volume to capture ions extracted from a source with about 35 keV of kinetic energy during transport [
20]. The ion storage time is limited not by the imperfections of the trap, but mainly by collisions with the residual gas in the vacuum chamber, which can be improved in a cryo-cooled apparatus. We will briefly describe the main features of the ion capture process in this section, followed by some experiments with the stored ions in subsequent sections.
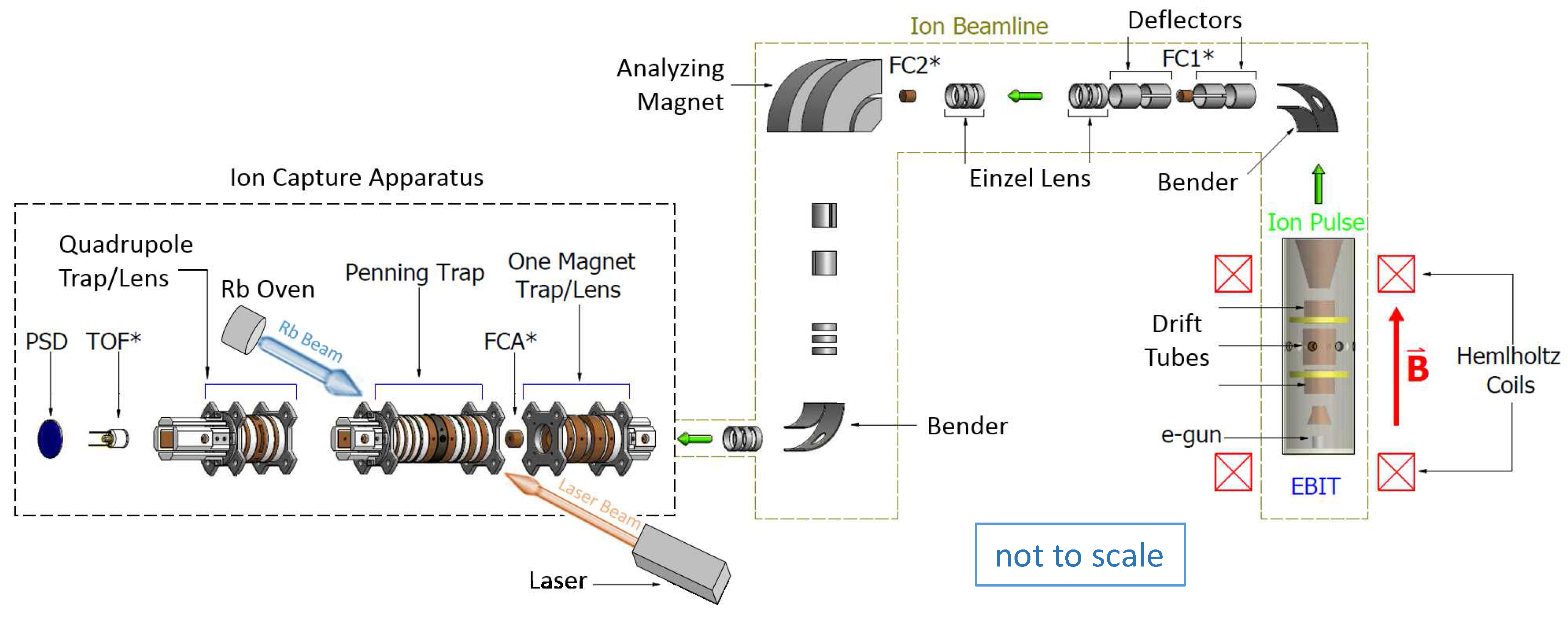
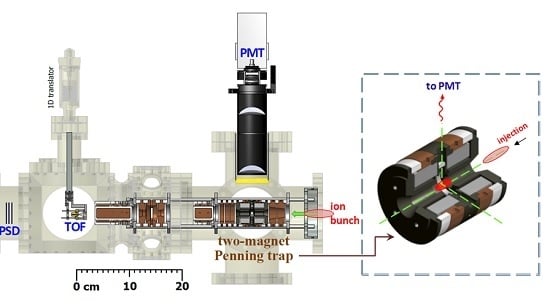
Figure 4 shows a schematic diagram of the setup, highlighting the EBIT, the ion beamline and the ion capture apparatus. The EBIT produces highly-charged ions by successive electron impact ionization. Various charge states are trapped in the energetic, intense electron beam of the EBIT; an ion-extraction beamline with an analyzing magnet can be used to isolate a single charge state of interest [
45]. More detailed descriptions of the EBIT and ion beamline at NIST can be found in [
46] and the references therein. It is important to emphasize here that electron impact ionization in an EBIT is well-controlled. An accelerated electron beam with a very narrow energy distribution is used, and a narrow beam-waist results from compression by a ≈ 3-T magnetic field, yielding very high current densities. The positively-charged ions are bound to the negative space-charge of the intense electron beam and undergo multiple collisions with the energetic electrons, which ionize them to successively higher charge states. The highest charge state attainable depends on the electron beam energy, which is set by the user.
Figure 4.
Overview of the experimental setup. The ion source is an electron beam ion trap (EBIT) (far right). The ion extraction beamline has an analyzing magnet for charge state selection and several Faraday cups (FC) to monitor the ions along the beamline. A unitary Penning trap has been installed at the end of the beamline to capture extracted ions. An atomic oven is used to send a Rb beam into the Penning trap where the atoms are excited by a laser. A time-of-flight (TOF) detector and a position-sensitive detector (PSD) are used to analyze the captured ions. Broken lines represent the boundary of evacuated space. Beamline elements labeled with an asterisk (*) are retractable.
Figure 4.
Overview of the experimental setup. The ion source is an electron beam ion trap (EBIT) (far right). The ion extraction beamline has an analyzing magnet for charge state selection and several Faraday cups (FC) to monitor the ions along the beamline. A unitary Penning trap has been installed at the end of the beamline to capture extracted ions. An atomic oven is used to send a Rb beam into the Penning trap where the atoms are excited by a laser. A time-of-flight (TOF) detector and a position-sensitive detector (PSD) are used to analyze the captured ions. Broken lines represent the boundary of evacuated space. Beamline elements labeled with an asterisk (*) are retractable.
3.1. Extraction of Ion Bunches
A unitary Penning trap, such as shown in
Figure 3, has a small confinement volume with a shallow trapping well depth. Moreover, the hole of the entrance endcap is only 8 mm in diameter. To capture ions coming out of a source with
keV kinetic energy (expected in the production of highly-ionized atoms), it would be ideal to compress the phase-space volume (coordinates, velocities) of the extracted ions as tightly as possible during transit to the capture trap, making ion bunches that can be phased with the pulse cycles of the trapping and detection process. Therefore, the EBIT is operated in a pulsed extraction mode.
A full schematic diagram and discussion of the ion capture process are provided in [
21]. To make an ion bunch, a fast electrical pulse (rise time ≈ 50 ns) is applied on one of the electrodes of the EBIT, ejecting the ions rapidly into the beamline. As shown in
Figure 4, the extracted ions undergo a 90-degree bend through an electrostatic bender and are further guided by the horizontal beamline to an analyzing magnet, where the different ionization stages are dispersed to select a specific charge state. The eight meter-long beamline contains various ion-optic elements for adjustments in alignment and ion pulse conditioning. In addition, the ion capture apparatus has some beam-conditioning structures that can be used during run-time optimization to minimize the width of the ion time-of-flight signal, as well as to maximize the number of ions captured.
3.2. Energy Distribution
Low temperature is ideal for certain measurements and applications, but it is particularly challenging to attain for highly-ionized atoms. Familiar cooling techniques involving the mechanical effects of coherent light (lasers) on neutral atoms [
47] and singly-ionized atoms [
48] are not readily applicable to highly-charged ions, in part because suitable transition energies are much higher than existing lasers can provide. Moreover, sources of highly-ionized atoms generally operate at much higher temperatures (
K) than the atomic ovens used to provide neutral atomic beams; in an EBIT, the ion energy distribution is of order
eV. Evaporative cooling of highly-charged ions stored in a Penning trap has been demonstrated recently [
49]. Highly-charged Ar ions have been stopped and sympathetically cooled by an ensemble of laser-cooled Be
ions, forming a multi-species Coulomb crystal in a linear radio-frequency (RF) trap [
50]. However, for studying transient phenomena, the application of a cooling technique may be limited by the cooling time constant, which can exceed the time scale of interest; an example is the study of the radiative decay of metastable states, as discussed in the next section. In the method used to inject highly-ionized atoms into a unitary Penning trap, a reduction in the temperature of the captured ions by roughly two orders of magnitude was attained rapidly without any active mechanism in the ion capture trap.
This fast mechanism is complex and not fully understood. It is likely that phase space compression is involved, since both temperature and trapping-volume reduction are attained with at least 10-times more ions than expected in the lowest 10 eV (the stored-ion temperature in energy units, kT) of a Boltzmann distribution with kT
eV (EBIT temperature). Energy is not conserved in this process due to particle loss as the ion bunch is focused and guided along the beamline; in fact, only one in 10 ions coming from the first electrostatic bender survive the transport to the analyzing magnet. There may also be further energy transfer/dissipation, via ion-ion collisions, from the selected ions to the rejected ion charge states as they enter the analyzing magnet. Phase space compression is necessary, but not sufficient for efficient trapping of an ion bunch. To minimize the energy of stored ions after an ion bunch is captured, the timing of the time-varying electric fields used to close the trap and the details of the deceleration process are important, as discussed in [
21]. Experimentally, we employ an eight-meter beamline with various ion-optics and two detectors—a time-of-flight (TOF) detector and a position-sensitive detector (PSD)—to facilitate phase-space compression of an ion bunch, so that it enters the trap as close to the trap axis as possible, with the narrowest velocity distribution attainable by tuning.
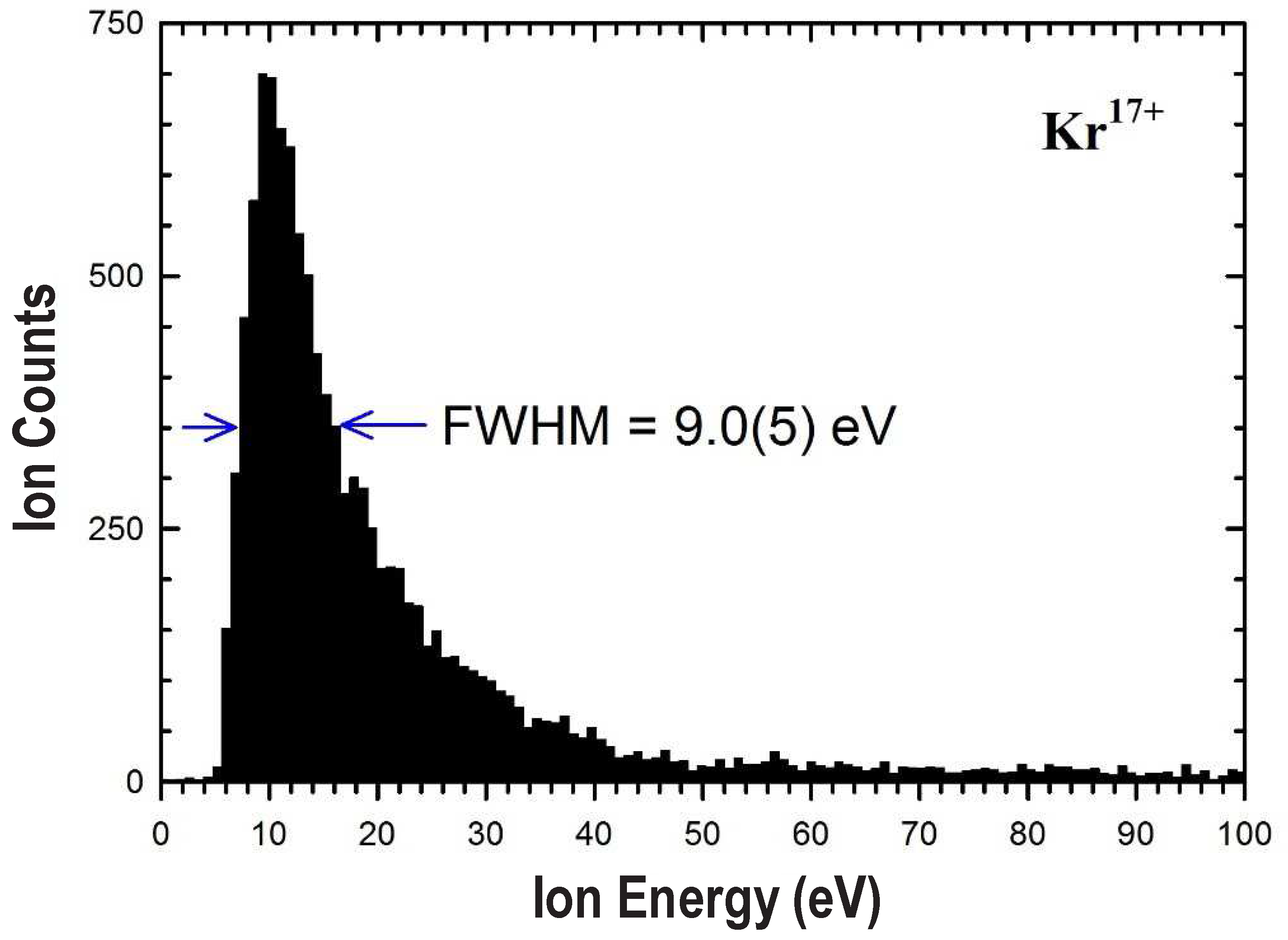
Figure 5.
Observed energy distribution of Kr ions escaping the confinement barrier along the trap axis as the voltage applied on the Penning trap ring electrode is ramped linearly to shallower well depths. The energy width at half-maximum is 9.0(5) eV. The measurement was made after 1 ms of storage.
Figure 5.
Observed energy distribution of Kr ions escaping the confinement barrier along the trap axis as the voltage applied on the Penning trap ring electrode is ramped linearly to shallower well depths. The energy width at half-maximum is 9.0(5) eV. The measurement was made after 1 ms of storage.
Figure 5 shows the energy distribution of Kr
ions measured after 1 ms of storage in a unitary Penning trap. This measurement employed an over-the-barrier technique, wherein the voltage applied on the Penning trap ring electrode is ramped up slowly, so that the axial-confinement well depth decreases gradually, allowing successively slower ions to escape over the known electrical potential barrier. The escaping ions for each ring voltage are guided to a time-of-flight (TOF) detector. The energy distribution has a full width at half maximum (FWHM) of 9.0 ± 0.5 eV, which is roughly a factor of
narrower than the energy spread of the ions extracted from the EBIT prior to beamline tuning. Although the FWHM for Kr
is about 64% larger than the FWHM of 5.5 ± 0.5 eV measured for Ar
[
21], we note that the FWHM energy width gives an upper limit for the ion temperature, since it does not account for the heating up of the escaping ions due to the conversion of the space-charge potential energy [
39], which increases with charge state. Thus, Kr
ions extracted from the EBIT and transported with ∼ 49 keV kinetic energy have been decelerated and captured rapidly in a compact Penning trap with an energy distribution of about 9 eV. With only 1 ms of ion storage time, this measurement is an estimate of the initial energy distribution, before any active cooling scheme has been implemented. Colder ion temperatures may be attainable by applying evaporative or sympathetic cooling techniques if sufficient time is available.
4. Electron Capture
Charge exchange with the background gas, also known as electron capture, is one of the loss mechanisms for highly-ionized atoms isolated in a trap. For a room-temperature apparatus, the electron-capture rate may limit the available time for studying or manipulating the ions of interest; for example, the time constant of a cooling technique must be much shorter than the charge-exchange rate to be effective in lowering the ion temperature appreciably.
Charge exchange has been studied extensively at high energies, because of its importance in astrophysics and plasma diagnostics. On the other hand, there is far less information available for electron capture at low energy, with the bulk of the experimental data coming from merged-beams experiments [
51,
52]. Understanding the low-energy regime is likely to become important for proposed applications, including atomic clock development, quantum information processing and precise tests of fundamental theory. For radiative-decay lifetime measurements using the stored-ion technique discussed in the next section, electron capture poses a systematic effect that must be evaluated to attain the best outcome. Various gases have been injected at controlled pressures into our ion capture apparatus to carefully study the charge exchange with fully-ionized neon (Ne
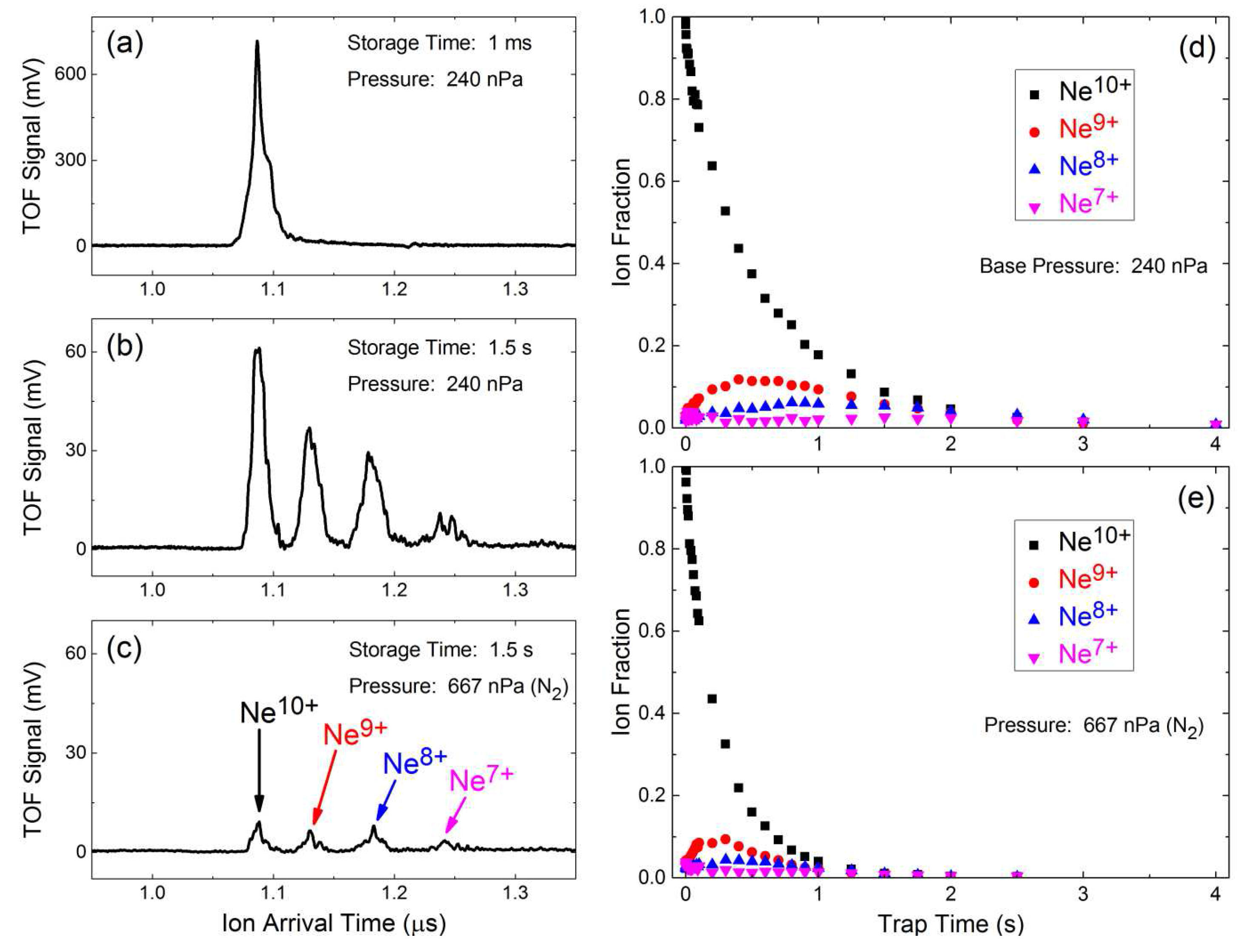
) isolated at low energy. The composition of a stored ion cloud is analyzed by pulsed ejection to the TOF detector, generating individual peaks for each ion species, with higher charge states arriving earlier.
At the base pressure (no injected gas), the TOF signal in
Figure 6a for a very short storage time of 1.0 ms shows that the bare neon nuclei are essentially unaffected by their storage in the Penning trap. If, however, the storage time is increased to 1.5 s, as shown in
Figure 6b, the charge state evolves, with Ne
, Ne
and Ne
all also being detected.
Figure 6c illustrates that when a background gas is injected into the trap, the total number of ions remaining in the trap after 1.5 s of storage is reduced, and the charge-exchange rates are also affected. Finally,
Figure 6d,e compares the evolution of the charge states for the base pressure (240 nPa) and 667 nPa of N
. Preliminary analysis of these data shows evidence of double-electron capture [
22], with further analysis underway.
Another experiment of interest is the production of one-electron ions in Rydberg states. For a certain range of nuclear charge Z, transitions between neighboring Rydberg states are in the optical domain, which can be measured precisely with an optical frequency comb. In particular, high angular momentum states are potentially useful for measuring fundamental constants, because the overlap of the electron wavefunction with the nucleus is negligible, and thus, the theory is greatly simplified for the extraction of fundamental constants. We are currently working with the experimental setup illustrated in
Figure 4, which incorporates a rubidium oven [
53] that can be used to inject an atomic beam through one of the holes in the trap midplane. The Rb atoms will be laser-excited to a Rydberg state so that the loosely-bound valence electron can be captured by a Ne
ion into a Rydberg state.
Figure 6.
Observed electron capture by fully-ionized neon stored in a unitary Penning trap. (a) The TOF signal of Ne within 1 ms of capture; (b) the TOF signal after 1.5 s of storage time at base pressure; (c) the TOF signal after 1.5 s of confinement in 667 nPa of nitrogen; (d) the charge state evolution at base pressure; and (e) the charge state evolution in 667 nPa of nitrogen.
Figure 6.
Observed electron capture by fully-ionized neon stored in a unitary Penning trap. (a) The TOF signal of Ne within 1 ms of capture; (b) the TOF signal after 1.5 s of storage time at base pressure; (c) the TOF signal after 1.5 s of confinement in 667 nPa of nitrogen; (d) the charge state evolution at base pressure; and (e) the charge state evolution in 667 nPa of nitrogen.
5. Radiative Lifetime of Metastable States
Applications of metastable states and forbidden transitions abound in various fields, including frequency-standard metrology, determination of fundamental constants, tests of the standard model and astrophysics (see the references in [
23]). Theoretical studies have found certain metastable states in highly-ionized atoms to be well suited for next-generation atomic clocks or quantum information experiments. Some are predicted to have very long lifetimes, but the uncertainties are large. The arsenal of tools for measuring radiative-decay lifetimes has grown, but there are not many results at the one percent level of precision [
54]. A unitary Penning trap offers a different method with the potential for precise measurements on metastable atomic states [
23].
The use of a unitary Penning trap to isolate ions for measuring radiative-decay lifetimes is briefly described here. This method has been demonstrated thoroughly with an improved lifetime determination for the metastable 3d D level in a Kr atom, which decays to the ground state 3d D, essentially via a magnetic-dipole (M1) transition. Interestingly, the ground configuration for the remaining 19 electrons of Kr is a closed shell [Ar] with one valence electron in a 3d orbital, an example of a configuration crossing or violation of the Madelung ordering rule in the K-like isoelectronic sequence.
Krypton gas is injected into the EBIT to produce Kr
ions by electron-impact ionization. Collisions also populate the upper fine-structure level
3d D
. An analyzing magnet selects the Kr
ions from the mixture of charge states extracted from the EBIT. The selected ions are guided to the ion capture apparatus (
Figure 7). The transit time from the EBIT to the unitary Penning trap is ≈ 22 μs, much shorter than the radiative decay lifetime of the
3d D
level. Under optimal conditions, a single-peaked ion pulse of width
ns is injected into the unitary Penning trap through the 8 mm-diameter hole of the entrance endcap. Within 1 ms after capture, the residual energy distribution of the stored ions is about 9 eV (roughly
-times lower than in the ion source) without any active cooling scheme [
21], reducing certain systematic effects.
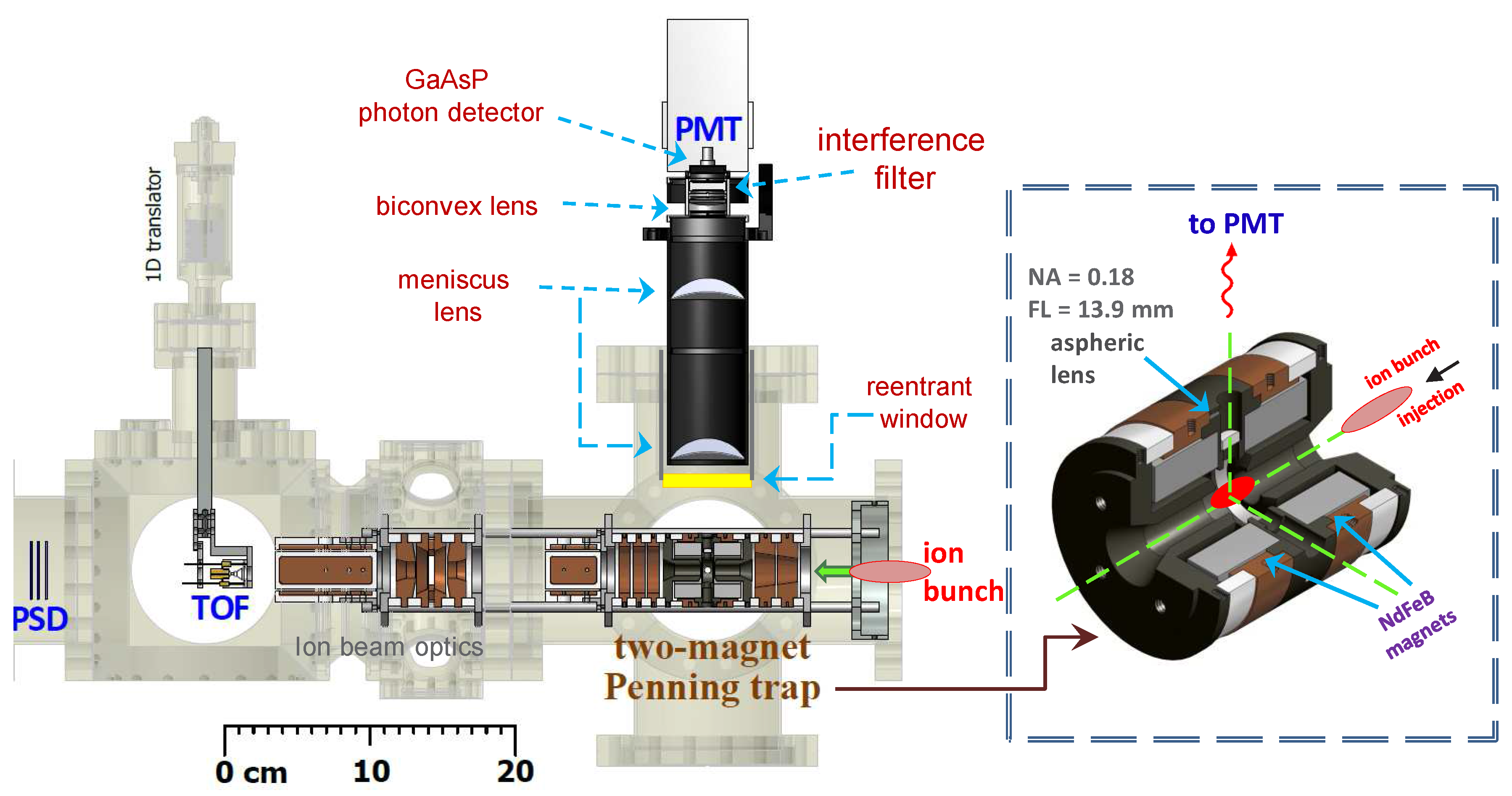
Figure 7.
Schematic diagram for the detection of fluorescence from Kr ions isolated in a unitary Penning trap (centered on the six-way cross). Ion bunches are periodically injected into the trap from the right. An aspheric lens collects photons emitted by the captured ions (see the inset in the three-dimensional perspective). Above the reentrant window, an optical setup with a narrow bandpass filter relays light to a photon detector. At the end of each data acquisition cycle, stored ions are counted and analyzed by ejection to a TOF detector. NA, numerical aperture; FL, focal length .
Figure 7.
Schematic diagram for the detection of fluorescence from Kr ions isolated in a unitary Penning trap (centered on the six-way cross). Ion bunches are periodically injected into the trap from the right. An aspheric lens collects photons emitted by the captured ions (see the inset in the three-dimensional perspective). Above the reentrant window, an optical setup with a narrow bandpass filter relays light to a photon detector. At the end of each data acquisition cycle, stored ions are counted and analyzed by ejection to a TOF detector. NA, numerical aperture; FL, focal length .
Figure 7 highlights the optical setup used for the collection of photons emitted by ions isolated in a unitary Penning trap. For Kr
ions, when the
3d D
level undergoes a magnetic dipole (M1) transition to the
3d D
ground state, a photon of wavelength 637 nm is emitted. An aspheric lens with a focal length (FL) of 13.9 mm is embedded in the ring electrode to collect a small amount of the 637 nm fluorescence, with an effective numerical aperture (NA) of 0.18 at a distance of 13.2 mm above the trap center. Increasing the NA would require enlarging the mounting hole in the Penning trap ring electrode, at the risk of perturbing the trapping fields. Outside the vacuum chamber, the collected light is relayed to a photomultiplier (PMT) via a lens system consisting of (1) two identical meniscus lenses (FL = 100 mm, 50.8-mm diameter), separated by 110 mm and (2) a biconvex lens (FL = 50 mm, 25.4-mm diameter, separated by 71 mm from the previous lens), which focuses the light onto the 5-mm active diameter of the photon detector via (3) an interference filter (central
nm with a bandpass FWHM = 10 nm). The lens system is mounted on a three-dimensional translator for optimization of light collection. Typically, the first meniscus lens is positioned about 72.5 mm from the center of the trap. For photon counting, we use a commercial system (Hamamatsu H7421-40) based on a GaAsP avalanche photodiode (APD) operated in a Geiger mode from 300 nm–720 nm, with a peak quantum efficiency of 40% at 580 nm [
31]. Two photons separated by 70 ns can be resolved. The dark count is typically 100 s
when the APD is operated at room temperature down to
. For our measurements, the APD is cooled to
with a thermoelectric (Peltier) cooler, reducing the
in situ dark counts to a rate of
s
.
PMT counts from the ion fluorescence are binned into 1-ms intervals by a fast multichannel scaler, which is gated to start synchronously with the ion capture. After accumulating PMT counts for a time equivalent to several decay lifetimes, we dump the ions, load a new excited population from the EBIT and repeat to build up statistics.
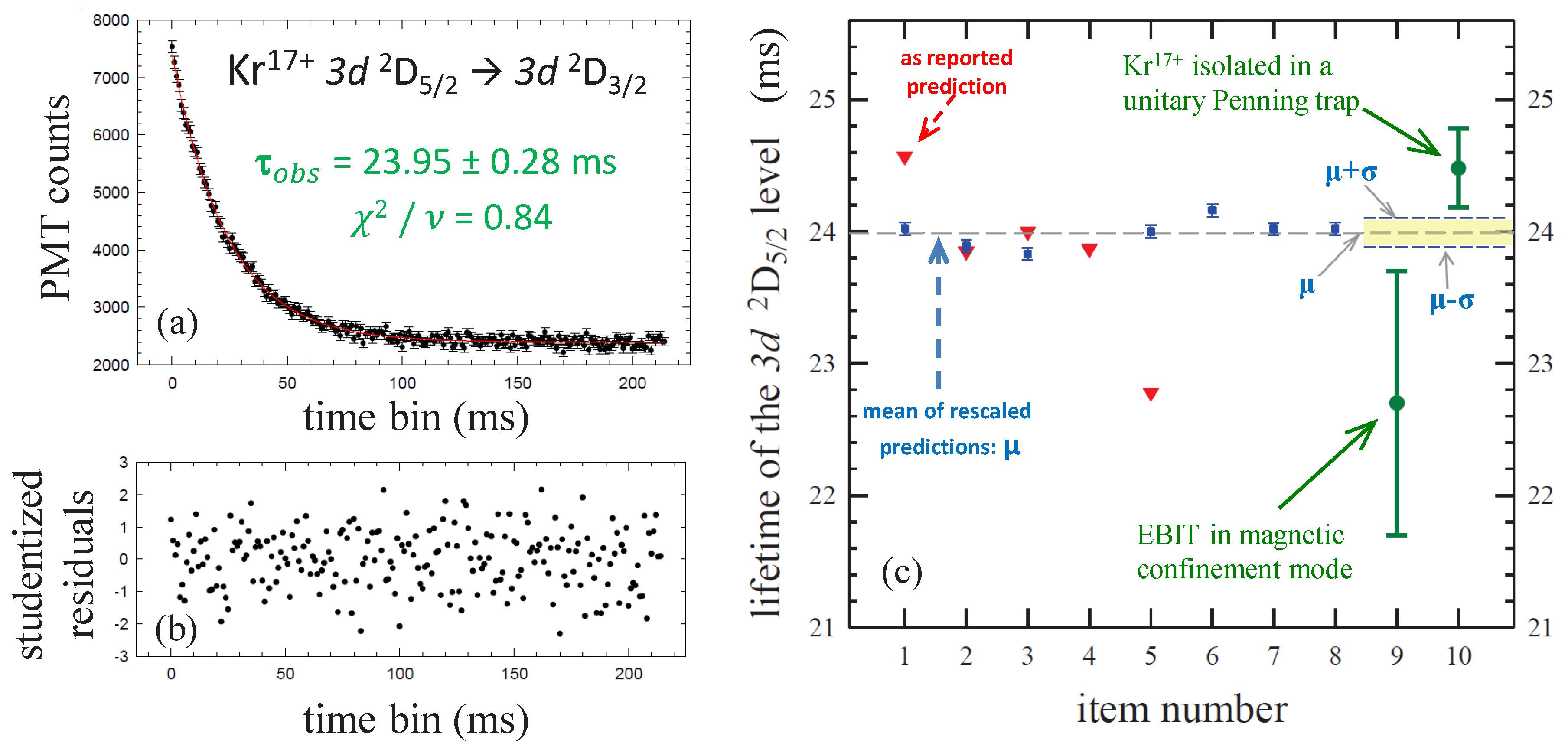
Figure 8a shows a sample of time-averaged PMT data. The decay fits well to a single exponential decay curve
, where the constant offset
c is generated by the dark count rate of the PMT. Related measurements of HCI lifetimes performed inside an EBIT (e.g., [
55]) rely on more complex curve fitting to account for the EBIT environment. In contrast, with extracted ions, the single exponential fit proves sufficient, as indicated by the chi-squared and distribution of residuals in
Figure 8b.
Figure 8.
(
a) Photomultiplier signal from Kr
ions captured in a trap with an ambient pressure of
Pa (
torr); the red line is the best fit to a single-exponential decay curve
; (
b) Studentized residuals
for the best fit; (
c) comparison of measurements (circle) with theoretical values, as reported (triangle) or adjusted (square).
Table 1 lists the sources of the items plotted in (
c). Adapted from
Figure 2 and
Figure 3 in [
23].
Figure 8.
(
a) Photomultiplier signal from Kr
ions captured in a trap with an ambient pressure of
Pa (
torr); the red line is the best fit to a single-exponential decay curve
; (
b) Studentized residuals
for the best fit; (
c) comparison of measurements (circle) with theoretical values, as reported (triangle) or adjusted (square).
Table 1 lists the sources of the items plotted in (
c). Adapted from
Figure 2 and
Figure 3 in [
23].
At the base pressure of the apparatus (
Pa), the measured lifetime of the Kr
3d D
level is
ms. This result does not take into account known systematic effects, in particular non-radiative processes that reduce the measured lifetime. A Stern–Volmer analysis corrects for pressure-dependent systematics, chief among which are collisional quenching of the metastable state and electron capture from background gas atoms. A precision leak valve allows the introduction of a controlled partial pressure of N
gas. The fluorescence decay rate (
Figure 8a) is measured at various pressure values and extrapolated back to a zero-pressure result.
Table 1.
Calculations and measurements for the lifetime
τ of the Kr
3d D
level. Data from
Table 1 in [
23].
Table 1.
Calculations and measurements for the lifetime τ of the Kr 3d D level. Data from Table 1 in [23].
| Item | Source/Method | λ (nm) | τ (ms) |
|---|
| | Calculation: | |
| 1 | [56] Dirac–Fock (single configuration approximation) | 642.0 | |
| | | adjusted | |
| 2 | [57] Relativistic Hartree–Fock | 636.82 | |
| | | adjusted | |
| 3 | [58] Cowan Code | 638.7 | |
| | | adjusted | |
| 4 | [59] Relativistic Hartree–Fock | – | |
| 5 | [60] Relativistic quantum-defect orbital | 626.2 | 22.78 |
| | | adjusted | |
| 6 | [61] Flexible Atomic Code | adjusted | |
| 7 | [62] Lowest-order relativistic many-body perturbation theory | adjusted | |
| 8 | [23] GRASP2K, a general-purpose relativistic atomic structure package | adjusted | |
| | Measurement: | |
| 9 | [59] Intra-EBIT experiment (magnetic confinement mode) | |
| 10 | [23] Isolation of Kr ions in a unitary Penning trap | |
Pressure-independent systematics (for example, a decay in collected fluorescence due to ion orbit instability) are studied through numerical modeling and simulation. The light collection efficiency is a function of the emitter location. Since the stored ions are distributed around the center of the trap, a change in ion cloud size can change the overall light collection slightly. Due to the dynamical equilibrium for radial confinement in a Penning trap, the ion cloud expands if there is a loss of angular momentum (arising from collisions with background gas atoms, for example). The low kinetic energy of the stored ions keeps such motional dependence small. We use the codes EQUILSOR, to model the spatial distribution of the ion cloud, and CPO (a charged particle optics software) [
31], to simulate the ion trajectories as they are ejected to the TOF detector. Model computations are checked against TOF measurements. Zemax [
31] software is then used to trace rays through our collection optics and to generate an optical transfer function relating the fluorescence collection efficiency to the ion position in the trap. The optical transfer function includes a measured correction for the angular dependence of the interference filter. By combining these simulations, we place bounds on the systematic errors related to experimental uncertainty in the initial size and metastable fraction of the ion cloud, along with possible dynamic effects, such as ion cloud expansion during the measurement period. In principle, the M1 transition rate is also perturbed by the presence of the electric and magnetic fields of the Penning trap, mainly via a shift in the transition wavelength. However, the correction is much smaller than the 1% level of measurement precision and, thus, is not included. Accounting for these small non-radiative losses, we determined that the
3d D
level has a radiative lifetime of
, slightly larger than the
observed lifetime in
Figure 8a.
Figure 8c compares this measurement of the Kr
3d D
lifetime with other works.
Table 1 enumerates theoretical predictions (plotted as squares and triangles) and experimental results (plotted as circles). In addition to listing calculated lifetimes as reported by each source, we also give the adjusted predictions based on a rescaling with the more precise Ritz wavelength for this transition if the wavelength used in the calculation is also provided by the source. Our experimental value obtained with a unitary Penning trap agrees well with various adjusted predictions at the one-percent level. The remarkable convergence of various theoretical methods within 0.5% for the
3d orbital when scaled to the same transition wavelength is discussed in [
23].
The only previous measurement of the Kr
3d D
lifetime was made in an EBIT operated in the magnetic confinement mode, wherein the electron beam is switched off momentarily to allow observation of the fluorescence without electron impact excitation [
59]. Our measurement with Kr
ions isolated in a unitary Penning trap is
ms longer than this previous measurement inside an EBIT. This mild discrepancy is 1.7-times the combined standard error (
). The technique of capturing Kr
ions in a unitary Penning trap yields three-times smaller uncertainty than the intra-EBIT measurement. An important difference is that thermal radiation from the EBIT electron gun drops to very low levels in the ion capture apparatus and, therefore, was not a significant contribution to the background noise; in contrast, thermal radiation was reported to be significant for the intra-EBIT measurement [
59]. Another benefit of isolating the Kr
ions in a unitary Penning trap is that the ions are stored at low energy (
eV) within 1 ms after capture [
21], which contributes to the reduction of systematic uncertainties associated with the ion motions. Moreover, since only one ion species is captured, complications that may arise from other charge states produced inside the ion source are not a concern. In brief, forbidden transitions can be studied precisely in a unitary Penning trap. This technique can be extended to other HCI lifetime measurements. Metastable states of highly-ionized atoms with forbidden transitions in the infrared region are of interest in planned space-telescope missions to study the first star formation and the age of re-ionization. In the apparatus shown in
Figure 7, the photon collection efficiency of order 1% for this trap tends to limit the signal-to-noise ratio and, hence, requires a long data acquisition time to achieve reasonable statistical uncertainty. Possibilities to improve the fluorescence collection include utilizing optical interference filters with higher transmission, designing a specialized unitary Penning trap and transferring the trapped ions to an RF trap with larger optical access.
6. A Miniature Electron Beam Ion Source/Trap
Electron beam ion sources and traps typically employ large superconducting coils for generating the magnetic field required for the adiabatic compression of the electron beam waist to attain the high current densities necessary for the production of very high charge states. In some applications, mobility is desirable; in addition, space allocation and operating cost may be constraining factors. Compact ion sources that require less maintenance have been developed for applications requiring ions with midscale ionization thresholds. The first step in this direction was the replacement of the liquid helium-cooled superconducting coils with a liquid nitrogen-cooled solenoid [
64]. High-T
Helmholtz coils have also been used successfully to build a low-energy EBIT [
65]. The most compact devices are attainable by the replacement of the current-carrying coils with rare-earth permanent magnets. Several compact EBIS/EBITs have been constructed employing rare-earth permanent magnets in various configurations for spectroscopy [
66,
67,
68].
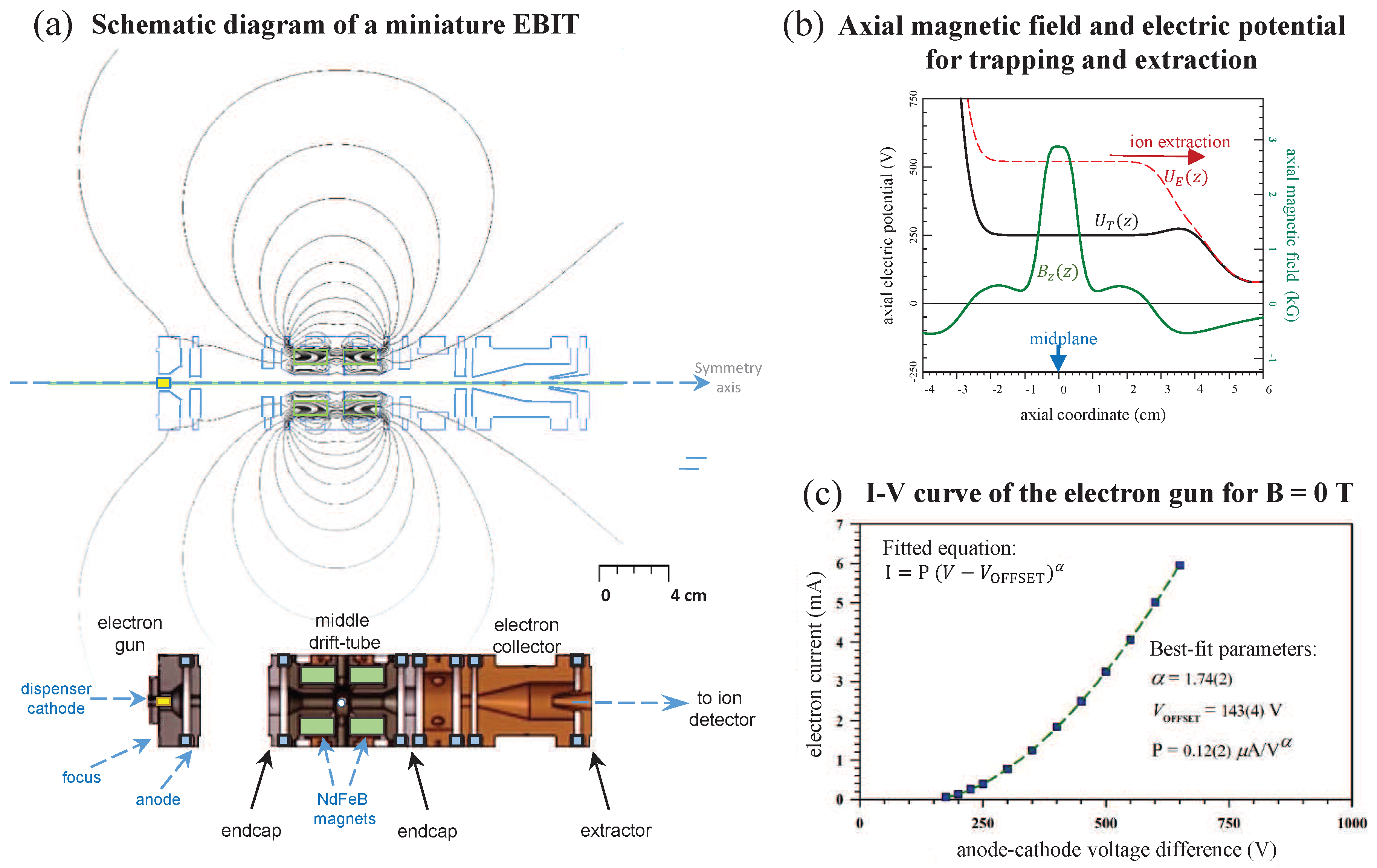
Figure 9.
A prototype for studying a miniature EBIT with ion extraction. The schematic diagram (a) shows an electron gun that can be repositioned relative to the drift tube assembly. The focus and anode of the electron gun are made of soft iron. The on-axis magnetic field (green line) and electric potential in the drift tube region for ion trapping (black line) and pulsed extraction (red dashed line) are shown in (b). The I-V curve of the electron gun (c) was measured independently with a Faraday cup biased at 600 V adjoining the anode, with a fit to the data as shown.
Figure 9.
A prototype for studying a miniature EBIT with ion extraction. The schematic diagram (a) shows an electron gun that can be repositioned relative to the drift tube assembly. The focus and anode of the electron gun are made of soft iron. The on-axis magnetic field (green line) and electric potential in the drift tube region for ion trapping (black line) and pulsed extraction (red dashed line) are shown in (b). The I-V curve of the electron gun (c) was measured independently with a Faraday cup biased at 600 V adjoining the anode, with a fit to the data as shown.
Our goal is to develop a miniature EBIT using rare-earth magnets in a configuration that serves also as an ion source for integration with an ion-capture apparatus, such as shown in
Figure 7. Many of the ions of interest have relatively low ionization thresholds (
keV), which are accessible to a compact EBIT. We have constructed a prototype to investigate the operating conditions of a miniature EBIT, wherein the middle drift tube has an architecture similar to a unitary Penning trap [
69].
Figure 9a shows the basic components. The electrodes of the two-magnet unitary Penning trap [
20] are shorted together to form the longer, middle drift tube of the EBIT. Two coaxial, annular disks, one on each side of this drift tube, serve as endcap electrodes that can be electrically biased at higher potentials for axial confinement of the ions, as illustrated by the black solid-line plot in
Figure 9b. Sintered NdFeB magnets are used to maximize the magnetic field. The magnetic field generated by the two NdFeB magnets embedded in the drift tube region (green solid-line plot in
Figure 9b) extends roughly over a centimeter, with a peak field strength of about 0.3 T at the midplane. A gas injected through one of the holes in the midplane serves as the initial source of atoms for electron impact ionization to produce the highly-ionized atoms to be studied. To extract these ions, the electrical potential of the central drift tube is rapidly pulsed higher than the voltage on the downstream endcap electrode (for example, see the red dashed-line plot in
Figure 9b).
The electron gun is constructed with a barium-tungsten dispenser cathode (5-mm diameter) rated for 3–5 A/cm
continuous thermionic emission of electrons in the operating temperature range of
C–
C; the focus and anode electrodes are made of soft iron to provide some magnetic shielding. The perveance can be obtained from the I-V curve shown in
Figure 9c and is approximately
for beam energies greater than 350 eV (allowing the exponent to vary as a free fitting parameter gives a slightly different value, as displayed in
Figure 9c). The electron gun assembly is mounted on a translation stage to allow variation of the distance between the cathode and the drift tube assembly. The electron beam passing through the drift tubes terminates in the electron collector, which is cooled by a thermo-electric chiller. Adjoining the collector is an extraction electrode to allow extraction of highly-ionized atoms. The apparatus for testing this miniature EBIT (miniEBIT) is shown in
Figure 10a; a more detailed description can be found in [
69].
In proof-of-principle experiments, both helium and neon were injected into the miniature EBIT of
Figure 9, and the resulting ions were extracted to a TOF detector. Examples of the TOF signals for an electron beam current of
mA accelerated to 645 eV can be seen in
Figure 10b,c. This simple prototype can be modified to improve performance. For example, the flat endcap electrodes can be replaced with drift tubes with additional magnets used to extend the high field region. More ion beam optics and secondary traps downstream from the miniEBIT can be added to allow for the re-capture and study of individual ion charge states. In particular, some electrodes are being redesigned to allow better focusing of the electron beam into the miniEBIT drift-tube region. To provide better control over the extracted ion bunch, the ion-beam optics will include one or more einzel lenses, as well as a charge-to-mass analyzer for selecting the charge state of interest.
We plan to install a compact Penning trap [
20] downstream to allow the isolation and further study of highly-ionized atoms. Similar to the current setup at the NIST EBIT (
Figure 4), a rubidium oven beam apparatus [
53] will also be added. This will be placed orthogonal to the ion path to allow the injection of the rubidium beam into the center of the re-capture Penning trap. A two- [
70] or three-laser excitation scheme [
71] can be used to excite the rubidium atoms to a Rydberg state. These Rydberg rubidium atoms will be injected into the Penning trap, where they will undergo resonant charge exchange [
72] with trapped, fully-ionized helium and neon ions to form one-electron ions in Rydberg states. Transitions between such high angular momentum states will be studied with the goal of comparing measurements with calculated energy levels, which are very precisely known, offering the possibility of a different determination of the Rydberg constant [
18,
19].
Figure 10.
(a) Schematic diagram of the apparatus for testing a miniature EBIT prototype. A retractable Faraday cup or a time-of-flight (TOF) detector can be used to analyze the extracted ion pulse. TOF ion signals are shown for (b) helium gas injection and (c) neon gas injection. The highest peak in (c) is likely due to He from an earlier experiment, but may include other background gas ions of the same charge-to-mass ratio.
Figure 10.
(a) Schematic diagram of the apparatus for testing a miniature EBIT prototype. A retractable Faraday cup or a time-of-flight (TOF) detector can be used to analyze the extracted ion pulse. TOF ion signals are shown for (b) helium gas injection and (c) neon gas injection. The highest peak in (c) is likely due to He from an earlier experiment, but may include other background gas ions of the same charge-to-mass ratio.
Other avenues of study involve metastable states of interest in developing novel quantum information systems or ultra-stable atomic clocks. Some of the proposed metastable states have very long lifetimes (e.g., see [
13]). However, the storage lifetime of ions isolated in a Penning trap is observed to be inversely proportional to the background gas pressure and is typically limited to roughly 1 s at the pressures achievable in a room-temperature ultra-high vacuum (UHV) system [
20]. To enable the study of long-lived metastable states, as well as to facilitate frequency comb-based spectroscopy, we plan to increase the ion-storage lifetime by incorporating a Gifford-McMahon-type cryocooler into the apparatus. This will be used to cool the re-capture trap, substantially lowering the background pressure inside the trap. Provided that possible instabilities due to trap imperfections are compensated, the ion storage lifetime can exceed 10 days in an apparatus which is cryo-cooled near four Kelvin, assuming conservatively that the resulting UHV pressure would be a million times better than attained in the system illustrated in
Figure 4.