Influence of Virtual Photon Process on the Generation of Squeezed Light from Atoms in an Optical Cavity
Abstract
:1. Introduction
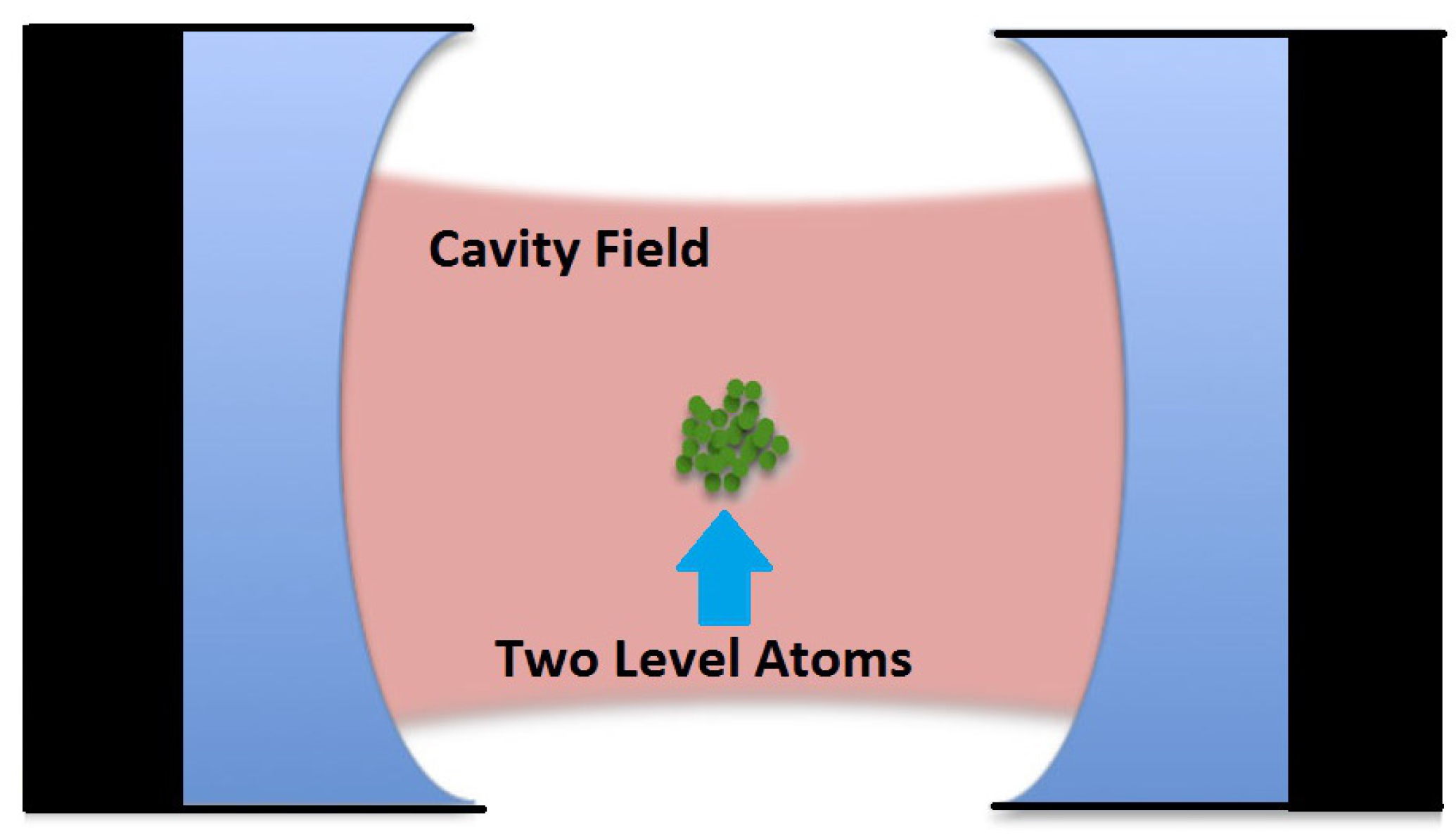
2. The Model
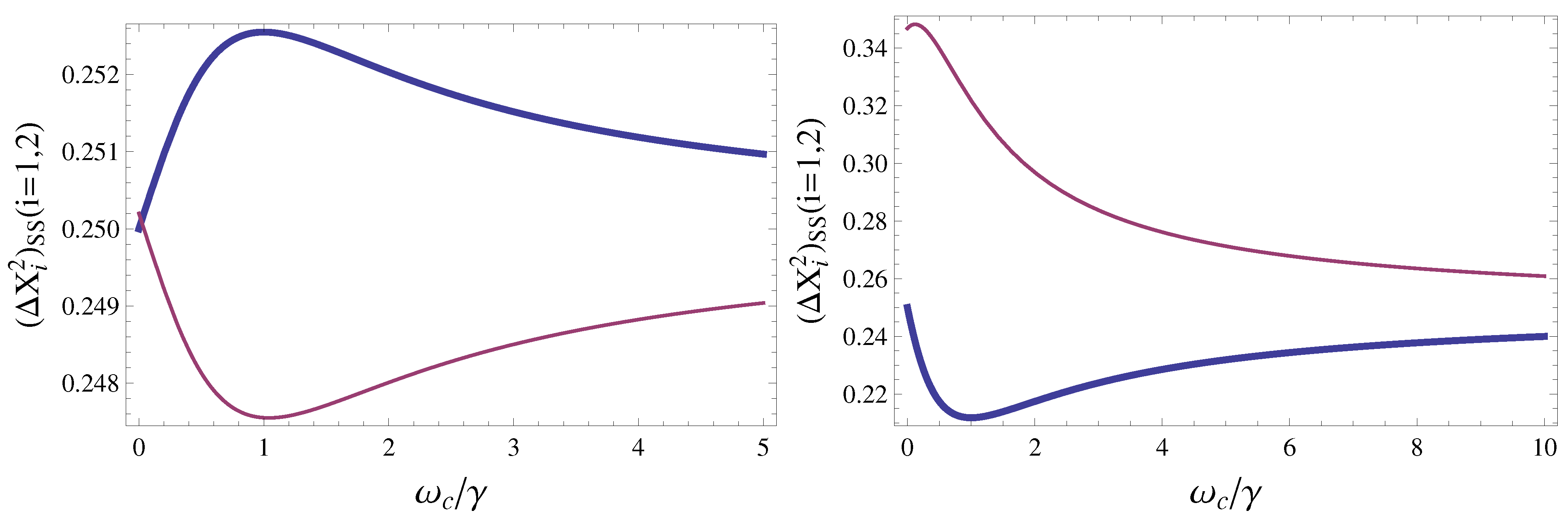
3. Squeezing of the Intra-Cavity Field
4. Squeezing of the Output Field
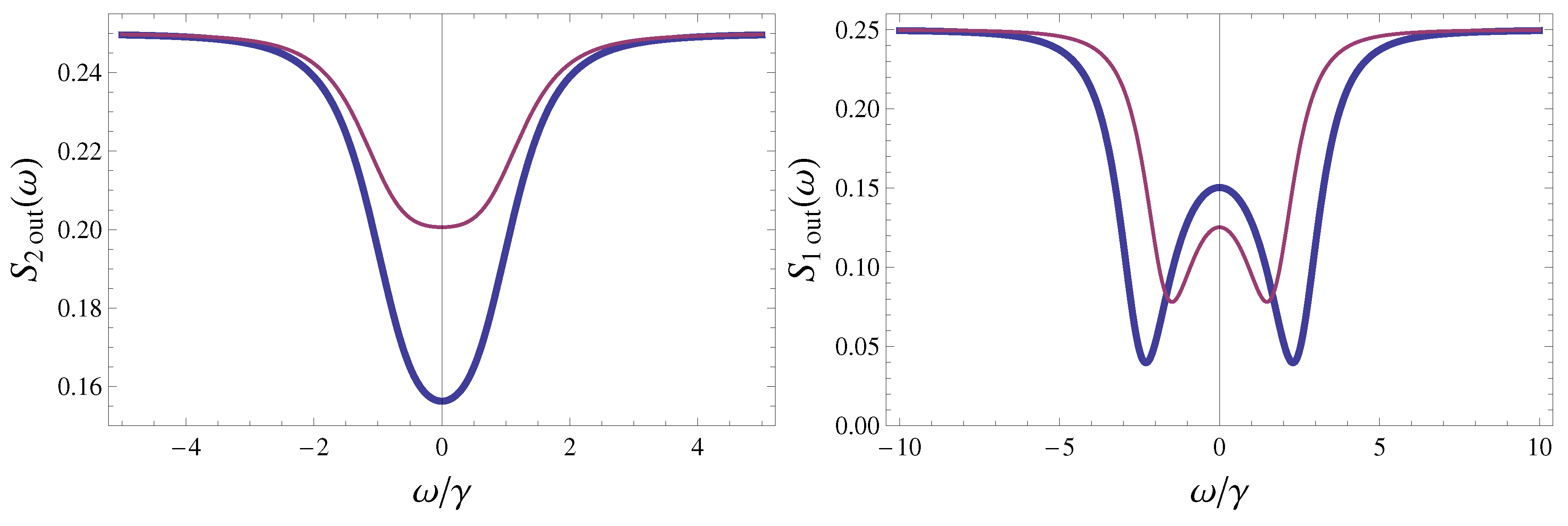
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Zoller, P.; Beth, Th.; Binosi, D.; Blatt, R.; Briegel, H.; Bruss, D.; Calarco, T.; Cirac, J.I.; Deutsch, D.; Eisert, J.; et al. Quantum information processing and communication. Eur. Phys. J. D 2005, 36, 203–228. [Google Scholar] [CrossRef]
- Briegel, H.J.; Dür, W.; Cirac, J.I.; Zoller, P. Quantum Repeaters: The Role of Imperfect Local Operations in Quantum Communication. Phys. Rev. Lett. 1998, 81, 5932–5935. [Google Scholar] [CrossRef]
- Kraus, B.; Cirac, J.I. Discrete Entanglement Distribution with Squeezed Light. Phys. Rev. Lett. 2004, 92, 013602. [Google Scholar] [CrossRef] [PubMed]
- Braunstein, S.L.; van Loock, P. Quantum information with continuous variables. Rev. Mod. Phys. 2005, 77, 513–577. [Google Scholar] [CrossRef]
- Keller, M.; Lange, B.; Hayasaka, K.; Lange, W.; Walther, H. Continuous generation of single photons with controlled waveform in an ion-trap cavity system. Nature 2004, 431, 1075–1078. [Google Scholar] [CrossRef] [PubMed]
- McKeever, J.; Boca, A.; Boozer, A.D.; Buck, J.R.; Kimble, H.J. Experimental realization of a one-atom laser in the regime of strong coupling. Nature 2003, 425, 268–271. [Google Scholar] [CrossRef] [PubMed]
- McKeever, J.; Boca, A.; Boozer, A.D.; Miller, R.; Buck, J.R.; Kuzmich, A.; Kimble, H.J. Deterministic Generation of Single Photons from One Atom Trapped in a Cavity. Science 2004, 303, 1992–1994. [Google Scholar] [CrossRef] [PubMed]
- Kuhn, A.; Hennrich, M.; Rempe, G. Deterministic Single-Photon Source for Distributed Quantum Networking. Phys. Rev. Lett. 2002, 89, 067901. [Google Scholar] [CrossRef] [PubMed]
- Wilk, T.; Webster, S.C.; Specht, H.P.; Rempe, G.; Kuhn, A. Polarization-Controlled Single Photons. Phys. Rev. Lett. 2007, 98, 063601. [Google Scholar] [CrossRef]
- Eisaman, M.D.; Childress, L.; André, A.; Massou, F.; Zibrov, A.S.; Lukin, M.D. Shaping Quantum Pulses of Light Via Coherent Atomic Memory. Phys. Rev. Lett. 2004, 93, 233602. [Google Scholar] [CrossRef] [PubMed]
- Neergaard-Nielsen, J.S.; Nielsen, B.M.; Hettich, C.; Mølmer, K.; Polzik, E.S. Generation of a Superposition of Odd Photon Number States for Quantum Information Networks. Phys. Rev. Lett. 2006, 97, 083604. [Google Scholar] [CrossRef] [PubMed]
- Matsukevich, D.N.; Chanelière, T.; Jenkins, S.D.; Lan, S.Y.; Kennedy, T.A.B.; Kuzmich, A. Deterministic Single Photons via Conditional Quantum Evolution. Phys. Rev. Lett. 2006, 97, 013601. [Google Scholar] [CrossRef] [PubMed]
- Darquie, B.; Jones, M.P.A.; Dingjan, J.; Beugnon, J.; Bergamini, S.; Sortais, Y.; Messin, G.; Browaeys, A.; Grangier, P. Controlled Single-Photon Emission from a Single Trapped Two-Level Atom. Science 2005, 309, 454–456. [Google Scholar] [CrossRef] [PubMed]
- Ourjoumtsev, A.; Brouri, R.T.; Laurat, J.; Grangier, P. Generating Optical Schrödinger Kittens for Quantum Information Processing. Science 2006, 312, 83–86. [Google Scholar] [CrossRef] [PubMed]
- Blinov, B.B.; Moehring, D.L.; Duan, L.M.; Monroe, C. Observation of entanglement between a single trapped atom and a single photon. Nature 2004, 428, 153–157. [Google Scholar] [CrossRef] [PubMed]
- Volz, J.; Weber, M.; Schlenk, D.; Rosenfeld, W.; Vrana, J.; Saucke, K.; Kurtsiefer, C.; Weinfurter, H. Observation of Entanglement of a Single Photon with a Trapped Atom. Phys. Rev. Lett. 2006, 96, 030404. [Google Scholar] [CrossRef] [PubMed]
- Walls, D.F.; Milburn, G.J. Quantum Optics; Springer: Berlin, Germany, 1994; pp. 127–138. [Google Scholar]
- Imamoglu, A.; Schmidt, H.; Woods, G.; Deutsch, M. Strongly Interacting Photons in a Nonlinear Cavity. Phys. Rev. Lett. 1997, 79, 1467–1470. [Google Scholar] [CrossRef]
- Parkins, A.S.; Kimble, H.J. Quantum state transfer between motion and light. J. Opt. B: Quantum Semiclassical Opt. 1999, 1, 496. [Google Scholar] [CrossRef]
- Morigi, G.; Eschner, J.; Mancini, S.; Vitali, D. Entangled Light Pulses from Single Cold Atoms. Phys. Rev. Lett. 2006, 96, 023601. [Google Scholar] [CrossRef] [PubMed]
- Morigi, G.; Eschner, J.; Mancini, S.; Vitali, D. Coherent generation of EPR-entangled light pulses mediated by a single trapped atom. Phys. Rev. A 2006, 73, 033822. [Google Scholar] [CrossRef]
- Vitali, D.; Morigi, G.; Eschner, J. Single cold atom as efficient stationary source of EPR-entangled light. Phys. Rev. A 2006, 74, 053814. [Google Scholar] [CrossRef]
- Vidal, S.F.; Zippilli, S.; Morigi, G. Nonlinear optics with two trapped atoms. Phys. Rev. A 2007, 76, 053829. [Google Scholar] [CrossRef]
- Bhattacherjee, A. Quantum noise reduction using a cavity with a Bose? Einstein condensate. J. Phys. B 2010, 43, 205301. [Google Scholar]
- Jaynes, E.T.; Cummings, F.W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef]
- Zucco, D.; Reuther, G.M.; Kohler, S.; Hänggi, P. Qubit-oscillator dynamics in the dispersive regime: Analytical theory beyond the rotating-wave approximation. Phys. Rev. A 2009, 80, 033846. [Google Scholar] [CrossRef]
- Emary, C.; Brandes, T. Chaos and the quantum phase transition in the Dicke model. Phys. Rev. E 2003, 67, 066203. [Google Scholar] [CrossRef]
- Raimond, J.M.; Brune, M.; Haroche, S. Manipulating quantum entanglement with atoms and photons in a cavity. Rev. Mod. Phys. 2001, 73, 565–582. [Google Scholar] [CrossRef]
- Klimov, A.B.; Saavedra, C. The Dicke model dynamics in a high detuning limit. Phys. Letts. A 1998, 247, 14–20. [Google Scholar]
- Seke, J. Squeezing and rabi oscillations in the Dicke model within and without rotating-wave approximation. Physica A 1995, 213, 587–596. [Google Scholar] [CrossRef]
- Seke, J. The effect of the counter-rotating terms on the Rabi oscillations and squeezing in the Dicke model with cavity losses. Phys. A 1997, 240, 635–646. [Google Scholar] [CrossRef]
- Viehman, O.; Delft, J.V.; Marquardt, F. Superradiant Phase Transitions and the Standard Description of Circuit QED. Phys. Rev. Letts. 2011, 107, 113602. [Google Scholar] [CrossRef]
- Nataf, P.; Ciuti, C. No-go theorem for superradiant quantum phase transitions in cavity QED and counter-example in circuit QED. Nat. Commun. 2010, 1, 72. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhattacherjee, A.B. Influence of Virtual Photon Process on the Generation of Squeezed Light from Atoms in an Optical Cavity. Atoms 2015, 3, 339-347. https://doi.org/10.3390/atoms3030339
Bhattacherjee AB. Influence of Virtual Photon Process on the Generation of Squeezed Light from Atoms in an Optical Cavity. Atoms. 2015; 3(3):339-347. https://doi.org/10.3390/atoms3030339
Chicago/Turabian StyleBhattacherjee, Aranya B. 2015. "Influence of Virtual Photon Process on the Generation of Squeezed Light from Atoms in an Optical Cavity" Atoms 3, no. 3: 339-347. https://doi.org/10.3390/atoms3030339
APA StyleBhattacherjee, A. B. (2015). Influence of Virtual Photon Process on the Generation of Squeezed Light from Atoms in an Optical Cavity. Atoms, 3(3), 339-347. https://doi.org/10.3390/atoms3030339




