Fully Relativistic Electron Impact Excitation Cross-Section and Polarization for Tungsten Ions
Abstract
:1. Introduction
2. Theoretical Background
| Transition Jb→J0 | Polarization, P | Transition Jb→J0 | Polarization, P |
|---|---|---|---|
| 1→0 | 3/2→1/2 | ||
| 1→2 | 3/2→3/2 | ||
| 2→1 | 3/2→5/2 | ||
| 2→2 | 5/2→3/2 | ||
| 2→3 | 5/2→5/2 | ||
| 3→2 | 7/2→5/2 | ||
| 3→3 | 7/2→9/2 | ||
| 3→4 | 9/2→9/2 | ||
| 4→3 | 11/2→11/2 | ||
| 4→4 | 5→4 | ||
| 6→6 |
3. Brief Review of the Earlier Work
3.1. L-Shell Excitation of Mg- through O-like Tungsten Ions
| Mg-like W62+ Ion | Na-like W63+ Ion | Ne-like W64+ Ion | ||||
|---|---|---|---|---|---|---|
| Lower Level | Upper Level | Lower Level | Upper Level | Lower Level | Upper Level | |
| | | | | |||
| F-like W65+ Ion | O-like W66+ Ion | |||||
| Lower Level | Upper Level | Lower Level | Upper Level | |||
| (1) b | ||||||
| (2) b | ||||||
| (1) a | ||||||
| (2) a | ||||||
3.2. M-Shell Excitation of Wn+ Tungsten Ions
3.2.1. Excitation of Co-like through Zn-like Tungsten Ions
| Ion | Zn-like W44+ | Cu-like W45+ | Ni-like W46+ | Co-like W47+ |
|---|---|---|---|---|
| Ground state | ||||
| Excited States | ||||
3.2.2. Excitation of Fe-like through Al-like Tungsten Ions
| W48+ | W49+ | ||
|---|---|---|---|
| Lower Level | Upper Level | Lower Level | Upper Level |
| W5°+ | W51+ | ||
| Lower Level | Upper Level | Lower Level | Upper Level |
| W52+ | |||
| Lower Level | Upper Level | ||
| W53+ | |||
| Lower Level | Upper Level | ||
| W54+ | W55+ | ||
| Lower Level | Upper Level | Lower Level | Upper Level |
| | | | |
| W56+ | W57+ | ||
| Lower Level | Upper Level | Lower Level | Upper Level |
| W58+ | W59+ | ||
| Lower Level | Upper Level | Lower Level | Upper Level |
| W6°+ | |||
| Lower Level | Upper Level | ||
| W61+ | |||
| Lower Level | Upper Level | ||
4. Present Calculations for M-Shell Excitation of K-like through Ne-like Tungsten Ions
| K-like W55+ | Ar-like W56+ | Cl-like W57+ | S-like W58+ | P-like W59+ |
|---|---|---|---|---|
| 3s23p63d 3s23p53d2 3s3p63d2 3p63d3 3s23p54p4d 3s3p53d3 | 3s23p6 3s23p53d 3s23p54s 3s23p54d 3s23p55s | 3s2 3p5 3s 3p53d 3p5 3d2 3s2 3p4 3d 3s2 3p44s 3s2 3p44d 3s 3p6 3p6 3d | 3s23p4 3s23p33d 3s23p23d2 3s3p33d2 3s3p5 3p53d | 3s23p3 3s23p23d 3s23p3d2 3s3p33d 3s3p23d2 3p5 3s3p4 3p43d |
| Si-like W6°+ | Al-like W61+ | Mg-like W62+ | Na-like W63+ | Ne-like W64+ |
| 3s23p2 3s23p3d 3s23d2 3s3p3 3s3p3d2 | 3s23p 3s3p3d 3s23d 3s3p2 3p23d 3p3 | 2p63s2 2p63s3p 2p63s3d 2p63p2 2p53s23p | 2p63s 2p63p 2p53p2 2p53s3d | 2s22p6 2s22p53s 2s22p53p 2s22p54p 2s22p43s3d 2s22p43p2 2s22p43d2 2s2p63s 2p63s2 2p63p2 |
| Ion | Key | Lower Level | Upper Level | EPresent | EMeasured[19] | EFAC[19] | EGRASP2 [19] | EPrevious | fPresent | fPrevious |
|---|---|---|---|---|---|---|---|---|---|---|
| W55+ | K-1 | 647.19 | 646.2 | 647.67 | 649.88 | 1.441 | ||||
| K-2 | 601.23 | 603.27 | 603.74 | 602.60 | 0.385 | |||||
| W56+ | Ar-1 | 631.80 | 630.03 | 631.41 | 632.35 | 0.722 | ||||
| W57+ | Cl-1 | 631.01 | 631.93 | 633.54 | 637.71 | 636.6a | 0.217 | 0.190 | ||
| Cl-2 | 624.90 | 625.74 | 626.63 | 628.53 | 631.7a | 0.203 | 0.196 | |||
| Cl-3 | 622.10 | 624.07 | 626.53 | 628.9a 622.9b | 0.315 | 0.294 | ||||
| W58+ | S-1 | 628.44 | 627.7 | 629.30 | 632.83 | 629.76c | 0.173 | 0.177c | ||
| S-2 | 622.54 | 623.57 | 627.61 | 623.92c 622.19b | 0.256 | 0.254c | ||||
| S-3 | 623.39 | 622.35 | 624.54 | 0.158 | ||||||
| S-4 | 615.23 | 615.40 | 616.35 | 619.74 | 618.29c | 0.263 | 0.262c | |||
| S-5 | 530.35 | 530.98 | 531.10 | 533.33 | 0.072 | |||||
| W59+ | P-1 | 621.48 | 622.54 | 626.53 | 622.28d 621.20b | 0.388 | 0.364d | |||
| P-2 | 619.41 | 621.72 | 624.73 | 620.85d 619.00b | 0.125 | 0.129d | ||||
| P-3 | 609.11 | 610.19 | 611.21 | 614.18 | 610.72d | 0.311 | 0.309d | |||
| P-4 | 515.43 | 515.70 | 515.78 | 516.67 | 517.83d | 0.042 | 0.043d | |||
| W6°+ | Si-1 | 611.60 | 611.6 | 612.90 | 613.78 | 611.86e | 0.923 | 0.880e | ||
| Si-2 | 543.63 | 543.96 | 544.60 | 544.65 | 546.09e | 0.172 | 0.174e | |||
| W61+ | Al-1 | 597.40 | 597.34 | 598.35 | 600.79 | 597.88f | 0.490 | 0.476f | ||
| Al-2 | 550.99 | 549.99 | 550.89 | 552.76 | 553.10f | 0.212 | 0.215f | |||
| Al-3 | 540.19 | 539.98 | 540.24 | 542.48 | 542.10f 539.53g | 0.116 | 0.124f 0.103g | |||
| Al-4 | 500.60 | 500.34 | 500.54 | 499.65 | 502.92f 500.34g | 0.0020 | 0.0021f 0.0019g | |||
| W62+ | Mg-1 | 579.87 | 580.12 | 580.45 | 573.42 | 0.322 | ||||
| Mg-2 | 545.03 | 545.35 | 546.16 | 544.87 | 0.641 | |||||
| W63+ | Na-1 | 533.27 | 533.20 | 533.56 | 533.28 | 0.283 | ||||
| W64+ | Ne-1 | 588.02 | 588.51 | 591.27 | 591.10 | 0.052 |
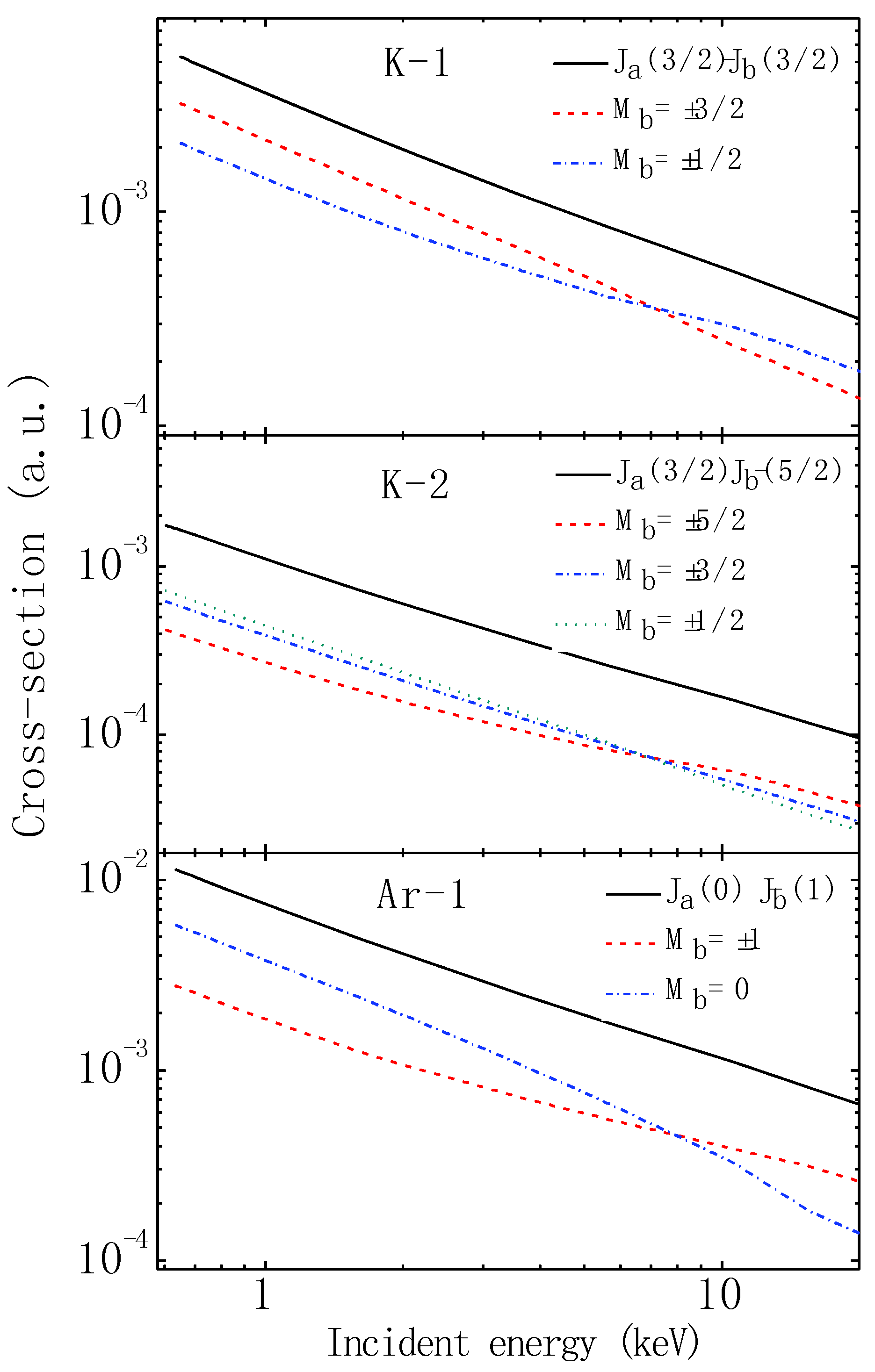
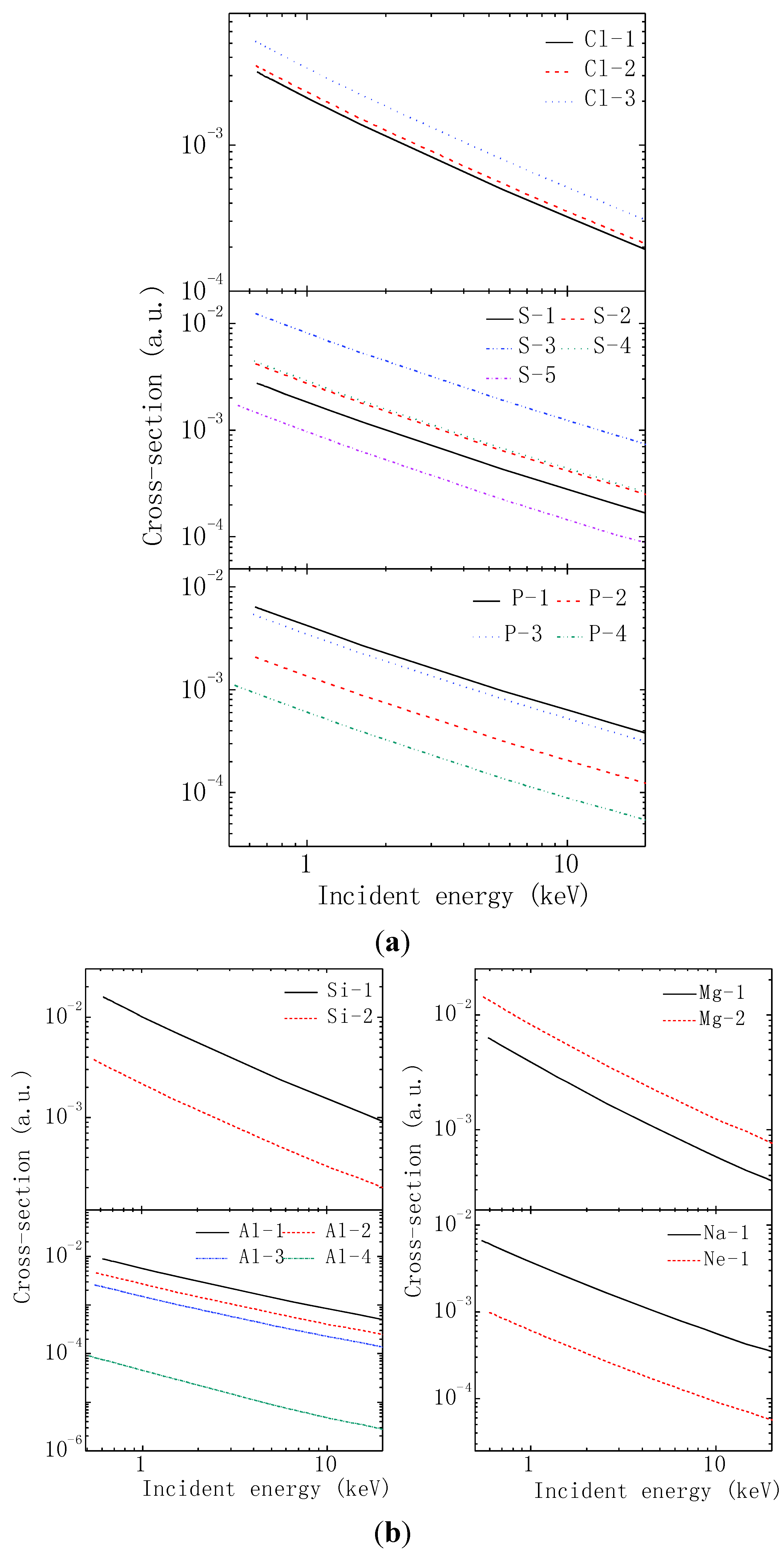
| Ion | Key | b0 | b1 | b2 | b3 | c0 | c1 | c2 |
|---|---|---|---|---|---|---|---|---|
| W55+ | K-1 | 3.11677(−1) | 2.23638(−3) | 8.52164(−7) | 5.85249(+1) | 2.71204(+0) | 9.80664(-3) | |
| K-2 | 4.48806(−2) | 1.73784(−4) | 2.53707(+1) | 1.16952(+0) | 7.96291(−2) | |||
| W56+ | Ar-1 | 1.13969(−2) | 4.47742(−4) | 5.95543(−10) | 3.55779(-5) | 7.01913(−1) | 1.90273(+0) | 7.96291(−2) |
| W57+ | Cl-1 | 9.25517(−2) | 3.81140(−4) | 2.88522(+1) | 1.27190(+0) | 1.90158(−5) | ||
| Cl-2 | 1.02397(−1) | 4.21701(−4) | 2.88731(+1) | 1. 28580(+0) | 1.93272(−5) | |||
| Cl-3 | 1.50742(−1) | 6.21858(−4) | 2.89651(+1) | 1.29560(+0) | 1.95184(−5) | |||
| W58+ | S-1 | 1.90654(−2) | 1.07145(−4) | 2.43210(−8) | 6.81444(+0) | 3.13430(−1) | 8.18660(−4) | |
| S-2 | 2.88122(−2) | 1.61719 (−4) | 3.63116(−8) | 6.81449(+0) | 3.16108(−1) | 8.23966(−4) | ||
| S-3 | 8.51184(−2) | 4.83359 (−4) | 1.11054(−7) | 6.81631(+0) | 3.16292(−1) | 8.37729(−4) | ||
| S-4 | 2.67276(−1) | 1.51345(−3) | 3.44237(−7) | 5.93855(+1) | 2.78957(+0) | 7.38151(−3) | ||
| S-5 | 1.02681(−1) | 7.06571(−4) | 2.65752(−7) | 5.93142(+1) | 3.29168(+0) | 1.18559(−2) | ||
| W59+ | P-1 | 8.05453(−2) | 3.25370(−4) | 1.25106(+1) | 5.60198(−1) | 8.27364(−4) | ||
| P-2 | 1.40812(−2) | 8.06080(−5) | 1.92106(−8) | 6.68179(+0) | 3.12933(−1) | 8.45658(−4) | ||
| P-3 | 3.64642(−2) | 2.10421(−4) | 5.02610(−8) | 6.68194(+0) | 3.18220(−1) | 8.69310(−4) | ||
| P-4 | 3.84554(−3) | 3.78456(−5) | 3.25047(−8) | 1.05095(-11) | 3.42358(+0) | 2.06440(−1) | 1.28072(−3) | |
| W6°+ | Si-1 | 4.04866(−1) | 1.62130(−3) | 2.52737(+1) | 1.15084(+0) | 1.69347(−3) | ||
| Si-2 | 9.68220(−2) | 3.63716(−4) | 2.53397(+1) | 1.28431(+0) | 1.65007(−3) | |||
| W61+ | Al-1 | 9.04079(−3) | 2.48386(−7) | 1.16146(−3) | 3.36091(−3) | 3.04110(+0) | 1.34588(−1) | |
| Al-2 | 4.64005(−3) | 1.12413(−7) | 6.48106(−4) | 2.40066(−3) | 3.04169(+0) | 1.45958(−1) | ||
| Al-3 Al-4 | 2.63551(−3) 9.14755(−5) | 1.23729(−4) 4.86592(−6) | 9.72385(−11) 3.16316(−12) | 1.30408(−5) 3.54016(−7) | 3.73498(−1) 1.35241(+0) | 2.13835(+0) 1.37690(+0) | 1.05531(−1) 7.26933(−2) | |
| W62+ | Mg-1 | 1.61410(−1) | 5.05668(−4) | 2.53830(+1) | 1.16343(+0) | 1.22164(−3) | ||
| Mg-2 | 3.76691(−1) | 1.39624(−3) | 2.60676(+1) | 1.31803(+0) | 1.67008(−3) | |||
| W63+ | Na-1 | 2.05206(−2) | 7.74583(−5) | 3.02309(+0) | 1.56720(−1) | 2.10181(−4) | ||
| W64+ | Ne-1 | 3.02868(−3) | 1.05254(−5) | 3.02448(+0) | 1.41603(−1) | 1.66132(−4) |
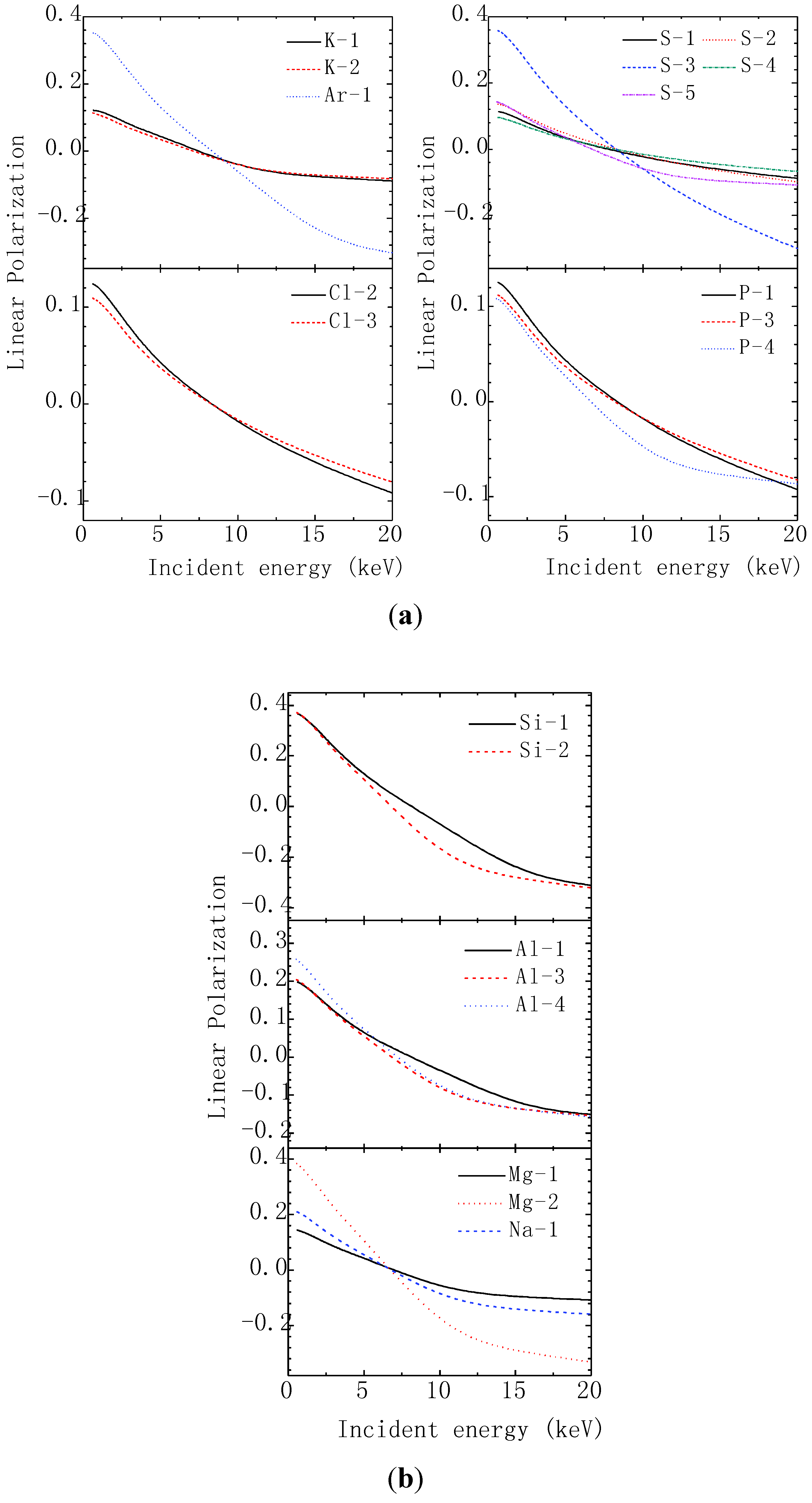
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Neu, R.; Dux, R.; Kallenbach, A.; Pütterich, T.; Balden, M.; Fuchs, J.C.; Herrmann, A.; Maggi, C.F.; O’Mullane, M.; Pugno, R.; et al. Tungsten: An option for divertor and main chamber plasma facing components in future fusion devices. Nucl. Fusion 2005, 45, 209–218. [Google Scholar]
- Ikeda, K. ITER on the road to fusion energy. Nucl. Fusion 2010, 50, 014002:1–014002:10. [Google Scholar] [CrossRef]
- Merolaa, M.; Loesserb, D.; Martina, A.; Chappuisa, P.; Mitteaua, R.; Komarova, V.; Pitts, R.A.; Gicquela, S.; Barabasha, V.; Giancarlia, L.; et al. ITER plasma-facing components. Fusion Eng. Des. 2010, 85, 2312–2322. [Google Scholar] [CrossRef]
- Inubushi, Y.; Kai, T.; Nakamura, T.; Fujioka, S.; Nishimura, H.; Mima, K. Analysis of x-ray polarization to determine the three-dimensionally anisotropic velocity distributions of hot electrons in plasma produced by ultrahigh intensity lasers. Phys. Rev. E 2007, 75, 026401:1–026401:5. [Google Scholar] [CrossRef]
- Beiersdorfer, P.; Slater, M. Measurement of the electron cyclotron energy component of the electron beam of an electron beam ion trap. Phys. Rev. E 2001, 64, 066408:1–066408:6. [Google Scholar] [CrossRef]
- Skinner, C.H. Atomic physics in the quest for fusion energy and ITER. Phys. Scr. 2009, 134, 014022:1–014022:4. [Google Scholar]
- CRP on spectroscopic and collisional data for tungsten. Available online: https://www-amdis.iaea.org/CRP/Tungsten/ (accessed on 21 January 2015).
- Watanabe, H.; Nakamura, N.; Kato, D.; Nakano, T.; Ohtani, S. X-Ray Spectra from Neon-like Tungsten Ions in the Interaction with Electrons. Plasma Fusion Res. Rapid Commun. 2007, 2, 27:1–27:3. [Google Scholar]
- Ralchenko, Y.; Draganić, I.N.; Tan, J.N.; Gillaspy, J.D.; Pomeroy, J.M.; Reader, J.; Feldman, U.; Holland, G.E. EUV spectra of highly-charged ions W54+–W63+ relevant to ITER diagnostics. J. Phys. B 2008, 41, 021003:1–021003:6. [Google Scholar] [CrossRef]
- Peacock, N.J.; O’ Mullane, M.G.; Barnsley, R.; Tarbutt, M. Anticipated X-ray and VUV spectroscopic data from ITER with appropriate diagnostic instrumentation. Can. J. Phys. 2008, 86, 277–284. [Google Scholar] [CrossRef]
- Pütterich, T.; Neu, R.; Dux, R.; Whiteford, A.D.; O’Mullane, M.G. The ASDEX Upgrade Team Modelling of measured tungsten spectra from ASDEX Upgrade and predictions for ITER. Plasma Phys. Control. Fusion 2008, 50, 085016:1–085016:26. [Google Scholar] [CrossRef]
- Biedermann, C.; Radtke, R.; Seidel, R.; Pütterich, T. Spectroscopy of highly charged tungsten ions relevant to fusion plasmas. Phys. Scr. 2009, 134, 014026:1–014026:6. [Google Scholar]
- Clementson, J.; Beiersdorfer, P.; Brown, G.V.; Gu, M.F.; Lundberg, H.; Podpaly, Y.; Träbert, E. Tungsten spectroscopy at the Livermore electron beam ion trap facility. Can. J. Phys. 2011, 89, 571–580. [Google Scholar] [CrossRef]
- Ralchenko, Y.; Draganić, I.N.; Osin, D.; Gillaspy, J.D.; Reader, J. Spectroscopy of diagnostically important magnetic-dipole lines in highly charged 3dn ions of tungsten. Phys. Rev. A 2011, 83, 032517:1–032517:10. [Google Scholar] [CrossRef]
- Kramida, A. Recent progress in spectroscopy of tungsten. Can. J. Phys. 2011, 89, 551–575. [Google Scholar] [CrossRef]
- Beiersdorfer, P.; Brown, G.V.; Graf, A.T.; Bitter, M.; Hill, K.W.; Kelley, R.L.; Kilbourne, C.A.; Leutenegger, M.A.; Porter, F.S. Rest-wavelength fiducials for the ITER core imaging x-ray spectrometer. Rev. Sci. Instrum. 2012, 83, 10E111:1–10E111:3. [Google Scholar]
- Gillaspy, J.D.; Osin, D.; Ralchenko, Y.; Reader, J.; Blundell, S.A. Transition energies of the D lines in Na-like ions. Phys. Rev. A 2013, 87, 062503:1–062503:10. [Google Scholar] [CrossRef]
- Clementson, J.; Beiersdorfer, P.; Brown, G.V.; Gu, M.F. Spectroscopy of M-shell x-ray transitions in Zn-like through Co-like W. Phys. Scr. 2010, 81, 015301:1–015301:8. [Google Scholar] [CrossRef]
- Clementson, J.; Beiersdorfer, P. Wavelength measurement of n = 3 to n = 3 transitions in highly charged tungsten ions. Phys. Rev. A 2010, 81, 052509:1–052509:7. [Google Scholar]
- Clementson, J.; Beiersdorfer, P.; Gu, M.F. X-ray spectroscopy of E2 and M3 transitions in Ni-like W. Phy. Rev. A 2010, 81, 012505:1–012505:6. [Google Scholar]
- Beiersdorfer, P.; Lepson, J.K.; Schneider, M.B.; Bode, M.P. L-shell x-ray emission from neonlike W64+. Phys. Rev. A 2012, 86, 012509:1–012509:10. [Google Scholar] [CrossRef]
- Lennartsson, T.; Clemenston, J.; Beiersdorfer, P. Experimental wavelengths for intrashell transitionsin tungsten ions with partially filled 3p and 3d subshells. Phys. Rev. A 2013, 87, 062505:1–062505:7. [Google Scholar] [CrossRef]
- Beiersdorfer, P.; Clementson, J.; Dunn, J.; Gu, M.F.; Morris, K.; Podpaly, Y.; Wang, E.; Bitter, M.; Feder, R.; Hill, K.W.; et al. The ITER core imaging x-ray spectrometer. J. Phys. B 2010, 43, 144008:1–144008:10. [Google Scholar]
- Fujimoto, T.; Iwamae, A. (Eds.) Plasma Polarization Spectroscopy; Springer Berlin Heidelberg: New York, NY, USA, 2008; Volume 44.
- Das, T.; Sharma, L.; Srivastava, R. Electron impact excitation of the M-shell electrons from Zn-like through Co-like tungsten ions. Phys. Scr. 2012, 86, 035301:1–035301:11. [Google Scholar] [CrossRef]
- Dipti; Das, T.; Sharma, L.; Srivastava, R. L-shell electron excitations of Mg- through O-like tungsten ions. Phys. Scr. 2014, 89, 085403:1–085403:13. [Google Scholar] [CrossRef]
- Dipti; Das, T.; Sharma, L.; Srivastava, R. Electron impact excitation and polarization studies of Fe-like W48+ to Al-like W61+ ions. Can. J. Phys. 2015, in press. [Google Scholar]
- Gangwar, R.K.; Sharma, L.; Srivastava, R.; Stauffer, A.D. Argon plasma modeling with detailed fine-structure cross sections. J. Appl. Phys. 2012, 111, 053307:1–053307:9. [Google Scholar] [CrossRef]
- Sharma, L.; Surzhykov, A.; Srivastava, R.; Fritzsche, S. Electron-impact excitation of singly charged metal ions. Phys. Rev. A 2011, 83, 062701:1–062701:8. [Google Scholar] [CrossRef]
- Madision, D.H.; Bartschat, K. The Distorted-Wave Method for Elastic Scattering and Atomic Excitation, Computational Atomic Physics: Electron and Positron Collision with Atoms and Ions; Bartschat, K., Ed.; Springer-Verlag: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Srivastava, R.; Stauffer, A.D.; Sharma, L. Excitation of the metastable states of the noble gases. Phys. Rev. A 2006, 74, 012715:1–012715:10. [Google Scholar]
- Parpia, F.A.; Fischer, C.F.; Grant, I.P. GRASP92: A package for large-scale relativistic atomic structure calculations. Comput. Phys. Commun. 1996, 94, 249–271. [Google Scholar] [CrossRef]
- Jönsson, P.; He, X.; Fischer, C.F.; Grant, I.P. The grasp2K relativistic atomic structure package. Comput. Phys. Commun. 2007, 177, 597–622. [Google Scholar] [CrossRef]
- Balashov, V.V.; Grum-Grzhimailo, A.N.; Kabachnik, N.M. Polarization and Correlation Phenomena in Atomic Collisions; Kluwer Academic/Plenum: New York, NY, USA, 2000. [Google Scholar]
- Chen, M.H.; Crasemann, B. Systematic trends of the oscillator strengths for n = 3 and 2 electric dipole transitions in oxygen-like ions. Phys. Rev. A 1989, 40, 4330:1–4330:7. [Google Scholar]
- Ivanova, E.P.; Gulov, A.V. Theoretical investigation of the neon isoelectronic sequence. At. Data Nucl. Data Tables 1991, 49, 1–64. [Google Scholar] [CrossRef]
- Vilkas, M.J.; López-Encarnación, J.M.; Ishikawa, Y. Relativistic multireference Møller–Plesset perturbation theory calculations of the energy levels and transition probabilities in Ne-like xenon, tungsten, and uranium ions. At. Data Nucl. Data Tables 2008, 94, 50–70. [Google Scholar] [CrossRef]
- Safronova, U.I.; Safronova, A.S.; Beiersdorfer, P. Excitation energies, radiative and autoionization rates, dielectronic satellite lines, and dielectronic recombination rates for excited states of Na-like W from Ne-like W. At. Data Nucl. Data Tables 2009, 95, 751–785. [Google Scholar] [CrossRef]
- Safronova, U.I.; Safronova, A.S.; Beiersdorfer, P. Excitation energies, radiative and autoionization rates, dielectronic satellite lines and dielectronic recombination rates for excited states of Mg-like W from Na-like W. J. Phys. B 2009, 42, 165010:1–165010:17. [Google Scholar]
- Zhang, H.L.; Sampson, D.H. Relativistic distorted wave collision strengths for excitation to the 88 n = 3 and n = 4 levels in all 71 neon-like ions with 22 ≤ Z ≤ 92. At. Data Nucl. Data Tables 1989, 43, 1–69. [Google Scholar] [CrossRef]
- Sampson, D.H.; Zhang, H.L.; Fontes, C.J. Relativistic distorted wave collision strengths and oscillator strengths for the 71 Na-like ions with 22 ≤ Z ≤ 92. At. Data Nucl. Data Tables 1990, 44, 209–271. [Google Scholar] [CrossRef]
- Sampson, D.H.; Zhang, H.L.; Fontes, C.J. Relativistic distorted-wave collision strengths and oscillator strengths for F-like ions with 22 ≤ Z ≤ 92. At. Data Nucl. Data Tables 1991, 48, 25–90. [Google Scholar] [CrossRef]
- Zhang, H.L.; Sampson, D.H. Relativistic Distorted-wave collision strengths and oscillator strengths for the 45 ∆n = 0 transition with n = 2 in the 79 O-like ions with 14 ≤ Z ≤ 92. At. Data Nucl. Data Tables 2002, 82, 357–389. [Google Scholar] [CrossRef]
- Zhang, H.L.; Sampson, D.H.; Fontes, C.J. Relativistic distorted wave collision strengths and oscillator strengths for the 33 Cu-like ions with 60 ≤ Z ≤ 92. At. Data Nucl. Data Tables 1990, 44, 273–304. [Google Scholar] [CrossRef]
- Zhang, H.L.; Sampson, D.H.; Fontes, C.J. Relativistic distorted-wave collision strengths and oscillator strengths for the 33Ni-like ions with 60 ≤ Z ≤ 92. At. Data Nucl. Data Tables 1991, 48, 91–163. [Google Scholar] [CrossRef]
- Xie, L.Y.; Ma, X.Y.; Dong, C.Z.; Wu, Z.W.; Shi, Y.L.; Jiang, J. Polarization of the nf→3d (n = 4, 5, 6) x-rays from tungsten ions following electron-impact excitation and dielectronic recombination processes. J. Quant. Spectrosc. Radiat. Transf. 2014, 141, 31–39. [Google Scholar] [CrossRef]
- Fournier, K.B. Atomic data and spectral line intensities for highly ionized tungsten (Co-like W47+to Rb-like W37+) in a high-temperature, low density plasma. At. Data Nucl. Data 1998, 68, 1–48. [Google Scholar] [CrossRef]
- Huang, K.N.; Kim, Y.K.; Cheng, K.T. Energy-level scheme and transition probabilities of Cl-like ions. At. Data Nucl. Data Tables 1983, 28, 355–377. [Google Scholar] [CrossRef]
- Huang, K.H. Energy-level scheme and transition probabilities of P-like ions. At. Data Nucl. Data Tables 1984, 30, 313–421. [Google Scholar] [CrossRef]
- Huang, K.H. Energy-level scheme and transition probabilities of Si-like ions. At. Data Nucl. Data Tables 1985, 32, 503–566. [Google Scholar] [CrossRef]
- Huang, K.N. Energy-level scheme and transition probabilities of Al-like ions. At. Data Nucl. Data Tables 1986, 34, 1–77. [Google Scholar] [CrossRef]
- Seely, J.F.; Brown, C.M.; Behring, W.E. Transitions in Fe-, Co-, Cu-, and Zn-like ions of W and Re. J. Opt. Soc. Am. B 1989, 6, 3–6. [Google Scholar] [CrossRef]
- Chou, H.S.; Chang, J.Y.; Chang, Y.S.; Huang, K.N. Energy-level scheme and transition probabilities of S-like. At. Data Nucl. Data Tables 1996, 62, 77–145. [Google Scholar] [CrossRef]
- Safronova, U.I.; Safronova, A.S. Wavelengths and transition rates for nl–n'l' transitions in Be-, B-, Mg-, Al-, Ca-, Zn-, Ag- and Yb-like tungsten ions. J. Phys. B 2010, 43, 074026:1–074026:15. [Google Scholar]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (ver. 5.2). Available online: http://physics.nist.gov/asd (accessed on 11 November 2014).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Priti; Dipti; Sharma, L.; Srivastava, R. Fully Relativistic Electron Impact Excitation Cross-Section and Polarization for Tungsten Ions. Atoms 2015, 3, 53-75. https://doi.org/10.3390/atoms3020053
Priti, Dipti, Sharma L, Srivastava R. Fully Relativistic Electron Impact Excitation Cross-Section and Polarization for Tungsten Ions. Atoms. 2015; 3(2):53-75. https://doi.org/10.3390/atoms3020053
Chicago/Turabian StylePriti, Dipti, Lalita Sharma, and Rajesh Srivastava. 2015. "Fully Relativistic Electron Impact Excitation Cross-Section and Polarization for Tungsten Ions" Atoms 3, no. 2: 53-75. https://doi.org/10.3390/atoms3020053
APA StylePriti, Dipti, Sharma, L., & Srivastava, R. (2015). Fully Relativistic Electron Impact Excitation Cross-Section and Polarization for Tungsten Ions. Atoms, 3(2), 53-75. https://doi.org/10.3390/atoms3020053






