Critical Assessment of Theoretical Calculations of Atomic Structure and Transition Probabilities: An Experimenter’s View
Abstract
:1. Introduction
1.1. Codes
2. Historical Remarks
2.1. Be-Like Ions
2.1.1. Resonance Transition Rate
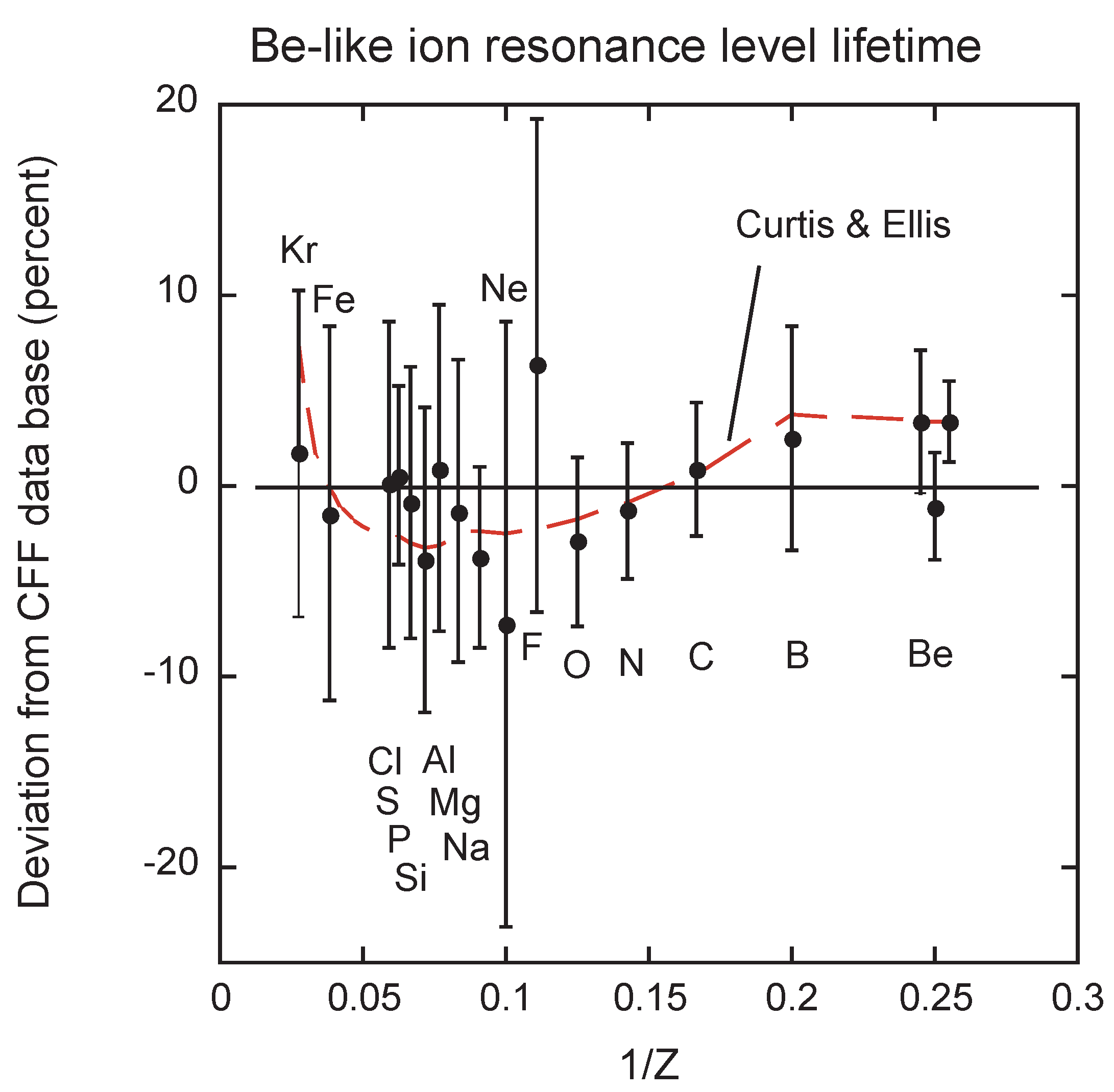
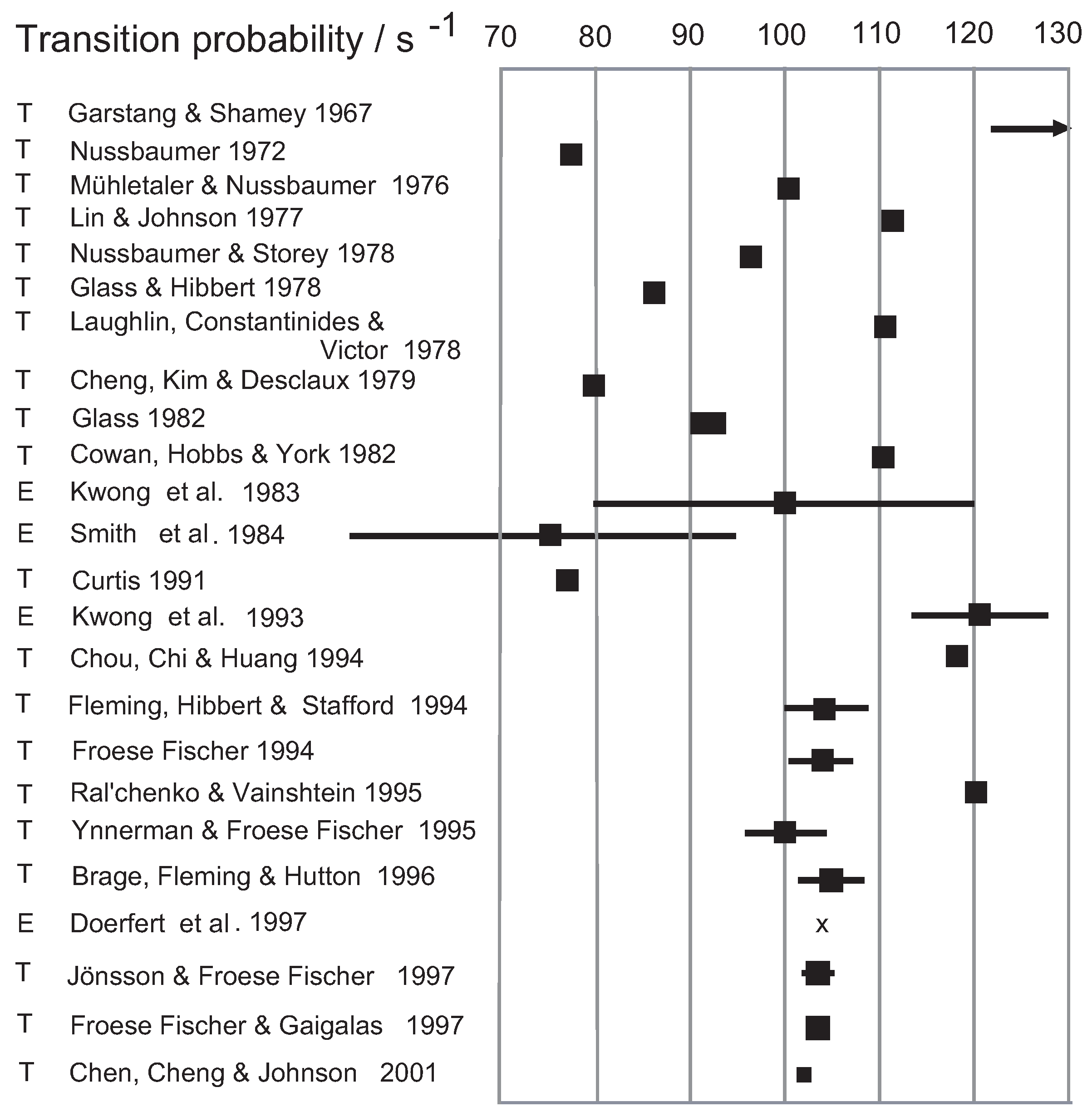
2.1.2. Intercombination Transition Rate
2.2. General Problems
3. Isoelectronic Sequences
3.1. H-Like Ions
3.2. He-Like Ions
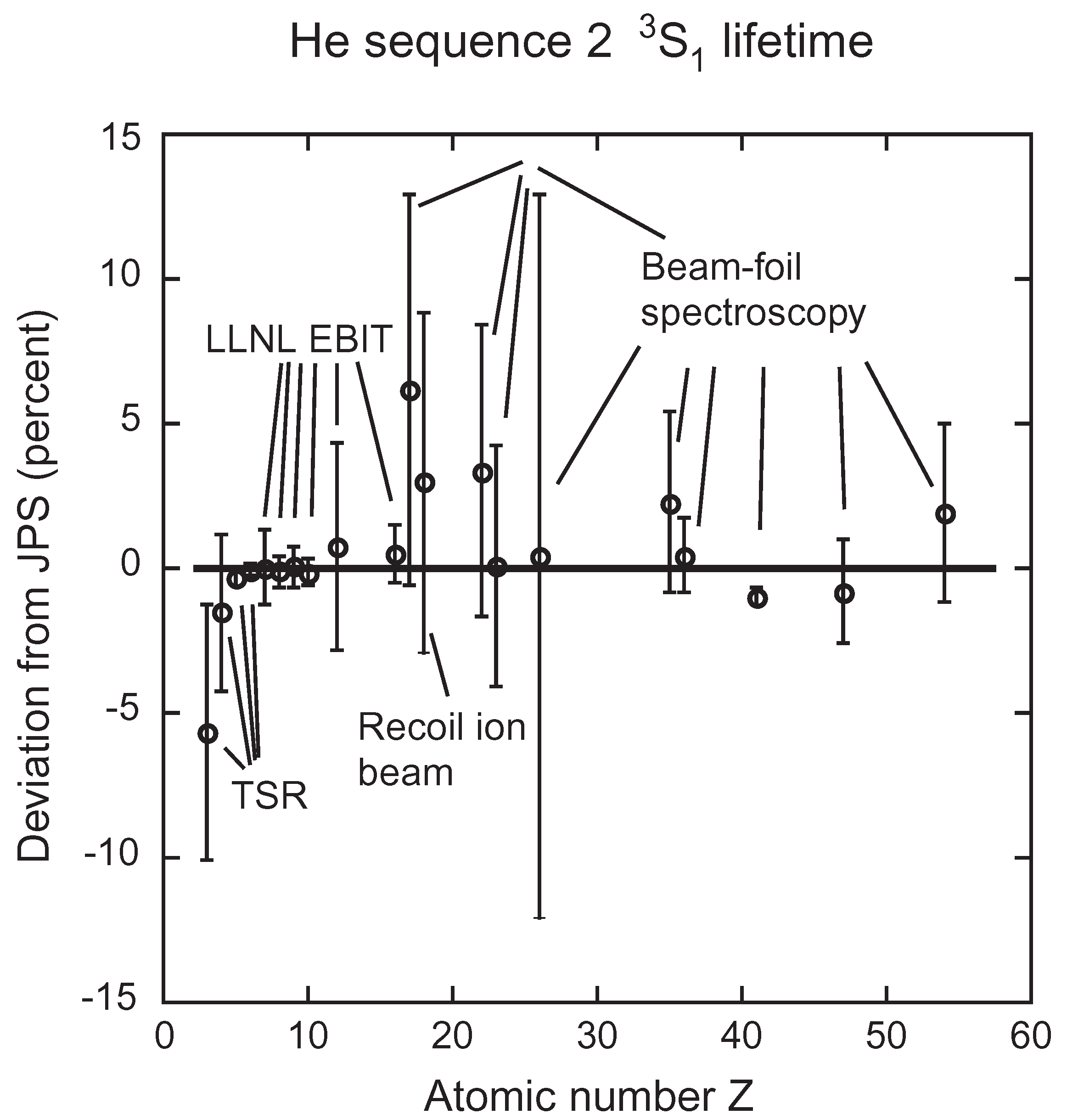
3.3. Li-Like Ions
3.3.1. Levels
3.3.2. Lifetimes
3.4. Be-Like Ions
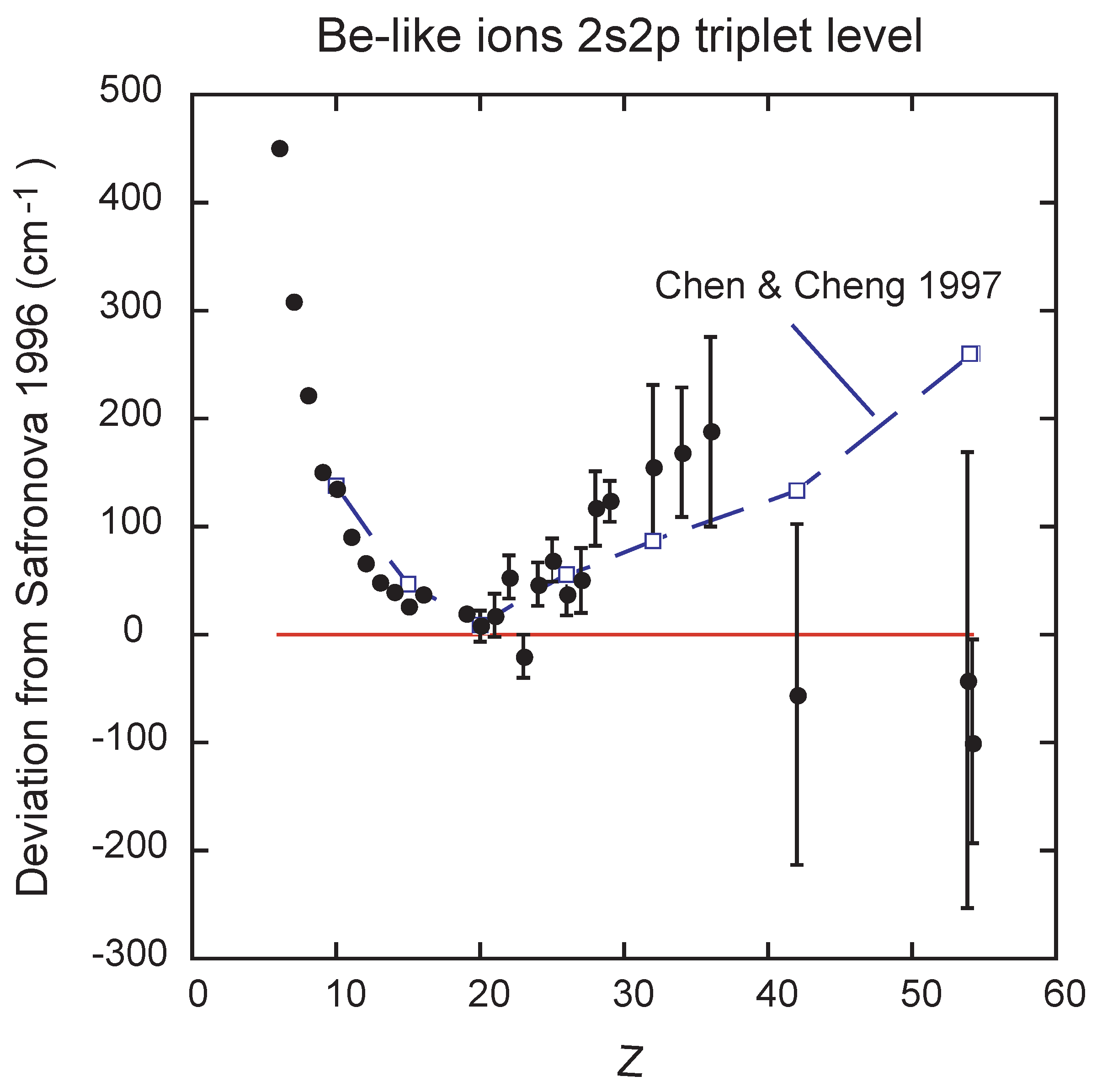
3.4.1. 2s2p Level Lifetimes
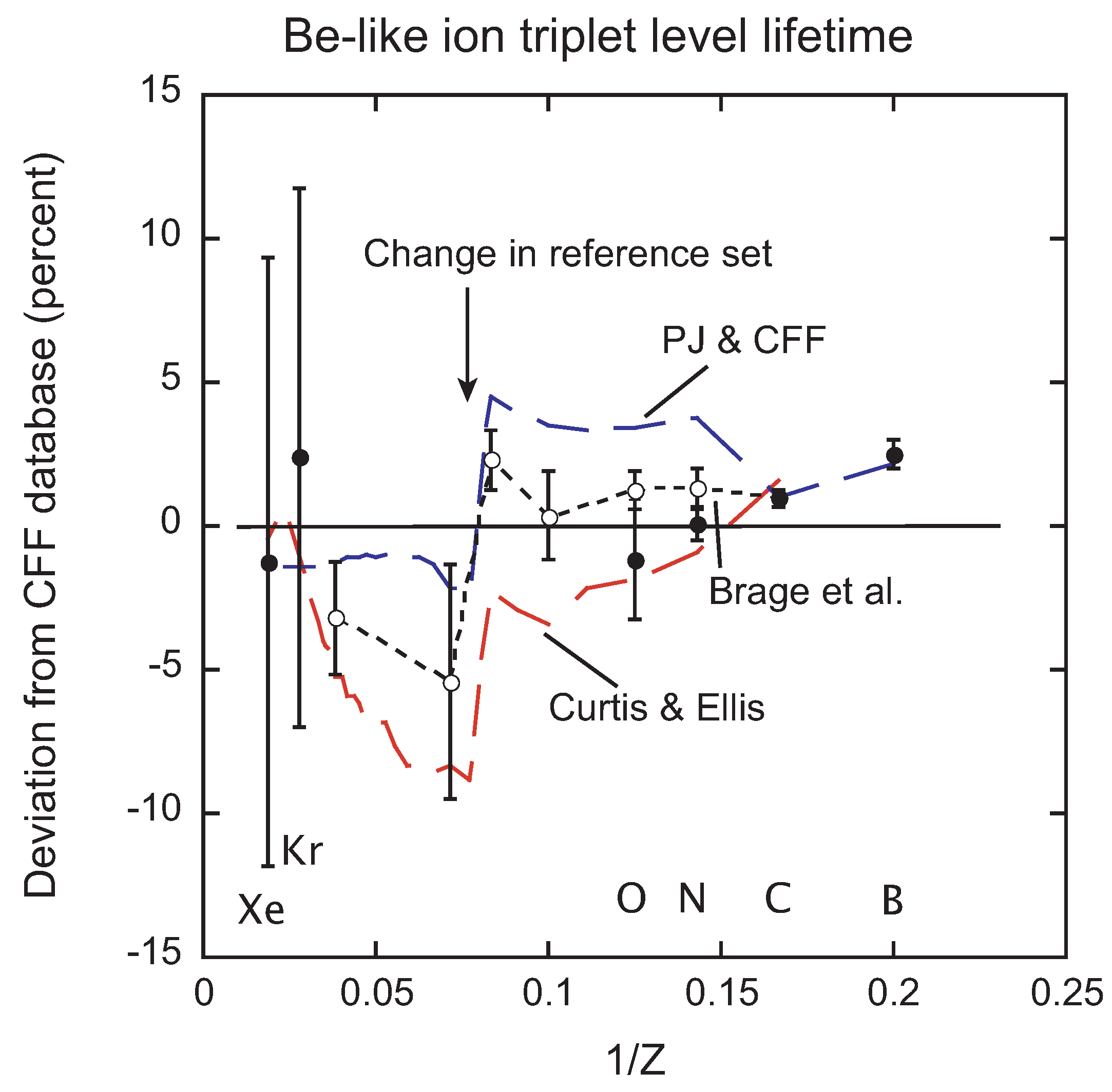
3.4.2. Displaced Level Lifetimes
3.4.3. Hyperfine-Induced Decays
3.5. B-Like Ions
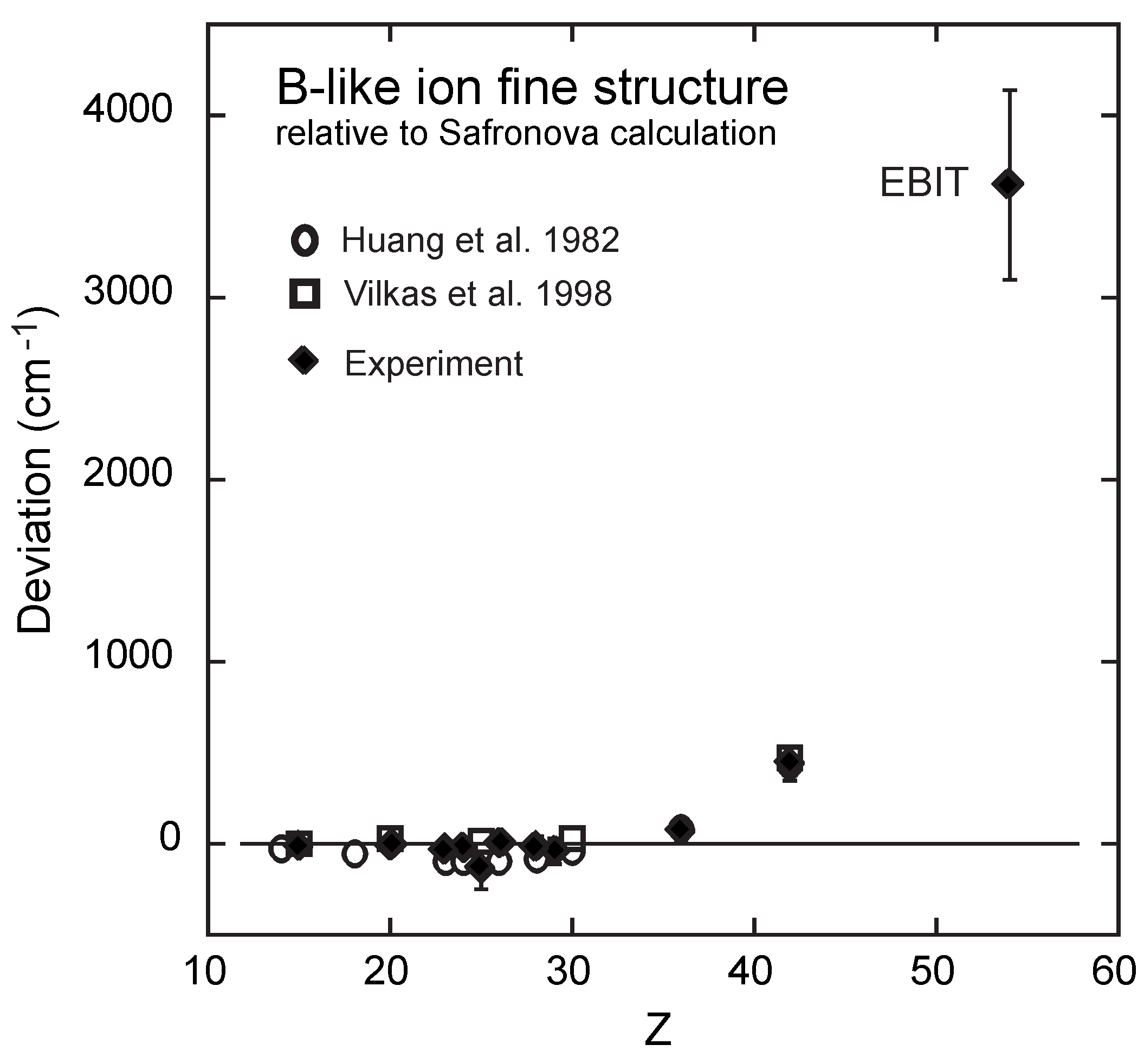
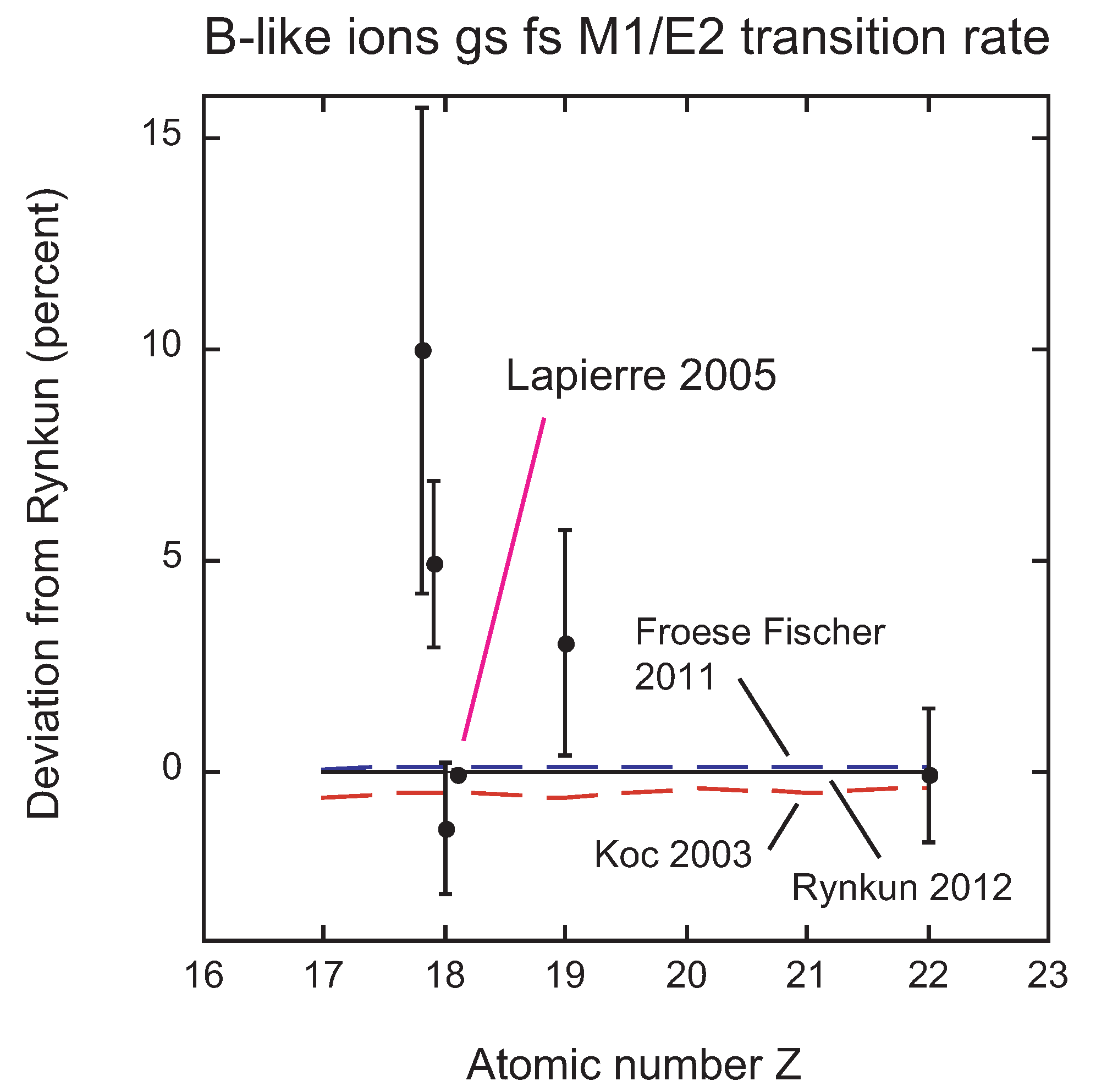
3.5.1. E1-Forbidden Transition Rates
3.6. CNO-Like Ions
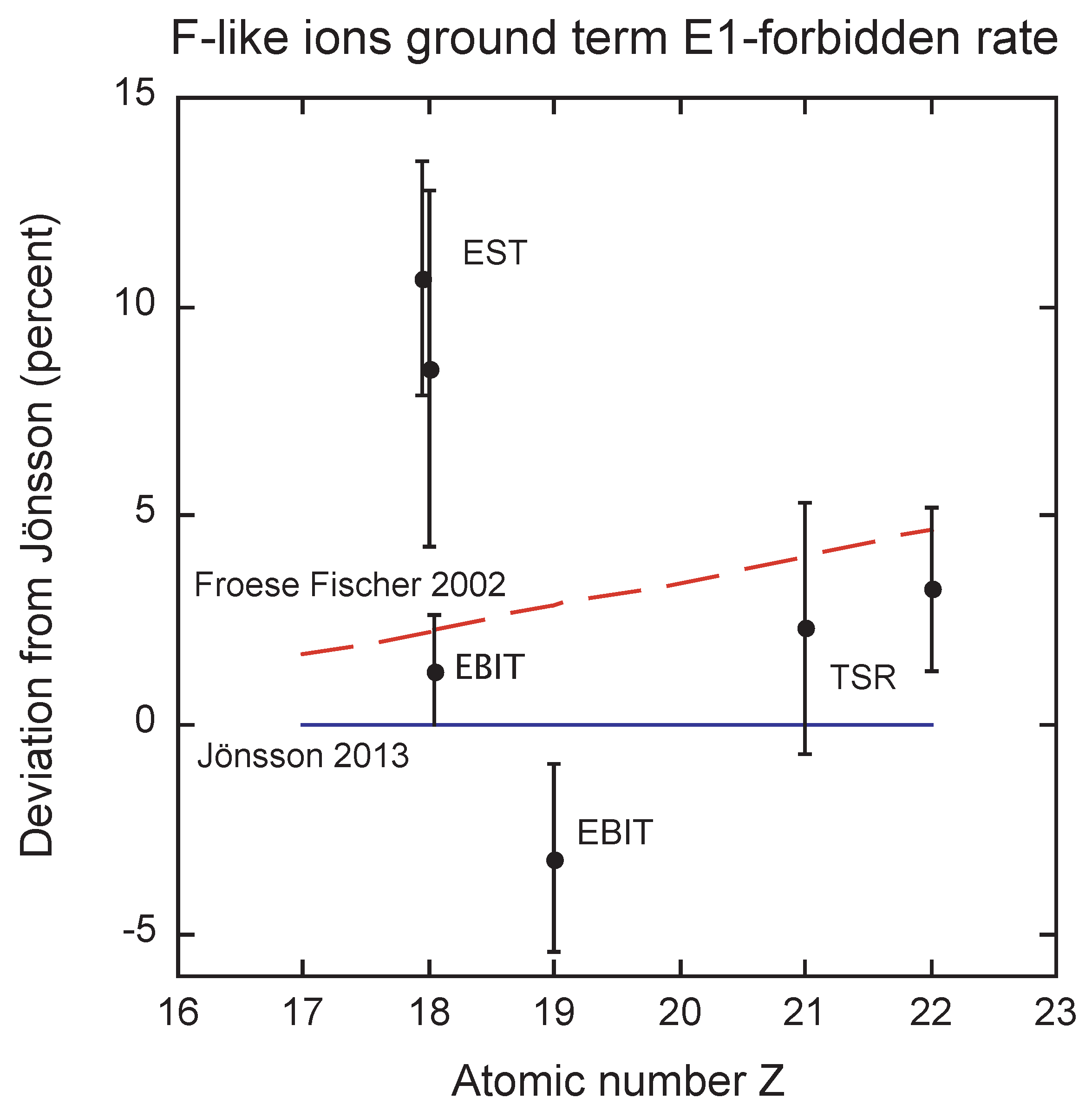
3.7. F-Like Ions

3.8. Ne-Like Ions
3.8.1. Levels
3.8.2. Lifetimes
3.8.3. Line Ratio
3.9. Na-Like Ions
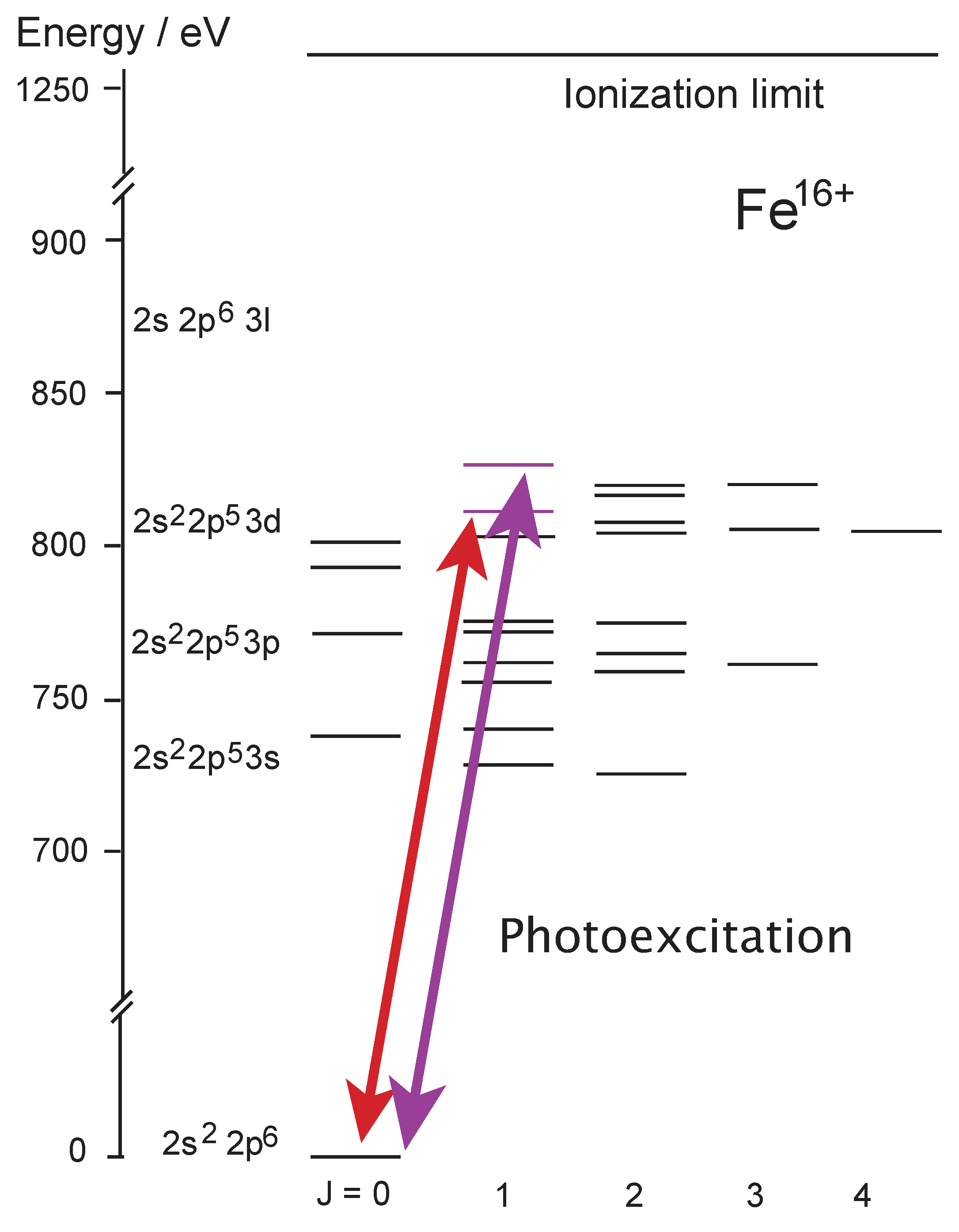
3.10. Mg-Like Ions
3.11. Al-Like Ions
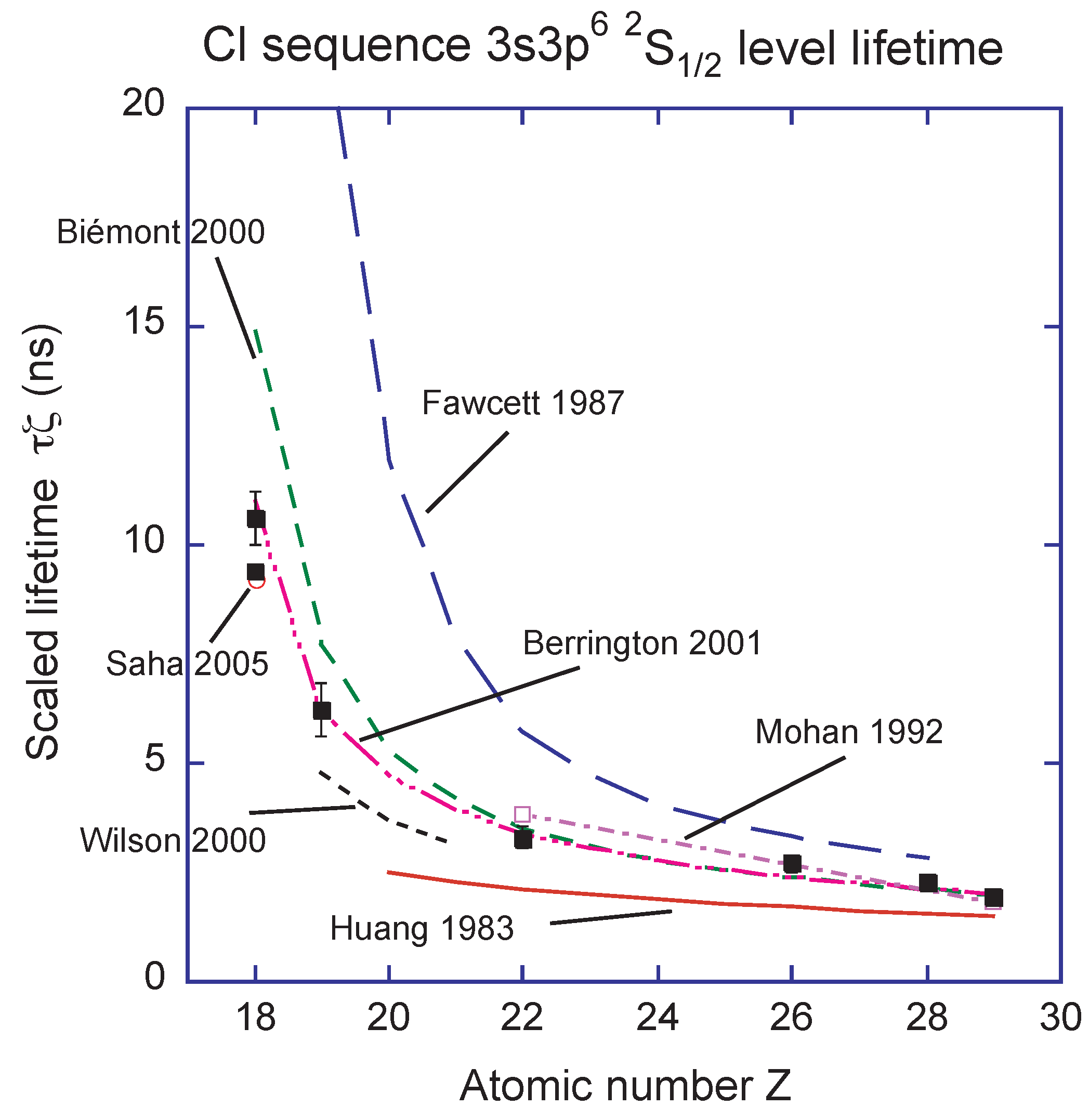
3.12. Si-Like Ions
3.13. P-Like Ions
3.14. S-Like Ions
3.15. Cl-Like Ions
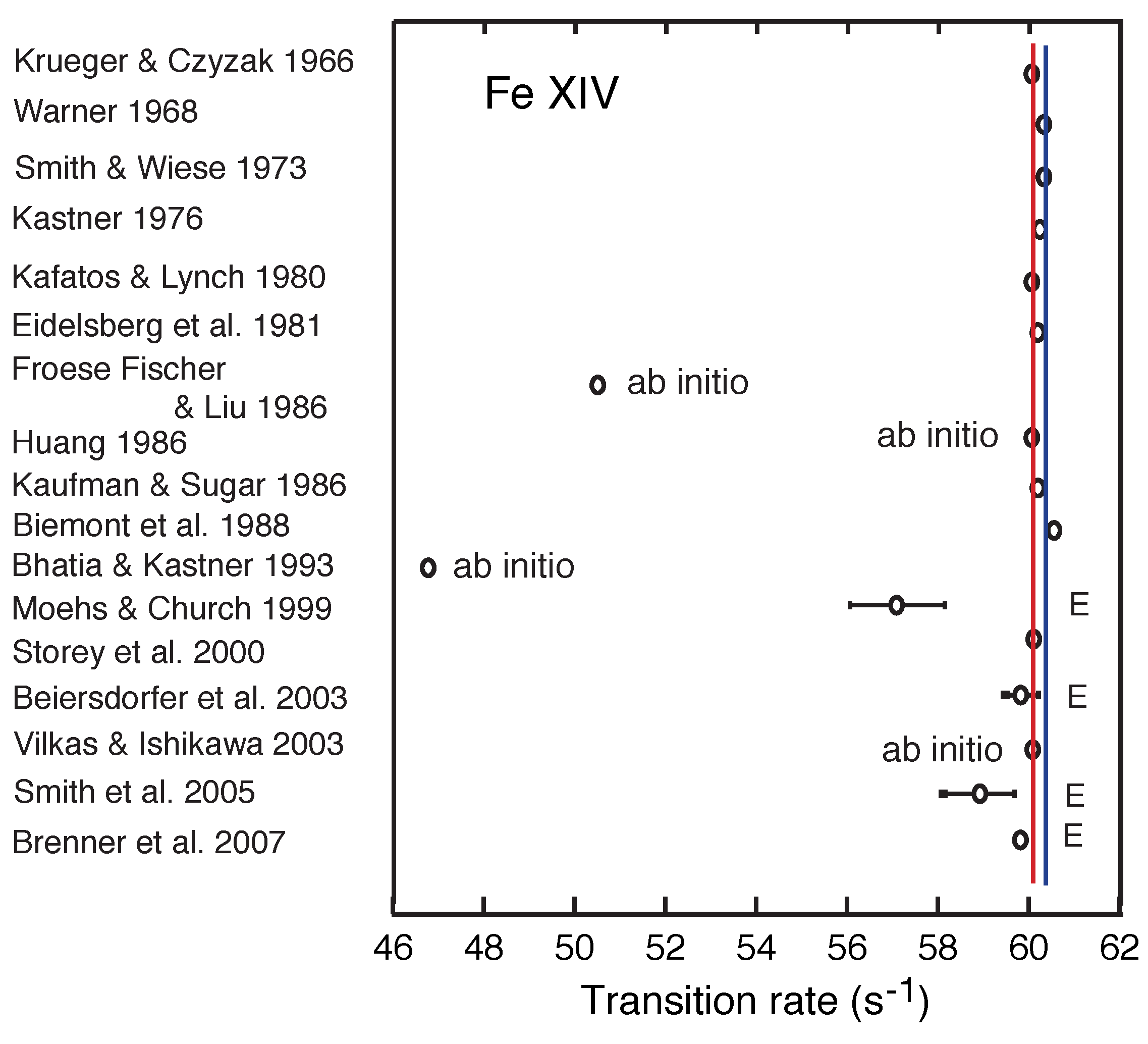
3.16. Ar-Like Ions
3.17. Cu-Like Ions
3.18. Zn-Like Ions
3.19. Ga-Like and Ge-Like Ions
4. Pm-Like, Sm-Like, Eu-Like Ions
5. W
6. Discussion
Acknowledgments
Conflicts of Interest
References
- Curtis, L.J.; Martinson, I. Recent Progress in Atomic-Structure Investigations with Fast-Ion Beams. Comments Atom. Molec. Phys. 1980, 10, 1–8. [Google Scholar]
- Martinson, I.; Ellis, D.G. Recent studies of intercombiantion lines in ions. Comments Atom. Mol. Phys. 1985, 16, 21–33. [Google Scholar]
- Ellis, D.G.; Martinson, I.; Träbert, E. Intercombination transitions in multiply ionized atoms. Comments Atom. Mol. Phys. 1989, 22, 241–262. [Google Scholar]
- Curtis, L.J.; Martinson, I. Lifetime Measurements in Multiply Ionized Atoms. Comments Atom. Mol. Phys. 1990, 24, 213–233. [Google Scholar]
- Curtis, L.J. Precision Oscillator Strength and Lifetime Measurements. In Atomic, Molecular, and Optical Physics Reference Book; Drake, G.W.F., Ed.; AIP Press: New York, NY, USA, 1996; pp. 206–212. [Google Scholar]
- Träbert, E. Atomic lifetime measurements with ion traps of many sizes. Phys. Scr. 2000, 61, 257–286. [Google Scholar]
- Träbert, E. Lifetime measurements of highly charged ions. Phys. Scr. T 2002, 100, 88–97. [Google Scholar]
- Träbert, E. Precise measurements of long atomic lifetimes using stored ion beams and ion traps. Can. J. Phys. 2002, 80, 1481–1503. [Google Scholar]
- Mannervik, S. Experimental lifetime studies of metastable levels. Phys. Scr. T 2003, 105, 67–75. [Google Scholar]
- Träbert, E. Atomic lifetime measurements using electron beam ion traps. Can. J. Phys. 2008, 86, 73–97. [Google Scholar]
- Träbert, E. Problems with accurate atomic lifetime measurements of multiply charged ions. Phys. Scr. 2009, 79, 068101. [Google Scholar]
- Träbert, E. In pursuit of high precision atomic lifetime measurements of multiply charged ions. J. Phys. B: At. Mol. Opt. Phys. 2010, 43, 074034. [Google Scholar] [CrossRef]
- Träbert, E. Radiative-lifetime measurements on highly-charged ions. In Accelerator-based Atomic Physics Techniques and Applications; Shafroth, S.M., Austin, J.C., Eds.; American Institute of Physics: Washington, DC, USA, 1997; pp. 567–607. [Google Scholar]
- Curtis, L.J. A diagrammatic mnemonic for computation of cascading level populations. Am. J. Phys. 1968, 36, 1123–1128. [Google Scholar]
- Curtis, L.J.; Berry, H.G.; Bromander, J. A meanlife measurement of the 3d 2D resonance doublet in Si II by a technique which exactly accounts for cascading. Phys. Lett. A 1971, 34, 169–170. [Google Scholar] [CrossRef]
- Engström, L. CANDY, a computer program to perform an ANDC analysis of cascade correlated decay curves. Nucl. Instrum. Meth. 1982, 202, 369–376. [Google Scholar]
- Engström, L. Studies of atomic decay properties using fast ion beam spectroscopy. Phys. Scr. 1989, 40, 17–24. [Google Scholar]
- Träbert, E.; Heckmann, P.H. Beam-foil lifetimes of Be-like ions of elements from Mg to S. Phys. Scr. 1980, 22, 489–492. [Google Scholar]
- Träbert, E.; Johnson, B.M.; Jones, K.W.; Gregory, D.C.; Kruse, T.H. Beam-foil lifetimes of n = 3 levels in Fe XIII to Fe XVI. II. Analysis of decay curves. Phys. Lett. A 1982, 87, 336–340. [Google Scholar]
- Träbert, E.; Doerfert, J.; Granzow, J.; Büttner, R.; Brauckhoff, J.; Nicolai, M.; Schartner, K.-H.; Folkmann, F.; Mokler, P.H. Lifetimes of n = 2 levels in foil-excited Kr32+ and Kr33+ ions. Phys. Lett. A 1995, 202, 91–98. [Google Scholar] [CrossRef]
- Träbert, E.; Curtis, L.J. Isoelectronic trends of line strength data in the Li and Be isoelectronic sequences. Phys. Scr. 2006, 74, C42–C50. [Google Scholar]
- Reistad, N.; Martinson, I. Accurate transition probabilities in ions obtained by isoelectronic smoothing of line strengths. Phys. Rev. A 1986, 34, 2632–2637. [Google Scholar]
- Träbert, E. Isoelectronic smoothing of oscillator strengths in the beryllium sequence. Z. Phys. D 1988, 9, 143–145. [Google Scholar]
- Curtis, L.J. Isoelectronic smoothing of line strengths in intermediate coupling. Phys. Scr. 1991, 43, 137–143. [Google Scholar]
- Hylleraas, E.A. Neue Berechnung der Energie des Heliums im Grundzustande, sowie des tiefsten Terms von Ortho-Helium. Z. Phys. 1929, 54, 347–366. [Google Scholar]
- Hylleraas, E.A. Über den Grundterm der Zweielektronenprobleme von H-, He, Li+, Be++ usw. Z. Phys. D 1930, 65, 209–225. [Google Scholar] [CrossRef]
- Jönsson, P.; Froese Fischer, C.; Träbert, E. On the status and perspectives of MCDF computations and measurements of transition data in the Be isoelectronic sequence. J. Phys. B: At. Mol. Opt. Phys. 1998, 31, 3497–3511. [Google Scholar]
- Froese Fischer, C. The MCHF/MCDHF collection. 2004. Available online: nlte.nist.gov/MCHF/ (accessed on 15 Nov 2013). [Google Scholar]
- Curtis, L.J.; Ellis, D.G. Predictive systematization of line strengths for the 2s2 - 2s2p resonance and intercombination transitions in the Be isoelectronic sequence. J. Phys. B: At. Mol. Opt. Phys. 1996, 29, 645–654. [Google Scholar]
- Martinson, I.; Gaupp, A.; Curtis, L.J. Comments on the Be I 2s2 1S - 2s2p 1P transition probability. J. Phys. B: At. Mol. Phys. 1974, 7, L463–L466. [Google Scholar] [CrossRef]
- Irving, R.E.; Henderson, M.; Curtis, L.J.; Martinson, I.; Bengtsson, P. Accurate transition probabilities for the 2s2 1S – 2s2p 1P transition in Be I and B II. Can. J. Phys. 1999, 77, 137–143. [Google Scholar] [CrossRef]
- Träbert, E.; Pinnington, E.H.; Kernahan, J.A.; Doerfert, J.; Granzow, J.; Heckmann, P.H.; Hutton, R. Beam-foil study of the lifetimes of n = 3 levels in Na-like Ca X, Mg-like Ca IX and Si-like Ca VII. J. Phys. B: At. Mol. Opt. Phys. 1996, 29, 2647–2659. [Google Scholar]
- Hutton, R.; Engström, L.; Träbert, E. Observation of a discrepancy between experimentally determined atomic lifetimes and relativistic predictions for highly ionized members of the Na I isoelectronic sequence. Phys. Rev. Lett. 1988, 60, 2469–2472. [Google Scholar]
- Träbert, E.; Doerfert, J.; Granzow, J.; Büttner, R.; Staude, U.; Schartner, K.H.; Rymuza, P.; Mokler, P.H.; Engström, L.; Hutton, R. Experimental n = 3 level lifetimes of Na-like heavy ions in the realm of massive relativistic effects. Phys. Lett. A 1994, 188, 355–360. [Google Scholar]
- Kink, I.; Hutton, R.; Nyström, B.; Martinson, I.; Ishii, K.; Ando, K.; Kambara, T.; Nakai, Y.; Kojima, T.M.; Awaya, Y. Lifetime of the 3p 2P3/2 level in Na-like Kr25+. Phys. Rev. A 1997, 55, 3229–3232. [Google Scholar] [CrossRef]
- Vasilyev, A.; Jasper, E.; Berry, H.G.; Livingston, A.E.; Curtis, L.J.; Cheng, S.; Dunford, R.W. Lifetime of the 3p 2P3/2 level in sodiumlike bromine (Br XXV). Phys. Rev. A 1998, 58, 732–735. [Google Scholar] [CrossRef]
- Schnabel, R.; Kock, M. f-value measurement of the Be I resonance line using a nonlinear time-resolved laser-induced-fluorescence technique. Phys. Rev. A 2000, 61, 062506. [Google Scholar]
- Verdebout, S.; Rynkun, P.; Jönsson, P.; Gaigalas, G.; Froese Fischer, C.; Godefroid, M. A partitioned correlation function interaction approach for describing electron correlation in atoms. J. Phys. B: At. Mol. Opt. Phys. 2013, 46, 085003. [Google Scholar]
- Wiese, W.L.; Smith, M.W.; Glennon, B.M. NSRDS-NBS4—Atomic Transition Probabilities; Government Printing Office: Washington, DC, USA, 1966; Volume I Hydrogen Through Neon, pp. 1–169.
- Kwong, H.S.; Smith, P.L.; Parkinson, W.H.; Knight, R.D. Transition probability of the C III 190.9 nm intersystem line. Bull. Am. Phys. Soc. 1983, 28, 781. [Google Scholar]
- Smith, P.L.; Kwong, H.S.; Johnson, B.C.; Parkinson, W.H. Measurements of A-values for C III (1909 Å) and O III (1660, 1666 Å) intersystem lines used in solar transition zone electron density determinations. Bull. Am. Astron. Soc. 1983, 15, 703. [Google Scholar]
- Smith, P.L.; Johnson, B.C.; Kwong, H.S.; Parkinson, W.H.; Knight, R.D. Measurements of transition probabilities for spin-changing lines of atomic ions used in diagnostics of astrophysical plasmas. Phys. Scr. T 1984, 8, 88–94. [Google Scholar]
- Kwong, V.H.S.; Fang, Z.; Gibbons, T.T.; Parkinson, W.H.; Smith, P.L. Measurement of the transition probability of the C III 190.9 nanometer intersystem line. Astrophys. J. 1993, 411, 431–437. [Google Scholar]
- Wiese, W.L.; Fuhr, J.R.; Deters, T.M. Atomic Transition Probabilities of Carbon, Nitrogen, and Oxygen: A Critical Data Compilation; Series: Journal of Physical and Chemical Reference Data, Monograph, No. 7; American Chemical Society: Washington, DC, USA, 1996; pp. 1–522. [Google Scholar]
- Chou, H.-S.; Chi, H.-S.; Huang, K.-N. Core polarization effects on the intercombination and resonance transitions in Be-like ions. Chin. J. Phys. 1994, 32, 261–268. [Google Scholar]
- Ral’chenko, Y.V.; Vainshtein, L.A. Intercombination transitions in Be-like ions. Phys. Rev. A 1995, 52, 2449–2452. [Google Scholar]
- Fleming, J.; Hibbert, A.; Stafford, R.P. The 1909 Å intercombination line in C III. Phys. Scr. 1994, 49, 316–322. [Google Scholar]
- Froese Fischer, C. Allowed transitions and intercombination lines in C III and C II. Phys. Scr. 1994, 49, 323–330. [Google Scholar]
- Ynnerman, A.; Froese Fischer, C. Multiconfigurational-Dirac-Fock computation of the 2s2 1S0 – 2s2p 3P1 spin-forbidden transition for the Be-like isoelectronic sequence. Phys. Rev. A 1995, 51, 2020–2030. [Google Scholar] [CrossRef]
- Doerfert, J.; Träbert, E.; Wolf, A.; Schwalm, D.; Uwira, O. Precision measurement of the electric dipole intercombination rate in C2+. Phys. Rev. Lett. 1997, 78, 4355–4358. [Google Scholar] [CrossRef]
- Curtis, L.J. Private Communication.
- Chen, M.H.; Cheng, K.T.; Johnson, W.R. Large-scale relativistic configuration-interaction computation of the 2s2 1S0 – 2s2p 3P1 intercombination transition in C III. Phys. Rev. A 2001, 64, 042507. [Google Scholar] [CrossRef]
- Kelly, R.L.; Palumbo, L.J. Atomic and Ionic Emission Lines Below 2000 Å, Hydrogen through Krypton; Naval Research Laboratory: Washington, DC, USA, 1973; pp. 1–1001. [Google Scholar]
- Vilkas, M.J.; Ishikawa, Y.; Träbert, E. Relativistic many-body perturbation computations of boron-like silicon, Si X. Phys. Scr. 2005, 72, 181–199. [Google Scholar] [CrossRef]
- Andrä, H.J.; Gaupp, A.; Wittmann, W. New method for precision lifetime measurements by laser excitation of fast-moving atoms. Phys. Rev. Lett. 1973, 31, 501–504. [Google Scholar] [CrossRef]
- Gaupp, A.; Kuske, P.; Andrä, H.J. Accurate lifetime measurements of the lowest 2P1/2 states in neutral lithium and sodium. Phys. Rev. A 1982, 26, 3351–3359. [Google Scholar] [CrossRef]
- Schulze-Hagenest, D. Ph.D. Thesis, University of Kaiserslautern, Kaiserslautern, Germany, 1979. cited in [56].
- Carlsson, J.; Sturesson, L. Accurate time-resolved laser spectroscopy on lithium atoms. Z. Phys. D 1989, 14, 281–287. [Google Scholar] [CrossRef]
- Carlsson, J. Laser spectroscopic studies of lifetimes in neutral atoms. Phys. Scr. 1989, 39, 442–446. [Google Scholar] [CrossRef]
- Carlsson, J.; Jönsson, P.; Sturesson, L.; Froese Fischer, C. Multi-configuration Hartree-Fock calculations and time-resolved laser spectroscopic studies of hyperfine constants in sodium. Phys. Scr. 1992, 46, 394–398. [Google Scholar] [CrossRef]
- McAlexander, W.I.; Abraham, E.R.I.; Ritchie, N.W.M.; Williams, C.J.; Stoof, H.T.C.; Hulet, R.G. Precise atomic radiative lifetime via photoassociative spectroscopy of ultracold lithium. Phys. Rev. A 1995, 51, R871–R874. [Google Scholar] [CrossRef] [PubMed]
- McAlexander, W.I.; Abraham, E.R.I.; Hulet, R.G. Radiative lifetime of the 2P state of lithium. Phys. Rev. A 1996, 54, R5–R8. [Google Scholar] [CrossRef] [PubMed]
- Volz, U.; Majerus, M.; Liebel, H.; Schmitt, A.; Schmoranzer, H. Precision lifetime measurements on Na I 3p 2P1/2 and 3p 2P3/2 by beam-gas-laser spectroscopy. Phys. REv. Lett. 1996, 76, 2862–2865. [Google Scholar] [CrossRef] [PubMed]
- Astner, G.; Curtis, L.J.; Liljeby, L.; Mannervik, S.; Martinson, I. A high precision beam-foil meanlife measurement of the 1s3p 1P level in He I. Z. Phys. A 1976, 279, 1–6. [Google Scholar] [CrossRef]
- Martinson, I. Private Communication.
- Cheng, K.T.; Kim, Y.-K.; Desclaux, J.P. Electric dipole, quadrupole, and magnetic dipole transition probabilities of ions isoelectronic to the first-row atoms, Li through F. At. Data Nucl. Data Tables 1979, 24, 111–189. [Google Scholar] [CrossRef]
- Huang, K.-N. Energy-level scheme and transition probabilities of Al-like ions. At. Data Nucl. Data Tables 1986, 34, 1–77. [Google Scholar] [CrossRef]
- Huang, K.-N. Energy-level scheme and transition probabilities of Si-like ions. At. Data Nucl. Data Tables 1985, 32, 503–566. [Google Scholar] [CrossRef]
- Huang, K.-N. Energy-level scheme and transition probabilities of P-like ions. At. Data Nucl. Data Tables 1984, 30, 313–421. [Google Scholar] [CrossRef]
- Huang, K.-N.; Kim, Y.-K.; Cheng, K.T.; Desclaux, J.P. Energy-level scheme and transition probabilities of Cl-like ions. At. Data Nucl. Data Tables 1983, 28, 355–377. [Google Scholar] [CrossRef]
- Huang, K.-N.; Johnson, W.R. Resonance transitions of Mg-and Zn-like ions from multiconfiguration relativistic random-phase approximation. Nucl. Instrum. Meth. Phys. Res. B 1985, 9, 502–504. [Google Scholar]
- Chou, H.-S.; Chi, H.-C.; Huang, K.-N. Relativistic excitation energies and oscillator strengths including core-polarization effects for the intercombination and resonance transitions in Mg-like ions. J. Phys. B: At. Mol. Opt. Phys. 1993, 26, 4079–4089. [Google Scholar] [CrossRef]
- Johnson, W.R.; Soff, B. The Lamb shift in hydrogen-like atoms, 1 ≤ Z ≤ 110. At. Data Nucl. Data Tables 1985, 33, 405–446. [Google Scholar] [CrossRef]
- Beiersdorfer, P.; Osterheld, A.; Scofield, J.; Crespo López-Urrutia, J.; Widmann, K. Measurement of QED and hyperfine splitting in the 2s1/2-2p3/2 X-ray transition in Li-like 209Bi80+. Phys. Rev. Lett. 1998, 80, 3022–3025. [Google Scholar] [CrossRef]
- Beiersdorfer, P.; Knapp, D.; Marrs, R.E.; Elliott, S.R.; Chen, M.H. Structure and Lamb shift of 2s1/2 - 2p3/2 levels in lithiumlike U89+ through neonlike U82+. Phys. Rev. Lett. 1993, 71, 3939–3942. [Google Scholar] [CrossRef] [PubMed]
- Beiersdorfer, P.; Chen, H.; Thorn, D.B.; Träbert, E. Measurement of the two-loop Lamb shift in lithiumlike U89+. Phys. Rev. Lett. 2005, 95, 233003. [Google Scholar] [CrossRef] [PubMed]
- Kozhedub, Y.S.; Andreev, O.V.; Shabaev, V.M.; Tupitsyn, I.I.; Brandau, C.; Kozhuharov, C.; Plunien, G.; Stöhlker, T. Nuclear deformation effect on the binding energies in heavy ions. Phys. Rev. A 2008, 77, 032501. [Google Scholar] [CrossRef]
- Shabaev, V.M.; Andreev, O.V.; Bondarev, A.I.; Glazov, D.A.; Kozhedub, Y.S.; Maiorova, A.V.; Plunien, G.; Tupitsyn, I.I.; Volotka, A.V. Quantum electrodynamics effects in heavy ions and atoms. AIP Conf. Proc. 2011, 1344, 60–69. [Google Scholar]
- Johnson, W.R.; Plante, D.R.; Sapirstein, J. Relativistic Computations of Transition Amplitudes in the Helium Isoelectronic Sequence. In Advances of Atomic, Molecular, and Optical Physics; Bederson, B., Walther, H., Eds.; Academic Press: San Diego, CA, USA, 1995; Volume 35, pp. 255–329. [Google Scholar]
- Toleikis, S.; Manil, B.; Berdermann, E.; Beyer, H.F.; Bosch, F.; Czanta, M.; Dunford, R.W.; Gumberidze, A.; Indelicato, P.; Kozhuharov, C.; et al. Lifetime of the 2 3P0 state of He-like 197Au. Phys. Rev. A 2004, 69, 022507. [Google Scholar] [CrossRef]
- Munger, C.T.; Gould, H. Lamb shift in heliumlike uranium (U90+). Phys. Rev. Lett. 1986, 57, 2927–2930. [Google Scholar] [CrossRef] [PubMed]
- Reuschl, R.; Gassner, T.; Spillmann, U.; Bräuning-Demian, A.; Ananyeva, A.; Beyer, H.; Blumenhagen, K.-H.; Chen, W.; Hagmann, S.; Hegewald, M.; et al. Lifetime measurement of the 2 3P0 state in He-like uranium. Phys. Scr. T 2013, 156, 014024. [Google Scholar]
- Trassinelli, M.; Kumar, A.; Beyer, H.F.; Indelicato, P.; Märtin, R.; Reuschl, R.; Kozhedub, Y.S.; Brandau, C.; Bräuning, H.; Geyer, S.; et al. Observation of the 2p3/2 → 2s1/2 intra-shell transition in He-like uranium. Europhys. Lett. 2009, 87, 63001. [Google Scholar] [CrossRef]
- Gabriel, A.H.; Jordan, C. Long wavelength satellites to the He-like ion resonance lines in the laboratory and the sun. Nature 1969, 221, 947–949. [Google Scholar] [CrossRef]
- Drake, G.W.F. Theory of relativistic magnetic dipole transitions: Lifetime of the metastable 2 3S state of the heliumlike ions. Phys. Rev. A 1971, 3, 908–915. [Google Scholar] [CrossRef]
- Lin, C.D. Ph.D. Thesis, Columbia University, New York, NY, USA, 1975.
- Schmidt, H.T.; Forck, P.; Grieser, M.; Habs, D.; Kenntner, J.; Miersch, G.; Repnow, R.; Schramm, U.; Schüssler, T.; Schwalm, D.; et al. High-precision measurement of the magnetic-dipole decay rate of metastable heliumlike carbon ions in a storage ring. Phys. Rev. Lett. 1994, 72, 1616–1619. [Google Scholar] [CrossRef] [PubMed]
- Saghiri, A.A.; Linkemann, J.; Schmitt, M.; Schwalm, D.; Wolf, A.; Bartsch, T.; Hoffknecht, A.; Müller, A.; Graham, W.G.; Price, A.D.; et al. Dielectronic recombination of ground-state and metastable Li+ ions. Phys. Rev. A 1999, 60, R3350–R3353. [Google Scholar] [CrossRef]
- Träbert, E.; Gwinner, G.; Knystautas, E.J.; Wolf, A. Heavy-ion storage-ring quest for atomic lifetimes in Li+ and Be2+. Can. J. Phys. 2003, 81, 941–952. [Google Scholar] [CrossRef]
- Crespo López-Urrutia, J.R.; Beiersdorfer, P.; Savin, D.W.; Widmann, K. Precision measurement of the lifetime of the 1s2s 3S1 metastable level in heliumlike O6+. Phys. Rev. A 1998, 58, 238–241. [Google Scholar] [CrossRef]
- Träbert, E.; Beiersdorfer, P.; Brown, G.V.; Smith, A.J.; Utter, S.B.; Gu, M.F.; Savin, D.W. Improved electron-beam ion-trap lifetime measurement of the 1s2s 3S1 level in Ne8+. Phys. Rev. A 1999, 60, 2034–2038. [Google Scholar] [CrossRef]
- Crespo López-Urrutia, J.R.; Beiersdorfer, P.; Widmann, K. Lifetime of the 1s2s 3S1 metastable level in He-like S14+ measured with an electron beam ion trap. Phys. Rev. A 2006, 74, 012507. [Google Scholar] [CrossRef]
- Dunford, R.W.; Church, D.A.; Liu, C.J.; Berry, H.G.; Raphaelian, M.L.A.; Hass, M.; Curtis, L.J. Lifetime of the 2 3S1 state of heliumlike 79Br33+. Phys. Rev. A 1990, 41, 4109–4111. [Google Scholar] [CrossRef] [PubMed]
- Birkett, B.B.; Briand, J.-P.; Charles, P.; Dietrich, D.D.; Finlayson, K.; Indelicato, P.; Liesen, D.; Simionovici, A. Hyperfine quenching and measurement of the 2 3P0 - 2 3P1 fine-structure splitting in heliumlike silver (Ag45+). Phys. Rev. A 1993, 47, R2454–R2457. [Google Scholar] [CrossRef] [PubMed]
- Simionovici, A.; Birkett, B.B.; Marrus, R.; Charles, P.; Indelicato, P.; Dietrich, D.D.; Finlayson, K. Cascade-free Doppler-tuned precision measurement of the 2 3S1 state in He-like niobium (93Nb39+). Phys. Rev. A 1994, 49, 3553–3556. [Google Scholar] [CrossRef] [PubMed]
- Marrus, R.; Charles, P.; Indelicato, P.; de Billy, L.; Tazi, C.; Briand, J.-P.; Simionovici, A.; Dietrich, D.D.; Bosch, F.; Liesen, D. Lifetime of the 2 3S1 state of heliumlike xenon (Xe52+). Phys. Rev. A 1989, 39, 3725–3727. [Google Scholar] [CrossRef] [PubMed]
- Hubricht, G.G.; Träbert, E. The argon 2 3S1 lifetime from a measurement on recoil ions. Z. Phys. D 1987, 7, 243–250. [Google Scholar] [CrossRef]
- Moos, H.W.; Woodworth, J.R. Observation of the forbidden 2 3S1 → 1 1S0 spontaneous emission line from helium and measurement of the transition rate. Phys. Rev. Lett. 1973, 30, 775–778. [Google Scholar] [CrossRef]
- Saathoff, G.; Reinhardt, S.; Karpuk, S.; Träbert, E. Quest for higher precision on the Li II M1 transition rate. 2004; unpublished. [Google Scholar]
- Kim, Y.-K.; Baik, D.H.; Indelicato, P.; Desclaux, J.P. Resonance transition energies of Li-, Na-, and Cu-like ions. Phys. Rev. A 1991, 44, 148–166. [Google Scholar] [CrossRef] [PubMed]
- Blundell, S.A. computations of the screened self-energy and vacuum polarization in Li-like, Na-like, and Cu-like ions. Phys. Rev. A 1993, 47, 1790–1803. [Google Scholar] [CrossRef] [PubMed]
- Träbert, E.; Beiersdorfer, P.; Lepson, J.K.; Chen, H. Extreme ultraviolet spectra of highly charged Xe ions. Phys. Rev. A 2003, 68, 042501. [Google Scholar] [CrossRef]
- Träbert, E.; Beiersdorfer, P.; Chen, H. Wavelengths of the 4s1/2-4p3/2 resonance lines in Cu- and Zn-like heavy ions. Phys. Rev. A 2004, 70, 032506. [Google Scholar] [CrossRef]
- Denne, B.; Magyar, G.; Jacquinot, J. Berylliumlike Mo XXXIX and lithiumlike Mo XL observed in the Joint European Torus. Phys. Rev. A 1989, 40, 3702–3705. [Google Scholar] [CrossRef] [PubMed]
- Büttner, R.; Staude, U.; Nicolai, M.; Braukhoff, J.; Schartner, K.-H.; Folkmann, F.; Mokler, P.H. Measurement of the 2s 2S1/2 - 2p 2P3/2 wavelength in Li-like nickel. Nucl. Instrum. Meth. Phys. Res. B 1995, 98, 41–44. [Google Scholar] [CrossRef]
- Staude, U.; Bosselmann, Ph.; Büttner, R.; Horn, D.; Schartner, K.-H.; Folkmann, F.; Livingston, A.E.; Ludziejewski, T.; Mokler, P.H. Measurements of 2s 2S1/2 − 2p 2P3/2,1/2 transition energies in lithiumlike heavy ions: Experiments and results for Ni25+ and Zn27+. Phys. Rev. A 1998, 58, 3516–3523. [Google Scholar] [CrossRef]
- Bosselmann, Ph.; Staude, U.; Horn, D.; Schartner, K.-H.; Folkmann, F.; Livingston, A.E.; Mokler, P.H. Measurements of 2s 2S1/2 - 2p 2P1/2,3/2 transition energies in lithiumlike heavy ions. II. Experimental results for Ag44+ and discussion along the isoelectronic series. Phys. Rev. A 1999, 59, 1874–1883. [Google Scholar] [CrossRef]
- Feili, D.; Bosselmann, Ph.; Schartner, K.-H.; Folkmann, F.; Livingston, A.E.; Träbert, E.; Ma, X.; Mokler, P.H. Measurements of 2s 2S1/2 - 2p 2P1/2,3/2 transition energies in lithiumlike heavy ions. III. Experimental results for Sn47+ and Xe51+. Phys. Rev. A 2000, 62, 022501. [Google Scholar] [CrossRef]
- Feili, D.; Bosselmann, Ph.; Schartner, K.-H.; Mokler, P.H.; Ma, X.; Livingston, A.E.; Folkmann, F.; Träbert, E. Access to two-photon QED contributions via 2s 2S1/2 - 2p 2P1/2 transitions in heavy Li-like ions. Phys. Scr. T 2001, 92, 300–302. [Google Scholar]
- Schweppe, J.; Belkacem, A.; Blumenfeld, L.; Claytor, N.; Feinberg, B.; Gould, H.; Kostroun, V.E.; Levy, L.; Misawa, S.; Mowat, J.R.; et al. Measurement of the Lamb shift in lithiumlike uranium (U89+). Phys. Rev. Lett. 1991, 66, 1434–1437. [Google Scholar] [CrossRef] [PubMed]
- Theodosiou, C.E.; Curtis, L.J.; El Mekki, M. computations of 2p Lifetimes in the Li Sequence. Phys. Rev. A 1991, 44, 7144–7157. [Google Scholar] [CrossRef] [PubMed]
- Aggarwal, K.M.; Keenan, F.P. Energy levels, radiative rates, and electron impact excitation rates for transitions in Li-like ions with 12 ≤ Z ≤ 20. At. Data Nucl. Data Tables 2013, 99, 156–248. [Google Scholar] [CrossRef]
- Aggarwal, K.M.; Keenan, F.P. Energy levels, radiative rates, and electron impact excitation rates for transitions in Li-like ions with 21 ≤ Z ≤ 28. At. Data Nucl. Data Tables 2013, 98, 1096–1108. [Google Scholar]
- Zou, Y.; Hutton, R.; Feili, D.; Neacsu, C.; Ma, X.; Schartner, K.-H.; Mokler, P.H. Precision lifetime measurement of the 2p 2P3/2 level for Li-like Ni by beam-foil spectroscopy. Nucl. Instrum. Meth. Phys. Res. B 2005, 235, 192–196. [Google Scholar] [CrossRef]
- Jasper, E.; Vasilyev, A.; Kukla, K.W.; Vogel Vogt, C.M.; Livingston, A.E.; Berry, H.G.; Cheng, S.; Curtis, L.J.; Dunford, R.W. Lifetime measurements for allowed and forbidden transitions. Phys. Scr. T 1999, 80, 466–468. [Google Scholar] [CrossRef]
- Kukla, K.W.; Livingston, A.E.; Vogel Vogt, C.M.; Berry, H.G.; Dunford, R.W.; Curtis, L.J.; Cheng, S. Extreme-ultraviolet wavelength and lifetime measurements in highly-ionized krypton. Can. J. Phys. 2005, 83, 1127–1139. [Google Scholar] [CrossRef]
- Epp, S.W.; Crespo López-Urrutia, J.R.; Brenner, G.; Mäckel, V.; Mokler, P.H.; Treusch, R.; Kuhlmann, M.; Yurkov, M.V.; Feldhaus, J.; Schneider, J.R.; et al. Soft X-ray laser spectroscopy on trapped highly charged ions at FLASH. Phys. Rev. Lett. 2007, 98, 183001. [Google Scholar] [CrossRef] [PubMed]
- Träbert, E.; Armour, I.A.; Bashkin, S.; Jelley, N.A.; O’Brien, R.; Silver, J.D. The x-ray spectra of H-like, He-like and Li-like silicon ions after foil excitation. J. Phys. B 1979, 12, 1665–1676. [Google Scholar] [CrossRef]
- Armour, I.A.; Fawcett, B.C.; Silver, J.D.; Träbert, E. X-ray spectra and satellite classification of foil-excited Mg and Al. J. Phys. B 1980, 13, 2701–2709. [Google Scholar] [CrossRef]
- Träbert, E.; Fawcett, B.C.; Silver, J.D. One- and two-electron one-photon satellite transitions in the x-ray spectrum of foil-excited F and Si. J. Phys. B 1982, 15, 3587–3597. [Google Scholar] [CrossRef]
- Mannervik, S.; Cederquist, H.; Träbert, E. On the EUV spectrum of Li I. Phys. Scr. 1986, 34, 143–145. [Google Scholar] [CrossRef]
- Mannervik, S.; Short, R.T.; Sonnek, D.; Träbert, E.; Möller, G.; Lodwig, V.; Heckmann, P.H.; Blanke, J.H.; Brand, K. Bound triply excited states in neutral lithium. Phys. Rev. A 1989, 39, 3964–3968. [Google Scholar] [CrossRef] [PubMed]
- Träbert, E.; Mannervik, S. Satellite lines from core-excited states in neutral lithium. Phys. Rev. A 1989, 40, 1667–1669. [Google Scholar] [CrossRef] [PubMed]
- Mannervik, S.; Cederquist, H.; Kisielinski, M. Determination of autoionization rates by means of optical emission spectroscopy. Phys. Scr. 1984, T8, 107–111. [Google Scholar] [CrossRef]
- Mannervik, S. Optical studies of multiply excited states. Phys. Scr. 1980, 40, 28–52. [Google Scholar] [CrossRef]
- Safronova, M.S.; Johnson, W.R.; Safronova, U. I Relativistic many-body computations of the energies of n = 2 states for the berylliumlike isoelectronic sequence. Phys. Rev. A 1996, 53, 4036–4053. [Google Scholar] [CrossRef] [PubMed]
- Safronova, U.I.; Johnson, W.R.; Safronova, M.S.; Derevianko, A. Relativistic many-body computations of transition probabilities for the 2l1 2l2 [LSJ] – 2l3 2l4 [L’S’J’] lines in Be-like ions. Phys. Scr. 1999, 59, 286–295. [Google Scholar] [CrossRef]
- Safronova, U.I.; Johnson, W.R.; Derevianko, A. Relativistic many-body computations of magnetic dipole transitions in Be-like ions. Phys. Scr. 1999, 60, 46–53. [Google Scholar] [CrossRef]
- Chen, M.H.; Cheng, K.T. Energy levels of the ground state and the 2s2p n(J = 1) excited states of berylliumlike ions: A large-scale, relativistic configuration-interaction computation. Phys. Rev. A 1997, 55, 166–174. [Google Scholar] [CrossRef]
- Möller, G.; Träbert, E.; Lodwig, V.; Wagner, C.; Heckmann, P.H.; Blanke, J.H.; Livingston, A.E.; Mokler, P.H. Experimental transition probability for the E1 intercombination transition in Be-like Xe50+. Z. Phys. D 1989, 11, 333–334. [Google Scholar] [CrossRef]
- Brage, T.; Fleming, J.; Hutton, R. A review of intercombination lines in beryllium-like ions. Mol. Phys. 2000, 98, 1057–1065. [Google Scholar] [CrossRef]
- Fawcett, B.C. Wavelengths and classifications of emission lines due to 2s22pn-2s2pn+1 and 2s2pn-2pn+1 transitions, Z ≤ 28. At. Data Nucl. Data Tables 1975, 16, 135–164. [Google Scholar] [CrossRef]
- Hutton, R.; Engström, L.; Träbert, E. Experimental oscillator strengths for the resonance lines in Na- and Mg-like iron. Nucl. Instrum. Meth. Phys. Res. B 1988, 31, 294–299. [Google Scholar] [CrossRef]
- Cheng, K.T.; Chen, M.H.; Johnson, W.R. Hyperfine quenching of the 2s2p 3P0 state of berylliumlike ions. Phys. Rev. A 2008, 77, 052504. [Google Scholar] [CrossRef]
- Träbert, E. E1-forbidden transition rates in ions of astrophysical interest. In Proceedings of the ASOS11 Conference, Mons, Belgium, 4–9 August 2013. Phys. Scr. T 2014, submitted.
- Kaufman, V.; Sugar, J. Forbidden lines in ns2 npk ground configurations and ns np excited configurations of beryllium through molybdenum atoms and ions. J. Phys. Chem. Ref. Data 1986, 15, 321–427. [Google Scholar] [CrossRef]
- Huang, K.-N.; Kim, Y.-K.; Cheng, K.T.; Desclaux, J.P. Correlation and relativistic effects in spin-orbit splitting. Phys. Rev. Lett. 1982, 48, 1245–1248. [Google Scholar] [CrossRef]
- Safronova, M.S.; Johnson, W.R.; Safronova, U.I. Relativistic many-body computations of energies of n = 2 states for boronlike ions. Phys. Rev. A 1996, 54, 2850–2862. [Google Scholar] [CrossRef] [PubMed]
- Merkelis, G.; Vilkas, M.J.; Gaigalas, G.; Kisielius, R. MBPT computation of energy spectra and E1 transition probabilities for boron isoelectronic sequence. Phys. Scr. 1995, 51, 233–251. [Google Scholar] [CrossRef]
- Vilkas, M.J.; Ishikawa, Y.; Koc, K. Second-order multiconfigurational Dirac-Fock computations on boronlike ions. Int. J. Quantum Chem. 1998, 70, 813–823. [Google Scholar] [CrossRef]
- Li, J.-G.; Jönsson, P.; Dong, C.-Z.; Gaigalas, G. Two-electron-one-photon M1 and E2 transitions between the states of the 2p3 and 2s22p odd configurations for B-like ions with 18 ≤ Z ≤ 92. J. Phys. B: At. Mol. Opt. Phys. 2010, 43, 035005. [Google Scholar] [CrossRef]
- Safronova, U.I.; Johnson, W.R.; Livingston, A.E. Relativistic many-body computations of electric-dipole transitions between n = 2 states in B-like ions. Phys. Rev. A 1999, 60, 996–1004, erratum 2000, 61, 039901. [Google Scholar]
- Jönsson, P.; Li, J.-G.; Gaigalas, G.; Dong, C.-Z. Hyperfine structures, isotope shifts, and transition rates of C II, N III, and O IV from relativistic configuration interaction computations. At. Data Nucl. Data Tables 2010, 96, 271–298. [Google Scholar] [CrossRef]
- Rynkun, P.; Jönsson, P.; Gaigalas, G.; Froese Fischer, C. Energies and E1, M1, E2, M2 transition rates for states of the 2s22p, 2s2p2, and 2p3 configurations in boron-like ions between N III and Zn XXVI. At. Data Nucl. Data Tables 2012, 98, 481–556. [Google Scholar] [CrossRef]
- Jönsson, P.; Ekman, J.; Gustafsson, S.; Hartman, H.; Karlsson, L.B.; du Rietz, R.; Gaigalas, G.; Godefroid, M.; Froese Fischer, C. Energy levels and transition rates for the boron isoelectronic sequence: Si X, Ti XVIII – Cu XXV. Astron. Astrophys. 2013, 559, A100. [Google Scholar] [CrossRef]
- Träbert, E.; Heckmann, P.H.; Schlagheck, W.; Buttlar, H.V. Beam-foil lifetime studies of highly ionized silicon. Phys. Scr. 1980, 21, 27–34. [Google Scholar] [CrossRef]
- Träbert, E.; Heckmann, P.H. EUV spectrum and lifetimes of foil-excited phosphorus. Phys. Scr. 1980, 21, 35–39. [Google Scholar] [CrossRef]
- Tordoir, X.; Biémont, E.; Garnir, H.P.; Dumont, P.-D.; Träbert, E. Atomic lifetimes and transition probabilities in boron-like (Na VII) and beryllium-like (Na VIII) sodium ions. Eur. Phys. J. D 1999, 6, 1–7. [Google Scholar] [CrossRef]
- Doerfert, J.S.; Träbert, E. Relative intensities of 2s22p 2P – 2s2p2 2S, 2P transitions in B-like ions of oxygen through chlorine. Phys. Scr. 1993, 47, 524–530. [Google Scholar] [CrossRef]
- Engström, L.; Kirm, M.; Bengtsson, P.; Maniak, S.T.; Curtis, L.J.; Träbert, E.; Doerfert, J.S.; Granzow, J. Extended analysis of intensity anomalies in the Al I isoelectronic sequence. Phys. Scr. 1995, 52, 516–521. [Google Scholar] [CrossRef]
- Träbert, E. On the transition rates of the FeX and Fe XIV coronal lines. Astron. Astrophys. 2004, 415, L39–L42. [Google Scholar] [CrossRef]
- Träbert, E.; Beiersdorfer, P.; Gwinner, G.; Pinnington, E.H.; Wolf, A. M1 transition rate in Cl12+ from an electron-beam ion trap and heavy-ion storage ring. Phys. Rev. A 2002, 66, 052507. [Google Scholar] [CrossRef]
- Moehs, D.P.; Church, D.A. Magnetic dipole transition rates from measured lfetimes of levels of Be-like and B-like argon ions. Phys. Rev. A 1998, 58, 1111–1114. [Google Scholar] [CrossRef]
- Serpa, F.G.; Gillaspy, J.D.; Träbert, E. Lifetime measurements in the ground configuration of Ar13+ and Kr22+ using an electron beam ion trap. J. Phys. B: At. Mol. Opt. Phys. 1998, 31, 3345–3352. [Google Scholar] [CrossRef]
- Träbert, E.; Beiersdorfer, P.; Utter, S.B.; Brown, G.V.; Chen, H.; Harris, C.L.; Neill, P.A.; Savin, D.W.; Smith, A.J. Experimental M1 tansition rates of coronal lines from Ar X, Ar XIV, and Ar XV. Astrophys. J. 2000, 541, 506–511. [Google Scholar] [CrossRef]
- Lapierre, A.; Jentschura, U.D.; Crespo López-Urrutia, J.R.; Braun, J.; Brenner, G.; Bruhns, H.; Fischer, D.; González Martínez, A.J.; Harman, Z.; Johnson, W.R.; et al. Relativistic electron correlation, quantum electrodynamics, and the lifetime of the 1s22s22p 2P level in boronlike argon. Phys. Rev. Lett. 2005, 95, 183001. [Google Scholar]
- Lapierre, A.; Crespo López-Urrutia, J.R.; Braun, J.; Brenner, G.; Bruhns, H.; Fischer, D.; González-Martínez, A.J.; Mironov, V.; Osborne, C.J.; Sikler, G.; et al. Lifetime measurement of the Ar XIV 1s22s22p 2P metastable level at the Heidelberg electron-beam ion trap. Phys. Rev. A 2006, 73, 052507. [Google Scholar]
- Träbert, E.; Gwinner, G.; Wolf, A.; Tordoir, X.; Calamai, A.G. Magnetic dipole transition rates in B-like and F-like titanium ions measured at a heavy-ion storage ring. Phys. Lett. A 1999, 264, 311–317. [Google Scholar] [CrossRef]
- Nemouchi, M.; Godefroid, M.R. Irreducible tensor fomathrm of the relativistic corrections to the M1 transition operator. J. Phys. B: At. Mol. Opt. Phys. 2009, 42, 175002. [Google Scholar] [CrossRef]
- Hibbert, A. Estimation of inaccuracies in oscillator strength computations. Phys. Scr. T 1996, 65, 104–109. [Google Scholar] [CrossRef]
- Brage, T.; Hibbert, A.; Leckrone, D.S. Transition rates of the intercombination UV0.01 multiplet in N II. Astrophys. J. 1997, 478, 423–429. [Google Scholar] [CrossRef]
- Träbert, E.; Wolf, A.; Pinnington, E.H.; Linkemann, J.; Knystautas, E.J.; Curtis, A.; Bhattacharya, N.; Berry, H.G. Measurement of the N1 2s2p3 5S level lifetime using a heavy-ion storage ring. Phys. Rev. A 1998, 58, 4449–4452. [Google Scholar]
- Jönsson, P.; Bieroń, J. Relativistic configuration interaction computations of energy levels, isotope shifts, hyperfine structures, and transition rates in the 2s22p2 - 2s2p3 transition array for the carbon-like sequence. J. Phys. B: At. Mol. Opt. Phys. 2010, 43, 074023. [Google Scholar] [CrossRef]
- Jönsson, P.; Rynkun, P.; Gaigalas, G. Energies, E1, M1, E2 transition rates, hyperfine structures, and Landé gJ factors for states of the 2s22p2, 2s2p3, and 2p4 configurations in carbon-like ions between F IV and Ni XXIII. At. Data Nucl. Data Tables 2011, 97, 648–691. [Google Scholar] [CrossRef]
- Rynkun, P.; Jönsson, P.; Gaigalas, G.; Froese Fischer, C. Energies and E1, M1, E2, and M2 transition rates for states of the 2s22p3, 2s2p4, and 2p5 configurations in nitrogen-like ions between F III and Kr XXX. At. Data Nucl. Data Tables 2013, 100, 315–402. [Google Scholar] [CrossRef]
- Träbert, E.; Calamai, A.G.; Gillaspy, J.D.; Gwinner, G.; Tordoir, X.; Wolf, A. Intercombination and forbidden transition rates in C- and N-like ions (O2+, F3+, and S9+) measured at a heavy-ion storage ring. Phys. Rev. A 2000, 62, 022507. [Google Scholar] [CrossRef]
- Träbert, E.; Wolf, A.; Pinnington, E.H.; Linkemann, J.; Knystautas, E.J.; Curtis, A.; Bhattacharya, N.; Berry, H.G. Heavy-ion storage ring measurement of forbidden transition rates between ground-configuration levels in Si6+ and Si8+ ions. Can. J. Phys. 1998, 5876, 899–906. [Google Scholar] [CrossRef]
- Träbert, E.; Grieser, M.; Hoffmann, J.; Krantz, C.; Repnow, R.; Wolf, A. Heavy-ion storage-ring-lifetime measurement of metastable levels in the C-, N-, and O-like ions of Si, P, and S. Phys. Rev. A 2012, 85, 042508. [Google Scholar] [CrossRef]
- Edlén, B. Comparison of theoretical and experimental level values of the n = 2 complex of ions isoelectronic with Li, Be, O and F. Phys. Scr. 1983, 28, 51–67. [Google Scholar] [CrossRef]
- Jönsson, P.; Alkauskas, A.; Gaigalas, G. Energies and E1, M1, E2 transition rates for states of the image and image configurations in fluorine-like ions between Si VI and W LXVI. At. Data Nucl. Data Tables 2013, 99, 431–446. [Google Scholar] [CrossRef]
- Jönsson, P.; Bengtsson, P.; Ekman, J.; Gustafsson, S.; Karlsson, L.B.; Gaigalas, G.; Froese Fischer, C.; Kato, D.; Murakami, I.; Sakaue, H.A.; et al. Relativistic CI computations of spectroscopic data for the 2p6 and 2p53l configurations in Ne-like ions between Mg III and Kr XXVII. At. Data Nucl. Data Tables 2014, 100, 1–154. [Google Scholar] [CrossRef]
- Träbert, E. Beam-foil lifetime study of Neon-like Ti12+. Z. Phys. D 1986, 1, 283–286. [Google Scholar] [CrossRef]
- Kirm, M.; Bengtsson, P.; Engström, L. Experimental investigation of atomic lifetimes for the 2p53l levels in Ne-like sulphur. Phys. Scr. 1996, 54, 167–173. [Google Scholar] [CrossRef]
- Träbert, E.; Jupén, C. Identification of 2s22p53p 1S0 decays in the spectra of Ne-like ions. Phys. Scr. 1987, 36, 586–590. [Google Scholar] [CrossRef]
- Ishikawa, Y.; López Encarnaciön, J.M.; Träbert, E. N = 3–3 transitions of Ne-like ions in the iron group, especially Ca10+ and Ti12+. Phys. Scr. 2009, 79, 025301. [Google Scholar] [CrossRef]
- DelZanna, G.; Ishikawa, Y. Benchmarking atomic data for astrophysics: Fe XVII EUV lines. Astron. Astrophys. 2009, 508, 1517–1526. [Google Scholar] [CrossRef]
- Beiersdorfer, P.; Träbert, E.; Lepson, J.K.; Brickhouse, N.S.; Golub, L. High-resolution laboratory measurements of coronal lines in the 198-218 Å region. Astrophys. J. Suppl. Ser. 2014. In print. [Google Scholar]
- Schectman, R.M.; Curtis, L.J.; Chojnacki, D.A. Redetermination of the meanlife of the 2p level in Ne I using cascade analysis. J. Opt. Soc. Am. 1973, 63, 99–100. [Google Scholar] [CrossRef]
- Westerlind, M.; Engström, L.; Bengtsson, P.; Curtis, L.J. Experimental lifetimes of the 2p5 3s 1P1 and 3P1 levels in Ne-like sulfur and chlorine. Phys. Rev. A 1992, 45, 6198–6201. [Google Scholar] [CrossRef] [PubMed]
- Curtis, L.J.; Maniak, S.T.; Ghrist, R.W.; Irving, R.E.; Ellis, D.G.; Henderson, M.; Kacher, M.H.; Träbert, E.; Granzow, J.; Bengtsson, P.; Engström, L. Measurements and data-based predictions for Δn = 1 resonance and intercombination transitions in the Be and Ne sequences. Phys. Rev. A 1995, 51, 4575–4582. [Google Scholar] [CrossRef] [PubMed]
- Träbert, E. Beam-foil Lifetimes of 2p53s 1,3P levels in Ne-like ions of Na through S. Phys. Scr. 1996, 53, 167–173. [Google Scholar] [CrossRef]
- Beiersdorfer, P.; Osterheld, A.L.; Decaux, V.; Widmann, K. Observation of Lifetime-Limited X-Ray Linewidths in Cold Highly Charged Ions. Phys. Rev. Lett. 1996, 77, 5353–5356. [Google Scholar] [CrossRef] [PubMed]
- Brown, G.V.; Beiersdorfer, P.; Widmann, K. Systematic measurement of the relative electron-impact excitation cross section of the 3d→ 2p 1P1 resonance and 3D1 intercombination lines in mid-Z neonlike ions. Phys. Rev. A 2001, 63, 032719. [Google Scholar] [CrossRef]
- Brown, G.V.; Beiersdorfer, P.; Liedahl, D.A.; Widmann, K.; Kahn, S.M.; Clothiaux, E.J. Laboratory measurements and identifications of the Fe XVIII-XXIV L-shell X-ray line emission. Astrophys. J. Suppl. Ser. 2002, 140, 589–607. [Google Scholar] [CrossRef]
- Gu, M.F. The flexibe atomic code. Can. J. Phys. 2008, 86, 675–689. [Google Scholar] [CrossRef]
- Brown, G.V.; Beiersdorfer, P. Reply to a comment. Phys. Rev. Lett. 2012, 108, 139302. [Google Scholar] [CrossRef]
- Bernitt, S.; Brown, G.V.; Rudolph, J.K.; Steinbrügge, R.; Graf, A.; Leutenegger, M.; Epp, S.W.; Eberle, S.; Kubicek, K.; Mäckel, V.; et al. An unexpectedly low oscillator strength as the origin of the Fe XVII emission problem. Nature 2012, 492, 225–228. [Google Scholar] [CrossRef] [PubMed]
- Cowan, T.E.; Bennett, C.L.; Dietrich, D.D.; Bixler, J.V.; Hailey, C.J.; Henderson, J.R.; Knapp, D.A.; Levine, M.A.; Marrs, R.E.; Schneider, M.B. Precision measurement of the 3s1/2-3p3/2 transition energy in Na-like platinum ions. Phys. Rev. Lett. 1991, 66, 1150–1153. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.H.; Cheng, K.T.; Beiersdorfer, P.; Sapirstein, J. Transition energies of the 3s-3p3/2 resonance lines in sodiumlike to phosphoruslike uranium. Phys. Rev. A 2003, 68, 022507. [Google Scholar] [CrossRef]
- Gillaspy, J.D.; Draganić, I.N.; Ralchenko, Yu.; Reader, J.; Tan, J.N.; Pomeroy, J.M.; Brewer, S.M. Measurement of the D-line doublet in high-Z highly charged sodiumlike ions. Phys. Rev. A 2009, 80, 010501. [Google Scholar] [CrossRef]
- Gillaspy, J.D.; Osin, D.; Ralchenko, Yu.; Reader, J.; Blundell, S.A. Transition energies of the D lines in Na-like ions. Phys. Rev. A 2013, 87, 062503. [Google Scholar] [CrossRef]
- Vilkas, M.J.; Ishikawa, Y.; Träbert, E. Relativistic multireference many-body perturbation theory computations on Au64+ - Au69+ ions. Eur. Phys. J. D 2006, 41, 77–93. [Google Scholar] [CrossRef]
- Träbert, E.; Wolf, A.; Linkemann, J.; Tordoir, X. Optical measurement of the B+ and Al+ intercombination and Sc12+ forbidden transition rates at a heavy-ion storage ring. J. Phys. B: At. Mol. Opt. Phys. 1999, 32, 537–552. [Google Scholar] [CrossRef]
- Johnson, B.C.; Smith, P.L.; Parkinson, W.H. Transition probability of the Al II 2669 intersystem line. Astrophys. J. 1986, 308, 1013–1017. [Google Scholar] [CrossRef]
- Träbert, E.; Hutton, R.; Martinson, I. Identification of intercombination transitions in Fe XIV and Fe XIII in the spectra of foil-excited ions and solar flares. Mon. Not. R. Astron. Soc. 1987, 227, 27p–31p. [Google Scholar] [CrossRef]
- Träbert, E.; Heckmann, P.H.; Hutton, R.; Martinson, I. Intercombination lines in delayed beam-foil spectra. J. Opt. Soc. Am. B 1988, 5, 2173–2182. [Google Scholar] [CrossRef]
- Träbert, E.; Staude, U.; Bosselmann, P.; Schartner, K.H.; Mokler, P.H.; Tordoir, X. Intercombination transition rates in Al-like Au66+ ions. Eur. Phys. J. D 1998, 2, 117–123. [Google Scholar]
- Santana, J.A.; Ishikawa, Y.; Träbert, E. Multireference Møller-Plesset perturbation theory results on levels and transition rates in Al-like ions of iron group elements. Phys. Scr. 2009, 79, 065301. [Google Scholar] [CrossRef]
- Vilkas, M.J.; Ishikawa, Y. Relativistic multireference many-body perturbation-theory computations on the multiple openshell states in siliconlike Ar and aluminumlike Fe ions. Phys. Rev. A 2003, 68, 012503. [Google Scholar] [CrossRef]
- Moehs, D.P.; Bhatti, M.I.; Church, D.A. Measurements and computations of metastable level lifetimes in FeX, FeXI, FeXII, FeXIII, and Fe XIV. Phys. Rev. A 2001, 63, 032515. [Google Scholar] [CrossRef]
- Träbert, E.; Gwinner, G.; Wolf, A.; Knystautas, E.J.; Garnir, H.-P.; Tordoir, X. M1/E2 transition rates in Fe X through Fe XIII measured at a heavy-ion storage ring. J. Phys. B: At. Mol. Opt. Phys. 2002, 35, 671–689. [Google Scholar] [CrossRef]
- Träbert, E.; Calamai, A.G.; Gwinner, G.; Knystautas, E.J.; Pinnington, E.H.; Wolf, A. M1/E2/M2 decay rates in Fe VII, Fe IX, Fe X and Fe XIII measured using a heavy-ion storage ring. J. Phys. B: At. Mol. Opt. Phys. 2003, 36, 1129–1141. [Google Scholar] [CrossRef]
- Beiersdorfer, P.; Träbert, E.; Pinnington, E.H. Experimental transition rate of the green coronal line of Fe XIV. Astrophys. J. 2003, 587, 836–840. [Google Scholar] [CrossRef]
- Smith, S.J.; Chutjian, A.; Lozano, J.A. Measurement of metastable lifetimes for transitions in Fe9+, Fe10+, and Fe13+. Phys. Rev. A 2005, 72, 062504. [Google Scholar] [CrossRef]
- Brenner, G.; Crespo López-Urrutia, J.R.; Harman, Z.; Mokler, P.H.; Ullrich, J. Lifetime determination of the Fe XIV 3s23p 2Pmetastable level. Phys. Rev. A 2007, 75, 032504. [Google Scholar] [CrossRef]
- Träbert, E.; Hoffmann, J.; Krantz, C.; Wolf, A.; Ishikawa, Y.; Santana, J.A. Atomic lifetime measurements on forbidden transitions of Al-, Si-, P- and S-like ions at a heavy-ion storage ring. J. Phys. B: At. Mol. Opt. Phys. 2009, 42, 025002. [Google Scholar] [CrossRef]
- Bengtsson, P.; Ando, K.; Kambara, T.; Awaya, Y.; Hutton, R. Intercombination lines in highly charged Al- and Si-like ions. Phys. Scr. T 1997, 73, 81–82. [Google Scholar] [CrossRef]
- Träbert, E. Contradictory observations in beam-foil EUV spectroscopy at high ion energies. Phys. Scr. 1999, 59, 443–445. [Google Scholar] [CrossRef]
- Ishikawa, Y.; Vilkas, M.J. Relativistic multireference Møller-Plesset perturbation theory computations on the term energy and lifetime of the 5S state in siliconlike ions with Z = 28–79. Phys. Scr. 2002, 65, 219–226. [Google Scholar] [CrossRef]
- Biémont, E. Energy-level scheme and oscillator strengths for the 3s-3p and 3p-3d transitions in silicon sequence for elements vanadium through nickel. Phys. Scr. 1986, 33, 324–335. [Google Scholar] [CrossRef]
- Biémont, E. 3s23p2 - 3s3p3, 3s23p2 - 3s23p3d, and 3s23p2 - 3s23p4s transitions in the silicon sequence for elements potassium through titanium. J. Opt. Soc. Am. B 1986, 3, 163–176. [Google Scholar] [CrossRef]
- Träbert, E. Solar EUV line identifications from delayed beam-foil spectra. Mon. Not. R. Astron. Soc. 1998, 297, 399–404. [Google Scholar] [CrossRef]
- Ishikawa, Y.; Vilkas, M.J. Relativistic multireference many-body perturbation-theory computations of the magnetic-dipole and electric-quadrupole transition probabilities of ions in the silicon isoelectronic sequence. Phys. Rev. A 2001, 63, 042506. [Google Scholar] [CrossRef]
- Vilkas, M.J.; Ishikawa, Y. High-accuracy computations of term energies and lifetimes of silicon-like ions with nuclear charges Z = 24–30. J. Phys. B: At. Mol. Opt. Phys. 2004, 37, 1803–1816. [Google Scholar] [CrossRef]
- Träbert, E.; Ishikawa, Y.; Santana, J.A.; Del Zanna, G. The 3s23p3d 3Fo term in the Si-like spectrum of Fe (Fe XIII). Can. J. Phys. 2011, 89, 403–412. [Google Scholar] [CrossRef]
- Del Zanna, G. Benchmarking atomic data for astrophysics: Fe XIII. Astron. Astrophys. 2011, 533, A12. [Google Scholar] [CrossRef]
- Del Zanna, G.; Storey, P.J. Atomic data for astrophysics: Fe XIII soft X-ray lines. Astron. Astrophys. 2012, 543, A144. [Google Scholar] [CrossRef]
- Froese Fischer, C. Towards accurate transition data for 3p2, 3p3, 3p4 levels of Fe, Co and Ni ions. J. Phys. B: At. Mol. Opt. Phys. 2010, 43, 074020. [Google Scholar] [CrossRef]
- Mendoza, C.; Zeippen, C.J. Transition probabilities for forbidden lines in the 3p2 configuration—II. Mon. Not. R. Astron. Soc. 1982, 199, 1025–1032. [Google Scholar] [CrossRef]
- Abou El-Maaref, A.; Uosif, M.A.M.; Allam, S.H.; El-Sherbini, Th.M. Energy levels, oscillator strengths and transition probabilities for Si-like P II, S III, Cl IV, Ar V and K VI. At. Data Nucl. Data Tables 2012, 98, 589–615. [Google Scholar] [CrossRef]
- Abou El-Maaref, A.; Allam, S.H.; El-Sherbini, Th.M. Energy levels, oscillator strengths and radiative rates for Si-like Zn XVII, Ga XVIII, Ge XIX, ans As XX. At. Data Nucl. Data Tables 2014, 100, 155–182. [Google Scholar] [CrossRef]
- Vilkas, M.J.; Ishikawa, Y. Relativistic many-body perturbation computations on extreme ultraviolet and soft-x-ray transition energies in siliconlike iron. Phys. Rev. A 2004, 69, 062503. [Google Scholar]
- Mendoza, C.; Zeippen, C.J. Transition probabilities for forbidden lines in the 3p3 configuration. Mon. Not. R. Astron. Soc. 1982, 198, 127–139. [Google Scholar] [CrossRef]
- Biémont, E.; Hansen, J.E. Radiative transition rates in the ground configuration of the phosphorus sequence from argon to ruthenium. Phys. Scr. 1985, 31, 509–518. [Google Scholar] [CrossRef]
- Biémont, E.; Palmeri, P.; Quinet, P.; Träbert, E.; Zeippen, C.J. Level lifetimes in 3p and 3d configurations of Fe XII. Eur. Phys. J. D 2002, 20, 37–44. [Google Scholar]
- Vilkas, M.J.; Ishikawa, Y. Relativistic multireference many-body perturbation theory calculations on ions of the phosphorus isoelectronic sequence. J. Phys. B: At. Mol. Opt. Phys. 2004, 37, 4763–4778. [Google Scholar] [CrossRef]
- Del Zanna, G.; Mason, H.E. Benchmarking atomic data for astrophysics: Fe XII. Astron. Astrophys. 2005, 433, 731–744. [Google Scholar] [CrossRef]
- Mendoza, C.; Zeippen, C.J. Transition probabilities for forbidden lines in the 3p4 configuration—III. Mon. Not. R. Astron. Soc. 1983, 202, 981–986. [Google Scholar] [CrossRef]
- Biémont, E.; Hansen, J.E. Forbidden transitions in 3p4 and 4p4 configurations. Phys. Scr. 1986, 34, 116–130. [Google Scholar] [CrossRef]
- Saloman, E.B.; Kim, Y.-K. Energy levels and transition probabilities in the ground-state configuration of sulfur-like ions. At. Data Nucl. Data Tables 1989, 41, 339–356. [Google Scholar] [CrossRef]
- Chou, H.-S.; Chang, J.-Y.; Chang, Y.-H.; Huang, K.-N. Energy-level scheme and transition probabilities of S-like ions. At. Data Nucl. Data Tables 1996, 62, 77–145. [Google Scholar] [CrossRef]
- Ishikawa, Y.; Vilkas, M.J. Relativistic many-body computations of excited-state energies and transition wavelengths for six-valence-electron sulfurlike ions. Phys. Rev. A 2008, 78, 042501. [Google Scholar] [CrossRef]
- Del Zanna, G. Benchmarking atomic data for astrophysics: Fe XI. Astron. Astrophys. 2010, 514, A41. [Google Scholar] [CrossRef]
- Del Zanna, G.; Storey, P.J. Atomic data for astrophysics: Fe XI soft X-ray lines. Astron. Astrophys. 2013, 549, A42. [Google Scholar] [CrossRef]
- Biémont, E.; Träbert, E. Transition rates of the resonance line doublet in the Cl I sequence, Ar II-Ge XVI. J. Phys. B: At. Mol. Opt. Phys. 2000, 33, 2939–2946. [Google Scholar] [CrossRef]
- Del Zanna, G.; Berrington, K.A.; Mason, H.E. Benchmarking atomic data for astrophysics: Fe X. Astron. Astrophys. 2004, 422, 731–749. [Google Scholar] [CrossRef]
- Del Zanna, G.; Berrington, K.A.; Mason, H.E. Atomic data for astrophysics: Fe X soft X-ray lines. Astron. Astrophys. 2012, 541, A90. [Google Scholar] [CrossRef]
- Ishikawa, Y.; SAntana, J.A.; Träbert, E. Relativistic multireference many-body perturbation theory for open-shell ions with multiple valence shell electrons: the transition rates and lifetimes of the excited levels in chlorinelike Fe X. J. Phys. B: At. Mol. Opt. Phys. 2010, 43, 074022. [Google Scholar] [CrossRef]
- Träbert, E.; Saathoff, G.; Wolf, A. M1/E2 decay rates in Co XI, Ni XII and Cu XIII measured at a heavy-ion storage ring. Can. J. Phys. 2004, 37, 945–952. [Google Scholar] [CrossRef]
- Träbert, E. Experimental checks on computations for Cl-, S- and P-like ions of the iron group elements. J. Phys. B: At. Mol. Opt. Phys. 1996, 29, L217–L224. [Google Scholar] [CrossRef]
- Dumont, P.D.; Garnir, H.P.; Baudinet-Robinet, Y.; Kapenyak, M. Lifetime measurements in Ti IV-VII using transitions observed in beam-foil spectroscopy between 400 and 800 Å. J. Opt. Soc. Am. 1981, 71, 502–503. [Google Scholar] [CrossRef]
- Mohan, M.; Singh, A.K.; Jha, A.K.S.; Jha, P. Level energies, oscillator strengths, and lifetimes for transitions in Ti VI. At. Data Nucl. Data Tables 2007, 93, 105–126. [Google Scholar] [CrossRef]
- Garnir, H.P.; Dumont, P.D.; Tordoir, X. Atomic lifetime measurement of K III. unpublished work.
- Lauer, S.; Liebel, H.; Vollweiler, F.; Schmoranzer, H.; Lagutin, B.M.; Demekhin, Ph.V.; Petrov, I.D.; Sukhorukov, V.L. Lifetimes of the ns1 np6 2S1=2 states of singly ionized argon, krypton and xenon. J. Phys. B: At. Mol. Opt. Phys. 1999, 32, 2015–2030. [Google Scholar] [CrossRef]
- Wilson, N.J.; Hibbert, A.; Bell, K.L. Oscillator Strengths for K III, Ca IV and Sc V. Phys. Scr. 2000, 61, 603–610. [Google Scholar] [CrossRef]
- Berrington, K.A.; Pelan, J.C.; Waldock, J.A. Oscillator strength for 3s23p5 - 3s3p6 in Cl-like ions. J. Phys. B: At. Mol. Opt. Phys. 2001, 34, L419–L424. [Google Scholar] [CrossRef]
- Saha, B.; Fritzsche, S. M1 and E2 transitions in Ar II. J. Phys. B: At. Mol. Opt. Phys. 2005, 38, 1161–1171. [Google Scholar] [CrossRef]
- Wagner, W.J.; House, L.L. Hartree-Fock computations of coronal forbidden lines in the Argon I isoelectronic sequence. Astrophys. J. 1969, 155, 677–686. [Google Scholar] [CrossRef]
- Wagner, W.J.; House, L.L. Emprically corrected computations of coronal visible lines from the 3p53d configuration. Astrophys. J. 1971, 166, 683–698. [Google Scholar] [CrossRef]
- Träbert, E.; Jupén, C.; Fritzsche, S. EUV line identifications and lifetime measurements in highly-charged ions of the iron group. Phys. Scr. T 1999, 80, 463–465. [Google Scholar] [CrossRef]
- Träbert, E.; Beiersdorfer, P.; Brown, G.V.; Chen, H.; Thorn, D.B.; Biémont, E. Experimental M1 transition rates in highly charged Kr ions. Phys. Rev. A 2001, 64, 042511. [Google Scholar] [CrossRef]
- Utter, S.B.; Beiersdorfer, P.; Träbert, E.; Clothiaux, E.J. Wavelengths of the 4s1/2-4p3/2 resonance lines in Cu-like heavy ions. Phys. Rev. A 2003, 67, 032502. [Google Scholar] [CrossRef]
- Vilkas, M.J.; Ishikawa, Y. Relativistic multireference many-body perturbation computations on multi-valence-electron systems: Benchmarks on Zn-like ions. Phys. Rev. A 2005, 72, 032512. [Google Scholar] [CrossRef]
- Ishikawa, Y.; Quiney, H.M.; Malli, G.L. Dirac-Fock-Breit self-consistent-field method: Gaussian basis-set computations on many-electron atoms. Phys. Rev. A 1991, 43, 3270–3278. [Google Scholar] [CrossRef] [PubMed]
- Malli, G.L.; Da Silva, A.B.F.; Ishikawa, Y. Universal Gaussian basis set for accurate ab initio relativistic Dirac-Fock computations. Phys. Rev. A 1993, 47, 143–146. [Google Scholar] [CrossRef] [PubMed]
- Blundell, S.A.; Johnson, W.R.; Safronova, M.S.; Safronova, U.I. Relativistic many-body computations of the energies of n = 4 states along the zinc isoelectronic sequence. Phys. Rev. A 2008, 77, 032507. [Google Scholar] [CrossRef]
- Blundell, S.A. computations of QED corrections in highly charged Zn-like ions. Can. J. Phys. 2009, 87, 55–65. [Google Scholar] [CrossRef]
- Safronova, U.I.; Safronova, M.S. Relativistic many-body computations of the oscillator strengths, transition rates and polarizabilities in Zn-like ions. J. Phys. B: At. Mol. Opt. Phys. 2010, 43, 074025. [Google Scholar] [CrossRef]
- Chen, M.H.; Cheng, K.T. A large-scale relativistic configuration-interaction approach: application to the 4s2 - 4s4p transition energies and E1 rates for Zn-like ions. J. Phys. B: At. Mol. Opt. Phys. 2010, 43, 074019. [Google Scholar] [CrossRef]
- Träbert, E.; Clementson, J.; Beiersdorfer, P.; Santana, J.A.; Ishikawa, Y. Measurements and computations of Zn-like heavy ions: an update. Can. J. Phys. 2011, 89, 639–645. [Google Scholar] [CrossRef]
- Träbert, E.; Clementson, J.; Beiersdorfer, P.; Santana, J.A.; Ishikawa, Y. Extreme-ultraviolet spectra of highly charged Pt ions with several valence-shell electrons: Observation and accurate computations. Phys. Rev. A 2010, 82, 062519. [Google Scholar] [CrossRef]
- Santana, J.A.; Ishikawa, Y.; Träbert, E. Relativistic MR-MP computations of the energy levels and transition probabilities in Ni- to Kr-like Pt ions. At. Data Nucl. Data Tables 2014, 100, 183–271. [Google Scholar] [CrossRef]
- Utter, S.B.; Beiersdorfer, P.; Träbert, E. Electron-beam ion-trap spectra of tungsten in the EUV. Can. J. Phys. 2002, 80, 1503–1515. [Google Scholar] [CrossRef]
- Träbert, E. EUV beam-foil observations of Cu-like ions through Ge-like ions of iodine. Phys. Scr. T 2011, 144, 014004. [Google Scholar] [CrossRef]
- Li, J.G.; Träbert, E.; Dong, C.Z. Energy levels, transition rates and lifetimes for low-lying levels in Cu-, Zn-, Ga- and Ge-like ions of iodine. Phys. Scr. 2011, 83, 015301. [Google Scholar] [CrossRef]
- Curtis, L.J.; Ellis, D.G. Alkali Spectra in the Promethium Isoelectronic Sequence. Phys. Rev. Lett. 1980, 45, 2099–2102. [Google Scholar] [CrossRef]
- Träbert, E.; Heckmann, P.H. Tentative Identification of the 5s-5p Transitions in Pm I-Like Au XIX. Z. Phys. D 1986, 1, 381–383. [Google Scholar] [CrossRef]
- Kaufman, V.; Träbert, E.; Heckmann, P.H.; Möller, G.; Lodwig, V.; Blanke, J.H. Search for intercombination lines in few-electron spectra of rare-earth sequence ions of Os through Au. Phys. Scr. 1990, 42, 705–713. [Google Scholar] [CrossRef]
- Vilkas, M.J.; Ishikawa, Y.; Träbert, E. Electric-dipole 5s-5p transitions in promethiumlike ions. Phys. Rev. A 2008, 77, 042510. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Kato, D.; Sakaue, H.A.; Murakami, I.; Nakamura, N. Spectroscopic study of promethiumlike bismuth with an electron-beam ion trap: Search for alkali-metal-like resonance lines. Phys. Rev. A 2014, 89, 010501. [Google Scholar] [CrossRef]
- Kramida, A.E.; Shirai, T. Energy levels and spectral lines of tungsten, W III through W LXXIV. At. Data Nucl. Data Tables 2009, 95, 305–474, Erratum: 2009, 95, 1051. [Google Scholar] [CrossRef]
- Beiersdorfer, P.; Osterheld, A.L.; Scofield, J.; Wargelin, B.; Marrs, R.E. Observation of magnetic octupole decay in atomic spectra. Phys. Rev. Lett. 1991, 67, 2272–2275. [Google Scholar] [CrossRef] [PubMed]
- Clementson, J.; Beiersdorfer, P.; Brown, G.V.; Gu, M.F. Spectroscopy of M-shell x-ray transitions in Zn-like through Co-like W. Phys. Scr. 2010, 81, 015301. [Google Scholar] [CrossRef]
- Clementson, J.; Beiersdorfer, P. Wavelength measurement of n = 3 to n = 3 transitions in highly charged tungsten ions. Phys. Rev. A 2010, 81, 052509. [Google Scholar] [CrossRef]
- Clementson, J.; Beiersdorfer, P.; Brown, G.V.; Gu, M.F.; Lundberg, H.; Podpaly, Y.; Träbert, E. Tungsten spectroscopy at the Livermore electron beam ion trap facility. Can. J. Phys. 2011, 89, 571–580. [Google Scholar] [CrossRef]
- Clementson, J.; Beiersdorfer, P.; Gu, M.F. X-ray spectroscopy of E2 and M3 transitions in Ni-like W. Phys. Rev. A 2010, 81, 052509. [Google Scholar] [CrossRef]
- Clementson, J.; Beiersdorfer, P.; Brage, T.; Gu, M.F. Atomic data and theoretical X-ray spectra of Ge-like through V-like W ions. At. Data Nucl. Data Tables 2014, 100, 577–649. [Google Scholar] [CrossRef]
- Träbert, E.; Beiersdorfer, P.; Pinnington, E.H.; Utter, S.B.; Vilkas, M.J.; Ishikawa, Y. Experiment and theory in interplay on high-Z few-electron ion spectra from foil-excited ion beams and electron beam ion traps. J. Phys.: Conf. Ser. 2007, 58, 93–96. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Yu.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (ver. 5.1), 2013. National Institute of Standards and Technology: Gaithersburg, MD, USA. Available online: http://physics.nist.gov/asd (accessed on 3 January 2014).
- Dere, K.P.; Landi, E.; Young, P.R.; Del Zanna, G.; Landini, M.; Mason, H.E. CHIANTI—An atomic database for emission lines IX. Ionization rates, recombination rates, ionization equilibria for the elements hydrogen through zinc and updated atomic data. Astron. Astrophys. 2009, 498, 915–929. [Google Scholar] [CrossRef]
- Landi, E.; Del Zanna, G.; Young, P.R.; Dere, K.P.; Mason, H.E. CHIANTI—An atomic data base for emission lines. XII. Version 7 of thedatabase. Astrophys. J. 2012, 744, 99. [Google Scholar] [CrossRef]
- Mäckel, V.; Klawitter, R.; Brenner, G.; Crespo López-Urrutia, J.R.; Ullrich, J. Laser spectroscopy on forbidden transitions in trapped highly charged Ar13+ ions. Phys. Rev. Lett. 2011, 107, 143002. [Google Scholar] [CrossRef] [PubMed]
© 2014 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Träbert, E. Critical Assessment of Theoretical Calculations of Atomic Structure and Transition Probabilities: An Experimenter’s View. Atoms 2014, 2, 15-85. https://doi.org/10.3390/atoms2010015
Träbert E. Critical Assessment of Theoretical Calculations of Atomic Structure and Transition Probabilities: An Experimenter’s View. Atoms. 2014; 2(1):15-85. https://doi.org/10.3390/atoms2010015
Chicago/Turabian StyleTräbert, Elmar. 2014. "Critical Assessment of Theoretical Calculations of Atomic Structure and Transition Probabilities: An Experimenter’s View" Atoms 2, no. 1: 15-85. https://doi.org/10.3390/atoms2010015
APA StyleTräbert, E. (2014). Critical Assessment of Theoretical Calculations of Atomic Structure and Transition Probabilities: An Experimenter’s View. Atoms, 2(1), 15-85. https://doi.org/10.3390/atoms2010015




