Fractatomic Physics: Atomic Stability and Rydberg States in Fractal Spaces

Abstract

We explore the physical quantum properties of atoms in fractal spaces, both as a theoretical generalization of normal integer-dimensional Euclidean spaces and as an experimentally realizable setting. We identify the threshold of fractality at which Ehrenfest atomic instability emerges, where the Schrödinger equation describing the wavefunction of a single electron orbiting around an atom becomes scale-free, and discuss the potential of observing this phenomena in laboratory settings. We then study the Rydberg states of stable atoms using the Wentzel–Kramers–Brillouin approximation, along with a proposed extension for the Langer modification, in general fractal dimensionalities. We show that fractal space atoms near instability explode in size even at low-number excited state, making them highly suitable to induce strong entanglements and foster long-range many-body interactions. We argue that atomic physics in fractal spaces—“fractatomic physics”—is a rich research avenue deserving of further theoretical and experimental investigations.

1. Introduction

Atomic physics lays the foundation for understanding the elementary constituents and basic interactions of matter [1]. Perhaps one of the simplest yet most thought-provoking theoretical findings about atoms is that, in terms of classical orbital stability, they cannot remain stable in Euclidean spaces above four dimensions [2,3,4], contributing to many anthropic arguments for why our universe has only three [5]. In laboratory settings, it is also possible to experimentally observe atomic instability around normal charges caused by massless (“relativistic”) quasi-electrons residing in two-dimensional lattice materials [6,7,8]. Exploring fundamentals in unconventional spaces can reveal new phenomena and offer unique insights into known physical principles [9,10,11,12,13], with vast potential for engineering applications and technologies [14,15]. An interesting class of spaces to investigate is fractal, whose geometry exhibits self-similarity across scales [16,17] and phenomena emerging within not only deviate significantly from their expected behaviors in conventional Euclidean spaces but also introduce new behaviors [18,19,20]. There have been many successes in generalizing and discovering novel physics by studying well-established models under fractality [21,22,23,24,25,26,27,28], using simple rules for vector calculus [29,30,31] founded on the assertion that mediums existing in fractal spaces can be effectively described using fractional continuous models [32,33].

In this report, we investigate the quantum aspects of Hydrogen-like atoms in fractal spaces. Each atom is a bound state of a stationary positively charged nucleus and a massive (“non-relativistic”) electron of negative charge. Here, we examine two distinct scenarios: one arises from mathematical curiosity, extending the concept of dimensionalities [29,34,35], while the other considers experimental implementation within three-dimensional Euclidean space of our universe [36]. To be more precise, in the former case (called the full fractal space), both the electrical field from the nucleus and the electron propagate within the same fractal space. In the later case (called the embedded fractal space), inspired by recent experiments for the atomic collapse on graphene [8], the electrical field spreads throughout all three dimensions, while the electron is a quasi-particle living on a fractal lattice embedded within those three dimensions. There have been studies on atomic physics in fractal spaces [37,38,39,40,41,42] and intersecting spaces without defined dimensionalities [43,44,45], but we believe we have offered a different perspective, i.e., on how atomic structure can be manipulated with fractality.

We begin by introducing a simple vector calculus formalism in fractal spaces. We briefly revisit the classical mechanics argument by Ehrenfest for why atoms should be unstable in higher-dimensional Euclidean spaces [2]. Then, under a quantum mechanical perspective, we demonstrate that the instability condition is triggered by the emergence of a scale-free Schrödinger equation describing the electron wavefunction around the nucleus [6]. This scale-free condition can be generalized for fractal spaces, allowing us to map out the boundary of fractality where the atomic transition from being stable to being unstable happens. We also find that there are macroscopic spatial structures in nature with fractional dimensions where atomic instability can occur, i.e., natural soil [21,46]. Thus, they might provide a “blueprint” for designing fractal lattices in the lab using nanoscale molecular engineering [47,48,49], through which we could search for the realization of Ehrenfest “non-relativistic” atomic instability phenomena [2,3,4]. Note that we need the ground-state of these embedded fractal space atoms to be much larger compared to the lattice spacing, which can be controlled by the effective mass of the quasi-electron orbitting around the seeded nucleus [8]. Finally, we investigate the physical properties of stable fractal space atoms by examining the behavior of their Rydberg (highly excited states [50,51]) energy levels, using the Wentzel–Kramers–Brillouin (WKB) approximation [52,53,54,55] with our proposed extension for the Langer modification [56,57]. We reveal that fractal space atoms exhibit a remarkable expansion in size as they approach the instability threshold, even at low-number excited states, as compared to that of their ground-state (which has been bounded by the lattice spacing for the fractality description to emerge). Consequently, these extremely gigantic atoms are effective at triggering robust entanglements and facilitating long-range many-body interactions [58,59]. These features might open up opportunities for advancing quantum technology [60] and proposing innovative applications, such as with quantum computing [61], quantum information [51], quantum simulation [62], and even novel materials with exotic properties [63].

2. Vector Calculus in Fractal Spaces

Fractal spaces introduce unconventional physics that require a corresponding adjustment of mathematics. To be precise, the standard vector calculus applied for Euclidean spaces has to be generalized. Let us begin with some fractal geometric characteristics. Fractal spaces can be distinguished by their unique topological attributes [64,65], in which the volume fractal dimension ${\mathcal{D}}_{\mathrm{v}}$ and the surface fractal dimension ${\mathcal{D}}_{\mathrm{s}}$ are the two most primary measures [46,66,67]. Consider a spherical ball $S$ of radius r in this space, with surface $\partial S$. The fractal dimensionalities $\dim \left(S\right)={\mathcal{D}}_{\mathrm{v}}$ and $\dim \left(\partial S\right)={\mathcal{D}}_{\mathrm{s}}$ can be positive non-integers. In general, the volume $\mathcal{V}\left(r\right)$ and the surface area of this ball $\mathcal{A}\left(r\right)$ follow power-law dependencies, i.e., $\mathcal{V}\left(r\right)\propto r^{{\mathcal{D}}_{\mathrm{v}}}$ and $\mathcal{A}\left(r\right)\propto r^{{\mathcal{D}}_{\mathrm{s}}}$, with the coefficients of proportionality depending on the particular spatial topology. For simplicity, we just assume these functions to be analytical continuations of those defined for hyperspheres [68]:

$$\mathcal{V}\left(r\right)={\displaystyle \frac{{\displaystyle {\pi }^{{\mathcal{D}}_{\mathrm{v}}/2}}}{{\displaystyle \Gamma \left(\frac{{\mathcal{D}}_{\mathrm{v}}+2}{2}\right)}}}{r}^{{\mathcal{D}}_{\mathrm{v}}}\mathrm{and}\mathcal{A}\left(r\right)={\displaystyle \frac{{\displaystyle 2{\pi }^{({\mathcal{D}}_{\mathrm{s}}+1)/2}}}{{\displaystyle \Gamma \left(\frac{{\mathcal{D}}_{\mathrm{s}}+1}{2}\right)}}}{r}^{{\mathcal{D}}_{\mathrm{s}}},$$

(1)

in which $\Gamma (\dots )$ refers to the Gamma function, an extension of the factorial function to complex numbers [69]. Besides ${\mathcal{D}}_{\mathrm{v}}>{\mathcal{D}}_{\mathrm{s}}$, the constraint of embedding in the physical three-dimensional Euclidean space also bounds the fractal dimensions, i.e., ${\mathcal{D}}_{\mathrm{v}}\le 3$, ${\mathcal{D}}_{\mathrm{s}}\le 2$.

We consider a Hydrogen-like atom, consisting of an atomic nucleus with a charge of $Z|q_{\mathrm{e}}|$ ($Z\in \mathbb{N}$), which remains fixed in space, and an outer electron of charge $-|q_{\mathrm{e}}|$ and mass $m_{\mathrm{e}}$, located at a distance denoted as r, away from the nucleus. Here, we consider the electron of this Hydrogen-like atom to be in a s-orbital with spherically symmetric wavefunctions, which should be a complex scalar function $\Psi \left(r\right)$. In this fractal space, the Laplacian operator $\Delta$ acting on any radial scalar function $S\left(r\right)$ gives the following [21]:

$$\Delta S\left(r\right)=F\left({\mathcal{D}}_{\mathrm{v}},{\mathcal{D}}_{\mathrm{s}}\right)\left\{\left[{\displaystyle \frac{1}{r^{2\left({\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}\right)-2}}}\right]{\partial }_r^2+\left[{\displaystyle \frac{-{\mathcal{D}}_{\mathrm{v}}+2{\mathcal{D}}_{\mathrm{s}}+1}{r^{2\left({\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}\right)-1}}}\right]{\partial }_r\right\}S\left(r\right),$$

(2)

where the pre-factor is given by the following:

$$F\left({\mathcal{D}}_{\mathrm{v}},{\mathcal{D}}_{\mathrm{s}}\right)={\displaystyle \frac{{\displaystyle \Gamma \left(\frac{{\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}}{2}\right)\Gamma \left(\frac{{\mathcal{D}}_{\mathrm{v}}}{2}\right)}}{{\displaystyle {\pi }^{\left({\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}\right)-1/2}\Gamma \left(\frac{{\mathcal{D}}_{\mathrm{s}}+1}{2}\right)}}}.$$

(3)

This result relies on an extension of the Green–Gauss theorem to fractal objects through fractional integrals in Euclidean spaces [22,70]. The Coulomb central interaction energy potential $U\left(r\right)$, felt by the electron due to the electrical field created by the nucleus, has the general form of a power-law:

$$U\left(r\right)=-\mathrm{sgn}\left(\kappa \right)\left|\mathbb{U}\right|r^{-\kappa },$$

(4)

in which $\mathrm{sgn}(\circ )$ is the sign-function (equals to $+1$ when $\circ >0$ and $-1$ when $★<0$). We choose this expression for $U\left(r\right)$ so that it can be seen easily that this is an attractive potential. As mentioned in the introduction, we look into the following two scenarios:

• The full fractal space, in which the electrical field and the electron propagate within the same fractal space. The coefficient $\left|\mathbb{U}\right|$ in the expression Equation (4) for the interacting energy potential can be found to be the following:

  $$\left|{\mathbb{U}}_{\mathrm{ful}}\right|=\left|{\displaystyle \frac{{\displaystyle \Gamma \left(\frac{{\mathcal{D}}_{\mathrm{s}}+1}{2}\right)}}{{\displaystyle 2{\kappa }_{\mathrm{ful}}{\pi }^{({\kappa }_{\mathrm{ful}}+1)/2}\Gamma \left(\frac{{\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}}{2}\right)}}}\right|Z{\left|q_{\mathrm{e}}\right|}^2\mathrm{and}{\kappa }_{\mathrm{ful}}=2{\mathcal{D}}_{\mathrm{s}}-{\mathcal{D}}_{\mathrm{v}}.$$

  (5)
  We show the derivation of this using fractal vector calculus in Appendix A.
• The embedded fractal space, where the electrical field spreads throughout the three-dimensional Euclidean space of our universe, while the electron is a quasi-particle residing on a fractal lattice embedded within those three dimensions. The coefficient $\left|\mathbb{U}\right|$ in the expression Equation (4) for the interacting energy potential has the familiar form:

  $$\left|{\mathbb{U}}_{\mathrm{emb}}\right|=\left({\displaystyle \frac{1}{4\pi }}\right)Z{\left|q_{\mathrm{e}}\right|}^2\mathrm{and}{\kappa }_{\mathrm{emb}}=1.$$

  (6)
  This can also be found by setting $\left({\mathcal{D}}_{\mathrm{v}},{\mathcal{D}}_{\mathrm{s}}\right)=\left(3,2\right)$ in Equation (5).

The former embarks on a mathematical adventure, while the latter is motivated by potential realizations within laboratory settings.

We emphasize that the assumption underlying all these mathematics— fractional continuous models for mediums on fractal spaces [32,33]—should not be viewed as definitive, but as a heuristic tool offering glimpses into the physics in fractal spaces [21]. Here, we have only adopted an effective “fractional-dimensional” continuum description (dimensionally continued Euclidean model) rather than an intrinsic analysis on a specific fractal set; a fully rigorous treatment on genuine fractals typically requires an appropriately defined fractal Laplacian/derivative operator, e.g., via Dirichlet forms or harmonic calculus. For the mathematics behind some of those representative approaches, see [71,72,73].

3. Atomic Instability

We investigate the dimensionalities of space, at which atoms become unstable, beginning with revisiting classical mechanics in Euclidean spaces, followed by expanding this argument into a quantum mechanical perspective in Euclidean spaces, and concluding with a complete and generalized model to describe atomic behaviors in fractal spaces. Note that $\mathcal{D}$-dimensional Euclidean spaces are special fractal spaces with volume, and surface dimensionalities are given by $\left({\mathcal{D}}_{\mathrm{v}},{\mathcal{D}}_{\mathrm{s}}\right)=\left(\mathcal{D},\mathcal{D}-1\right)$, in which $\mathcal{D}$ is a natural number, i.e., $\mathcal{D}\in \mathbb{N}$.

3.1. Ehrenfest Finding in Euclidean Spaces

In classical mechanics, the planetary model depicts Hydrogen-like atoms with an electron orbiting around the nucleus in planar [74,75,76]. The electrical potential $U\left(r\right)$ created around the nucleus is spherical-symmetric, therefore angular momentum L is conserved. Consider the radial motion $r\left(t\right)$ of the electron (t represents time), we can define an effective potential $U_{\mathrm{eff}}\left(r\right)$ in which the radial acceleration $\ddot{r}=m_{\mathrm{e}}^{-1}{\partial }_r{U}_{\mathrm{eff}}\left(r\right)$:

$$U_{\mathrm{eff}}\left(r\right)=U\left(r\right)+{\displaystyle \frac{L^2}{2m_{\mathrm{e}}{r}^2}}$$

(7)

The extra energy-term $L^2/2m_{\mathrm{e}}{r}^2$ is the kinetic energy stored inside the compact angular dimension [77]. Following from Equation (5), in $\mathcal{D}$-dimensional Euclidean spaces:

$${\kappa }_{\mathrm{ful}}=\mathcal{D}-2\mathrm{and}\mathrm{therefore}U\left(r\right)\propto -r^{-\left(\mathcal{D}-2\right)},$$

(8)

which means that, for $\mathcal{D}\ge 4$, the effetive potential $U_{\mathrm{eff}}\left(r\right)$ in Equation (7) has no minimum except at $r=0$ and $r=+\infty$ (corresponding to atomic collapse and atomic deconfinement). There is no stable orbit for an electron around the nucleus; hence, classically, an atom cannot be stable in Euclidean spaces with dimensions $\mathcal{D}=4$ and above.

3.2. Scale-Free Schrödinger Equation in Euclidean Spaces

Going from classical to quantum mechanics [78,79,80,81], the stationary state of an atom can be described by the time-independent Schödinger equation:

$$\widehat{H}\Psi \left(r\right)=E\Psi \left(r\right),\widehat{H}=-{\displaystyle \frac{{\hslash }^2}{2m_{\mathrm{e}}}}\Delta +U\left(r\right),$$

(9)

in which $\Psi \left(r\right)$, $m_e$, and E are the wavefunction, the mass, and the corresponding energy of the outer electron around the nucleus, respectively. $\widehat{H}$ is the Hamiltonian operator, ℏ is the reduced Planck constant, and $\Delta$ is the Laplacian operator. The Schödinger equation becomes scale-free when an homogeneous rescaling of $r\to \gamma r$ leads to a rescaling of $\widehat{H}\to {\gamma }^{\prime }\widehat{H}$. When this occurs, the atomic spectrum becomes continuous. This is because if the wavefunction $\Psi \left(r\right)$ is a solution of Equation (9) with energy E, then the rescaled wavefunction $\Psi \left(\gamma r\right)$ with rescaled energy ${\gamma }^{\prime }E$ is also a solution. If the bound state requires $E<0$, then the possible energy for bound states is unbounded from below (the energy can be arbitrarily negatively large, indicating no well-defined ground-state and thus atomic instability).

For the scale-free condition to be satisfied, the Laplacian $\Delta$ and the power-law energy potential $U\left(r\right)$ must have the same spatial-scaling. In Euclidean spaces, $\Delta \propto r^{-2}$ (as a second-derivative in space); hence, we obtain scale independence when $U\left(r\right)\propto r^{-2}$. From Equation (8), we know that $U\left(r\right)\propto r^{-(\mathcal{D}-2)}$; hence, the scale-free critical dimension should be at $\mathcal{D}-2=2$, i.e., $\mathcal{D}=4$–; in other words, for $\mathcal{D}\ge 4$, the quantum problem enters the unstable regime. This is also the smallest dimensionality of Euclidean spaces where Ehrenfest atomic instability is expected to emerge in classical mechanics, as explained in Section 3.1.

3.3. Scale-Free Schrödinger Equation in Fractal Spaces

In a general fractal spaces, the Laplacian operator scales differently. From Equation (2), we have the scaling rule $\Delta \propto r^{-2\left({\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}\right)}$. For a power-law energy potential $U\left(r\right)$ as in Equation (4), the scale-free condition emerges when the range of interaction $\kappa$ satisfies the following:

$$\kappa =2\left({\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}\right).$$

(10)

Let us look at this closer in two scenarios of interests:

• The full fractal space has ${\kappa }_{\mathrm{ful}}=2{\mathcal{D}}_{\mathrm{s}}-{\mathcal{D}}_{\mathrm{v}}$, as found in Equation (5). Therefore, the fractality for scale-free atoms is as follows:

  $${\displaystyle \frac{{\mathcal{D}}_{\mathrm{v}}}{{\mathcal{D}}_{\mathrm{s}}}}={\displaystyle \frac{4}{3}}.$$

  (11)
  This agrees with what we have found in Section 3.2 for Euclidean spaces.
• The embedded fractal space has ${\kappa }_{\mathrm{emb}}=1$, see Equation (6). Thus, scale-free atoms can be found at fractality satisfies the following:

  $${\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}={\displaystyle \frac{1}{2}}.$$

  (12)
  This indicates that the radial dimension should exhibits a strong fractal characteristics.

With Equation (11) or Equation (12) serving as the transition upper thresholds—below which the atom becomes unstable—in dimensionality space $\left({\mathcal{D}}_{\mathrm{v}},{\mathcal{D}}_{\mathrm{s}}\right)$, we can see that the fractality found in natural soil [46] can give us unstable atoms in both cases, e.g., $\left({\mathcal{D}}_{\mathrm{v}},{\mathcal{D}}_{\mathrm{s}}\right)=\left(1.79,1.48\right)$, since ${\mathcal{D}}_{\mathrm{v}}/{\mathcal{D}}_{\mathrm{s}}\approx 1.21<4/3$ and ${\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}\approx 0.31<1/2$ [21,46].

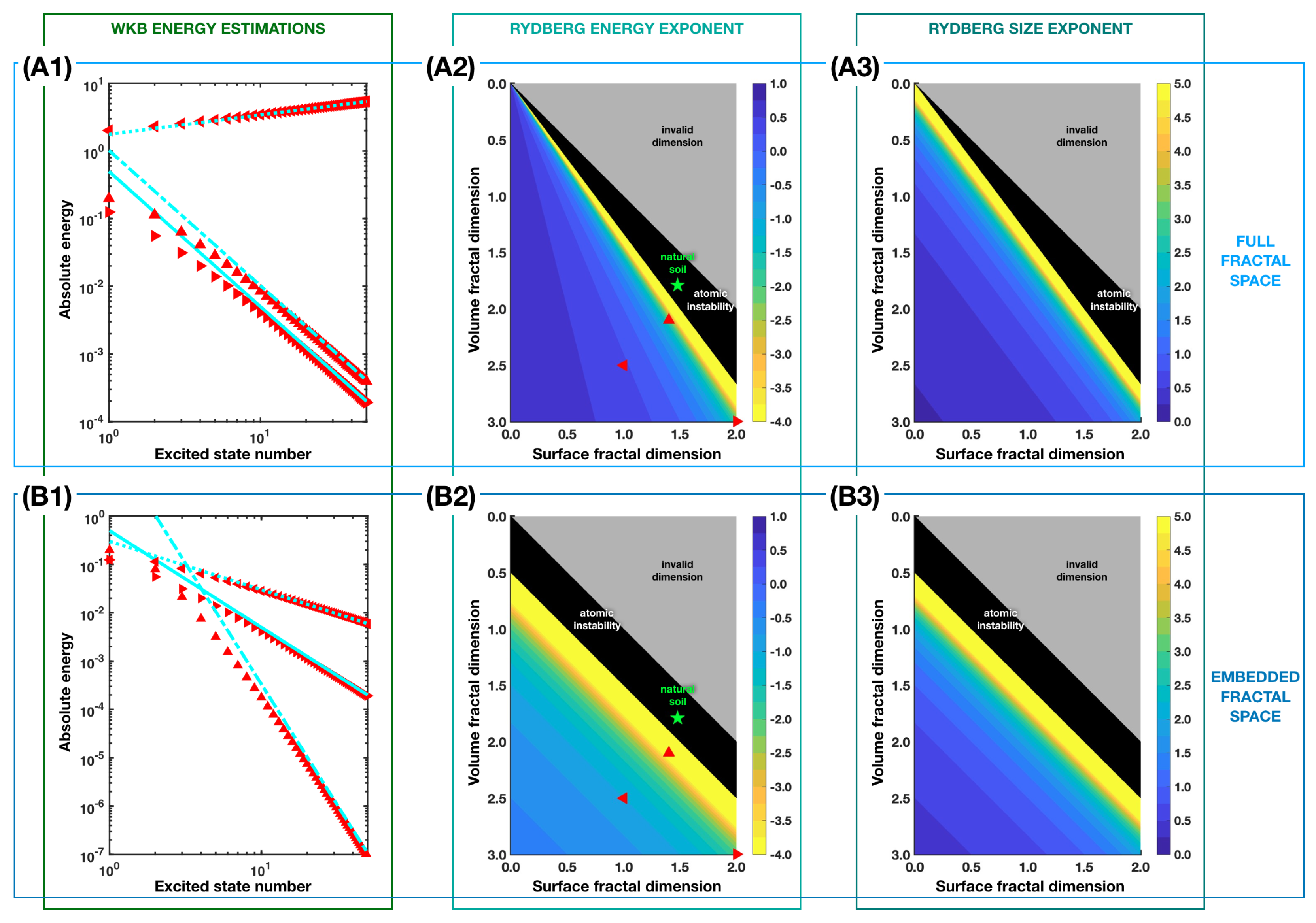
4. Rydberg States

In Section 3.3, we have found that atoms are stable in ${\mathcal{D}}_{\mathrm{v}}/{\mathcal{D}}_{\mathrm{s}}>4/3$ for the full fractal space and ${\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}>1/2$ for the embedded fractal space. We can further explore some quantum mechanical properties of these stable fractal space atoms. Let us demonstrate that by investigating the Rydberg states of Hydrogen-like atoms. To be precise, we study how their excited state energy-level $E\left(n\right)$ depends on their large quantum number $n\gg 1$, $n\in \mathbb{N}$ [50,51]. Note that this model aims to understand the overall scaling of atomic energy without considering special contributions, e.g., from quantum defects [82].

We define the rescaled radius and the rescaled energy as follows:

$$\tilde{r}=r{\left[{\displaystyle \frac{{\hslash }^{2}F\left({\mathcal{D}}_{\mathrm{v}},{\mathcal{D}}_{\mathrm{s}}\right)}{m_{\mathrm{e}}\left|\mathbb{U}\right|}}\right]}^{{\displaystyle \frac{1}{\kappa -2\left({\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}\right)}}},\tilde{E}=E{\left|\mathbb{U}\right|}^{-1}{\left[{\displaystyle \frac{m_{\mathrm{e}}\left|\mathbb{U}\right|}{{\hslash }^{2}F\left({\mathcal{D}}_{\mathrm{v}},{\mathcal{D}}_{\mathrm{s}}\right)}}\right]}^{{\displaystyle \frac{\kappa }{\kappa -2\left({\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}\right)}}},$$

(13)

in which $F\left({\mathcal{D}}_{\mathrm{v}},{\mathcal{D}}_{\mathrm{s}}\right)$ is given by Equation (3). We rewrite the Schrödinger equation from Equation (9), using the fractal Laplacian operator in Equation (2) and the power-law potential $U\left(r\right)$ in Equation (4), as follows:

$$\left\{{\partial }_{\tilde{r}}^2+\left[{\displaystyle \frac{-{\mathcal{D}}_{\mathrm{v}}+2{\mathcal{D}}_{\mathrm{s}}+1}{\tilde{r}}}\right]{\partial }_{\tilde{r}}+2{\tilde{r}}^{2\left({\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}\right)-2}\left[\tilde{E}+\mathrm{sgn}\left(\kappa \right){\tilde{r}}^{-\kappa }\right]\right\}\Psi \left(\tilde{r}\right)=0.$$

(14)

Note that, since we consider only the spherical-symmetric s-orbital sector, the centrifugal term gives no contribution. We then define the rescaled wavefunction

$$\tilde{\Psi }\left(\tilde{r}\right)={\tilde{r}}^{{\displaystyle \frac{-{\mathcal{D}}_{\mathrm{v}}+2{\mathcal{D}}_{\mathrm{s}}+1}{2}}}\Psi \left(\tilde{r}\right)$$

(15)

to further simplify the Schrödinger equation:

$$\left({\partial }_{\tilde{r}}^2+\left\{2{\tilde{r}}^{2\left({\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}\right)-2}\left[\tilde{E}+\mathrm{sgn}\left(\kappa \right){\tilde{r}}^{-\kappa }\right]-\left[{\displaystyle \frac{{\left(-{\mathcal{D}}_{\mathrm{v}}+2{\mathcal{D}}_{\mathrm{s}}\right)}^2-1}{4}}\right]{\tilde{r}}^{-2}\right\}\right)\tilde{\Psi }\left(\tilde{r}\right)=0.$$

(16)

For analytical tractability, instead of solving Equation (16) directly, we use the WKB approximation [52,53,54,55]. The estimated radial momentum of the electron can be found by replacing ${\partial }_{\tilde{r}}$ with $i{\tilde{p}}_r\left(\tilde{r}\right)$ in Equation (16):

$${\tilde{p}}_r\left(\tilde{r}\right)={\left\{2{\tilde{r}}^{2\left({\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}\right)-2}\left[\tilde{E}+\mathrm{sgn}\left(\kappa \right){\tilde{r}}^{-\kappa }\right]-\left[{\displaystyle \frac{{\left(-{\mathcal{D}}_{\mathrm{v}}+2{\mathcal{D}}_{\mathrm{s}}\right)}^2-1}{4}}\right]{\tilde{r}}^{-2}\right\}}^{1/2}.$$

(17)

It is important to mention that the WKB approximation has long been known to be problematic in general dimensions. To address this, a trick like the generalized Langer modification is often used for more accurate estimations of eigenenergies [56,57]. Here, we follow the simple proposal made in [57], applying it for the spherical mode of the wavefunction and extending its applicability to fractal spaces. We modify the radial momentum in Equation (17) to the following:

$${\tilde{p}}_r\left(\tilde{r}\right)\stackrel{\mathrm{modify}}{\to }{\tilde{p}}_r^{\prime }\left(\tilde{r}\right)={\left\{2{\tilde{r}}^{2\left({\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}\right)-2}\left[\tilde{E}+\mathrm{sgn}\left(\kappa \right){\tilde{r}}^{-\kappa }\right]-\left[{\displaystyle \frac{{\left(-{\mathcal{D}}_{\mathrm{v}}+2{\mathcal{D}}_{\mathrm{s}}\right)}^2}{4}}\right]{\tilde{r}}^{-2}\right\}}^{1/2},$$

(18)

which can ensure that the estimations for the energy spectrums $\tilde{E}\left(n\right)$ in Euclidean spaces of $\mathcal{D}\in \mathbb{N}$ dimensions are reasonably good. This change has the benefit of being simple, yet rather far from being trivial, so we provide a detailed explanation in Appendix B. To obtain the exact correct eigenstate energies, we need to also change the Maslov index $\mu =2\stackrel{\mathrm{modify}}{\to }{\mu }^{\prime }$ in a very complicated manner [57,83].

We have mentioned how the WKB approximation can be used to estimate the eigenstate energies, but we have not yet explained the method. Let us do that now. To find $\tilde{E}\left(n\right)$, we choose the ansatz

$$\tilde{E}=-\mathrm{sgn}\left(\kappa \right)\left|\tilde{E}\right|$$

(19)

and impose the Wilson–Sommerfeld quantization condition [84]:

$${\displaystyle \frac{1}{2}}\oint {\tilde{p}}_r^{\prime }\left(\tilde{r}\right)d\tilde{r}={\int }_{{\tilde{r}}_{min}}^{{\tilde{r}}_{max}}{\tilde{p}}_r^{\prime }\left(\tilde{r}\right)d\tilde{r}=\pi \left[(n-1)+{\displaystyle \frac{\mu }{4}}\right]\mathrm{in}\mathrm{which}{\tilde{p}}_r^{\prime }\left({\tilde{r}}_{min}\right)={\tilde{p}}_r^{\prime }\left({\tilde{r}}_{max}\right)=0.$$

(20)

Note that $n=1$ corresponds to the ground-state in this counting convention. For simplicity, we keep using the Maslov index $\mu =2$, since the bound radial motion has two turning points (each contributing a phase shift of $\pi /2$). We numerically investigate the solution $\left|\tilde{E}\right|\left(n\right)$ and the corresponding ${\tilde{r}}_{max}$ of Equation (20) in Figure 1(A1,B1) for some representative fractalities.

Inside the square root of the modified radial momentum, which is given by Equation (17), there are three radial-dependent terms with exponents $2\left({\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}\right)-2$, $2\left({\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}\right)-2-\kappa$, and $-2$. Since ${\mathcal{D}}_v>{\mathcal{D}}_s$ and the atomic stability condition in Equation (10) requires $\kappa <2\left({\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}\right)$, the third exponent should always be the smallest. For $n\gg 1$, the atomic size becomes large, then following from Equations (18)–(20), we can use the approximation:

$${\int }_0^{{\tilde{r}}_{max}}{\left[2{\tilde{r}}^{2\left({\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}\right)-2}\mathrm{sgn}\left(\kappa \right)\left(-\left|\tilde{E}\right|+{\tilde{r}}^{-\kappa }\right)\right]}^{1/2}d\tilde{r}\approx \pi n\mathrm{where}{\tilde{r}}_{max}\approx {\left|\tilde{E}\right|}^{-1/\kappa }.$$

(21)

This approximation is unaffected by how the Maslov index $\mu$ is chosen. We estimate the scaling of energy levels and sizes for fractal-space-atom Rydberg states to be the following:

$$\left|\tilde{E}\right|\propto n^{-{\displaystyle \frac{2\kappa }{2\left({\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}\right)-\kappa }}},{\tilde{r}}_{max}\propto n^{{\displaystyle \frac{2}{2\left({\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}\right)-\kappa }}}.$$

(22)

We show their derivation in Appendix C. Let us look at them closer, in each of the two scenarios of interests:

• The full fractal space has ${\kappa }_{\mathrm{ful}}=2{\mathcal{D}}_{\mathrm{s}}-{\mathcal{D}}_{\mathrm{v}}$, as previously found in Equation (5). Thus:

  $$\left|\tilde{E}\right|\propto n^{-{\displaystyle \frac{2\left(2{\mathcal{D}}_{\mathrm{s}}-{\mathcal{D}}_{\mathrm{v}}\right)}{3{\mathcal{D}}_{\mathrm{v}}-4{\mathcal{D}}_{\mathrm{s}}}}},{\tilde{r}}_{max}\propto n^{{\displaystyle \frac{2}{3{\mathcal{D}}_{\mathrm{v}}-4{\mathcal{D}}_{\mathrm{s}}}}}.$$

  (23)
• The embedded fractal space has ${\kappa }_{\mathrm{emb}}=1$, from Equation (6). Therefore:

  $$\left|\tilde{E}\right|\propto n^{-{\displaystyle \frac{2}{2\left({\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}\right)-1}}},{\tilde{r}}_{max}\propto n^{{\displaystyle \frac{2}{2\left({\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}\right)-1}}}.$$

  (24)

These results are also in agreement with our representative numerical findings shown in Figure 1(A1,B1). We plot them as surface functions of fractality $\left({\mathcal{D}}_{\mathrm{v}},{\mathcal{D}}_{\mathrm{s}}\right)$, for the full fractal space in Figure 1(A2,A3), and for the embedded fractal space in Figure 1(B2,B3).

In the vicinity of the scale-free threshold, i.e., $\kappa \to 2\left({\mathcal{D}}_{\mathrm{v}}-{\mathcal{D}}_{\mathrm{s}}\right)$ from below as found in Equation (10), the atomic size explodes after the stable fractal space atoms are excited from the ground-state size, which follows directly from Equation (22) as ${\tilde{r}}_{max}\propto n^{1/0^{+}}$. For comparison, the usual case of a Rydberg atom in $\mathcal{D}=$ three-dimensional Euclidean space has the atomic size scales as $\propto n^2$ [50]. This ability to drastically bloat up even at low-excited states can help generating long-distance interactions in cold neutral atom systems. This allows atoms to interact on a macroscopic scale, facilitating long-distance quantum communication [85]. Additionally, the strength of the Rydberg–Rydberg interactions will increase greatly, which is crucial for technologies such as quantum computing [86,87,88] and quantum simulation [89,90,91]. With stronger interactions, entanglement between atoms occurs rapidly, enabling a significantly higher number of operations within a time that is negligible to the atoms’ decoherence time. In quantum simulation, the fast growth of entanglement enables us to study system dynamics on a longer timescale. This capability holds promise in gaining insight into systems exhibiting glass-like dynamics and slow thermalization (many-body localization regime [92]), which are typically challenging to observe in traditional laboratory settings due to thermalization occurring at an inaccessible time.

5. Conclusions

In this report, we give some remarks about atomic physics in fractal spaces. Beyond being merely a mathematical curiosity, we have demonstrated the potential in laboratory settings to observe the Ehrenfest atomic instability and approach the scale-free boundary of fractality to create atoms that explode after becoming excited. These exotic properties of fractal space atoms can be of relevance to the development of quantum engineering [93]. Here, we have only scratched the surface of a deep topic that requires further research attempts. On a single atom level, we have yet to fully comprehend the intricacies of angular modes beyond spherical configurations [94,95,96], scattering [97,98] and resonances [99], and we also do not consider atoms possessing many electrons [100]. On a many-atom level, it remains largely untouched, leaving a vast uncharted territory awaiting exploration [101,102,103]. We hope our work can ignite some interest in fractal space atoms, not just as a theoretical adventure, but also as an experimental quest that one can realistically pursue.