Accurate Nonrelativistic Energy Calculations for Helium 1snp^1,3P (n = 2 to 27) States via Correlated B-Spline Basis Functions

Abstract

Rydberg atoms play a crucial role in testing atomic structure theory, quantum computing and simulation. Measurements of transition frequencies from the $2^{1,3}S$ states to Rydberg ${}^{1,3}P$ states have reached a precision of several kHz, which poses significant challenges for theoretical calculations, since the accuracy of variational energy calculations decreases rapidly with increasing principal quantum number n. Recently the complex “triple” Hylleraas basis was employed to attain the ionization energy of helium $24{}^{1}P$ state with high accuracy. Different from it, we extended the correlated B-spline basis functions (C-BSBFs) to calculate the Rydberg states of helium. The nonrelativistic energies of $1snp$${}^{1,3}P$ states up to $n=27$ achieve at least 14 significant digits using a unified basis set, thereby greatly reducing the complexity of the optimization process. Results of geometric structure parameters and cusp conditions were presented as well. Both the global operator and direct calculation methods are employed and cross-checked for contact potentials. This C-BSBF method not only obtains high-accuracy energies across all studied levels but also confirms the effectiveness of the C-BSBFs in depicting long-range and short-range correlation effects, laying a solid foundation for future high-accuracy Rydberg-state calculations with relativistic and QED corrections included in helium atom and low-Z helium-like ions.

1. Introduction

As the simplest multi-electron system, helium plays an important role in experimental tests of bound-state quantum electrodynamics (QED) due to its high-resolution spectroscopy [1,2], with measurements now achieving part-per-trillion (ppt) precision [3,4,5,6]. Moreover, helium is among the few-electron atomic systems for which ab initio calculations, including higher-order relativistic and QED corrections, can achieve high numerical accuracy [7,8,9,10,11]. However, the significant discrepancies between theory and experiment remain puzzling. In particular, the ionization energy of the metastable $2{}^{3}S$ state differs by $9\sigma$ [9,12] and the experimentally measured transition frequencies of $3{}^{3}D$ state, with the $3{}^{3}D\leftarrow 2{}^{3}S$ and $3{}^{3}D\leftarrow 2{}^{3}P_0$ differ from theoretical calculations by $6\sigma$ [9,13,14] and $15\sigma$ [13,15,16], respectively. These discrepancies require further investigation, as they may signify inherent limitations or unresolved issues within the theoretical framework.

Rydberg atoms exhibit distinctive quantum properties, such as long lifetimes and high sensitivity to external fields [17,18]. Consequently, spectral transitions from low-energy states to Rydberg states serve as valuable tools for probing atomic structures and offer an effective approach to investigating the above discrepancies. Sansonetti and Gillaspy [19] and Lichten et al. [20] measured transitions from the $2{}^{1}S$ state to the $n{}^{1}P$ ($n=7-74$) and $n{}^{1}D$ ($n=7-20$) excited states, respectively, determining the ionization energy of the $2{}^{1}S$ state with precisions of 0.22 ppb and 0.16 ppb. Recently, Clausen et al. [12,21,22] determined the ionization energies of the $2{}^{1}S$ and $2{}^{3}S$ metastable states through Rydberg-series spectroscopy, achieving significantly improved precisions of 33 and 7 ppt, respectively. All these experiments rely on the semi-empirical quantum defect theory to interpret spectral data; however, discrepancies between experimental measurements and theoretical predictions remain. Thus, further verification through ab initio calculations is essential to resolve these discrepancies and refine the accuracy of atomic structure determinations.

From a theoretical perspective, ab initio calculations of accurate energy spectra for Rydberg states exhibit characteristic multiscale features. Physical processes span three distinct spatial regimes—the atomic core region (∼1 a.u.), low-lying states (∼10 a.u.), and high Rydberg states (>1000 a.u.). The coupling across these widely separated length scales poses a fundamental difficulty in establishing a unified and accurate theoretical description. To address these challenges, Hylleraas-type basis sets [23,24] have been extensively employed to achieve highly precise energy level calculations for helium. Aznabaev et al. [8] provided exceptionally precise nonrelativistic energies for helium states up to $n=4$ using explicitly correlated exponential (ECE) basis sets, achieving between 28 and 35 significant digits of accuracy. Drake and Yan [7] calculated energies for states up to $n=10$ and angular momentum $L=7$, employing “double” Hylleraas basis sets and achieving accuracies of 14–18 significant digits. Extending this approach to higher Rydberg states, Bondy et al. [25] recently performed ab initio calculations of the ionization energy for the helium $24{}^{1}P$ state, incorporating relativistic and QED effects using “triple” Hylleraas basis sets. Their results represent significant progress in accurately describing high Rydberg states.

In computational atomic physics, B-spline basis functions have been widely employed due to their linear independence, completeness, and capability to accurately model both bound and continuum states within finite spherical cavities [26,27,28,29,30]. Compared to Hylleraas-type basis sets, B-spline basis sets enable the simultaneous and accurate treatment of atomic systems spanning several orders of magnitude in scale, while requiring fewer adjustable basis-set parameters. However, traditional B-spline methods encounter limitations when calculating systems characterized by strong electron correlation interactions, primarily due to the significant role played by interelectronic distances in accurately representing two-electron wave functions [31]. To overcome these limitations, Yang et al. developed explicitly correlated B-spline basis functions (C-BSBFs), which incorporate explicit interelectronic correlation into the basis set. This method has demonstrated substantial success in the calculation of energy levels, static dipole polarizabilities [32], and Bethe logarithms [33] for helium singlet states. Recently, Fang et al. further advanced this methodology by successfully computing leading relativistic and QED corrections within the nonrelativistic quantum electrodynamics (NRQED) framework [34], as well as determining the dipole polarizabilities for both singlet and triplet S states up to principal quantum number $n=7$, achieving an accuracy exceeding 0.2 ppm [35]. The combination of these advancements has facilitated accurate and reliable calculations of helium energies for states with high principal quantum numbers using ab initio methods.

In this paper, we extend the C-BSBF method to a full sequence of helium $1snp$${}^{1,3}P$ states up to $n=27$, achieving unified, high-accuracy nonrelativistic energy calculations within a single diagonalization. Building on its successful application to low-lying states, the method is now extended to the accurate computation of highly Rydberg states. To support this extension, we implement an adaptive integration algorithm that rigorously controls numerical precision, thereby ensuring stable and reliable evaluation of two-electron integrals over the broad radial domains needed to accurately describe Rydberg states, which extend to much larger distances. To demonstrate the accuracy of the obtained wave functions over both short-range and long-range regions, we thoroughly analyze geometric structure parameters, cusp conditions, and two-particle contact potentials. Specifically, for evaluating the contact potentials, both the global operator and direct calculation methods are employed and cross-checked. This cross-check enables an informed choice between these methods, guided by the cusp conditions and the computational accuracy requirements. These results confirm that the wave functions obtained through the C-BSBF method accurately depict both the long-range and short-range asymptotic behaviors of helium, laying a solid foundation for future inclusion of relativistic and QED corrections. Atomic units (a.u.) are used throughout this paper.

2. Theory and Method

2.1. Correlated B-Spline Basis Functions

Helium is a three-body system composed of two electrons and one nucleus. The nonrelativistic Hamiltonian of the system with an infinite mass nucleus can be formulated as:

$$\begin{array}{c}\hfill H=\sum _{i=1}^2\left({\displaystyle \frac{{\mathbf{p}}_i^2}{2}}-{\displaystyle \frac{Z}{r_i}}\right)+{\displaystyle \frac{1}{r_{12}}},\end{array}$$

(1)

where ${\mathbf{p}}_i$ and $r_i$ is the momentum operator and the coordinate of the ith electron to the nucleus, $r_{12}$ is the interelectronic coordinate, and the nuclear charge $Z=2$ for helium.

For a given principal quantum number n, orbital angular momentum L, and total spin S, a specific atomic state $n{}^{2S+1}L$ is uniquely determined. The trial wave functions of helium can be expanded by the following C-BSBFs in which the interelectronic coordinate $r_{12}$ is included explicitly [27,34],

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\varphi }_{ij,c,{\mathsf{\ell }}_1{\mathsf{\ell }}_2}& =r_{12}^c{B}_i^k\left(r_1\right)B_j^k\left(r_2\right){\mathcal{Y}}_{{\mathsf{\ell }}_1{\mathsf{\ell }}_2}^{LM}\left({\widehat{\mathbf{r}}}_1,{\widehat{\mathbf{r}}}_2\right)\hfill \\ & \hfill +{\left(-1\right)}^{{\mathsf{\ell }}_1+{\mathsf{\ell }}_2-L+S}{r}_{12}^c{B}_j^k\left(r_1\right)B_i^k\left(r_2\right){\mathcal{Y}}_{{\mathsf{\ell }}_2{\mathsf{\ell }}_1}^{LM}\left({\widehat{\mathbf{r}}}_1,{\widehat{\mathbf{r}}}_2\right),\hfill \end{array}\end{array}$$

(2)

where c is the power of the $r_{12}$ coordinate. In the present calculations, c is restricted to be 0 and 1. The vectorcoupled product of spherical harmonics ${\mathcal{Y}}_{{\mathsf{\ell }}_1{\mathsf{\ell }}_2}^{LM}\left({\widehat{\mathbf{r}}}_1,{\widehat{\mathbf{r}}}_2\right)$ is given by

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathcal{Y}}_{{\mathsf{\ell }}_1{\mathsf{\ell }}_2}^{LM}\left({\widehat{\mathbf{r}}}_1,{\widehat{\mathbf{r}}}_2\right)=\sum _{m_1{m}_2}〈{\mathsf{\ell }}_1{m}_1{\mathsf{\ell }}_2{m}_2\mid LM〉Y_{{\mathsf{\ell }}_1{m}_1}\left({\widehat{\mathbf{r}}}_1\right)Y_{{\mathsf{\ell }}_2{m}_2}\left({\widehat{\mathbf{r}}}_2\right),\end{array}\end{array}$$

(3)

with $〈{\mathsf{\ell }}_1{\mathsf{\ell }}_2{m}_1{m}_2\mid LM〉$ being the Clebsch–Gordan coefficient, and ${\mathsf{\ell }}_1$ and ${\mathsf{\ell }}_2$ are the orbital angular momentum, both less than the parameter ${\mathsf{\ell }}_{\max }$. $B_i^k\left(r\right)$ is a B-spline of order k, where i denotes the serial number [27,34,35]. The exponential knots sequence is used to define B splines:

$$\left\{\begin{array}{cc}{t}_i=0,\hfill & i=1,2,\dots ,k-1,\hfill \\ t_{i+k-1}=R_0{\displaystyle \frac{exp\left(\gamma \frac{i-1}{N-2}\right)-1}{exp\left(\gamma \right)-1}},\hfill & i=1,2,\dots ,N-1,\hfill \\ t_i=R_0,\hfill & i=N+k-1,N+k,\hfill \end{array}\right.$$

(4)

where $\gamma =\tau R_0$ with $\tau$ being an adjustable knot parameter utilized to modify the knot sequence, $R_0$ is the cavity radius and N is the total number of B-splines. If basis-set parameters (N, k, $R_0$, $\tau$, and ${\mathsf{\ell }}_{\max }$) are given, the basis set of C-BSBFs is fully constructed.

After the construction of the basis set, for a system characterized by a well-defined Hamiltonian, the Schrödinger equation can be written in the matrix form through Rayleigh–Ritz variational method:

$$\begin{array}{c}\hfill HC=ESC,\end{array}$$

(5)

where E is the eigenenergy and C the corresponding eigenvector, and H and S are the Hamiltonian and the overlap matrix, respectively. The energy eigenvalues and the corresponding wave functions can be obtained by diagonalizing the Hamiltonian matrix.

2.2. Geometric Structure Parameters

The calculation of radial and angular geometric structure parameters in two-electron system can assist in understanding quantum correlation effects by enabling different types of measurements and characterizations of the quantum many-body system from a classical perspective. The expectation values $〈r^m〉$ and $〈r_{12}^m〉$, where m takes positive integer values, serve as important descriptors of the long-range asymptotic behavior of the system’s wave function. Moreover, they play a crucial role in the calculation of transition matrix elements in few-electron atomic systems, as well as in the approximation of atomic multipole polarizabilities [36].

In spherical coordinates, the evaluation of the integrals involving $r_{12}^m$ requires decomposing them into their radial and angular dimensions. The Laplace expansion provided by Sack [37] generalizes to arbitrary powers and functions of $r_{12}$, facilitating the evaluation of integrals involving different powers of $r_{12}$. The term $r_{12}^m$ can be expanded in the following form:

$$\begin{array}{c}\hfill r_{12}^m=\sum _{\mathsf{\ell }=0}^{\infty }{R}_{m\mathsf{\ell }}(r_1,r_2)P_{\mathsf{\ell }}(cos{\theta }_{12}),\end{array}$$

(6)

where $cos{\theta }_{12}={\widehat{\mathbf{r}}}_1·{\widehat{\mathbf{r}}}_2$ and $P_{\mathsf{\ell }}(cos{\theta }_{12})$ is the Legendre polynomial. The radial function $R_{m\mathsf{\ell }}(r_1,r_2)$ has been expressed by Sack [37] as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill R_{m\mathsf{\ell }}(r_1,r_2)& \hfill ={\displaystyle \frac{{\left(-\frac{1}{2}m\right)}_{\mathsf{\ell }}}{{\left(\frac{1}{2}\right)}_{\mathsf{\ell }}}}{r}_{>}^m{\left({\displaystyle \frac{r_{<}}{r_{>}}}\right)}^{\mathsf{\ell }}{}_{2}F_1\left(l-{\displaystyle \frac{1}{2}}m,-{\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}m;l+{\displaystyle \frac{3}{2}};{\displaystyle \frac{r_{<}^2}{r_{>}^2}}\right),\hfill \end{array}\end{array}$$

(7)

where $r_{<}=min(r_1,r_2)$, $r_{>}=max(r_1,r_2)$, and ${}_{2}F_1(\alpha ,\beta ;\gamma ;x)$ is the hypergeometric function.

In the calculations, cases with $m=-1$ and $m=-2$ will be encountered. For $m=-1$, the associated hypergeometric function simplifies to a terminating series. This leads to a natural truncation of the corresponding radial wave function $R_{m\mathsf{\ell }}(r_1,r_2)$, whose explicit expression can be obtained in closed form. In this case, the inter-electronic Coulomb interaction can be expanded as [38]:

$$\begin{array}{c}\hfill r_{12}^{-1}=\sum _{\mathsf{\ell }=0}^{\infty }{\displaystyle \frac{r_{<}^{\mathsf{\ell }}}{r_{>}^{\mathsf{\ell }+1}}}{P}_{\mathsf{\ell }}(cos{\theta }_{12}).\end{array}$$

(8)

For $m=-2$, analytic expressions can be obtainable for specific values of ℓ, such as $\mathsf{\ell }=0$ and $\mathsf{\ell }=1$:

$$\begin{array}{c}\hfill R_{-2,0}\left(r_1,r_2\right)={\displaystyle \frac{{tanh}^{-1}\left(x\right)}{x{r}_{>}^2}},\end{array}$$

(9)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill R_{-2,1}\left(r_1,r_2\right)& \hfill ={\displaystyle \frac{3}{2r_{<}^2}}\left[\left(x^2+1\right){tanh}^{-1}\left(x\right)-1\right],\hfill \end{array}\end{array}$$

(10)

where $x=r_{<}/r_{>}$. By employing the recurrence relations of the hypergeometric function, one can obtain expressions for arbitrary values of ℓ:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\displaystyle \frac{r_1^2+r_2^2}{r_1{r}_2}}{R}_{m,\mathsf{\ell }}-{\displaystyle \frac{\mathsf{\ell }+2+\frac{1}{2}m}{\mathsf{\ell }+\frac{3}{2}}}{R}_{m,\mathsf{\ell }+1}-{\displaystyle \frac{\mathsf{\ell }-1-\frac{1}{2}m}{\mathsf{\ell }-\frac{1}{2}}}{R}_{m,\mathsf{\ell }-1}=0.\end{array}\end{array}$$

(11)

2.3. Contact Interaction

In addition to the long-range asymptotic behavior, the analysis of the short-range asymptotic behavior of the wave function, which can be examined by evaluating the Dirac delta function, is equally crucial. Meanwhile, the accurate computation of the Dirac delta function is essential for various important physical processes including atomic hyperfine structure. For example, within the framework of NRQED, both the relativistic effects $m{\alpha }^4$ and the radiative effects $m{\alpha }^5$ involve the evaluation of delta functions ${\delta }^3\left(r_i\right)$ and ${\delta }^3\left(r_{12}\right)$ [39]. The contact potentials ${\delta }^3\left(r_i\right)$ and ${\delta }^3\left(r_{12}\right)$ can be evaluated using both the global operator method proposed by Drachman [40] and the direct calculation method. The equivalent form of the global operator is used to compute the expectation values of ${\delta }^3\left(r_i\right)$ and ${\delta }^3\left(r_{12}\right)$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill 4\pi 〈\psi \left|{\delta }^3\left(r_i\right)\right|\psi 〉=& \hfill 4\langle \psi |r_i^{-1}(E_{\psi }-V)|\psi \rangle -2\sum _{s=1}^2\langle {\nabla }_s\psi |r_i^{-1}|{\nabla }_s\psi \rangle ,\hfill \end{array}\end{array}$$

(12)

and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill 4\pi 〈\psi \left|{\delta }^3\left(r_{12}\right)\right|\psi 〉=& \hfill 2\langle \psi |r_{12}^{-1}(E_{\psi }-V)|\psi \rangle -\sum _{s=1}^2\langle {\nabla }_s\psi |r_{12}^{-1}|{\nabla }_s\psi \rangle ,\hfill \end{array}\end{array}$$

(13)

where $V=-Z/r_1-Z/r_2+1/r_{12}$ and $E_{\psi }$ is the corresponding eigenvalue of the two-electron wave function $\psi$. Compared to the global operator method, the direct calculation method requires higher wave function accuracy, especially near the coalescence points where the cusp conditions need to be well satisfied [41]

$$\begin{array}{c}\hfill \mathrm{cusp}\left(r_{ij}\right)={\displaystyle \frac{〈\psi \left|{\delta }^3\left(r_{ij}\right)\frac{\partial }{\partial r_{ij}}\right|\psi 〉}{〈\psi \left|{\delta }^3\left(r_{ij}\right)\right|\psi 〉}},\end{array}$$

(14)

and exact cusp values are

$$\begin{array}{c}\hfill {\mathrm{cusp}}^{\mathrm{exact}}\left(r_{ij}\right)=q_i{q}_j{\displaystyle \frac{m_i{m}_j}{m_i+m_j}},\end{array}$$

(15)

where $q_i$ and $q_j$ are the charges, and $m_i$ and $m_j$ the masses of the particles. By examining the deviation measure

$$\begin{array}{c}\hfill C_{ij}=\left|1-{\displaystyle \frac{\mathrm{cusp}\left(r_{ij}\right)}{{\mathrm{cusp}}^{\mathrm{exact}}\left(r_{ij}\right)}}\right|,\end{array}$$

(16)

we can assess whether the trial wave function accurately describes the asymptotic behavior between particles, which is crucial for the computational accuracy of singular operators. This condition provides an effective criterion for verifying the accuracy of the wave functions constructed through the C-BSBF method near electron–nuclear and electron–electron coalescence points.

3. Results and Discussions

The C-BSBFs on an exponential knot are generated by confining B-spline basis functions within a spherical boundary [27], where the accuracy of energy levels and wave function calculations critically relies on the optimal selection of the cavity radius. To investigate the energies of Rydberg states, we systematically analyzed the influence of the B-spline knot parameter $\tau$ and ${\mathsf{\ell }}_{\max }$ on the convergence behavior of the energies under different cavity radii $R_0$, in order to select the most appropriate set of parameters. Following the recent experimental data reported by the Merkt’s group on ionization energies of Rydberg ${}^{1}P$ ($n=24$–100) [22] and ${}^{3}P$ (n = 27–55) [12] states in helium, an appropriate cavity radius should be chosen to ensure computational accuracy in nonrelativistic energy calculations up to $n=27$. In order to achieve stable and high numerical accuracy, the calculations used quadruple precision and the number of B-splines used in the following computations is N = 70–80, using the expression [35] of

$$\begin{array}{c}\hfill {\langle \widehat{O}\rangle }_{\mathrm{Extrap}.}={\langle \widehat{O}\rangle }_{N=80}+{\displaystyle \frac{{\left[{\langle \widehat{O}\rangle }_{N=80}-{\langle \widehat{O}\rangle }_{N=75}\right]}^2}{{\langle \widehat{O}\rangle }_{N=75}-{\langle \widehat{O}\rangle }_{N=70}}},\end{array}$$

(17)

where $\widehat{O}$ represents an arbitrary operator, and the B-spline orders $k=13$. The numerical uncertainty is twice the maximum difference between the extrapolated result and those calculated with the last three largest numbers of B-splines N.

We analyzed the convergence behavior of the nonrelativistic energies for various principal quantum numbers across three different cavity radii to identify the optimal cavity radius. The choice of knot parameter is guided by the calculated energies of the lowest state for a given $(L,S)$ within each cavity, and the optimal values are determined according to the variational principle. The convergence results are summarized in

Table 1. The convergence of nonrelativistic energies for $n{}^{1}P$ states of helium with the number of B-splines N increased under different cavity radii $R_0$. The order of B-splines is $k=13$ and ${\mathsf{\ell }}_{\max }=4$. The knot parameters $\tau$ are chosen as 0.0043, 0.0038 and 0.0032 for $R_0=$ 1700 a.u., 2000 a.u. and 2400 a.u., respectively. The convergent uncertainty, defined as the maximum difference between extrapolated result and those calculated with the last three largest numbers of B-splines N, is given in parentheses.

n	N	${\mathit{R}}_0=1700$ a.u.	${\mathit{R}}_0=2000$ a.u.	${\mathit{R}}_0=2400$ a.u.
2	70	−2.123 843 086 498 088 063	−2.123 843 086 498 088 069	−2.123 843 086 498 087 979
	75	−2.123 843 086 498 088 185	−2.123 843 086 498 088 191	−2.123 843 086 498 088 118
	80	−2.123 843 086 498 088 278	−2.123 843 086 498 088 284	−2.123 843 086 498 088 223
	Extrap.	−2.123 843 086 498 088 3(2)	−2.123 843 086 498 088 4(3)	−2.123 843 086 498 088 3(3)
	Ref. [8]			−2.123 8430 864 9810136
10	70	−2.004 987 983 802 218 155 81	−2.004 987 983 802 218 155 88	−2.004 987 983 802 218 155 17
	75	−2.004 987 983 802 218 156 73	−2.004 987 983 802 218 156 80	−2.004 987 983 802 218 156 22
	80	−2.004 987 983 802 218 157 42	−2.004 987 983 802 218 157 49	−2.004 987 983 802 218 157 01
	Extrap.	−2.004 987 983 802 218 158(2)	−2.004 987 983 802 218 158(2)	−2.004 987 983 802 218 158(3)
	Ref. [42]			−2.004 987 983 802 22(4)
24	70	−2.000 867 180 601	−2.000 867 180 846 168 99	−2.000 867 180 846 170 020
	75	−2.000 867 180 680	−2.000 867 180 846 169 45	−2.000 867 180 846 170 083
	80	−2.000 867 180 729	−2.000 867 180 846 169 70	−2.000 867 180 846 170 099
	Extrap.	−2.000 867 180 8(2)	−2.000 867 180 846 170(1)	−2.000 867 180 846 170 1(1)
	Ref. [25]			−2.000 867 180 846 170 111 282 a
27	70	−2.000 680 91	−2.000 685 250 58	−2.000 685 256 528 875 1
	75	−2.000 681 62	−2.000 685 252 38	−2.000 685 256 528 878 1
	80	−2.000 682 16	−2.000 685 253 55	−2.000 685 256 528 879 7
Extrap.		−2.000 683(2)	−2.000 685 254(3)	−2.000 685 256 528 88(1)

^a The nonrelativistic energy results of −2.000 867 180 846 170 111 282 23(6) for the $24{}^{1}P$ state was reported, with the use of “triple” Hylleraas basis sets by Bondy et al. [25].

. The energies of both low-lying (e.g., $n=2$) and low Rydberg (e.g., $n=10$) states remain consistent across all tested cavity radii, exhibiting negligible differences and excellent agreement with the values reported in Refs. [8,42]. In contrast, for higher Rydberg states such as $n=24$ state, $R_0=1700$ a.u. no longer provides adequate accuracy, while results from 2000 and 2400 a.u. agree to within 15 significant digits and match the value reported by Bondy et al. [25]. For $n=27$ state, only the $R_0=2400$ a.u. yields convergence at the 14 digits, offering improvements of up to five orders of magnitude over $R_0=2000$ a.u.. Based on the convergence behavior, the cavity radius of 2400 a.u. is selected to ensure high-accuracy results for all states up to $n=27$.

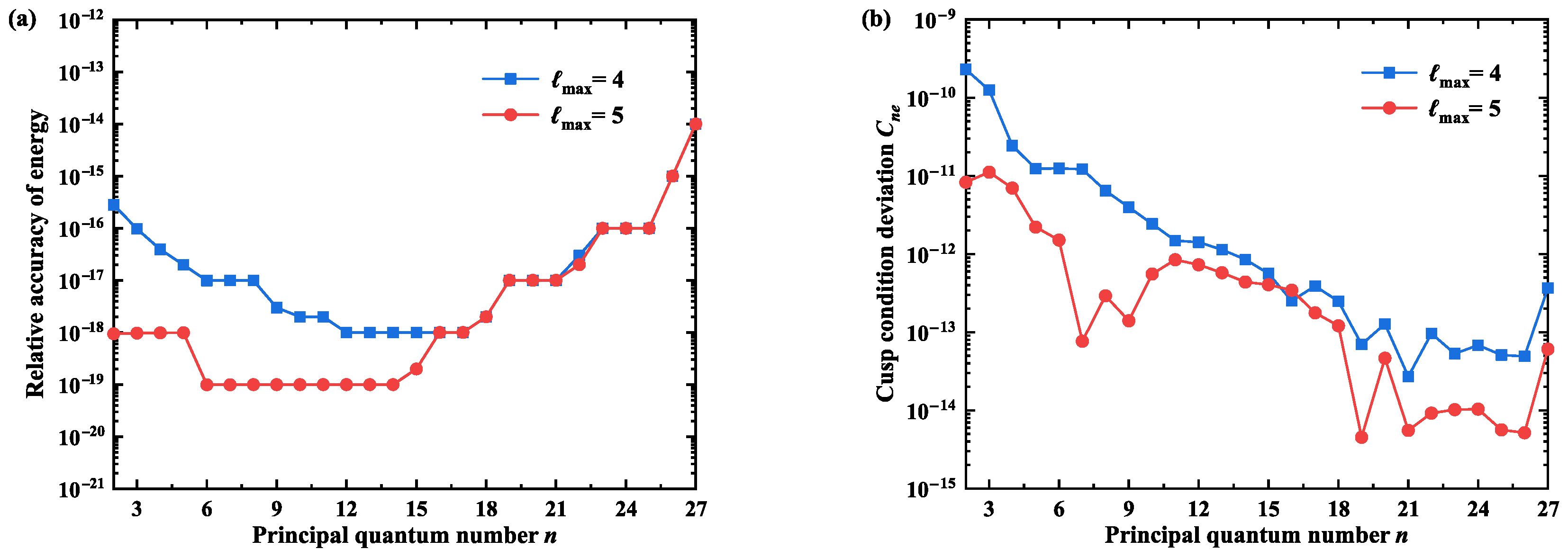
As shown in Table 1, the calculated energies for the $2{}^{1}P$ state under three different cavity radii exhibit slight discrepancies compared to the value reported in Ref. [8]. These differences primarily arise from truncation at ${\mathsf{\ell }}_{max}=4$, which may insufficiently account for contributions from higher-angular-momentum components. To address this, we increased the ${\mathsf{\ell }}_{max}$ from 4 to 5 and systematically compared the resulting relative accuracy of energy uncertainties and deviations in the electron–nucleus cusp condition $C_{ne}$ across various principal quantum numbers. The corresponding results are presented in Figure 1. As shown in Figure 1a, increasing ${\mathsf{\ell }}_{max}$ from 4 to 5 improves the accuracy by one to two orders of magnitude for excited states with $n<16$, underscoring the critical role of higher ${\mathsf{\ell }}_{max}$ in energy calculations. For higher Rydberg states with $n\ge 16$, the accuracy remains nearly unchanged between the two cases, mainly due to the current limitation in the number of B-splines, which restricts the contributions from higher ${\mathsf{\ell }}_{max}$.

Furthermore, analysis of the electron–nucleus cusp condition deviation $C_{ne}$ in Figure 1b indicates that including higher ${\mathsf{\ell }}_{max}$ consistently enhances the asymptotic behavior of the wave function near the nucleus. For example, the basis set convergence of the nonrelativistic energies for the $2{}^{1}P$ and $24{}^{1}P$ states with ${\mathsf{\ell }}_{max}=5$ is presented in

Table 2. The convergence of nonrelativistic energy for the $2{}^{1}P$ and $24{}^{1}P$ states of helium with the number of B-splines N increased. The cavity radius is $R_0=2400$ a.u., and the order of B-splines is $k=13$ and ${\mathsf{\ell }}_{\max }=5$. Numbers in parentheses give the numerical uncertainties.

N	$2{}^1\mathit{P}$	$24{}^1\mathit{P}$
70	−2.123 843 086 498 101 342 45	−2.000 867 180 846 170 026 09
75	−2.123 843 086 498 101 342 92	−2.000 867 180 846 170 088 95
80	−2.123 843 086 498 101 343 24	−2.000 867 180 846 170 105 32
Extrap.	−2.123 843 086 498 101 343(2)	−2.000 867 180 846 170 1(2)
Ref. [8]	−2.123 843 086 498 101 359 247
Ref. [25]		−2.000 867 180 846 170 111 282 23(6)

. This table further demonstrates that for the $2{}^{1}P$ state, incorporating higher-order ${\mathsf{\ell }}_{max}$ is essential for achieving high-accuracy calculations. These results highlight that obtaining precise energies for large-n states requires not only sufficiently large cavity sizes to capture the asymptotic behavior but also the inclusion of higher-order ${\mathsf{\ell }}_{max}$ to accurately describe electron correlation effects. For all subsequent calculations, we selected the parameters $R_0=2400$ a.u., $k=13$, and ${\mathsf{\ell }}_{max}=5$, with a maximum basis set size of 64,000, as summarized in

Table 3. Adjustable basis-set parameters used in the C-BSBFs calculations.

Symbol	Description	Value(s)
N	Number of B-spline functions	70, 75, 80
k	Order of B-spline functions	13
$\tau$	Adjustable knot parameter	0.0032
$R_0$	Cavity radius	2400 a.u.
${\mathsf{\ell }}_{\max }$	Angular partial-wave cutoff parameter	5

. It takes approximately 15 hours for a full diagonalization using 192-core parallel processing. The same basis-set parameters were employed in the calculations presented in

Table 4. Nonrelativistic energies of helium $n{}^{1,3}P$ states with infinite mass nucleus. Numbers in parentheses give the numerical uncertainties.

n	${}^1\mathit{P}$	Ref. [8,42]	${}^3\mathit{P}$	Ref. [8,42]
2	−2.123 843 086 498 101 343(2)	−2.123 843 086 498 101 359	−2.133 164 190 779 283 204(2)	−2.133 164 190 779 283 205 15
3	−2.055 146 362 091 943 533(2)	−2.055 146 362 091 943 537	−2.058 081 084 274 275 331 2(2)	−2.058 081 084 274 275 331 34
4	−2.031 069 650 450 240 713(2)	−2.031 069 650 450 240 715	−2.032 324 354 296 630 331 9(2)	−2.032 324 354 296 630 331 95
5	−2.019 905 989 900 846 448(2)	−2.019 905 989 900 83(2)	−2.020 551 187 256 267 788 3(2)	−2.020 551 187 256 25(1)
6	−2.013 833 979 671 740 102 0(2)	−2.013 833 979 671 73(2)	−2.014 207 958 773 750 591 33(4)	−2.014 207 958 773 74(1)
7	−2.010 169 314 529 388 984 6(2)	−2.010 169 314 529 35(2)	−2.010 404 960 007 971 431 26(2)	−2.010 404 960 007 94(2)
8	−2.007 789 127 133 235 895 0(2)	−2.007 789 127 133 22(2)	−2.007 947 013 771 161 505 27(2)	−2.007 947 013 771 12(1)
9	−2.006 156 384 652 853 818 2(2)	−2.006 156 384 652 86(5)	−2.006 267 267 366 409 032 58(2)	−2.006 267 267 366 41(4)
10	−2.004 987 983 802 218 239 4(2)	−2.004 987 983 802 22(4)	−2.005 068 805 497 707 316 44(2)	−2.005 068 805 497 8(1)
11	−2.004 123 191 922 332 652 5(2)		−2.004 183 903 199 590 642 4(2)
12	−2.003 465 252 704 885 798 2(2)		−2.003 512 006 535 142 745 6(2)
13	−2.002 953 093 958 149 784 8(2)		−2.002 989 859 764 908 816 3(2)
14	−2.002 546 625 370 190 968 0(2)		−2.002 576 056 426 625 769 1(2)
15	−2.002 218 647 104 088 301 6(4)		−2.002 242 571 222 150 326 4(2)
16	−2.001 950 177 973 979 341(2)		−2.001 969 887 403 296 967(2)
17	−2.001 727 645 999 910 517(2)		−2.001 744 075 191 087 356(2)
18	−2.001 541 138 760 913 625(4)		−2.001 554 976 940 232 727(4)
19	−2.001 383 280 102 341 61(2)		−2.001 395 044 604 295 125(6)
20	−2.001 248 489 450 687 61(2)		−2.001 258 574 692 820 42(2)
21	−2.001 132 481 733 017 53(2)		−2.001 141 192 656 477 68(2)
22	−2.001 031 922 552 162 28(4)		−2.001 039 497 912 816 70(4)
23	−2.000 944 185 877 955 8(2)		−2.000 950 814 760 962 2(2)
24	−2.000 867 180 846 170 1(2)	−2.000 867 180 846 170 111 a	−2.000 873 014 566 616 7(2)	−2.000 873 014 566 616 659 39 a
25	−2.000 799 226 024 103 1(2)		−2.000 804 386 829 929 1(2)
26	−2.000 738 956 837 743(2)		−2.000 743 544 360 330(2)
27	−2.000 685 256 528 88(2)		−2.000 689 352 623 57(2)

^a The nonrelativistic energy results of −2.000 867 180 846 170 111 282 23(6) and −2.000 873 014 566 616 659 392 40(9) for the $24{}^{1,3}P$ states were reported, respectively, with the use of “triple” Hylleraas basis sets by Bondy et al. [25].

, Table 5, Table 6, Table 7 and Table 8, as listed in Table 3.

Table 4 summarizes the energies of the ${}^{1,3}P$ states up to $n=27$ obtained from a single diagonalization. For low-lying states such as the $2{}^{1}P$ state, the calculated energy is -2.123 843 086 498 101 343(2), demonstrating improved numerical accuracy compared to the ${\mathsf{\ell }}_{max}=4$ results shown in Table 1. The result with ${\mathsf{\ell }}_{max}=5$ deviates from the reference value [8] only at the 17th decimal place, with a discrepancy on the order of ${10}^{-17}$. This exceptional level of agreement confirms the reliability of the calculation and indicates that increasing ${\mathsf{\ell }}_{max}$ further validates the numerical precision. For high Rydberg states, such as $n=24$, the energies of the ${}^{1,3}P$ states are -2.000 867 180 846 170 1(2) and -2.000 873 014 566 616 7(2), respectively, achieving 16 significant digits. These results are in excellent agreement with the nonrelativistic energies reported by Bondy et al. [25], which are accurate to 23 significant figures. We have additionally obtained energies for higher principal quantum numbers ($n=25$ to 27) with an accuracy of at least 14 significant digits. The present precision of the nonrelativistic energies adequately meets the accuracy demands of subsequent relativistic and QED correction computations. Using the same basis set construction and parameters, we have also extended the C-BSBF method to the calculation of Rydberg S and D states, with preliminary results demonstrating that comparable accuracy is attainable.

Based on the nonrelativistic energies and wave functions, the geometric structure parameters of helium can be evaluated numerically, as shown in Table 5 and Table 6. For the $n=$ 2–3 states, these expectation values are in excellent agreement with corresponding reference data reported by Drake [43], obtained using the Hylleraas basis set. For instance, the obtained value of $\langle r_1\rangle$ for the $2{}^{1}P$ state is 2.910 684 342 443 034(2), which agrees with Drake’s result of 2.910 684 342 443 036(18) within uncertainty. For $n=$ 4–6 states, our calculation results of those radial parameters for those states are consistent with those reported by Jiao [44] using the Hylleraas configuration interaction (HyCI) basis set, and by Yu et al. [45] based on the Hylleraas-B-spline CI basis set. As the principal quantum number increases, these results also retain at least eight significant digits for all states up to $n=27$. The present results are not only applicable to the evaluation of physical observables such as polarizabilities, but also confirm that the wave functions constructed using the C-BSBFs accurately capture the long-range asymptotic behavior of helium. The expectation values of $cos{\theta }_{12}$ are also included and show good agreement with the results of Yu et al. [45]. These values provide a valuable reference for comparing the angular properties across different states.

Employing the C-BSBFs, we also calculated the expectation values of the two-particle contact potentials for $n{}^{1,3}P$ using both the global operator and direct calculation methods, along with the corresponding cusp condition deviations obtained with the maximum number of B-splines, as summarized in Table 7 and Table 8. For $〈{\delta }^3\left(r_1\right)〉$ of the $2{}^{1}P$ state, the global operator method yields 1.274 392 886 328 85(4), in agreement with the direct calculation method within uncertainty and reaching 12-digit accuracy. However, a slight deviation is observed compared to Drake’s result, 1.274 392 886 363 6(18) [43]. Similarly, for the $2{}^{3}P$ and $3{}^{3}P$ states, the two methods remain consistent, while differences from Drake’s values appear at the tenth and ninth decimal digits, respectively. As the principal quantum number n increases, the global operator method maintains at least 12 significant digits for the Rydberg states in the range $n=10$–25. However, its accuracy declines to 6–9 digits for $n=26$–27 states, primarily due to the limited size of the B-spline cavity, which constrains the overall wave function accuracy and prevents the method from fully realizing its potential. In contrast, the direct calculation method achieves a stable accuracy of 12–14 significant digits. This high accuracy primarily stems from the ability of the wave functions constructed by C-BSBFs to precisely describe the short-range behavior near the nucleus, as evidenced by the electron–nucleus cusp condition deviations being within the range of ${10}^{-11}$ to ${10}^{-14}$. Therefore, when the wave function constructed by C-BSBFs accurately depicts the short-range asymptotic behavior, the ${\delta }^3\left(r_1\right)$ can be reliably evaluated using direct calculation method, which can reduce the overall computational complexity.

Table 5. Expectation values of operator $r_1$, $r_1^2$, $r_{12}$, $r_{12}^2$ and $cos{\theta }_{12}$ for the $n{}^{1}P$ states of helium. For each principal quantum number n, the first row corresponds to the calculated values from the present work, while the second rows list the reference values from prior studies for comparison. The numbers in square brackets are the power of 10.

n	$〈{\mathit{r}}_1〉$	$〈{\mathit{r}}_1^2〉$	$〈{\mathit{r}}_{12}〉$	$〈{\mathit{r}}_{12}^2〉$	$〈cos{\mathit{\theta }}_{12}〉$
2	2.910 684 342 4	15.765 654 942	5.138 328 372 1	31.598 515 996	−4.773 133 917[−3]
	2.910 684 342 4 a	15.765 654 942 a	5.138 328 372 1 a	31.598 515 996 a	−4.773 133 9[−3] b
3	6.679 547 332 5	91.872 907 566	12.638 017 449	183.786 627 76	−1.176 869 938[−3]
	6.679 547 332 5 a	91.872 907 567 a	12.638 017 449 a	183.786 627 76 a	−1.176 869 9[−3] b
4	11.947 784 061	304.072 624 96	23.161 657 910	608.171 287 23	−4.683 944 738[−4]
	11.947 784 058 c	304.072 625 b	23.161 657 905 c	608.171 287 b	−4.683 944 7[−4] b
5	18.715 965 731	757.728 282 24	36.692 165 776	1 515.474 402 9	−2.337 613 090[−4]
	18.715 965 697 c	757.728 28 b	36.692 165 708 c	1 515.474 40 b	−2.337 613 09[−4] b
6	26.984 138 887	1 588.203 285 3	53.225 356 783	3 176.419 500 0	−1.334 772 820[−4]
	26.984 138 799 c		53.225 356 606 c
7	36.752 310 354	2 960.861 051 3	72.759 807 125	5 921.731 885 2	−8.339 796 783[−5]
8	48.020 481 475	5 071.065 002 3	95.294 925 579	10 142.137 657	−5.559 295 139[−5]
9	60.788 652 556	8 144.178 562 7	120.830 431 06	16 288.363 271	−3.891 480 395[−5]
10	75.056 823 665	12 435.565 157	149.366 176 11	24 871.135 357	−2.830 280 441[−5]
11	90.824 994 810	18 230.588 211	180.902 077 34	36 461.180 634	−2.122 842 412[−5]
12	108.093 165 99	25 844.611 150	215.438 084 72	51 689.225 870	−1.633 073 293[−5]
13	126.861 337 19	35 622.997 400	252.974 166 74	71 245.997 864	−1.283 225 434[−5]
14	147.129 508 41	47 941.110 387	293.510 302 80	95 882.223 431	−1.026 657 048[−5]
15	168.897 679 64	63 204.313 535	337.046 478 91	126 408.629 40	−8.342 192 540[−6]
16	192.165 850 89	81 847.970 271	383.582 685 36	163 695.942 60	−6.870 516 117[−6]
17	216.934 022 15	104 337.444 02	433.118 915 19	208 674.889 87	−5.725 805 231[−6]
18	243.202 193 41	131 168.098 21	485.655 163 34	262 336.198 06	−4.822 028 525[−6]
19	270.970 364 67	162 865.296 26	541.191 426 05	325 730.594 00	−4.098 962 237[−6]
20	300.238 535 94	199 984.401 61	599.727 700 48	399 968.804 55	−3.513 587 743[−6]
21	331.006 707 22	243 110.777 67	661.263 984 43	486 221.556 56	−3.034 617 401[−6]
22	363.274 878 49	292 859.787 88	725.800 276 21	585 719.576 86	−2.638 924 478[−6]
23	397.043 049 77	349 876.795 65	793.336 574 49	699 753.592 31	−2.309 163 081[−6]
24	432.311 221 05	414 837.164 41	863.872 878 21	829 674.329 76	−2.032 149 681[−6]
25	469.079 392 33	488 446.257 60	937.409 186 50	976 892.516 06	−1.797 742 602[−6]
26	507.347 563 61	571 439.438 63	1 013.945 498 7	1 142 878.878 1	−1.598 053 490[−6]
27	547.115 735	664 582.071	1 093.481 814	1 329 164.14	−1.426 884[−6]

^a Ref. [43]. ^b Ref. [45]. ^c Ref. [44].

Table 5. Expectation values of operator $r_1$, $r_1^2$, $r_{12}$, $r_{12}^2$ and $cos{\theta }_{12}$ for the $n{}^{1}P$ states of helium. For each principal quantum number n, the first row corresponds to the calculated values from the present work, while the second rows list the reference values from prior studies for comparison. The numbers in square brackets are the power of 10.

n	$〈{\mathit{r}}_1〉$	$〈{\mathit{r}}_1^2〉$	$〈{\mathit{r}}_{12}〉$	$〈{\mathit{r}}_{12}^2〉$	$〈cos{\mathit{\theta }}_{12}〉$
2	2.910 684 342 4	15.765 654 942	5.138 328 372 1	31.598 515 996	−4.773 133 917[−3]
	2.910 684 342 4 a	15.765 654 942 a	5.138 328 372 1 a	31.598 515 996 a	−4.773 133 9[−3] b
3	6.679 547 332 5	91.872 907 566	12.638 017 449	183.786 627 76	−1.176 869 938[−3]
	6.679 547 332 5 a	91.872 907 567 a	12.638 017 449 a	183.786 627 76 a	−1.176 869 9[−3] b
4	11.947 784 061	304.072 624 96	23.161 657 910	608.171 287 23	−4.683 944 738[−4]
	11.947 784 058 c	304.072 625 b	23.161 657 905 c	608.171 287 b	−4.683 944 7[−4] b
5	18.715 965 731	757.728 282 24	36.692 165 776	1 515.474 402 9	−2.337 613 090[−4]
	18.715 965 697 c	757.728 28 b	36.692 165 708 c	1 515.474 40 b	−2.337 613 09[−4] b
6	26.984 138 887	1 588.203 285 3	53.225 356 783	3 176.419 500 0	−1.334 772 820[−4]
	26.984 138 799 c		53.225 356 606 c
7	36.752 310 354	2 960.861 051 3	72.759 807 125	5 921.731 885 2	−8.339 796 783[−5]
8	48.020 481 475	5 071.065 002 3	95.294 925 579	10 142.137 657	−5.559 295 139[−5]
9	60.788 652 556	8 144.178 562 7	120.830 431 06	16 288.363 271	−3.891 480 395[−5]
10	75.056 823 665	12 435.565 157	149.366 176 11	24 871.135 357	−2.830 280 441[−5]
11	90.824 994 810	18 230.588 211	180.902 077 34	36 461.180 634	−2.122 842 412[−5]
12	108.093 165 99	25 844.611 150	215.438 084 72	51 689.225 870	−1.633 073 293[−5]
13	126.861 337 19	35 622.997 400	252.974 166 74	71 245.997 864	−1.283 225 434[−5]
14	147.129 508 41	47 941.110 387	293.510 302 80	95 882.223 431	−1.026 657 048[−5]
15	168.897 679 64	63 204.313 535	337.046 478 91	126 408.629 40	−8.342 192 540[−6]
16	192.165 850 89	81 847.970 271	383.582 685 36	163 695.942 60	−6.870 516 117[−6]
17	216.934 022 15	104 337.444 02	433.118 915 19	208 674.889 87	−5.725 805 231[−6]
18	243.202 193 41	131 168.098 21	485.655 163 34	262 336.198 06	−4.822 028 525[−6]
19	270.970 364 67	162 865.296 26	541.191 426 05	325 730.594 00	−4.098 962 237[−6]
20	300.238 535 94	199 984.401 61	599.727 700 48	399 968.804 55	−3.513 587 743[−6]
21	331.006 707 22	243 110.777 67	661.263 984 43	486 221.556 56	−3.034 617 401[−6]
22	363.274 878 49	292 859.787 88	725.800 276 21	585 719.576 86	−2.638 924 478[−6]
23	397.043 049 77	349 876.795 65	793.336 574 49	699 753.592 31	−2.309 163 081[−6]
24	432.311 221 05	414 837.164 41	863.872 878 21	829 674.329 76	−2.032 149 681[−6]
25	469.079 392 33	488 446.257 60	937.409 186 50	976 892.516 06	−1.797 742 602[−6]
26	507.347 563 61	571 439.438 63	1 013.945 498 7	1 142 878.878 1	−1.598 053 490[−6]
27	547.115 735	664 582.071	1 093.481 814	1 329 164.14	−1.426 884[−6]

^a Ref. [43]. ^b Ref. [45]. ^c Ref. [44].

Table 6. Expectation values of operator $r_1$, $r_1^2$, $r_{12}$, $r_{12}^2$ and $cos{\theta }_{12}$ for the $n{}^{3}P$ states of helium. For each principal quantum number n, the first row corresponds to the calculated values from the present work, while the second rows list the reference values from prior studies for comparison. The numbers in square brackets are the power of 10.

n	$〈{\mathit{r}}_1〉$	$〈{\mathit{r}}_1^2〉$	$〈{\mathit{r}}_{12}〉$	$〈{\mathit{r}}_{12}^2〉$	$〈cos{\mathit{\theta }}_{12}〉$
2	2.673 961 655 2	13.211 740 573	4.699 955 007 5	26.642 793 447	−3.671 932 603[−2]
	2.673 961 655 2 a	13.211 740 573 a	4.699 955 007 5 a	26.642 793 447 a	−3.671 932 60[−2] b
3	6.321 128 044 5	82.109 891 976	11.931 203 148	164.302 878 72	−1.042 038 644[−2]
	6.321 128 044 5 a	82.109 891 976 a	11.931 203 148 a	164.302 878 72 a	−1.042 038 64[−2] b
4	11.468 700 443	279.935 257 54	22.207 622 661	559.913 902 50	−4.293 016 327[−3]
	11.468 700 443 c	279.935 257 b	22.207 622 662 c	559.913 902 b	−4.293 016 32[−3] b
5	18.116 274 445	709.635 959 83	35.494 869 430	1 419.298 518 0	−2.167 819 079[−3]
	18.116 274 453 c	709.635 960 b	35.494 869 447 c	1 419.298 5 b	−2.167 819 078[−3] b
6	26.263 842 175	1 504.162 752 0	51.785 959 700	3 008.343 461 9	−1.243 391 760[−3]
	26.263 842 205 c		51.785 959 760 c
7	35.911 406 361	2 826.466 717 6	71.078 747 733	5 652.946 368 2	−7.781 853 591[−4]
8	47.058 968 678	4 869.499 012 5	93.372 399 136	9 739.007 780 6	−5.189 702 606[−4]
9	59.706 529 968	7 856.210 814 2	118.666 535 20	15 712.429 248	−3.632 347 222[−4]
10	73.854 090 667	12 039.553 308	146.960 964 05	24 079.112 731	−2.640 808 307[−4]
11	89.501 651 007	17 702.477 682	178.255 580 08	35 404.960 380	−1.979 742 057[−4]
12	106.649 211 12	25 157.935 127	212.550 321 32	50 315.874 442	−1.522 161 151[−4]
13	125.296 771 09	34 748.876 832	249.845 149 46	69 497.757 214	−1.195 416 550[−4]
14	145.444 330 95	46 848.253 989	290.140 039 76	93 696.511 025	−9.558 920 113[−5]
15	167.091 890 74	61 859.017 790	333.434 975 73	123 718.038 22	−7.763 200 516[−5]
16	190.239 450 49	80 214.119 424	379.729 945 97	160 428.241 16	−6.390 561 504[−5]
17	214.887 010 20	102 376.510 08	429.024 942 45	204 753.022 21	−5.323 383 901[−5]
18	241.034 569 88	128 839.140 96	481.319 959 35	257 678.283 74	−4.481 206 256[−5]
19	268.682 129 54	160 124.963 25	536.614 992 37	320 249.928 13	−3.807 719 178[−5]
20	297.829 689 18	196 786.928 14	594.910 038 31	393 573.857 74	−3.262 712 841[−5]
21	328.477 248 82	239 407.986 82	656.205 094 70	478 815.974 96	−2.816 952 450[−5]
22	360.624 808 44	288 601.090 48	720.500 159 64	577 202.182 16	−2.448 836 350[−5]
23	394.272 368 06	345 009.190 32	787.795 231 65	690 018.381 73	−2.142 168 356[−5]
24	429.419 927 67	409 305.237 51	858.090 309 55	818 610.476 04	−1.884 643 194[−5]
25	466.067 487 27	482 192.183 28	931.385 392 40	964 384.367 50	−1.666 798 169[−5]
26	504.215 046 88	564 402.978 79	1 007.680 479 4	1 128 805.958 4	−1.481 275 615[−5]
27	543.862 606	656 700.575	1 086.975 570	1 313 401.151	−1.322 296 19[−5]

^a Ref. [43]. ^b Ref. [45]. ^c Ref. [44].

Table 6. Expectation values of operator $r_1$, $r_1^2$, $r_{12}$, $r_{12}^2$ and $cos{\theta }_{12}$ for the $n{}^{3}P$ states of helium. For each principal quantum number n, the first row corresponds to the calculated values from the present work, while the second rows list the reference values from prior studies for comparison. The numbers in square brackets are the power of 10.

n	$〈{\mathit{r}}_1〉$	$〈{\mathit{r}}_1^2〉$	$〈{\mathit{r}}_{12}〉$	$〈{\mathit{r}}_{12}^2〉$	$〈cos{\mathit{\theta }}_{12}〉$
2	2.673 961 655 2	13.211 740 573	4.699 955 007 5	26.642 793 447	−3.671 932 603[−2]
	2.673 961 655 2 a	13.211 740 573 a	4.699 955 007 5 a	26.642 793 447 a	−3.671 932 60[−2] b
3	6.321 128 044 5	82.109 891 976	11.931 203 148	164.302 878 72	−1.042 038 644[−2]
	6.321 128 044 5 a	82.109 891 976 a	11.931 203 148 a	164.302 878 72 a	−1.042 038 64[−2] b
4	11.468 700 443	279.935 257 54	22.207 622 661	559.913 902 50	−4.293 016 327[−3]
	11.468 700 443 c	279.935 257 b	22.207 622 662 c	559.913 902 b	−4.293 016 32[−3] b
5	18.116 274 445	709.635 959 83	35.494 869 430	1 419.298 518 0	−2.167 819 079[−3]
	18.116 274 453 c	709.635 960 b	35.494 869 447 c	1 419.298 5 b	−2.167 819 078[−3] b
6	26.263 842 175	1 504.162 752 0	51.785 959 700	3 008.343 461 9	−1.243 391 760[−3]
	26.263 842 205 c		51.785 959 760 c
7	35.911 406 361	2 826.466 717 6	71.078 747 733	5 652.946 368 2	−7.781 853 591[−4]
8	47.058 968 678	4 869.499 012 5	93.372 399 136	9 739.007 780 6	−5.189 702 606[−4]
9	59.706 529 968	7 856.210 814 2	118.666 535 20	15 712.429 248	−3.632 347 222[−4]
10	73.854 090 667	12 039.553 308	146.960 964 05	24 079.112 731	−2.640 808 307[−4]
11	89.501 651 007	17 702.477 682	178.255 580 08	35 404.960 380	−1.979 742 057[−4]
12	106.649 211 12	25 157.935 127	212.550 321 32	50 315.874 442	−1.522 161 151[−4]
13	125.296 771 09	34 748.876 832	249.845 149 46	69 497.757 214	−1.195 416 550[−4]
14	145.444 330 95	46 848.253 989	290.140 039 76	93 696.511 025	−9.558 920 113[−5]
15	167.091 890 74	61 859.017 790	333.434 975 73	123 718.038 22	−7.763 200 516[−5]
16	190.239 450 49	80 214.119 424	379.729 945 97	160 428.241 16	−6.390 561 504[−5]
17	214.887 010 20	102 376.510 08	429.024 942 45	204 753.022 21	−5.323 383 901[−5]
18	241.034 569 88	128 839.140 96	481.319 959 35	257 678.283 74	−4.481 206 256[−5]
19	268.682 129 54	160 124.963 25	536.614 992 37	320 249.928 13	−3.807 719 178[−5]
20	297.829 689 18	196 786.928 14	594.910 038 31	393 573.857 74	−3.262 712 841[−5]
21	328.477 248 82	239 407.986 82	656.205 094 70	478 815.974 96	−2.816 952 450[−5]
22	360.624 808 44	288 601.090 48	720.500 159 64	577 202.182 16	−2.448 836 350[−5]
23	394.272 368 06	345 009.190 32	787.795 231 65	690 018.381 73	−2.142 168 356[−5]
24	429.419 927 67	409 305.237 51	858.090 309 55	818 610.476 04	−1.884 643 194[−5]
25	466.067 487 27	482 192.183 28	931.385 392 40	964 384.367 50	−1.666 798 169[−5]
26	504.215 046 88	564 402.978 79	1 007.680 479 4	1 128 805.958 4	−1.481 275 615[−5]
27	543.862 606	656 700.575	1 086.975 570	1 313 401.151	−1.322 296 19[−5]

^a Ref. [43]. ^b Ref. [45]. ^c Ref. [44].

Table 7. Expectation values of operator ${\delta }^3\left(r_1\right)$ and ${\delta }^3\left(r_{12}\right)$, and the cusp condition deviation for the $n{}^{1}P$ states of helium. For each principal quantum number n, the first row corresponds to the calculated values from the present work, while the second rows list the reference values from prior studies for comparison. “Direct” and “Global” refer to the results obtained via the direct calculation and global operator methods, respectively. The fourth column $C_{ne}$ and last column $C_{ee}$ represent electron–nucleus and electron–electron cusp condition deviation, with values closer to zero indicating better agreement with the exact cusp conditions. The numbers in parentheses and square brackets are the numerical uncertainties and power of 10, respectively.

n	$〈{\mathit{\delta }}^3\left({\mathit{r}}_1\right)〉$			$〈{\mathit{\delta }}^3\left({\mathit{r}}_{12}\right)〉$
	Direct	Global	${\mathbf{C}}_{\mathbf{ne}}$	Direct	Global	${\mathbf{C}}_{\mathbf{ee}}$
2	1.274 392 886 329(8)	1.274 392 886 328 85(4)	8.298[−12]	7.351 690(2)[−4]	7.351 688 767(4)[−4]	5.318[−6]
		1.274 392 886 363 6(18) a			7.351 688 78(4)[−4] a
3	1.273 627 290 829(4)	1.273 627 290 828 82(2)	1.117[−11]	2.520 145(2)[−4]	2.520 144 150(2)[−4]	5.155[−6]
		1.273 627 289 01(6) a			2.520 144 18(16)[−4] a
4	1.273 405 800 160(2)	1.273 405 800 159 7(2)	6.973[−12]	1.114 641(2)[−4]	1.114 640 437(2)[−4]	5.105[−6]
5	1.273 324 985 047(2)	1.273 324 985 047 0(2)	2.209[−12]	5.831 674(2)[−5]	5.831 673 552(4)[−5]	5.082[−6]
6	1.273 289 047 895 6(2)	1.273 289 047 895 6(2)	1.508[−12]	3.414 891(2)[−5]	3.414 890 348(2)[−5]	5.070[−6]
7	1.273 270 734 118 5(4)	1.273 270 734 118 4(2)	7.646[−14]	2.166 031(2)[−5]	2.166 030 436(2)[−5]	5.063[−6]
8	1.273 260 444 748 0(2)	1.273 260 444 747 9(4)	2.914[−13]	1.457 971(2)[−5]	1.457 970 456(2)[−5]	5.058[−6]
9	1.273 254 226 103 4(2)	1.273 254 226 103 3(4)	1.395[−13]	1.027 368(2)[−5]	1.027 367 914(2)[−5]	5.055[−6]
10	1.273 250 248 938 9(2)	1.273 250 248 938 8(4)	5.528[−13]	7.507 527(2)[−6]	7.507 525 62(2)[−6]	5.053[−6]
11	1.273 247 587 906 8(4)	1.273 247 587 906 6(8)	8.465[−13]	5.650 719(2)[−6]	5.650 717 88(2)[−6]	5.051[−6]
12	1.273 245 740 668 7(2)	1.273 245 740 668(2)	7.296[−13]	4.358 580(2)[−6]	4.358 578 93(2)[−6]	5.050[−6]
13	1.273 244 418 461 9(2)	1.273 244 418 462(2)	5.768[−13]	3.431 934(2)[−6]	3.431 933 47(2)[−6]	5.049[−6]
14	1.273 243 447 248 3(2)	1.273 243 447 248(2)	4.371[−13]	2.750 252(2)[−6]	2.750 250 17(2)[−6]	5.048[−6]
15	1.273 242 717 873 2(2)	1.273 242 717 873(2)	4.065[−13]	2.237 692(2)[−6]	2.237 691 34(2)[−6]	5.047[−6]
16	1.273 242 159 510 89(8)	1.273 242 159 510(4)	3.447[−13]	1.844 923(2)[−6]	1.844 922 79(2)[−6]	5.047[−6]
17	1.273 241 724 837 80(6)	1.273 241 724 837(4)	1.774[−13]	1.538 912(2)[−6]	1.538 912 14(2)[−6]	5.047[−6]
18	1.273 241 381 414 75(4)	1.273 241 381 414(2)	1.206[−13]	1.296 978(2)[−6]	1.296 977 46(2)[−6]	5.046[−6]
19	1.273 241 106 499 21(2)	1.273 241 106 499(2)	4.531[−15]	1.103 194(2)[−6]	1.103 193 97(2)[−6]	5.046[−6]
20	1.273 240 883 825 34(2)	1.273 240 883 825(2)	4.641[−14]	9.461 584(2)[−7]	9.461 582 20(2)[−7]	5.046[−6]
21	1.273 240 701 550 25(2)	1.273 240 701 550(2)	5.545[−15]	8.175 591(2)[−7]	8.175 590 04(2)[−7]	5.045[−6]
22	1.273 240 550 912 14(2)	1.273 240 550 912(2)	9.206[−15]	7.112 420(2)[−7]	7.112 419 33(2)[−7]	5.045[−6]
23	1.273 240 425 334 18(2)	1.273 240 425 334(2)	1.016[−14]	6.225 839(2)[−7]	6.225 838 52(2)[−7]	5.045[−6]
24	1.273 240 319 814 35(2)	1.273 240 319 814(2)	1.039[−14]	5.480 664(2)[−7]	5.480 662 68(2)[−7]	5.045[−6]
25	1.273 240 230 502 47(2)	1.273 240 230 503(2)	5.635[−15]	4.849 794(2)[−7]	4.849 793 4(2)[−7]	5.045[−6]
26	1.273 240 154 402 27(2)	1.273 240 155(2)	5.168[−15]	4.312 132(2)[−7]	4.312 10(6)[−7]	5.045[−6]
27	1.273 240 089 158 2(4)	1.273 241(2)	6.072[−14]	3.851 083(2)[−7]	3.83(4)[−7]	5.045[−6]

^a Ref. [43].

Table 7. Expectation values of operator ${\delta }^3\left(r_1\right)$ and ${\delta }^3\left(r_{12}\right)$, and the cusp condition deviation for the $n{}^{1}P$ states of helium. For each principal quantum number n, the first row corresponds to the calculated values from the present work, while the second rows list the reference values from prior studies for comparison. “Direct” and “Global” refer to the results obtained via the direct calculation and global operator methods, respectively. The fourth column $C_{ne}$ and last column $C_{ee}$ represent electron–nucleus and electron–electron cusp condition deviation, with values closer to zero indicating better agreement with the exact cusp conditions. The numbers in parentheses and square brackets are the numerical uncertainties and power of 10, respectively.

n	$〈{\mathit{\delta }}^3\left({\mathit{r}}_1\right)〉$			$〈{\mathit{\delta }}^3\left({\mathit{r}}_{12}\right)〉$
	Direct	Global	${\mathbf{C}}_{\mathbf{ne}}$	Direct	Global	${\mathbf{C}}_{\mathbf{ee}}$
2	1.274 392 886 329(8)	1.274 392 886 328 85(4)	8.298[−12]	7.351 690(2)[−4]	7.351 688 767(4)[−4]	5.318[−6]
		1.274 392 886 363 6(18) a			7.351 688 78(4)[−4] a
3	1.273 627 290 829(4)	1.273 627 290 828 82(2)	1.117[−11]	2.520 145(2)[−4]	2.520 144 150(2)[−4]	5.155[−6]
		1.273 627 289 01(6) a			2.520 144 18(16)[−4] a
4	1.273 405 800 160(2)	1.273 405 800 159 7(2)	6.973[−12]	1.114 641(2)[−4]	1.114 640 437(2)[−4]	5.105[−6]
5	1.273 324 985 047(2)	1.273 324 985 047 0(2)	2.209[−12]	5.831 674(2)[−5]	5.831 673 552(4)[−5]	5.082[−6]
6	1.273 289 047 895 6(2)	1.273 289 047 895 6(2)	1.508[−12]	3.414 891(2)[−5]	3.414 890 348(2)[−5]	5.070[−6]
7	1.273 270 734 118 5(4)	1.273 270 734 118 4(2)	7.646[−14]	2.166 031(2)[−5]	2.166 030 436(2)[−5]	5.063[−6]
8	1.273 260 444 748 0(2)	1.273 260 444 747 9(4)	2.914[−13]	1.457 971(2)[−5]	1.457 970 456(2)[−5]	5.058[−6]
9	1.273 254 226 103 4(2)	1.273 254 226 103 3(4)	1.395[−13]	1.027 368(2)[−5]	1.027 367 914(2)[−5]	5.055[−6]
10	1.273 250 248 938 9(2)	1.273 250 248 938 8(4)	5.528[−13]	7.507 527(2)[−6]	7.507 525 62(2)[−6]	5.053[−6]
11	1.273 247 587 906 8(4)	1.273 247 587 906 6(8)	8.465[−13]	5.650 719(2)[−6]	5.650 717 88(2)[−6]	5.051[−6]
12	1.273 245 740 668 7(2)	1.273 245 740 668(2)	7.296[−13]	4.358 580(2)[−6]	4.358 578 93(2)[−6]	5.050[−6]
13	1.273 244 418 461 9(2)	1.273 244 418 462(2)	5.768[−13]	3.431 934(2)[−6]	3.431 933 47(2)[−6]	5.049[−6]
14	1.273 243 447 248 3(2)	1.273 243 447 248(2)	4.371[−13]	2.750 252(2)[−6]	2.750 250 17(2)[−6]	5.048[−6]
15	1.273 242 717 873 2(2)	1.273 242 717 873(2)	4.065[−13]	2.237 692(2)[−6]	2.237 691 34(2)[−6]	5.047[−6]
16	1.273 242 159 510 89(8)	1.273 242 159 510(4)	3.447[−13]	1.844 923(2)[−6]	1.844 922 79(2)[−6]	5.047[−6]
17	1.273 241 724 837 80(6)	1.273 241 724 837(4)	1.774[−13]	1.538 912(2)[−6]	1.538 912 14(2)[−6]	5.047[−6]
18	1.273 241 381 414 75(4)	1.273 241 381 414(2)	1.206[−13]	1.296 978(2)[−6]	1.296 977 46(2)[−6]	5.046[−6]
19	1.273 241 106 499 21(2)	1.273 241 106 499(2)	4.531[−15]	1.103 194(2)[−6]	1.103 193 97(2)[−6]	5.046[−6]
20	1.273 240 883 825 34(2)	1.273 240 883 825(2)	4.641[−14]	9.461 584(2)[−7]	9.461 582 20(2)[−7]	5.046[−6]
21	1.273 240 701 550 25(2)	1.273 240 701 550(2)	5.545[−15]	8.175 591(2)[−7]	8.175 590 04(2)[−7]	5.045[−6]
22	1.273 240 550 912 14(2)	1.273 240 550 912(2)	9.206[−15]	7.112 420(2)[−7]	7.112 419 33(2)[−7]	5.045[−6]
23	1.273 240 425 334 18(2)	1.273 240 425 334(2)	1.016[−14]	6.225 839(2)[−7]	6.225 838 52(2)[−7]	5.045[−6]
24	1.273 240 319 814 35(2)	1.273 240 319 814(2)	1.039[−14]	5.480 664(2)[−7]	5.480 662 68(2)[−7]	5.045[−6]
25	1.273 240 230 502 47(2)	1.273 240 230 503(2)	5.635[−15]	4.849 794(2)[−7]	4.849 793 4(2)[−7]	5.045[−6]
26	1.273 240 154 402 27(2)	1.273 240 155(2)	5.168[−15]	4.312 132(2)[−7]	4.312 10(6)[−7]	5.045[−6]
27	1.273 240 089 158 2(4)	1.273 241(2)	6.072[−14]	3.851 083(2)[−7]	3.83(4)[−7]	5.045[−6]

^a Ref. [43].

For $〈{\delta }^3\left(r_{12}\right)〉$, the expectation values for the triplet states are zero and hence omitted from Table 8. Due to the complexity of electron–electron correction, the wave functions constructed by C-BSBFs show relatively lower accuracy in describing electron–electron interactions, with cusp condition deviations on the order of ${10}^{-6}$. Therefore, the direct calculation method is somewhat limited in accuracy for $〈{\delta }^3\left(r_{12}\right)〉$. Conversely, the global operator method, which does not rely entirely on the accurate local behavior of the wave function near the electron–electron coalescence point, exhibits better computational stability and achieves an accuracy of 8-10 significant digits. Specifically, for $n=$ 2–3 states, our results show excellent agreement with those reported by Drake [43]. Both the global operator and direct calculation methods yield consistent values within uncertainties. Accordingly, in cases where the cusp condition at the electron–electron coalescence point is poorly satisfied, the global operator method is preferable for evaluating the two-electron contact potential ${\delta }^3\left(r_{12}\right)$.

The reduction in accuracy of the global operator method for the $n=26$–27 states can be effectively addressed by systematically optimizing the cavity radius, thereby enabling the method to achieve a level of accuracy comparable to that of the direct calculation method. It is important to note that, for states with principal quantum numbers $n=2$–25, both the global operator and direct calculation methods have achieved the accuracy required for evaluating relativistic and QED corrections.

Table 8. Expectation values of operator ${\delta }^3\left(r_1\right)$ and the cusp condition deviation for the $n{}^{3}P$ states of helium. For each principal quantum number n, the first row corresponds to the calculated values from the present work, while the second rows list the reference values from prior studies for comparison. “Direct” and “Global” refer to the results obtained via the direct calculation and global operator methods, respectively. The last column $C_{ne}$ represents electron–nucleus cusp condition deviation, with values closer to zero indicating better agreement with the exact cusp conditions. The numbers in parentheses and square brackets are the numerical uncertainties and power of 10, respectively.

n	Direct	Global	${\mathit{C}}_{\mathbf{ne}}$
2	1.258 860 605 106(8)	1.258 860 605 106 90(8)	8.839[−11]
		1.258 860 605 073(4) a
3	1.269 121 799 542(4)	1.269 121 799 541 72(2)	3.411[−11]
		1.269 121 797 96(3) a
4	1.271 538 194 169(2)	1.271 538 194 168 72(6)	1.600[−11]
5	1.272 379 289 175(2)	1.272 379 289 174 7(2)	9.261[−12]
6	1.272 745 777 445 7(2)	1.272 745 777 445 6(2)	4.154[−12]
7	1.272 930 384 442 1(2)	1.272 930 384 442 1(2)	1.787[−12]
8	1.273 033 309 053 4(2)	1.273 033 309 053 4(2)	1.924[−12]
9	1.273 095 169 969 9(2)	1.273 095 169 969 8(4)	8.103[−13]
10	1.273 134 566 368 6(2)	1.273 134 566 368 5(4)	2.500[−13]
11	1.273 160 837 411 9(2)	1.273 160 837 411 8(6)	1.300[−12]
12	1.273 179 024 543 7(2)	1.273 179 024 543(2)	1.252[−12]
13	1.273 192 012 889 3(2)	1.273 192 012 889(2)	1.547[−13]
14	1.273 201 535 015 3(2)	1.273 201 535 015(2)	2.481[−13]
15	1.273 208 674 275 0(2)	1.273 208 674 274(4)	6.064[−13]
16	1.273 214 131 802 71(8)	1.273 214 131 802(4)	5.352[−13]
17	1.273 218 375 035 22(6)	1.273 218 375 035(2)	3.452[−13]
18	1.273 221 723 771 28(4)	1.273 221 723 771(2)	2.496[−13]
19	1.273 224 401 834 64(2)	1.273 224 401 834(2)	1.217[−13]
20	1.273 226 569 066 32(2)	1.273 226 569 066(2)	1.335[−13]
21	1.273 228 341 686 62(2)	1.273 228 341 687(2)	9.334[−14]
22	1.273 229 805 575 38(2)	1.273 229 805 575(2)	5.764[−14]
23	1.273 231 025 125 24(2)	1.273 231 025 125(2)	7.196[−14]
24	1.273 232 049 261 24(2)	1.273 232 049 261(2)	4.454[−14]
25	1.273 232 915 607 79(2)	1.273 232 915 608(2)	5.156[−14]
26	1.273 233 653 420 36(2)	1.273 233 654(2)	4.066[−14]
27	1.273 234 29(2)	1.273 234 6(6)	6.093[−14]

^a Ref. [43].

Table 8. Expectation values of operator ${\delta }^3\left(r_1\right)$ and the cusp condition deviation for the $n{}^{3}P$ states of helium. For each principal quantum number n, the first row corresponds to the calculated values from the present work, while the second rows list the reference values from prior studies for comparison. “Direct” and “Global” refer to the results obtained via the direct calculation and global operator methods, respectively. The last column $C_{ne}$ represents electron–nucleus cusp condition deviation, with values closer to zero indicating better agreement with the exact cusp conditions. The numbers in parentheses and square brackets are the numerical uncertainties and power of 10, respectively.

n	Direct	Global	${\mathit{C}}_{\mathbf{ne}}$
2	1.258 860 605 106(8)	1.258 860 605 106 90(8)	8.839[−11]
		1.258 860 605 073(4) a
3	1.269 121 799 542(4)	1.269 121 799 541 72(2)	3.411[−11]
		1.269 121 797 96(3) a
4	1.271 538 194 169(2)	1.271 538 194 168 72(6)	1.600[−11]
5	1.272 379 289 175(2)	1.272 379 289 174 7(2)	9.261[−12]
6	1.272 745 777 445 7(2)	1.272 745 777 445 6(2)	4.154[−12]
7	1.272 930 384 442 1(2)	1.272 930 384 442 1(2)	1.787[−12]
8	1.273 033 309 053 4(2)	1.273 033 309 053 4(2)	1.924[−12]
9	1.273 095 169 969 9(2)	1.273 095 169 969 8(4)	8.103[−13]
10	1.273 134 566 368 6(2)	1.273 134 566 368 5(4)	2.500[−13]
11	1.273 160 837 411 9(2)	1.273 160 837 411 8(6)	1.300[−12]
12	1.273 179 024 543 7(2)	1.273 179 024 543(2)	1.252[−12]
13	1.273 192 012 889 3(2)	1.273 192 012 889(2)	1.547[−13]
14	1.273 201 535 015 3(2)	1.273 201 535 015(2)	2.481[−13]
15	1.273 208 674 275 0(2)	1.273 208 674 274(4)	6.064[−13]
16	1.273 214 131 802 71(8)	1.273 214 131 802(4)	5.352[−13]
17	1.273 218 375 035 22(6)	1.273 218 375 035(2)	3.452[−13]
18	1.273 221 723 771 28(4)	1.273 221 723 771(2)	2.496[−13]
19	1.273 224 401 834 64(2)	1.273 224 401 834(2)	1.217[−13]
20	1.273 226 569 066 32(2)	1.273 226 569 066(2)	1.335[−13]
21	1.273 228 341 686 62(2)	1.273 228 341 687(2)	9.334[−14]
22	1.273 229 805 575 38(2)	1.273 229 805 575(2)	5.764[−14]
23	1.273 231 025 125 24(2)	1.273 231 025 125(2)	7.196[−14]
24	1.273 232 049 261 24(2)	1.273 232 049 261(2)	4.454[−14]
25	1.273 232 915 607 79(2)	1.273 232 915 608(2)	5.156[−14]
26	1.273 233 653 420 36(2)	1.273 233 654(2)	4.066[−14]
27	1.273 234 29(2)	1.273 234 6(6)	6.093[−14]

^a Ref. [43].

4. Summary and Outlook

In this paper, we employed the C-BSBF method to systematically investigate the energy convergence behavior of helium $n{}^{1,3}P$ states confined in a finite cavity. B-spline functions, owing to their completeness and linear independence, are well-suited for addressing multiscale problems spanning several orders of magnitude, while effectively maintaining numerical stability as the basis set is expanded. By optimizing the knot parameters and cavity radius, we achieve high-accuracy nonrelativistic energy calculations for Rydberg states with principal quantum numbers up to $n=27$ within a single diagonalization. The results demonstrate that all calculated energies achieve an accuracy of at least 14 significant digits, and the expectation values of geometric structure parameters exhibit excellent numerical stability and agree with existing theoretical data. These confirm the effectiveness of wave functions constructed using C-BSBFs and accurately depict the long-range asymptotic behavior of helium.

For the contact potentials ${\delta }^3\left(r_1\right)$ and ${\delta }^3\left(r_{12}\right)$, both the global operator and direct calculation methods have been systematically investigated. In addition, we evaluated the electron–electron and electron–nucleus cusp deviations of the wave functions. The electron–nucleus cusp deviation for $\delta \left(r_1\right)$ is on the order of ${10}^{-14}$, confirming that the short-range behavior is well described and allowing accurate evaluation via direct calculation method. In contrast, the cusp deviation for $\delta \left(r_{12}\right)$ reaches approximately ${10}^{-6}$, indicating that the global operator method is more appropriate in this case. Therefore, an appropriate choice between the global operator and direct calculation methods can be made based on the cusp conditions and the required computational accuracy. The results demonstrate that wave functions constructed by C-BSBFs are capable of accurately depicting the short-range asymptotic behavior of helium.

Owing to the flexibility of the B-spline basis construction, the C-BSBF method can be extended to the calculation of Rydberg ${}^{1,3}S$ and ${}^{1,3}D$ states using the same basis configuration and parameters. Preliminary results show that the nonrelativistic energies of these states can be obtained with comparable accuracy to that of ${}^{1,3}P$ states. Building on these results, we can further evaluate atomic properties of Rydberg states, such as electric dipole transition probabilities, radiative lifetimes, and polarizabilities. These properties are essential for interpreting high-precision spectroscopic measurements and for modeling Rydberg atom behavior in external fields.

Moving forward, building on the demonstrated success of the C-BSBF method in relativistic and QED correction calculations [34], and supported by the present high-accuracy results for nonrelativistic energies and contact potentials, this method can be extended to compute relativistic and QED corrections for higher Rydberg states, including effects such as fine structure and the Bethe logarithm. By increasing the cavity radius $R_0$, calculations for even higher principal quantum number states (n ∼40) can be performed, further broadening the applicability of this method. Moreover, the inclusion of these corrections will enable direct comparison with experimental measurements, while also allowing for the theoretical determination of accurate quantum defect parameters, allowing precise predictions of energy levels for higher principal quantum numbers. Combined with spectroscopic measurements [12,21,22,46] and a series of ab initio calculations of Rydberg ionization energies, this method holds promise for further improving the accuracy of ionization energies of low-lying states without using Rydberg–Ritz formula. Furthermore, the C-BSBF method can also be extended to low-Z helium-like ions (such as ${\mathrm{Li}}^{+}$), where it can be applied to the calculation of two-photon transitions and related radiative processes. These few-body systems serve as ideal platforms for testing fundamental aspects of atomic structure theory, as they are sensitive to relativistic, QED, and electron-correlation effects. Accurate two-photon transitions are essential for interpreting high-precision spectroscopic measurements and for providing reliable benchmarks for future theoretical and experimental investigations.