Informational Entropy Analysis of Artificial Helium Atoms
Abstract
1. Introduction
2. Theoretical Background
2.1. System of Interest
2.1.1. Center of Mass Motion
2.1.2. Relative Motion Between the Two Electrons
2.2. Shannon Informational Entropies
3. Results
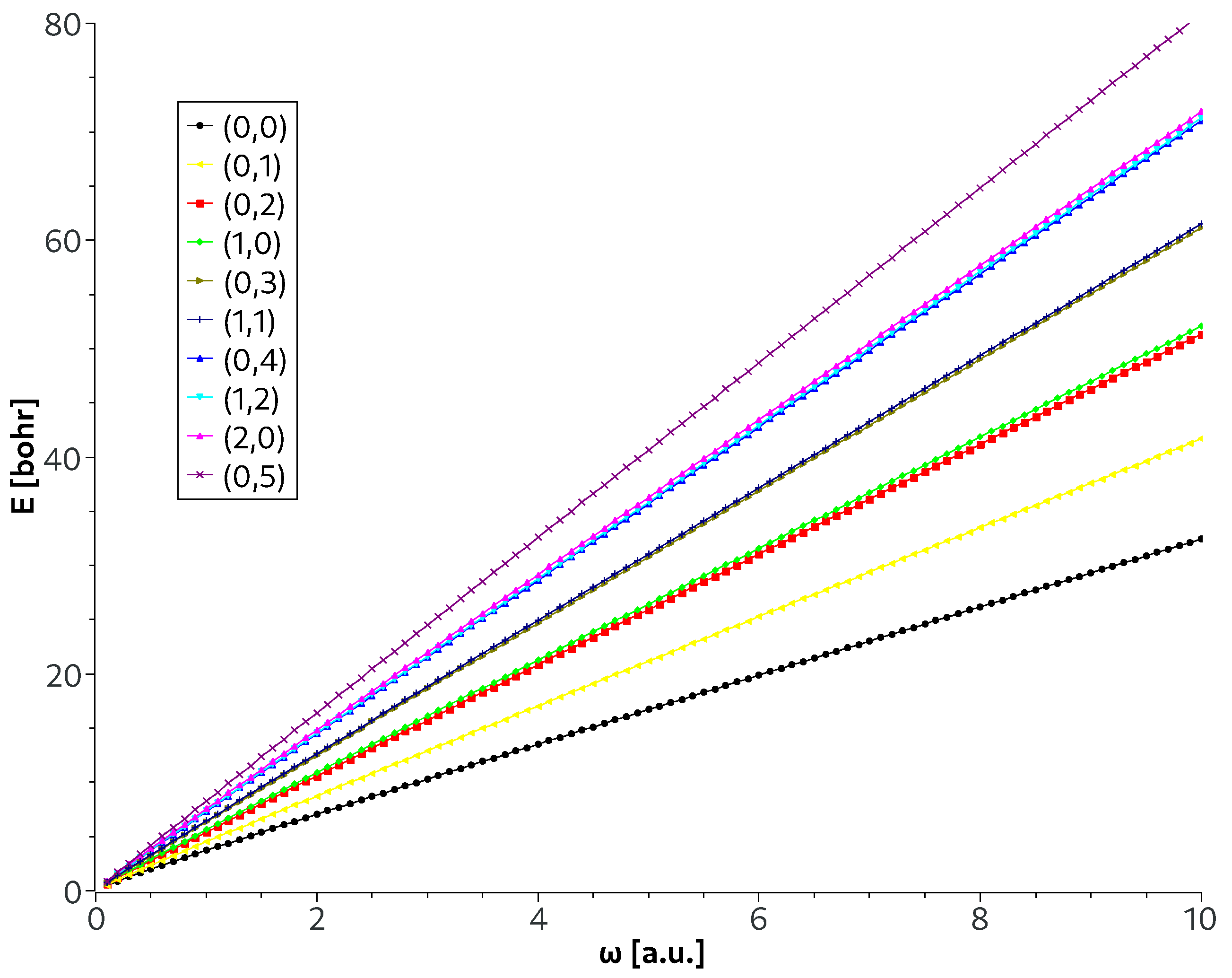
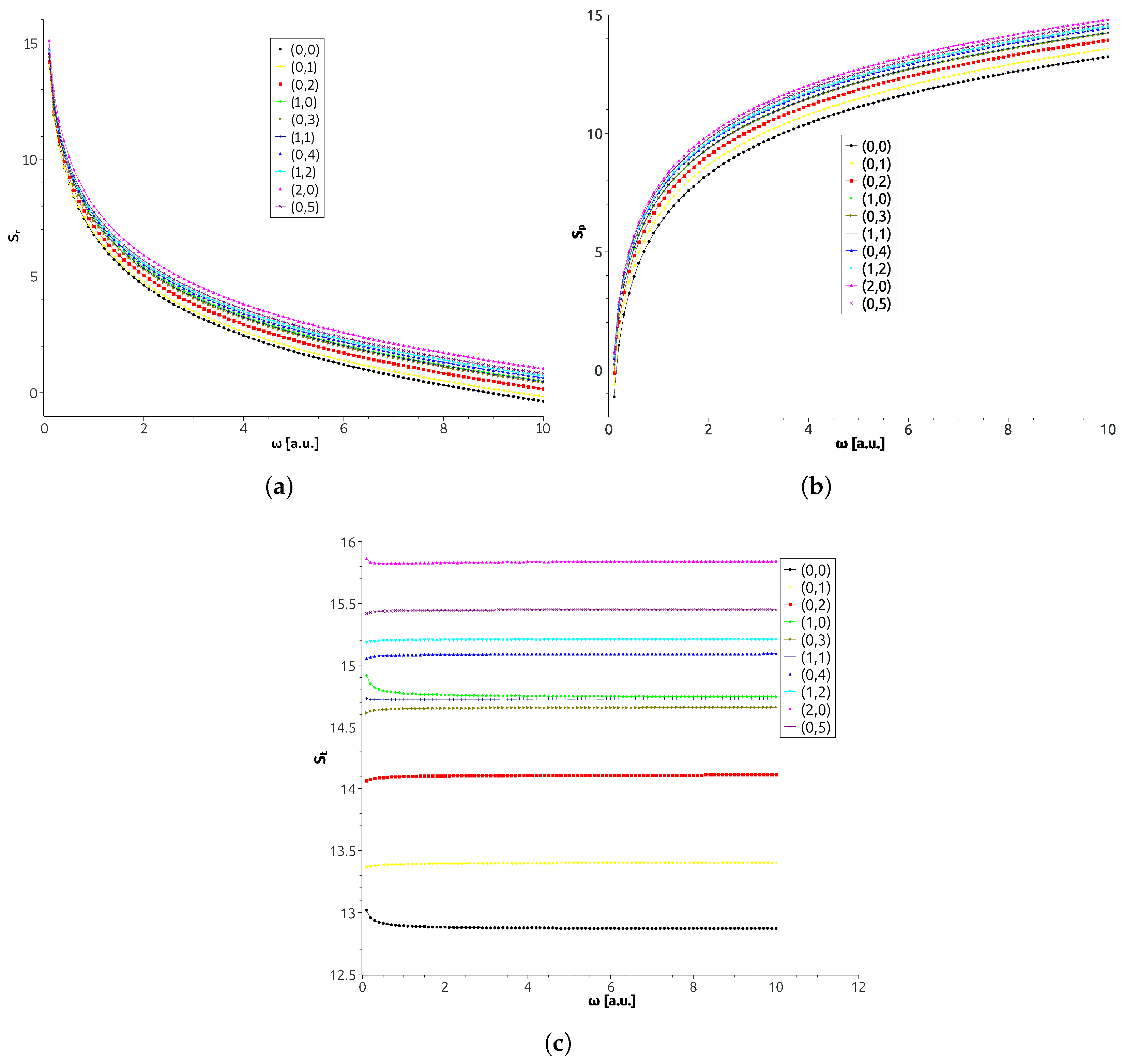
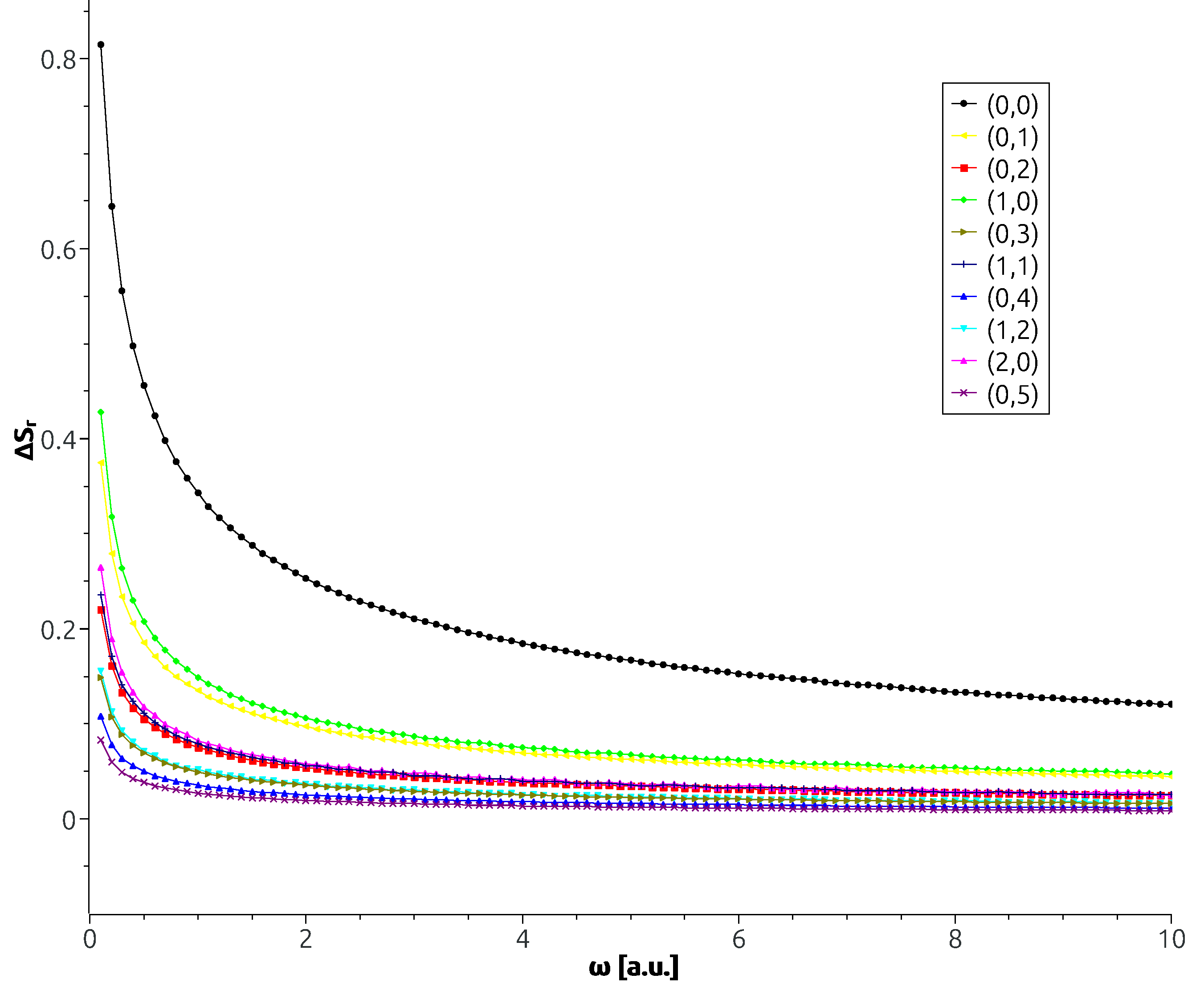
3.1. Spherical Artificial Helium Atom
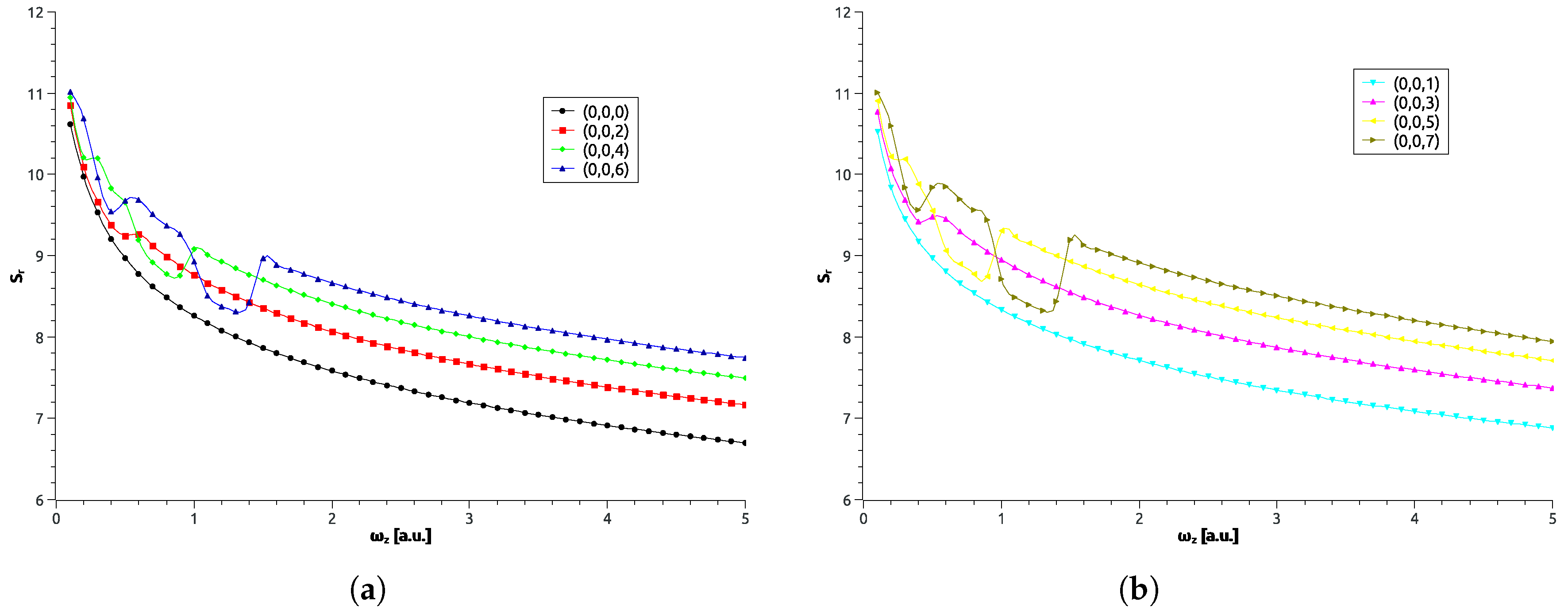
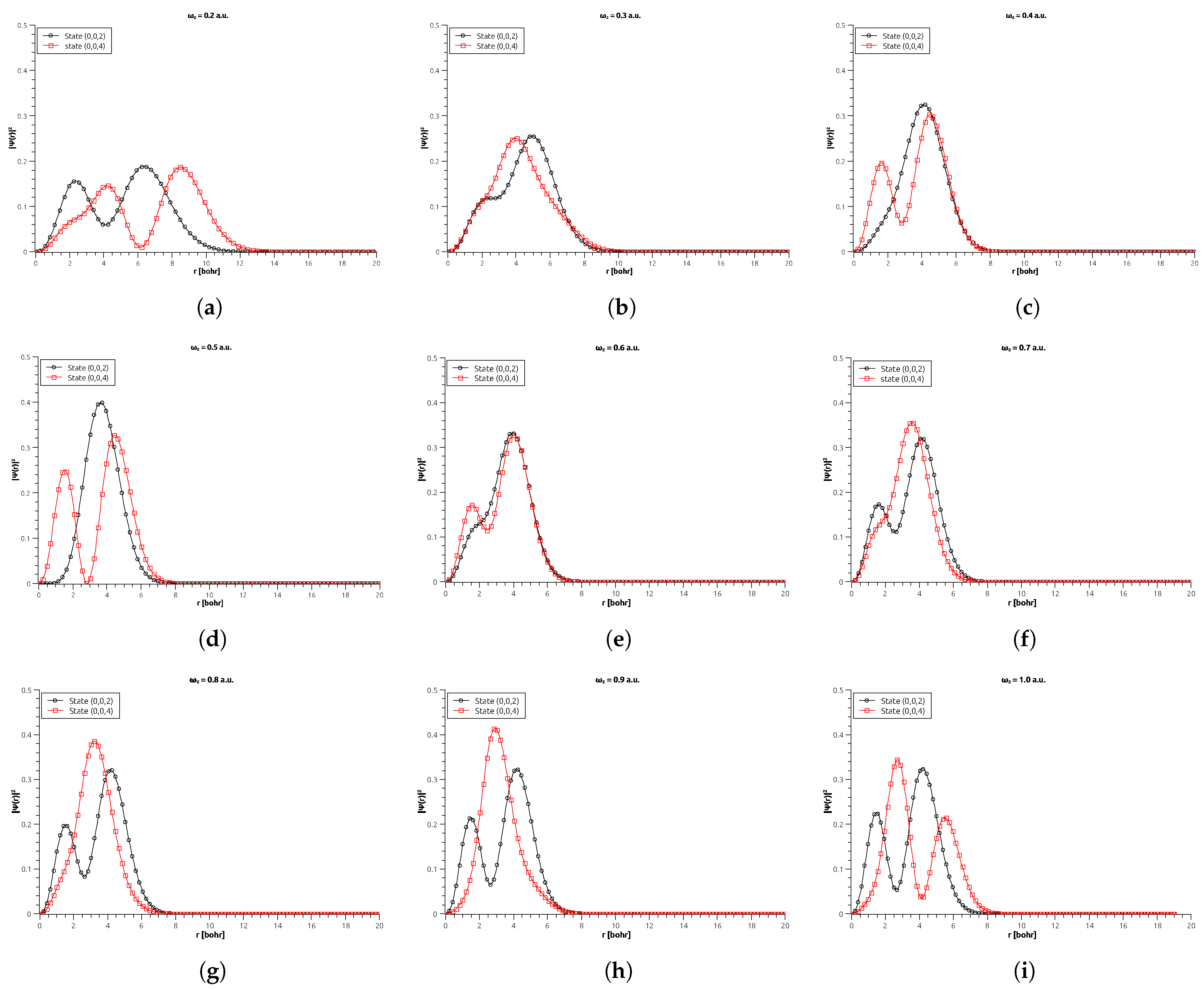
3.2. Cylindrical Artificial Helium Atom
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Knoss, R.W. (Ed.) Quantum Dots Research, Technology and Applications; Nova Science Publishers: New York, NY, USA, 2009. [Google Scholar]
- Kastner, M.A. The single-electron transistor. Rev. Mod. Phys. 1992, 64, 849. [Google Scholar] [CrossRef]
- Lee, Y.; Jun, H.; Park, S.; Kim, D.Y.; Lee, S. Transport Characteristics of Silicon Multi-Quantum-Dot Transistor Analyzed by Means of Experimental Parametrization Based on Single-Hole Tunneling Model. Nanomaterials 2023, 13, 1809. [Google Scholar] [CrossRef]
- Wu, J.; Wang, Z.M. (Eds.) Quantum Dot Solar Cells; Springer: New York, NY, USA, 2014. [Google Scholar]
- Cavassilas, N.; Suchet, D.; Delamarre, A.; Guillemoles, J.; Michelini, F.; Bescond, M.; Lannoo, M. Optimized Operation of Quantum-Dot Intermediate-Band Solar Cells Deduced from Electronic Transport Modeling. Phys. Rev. Appl. 2020, 13, 044035. [Google Scholar] [CrossRef]
- Jang, E.; Jang, H. Review: Quantum Dot Light-Emitting Diodes. Chem. Rev. 2023, 123, 4663. [Google Scholar] [CrossRef] [PubMed]
- Yu, R.; Yin, F.; Zhou, D.; Zhu, H.; Ji, W. Efficient Quantum-Dot Light-Emitting Diodes Enabled via a Charge Manipulating Structure. J. Phys. Chem. Lett. 2023, 14, 4548. [Google Scholar] [CrossRef]
- Tóth, G.; Lent, C.S. Quantum computing with quantum-dot cellular automata. Phys. Rev. A 2001, 63, 052315. [Google Scholar] [CrossRef]
- Jefferson, J.H.; Fearn, M.; Tipton, D.L.J.; Spiller, T.P. Two-electron quantum dots as scalable qubits. Phys. Rev. A 2002, 66, 042328. [Google Scholar] [CrossRef]
- Chiquito, A.J. Pontos quânticos: Átomos artificiais e transistores atômicos. Rev. Bras. Ensino Fis. 2001, 23, 159. [Google Scholar] [CrossRef]
- Bimberg, D.; Grundmann, M.; Ledentsov, N.N. Quantum Dot Heterostructures; Wiley: Chichester, UK, 1999. [Google Scholar]
- Ashoori, R.C. Electrons in artificial atoms. Nature 1996, 379, 413. [Google Scholar] [CrossRef]
- Kastner, M.A. The single electron transistor and artificial atoms. Ann. Phys. 2000, 512, 885. [Google Scholar] [CrossRef]
- Sako, T.; Diercksen, G.H.F. Confined quantum systems: A comparison of the spectral properties of the two-electron quantum dot, the negative hydrogen ion and the helium atom. J. Phys. B At. Mol. Opt. Phys. 2003, 36, 1681. [Google Scholar] [CrossRef]
- Reimann, S.M.; Manninen, M. Electronic structure of quantum dots. Rev. Mod. Phys. 2002, 74, 1283. [Google Scholar] [CrossRef]
- Maniero, A.; Prudente, F.; de Carvalho, C.; Jalbert, G. 3D two-electron double quantum dot: Comparison between the behaviour of some physical quantities under two different confinement potentials in the presence of a magnetic field. Physica B 2023, 657, 414818. [Google Scholar] [CrossRef]
- Kouwenhoven, L.P.; Austing, D.G.; Tarucha, S. Few-electron quantum dots. Rep. Prog. Phys. 2001, 64, 701. [Google Scholar] [CrossRef]
- Chan, I.H.; Fallahi, P.; Vidan, A.; Westervelt, R.M.; Hanson, M.; Gossard, A.C. Few-electron double quantum dots. Nanotechnology 2004, 15, 609. [Google Scholar] [CrossRef]
- Alivisatos, A.P. Semiconductor Clusters, Nanocrystals, and Quantum Dots. Science 1996, 271, 933. [Google Scholar] [CrossRef]
- Brauman, J.I. Clusters. Science 1996, 271, 889. [Google Scholar] [CrossRef]
- Adamowski, J.; Sobkowicz, M.; Szafran, B.; Bednarek, S. Electron pair in a Gaussian confining potential. Phys. Rev. B 2000, 62, 4234. [Google Scholar] [CrossRef]
- Kasapoglu, E.; Yücel, M.B.; Duque, C.A. Harmonic-Gaussian Symmetric and Asymmetric Double Quantum Wells: Magnetic Field Effects. Nanomaterials 2023, 13, 892. [Google Scholar] [CrossRef]
- Maniero, A.M.; de Carvalho, C.R.; Prudente, F.V.; Jalbert, G. Effect of a laser field in the confinement potential of two electrons in a double quantum dot. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 095103. [Google Scholar] [CrossRef]
- Durak, S.; Sakiroglu, S. Theoretical investigation of laser field effect on nonlinear optical properties of quantum dots. Physica B 2023, 650, 414575. [Google Scholar] [CrossRef]
- Maniero, A.M.; de Carvalho, C.R.; Prudente, F.V.; Jalbert, G. Oscillating properties of a two-electron quantum dot in the presence of a magnetic field. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 185001. [Google Scholar] [CrossRef]
- Chaudhuri, S. Two-electron quantum dot in a magnetic field: Analytic solution for finite potential model. Physica E 2021, 128, 114571. [Google Scholar] [CrossRef]
- Plastino, A.R.; Plastino, A. Maximum entropy and approximate descriptions of pure states. Phys. Lett. A 1993, 181, 446–449. [Google Scholar] [CrossRef]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; Illini Books: Champaign, IL, USA, 1949. [Google Scholar]
- Rioul, O. Théorie de L’Information et du Codage; Lavoisier: Paris, France, 2007. [Google Scholar]
- Björk, G. Information gain when measuring an unknown qubit. Eur. J. Phys. 2018, 39, 015403. [Google Scholar] [CrossRef]
- Ricotta, C. Bridging the gap between ecological diversity indices and measures of biodiversity with Shannon’s entropy: Comment to Izsák and Papp. Ecol. Modell. 2002, 152, 1. [Google Scholar] [CrossRef]
- Dabas, S.; Joshi, R. A numerical evaluation of Shannon entropy for modified Hulthen potential. Eur. Phys J. D 2022, 76, 95. [Google Scholar] [CrossRef]
- Singh, S.; Saha, A. Shannon Information Entropy Sum of a Free Particle in Three Dimensions Using Cubical and Spherical Symmetry. J. Sci. Res. 2023, 15, 71. [Google Scholar] [CrossRef]
- Santos, A.J.; Prudente, F.V.; Guimarães, M.N.; Nascimento, W.S. A Study of Strong Confinement Regions Using Informational Entropy. Quantum Rep. 2022, 4, 544–557. [Google Scholar] [CrossRef]
- Salazar, S.J.C.; Laguna, H.G.; Dahiya, B.; Prasad, V.; Sagar, R.P. Shannon information entropy sum of the confined hydrogenic atom under the influence of an electric field. Eur. Phys. J. D 2021, 75, 127. [Google Scholar] [CrossRef]
- Nascimento, W.S.; Prudente, F.V. Shannon entropy: A study of confined hydrogenic-like atoms. Chem. Phys. Lett. 2018, 691, 401. [Google Scholar] [CrossRef]
- Estañón, C.R.; Montgomery, H.E., Jr.; Angulo, J.C.; Aquino, N. The confined helium atom: An information–theoretic approach. Int. J. Quantum Chem. 2024, 124, e27358. [Google Scholar] [CrossRef]
- Nascimento, W.S.; de Almeida, M.M.; Prudente, F.V. Coulomb Correlation and Information Entropies in Confined Helium-Like Atoms. Eur. Phys. J. D 2021, 75, 171. [Google Scholar] [CrossRef]
- Ou, J.H.; Ho, Y.K. Shannon Information Entropy in Position Space for the Ground and Singly Excited States of Helium with Finite Confinements. Atoms 2017, 5, 15. [Google Scholar] [CrossRef]
- Verma, N.; Joshi, R. Shannon entropy for hydrogen atom in Debye and quantum plasma environment. Phys. Plasmas 2023, 30, 063905. [Google Scholar] [CrossRef]
- Zan, L.R.; Jiao, L.G.; Ma, J.; Ho, Y.K. Information-theoretic measures of hydrogen-like ions in weakly coupled Debye plasmas. Phys. Plasmas 2017, 24, 122101. [Google Scholar] [CrossRef]
- Shafeekali, H.; Olendski, O. Quantum-information theory of magnetic field influence on circular dots with different boundary conditions. Phys. Scr. 2023, 98, 085107. [Google Scholar] [CrossRef]
- Liu, X.; Xie, X.; Wang, D.; Wang, C.; Zhao, Y.; Zhang, S. The effect of in-doping on the quantum information entropy of hydrogenic impurity states in the InxGa1-xN semiconductor quantum dot. Philos. Mag. 2023, 103, 892–913. [Google Scholar] [CrossRef]
- Nascimento, W.S.; Maniero, A.M.; Prudente, F.V.; de Carvalho, C.R.; Jalbert, G. Electron confinement study in a double quantum dot by means of Shannon entropy information. Physica B 2024, 677, 415692. [Google Scholar] [CrossRef]
- Nascimento, W.S.; Maniero, A.M.; Prudente, F.V.; de Carvalho, C.R.; Jalbert, G. Informational analysis of the confinement of an electron in an asymmetric double quantum dot. Physica B 2025, 699, 416769. [Google Scholar] [CrossRef]
- González-Férez, R.; Dehesa, J.S. Shannon Entropy as an Indicator of Atomic Avoided Crossings in Strong Parallel Magnetic and Electric Fields. Phys. Rev. Lett. 2003, 91, 113001. [Google Scholar] [CrossRef]
- González-Férez, R.; Dehesa, J.S. Characterization of atomic avoided crossings by means of Fisher’s information. Eur. Phys. J. D 2005, 32, 39. [Google Scholar] [CrossRef]
- Prudente, F.V.; Guimarães, M.N. Confined Quantum Systems Using the Finite Element and Discrete Variable Representation Methods. In Electronic Structure of Quantum Confined Atoms and Molecules; Sen, K.D., Ed.; Springer International Publishing: Oxford, UK, 2014; Chapter 5; p. 101. [Google Scholar] [CrossRef]
- Sen, K.D. (Ed.) Statistical Complexity: Applications in Electronic Struture; Springer: Dordrecht, The Netherlands, 2011. [Google Scholar] [CrossRef]
- Nascimento, W.S.; de Almeida, M.M.; Prudente, F.V. Information and quantum theories: An analysis in one-dimensional systems. Eur. J. Phys. 2020, 41, 025405. [Google Scholar] [CrossRef]
- Corzo, H.H.; Laguna, H.G.; Sagar, R.P. Localization-delocalization phenomena in a cyclic box. J. Math. Chem. 2012, 50, 233. [Google Scholar] [CrossRef]
- Bialynicki-Birula, I.; Mycielski, J. Uncertainty relations for information entropy in wave mechanics. Commun. Math. Phys. 1975, 44, 129. [Google Scholar] [CrossRef]
- Prudente, F.V.; Costa, L.S.; Vianna, J.D.M. A study of two-electron quantum dot spectrum using discrete variable representation method. J. Chem. Phys. 2005, 123, 224701. [Google Scholar] [CrossRef]
- Cordeiro, R.N. Sistemas de Dois Elétrons Confinados Harmonicamente Usando Coordenadas Hiperesféricas e Método do Elemento Finito. Master’s Thesis, Physics Institute—Federal University of Bahia, Salvador, Brazil, 2022. [Google Scholar]
- Manzano, D.; Plastino, A.R.; Dehesa, J.S.; Koga, T. Quantum entanglement in two-electron atomic models. J. Phys. A Math. Theor. 2010, 43, 275301. [Google Scholar] [CrossRef]
- Nazmitdinov, R.G.; Simonović, N.S.; Plastino, A.R.; Chizhov, A.V. Shape transitions in excited states of two-electron quantum dots in a magnetic field. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 205503. [Google Scholar] [CrossRef]


| Cordeiro [54] | Present | Cordeiro [54] | Present | |
|---|---|---|---|---|
| 0.1 | 14.1560 | 14.1564 | 14.7033 | 14.7037 |
| 0.25 | 11.1877 | 11.1880 | 11.8127 | 11.8137 |
| 0.5 | 8.9695 | 8.9697 | 9.6539 | 9.6545 |
| 1.0 | 6.7766 | 6.7767 | 7.5157 | 7.5168 |
| 4.0 | 2.4600 | 2.4599 | 3.2836 | 3.2836 |
| 14.1564 | −1.1391 | 8.9697 | 3.9425 | 2.4599 | 10.4151 | |
| 13.9867 | −0.6189 | 8.9695 | 4.4120 | 2.6151 | 10.7823 | |
| 14.1879 | −0.1239 | 9.2439 | 4.8475 | 2.9391 | 11.1698 | |
| 14.7037 | 0.2114 | 9.6545 | 5.1396 | 3.2836 | 11.4654 | |
| 14.3877 | 0.2264 | 9.4802 | 5.1598 | 3.1978 | 11.4571 | |
| 14.5077 | 0.2218 | 9.5551 | 5.1674 | 3.2457 | 11.4798 | |
| 14.5636 | 0.4904 | 9.6771 | 5.3993 | 3.4069 | 11.6820 | |
| 14.6687 | 0.5136 | 9.7576 | 5.4410 | 3.4726 | 11.7336 | |
| 15.0980 | 0.7638 | 10.1232 | 5.6979 | 3.8091 | 12.0280 | |
| 14.7173 | 0.7004 | 9.8439 | 5.5929 | 3.5812 | 11.8660 | |
| 10.6205 | 8.2612 | 6.9117 | |||
| 10.5241 | 8.5527 | 7.1609 | |||
| 10.8540 | 8.7503 | 7.3573 | |||
| 10.7673 | 8.7640 | 7.3840 | |||
| 10.9458 | 8.3347 | 7.5045 | |||
| 10.9072 | 8.8962 | 7.6054 | |||
| 11.2061 | 8.7798 | 7.6204 | |||
| 11.0205 | 9.0014 | 7.7588 | |||
| 11.0988 | 9.0109 | 7.7166 | |||
| 11.0079 | 9.1536 | 7.7154 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guimarães, M.N.; Cordeiro, R.N.; Nascimento, W.S.; Prudente, F.V. Informational Entropy Analysis of Artificial Helium Atoms. Atoms 2025, 13, 42. https://doi.org/10.3390/atoms13050042
Guimarães MN, Cordeiro RN, Nascimento WS, Prudente FV. Informational Entropy Analysis of Artificial Helium Atoms. Atoms. 2025; 13(5):42. https://doi.org/10.3390/atoms13050042
Chicago/Turabian StyleGuimarães, Marcilio N., Rafael N. Cordeiro, Wallas S. Nascimento, and Frederico V. Prudente. 2025. "Informational Entropy Analysis of Artificial Helium Atoms" Atoms 13, no. 5: 42. https://doi.org/10.3390/atoms13050042
APA StyleGuimarães, M. N., Cordeiro, R. N., Nascimento, W. S., & Prudente, F. V. (2025). Informational Entropy Analysis of Artificial Helium Atoms. Atoms, 13(5), 42. https://doi.org/10.3390/atoms13050042






