Electron Scattering from Superheavy Elements: Copernicium and Oganesson
Abstract
1. Introduction
2. Methodology
2.1. Relativistic Case
2.2. Non-Relativistic Case
3. Results and Discussion
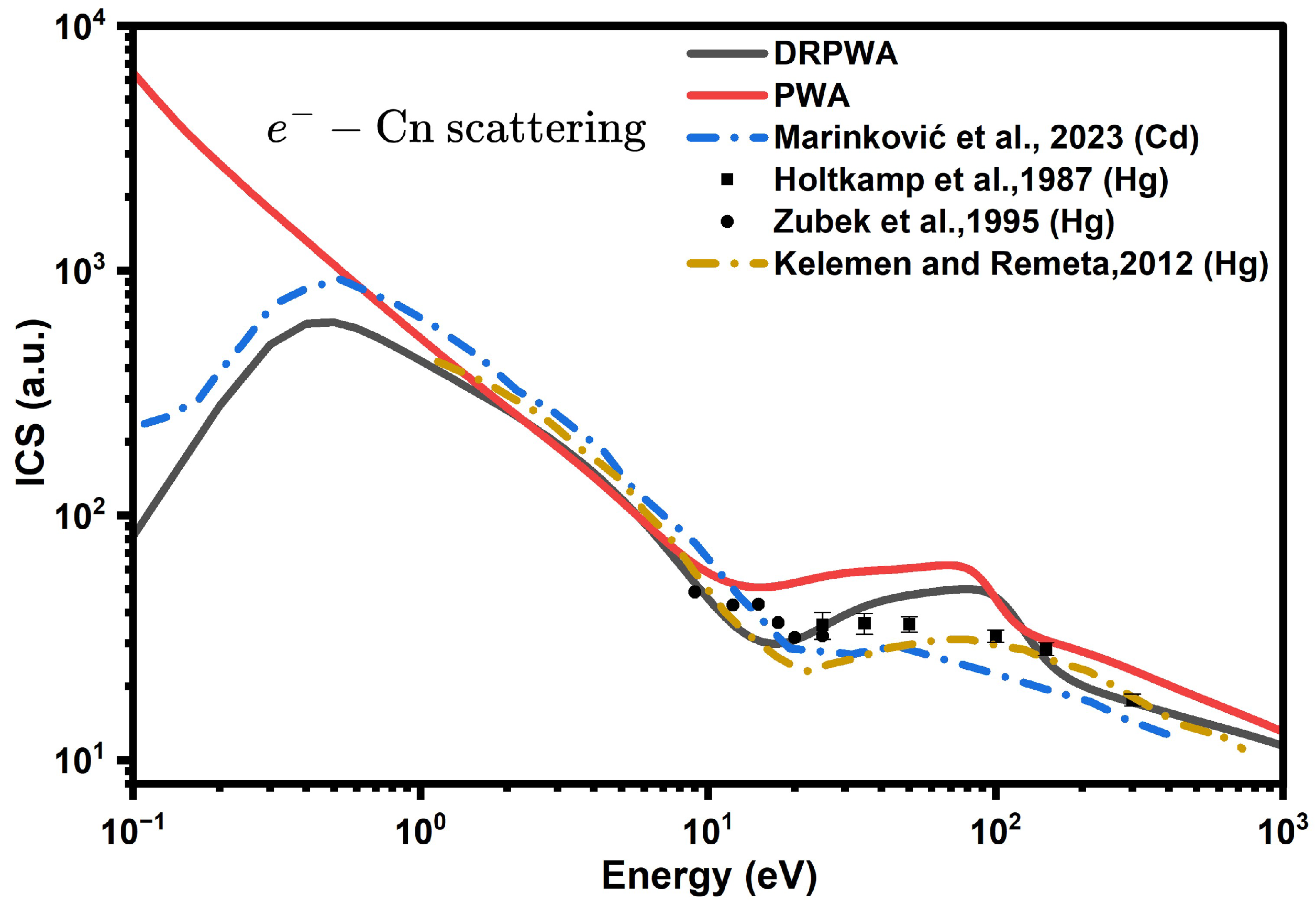
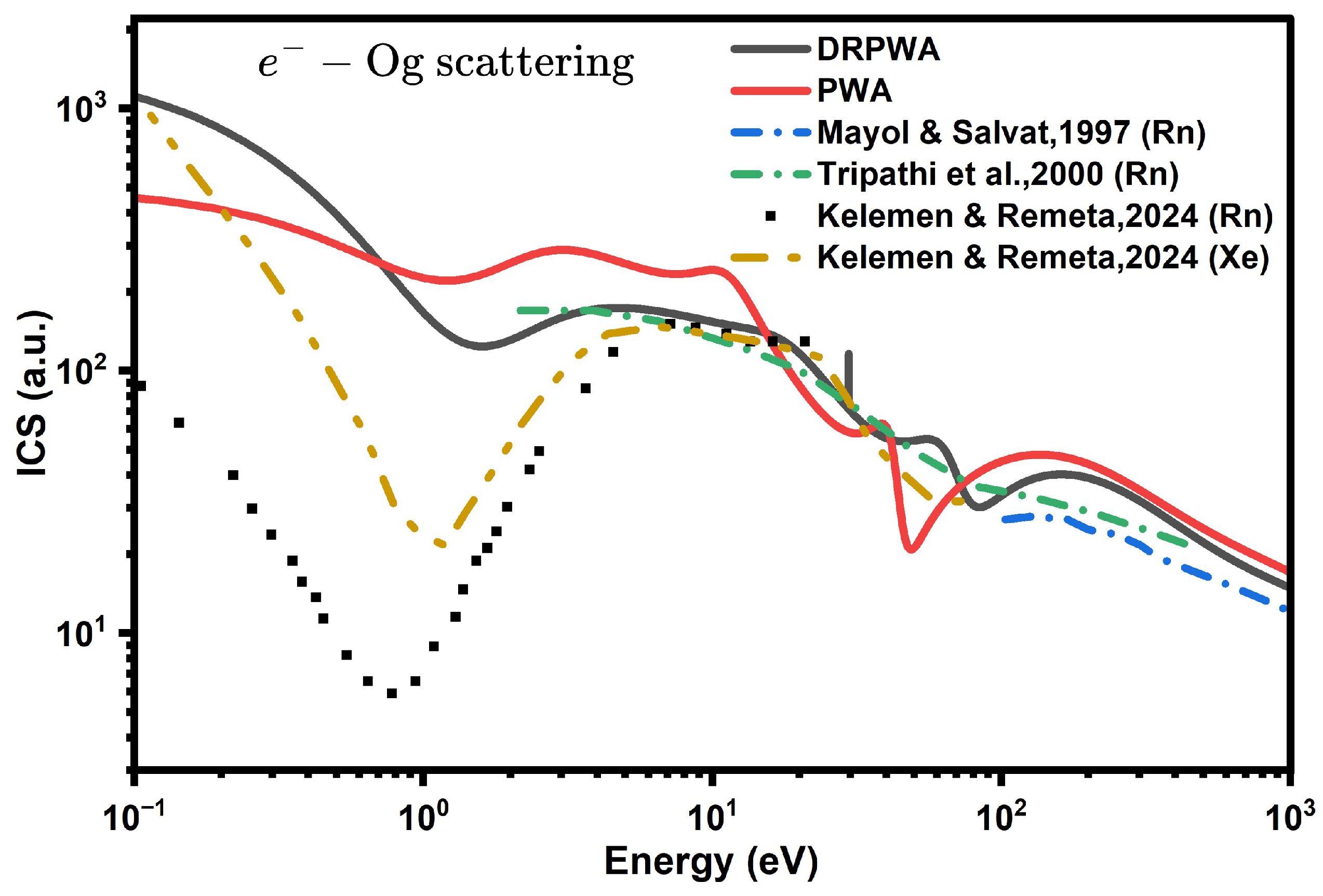
3.1. Integral Cross-Section for Electron Scattering from Copernicium and Oganesson
3.2. Scattering Length
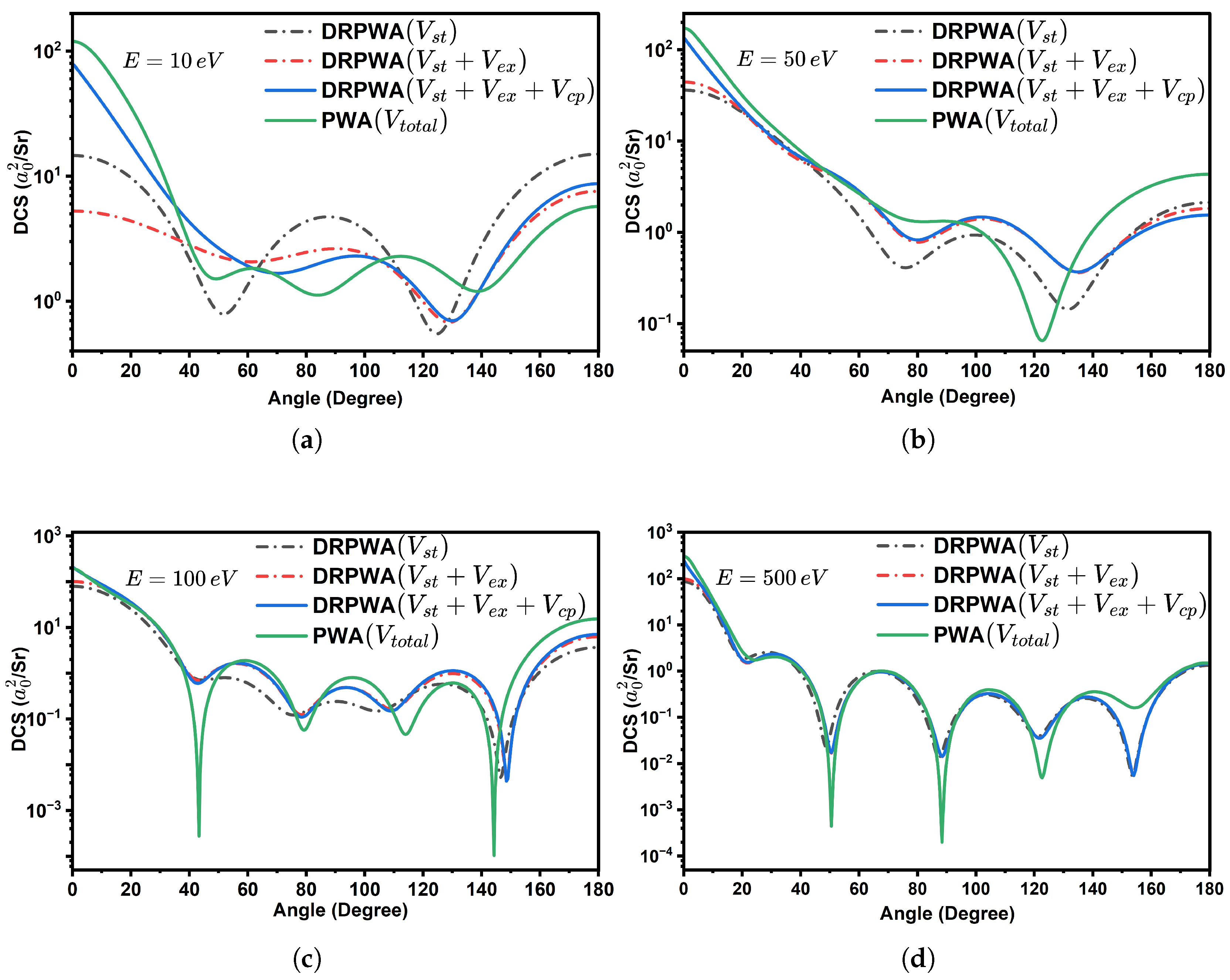
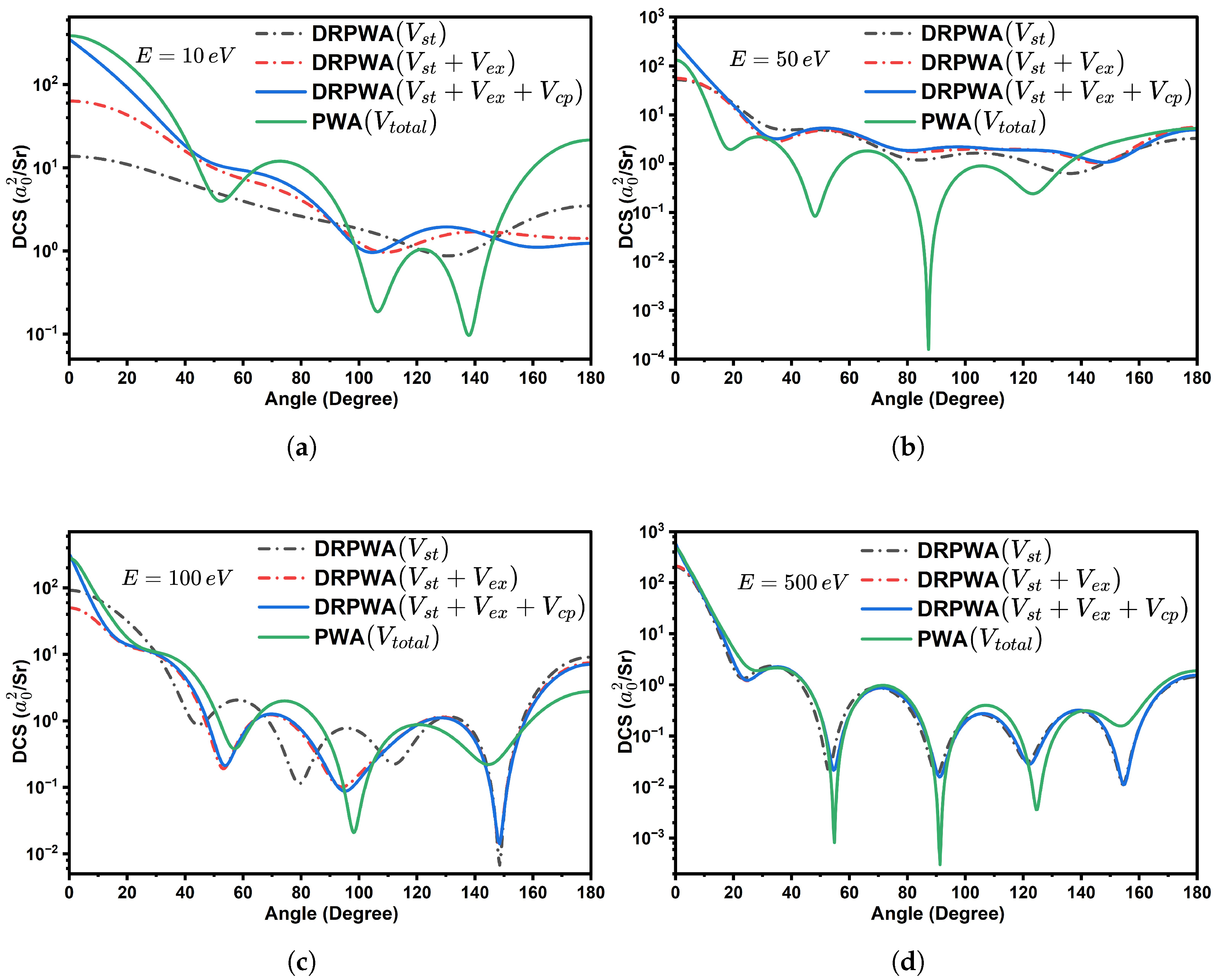
3.3. Differential Cross-Section for – Cn and – Og Scattering
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zvára, I. State of art in experimental studies and theory of superheavy elements. Czechoslov. J. Phys. 2003, 53, A281–A290. [Google Scholar] [CrossRef]
- Pershina, V. Electronic structure and chemical properties of superheavy elements. Russ. Chem. Rev. 2009, 78, 1153. [Google Scholar] [CrossRef]
- Zaitsevskii, A.V.; Rykova, E.A.; Titov, A.V. Theoretical studies on the structures and properties of superheavy element compounds. Russ. Chem. Rev. 2008, 77, 205. [Google Scholar] [CrossRef]
- Dzuba, V.; Flambaum, V. Electron structure of superheavy elements Uut, Fl and Uup (Z = 113 to 115). Hyperfine Interact. 2016, 237, 160. [Google Scholar] [CrossRef]
- Kumar, R.; Chattopadhyay, S.; Angom, D.; Mani, B.K. Relativistic coupled-cluster calculation of the electric dipole polarizability and correlation energy of Cn, Nh+, and Og: Correlation effects from lighter to superheavy elements. Phys. Rev. A 2021, 103, 062803. [Google Scholar] [CrossRef]
- Yakushev, A.; Khuyagbaatar, J.; Düllmann, C.E.; Block, M.; Cantemir, R.; Cox, D.; Dietzel, D.; Giacoppo, F.; Hrabar, Y.; Iliaš, M.; et al. Manifestation of relativistic effects in the chemical properties of nihonium and moscovium revealed by gas chromatography studies. Front. Chem. 2024, 12, 1474820. [Google Scholar] [CrossRef]
- Giuliani, S.A.; Matheson, Z.; Nazarewicz, W.; Olsen, E.; Reinhard, P.G.; Sadhukhan, J.; Schuetrumpf, B.; Schunck, N.; Schwerdtfeger, P. Colloquium: Superheavy elements: Oganesson and beyond. Rev. Mod. Phys. 2019, 91, 011001. [Google Scholar] [CrossRef]
- Hofmann, S.; Ninov, V.; Heßberger, F.; Armbruster, P.; Folger, H.; Münzenberg, G.; Schött, H.; Popeko, A.; Yeremin, A.; Saro, S.; et al. The new element 112. Z. Phys. A Hadron. Nucl. 1996, 354, 229–230. [Google Scholar] [CrossRef]
- Mewes, J.M.; Smits, O.R.; Kresse, G.; Schwerdtfeger, P. Copernicium: A relativistic noble liquid. Angew. Chem. Int. Ed. 2019, 58, 17964–17968. [Google Scholar] [CrossRef]
- Liu, H.; Han, J.; Yu, Y.; Ge, Y.; Liu, Y.; Huang, Z. Relativistic Calculations of Energy Levels, Field Shift Factors, and Polarizabilities of Mercury and Copernicium. arXiv 2025, arXiv:2507.18490. [Google Scholar] [CrossRef]
- Fricke, B.; Waber, J.T. Theoretical Predictions of the Chemistry of Superheavy Elements. Continuation of the Periodic Table up to z = 184; Technical Report; Northwestern Univ.: Evanston, IL, USA, 1971. [Google Scholar]
- Pershina, V.; Bastug, T. Relativistic effects on experimentally studied gas-phase properties of the heaviest elements. Chem. Phys. 2005, 311, 139–150. [Google Scholar] [CrossRef]
- Yu, Y.; Li, J.; Dong, C.; Ding, X.; Fritzsche, S.; Fricke, B. The excitation energies, ionization potentials and oscillator strengths of neutral and ionized species of Uub (Z= 112) and the homologue elements Zn, Cd and Hg. Eur. Phys. J. D 2007, 44, 51–56. [Google Scholar] [CrossRef]
- Smits, O.R.; Mewes, J.M.; Jerabek, P.; Schwerdtfeger, P. Oganesson: A noble gas element that is neither noble nor a gas. Angew. Chem. Int. Ed. 2020, 59, 23636–23640. [Google Scholar] [CrossRef] [PubMed]
- Oganessian, Y.T.; Utyonkov, V.; Lobanov, Y.V.; Abdullin, F.S.; Polyakov, A.; Sagaidak, R.; Shirokovsky, I.; Tsyganov, Y.S.; Voinov, A.; Gulbekian, G.; et al. Synthesis of the isotopes of elements 118 and 116 in the Cf 249 and Cm 245+ Ca 48 fusion reactions. Phys. Rev. C—Nuclear Phys. 2006, 74, 044602. [Google Scholar] [CrossRef]
- Santhosh, K.; Safoora, V. Theoretical studies on the synthesis of SHE 290-302 Og (Z = 118) using 48Ca, 45Sc, 50Ti, 51V, 54Cr, 55Mn, 58Fe, 59Co and 64Ni induced reactions. Eur. Phys. J. A 2018, 54, 80. [Google Scholar] [CrossRef]
- Jerabek, P.; Schuetrumpf, B.; Schwerdtfeger, P.; Nazarewicz, W. Electron and Nucleon Localization Functions of Oganesson: Approaching the Thomas-Fermi Limit. Phys. Rev. Lett. 2018, 120, 053001. [Google Scholar] [CrossRef] [PubMed]
- Mewes, J.M.; Jerabek, P.; Smits, O.R.; Schwerdtfeger, P. Oganesson Is a Semiconductor: On the Relativistic Band-Gap Narrowing in the Heaviest Noble-Gas Solids. Angew. Chem. Int. Ed. 2019, 58, 14260–14264. [Google Scholar] [CrossRef]
- Lackenby, B.G.; Dzuba, V.A.; Flambaum, V.V. Atomic structure calculations of superheavy noble element oganesson (Z = 118). Phys. Rev. A 2018, 98, 042512. [Google Scholar] [CrossRef]
- Kaygorodov, M.; Skripnikov, L.; Tupitsyn, I.; Eliav, E.; Kozhedub, Y.; Malyshev, A.; Oleynichenko, A.; Shabaev, V.; Titov, A.; Zaitsevskii, A. Electron affinity of oganesson. Phys. Rev. A 2021, 104, 012819. [Google Scholar] [CrossRef]
- Jose, J.; Baral, S.; Deshmukh, P.C.; Manson, S.T. Relativistic and correlation effects in the photoionization dynamics of oganesson (Z = 118): Spin-orbit-interaction-activated interchannel coupling effects. Phys. Rev. A 2020, 102, 022813. [Google Scholar] [CrossRef]
- Walker, D. Relativistic effects in low energy electron scattering from atoms. Adv. Phys. 1971, 20, 257–323. [Google Scholar] [CrossRef]
- Lam, L.S.F. Relativistic effects in electron scattering by atoms. III. Elastic scattering by krypton, xenon and radon. J. Phys. B At. Mol. Phys. 1982, 15, 119. [Google Scholar] [CrossRef]
- Kapil, K.S.; Vats, R. Elastic positron scattering by radon and radium atoms. Phys. Scr. 2012, 85, 045304. [Google Scholar] [CrossRef]
- Haque, M.; Haque, A.; Bhattacharjee, P.P.; Uddin, M.A.; Patoary, M.A.R.; Basak, A.; Maaza, M.; Saha, B. Relativistic treatment of scattering of electrons and positrons by mercury atoms. Mol. Phys. 2019, 117, 2303–2319. [Google Scholar] [CrossRef]
- Baluja, K.; Jain, A. Positron scattering from rare gases (He, Ne, Ar, Kr, Xe, and Rn): Total cross sections at intermediate and high energies. Phys. Rev. A 1992, 46, 1279. [Google Scholar] [CrossRef] [PubMed]
- Parpia, F.A.; Fischer, C.F.; Grant, I.P. GRASP92: A package for large-scale relativistic atomic structure calculations. Comput. Phys. Commun. 1996, 94, 249–271. [Google Scholar] [CrossRef]
- Furness, J.; McCarthy, I. Semiphenomenological optical model for electron scattering on atoms. J. Phys. B At. Mol. Phys. 1973, 6, 2280. [Google Scholar] [CrossRef]
- Salvat, F. Optical-model potential for electron and positron elastic scattering by atoms. Phys. Rev. A 2003, 68, 012708. [Google Scholar] [CrossRef]
- Cheng, Y. Relativistic and electron-correlation effects in static dipole polarizabilities for group 12 elements. Phys. Chem. Chem. Phys. 2025, 27, 3430–3441. [Google Scholar] [CrossRef] [PubMed]
- Mittleman, M.H.; Watson, K.M. Effects of the Pauli principle on the scattering of high-energy electrons by atoms. Ann. Phys. 1960, 10, 268–279. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048. [Google Scholar] [CrossRef]
- Salvat, F.; Jablonski, A.; Powell, C.J. Elsepa—Dirac partial-wave calculation of elastic scattering of electrons and positrons by atoms, positive ions and molecules (new version announcement). Comput. Phys. Commun. 2021, 261, 107704. [Google Scholar] [CrossRef]
- Marinković, B.; McEachran, R.; Fursa, D.; Bray, I.; Umer, H.; Blanco, F.; García, G.; Brunger, M.; Campbell, L.; Jones, D. Cross sections for electron scattering from cadmium: Theory and experiment. J. Phys. Chem. Ref. Data 2023, 52, 023102. [Google Scholar] [CrossRef]
- Holtkamp, G.; Jost, K.; Peitzmann, F.; Kessler, J. Absolute differential cross sections for elastic electron scattering from mercury. J. Phys. B At. Mol. Phys. 1987, 20, 4543. [Google Scholar] [CrossRef]
- Zubek, M.; Danjo, A.; King, G. Differential cross sections for elastic electron scattering by mercury in the energy range 9 to 25 eV. J. Phys. B: At. Mol. Opt. Phys. 1995, 28, 4117. [Google Scholar] [CrossRef]
- Kelemen, V.; Remeta, E.Y. Critical minima and spin polarization in the elastic electron scattering by the mercury atoms. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 185202. [Google Scholar] [CrossRef]
- Mayol, R.; Salvat, F. Total and transport cross sections for elastic scattering of electrons by atoms. At. Data Nucl. Data Tables 1997, 65, 55–154. [Google Scholar] [CrossRef]
- Tripathi, A.; Jain, A. Spin polarization and cross sections in elastic scattering of electrons from Yb, Rn, and Ra atoms. Phys. Rev. A 2000, 61, 032713. [Google Scholar] [CrossRef]
- Kelemen, V.; Remeta, E.Y. Features in the electron elastic scattering cross sections of atoms Sb, Xe and Bi, Rn. J. Phys. B At. Mol. Opt. Phys. 2024, 57, 245001. [Google Scholar] [CrossRef]
- Joachain, C.J. Quantum Collision Theory; North-Holland: Amsterdam, The Netherlands, 1975. [Google Scholar]
- Regal, C.; Jin, D. Measurement of positive and negative scattering lengths in a Fermi gas of atoms. Phys. Rev. Lett. 2003, 90, 230404. [Google Scholar] [CrossRef]
- Syty, P.; Piłat, M.P.; Sienkiewicz, J.E. Calculation of electron scattering lengths on Ar, Kr, Xe, Rn and Og atoms. J. Phys. B At. Mol. Opt. Phys. 2024, 57, 175202. [Google Scholar] [CrossRef]
- Fedus, K.; Karwasz, G. Semi-empirical prediction of bound and virtual states in low-energy positron and electron scattering by atoms and molecules. Eur. Phys. J. D 2025, 79, 43. [Google Scholar] [CrossRef]
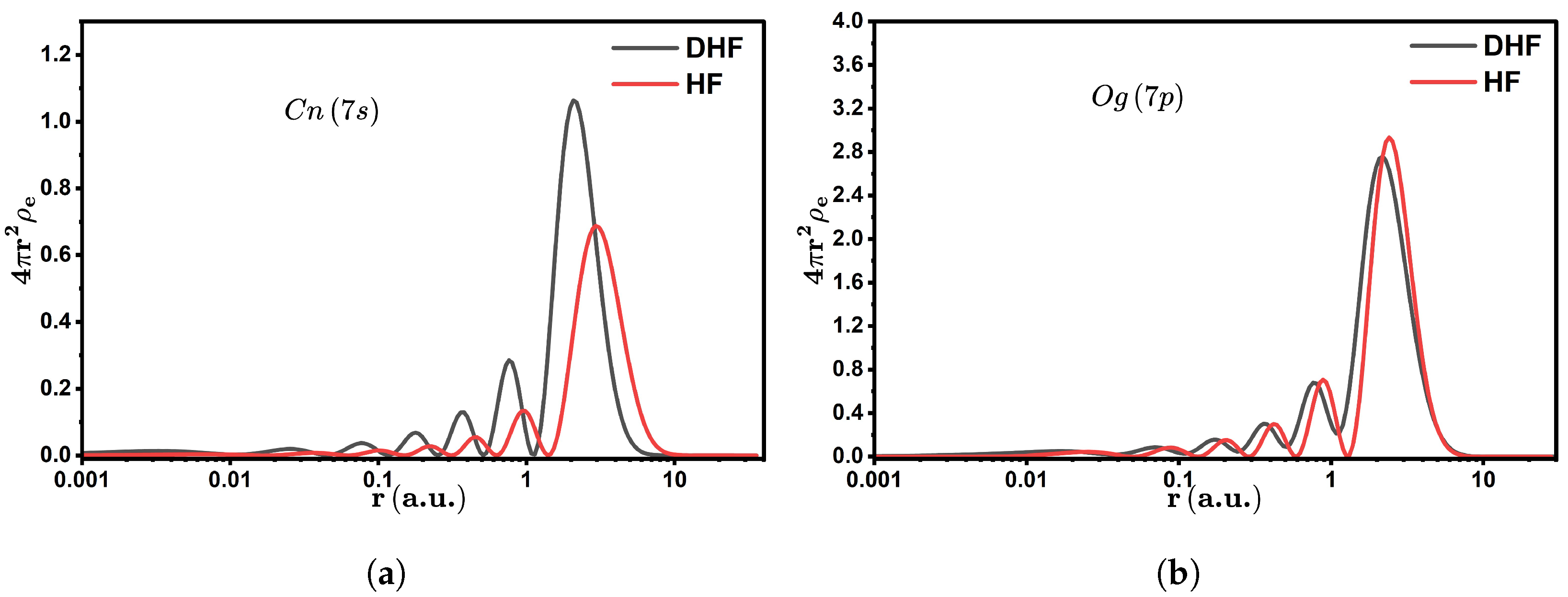
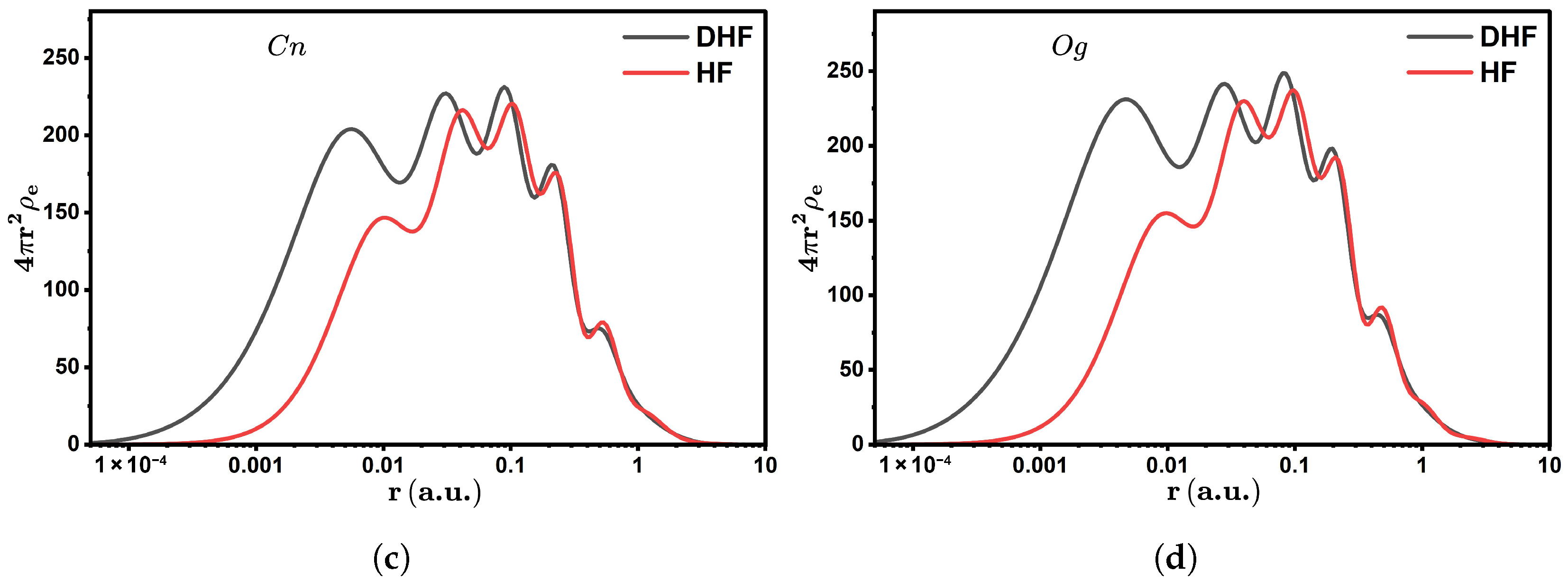
| Atom | Relativistic Subshells | Energy (eV) | Non-Relativistic Subshells | Energy (eV) |
|---|---|---|---|---|
| Cn | 15.311 12.027 12.274 | 18.941 6.478 | ||
| Og | 35.289 20.119 8.315 | 21.058 10.732 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarswat, S.; Baral, S.; Jose, J. Electron Scattering from Superheavy Elements: Copernicium and Oganesson. Atoms 2025, 13, 94. https://doi.org/10.3390/atoms13110094
Sarswat S, Baral S, Jose J. Electron Scattering from Superheavy Elements: Copernicium and Oganesson. Atoms. 2025; 13(11):94. https://doi.org/10.3390/atoms13110094
Chicago/Turabian StyleSarswat, Shruti, Saumyashree Baral, and Jobin Jose. 2025. "Electron Scattering from Superheavy Elements: Copernicium and Oganesson" Atoms 13, no. 11: 94. https://doi.org/10.3390/atoms13110094
APA StyleSarswat, S., Baral, S., & Jose, J. (2025). Electron Scattering from Superheavy Elements: Copernicium and Oganesson. Atoms, 13(11), 94. https://doi.org/10.3390/atoms13110094






