Applicability of Bispectral Analysis to Causality Determination within and between Ensembles of Unstable Plasma Waves

Abstract

Turbulence implies nonlinear wave–wave coupling, and determining cause and effect of either is important to understand mixing responsible for enhanced number, momentum, or energy (NME) transport. To explain the identification of parent and daughter modes via a look-up table, we sketch the framework of bispectral analysis without repeating the mathematical formalism of earlier bispectrum researchers. We then apply this technique to a test signal and plasma fluctuation data from the WVU-Q machine, where the inhomogeneous energy density-driven spectrum exhibited a degree of coupling to lower frequencies that was absent in the case of the related, single-eigenmode, current-driven spectrum.

1. Introduction

Establishing a causal relationship between physical properties, mechanisms, and events is important for understanding plasma dynamics, validating models, and isolating the factors that influence plasma conditions. Methods for doing this are not new, and we do not delve into the subject beyond the familiar level. However, we cite van Milligen et al. [1], who employed the transfer entropy technique, measuring information transfer to conclude that the causal relationship between nonlinearly interacting fields in complex systems can be unraveled, as demonstrated in an electron-cyclotron-resonance-heated stellarator plasma [2]. In our paper, we claim that our documentation of causality unambiguously exceeds the minimum threshold of credible fluctuation correlation, with the help of bispectral analysis. This paper includes a brief overview (Section 2), ample technique description (Section 3 and Section 4), and key experimental results and interpretation (Section 5) of two categories of plasma fluctuations: one driven by magnetic field-aligned current [3] and the other driven by shear in plasma flow [4], where the shear and the flow are both perpendicular to the magnetic field and to each other.

Our objective is to distinguish two parent waves from the daughter wave in a broadband spectrum of three-wave interactions so that coupling and cause and effect can be recognized. To establish signatures of actual wave–wave coupling and to distinguish these from artifact signatures, we establish that the (broadband, ion-cyclotron range, shear-driven) inhomogeneous energy-density driven spectrum, as evidenced by plasma fluctuation data from the WVU-Q machine [5,6], is shown to exhibit a degree of coupling to various spectral components of the lower-frequency drift-wave oscillations [7] that is absent in the case of the (narrowband, ion-cyclotron range, current-driven) electrostatic ion-cyclotron spectrum. First, we describe the algorithm used to identify the parent waves and fraction of power associated with three-wave coupling.

2. Background

2.1. Bispectrum (B)

The Fourier spectrum of the autocorrelation function is the second-order cumulant spectrum and is identical to the conventional power spectrum. The power spectrum’s frequency components are insensitive to phase coherence among those components, whereas the cross-correlation function yields the statistical phase- and amplitude-dependent spatiotemporal similarities between same-frequency (or same-wavenumber) fluctuations acquired at separate times or positions. In contrast, the third-order cumulant spectrum, called the bispectrum B(ω_j, ω_k), is the Fourier transform of the triple correlation function and will be non-zero only if there is a statistical phase dependence between waves at ω_j, ω_k, and (ω_j + ω_k). The wavenumbers relate similarly for k_j, k_k, and (k_j + k_k), but we emphasize ω-space here):

$$B\left({\mathsf{\omega }}_j,{\mathsf{\omega }}_k\right),=\mathrm{E}\left[\mathsf{\Phi }\left({\mathsf{\omega }}_j\right)\mathsf{\Phi }\left({\mathsf{\omega }}_k\right){\mathsf{\Phi }}^{*}({\mathsf{\omega }}_j+{\mathsf{\omega }}_k)\right]$$

(1)

where E is the expectation operator and Φ is the Fourier amplitude of a time series measured at a single point. For spontaneously excited independent waves, the phase of each will be statistically independent, and the resulting sum (net) phase will be randomly distributed over the interval −π to π. As a result, the average of the Fourier convolution and consequently the bispectrum should vanish. If, instead, some oscillations are excited due to nonlinear interactions with other oscillations, their sum phase will be the same for each realization and therefore the average will not go to zero. Thus, the bispectrum measures the degree of the statistical dependence between three waves and provides a means of verifying and quantifying the coupling between the observed waves [8].

2.2. Bicoherence Spectrum (b²)

The bispectrum B(ω_j, ω_k) is dependent not only on the degree of coupling but also on the amplitudes of the involved spectral components. A normalized bispectrum, referred to as the bicoherence spectrum b²(ω_j, ω_k), is bounded by zero and one, and is a measure of the fraction of power at a given frequency that is due to quadratic coupling interactions.

$$b^2\left({\mathsf{\omega }}_j,{\mathsf{\omega }}_k\right)={\displaystyle \frac{{\left|B\left({\mathsf{\omega }}_j,{\mathsf{\omega }}_k\right)\right|}^2}{\mathrm{E}\left[|\mathsf{\Phi }\left({\mathsf{\omega }}_j\right)\mathsf{\Phi }\left({\mathsf{\omega }}_k\right){|}^2\right]E\left[|\mathsf{\Phi }({\mathsf{\omega }}_j+{\mathsf{\omega }}_k){|}^2\right]}}$$

(2)

The magnitude of the bicoherence spectrum provides a quantitative measure of the degree of coupling between three waves at ω_j, ω_k, and ω_j + ω_k, and can be used to measure the ratio of the spectral power of correlated daughter waves to the total power at a given frequency. According to [8], b² can be interpreted (with caveats noted in the pitfalls section) as:

$$b^2\left({\mathsf{\omega }}_j,{\mathsf{\omega }}_k\right)={\displaystyle \frac{{Power}_{coupled}}{{Power}_{coupled}+{Power}_{not coupled}}}$$

(3)

2.3. Biphase (β)

The phase of the bispectrum, or “biphase” β(ω_j, ω_k), is equal to θ(ω_j) + θ(ω_k) − θ(ω_j + ω_k), so the sign of the real part of the bispectrum gives information about the phase relation of the daughter with respect to the beating of the two parent waves, even with no knowledge of coupling coefficients or wavenumbers. Intrator et al. [9] used the sign of the real part of the same bispectrum to show that the daughters of the interaction tend to cancel [negative Re(B)] or reinforce [positive Re(B)] ponderomotive forces induced by the radio-frequency parent waves. If the sign of the real part of the bispectrum is positive (corresponding to a biphase of less than ±π/2), the daughter wave will constructively interfere with the beating of the two parent waves.

The growth or damping of a wave at ω_m due to the nonlinear coupling of waves at ω_j and ω_k, and is determined by the sign of the real part of B(ω_j, ω_k) and the biphase. For instance, if the coupling coefficient is known to be real and positive and the wave vector of the daughter is aligned with the positive-x axis, the sign of the real part of the bispectrum would determine whether the amplitude of the daughter wave were increasing or decreasing as it traveled in the x direction, taken as an arbitrary reference direction. This only applies to the portion of oscillations at ω_m that are due to the interaction of waves at frequencies ω_j and ω_k.

2.4. Symmetry Properties Used to Simplify Computation and Graphing

The time series used for bispectral analysis consists of N points sampled at an interval Δt, yielding an elementary bandwidth of Δf (=1/(NΔt)), commonly expressed in terms of angular frequency Δω). The bispectrum, since it involves Fourier components at jΔω, kΔω, and jΔω + kΔω, is defined only in the interval j < _N/2, k < _N/2, and j + k < _N/2, which defines the boundaries of the hexagon in Figure 1. Using the symmetry relations B(ω_j, ω_k) = B(ω_k, ω_j) = B*(−ω_j, ω_k), Kim and Powers [10] show that it is sufficient to calculate the bispectrum over regions A and B of the hexagon. Changing variables (j’ → −k, and k’ → j + k) and using the relations B(ω_j, ω_k) = B*(−ω_k, ω_j, + ω_k) = B*(−ω_j, ω_j + ω_k) eliminates all but the triangular region A, which is one-twelfth of the total computation region. In Figure 1, region A contains the sum interactions and B contains the difference interactions. The advantage of plotting both regions is that all the interactions involving a given frequency are represented on a single line (ω_j + ω_k = ω_m = constant). In the compact representation, these interactions are represented on three separate lines: ω_j + ω_k = ω_m, ω_j = ω_m, ω_k = ω_m.

2.5. Interpretation Pitfalls

2.5.1. False Positives and Negatives

The bispectrum must be interpreted with caution, since there are instances where phase coherence between waves will not be indicated by a bispectral feature, and other instances where the bispectrum may give a false indication of coupling. The first situation occurs when the phase difference between the daughter and the beating of the parent waves averages ±π/2. In this case, only the imaginary part of the bispectrum will be non-zero: if the dispersion relation prohibits three-wave coupling, higher-order wave interactions may become more important, requiring a trispectral analysis. The second situation occurs much more frequently, and can be attributed to a variety of mechanisms. Both the frequency and wavenumber selection criteria must be satisfied for true quadratic coupling. The bispectrum will still be non-zero for phase coherent waves even when k_m ≠ k_i + k_k, provided the frequencies sum to zero. Conversely, because of the limited spectral resolution associated with finite record lengths, it is possible to obtain a significant peak in the bispectrum even when the frequency selection rule is not precisely satisfied.

2.5.2. Filtering

Filtering effects also need to be considered. When filters are used to eliminate aliased Fourier spectral components or amplifier noise, they introduce frequency-dependent phase shifts. Since the bispectrum will be non-zero for any constant phase relation between three waves, the magnitude of B is expected to remain unaffected by filtering, but this is not necessarily so for the biphase and the other phase-dependent quantities.

2.5.3. Turbulence and Spectral Broadening

The presence of many modes will reduce the typical value of b² by an amount δ, which Tsui et al. [11] ascribed to turbulent spectral broadening:

$$\sum _{j,k}{b}^2\left({\omega }_j,{\omega }_k\right)=1-{\mathsf{\delta }}^2$$

(4)

Though a relatively large value of b² at (ω_j, ω_k) is indicative of coherent nonlinear coupling, which may lead to turbulence, a fully turbulent state would be characterized by small values for b² because of the broadband distribution of spectral features. The fraction of power due to nonlinear coupling can be approximated best by b² if only a few modes are involved in the interaction and if the spectral peaks are not too broad. In practice, a more meaningful value of bicoherence is approximated by summing all j and k values that satisfy the resonant conditions (of frequency and wavenumber) for a given ω_m (=ω_j + ω_k). A value near unity for that sum would indicate coherent wave coupling, and anything less would imply the presence of turbulent frequency broadening.

3. Causality Determination

Now we apply these concepts of nonlinear coupling to interpreting the roles of waves associated with narrowband and broadband turbulence and to making comparisons. Specifically, we describe an algorithm to identify the parent waves involved in a quadratic coupling interaction and to tabulate the signatures of such an interaction in

Table 1. Bispectral features and respective coupling roles of a quadratic coupling interaction (inspired by [12]).

For Parents at	Freq of “Sum-Frequency Daughter”	Freq of “Diff-Frequency Daughter”	Coordinates of Feature Representing Interaction of Parents with Sum-Freq Daughter	Coordinates of Feature Representing Interaction of Parents with Diff-Freq Daughter
ωj and ωk	ωj + ωk	ωj − ωk	ωj, ωk	ωk, ωj − ωk
(ωj + ωk) and ωk	ωj + 2ωk	ωj	ωj + ωk, ωk	ωj, ωk
(ωj + ωk) and ωj	ωk +2ωj	ωk	ωj + ωk, ωj	ωj, ωk

and

Table 2. Aid in causality determination for a given bispectral feature at coordinate ω_j and ω_k.

If There Is Also a Feature with Coordinates:	Then the Parent Frequencies Are:
(ωk, ωj − ωk) or (ωj − ωk, ωk)	ωj and ωk
(ωj + ωk, ωk)	(ωj + ωk) and ωk
(ωj + ωk, ωj)	(ωj + ωk) and ωj

.

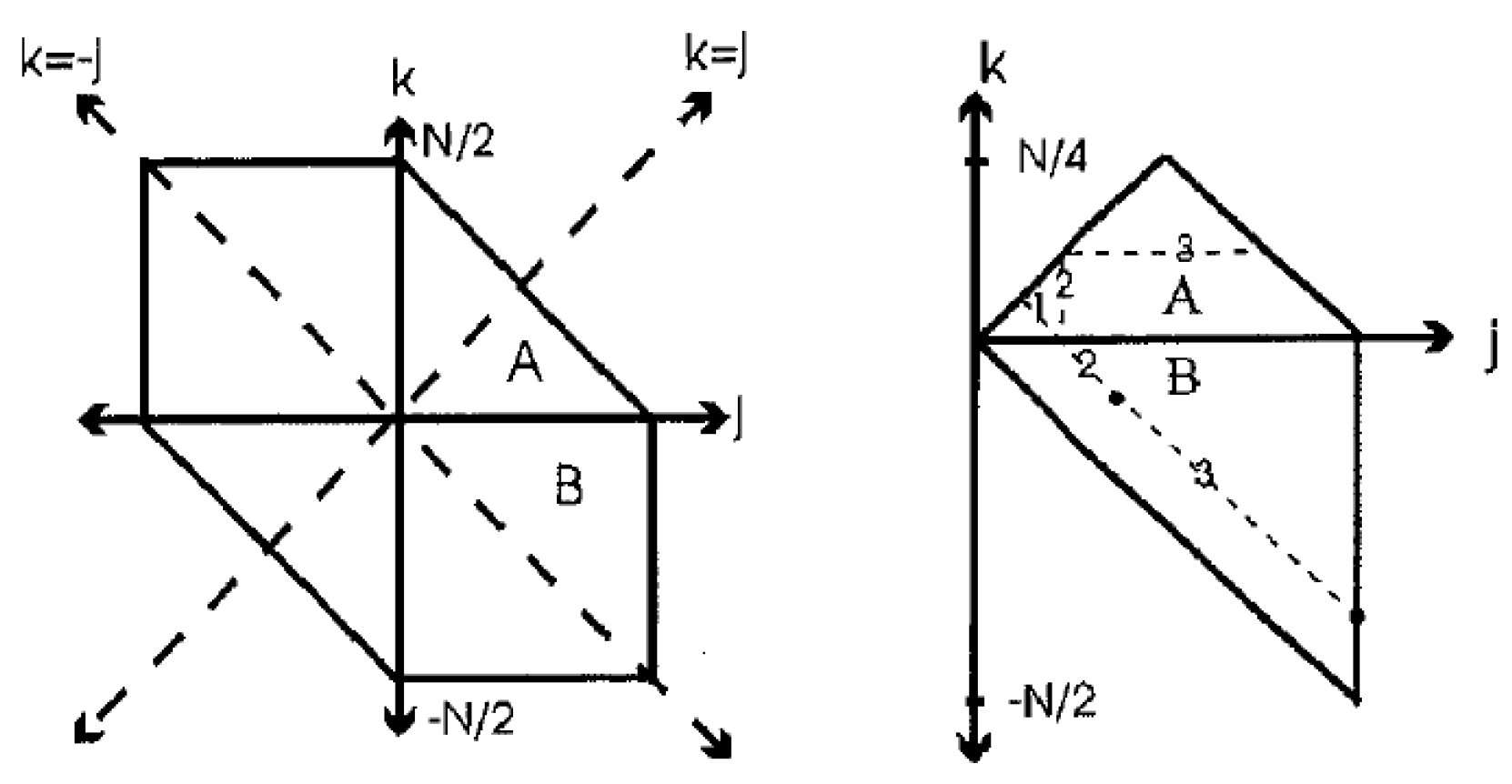
A non-zero value of B(ω_j, ω_k) indicates a quadratic coupling of two modes, but the parent modes are not necessarily ω_j and ω_k (see Table 2). Since quadratic coupling produces both a sum and a difference frequency, other candidate pairs (ω_j with ω_j + ω_k and ω_k with ω_j + ω_k) can be investigated by looking for bispectrum peaks at the corresponding sum and difference frequencies. The generally accepted convention of plotting the bispectrum over a triangular region where ω_j > _0, ω_j > ω_k, and ω_j < ω_{j max} − ω_k exploits certain symmetry properties. In this condensed representation, any observed bispectral feature represents a three-wave interaction involving the modes on the axes, say, ω_j and ω_k, and a third (daughter) mode at the sum, ω_j + ω_k. The three-wave interaction involving a daughter at the difference frequency would be represented, in this case, by a bispectral feature at (ω_k, ω_j − ω_k), where again, the sum of the mode locations gives the third (daughter) wave involved in the interaction, i.e., ω_j (see first row of Table 1).

From Equation (1), the bispectrum is non-zero if the spectral features at ω_j, ω_k and their sum frequency ω_j + ω_k are phase-correlated. Thus, we must inspect all the possible difference interactions between those three waves to find the parents. In Table 1, row 1, for example, a feature at (ω_j, ω_k) represents the three-wave relationship with the parents and the “sum-frequency daughter” (column 4). A feature at (ω_k, ω_j − ω_k) represents the three-wave relationship with the “difference-frequency daughter” (column 5).

For a parent at ω_j and another parent at frequency ω_k, we would expect to see bispectrum peaks at (ω_j, ω_j) or (ω_k, ω_k) only if harmonics of the parents were present in the signal. Because we plot the bispectrum only in the region where ω_j > ω_k, the only plotted (non-negative) difference-frequency daughter is at ω_j − ω_k.

While helpful in understanding where bispectral features can be expected when the parent frequencies are known, Table 1 does not help us evaluate experimental data where the identity of the parent waves might not be known in advance. To facilitate the identification of parent waves, we found it helpful to rearrange Table 1 for a given bispectral feature at coordinates (ω_j, ω_k).

The first row of Table 2 means a bispectral feature at (ω_k, ω_j − ω_k) and represents a difference-frequency–daughter interaction (thus the (ω_j, ω_k) feature represents the sum-frequency–daughter interaction), whereas the second and third rows correspond to sum-frequency–daughter interactions (meaning the (ω_j, ω_k) feature represents the difference-frequency–daughter interaction). There are two options listed in the first row of Table 2, because the bispectrum is typically plotted only in the region where the first coordinate is larger than the second (see Figure 1), so the order of coordinates depends on the relative magnitudes of ω_j and ω_k. For example, in row 1, if ω_j > 2ω_k, the (ω_k, ω_j − ω_k) point would not be plotted.

Accordingly, for a given spectral feature in a fast Fourier transform (FFT), the bispectrum should make it possible to determine if that feature corresponds to an independent mode or is the result of nonlinear coupling between two waves. In practice, the identification of coupled modes is complicated by the broadness of spectral peaks typical of a nonstationary or inhomogeneous plasma process, and the occasional absence of one of the daughters (there is no guarantee that both daughters are resonant or are natural modes of the system), but it is often possible to identify the parents of the interaction, even within a turbulent-looking FFT, from the bispectrum with the help of Table 2. This will be demonstrated with a test signal in Section 4 and experimental plasma data in Section 5.

4. Test Signal Tutorial

For example, consider a test signal (from [8]) comprised of three cosine waves with random phase angles and ω_a + ω_b = ω_c:

cos(ω_at + θ_a) + cos(ω_bt + θ_b) + cos(ω_ct + θ_c)

(5)

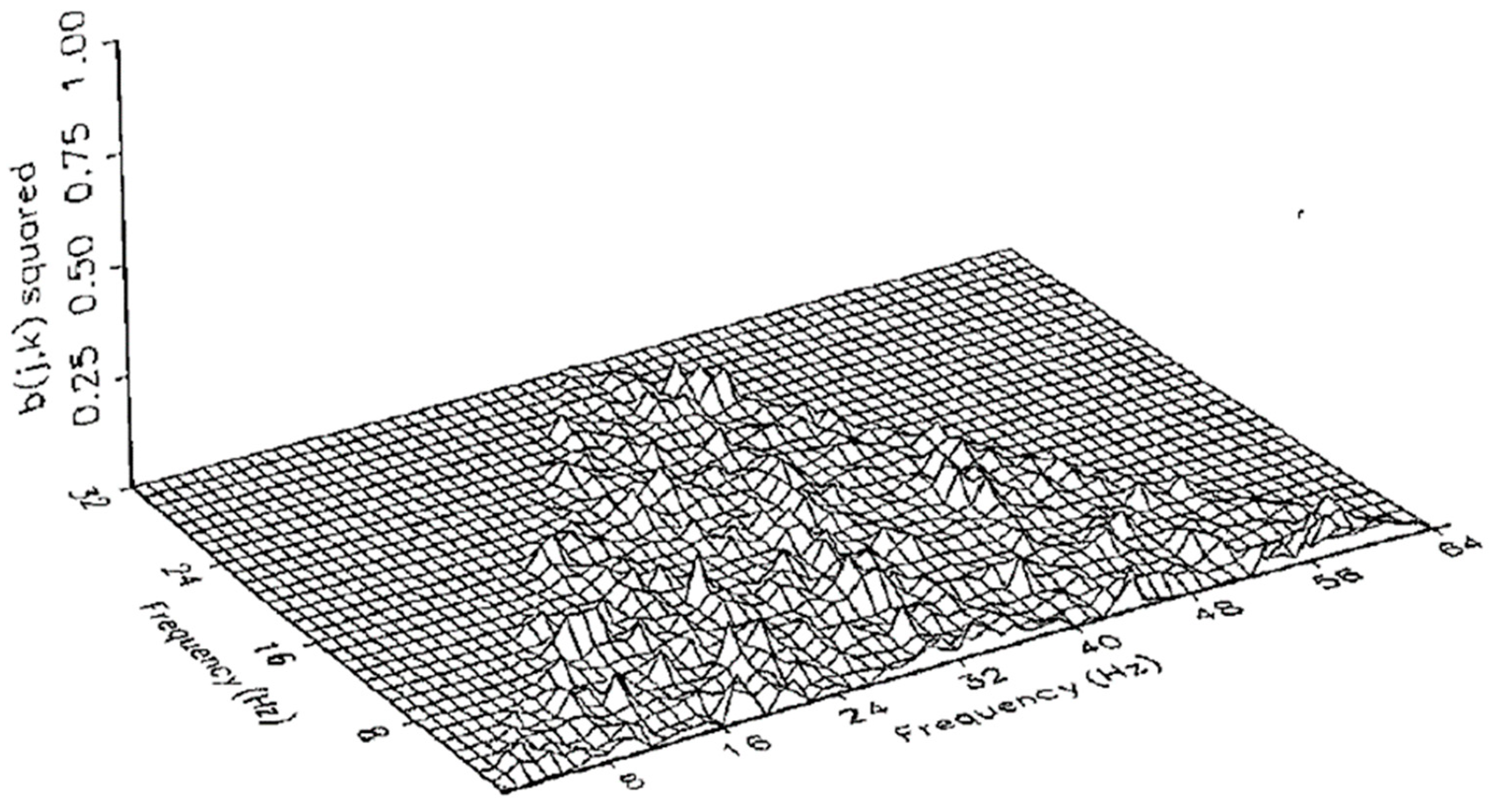
In sum, 64 records of 128-point time series were generated with random noise added to each record. Phase-incoherent waves such as this produce no bispectrum peaks, even if the wavenumber selection rule ω_a + ω_b = ω_c is met (Figure 2).

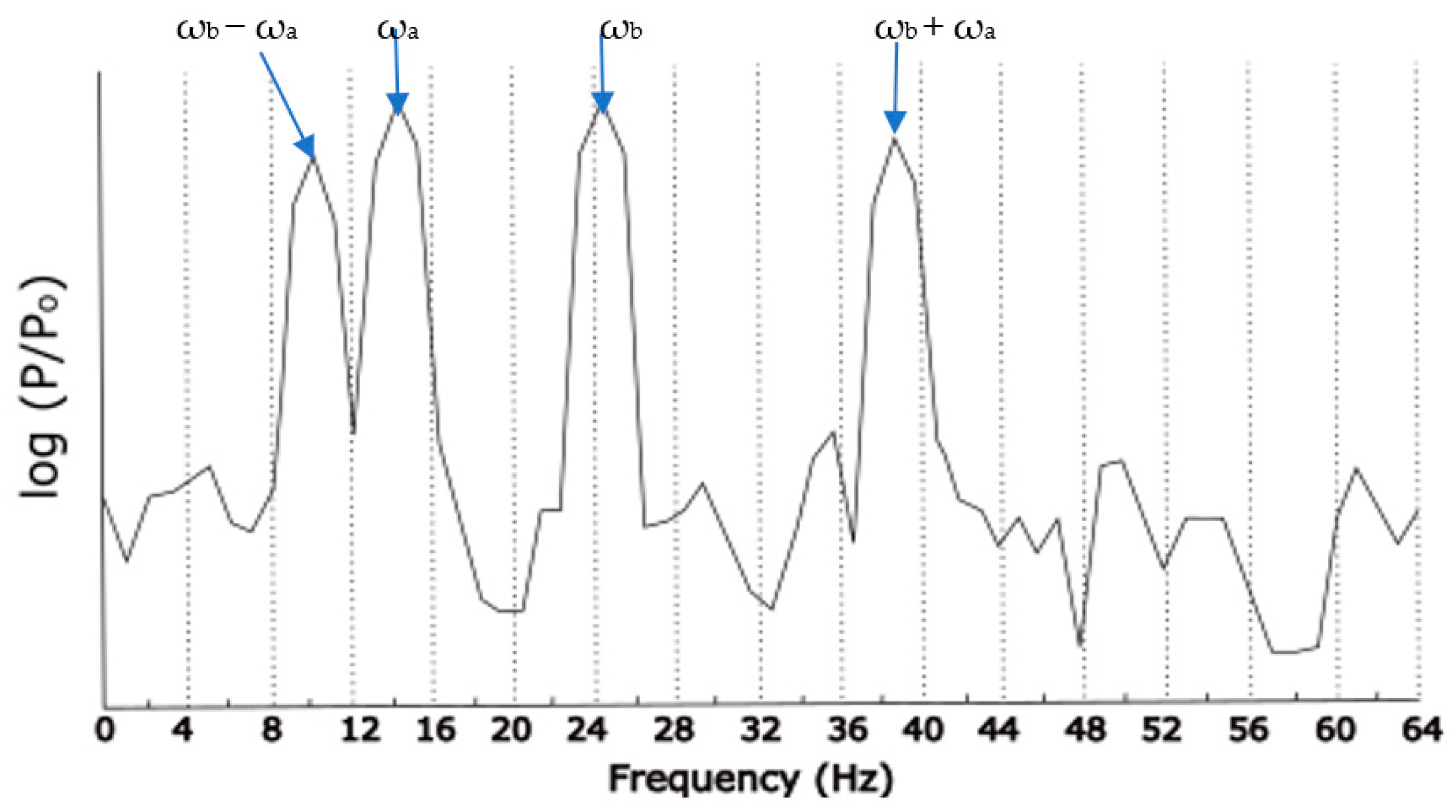
However, if we use a test signal that includes coupled cosines (see Figure 3), such as:

cos(ω_at + θ_a) + cos(ω_bt + θ_b) + 0.5cos(ω_ct + θ_c) + cos(ω_at + θ_a) cos(ω_bt + θ_b)

(6)

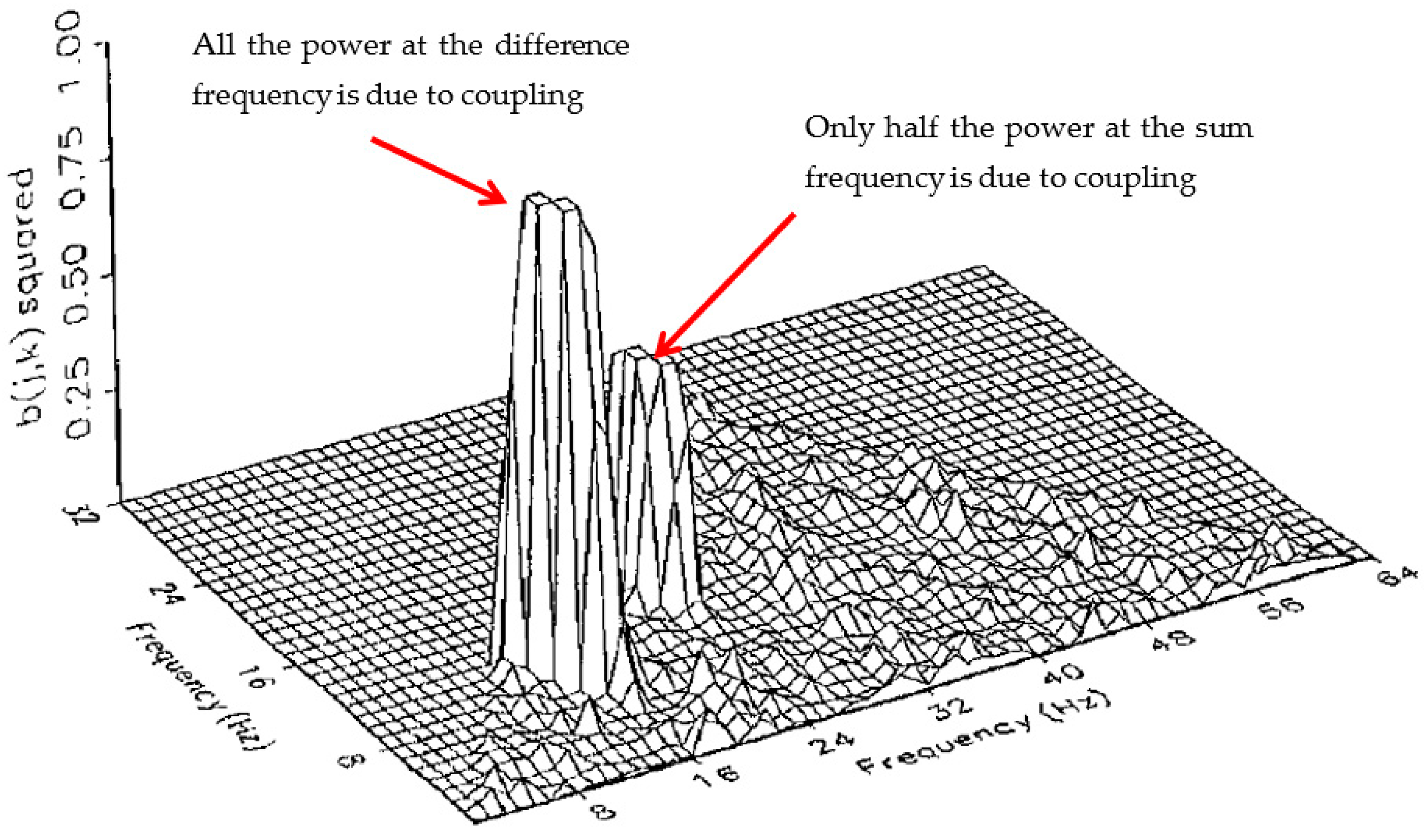
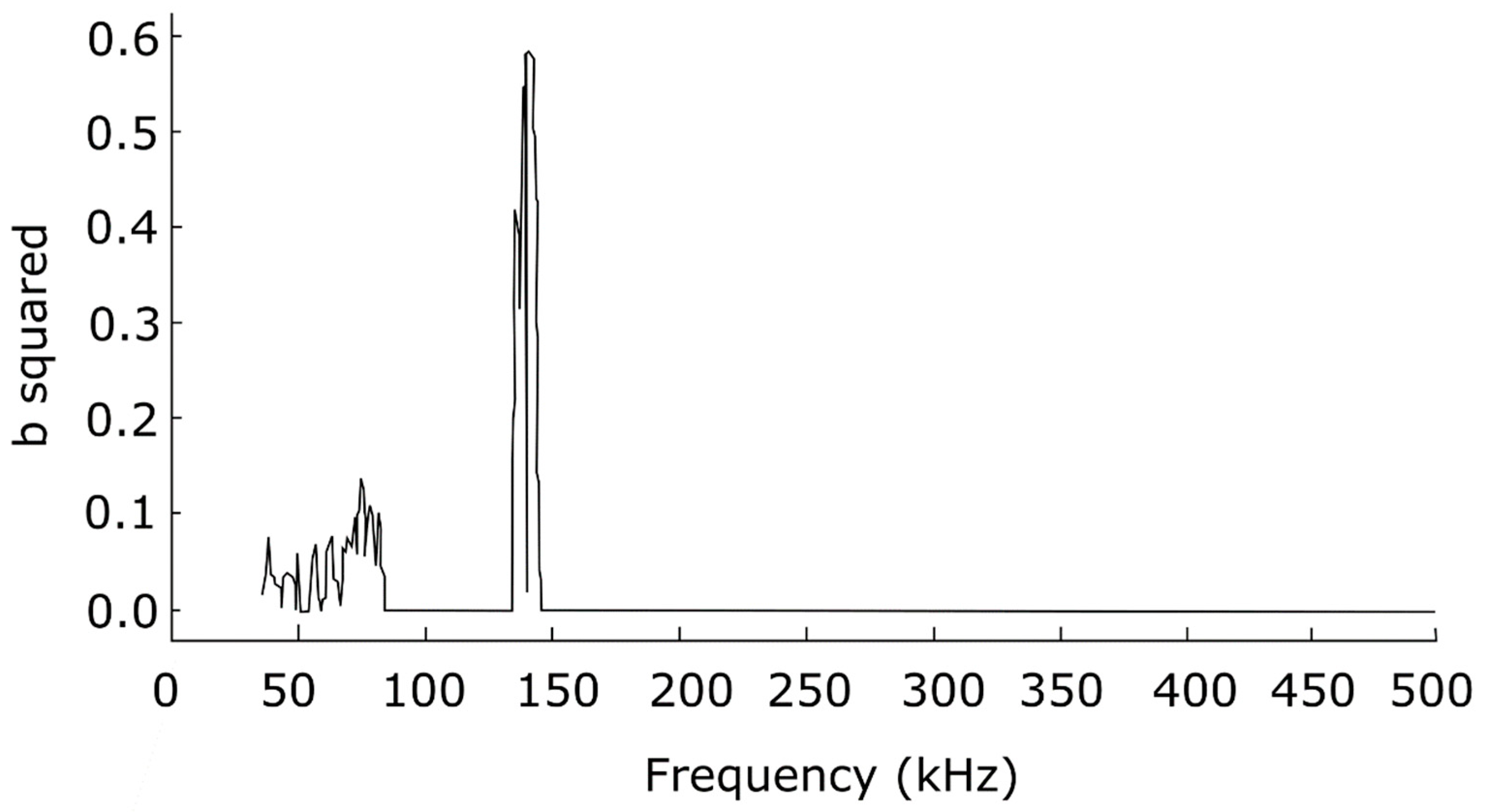
Then the bispectrum would produce peaks proportional to the fraction of power due to coupling (see Figure 4).

This is because cos(a) cos(b) = ½ [cos(a + b) + cos(a − b)], so we would expect Fourier components at the sum and difference frequencies as shown in Figure 3, but only half of the power at the sum frequency ω_c is due to coupling (the other half is not phase-coherent), so the amplitude of b² is 0.5 there.

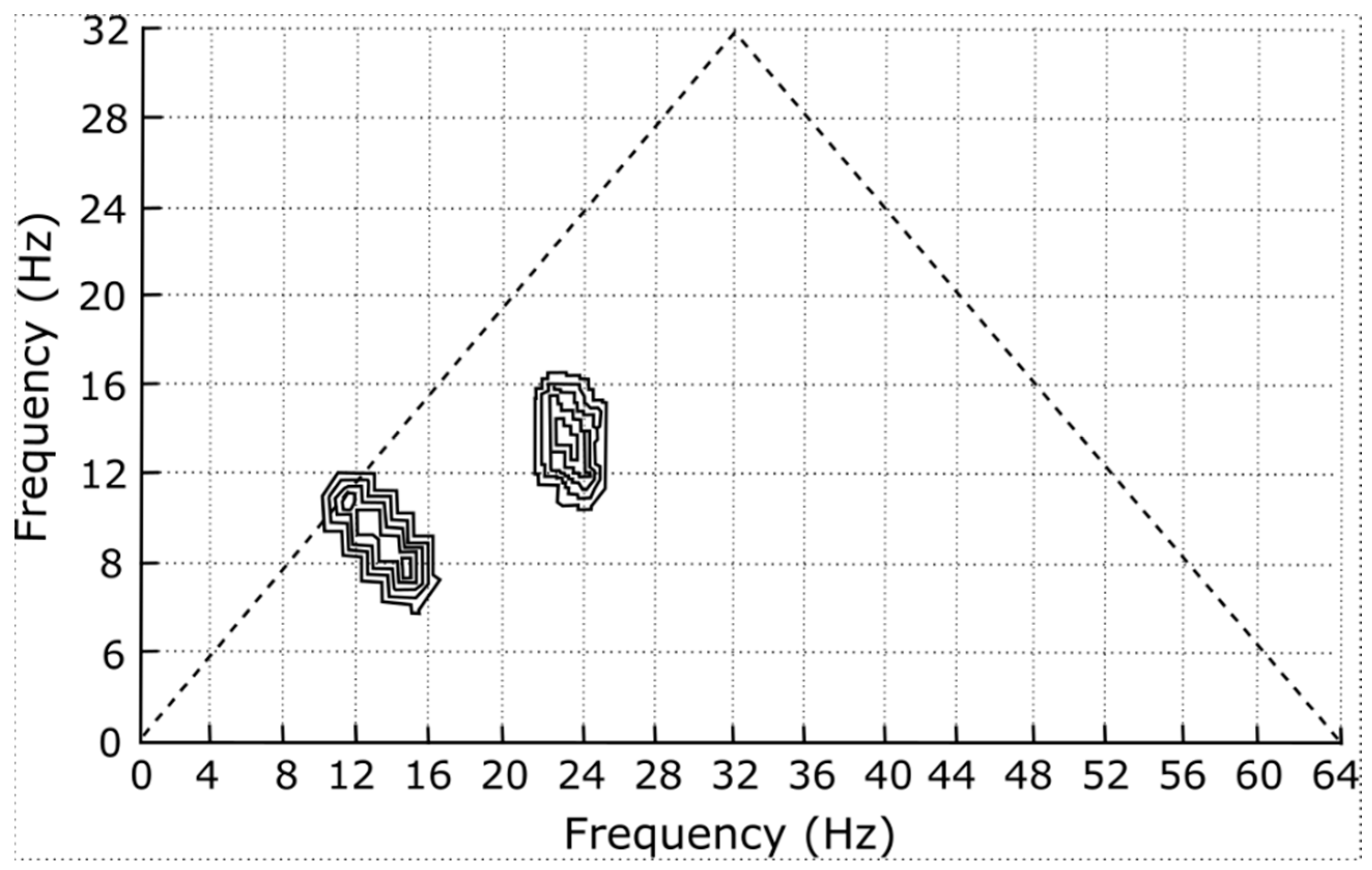
In the absence of any information about this computer-generated test signal, we could still identify the parents of any wave–wave interactions from a contour plot of the bispectrum (see Figure 5).

Here is how we might use Table 2 to find the parents:

For peak at (ω_j, ω_k) = (24, 14):

Is there a difference-frequency peak at (14, 10)? Yes.

Is there a sum-frequency peak at (38, 14)? No.

Is there a sum-frequency peak at (38, 24)? No.

The first row of Table 2 indicates that the parent frequencies are therefore 14 Hz and 24 Hz, and the magnitude of this peak tells us what fraction of the power at the difference frequency (10 Hz) is due to coupling.

For peak at (ω_j, ω_k) = (14, 10):

Is there a difference-frequency peak at (10, 4)? No.

Is there a sum-frequency peak at (24, 10)? No.

Is there a sum-frequency peak at (24, 14)? Yes.

The third row of Table 2 indicates that the parents are at the sum frequency, 24 Hz, and ω_j (14 Hz), and the magnitude of this peak tells us what fraction of the power at the sum frequency (38 Hz) is due to coupling.

5. Bispectral Analysis of Interfacial Broadband Cyclotron Waves

As an application of bispectral techniques to a turbulent-mixing paradigm, we analyze previously acquired plasma fluctuation data [13,14,15,16]. Two related categories of waveforms are used. One category is associated with (broadband, ion-cyclotron-range, shear-driven) inhomogeneous energy-density driven (IEDD) instability, and the other is associated with (narrowband, ion-cyclotron range, current-driven) electrostatic ion-cyclotron (CDEIC) instability. For the same value of magnetic field-aligned plasma current, IEDDI waves have significantly larger wave amplitude than CDEIC waves because of the contribution of E × B velocity-shear inhomogeneity to the instability growth rate. The setup for this experiment is documented in [13,17,18,19]. The sampling frequency for each 1024-point realization was one mega-sample per second, and a bandpass filter (10 kHz to 240 kHz) was used to suppress drift waves at 3 kHz and eliminate interference at 240 kHz.

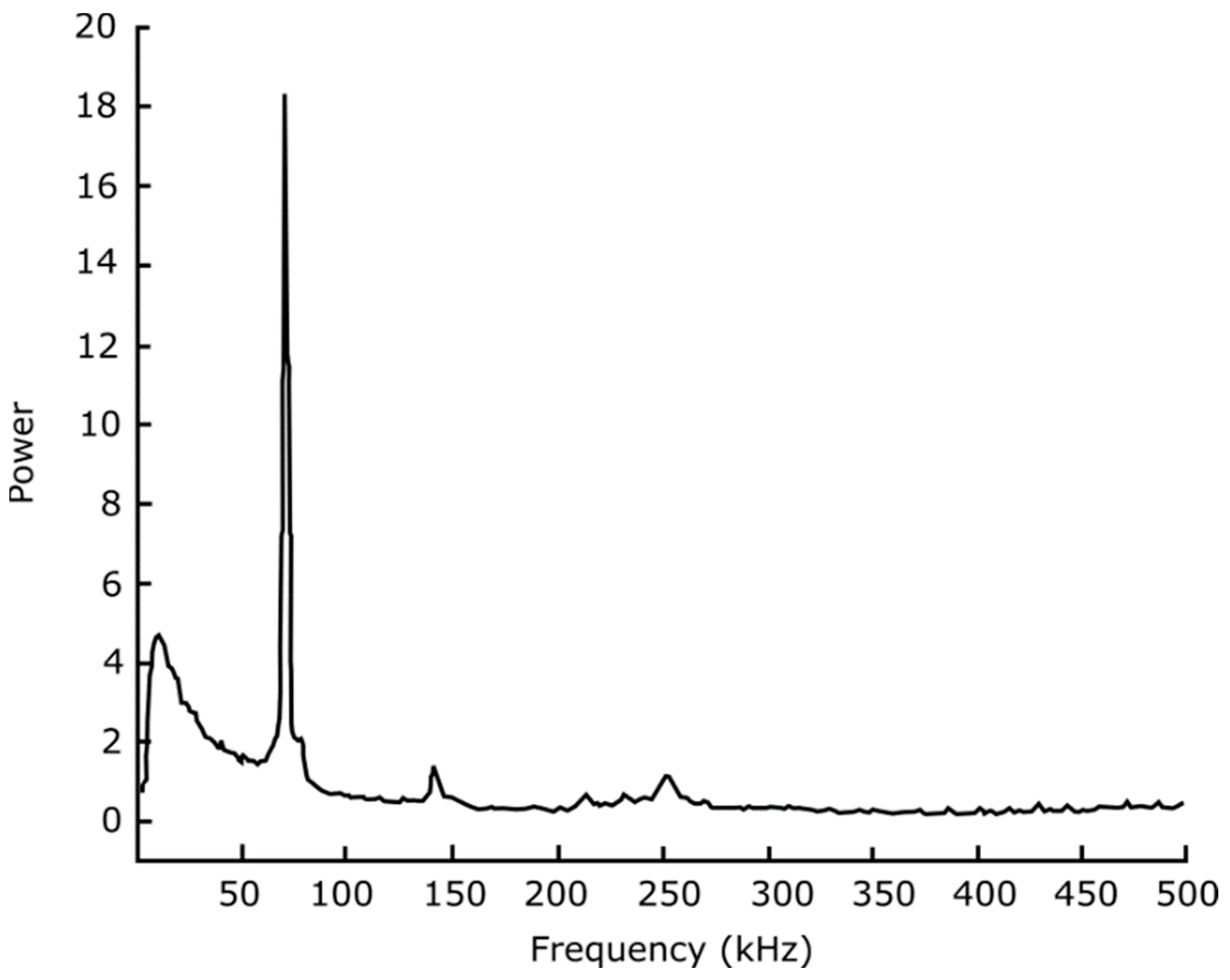
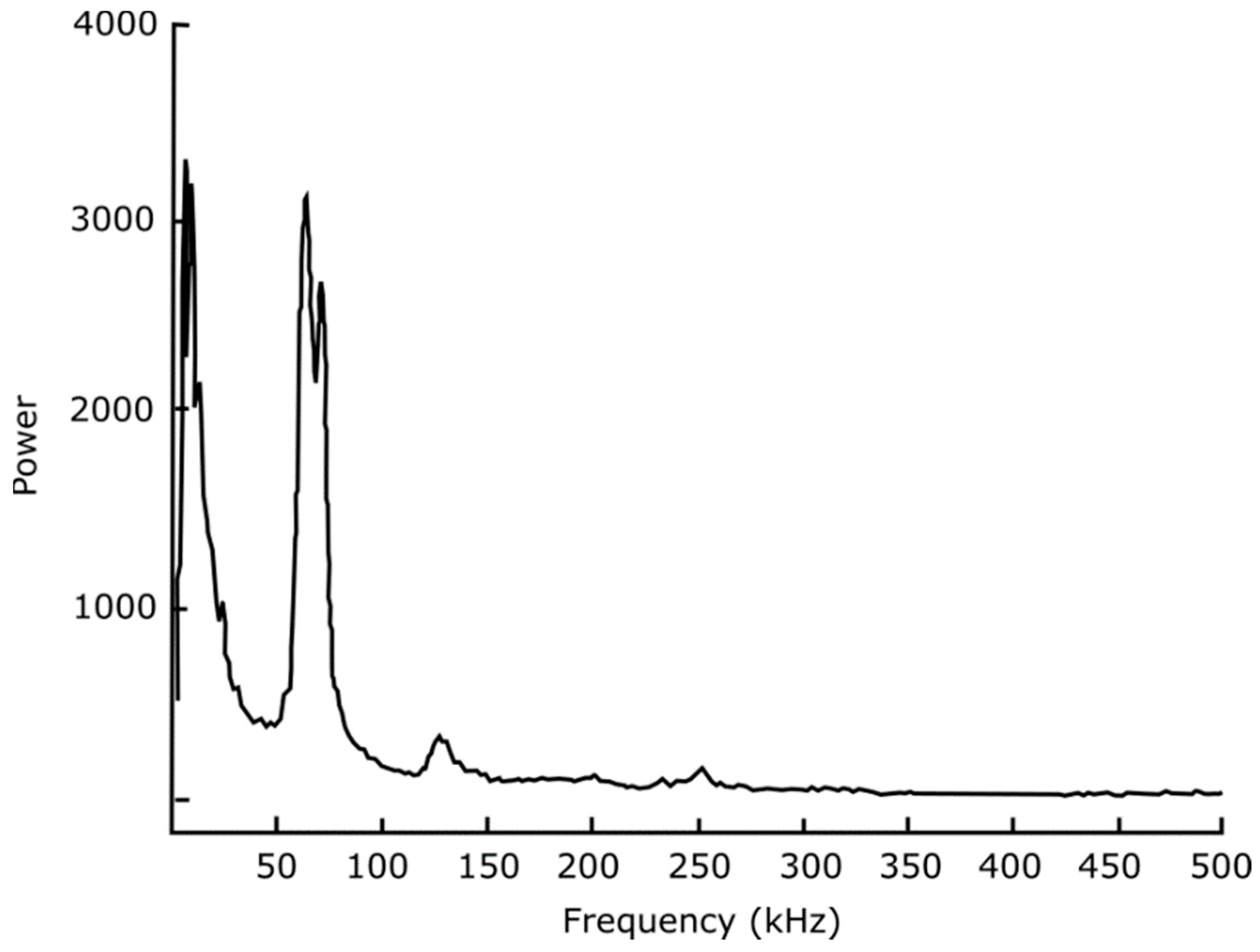
The average power spectra of the two plasma instabilities, shown in Figure 6 and Figure 7, are quite distinct. The CDEIC mode, seen at 71 kHz, is almost monochromatic, and the spectrum displays only small relative amounts of energy in the 5–10 kHz frequency range. Conversely, the frequency spectrum associated with the IEDDI mode, seen at approximately 65 kHz, is broadband with significantly more relative power in the 5 kHz–25 kHz range. These low-frequency fluctuations have been identified as drift waves by their three-dimensional mode characteristics and magnetic field-dependent frequency.

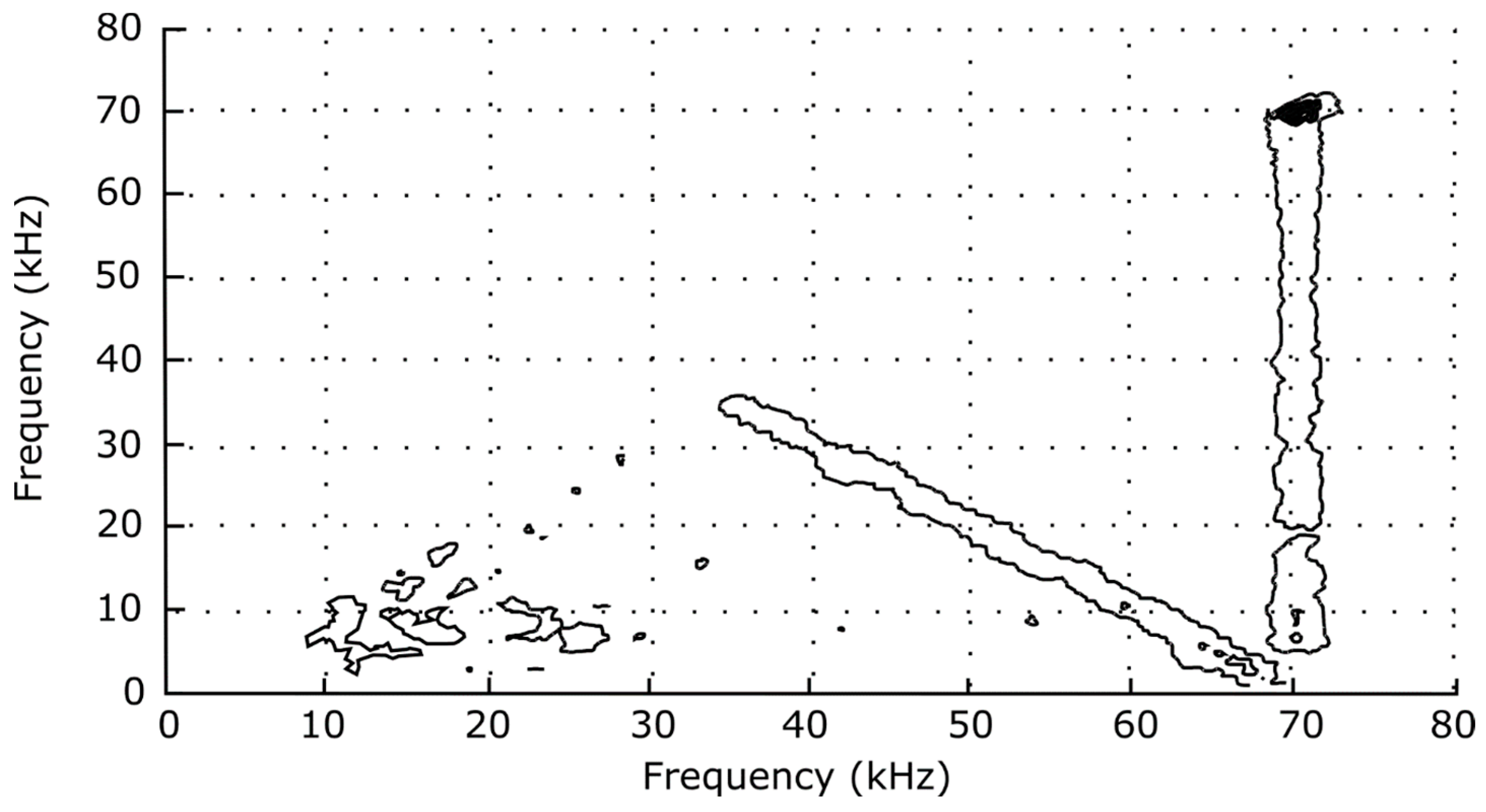
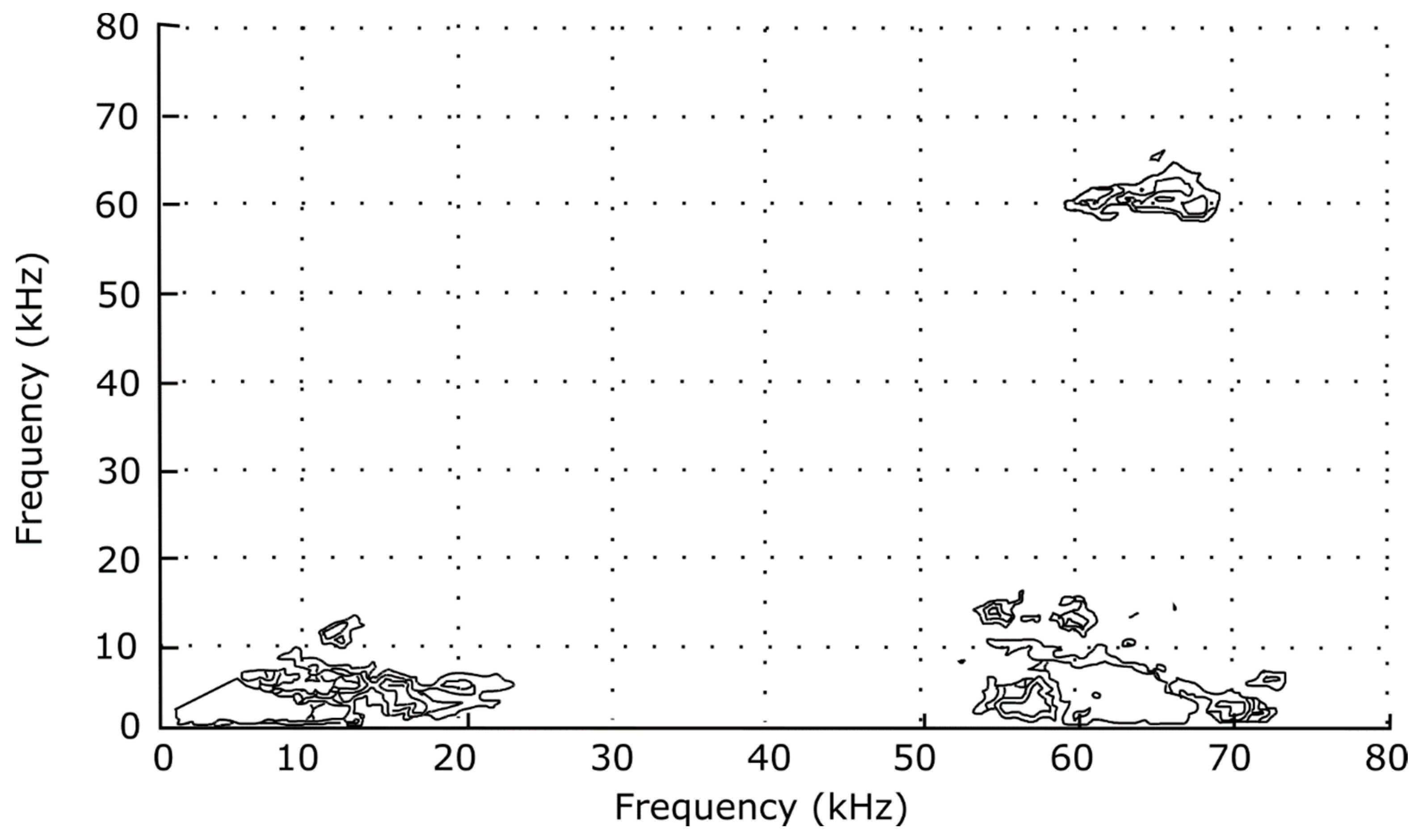
The coherency of the CDEIC spectrum is particularly evident in the contour plot of the bispectrum and bicoherence spectrum (Figure 8 and Figure 9), where the most significant feature indicates “coupling” of f_CDEIC with its first harmonic. Also note the 71 kHz iso-daughter line starting at 35.5 kHz and sloping down to the right. Every possible combination of frequencies satisfying the selection rule for ω_j + ω_k = 71 kHz exhibits some, albeit much smaller, degree of coherence with the CDEIC spectrum, implying that 71 kHz is just one of the many components required in the Fourier decomposition of the longer-wavelength pulse shapes. Such a bispectrum would be expected from any time series containing the sum of a periodic, non-sinusoidal low-frequency waveform and a sinusoidal high-frequency waveform and should not be interpreted as an indication of significant active nonlinear coupling.

The cluster in the lower left-hand corner of the bispectrum plot of Figure 8, however, is indicative of some nonlinear interactions present among the low-frequency fluctuations, a result consistent with previous experiments on drift wave-type turbulence in tokamaks [11] and linear plasma discharges [13,20]. Tsui [11], in particular, used the Hasegawa–Mima drift-wave turbulence equation to derive Equation (4), showing that δ² increases with turbulence broadening of spectral components.

As an interesting confirmation of Tsui’s result in the present experiment, the sum of the squared bicoherence of the interactions involving each frequency was calculated using the program documented in [13,17]. The bicoherence of all interactions at a certain frequency lies along three separate lines in the reduced triangular region.

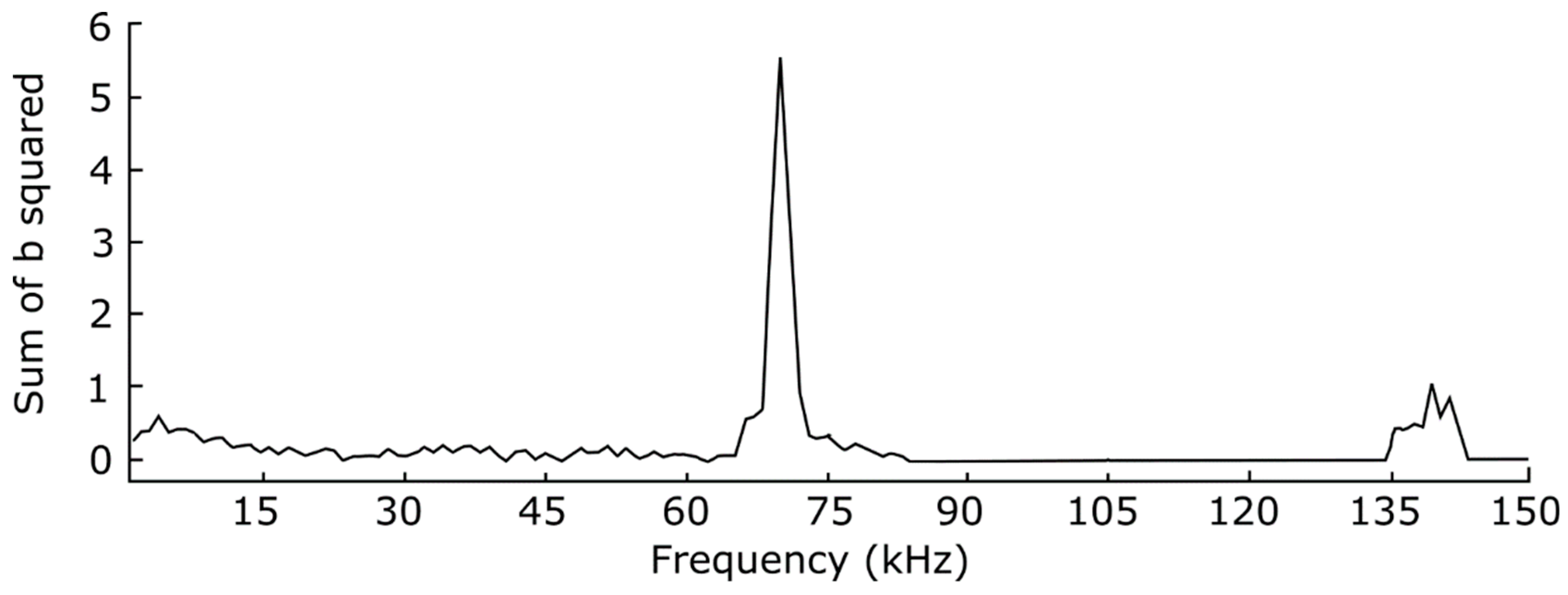
Figure 10 is the bicoherence of all interactions involving the mode at 71 kHz, where the x axis is the frequency of one of the triplets satisfying ω_m = ω_j + ω_k, for ω_m fixed at 71 kHz. The amplitude of the cluster at 35 to 70 kHz, though smaller than the self-coherent 71 kHz peak, is still much larger than the statistical uncertainty of 1/M = 0.009.

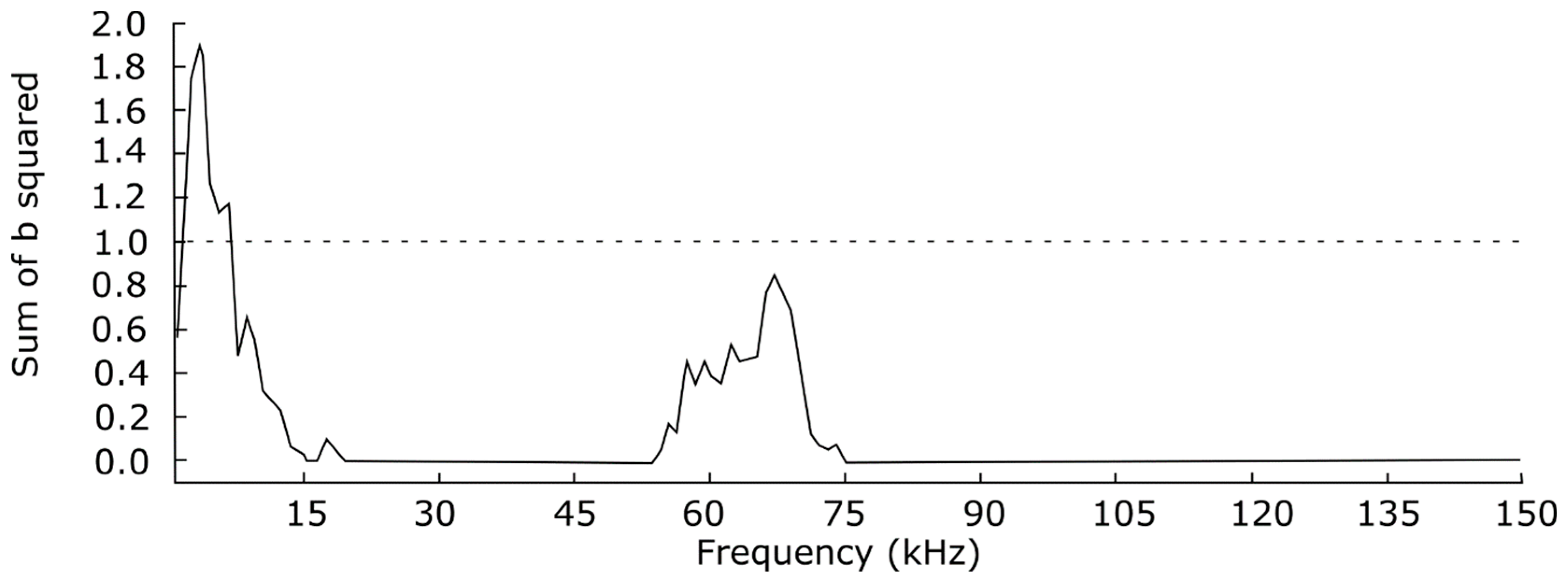
Plotting the area under each such curve as a function of the interaction frequency produces the graph shown in Figure 11. For the range of frequencies associated with drift-wave turbulence, the sum is indeed less than one. The difference of 0.4 between unity and the sum of b² for f_drift = 3 kHz is attributed to the spectral broadening term δ².

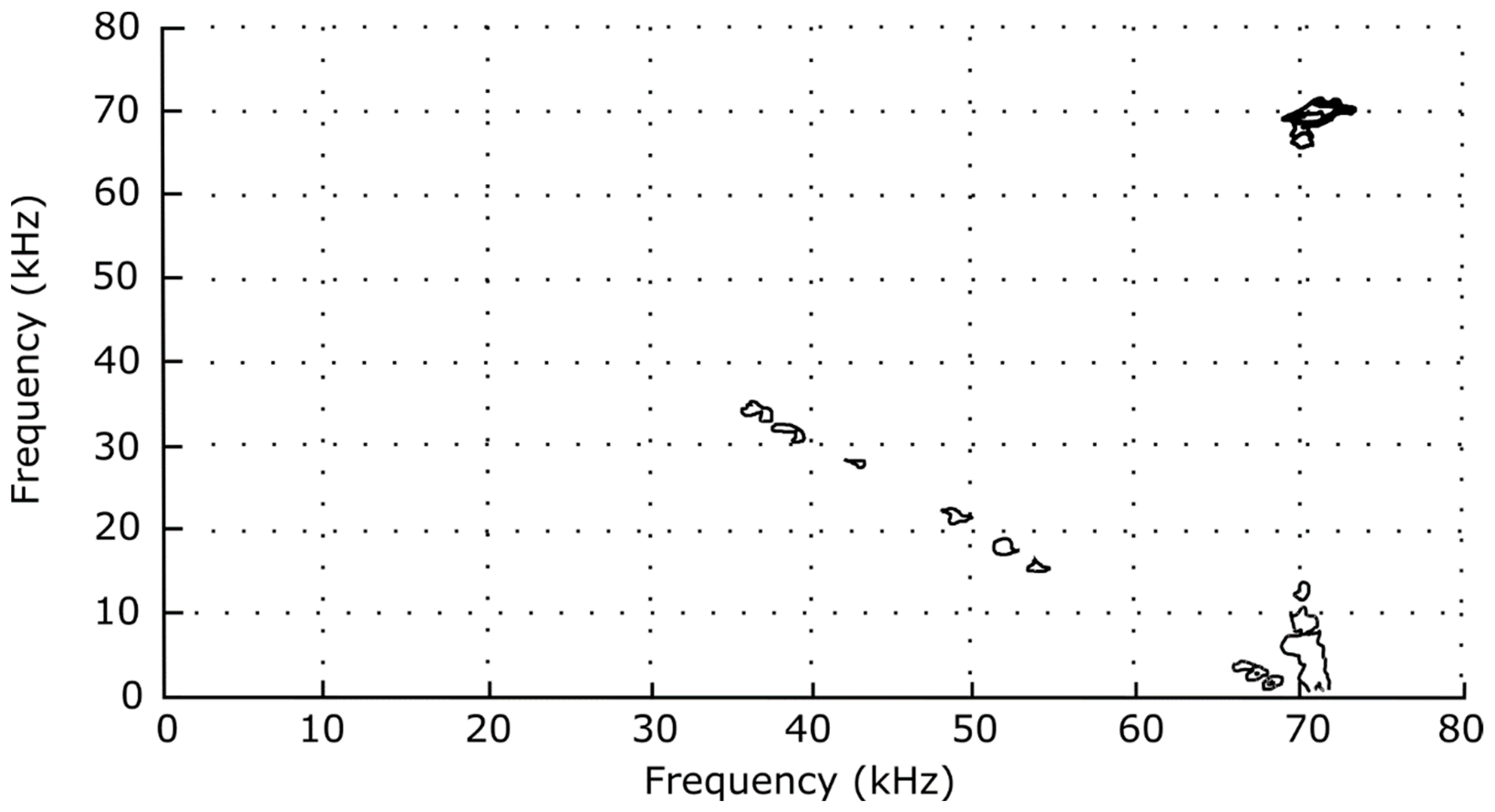
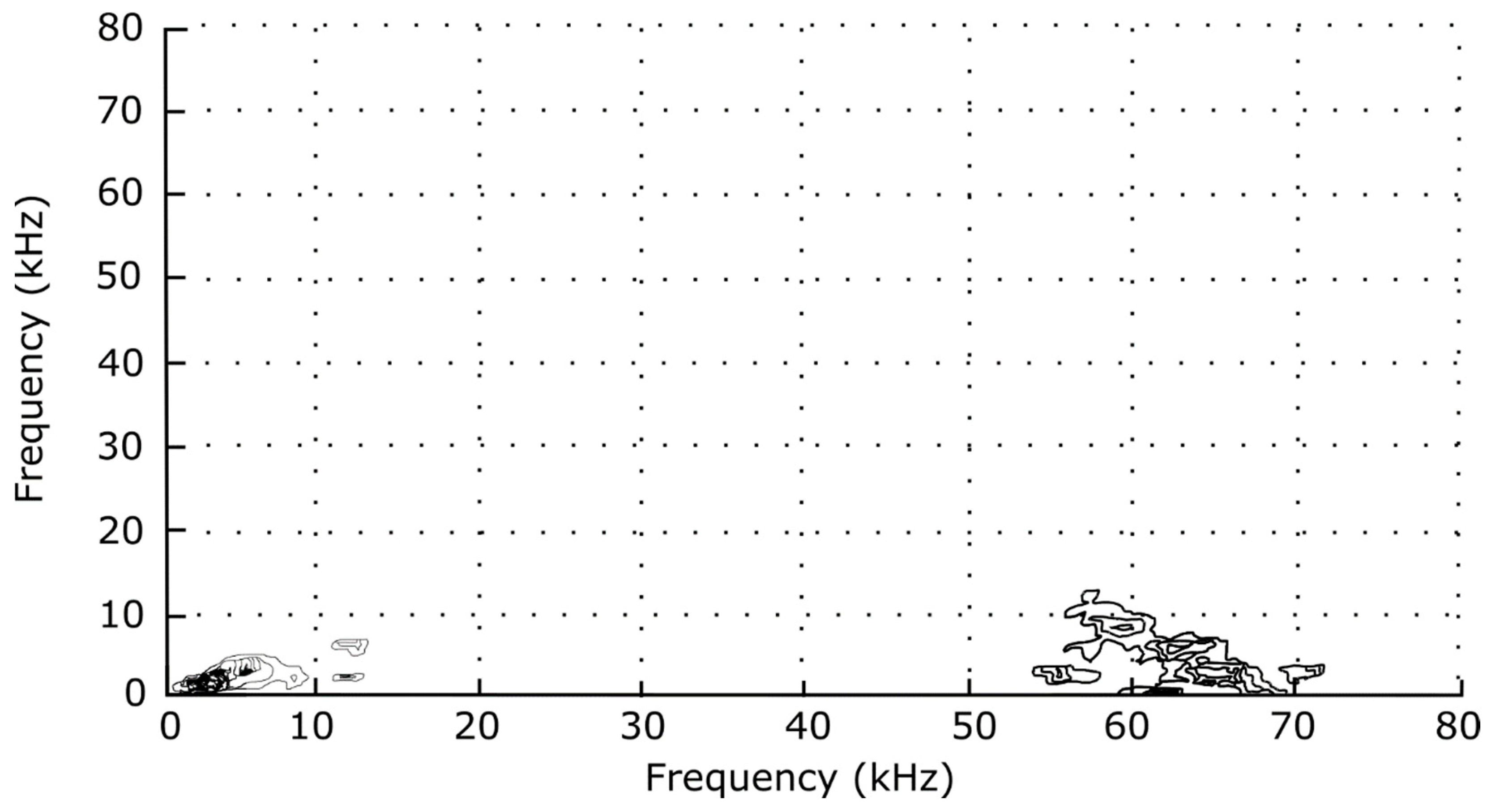
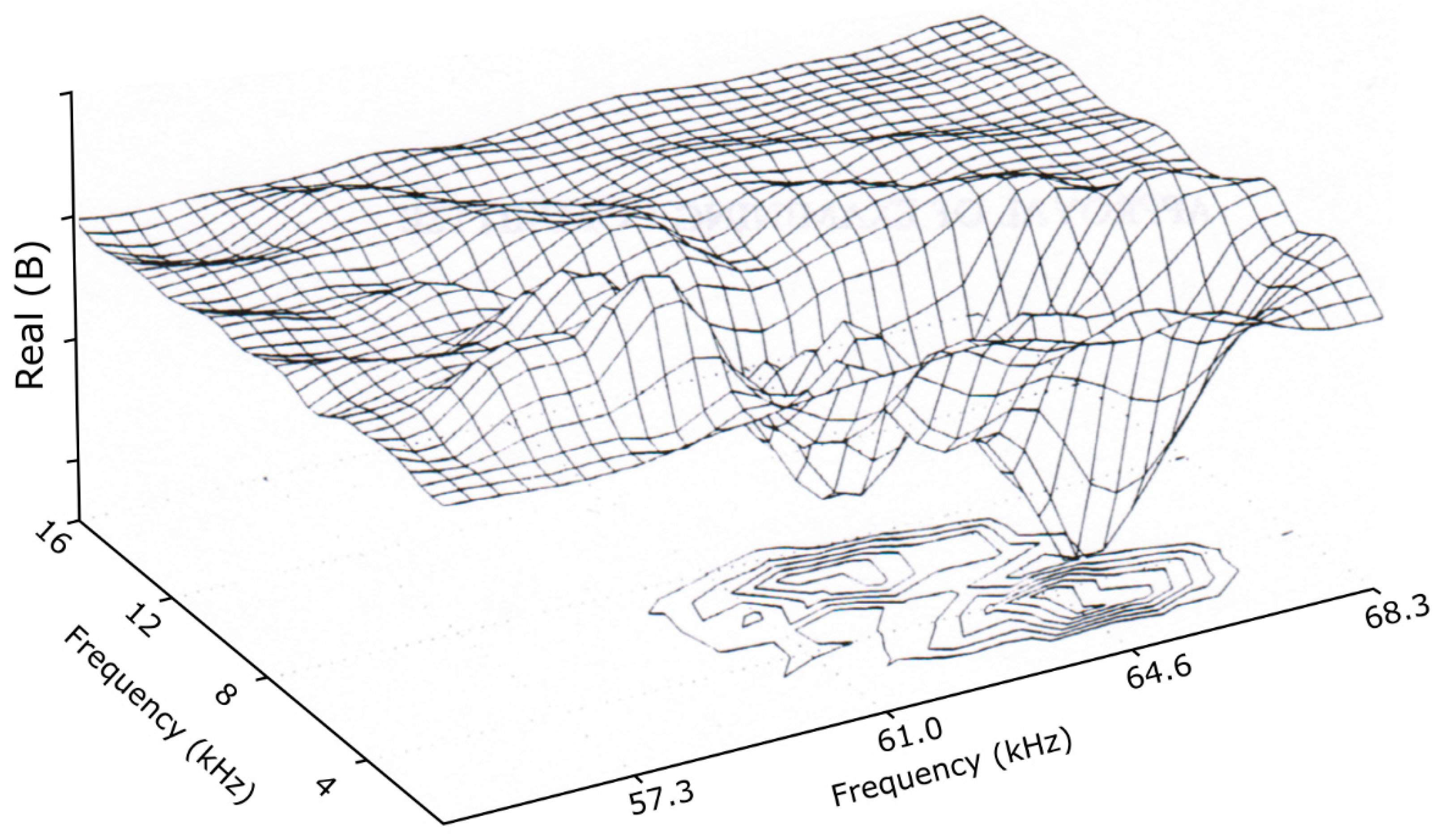
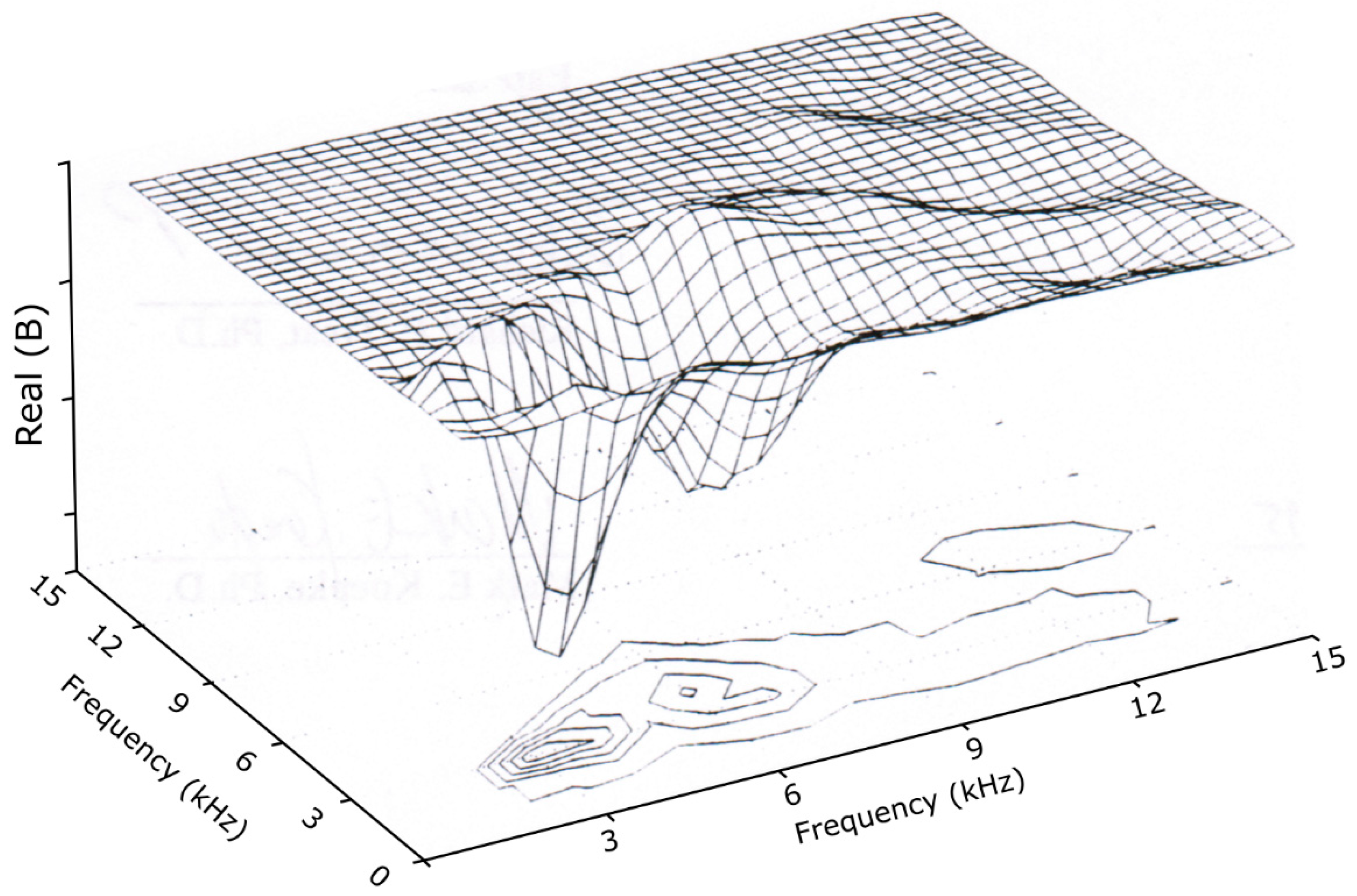
In contrast, the IEDD bispectrum indicates a coupling of the high-frequency spectrum to drift waves that is absent in the CDEIC fluctuations (see Figure 12 and Figure 13 and [19]). Inspection of the 3D surface plots of the low-frequency group (Figure 14) and the high-frequency group (Figure 15) reveals the four most significant spectral features: (f_j, f_k) = (3, 3), (6, 3), (62, 6), and (65, 3), all in kHz. The third feature, evaluated with the help of Table 2, unequivocally points to parents at (68, 62), and the fourth feature probably indicates parent waves at (68, 65).

The low-frequency peaks are more ambiguous, since none of the rows of Table 2 can be eliminated with a significant degree of certainty, except for the (9,6) parent of the second feature. The power spectrum suggests the formation of harmonics of the 3 kHz wave. The presence of the (3,3) peak on the bispectrum confirms that the mode at the 6 kHz peak is indeed the second harmonic of 3 kHz, and not a self-excited mode. In summary, bispectral analysis suggests a “mixing down” of the IEDD spectrum into the lower-frequency drift spectrum and a coupling among various spectral components of the drift-wave oscillations.

A few words of caution are perhaps in order. First, resonant wave–wave interactions can be only partially verified without a corresponding k-space analysis, since the wavenumbers of the three modes may or may not satisfy the wavenumber selection criteria required for quadratic coupling to an acceptable degree of precision. Second, no correction has been made to offset the frequency-dependent phase shifts introduced by the bandpass filtering of the time-series data, so even a priori knowledge of wavenumbers and coupling coefficients would be subject to a complicated interpretation of the biphase. A filter similar to the one used to collect the plasma data was used to measure the phase shifts of a generated sine wave at the frequencies of interest. The result was −72 degrees at 6 kHz, +22 degrees at 62 kHz, and +24 degrees at 68 kHz, where the plus sign indicates that the output lags the input. Using this convention, and letting ϕ be the phase shift introduced by the filter:

β_uncorrected = (θ_j + ϕ_j) + (θ_k + ϕ_k) + (θ_m + ϕ_m) = β_corrected + ϕ_j + ϕ_k + ϕ_m

gives a β_corrected (68 kHz, 62 kHz) value of −4 ± 12°. This indicates a reinforcing phase relation of the parent waves with respect to the low-frequency daughter wave.

The plot of summed bicoherence vs. interaction frequency for the IEDD data provides an additional indication that something other than the coupling of drift waves among themselves is responsible for the growth in low-frequency turbulence (see Figure 16).

Compared to drift waves in the CDEIC case, drift waves present in the IEDD spectrum seem to exhibit a much stronger degree of coherence—in fact, more than is allowed for drift-wave nonlinear interactions. One could infer that the difference is the result of coupling with the higher-frequency IEDD instability (harmonic generation of drift waves is not excluded in Tsui’s derivation). It may be plausible that this coupling is facilitated by the more broadband spectrum associated with IEDD fluctuations and is inhibited by the narrow CDEIC wave spectrum. Also note that at the center frequency of the IEDD mode, the sum of the squared bicoherence is close to one. In the context of three-wave coupling models, a value of one indicates coherent wave coupling [10]. The low value of this sum at intermediate (20 kHz–55 kHz) and high frequencies (greater than 75 kHz) is consistent with random, non-coherent interactions among the background turbulence (a somewhat surprising result, given the relatively high power of the intermediate frequencies).

6. Conclusions

Our experimental efforts to identify shear-driven and shear-modified mechanisms have contributed to linking the cause and effect of plasma heating, mixing, and transport. Applying a radially localized radial electric field reduces the parallel-to-B current threshold for exciting ion-cyclotron turbulence, broadens the wave spectrum in the ion-cyclotron-range, strengthens the amplitude and frequency range of the lower-frequency drift-wave spectrum, and increases the coherence between ion-cyclotron spectral components and between those components and drift-wave spectral components. This represents the direct relevance of this work to non-equilibrium dynamics, interfaces and mixing. Compared to drift waves in the CDEIC case, the drift waves present in the IEDD spectrum exhibit a stronger degree of coherence—probably as a result of coupling with the higher-frequency IEDD instability. It may be plausible that this coupling is facilitated by the more broadband spectrum associated with IEDD fluctuations and is inhibited by the narrow CDEIC wave spectrum. In contrast, the background turbulence is characterized by random, non-coherent interactions.

We offer an identification scheme for parents and daughter, which is the second novel dimension of this work. We distinguish narrowband from broadband (turbulence) waves, the difference being the enhancement of the low-frequency drift waves. Specifically, a method of determining causality is proposed and subjected to empirical tests with these signals. The proposed method is shown to be valid (with some limitations) in experimental systems. A bispectral analysis of two distinct plasma instabilities reveals a degree of coupling of the IEDD mode to drift waves that is absent in the CDEIC fluctuations. It is concluded, with acceptable ambiguity, that the parents of the nonlinear interaction are the high-frequency IEDD modes. The quadratic coupling of these waves produces daughters at a difference frequency that tends to increase the power of the drift waves.