Abstract
The present paper discusses a number of topics relevant to line broadening in the presence of periodic oscillatory fields. Specifically, we discuss the applicablility of the expression usually employed to compute the autocorrelation function, the dressing, accounting for random phases, neglecting fine structure and numerical issues associated with stiffnes.
1. Introduction
Apart from natural broadening, all line broadening of an atomic system requires a stochastic, random medium [1]. Pressure broadening in particular involves the interactions of the atomic system with the random medium. When, in addition to the random medium, a non-random electric or magnetic field, either externally (e.g., lasers) or internally (e.g., plasma waves from various instabilities) generated, is applied, the line profile may be modified in significant ways [2,3,4,5,6,7,8,9,10,11,12,13,14,15]. In the present work, we ignore the effect of such a field on trajectories and distribution functions [16,17,18] and focus on the lineshape computation, both with respect to the emergence of satellites [19,20] and width modifications [21,22,23]. An old and well-known result is that, in the absence of a plasma and for hydrogen-like lines without fine structure, one obtains the Blokhintsev satellites. For a line with upper state n and lower state , with no fine structure in the absence of a medium (plasma) and in the presence of a linearly polarized field of magnitude E and frequency , the profile as a function of frequency is [20]
with and as parabolic numbers of the upper and lower levels, respectively, denoting the p th Bessel function of the first kind, the Dirac -function and the Bohr radius.
2. The Lineshape Formula
Typically, lineshape calculations employ the autocorrelation function C(t), i.e., the Fourier transform of the line profile , defined as (neglecting the density matrix)
with denoting the statistical average over plasma [1] and and denoting the complete set of states of the upper and lower levels of the line profile in question, respectively, and is the time evolution operator for time t. Throughout the present work, the Einstein summation convention is followed, i.e., repeated indices are summed over and states that start with , e.g., refer to a complete set of upper-level states and, similarly, states that start with a , e.g., refer to a complete set of lower-level states. There is also the power spectrum formula discussed below. In [24], the two were compared and the power spectrum method was shown to provide better variance, although the two methods give the same results and the same speed of convergence. In this work, we also show that in the case of external time-dependent (oscillatory) fields, the power spectrum and dipole autocorrelation formulas give, in principle, results.
Equation (2) is particularly attractive, since one often has a code that solves for the atomic U -matrices evolution in the presence of the plasma fields, so it would be easy to just add the oscillatory field to the plasma fields.
However, this form, which assumes stationary processes, is applicable here. To illustrate this, it is important to note that, for hydrogen-like species without fine structure in an external, linearly polarized electric field in the z-direction without a plasma, one can solve in the parabolic basis, so that the time evolution operator (U-matrix) is:
with denoting the diagonal z-matrix element in the parabolic basis and . We get a similar expression for the lower level. Therefore,
with denoting the diagonal z-matrix element for the lower level .
Using the identity
we obtain
This disagrees with the Blokhintsev result, which involves and can produce negative profiles, as is negative for certain ranges of x.
In contrast, the expression for the line profile in direction without assuming stationarity (referred to as the power spectrum formula) is based on the radiation formula in direction e:
where is the power radiated in direction e, is the population of the upper level , d the dipole moment, the component of the dipole moment in the e direction and in principle complete sets of states. If we assume the density matrix to be trivial (i.e., diagonal and time-independent [25]), the line profile reads as follows:
and may then be written as (by using )
The line profile then is shown to be [6] a product of three factors:
where the dipole term D is purely atomic,
and the plasma-independent (but field-dependent) matrix S is
is the time evolution for the atomic system plus periodic field and U is determined by
with
and is the emitter–plasma interaction, i.e., the interaction of the electron involved in the transition of the line in question with the plasma electrons and ions. Thus, the emitter does not experience the perturbation by the plasma electrons and ions, but the “dressed” perturbation , which generally oscillates faster than .
S determines the satellite structure and intensity, D determines the total line intensity and determines the broadening of each satellite. In the case without a periodic field, , with denoting the energy of the ith state, and S reduces to
With this formalism that does not assume stationarity, and for a hydrogen-like line without fine structure, we recover the Blokhintsev results; the U-matrices describing the plasma interactions are simply the identity matrix and the line profile reduces to the product of D and S:
If we now substitute for the expression from Equation (3) and make use of the expansion (5), we obtain a sum of squares of Bessel functions , as in the Blokhintsev result [6]. Thus the lineshape formula (Equation (10)) is different from the one routinely used for Stark-broadening calculations, i.e., the Fourier transform of Equation (2).
3. Approximations on the Electron and Ion Treatments
From Equation (13), we see that dressing of affects electrons and ions. This implies that one should apply dressing to both electrons and ions instead of applying dressing to only electrons or only ions. Neglecting to dress in either electron or ions will tend to the widths, since the change of sign of the interaction effectively decreases the rate of decay of the autocorrelation function [21,22,23]. This can be important.
4. Adding Randomness to the Oscillatory Field
Intuitively, additional randomness should enhance broadening. Broadening is in general enhanced by the following [1]: (a) inhomogeneous mechanisms (the positions of components change, akin to quasistatic broadening where the heavier ions are considered static on the time scale of the inverse half-width (HWHM) of the line and (b) homogeneous mechanisms, where loss of memory is due to random phases (and hence an average that tends to 0) in the U-matrices for long times.
In real plasmas, different emitters may see the following:
- Different phases (e.g., plasma oscillations, such as Langmuir turbulence and, although the electric field that two different emitters experience as a function of time may have the same frequency and peak amplitude, their phases may be different, e.g., one emitter experiences an oscillatory field , the other , etc.
- Different field peak magnitudes (e.g., damping, i.e., the maximum field at an emiiter at point may be smaller than the maximum at an emitter at point ).
- Different frequencies (broadband frequency/dispersion).
The last two are hard to treat, mainly because it is hard to come up with realistic and tractable models, as models typically assume some sort of linearly polarized field with, at most, random phases. They will clearly, especially in the case of different frequencies, have at least an inhomogeneous contribution. However, the first scenario, i.e., emitters seeing different phases, means that their lineshape contributions will have the same S and will simply result in the calculated being added after multiplication with a phase factor. The details are given in Appendix A. So the point is that different phases do affect the positions (or intensities) of the components (which are controlled by S), i.e., there is no inhomogeneous type broadening. This can be exploited numerically, because if randomness is only in the phases of the different oscillatory field experienced by different emitters, then needs to be computed once and for all (for zero phase), and the positions and intensities are determined once. Furthermore, for a periodic field with a phase can be simply obtained in terms of in a periodic field with phase 0. Of course, we still need to solve the Schrödinger equation to obtain .
5. Numerical Solution: Stiffness Issues
Typically, Stark-broadening calculations involve similar magnitudes of interaction and thus do not exhibit stiffness. However, when we add a strong periodic external field, and especially arbitrarily strong static fields, we have a complete renormalization of the atomic system and, as a result, stiffness may appear. We illustrate this in Figure 1 with a calculation of [26], which shows different time scales for the various components, although stiffness is not yet extreme. This calculation refers to experimental results claiming to have diagnosed Langmuir and ion-acousting turbulence with the stated parameters [27]. As discussed in Ref. [6], solving the Schrödinger equation in an oscillatory field can be a stiff problem. Hence, in the present approach, one solves for , i.e., the 0th order Hamiltonian consisting of the atomic Hamiltonian plus the periodic field (oscillatory plus static) using a stiff solver (actually a symplectic integrator that preserves unitarity [28]) and a non-stiff integrator for the interaction Hamiltonian. Alternatively, one could include the periodic field with the plasma particle fields, which should also be done using a stiff integrator.
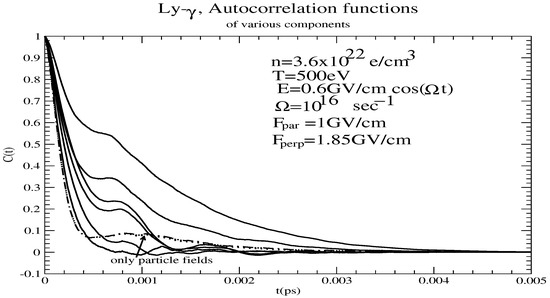
Figure 1.
Autocorrelation functions (solid) for the H-like Si Lyman line components in a plasma with electron density e/cm3 and temperature 500 eV under the action of a linearly polarized field of 0.6 GV/cm and frequency s−1 in the z-direction and a static field with components parallel and perpendicular to the oscillatory field of 1 and 1.85 GV/cm, respectively. Also shown are the autocorrelation functions without the static and oscillatory field (only particle fields) without (dashed) and with (dotted) fine structure.
For a periodic field (such as a laser), using the Floquet theory represents a way to significantly optimize the calculation if stiffness is an issue. Compared to solving the Schrödinger equation in the external plus plasma particle field, which may be dominated by the external field for high field amplitudes, the alternative algorithm can be more efficient.
Since the periodic (which may involve constant terms) field amplitude may well exceed the plasma microfield, even by orders of magnitude, if we solve for the total (deterministic laser plus stochastic plasma) field, the change over a given time step can de dominated by the deterministic field. Thus, it is numerically convenient to use the interaction picture after having solved the 0th order Hamiltonian with the periodic field; it also accurately identifies the satellite positions. In other words, only , which will be solved once, requires a stiff solver [28]; may be solved by non-stiff integrators. In addition, if a numerical solution is necessary, it is important that we only need for the laser (or turbulent field) period, not the time of interest for which may be much larger.
On the other hand, the spectrum consists of features at the Floquet exponents, shifted by the Blokhintsev structure, i.e., integer multiples of the laser frequency . These Floquet exponents, indexed by k, and Blokhintsev satellites couple and, in general, involve more time evolutions than usual. For instance, for Lyman lines, it would normally suffice to solve the systems for the upper level with the principal quantum number n:
i.e., we would only need to solve for the evolution of the states (i, k is any state of the upper level and np is any “p” state of the upper level, i.e., with angular momentum quantum number 1). This is no longer the case, making calculations (in this respect) harder.
6. Role of Fine Structure
As shown in [6], the Floquet exponents arise from time-independent terms. For hydrogen lines without fine structure, these are due to the zeroth (constant) component of the oscillatory field and from other possible constant fields. With fine structure, there is an additional contribution due to the time-independent fine structure terms in the 0th order Hamiltonian. The importance of fine structure then depends not on the magnitude of the oscillatory field, but on the magnitude of its constant component compared to the fine structure. We illustrate by showing calculations for hydrogen with and without fine structure. Figure 2 and Figure 3 both consider the joint action of two perpendicular fields, one static field with magnitude 1 GV/cm and an oscillatory field with GV/cm and s−1 and s−1, respectively. These figures display the positions (in units of ) and intensities for calculations with and without fine structure and show important differences. For example, in Figure 3, the component at about is the strongest one in the calculation without fine structure, but is hardly noticeable in the calculation with fine structure. Thus, especially if one wants to use these positions to infer information, accounting for fine structure can be quite important.
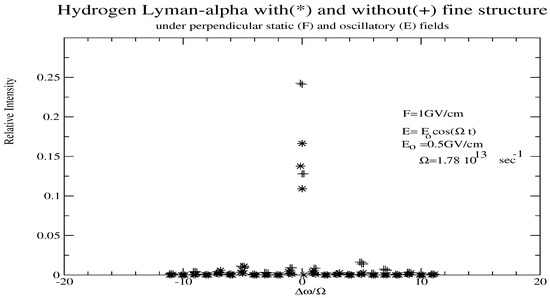
Figure 2.
Positions and intensities for the hydrogen Lyman line under the action of perpendicular static and oscillatory fields, respectively, without (+) and with (*) fine structure.
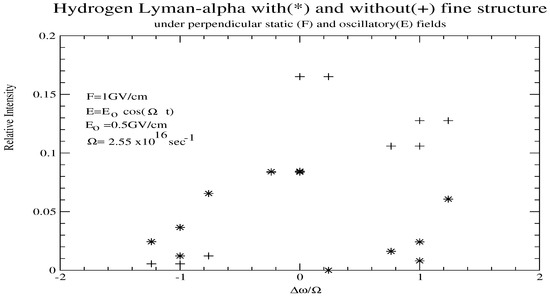
Figure 3.
Positions and intensities for the hydrogen Lyman line under the action of perpendicular static and oscillatory fields, respectively, without (+) and with (*) fine structure.
7. Conclusions
This article stressed a number of important aspects of the effects of oscillatory electric fields on lineshapes in plasmas. Specifially, it was shown that the usual formula employed in calculations without an external field, which assumes stationarity, does not recover the correct Blokhintsev limit. For small fields, this does not make much of a difference [29], but it can be important for larger fields. It was also shown that dressing either electrons or ions alone is theoretically suspect, that random phases of the oscillatory electric fields do not alter the satellite positions and intensities—something that is also numerically convenient—but they do in principle affect the width and that stiffness may be an issue, which may be handled by solving once and for all by computing the atomic plus oscillatory field time evolution. In addition, we discussed the effect of neglecting fine structure on the satellite positions and intensities and showed that the neglect of fine structure can result in incorrect spectral positions and intensities.
Funding
This research received no external funding.
Data Availability Statement
Data are available upon request from the author.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A. Random Phases
Let be the time evolution operator for a field with 0 phase and let be the time evolution for the same field with phase , i.e., . For example, if is a linearly polarized field with time dependence , then has the time dependence . Then, it is simple to see that if , with being I the unit matrix, then
with being the solution for and the unit matrix.
Therefore, , the S in a field with phase , can be written in terms of . Specifically, we will contrast
for zero phase to the corresponding expression for phase :
where we switched to the integration variable with
Thus, whereas the zero phase result was
the profile with nonzero random phases is
This means that and, hence, the positions and intensities remain unchanged in the presence of a random phase in the interaction, and the part that is responsible for broadening, {Ua} is weighted by a random phase factor, F(ϕ). If the phases are not uniformly random, a probability density for ϕ should multiply this expression.
References
- Alexiou, S. Overview of plasma line broadening. High Energy Density Phys. 2009, 5, 225–233. [Google Scholar] [CrossRef]
- Peyrusse, O. Stark-profile calculations for spectral lines of hydrogenic ions in plasmas submitted to a strong oscillating electric field. Phys. Scr. 1997, 56, 371–380. [Google Scholar] [CrossRef]
- Sauvan, P.; Dalimier, E. Floquet-Liouville approach for calculating Stark profiles in plasmas in the presence of a strong oscillating field. Phys. Rev. E 2009, 79, 036405. [Google Scholar] [CrossRef]
- Baranger, M.; Mozer, B. Light as a Plasma Probe. Phys. Rev. 1961, 1123, 25–28. [Google Scholar] [CrossRef]
- Lisitsa, V. Atoms in Plasma; Springer: Berlin/Heidelberg, Germany, 1994; ISBN 3-540-57580-4. [Google Scholar]
- Alexiou, S. Methods for Line Shapes in Plasmas in the Presence of External Electric Fields. Atoms 2021, 9, 30. [Google Scholar] [CrossRef]
- Oks, E.A. Plasma Spectroscopy: The Influence of Microwave and Laser Fields; Springer Series on Atoms and Plasmas; Springer: New York, NY, USA, 1995; Volume 9, ISBN 3-540-54100-4. [Google Scholar]
- Cohn, A.; Bakshi, P.; Kalman, G. Linear Stark Effect Due to Resonant Interactions of Static and Dynamic Fields. Phys. Rev. Lett. 1972, 29, 324–326, Erratum in Phys. Rev. Lett. 1973, 31, 620–620.. [Google Scholar] [CrossRef]
- Bakshi, P.; Kalman, G.; Cohn, A. Hydrogenic Stark-Zeeman Spectra for Combined Static and Dynamic Fields. Phys. Rev. Lett. 1973, 31, 1576–1579. [Google Scholar] [CrossRef]
- Deutsch, C.; Bekefi, G. Stark-broadening calculations of the Lyman-α line in a turbulent plasma. Phys. Rev. 1976, 14, 854–862. [Google Scholar] [CrossRef]
- Oks, E.; Böddeker, S.; Kunze, H.J. Spectroscopy of atomic hydrogen in dense plasmas in the presence of dynamic fields: Intra-Stark spectroscopy. Phys. Rev. A 1991, 44, 8338–8347. [Google Scholar] [CrossRef] [PubMed]
- Nee, T.-J.A.; Griem, H.R. Measurement of hydrogen n-α line Stark profiles in a turbulent plasma. Phys. Rev. A 1976, 14, 1853–1868. [Google Scholar] [CrossRef]
- Nee, T.-J. Calculation of helium plasma satellites in turbulent plasmas. J. Quant. Spectrosc. Radiat. Transf. 1987, 38, 213–224. [Google Scholar] [CrossRef]
- Griem, H.R.; Kunze, H.J. Stark Broadening of Two Ionized-Helium Lines by Collective Electric Fields in a Laboratory Plasma. Phys. Rev. Lett. 1969, 23, 1279–1281. [Google Scholar] [CrossRef]
- Sarid, E.; Maron, Y.; Troyanksi, L. Spectroscopic investigation of fluctuating anisotropic electric fields in a high-power diode plasma. Phys. Rev. E 1993, 48, 1364–1374. [Google Scholar] [CrossRef] [PubMed]
- Balakin, A.A. Operator of pair electron-ion collisions in alternating electromagnetic fields. Plasma Phys. Rep. 2008, 34, 1046–1053. [Google Scholar] [CrossRef]
- Rosato, J. Hydrogen Line Shapes in Plasmas with Large Magnetic Fields. Atoms 2020, 8, 74. [Google Scholar] [CrossRef]
- Alexiou, S. Line Shapes in a Magnetic Field: Trajectory Modifications I: Electrons. Atoms 2019, 7, 52. [Google Scholar] [CrossRef]
- Blokhintsev, O. Theory of the Stark Effect in a Time-Dependent Field. Phys. Z. Sowjet. 1933, 4, 501–515. [Google Scholar]
- Letunov, A.Y.; Lisitsa, V.S. Stark–Zeeman and Blokhintsev Spectra of Rydberg Atoms. JETP 2020, 131, 696–706. [Google Scholar] [CrossRef]
- Alexiou, S.; Weingarten, A.; Maron, Y.; Sarfaty, M.; Krasik, Y.E. Novel Spectroscopic Method for Analysis of Nonthermal Electric Fields in Plasmas. Phys. Rev. Lett. 1995, 75, 3126–3129. [Google Scholar] [CrossRef]
- Weingarten, A.; Alexiou, S.; Maron, Y.; Sarfaty, M.; Krasik, Y.E.; Kingsep, Y. Observation of nonthermal turbulent electric fields in a nanosecond plasma opening switch experiment. Phys. Rev. E 1999, 59, 1096–1110. [Google Scholar] [CrossRef]
- Alexiou, S. X-ray laser line narrowing: New developments. J. Quant. Spectrosc. Radiat. Transfer. 2001, 71, 139–146. [Google Scholar] [CrossRef]
- Rosato, J.; Marandet, Y.; Stamm, R. Quantifying the statistical noise in computer simulations of Stark broadening. J. Quant. Spectrosc. Radiat. Transfer. 2020, 249, 107002–107010. [Google Scholar] [CrossRef]
- Stambulchik, E.; Kroupp, E.; Maron, Y.; Malka, V. On the Stark Effect of the OI 777-nm Triplet in Plasma and Laser Fields. Atoms 2020, 8, 84. [Google Scholar] [CrossRef]
- Alexiou, S. Analysis of Plasma Emission Experiments and ‘Dips’. Atoms 2023, 11, 29. [Google Scholar] [CrossRef]
- Dalimier, E.; Pikuz, T.A.; Angelo, P. Mini-Review of Intra-Stark X-ray Spectroscopy of Relativistic Laser—Plasma Interactions. Atoms 2018, 6, 45. [Google Scholar] [CrossRef]
- Hairer, E.; Wanner, G. Solving ordinary differential equations II. In Stiff and Differential-Algebraic Problems, 2nd ed.; Springer Series in Computational Mathematics 14; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Hannachi, I.; Alexiou, S.; Stamm, R. Line shape code comparison of the effect of periodic fields on hydrogen lines. Atoms 2024. in print. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).