Next Article in Journal
Long-Lived Levels in Multiply and Highly Charged Ions
Previous Article in Journal
Optical Extreme Learning Machines with Atomic Vapors
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atoms
Volume 12
Issue 2
10.3390/atoms12020011
atoms-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

FeC4H22+ Encompassing Planar Tetracoordinate Iron: Structure and Bonding Patterns

by
Shilpa Shajan
1,
Kandasamy Thirunavukkarsu
2,
Vijayanand Chandrasekaran
1,*,
Venkatesan S. Thimmakondu
3,* and
Krishnan Thirumoorthy
1,*
1
Department of Chemistry, School of Advanced Sciences, Vellore Institute of Technology, Vellore 632014, India
2
Vel Tech Rangarajan Dr Sagunthala R&D Institute of Science and Technology, Avadi, Chennai 600062, India
3
Department of Chemistry and Biochemistry, San Diego State University, San Diego, CA 92182-1030, USA
*
Authors to whom correspondence should be addressed.
Atoms 2024, 12(2), 11; https://doi.org/10.3390/atoms12020011
Submission received: 28 December 2023 / Revised: 7 February 2024 / Accepted: 14 February 2024 / Published: 18 February 2024
(This article belongs to the Section Quantum Chemistry, Computational Chemistry and Molecular Physics)
Browse Figures
Versions Notes

Abstract

:
The singlet, triplet, and quintet electronic states of the Fe C 4 H 2 2 + system are theoretically explored using quantum chemical methods, and 39 isomers are identified in the singlet electronic state and 4 isomers in both triplet and quintet electronic states. A molecule with a planar tetracoordinate iron (ptFe) is found on the potential energy surface of singlet and triplet electronic states. The bonding features of ptFe in the singlet electronic state are analyzed with natural bond orbital (NBO) analysis, adaptive natural density partitioning (AdNDP), and molecular orbital analysis. The resultant data delineate that the ptFe is stabilized through electron delocalization in the ptFe system.

1. Introduction

The study of transition metal clusters, especially first-row transition metal clusters, has sparked the interest of several research groups over the years due to the clusters’ unique structural, electronic, magnetic, and catalytic properties [1,2,3,4,5]. Iron (Fe) is one of the universe’s most prevalent heavy and refractory elements. Iron–carbon clusters have provided an in-depth understanding of geometrical properties, electronic structures, and magnetism among the transition metal clusters because of iron’s position between early and late transition metals due to experimental measurements [6,7,8] and theoretical calculations [9,10,11]. Experimental studies on the iron–carbon clusters include mass spectrometry, infrared isolation matrix spectrometry, anion photoelectron spectroscopy, and gas-phase ion chromatography [7,8,12,13,14,15,16]. FeCn (n ≤ 8) [17,18,19,20] and FenC (n ≤ 13) [21,22,23] iron–carbon clusters have been theoretically examined in the past, and some of them have been reported experimentally [24]. The clusters of iron, carbon, and hydrogen have also been the subject of similar studies. In 1987, for the first time, neutral FeCHn (n = 0–3) systems were produced and characterized in the gas phase by Schwarz et al. using neutralization–reionization mass spectrometry (NRMS) [25]. Fan et al. have investigated FeCn and FeCnH (n = 2) clusters via anion photoelectron spectroscopy [26]. The cation of the FeCH2 cluster was also investigated experimentally via photofragment spectroscopy [27]. In 2003, Boesl et al. identified the FeC4H2 neutral complex experimentally using mass selective photo-detachment photoelectron spectroscopy [28]. In 2013, Chandra and coworkers conducted studies on the molecular and spectroscopic properties of iron-containing ring molecules, including theoretical studies on cyclic compounds like FeC2, FeC3, FeC3H2, FeC2H2, FeC2H4, and FeC3H4, which are of astrophysical interest [29]. Transition metal clusters have gained potential applications in various fields since the discovery of metallocarbohedrene in 1992 [30]. The list extends from materials to the emerging field of nanotechnology and also exhibits remarkable applications in organic chemistry [16,31,32,33,34]. A prominent instance is the challenging activation of methane by iron carbide cluster ions [5,35]. Another interesting application of these compounds is their catalytic activity in oxygen reduction, COx (x = 1, 2) reduction, and also in Fischer–Tropsch synthesis [36,37,38,39]. Energy and hydrogen storage are further applications of these compounds [40,41,42,43]. The prospective applications of these iron–carbon clusters extend beyond material science; other significant areas include surface chemistry, astrochemistry, and combustion chemistry.
On the other hand, there have been extensive studies on aberrant molecules that deviate from the accepted notions in chemistry ever since H. J. Monkhorst proposed the concept of planar tetracoordinate carbon (ptC) in 1968 [44]. In 1970, Hoffman and co-workers proposed ways to stabilize the ptC [45], which in turn spurred unrelenting experimental and computational investigations into “planar hypercoordinate” chemistry [46,47,48,49,50,51,52,53,54]. In 1976, Schleyer and coworkers identified ptC as local minima in lithium-substituted cyclopropane and cyclopropene computationally and marked the beginning of the theoretical [45,55,56,57,58,59,60,61,62] and experimental [63,64,65] investigations in this area. A lot of attention has been paid to this field recently as a result of the tremendous theoretical and experimental progress made in the pursuit of a stable compound using planar hypercoordinate compounds. The exploration of planar tetracoordinate chemistry has also extended to the hetero atoms and also to the transition metals. In 2003, Frenking and co-workers predicted, theoretically, a novel type of a transition metal-centered aromatic compound in which planar pentacoordinate iron was first introduced [66]. In the same year, Tanaka et al.’s experimental and theoretical studies on Au5Zn+ revealed the lowest energy isomer as a planar tetracoordinate Zn, which is stabilized via σ aromaticity [67,68]. Later, in 2004, the same group further identified planar motifs in gold clusters doped with transition metals, including planar tetracoordinate iron [69]. In 2006, Lievens, Nguyen, and co-workers explored the flat structural motifs in Ag5X0/–/+(X = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni), where planar tetra and pentacoordinate iron were reported [70,71]. In 2005, Wang and co-workers discovered planar hexacoordinate species in transition metal-doped gold clusters, M@Au6 (M = Ti, V, Cr) [72]. This research trend was expanded to include other transition metals from Sc to Ni, and planar hexacoordinate molecules were discovered in these gold clusters by Zhang et al. [73]. Planar heptacoordinate Sc was identified as the global minimum in the Cu7Sc cluster in 2008 by Nguyen and co-workers [74]. Li, Schleyer, and co-workers investigated unconventional planar motifs with hepta-, octa-, nona-, and decacoordinate first-row transition metals enclosed by boron rings with many neutral and charged molecules including planar octa- and nonacoordinate iron as global minima [75,76]. Later, in 2012, Romanescu et al. experimentally reported both the planar octa- and nonacoordinate in Fe B 8 − and Fe B 9 − clusters [77]. Zhang et al. attempted to design graphene-like materials containing planar hypercoordinate transition metal atoms by constructing FeB6 monolayers [78]. Zhao and co-workers recently developed a stable FeSi2 monolayer with planar hexacoordinate Fe atoms [79]. Thimmakondu and co-workers studied the interaction of planar pentacoordinate carbon within a ferrocene derivative [80]. Planar pentacoordinate Zn group elements supported by lithium clusters were found to be global minima by Guha and co-workers [81]. Very recently, planar hexacoordinate transition metals in star structures were identified as global minima [82]. In this direction, the present work aimed to find various geometries of Fe C 4 H 2 2 + as they are astronomically relevant molecules. Since the four-carbon cumulene carbene, butatrienylidene (C4H2), has already been detected in the interstellar medium (ISM) [83], this study explored the species that might potentially mix with transition metals like iron. It is noted here that, in total, eight cumulene carbene molecules of the type CnH2 (n = 3 to 10) are well-known in the laboratory [84,85,86,87,88], and among them, four lower homologues (n = 3 to 6) have already been identified in the ISM [83,89,90,91]. Despite being the most abundant metal in the universe, iron is less common in the ISM, and hitherto, many have strived to find the missing iron in the interstellar medium [92]. Very recently, for the first time, FeC radical was detected in the envelope of IRC+10216 [93].
In the present work, the isomers of Fe C 4 H 2 2 + in their singlet, triplet, and quintet electronic states are explored, with an emphasis on planar tetracoordinate iron (ptFe) in the singlet electronic state, and the bonding features of the ptFe structure are also analyzed. This study explores the isomers of Fe C 4 H 2 2 + , where a ptFe is serendipitously identified and is a local minimum. It is noteworthy that iron is in a +2 oxidation state, which is a more commonly occurring oxidation state, and therefore, the Fe C 4 H 2 2 + system is taken into account here. Iron (II) is integral to various fields of chemistry, including redox reactions, coordination chemistry, and biological systems [94,95,96,97]. For brevity, the interaction of counter ions that can neutralize the system was not considered in the current study.

2. Computational Calculation Methodology

The geometries of all isomers of Fe C 4 H 2 2 + were generated by chemical intuition. Quantum chemical calculations on the singlet electronic state of the system were carried out using the Density Functional Theory (DFT) approach. The possible structures were optimized using the ωB97X–D hybrid functional method that uses a version of Grimme’s D2 dispersion model. The Restricted Open-Shell Hartree–Fock (ROHF) method was utilized for the triplet and quintet electronic states optimization [98]. The effective core potential (ECP), Stuttgart/Dresden, SDD was used for iron metal, and the large 6–311++G (2d, 2p) basis set for carbon and hydrogen atoms for the investigated system [99,100,101,102]. Relativistic effects were significant for molecules containing heavy metals and transition metals; hence, the ECP was considered for the iron system. ECP was used to replace the core with analytical functions that more effectively and precisely represent the combined nuclear-electronic core to the remaining electrons [103]. To confirm whether the stationary point obtained on the potential energy surface (PES) is a minimum or a transition state, or an nth order saddle point, harmonic vibrational frequencies were computed for all the energy-minimized geometries at the same level. All the computational calculations were carried out with the Gaussian suite of programs [104]. Natural bond orbital (NBO) analysis was carried out at the same level of theory. NBO analysis provides information on the charge distribution of the atoms in the molecules and also the Wiberg bond index (WBI) values that are the electronic parameters related to the electron density between atoms. NBO 3.1 implemented in Gaussian 16 was utilized for this purpose [105,106]. Adaptive natural density partitioning (AdNDP) analysis was utilized to further investigate the bonding characteristics [107,108]. A topological analysis of the ptFe isomer was carried out using the Multiwfn program [109,110] with the wavefunction file generated by the Gaussian program [104].

3. Results and Discussions

The potential energy surface (PES) of Fe C 4 H 2 2 + in the singlet, triplet, and quintet electronic states was explored. The ten energetically low-lying isomers of the singlet electronic state of the Fe C 4 H 2 2 + system are shown in Figure 1 with their relative energies, point groups, number of imaginary frequencies, and dipole moments. All other optimized isomers of Fe C 4 H 2 2 + in the singlet electronic state are provided in the Supplementary Material. For brevity, the total electronic energies, zero-point vibrational energy (ZPVE) corrections, ZPVE-corrected total energies (E+ZPVE), absolute dipole moments, relative energies without (∆E) and with ZPVE corrections (∆E + ZPVE), and the number of imaginary frequencies (NImag) are provided in Table S1 in the Supplementary Material. In the unrestricted UωB97X–D approach (results are provided in the Supporting Information), the optimization of the quintet and triplet electronic states shows significant and non-trivial spin contamination. Therefore, we made an effort to optimize the geometries in the triplet and quintet electronic states with the ROHF wavefunction to prevent spin contamination. Nevertheless, in the triplet and quintet electronic states without spin contamination, the number of optimal geometries was lowered to four. The optimized geometries of the triplet and quintet electronic states with ROHF are shown in Figure 2. Isomers 1s, 1t, and 1q are the global minima of the singlet, triplet, and quintet electronic states, respectively. 1s has a linear structure, and the structure like iron is directly attached to the cumulene carbene. As cumulene carbene has already been detected in the interstellar medium (ISM) [83], the global minimum of singlet electronic state 1s suggests that the presence of iron atoms in the ISM might be in the form of these iron hydrogenated carbides. The isovalent pentatetraenylidene, an isomer of C5H2, has already been a familiar molecule in the laboratory as well as in the ISM [84,90]. As 1s is a global minimum, it has a higher chance of being viable in the laboratory. It is also polar with a dipole moment value of 1.25 Debye indicating feasible detection in the ISM. 4s contains planar tetracoordinate iron (ptFe), which should be considered an accidental surprise in the PES of the singlet electronic state. 1t also contains ptFe, which has been identified as a global minimum in the PES of the triplet electronic state. 1q has a cyclic structure that is a local minimum in the singlet electronic state, and a similar geometry has been identified as a local minimum (2t) in the triplet electronic state. The main focus of the present work was on isomer 4s, which contains ptFe in the singlet electronic state. It lies ~28.15 kcal mol−1 above its lowest energy isomer, 1s. The point group of 4s is C2v, and its dipole moment value is 1.16 Debye. To probe into the ptFe, the chemical bonding characteristic features were investigated in detail.

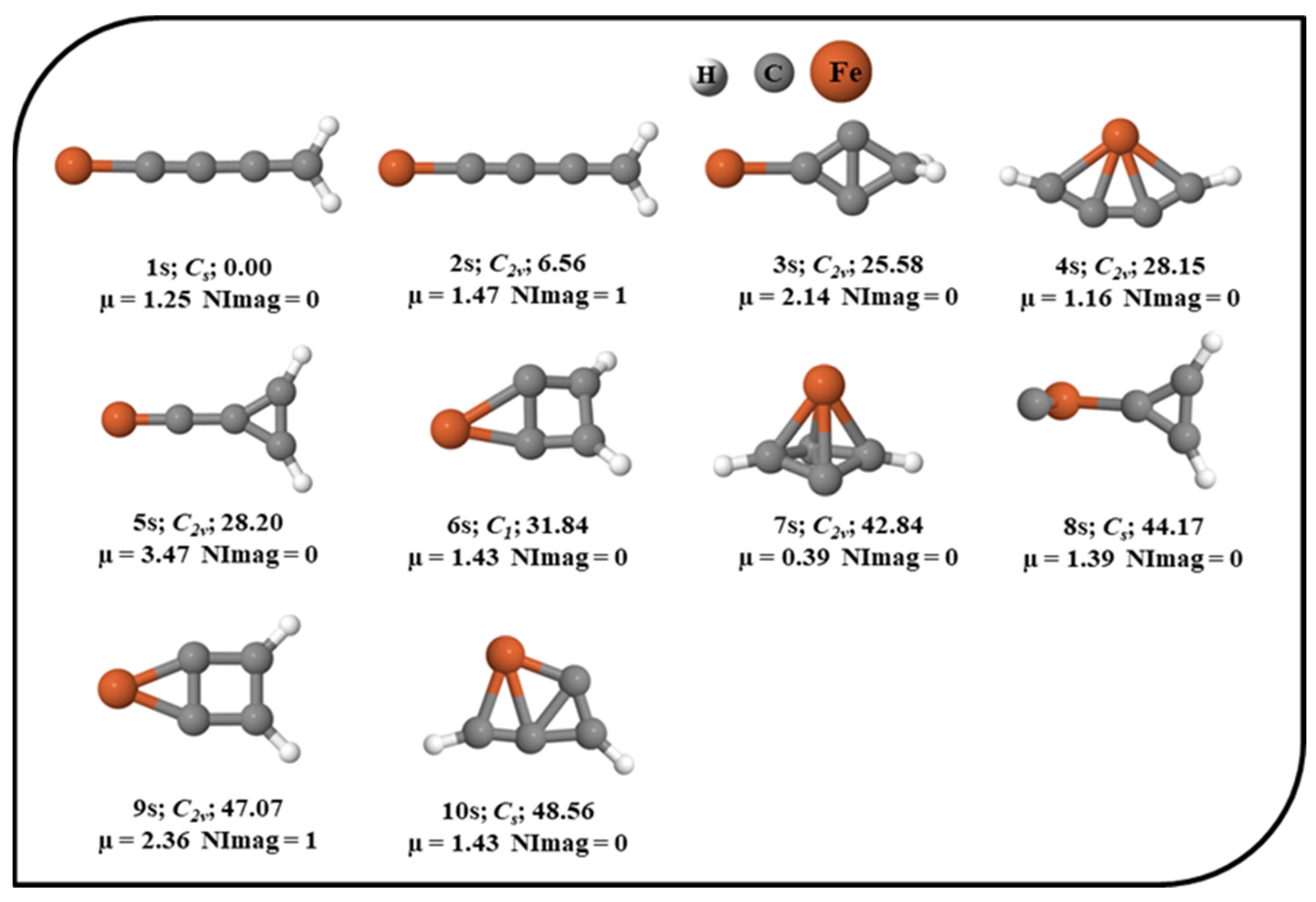
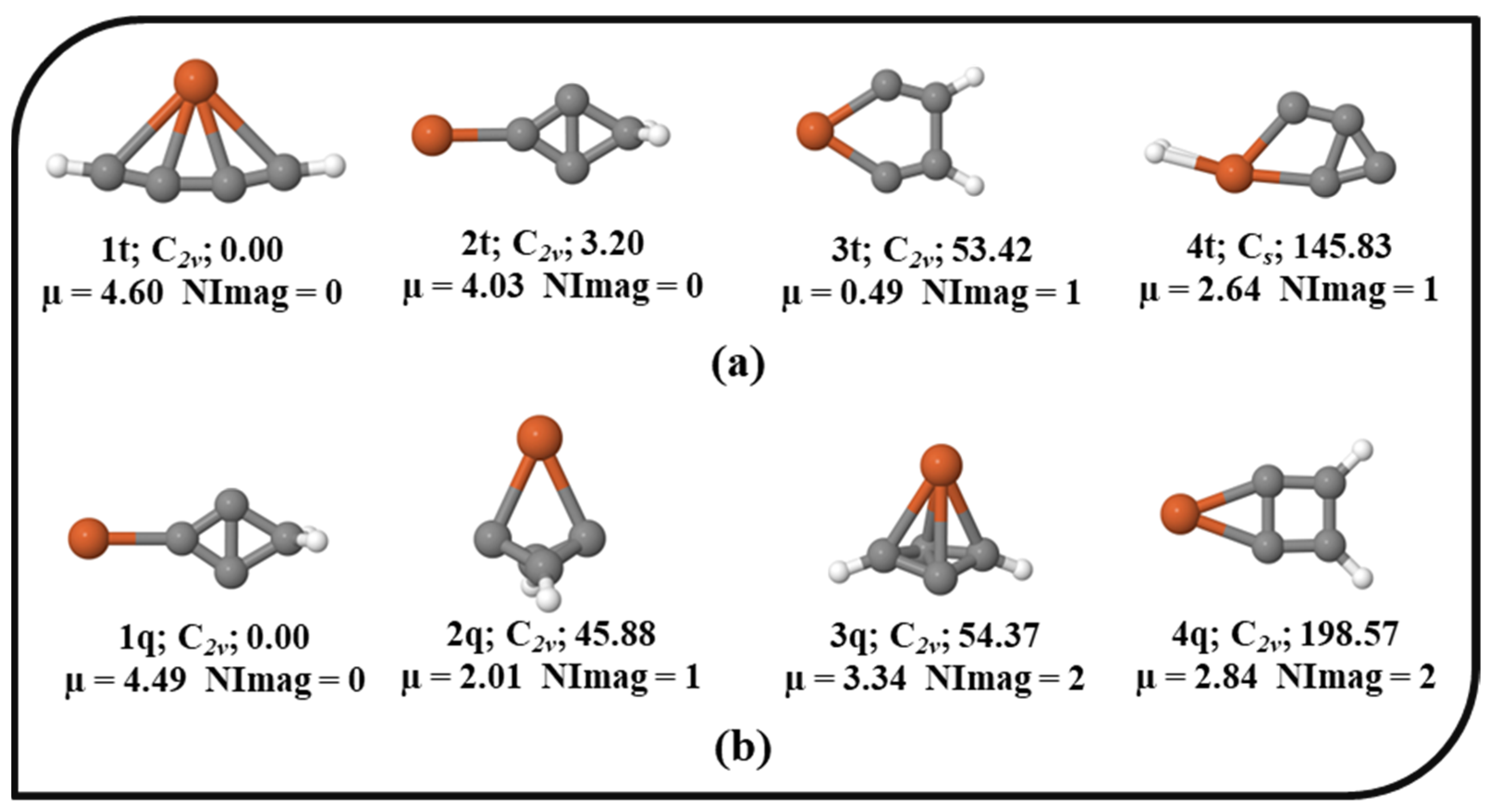
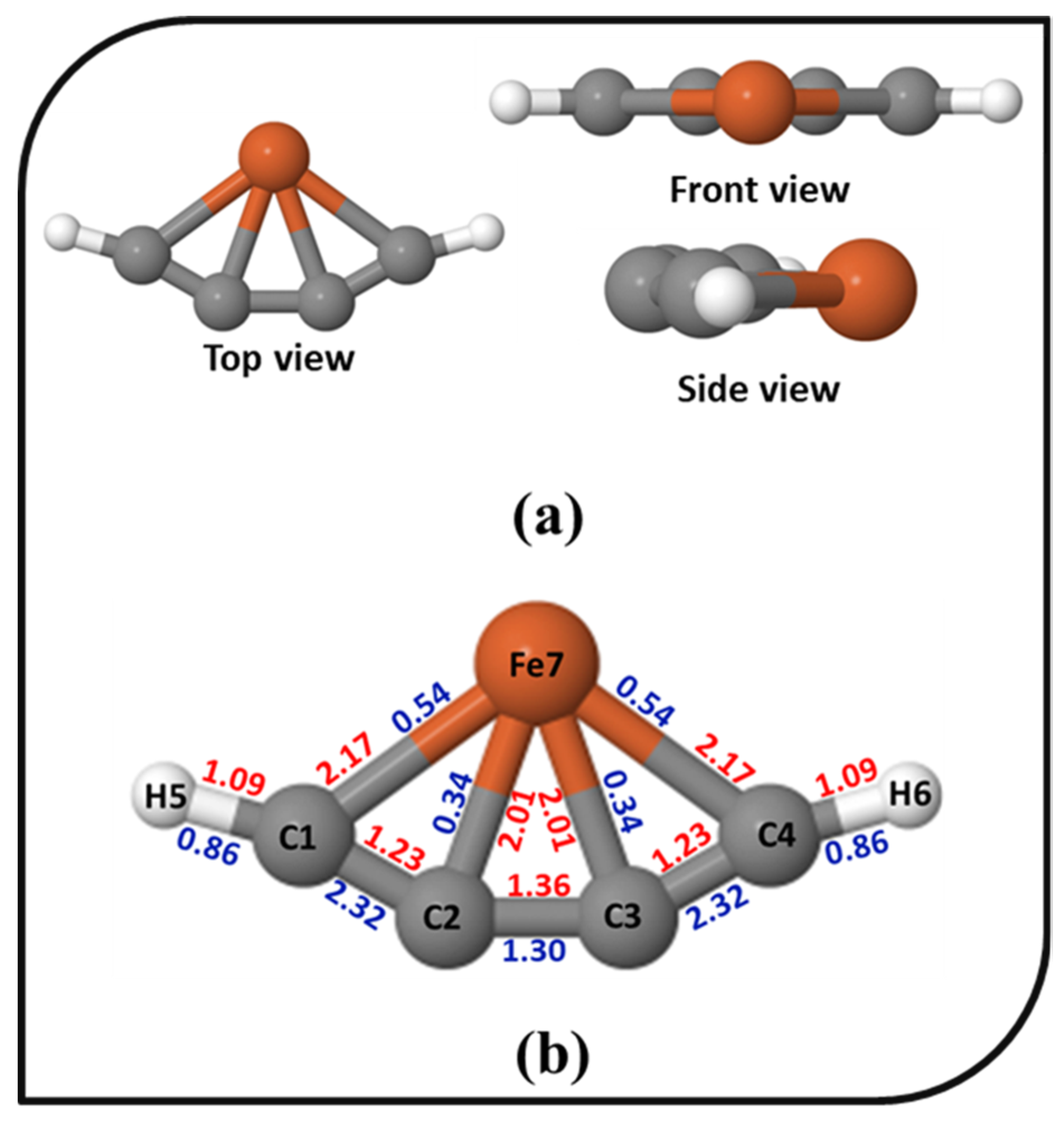
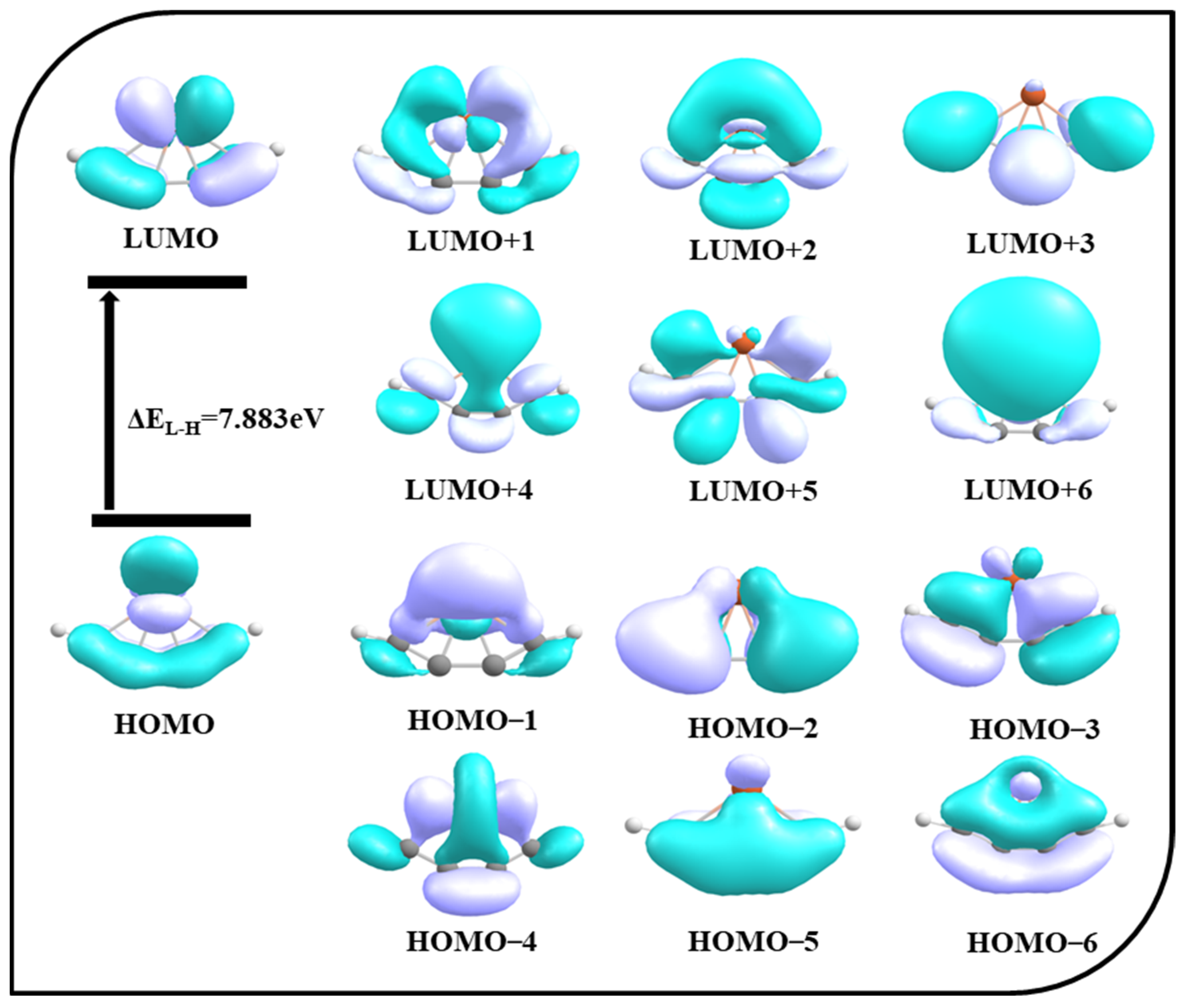
3.1. Bonding, Wiberg Bond Indices, and Molecular Orbital Analysis

The bonding scenario of 4s exhibiting ptFe was analyzed. The different views, bond lengths, and WBI values of 4s are shown in Figure 3. The Fe–C bond lengths in the ptFe are 2.01 and 2.17 Å, which are in close agreement with the bond lengths already reported in iron–carbon-based molecules [69,71,111,112,113]. The carbon–carbon bond lengths in 4s are also similar to the reported iron–carbon-based molecules [23,112], and also, it has electron delocalization along the carbon chain. The electronic characteristics associated with the overlap of the electron populations between two atoms are measured using the WBI. Here, the WBI values of ptFe indicate its chemical bonding characteristics. For 4s, the WBI values for C2–Fe and C3–Fe are 0.34, and C1–Fe and C4–Fe are 0.54, indicating the existence of covalent interaction between iron and carbon atoms. These values are in good agreement with the values reported in iron–carbon- and boron-based clusters [75,76]. The carbon–carbon WBI values range from 1.30 to 2.32, reflecting the bonding features arising from the delocalization of electrons. The natural bond orbital (NBO) analysis provides insight into the natural atomic charges (NAC) of the system. The NAC on 4s are depicted in Figure S3 in the Supplementary Material. According to the NAC, the metal center in the ptFe shows a large positive value of 1.257. The NAC on the carbon atoms are low, indicating a large charge transfer between iron and the carbon atoms. The polarity of the system varies because of the differences in electronegativities between carbon and iron. Electrostatic attraction results from this, which makes the ptFe more stable.
To extract more information on bonding, a molecular orbital analysis is carried out. The molecular orbitals of 4s are shown in Figure 4. HOMO, HOMO–2, and HOMO–5 are π delocalization orbitals, whereas HOMO–1, HOMO–3, HOMO–4, and HOMO–6 are σ delocalization orbitals. HOMO–6 clearly shows the covalent interaction between iron and carbon atoms from the overlap of the orbitals. The LUMO to LUMO+6 orbitals are also depicted in Figure 4. The HOMO-LUMO gap is 7.883 eV. Along with σ and π delocalizations, this large energy gap also plays an important role in maintaining the stability of the ptFe.

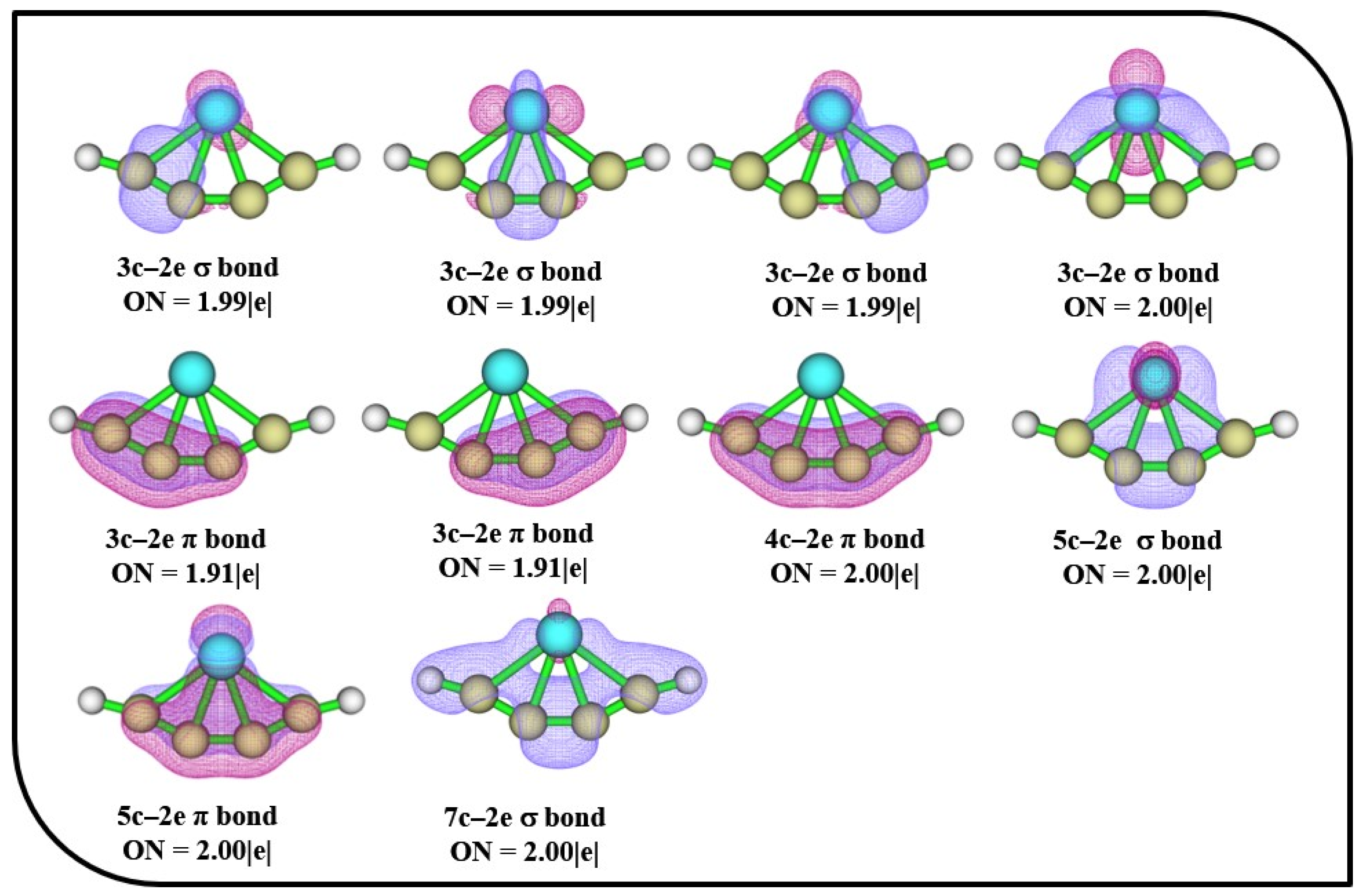
3.2. Adaptive Natural Density Partitioning (AdNDP) Analysis

The AdNDP analysis wass employed to comprehend the nature of bonding in the ptFe isomer. This method is an extension of NBO and a powerful approach for the analysis of electron density. The chemical bonding in molecules with non-classical bonding patterns may be described succinctly and simply using this technique. In using this method, the charge density is divided into components with the highest possible degree of localized electron pairs, such as n-center two-electron (nc–2e) bonds, which include core electrons, lone pairs (LPs), and multicentered two-electron bonds like 2c–2e. AdNDP is an excellent implementation to search for delocalized n-center two-electron bonds (n < 2) due to the extension of the Lewis description.
The AdNDP bonding patterns of 4s with occupation numbers (ONs) are depicted in Figure 5. The four 3c–2e σ bonds in 4s have ON values of 1.99 |e| and 2.00|e|, which ascertain the electron density localized between the planar tetracoordinate center and their adjacent atoms. The presence of 3c–2e, 4c–2e, and 5c–2e π bonds confirms the presence of alternate delocalized π bonds in the ptFe, which aid in the stabilization of the molecule. The stability of the ptFe is additionally supported by the presence of 5c–2e and 7c–2e σ bonds.

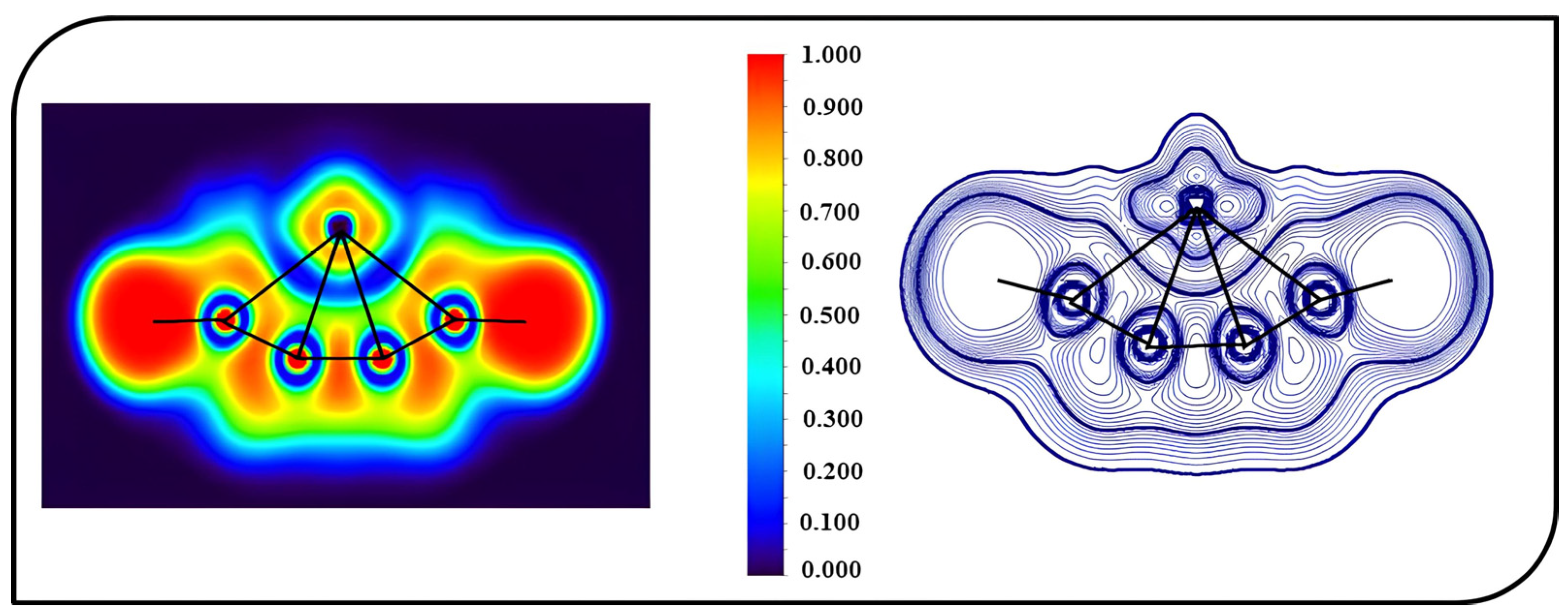
3.3. Topological Analysis: Electron Localization Function and Laplacian of Electron Density

A topological analysis was carried out to shed light on the bonding characteristics of ptFe. The electron localization function (ELF) and Laplacian of electron density (Δ2ρ(r)) were used for the investigation of the topologies of the molecules, which depict the localization of electron pairs and can be used to visualize delocalized bonds. The color-filled map of the ELF and the contour map of the Laplacian of electron density (Δ2ρ(r)) for 4s are shown in Figure 6. The interaction between the d-orbitals of iron and adjacent atoms can be observed from the ELF plots. From the contour plot, it is clear that the carbon chain has localized electron density, demonstrating high electron localization that fosters the stability of the ptFe. In 4s, the electron density for peripheral carbon atoms is higher, resulting in a higher WBI value of 0.54 when compared to the inner carbon atom, which has a value of 0.34. The plots generated show the interaction between the iron atom and the surrounding carbon atoms and also the delocalization of electron densities within the molecule.

3.4. IR and Raman Spectra

The IR (infrared) and Raman spectra for 4s computed in silico are provided in the Supplementary Material in Figure S4, which assist further experimental observations. The observed vibrational frequencies in the stimulated spectra are due to the C=C, Fe–C, and C–H bonds. The absorptions for allenic C=C asymmetric and symmetric stretching occur around 1956 cm−1 and 2119 cm−1, respectively. The symmetric and asymmetric stretching of C–H is around 3240 cm−1. The Fe–C asymmetric stretching is at 598 cm−1, whereas in the Raman spectra, the Fe–C mode is observed at 499 cm−1. The IR and Raman spectra were generated with the Gaussian program [101]. The computationally predicted IR and Raman spectra would be useful for the detection of the 4s structure in the experimental laboratory.

4. Conclusions

The isomers of the Fe C 4 H 2 2 + system in the singlet electronic state were investigated first with the DFT method, whereas triplet and quintet electronic states were explored using the ROHF method. Planar tetracoordinate iron (ptFe) was found on the PES while exploring the isomers of the Fe C 4 H 2 2 + system. A thorough bonding analysis was performed on the 4s ptFe isomer. Different methods such as the AdNDP, WBI, NBO, and ELF were used to obtain insight into the structural characteristics. The delocalized bonds that stabilize the ptFe in the singlet electronic state are well supported by the AdNDP, NBO, and WBI. The WBI values in 4s indicate the covalent characteristics of the Fe–C bond in the ptFe. The electron density around carbon and iron in the color-filled ELF plot depicts the stability of the ptFe. The topological analysis through the ELF and the Laplacian of electron density (Δ2ρ(r)) confirms the interaction between ptFe and the carbon atoms surrounding them. The stable nature of the ptFe is also attained through favorable molecular orbital interactions. The computed IR and Raman spectra of the ptFe could be useful for experimentalists for identification in the laboratory in the future. The results of the present work provide new directions to theoretical and experimental studies on flat transition metal–carbon hydride chemistry.

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/atoms12020011/s1. The optimized geometries of Fe C 4 H 2 2 + in the singlet electronic state are shown in Figure S1; the AdNDP bonding patterns of 4s in the singlet electronic state with occupation numbers (ON) are shown in Figure S2; NBO charges (in |e|) on 4s obtained using the ωB97X–D functional with SDD and 6–311++G (2d, 2p) basis sets are shown in Figure S3; the IR vibrational spectrum and Raman spectrum of 4s obtained using the ωB97X–D functional with SDD and 6–311++G (2d, 2p) basis sets are shown in Figure S4; the isomers of Fe C 4 H 2 2 + in the triplet and quintet electronic states with ZPVE-corrected relative energies (in kcal mol−1), dipole moments (in Debye), and the number of imaginary frequencies (NImag) obtained using the (U)ωB97X–D functional with SDD and 6–311++G (2d, 2p) basis sets in Figures S5 and S6, respectively, total energy (in a.u), zero-point correction (in a.u), ZPVE-corrected total energy (E+ZPVE; in a.u), relative energy (ΔE + ZPVE; in kcal mol–1), dipole moment (in Debye), and the number of imaginary frequencies (NImag) of Fe C 4 H 2 2 + in the singlet electronic state calculated at the ωB97X–D functional with SDD and 6–311++G (2d, 2p) basis sets are listed in Table S1, and triplet and quintet electronic states calculated using ROHF with SDD and 6–311++G (2d, 2p) basis sets are listed in Tables S2 and S3, respectively; the Cartesian coordinates of all the isomers of Fe C 4 H 2 2 + in the singlet, triplet, and quintet electronic states are listed in Tables S4, S5, and S6, respectively; and the total energy (in a.u), point group, zero-point correction (in a.u), ZPVE-corrected total energy (E + ZPVE; in a.u), relative energy (ΔE + ZPVE; in kcal mol−1), dipole moment (in Debye), the number of imaginary frequencies (NImag), the expectation value of the total spin, <S2>, and calculated %error for the spin contamination of Fe C 4 H 2 2 + in their corresponding triplet and quintet electronic states calculated using (U)ωB97X–D functional with SDD and 6-311++G (2d, 2p) basis sets are listed in Tables S7 and S8, respectively.

Author Contributions

Conceptualization, V.S.T., V.C. and K.T. (Krishnan Thirumoorthy); Investigation, S.S., V.S.T., V.C., K.T. (Kandasamy Thirunavukkarsu) and K.T. (Krishnan Thirumoorthy); Methodology, S.S., V.S.T., V.C., K.T. (Kandasamy Thirunavukkarsu) and K.T. (Krishnan Thirumoorthy); Supervision, V.S.T., V.C., K.T. (Kandasamy Thirunavukkarsu) and K.T. (Krishnan Thirumoorthy); Visualization, S.S. and K.T. (Krishnan Thirumoorthy); Writing—Original Draft, S.S.; Writing—Review and Editing, V.S.T., V.C. and K.T. (Krishnan Thirumoorthy). All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data are available in the article or Supplementary Materials.

Acknowledgments

The computational facility provided at the VIT, Vellore, to carry out this work is gratefully acknowledged.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Miralrio, A.; Hernández-Hernández, A.; Pescador-Rojas, J.A.; Sansores, E.; López-Pérez, P.A.; Martínez-Farías, F.; Cortes, E.R. Theoretical Study of the Stability and Properties of Magic Numbers (m = 5, n = 2) and (m = 6, n = 3) of Bimetallic Bismuth-Copper Nanoclusters; Bim Cun. Int. J. Quantum Chem. 2017, 117, e25449. [Google Scholar] [CrossRef]
  2. Billas, I.M.L.; De Heer, W.A.; Chatelain, A. Magnetic Properties of Small Iron Systems: From Ferromagnetic Resonance of Precipitated Particles in Silica to Stern-Gerlach Deflections in Molecular Beam. J. Non Cryst. Solids 1994, 179, 316–323. [Google Scholar] [CrossRef]
  3. Castro, M. The role of the Jahn-teller distortions on the structural, binding, and magnetic properties of small Fen clusters, n ≤ 7. Int. J. Quantum Chem. 1997, 64, 223–230. [Google Scholar] [CrossRef]
  4. Fehlner, T.; Halet, J.F.; Saillard, J.Y. Molecular Clusters: A Bridge to Solid-State Chemistry; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
  5. Li, H.-F.; Li, Z.-Y.; Liu, Q.-Y.; Li, X.-N.; Zhao, Y.-X.; He, S.-G. Methane Activation by Iron-Carbide Cluster Anions FeC6−. J. Phys. Chem. Lett. 2015, 6, 2287–2291. [Google Scholar] [CrossRef] [PubMed]
  6. Allen, M.D.; Pesch, T.C.; Ziurys, L.M. The pure rotational spectrum of FeC (X3Δi). Astrophys. J. 1996, 472, L57. [Google Scholar] [CrossRef]
  7. Chu, C.J.; Kafafi, Z.H.; Margrave, J.L.; Hauge, R.H.; Billups, W.E. Matrix-Isolation Studies of the Reactions of Ground- and Excited-State Atomic Iron with Cyclopropane. Organometallics 2000, 19, 39–48. [Google Scholar] [CrossRef]
  8. Balfour, W.J.; Cao, J.; Prasad, C.V.V.; Qian, C.X.W. Electronic Spectroscopy of Jet-Cooled Iron Monocarbide. The 3Δi←3Δi Transition near 493 nm. J. Chem Phys. 1995, 103, 4046–4051. [Google Scholar] [CrossRef]
  9. Tzeli, D.; Mavridis, A. Accurate Ab Initio Calculations of the Ground States of FeC, FeC+, and FeC−. J. Chem. Phys. 2010, 132, 194312. [Google Scholar] [CrossRef]
  10. Tzeli, D.; Mavridis, A. Theoretical Investigation of Iron Carbide, FeC. J. Chem. Phys. 2002, 116, 4901–4921. [Google Scholar] [CrossRef]
  11. Li, C.G.; Zhang, J.; Zhang, W.Q.; Tang, Y.N.; Ren, B.Z.; Hu, Y.F. First-Principle Study of Structural, Electronic and Magnetic Properties of (FeC)n (n = 1–8) and (FeC)8TM (TM = V, Cr, Mn and Co) Clusters. Sci. Rep. 2017, 7, 17516. [Google Scholar] [CrossRef]
  12. Steglich, M.; Chen, X.; Johnson, A.; Maier, J.P. UV Spectra of Iron-Doped Carbon Clusters FeCn n = 3–6. Int. J. Mass Spectrom. 2014, 365–366, 351–355. [Google Scholar] [CrossRef]
  13. Huisken, F.; Kohn, B.; Alexandrescu, R.; Morjan, I. Reactions of Iron Clusters with Oxygen and Ethylene: Observation of Particularly Stable Species. J. Chem. Phys. 2000, 113, 6579–6584. [Google Scholar] [CrossRef]
  14. Ball, D.W.; Pong, R.G.S.; Kafafi’, Z.H. Reactions of Atomic and Diatomic Iron with Allene in Solid Argon. J. Am. Chem. Soc. 1993, 115, 2864–2870. [Google Scholar] [CrossRef]
  15. Glukhovtsev, M.N.; Bach, R.D.; Nagel, C.J. Performance of the B3LYP/ECP DFT Calculations of Iron-Containing Compounds. J. Phys. Chem. A 1997, 101, 316–323. [Google Scholar] [CrossRef]
  16. Pilgrim, J.S.; Duncan, M.A. Metallo-Carbohedrenes: Chromium, Iron, and Molybdenum Analogs. J. Am. Chem. Soc. 1993, 115, 6958–6961. [Google Scholar] [CrossRef]
  17. Nash, B.K.; Rao, B.K.; Jena, P. Equilibrium Structure and Bonding of Small Iron-Carbon Clusters. J. Chem. Phys. 1996, 105, 11020–11023. [Google Scholar] [CrossRef]
  18. Noya, E.G.; Longo, R.C.; Gallego, L.J. Geometric Structure and Electronic Properties of Neutral and Anionic Fe2C3 and Fe2C4 Clusters, as Obtained by Density-Functional Calculations. J. Chem. Phys. 2004, 120, 2069–2070. [Google Scholar] [CrossRef]
  19. Noya, E.G.; Longo, R.C.; Gallego, L.J. Density-Functional Calculations of the Structures, Binding Energies, and Spin Multiplicities of Fe-C Clusters. J. Chem. Phys. 2003, 119, 11130–11134. [Google Scholar] [CrossRef]
  20. Largo, L.; Barrientos, C.; Redondo, P. Small Iron Doped Carbon Clusters: A Comparison with Early and Late First-Row Transition Metal Doped Clusters. J. Chem. Phys. 2009, 130, 134304. [Google Scholar] [CrossRef]
  21. Zhang, B.; Cao, B.B.; Chen, C.; Zhang, J.; Duan, H.M. Density-Functional Theory Study on Neutral and Charged MnC2 (M = Fe, Co, Ni, Cu; n = 1–5) Clusters. J. Clust. Sci. 2013, 24, 197–207. [Google Scholar] [CrossRef]
  22. Limon, P.; Miralrio, A.; Castro, M. Characterization of Magnetic Series of Iron-Carbon Clusters FeNC0, ±1 (n ≤ 13). J. Phys. Chem. C 2020, 124, 9484–9495. [Google Scholar] [CrossRef]
  23. Zhang, Z.X.; Cao, B.B.; Duan, H.M. Density-Functional Calculations of MnC(M = Fe, Co, Ni, Cu, n = 1–6) Clusters. J. Mol. Struct. Theochem 2008, 863, 22–27. [Google Scholar] [CrossRef]
  24. Wang, L.-S.; Li, X. Vibrationally Resolved Photoelectron Spectroscopy of the First Row Transition Metal and C3 Clusters: MC3− (M=Sc, V, Cr, Mn, Fe, Co, and Ni). J. Chem. Phys. 2000, 112, 3602–3608. [Google Scholar] [CrossRef]
  25. Lebrilla, C.B.; Drewello, T.; Schwarz, H. Formation and Detection of Neutral FeCHx (x = 0–3) Using Neutralization-Reionization Mass Spectrometry (NRMS). Organometallics. 1987, 6, 2268–2270. [Google Scholar] [CrossRef]
  26. Fan, J.; Wang, L.-S. A Study of FeC2 and FeC2H by Anion Photoelectron Spectroscopy. J. Phys. Chem. 1994, 98, 11814–11817. [Google Scholar] [CrossRef]
  27. Husband, J.; Aguirre, F.; Thompson, C.J.; Laperle, C.M.; Metz, R.B. Photofragment Spectroscopy of FeCH2+, CoCH2+, and NiCH2+ near the M+-CH2 Dissociation Threshold. J. Phys. Chem. A 2000, 104, 2020–2024. [Google Scholar] [CrossRef]
  28. Drechsler, G.; Boesl, U. Mass Selective Photodetachment Photoelectron Spectroscopy: Small Transition Metal (Fe, Ni) Carbon Hydrogen Compounds. Int. J. Mass Spectrom. 2003, 228, 1067–1082. [Google Scholar] [CrossRef]
  29. Chang, C.; Patzer, A.B.C.; Kegel, W.H.; Chandra, S. Small Fe Bearing Ring Molecules of Possible Astrophysical Interest: Molecular Properties and Rotational Spectra. Astrophys. Space Sci. 2013, 347, 315–325. [Google Scholar] [CrossRef]
  30. Guo, B.C.; Kerns, K.P.; Castleman, A.W., Jr. Ti8C12+-metallo-carbohedrenes: A New Class of Molecular Clusters? Science 1992, 255, 1411–1413. [Google Scholar] [CrossRef]
  31. Ryzhkov, M.V.; Delley, B. Geometry, electronic structure, and magnetic ordering of iron-carbon nanoparticles. Theor. Chem. Acc. 2012, 131, 1144. [Google Scholar] [CrossRef]
  32. Ryzhkov, M.V.; Ivanovskii, A.L.; Delley, B.T. Electronic Structure and Geometry Optimization of Nanoparticles Fe2C, FeC2, Fe3C, FeC3 and Fe2C2. Chem Phys Lett. 2005, 404, 400–408. [Google Scholar] [CrossRef]
  33. Hensley, B.S.; Draine, B.T. Thermodynamics and charging of interstellar iron nanoparticles. Astrophys. J. 2017, 834, 134. [Google Scholar] [CrossRef]
  34. Rohmer, M.M.; Bénard, M.; Poblet, J.-M. Structure, Reactivity, and Growth Pathways of Metallocarbohedrenes M8C12 and Transition Metal/Carbon Clusters and Nanocrystals: A Challenge to Computational Chemistry. Chem. Rev. 2000, 100, 495–542. [Google Scholar] [CrossRef]
  35. Geng, C.; Li, J.; Weiske, T.; Schwarz, H. A Reaction-Induced Localization of Spin Density Enables Thermal C−H Bond Activation of Methane by Pristine FeC4+. Chem. A Eur. J. 2019, 25, 12940–12945. [Google Scholar] [CrossRef]
  36. Hu, Y.; Jensen, J.O.; Zhang, W.; Cleemann, L.N.; Xing, W.; Bjerrum, N.J.; Li, Q. Hollow Spheres of Iron Carbide Nanoparticles Encased in Graphitic Layers as Oxygen Reduction Catalysts. Angew. Chem. Int. Ed. 2014, 53, 3675–3679. [Google Scholar] [CrossRef]
  37. Li, S.; Yang, J.; Song, C.; Zhu, Q.; Xiao, D.; Ma, D. Iron Carbides: Control Synthesis and Catalytic Applications in COx Hydrogenation and Electrochemical HER. Adv. Mater. 2019, 31, e1901796. [Google Scholar] [CrossRef]
  38. Wang, X.; Zhu, K.; Ju, Y.; Li, Y.; Li, W.; Xu, J.; Hou, Y. Iron Carbides: Magic Materials with Magnetic and Catalytic Properties. J. Magn. Magn. Mater. 2019, 489, 165432. [Google Scholar] [CrossRef]
  39. Li, Y.; Li, Z.; Ahsen, A.; Lammich, L.; Mannie, G.J.A.; Niemantsverdriet, J.W.H.; Lauritsen, J.V. Atomically Defined Iron Carbide Surface for Fischer-Tropsch Synthesis Catalysis. ACS Catal. 2019, 9, 1264–1273. [Google Scholar] [CrossRef]
  40. Miyaoka, H.; Ichikawa, T.; Fujii, T.; Ishida, W.; Isobe, S.; Fuji, H.; Kojima, Y. Anomalous Hydrogen Absorption on Non-Stoichiometric Iron-Carbon Compound. J. Alloys Compd. 2010, 507, 547–550. [Google Scholar] [CrossRef]
  41. Wu, X.; Dong, J.; Qiu, M.; Li, Y.; Zhang, Y.; Zhang, H.; Zhang, J. Subnanometer Iron Clusters Confined in a Porous Carbon Matrix for Highly Efficient Zinc-Air Batteries. Nanoscale Horiz. 2020, 5, 359–365. [Google Scholar] [CrossRef]
  42. Fan, D.; Chen, C.; Lu, S.; Li, X.; Jiang, M.; Hu, X. Highly Stable Two-Dimensional Iron Monocarbide with Planar Hypercoordinate Moiety and Superior Li-Ion Storage Performance. ACS Appl. Mater. Interfaces. 2020, 12, 30297–30303. [Google Scholar] [CrossRef]
  43. Xiang, T.; Chen, Z.; Rao, Z.; Yan, M.; Feng, Z.; Li, X.; Yang, H.; Huang, J.; Shen, X. Hierarchical Fe/Fe3C/C Nanofibers as Anodes for High Capacity and Rate in Lithium Ion Batteries. Ionics 2021, 27, 3663–3669. [Google Scholar] [CrossRef]
  44. Monkhorst, H.J. Activation Energy for Interconversion of Enantiomers Containing an Asymmetric Carbon Atom without Breaking Bonds. Chem. Commun. 1968, 18, 1111–1112. [Google Scholar] [CrossRef]
  45. Erker, G. Planar-Tetracoordinate Carbon: Making Stable Anti-van’t Hoff/LeBel Compounds. Comments Inorg. Chem. 1992, 13, 111–131. [Google Scholar] [CrossRef]
  46. Hoffmann, R.; Alder, R.W.; Wilcox, C.F., Jr. Planar tetracoordinate carbon. J. Am. Chem. Soc. 1970, 92, 4992–4993. [Google Scholar] [CrossRef]
  47. Ravell, E.; Jalife, S.; Barroso, J.; Orozco-Ic, M.; Hernández-Juárez, G.; Ortiz-Chi, F.; Pan, S.; Cabellos, J.L.; Merino, G. Structure and Bonding in CE5−(E=Al-Tl) Clusters: Planar Tetracoordinate Carbon versus Pentacoordinate Carbon. Chem. Asian J. 2018, 13, 1467–1473. [Google Scholar] [CrossRef]
  48. Sarkar, P.; Thirumoorthy, K.; Anoop, A.; Thimmakondu, V.S. Planar Pentacoordinate Carbon in [XC7H2]2+ (X = Be and Mg) and Its Derivatives. Phys. Chem. Chem. Phys. 2022, 24, 27606–27611. [Google Scholar] [CrossRef]
  49. Leyva-Parra, L.; Diego, L.; Yañez, O.; Inostroza, D.; Barroso, J.; Vásquez-Espinal, A.; Merino, G.; Tiznado, W. Planar Hexacoordinate Carbons: Half Covalent, Half Ionic. Angew. Chem. Int. Ed. 2021, 60, 8700–8704. [Google Scholar] [CrossRef]
  50. Jimenez-Halla, J.O.C.; Wu, Y.-B.; Wang, Z.-X.; Islas, R.; Heine, T.; Merino, G. CAl4Be and CAl3Be2-: Global Minima with a Planar Pentacoordinate Carbon Atom. Chem. Commun. 2010, 46, 8776–8778. [Google Scholar] [CrossRef] [PubMed]
  51. Yañez, O.; Báez-Grez, R.; Garza, J.; Pan, S.; Barroso, J.; Vásquez-Espinal, A.; Merino, G.; Tiznado, W. Embedding a Planar Hypercoordinate Carbon Atom into a [4n+2] π-System. ChemPhysChem 2020, 21, 145–148. [Google Scholar] [CrossRef]
  52. Wang, L.-M.; Huang, W.; Averkiev, B.B.; Boldyrev, A.I.; Wang, L.-S. CB7-: Experimental and Theoretical Evidence against Hypercoordinate Planar Carbon. Angew. Chem. Int. Ed. 2007, 46, 4550–4553. [Google Scholar] [CrossRef]
  53. Malhan, A.H.; Thimmakondu, V.S.; Thirumoorthy, K. Five Bonds to Carbon through Tri-Coordination in Al3C3−/0. Chemistry 2023, 5, 1113–1123. [Google Scholar] [CrossRef]
  54. Malhan, A.H.; Thirumoorthy, K. Global minimum and a heap of low-lying isomers with planar tetracoordinate carbon in CAl3MgH2-system. Phys. Chem. Chem. Phys. 2024, 26, 3804–3809. [Google Scholar] [CrossRef]
  55. Cui, Z.-H.; Contreras, M.; Ding, Y.-H.; Merino, G. Planar Tetracoordinate Carbon versus Planar Tetracoordinate Boron: The Case of CB4 and Its Cation. J. Am. Chem. Soc. 2011, 133, 13228–13231. [Google Scholar] [CrossRef] [PubMed]
  56. Collins, J.B.; Dill, J.D.; Jemmis, E.D.; Apeloig, Y.; Schleyer, P.V.R.; Seeger, R.; Pople, J.A. Stabilization of planar tetracoordinate carbon. J. Am. Chem. Soc. 1976, 98, 5419–5427. [Google Scholar] [CrossRef]
  57. Thimmakondu, V.S.; Thirumoorthy, K. Si3C2H2 Isomers with a Planar Tetracoordinate Carbon or Silicon Atom(s). Comput. Theor. Chem. 2019, 1157, 40–46. [Google Scholar] [CrossRef]
  58. Das, P.; Khatun, M.; Anoop, A.; Chattaraj, P.K. CSinGe4−n2+ (n = 1–3): Prospective Systems Containing Planar Tetracoordinate Carbon (ptC). Phys. Chem. Chem. Phys. 2022, 24, 16701–16711. [Google Scholar] [CrossRef]
  59. Bai, L.-X.; Barroso, J.; Orozco-Ic, M.; Ortiz-Chi, F.; Guo, J.-C.; Merino, G. CAl11−: A Molecular Rotor with a Quasi-Planar Tetracoordinate Carbon. Chem. Commun. 2023, 59, 4966–4969. [Google Scholar] [CrossRef]
  60. Malhan, A.H.; Sobinson, S.; Job, N.; Shajan, S.; Mohanty, S.P.; Thimmakondu, V.S.; Thirumoorthy, K. Al2C4H2 Isomers with the Planar Tetracoordinate Carbon (PtC)/Aluminum (PtAl). Atoms 2022, 10, 112. [Google Scholar] [CrossRef]
  61. Job, N.; Khatun, M.; Thirumoorthy, K.; Sasanka Sankhar Reddy, C.H.; Chandrasekaran, V.; Anoop, A.; Thimmakondu, V.S. Cal4mg0/−: Global Minima with a Planar Tetracoordinate Carbon Atom. Atoms 2021, 9, 24. [Google Scholar] [CrossRef]
  62. Thirumoorthy, K.; Chandrasekaran, V.; Cooksy, A.L.; Thimmakondu, V.S. Kinetic Stability of Si2C5H2 Isomer with a Planar Tetracoordinate Carbon Atom. Chemistry 2020, 3, 13–27. [Google Scholar] [CrossRef]
  63. Xu, J.; Zhang, X.; Yu, S.; Ding, Y.-H.; Bowen, K.H. Identifying the Hydrogenated Planar Tetracoordinate Carbon: A Combined Experimental and Theoretical Study of CAl4H and CAl4H−. J. Phys. Chem. Lett. 2017, 8, 2263–2267. [Google Scholar] [CrossRef] [PubMed]
  64. Ebner, F.; Greb, L. Calix[4]Pyrrole Hydridosilicate: The Elusive Planar Tetracoordinate Silicon Imparts Striking Stability to Its Anionic Silicon Hydride. J. Am. Chem. Soc. 2018, 140, 17409–17412. [Google Scholar] [CrossRef] [PubMed]
  65. Li, X.; Wang, L.-S.; Boldyrev, A.I.; Simons, J. Tetracoordinated Planar Carbon in the Al4C- Anion. A Combined Photoelectron Spectroscopy and Ab Initio Study. J. Am. Chem. Soc. 1999, 121, 6033–6038. [Google Scholar] [CrossRef]
  66. Lein, M.; Frunzke, J.; Frenking, G. A Novel Class of Aromatic Compounds: Metal-Centered Planar Cations [Fe(Sb5)]+ and [Fe(Bi5)]+. Angew. Chem. Int. Ed. 2003, 42, 1303–1306. [Google Scholar] [CrossRef]
  67. Tanaka, H.; Neukermans, S.; Janssens, E.; Silverans, R.E.; Lievens, P. σ Aromaticity of the Bimetallic Au5Zn+ Cluster. J. Am. Chem. Soc. 2003, 125, 2862–2863. [Google Scholar] [CrossRef]
  68. Neukermans, S.; Janssens, E.; Tanaka, H.; Silverans, R.E.; Lievens, P. Element- and Size-Dependent Electron Delocalization in AuNX+ Clusters (X = Sc, Ti, V, Cr, Mn, Fe, Co, Ni). Phys. Rev. Lett. 2003, 90, 033401. [Google Scholar] [CrossRef]
  69. Janssens, E.; Tanaka, H.; Neukermans, S.; Silverans, R.E.; Lievens, P. Electron Delocalization in AuNXM (X=Sc, Ti, Cr, Fe) Clusters: A Density Functional Theory and Photofragmentation Study. Phys. Rev. B 2004, 69, 085402. [Google Scholar] [CrossRef]
  70. Hou, X.-J.; Janssens, E.; Lievens, P.; Nguyen, M.T. Theoretical Study of the Geometric and Electronic Structure of Neutral and Anionic Doped Silver Clusters, Ag5X0,− with X = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni. J. Chem. Phys. 2006, 330, 365–379. [Google Scholar] [CrossRef]
  71. Janssens, E.; Hou, X.J.; Nguyen, M.T.; Lievens, P. The Geometric, Electronic, and Magnetic Properties of Ag5X + (X=Sc, Ti, V, Cr, Mn, Fe, Co, and Ni) Clusters. J. Chem. Phys. 2006, 124, 184319. [Google Scholar] [CrossRef]
  72. Li, X.; Kiran, B.; Cui, L.-F.; Wang, L.-S. Magnetic Properties in Transition-Metal-Doped Gold Clusters: M@Au6 (M = Ti, V, Cr). Phys. Rev. Lett. 2005, 95, 253401. [Google Scholar] [CrossRef]
  73. Zhang, M.; He, L.-M.; Zhao, L.-X.; Feng, X.-J.; Luo, Y.-H. Tuning Magnetic Moments by 3d Transition-Metal-Doped Au6 Clusters. J. Phys. Chem. C 2009, 113, 6491–6496. [Google Scholar] [CrossRef]
  74. Höltzl, T.; Janssens, E.; Veldeman, N.; Veszprémi, T.; Lievens, P.; Nguyen, M.T. The Cu7Sc Cluster Is a Stable σ-Aromatic Seven-Membered Ring. ChemPhysChem. 2008, 9, 833–838. [Google Scholar] [CrossRef]
  75. Pu, Z.; Ito, K.; Schleyer, P.V.R.; Li, Q.-S. Planar Hepta-, Octa-, Nona-, and Decacoordinate First Row d-Block Metals Enclosed by Boron Rings. Inorg. Chem. 2009, 48, 10679–10686. [Google Scholar] [CrossRef] [PubMed]
  76. Ito, K.; Pu, Z.; Li, Q.-S.; Schleyer, P.V.R. Cyclic Boron Clusters Enclosing Planar Hypercoordinate Cobalt, Iron, and Nickel. Inorg. Chem. 2008, 47, 10906–10910. [Google Scholar] [CrossRef]
  77. Romanescu, C.; Galeev, T.R.; Sergeeva, A.P.; Li, W.-L.; Wang, L.-S.; Boldyrev, A.I. Experimental and Computational Evidence of Octa- and Nona-Coordinated Planar Iron-Doped Boron Clusters: Fe©B8- and Fe©B9-. J. Organomet. Chem. 2012, 721–722, 148–154. [Google Scholar] [CrossRef]
  78. Zhang, H.; Li, Y.; Hou, J.; Tu, K.; Chen, Z. FeB6 Monolayers: The Graphene-like Material with Hypercoordinate Transition Metal. J. Am. Chem. Soc. 2016, 138, 5644–5651. [Google Scholar] [CrossRef]
  79. Zhao, Y.; Liu, Q.; Xing, J.; Jiang, X.; Zhao, J. FeSi2: A Two-Dimensional Ferromagnet Containing Planar Hexacoordinate Fe Atoms. Nanoscale Adv. 2022, 4, 600–607. [Google Scholar] [CrossRef] [PubMed]
  80. Shajan, S.; Guo, J.-C.; Sinjari, A.; Thirumoorthy, K.; Thimmakondu, V.S. Pentacoordinate Carbon Atoms in a Ferrocene Dication Derivative—[Fe(Si2-η5-C5H2)2]2+. Chemistry 2022, 4, 1092–1100. [Google Scholar] [CrossRef]
  81. Kalita, A.J.; Baruah, I.; Sarmah, K.; Borah, R.R.; Yashmin, F.; Guha, A.K. Planar Pentacoordinate Zinc Group Elements Stabilized by Multicentric Bonds. Inorg. Chem. 2022, 61, 1259–1263. [Google Scholar] [CrossRef]
  82. Bai, L.-X.; Guo, J.-C. σ-Aromatic MAl6S6 (M = Ni, Pd, Pt) Stars Containing Planar Hexacoordinate Transition Metals. Molecules 2023, 28, 942. [Google Scholar] [CrossRef]
  83. Killian, T.C.; Gottlieb, C.A.; Gottlieb, E.W.; Vrtilek, J.M.; Thaddeus, P. Laboratory Detection of a Second Carbon Chain Carbene—Butatrienylidene, H2CCCC. Astrophys. J. 1990, 365, L89–L92. [Google Scholar] [CrossRef]
  84. McCarthy, M.C.; Travers, M.J.; Kovács, A.; Chen, W.; Novick, S.E.; Gottlieb, C.A.; Thaddeus, P. Detection and characterization of the cumulene carbenes H2C5 and H2C6. Science 1997, 275, 518–520. [Google Scholar] [CrossRef]
  85. McCarthy, M.C.; Travers, M.J.; Kovács, A.; Gottlieb, C.A.; Thaddeus, P. Eight new carbon chain molecules. Astrophys. J. Suppl. Ser. 1997, 113, 105. [Google Scholar] [CrossRef]
  86. Maier, G.; Reisenauer, H.P.; Schwab, W.; Carsky, P.; Hess, B.A., Jr.; Schaad, L.J. Vinylidene carbene: A new C3H2 species. J. Am. Chem. Soc. 1987, 109, 5183–5188. [Google Scholar] [CrossRef]
  87. McCarthy, M.C.; Travers, M.J.; Gottlieb, C.A.; Thaddeus, P. Laboratory detection of the ring-chain molecule C7H2. Astrophys. J. 1997, 483, L139. [Google Scholar] [CrossRef]
  88. Apponi, A.J.; McCarthy, M.C.; Gottlieb, C.A.; Thaddeus, P. Laboratory detection of four new cumulene carbenes: H2C7, H2C8, H2C9, and D2C10. Astrophys. J. 2000, 530, 357. [Google Scholar] [CrossRef]
  89. Kawaguchi, K.; Kaifu, N.; Ohishi, M.; Ishikawa, S.I.; Hirahara, Y.; Yamamoto, S.; Irvine, W.M. Observations of cumulene carbenes, H2CCCC and H2CCC, in TMC-1. Publ. Astron. Soc. Jpn. 1991, 43, 607–619. [Google Scholar]
  90. Cabezas, C.; Tercero, B.; Agúndez, M.; Marcelino, N.; Pardo, J.R.; de Vicente, P.; Cernicharo, J. Cumulene carbenes in TMC-1: Astronomical discovery of l-H2C5. Astron. Astrophys. 2021, 650, L9. [Google Scholar] [CrossRef] [PubMed]
  91. Langer, W.D.; Velusamy, T.; Kuiper, T.B.H.; Peng, R.M.M.C.; McCarthy, M.C.; Travers, M.J.; Thaddeus, P. First astronomical detection of the cumulene carbon chain molecule H2C6 in TMC-1. Astrophys. J. 1997, 480, L63. [Google Scholar] [CrossRef] [PubMed]
  92. Kimura, Y.; Tanaka, K.K.; Nozawa, T.; Takeuchi, S.; Inatomi, Y. Pure Iron Grains Are Rare in the Universe. Sci. Adv. 2017, 3, e1601992. [Google Scholar] [CrossRef]
  93. Koelemay, L.A.; Ziurys, L.M. Elusive Iron: Detection of the FeC Radical (X3Δi) in the Envelope of IRC + 10216. Astrophys. J. Lett. 2023, 958, L6. [Google Scholar] [CrossRef]
  94. Hawrelak, E.J.; Bernskoetter, W.H.; Lobkovsky, E.; Yee, G.T.; Bill, E.; Chirik, P.J. Square planar vs tetrahedral geometry in four coordinate iron (II) complexes. Inorg. Chem. 2005, 44, 3103–3111. [Google Scholar] [CrossRef]
  95. Ghosh, A.K.; Neogi, S.; Ghosh, P.; Hajra, A. Synergistic Photoredox and Iron (II) Catalyzed Carbophosphorothiolation of Vinyl Arenes. Adv. Synth. Catal. 2023, 365, 2271–2278. [Google Scholar] [CrossRef]
  96. Varga, Z.; Verma, P.; Truhlar, D.G. Hyper open-shell states: The lowest excited spin states of o atom, Fe2+ ion, and FeF2. J. Am. Chem. Soc 2017, 139, 12569–12578. [Google Scholar] [CrossRef]
  97. Athanasopoulos, E.; Conradie, J. Substituent effect on the oxidation and reduction of electronically altered iron (II)-terpyridine derivatives-DFT study. Inorganica Chim. Acta 2023, 555, 121599. [Google Scholar] [CrossRef]
  98. Chai, J.D.; Head-Gordon, M. Long-Range Corrected Hybrid Density Functionals with Damped Atom-Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
  99. Young, D. Computational Chemistry: A Practical Guide for Applying Techniques to Real World Problems; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
  100. Fuentealba, P.; Stoll, H.; Von Szentpaly, L.; Schwerdtfeger, P.; Preuss, H. On the reliability of semi-empirical pseudopotentials: Simulation of Hartree-Fock and Dirac-Fock results. J. Phys. B At. Mol. Phys. 1983, 16, L323. [Google Scholar] [CrossRef]
  101. Fuentealba, P.; Preuss, H.; Stoll, H.; Von Szentpály, L. A proper account of core-polarization with pseudopotentials: Single valence-electron alkali compounds. Chem. Phys. Lett. 1982, 89, 418–422. [Google Scholar] [CrossRef]
  102. Pershina, V. Electronic Structure and Properties of Superheavy Elements. Nucl. Phys. A 2014, 944, 578–613. [Google Scholar] [CrossRef]
  103. Clark, T.; Chandrasekhar, J.; Spitznagel, G.W.; Von Ragué Schleyer, P. Efficient Diffuse Function-Augmented Basis Sets for Anion Calculations. III. The 3-21+G Basis Set for First-Row Elements, Li-F. J. Comput. Chem. 1983, 4, 294–301. [Google Scholar] [CrossRef]
  104. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision B.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  105. Glendening, E.D.; Weinhold, F. Natural resonance theory: I. General formalism. J. Comput. Chem. 1998, 19, 593–609. [Google Scholar] [CrossRef]
  106. Reed, A.E.; Weinstock, R.B.; Weinhold, F. Natural Population Analysis. J. Chem. Phys. 1985, 83, 735–746. [Google Scholar] [CrossRef]
  107. Zubarev, D.Y.; Boldyrev, A.I. Developing Paradigms of Chemical Bonding: Adaptive Natural Density Partitioning. Phys. Chem. Chem. Phys. 2008, 10, 5207–5217. [Google Scholar] [CrossRef]
  108. Zubarev, D.Y.; Boldyrev, A.I. Revealing Intuitively Assessable Chemical Bonding Patterns in Organic Aromatic Molecules via Adaptive Natural Density Partitioning. J. Org. Chem. 2008, 73, 9251–9258. [Google Scholar] [CrossRef] [PubMed]
  109. Becke, A.D.; Edgecombe, K.E. A Simple Measure of Electron Localization in Atomic and Molecular Systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
  110. Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
  111. Limon, P.; Miralrio, A.; Castro, M. Small Binary Iron-Carbon Clusters with Persistent High Magnetic Moments. A Theoretical Characterization. Int. J. Quantum Chem. 2019, 119, e25932. [Google Scholar] [CrossRef]
  112. Redondo, P.; Largo, L.; Barrientos, C. Charged FeCn Clusters: A Comparison with TMCn+/TMCn− (TM = Sc, Ti, V, Co and Zn, n = 1–8) Systems. J. Chem. Phys. 2009, 364, 1–13. [Google Scholar] [CrossRef]
  113. Fan, J.; Lou, L.; Wang, L.-S. FeCn− and FeCnH− (n = 3,4): A Photoelectron Spectroscopic and Density Functional Study. J. Chem. Phys. 1995, 102, 2701–2707. [Google Scholar] [CrossRef]
Atoms 12 00011 g001
Figure 1. Ten low-lying isomers of Fe C 4 H 2 2 + in their corresponding singlet electronic state with the ZPVE-corrected relative energies (in kcal mol−1), point groups, dipole moments (in Debye), and the number of imaginary frequencies (NImag) obtained using the ωB97X–D functional with SDD and 6–311++G (2d, 2p) basis sets.
Figure 1. Ten low-lying isomers of Fe C 4 H 2 2 + in their corresponding singlet electronic state with the ZPVE-corrected relative energies (in kcal mol−1), point groups, dipole moments (in Debye), and the number of imaginary frequencies (NImag) obtained using the ωB97X–D functional with SDD and 6–311++G (2d, 2p) basis sets.
Atoms 12 00011 g001
Atoms 12 00011 g002
Figure 2. The isomers of Fe C 4 H 2 2 + in their corresponding (a) triplet and (b) quintet electronic states with the ZPVE-corrected relative energies (in kcal mol−1), point groups, dipole moments (in Debye), and the number of imaginary frequencies (NImag) obtained using the ROHF method with SDD and 6–311++G (2d, 2p) basis sets.
Figure 2. The isomers of Fe C 4 H 2 2 + in their corresponding (a) triplet and (b) quintet electronic states with the ZPVE-corrected relative energies (in kcal mol−1), point groups, dipole moments (in Debye), and the number of imaginary frequencies (NImag) obtained using the ROHF method with SDD and 6–311++G (2d, 2p) basis sets.
Atoms 12 00011 g002
Atoms 12 00011 g003
Figure 3. (a) The top, front, and side views of the ptFe, 4s; (b) The bond lengths (in Å, red) and the Wiberg bond indices (in blue) of 4s obtained using the ωB97X–D functional with SDD and 6–311++G (2d, 2p) basis sets.
Figure 3. (a) The top, front, and side views of the ptFe, 4s; (b) The bond lengths (in Å, red) and the Wiberg bond indices (in blue) of 4s obtained using the ωB97X–D functional with SDD and 6–311++G (2d, 2p) basis sets.
Atoms 12 00011 g003
Atoms 12 00011 g004
Figure 4. Molecular orbitals of 4s obtained using the ωB97X–D functional with SDD and 6–311++G (2d, 2p) basis sets.
Figure 4. Molecular orbitals of 4s obtained using the ωB97X–D functional with SDD and 6–311++G (2d, 2p) basis sets.
Atoms 12 00011 g004
Atoms 12 00011 g005
Figure 5. AdNDP bonding patterns of 4s with occupation numbers (ONs) were obtained using the ωB97X–D functional with SDD and 6–311++G (2d, 2p) basis sets.
Figure 5. AdNDP bonding patterns of 4s with occupation numbers (ONs) were obtained using the ωB97X–D functional with SDD and 6–311++G (2d, 2p) basis sets.
Atoms 12 00011 g005
Atoms 12 00011 g006
Figure 6. Color-filled map of the ELF and the contour map of the Laplacian of electron density (Δ2ρ(r)) for 4s obtained using the ωB97X–D functional with SDD and 6–311++G (2d, 2p) basis sets.
Figure 6. Color-filled map of the ELF and the contour map of the Laplacian of electron density (Δ2ρ(r)) for 4s obtained using the ωB97X–D functional with SDD and 6–311++G (2d, 2p) basis sets.
Atoms 12 00011 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Shajan, S.; Thirunavukkarsu, K.; Chandrasekaran, V.; Thimmakondu, V.S.; Thirumoorthy, K. FeC4H22+ Encompassing Planar Tetracoordinate Iron: Structure and Bonding Patterns. Atoms 2024, 12, 11. https://doi.org/10.3390/atoms12020011

AMA Style

Shajan S, Thirunavukkarsu K, Chandrasekaran V, Thimmakondu VS, Thirumoorthy K. FeC4H22+ Encompassing Planar Tetracoordinate Iron: Structure and Bonding Patterns. Atoms. 2024; 12(2):11. https://doi.org/10.3390/atoms12020011

Chicago/Turabian Style

Shajan, Shilpa, Kandasamy Thirunavukkarsu, Vijayanand Chandrasekaran, Venkatesan S. Thimmakondu, and Krishnan Thirumoorthy. 2024. "FeC4H22+ Encompassing Planar Tetracoordinate Iron: Structure and Bonding Patterns" Atoms 12, no. 2: 11. https://doi.org/10.3390/atoms12020011

APA Style

Shajan, S., Thirunavukkarsu, K., Chandrasekaran, V., Thimmakondu, V. S., & Thirumoorthy, K. (2024). FeC4H22+ Encompassing Planar Tetracoordinate Iron: Structure and Bonding Patterns. Atoms, 12(2), 11. https://doi.org/10.3390/atoms12020011

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop