Calculation of the Breit–Rosenthal Effect in Bi I
Abstract
:1. Introduction
2. Method
The States Studied in Bi
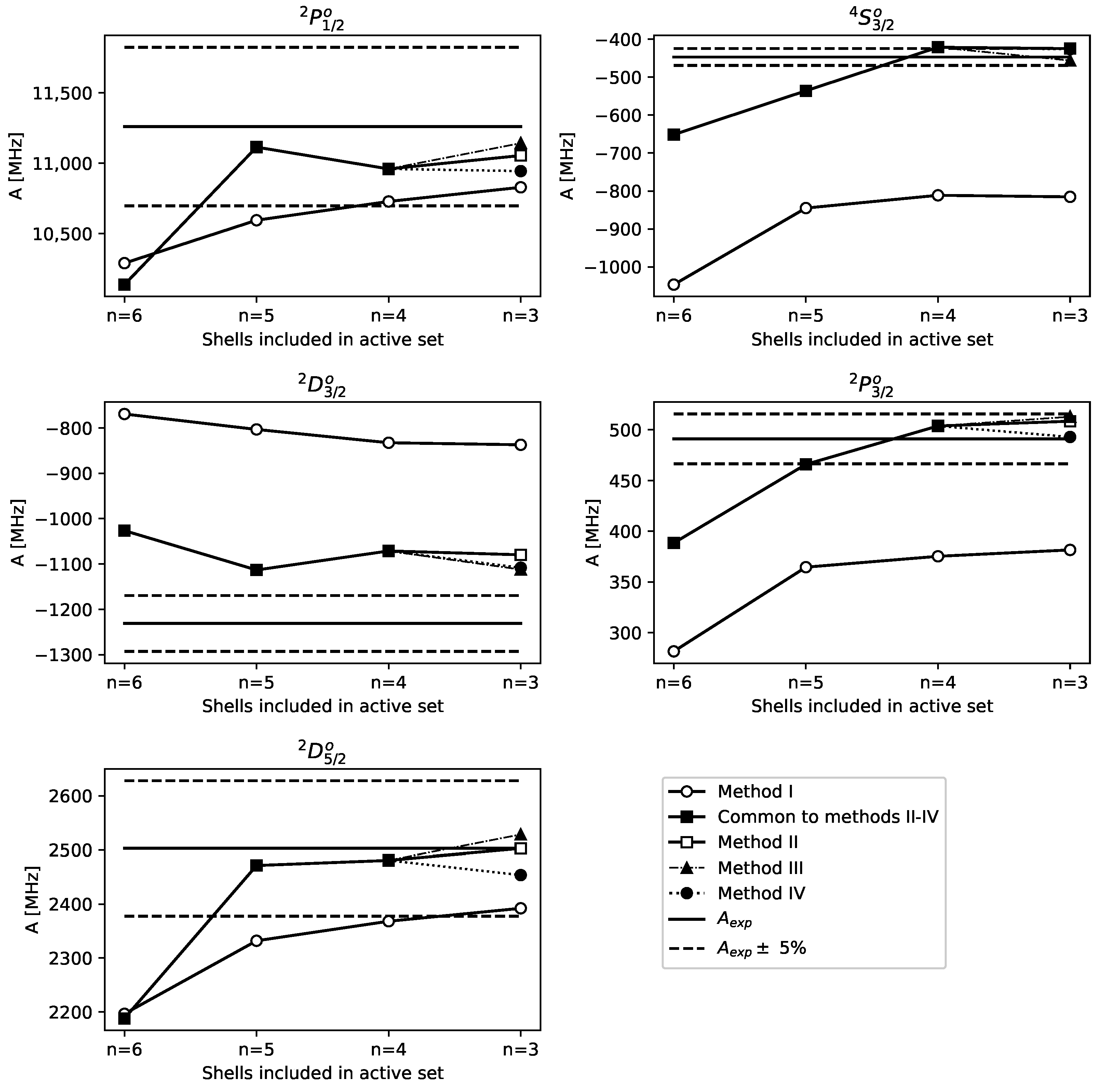
3. Calculations
Calculation of BR Effect
4. Systematics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rosenthal, J.E.; Breit, G. The Isotope Shift in Hyperfine Structure. Phys. Rev. 1932, 41, 459–470. [Google Scholar] [CrossRef]
- Bohr, A.; Weisskopf, V. The influence of nuclear structure on the hyperfine structure of heavy elements. Phys. Rev. 1950, 77, 94. [Google Scholar] [CrossRef]
- Persson, J. Table of hyperfine anomaly in atomic systems—2023. At. Data Nucl. Data Tables 2023, 154, 101589. [Google Scholar] [CrossRef]
- Heggset, T.; Persson, J.R. Calculation of the Differential Breit–Rosenthal Effect in the 6 s 6 p 3 P 1, 2 States of Hg. Atoms 2020, 8, 86. [Google Scholar] [CrossRef]
- Karlsen, M.K.; Persson, J.R. Calculation of the Differential Breit-Rosenthal Effect in Pb. Atoms 2024, 12, 5. [Google Scholar] [CrossRef]
- Rosenberg, H.; Stroke, H. Effect of a diffuse nuclear charge distribution on the hyperfine-structure interaction. Phys. Rev. A 1972, 5, 1992. [Google Scholar] [CrossRef]
- Angeli, I.; Marinova, K. Table of experimental nuclear ground state charge radii: An update. At. Data Nucl. Data Tables 2013, 99, 69–95. [Google Scholar] [CrossRef]
- Fischer, C.F.; Gaigalas, G.; Jönsson, P.; Bieron, J. GRASP2018—A Fortran 95 version of the general relativistic atomic structure package. Comput. Phys. Commun. 2019, 237, 184–187. [Google Scholar] [CrossRef]
- Jönsson, P.; Godefroid, M.; Gaigalas, G.; Ekman, J.; Grumer, J.; Li, W.; Li, J.; Brage, T.; Grant, I.P.; Bieroń, J.; et al. An Introduction to Relativistic Theory as Implemented in GRASP. Atoms 2023, 11, 7. [Google Scholar] [CrossRef]
- Fischer, C.F.; Godefroid, M.; Brage, T.; Jönsson, P.; Gaigalas, G. Advanced multiconfiguration methods for complex atoms: I. Energies and wave functions. J. Phys. At. Mol. Opt. Phys. 2016, 49, 182004. [Google Scholar] [CrossRef]
- Grant, I.P. Relativistic Quantum Theory of Atoms and Molecules: Theory and Computation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; Volume 40. [Google Scholar]
- Røger, T.A. On the Effects of a Non-Infinitesimal Nuclear Charge Distribution on the Hyperfine Spectrum of Bi I. Master’s Thesis, Norwegian University of Science and Technology (NTNU), Trondheim, Norway, 2024. [Google Scholar]
- Stone, N. Table of nuclear magnetic dipole and electric quadrupole moments. At. Data Nucl. Data Tables 2005, 90, 75–176. [Google Scholar] [CrossRef]
- Wilman, S.; Elantkowska, M.; Ruczkowski, J. Fine- and hyperfine structure semi-empirical studies of the neutral and singly ionised bismuth. Determination of the nuclear quadrupole moment of 209Bi. J. Quant. Spectrosc. Radiat. Transf. 2021, 275, 107892. [Google Scholar] [CrossRef]
- Bieroń, J.; Pyykkö, P. Nuclear Quadrupole Moments of Bismuth. Phys. Rev. Lett. 2001, 87, 133003. [Google Scholar] [CrossRef] [PubMed]
- Själander, M.; Jahre, M.; Tufte, G.; Reissmann, N. EPIC: An Energy-Efficient, High-Performance GPGPU Computing Research Infrastructure. arXiv 2019, arXiv:1912.05848. [Google Scholar]

| States | A (MHz) |
|---|---|
| −446.937 (1) | |
| −1231.02 (15) | |
| 2502.86 (1) | |
| 11,260.2 (1.5) | |
| 491.028 (1) |
| MR (6sp SD): | 10,135.23 | −652.01 | −1027.07 | 387.69 | 2186.77 |
| Method I: | 10,829.14 | −815.39 | −837.15 | 381.59 | 2392.19 |
| Method II: | 11,054.69 | −424.78 | −1079.71 | 508.46 | 2502.79 |
| Method III: | 11,142.64 | −456.14 | −1112.18 | 512.90 | 2528.48 |
| Method IV: | 10,944.31 | −426.49 | −1108.15 | 492.92 | 2453.71 |
| Experiment: | 11,260.2 (1.5) | −446.937 (1) | −1231.02 (15) | 491.028 (1) | 2502.86 (1) |
| Method | Number of CSFs | (%) | (%) | (%) |
|---|---|---|---|---|
| MR | 1 | 55.52 | 9.99 | 45.88 |
| I | 6865 | 91.39 | 3.83 | 82.44 |
| II | 41,723 | 13.84 | 0.00 | 12.29 |
| III | 203,299 | 10.92 | 1.02 | 9.65 |
| IV | 29,389 | 11.51 | 0.39 | 9.98 |
| Mthd. | Var. | |||||
|---|---|---|---|---|---|---|
| I | −0.039 | −0.167 | −0.131 | 0.169 | −0.013 | |
| 3.83 | 82.44 | 32.00 | 22.29 | 4.42 | ||
| II | −0.040 | −0.248 | −0.109 | 0.095 | −0.017 | |
| 1.83 | 4.96 | 12.29 | 3.55 | 0.00 | ||
| III | −0.039 | −0.249 | −0.110 | 0.103 | −0.016 | |
| 1.04 | 2.06 | 9.65 | 4.45 | 1.02 | ||
| IV | −0.039 | −0.253 | −0.110 | 0.108 | −0.014 | |
| 2.81 | 4.58 | 9.98 | 0.39 | 1.96 |
| State | |
|---|---|
| −0.250 (13) | |
| −0.110 (11) | |
| −0.016 (2) | |
| −0.039 (2) | |
| 0.102 (6) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Røger, T.A.; Persson, J.R. Calculation of the Breit–Rosenthal Effect in Bi I. Atoms 2024, 12, 72. https://doi.org/10.3390/atoms12120072
Røger TA, Persson JR. Calculation of the Breit–Rosenthal Effect in Bi I. Atoms. 2024; 12(12):72. https://doi.org/10.3390/atoms12120072
Chicago/Turabian StyleRøger, Tarje Arntzen, and Jonas R. Persson. 2024. "Calculation of the Breit–Rosenthal Effect in Bi I" Atoms 12, no. 12: 72. https://doi.org/10.3390/atoms12120072
APA StyleRøger, T. A., & Persson, J. R. (2024). Calculation of the Breit–Rosenthal Effect in Bi I. Atoms, 12(12), 72. https://doi.org/10.3390/atoms12120072







