Abstract
We report here an R-matrix study of electron collision with the BeO molecular ion in its X ground state and at a single bond length, namely its equilibrium . Firstly, a good quality configuration interaction calculation is performed for the BeO ground and excited states. We then perform scattering calculations using the R-matrix method to yield the cross-section for electronic excitation to several of its excited states. The electron impact dissociation of BeO through the two lowest dissociation channels, namely the Be + O and Be + O dissociation channels, is estimated using the electronic excitation cross-sections. Rotational excitation cross-sections are provided for the rotational transitions. Our calculations also yield e + BeO neutral Feshbach resonances and their widths which we present systematically categorized by their symmetry and quantum defects, and BeO-bound Rydberg states at the BeO equilibrium. The full potential energy curves for the resonant states, their widths and the bound Rydberg states, whose details we propose to give in a subsequent work, can be the starting point of other collision calculations.
1. Introduction
Beryllium is chosen presently as the plasma-facing wall material for fusion devices such as JET and ITER [1,2,3]. The interaction of the plasma in the edge regions with the walls can cause beryllium to enter into the plasma by sputtering [4,5], and this can subsequently lead to the formation of different molecular and molecular ion species containing beryllium as impurities by reaction with other atoms, molecules and ions in the plasma. Although the main components of the plasma are hydrogen, deuterium, tritium and helium, numerous other molecules can be present in the plasma either as trace gases in the fuel or due to their artificial introduction to modify plasma characteristics. This can lead to the formation of many beryllium-containing molecular and ion species. Particularly, since beryllium is also known to be a good “oxygen getter” [3,6], it is easily oxidized by traces of oxygen in the fuel to form BeO [4]. Consequently, this also implies the presence of BeO and BeO ions as impurities in the plasma in the edge regions. The presence of BeO is the principal motivation for the present work as collision data are required on all molecular and ion species in the plasma for plasma modeling and for estimating beryllium release.
As a molecular ion species, BeO is studied very little. In fact, we are aware of only two known works, the first by Partridge, Langhoff and Bauschlicher, Jr. [7], in which they obtained the spectroscopic parameters of BeO among other alkaline earth metal oxide, fluoride and hydroxide positive ions at the self-consistent field (SCF) and singles plus doubles configuration interaction (SDCI) level. The second, and more detailed work by Ghalila et al. [8], is an electronic structure calculation using large Gaussian basis sets and highly correlated wave functions. This latter work not only reported a stable ground state of symmetry having a deep minimum at but also many other excited states and their properties. It also reported a simulation of the BeO(X ) ionization spectrum.
In a previous work [9], we had studied electron collision with the neutral BeO molecule and reported cross-sections in considerable detail. In this work, we report a study on the electron collision with its positive ion BeO. We present cross-sections for electronic excitation to several of its electronically excited states, with electron impact dissociation through the lowest two dissociation channels, namely Be + O and Be + O. We also report e + BeO neutral Feshbach resonances at the BeO equilibrium and their widths categorized by their quantum defects and bound states of BeO calculated at the BeO equilibrium. Finally, we give cross-sections for the rotational excitation of BeO from its ground state to few of its rotationally excited states.
2. Theory
Our calculations are based on the molecular R-matrix method which has now become state of the art in electron–molecule collision calculations. While a detailed discussion on this is omitted for brevity and to avoid repetition, it can nonetheless be found in [10,11], of which we present a brief exposition below.
The R-matrix method starts by the division of the configuration space into an inner and an outer region by a sphere of radius a, taken here to be 10 . In the inner region, the -electron wave function of the N-electron target and the incident electron is expressed as close coupling expansion,
in Equation (1), is an antisymmetrization operator, and are, respectively, the coordinates of the N target electrons and the continuum electron, is the ith target state wave function and are continuum orbitals. The are square integrable functions taken to represent electron correlation and polarization of the target in presence of the incident electron, and are obtained by allowing the incident electron to occupy the target molecular orbitals. The coefficients and are variationally determined.
The inner region wave function is then used to build an R-matrix at the boundary of the R-matrix sphere. To construct the wave function in the outer region, the R-matrix is propagated to a certain asymptotic distance whose choice depends on the nature of the calculation. For bound-state calculations, typically = 40–50 is normally sufficient, while for scattering calculations, where outer region solutions do not die out even at asymptotic distances, a much larger value of is usually necessary. At , the R-matrix is then matched to known asymptotic functions obtained from a Gailitis expansion [12]. The scattering information is contained in the K-matrix which is obtained from the matching procedure. Once the K-matrix is known, it is used to build a T-matrix, which is related to the K-matrix as
where . Scattering cross-sections can be obtained from the T-matrix, while resonance parameters are obtainable from the K-matrix itself. The calculations of bound states, however, follow a different route not involving the K-matrix. These are discussed in more detail later.
3. Calculations
3.1. Calculation of the BeO Target
An accurate description of the target molecular ion, here BeO, is necessary for performing subsequent scattering calculations. We used Slater-type orbitals (STOs) as basis sets and the diatomic version of the UK molecular R-matrix codes for the present calculations. The diatomic codes and the use of STOs have become rather old-fashioned and more modern versions of the codes which can use large Gaussian basis sets (UKRMol) [13] or B-spline basis sets (UKRmol+) [14] are available. However, from past experiences (see, for example [9,15,16]), we know that even small STO bases, if chosen properly, are able to give reasonably accurate calculation while consuming very little computational resources and CPU time.
We tested several STO basis sets. Finally, for the present work, we chose the STOs of Bagus et al. [17] for Be and the STOs of Cade and Huo [18] for O, each of which contained five s-type, four p-type, two d-type and one f-type Slater functions as these gave the best target vertical excitation energies (VEEs) in comparison to the only existing work of Ghalila et al. [8]. The STOs were used to build a molecular basis consisting of 24 , 14 , 6 and 2 molecular orbitals (MOs) which were then used to perform a Hartree–Fock self-consistent field (SCF) calculation. Finally, 44 SCF MOs (24 , 14 and 6 ) were used in a configuration interaction (CI) calculation.
For calculation of the target states , we constructed several complete active space (CAS) CI models. In each of these models, six electrons were frozen in orbitals while the remaining five electrons were allowed to move in the target CAS defined as follows. For model M1, the CAS was defined by –10, 1–3), for model M2 the CAS was chosen as –10–, while for the model M3 it was taken to be ––. A comparison of vertical excitation energies computed with each of these model is shown in Table 1.


Table 1.
Comparison of vertical excitation energies (in eV) from the X ground state of the BeO molecular ion at the BeO equilibrium to 14 of its excited states calculated using the CASCI models M1, M2 and M3 as described in the text, with the adiabatic excitation energies and the estimated VEEs of Ghalila et al. [8]. The absolute ground state energies computed with models M1, M2, and M3 are −89.175473 Hartree, −89.185409 Hartree and −89.184491 Hartree, respectively. (Absolute ground state energies from Ref. [8] are unavailable.)
Table 1.
Comparison of vertical excitation energies (in eV) from the X ground state of the BeO molecular ion at the BeO equilibrium to 14 of its excited states calculated using the CASCI models M1, M2 and M3 as described in the text, with the adiabatic excitation energies and the estimated VEEs of Ghalila et al. [8]. The absolute ground state energies computed with models M1, M2, and M3 are −89.175473 Hartree, −89.185409 Hartree and −89.184491 Hartree, respectively. (Absolute ground state energies from Ref. [8] are unavailable.)
| Target States | Model M1 | Model M2 | Model M3 | Ghalila et al. | Ghalila et al. VEE |
|---|---|---|---|---|---|
| X | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1 | 1.58 | 1.48 | 1.71 | 1.16 | 1.28 |
| 1 | 3.94 | 3.71 | 3.71 | 2.92 | 3.77 |
| 1 | 4.14 | 3.88 | 3.92 | 3.15 | 4.11 |
| 2 | 5.80 | 5.44 | 5.68 | 4.92 | 5.51 |
| 1 | 6.00 | 5.88 | 5.78 | 5.04 | 5.93 |
| 2 | 7.27 | 7.13 | 7.08 | 6.11 | 6.93 |
| 2 | 7.92 | 7.24 | 7.74 | 6.12 | 7.12 |
| 3 | 7.74 | 7.45 | 7.68 | 6.21 | 7.39 |
| 4 | 8.64 | 8.15 | 8.46 | 6.91 | 8.14 |
| 1 | 9.28 | 8.47 | 9.21 | 7.34 | 8.19 |
| 1 | 9.47 | 8.72 | 9.40 | 7.51 | 8.51 |
| 2 | 9.62 | 8.92 | 9.54 | 7.57 | 8.74 |
| 2 | 9.73 | 9.07 | 9.64 | 7.79 | 9.09 |
| 2 | 11.77 | 11.12 | 11.75 | 7.83 | 9.18 |
a Ghalila et al. [8]. b VEEs estimated from Figure 1 of Ghalila et al. [8].
From Table 1, it is clear that the VEEs produced by model M2 are in excellent agreement with the estimated VEES of Ghalila et al. [8]. The dipole moment computed with model M2 at is 2.199 a.u., while the dipole transition moment for the X transition at is found to be 0.077 a.u. and agrees excellently with the value of 0.083 a.u. estimated from Figure 3 of Ghalila et al. [8] et al. We therefore adopted model M2 for subsequent scattering calculations.
Figure 1 shows the potential energy curves (PECs) of the ground and few of the excited states of BeO. We also included the ground state PEC of Ghalila et al. [8] shifted down by 0.035 Hartree for a comparison. Although the minima of the ground states from the two calculations are slightly different from each other, for scattering calculations only the relative position of the curves are significant as the incident electron energy is measured relative to the ground state minimum. Table 1 confirms that, for the M2 model chosen, the VEEs, and hence the relative positions of the curves, are in excellent agreement with those obtained by Ghalila et al. [8]. We propose to make a more accurate model of the BeO curves in a future work wherein we intend to study the bound and resonant states of BeO in full detail.
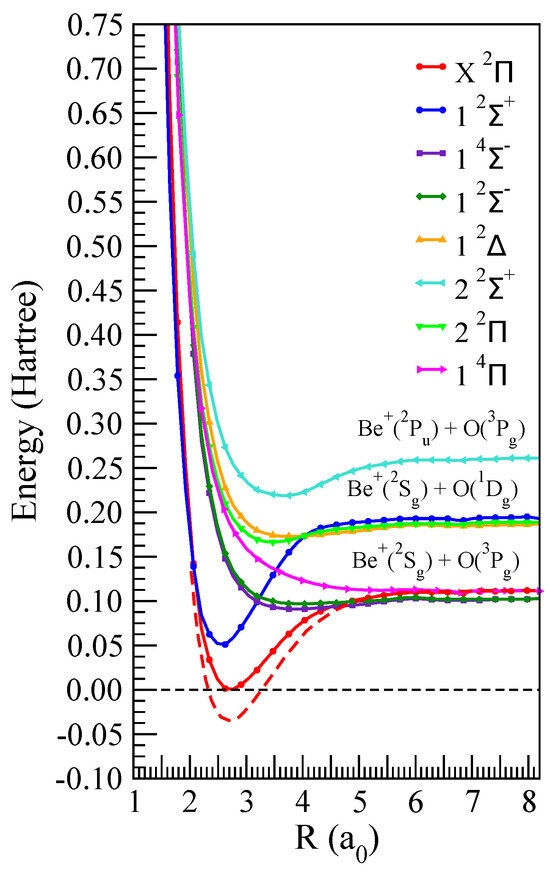
Figure 1.
Potential energy of the ground and few excited states of the BeO molecular ion. Curves with symbols: present calculation. Bottom−most dashed curve: X ground state of Ghalila et al. [8] shifted down by 0.035 Hartree (≈0.95 eV).
3.2. Inner-Region Solutions
For the inner-region solutions in Equation (1), we used 44 SCF MOs described above and a target CAS defined by model M2. The SCF MOs were supplemented with continuum functions for describing the scattered electron. Due to the ionic nature of the target, the radial parts of were represented by Coulomb functions which were obtained as a partial wave expansion about the target center of mass, and those partial waves with and were included in the expansion. The radial parts of the Coulomb functions were calculated numerically as solutions of the radial Coulomb equation with an isotropic Coulomb potential, retaining those solutions with energies below 10 Ryd using an R-matrix box radius 10 , and a Buttle [19] correction was used to mitigate the effects of this truncation. This resulted in 157 (63, 52, 42) continuum functions which were Schmidt orthogonalized to the target SCF orbitals. For the inner-region calculations, we used 12, 6 and 2 target SCF orbitals which allowed for two unoccupied virtual orbitals (VOs) per symmetry, and a CAS-CI wave function described by the model M2 above. The target VOs were treated in the same way as continuum function in Equation (1) and were contracted in the CI expansion [20].
We conducted extensive tests on different scattering models by varying the number and nature of the target states coupled in Equation (1) to obtain accurate values of BeO-bound states, resonance parameters and convergence in cross-sections. Our final calculations were performed using three scattering models which used up to 8, 10 and 12 target states in energy order, as given in Table 1. Henceforth, we will refer to these as the 8-state, 10-state and the 12-state scattering models.
3.3. Outer-Region Solutions and Scattering Calculations
All scattering calculations were performed at a single bond length, namely the BeO equilibrium . The inner-region solutions obtained were used to build an R-matrix at the boundary of the R-matrix sphere. For the outer-region solutions, it is more robust to propagate the R-matrix in the external region rather than the wave function itself (see, for example, [21]). The R-matrix was propagated in the outer region to an asymptotic distance in a potential which, in addition to the Coulomb potential of the target, contained the dipole and quadrupole potentials of the target ion. It was then matched at with suitable asymptotic functions obtained from a Gailitis expansion [12]. For scattering calculations, the matching at gives the K-matrix which is related to the T-matrix through the relation
where is the identity matrix and . All scattering cross-sections are then calculated from the T-matrix. The scattering cross-section for transition between an initial state labeled by i and a final state with label f is given by [11]
in Equation (4), are the total angular momentum and spin of the initial target state, are the angular momenta of the scattered electron coupled to the initial and final target states and , the total angular momentum, spin and parity of the full system.
The calculations of bound states, however, follow a different route for which a lower value of is required and is discussed below.
4. Results
4.1. Bound States of BeO
In the R-matrix formalism, the scattered electron in the inner region may be recaptured by the target ion to form a bound state, and for this the radial part of the -electron wave function in Equation (1) representing a bound state must decrease exponentially over a large distance (see [10]). For bound-state calculations, the R-matrix was propagated to and matched with exponentially decreasing functions obtained from Gailitis expansions [12]. It can be shown [22] that the bound states of the e + BeO system occur as the roots of an energy-dependent determinant , and these roots were searched for using a non-linear quantum defect grid of Rabadán and Tennyson [23] to obtain the bound states of BeO.
Table 2 shows a comparison of the vertical excitation energies of some of the bound states of the BeO molecule. In a previous work [9] on electron collision with the BeO molecule, we had obtained the vertical excitation energies of the BeO molecules using a CI calculation. Table 2 shows that our present values of the vertical excitation energies are close to the values we obtained in our previous work [9] and the estimated VEEs of Buenker et al. [24]. The deviations of our present VEEs from our previous calculations, and their closeness to the adiabatic energies of the works of Buenker et al. [24] and Kalemos [25] are likely due to two reasons. The absolute energy of our BeO ground state is slightly higher than that obtained by Buenker et al. [24] and Kalemos [25], which makes our VEEs slightly low. Secondly, our VEEs are calculated at the BeO equilibrium , while the of Buenker et al. [24] and Kalemos [25] and the VEEs in our earlier calculations are computed at the BeO equilibrium .

Table 2.
Vertical excitation energies for the bound states of the BeO molecule at the BeO equilibrium for some of the low lying states.
4.2. Resonances
A general feature of electron collision with positive ions is the occurrence of numerous neutral Feshbach resonances. For the detection of these resonances, the R-matrix was propagated to 100 and matched with suitable asymptotic functions outlined above to obtain the K-matrix, whose diagonal elements determine the eigenphase sum given by
The eigenphase sum is known to undergo a characteristic jump by near a resonance, causing its second derivative to change sign around the energy position at which the resonance occurs. The resonance positions were located by tracking this change in sign of the second derivative of numerically over an energy grid of 0.005 eV and fitting to a Breit–Wigner profile [26]
where and are the actual resonance position and width of the resonance, and is the background which represents the underlying trend of the eigenphase sum near the resonance.
Typical eigenphase sums of , , , symmetries of the e + BeO system are shown in Figure 2. The eigenphase sum show numerous sharp oscillations corresponding to the resonances. We tabulated some of these resonances in Table 3 whose parent state is the first excited state of BeO. As can be seen from the effective quantum numbers, many of the resonances fall in a Rydberg series. Also, several of the resonances have very narrow widths, indicating that they are very close to the BeO ground state and are likely to cross it from above to become bound states. A more precise understanding of this requires the construction of diabatic states by correlating resonances above the ion and bound states below it. This is more involved and is not attempted here.
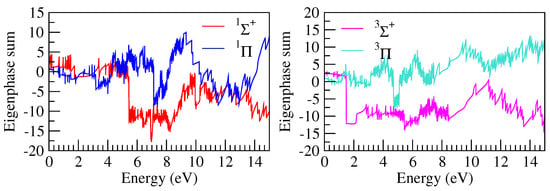
Figure 2.
Typical eigenphase sums for , (left panel) and , (right panel) overall symmetries of the e + BeO system.

Table 3.
Resonance positions , widths (in Rydbergs) and effective quantum numbers for some of the resonances with singlet and triplet symmetry below the first excited state of the BeO molecule at . (Figures in brackets indicate powers of 10).
4.3. Cross-Sections and Rate Coefficients
4.3.1. Electron Impact Excitation
In this section, we present cross-sections and rate coefficients for electron impact excitation from the X ground state of the BeO ion to some of its electronically excited states. Since the cross-sections are highly oscillatory due to presence of many Feshbach resonances, it is difficult to compare the convergence patterns of the cross-section curves. Therefore, we have verified convergence in our calculation with respect to the Maxwell isotropic rate coefficients (computed from the cross-sections, see details below) which are smooth due to the convolution of the cross-section with the isotropic Maxwell distribution. We computed cross-sections and the Maxwellian rate coefficients in the 8-state, 10-state and the 12-state models described above. Since the inclusion of too many states causes pseudo-resonances as our higher lying states are not likely to be modeled very accurately, and as our rates have converged in the 10-state model, we presented our final cross sections in the 10-state model.
BeO has a large permanent dipole moment at about 5.589 D, which makes it necessary to include a large number of partial waves in the outer-region calculation. The higher-order partial waves for , excluded in our cross-section calculation, are therefore accounted for through a Born correction to the excitation cross-sections. The excitation cross-sections, together with the Born corrections, which are relevant only for the dipole-allowed transitions, are shown in Figure 3. The Born corrections are largest for the and excitations. Particularly, the corrections to the cross-sections are largest for the case and are nearly two orders of magnitude more than the actual cross-sections at the maximum.
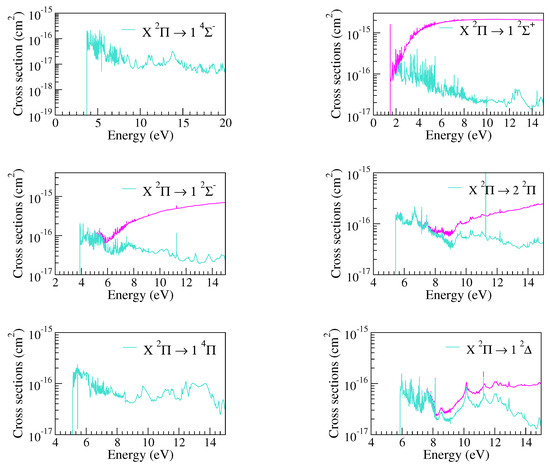
Figure 3.
(Left panels): cross-sections for electron impact excitation of the BeO molecule from its X ground state to the states indicated in the figures and dissociating to the Be(S) + O(P) limit. (Right panels): the same as left panels, but for states dissociating to the Be(S) + O(D) limit. The Born correction to the cross−section, wherever relevant, is given by the topmost curve (magenta, color online).
The left panels in Figure 3 show our cross-sections for excitation from the X ground state of BeO to the and states, all of which dissociate to the Be(S) + O(P) limit with eV. The cross-sections for excitation to the and states are small as they are dipole-forbidden. The large cross-section for the state for energies greater than 6 eV indicate a preferential excitation to this state over the or states.
The right panels in Figure 3 display cross-sections for excitation to the states and , which dissociate to the Be(S) + O(D) limit with eV. Generally, the uncorrected excitation cross-sections show a similar behavior with large cross-sections near the threshold and decreasing with an increase in incident energies due to the opening of other dissociation channels. However, the Born-corrected cross-sections rise rapidly beyond a certain energy and stabilize for larger energies. At the high energy end, the Born-corrected cross-sections are significantly larger than the uncorrected ones in all cases.
In Figure 4, we displayed the rate coefficients computed from the cross-sections for excitation from the X ground state to the first two states dissociating to the Be(S) + O(P) and the Be(S) + O(D) limits, computed in the 8-, 10- and 12-state models. The rate coefficients, presented in the electron temperature range of 0–80,000 K which correspond approximately to the incident energy range of 0–8 eV, are obtained with the aim of demonstrating convergence and hence are computed from the original cross-sections rather than the Born-corrected ones. It is clear from Figure 4 that, in all cases, convergence is obtained in the 10-state model and an additional calculation in the 12-state model confirms this.
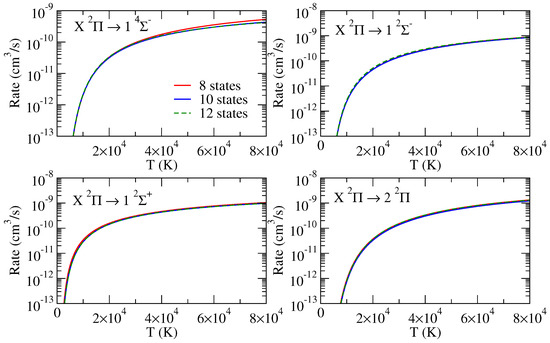
Figure 4.
Rate coefficients for excitation to some of the states (indicated in each panel) approaching the Be(S) + O(P) dissociation limit (top panels) and the Be(S) + O(D) dissociation limit (bottom panels). Convergence pattern in the rate coefficients is shown for 8-state (red curve), 10-state (blue curve) and 12-state (green dashed curve) models in each figure.
4.3.2. Electron Impact Dissociation
The lowest two dissociation channels are the BeO, the Be(S) + O(P) (threshold 4 eV) and the Be(S) + O(D) (threshold 5.91 eV) channels, which we subsequently refer to as the first and second dissociation channels, respectively. The X and the 1 states dissociated to the Be(S) + O(P), while the and the 1 dissociate to the next higher one, that is, the Be(S) + O(D) channel. We have approximately calculated the dissociation cross-sections by assuming that excitation to the states approaching a particular dissociation channel above the dissociation threshold of that channel results in dissociation. This approximation has proved to give a reasonable estimate of the dissociation cross-sections in many of our earlier studies (see [16] for example).
Figure 5 shows our estimates of the dissociation cross-sections for the lowest two dissociation channels. The dissociation cross-sections for higher dissociation channels are small and are not presented. The excitation cross-sections used in the calculation of dissociation cross-sections are taken to be the Born-corrected ones wherever relevant.
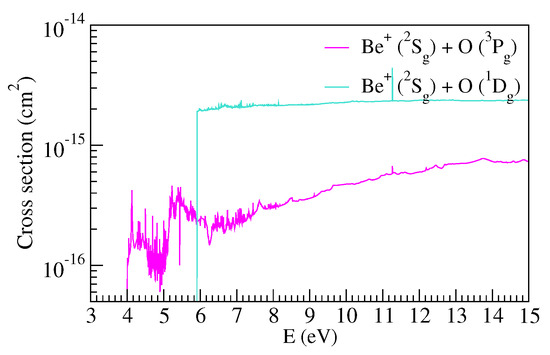
Figure 5.
Cross-section for electron impact dissociation of the BeO molecule in its ground state to the Be(S) + O(P) and the Be(S) + O(D) channels at the equilibrium . Cross-sections are Born-corrected.
The dissociation cross-section corresponding to the first (lowest) channel is significantly lower than that corresponding to the second dissociation channel. The reason behind this can be understood from the excitation cross-sections. From Figure 1, we see that the first excited state is the 1 state, which dissociates to the second dissociation channel. Consequently, the probability of excitation to this state is significantly higher than excitation to other excited states. The Born-corrected cross-section for the X excitation is therefore much higher than similar cross-sections for excitation to other higher lying states, as can be seen from Figure 3. Since our dissociation cross-sections are built from excitation cross-sections, the dissociation cross-section for the second channel is significantly higher due to a large contribution from the excitation cross-section for the X excitation. We therefore expect a significant proportion of O(D) (corresponding to the second dissociation channel) to be produced over O(P) due to dissociation. It is also interesting to note that dissociation will principally produce Be ions in preference to neutral Be, because the lowest three dissociation channels produce Be.
4.3.3. Rotational Excitation
Rotational excitation is important at low collisional energies. We have therefore obtained cross-sections for the rotational excitation of the BeO ion from its rotational ground state to the rotationally excited states .
The cross-sections were computed from the T-matrix elements for partial waves and were supplemented, for larger ℓ, with the cross-sections obtained in the Coulomb–Born (CB) approximation [27,28], where the cross-section for a rotational transition from a rotational state j to a state is given by
in Equation (7), is the cross-section computed from the T matrix, is the cross-section computed in the CB approximation and represents the partial cross-section in the CB approximation for those ℓ which have already been included in , and therefore need to be subtracted out.
The cross-sections for rotational excitations are shown in Figure 6 and are truncated close to the threshold. As is well known (see [16] for example), the transitions are dipole-driven, while transitions are driven primarily by short-range interactions which make them susceptible to resonance effects, which can be seen as oscillations in the cross-section curves for and .
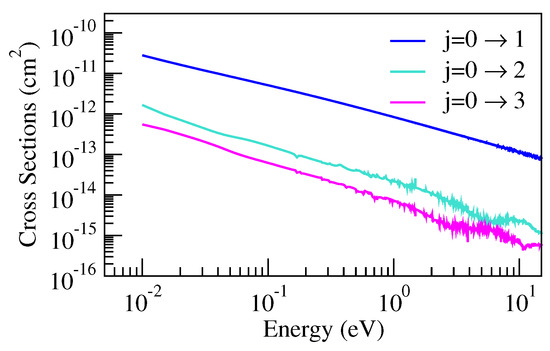
Figure 6.
Cross-section for rotational excitation of the BeO ion from its ground state () to the rotationally excited states with .
5. Conclusions
In this work, we studied electron collision with the BeO molecule with the goal of providing electron collision cross-sections and identifying Feshbach resonances in the e + BeO system. We presented some of these Feshbach resonances with the parent state and their widths characterized by their quantum defects.
Collision cross-sections for electronic excitation from the ground state of BeO to several of its excited states which dissociate to the lowest two dissociation channels were calculated, and rate coefficients corresponding to some of these cross-sections have been obtained. We demonstrated convergence in our calculations with respect to rate coefficients obtained from the cross-sections using scattering models constructed including up to 8, 10 and 12 target states.
The electronic excitation cross-sections have been used to estimate cross-sections for dissociation into the lowest two dissociation channels, namely the Be(S) + O(P) and the Be(S) + O(D) channels. Our estimates predict a significantly higher yield of O( over O beyond 6 eV incident energy. Finally, we also provided cross-sections for rotational excitation from the rotational ground state to the rotationally excited states , as these are likely to be important in low-energy collisions.
In a subsequent work, we hope to undertake a more detailed calculation on the bound and resonant states of BeO which will be helpful in initiating further studies in dissociative recombination of the BeO ion. Apart from the potential energy curves of BeO and the bound states of the BeO molecule presented in this paper, none of the other results were obtained before and these results are being reported for the first time.
Author Contributions
Conceptualization and methodology, K.C.; supervision, K.C. and A.B.; calculations, N.M. and K.C.; data curation, K.C. and N.M.; writing—original draft preparation, K.C., A.B and N.M.; writing—review and editing, A.B., K.C. and N.M.; project administration and funding acquisition, K.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Engineering Research Board (SERB), India, through the Core Research Grant CRG/2021/000357 provided to K.C.
Data Availability Statement
The data presented in this paper will be made available from the IAEA CollisionDB database https://db-amdis.org/collisiondb/ after publication of the paper.
Acknowledgments
K.C. thanks SERB, India, for financial support under the Core Research Grant CRG/2021/00357. N.M. acknowledges financial support from SERB, India, in the form of a research fellowship provided through the grant CRG/2021/00357.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Raffray, A.R.; Federici, G.; Barabash, V.; Pacher, H.D.; Bartels, H.W.; Cardella, A.; Jakeman, R.; Ioki, K.; Janeschitz, G.; Parker, R.; et al. Beryllium application in ITER plasma facing components. Fusion Eng. Des. 1997, 37, 261–286. [Google Scholar] [CrossRef]
- Pitts, R.A.; Carpentier, A.; Escourbiac, F.; Hirai, T.; Komarov, V.; Kukushkin, A.S.; Lisgo, S.; Loarte, A.; Merola, M.; Mitteau, R.; et al. Physics basis and design of the ITER plasma-facing components. J. Nucl. Mater. 2011, 415, S957–S964. [Google Scholar] [CrossRef]
- Makepeace, C.; Pardanaud, C.; Roubin, P.; Borodkina, I.; Ayres, C.; Coad, P.; Baron-Wiechec, A.; Jepu, I.; Heinola, K.; Widdowson, A.; et al. The effect of beryllium oxide on retention in JET ITER-like wall tiles. J. Nucl. Mater. 2019, 19, 346. [Google Scholar] [CrossRef]
- Hodille, E.A.; Byggmäster, J.; Safi, E.; Nordlund, K. Sputtering of beryllium oxide by deuterium at various temperatures simulated with molecular dynamics. Pys. Scr. 2020, T171, 014024. [Google Scholar] [CrossRef]
- Romazanov, J.; Kirschner, A.; Brezinsek, S.; Pitts, R.A.; Borodin, D.; Rode, S.; Navarro, M.X.; Schmid, K.; Veshchev, E.S.; Neverov, V.S.; et al. Beryllium erosion and redeposition in ITER H, He and D–T discharges. Nucl. Fusion 2022, 62, 036011. [Google Scholar] [CrossRef]
- Cardella, A.; Barabash, V.; Ioki, K.; Yamada, M.; Hatano, T.; Ohara, Y.; Lorenzetto, P.; Merola, M.; Mazul, I.; Strebkov, Y. Application of Beryllium as First Wall Armour for ITER Primary, Baffle, and Limiter Modules. Fusion Technol. 2020, 38, 326. [Google Scholar] [CrossRef]
- Partridge, H.; Langhoff, S.R.; Bauschlicher, W., Jr. Ab initio calculations on the positive ions of the alkalineearth oxides, fluorides, and hydroxides. J. Chem. Phys. 1986, 84, 4489. [Google Scholar] [CrossRef]
- Ghalila, H.; Lahmar, S.; Ben Lakhdar, Z.; Hochlaf, M. Spectroscopy and metastability of BeO+. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 205101. [Google Scholar] [CrossRef]
- Mukherjee, N.; Chakrabarti, K. Theoretical study of low energy electron collisions with the BeO molecule. J. Phys. B At. Mol. Opt. Phys. 2023, 56, 015202. [Google Scholar] [CrossRef]
- Tennyson, J. Electron–molecule collision calculations using the R-matrix method. Phys. Rep. 2010, 491, 29–76. [Google Scholar] [CrossRef]
- Burke, P.G. R-Matrix Theory of Atomic Collisions; Springer: Berlin, Germany, 2011. [Google Scholar]
- Noble, C.J.; Nesbet, R.K. CFASYM, A Program for the Calculation of the Asymptotic Solutions of the Coupled Equations of Electron Collision Theory. Comput. Phys. Commun. 1984, 33, 399. [Google Scholar] [CrossRef]
- Carr, J.M.; Galiatsatos, P.G.; Gorfinkiel, J.D.; Harvey, A.G.; Lysaght, M.A.; Madden, D.; Mašín, Z.; Plummer, M.; Tennyson, J.; Varambhia, H.N. UKRmol: A low-energy electron- and positron-molecule scattering suite. Euro. Phys. J. D 2012, 66, 58. [Google Scholar] [CrossRef]
- Mašín, Z.; Benda, J.; Gorfinkiel, J.D.; Harvey, A.G.; Tennyson, J. UKRmol+: A suite for modelling electronic processes in molecules interacting with electrons, positrons and photons using the R-matrix method. Comput. Phys. Commun. 2020, 249, 107092. [Google Scholar] [CrossRef]
- Ghosh, R.; Chakrabarti, K.; Choudhury, B.S. Electron induced processes in CH: An R-matrix study of electronic excitation, dissociation and dissociative attachment. Plasma Sources Sci. Technol. 2020, 29, 095016. [Google Scholar] [CrossRef]
- Ghosh, R.; Chakrabarti, K.; Choudhury, B.S. Electron impact studies on the imidogen (NH+) molecular ion. Plasma Sources Sci. Technol. 2022, 31, 065005. [Google Scholar] [CrossRef]
- Bagus, P.S.; Moser, C.M.; Goethals, P.; Verhaegen, G. Accurate ab initio calculation of the BeH molecule. I. The X 2Π+ and A 2Π states. J. Chem. Phys. 1973, 58, 1886. [Google Scholar] [CrossRef]
- Cade, P.E.; Huo, H. Hartree-Fock-Roothaan Wavefunctions for Diatomic Molecules. Atomic Data Nucl. Data Tables 1973, 13, 415. [Google Scholar] [CrossRef]
- Buttle, P.J.A. Solution of Coupled Equations by R-Matrix Techniques. Phys. Rev. 1967, 160, 719. [Google Scholar] [CrossRef]
- Tennyson, J. A new algorithm for Hamiltonian matrix construction in electron–molecule collision calculations. J. Phys. B At. Mol. Opt. Phys. 1996, 29, 1817–1828. [Google Scholar] [CrossRef]
- Chakrabarti, K.; Dinda, S. Calculated cross sections for electron collisions with the BeN molecule. Plasma Phys. Control. Fusion 2023, 65, 085017. [Google Scholar] [CrossRef]
- Sarpal, B.K.; Branchett, S.E.; Tennyson, J.; Morgan, L.A. Bound states using the R-matrix method: Rydberg states of HeH. J. Phys. B At. Mol. Opt. Phys. 1991, 24, 3685–3699. [Google Scholar] [CrossRef]
- Rabádan, I.; Tennyson’, J. R-Matrix calculation of the bound and continuum states of the e–NO+ system. J. Phys. B At. Mol. Opt. Phys. 1996, 29, 3747. [Google Scholar] [CrossRef]
- Buenker, R.J.; Leibermann, H.P.; Pichl, L.; Tachikawa, M.; Kimura, M. Role of the electric dipole moment in positron binding to the ground and excited states of the BeO molecule. J. Chem. Phys. 2007, 126, 104305. [Google Scholar] [CrossRef] [PubMed]
- Kalemos, A. The nature of the chemical bond in BeO0,-, BeOBe+,0,-, and in their hydrogenated products HBeO0,-, BeOH, HBeOH, BeOBeH+,0,-, and HBeOBeH. J. Chem. Phys. 2017, 29, 104307. [Google Scholar] [CrossRef]
- Tennyson, J.; Noble, C.J. RESON: For the automatic detection and fitting of Breit-Wigner resonances. Comput. Phys. Commun. 1984, 33, 421. [Google Scholar] [CrossRef]
- Rabadán, I.; Sarpal, B.K.; Tennyson, J. On the calculation of electron impact rotational excitation cross sections for molecular ions. J. Phys. B At. Mol. Opt. Phys. 1998, 31, 2077. [Google Scholar] [CrossRef]
- Rabadán, I.; Tennyson, J. ROTIONS: A program for the calculation of rotational excitation cross sections in electron molecular ion collisions. Comput. Phys. Commun. 1998, 114, 129. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).