Shape Coexistence in Even–Even Nuclei: A Theoretical Overview
Abstract
1. Introduction
1.1. Statement of Purpose
1.2. Outline
2. Theoretical Approaches to Shape Coexistence
2.1. The Nuclear Shell Model
2.1.1. The Tensor Force
2.2. Self-Consistent Mean-Field Models
2.3. Nuclear Deformation and the Nuclear Collective Model
2.4. The SU(3) Symmetry
2.4.1. The SU(3) Symmetry of Elliott
2.4.2. The Pseudo-SU(3) Symmetry
2.4.3. The Quasi-SU(3) Symmetry
2.4.4. The Proxy-SU(3) Symmetry
2.4.5. The SU(3) Symmetry in the Symplectic Model
2.4.6. The Dual-Shell Mechanism
2.5. Algebraic Models Using Bosons
2.6. Shape/Phase Transitions and Critical Point Symmetries
2.7. The O(6) Symmetry
2.8. The Nature of States
2.9. Multiple Shape Coexistence
2.10. Islands of Inversion
3. The Z ≈ 82 Region
3.1. The Hg (Z = 80) Isotopes
3.2. The Pb (Z = 82) Isotopes
3.3. The Po (Z = 84) Isotopes
3.4. The Rn (Z = 86) Isotopes
3.5. Heavy Nuclei Beyond Z = 86
3.6. The Pt (Z = 78) Isotopes
4. The Z = 68–76 Desert
4.1. The Os (Z = 76) Isotopes
4.2. The W (Z = 74) Isotopes
4.3. The Hf (Z = 72) Isotopes
4.4. The Yb (Z = 70) Isotopes
4.5. The Er (Z = 68) Isotopes
5. The Z ≈ , Region
5.1. The Sm (Z = 62) Isotopes
5.1.1. Sm (Z = 62) Isotopes above N = 82
5.1.2. Sm (Z = 62) Isotopes below N = 82
5.2. The Gd (Z = 64) Isotopes
5.2.1. Gd (Z = 64) Isotopes above N = 82
5.2.2. Gd (Z = 64) Isotopes below N = 82
5.3. The Dy (Z = 66) Isotopes
5.4. The Nd (Z = 60) Isotopes
5.4.1. Nd (Z = 60) Isotopes above N = 82
5.4.2. Nd (Z = 60) Isotopes below N = 82
5.5. Shape Coexistence and Shape/Phase Transition at
6. The Z = 54–58 Desert
6.1. The Ce (Z = 58) Isotopes
6.2. The Ba (Z = 56) Isotopes
6.3. The Xe (Z = 54) Isotopes
7. The Region
7.1. The Sn (Z = 50) Isotopes
7.2. The Cd (Z = 48) Isotopes
7.3. The Te (Z = 52) Isotopes
7.4. The Pd (Z = 46) Isotopes
8. The , Region
8.1. The Zr (Z = 40) Isotopes
8.1.1. Zr (Z = 40) Isotopes above N = 50
8.1.2. Zr (Z = 40) Isotopes below N = 50
8.2. The Sr (Z = 38) Isotopes
8.2.1. Sr (Z = 38) Isotopes above N = 50
8.2.2. Sr (Z = 38) Isotopes below N = 50
8.3. The Mo (Z = 42) Isotopes
8.3.1. Mo (Z = 42) Isotopes above N = 50
8.3.2. Mo (Z = 42) Isotopes below N = 50
8.4. The Ru (Z = 44) Isotopes
8.5. Shape Coexistence and Shape/Phase Transition at
9. The , Region
9.1. The Kr (Z = 36) Isotopes
9.1.1. Kr (Z = 36) Isotopes below N = 50
9.1.2. Kr (Z = 36) Isotopes above N = 50
9.2. The Se (Z = 34) Isotopes
9.2.1. Se (Z = 34) Isotopes below N = 50
9.2.2. Se (Z = 34) Isotopes above N = 50
9.3. The Ge (Z = 32) Isotopes
9.3.1. Ge (Z = 32) Isotopes below N = 50
9.3.2. Ge (Z = 32) Isot4opes above N = 50
9.4. The Zn (Z = 30) Isotopes
9.5. Shape Coexistence and Shape/Phase Transition at
10. The Light Nuclei at and below Z ≈ 28
10.1. The Ni (Z = 28) Isotopes
10.2. The Fe (Z = 26) Isotopes
10.3. The Cr (Z = 24) Isotopes
10.4. The Ti (Z = 22) Isotopes
10.5. The Ca (Z = 20) Isotopes
10.6. The Ar (Z = 18) Isotopes
10.7. The S (Z = 16) Isotopes
10.8. The Si (Z = 14) Isotopes
10.9. The Mg (Z = 12) Isotopes
10.10. The Ne (Z = 10) Isotopes
10.11. The O (Z = 8) Isotopes
10.12. The C (Z = 6) Isotopes
10.13. The Be (Z = 4) Isotopes
11. The Nuclei
11.1. Pairs in Nuclei
12. Islands of Inversion
13. Unified Perspectives for Shape Coexistence
13.1. Islands of Shape Coexistence and Shape/Phase Transitions
13.2. Systematics of Data
13.3. Comparison to Earlier Compilations
14. Conclusions
15. Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 5DQCH | five-dimensional quadrupole collective Hamiltonian |
| CDFT | covariant density functional theory |
| CPS | critical point symmetry |
| GCM | generator coordinate method |
| HF | Hartree–Fock |
| HFB | Hartree–Fock–Bogoliubov |
| IBM | interacting boson model |
| IBM-CM | interacting boson model with configuration mixing |
| MCSM | Monte Carlo shell model |
| PDS | partial dynamical symmetry |
| PPQ | pairing plus quadrupole |
| RHB | relativistic Hartree–Bogoliubov |
| RMF | relativistic mean field |
| SANCSM | symmetry-adapted no-core shell model |
| SC | shape coexistence |
| SPT | shape/phase transition |
| TDHFB | time-dependent Hartree–Fock–Bogoliubov |
| VAMPIR | variation after mean-field projection in realistic model spaces |
Appendix A. Theoretical Methods
Appendix A.1. Theoretical Approaches
| BCS approximation | Section 2.2 |
| beyond-mean-field approach | Section 2.2 |
| collective model of Bohr and Mottelson | Section 2.3 |
| covariant density functional theory (CDFT) | Section 3.1 |
| critical point symmetry (CPS) | Section 2.6 |
| density functional theory (DFT) | Section 2.2 |
| dual shell mechanism | Section 2.4.6 |
| E(5) CPS | Section 2.6 |
| Elliott SU(3) model | Section 2.4.1 |
| extended IBM | Section 2.5 |
| five-dimensional quadrupole collective Hamiltonian (5DQCH) | Section 2.2 |
| generator coordinate method (GCM) | Section 2.2 |
| Gogny interaction | Section 2.2 |
| Hartree–Fock (HF) | Section 2.2 |
| Hartree–Fock–Bogoliubov (HFB) | Section 2.2 |
| IBM with configuration mixing (IBM-CM) | Section 2.5 |
| interacting boson model (IBM) | Section 2.5 |
| Monte Carlo shell model (MCSM) | Section 2.1 |
| Nilsson model | Section 2.3 |
| no-core shell model | Section 2.1 |
| O(6) symmetry | Section 2.7 |
| pairing interaction | Section 2.3 |
| pairing plus quadrupole (PPQ) model | Section 2.3 |
| partial dynamical symmetry (PDS) | Section 2.5 |
| proxy-SU(3) symmetry | Section 2.4.4 |
| quasi-SU(3) symmetry | Section 2.4.3 |
| pseudo-SU(3) symmetry | Section 2.4.2 |
| relativistic mean field (RMF) | Section 2.2 |
| shape/phase transition (SPT) | Section 2.6 |
| Skyrme interaction | Section 2.2 |
| spdf-IBM | Section 2.5 |
| symmetry-adapted no-core shell model (SANCSM) | Section 2.1 |
| symplectic model | Section 2.4.5 |
| tensor force | Section 2.1.1 |
| time-dependent Hartree–Fock–Bogoliubov (TDHFB) | Section 2.2 |
| VAMPIR | Section 2.2 |
| X(5) CPS | Section 2.6 |
| Z(5) CPS | Section 2.6 |
Appendix A.2. The Constrained HFB Theory
Appendix A.3. The Cranking Model and the Routhians
Appendix A.4. The Deformed Woods–Saxon Potential
Appendix A.5. The Nilsson–Strutinsky Model
Appendix A.6. The Particle-Plus-Rotor Model
Appendix A.7. The Projection Method
References
- Morinaga, H. Interpretation of Some of the Excited States of 4n Self-Conjugate Nuclei. Phys. Rev. 1956, 101, 254. [Google Scholar] [CrossRef]
- Heyde, K.; Van Isacker, P.; Waroquier, M.; Wood, J.L.; Meyer, R.A. Coexistence in odd-mass nuclei. Phys. Rep. 1983, 102, 291. [Google Scholar] [CrossRef]
- Wood, J.L.; Heyde, K.; Nazarewicz, W.; Huyse, M.; Van Duppen, P. Coexistence in even-mass nuclei. Phys. Rep. 1992, 215, 101. [Google Scholar] [CrossRef]
- Heyde, K.; Wood, J.L. Shape coexistence in atomic nuclei. Rev. Mod. Phys. 2011, 83, 1467. [Google Scholar] [CrossRef]
- Heyde, K.; Wood, J.L. Nuclear shapes: From earliest ideas to multiple shape coexisting structures. Phys. Scr. 2016, 91, 083008. [Google Scholar] [CrossRef]
- Poves, A. Shape coexistence in nuclei. J. Phys. G Nucl. Part. Phys. 2016, 43, 020401. [Google Scholar] [CrossRef][Green Version]
- Wood, J.L.; Heyde, K. A focus on shape coexistence in nuclei. J. Phys. G Nucl. Part. Phys. 2016, 43, 020402. [Google Scholar] [CrossRef]
- Garrett, P.E.; Zielińska, M.; Clément, E. An experimental view on shape coexistence in nuclei. Prog. Part. Nucl. Phys. 2022, 124, 103931. [Google Scholar] [CrossRef]
- Nobel Foundation. Nobel Lectures, Physics 1963–1970; Elsevier: Amsterdam, The Netherlands, 1972. [Google Scholar]
- Nobel Foundation. Nobel Lectures, Physics 1971–1980; Lundqvist, S., Ed.; World Scientific: Singapore, 1992. [Google Scholar]
- Bark, R.A.; Dracoulis, G.D.; Stuchbery, A.E. Shape coexistence or particle alignment in the light osmium isotopes 171Os, 172Os and 173Os. Nucl. Phys. A 1990, 514, 503. [Google Scholar] [CrossRef]
- Davidson, P.M.; Dracoulis, G.D.; Kibédi, T.; Byrne, A.P.; Anderssen, S.S.; Baxter, A.M.; Fabricius, B.; Lane, G.J.; Stuchbery, A.E. Non-yrast states and shape co-existence in 172Os. Nucl. Phys. A 1994, 568, 90. [Google Scholar] [CrossRef]
- Joss, D.T.; King, S.L.; Page, R.D.; Simpson, J.; Keenan, A.; Amzal, N.; Bäck, T.; Bentley, M.A.; Cederwall, B.; Cocks, J.F.; et al. Identification of excited states in 167Os and 168Os: Shape coexistence at extreme neutron deficiency. Nucl. Phys. A 2001, 689, 631. [Google Scholar] [CrossRef]
- Kibédi, T.; Dracoulis, G.D.; Byrne, A.P.; Davidson, P.M. Low-spin non-yrast states in light tungsten isotopes and the evolution of shape coexistence. Nucl. Phys. A 2001, 688, 669. [Google Scholar] [CrossRef]
- Paul, E.S.; Fossan, D.B.; Liang, Y.; Ma, R.; Xu, N. Shape coexistence in 132Ba. Phys. Rev. C 1989, 40, 1255. [Google Scholar] [CrossRef]
- Procter, M.G.; Cullen, D.M.; Scholey, C.; Niclasen, B.; Mason, P.J.R.; Rigby, S.V.; Dare, J.A.; Dewald, A.; Greenlees, P.T.; Iwasaki, H.; et al. Lifetime measurements and shape coexistence in 144Dy. Phys. Rev. C 2010, 81, 054320. [Google Scholar] [CrossRef]
- Revill, J.P.; Paul, E.S.; Wang, X.; Riley, M.A.; Simpson, J.; Janssens, R.V.F.; Ollier, J.; Boston, A.J.; Carpenter, M.P.; Chiara, C.J.; et al. Quadrupole moments of coexisting collective shapes at high spin in 154Er. Phys. Rev. C 2013, 88, 031304. [Google Scholar] [CrossRef]
- Smith, M.B.; Appelbe, D.E.; Twin, P.J.; Beausang, C.W.; Beck, F.A.; Bentley, M.A.; Cullen, D.M.; Curien, D.; Dagnall, P.J.; de France, G.; et al. Deformed rotational cascades in 152Dy: Further evidence for shape coexistence at high spin. Phys. Rev. C 2000, 61, 034314. [Google Scholar] [CrossRef]
- Fant, B.; Tanner, R.J.; Butler, P.A.; James, A.N.; Jones, G.D.; Poynter, R.J.; White, C.A.; Ying, K.L.; Love, D.J.G.; Simpson, J.; et al. Search for shape coexistence in 194Pb. J. Phys. G Nucl. Part. Phys. 1991, 17, 319. [Google Scholar]
- Ionescu-Bujor, M.; Iordachescu, A.; Mǎrginean, N.; UR, C.A.; Bucurescu, D.; Suliman, G.; Balabanski, D.L.; Brandolini, F.; Chmel, S.; Detistov, P.; et al. Shape coexistence in neutron-deficient Pb nuclei probed by quadrupole moment measurements. Phys. Lett. B 2007, 650, 141. [Google Scholar] [CrossRef]
- Ionescu-Bujor, M.; Iordachescu, A.; Ur, C.A.; Marginean, N.; Suliman, G.; Bucurescu, D.; Brandolini, F.; Della Vedova, F.; Chmel, S.; Lenzi, S.M.; et al. g factors of coexisting isomeric states in 188Pb. Phys. Rev. C 2010, 81, 024323. [Google Scholar] [CrossRef]
- Mare, A.S.; Petrovici, A. Shape coexistence and isomeric states in 94Pd within a beyond-mean-field approach. Phys. Rev. C 2022, 106, 054306. [Google Scholar] [CrossRef]
- Nara Singh, B.S.; Liu, Z.; Wadsworth, R.; Grawe, H.; Brock, T.S.; Boutachkov, P.; Braun, N.; Blazhev, A.; Górska, M.; Pietri, S.; et al. 16+ spin-gap isomer in 96Cd. Phys. Rev. Lett. 2011, 107, 172502. [Google Scholar] [CrossRef] [PubMed]
- Oi, M.; Walker, P.M.; Ansari, A. Shape coexistence and tilted-axis rotation in neutron-rich hafnium isotopes. Phys. Lett. B 2001, 505, 75. [Google Scholar] [CrossRef][Green Version]
- Dudek, J.; Nazarewicz, W.; Rowley, N. Shape coexistence effects and superdeformation in 84Zr. Phys. Rev. C 1987, 35, 1489. [Google Scholar] [CrossRef] [PubMed]
- Dudek, J.; Nazarewicz, W.; Szymanski, Z.; Leander, G.A. Abundance and systematics of nuclear superdeformed states; relation to the pseudospin and pseudo-SU(3) symmetries. Phys. Rev. Lett. 1987, 59, 1405. [Google Scholar] [CrossRef] [PubMed]
- Lagergren, K.; Cederwall, B.; Bäck, T.; Wyss, R.; Ideguchi, E.; Johnson, A.; Ataç, A.; Axelsson, A.; Azaiez, F.; Bracco, A.; et al. Coexistence of Superdeformed Shapes in 154Er. Phys. Rev. Lett. 2001, 87, 022502. [Google Scholar] [CrossRef]
- Grahn, T.; Petts, A.; Scheck, M.; Butler, P.; Page, R.; Dewald, A.; Jolie, J.; Melon, B.; Pissulla, T.; Hornillos, M.; et al. Evolution of collectivity in 180Hg and 182Hg. Phys. Rev. C 2009, 80, 014324. [Google Scholar] [CrossRef]
- Leandri, J.; Piepenbring, R. Coupled Kπ=0+ and Kπ=0− vibrations in 152Sm. Phys. Lett. B 1989, 232, 437. [Google Scholar] [CrossRef]
- Urban, W.; Lieder, R.M.; Gast, W.; Hebbinghaus, G.; Krämer-Flecken, A.; Blume, K.P.; Hübel, H. Evidence for coexistence of reflection asymmetric and symmetric shapes in 150Sm. Phys. Lett. B 1987, 185, 331. [Google Scholar] [CrossRef]
- Zhu, S.J.; Wang, E.H.; Hamilton, J.H.; Ramayya, A.V.; Liu, Y.X.; Brewer, N.T.; Luo, Y.X.; Rasmussen, J.O.; Xiao, Z.G.; Huang, Y.; et al. Coexistence of Reflection Asymmetric and Symmetric Shapes in 144Ba. Phys. Rev. Lett. 2020, 124, 032501. [Google Scholar] [CrossRef]
- Haxel, O.; Jensen, J.H.D.; Suess, H.E. On the “Magic Numbers” in Nuclear Structure. Phys. Rev. 1949, 75, 1766. [Google Scholar] [CrossRef]
- Heyde, K.L.G. The Nuclear Shell Model; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Mayer, M.G. On Closed Shells in Nuclei. Phys. Rev. 1948, 74, 235. [Google Scholar] [CrossRef]
- Mayer, M.G. On Closed Shells in Nuclei. II. Phys. Rev. 1949, 75, 1969. [Google Scholar] [CrossRef]
- Mayer, M.G.; Jensen, J.H.D. Elementary Theory of Nuclear Shell Structure; Wiley: New York, NY, USA, 1955. [Google Scholar]
- Talmi, I. Simple Models of Complex Nuclei: The Shell Model and the Interacting Boson Model; Harwood: Chur, Switzerland, 1993. [Google Scholar]
- Iachello, F. Lie Algebras and Applications; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Moshinsky, M.; Smirnov, Y.F. The Harmonic Oscillator in Modern Physics; Harwood: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Wybourne, B.G. Classical Groups for Physicists; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Woods, R.D.; Saxon, D.S. Diffuse Surface Optical Model for Nucleon-Nuclei Scattering. Phys. Rev. 1954, 95, 577. [Google Scholar] [CrossRef]
- Bethe, H.A.; Bacher, R.F. Nuclear Physics A. Stationary States of Nuclei. Rev. Mod. Phys. 1936, 8, 82. [Google Scholar] [CrossRef]
- Elsasser, W.M. Sur le principe de Pauli dans les noyaux-II. J. Phys. Radium 1934, 5, 389–397. [Google Scholar] [CrossRef]
- Elsasser, W.M. Sur le principe de Pauli dans les noyaux-III. J. Phys. Radium 1934, 5, 635–639. [Google Scholar] [CrossRef]
- Caurier, E.; Martínez-Pinedo, G.; Nowacki, F.; Poves, A.; Zuker, A.P. The shell model as a unified view of nuclear structure. Rev. Mod. Phys. 2005, 77, 427. [Google Scholar] [CrossRef]
- Poves, A. Shape coexistence: The shell model view. J. Phys. G Nucl. Part. Phys. 2016, 43, 024010. [Google Scholar] [CrossRef]
- Caurier, E.; Nowacki, F.; Poves, A. Large-scale shell model calculations for exotic nuclei. Eur. Phys. J. A 2002, 15, 145. [Google Scholar] [CrossRef]
- Caurier, E.; Menéndez, J.; Nowacki, F.; Poves, A. Coexistence of spherical states with deformed and superdeformed bands in doubly magic 40Ca: A shell-model challenge. Phys. Rev. C 2007, 75, 054317. [Google Scholar] [CrossRef]
- Caurier, E.; Nowacki, F.; Poves, P. Merging of the islands of inversion at N = 20 and N = 28. Phys. Rev. C 2014, 90, 014302. [Google Scholar] [CrossRef]
- Lenzi, S.M.; Nowacki, F.; Poves, A.; Sieja, K. Island of inversion around 64Cr. Phys. Rev. C 2010, 82, 054301. [Google Scholar] [CrossRef]
- Valiente-Dobón, J.J.; Poves, A.; Gadea, A.; Fernández-Domínguez, B. Broken mirror symmetry in 36S and 36Ca. Phys. Rev. C 2018, 98, 011302. [Google Scholar] [CrossRef]
- Honma, M.; Mizusaki, T.; Otsuka, T. Diagonalization of Hamiltonians for Many-Body Systems by Auxiliary Field Quantum Monte Carlo Technique. Phys. Rev. Lett. 1995, 75, 1284. [Google Scholar] [CrossRef]
- Honma, M.; Mizusaki, T.; Otsuka, T. Nuclear Shell Model by the Quantum Monte Carlo Diagonalization Method. Phys. Rev. Lett. 1996, 77, 3315. [Google Scholar] [CrossRef] [PubMed]
- Mizusaki, T.; Honma, M.; Otsuka, T. Quantum Monte Carlo diagonalization with angular momentum projection. Phys. Rev. C 1996, 53, 2786. [Google Scholar] [CrossRef] [PubMed]
- Otsuka, T.; Honma, M.; Mizusaki, T. Structure of the N=Z=28 Closed Shell Studied by Monte Carlo Shell Model Calculation. Phys. Rev. Lett. 1998, 81, 1588. [Google Scholar] [CrossRef]
- Otsuka, T.; Honma, M.; Mizusaki, T.; Shimizu, N.; Utsuno, Y. Monte Carlo shell model for atomic nuclei. Prog. Part. Nucl. Phys. 2001, 47, 319. [Google Scholar] [CrossRef]
- Shimizu, N.; Otsuka, T.; Mizusaki, T.; Honma, M. Transition from Spherical to Deformed Shapes of Nuclei in the Monte Carlo Shell Model. Phys. Rev. Lett. 2001, 86, 1171. [Google Scholar] [CrossRef]
- Shimizu, N.; Abe, T.; Tsunoda, Y.; Utsuno, Y.; Yoshida, T.; Mizusaki, T.; Honma, M.; Otsuka, T. New-generation Monte Carlo shell model for the K computer era. Prog. Theor. Exp. Phys. 2012, 2012, 01A205. [Google Scholar] [CrossRef]
- Yoshida, S.; Shimizu, N.; Togashi, T.; Otsuka, T. Uncertainty quantification in the nuclear shell model. Phys. Rev. C 2018, 98, 061301. [Google Scholar] [CrossRef]
- Hasegawa, M.; Kaneko, K.; Mizusaki, T.; Sun, Y. Phase transition in exotic nuclei along the N = Z line. Phys. Lett. B 2007, 656, 51. [Google Scholar] [CrossRef]
- Kaneko, K.; Hasegawa, H.; Mizusaki, T. Shape transition and oblate-prolate coexistence in N = Z fpg-shell nuclei. Phys. Rev. C 2004, 70, 051301. [Google Scholar] [CrossRef]
- Kaneko, K.; Casten, R.F.; Hasegawa, M.; Mizusaki, T.; Zhang, J.-Y.; McCutchan, E.A.; Zamfir, N.V.; Krücken, R. Anomalous behavior of the first excited 0+ state in N≈Z nuclei. Phys. Rev. C 2005, 71, 014319. [Google Scholar] [CrossRef]
- Kaneko, K.; Mizusaki, T.; Sun, Y.; Tazaki, S. Toward a unified realistic shell-model Hamiltonian with the monopole-based universal force. Phys. Rev. C 2014, 89, 011302. [Google Scholar] [CrossRef]
- Kaneko, K.; Mizusaki, T.; Sun, Y.; Tazaki, S. Systematical shell-model calculation in the pairing-plus-multipole Hamiltonian with a monopole interaction for the pf5/2g9/2 shell. Phys. Rev. C 2015, 92, 044331. [Google Scholar] [CrossRef]
- Kaneko, K.; Sun, Y.; Wadsworth, R. Shape coexistence and shape transition in self-conjugate nucleus 72Kr and the tensor force. Phys. Scr. 2017, 92, 114008. [Google Scholar] [CrossRef]
- Lay, J.A.; Vitturi, A.; Fortunato, L.; Tsunoda, Y.; Togashi, T.; Otsuka, T. Two-particle transfer processes as a signature of shape phase transition in Zirconium isotopes. Phys. Lett. B 2023, 838, 137719. [Google Scholar] [CrossRef]
- Mizusaki, T.; Otsuka, T.; Utsuno, Y.; Honma, M.; Sebe, T. Shape coexistence in doubly-magic 56Ni by the Monte Carlo shell model. Phys. Rev. C 1999, 59, R1846. [Google Scholar] [CrossRef]
- Mizusaki, T.; Otsuka, T.; Honma, M.; Brown, B.A. Spherical-deformed shape coexistence for the pf shell in the nuclear shell model. Phys. Rev. C 2001, 63, 044306. [Google Scholar] [CrossRef]
- Reinhard, P.-G.; Dean, D.J.; Nazarewicz, W.; Dobaczewski, J.; Maruhn, J.A.; Strayer, M.R. Shape coexistence and the effective nucleon-nucleon interaction. Phys. Rev. C 1999, 60, 014316. [Google Scholar] [CrossRef]
- Shimizu, N.; Utsuno, Y.; Mizusaki, T.; Honma, M.; Tsunoda, Y.; Otsuka, T. Variational procedure for nuclear shell-model calculations and energy-variance extrapolation. Phys. Rev. C 2012, 85, 054301. [Google Scholar] [CrossRef]
- Togashi, T.; Tsunoda, Y.; Otsuka, T.; Shimizu, N. Quantum Phase Transition in the Shape of Zr isotopes. Phys. Rev. Lett. 2016, 117, 172502. [Google Scholar] [CrossRef]
- Togashi, T.; Tsunoda, Y.; Otsuka, T.; Shimizu, N.; Honma, M. Novel Shape Evolution in Sn Isotopes from Magic Numbers 50 to 82. Phys. Rev. Lett. 2018, 121, 062501. [Google Scholar] [CrossRef] [PubMed]
- Tsunoda, Y.; Otsuka, T.; Shimizu, N.; Honma, M.; Utsuno, Y. Novel shape evolution in exotic Ni isotopes and configuration-dependent shell structure. Phys. Rev. C 2014, 89, 031301. [Google Scholar] [CrossRef]
- Utsuno, Y.; Otsuka, T.; Brown, B.A.; Honma, M.; Mizusaki, T.; Shimizu, N. Shape transitions in exotic Si and S isotopes and tensor-force-driven Jahn-Teller effect. Phys. Rev. C 2012, 86, 051301. [Google Scholar] [CrossRef]
- Utsuno, Y.; Shimizu, N.; Otsuka, T.; Yoshida, T.; Tsunoda, Y. Nature of Isomerism in Exotic Sulfur Isotopes. Phys. Rev. Lett. 2015, 114, 032501. [Google Scholar] [CrossRef]
- Navrátil, P.; Vary, J.P.; Barrett, B.R. Properties of 12C in the Ab Initio Nuclear Shell Model. Phys. Rev. Lett. 2000, 84, 5728. [Google Scholar] [CrossRef]
- Navrátil, P.; Vary, J.P.; Barrett, B.R. Large-basis ab initio no-core shell model and its application to 12C. Phys. Rev. C 2000, 62, 054311. [Google Scholar] [CrossRef]
- Dytrych, T.; Sviratcheva, K.D.; Draayer, J.P.; Bahri, C.; Vary, J.P. Ab initio symplectic no-core shell model. J. Phys. G Nucl. Part. Phys. 2008, 35, 123101. [Google Scholar] [CrossRef]
- Launey, K.D.; Draayer, J.P.; Dytrych, T.; Sun, G.-H.; Dong, S.-H. Approximate symmetries in atomic nuclei from a large-scale shell-model perspective. Int. J. Mod. Phys. E 2015, 24, 1530005. [Google Scholar] [CrossRef]
- Launey, K.D.; Dytrych, T.; Draayer, J.P. Symmetry-guided large-scale shell-model theory. Prog. Part. Nucl. Phys. 2016, 89, 101. [Google Scholar] [CrossRef]
- Launey, K.D.; Dytrych, T.; Sargsyan, G.H.; Baker, R.B.; Draayer, J.P. Emergent symplectic symmetry in atomic nuclei: Ab initio symmetry-adapted no-core shell model. Eur. Phys. J. Spec. Top. 2020, 229, 2429. [Google Scholar] [CrossRef]
- Launey, K.D.; Mercenne, A.; Dytrych, T. Nuclear Dynamics and Reactions in the Ab Initio Symmetry-Adapted Framework. Annu. Rev. Nucl. Part. Sci. 2021, 71, 253. [Google Scholar] [CrossRef]
- Heyde, K.; Van Isacker, P.; Casten, R.F.; Wood, J.L. A shell-model interpretation of intruder states and the onset of deformation in even-even nuclei. Phys. Lett. B 1985, 155, 303. [Google Scholar] [CrossRef]
- Heyde, K.; De Coster, C.; Ryckebusch, J.; Waroquier, M. Equivalence of the spherical and deformed shell-model approach to intruder states. Phys. Lett. B 1989, 218, 287. [Google Scholar] [CrossRef]
- Heyde, K.; Meyer, R.A. Possible evidence for four-particle, four-hole excitations in 146Gd. Phys. Rev. C 1990, 41, 280. [Google Scholar] [CrossRef]
- Heyde, K. A shell-model description of intruder states and shape coexistence. Nucl. Phys. A 1990, 507, 149c. [Google Scholar] [CrossRef]
- Wenes, G.; Van Isacker, P.; Waroquier, M.; Heyde, K.; Van Maldeghem, J. Collective bands in doubly-even Sn nuclei: Energy spectra and electromagnetic decay properties. Phys. Rev. C 1981, 23, 2291. [Google Scholar] [CrossRef]
- Fortune, H.T. Shape coexistence and mixing in 96Zr. Phys. Rev. C 2017, 95, 054313. [Google Scholar] [CrossRef]
- Fortune, H.T. Coexistence and B(E2)’s in 98Sr. Nucl. Phys. A 2017, 957, 184–187. [Google Scholar] [CrossRef]
- Fortune, H.T. Coexistence and mixing in 76Se. Phys. Rev. C 2019, 99, 054320. [Google Scholar] [CrossRef]
- Carchidi, M.; Fortune, H.T. Coexistence in the even zinc isotopes. Phys. Rev. C 1988, 37, 556–570. [Google Scholar] [CrossRef]
- Fortune, H.T. Nature of collectivity in Pd isotopes. J. Phys. G Nucl. Phys. 1985, 11, 1305–1308. [Google Scholar] [CrossRef]
- Fortune, H.T.; Carchidi, M. Coexistence and B(E2)’s in even Ge nuclei. Phys. Rev. C 1987, 36, 2584–2589. [Google Scholar] [CrossRef]
- Fortune, H.T. Coexistence and B(E2) values in 72Ge. Phys. Rev. C 2016, 94, 024318. [Google Scholar] [CrossRef]
- Fortune, H.T. Mixing of higher-J states in 72Ge. Phys. Rev. C 2017, 95, 044317. [Google Scholar] [CrossRef]
- Fortune, H.T. Nature of first two rotational bands in 152Sm. Nucl. Phys. A 2017, 966, 47–53. [Google Scholar] [CrossRef]
- Fortune, H.T. Band mixing and structure of 106,108Pd. Phys. Rev. C 2018, 98, 064303. [Google Scholar] [CrossRef]
- Fortune, H.T. Band mixing in 154Gd. Eur. Phys. J. A 2018, 54, 178. [Google Scholar] [CrossRef]
- Fortune, H.T. Band mixing in 74,76,78Kr. Eur. Phys. J. A 2018, 54, 229. [Google Scholar] [CrossRef]
- Fortune, H.T. Coexistence and mixing in 182,184Hg. Phys. Rev. C 2019, 100, 044303. [Google Scholar] [CrossRef]
- Majarshin, A.J.; Luo, Y.-A.; Pan, F.; Fortune, H.T.; Draayer, J.P. Nuclear structure and band mixing in 194Pt. Phys. Rev. C 2021, 103, 024317. [Google Scholar] [CrossRef]
- Otsuka, T.; Suzuki, T.; Fujimoto, R.; Grawe, H.; Akaishi, Y. Evolution of Nuclear Shells due to the Tensor Force. Phys. Rev. Lett. 2005, 95, 232502. [Google Scholar] [CrossRef] [PubMed]
- Yukawa, H. On the Interaction of Elementary Particles. I. Proc. Phys. Math. Soc. Jpn. 1935, 17, 48. [Google Scholar]
- Nilsson, S.G.; Ragnarsson, I. Shapes and Shells in Nuclear Structure; Cambridge U. Press: Cambridge, UK, 1995. [Google Scholar]
- Otsuka, T.; Tsunoda, Y. The role of shell evolution in shape coexistence. J. Phys. G Nucl. Part. Phys. 2016, 43, 024009. [Google Scholar] [CrossRef]
- Otsuka, T. Exotic nuclei and nuclear forces. Phys. Scr. 2013, T152, 014007. [Google Scholar] [CrossRef]
- Otsuka, T.; Gade, A.; Sorlin, O.; Suzuki, T.; Utsuno, Y. Evolution of shell structure in exotic nuclei. Rev. Mod. Phys. 2020, 92, 015002. [Google Scholar] [CrossRef]
- Kratzer, A. Die ultraroten Rotationsspektren der Halogenwasserstoffe. Z. Phys. 1920, 3, 289. [Google Scholar] [CrossRef]
- Bender, M.; Heenen, P.-H.; Reinhard, P.-G. Self-consistent mean-field models for nuclear structure. Rev. Mod. Phys. 2003, 75, 121. [Google Scholar] [CrossRef]
- Greiner, W.; Maruhn, J.A. Nuclear Models; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Ring, P.; Schuck, P. The Nuclear Many-Body Problem; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175. [Google Scholar] [CrossRef]
- Delaroche, J.-P.; Girod, M.; Libert, J.; Goutte, H.; Hilaire, S.; Péru, S.; Pillet, N.; Bertsch, G.F. Structure of even-even nuclei using a mapped collective Hamiltonian and the D1S Gogny interaction. Phys. Rev. C 2010, 81, 014303. [Google Scholar] [CrossRef]
- Gogny, D. Hartree-Fock Bogolyubov method with density-dependent interaction. In Proceedings of the International Conference on Nuclear Physics, Munich, Germany, 27 August–1 September 1973; de Boer, J., Mang, H.J., Eds.; North Holland: Amsterdam, The Netherlands, 1973; p. 48. [Google Scholar]
- Gogny, D. Perturbation theory with a soft core two nucleon interaction. In Proceedings of the International Conference on Nuclear Self-Consistent Fields, Trieste, Italy, 24–28 February 1975; Ripka, G., Porneuf, M., Eds.; North Holland: Amsterdam, The Netherlands, 1975; p. 149. [Google Scholar]
- Erler, J.; Klüpfel, P.; Reinhard, P.-G. Self-consistent nuclear mean-field models: Example Skyrme–Hartree–Fock. J. Phys. G Nucl. Part. Phys. 2011, 38, 033101. [Google Scholar] [CrossRef]
- Skyrme, T.H.R. CVII. The nuclear surface. Phil. Mag. 1956, 1, 1043. [Google Scholar] [CrossRef]
- Skyrme, T.H.R. The spin-orbit interaction in nuclei. Nucl. Phys. 1959, 9, 615. [Google Scholar] [CrossRef]
- Lalazissis, G.A.; König, J.; Ring, P. New parametrization for the Lagrangian density of relativistic mean field theory. Phys. Rev. C 1997, 55, 540. [Google Scholar] [CrossRef]
- Lalazissis, G.A.; Niksić, T.; Vretenar, D.; Ring, P. New relativistic mean-field interaction with density-dependent meson-nucleon couplings. Phys. Rev. C 2005, 71, 024312. [Google Scholar] [CrossRef]
- Niksić, T.; Vretenar, D.; Ring, P.; Lalazissis, G.A. Shape coexistence in the relativistic Hartree-Bogoliubov approach. Phys. Rev. C 2002, 65, 054320. [Google Scholar] [CrossRef]
- Niksić, T.; Vretenar, D.; Ring, P. Beyond the relativistic mean-field approximation: Configuration mixing of angular-momentum-projected wave functions. Phys. Rev. C 2006, 73, 034308. [Google Scholar] [CrossRef]
- Niksić, T.; Vretenar, D.; Ring, P. Beyond the relativistic mean-field approximation. II. Configuration mixing of mean-field wave functions projected on angular momentum and particle number. Phys. Rev. C 2006, 74, 064309. [Google Scholar] [CrossRef]
- Niksić, T.; Li, Z.P.; Vretenar, D.; Próchniak, L.; Meng, J.; Ring, P. Beyond the relativistic mean-field approximation. III. Collective Hamiltonian in five dimensions. Phys. Rev. C 2009, 79, 034303. [Google Scholar] [CrossRef]
- Ring, P.; Gambhir, Y.K.; Lalazissis, G.A. Computer program for the relativistic mean field description of the ground state properties of even-even axially deformed nuclei. Comp. Phys. Commun. 1997, 105, 77. [Google Scholar] [CrossRef]
- Tian, Y.; Ma, Z.Y.; Ring, P. A finite range pairing force for density functional theory in superfluid nuclei. Phys. Lett. B 2009, 676, 44. [Google Scholar] [CrossRef]
- Tian, Y.; Ma, Z.-Y.; Ring, P. Axially deformed relativistic Hartree Bogoliubov theory with a separable pairing force. Phys. Rev. C 2009, 80, 024313. [Google Scholar] [CrossRef]
- Vretenar, D.; Afanasjev, A.V.; Lalazissis, G.A.; Ring, P. Relativistic Hartree–Bogoliubov theory: Static and dynamic aspects of exotic nuclear structure. Phys. Rep. 2005, 409, 101. [Google Scholar]
- Niksić, T.; Paar, N.; Vretenar, D.; Ring, P. DIRHB—A relativistic self-consistent mean-field framework for atomic nuclei. Comp. Phys. Commun. 2014, 185, 1808. [Google Scholar] [CrossRef]
- Egido, J.L.; Robledo, L.M.; Rodríguez-Guzmán, R.R. Unveiling the Origin of Shape Coexistence in Lead Isotopes. Phys. Rev. Lett. 2004, 93, 082502. [Google Scholar] [CrossRef]
- Egido, J.L.; Jungclaus, A. Predominance of Triaxial Shapes in Transitional Super-Heavy Nuclei: Ground-State Deformation and Shape Coexistence along the Flerovium (Z = 114) Chain of Isotopes. Phys. Rev. Lett. 2020, 125, 192504. [Google Scholar] [CrossRef] [PubMed]
- Girod, M.; Delaroche, J.-P.; Görgen, A.; Obertelli, A. The role of triaxiality for the coexistence and evolution of shapes in light krypton isotopes. Phys. Lett. B 2009, 676, 39. [Google Scholar] [CrossRef]
- Guo, L.; Maruhn, J.A.; Reinhard, P.-G. Triaxiality and shape coexistence in germanium isotopes. Phys. Rev. C 2007, 76, 034317. [Google Scholar] [CrossRef]
- Péru, S.; Martini, M. Mean field based calculations with the Gogny force: Some theoretical tools to explore the nuclear structure. Eur. Phys. J. A 2014, 50, 88. [Google Scholar] [CrossRef]
- Robledo, L.M.; Rodríguez-Guzmán, R.R.; Sarriguren, P. Evolution of nuclear shapes in medium mass isotopes from a microscopic perspective. Phys. Rev. C 2008, 78, 034314. [Google Scholar] [CrossRef]
- Rodríguez, T.R.; Egido, J.L. A beyond mean field analysis of the shape transition in the Neodymium isotopes. Phys. Lett. B 2008, 663, 49. [Google Scholar] [CrossRef]
- Rodríguez, T.R.; Egido, J.L. Study of shape transitions in N∼90 isotopes with beyond mean field calculations. AIP Conf. Proc. 2009, 1090, 419. [Google Scholar]
- Rodríguez, T.R.; Egido, J.L. Multiple shape coexistence in the nucleus 80Zr. Phys. Lett. B 2011, 705, 255. [Google Scholar] [CrossRef]
- Rodríguez, T.R. Structure of krypton isotopes calculated with symmetry-conserving configuration-mixing methods. Phys. Rev. C 2014, 90, 034306. [Google Scholar] [CrossRef]
- Rodríguez-Guzmán, R.R.; Egido, J.L.; Robledo, L.M. Beyond mean field description of shape coexistence in neutron-deficient Pb isotopes. Phys. Rev. C 2004, 69, 054319. [Google Scholar] [CrossRef]
- Bender, M.; Bonche, P.; Heenen, P.-H. Shape coexistence in neutron-deficient Kr isotopes: Constraints on the single-particle spectrum of self-consistent mean-field models from collective excitations. Phys. Rev. C 2006, 74, 024312. [Google Scholar] [CrossRef]
- Duguet, T.; Bender, M.; Bonche, P.; Heenen, P.-H. Shape coexistence in 186Pb: Beyond-mean-field description by configuration mixing of symmetry restored wave functions. Phys. Lett. B 2003, 559, 201. [Google Scholar] [CrossRef]
- Fu, Y.; Tong, H.; Wang, X.F.; Wang, H.; Wang, D.Q.; Wang, X.Y.; Yao, J.M. Microscopic analysis of shape transition in neutron-deficient Yb isotopes. Phys. Rev. C 2018, 97, 014311. [Google Scholar] [CrossRef]
- Rodríguez-Guzmán, R.; Sarriguren, P. E(5) and X(5) shape phase transitions within a Skyrme-Hartree-Fock + BCS approach. Phys. Rev. C 2007, 76, 064303. [Google Scholar] [CrossRef]
- Sarriguren, P.; Rodríguez-Guzmán, R.; Robledo, L.M. Shape transitions in neutron-rich Yb, Hf, W, Os, and Pt isotopes within a Skyrme Hartree-Fock + BCS approach. Phys. Rev. C 2008, 77, 064322. [Google Scholar] [CrossRef]
- Skalski, J.; Heenen, P.-H.; Bonche, P. Shape coexistence and low-lying collective states in A≈100 Zr nuclei. Nucl. Phys. A 1993, 559, 221. [Google Scholar] [CrossRef]
- Werner, T.R.; Sheikh, J.A.; Nazarewicz, W.; Strayer, M.R.; Umar, A.S.; Misu, M. Shape coexistence around : The deformed N = 28 region. Phys. Lett. B 1994, 335, 259. [Google Scholar] [CrossRef][Green Version]
- Yao, J.M.; Bender, M.; Heenen, P.-H. Systematics of low-lying states of even-even nuclei in the neutron-deficient lead region from a beyond-mean-field calculation. Phys. Rev. C 2013, 87, 034322. [Google Scholar] [CrossRef]
- Abusara, H.; Ahmad, S.; Othman, S. Triaxiality softness and shape coexistence in Mo and Ru isotopes. Phys. Rev. C 2017, 95, 054302. [Google Scholar] [CrossRef]
- Abusara, H.; Ahmad, S. Shape evolution in Kr, Zr, and Sr isotopic chains in covariant density functional theory. Phys. Rev. C 2017, 96, 064303. [Google Scholar] [CrossRef]
- Choi, Y.-B.; Lee, C.-H.; Mun, M.-H.; Kim, Y. Bubble nuclei with shape coexistence in even-even isotopes of Hf to Hg. Phys. Rev. C 2022, 105, 024306. [Google Scholar] [CrossRef]
- Heyde, K.; De Coster, C.; Van Duppen, P.; Huyse, M.; Wood, J.L.; Nazarewicz, W. Comment on “Shape and superdeformed structure in Hg isotopes in relativistic mean field model” and “Structure of neutron-deficient Pt, Hg, and Pb isotopes”. Phys. Rev. C 1996, 53, 1035. [Google Scholar] [CrossRef]
- Kim, S.; Mun, M.-H.; Cheoun, M.-K.; Ha, E. Shape coexistence and neutron skin thickness of Pb isotopes by the deformed relativistic Hartree-Bogoliubov theory in continuum. Phys. Rev. C 2022, 105, 034340. [Google Scholar] [CrossRef]
- Kumar, P.; Dhiman, S.K. Microscopic study of shape evolution and ground state properties in even-even Cd isotopes using covariant density functional theory. Nucl. Phys. A 2020, 1001, 121935. [Google Scholar] [CrossRef]
- Kumar, P.; Thakur, V.; Thakur, S.; Kumar, V.; Dhiman, S.K. Nuclear shape evolution and shape coexistence in Zr and Mo isotopes. Eur. Phys. J. A 2021, 57, 36. [Google Scholar] [CrossRef]
- Maharana, J.P.; Gambhir, Y.K.; Sheikh, J.A.; Ring, P. Shape coexistence and extreme deformations near A = 80. Phys. Rev. C 1992, 46, R1163. [Google Scholar] [CrossRef] [PubMed]
- Meng, J.; Zhang, W.; Zhou, S.G.; Toki, H.; Geng, L.S. Shape evolution for Sm isotopes in relativistic mean-field theory. Eur. Phys. J. A 2005, 25, 23. [Google Scholar] [CrossRef]
- Naz, T.; Bhat, G.H.; Jehangir, S.; Ahmad, S.; Sheikh, J.A. Microscopic description of structural evolution in Pd, Xe, Ba, Nd, Sm, Gd and Dy isotopes. Nucl. Phys. A 2018, 979, 1. [Google Scholar] [CrossRef]
- Niksić, T.; Vretenar, D.; Lalazissis, G.A.; Ring, P. Microscopic Description of Nuclear Quantum Phase Transitions. Phys. Rev. Lett. 2007, 99, 092502. [Google Scholar] [CrossRef]
- Patra, S.K.; Yoshida, S.; Takigawa, N.; Praharaj, C.R. Shape and superdeformed structure in Hg isotopes in relativistic mean field model. Phys. Rev. C 1994, 50, 1924. [Google Scholar] [CrossRef]
- Ren, Z. Shape coexistence in even-even superheavy nuclei. Phys. Rev. C 2002, 65, 051304. [Google Scholar] [CrossRef]
- Sharma, M.M.; Ring, P. Relativistic mean-field description of neutron-deficient platinum isotopes. Phys. Rev. C 1992, 46, 1715. [Google Scholar] [CrossRef]
- Sharma, S.; Devi, R.; Khosa, S.K. Microscopic study of evolution of shape change across even-even mass chain of tellurium isotopes using relativistic Hartree-Bogoliubov model. Nucl. Phys. A 2019, 988, 9. [Google Scholar] [CrossRef]
- Sheng, Z.-Q.; Guo, J.-Y. Systematic analysis of critical point nuclei in the rare-earth region with relativistic mean field theory. Mod. Phys. Lett. A 2005, 20, 2711. [Google Scholar] [CrossRef]
- Takigawa, N.; Yoshida, S.; Hagino, K.; Patra, S.K.; Praharaj, C.R. Reply to “Comment on `Shape and superdeformed structure in Hg isotopes in relativistic mean field model’ and `Structure of neutron-deficient Pt, Hg, and Pb isotopes”’. Phys. Rev. C 1996, 53, 1038. [Google Scholar] [CrossRef] [PubMed]
- Thakur, S.; Kumar, P.; Thakur, V.; Kumar, V.; Dhiman, S.K. Shape transitions and shell structure study in zirconium, molybdenum and ruthenium. Nucl. Phys. A 2021, 1014, 122254. [Google Scholar] [CrossRef]
- Thakur, S.; Kumar, P.; Thakur, V.; Kumar, V.; Dhiman, S.K. Nuclear Shape Evolution in Palladium Isotopes. Acta Phys. Pol. B 2021, 52, 1433. [Google Scholar] [CrossRef]
- Wang, G.; Fang, X.-Z.; Guo, J.-Y. Analysis of shape evolution for Pt isotopes with relativistic mean field theory. Acta Phys. Sin. 2012, 61, 102101. [Google Scholar] [CrossRef]
- Wu, X.Y.; Mei, H.; Yao, J.M.; Zhou, X.-R. Beyond-mean-field study of the hyperon impurity effect in hypernuclei with shape coexistence. Phys. Rev. C 2017, 95, 034309. [Google Scholar] [CrossRef]
- Yoshida, S.; Patra, S.K.; Takigawa, N.; Praharaj, C.R. Structure of neutron-deficient Pt, Hg, and Pb isotopes. Phys. Rev. C 1994, 50, 1398. [Google Scholar] [CrossRef]
- Yu, M.; Zhang, P.-F.; Ruan, T.-N.; Guo, J.-Y. Shape evolution for Ce isotopes in relativistic mean-field theory. Int. J. Mod. Phys. E 2006, 15, 939. [Google Scholar] [CrossRef]
- Dobaczewski, J. Current Developments in Nuclear Density Functional Methods. J. Phys. Conf. Ser. 2011, 312, 092002. [Google Scholar] [CrossRef]
- Dobaczewski, J.; Bennaceur, K.; Raimondi, F. Effective theory for low-energy nuclear energy density functionals. J. Phys. G Nucl. Part. Phys. 2012, 39, 125103. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Drut, J.E.; Furnstahl, R.J.; Platter, L. Toward ab initio density functional theory for nuclei. Prog. Part. Nucl. Phys. 2010, 64, 120. [Google Scholar] [CrossRef]
- Garrett, P.E.; Rodríguez, T.R.; Varela, A.D.; Green, K.L.; Bangay, J.; Finlay, A.; Austin, R.A.E.; Ball, G.C.; Garnsworthy, A.B.; Grinyer, G.F.; et al. Multiple Shape Coexistence in 110,112Cd. Phys. Rev. Lett. 2019, 123, 142502. [Google Scholar] [CrossRef]
- Garrett, P.E.; Rodríguez, T.R.; Diaz Varela, A.; Green, K.L.; Bangay, J.; Finlay, A.; Austin, R.A.E.; Ball, G.C.; Bandyopadhyay, D.S.; Bildstein, V.; et al. Shape coexistence and multiparticle-multihole structures in 110,112Cd. Phys. Rev. C 2020, 101, 044302. [Google Scholar] [CrossRef]
- Dobaczewski, J.; Skalski, J. The quadrupole vibrational inertial function in the adiabatic time-dependent Hartree-Fock-Bogolyubov approximation. Nucl. Phys. A 1981, 369, 123. [Google Scholar] [CrossRef]
- Ebata, S.; Kimura, M. Quenching of N = 28 shell gap and a low-lying quadrupole mode in the vicinity of neutron-rich N = 28 isotones. JPS Conf. Proc. 2015, 6, 030093. [Google Scholar]
- Próchniak, L. E(5) and X(5) Dynamical Symmetries from a Microscopic Perspective. Acta Phys. Pol. B 2007, 38, 1605. [Google Scholar]
- Petrovici, A.; Schmid, K.W.; Grümmer, F.; Faessler, A. Shape coexistence at high spins in the nuclei 68Ge and 72Se. Nucl. Phys. A 1989, 504, 277. [Google Scholar] [CrossRef]
- Petrovici, A.; Schmid, K.W.; Grümmer, F.; Faessler, A. Some new aspects of the shape coexistence in the A = 70 mass region. Nucl. Phys. A 1990, 517, 108. [Google Scholar] [CrossRef]
- Petrovici, A.; Hammarén, E.; Schmid, K.W.; Grümmer, F.; Faessler, A. Shape coexistence in the A∼70 region including neutron-proton interaction and unnatural-parity correlations in the mean field. Nucl. Phys. A 1992, 549, 352. [Google Scholar] [CrossRef]
- Petrovici, A.; Schmid, K.W.; Faessler, A. Shape coexistence and shape transition in N≃Z nuclei from krypton to molybdenum. Nucl. Phys. A 1996, 605, 290. [Google Scholar] [CrossRef]
- Petrovici, A.; Schmid, K.W.; Faessler, A. Microscopic aspects of shape coexistence in 72Kr and 74Kr. Nucl. Phys. A 2000, 665, 333. [Google Scholar] [CrossRef]
- Petrovici, A.; Schmid, K.W.; Faessler, A. Variational approach to shape coexistence in 56Ni. Nucl. Phys. A 2001, 689, 707. [Google Scholar] [CrossRef]
- Petrovici, A.; Schmid, K.W.; Faessler, A. Shape coexistence and center-of-mass effects in N=Z medium mass nuclei. Nucl. Phys. A 2002, 708, 190. [Google Scholar] [CrossRef]
- Petrovici, A.; Schmid, K.W.; Faessler, A. Variational approach to shape coexistence in 68Se. Nucl. Phys. A 2002, 710, 246. [Google Scholar] [CrossRef]
- Petrovici, A. Triple shape coexistence and shape evolution in the N = 58 Sr and Zr isotopes. Phys. Rev. C 2012, 85, 034337. [Google Scholar] [CrossRef]
- Petrovici, A. Isospin-symmetry breaking and shape coexistence in A≈70 analogs. Phys. Rev. C 2015, 91, 014302. [Google Scholar] [CrossRef]
- Petrovici, A.; Andrei, O. Weak interaction rates and shape coexistence for the Z=N+2 isotopes 70Kr and 74Sr. Phys. Rev. C 2015, 92, 064305. [Google Scholar] [CrossRef]
- Petrovici, A.; Andrei, O. Stellar weak interaction rates and shape coexistence for 68Se and 72Kr waiting points. Eur. Phys. J. A 2015, 51, 133. [Google Scholar] [CrossRef]
- Petrovici, A. Shape evolution in proton-rich and neutron-rich Kr isotopes within the beyond-mean-field approach. Phys. Scr. 2017, 92, 064003. [Google Scholar] [CrossRef]
- Petrovici, A.; Andrei, O.; Chilug, A. Exotic phenomena in medium mass N≃Z nuclei within the beyond-mean-field approach. Phys. Scr. 2018, 93, 114001. [Google Scholar] [CrossRef]
- Petrovici, A.; Mare, A.S. Triple shape coexistence and β decay of 96Y to 96Zr. Phys. Rev. C 2020, 101, 024307. [Google Scholar] [CrossRef]
- Schmid, K.W.; Grümmer, F.; Kyotoku, M.; Faessler, A. Selfconsistent description of non-yrast states in nuclei: The excited VAMPIR approach. Nucl. Phys. A 1986, 452, 493. [Google Scholar] [CrossRef]
- Matsuyanagi, K.; Matsuo, M.; Nakatsukasa, T.; Yoshida, K.; Hinohara, N.; Sato, K. Microscopic derivation of the quadrupole collective Hamiltonian for shape coexistence/mixing dynamics. J. Phys. G Nucl. Part. Phys. 2016, 43, 024006. [Google Scholar] [CrossRef]
- Hinohara, N.; Nakatsukasa, T.; Matsuo, M.; Matsuyanagi, K. Microscopic description of oblate-prolate shape mixing in proton-rich Se isotopes. Phys. Rev. C 2009, 80, 014305. [Google Scholar] [CrossRef]
- Hinohara, N.; Sato, K.; Nakatsukasa, T.; Matsuo, M.; Matsuyanagi, K. Microscopic description of large-amplitude shape-mixing dynamics with inertial functions derived in local quasiparticle random-phase approximation. Phys. Rev. C 2010, 82, 064313. [Google Scholar] [CrossRef]
- Hinohara, N.; Kanada-En’yo, Y. Triaxial quadrupole deformation dynamics in sd-shell nuclei around 26Mg. Phys. Rev. C 2011, 83, 014321. [Google Scholar] [CrossRef]
- Hinohara, N.; Sato, K.; Yoshida, K.; Nakatsukasa, T.; Matsuo, M.; Matsuyanagi, K. Shape fluctuations in the ground and excited 0+ states of 30,32,34 Mg. Phys. Rev. C 2011, 84, 061302. [Google Scholar] [CrossRef]
- Sato, K.; Hinohara, N. Shape mixing dynamics in the low-lying states of proton-rich Kr isotopes. Nucl. Phys. A 2011, 849, 53. [Google Scholar] [CrossRef]
- Sato, K.; Hinohara, N.; Yoshida, K.; Nakatsukasa, T.; Matsuo, M.; Matsuyanagi, K. Shape transition and fluctuations in neutron-rich Cr isotopes around N = 40. Phys. Rev. C 2012, 86, 024316. [Google Scholar] [CrossRef]
- Yoshida, K.; Hinohara, N. Shape changes and large-amplitude collective dynamics in neutron-rich Cr isotopes. Phys. Rev. C 2011, 83, 061302. [Google Scholar] [CrossRef]
- Nomura, K.; Shimizu, N.; Otsuka, T. Mean-Field Derivation of the Interacting Boson Model Hamiltonian and Exotic Nuclei. Phys. Rev. Lett. 2008, 101, 142501. [Google Scholar] [CrossRef] [PubMed]
- Nomura, K.; Shimizu, N.; Otsuka, T. Formulating the interacting boson model by mean-field methods. Phys. Rev. C 2010, 81, 044307. [Google Scholar] [CrossRef]
- Nomura, K.; Otsuka, T.; Shimizu, N.; Guo, L. Microscopic formulation of the interacting boson model for rotational nuclei. Phys. Rev. C 2011, 83, 041302. [Google Scholar] [CrossRef]
- Nomura, K.; Otsuka, T.; Rodríguez-Guzmán, R.; Robledo, L.M.; Sarriguren, P.; Regan, P.H.; Stevenson, P.D.; Podolyák, Z. Spectroscopic calculations of the low-lying structure in exotic Os and W isotopes. Phys. Rev. C 2011, 83, 054303. [Google Scholar] [CrossRef]
- Nomura, K.; Shimizu, N.; Vretenar, D.; Niksić, T.; Otsuka, T. Robust Regularity in γ-Soft Nuclei and Its Microscopic Realization. Phys. Rev. Lett. 2012, 108, 132501. [Google Scholar] [CrossRef]
- Arima, A.; Iachello, F. Collective Nuclear States as Representations of a SU(6) Group. Phys. Rev. Lett. 1975, 35, 1069. [Google Scholar] [CrossRef]
- Casten, R.F. (Ed.) Algebraic Approaches to Nuclear Structure: Interacting Boson and Fermion Models; Harwood: Chur, Switzerland, 1993. [Google Scholar]
- Frank, A.; Van Isacker, P. Symmetry Methods in Molecules and Nuclei; S y G Editores: Ciudad de Mexico, Mexico, 2005. [Google Scholar]
- Iachello, F.; Arima, A. The Interacting Boson Model; Cambridge U. Press: Cambridge, UK, 1987. [Google Scholar]
- Iachello, F.; Van Isacker, P. The Interacting Boson-Fermion Model; Cambridge U. Press: Cambridge, UK, 1991. [Google Scholar]
- Nomura, K.; Otsuka, T.; Rodríguez-Guzmán, R.; Robledo, L.M.; Sarriguren, P. Structural evolution in Pt isotopes with the interacting boson model Hamiltonian derived from the Gogny energy density functional. Phys. Rev. C 2011, 83, 014309. [Google Scholar] [CrossRef]
- Nomura, K.; Niksić, T.; Otsuka, T.; Shimizu, N.; Vretenar, D. Quadrupole collective dynamics from energy density functionals: Collective Hamiltonian and the interacting boson model. Phys. Rev. C 2011, 84, 014302. [Google Scholar] [CrossRef]
- Nomura, K.; Otsuka, T.; Rodríguez-Guzmán, R.; Robledo, L.M.; Sarriguren, P. Collective structural evolution in neutron-rich Yb, Hf, W, Os, and Pt isotopes. Phys. Rev. C 2011, 84, 054316. [Google Scholar] [CrossRef]
- Nomura, K.; Rodríguez-Guzmán, R.; Robledo, L.M.; Shimizu, N. Shape coexistence in lead isotopes in the interacting boson model with a Gogny energy density functional. Phys. Rev. C 2012, 86, 034322. [Google Scholar] [CrossRef]
- Nomura, K.; Rodríguez-Guzmán, R.; Robledo, L.M. Shape evolution and the role of intruder configurations in Hg isotopes within the interacting boson model based on a Gogny energy density functional. Phys. Rev. C 2013, 87, 064313. [Google Scholar] [CrossRef]
- Nomura, K.; Rodríguez-Guzmán, R.; Robledo, L.M. Structural evolution in A≈100 nuclei within the mapped interacting boson model based on the Gogny energy density functional. Phys. Rev. C 2016, 94, 044314. [Google Scholar] [CrossRef]
- Nomura, K.; Otsuka, T.; Van Isacker, P. Shape coexistence in the microscopically guided interacting boson model. J. Phys. G Nucl. Part. Phys. 2016, 43, 024008. [Google Scholar] [CrossRef]
- Nomura, K.; Rodríguez-Guzmán, R.; Robledo, L.M. Structural evolution in germanium and selenium nuclei within the mapped interacting boson model based on the Gogny energy density functional. Phys. Rev. C 2017, 95, 064310. [Google Scholar] [CrossRef]
- Nomura, K.; Rodríguez-Guzmán, R.; Humadi, Y.M.; Robledo, L.M.; Abusara, H. Structure of krypton isotopes within the interacting boson model derived from the Gogny energy density functional. Phys. Rev. C 2017, 96, 034310. [Google Scholar] [CrossRef]
- Nomura, K.; Jolie, J. Structure of even-even cadmium isotopes from the beyond-mean-field interacting boson model. Phys. Rev. C 2018, 98, 024303. [Google Scholar] [CrossRef]
- Nomura, K.; Zhang, Y. Two-neutron transfer reactions and shape phase transitions in the microscopically formulated interacting boson model. Phys. Rev. C 2019, 99, 024324. [Google Scholar] [CrossRef]
- Nomura, K.; Rodríguez-Guzmán, R.; Robledo, L. M > β decay of even-A nuclei within the interacting boson model with input based on nuclear density functional theory. Phys. Rev. C 2020, 101, 044318. [Google Scholar] [CrossRef]
- Nomura, K.; Vretenar, D.; Li, Z.P.; Xiang, J. Pairing vibrations in the interacting boson model based on density functional theory. Phys. Rev. C 2020, 102, 054313. [Google Scholar] [CrossRef]
- Thomas, T.; Nomura, K.; Werner, V.; Ahn, T.; Cooper, N.; Duckwitz, H.; Hinton, M.; Ilie, G.; Jolie, J.; Petkov, P.; et al. Evidence for shape coexistence in 98Mo. Phys. Rev. C 2013, 88, 044305. [Google Scholar] [CrossRef]
- Thomas, T.; Werner, V.; Jolie, J.; Nomura, K.; Ahn, T.; Cooper, N.; Duckwitz, H.; Fitzler, A.; Fransen, C.; Gade, A.; et al. Nuclear structure of 96,98Mo: Shape coexistence and mixed-symmetry states. Nucl. Phys. A 2016, 947, 203–233. [Google Scholar] [CrossRef]
- Li, Z.P.; Niksić, T.; Vretenar, D.; Meng, J.; Lalazissis, G.A.; Ring, P. Microscopic analysis of nuclear quantum phase transitions in the N≈90 region. Phys. Rev. C 2009, 79, 054301. [Google Scholar] [CrossRef]
- Li, Z.P.; Niksić, T.; Vretenar, D.; Meng, J. Microscopic analysis of order parameters in nuclear quantum phase transitions. Phys. Rev. C 2009, 80, 061301. [Google Scholar] [CrossRef]
- Li, Z.P.; Niksić, T.; Vretenar, D. Coexistence of nuclear shapes: Self-consistent mean-field and beyond. J. Phys. G Nucl. Part. Phys. 2016, 43, 024005. [Google Scholar] [CrossRef]
- Lu, K.Q.; Li, Z.X.; Li, Z.P.; Yao, J.M.; Meng, J. Global study of beyond-mean-field correlation energies in covariant energy density functional theory using a collective Hamiltonian method. Phys. Rev. C 2015, 91, 027304. [Google Scholar] [CrossRef]
- Niksić, T.; Vretenar, D.; Ring, P. Relativistic nuclear energy density functionals: Mean-field and beyond. Prog. Part. Nucl. Phys. 2011, 66, 519. [Google Scholar] [CrossRef]
- Quan, S.; Chen, Q.; Li, Z.P.; Niksić, T.; Vretenar, D. Global analysis of quadrupole shape invariants based on covariant energy density functionals. Phys. Rev. C 2017, 95, 054321. [Google Scholar] [CrossRef]
- Yang, Y.L.; Wang, Y.K.; Zhao, P.W.; Li, Z.P. Nuclear landscape in a mapped collective Hamiltonian from covariant density functional theory. Phys. Rev. C 2021, 104, 054312. [Google Scholar] [CrossRef]
- Li, Z.P.; Niksić, T.; Vretenar, D.; Meng, J. Microscopic description of spherical to γ–soft shape transitions in Ba and Xe nuclei. Phys. Rev. C 2010, 81, 034316. [Google Scholar] [CrossRef]
- Li, Z.P.; Niksić, T.; Vretenar, D.; Ring, P.; Meng, J. Relativistic energy density functionals: Low-energy collective states of 240Pu and 166Er. Phys. Rev. C 2010, 81, 064321. [Google Scholar] [CrossRef]
- Li, Z.P.; Yao, J.M.; Vretenar, D.; Niksić, T.; Chen, H.; Meng, J. Energy density functional analysis of shape evolution in N = 28 isotones. Phys. Rev. C 2011, 84, 054304. [Google Scholar] [CrossRef]
- Majola, S.N.T.; Shi, Z.; Song, B.Y.; Li, Z.P.; Zhang, S.Q.; Bark, R.A.; Sharpey-Schafer, J.F.; Aschman, D.G.; Bvumbi, S.P.; Bucher, T.D.; et al. β and γ bands in N = 88, 90, and 92 isotones investigated with a five-dimensional collective Hamiltonian based on covariant density functional theory: Vibrations, shape coexistence, and superdeformation. Phys. Rev. C 2019, 100, 044324. [Google Scholar] [CrossRef]
- Xiang, J.; Li, Z.P.; Li, Z.X.; Yao, J.M.; Meng, J. Covariant description of shape evolution and shape coexistence in neutron-rich nuclei at N≈60. Nucl. Phys. A 2012, 873, 1. [Google Scholar] [CrossRef]
- Xiang, J.; Li, Z.P.; Long, W.H.; Niksić, T.; Vretenar, D. Shape evolution and coexistence in neutron-deficient Nd and Sm nuclei. Phys. Rev. C 2018, 98, 054308. [Google Scholar] [CrossRef]
- Yang, X.Q.; Wang, L.J.; Xiang, J.; Wu, X.Y.; Li, Z.P. Microscopic analysis of prolate-oblate shape phase transition and shape coexistence in the Er-Pt region. Phys. Rev. C 2021, 103, 054321. [Google Scholar] [CrossRef]
- Rainwater, J. Nuclear Energy Level Argument for a Spheroidal Nuclear Model. Phys. Rev. 1950, 79, 432. [Google Scholar] [CrossRef]
- Bohr, A. The coupling of nuclear surface oscillations to the motion of individual nucleons. Dan. Mat. Fys. Medd. 1952, 26, 14. [Google Scholar]
- Bohr, A.; Mottelson, B.R. Collective and individual-particle aspects of nuclear structure. Dan. Mat. Fys. Medd. 1953, 27, 16. [Google Scholar]
- Bohr, A.; Mottelson, B.R. Nuclear Structure Vol. I: Single-Particle Motion; World Scientific: Singapore, 1998. [Google Scholar]
- Bohr, A.; Mottelson, B.R. Nuclear Structure Vol. II: Nuclear Deformations; World Scientific: Singapore, 1998. [Google Scholar]
- Nilsson, S.G. Binding states of individual nucleons in strongly deformed nuclei. Dan. Mat. Fys. Medd. 1955, 29, 16. [Google Scholar]
- Ragnarsson, I.; Nilsson, S.G. Shell structure in nuclei. Phys. Rep. 1978, 45, 1. [Google Scholar] [CrossRef]
- Lederer, C.M.; Shirley, V.S. (Eds.) Table of Isotopes, 7th ed.; Wiley: New York, NY, USA, 1978. [Google Scholar]
- Baranger, M.; Kumar, K. Nuclear deformations in the pairing-plus-quadrupole model: (I). The single-j shell. Nucl. Phys. 1965, 62, 113. [Google Scholar] [CrossRef]
- Baranger, M.; Kumar, K. Nuclear deformations in the pairing-plus-quadrupole model: (II). Discussion of validity of the model. Nucl. Phys. A 1968, 110, 490. [Google Scholar] [CrossRef]
- Kumar, K.; Baranger, M. Nuclear deformations in the pairing-plus-quadrupole model: (III). Static nuclear shapes in the rare-earth region. Nucl. Phys. A 1968, 110, 529. [Google Scholar] [CrossRef]
- Brink, D.M.; Broglia, R.A. Nuclear Superfluidity: Pairing in Finite Systems; Cambridge U. Press: Cambridge, UK, 2005. [Google Scholar]
- Shlomo, S.; Talmi, I. Shell-model hamiltonians with generalized seniority eigenstates. Nucl. Phys. A 1972, 198, 81. [Google Scholar] [CrossRef]
- Talmi, I. Effective Interactions and Coupling Schemes in Nuclei. Rev. Mod. Phys. 1962, 34, 704. [Google Scholar] [CrossRef]
- Talmi, I. Generalized seniority and structure of semi-magic nuclei. Nucl. Phys. A 1971, 172, 1. [Google Scholar] [CrossRef]
- Talmi, I. Coupling schemes in nuclei. Riv. Nuovo C. 1973, 3, 85. [Google Scholar] [CrossRef]
- Talmi, I. Effective interactions and coupling schemes in nuclei. Nucl. Phys. A 1994, 570, 319c. [Google Scholar] [CrossRef]
- Casten, R.F. Possible Unified Interpretation of Heavy Nuclei. Phys. Rev. Lett. 1985, 54, 1991. [Google Scholar] [CrossRef]
- Casten, R.F. NpNn systematics in heavy nuclei. Nucl. Phys. A 1985, 443, 1. [Google Scholar] [CrossRef]
- Casten, R.F. Nuclei far off stability in the NpNn scheme. Phys. Rev. C 1986, 33, 1819. [Google Scholar] [CrossRef] [PubMed]
- Casten, R.F. Nuclear Structure from a Simple Perspective; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Casten, R.F.; Brenner, D.S.; Haustein, P.E. Valence p-n interactions and the development of collectivity in heavy nuclei. Phys. Rev. Lett. 1987, 58, 658. [Google Scholar] [CrossRef] [PubMed]
- Bender, M.; Heenen, P.-H. What can be learned from binding energy differences about nuclear structure: The example of δVpn. Phys. Rev. C 2011, 83, 064319. [Google Scholar] [CrossRef]
- Bonatsos, D.; Karampagia, S.; Cakirli, R.B.; Casten, R.F.; Blaum, K.; Amon Susam, L. Emergent collectivity in nuclei and enhanced proton-neutron interactions. Phys. Rev. C 2013, 88, 054309. [Google Scholar] [CrossRef]
- Brenner, D.S.; Wesselborg, C.; Casten, R.F.; Warner, D.D.; Zhang, J.-Y. Empirical p-n interactions: Global trends, configuration sensitivity and N = Z enhancements. Phys. Lett. B 1990, 243, 1–6. [Google Scholar] [CrossRef]
- Brenner, D.S.; Cakirli, R.B.; Casten, R.F. Valence proton-neutron interactions throughout the mass surface. Phys. Rev. C 2006, 73, 034315. [Google Scholar] [CrossRef]
- Cakirli, R.B.; Brenner, D.S.; Casten, R.F.; Millman, E.A. Proton-Neutron Interactions and the New Atomic Masses. Phys. Rev. Lett. 2005, 94, 092501, Erratum in Phys. Rev. Lett. 2005, 95, 119903. [Google Scholar] [CrossRef]
- Cakirli, R.B.; Casten, R.F. Direct Empirical Correlation between Proton-Neutron Interaction Strengths and the Growth of Collectivity in Nuclei. Phys. Rev. Lett. 2006, 96, 132501. [Google Scholar] [CrossRef]
- Cakirli, R.B.; Blaum, K.; Casten, R.F. Indication of a mini-valence Wigner-like energy in heavy nuclei. Phys. Rev. C 2010, 82, 061304. [Google Scholar] [CrossRef]
- Cakirli, R.B.; Casten, R.F. Nuclear binding and nuclear structure. Int. J. Mass Spectrom. 2013, 187, 349–350. [Google Scholar] [CrossRef]
- Oktem, Y.; Cakirli, R.B.; Casten, R.F.; Casperson, R.J.; Brenner, D.S. Simple interpretation of proton-neutron interactions in rare earth nuclei. Phys. Rev. C 2006, 74, 027304. [Google Scholar] [CrossRef]
- Stoitsov, M.; Cakirli, R.B.; Casten, R.F.; Nazarewicz, W.; Satuła, W. Empirical Proton-Neutron Interactions and Nuclear Density Functional Theory: Global, Regional, and Local Comparisons. Phys. Rev. Lett. 2007, 98, 132502. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.-Y.; Casten, R.F.; Brenner, D.S. Empirical proton-neutron interaction energies. Linearity and saturation phenomena. Phys. Lett. B 1989, 227, 1. [Google Scholar] [CrossRef]
- Casten, R.F.; Cakirli, R.B. The evolution of collectivity in nuclei and the proton–neutron interaction. Phys. Scr. 2016, 91, 033004. [Google Scholar] [CrossRef]
- Ait Ben Mennana, A.; Benjedi, R.; Budaca, R.; Buganu, P.; El Bassem, Y.; Lahbas, A.; Oulne, M. Mixing of the coexisting shapes in the ground states of 74Ge and 74Kr. Phys. Scr. 2021, 96, 125306. [Google Scholar] [CrossRef]
- Ait Ben Mennana, A.; Benjedi, R.; Budaca, R.; Buganu, P.; El Bassem, Y.; Lahbas, A.; Oulne, M. Shape and structure for the low-lying states of the 80Ge nucleus. Phys. Rev. C 2022, 105, 034347. [Google Scholar] [CrossRef]
- Budaca, R.; Buganu, P.; Budaca, A.I. Bohr Model Solution for a Shape Coexisting Potential. Bulg. J. Phys. 2017, 44, 319. [Google Scholar]
- Budaca, R.; Buganu, P.; Budaca, A.I. Bohr model description of the critical point for the first order shape phase transition. Phys. Lett. B 2018, 776, 26. [Google Scholar] [CrossRef]
- Budaca, R.; Buganu, P.; Budaca, A.I. Geometrical model description of shape coexistence in Se isotopes. Nucl. Phys. A 2019, 990, 137. [Google Scholar] [CrossRef]
- Budaca, R.; Budaca, A.I.; Buganu, P. Application of the Bohr Hamiltonian with a double-well sextic potential to collective states in Mo isotopes. J. Phys. G Nucl. Part. Phys. 2019, 46, 125102. [Google Scholar] [CrossRef]
- Georgoudis, P.E.; Leviatan, A. Aspects of Shape Coexistence in the Geometric Collective Model of Nuclei. J. Phys. Conf. Ser. 2018, 966, 012043. [Google Scholar] [CrossRef]
- Budaca, R.; Budaca, A.I. Stepped infinite square well potential for collective excitations in even–even nuclei. Eur. Phys. J. Plus 2021, 136, 983. [Google Scholar] [CrossRef]
- Mardyban, E.V.; Kolganova, E.A.; Shneidman, T.M.; Jolos, R.V.; Pietralla, N. Description of the low-lying collective states of 96Zr based on the collective Bohr Hamiltonian including the triaxiality degree of freedom. Phys. Rev. C 2020, 102, 034308. [Google Scholar] [CrossRef]
- Mardyban, E.V.; Kolganova, E.A.; Shneidman, T.M.; Jolos, R.V. Evolution of the phenomenologically determined collective potential along the chain of Zr isotopes. Phys. Rev. C 2022, 105, 024321. [Google Scholar] [CrossRef]
- Sato, K.; Hinohara, N.; Nakatsukasa, T.; Matsuo, M.; Matsuyanagi, K. A model analysis of triaxial deformation dynamics in oblate-prolate shape coexistence phenomena. Prog. Theor. Phys. 2010, 123, 129–155. [Google Scholar] [CrossRef]
- Elliott, J.P. Collective motion in the nuclear shell model. I. Classification schemes for states of mixed configurations. Proc. R. Soc. A Ser. A 1958, 245, 128. [Google Scholar]
- Elliott, J.P. Collective motion in the nuclear shell model II. The introduction of intrinsic wave-functions. Proc. R. Soc. A Ser. A 1958, 245, 562. [Google Scholar]
- Elliott, J.P.; Harvey, M. Collective motion in the nuclear shell model III. The calculation of spectra. Proc. R. Soc. A Ser. A 1963, 272, 557. [Google Scholar]
- Elliott, J.P.; Wilsdon, C.E. Collective motion in the nuclear shell model IV. Odd-mass nuclei in the sd shell. Proc. R. Soc. A Ser. A 1968, 302, 509. [Google Scholar]
- Harvey, M. The nuclear SU3 model. Adv. Nucl. Phys. 1968, 1, 67. [Google Scholar]
- Gilmore, R. Lie Groups, Lie Algebras, and Some of Their Applications; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Kota, V.K.B. SU(3) Symmetry in Atomic Nuclei; Springer Nature: Singapore, 2020. [Google Scholar]
- Rowe, D.J.; Wood, J.L. Fundamentals of Nuclear Models: Foundation Models; World Scientific: Singapore, 2010. [Google Scholar]
- Bonatsos, D.; Klein, A. Exact boson mappings for nuclear neutron (proton) shell-model algebras having SU(3) subalgebras. Ann. Phys. 1986, 169, 61. [Google Scholar] [CrossRef]
- Arima, A.; Harvey, M.; Shimizu, K. Pseudo LS coupling and pseudo SU3 coupling schemes. Phys. Lett. B 1969, 30, 517. [Google Scholar] [CrossRef]
- Bahri, C.; Draayer, J.P.; Moszkowski, S.A. Pseudospin symmetry in nuclear physics. Phys. Rev. Lett. 1992, 68, 2133. [Google Scholar] [CrossRef]
- Draayer, J.P.; Weeks, K.J.; Hecht, K.T. Strength of the Qπ·Qν interaction and the strong-coupled pseudo-SU(3) limit. Nucl. Phys. A 1982, 381, 1. [Google Scholar] [CrossRef]
- Draayer, J.P.; Weeks, K.J. Shell-Model Description of the Low-Energy Structure of Strongly Deformed Nuclei. Phys. Rev. Lett. 1983, 51, 1422. [Google Scholar] [CrossRef]
- Draayer, J.P.; Weeks, K.J. Towards a shell model description of the low-energy structure of deformed nuclei I. Even-even systems. Ann. Phys. 1984, 156, 41. [Google Scholar] [CrossRef]
- Ginocchio, J.N. Pseudospin as a Relativistic Symmetry. Phys. Rev. Lett. 1997, 78, 436. [Google Scholar] [CrossRef]
- Hecht, K.T.; Adler, A. Generalized seniority for favored J≠0 pairs in mixed configurations. Nucl. Phys. A 1969, 137, 129. [Google Scholar] [CrossRef]
- Ratna Raju, R.D.; Draayer, J.P.; Hecht, K.T. Search for a coupling scheme in heavy deformed nuclei: The pseudo SU(3) model. Nucl. Phys. A 1973, 202, 433. [Google Scholar] [CrossRef]
- Castaños, O.; Moshinsky, M.; Quesne, C. Transformation from U(3) to pseudo U(3) basis. In Group Theory and Special Symmetries in Nuclear Physics (AnnArbor, 1991); Draayer, J.P., Jänecke, J., Eds.; World Scientific: Singapore, 1992; p. 80. [Google Scholar]
- Castaños, O.; Moshinsky, M.; Quesne, C. Transformation to pseudo-SU(3) in heavy deformed nuclei. Phys. Lett. B 1992, 277, 238. [Google Scholar] [CrossRef]
- Castaños, O.; Velázquez, A.V.; Hess, P.O.; Hirsch, J.G. Transformation to pseudo-spin-symmetry of a deformed Nilsson hamiltonian. Phys. Lett. B 1994, 321, 303. [Google Scholar] [CrossRef]
- Bonatsos, D.; Assimakis, I.E.; Martinou, A. Proton-Neutron Pairs in Heavy Deformed Nuclei. Bulg. J. Phys. 2015, 42, 439. [Google Scholar]
- Martinou, A.; Assimakis, I.E.; Minkov, N.; Bonatsos, D. Emergence of SU(3) symmetry in heavy deformed nuclei. Nucl. Theory 2016, 35, 224. [Google Scholar]
- Castaños, O.; Draayer, J.P.; Leschber, L. Towards a shell-model description of the low-energy structure of deformed nuclei II. Electromagnetic properties of collective M1 bands. Ann. Phys. 1987, 180, 290. [Google Scholar] [CrossRef]
- Vargas, C.E.; Hirsch, J.G.; Draayer, J.P. Pseudo SU(3) shell model: Normal parity bands in odd-mass nuclei. Nucl. Phys. A 2000, 673, 219. [Google Scholar] [CrossRef]
- Weeks, K.J.; Draayer, J.P. Shell-model predictions for unique parity yrast configurations of odd-mass deformed nuclei. Nucl. Phys. A 1983, 393, 69. [Google Scholar] [CrossRef]
- Troltenier, D.; Bahri, C.; Draayer, J.P. Generalized pseudo-SU(3) model and pairing. Nucl. Phys. A 1995, 586, 53. [Google Scholar] [CrossRef]
- Troltenier, D.; Bahri, C.; Draayer, J.P. Effects of pairing in the pseudo-SU(3) model. Nucl. Phys. A 1995, 589, 75. [Google Scholar] [CrossRef][Green Version]
- Castaños, O.; Hirsch, J.G.; Civitarese, O.; Hess, P.O. Double-beta decay in the pseudo SU(3) scheme. Nucl. Phys. A 1994, 571, 276. [Google Scholar] [CrossRef]
- Hirsch, J.G.; Castaños, O.; Hess, P.O. Neutrinoless double beta decay in heavy deformed nuclei. Nucl. Phys. A 1995, 582, 124. [Google Scholar] [CrossRef]
- Zuker, A.P.; Retamosa, J.; Poves, A.; Caurier, E. Spherical shell model description of rotational motion. Phys. Rev. C 1995, 52, R1741. [Google Scholar] [CrossRef]
- Zuker, A.P.; Poves, A.; Nowacki, F.; Lenzi, S.M. Nilsson-SU3 self-consistency in heavy N = Z nuclei. Phys. Rev. C 2015, 92, 024320. [Google Scholar] [CrossRef]
- Kaneko, K.; Shimizu, N.; Mizusaki, T.; Sun, Y. Quasi-SU(3) coupling of (1h11/2, 2f7/2) across the N = 82 shell gap: Enhanced E2 collectivity and shape evolution in Nd isotopes. Phys. Rev. C 2021, 103, L021301. [Google Scholar] [CrossRef]
- Kaneko, K.; Sun, Y.; Shimizu, N.; Mizusaki, T. Quasi-SU(3) Coupling Induced Oblate-Prolate Shape Phase Transition in the Casten Triangle. Phys. Rev. Lett. 2023, 130, 052501. [Google Scholar] [CrossRef]
- Bonatsos, D.; Assimakis, I.E.; Minkov, N.; Martinou, A.; Cakirli, R.B.; Casten, R.F.; Blaum, K. Proxy-SU(3) symmetry in heavy deformed nuclei. Phys. Rev. C 2017, 95, 064325. [Google Scholar] [CrossRef]
- Bonatsos, D.; Assimakis, I.E.; Minkov, N.; Martinou, A.; Sarantopoulou, S.; Cakirli, R.B.; Casten, R.F.; Blaum, K. Analytic predictions for nuclear shapes, prolate dominance, and the prolate-oblate shape transition in the proxy-SU(3) model. Phys. Rev. C 2017, 95, 064326. [Google Scholar] [CrossRef]
- Bonatsos, D. Prolate over oblate dominance in deformed nuclei as a consequence of the SU(3) symmetry and the Pauli principle. Eur. Phys. J. A 2017, 53, 148. [Google Scholar] [CrossRef]
- Bonatsos, D.; Martinou, A.; Sarantopoulou, S.; Assimakis, I.E.; Peroulis, S.; Minkov, N. Parameter-free predictions for the collective deformation variables β and γ within the pseudo-SU(3) scheme. Eur. Phys. J. Spec. Top. 2020, 229, 2367. [Google Scholar] [CrossRef]
- Bonatsos, D.; Martinou, A.; Peroulis, S.K.; Mertzimekis, T.J.; Minkov, N. The Proxy-SU(3) Symmetry in Atomic Nuclei. Symmetry 2023, 15, 169. [Google Scholar] [CrossRef]
- Martinou, A.; Bonatsos, D.; Karakatsanis, K.E.; Sarantopoulou, S.; Assimakis, I.E.; Peroulis, S.K.; Minkov, N. Why nuclear forces favor the highest weight irreducible representations of the fermionic SU(3) symmetry. Eur. Phys. J. A 2021, 57, 83. [Google Scholar] [CrossRef]
- Martinou, A.; Bonatsos, D.; Minkov, N.; Assimakis, I.E.; Peroulis, S.K.; Sarantopoulou, S.; Cseh, J. Proxy-SU(3) symmetry in the shell model basis. Eur. Phys. J. A 2020, 56, 239. [Google Scholar] [CrossRef]
- Bonatsos, D.; Sobhani, H.; Hassanabadi, H. Shell model structure of proxy-SU(3) pairs of orbitals. Eur. Phys. J. Plus 2020, 135, 710. [Google Scholar] [CrossRef]
- de-Shalit, A.; Goldhaber, M. Mixed Configurations in Nuclei. Phys. Rev. 1953, 92, 1211. [Google Scholar] [CrossRef]
- Castaños, O.; Draayer, J.P.; Leschber, Y. Shape variables and the shell model. Z. Phys. A 1988, 329, 33. [Google Scholar]
- Draayer, J.P.; Park, S.C.; Castaños, O. Shell-Model Interpretation of the Collective-Model Potential-Energy Surface. Phys. Rev. Lett. 1989, 62, 20. [Google Scholar] [CrossRef]
- Martinou, A.; Bonatsos, D.; Metzimekis, T.J.; Karakatsanis, K.E.; Assimakis, I.E.; Peroulis, S.K.; Sarantopoulou, S.; Minkov, N. The islands of shape coexistence within the Elliott and the proxy-SU(3) Models. Eur. Phys. J. A 2021, 57, 84. [Google Scholar] [CrossRef]
- Martinou, A.; Bonatsos, D.; Peroulis, S.K.; Karakatsanis, K.E.; Mertzimekis, T.J.; Minkov, N. Islands of Shape Coexistence: Theoretical Predictions and Experimental Evidence. Symmetry 2023, 15, 29. [Google Scholar] [CrossRef]
- Rosensteel, G.; Rowe, D.J. Nuclear Sp(3,R) Model. Phys. Rev. Lett. 1977, 38, 10. [Google Scholar] [CrossRef]
- Rosensteel, G.; Rowe, D.J. On the algebraic formulation of collective models III. The symplectic shell model of collective motion. Ann. Phys. 1980, 126, 343. [Google Scholar] [CrossRef]
- Rowe, D.J. Microscopic theory of the nuclear collective model. Rep. Prog. Phys. 1985, 48, 1419. [Google Scholar] [CrossRef]
- Dytrych, T.; Sviratcheva, K.D.; Bahri, C.; Draayer, J.P.; Vary, J.P. Evidence for Symplectic Symmetry in Ab Initio No-Core Shell Model Results for Light Nuclei. Phys. Rev. Lett. 2007, 98, 162503. [Google Scholar] [CrossRef] [PubMed]
- Dytrych, T.; Sviratcheva, K.D.; Bahri, C.; Draayer, J.P.; Vary, J.P. Dominant role of symplectic symmetry in ab initio no-core shell model results for light nuclei. Phys. Rev. C 2007, 76, 014315. [Google Scholar] [CrossRef]
- Dytrych, T.; Launey, K.D.; Draayer, J.P.; Maris, P.; Vary, J.P.; Saule, E.; Catalyurek, U.; Sosonkina, M.; Langr, D.; Caprio, M.A. Collective Modes in Light Nuclei from First Principles. Phys. Rev. Lett. 2013, 111, 252501. [Google Scholar] [CrossRef] [PubMed]
- Dreyfuss, A.C.; Launey, K.D.; Dytrych, T.; Draayer, J.P.; Bahri, C. Hoyle state and rotational features in Carbon-12 within a no-core shell-model framework. Phys. Lett. B 2013, 727, 511. [Google Scholar] [CrossRef]
- Dreyfuss, A.C.; Launey, K.D.; Dytrych, T.; Draayer, J.P.; Baker, R.B.; Deibel, C.M.; Bahri, C. Understanding emergent collectivity and clustering in nuclei from a symmetry-based no-core shell-model perspective. Phys. Rev. C 2017, 95, 044312. [Google Scholar] [CrossRef]
- Dytrych, T.; Sviratcheva, K.D.; Bahri, C.; Draayer, J.P.; Vary, J.P. Highly deformed modes in the ab initio symplectic no-core shell model. J. Phys. G Nucl. Part. Phys. 2008, 35, 095101. [Google Scholar] [CrossRef]
- Tobin, G.K.; Ferriss, M.C.; Launey, K.D.; Dytrych, T.; Draayer, J.P.; Dreyfuss, A.C.; Bahri, C. Symplectic no-core shell-model approach to intermediate-mass nuclei. Phys. Rev. C 2014, 89, 034312. [Google Scholar] [CrossRef]
- Dytrych, T.; Launey, K.D.; Draayer, J.P.; Rowe, D.J.; Wood, J.L.; Rosensteel, G.; Bahri, C.; Langr, D.; Baker, R.B. Physics of Nuclei: Key Role of an Emergent Symmetry. Phys. Rev. Lett. 2020, 124, 042501. [Google Scholar] [CrossRef]
- Casten, R.F.; McCutchan, E.A. Quantum phase transitions and structural evolution in nuclei. J. Phys. G Nucl. Part. Phys. 2007, 34, R285. [Google Scholar] [CrossRef]
- Casten, R.F. Quantum phase transitions and structural evolution in nuclei. Prog. Part. Nucl. Phys. 2009, 62, 183. [Google Scholar] [CrossRef]
- 0 Database. Available online: https://www.nndc.bnl.gov/nudat3 (accessed on 31 January 2023).
- Brenner, D.S. Are There X(5) Nuclei In The A∼80 and A∼100 Regions? AIP Conf. Proc. 2002, 638, 223. [Google Scholar]
- Hutter, C.; Krücken, R.; Aprahamian, A.; Barton, C.J.; Beausang, C.W.; Caprio, M.A.; Casten, R.F.; Chou, W.-T.; Clark, R.M.; Cline, D.; et al. B(E2) values and the search for the critical point symmetry X(5) in 104Mo and 106Mo. Phys. Rev. C 2003, 67, 054315. [Google Scholar] [CrossRef]
- Regan, P.H.; Yamamoto, A.D.; Beausang, C.W.; Zamfir, N.V.; Casten, R.F.; Zhang, J.-Y.; Caprio, M.A.; Gúrdal, G.; Hecht, A.A.; Hutter, C.; et al. The Highs And Lows Of The A=100 Region: Vibration-To-Rotation Evolution In Mo And Ru Isotopes. AIP Conf. Proc. 2003, 656, 422. [Google Scholar]
- Bizzeti, P.G.; Bizzeti-Sona, A.M. Evidence of X(5) symmetry for nγ=0, 1, 2 bands in 104Mo. Phys. Rev. C 2002, 66, 031301. [Google Scholar] [CrossRef]
- Bizzeti, P.G.; Bizzeti-Sona, A.M.; Tonev, D.; Ur, C.A.; Dewald, A.; Giannatiempo, A.; Melon, B.; Bazzacco, D.; Costin, A.; de Angelis, G.; et al. Transition probabilities in the X(5) candidate 122Ba. Phys. Rev. C 2010, 82, 054311. [Google Scholar] [CrossRef]
- Fransen, C.; Pietralla, N.; Linnemann, A.; Werner, V.; Bijker, R. Low-spin γ-ray spectroscopy of the (critical-point?) nucleus 122Ba. Phys. Rev. C 2004, 69, 014313. [Google Scholar] [CrossRef]
- Clark, R.M.; Cromaz, M.; Deleplanque, M.A.; Descovich, M.; Diamond, R.M.; Fallon, P.; Firestone, R.B.; Lee, I.Y.; Macchiavelli, A.O.; Mahmud, H.; et al. Searching for X(5) behavior in nuclei. Phys. Rev. C 2003, 68, 037301. [Google Scholar] [CrossRef]
- Balabanski, D.L.; Gladnishki, K.A.; Lo Bianco, G.; Saltarelli, A.; Zamfir, N.V.; McCutchan, E.A.; Ai, H.; Casten, R.F.; Heinz, A.; Meyer, D.A.; et al. Evidence for X(5) critical point symmetry in 128Ce. Int. J. Mod. Phys. E 2006, 15, 1735. [Google Scholar] [CrossRef]
- Casten, R.F.; Zamfir, N.V.; Krücken, R. Comment on “Reexamination of the N = 90 transitional nuclei 150Nd and 152Sm”. Phys. Rev. C 2003, 68, 059801. [Google Scholar] [CrossRef]
- Mertz, A.F.; McCutchan, E.A.; Casten, R.F.; Casperson, R.J.; Heinz, A.; Huber, B.; Lüttke, R.; Qian, J.; Shoraka, B.; Terry, J.R.; et al. First experimental test of X(5) critical-point symmetry in the A∼130 mass region: Low-spin states and the collective structure of 130Ce. Phys. Rev. C 2008, 77, 014307. [Google Scholar] [CrossRef]
- Clark, R.M.; Cromaz, M.; Deleplanque, M.A.; Diamond, R.M.; Fallon, P.; Görgen, A.; Lee, I.Y.; Macchiavelli, A.O.; Stephens, F.S.; Ward, D. Reexamination of the N = 90 transitional nuclei 150Nd and 152Sm. Phys. Rev. C 2003, 67, 041302. [Google Scholar] [CrossRef]
- Krücken, R.; Albanna, B.; Bialik, C.; Casten, R.F.; Cooper, J.R.; Dewald, A.; Zamfir, N.V.; Barton, C.J.; Beausang, C.W.; Caprio, M.A.; et al. B(E2) values in 150Nd and the critical point symmetry X(5). Phys. Rev. Lett. 2002, 88, 232501. [Google Scholar] [CrossRef]
- Zhang, D.-L.; Zhao, H.-Y. Empirical example of nucleus with transitional dynamical symmetry X(5). Chin. Phys. Lett. 2002, 19, 779. [Google Scholar]
- Börner, H.G.; Mutti, P.; Jentschel, M.; Zamfir, N.V.; Casten, R.F.; McCutchan, E.A.; Krücken, R. Low-energy phonon structure of 150Sm. Phys. Rev. C 2006, 73, 034314. [Google Scholar] [CrossRef]
- Bijker, R.; Casten, R.F.; Zamfir, N.V.; McCutchan, E.A. Test of X(5) for the γ degree of freedom. Phys. Rev. C 2003, 68, 064304, Erratum in Phys. Rev. C 2004, 69, 059901. [Google Scholar] [CrossRef]
- Casten, R.F.; Wilhelm, M.; Radermacher, E.; Zamfir, N.V.; von Brentano, P. The first excited 0+ state in 152Sm. Phys. Rev. C 1998, 57, R1553. [Google Scholar] [CrossRef]
- Casten, R.F.; Zamfir, N.V. Empirical Realization of a Critical Point Description in Atomic Nuclei. Phys. Rev. Lett. 2001, 87, 052503. [Google Scholar] [CrossRef]
- Jolie, J.; Cejnar, P.; Dobes, J. Phase coexistence in the interacting boson model and 152Sm. Phys. Rev. C 1999, 60, 061303. [Google Scholar] [CrossRef]
- Klug, T.; Dewald, A.; Werner, V.; von Brentano, P.; Casten, R.F. The B(E2:→) value in 152Sm and β-softness in phase coexisting structures. Phys. Lett. B 2000, 495, 55. [Google Scholar] [CrossRef]
- Kulp, W.D.; Wood, J.L.; Allmond, J.M.; Eimer, J.; Furse, D.; Krane, K.S.; Loats, J.; Schmelzenbach, P.; Stapels, C.J.; Larimer, R.-M.; et al. N = 90 region: The decays of 152Eum,g to 152Sm. Phys. Rev. C 2007, 76, 034319. [Google Scholar] [CrossRef]
- Kulp, W.D.; Wood, J.L.; Garrett, P.E.; Wu, C.Y.; Cline, D.; Allmond, J.M.; Bandyopadhyay, D.; Dashdorj, D.; Choudry, S.N.; Hayes, A.B.; et al. Search for intrinsic collective excitations in 152Sm. Phys. Rev. C 2008, 77, 061301. [Google Scholar] [CrossRef]
- Zamfir, N.V.; Casten, R.F.; Caprio, M.A.; Beausang, C.W.; Krücken, R.; Novak, J.R.; Cooper, J.R.; Cata-Danil, G.; Barton, C.J. B(E2) values and phase coexistence in 152Sm. Phys. Rev. C 1999, 60, 054312. [Google Scholar] [CrossRef]
- Zamfir, N.V.; Börner, H.G.; Pietralla, N.; Casten, R.F.; Berant, Z.; Barton, C.J.; Beausang, C.W.; Brenner, D.S.; Caprio, M.A.; Cooper, J.R.; et al. Lifetime and B(E2) values for the level in 152Sm. Phys. Rev. C 2002, 65, 067305. [Google Scholar] [CrossRef]
- Zhang, J.-Y.; Caprio, M.A.; Zamfir, N.V.; Casten, R.F. Phase/shape coexistence in 152Sm in the geometric collective model. Phys. Rev. C 1999, 60, 061304. [Google Scholar] [CrossRef]
- Adam, J.; Dobes, J.; Honusek, M.; Kalinnikov, V.G.; Mrázek, J.; Pronskikh, V.S.; Caloun, P.; Lebedev, N.A.; Stegailov, V.I.; Tsoupko-Sitnikov, V.M. Properties of 152Gd collective states. Eur. Phys. J. A 2003, 18, 605. [Google Scholar] [CrossRef]
- Dewald, A.; Möller, O.; Tonev, D.; Fitzler, A.; Saha, B.; Jessen, K.; Heinze, S.; Linnemann, A.; Jolie, J.; Zell, K.O.; et al. Shape changes and test of the critical-point symmetry X(5) in N = 90 nuclei. Eur. Phys. J. A 2003, 20, 173. [Google Scholar] [CrossRef]
- Tonev, D.; Dewald, A.; Klug, T.; Petkov, P.; Jolie, J.; Fitzler, A.; Möller, O.; Heinze, S.; von Brentano, P.; Casten, R.F. Transition probabilities in 154Gd: Evidence for X(5) critical point symmetry. Phys. Rev. C 2004, 69, 034334. [Google Scholar] [CrossRef]
- Caprio, M.A.; Zamfir, N.V.; Casten, R.F.; Barton, C.J.; Beausang, C.W.; Cooper, J.R.; Hecht, A.A.; Krücken, R.; Newman, H.; Novak, J.R.; et al. Low-spin structure of 156Dy through γ-ray spectroscopy. Phys. Rev. C 2002, 66, 054310. [Google Scholar] [CrossRef]
- Möller, O.; Dewald, A.; Petkov, P.; Saha, B.; Fitzler, A.; Jessen, K.; Tonev, D.; Klug, T.; Heinze, S.; Jolie, J.; et al. Electromagnetic transition strengths in 156Dy. Phys. Rev. C 2006, 74, 024313. [Google Scholar] [CrossRef]
- McCutchan, E.A.; Zamfir, N.V.; Casten, R.F.; Ai, H.; Amro, H.; Babilon, M.; Brenner, D.S.; Gürdal, G.; Heinz, A.; Hughes, R.O.; et al. Lifetime measurements of yrast states in 162Yb and 166Hf. Phys. Rev. C 2006, 73, 034303. [Google Scholar] [CrossRef]
- McCutchan, E.A.; Zamfir, N.V.; Casten, R.F.; Caprio, M.A.; Ai, H.; Amro, H.; Beausang, C.W.; Hecht, A.A.; Meyer, D.A.; Ressler, J.J. γ-ray spectroscopy of 166Hf: X(5) in N>90? Phys. Rev. C 2005, 71, 024309. [Google Scholar] [CrossRef]
- McCutchan, E.A.; Casten, R.F.; Werner, V.; Wolf, A.; Berant, Z.; Casperson, R.J.; Heinz, A.; Lüttke, R.; Shoraka, B.; Terry, J.R.; et al. β decay study of 168Hf and a test of new geometrical models. Phys. Rev. C 2007, 76, 064307. [Google Scholar] [CrossRef]
- Costin, A.; Ahn, T.; Bochev, B.; Dusling, K.; Li, T.C.; Pietralla, N.; Rainovski, G.; Rother, W. Lifetime measurement for the state of 170Hf. Phys. Rev. C 2006, 74, 067301. [Google Scholar] [CrossRef]
- Dewald, A.; Möller, O.; Saha, B.; Jessen, K.; Fitzler, A.; Melon, B.; Pissulla, T.; Heinze, S.; Jolie, J.; Zell, K.O.; et al. Test of the critical point symmetry X(5) in the mass A = 180 region. J. Phys. G Nucl. Part. Phys. 2005, 31, S1427. [Google Scholar] [CrossRef]
- Aoi, N.; Suzuki, H.; Takeshita, E.; Takeuchi, S.; Ota, S.; Baba, H.; Bishop, S.; Fukui, T.; Hashimoto, Y.; Ong, H.J.; et al. Shape transition observed in neutron-rich pf-shell isotopes studied via proton inelastic scattering. Nucl. Phys. A 2008, 805, 400c. [Google Scholar] [CrossRef]
- Gadea, A. First results of the CLARA-PRISMA setup installed at LNL. Eur. Phys. J. A 2005, 25, 421. [Google Scholar] [CrossRef]
- Gadea, A. The CLARA-PRISMA setup installed at LNL: First results. J. Phys. G Nucl. Part. Phys. 2005, 31, S1443. [Google Scholar]
- Mărginean, N.; Lenzi, S.M.; Gadea, A.; Farnea, E.; Freeman, S.J.; Napoli, D.R.; Bazzacco, D.; Beghini, S.; Behera, B.R.; Bizzeti, P.G.; et al. Shape transitions far from stability: The nucleus 58Cr. Phys. Lett. B 2006, 633, 696. [Google Scholar] [CrossRef]
- Bettermann, L.; Régis, J.-M.; Materna, T.; Jolie, J.; Köster, U.; Moschner, K.; Radeck, D. Lifetime measurement of excited states in the shape-phase-transitional nucleus 98Zr. Phys. Rev. C 2010, 82, 044310. [Google Scholar] [CrossRef]
- Frank, A.; Alonso, C.E.; Arias, J.M. Search for E(5) symmetry in nuclei: The Ru isotopes. Phys. Rev. C 2001, 65, 014301. [Google Scholar] [CrossRef]
- Radeck, D.; Blazhev, A.; Albers, M.; Bernards, C.; Dewald, A.; Fransen, C.; Heidemann, M.; Jolie, J.; Melon, B.; Mücher, D.; et al. First measurement of lifetimes in the yrast band of 100Pd. Phys. Rev. C 2009, 80, 044331. [Google Scholar] [CrossRef]
- Clark, R.M.; Cromaz, M.; Deleplanque, M.A.; Descovich, M.; Diamond, R.M.; Fallon, P.; Lee, I.Y.; Macchiavelli, A.O.; Mahmud, H.; Rodriguez-Vieitez, R.; et al. Searching for E(5) behavior in nuclei. Phys. Rev. C 2004, 69, 064322. [Google Scholar] [CrossRef]
- Konstantinopoulos, T.; Ashley, S.F.; Axiotis, M.; Spyrou, A.; Harissopulos, S.; Dewald, A.; Litzinger, J.; Möller, O.; Müller-Gatterman, C.; Petkov, P.; et al. Lifetime measurements in 102Pd: Searching for empirical proof of the E(5) critical-point symmetry in nuclear structure. Phys. Rev. C 2016, 93, 014320. [Google Scholar] [CrossRef]
- Zhang, D.-L.; Liu, Y.-X. Empirical example of possible E(5) symmetry nucleus 108Pd. Phys. Rev. C 2002, 65, 057301. [Google Scholar] [CrossRef]
- Zhang, D.-L.; Wang, H.-L. An IBM2 Description of the E(5) Symmetry in 134Ba and 108Pd. Commun. Theor. Phys. 2002, 38, 71. [Google Scholar]
- Kirson, M.W. Comment on “Searching for E(5) behavior in nuclei”. Phys. Rev. C 2004, 70, 049801. [Google Scholar] [CrossRef]
- Zhang, J.-F.; Long, G.-L.; Sun, Y.; Zhu, S.-J.; Liu, F.-Y.; Jia, Y. Description of 114Cd in the E(5) Symmetry. Chin. Phys. Lett. 2003, 20, 1231. [Google Scholar]
- Ghiţă, D.G.; Căta-Danil, G.; Bucurescu, D.; Căta-Danil, I.; Ivascu, M.; Mihai, C.; Suliman, G.; Stroe, L.; Sava, T.; Zamfir, N.V. 124Te and the E(5) critical point symmetry. Int. J. Mod. Phys. A 2008, 17, 1453. [Google Scholar] [CrossRef]
- Hicks, S.F.; Vanhoy, J.R.; Burkett, P.G.; Champine, B.R.; Etzkorn, S.J.; Garrett, P.E.; Yates, S.W.; Yeh, M. Lifetimes in 124Te: Examining critical-point symmetry in the Te nuclei. Phys. Rev. C 2017, 95, 034322. [Google Scholar] [CrossRef]
- Coquard, L.; Pietralla, N.; Ahn, T.; Rainovski, G.; Bettermann, L.; Carpenter, M.P.; Janssens, R.V.F.; Leske, J.; Lister, C.J.; Möller, O.; et al. Robust test of E(5) symmetry in 128Xe. Phys. Rev. C 2009, 80, 061304. [Google Scholar] [CrossRef]
- Peters, E.E.; Ross, T.J.; Ashley, S.F.; Chakraborty, A.; Crider, B.P.; Hennek, M.D.; Liu, S.H.; McEllistrem, M.T.; Mukhopadhyay, S.; Prados-Estévez, F.M.; et al. 0+ states in 130,132Xe: A search for E(5) behavior. Phys. Rev. C 2016, 94, 024313. [Google Scholar] [CrossRef]
- Zhang, D.-L.; Liu, Y.-X. Evidence for a Possible E(5) Symmetry in 130Xe. Chin. Phys. Lett. 2003, 20, 1028–1030. [Google Scholar]
- Pascu, S.; Căta-Danil, G.; Bucurescu, D.; Mărginean, N.; Müller, C.; Zamfir, N.V.; Graw, G.; Gollwitzer, A.; Hofer, D.; Valnion, B.D. Structure investigation with the (p, t) reaction on 132,134Ba nuclei. Phys. Rev. C 2010, 81, 014304. [Google Scholar] [CrossRef]
- Arias, J.M. E2 transitions and quadrupole moments in the E(5) symmetry. Phys. Rev. C 2001, 63, 034308. [Google Scholar] [CrossRef]
- Casten, R.F.; Zamfir, N.V. Evidence for a Possible E(5) Symmetry in 134Ba. Phys. Rev. Lett. 2000, 85, 3584. [Google Scholar] [CrossRef]
- Luo, Y.-A.; Zhang, X.-B.; Pan, F.; Ning, P.-Z.; Draayer, J.P. Magnetic excitations in the nucleon-pair shell model. Phys. Rev. C 2001, 64, 047302. [Google Scholar] [CrossRef]
- ENSDF Database. Available online: https://www.nndc.bnl.gov/ensdf (accessed on 31 January 2023).
- Bonatsos, D.; Martinou, A.; Peroulis, S.; Mertzimekis, T.; Minkov, N. Signatures for shape coexistence and shape/phase transitions in even-even nuclei. J. Phys. G Nucl. Part. Phys. 2023, 50, 075105. [Google Scholar] [CrossRef]
- Arima, A.; Iachello, F. Interacting boson model of collective states I. The vibrational limit. Ann. Phys. 1976, 99, 253. [Google Scholar] [CrossRef]
- Arima, A.; Iachello, F. Interacting boson model of collective nuclear states II. The rotational limit. Ann. Phys. 1978, 111, 201. [Google Scholar] [CrossRef]
- Arima, A.; Iachello, F. Interacting boson model of collective nuclear states IV. The O(6) limit. Ann. Phys. 1979, 123, 468. [Google Scholar] [CrossRef]
- Feng, D.H.; Gilmore, R.; Deans, S.R. Phase transitions and the geometric properties of the interacting boson model. Phys. Rev. C 1981, 23, 1254. [Google Scholar] [CrossRef]
- Iachello, F.; Zamfir, N.V.; Casten, R.F. Phase Coexistence in Transitional Nuclei and the Interacting-Boson Model. Phys. Rev. Lett. 1998, 81, 1191. [Google Scholar] [CrossRef]
- Alhassid, Y.; Leviatan, A. Partial dynamical symmetry. J. Phys. A Math. Gen. 1992, 25, L1265–L1271. [Google Scholar] [CrossRef]
- Leviatan, A. Partial dynamical symmetries. Prog. Part. Nucl. Phys. 2011, 66, 93–143. [Google Scholar] [CrossRef]
- Leviatan, A.; Shapira, D. Algebraic benchmark for prolate-oblate coexistence in nuclei. Phys. Rev. C 2016, 93, 051302. [Google Scholar] [CrossRef]
- Leviatan, A.; Gavrielov, N. Partial dynamical symmetries and shape coexistence in nuclei. Phys. Scr. 2017, 92, 114005. [Google Scholar] [CrossRef]
- Engel, J.; Iachello, F. Quantization of Asymmetric Shapes in Nuclei. Phys. Rev. Lett. 1985, 54, 1126. [Google Scholar] [CrossRef]
- Engel, J.; Iachello, F. Interacting boson model of collective octupole states: (I). The rotational limit. Nucl. Phys. A 1987, 472, 61. [Google Scholar] [CrossRef]
- Kusnezov, D.; Iachello, F. A study of collective octupole states in barium in the interacting boson model. Phys. Lett. B 1988, 209, 420. [Google Scholar] [CrossRef]
- Kusnezov, D.F.; Henry, E.A.; Meyer, R.A. An octupole two-phonon multiplet in 96Zr and its description within the spdf interacting boson model. Phys. Lett. B 1989, 228, 11. [Google Scholar] [CrossRef]
- Zamfir, N.V.; Kusnezov, D. Octupole correlations in the transitional actinides and the spdf interacting boson model. Phys. Rev. C 2001, 63, 054306. [Google Scholar] [CrossRef]
- Zamfir, N.V.; Kusnezov, D. Octupole correlations in U and Pu nuclei. Phys. Rev. C 2003, 67, 014305. [Google Scholar] [CrossRef]
- De Coster, C.; Heyde, K.; Decroix, B.; Van Isacker, P.; Jolie, J.; Lehmann, H.; Wood, J.L. Particle-hole excitations in the interacting boson model (I) General structure and symmetries. Nucl. Phys. A 1996, 600, 251. [Google Scholar] [CrossRef]
- De Coster, C.; Decroix, B.; Heyde, K.; Wood, J.L.; Jolie, J.; Lehmann, H. Particle-hole excitations in the interacting boson model (III): The O(6)-SU(3) coupling. Nucl. Phys. A 1997, 621, 802. [Google Scholar] [CrossRef]
- De Coster, C.; Decroix, B.; Heyde, K.; Jolie, J.; Lehmann, H.; Wood, J.L. Particle-hole excitations in the interacting boson model (IV). The U(5)-SU(3) coupling. Nucl. Phys. A 1999, 651, 31. [Google Scholar] [CrossRef]
- De Coster, C.; De Beule, J.; Decroix, B.; Heyde, K.; Oros, A.M.; Van Isacker, P. An algebraic approach to shape coexistence. J. Phys. G Nucl. Part. Phys. 1999, 25, 671. [Google Scholar] [CrossRef]
- Decroix, B.; De Beule, J.; De Coster, C.; Heyde, K. SU(4) symmetry in the extended proton-neutron interacting boson model: Multiplets and symmetry breaking. Phys. Lett. B 1998, 439, 237. [Google Scholar] [CrossRef][Green Version]
- Decroix, B.; De Beule, J.; De Coster, C.; Heyde, K.; Oros, A.M.; Van Isacker, P. Particle-hole excitations in the interacting boson models IBM-2 and IBM-3. Phys. Rev. C 1998, 57, 2329. [Google Scholar] [CrossRef]
- Decroix, B.; De Coster, C.; Heyde, K.; Oros, A.M.; De Beule, J.; Van Isacker, P. The extended proton-neutron interacting boson model and possible applications. J. Phys. G Nucl. Part. Phys. 1999, 25, 855. [Google Scholar] [CrossRef]
- Lehmann, H.; Jolie, J.; De Coster, C.; Decroix, B.; Heyde, K.; Wood, J.L. Particle-hole excitations in the interacting boson model (II): The U(5)-O(6) coupling. Nucl. Phys. A 1997, 621, 767. [Google Scholar] [CrossRef]
- Duval, P.D.; Barrett, B.R. Configuration mixing in the interacting boson model. Phys. Lett. B 1981, 100, 223. [Google Scholar] [CrossRef]
- Duval, P.D.; Barrett, B.R. Quantitative description of configuration mixing in the interacting boson model. Nucl. Phys. A 1982, 376, 213. [Google Scholar] [CrossRef]
- Frank, A.; Van Isacker, P.; Vargas, C.E. Evolving shape coexistence in the lead isotopes: The geometry of configuration mixing in nuclei. Phys. Rev. C 2004, 69, 034323. [Google Scholar] [CrossRef]
- García-Ramos, J.E.; Hellemans, V.; Heyde, K. Platinum nuclei: Concealed configuration mixing and shape coexistence. Phys. Rev. C 2011, 84, 014331. [Google Scholar] [CrossRef]
- García-Ramos, J.E.; Heyde, K. Nuclear shape coexistence: A study of the even-even Hg isotopes using the interacting boson model with configuration mixing. Phys. Rev. C 2014, 89, 014306. [Google Scholar] [CrossRef]
- García-Ramos, J.E.; Heyde, K.; Robledo, L.M.; Rodríguez-Guzmán, R. Shape evolution and shape coexistence in Pt isotopes: Comparing interacting boson model configuration mixing and Gogny mean-field energy surfaces. Phys. Rev. C 2014, 89, 034313. [Google Scholar] [CrossRef]
- García-Ramos, J.E.; Heyde, K. Nuclear shape coexistence in Po isotopes: An interacting boson model study. Phys. Rev. C 2015, 92, 034309. [Google Scholar] [CrossRef]
- García-Ramos, J.E.; Heyde, K. Quest of shape coexistence in Zr isotopes. Phys. Rev. C 2019, 100, 044315. [Google Scholar] [CrossRef]
- García-Ramos, J.E.; Heyde, K. Subtle connection between shape coexistence and quantum phase transition: The Zr case. Phys. Rev. C 2020, 102, 054333. [Google Scholar] [CrossRef]
- Gavrielov, N.; Leviatan, A.; Iachello, F. Intertwined quantum phase transitions in the Zr isotopes. Phys. Rev. C 2019, 99, 064324. [Google Scholar] [CrossRef]
- Gavrielov, N.; Leviatan, A.; Iachello, F. Interplay between shape-phase transitions and shape coexistence in the Zr isotopes. Phys. Scr. 2020, 95, 024001. [Google Scholar] [CrossRef]
- Gavrielov, N.; Leviatan, A.; Iachello, F. Zr isotopes as a region of intertwined quantum phase transitions. Phys. Rev. C 2022, 105, 014305. [Google Scholar] [CrossRef]
- Harder, M.K.; Tang, K.T.; Van Isacker, P. An IBM description of coexistence in the platinum isotopes. Phys. Lett. B 1997, 405, 25. [Google Scholar] [CrossRef]
- Hellemans, V.; De Baerdemacker, S.; Heyde, K. Configuration mixing in the neutron-deficient 186-196Pb isotopes. Phys. Rev. C 2008, 77, 064324. [Google Scholar] [CrossRef]
- Maya-Barbecho, E.; García-Ramos, J.E. Shape coexistence in Sr isotopes. Phys. Rev. C 2022, 105, 034341. [Google Scholar] [CrossRef]
- Morales, I.O.; Frank, A.; Vargas, C.E.; Van Isacker, P. Shape coexistence and phase transitions in the platinum isotopes. Phys. Rev. C 2008, 78, 024303. [Google Scholar] [CrossRef]
- Casten, R.F. Shape phase transitions and critical-point phenomena in atomic nuclei. Nat. Phys. 2006, 2, 811. [Google Scholar] [CrossRef]
- Cejnar, P.; Jolie, J. Quantum phase transitions in the interacting boson model. Prog. Part. Nucl. Phys. 2009, 62, 210. [Google Scholar] [CrossRef]
- Cejnar, P.; Jolie, J.; Casten, R.F. Quantum phase transitions in the shapes of atomic nuclei. Rev. Mod. Phys. 2010, 82, 2155. [Google Scholar] [CrossRef]
- Iachello, F. Dynamic Symmetries at the Critical Point. Phys. Rev. Lett. 2000, 85, 3580. [Google Scholar] [CrossRef]
- Iachello, F. Analytic Description of Critical Point Nuclei in a Spherical-Axially Deformed Shape Phase Transition. Phys. Rev. Lett. 2001, 87, 052502. [Google Scholar] [CrossRef]
- Scholten, O.; Iachello, F.; Arima, A. Interacting boson model of collective nuclear states III. The transition from SU(5) to SU(3). Ann. Phys. 1978, 115, 325. [Google Scholar] [CrossRef]
- Jolie, J.; Casten, R.F.; von Brentano, P.; Werner, V. Quantum Phase Transition for γ-Soft Nuclei. Phys. Rev. Lett. 2001, 87, 162501. [Google Scholar] [CrossRef] [PubMed]
- Jolie, J.; Cejnar, P.; Casten, R.F.; Heinze, S.; Linnemann, A.; Werner, V. Triple Point of Nuclear Deformations. Phys. Rev. Lett. 2002, 89, 182502. [Google Scholar] [CrossRef] [PubMed]
- Warner, D. A triple point in nuclei. Nature 2002, 420, 614. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Casten, R.F.; Zamfir, N.V. A structural triangle for the geometric collective model. Phys. Lett. B 1997, 407, 201. [Google Scholar] [CrossRef]
- Iachello, F. Phase Transitions in Angle Variables. Phys. Rev. Lett. 2003, 91, 132502. [Google Scholar] [CrossRef] [PubMed]
- Bonatsos, D.; Lenis, D.; Petrellis, D.; Terziev, P.A. Z(5): Critical point symmetry for the prolate to oblate nuclear shape phase transition. Phys. Lett. B 2004, 588, 172. [Google Scholar] [CrossRef]
- Bonatsos, D.; Lenis, D.; Petrellis, D.; Terziev, P.A.; Yigitoglu, I. X(3): An exactly separable γ-rigid version of the X(5) critical point symmetry. Phys. Lett. B 2006, 632, 238–242. [Google Scholar] [CrossRef]
- Bonatsos, D.; Lenis, D.; Petrellis, D.; Terziev, P.A.; Yigitoglu, I. γ-rigid solution of the Bohr Hamiltonian for γ=30o compared to the E(5) critical point symmetry. Phys. Lett. B 2005, 621, 102–108. [Google Scholar] [CrossRef]
- Budaca, R.; Budaca, A.I. Emergence of Euclidean dynamical symmetry as a consequence of shape phase mixing. Phys. Lett. B 2016, 759, 349–353. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, F.; Liu, Y.-X.; Luo, Y.-A.; Draayer, J.P. γ-rigid solution of the Bohr Hamiltonian for the critical point description of the spherical to γ-rigidly deformed shape phase transition. Phys. Rev. C 2017, 96, 034323. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.-X.; Pan, F.; Sun, Y.; Draayer, J.P. Euclidean dynamical symmetry in nuclear shape phase transitions. Phys. Lett. B 2014, 732, 55–58. [Google Scholar] [CrossRef]
- Bonatsos, D.; Lenis, D.; Petrellis, D. Special solutions of the Bohr hamiltonian related to shape phase transitions in nuclei. Rom. Rep. Phys. 2007, 59, 273. [Google Scholar]
- Rosensteel, G.; Rowe, D.J. Phase transitions and quasi-dynamical symmetry in nuclear collective models, III: The U(5) to SU(3) phase transition in the IBM. Nucl. Phys. A 2005, 759, 92. [Google Scholar] [CrossRef]
- Rowe, D.J. Quasidynamical Symmetry in an Interacting Boson Model Phase Transition. Phys. Rev. Lett. 2004, 93, 122502. [Google Scholar] [CrossRef]
- Rowe, D.J. Phase transitions and quasidynamical symmetry in nuclear collective models: I. The U(5) to O(6) phase transition in the IBM. Nucl. Phys. A 2004, 745, 47. [Google Scholar] [CrossRef]
- Turner, P.S.; Rowe, D.J. Phase transitions and quasidynamical symmetry in nuclear collective models. II. The spherical vibrator to gamma-soft rotor transition in an SO(5)-invariant Bohr model. Nucl. Phys. A 2005, 756, 333–355. [Google Scholar] [CrossRef]
- Heyde, K.; Jolie, J.; Fossion, R.; De Baerdemacker, S.; Hellemans, V. Phase transitions versus shape coexistence. Phys. Rev. C 2004, 69, 054304. [Google Scholar] [CrossRef]
- Federman, P.; Pittel, S. Towards a unified microscopic description of nuclear deformation. Phys. Lett. B 1977, 69, 385. [Google Scholar] [CrossRef]
- Federman, P.; Pittel, S. Hartree-Fock-Bogolyubov study of deformation in the Zr-Mo region. Phys. Lett. B 1978, 77, 29. [Google Scholar] [CrossRef]
- Federman, P.; Pittel, S.; Campos, R. Microscopic study of the shape transition in the zirconium isotopes. Phys. Lett. B 1979, 82, 9. [Google Scholar] [CrossRef]
- Federman, P.; Pittel, S. Unified shell-model description of nuclear deformation. Phys. Rev. C 1979, 20, 820. [Google Scholar] [CrossRef]
- Hammad, M.M. On the conformable fractional E(5) critical point symmetry. Nucl. Phys. A 2021, 1011, 122203. [Google Scholar] [CrossRef]
- Herrmann, R. Fractional Calculus—An Introduction for Physicists; World Scientific: Singapore, 2011. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Hammad, M.M. Conformable fractional Bohr Hamiltonian with Bonatsos and double-well sextic potentials. Phys. Scr. 2021, 96, 115304. [Google Scholar] [CrossRef]
- Hammad, M.M.; Yaqut, A.S.H.; Abdel-Khalek, M.A.; Doma, S.B. Analytical study of conformable fractional Bohr Hamiltonian with Kratzer potential. Nucl. Phys. A 2021, 1015, 122307. [Google Scholar] [CrossRef]
- Hammad, M.M.; Yahia, M.M.; Bonatsos, D. Triaxial nuclei and analytical solutions of the conformable fractional Bohr Hamiltonian with some exponential-type potentials. Nucl. Phys. A 2023, 1030, 122576. [Google Scholar] [CrossRef]
- Leviatan, A.; Novoselsky, A.; Talmi, I. O(5) symmetry in IBA-1—The O(6)—U(5) transition region. Phys. Lett. B 1986, 172, 144. [Google Scholar]
- Jolie, J.; Linnemann, A. Prolate-oblate phase transition in the Hf-Hg mass region. Phys. Rev. C 2003, 68, 031301. [Google Scholar] [CrossRef]
- Jolie, J.; Lehmann, H. On the influence of the O(5) symmetry on shape coexistence in atomic nuclei. Phys. Lett. B 1995, 342, 1. [Google Scholar]
- Lehmann, H.; Jolie, J. The U(5)-O(6) model: An analytical approach to shape coexistence. Nucl. Phys. A 1995, 588, 623. [Google Scholar] [CrossRef]
- Nakatsukasa, T.; Walet, N.R. Collective coordinates, shape transitions, and shape coexistence: A microscopic approach. Phys. Rev. C 1998, 58, 3397. [Google Scholar]
- Kaup, U.; Barrett, B.R. Nuclear shape coexistence in a schematic model. Phys. Rev. C 1990, 42, 981. [Google Scholar] [CrossRef]
- Ginocchio, J.N. On a generalization of quasispin to monopole and quadrupole pairing. Phys. Lett. B 1979, 85, 9–13. [Google Scholar] [CrossRef]
- Ginocchio, J.N. A schematic model for monopole and quadrupole pairing in nuclei. Ann. Phys. 1980, 126, 234–276. [Google Scholar] [CrossRef]
- Garrett, P.E. Characterization of the β vibration and states in deformed nuclei. J. Phys. G Nucl. Part. Phys. 2001, 27, R1. [Google Scholar]
- Zganjar, E.F.; Wood, J.L. Electric monopole transitions and shape coexistence in nuclei. Nucl. Phys. A 1990, 520, 427c. [Google Scholar] [CrossRef]
- Aprahamian, A. What is the nature of Kπ=0+ bands in deformed nuclei? AIP Conf. Proc. 2002, 638, 77. [Google Scholar]
- Aprahamian, A.; Lesher, S.R.; Stratman, A. First Excited 0+ States in Deformed Nuclei. Bulg. J. Phys. 2017, 44, 372. [Google Scholar]
- Lesher, S.R.; Aprahamian, A.; Trache, L.; Oros-Peusquens, O.; Deyliz, S.; Gollwitzer, A.; Hertenberger, R.; Valnion, B.D.; Graw, G. New 0+ states in 158Gd. Phys. Rev. C 2002, 66, 051305. [Google Scholar] [CrossRef]
- Lesher, S.R.; Orce, J.N.; Ammar, Z.; Hannant, C.D.; Merrick, M.; Warr, N.; Brown, T.B.; Boukharouba, N.; Fransen, C.; Scheck, M.; et al. Study of 0+ excitations in 158Gd with the (n,n’γ) reaction. Phys. Rev. C 2007, 76, 034318. [Google Scholar] [CrossRef]
- Zamfir, N.V.; Zhang, J.-Y.; Casten, R.F. Interpreting recent measurements of 0+ states in 158Gd. Phys. Rev. C 2002, 66, 057303. [Google Scholar] [CrossRef]
- Hirsch, J.G.; Popa, G.; Lesher, S.R.; Aprahamian, A.; Vargas, C.E.; Draayer, J.P. Low energy 0+ excitations in 158Gd. Rev. Mex. Fis. 2006, S52, 69. [Google Scholar]
- Popa, G.; Hirsch, J.G.; Draayer, J.P. Shell model description of normal parity bands in even-even heavy deformed nuclei. Phys. Rev. C 2000, 62, 064313. [Google Scholar] [CrossRef]
- Popa, G.; Georgieva, A. Description of heavy deformed nuclei within the pseudo-SU(3) shell model. J. Phys. G Conf. Ser. 2012, 403, 012009. [Google Scholar] [CrossRef]
- Lo Iudice, N.; Sushkov, A.V.; Shirikova, N.Y. Microscopic structure of low-lying 0+ states in the deformed 158Gd. Phys. Rev. C 2004, 70, 064316. [Google Scholar] [CrossRef]
- Gerçceklioğlu, M. Excited 0+ states in 156,158,160,162Gd. Ann. Phys. 2005, 14, 312. [Google Scholar] [CrossRef]
- Asai, M.; Sekine, T.; Osa, A.; Koizumi, M.; Kojima, Y.; Shibata, M.; Yamamoto, H.; Kawade, K. Energy systematics of low-lying 0+ states in neutron-deficient Ba nuclei. Phys. Rev. C 1997, 56, 3045. [Google Scholar] [CrossRef]
- Balabanski, D.L.; Lo Bianco, G.; Atanasova, L.; Blasi, N.; Das Gupta, S.; Detistov, P.; Gladnishki, K.; Fortunato, L.; Kusoglu, A.; Nardelli, S.; et al. E0 decay and lifetimes of states in the rare-earth region: The case of 156Dy and 160Er. In Proceedings of the 30th International Workshop on Nuclear Theory, Rila Mountains, Bulgaria, 27 June–1 July 2011; Georgieva, A., Minkov, N., Eds.; Heron Press: Sofia, Bulgaria, 2011. [Google Scholar]
- Bucurescu, D.; Graw, G.; Hertenberger, R.; Wirth, H.-F.; Lo Iudice, N.; Sushkov, A.V.; Shirikova, N.Y.; Sun, Y.; Faestermann, T.; Krücken, R.; et al. High-resolution study of 0+ and 2+ excitations in 168Er with the (p, t) reaction. Phys. Rev. C 2006, 73, 064309. [Google Scholar] [CrossRef]
- Meyer, D.A.; Wood, V.; Casten, R.F.; Fitzpatrick, C.R.; Graw, G.; Bucurescu, D.; Jolie, J.; von Brentano, P.; Hertenberger, R.; Wirth, H.-F.; et al. Enhanced density of low-lying 0+ states: A corroboration of shape phase transitional behavior. Phys. Lett. B 2006, 638, 44. [Google Scholar] [CrossRef]
- Meyer, D.A.; Wood, V.; Casten, R.F.; Fitzpatrick, C.R.; Graw, G.; Bucurescu, D.; Jolie, J.; von Brentano, P.; Hertenberger, R.; Wirth, H.-F.; et al. Extensive investigation of 0+ states in rare earth region nuclei. Phys. Rev. C 2006, 74, 044309. [Google Scholar] [CrossRef]
- Suliman, G.; Bucurescu, D.; Hertenberger, R.; Wirth, H.-F.; Faestermann, T.; Krücken, R.; Behrens, T.; Bildstein, V.; Eppinger, K.; Hinke, C.; et al. Study of the 130Ba nucleus with the (p, t) reaction. Eur. Phys. J. A 2008, 36, 243. [Google Scholar] [CrossRef]
- Popa, G.; Georgieva, A.; Draayer, J.P. Systematics in the structure of low-lying, nonyrast bandhead configurations of strongly deformed nuclei. Phys. Rev. C 2004, 69, 064307. [Google Scholar] [CrossRef]
- Popa, G.; Aprahamian, A.; Georgieva, A.; Draayer, J.P. Systematics in the structure of low-lying, non-yrast band-head configurations of strongly deformed nuclei. Eur. Phys. J. A 2005, 25, s01, 451. [Google Scholar] [CrossRef]
- Gerçeklioğlu, M. Transfer strengths to the 0+ states excited by (p, t) reactions in 130,132,134Ba. Phys. Rev. C 2010, 82, 024306. [Google Scholar] [CrossRef]
- Gerçeklioğlu, M. The 0+ states excited by (p, t) reaction in 170Yb. Eur. Phys. J. A 2012, 48, 141. [Google Scholar] [CrossRef]
- Cakirli, R.B.; Casten, R.F. Anomalies in the Behavior of the First Excited K = 0 Band in Deformed Nuclei. Bulg. J. Phys. 2017, 44, 380. [Google Scholar]
- Aprahamian, A.; Brenner, D.S.; Casten, R.F.; Gill, R.L.; Piotrowski, A.; Heyde, K. Observation of 0+ states in 118Cd and the systematics of intruder states. Phys. Lett. B 1984, 140, 22. [Google Scholar] [CrossRef]
- Garrett, P.E.; Wood, J.L. On the robustness of surface vibrational modes: Case studies in the Cd region. J. Phys. G Nucl. Part. Phys. 2010, 37, 064028, Erratum in J. Phys. G Nucl. Part. Phys. 2010, 37, 069701. [Google Scholar] [CrossRef]
- Garrett, P.E.; Green, K.L.; Austin, R.A.E.; Ball, G.C.; Byopadhyay, D.S.; Colosimo, S.; Cross, D.S.; Demand, G.A.; Grinyer, G.F.; Hackman, G. Using β-decay to Map the E2 Strength in the Cd Isotopes and the Downfall of Vibrational Motion. Acta Phys. Pol. B 2011, 42, 799. [Google Scholar] [CrossRef]
- Garrett, P.E. Shape coexistence at low spin in the Z = 50 region and its spectroscopic signatures. J. Phys. G Nucl. Part. Phys. 2016, 43, 084002. [Google Scholar] [CrossRef]
- Garrett, P.E.; Wood, J.L.; Yates, S.W. Critical insights into nuclear collectivity from complementary nuclear spectroscopic methods. Phys. Scr. 2018, 93, 063001. [Google Scholar] [CrossRef]
- Burke, D.G. Search for experimental evidence supporting the multiphonon description of excited states in 152Sm. Phys. Rev. C 2002, 66, 024312. [Google Scholar] [CrossRef]
- Wirth, H.-F.; Graw, G.; Christen, S.; Cutoiu, D.; Eisermann, Y.; Günther, C.; Hertenberger, R.; Jolie, J.; Levon, A.I.; Möller, O.; et al. 0+ states in deformed actinide nuclei by the (p, t) reaction. Phys. Rev. C 2004, 69, 044310. [Google Scholar] [CrossRef]
- Lo Iudice, N.; Sushkov, A.V.; Shirikova, N.Y. Microscopic structure of low-lying 0+ states in deformed nuclei. Phys. Rev. C 2005, 72, 034303. [Google Scholar] [CrossRef]
- Sharpey-Schafer, J.F.; Mullins, S.M.; Bark, R.A.; Gueorguieva, E.; Kau, J.; Komati, F.; Lawrie, J.J.; Maine, P.; Minkova, A.; Murray, S.H.T.; et al. Shape Transitional Nuclei: What can we learn from the Yrare States? or Hello the Double Vacuum; Goodbye β-vibrations! AIP Conf. Proc. 2008, 1012, 19. [Google Scholar]
- Sharpey-Schafer, J.F.; Bark, R.A.; Bvumbi, S.P.; Lawrie, E.A.; Lawrie, J.J.; Madiba, T.E.; Majola, S.N.T.; Minkova, A.; Mullins, S.M.; Papka, P.; et al. A double vacuum, configuration dependent pairing and lack of β-vibrations in transitional nuclei: Band structure of N = 88 to N = 91 Nuclei. Nucl. Phys. A 2010, 834, 45c. [Google Scholar] [CrossRef]
- Sharpey-Schafer, J.F.; Mullins, S.M.; Bark, R.A.; Kau, J.; Komati, F.; Lawrie, E.A.; Lawrie, J.J.; Madiba, T.E.; Maine, P.; Minkova, A.; et al. Congruent band structures in 154Gd: Configuration-dependent pairing, a double vacuum and lack of β-vibrations. Eur. Phys. J. A 2011, 47, 5. [Google Scholar] [CrossRef]
- Sharpey-Schafer, J.F.; Madiba, T.E.; Bvumbi, S.P.; Lawrie, E.A.; Lawrie, J.J.; Minkova, A.; Mullins, S.M.; Papka, P.; Roux, D.G.; Timár, J. Blocking of coupling to the excitation in 154Gd by the [505]11/2- neutron in 155Gd. Eur. Phys. J. A 2011, 47, 6. [Google Scholar] [CrossRef]
- Sharpey-Schafer, J.F.; Bark, R.A.; Bvumbi, S.P.; Dinoko, T.R.S.; Majola, S.N.T. “Stiff” deformed nuclei, configuration dependent pairing and the β and γ degrees of freedom. Eur. Phys. J. A 2019, 55, 15. [Google Scholar] [CrossRef]
- Kibédi, T.; Spear, R.H. Electric monopole transitions between 0+ states for nuclei throughout the periodic table. At. Data Nucl. Data Tables 2005, 89, 77. [Google Scholar] [CrossRef]
- Wood, J.L.; Zganjar, E.F.; De Coster, C.; Heyde, K. Electric monopole transitions from low energy excitations in nuclei. Nucl. Phys. A 1999, 651, 323. [Google Scholar] [CrossRef]
- Zganjar, E.F. Conversion electron spectroscopy and its role in identifying shape coexisting structures in nuclei via E0 transitions. J. Phys. G Nucl. Part. Phys. 2016, 43, 024013. [Google Scholar] [CrossRef]
- Andreyev, A.N.; Huyse, M.; Van Duppen, P.; Weissman, L.; Ackermann, D.; Gerl, J.; Hessberger, F.P.; Hofmann, S.; Kleinböhl, A.; Münzenberg, G.; et al. A triplet of differently shaped spin-zero states in the atomic nucleus 186Pb. Nature 2000, 405, 430. [Google Scholar] [CrossRef] [PubMed]
- Le Coz, Y.; Becker, F.; Kankaanpää, H.; Korten, W.; Mergel, E.; Butler, P.A.; Cocks, J.F.C.; Dorvaux, O.; Hawcroft, D.; Helariutta, K.; et al. Evidence of multiple shape-coexistence in 188Pb. EPJdirect 1999, A3, 1. [Google Scholar]
- Cruz, S.; Bender, P.C.; Krucken, R.; Wimmer, K.; Ames, F.; Andreoiu, C.; Austin, R.A.E.; Bancroft, C.S.; Braid, R.; Bruhn, T.; et al. Shape coexistence and mixing of low-lying 0+ states in 96Sr. Phys. Lett. B 2018, 786, 94. [Google Scholar] [CrossRef]
- Little, D.; Ayangeakaa, A.D.; Janssens, R.V.F.; Zhu, S.; Tsunoda, Y.; Otsuka, T.; Brown, B.A.; Carpenter, M.P.; Gade, A.; Rhodes, D.; et al. Multistep Coulomb excitation of 64Ni: Shape coexistence and nature of low-spin excitations. Phys. Rev. C 2022, 106, 044313. [Google Scholar] [CrossRef]
- Warburton, E.K.; Becker, J.A.; Brown, B.A. Mass systematics for A = 29–44 nuclei: The deformed A ∼ 32 region. Phys. Rev. C 1990, 41, 1147. [Google Scholar] [CrossRef]
- Nowacki, F.; Poves, A.; Caurier, E.; Bounthong, B. Shape Coexistence in 78Ni as the Portal to the Fifth Island of Inversion. Phys. Rev. Lett. 2016, 117, 272501. [Google Scholar] [CrossRef] [PubMed]
- Brown, B.A. Islands of insight in the nuclear chart. Physics 2010, 3, 104. [Google Scholar] [CrossRef]
- Sorlin, O. Shell Evolutions and Nuclear Forces. EPJ Web Conf. 2014, 66, 01016. [Google Scholar] [CrossRef]
- Miyagi, T.; Stroberg, S.R.; Holt, J.D.; Shimizu, N. Ab initio multishell valence-space Hamiltonians and the island of inversion. Phys. Rev. C 2020, 102, 034320. [Google Scholar] [CrossRef]
- Doornenbal, P.; Scheit, H.; Takeuchi, S.; Aoi, N.; Li, K.; Matsushita, M.; Steppenbeck, D.; Wang, H.; Baba, H.; Ideguchi, E.; et al. Mapping the deformation in the “island of inversion”: Inelastic scattering of 30Ne and 36Mg at intermediate energies. Phys. Rev. C 2016, 93, 044306. [Google Scholar] [CrossRef]
- Doornenbal, P.; Scheit, H.; Takeuchi, S.; Utsuno, Y.; Aoi, N.; Li, K.; Matsushita, M.; Steppenbeck, D.; Wang, H.; Baba, H.; et al. Low-Z shore of the “island of inversion” and the reduced neutron magicity toward 28O. Phys. Rev. C 2017, 95, 041301. [Google Scholar] [CrossRef]
- MacGregor, P.T.; Sharp, D.K.; Freeman, S.J.; Hoffman, C.R.; Kay, B.P.; Tang, T.L.; Gaffney, L.P.; Baader, E.F.; Borge, M.J.G.; Butler, P.A.; et al. Evolution of single-particle structure near the N = 20 island of inversion. Phys. Rev. C 2021, 104, L051301. [Google Scholar] [CrossRef]
- Pritychenko, B.V.; Glasmacher, T.; Cottle, P.D.; Ibbotson, R.W.; Kemper, K.W.; Miller, K.L.; Riley, L.A.; Scheit, H. Transition to the “island of inversion”: Fast-beam γ-ray spectroscopy of 28, 30Na. Phys. Rev. C 2002, 66, 024325. [Google Scholar] [CrossRef]
- Scheit, H. Spectroscopy in and around the Island of Inversion. J. Phys. Conf. Ser. 2011, 312, 092010. [Google Scholar] [CrossRef]
- Wimmer, K.; Kröll, T.; Krücken, R.; Bildstein, V.; Gernhäuser, R.; Bastin, B.; Bree, N.; Diriken, J.; Duppen, P.V.; Huyse, M.; et al. Discovery of the Shape Coexisting 0+ State in 32Mg by a Two Neutron Transfer Reaction. Phys. Rev. Lett. 2010, 105, 252501. [Google Scholar] [CrossRef] [PubMed]
- Choudhary, V.; Horiuchi, W.; Kimura, M.; Chatterjee, R. Enormous nuclear surface diffuseness of Ne and Mg isotopes in the island of inversion. Phys. Rev. C 2021, 104, 054313. [Google Scholar] [CrossRef]
- Doornenbal, P.; Scheit, H.; Takeuchi, S.; Aoi, N.; Li, K.; Matsushita, M.; Steppenbeck, D.; Wang, H.; Baba, H.; Crawford, H.; et al. In-Beam γ-Ray Spectroscopy of 34,36,38Mg: Merging the N = 20 and N = 28 Shell Quenching. Phys. Rev. Lett. 2013, 111, 212502. [Google Scholar] [CrossRef]
- Gade, A. Reaching into the N = 40 Island of Inversion with Nucleon Removal Reactions. Physics 2021, 3, 1226. [Google Scholar] [CrossRef]
- Horiuchi, W.; Inakura, T.; Michimasa, S. Large enhancement of total reaction cross sections at the edge of the island of inversion in Ti, Cr, and Fe isotopes. Phys. Rev. C 2022, 105, 014316. [Google Scholar] [CrossRef]
- Ljungvall, J.; Görgen, A.; Obertelli, A.; Korten, W.; Clément, E.; de France, G.; Bürger, A.; Delaroche, J.-P.; Dewald, A.; Gadea, A.; et al. Onset of collectivity in neutron-rich Fe isotopes: Toward a new island of inversion? Phys. Rev. C 2010, 81, 061301. [Google Scholar] [CrossRef]
- Porter, W.S.; Ashrafkhani, B.; Bergmann, J.; Brown, C.; Brunner, T.; Cardona, J.D.; Curien, D.; Dedes, I.; Dickel, T.; Dudek, J.; et al. Mapping the N = 40 island of inversion: Precision mass measurements of neutron-rich Fe isotopes. Phys. Rev. C 2022, 105, L041301. [Google Scholar] [CrossRef]
- Rocchini, M.; Garrett, P.; Zielińska, M.; Lenzi, S.; Dao, D.; Nowacki, F.; Bildstein, V.; MacLean, A.; Olaizola, B.; Ahmed, Z.; et al. First Evidence of Axial Shape Asymmetry and Configuration Coexistence in 74Zn : Suggestion for a Northern Extension of the N = 40 Island of Inversion. Phys. Rev. Lett. 2023, 130, 122502. [Google Scholar] [CrossRef]
- Louchart, C.S.C.; Obertelli, A.; Werner, V.; Doornenbal, P.; Nowacki, F.; Authelet, G.; Baba, H.; Calvet, D.; Château, F.; Corsi, A. Extension of the N = 40 Island of Inversion towards N = 50 : Spectroscopy of 66Cr, 70, 72Fe. Phys. Rev. Lett. 2015, 115, 192501. [Google Scholar]
- Kortelahti, M.O.; Zganjar, E.F.; Wood, J.L.; Bingham, C.R.; Carter, H.K.; Toth, K.S.; Hamilton, J.H.; Kormicki, J.; Chaturvedi, L.; Newbolt, W.B. Shape coexistence in 190Hg. Phys. Rev. C 1991, 43, 484. [Google Scholar] [CrossRef]
- Siciliano, M.; Zanon, I.; Goasduff, A.; John, P.R.; Rodríguez, T.R.; Péru, S.; Deloncle, I.; Libert, J.; Zielińska, M.; Ashad, D.; et al. Shape coexistence in neutron-deficient 188Hg investigated via lifetime measurements. Phys. Rev. C 2020, 102, 014318. [Google Scholar] [CrossRef]
- Hamilton, J.H.; Ramayya, A.V.; Bosworth, E.L.; Lourens, W.; Cole, J.D.; van Nooijen, B.; Garcia-Bermudez, G.; Martin, B.; Rao, B.N.; Kawakami, H.; et al. Crossing of Near-Spherical and Deformed Bands in 186,188Hg and New Isotopes 186,188Tl. Phys. Rev. Lett. 1975, 35, 562. [Google Scholar] [CrossRef]
- Proetel, D.; Diamond, R.M.; Kienle, P.; Leigh, J.R.; Maier, K.H.; Stephens, F.S. Evidence for Strongly Deformed Shapes in 186Hg. Phys. Rev. Lett. 1973, 31, 896. [Google Scholar] [CrossRef]
- Proetel, D.; Diamond, R.M.; Stephens, F.S. Nuclear deformations in 186Hg from lifetime measurements. Phys. Lett. B 1974, 48, 102. [Google Scholar] [CrossRef][Green Version]
- Rud, N.; Ward, D.; Andrews, H.R.; Graham, R.L.; Geiger, J.S. Lifetimes in the Ground-State Band of 184Hg. Phys. Rev. Lett. 1973, 31, 1421. [Google Scholar] [CrossRef]
- Cole, J.D.; Ramayya, A.V.; Hamilton, J.H.; Kawakami, H.; van Nooijen, B.; Nettles, W.G.; Riedinger, L.L.; Turner, F.E.; Bingham, C.R.; Carter, H.K.; et al. Shape coexistence in 186Hg and the decay of 186Tl. Phys. Rev. C 1977, 16, 2010. [Google Scholar] [CrossRef]
- Gaffney, L.P.; Hackstein, M.; Page, R.D.; Grahn, T.; Scheck, M.; Butler, P.A.; Bertone, P.F.; Bree, N.; Carroll, R.J.; Carpenter, M.P.; et al. Shape coexistence in neutron-deficient Hg isotopes studied via lifetime measurements in 184,186Hg and two-state mixing calculations. Phys. Rev. C 2014, 89, 024307, Erratum in Phys. Rev. C 2014, 89, 059905(E). [Google Scholar] [CrossRef]
- Ma, W.C.; Ramayya, A.V.; Hamilton, J.H.; Robinson, S.J.; Cole, J.D.; Zganjar, E.F.; Spejewski, E.H.; Bengtsson, R.; Nazarewicz, W.; Zhang, J.-Y. The structure of high spin states in 184 Hg and 186 Hg. Phys. Lett. B 1986, 167, 277. [Google Scholar] [CrossRef]
- Bree, N.; Wrzosek-Lipska, K.; Petts, A.; Andreyev, A.; Bastin, B.; Bender, M.; Blazhev, A.; Bruyneel, B.; Butler, P.A.; Butterworth, J.; et al. Shape Coexistence in the Neutron-Deficient Even-Even 182–188Hg Isotopes Studied via Coulomb Excitation. Phys. Rev. Lett. 2014, 112, 162701. [Google Scholar] [CrossRef]
- Cole, J.D.; Hamilton, J.H.; Ramayya, A.V.; Lourens, W.; van Nooijen, B.; Kawakami, H.; Mink, L.A.; Spejewski, E.H.; Carter, H.K.; Mlekodaj, R.L.; et al. Decay of 188TI and observed shape coexistence in the bands of 188Hg. Phys. Rev. C 1984, 30, 1267. [Google Scholar] [CrossRef]
- Ma, W.C.; Ramayya, A.V.; Hamilton, J.H.; Robinson, S.J.; Barclay, M.E.; Zhao, K.; Cole, J.D.; Zganjar, E.F.; Spejewski, E.H. Ground state shaoe and crossing of near spherical and deformed bands in 182 Hg. Phys. Lett. B 1984, 139, 276. [Google Scholar] [CrossRef]
- Olaizola, B.; Garnsworthy, A.B.; Ali, F.A.; Andreoiu, C.; Ball, G.C.; Bernier, N.; Bidaman, H.; Bildstein, V.; Bowry, M.; Caballero-Folch, R.; et al. Shape coexistence in the neutron-deficient lead region: A systematic study of lifetimes in the even-even 188--200Hg with the GRIFFIN spectrometer at TRIUMF. Phys. Rev. C 2019, 100, 024301. [Google Scholar] [CrossRef]
- Wrzosek-Lipska, K.; Gaffney, L.P. Unique and complementary information on shape coexistence in the neutron-deficient Pb region derived from Coulomb excitation. J. Phys. G Nucl. Part Phys. 2016, 43, 024012. [Google Scholar] [CrossRef]
- Carpenter, M.P.; Janssens, R.V.F.; Amro, H.; Blumenthal, D.J.; Brown, L.T.; Seweryniak, D.; Woods, P.J.; Ackermann, D.; Ahmad, I.; Davids, C.; et al. Excited States in 176,178Hg and Shape Coexistence in Very Neutron-Deficient Hg Isotopes. Phys. Rev. Lett. 1997, 78, 3650. [Google Scholar] [CrossRef]
- Dracoulis, G.D.; Stuchbery, A.E.; Macchiavelli, A.O.; Beausang, C.W.; Burde, J.; Deleplanque, M.A.; Diamond, R.M.; Stephens, F.S. Shape co-existence in 180Hg and delineation of the midshell minimum. Phys. Lett. B 1988, 208, 365. [Google Scholar] [CrossRef]
- Elseviers, J.; Andreyev, A.; Antalic, S.; Barzakh, A.; Bree, N.; Cocolios, T.; Comas, V.; Diriken, J.; Fedorov, D.; Fedosseyev, V.N.; et al. Shape coexistence in 180Hg studied through the β decay of 180Tl. Phys. Rev. C 2011, 84, 034307. [Google Scholar] [CrossRef]
- Kondev, F.G.; Carpenter, M.P.; Janssens, R.V.F.; Wiedenhöver, I.; Alcorta, M.; Bhattacharyya, P.; Brown, L.T.; Davids, C.N.; Fischer, S.M.; Khoo, T.L.; et al. Complex band structure in neutron-deficient 178Hg. Phys. Rev. C 1999, 61, 011303. [Google Scholar] [CrossRef]
- Kondev, F.G.; Janssens, R.V.F.; Carpenter, M.P.; Abu Saleem, K.; Ahmad, I.; Alcorta, M.; Amro, H.; Bhattacharyya, P.; Brown, L.T.; Caggiano, T.; et al. Interplay between octupole and quasiparticle excitations in 178Hg and 180Hg. Phys. Rev. C 2000, 62, 044305. [Google Scholar] [CrossRef]
- Müller-Gatermann, C.; Dewald, A.; Fransen, C.; Auranen, K.; Badran, H.; Beckers, M.; Blazhev, A.; Blazhev, A.; Cullen, D.M.; Fruet, G.; et al. Shape coexistence in 178Hg. Phys. Rev. C 2019, 99, 054325. [Google Scholar] [CrossRef]
- Bengtsson, R.; Bengtsson, T.; Dudek, J.; Leander, G.; Nazarewicz, W.; Zhang, J.-Y. Shape coexistence and shape transitions in even-even Pt and Hg isotopes. Phys. Lett. B 1987, 183, 1. [Google Scholar] [CrossRef]
- Delion, D.S.; Liotta, R.J.; Qi, C.; Wyss, R. Probing shape coexistence by α decays to 0+ states. Phys. Rev. C 2014, 90, 061303. [Google Scholar]
- Jiao, C.F.; Shi, Y.; Liu, H.L.; Xu, F.R.; Walker, P.M. Shape-coexisting rotation in neutron-deficient Hg and Pb nuclei. Phys. Rev. C 2015, 91, 034309. [Google Scholar] [CrossRef]
- Shi, Y.; Xu, F.R.; Liu, H.L.; Walker, P.M. Multi-quasiparticle excitation: Extending shape coexistence in A∼190 neutron-deficient nuclei. Phys. Rev. C 2010, 82, 044314. [Google Scholar] [CrossRef]
- Richards, J.D.; Berggren, T.; Bingham, C.R.; Nazarewicz, W.; Wauters, J. α decay and shape coexistence in the α-rotor model. Phys. Rev. C 1997, 56, 1389. [Google Scholar] [CrossRef]
- Zhang, J.-Y.; Hamilton, J.H. Theoretical calculations of the different shape coexistence observed in 190Hg. Phys. Lett. B 1991, 260, 11. [Google Scholar] [CrossRef]
- Nazarewicz, W. Variety of shapes in the mercury and lead isotopes. Phys. Lett. B 1993, 305, 195. [Google Scholar] [CrossRef]
- Bonatsos, D.; Karakatsanis, K.E.; Martinou, A.; Mertzimekis, T.J.; Minkov, N. Microscopic origin of shape coexistence in the N = 90, Z = 64 region. Phys. Lett. B 2022, 829, 137099. [Google Scholar] [CrossRef]
- Bonatsos, D.; Karakatsanis, K.E.; Martinou, A.; Mertzimekis, T.J.; Minkov, N. Islands of shape coexistence from single-particle spectra in covariant density functional theory. Phys. Rev. C 2022, 106, 044323. [Google Scholar] [CrossRef]
- Penninga, J.; Hesselink, W.H.A.; Balanda, A.; Stolk, A.; Verheul, H.; van Klinken, J.; Riezebos, H.J.; de Voigt, M.J.A. Proton particle-hole states and collective excitations in 196Pb. Nucl. Phys. A 1987, 471, 535. [Google Scholar] [CrossRef]
- Van Duppen, P.; Coenen, E.; Deneffe, K.; Huyse, M.; Heyde, K.; Van Isacker, P. Observation of Low-Lying Jπ=0+ States in the Single-Closed-Shell Nuclei 192-198Pb. Phys. Rev. Lett. 1984, 52, 1974. [Google Scholar] [CrossRef]
- Van Duppen, P.; Coenen, E.; Deneffe, K.; Huyse, M.; Wood, J.L. β+/electron-capture decay of 192,194,196,198,200Bi: Experimental evidence for low lying 0+ states. Phys. Rev. C 1987, 35, 1861. [Google Scholar] [CrossRef] [PubMed]
- Allatt, R.G.; Page, R.D.; Leino, M.; Enqvist, T.; Eskola, K.; Greenlees, P.T.; Jones, P.; Julin, R.; Kuusiniemi, P.; Trzaska, W.H.; et al. Fine structure in 192Po α-decay and shape coexistence in 188Pb. Phys. Lett. B 1998, 437, 29. [Google Scholar] [CrossRef]
- Dracoulis, G.D.; Lane, G.J.; Byrne, A.P.; Baxter, A.M.; Kibédi, T.; Macchiavelli, A.O.; Fallon, P.; Clark, R.M. Isomer bands, E0 transitions, and mixing due to shape coexistence in . Phys. Rev. C 2003, 67, 051301. [Google Scholar] [CrossRef]
- Dracoulis, G.D.; Lane, G.J.; Byrne, A.P.; Kibédi, T.; Baxter, A.M.; Macchiavèlli, A.O.; Fallon, P.; Clark, R.M. Spectroscopy of 82188Pb106: Evidence for shape coexistence. Phys. Rev. C 2004, 69, 054318. [Google Scholar] [CrossRef]
- Pakarinen, J.; Darby, I.G.; Eeckhaudt, S.; Enqvist, T.; Grahn, T.; Greenlees, P.T.; Hellemans, V.; Heyde, K.; Johnston-Theasby, F.; Jones, P.; et al. Evidence for oblate structure in 186Pb. Phys. Rev. C 2005, 72, 011304. [Google Scholar] [CrossRef]
- Cocks, J.F.C.; Muikku, M.; Korten, W.; Wadsworth, R.; Chmel, S.; Domscheit, J.; Greenlees, P.T.; Helariutta, K.; Hibbert, I.; Houry, M.; et al. First observation of excited states in 184Pb: Spectroscopy beyond the neutron mid-shell. Eur. Phys. J. A 1998, 3, 17. [Google Scholar] [CrossRef]
- Jenkins, D.G.; Muikku, M.; Greenlees, P.T.; Hauschild, K.; Helariutta, K.; Jones, P.M.; Julin, R.; Juutinen, S.; Kankaanpää, H.; Kelsall, N.S.; et al. First observation of excited states in 182Pb. Phys. Rev. C 2000, 62, 021302. [Google Scholar] [CrossRef]
- Rahkila, P.; Jenkins, D.G.; Pakarinen, J.; Gray-Jones, C.; Greenlees, P.T.; Jakobsson, U.; Jones, P.; Julin, R.; Juutinen, S.; Ketelhut, S.; et al. Shape coexistence at the proton drip-line: First identification of excited states in 180Pb. Phys. Rev. C 2010, 82, 011303. [Google Scholar] [CrossRef]
- Julin, R.; Grahn, T.; Pakarinen, J.; Rahkila, P. In-beam spectroscopic studies of shape coexistence and collectivity in the neutron-deficient Zapprox82 nuclei. J. Phys. G Nucl. Part. Phys. 2016, 43, 024004. [Google Scholar] [CrossRef]
- Xu, C.; Ren, Z. α transitions to coexisting 0+ states in Pb and Po isotopes. Phys. Rev. C 2007, 75, 044301. [Google Scholar] [CrossRef]
- Alber, D.; Alfier, R.; Bach, C.E.; Fossan, D.B.; Grawe, H.; Kluge, H.; Lach, M.; Maier, K.H.; Schramm, M.; Schubart, R.; et al. Quadrupole and octupole collectivity in light Po isotopes. Z. Phys. A 1991, 339, 225. [Google Scholar] [CrossRef]
- Grahn, T.; Dewald, A.; Moller, O.; Julin, R.; Beausang, C.W. Collectivity and Configuration Mixing in 186,188Pb and 194Po. Phys. Rev. Lett. 2006, 97, 062501. [Google Scholar] [CrossRef]
- Grahn, T.; Dewald, A.; Möller, O.; Julin, R.; Beausang, C.W.; Christen, S.; Darby, I.G.; Eeckhaudt, S.; Greenlees, P.T.; Görgen, A. Lifetimes of intruder states in 186,188Pb and 194Po. Nucl. Phys. A 2008, 801, 83. [Google Scholar] [CrossRef][Green Version]
- Helariutta, K.; Cocks, J.F.C.; Enqvist, T.; Greenlees, P.T.; Jones, P.; Julin, R.; Juutinen, S.; Jämsen, P.; Kankaanpää, H.; Kettunen, H.; et al. Gamma-ray spectroscopy of 192-195Po. Eur. Phys. J. A 1999, 6, 289. [Google Scholar] [CrossRef]
- Younes, W.; Cizewski, J.A. Systematical behavior of even—A polonium isotopes. Phys. Rev. C 1997, 55, 1218. [Google Scholar] [CrossRef]
- Bijnens, N.; Decrock, P.; Franchoo, S.; Gaelens, M.; Huyse, M.; Hwang, H.-Y.; Reusen, I.; Szerypo, J.; von Schwarzenberg, J.; Vancraeynest, G.; et al. Study of 200,202Po through β+ and electron-capture decay and the manifestation of shape coexistence in the lighter Po isotopes. Phys. Rev. C 1998, 58, 754. [Google Scholar] [CrossRef]
- Kesteloot, N.; Bastin, B.; Gaffney, L.P.; Wrzosek-Lipska, K.; Auranen, K.; Bauer, C.; Bender, M.; Bildstein, V.; Blazhev, A.; Bonig, S.; et al. Deformation and mixing of coexisting shapes in neutron-deficient polonium isotopes. Phys. Rev. C 2015, 92, 054301. [Google Scholar] [CrossRef]
- Oros, A.M.; Heyde, K.; De Coster, C.; Decroix, B.; Wyss, R.; Barrett, B.R.; Navratil, P. Shape coexistence in the light Po isotopes. Nucl. Phys. A 1999, 645, 107. [Google Scholar] [CrossRef]
- Agbemava, S.E.; Afanasjev, A.V.; Nakatsukasa, T.; Ring, P. Covariant density functional theory: Reexamining the structure of superheavy nuclei. Phys. Rev. C 2015, 92, 054310. [Google Scholar] [CrossRef]
- Prassa, V.; Nikšić, T.; Lalazissis, G.A.; Vretenar, D. Relativistic energy density functional description of shape transitions in superheavy nuclei. Phys. Rev. C 2012, 86, 024317. [Google Scholar] [CrossRef]
- Prassa, V.; Nikšić, T.; Vretenar, D. Structure of transactinide nuclei with relativistic energy density functionals. Phys. Rev. C 2013, 88, 044324. [Google Scholar] [CrossRef]
- Garg, U.; Chaudhury, A.; Drigert, M.W.; Funk, E.G.; Mihelich, J.W.; Radford, D.C.; Helppi, H.; Holzmann, R.; Janssens, R.V.F.; Khoo, T.L.; et al. Lifetime measurements in 184Pt and the shape coexistence picture. Phys. Lett. B 1986, 180, 319. [Google Scholar] [CrossRef]
- Larabee, A.J.; Carpenter, M.P.; Riedinger, L.L.; Courtney, L.H.; Waddington, J.C.; Janzen, V.P.; Nazarewicz, W.; Zhang, J.-Y.; Bengtsson, R.; Lèander, G.A. Shape coexistence and alignment processes in the light Pt and Au region. Phys. Lett. B 1986, 169, 21. [Google Scholar] [CrossRef]
- Xu, Y.; Krane, K.S.; Gummin, M.A.; Jarrio, M.; Wood, J.L.; Zganjar, E.F.; Carter, H.K. Shape coexistence and electric monopole transitions in 184Pt. Phys. Rev. Lett. 1992, 68, 3853. [Google Scholar] [CrossRef] [PubMed]
- Davidson, P.M.; Dracoulis, G.D.; Kibédi, T.; Byrne, A.P.; Anderssen, S.S.; Baxter, A.M.; Fabricius, B.; Lane, G.J.; Stuchbery, A.E. Non-yrast states and shape co-existence in light Pt isotopes. Nucl. Phys. A 1999, 657, 219. [Google Scholar] [CrossRef]
- Dracoulis, G.D.; Stuchbery, A.E.; Byrne, A.P.; Poletti, A.R.; Poletti, S.J.; Gerl, J.; Bark, R.A. Shape coexistence in very neutron-deficient Pt isotopes. J. Phys. G Nucl. Phys. 1986, 12, L97. [Google Scholar] [CrossRef]
- Dracoulis, G.D.; Fabricius, B.; Stuchbery, A.E.; Macchiavelli, A.O.; Korten, W.; Azaiez, F.; Rubel, E.; Deleplanque, M.A.; Diamond, R.M.; Stephens, F.S. Shape coexistence from the structure of the yrast band in 174Pt. Phys. Rev. C 1991, 44, R1246. [Google Scholar] [CrossRef]
- Gladnishki, K.A.; Petkov, P.; Dewald, A.; Fransen, C.; Hackstein, M.; Jolie, J.; Pissulla, T.; Rother, W.; Zell, K.O. Yrast electromagnetic transition strengths and shape coexistence in 182Pt. Nucl. Phys. A 2012, 877, 19. [Google Scholar] [CrossRef]
- Goon, J.T.M.; Hartley, D.J.; Riedinger, L.L.; Carpenter, M.P.; Kondev, F.G.; Janssens, R.V.F.; Abu Saleem, K.H.; Ahmad, I.; Amro, H.; Cizewski, J.A.; et al. Shape coexistence and band crossings in 174Pt. Phys. Rev. C 2004, 70, 014309. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Biswas, D.C.; Tanel, S.K.; Danu, L.S.; Joshi, B.N.; Prajapati, G.K.; Nag, S.; Trivedi, T.; Saha, S.; Sethi, J.; et al. Coexisting shape- and high-K isomers in the shape transitional nucleus 188Pt. Phys. Lett. B 2014, 739, 462. [Google Scholar] [CrossRef][Green Version]
- Stuchbery, A.E.; Anderssen, S.S.; Byrne, A.P.; Davidson, P.M.; Dracoulis, G.D.; Lane, G.J. Measured Magnetic Moments and Shape Coexistence in the Neutron-Deficient Nuclei 184,186,188Pt. Phys. Rev. Lett. 1996, 76, 2246. [Google Scholar] [CrossRef] [PubMed]
- McCutchan, E.A.; Casten, R.F.; Zamfir, N.V. Simple interpretation of shape evolution in Pt isotopes without intruder states. Phys. Rev. C 2005, 71, 061301. [Google Scholar] [CrossRef]
- Budaca, R.; Budaca, A.I. Shape phase mixing in critical point nuclei. Phys. Rev. C 2016, 94, 054306. [Google Scholar] [CrossRef]
- Stevenson, P.D.; Brine, M.P.; Podolyak, Z.; Regan, P.H.; Walker, P.M.; Rikovska Stone, J. Shape evolution in the neutron-rich tungsten region. Phys. Rev. C 2005, 72, 047303. [Google Scholar] [CrossRef]
- Kumar, R.; Govil, I.M.; Dhal, A.; Chaturvedi, L.; Praharaj, C.R.; Rath, A.K.; Kiran Kumar, G.; Basu, S.K.; Chakraborty, A.; Krishichayan; et al. Triaxial shape coexistence and new aligned band in 178Os. Phys. Rev. C 2009, 80, 054319. [Google Scholar] [CrossRef]
- Tanabe, K.; Sugawara-Tanabe, K. Shape coexistence at high spins in 158Er and 160Yb predicted by the self-consistent calculation. Phys. Lett. B 1984, 135, 353. [Google Scholar] [CrossRef]
- Rowe, D.J. The emergence of deformation and rotational states in the many-nucleon quantum theory of nuclei. J. Phys. G Nucl. Part. Phys. 2016, 43, 024011. [Google Scholar] [CrossRef]
- Rowe, D.J. Nuclear shape coexistence from the perspective of an algebraic many-nucleon version of the Bohr-Mottelson unified model. Phys. Rev. C 2020, 101, 054301. [Google Scholar] [CrossRef]
- Bjerregaard, J.H.; Hansen, O.; Nathan, O.; Hinds, S. The (t, p) reaction with the even isotopes of Sm. Nucl. Phys. 1966, 86, 145. [Google Scholar] [CrossRef]
- McLatchie, W.; Kitching, J.E.; Darcey, W. The reaction 154Sm (p, t) 152Sm and further evidence for shape coexistence in 152Sm. Phys. Lett. B 1969, 30, 529. [Google Scholar] [CrossRef]
- Casten, R.F.; Kusnezov, D.; Zamfir, N.V. Phase Transitions in Finite Nuclei and the Integer Nucleon Number Problem. Phys. Rev. Lett. 1999, 82, 5000. [Google Scholar] [CrossRef]
- Garrett, P.E.; Kulp, W.D.; Wood, J.L.; Byopadhyay, D.; Choudry, S.; Dashdorj, D.; Lesher, S.R.; McEllistrem, M.T.; Mynk, M.; Orce, J.N.; et al. New Features of Shape Coexistence in 152Sm. Phys. Rev. Lett. 2009, 103, 062501. [Google Scholar] [CrossRef] [PubMed]
- Basak, S.; Alam, S.S.; Kumar, D.; Saha, A.; Bhattacharjee, T. Shape coexistence scenario in 150Sm from a γ-γ fast-timing measurement. Phys. Rev. C 2021, 104, 024320. [Google Scholar] [CrossRef]
- Passoja, A.; Julin, R.; Kantele, J.; Luontama, M.; Vergnes, M. E0 transitions in 70Ge and shape-coexistence interpretation of even-mass Ge isotopes. Nucl. Phys. A 1985, 441, 261. [Google Scholar] [CrossRef]
- Gupta, J.B.; Hamilton, J.H. Outstanding problems in the band structures of 152Sm. Phys. Rev. C 2017, 96, 034321. [Google Scholar] [CrossRef]
- Rajbanshi, S.; Bisoi, A.; Nag, S.; Saha, S.; Sethi, J.; Trivedi, T.; Bhattacharjee, T.; Bhattacharyya, S.; Chattopadhyay, S.; Gangopadhyay, G.; et al. Shape coexistence in the near-spherical 142Sm nucleus. Phys. Rev. C 2014, 89, 014315. [Google Scholar] [CrossRef]
- Cardona, M.A.; Lunardi, S.; Bazzacco, D.; de Angelis, G.; Roca, V. Shape coexistence in 140Sm and the onset of deformation below N = 82 from lifetime measurements. Phys. Rev. C 1991, 44, 891. [Google Scholar] [CrossRef]
- Casten, R.F.; Warner, D.D.; Brenner, D.S.; Gill, R.L. Relation between the Z = 64 Shell Closure and the Onset of Deformation at N = 88–90. Phys. Rev. Lett. 1981, 47, 1433. [Google Scholar] [CrossRef]
- Petrache, C.M.; Walker, P.M.; Guo, S.; Chen, Q.B.; Frauendorf, S.; Liu, Y.X.; Wyss, R.A.; Mengoni, D.; Qiang, Y.H.; Astier, A.; et al. Diversity of shapes and rotations in the γ-soft 130Ba nucleus: First observation of a t-band in the A = 130 mass region. Phys. Lett. B 2019, 795, 241. [Google Scholar] [CrossRef]
- Bron, J.; Hesselink, W.H.A.; Van Poelgeest, A.; Zalmstra, J.J.A.; Uitzinger, M.J.; Verheul, H.; Heyde, K.; Waroquier, M.; Vincx, H.; Van Isacker, P. Collective bands in even mass Sn isotopes. Nucl. Phys. A 1979, 318, 335. [Google Scholar] [CrossRef]
- Cross, D.S.; Pore, J.L.; Andreoiu, C.; Ball, G.C.; Bender, P.C.; Chester, A.S.; Churchman, R.; Demand, G.A.; Diaz Varela, A.; Dunlop, R.; et al. Conversion-electron spectroscopy and gamma-gamma angular correlation measurements in 116Sn. Eur. Phys. J. A 2017, 53, 216. [Google Scholar] [CrossRef]
- Harada, H.; Murakami, T.; Yoshida, K.; Kasagi, J.; Inamura, T.; Kubo, T. Intruder deformed bands in 110Sn and 112Sn. Phys. Lett. B 1988, 207, 17. [Google Scholar] [CrossRef]
- Harada, H.; Sugawara, M.; Kusakari, H.; Shinohara, H.; Ono, Y.; Furuno, K.; Hosoda, T.; Adachi, M.; Matsuki, S.; Kawamura, N. High-spin states in 114Sn. Phys. Rev. C 1989, 39, 132. [Google Scholar] [CrossRef]
- Petrache, C.M.; Régis, J.-M.; Andreoiu, C.; Spieker, M.; Michelagnoli, C.; Garrett, P.E.; Astier, A.; Dupont, E.; Garcia, F.; Guo, S.; et al. Collectivity of the 2p-2h proton intruder band of 116Sn. Phys. Rev. C 2019, 99, 024303. [Google Scholar] [CrossRef]
- Pore, J.L.; Cross, D.S.; Andreoiu, C.; Ashley, R.; Ball, G.C.; Bender, P.C.; Chester, A.S.; Diaz Varela, A.; Demand, G.A.; Dunlop, R.; et al. Study of the β-decay of 116m1In: A new interpretation of low-lying 0+ states in 116Sn. Eur. Phys. J. A 2017, 53, 27. [Google Scholar] [CrossRef]
- Schimmer, M.; Wirowski, R.; Albers, S.; Böhm, G.; Dewald, A.; Gelberg, A.; von Brentano, P. Observation of a new deformed structure in 114Sn. Z. Phys. A 1991, 338, 117. [Google Scholar] [CrossRef]
- Spieker, M.; Petkov, P.; Litvinova, E.; Müller-Gatermann, C.; Pickstone, S.G.; Prill, S.; Scholz, P.; Zilges, A. Shape coexistence and collective low-spin states in 112,114Sn studied with the (p, p’ γ) Doppler-shift attenuation coincidence technique. Phys. Rev. C 2018, 97, 054319. [Google Scholar] [CrossRef]
- Viggars, D.A.; Taylor, H.W.; Singh, B.; Waddington, J.C. Observation of collective behavior in 110Sn. Phys. Rev. C 1987, 36, 1006. [Google Scholar] [CrossRef]
- Wolińska-Cichocka, M.; Kownacki, J.; Urban, W.; Ruchowska, E.; Płóciennik, W.A.; Bekman, B.; Droste, C.; Gast, W.; Lieder, R.; Mȩczyński, W.; et al. Gamma-ray spectroscopy in 110Sn and 111Sn. Eur. Phys. J. A 2005, 24, 259. [Google Scholar] [CrossRef]
- Azaiez, F.; Andriamonje, S.; Chemin, J.F.; Fidah, M.; Scheurer, J.N.; Bastin, G.; Thibaud, J.P.; Beck, F.; Costa, G.; Bruandet, J.F.; et al. High-spin states in neutron deficient 106Sn and 108Sn isotopes. Nucl. Phys. A 1989, 501, 401. [Google Scholar] [CrossRef]
- Juutinen, S.; Mäkelä, E.; Julin, R.; Piiparinen, M.; Törmänen, S.; Virtanen, A.; Adamides, E.; Ataç, A.; Blomqvist, J.; Cederwall, B.; et al. Coexistence of collective and quasiparticle structures in 106Sn and 108Sn. Nucl. Phys. A 1997, 617, 74. [Google Scholar] [CrossRef]
- Wadsworth, R.; Andrews, H.R.; Clark, R.M.; Fossan, D.B.; Galindo-Uribarri, A.; Hughes, J.R.; Janzen, V.P.; LaFosse, D.R.; Mullins, S.M.; Paul, E.S.; et al. Intruder bands in 108Sn. Nucl. Phys. A 1993, 559, 461. [Google Scholar] [CrossRef]
- Wadsworth, R.; Beausang, C.W.; Cromaz, M.; DeGraaf, J.; Drake, T.E.; Fossan, D.B.; Flibotte, S.; Galindo-Uribarri, A.; Hauschild, K.; Hibbert, I.M.; et al. Smooth band termination in 108Sn. Phys. Rev. C 1996, 53, 2763. [Google Scholar] [CrossRef] [PubMed]
- Song, T.; Yang, L.M. Microscopic investigation of pair excitation and shape coexistence in even-even nuclei. Phys. Rev. C 1989, 40, 1782. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.M.; Song, T.; Wang, X.H. Microscopic treatment of shape coexistence in even-even nuclei and related extension of IBM. Phys. Lett. B 1986, 175, 6. [Google Scholar] [CrossRef]
- Meyer, R.A.; Peker, L. Evidence for the coexistence of shapes in even-mass Cd nuclei. Z. Phys. A 1977, 283, 379. [Google Scholar] [CrossRef]
- Fahlander, C.; Bäcklin, A.; Hasselgren, L.; Kavka, A.; Mittal, V.; Svensson, L.E.; Varnestig, B.; Cline, D.; Kotlinski, B.; Grein, H.; et al. Quadrupole collective properties of 114Cd. Nucl. Phys. A 1988, 485, 327. [Google Scholar] [CrossRef]
- Kern, J.; Bruder, A.; Drissi, S.; Ionescu, V.A.; Kusnezov, D. Study of 110Cd by the 108Pd (α,2nγ) reaction. Nucl. Phys. A 1990, 512, 1. [Google Scholar] [CrossRef]
- Kusnezov, D.; Bruder, A.; Ionescu, V.; Kern, J.; Rast, M.; Heyde, K.; Van Isacker, P.; Moreau, J.; Waroquier, M.; Meyer, R.A. Mixing of the ground band and two-particle four-hole intruder band in 110Cd. Helv. Phys. Acta 1987, 60, 456. [Google Scholar]
- Garrett, P.E.; Rodríguez, T.R.; Diaz Varela, A.; Green, K.L.; Bangay, J.; Finlay, A.; Austin, R.A.E.; Ball, G.C.; Bandyopadhyay, D.S.; Bildstein, V.; et al. Multiple Shape Coexistence in 110,112Cd and Beyond Mean Field Calculations. J. Phys. Conf. Ser. 2020, 1643, 012131. [Google Scholar] [CrossRef]
- Kumpulainen, J.; Julin, R.; Kantele, J.; Passoja, A.; Trzaska, W.H.; Verho, E.; Väärämäki, J. New features in systematics of low-spin states in even 106-120Cd. Z. Phys. A At. Nucl. 1990, 335, 109. [Google Scholar] [CrossRef]
- Kumpulainen, J.; Julin, R.; Kantele, J.; Passoja, A.; Trzaska, W.H.; Verho, E.; Väärämäki, J.; Cutoiu, D.; Ivascu, M. Systematic study of low-spin states in even Cd nuclei. Phys. Rev. C 1992, 45, 640. [Google Scholar] [CrossRef] [PubMed]
- Gray, T.J.; Allmond, J.M.; Janssens, R.V.F.; Korten, W.; Stuchbery, A.E.; Wood, J.L.; Ayangeakaa, A.D.; Bottoni, S.; Bucher, B.M.; Campbell, C.M.; et al. E2 rotational invariants of and states for 106Cd: The emergence of collective rotation. Phys. Lett. B 2022, 834, 137446. [Google Scholar] [CrossRef]
- Aprahamian, A.; Brenner, D.S.; Casten, R.F.; Gill, R.L.; Piotrowski, A. First observation of a near-harmonic vibrational nucleus. Phys. Rev. Lett. 1987, 59, 535. [Google Scholar] [CrossRef]
- Nomura, K.; Karakatsanis, K.E. Collective-model description of shape coexistence and intruder states in cadmium isotopes based on a relativistic energy density functional. Phys. Rev. C 2022, 106, 064317. [Google Scholar] [CrossRef]
- Rikovska, J.; Stone, N.J.; Green, V.R.; Walker, P.M. IBA-2 model calculation on even mass tellurium isotopes compared with results of recent nuclear orientation experiments. Hyperfine Interact. 1985, 22, 405. [Google Scholar] [CrossRef]
- Rikovska, J.; Stone, N.J.; Walters, W.B. Dynamical symmetries in even-even Te nuclides. Phys. Rev. C 1987, 36, 2162. [Google Scholar] [CrossRef]
- Rikovska, J.; Stone, N.J.; Walker, P.M.; Walters, W.B. Intruder states in even-even Te nuclei. Nucl. Phys. A 1989, 505, 145. [Google Scholar] [CrossRef]
- Walker, P.M.; Ashworth, C.J.; Grant, I.S.; Green, V.R.; Rikovska, J.; Shaw, T.L.; Stone, N.J. E0 transitions in the light tellurium isotopes: Evidence for intruder states. J. Phys. G Nucl. Phys. 1987, 13, L195. [Google Scholar] [CrossRef]
- Abood, S.N.; Najim, L.A. Interacting boson model (IBM-2) calculations of selected even-even Te nuclei. Adv. Appl. Sci. Res. 2013, 4, 444. [Google Scholar]
- Sabri, H.; Jahangiri, Z.; Mohammadi, M.A. Investigation of shape coexistence in 118-128Te isotopes. Nucl. Phys. A 2016, 946, 11. [Google Scholar] [CrossRef]
- Gupta, J.B. Spectral features of vibrational Te isotopes. Phys. Rev. C 2023, 107, 034315. [Google Scholar] [CrossRef]
- Lhersonneau, G.; Wang, J.C.; Hankonen, S.; Dendooven, P.; Jones, P.; Julin, R.; Äystö, J. Decays of 110Rh and 112Rh to the near neutron midshell isotopes 110Pd and 112Pd. Phys. Rev. C 1999, 60, 014315. [Google Scholar] [CrossRef]
- Prados-Estévez, F.M.; Peters, E.E.; Chakraborty, A.; Mynk, M.G.; Bandyopadhyay, D.; Boukharouba, N.; Choudry, S.N.; Crider, B.P.; Garrett, P.E.; Hicks, S.F.; et al. Collective quadrupole behavior in 106Pd. Phys. Rev. C 2017, 95, 034328. [Google Scholar] [CrossRef]
- Svensson, L.E.; Fahlander, C.; Hasselgren, L.; Bäcklin, A.; Westerberg, L.; Cline, D.; Czosnyka, T.; Wu, C.Y.; Diamond, R.M.; Kluge, H. Multiphonon vibrational states in 106,108Pd. Nucl. Phys. A 1995, 584, 547. [Google Scholar] [CrossRef]
- Peters, E.E.; Prados-Estévez, F.M.; Chakraborty, A.; Mynk, M.G.; Bandyopadhyay, D.; Choudry, S.N.; Crider, B.P.; Garrett, P.E.; Hicks, S.F.; Kumar, A.; et al. E0 transitions in 106Pd: Implications for shape coexistence. Eur. Phys. J. A 2016, 52, 96. [Google Scholar] [CrossRef][Green Version]
- Zamfir, N.V.; Caprio, M.A.; Casten, R.F.; Barton, C.J.; Beausang, C.W.; Berant, Z.; Brenner, D.S.; Chou, W.T.; Cooper, J.R.; Hecht, A.A.; et al. 102Pd: An E(5) nucleus? Phys. Rev. C 2002, 65, 044325. [Google Scholar] [CrossRef]
- Hosseinnezhad, A.; Jalili Majarshin, A.; Luo, Y.A.; Ahmadian, D.; Sabri, H. Deformation in 92–128 Pd isotopes. Nucl. Phys. A 2022, 1028, 122523. [Google Scholar] [CrossRef]
- Ansari, S.; Régis, J.; Jolie, J.; Saed-Samii, N.; Warr, N.; Korten, W.; Zielińska, M.; Salsac, M.; Blanc, A.; Jentschel, M.; et al. Experimental study of the lifetime and phase transition in neutron-rich 98,100,102Zr. Phys. Rev. C 2017, 96, 054323. [Google Scholar] [CrossRef]
- Heyde, K.; Meyer, R.A. Comment on “Monopole strength and shape coexistence in the A≃100 mass region”. Phys. Rev. C 1990, 42, 790. [Google Scholar] [CrossRef]
- Mach, H.; Moszyǹski, M.; Gill, R.L.; Wohn, F.K.; Winger, J.A.; Hill, J.C.; Molnár, G.; Sistemich, K. Deformation and shape coexistence of 0+ states in 98Sr and 100Zr. Phys. Lett. B 1989, 230, 21. [Google Scholar] [CrossRef]
- Mach, H.; Moszyǹski, M.; Gill, R.L.; Molnár, G.; Wohn, F.K.; Winger, J.A.; Hill, J.C. Monopole strength and shape coexistence in the A ≃ 100 mass region. Phys. Rev. C 1990, 41, 350. [Google Scholar] [CrossRef] [PubMed]
- Mach, H.; Moszyǹski, M.; Gill, R.L.; Molnár, G.; Wohn, F.K.; Winger, J.A.; Hill, J.C. Reply to “Comment on `Monopole strength and shape coexistence in the A ≃ 100 mass region”’. Phys. Rev. C 1990, 42, 793. [Google Scholar] [CrossRef] [PubMed]
- Wohn, F.K.; Hill, J.C.; Howard, C.B.; Sistemich, K.; Petry, R.F.; Gill, R.L.; Mach, H.; Piotrowski, A. Shape coexistence and level structure of 100Zr from decay of the low-spin isomer of 100Y. Phys. Rev. C 1986, 33, 677. [Google Scholar] [CrossRef]
- Singh, P.; Korten, W.; Hagen, T.; Görgen, A.; Grente, L.; Salsac, M.-D.; Farget, F.; Clément, E.; de France, G.; Braunroth, T.; et al. Evidence for Coexisting Shapes through Lifetime Measurements in 98Zr. Phys. Rev. Lett. 2018, 121, 192501. [Google Scholar] [CrossRef]
- Witt, W.; Werner, V.; Pietralla, N.; Albers, M.; Ayangeakaa, A.D.; Bucher, B.; Carpenter, M.P.; Cline, D.; David, H.M.; Hayes, A.; et al. Sub-shell closure and shape coexistence in the transitional nucleus 98Zr. Phys. Rev. C 2018, 98, 041302. [Google Scholar] [CrossRef]
- Kremer, C.; Aslanidou, S.; Bassauer, S.; Hilcker, M.; Krugmann, A.; von Neumann-Cosel, P.; Otsuka, T.; Pietralla, N.; Ponomarev, V.Y.; Shimizu, N.; et al. First Measurement of Collectivity of Coexisting Shapes Based on Type II Shell Evolution: The Case of 96Zr. Phys. Rev. Lett. 2016, 117, 172503. [Google Scholar] [CrossRef]
- Witt, W.; Pietralla, N.; Werner, V.; Beck, T. Data on the structural coexistence in the 96Zr nucleus. Eur. Phys. J. A 2019, 55, 79. [Google Scholar] [CrossRef]
- Chakraborty, A.; Peters, E.E.; Crider, B.P.; Andreoiu, C.; Bender, P.C.; Cross, D.S.; Demand, G.A.; Garnsworthy, A.B.; Garrett, P.E.; Hackman, G.; et al. Collective Structure in 94Zr and Subshell Effects in Shape Coexistence. Phys. Rev. Lett. 2013, 110, 022504. [Google Scholar] [CrossRef]
- Paul, N.; Corsi, A.; Obertelli, A.; Doornenbal, P.; Authelet, G.; Baba, H.; Bally, B.; Bender, M.; Calvet, D.; Château, F.; et al. Are There Signatures of Harmonic Oscillator Shells Far from Stability? First Spectroscopy of 110Zr. Phys. Rev. Lett. 2017, 118, 032501. [Google Scholar]
- García-Ramos, J.E.; Heyde, K. On the nature of the shape coexistence and the quantum phase transition phenomena: Lead region and Zr isotopes. EPJ Web Conf. 2018, 178, 05005. [Google Scholar] [CrossRef]
- Wu, C.Y.; Hua, H.; Cline, D. Shape coexistence and their configuration mixing in 98Sr and 100Zr. Phys. Rev. C 2003, 68, 034322. [Google Scholar] [CrossRef]
- Sazonov, D.A.; Kolganova, E.A.; Shneidman, T.M.; Jolos, R.V.; Pietralla, N.; Witt, W. Description of shape coexistence in 96Zr based on the quadrupole-collective Bohr Hamiltonian. Phys. Rev. C 2019, 99, 031304. [Google Scholar] [CrossRef]
- Zheng, S.J.; Xu, F.R.; Shen, S.F.; Liu, H.L.; Wyss, R.; Yan, Y.P. Shape coexistence and triaxiality in nuclei near 80Zr. Phys. Rev. C 2014, 90, 064309. [Google Scholar] [CrossRef]
- Clément, E.; Zielińska, M.; Görgen, A.; Korten, W.; Péru, S.; Libert, J.; Goutte, H.; Hilaire, S.; Bastin, B.; Bauer, C.; et al. Spectroscopic Quadrupole Moments in 96,98Sr: Evidence for Shape Coexistence in Neutron-Rich Strontium Isotopes at N = 60. Phys. Rev. Lett. 2016, 116, 022701, Erratum in Phys. Rev. Lett. 2016 , 117, 099902. [Google Scholar] [CrossRef]
- Clément, E.; Zielińska, M. Shape coexistence in neutron-rich strontium isotopes at N = 60. Phys. Scr. 2017, 92, 084002. [Google Scholar] [CrossRef]
- Görgen, A.; Korten, W. Coulomb excitation studies of shape coexistence in atomic nuclei. J. Phys. G Nucl. Part Phys. 2016, 43, 024002. [Google Scholar] [CrossRef]
- Park, J.; Garnsworthy, A.B.; Krücken, R.; Andreoiu, C.; Ball, G.C.; Bender, P.C.; Chester, A.; Close, A.; Finlay, P.; Garrett, P.E.; et al. Shape coexistence and evolution in 98Sr. Phys. Rev. C 2016, 93, 014315. [Google Scholar] [CrossRef]
- Régis, J.-M.; Jolie, J.; Saed-Samii, N.; Warr, N.; Pfeiffer, M.; Blanc, A.; Jentschel, M.; Köster, U.; Mutti, P.; Soldner, T.; et al. Abrupt shape transition at neutron number N = 60: B(E2) values in 94,96,98Sr from fast γ-γ timing. Phys. Rev. C 2017, 95, 054319, Erratum in Phys. Rev. C 2017 , 95, 069902. [Google Scholar] [CrossRef]
- Schussler, F.; Pinston, J.A.; Monnand, E.; Moussa, A.; Jung, G.; Koglin, E.; Pfeiffer, B.; Janssens, R.V.F.; van Klinken, J. Discovery of a very low-lying 0+ state in 98Sr and shape coexistence implication in 98Sr. Nucl. Phys. A 1980, 339, 415. [Google Scholar] [CrossRef]
- Baktash, C.; Garcia-Bermudez, G.; Sarantites, D.G.; Nazarewicz, W.; Abenante, V.; Beene, J.R.; Griffin, H.C.; Halbert, M.L.; Hensley, D.C.; Johnson, N.R.; et al. Shape coexistence and disappearance of pairing correlations in 82Sr. Phys. Lett. B 1991, 255, 174. [Google Scholar] [CrossRef][Green Version]
- Esmaylzadeh, A.; Karayonchev, V.; Nomura, K.; Jolie, J.; Beckers, M.; Blazhev, A.; Dewald, A.; Fransen, C.; Gerst, R.-B.; Häfner, G.; et al. Lifetime measurements to investigate γ softness and shape coexistence in 102Mo. Phys. Rev. C 2021, 104, 064314. [Google Scholar] [CrossRef]
- Ha, J.; Sumikama, T.; Browne, F.; Hinohara, N.; Bruce, A.M.; Choi, S.; Nishizuka, I.; Nishimura, S.; Doornenbal, P.; Lorusso, G.; et al. Shape evolution of neutron-rich 106,108,110Mo isotopes in the triaxial degree of freedom. Phys. Rev. C 2020, 101, 044311. [Google Scholar] [CrossRef]
- Garrett, P.E.; Makhathini, L.; Bark, R.A.; Rodríguez, T.R.; Valbuena, S.; Bildstein, V.; Bucher, T.D.; Burbadge, C.; Dubey, R.; Faestermann, T.; et al. Observation of the and γ bands in 98Ru, and shape coexistence in the Ru isotopes. Phys. Lett. B 2020, 809, 135762. [Google Scholar] [CrossRef]
- Becker, F.; Korten, W.; Hannachi, F.; Paris, P.; Buforn, N.; Chandler, C.; Houry, M.; Hübel, H.; Jansen, A.; Le Coz, Y.; et al. Investigation of prolate-oblate shape-coexistence in 74Kr. Eur. Phys. J. A 1999, 4, 103. [Google Scholar] [CrossRef]
- Briz, J.A.; Nácher, E.; Borge, M.J.G.; Algora, A.; Rubio, B.; Dessagne, P.; Maira, A.; Cano-Ott, D.; Courtin, S.; Escrig, D.; et al. Shape study of the N = Z nucleus 72Kr via β decay. Phys. Rev. C 2015, 92, 054326. [Google Scholar] [CrossRef]
- Clément, E.; Görgen, A.; Korten, W.; Bouchez, E.; Chatillon, A.; Delaroche, J.; Girod, M.; Goutte, H.; Huerstel, A.; Coz, Y.; et al. Shape coexistence in neutron-deficient krypton isotopes. Phys. Rev. C 2007, 75, 054313. [Google Scholar] [CrossRef]
- Dejbakhsh, H.; Cormier, T.M.; Zhao, X.; Ramayya, A.V.; Chaturvedi, L.; Zhu, S.; Kormicki, J.; Hamilton, J.H.; Satteson, M.; Lee, I.Y.; et al. Signature of the shape coexistence in 72Kr: Discontinuities of the moment of inertia at low spin. Phys. Lett. B 1990, 249, 195. [Google Scholar] [CrossRef]
- Korten, W.; Bouchez, E.; Clément, E.; Chatillon, A.; Görgen, A.; Le Coz, Y.; Theisen, C.; Wilson, J.; Casandjian, J.M.; de France, G.; et al. Shape coexistence in Krypton isotopes studied through Coulomb excitation of radioactive Krypton ion beams. Nucl. Phys. A 2004, 746, 90c. [Google Scholar] [CrossRef]
- Piercey, R.B.; Ramayya, A.V.; Hamilton, J.H.; Sun, X.J.; Zhao, Z.Z.; Robinson, R.L.; Kim, H.J.; Wells, J.C. Collective band structure to high spin and shape coexistence in 76Kr. Phys. Rev. C 1982, 25, 1941. [Google Scholar] [CrossRef]
- Varley, B.J.; Campbell, M.; Chishti, A.A.; Gelletly, W.; Goettig, L.; Lister, C.J.; James, A.N.; Skeppstedt, O. Evidence for shape coexistence in the N = Z nucleus . Phys. Lett. B 1987, 194, 463. [Google Scholar] [CrossRef]
- Wimmer, K.; Arici, T.; Korten, W.; Doornenbal, P.; Delaroche, J.-P.; Girod, M.; Libert, J.; Rodríguez, T.R.; Aguilera, P.; Algora, A.; et al. Shape coexistence revealed in the N = Z isotope 72Kr through inelastic scattering. Eur. Phys. J. A 2020, 56, 159. [Google Scholar] [CrossRef]
- Wimmer, K.; Korten, W.; Arici, T.; Doornenbal, P.; Aguilera, P.; Algora, A.; Ando, T.; Baba, H.; Blank, B.; Boso, A.; et al. Shape coexistence and isospin symmetry in A = 70 nuclei: Spectroscopy of the Tz=-1 nucleus 70Kr. Phys. Lett. B 2018, 785, 441. [Google Scholar] [CrossRef]
- Wimmer, K.; Korten, W.; Doornenbal, P.; Arici, T.; Aguilera, P.; Algora, A.; Ando, T.; Baba, H.; Blank, B.; Boso, A.; et al. Shape Changes in the Mirror Nuclei 70Kr and 70Se. Phys. Rev. Lett. 2021, 126, 072501. [Google Scholar] [CrossRef]
- Almehed, D.; Walet, N.R. Shape coexistence in 72Kr at finite angular momentum. Phys. Lett. B 2004, 604, 163. [Google Scholar] [CrossRef]
- Budaca, R.; Budaca, A.I. Coexistence, mixing and fluctuation of nuclear shapes. EPL 2018, 123, 42001. [Google Scholar] [CrossRef]
- Albers, M.; Warr, N.; Nomura, K.; Blazhev, A.; Jolie, J.; Mücher, D.; Bastin, B.; Bauer, C.; Bernards, C.; Bettermann, L.; et al. Evidence for a Smooth Onset of Deformation in the Neutron-Rich Kr Isotopes. Phys. Rev. Lett. 2012, 108, 062701, Erratum in Phys. Rev. Lett. 2012, 109, 209904; Phys. Rev. Lett. 2015, 114, 189902. [Google Scholar] [CrossRef]
- Dudouet, J.; Lemasson, A.; Duchêne, G.; Rejmund, M.; Clément, E.; Michelagnoli, C.; Didierjean, D.; Korichi, A.; Maquart, G.; Stezowski, O.; et al. –Low-Z Boundary of the Island of Deformation at N = 60. Phys. Rev. Lett. 2017, 118, 162501. [Google Scholar] [CrossRef]
- Flavigny, F.; Doornenbal, P.; Obertelli, A.; Delaroche, J.-P.; Girod, M.; Libert, J.; Rodriguez, T.R.; Authelet, G.; Baba, H.; Calvet, D.; et al. Shape Evolution in Neutron-Rich Krypton Isotopes Beyond N = 60: First Spectroscopy of 98,100Kr. Phys. Rev. Lett. 2017, 118, 242501. [Google Scholar] [CrossRef]
- Delafosse, C.; Verney, D.; Marević, P.; Gottardo, A.; Michelagnoli, C.; Lemasson, A.; Goasduff, A.; Ljungvall, J.; Clément, E.; Korichi, A.; et al. Pseudospin Symmetry and Microscopic Origin of Shape Coexistence in the 78Ni Region: A Hint from Lifetime Measurements. Phys. Rev. Lett. 2018, 121, 192502. [Google Scholar] [CrossRef]
- Hamilton, J.H.; Ramayya, A.V.; Pinkston, W.T.; Ronningen, R.M.; Garcia-Bermudez, G.; Carter, H.K.; Robinson, R.L.; Kim, H.J.; Sayer, R.O. Evidence for Coexistence of Spherical and Deformed Shapes in 72Se. Phys. Rev. Lett. 1974, 32, 239. [Google Scholar] [CrossRef]
- Hamilton, J.H.; Crowell, H.L.; Robinson, R.L.; Ramayya, A.V.; Collins, W.E.; Ronningen, R.M.; Maruhn-Rezwani, V.; Maruhn, J.A.; Singhal, N.C.; Kim, H.J.; et al. Lifetime Measurements to Test the Coexistence of Spherical and Deformed Shapes in 72Se. Phys. Rev. Lett. 1976, 36, 340. [Google Scholar] [CrossRef]
- Ljungvall, J.; Görgen, A.; Girod, M.; Delaroche, J.-P.; Dewald, A.; Dossat, C.; Farnea, E.; Korten, W.; Melon, B.; Menegazzo, R.; et al. Shape Coexistence in Light Se Isotopes: Evidence for Oblate Shapes. Phys. Rev. Lett. 2008, 100, 102502. [Google Scholar] [CrossRef] [PubMed]
- McCutchan, E.A.; Lister, C.J.; Ahn, T.; Casperson, R.J.; Heinz, A.; Ilie, G.; Qian, J.; Williams, E.; Winkler, R.; Werner, V. Shape coexistence in 72Se investigated following the β decay of 72Br. Phys. Rev. C 2011, 83, 024310. [Google Scholar] [CrossRef]
- Palit, R.; Jain, H.C.; Joshi, P.K.; Sheikh, J.A.; Sun, Y. Shape coexistence in 72Se. Phys. Rev. C 2001, 63, 024313. [Google Scholar] [CrossRef]
- Mukherjee, A.; Bhattacharya, S.; Trivedi, T.; Singh, R.P.; Muralithar, S.; Negi, D.; Palit, R.; Nag, S.; Rajbanshi, S.; Kumar Raju, M.; et al. Shape coexistence and octupole correlations in 72Se. Phys. Rev. C 2022, 105, 014322. [Google Scholar] [CrossRef]
- Cottle, P.D.; Holcomb, J.W.; Johnson, T.D.; Stuckey, K.A.; Tabor, S.L.; Womble, P.C.; Buccino, S.G.; Durham, F.E. Shape coexistence and octupole vibrations in 74Se. Phys. Rev. C 1990, 42, 1254. [Google Scholar] [CrossRef]
- McCutchan, E.A.; Lister, C.J.; Ahn, T.; Anagnostatou, V.; Cooper, N.; Elvers, M.; Goddard, P.; Heinz, A.; Ilie, G.; Radeck, D.; et al. Shape coexistence and high-K states in 74Se populated following the β decay of 74Br. Phys. Rev. C 2013, 87, 014307. [Google Scholar] [CrossRef]
- Fischer, S.M.; Balamuth, D.P.; Hausladen, P.A.; Lister, C.J.; Carpenter, M.P.; Seweryniak, D.; Schwartz, J. Evidence for Collective Oblate Rotation in N = Z 68Se. Phys. Rev. Lett. 2000, 84, 4064. [Google Scholar] [CrossRef]
- Jenkins, D.G.; Balamuth, D.P.; Carpenter, M.P.; Lister, C.J.; Fischer, S.M.; Clark, R.M.; Macchiavelli, A.O.; Fallon, P.; Svensson, C.E.; Kelsall, N.S.; et al. Stability of oblate shapes in the vicinity of N=Z=34 68Se: Bands in 69Se and 67As. Phys. Rev. C 2001, 64, 064311. [Google Scholar] [CrossRef]
- Obertelli, A.; Baugher, T.; Bazin, D.; Boissinot, S.; Delaroche, J.-P.; Dijon, A.; Flavigny, F.; Gade, A.; Girod, M.; Glasmacher, T.; et al. First spectroscopy of 66Se and 65As: Investigating shape coexistence beyond the N=Z line. Phys. Lett. B 2011, 701, 417. [Google Scholar] [CrossRef]
- Gupta, J.B.; Hamilton, J.H. Empirical study of the shape evolution and shape coexistence in Zn, Ge and Se isotopes. Nucl. Phys. A 2019, 983, 20. [Google Scholar] [CrossRef]
- Gratchev, I.N.; Simpson, G.S.; Thiamova, G.; Ramdhane, M.; Sieja, K.; Blanc, A.; Jentschel, M.; Köster, U.; Mutti, P.; Soldner, T.; et al. Identification of excited states and collectivity in 88Se. Phys. Rev. C 2017, 95, 051302. [Google Scholar] [CrossRef]
- Lizarazo, C.; Söderström, P.-A.; Werner, V.; Pietralla, N.; Walker, P.; Dong, G.; Xu, F.; Rodríguez, T.; Browne, F.; Doornenbal, P.; et al. Metastable States of 92,94Se: Identification of an Oblate K Isomer of 94Se and the Ground-State Shape Transition between N = 58 and 60. Phys. Rev. Lett. 2020, 124, 222501. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Doornenbal, P.; Obertelli, A.; Rodríguez, T.R.; Authelet, G.; Baba, H.; Calvet, D.; Browne, F.; Bruce, A.; Nobs, C. Low-lying structure and shape evolution in neutron-rich Se isotopes. Phys. Rev. C 2017, 95, 041302. [Google Scholar] [CrossRef]
- Lecomte, R.; Kajrys, G.; Landsberger, S.; Paradis, P.; Monaro, S. Shape coexistence and shape transitions in the even-A Ge nuclei. Phys. Rev. C 1982, 25, 2812, Erratum in Phys. Rev. C 1982, 26, 1334. [Google Scholar] [CrossRef]
- Ayangeakaa, A.D.; Janssens, R.V.F.; Wu, C.Y.; Allmond, J.M.; Wood, J.L.; Zhu, S.; Albers, M.; Almaraz-Calderon, S.; Bucher, B.; Carpenter, M.P.; et al. Shape coexistence and the role of axial asymmetry in 72Ge. Phys. Lett. B 2016, 754, 254. [Google Scholar] [CrossRef]
- Turkan, N.; Maras, I. E(5) behaviour of the Ge isotopes. Math. Comput. Appl. 2010, 15, 428. [Google Scholar] [CrossRef]
- Hwang, J.K.; Hamilton, J.H.; Ramayya, A.V.; Brewer, N.T.; Luo, Y.X.; Rasmussen, J.O.; Zhu, S.J. Possible excited deformed rotational bands in 82Ge. Phys. Rev. C 2011, 84, 024305. [Google Scholar] [CrossRef]
- Ahn, S.; Bardayan, D.W.; Jones, K.L.; Adekola, A.S.; Arbanas, G.; Blackmon, J.C.; Chae, K.Y.; Chipps, K.A.; Cizewski, J.A.; Hardy, S.; et al. Direct neutron capture cross section on 80Ge and probing shape coexistence in neutron-rich nuclei. Phys. Rev. C 2019, 100, 044613. [Google Scholar] [CrossRef]
- Gottardo, A.; Verney, D.; Delafosse, C.; Ibrahim, F.; Roussière, B.; Sotty, C.; Roccia, S.; Andreoiu, C.; Costache, C.; Delattre, M.C.; et al. First Evidence of Shape Coexistence in the 78Ni Region: Intruder State in 80Ge. Phys. Rev. Lett. 2016, 116, 182501. [Google Scholar] [CrossRef]
- Garcia, F.H.; Andreoiu, C.; Ball, G.C.; Bell, A.; Garnsworthy, A.B.; Nowacki, F.; Petrache, C.M.; Poves, A.; Whitmore, K.; Ali, F.A.; et al. Absence of Low-Energy Shape Coexistence in 80Ge: The Nonobservation of a Proposed Excited Level at 639 keV. Phys. Rev. Lett. 2020, 125, 172501. [Google Scholar] [CrossRef]
- Koizumi, M.; Seki, A.; Toh, Y.; Osa, A.; Utsuno, Y.; Kimura, A.; Oshima, M.; Hayakawa, T.; Hatsukawa, Y.; Katakura, J.; et al. Multiple Coulomb excitation experiment of 68Zn. Nucl. Phys. A 2004, 730, 46. [Google Scholar] [CrossRef]
- Rocchini, M.; Hadyńska-Klȩk, K.; Nannini, A.; Goasduff, A.; Zielińska, M.; Testov, D.; Rodríguez, T.R.; Gargano, A.; Nowacki, F.; Gregorio, G.D.; et al. Onset of triaxial deformation in 66Zn and properties of its first excited 0+ state studied by means of Coulomb excitation. Phys. Rev. C 2021, 103, 014311. [Google Scholar] [CrossRef]
- Shiga, Y.; Yoneda, K.; Steppenbeck, D.; Aoi, N.; Doornenbal, P.; Lee, J.; Liu, H.; Matsushita, M.; Takeuchi, S.; Wang, H.; et al. Investigating nuclear shell structure in the vicinity of 78Ni: Low-lying excited states in the neutron-rich isotopes 80,82Zn. Phys. Rev. C 2016, 93, 024320, Erratum in Phys. Rev. C 2016, 93, 049904. [Google Scholar] [CrossRef]
- Van de Walle, J.; Aksouh, F.; Behrens, T.; Bildstein, V.; Blazhev, A.; Cederkäll, J.; Clément, E.; Cocolios, T.E.; Davinson, T.; Delahaye, P.; et al. Low-energy Coulomb excitation of neutron-rich zinc isotopes. Phys. Rev. C 2009, 79, 014309. [Google Scholar] [CrossRef]
- Orlandi, R.; Mücher, D.; Raabe, R.; Jungclaus, A.; Pain, S.D.; Bildstein, V.; Chapman, R.; de Angelis, G.; Johansen, J.G.; Van Duppen, P.; et al. Single-neutron orbits near 78Ni: Spectroscopy of the isotope 79Zn. Phys. Lett. B 2015, 740, 298. [Google Scholar] [CrossRef]
- Yang, X.F.; Wraith, C.; Xie, L.; Babcock, C.; Billowes, J.; Bissell, M.L.; Blaum, K.; Cheal, B.; Flanagan, K.T.; Garcia Ruiz, R.F.; et al. Isomer Shift and Magnetic Moment of the Long-Lived 1/2+ Isomer in : Signature of Shape Coexistence near 78Ni. Phys. Rev. Lett. 2016, 116, 182502. [Google Scholar] [CrossRef] [PubMed]
- Chiara, C.J.; Broda, R.; Walters, W.B.; Janssens, R.V.F.; Albers, M.; Alcorta, M.; Bertone, P.F.; Carpenter, M.P.; Hoffman, C.R.; Lauritsen, T.; et al. Low-spin states and the non-observation of a proposed 2202-keV, 0+ isomer in 68Ni. Phys. Rev. C 2012, 86, 041304. [Google Scholar] [CrossRef]
- Crider, B.P.; Prokop, C.J.; Liddick, S.N.; Al-Shudifat, M.; Ayangeakaa, A.D.; Carpenter, M.P.; Carroll, J.J.; Chen, J.; Chiara, C.J.; David, H.M.; et al. Shape coexistence from lifetime and branching-ratio measurements in 68,70Ni. Phys. Lett. B 2016, 763, 108. [Google Scholar] [CrossRef]
- Dijon, A.; Clément, E.; France, G.D.; Angelis, G.D.; Duchêne, G.; Dudouet, J.; Franchoo, S.; Gadea, A.; Gottardo, A.; Hüyük, T.; et al. Discovery of a new isomeric state in 68Ni: Evidence for a highly deformed proton intruder state. Phys. Rev. C 2012, 85, 031301. [Google Scholar] [CrossRef]
- Flavigny, F.; Pauwels, D.; Radulov, D.; Darby, I.J.; de Witte, H.; Diriken, J.; Fedorov, D.V.; Fedosseev, V.N.; Prieto, F.; Mario, L.; et al. Characterization of the low-lying 0+ and 2+ states in 68Ni via β decay of the low-spin 68Co isomer. Phys. Rev. C 2015, 91, 034310. [Google Scholar] [CrossRef]
- Flavigny, F.; Elseviers, J.; Andreyev, A.; Bauer, C.; Bildstein, V.; Blazhev, A.; Brown, B.A.; Witte, H.; Diriken, J.; Fedosseev, V.; et al. Microscopic structure of coexisting 0+ states in 68Ni probed via two-neutron transfer. Phys. Rev. C 2019, 99, 054332. [Google Scholar] [CrossRef]
- Recchia, F.; Chiara, C.J.; Janssens, R.V.F.; Weisshaar, D.; Gade, A.; Walters, W.B.; Albers, M.; Alcorta, M.; Bader, V.M.; Baugher, T.; et al. Configuration mixing and relative transition rates between low-spin states in 68Ni. Phys. Rev. C 2013, 88, 041302. [Google Scholar] [CrossRef]
- Suchyta, S.; Liddick, S.N.; Tsunoda, Y.; Otsuka, T.; Bennett, M.B.; Chemey, A.; Honma, M.; Larson, N.; Prokop, C.J.; Quinn, S.J.; et al. Shape coexistence in 68Ni. Phys. Rev. C 2014, 89, 021301. [Google Scholar] [CrossRef]
- Chiara, C.; Weisshaar, D.; Janssens, R.; Tsunoda, Y.; Otsuka, T.; Harker, J.; Walters, W.; Recchia, F.; Albers, M.; Alcorta, M.; et al. Identification of deformed intruder states in semi-magic 70Ni. Phys. Rev. C 2015, 91, 044309. [Google Scholar] [CrossRef]
- Prokop, C.J.; Crider, B.P.; Liddick, S.N.; Ayangeakaa, A.D.; Carpenter, M.P.; Carroll, J.J.; Chen, J.; Chiara, C.J.; David, H.M.; Dombos, A.C.; et al. New low-energy 0+ state and shape coexistence in 70Ni. Phys. Rev. C 2015, 92, 061302, Erratum in Phys. Rev. C 2016, 93, 019901(E). [Google Scholar] [CrossRef]
- Broda, R.; Pawłat, T.; Królas, W.; Janssens, R.V.F.; Zhu, S.; Walters, W.B.; Fornal, B.; Chiara, C.J.; Carpenter, M.P.; Hoteling, N.; et al. Spectroscopic study of the 64,66,68Ni isotopes populated in 64Ni + 238U collisions. Phys. Rev. C 2012, 86, 064312. [Google Scholar] [CrossRef]
- Leoni, S.; Fornal, B.; Mărginean, N.; Sferrazza, M.; Tsunoda, Y.; Otsuka, T.; Bocchi, G.; Crespi, F.C.L.; Bracco, A.; Aydin, S.; et al. Multifaceted Quadruplet of Low-Lying Spin-Zero States in 66Ni: Emergence of Shape Isomerism in Light Nuclei. Phys. Rev. Lett. 2017, 118, 162502. [Google Scholar] [CrossRef]
- Olaizola, B.; Fraile, L.M.; Mach, H.; Poves, A.; Nowacki, F.; Aprahamian, A.; Briz, J.A.; Cal-González, J.; Ghiţa, D.; Köster, U.; et al. Search for shape-coexisting 0+ states in 66Ni from lifetime measurements. Phys. Rev. C 2017, 95, 061303. [Google Scholar] [CrossRef]
- Mărginean, N.; Little, D.; Tsunoda, Y.; Leoni, S.; Janssens, R.V.F.; Fornal, B.; Otsuka, T.; Michelagnoli, C.; Stan, L.; Crespi, F.C.L.; et al. Shape Coexistence at Zero Spin in 64Ni Driven by the Monopole Tensor Interaction. Phys. Rev. Lett. 2020, 125, 102502. [Google Scholar] [CrossRef] [PubMed]
- Gade, A.; Liddick, S.N. Shape coexistence in neutron-rich nuclei. J. Phys. G Nucl. Part. Phys. 2016, 43, 024001. [Google Scholar] [CrossRef]
- Olivier, L.; Franchoo, S.; Niikura, M.; Vajta, Z.; Sohler, D.; Doornenbal, P.; Obertelli, A.; Tsunoda, Y.; Otsuka, T.; Authelet, G.; et al. Persistence of the Z = 28 Shell Gap Around 78Ni: First Spectroscopy of 79Cu. Phys. Rev. Lett. 2017, 119, 192501. [Google Scholar] [CrossRef] [PubMed]
- Welker, A.; Althubiti, N.A.S.; Atanasov, D.; Blaum, K.; Cocolios, T.E.; Herfurth, F.; Kreim, S.; Lunney, D.; Manea, V.; Mougeot, M.; et al. Binding Energy of 79Cu: Probing the Structure of the Doubly Magic 78Ni from Only One Proton Away. Phys. Rev. Lett. 2017, 119, 192502. [Google Scholar] [CrossRef] [PubMed]
- Porquet, M.-G.; Sorlin, O. Evolution of the N = 50 gap from Z = 30 to Z = 38 and extrapolation toward 78Ni. Phys. Rev. C 2012, 85, 014307. [Google Scholar] [CrossRef]
- Klintefjord, M.; Ljungvall, J.; Görgen, A.; Lenzi, S.M. Measurement of lifetimes in 62,64Fe, 61,63Co, and 59Mn. Phys. Rev. C 2017, 95, 024312. [Google Scholar] [CrossRef]
- Lunardi, S.; Lenzi, S.M.; Della Vedova, F.; Farnea, E.; Gadea, A.; Mărginean, N.; Bazzacco, D.; Beghini, S.; Bizzeti, P.G.; Bizzeti-Sona, A.M.; et al. Spectroscopy of neutron-rich Fe isotopes populated in the 64Ni+238U reaction. Phys. Rev. C 2007, 76, 034303. [Google Scholar] [CrossRef]
- Rother, W.; Dewald, A.; Iwasaki, H.; Lenzi, S.M.; Starosta, K.; Bazin, D.; Baugher, T.; Brown, B.A.; Crawford, H.L.; Fransen, C.; et al. Enhanced Quadrupole Collectivity at N = 40: The Case of Neutron-Rich Fe Isotopes. Phys. Rev. Lett. 2011, 106, 022502. [Google Scholar] [CrossRef]
- Olaizola, B.; Fraile, L.M.; Mach, H.; Poves, A.; Aprahamian, A.; Briz1, J.A.; Cal-González, J.; Ghiţa, D.; Köster, U.; Kurcewicz, W.; et al. Beta decay of 66Mn to the N = 40 nucleus 66Fe. J. Phys. G Nucl. Part. Phys. 2017, 44, 125103. [Google Scholar] [CrossRef]
- Liddick, S.N.; Abromeit, B.; Ayres, A.; Bey, A.; Bingham, C.R.; Brown, B.A.; Cartegni, L.; Crawford, H.L.; Darby, I.G.; Grzywacz, R.; et al. Low-energy level schemes of 66,68Fe and inferred proton and neutron excitations across Z = 28 and N = 40. Phys. Rev. C 2013, 87, 014325. [Google Scholar] [CrossRef]
- Arnswald, K.; Braunroth, T.; Seidlitz, M.; Coraggio, L.; Reiter, P.; Birkenbach, B.; Blazhev, A.; Dewald, A.; Fransen, C.; Fu, B.; et al. Enhanced collectivity along the N = Z line: Lifetime measurements in 44Ti, 48Cr, and 52Fe. Phys. Lett. B 2017, 772, 599. [Google Scholar] [CrossRef]
- Carpenter, M.P.; Janssens, R.V.F.; Zhu, S. Shape coexistence in neutron-rich nuclei near N = 40. Phys. Rev. C 2013, 87, 041305. [Google Scholar] [CrossRef]
- Liddick, S.N.; Suchyta, S.; Abromeit, B.; Ayres, A.; Bey, A.; Bingham, C.R.; Bolla1, M.; Carpenter, M.P.; Cartegni, L.; Chiara, C.J.; et al. Shape coexistence along N = 40. Phys. Rev. C 2011, 84, 061305. [Google Scholar] [CrossRef]
- Kumar, R.; Chamoli, S.K.; Govil, I.M.; Dhal, A.; Sinha, R.K.; Chaturvedi, L.; Naik, Z.; Praharaj, C.R.; Muralithar, S.; Singh, R.P.; et al. Shape coexistence and high spin states in 52Cr. Phys. Rev. C 2007, 76, 034301. [Google Scholar] [CrossRef]
- Rowe, D.J.; Wood, J.L. A relationship between isobaric analog states and shape coexistence in nuclei. J. Phys. G Nucl. Part. Phys. 2018, 45, 06LT01. [Google Scholar] [CrossRef]
- O’Leary, C.D.; Bentley, M.A.; Brown, B.A.; Appelbe, D.E.; Bark, R.A.; Cullen, D.M.; Ertürk, S.; Maj, A.; Merchant, A.C. Nonyrast high-spin states in N = Z 44Ti. Phys. Rev. C 2000, 61, 064314. [Google Scholar] [CrossRef]
- Schielke, S.; Hohn, D.; Speidel, K.-H.; Kenn, O.; Leske, J.; Gemein, N.; Offer, M.; Gerber, J.; Maier-Komor, P.; Zell, O.; et al. Evidence for 40Ca core excitation from g factor and B(E2) measurements on the states of 42,44Ca. Phys. Lett. B 2003, 571, 29. [Google Scholar] [CrossRef]
- Simpson, J.J.; Dixon, W.R.; Storey, R.S. Evidence for Rotational Bands in 44Ti. Phys. Rev. Lett. 1973, 31, 946. [Google Scholar] [CrossRef]
- Schielke, S.; Speidel, K.-H.; Kenn, O.; Leske, J.; Gemein, N.; Offer, M.; Sharon, Y.Y.; Zamick, L.; Gerber, J.; Maier-Komor, P. First measurement and shell model interpretation of the g factor of the state in self-conjugate radioactive 44Ti. Phys. Lett. B 2003, 567, 153. [Google Scholar] [CrossRef][Green Version]
- Middleton, R.; Garrett, J.D.; Fortune, H.T. Search for multiparticle-multihole states of 40Ca with the 32S(12C,α) reaction. Phys. Lett. B 1972, 39, 339. [Google Scholar] [CrossRef]
- Ellegaard, C.; Lien, J.R.; Nathan, O.; Sletten, G.; Ingebretsen, F.; Osnes, E.; Tjøm, P.O.; Hansen, O.; Stock, R. The (1f)2 multiplet in 42Ca. Phys. Lett. B 1972, 40, 641. [Google Scholar] [CrossRef]
- Hadyńska-Klȩk, K.; Napiorkowski, P.J.; Zielinska, M.; Srebrny, J.; Maj, A.; Azaiez, F.; aliente Dobon, J.J.; Kicinska-Habior, M.; Nowacki, F.; Naïdja, H.; et al. Superdeformed and Triaxial States in 42Ca. Phys. Rev. Lett. 2016, 117, 062501. [Google Scholar] [CrossRef]
- Hadyńska-Klȩk, K.; Napiorkowski, P.J.; Zielinska, M.; Srebrny, J.; Maj, A.; Azaiez, F.; aliente Dobon, J.J.; Kicinska-Habior, M.; Nowacki, F.; Naïdja, H.; et al. Quadrupole collectivity in 42Ca from low-energy Coulomb excitation with AGATA. Phys. Rev. C 2018, 97, 024326. [Google Scholar] [CrossRef]
- Flynn, E.R.; Hansen, O.; Casten, R.F.; Garrett, J.D.; Ajzenberg-Selove, F. The (t, p) reaction on 36, 38, 40Ar. Nucl. Phys. A 1975, 246, 117. [Google Scholar] [CrossRef]
- Ideguchi, E.; Ota, S.; Morikawa, T.; Oshima, M.; Koizumi, M.; Toh, Y.; Kimura, A.; Harada, H.; Furutaka, K.; Nakamura, S.; et al. Superdeformation in asymmetric N>Z nucleus 40Ar. Phys. Lett. B 2010, 686, 18. [Google Scholar] [CrossRef]
- Speidel, K.-H.; Schielke, S.; Leske, J.; Gerber, J.; Maier-Komor, P.; Robisnon, S.J.O.; Sharon, Y.Y.; Zamick, L. Experimental g factors and B(E2) values in Ar isotopes: Crossing the N = 20 semi-magic divide. Phys. Lett. B 2006, 632, 207. [Google Scholar] [CrossRef]
- Stefanova, E.A.; Benczer-Koller, N.; Kumbartzki, G.J.; Sharon, Y.Y.; Zamick, L.; Robinson, S.J.Q.; Bernstein, L.; Cooper, J.R.; Judson, D.; Taylor, M.J.; et al. Near spherical shell-model structure of the 2 + 1 state in 40Ar from g-factor measurements. Phys. Rev. C 2005, 72, 014309. [Google Scholar] [CrossRef]
- Svensson, C.E.; Macchiavelli, A.O.; Juodagalvis, A.; Poves, A.; Ragnarsson, I.; Åberg, S.; Appelbe, D.E.; Austin, R.A.E.; Baktash, C.; Ball, G.C.; et al. Superdeformation in the N = Z Nucleus 36Ar: Experimental, Deformed Mean Field, and Spherical Shell Model Descriptions. Phys. Rev. Lett. 2000, 85, 2693. [Google Scholar] [CrossRef]
- Meisel, Z.; George, S.; Ahn, S.; Browne, J.; Bazin, D.; Brown, B.A.; Carpino, J.F.; Chung, H.; Cyburt, R.H.; Estradé, A.; et al. Mass Measurements Demonstrate a Strong N = 28 Shell Gap in Argon. Phys. Rev. Lett. 2015, 114, 022501. [Google Scholar] [CrossRef]
- Cottle, P.D.; Kemper, K.W. Persistence of the N = 28 shell closure in neutron-rich nuclei. Phys. Rev. C 1998, 58, 3761. [Google Scholar] [CrossRef]
- Force, C.; Grévy, S.; Gaudefroy, L.; Sorlin, O.; Cáceres, L.; Rotaru, F.; Mrazek, J.; Achouri, N.L.; Angélique, J.C.; Azaiez, F.; et al. Prolate-Spherical Shape Coexistence at N = 28 in 44S. Phys. Rev. Lett. 2010, 105, 102501. [Google Scholar] [CrossRef]
- Longfellow, B.; Weisshaar, D.; Gade, A.; Brown, B.A.; Bazin, D.; Brown, K.W.; Elman, B.; Pereira, J.; Rhodes, D.; Spieker, M.; et al. Shape Changes in the N = 28 Island of Inversion: Collective Structures Built on Configuration-Coexisting States in 43S. Phys. Rev. Lett. 2020, 125, 232501. [Google Scholar] [CrossRef] [PubMed]
- Sarazin, F.; Savajols, H.; Mittig, W.; Nowacki, F.; Orr, N.A.; Ren, Z.; Roussel-Chomaz, P.; Auger, G.; Baiborodin, D.; Belozyorov, A.V.; et al. Shape Coexistence and the N = 28 Shell Closure Far from Stability. Phys. Rev. Lett. 2000, 84, 5062. [Google Scholar] [CrossRef] [PubMed]
- Mittig, W.; Savajols, H.; Baiborodin, D.; Casandjian, J.M.; Demonchy, C.E.; Roussel-Chomaz, P.; Sarazin, F.; Dlouhý, Z.; Mrazek, J.; Belozyorov, A.V.; et al. Shape coexistence and the N = 20 shell closure far from stability by inelastic scattering. Eur. Phys. J. A 2002, 15, 157. [Google Scholar] [CrossRef]
- Rotaru, F.; Negoita, F.; Grévy, S.; Mrazek, J.; Lukyanov, S.; Owacki, F.; Poves, A.; Sorlin, O.; Borcea, C.; Borcea, R.; et al. Unveiling the Intruder Deformed State in 34Si. Phys. Rev. Lett. 2012, 109, 092503. [Google Scholar] [CrossRef] [PubMed]
- Macchiavelli, A.O.; Crawford, H.L.; Campbell, C.M.; Clark, R.M.; Cromaz, M.; Fallon, P.; Lee, I.Y.; Gade, A.; Poves, A.; Rice, E.; et al. Structure of 43P and 42Si in a two-level shape-coexistence model. Phys. Rev. C 2022, 105, 014309. [Google Scholar] [CrossRef]
- Ragnarsson, I.; Åberg, S. Shape coexistence and high-spin states in 28Si. Phys. Lett. B 1982, 114, 387. [Google Scholar] [CrossRef]
- Sheline, R.K.; Kubono, S.; Morita, K.; Tanaka, M.H. Coexistence of three different shapes in 28Si. Phys. Lett. B 1982, 119, 263. [Google Scholar] [CrossRef]
- Kitamura, N.; Wimmer, K.; Shimizu, N.; Bader, V.M.; Bancroft, C.; Barofsky, D.; Baugher, T.; Bazin, D.; Berryman, J.S.; Bildstein, V.; et al. Structure of 30Mg explored via in-beam γ-ray spectroscopy. Phys. Rev. C 2020, 102, 054318. [Google Scholar] [CrossRef]
- Nishibata, H.; Tajiri, K.; Shimoda, T.; Odahara, A.; Morimoto, S.; Kanaya, S.; Yagi, A.; Kanaoka, H.; Pearson, M.R.; Levy, C.D.P.; et al. Structure of the neutron-rich nucleus 30Mg. Phys. Rev. C 2020, 102, 054327. [Google Scholar] [CrossRef]
- Schwerdtfeger, W.; Thirolf, P.G.; Wimmer, K.; Habs, D.; Mach, H.; Rodriguez, T.R.; Bildstein, V.; Egido, J.L.; Fraile, L.M.; Gernhäuser, R.; et al. Shape Coexistence Near Neutron Number N = 20: First Identification of the E0 Decay from the Deformed First Excited Jπ=0+ State in 30Mg. Phys. Rev. Lett. 2009, 103, 012501. [Google Scholar] [CrossRef] [PubMed]
- Dowie, J.T.H.; Kibedi, T.; Jenkins, D.J.; Stuchbery, A.E.; Akber, A.; Alshammari, H.; Aoi, N.; Abaraham, A.; Bignell, L.; Vernon Chisapi, M.V.; et al. Evidence for shape coexistence and superdeformation in 24Mg. Phys. Lett. B 2020, 811, 135855. [Google Scholar] [CrossRef]
- Murray, I.; MacCormick, M.; Bazin, D.; Doornenbal, P.; Aoi, N.; Baba, H.; Crawford, H.; Fallon, P.; Li, K.; Lee, J.; et al. Spectroscopy of strongly deformed 32Ne by proton knockout reactions. Phys. Rev. C 2019, 99, 011302. [Google Scholar] [CrossRef]
- Dombrádi, Z.; Elekes, Z.; Saito, A.; Aoi, N.; Baba, H.; Demichi, K.; Fülöp, Z.; Gibelin, J.; Gomi, T.; Hasegawa, H.; et al. Vanishing N = 20 Shell Gap: Study of Excited States in 27,28Ne. Phys. Rev. Lett. 2006, 96, 182501. [Google Scholar] [CrossRef]
- Brown, G.E.; Green, A.M. Even parity states of 16O and 17O. Nucl. Phys. 1966, 75, 401. [Google Scholar] [CrossRef]
- Brown, G.E.; Green, A.M. Nuclear coexistence in the oxygen region and realistic nucleon-nucleon forces. Nucl. Phys. 1966, 85, 87. [Google Scholar] [CrossRef]
- Unna, I.; Talmi, I. Energies of Ground and Excited Nuclear Configurations in the First p1/2 Region. Phys. Rev. 1958, 112, 452. [Google Scholar] [CrossRef]
- Franzini, P.; Radicati, L.A. On the validity of the supermultiplet model. Phys. Lett. 1963, 6, 322–324. [Google Scholar] [CrossRef]
- Hecht, K.T.; Pang, S.C. On the Wigner Supermultiplet Scheme. J. Math. Phys. 1969, 10, 1571. [Google Scholar] [CrossRef]
- Van Isacker, P.; Pittel, S. Symmetries and deformations in the spherical shell model. Phys. Scr. 2016, 91, 023009. [Google Scholar] [CrossRef]
- Wigner, E. On the Consequences of the Symmetry of the Nuclear Hamiltonian on the Spectroscopy of Nuclei. Phys. Rev. 1937, 51, 106. [Google Scholar] [CrossRef]
- Rowe, D.J.; Thiamova, G.; Wood, J.L. Implications of Deformation and Shape Coexistence for the Nuclear Shell Model. Phys. Rev. Lett. 2006, 97, 202501. [Google Scholar] [CrossRef] [PubMed]
- Hoyle, F. On Nuclear Reactions Occurring in Very Hot STARS. I. the Synthesis of Elements from Carbon to Nickel. Astrophys. J. Suppl. 1954, 1, 121. [Google Scholar]
- Fynbo, H.O.U.; Freer, M. Viewpoint: Rotations of the Hoyle state in 12C. Physics 2011, 4, 94. [Google Scholar] [CrossRef]
- Itoh, M.; Akimune, H.; Fujiwara, M.; Garg, U.; Hashimoto, N.; Kawabata, T.; Kawase, K.; Kishi, S.; Murakami, T.; Nakanishi, K.; et al. Candidate for the 2+ excited Hoyle state at Ex∼10 MeV in 12C. Phys. Rev. C 2011, 84, 054308. [Google Scholar] [CrossRef]
- Freer, M.; Fynbo, H.O.U. The Hoyle state in 12C. Prog. Part. Nucl. Phys. 2014, 78, 1. [Google Scholar] [CrossRef]
- Tohsaki, A.; Horiuchi, H.; Schuck, P.; Röpke, G. Colloquium: Status of α-particle condensate structure of the Hoyle state. Rev. Mod. Phys. 2017, 89, 011002. [Google Scholar] [CrossRef]
- Freer, M.; Horiuchi, H.; Kanada-En’yo, Y.; Lee, D.; Meissner, U.-G. Microscopic clustering in light nuclei. Rev. Mod. Phys. 2018, 90, 035004. [Google Scholar] [CrossRef]
- Takemoto, H.; Myo, T.; Horiuchi, H.; Toki, H.; Isaka, M.; Lyu, M.; Zhao, Q.; Wan, N. Appearance of the Hoyle state and its breathing mode in 12C despite strong short-range repulsion of the nucleon-nucleon potential. Phys. Rev. C 2023, 107, 044304. [Google Scholar] [CrossRef]
- Iwasaki, H.; Motobayashi, T.; Akiyoshi, H.; Ando, Y.; Fukuda, N.; Fujiwara, H.; Fülöp, Z.; Hahn, K.I.; Higurashi, Y.; Hirai, M.; et al. Low-lying intruder 1− state in 12Be and the melting of the N = 8 shell closure. Phys. Lett. B 2000, 491, 8. [Google Scholar] [CrossRef]
- Navin, A.; Anthony, D.W.; Aumann, T.; Baumann, T.; Bazin, D.; Blumenfeld, Y.; Brown, B.A.; Glasmacher, T.; Hansen, P.G.; Ibbotson, R.W.; et al. Direct Evidence for the Breakdown of the N = 8 Shell Closure in 12Be. Phys. Rev. Lett. 2000, 85, 266. [Google Scholar] [CrossRef]
- Lyu, M.; Yoshida, K.; Kanada-En’yo, Y.; Ogata, K. Direct probing of the cluster structure in 12Be via the α-knockout reaction. Phys. Rev. C 2019, 99, 064610. [Google Scholar] [CrossRef]
- Van Isacker, P.; Warner, D.D.; Brenner, D.S. Test of Wigner’s Spin-Isospin Symmetry from Double Binding Energy Differences. Phys. Rev. Lett. 1995, 74, 4607. [Google Scholar] [CrossRef]
- Kota, V.K.B.; Sahu, R. Structure of Medium Mass Nuclei: Deformed Shell Model and Spin-Isospin Interacting Boson Model; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Cederwall, B.; Moradi, F.G.; Bäck, T.; Johnson, A.; Blomqvist, J.; Clément, E.; de France, G.; Wadsworth, R.; Andgren, K.; Lagergren, K.; et al. Evidence for a spin-aligned neutron–proton paired phase from the level structure of 92Pd. Nature 2011, 469, 68. [Google Scholar] [CrossRef] [PubMed]
- Qi, C.; Blomqvist, J.; Bäck, T.; Cederwall, B.; Johnson, A.; Liotta, R.J.; Wyss, R. Spin-aligned neutron-proton pair mode in atomic nuclei. Phys. Rev. C 2011, 84, 021301. [Google Scholar] [CrossRef]
- Qi, C.; Blomqvist, J.; Bäck, T.; Cederwall, B.; Johnson, A.; Liotta, R.J.; Wyss, R. Coherence features of the spin-aligned neutron–proton pair coupling scheme. Phys. Scr. 2012, T150, 014031. [Google Scholar] [CrossRef]
- Qi, C.; Wyss, R. N = Z nuclei: A laboratory for neutron–proton collective mode. Phys. Scr. 2016, 91, 013009. [Google Scholar] [CrossRef]
- Robinson, S.J.Q.; Fan, C.; Harper, M.; Zamick, L. On the vibrational model of 92Pd and comparison with 48Cr. Int. J. Mod. Phys. E 2021, 30, 2150047. [Google Scholar] [CrossRef]
- Xu, Z.X.; Qi, C.; Blomqvist, J.; Liotta, R.J.; Wyss, R. Multistep shell model description of spin-aligned neutron–proton pair coupling. Nucl. Phys. A 2012, 877, 51. [Google Scholar] [CrossRef]
- Sambataro, M.; Sandulescu, N. Four-Body Correlations in Nuclei. Phys. Rev. Lett. 2015, 115, 112501. [Google Scholar] [CrossRef]
- Sambataro, M.; Sandulescu, N. Quarteting and spin-aligned proton-neutron pairs in heavy N = Z nuclei. Phys. Rev. C 2015, 91, 064318. [Google Scholar] [CrossRef]
- Zerguine, S.; Van Isacker, P. Spin-aligned neutron-proton pairs in N = Z nuclei. Phys. Rev. C 2011, 83, 064314. [Google Scholar] [CrossRef]
- Frauendorf, S.; Macchiavelli, A.O. Overview of neutron–proton pairing. Prog. Part. Nucl. Phys. 2014, 78, 24. [Google Scholar] [CrossRef]
- Cederwall, B.; Liu, X.; Aktas, O.; Ertoprak, A.; Zhang, W.; Qi, C.; Clement, E.; De France, G.; Ralet, D.; Gadea, A.; et al. Isospin Properties of Nuclear Pair Correlations from the Level Structure of the Self-Conjugate Nucleus 88Ru. Phys. Rev. Lett. 2020, 124, 062501. [Google Scholar] [CrossRef] [PubMed]
- Sambataro, M.; Sandulescu, N.; Johnson, C.W. Isoscalar and isovector pairing in a formalism of quartets. Phys. Lett. B 2015, 740, 137. [Google Scholar] [CrossRef]
- Sambataro, M.; Sandulescu, N. Isoscalar-isovector proton-neutron pairing and quartet condensation in N = Z nuclei. Phys. Rev. C 2016, 93, 054320. [Google Scholar] [CrossRef]
- Sandulescu, N.; Negrea, D.; Gambacurta, D. Proton-neutron pairing in N = Z nuclei: Quartetting versus pair condensation. Phys. Lett. B 2015, 751, 348–351. [Google Scholar] [CrossRef][Green Version]
- Darai, J.; Cseh, J.; Jenkins, D.G. Shape isomers and clusterization in the 28Si nucleus. Phys. Rev. C 2012, 86, 064309. [Google Scholar] [CrossRef]
- Cseh, J.; Algora, A.; Darai, J.; Hess, P.O. Deformation dependence of nuclear clusterization. Phys. Rev. C 2004, 70, 034311. [Google Scholar] [CrossRef]
- Cseh, J.; Darai, J.; Sciani, W.; Otani, Y.; Lépine-Szily, A.; Benjamim, E.A.; Chamon, L.C.; Lichtenthäler Filho, R. Elongated shape isomers in the 36Ar nucleus. Phys. Rev. C 2009, 80, 034320. [Google Scholar] [CrossRef]
- Satuła, W.; Wyss, R. Competition between T = 0 and T = 1 pairing in proton-rich nuclei. Phys. Lett. B 1997, 393, 1. [Google Scholar] [CrossRef]
- Terasaki, J.; Wyss, R.; Heenen, P.-H. Onset of T = 0 pairing and deformations in high spin states of the N = Z nucleus 48Cr. Phys. Lett. B 1998, 437, 1. [Google Scholar] [CrossRef][Green Version]
- Lei, Y.; Pittel, S.; Sandulescu, N.; Poves, A.; Thakur, B.; Zhao, Y.M. Systematic study of proton-neutron pairing correlations in the nuclear shell model. Phys. Rev. C 2011, 84, 044318. [Google Scholar] [CrossRef]
- Poves, A.; Martinez-Pinedo, G. Pairing and the structure of the pf-shell N∼Z nuclei. Phys. Lett. B 1998, 430, 203. [Google Scholar] [CrossRef]
- de Angelis, G.; Fahlander, C.; Gadea, A.; Farnea, E.; Gelletly, W.; Aprahamian, A.; Axelsson, A.; Bazzacco, D.; Becker, F.; Bizzeti, P.G.; et al. T = 0 pairing correlations and band crossing phenomena in N = Z nuclei. Nucl. Phys. A 1998, 630, 426c. [Google Scholar] [CrossRef]
- Rudolph, D.; Baktash, C.; Satuła, W.; Dobaczewski, J.; Nazarewicz, W.; Brinkman, M.J.; Devlin, M.; Jin, H.-Q.; LaFosse, D.R.; Riedinger, L.L.; et al. High-spin γ-ray spectroscopy in the vicinity of 56Ni. Nucl. Phys. A 1998, 630, 417c. [Google Scholar] [CrossRef]
- Rudolph, D.; Baktash, C.; Brinkman, M.J.; Caurier, E.; Dean, D.J.; Devlin, M.; Dobaczewski, J.; Heenen, P.-H.; Jin, H.-Q.; LaFosse, D.R.; et al. Rotational Bands in the Doubly Magic Nucleus 56Ni. Phys. Rev. Lett. 1999, 82, 3763. [Google Scholar] [CrossRef]
- Svensson, C.E.; Rudolph, D.; Baktash, C.; Bentley, M.A.; Cameron, J.A.; Carpenter, M.P.; Devlin, M.; Eberth, J.; Flibotte, S.; Galindo-Uribarri, A.; et al. Decay Out of the Doubly Magic Superdeformed Band in the N = Z Nucleus 60Zn. Phys. Rev. Lett. 1999, 82, 3400. [Google Scholar] [CrossRef]
- Dobaczewski, J.; Dudek, J.; Wyss, R. T = 0 neutron-proton pairing correlations in the superdeformed rotational bands around 60Zn. Phys. Rev. C 2003, 67, 034308. [Google Scholar] [CrossRef]
- Šimkovic, F.; Moustakidis, C.C.; Pacearescu, L.; Faessler, A. Proton-neutron pairing in the deformed BCS approach. Phys. Rev. C 2003, 68, 054319. [Google Scholar] [CrossRef]
- Yoshida, K. Proton-neutron pairing vibrations in N = Z nuclei: Precursory soft mode of isoscalar pairing condensation. Phys. Rev. C 2014, 90, 031303. [Google Scholar] [CrossRef]
- Sagawa, H.; Tanimura, Y.; Hagino, K. Competition between T = 1 and T = 0 pairing in pf-shell nuclei with N = Z. Phys. Rev. C 2013, 87, 034310. [Google Scholar] [CrossRef]
- Darai, J.; Cseh, J.; Antonenko, N.V.; Royer, G.; Algora, A.; Hess, P.O.; Jolos, R.V.; Scheid, W. Clusterization in the shape isomers of the 56Ni nucleus. Phys. Rev. C 2011, 84, 024302. [Google Scholar] [CrossRef]
- Macchiavelli, A.O.; Fallon, P.; Clark, R.M.; Cromaz, M.; Deleplanque, M.A.; Diamond, R.M.; Lane, G.J.; Lee, I.Y.; Stephens, F.S.; Svensson, C.E.; et al. Collective T = 0 pairing in N = Z nuclei? Pairing vibrations around 56Ni revisited. Phys. Lett. B 2000, 480, 1. [Google Scholar]
- Sagawa, H.; Bai, C.L.; Colò, G. Isovector spin-singlet (T = 1, S = 0) and isoscalar spin-triplet (T = 0, S = 1) pairing interactions and spin-isospin response. Phys. Scr. 2016, 91, 083011. [Google Scholar] [CrossRef]
- Skoda, S.; Fiedler, B.; Becker, F.; Eberth, J.; Freund, S.; Steinhardt, T.; Stuch, O.; Thelen, O.; Thomas, H.G.; Käubler, L.; et al. Identification of excited states in the N = Z nucleus 68Se with cluster detectors. Phys. Rev. C 1998, 58, R5. [Google Scholar] [CrossRef]
- Lieb, K.P.; Harder, A.; Rudolph, D.; Dönau, F.; Gelletly, W.; Gross, C.J.; Jungclaus, A.; Sheikh, J.A.; EUROGRAM 1 Collaboration; NORDBALL Collaboration. High-spin spectroscopy near the deformed N≈Z≈38 shell gap: The light Rb isotopes. Prog. Part. Nucl. Phys. 1997, 38, 101. [Google Scholar] [CrossRef]
- Tsunoda, N.; Otsuka, T.; Takayanagi, K.; Shimizu, N.; Suzuki, T.; Utsuno, Y.; Yoshida, S.; Ueno, H. The impact of nuclear shape on the emergence of the neutron dripline. Nature 2020, 587, 66. [Google Scholar] [CrossRef]
- Neufcourt, L.; Cao, Y.; Giuliani, S.A.; Nazarewicz, W.; Olsen, E.; Tarasov, O.B. Quantified limits of the nuclear landscape. Phys. Rev. C 2020, 101, 044307. [Google Scholar] [CrossRef]
- Stroberg, S.R.; Holt, J.D.; Schwenk, A.; Simonis, J. Ab Initio Limits of Atomic Nuclei. Phys. Rev. Lett. 2021, 126, 022501. [Google Scholar] [CrossRef] [PubMed]
- Fortune, H.T. Proposed new classification among coexistence nuclei. Nucl. Phys. A 2020, 1004, 122063. [Google Scholar] [CrossRef]
- Ahmad, I.; Butler, P.A. Octupole Shapes in Nuclei. Annu. Rev. Nucl. Part. Sci. 1993, 43, 71–116. [Google Scholar] [CrossRef]
- Butler, P.A.; Nazarewicz, W. Intrinsic reflection asymmetry in atomic nuclei. Rev. Mod. Phys. 1996, 68, 349. [Google Scholar] [CrossRef]
- Butler, P.A. Octupole collectivity in nuclei. J. Phys. G Nucl. Part. Phys. 2016, 43, 073002. [Google Scholar] [CrossRef]
- Phillips, W.R.; Ahmad, I.; Emling, H.; Holzmann, R.; Janssens, R.V.F.; Khoo, T.-L.; Drigert, M.W. Octupole deformation in neutron-rich barium isotopes. Phys. Rev. Lett. 1986, 57, 3257. [Google Scholar] [CrossRef]
- Schüler, P.; Lauterbach, C.; Agarwal, Y.K.; De Boer, J.; Blume, K.P.; Butler, P.A.; Euler, K.; Fleischmann, C.; Günther, C.; Hauber, E.; et al. High-spin states in 224,226,228Th and the systematics of octupole effects in even Th isotopes. Phys. Lett. B 1986, 174, 241. [Google Scholar] [CrossRef]
- Leander, G.A.; Sheline, R.K.; Möller, P.; Olanders, P.; Ragnarsson, I.; Sierk, A.J. The breaking of intrinsic reflection symmetry in nuclear ground states. Nucl. Phys. A 1982, 388, 452–476. [Google Scholar] [CrossRef]
- Inglis, D.R. Particle Derivation of Nuclear Rotation Properties Associated with a Surface Wave. Phys. Rev. 1954, 96, 1059–1065. [Google Scholar] [CrossRef]
- Inglis, D.R. Nuclear Moments of Inertia due to Nucleon Motion in a Rotating Well. Phys. Rev. 1956, 103, 1786–1795. [Google Scholar] [CrossRef]
- Kerman, A.K. Pairing forces and nuclear collective motion. Ann. Phys. 1961, 12, 300–329. [Google Scholar] [CrossRef]
- Nazarewicz, W.; Dudek, J.; Bengtsson, R.; Bengtsson, T.; Ragnarsson, I. Microscopic study of the high-spin behaviour in selected A≈80 nuclei. Nucl. Phys. A 1985, 435, 397–447. [Google Scholar] [CrossRef]
- Cwiok, S.; Dudek, J.; Nazarewicz, W.; Skalski, J.; Werner, T. Single-particle energies, wave functions, quadrupole moments and g-factors in an axially deformed woods-saxon potential with applications to the two-centre-type nuclear problems. Comp. Phys. Commun. 1987, 46, 379–399. [Google Scholar] [CrossRef]
- Strutinsky, V.M. Shell effects in nuclear masses and deformation energies. Nucl. Phys. A 1967, 95, 420. [Google Scholar] [CrossRef]


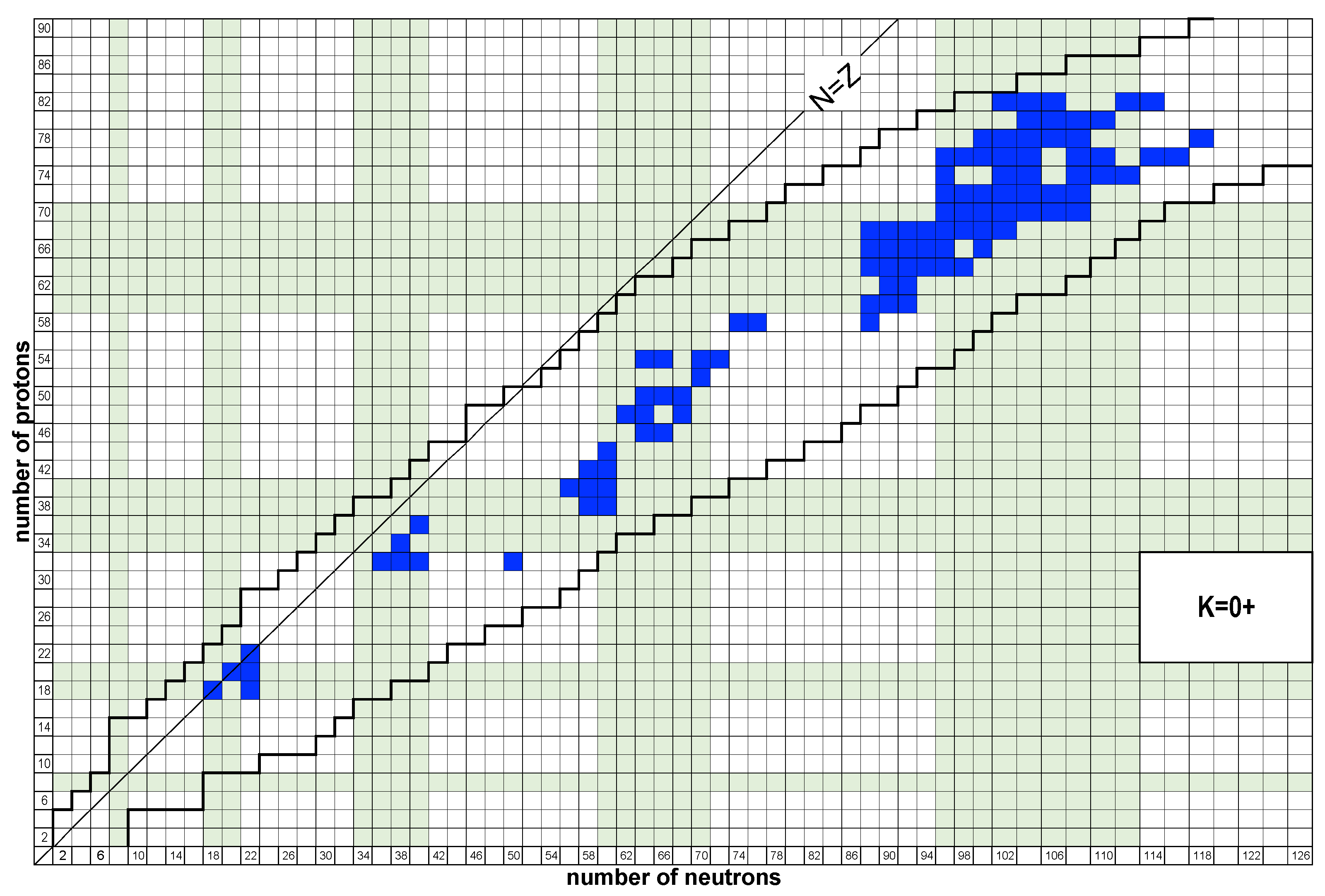
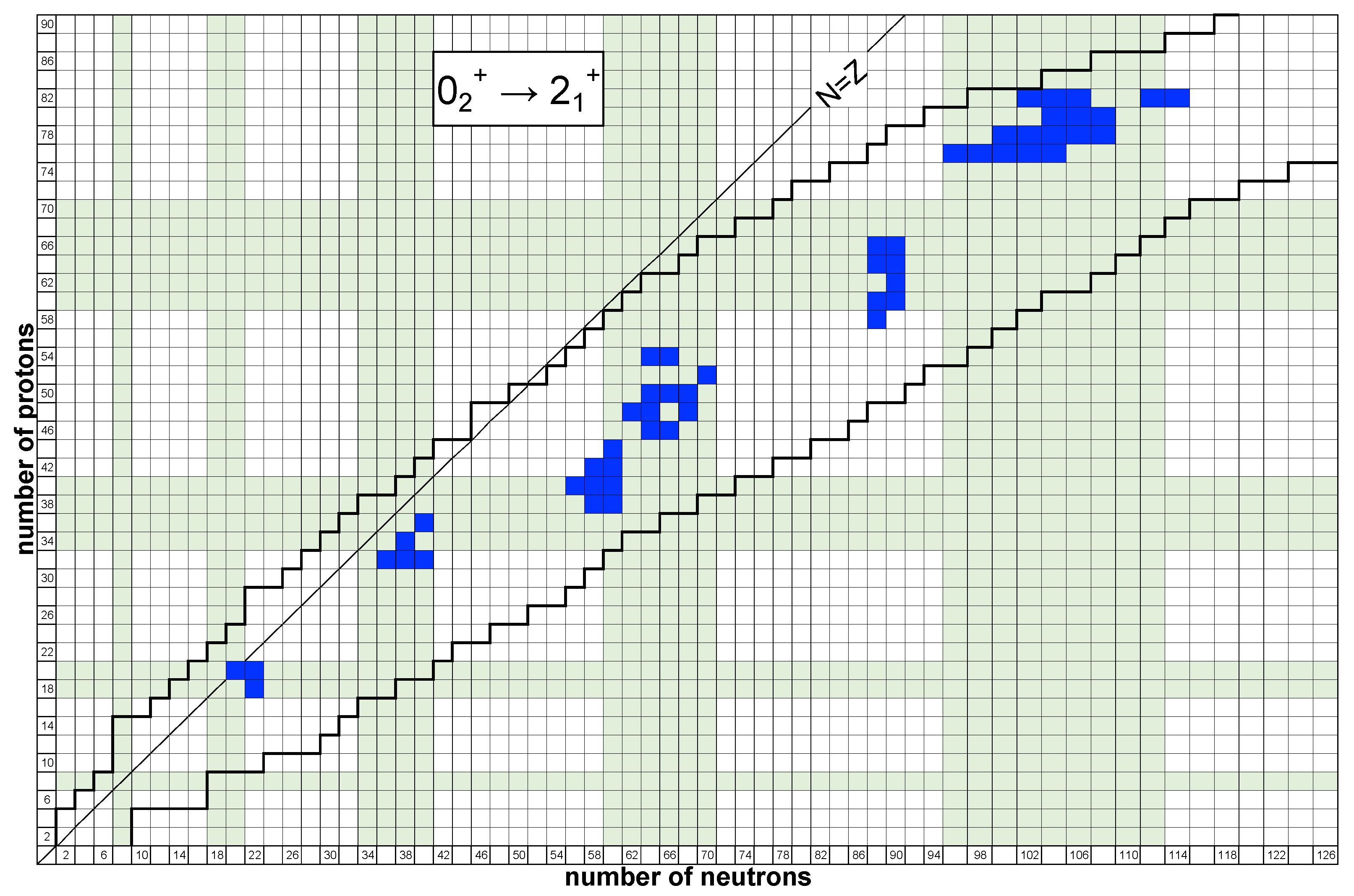
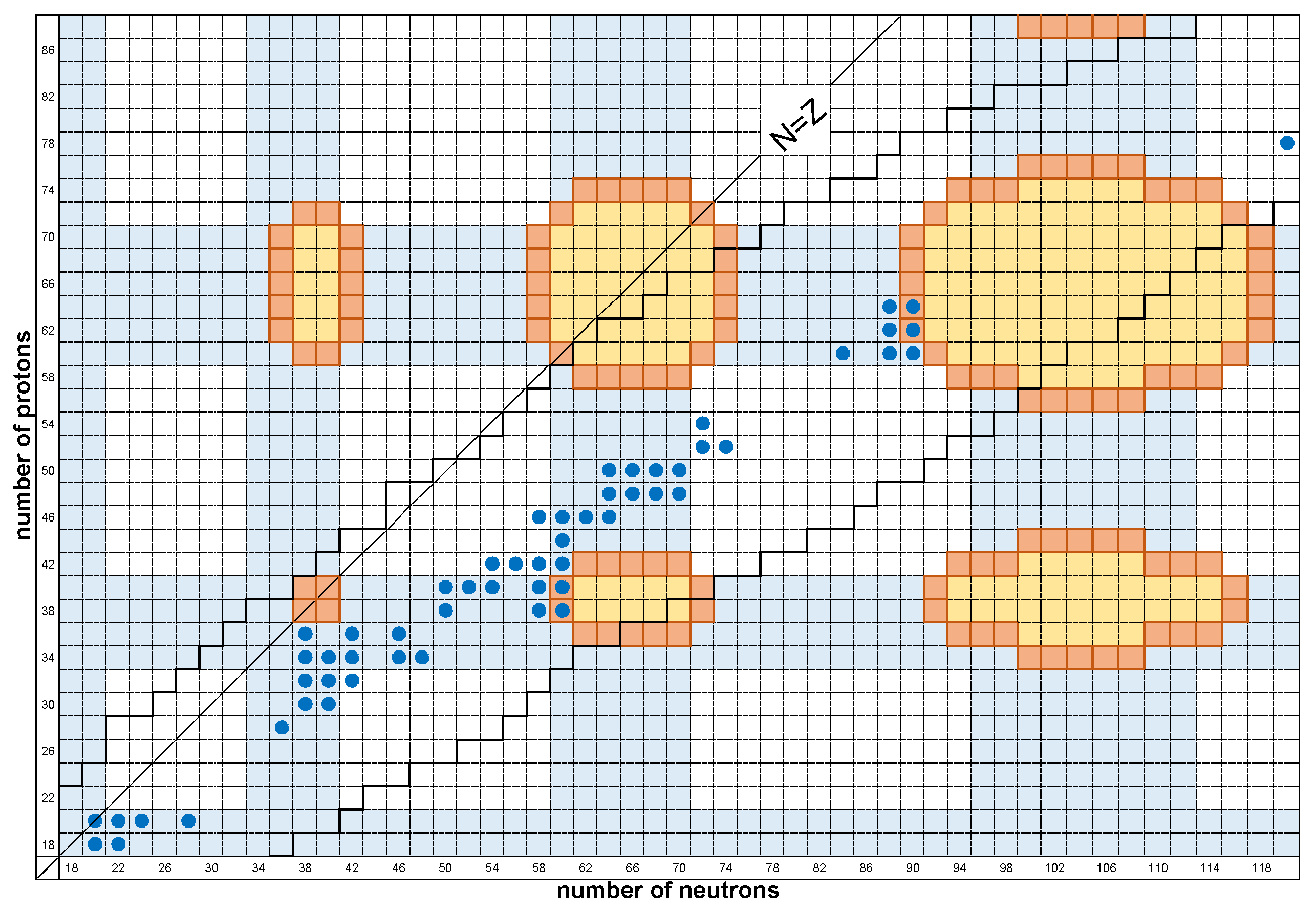
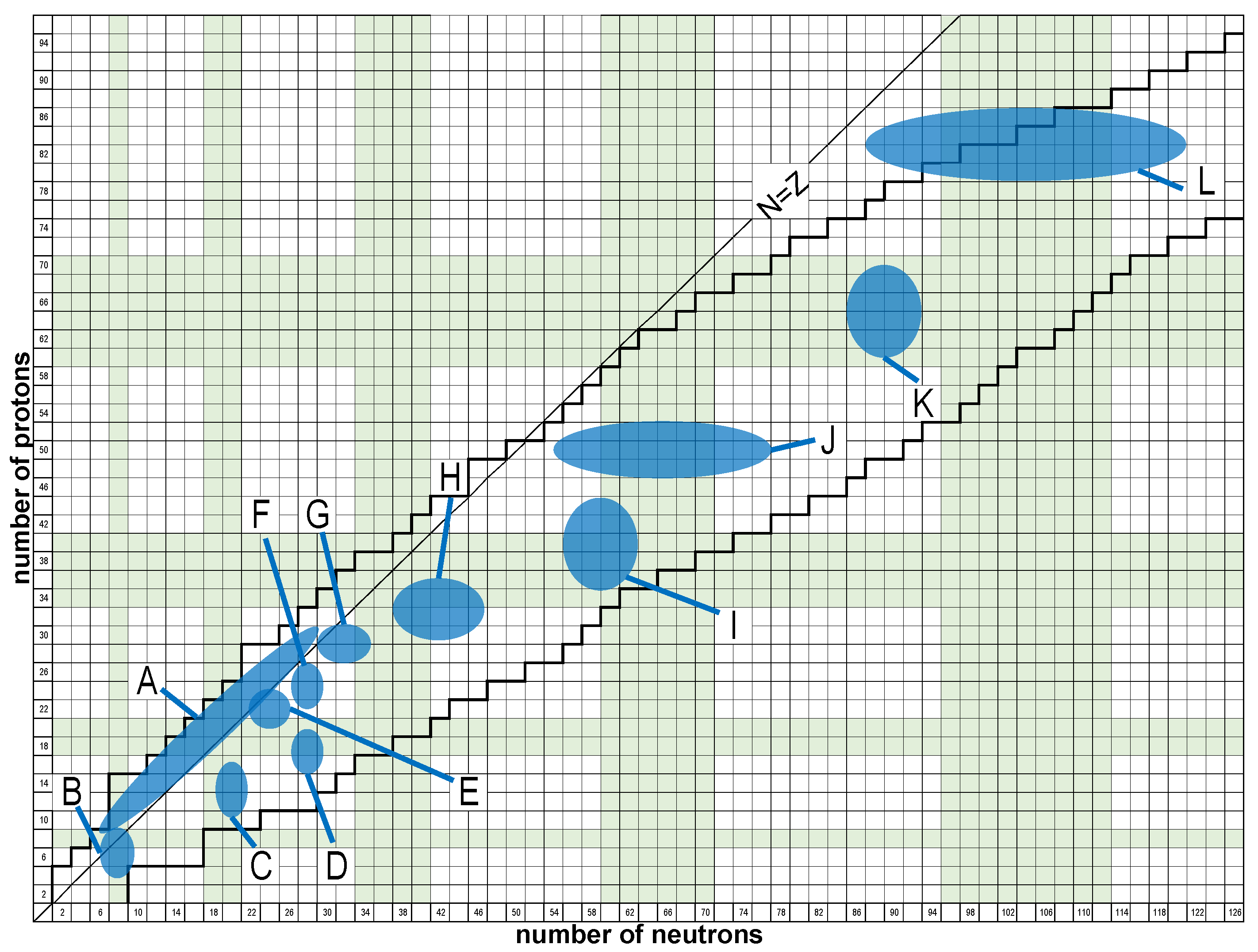
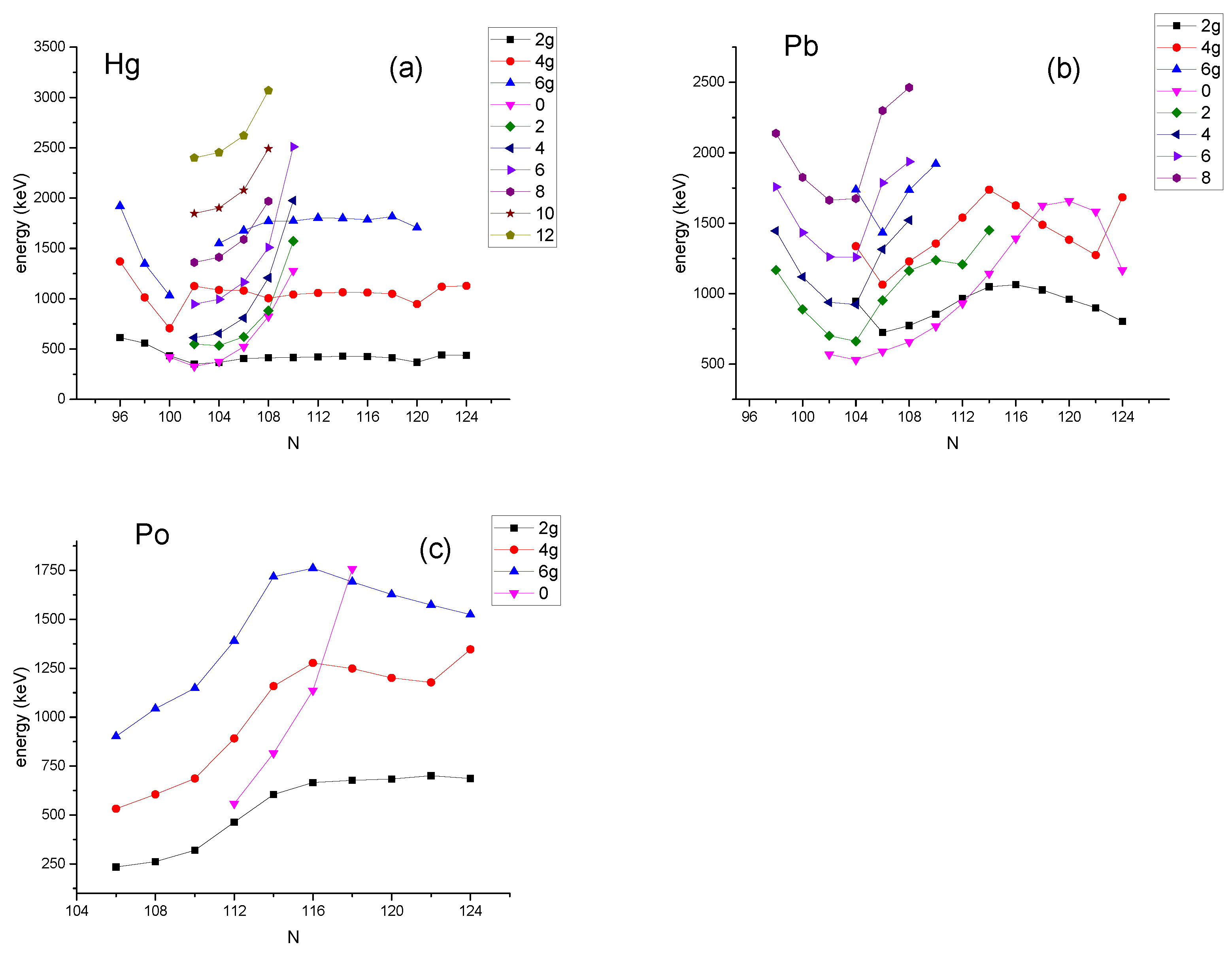
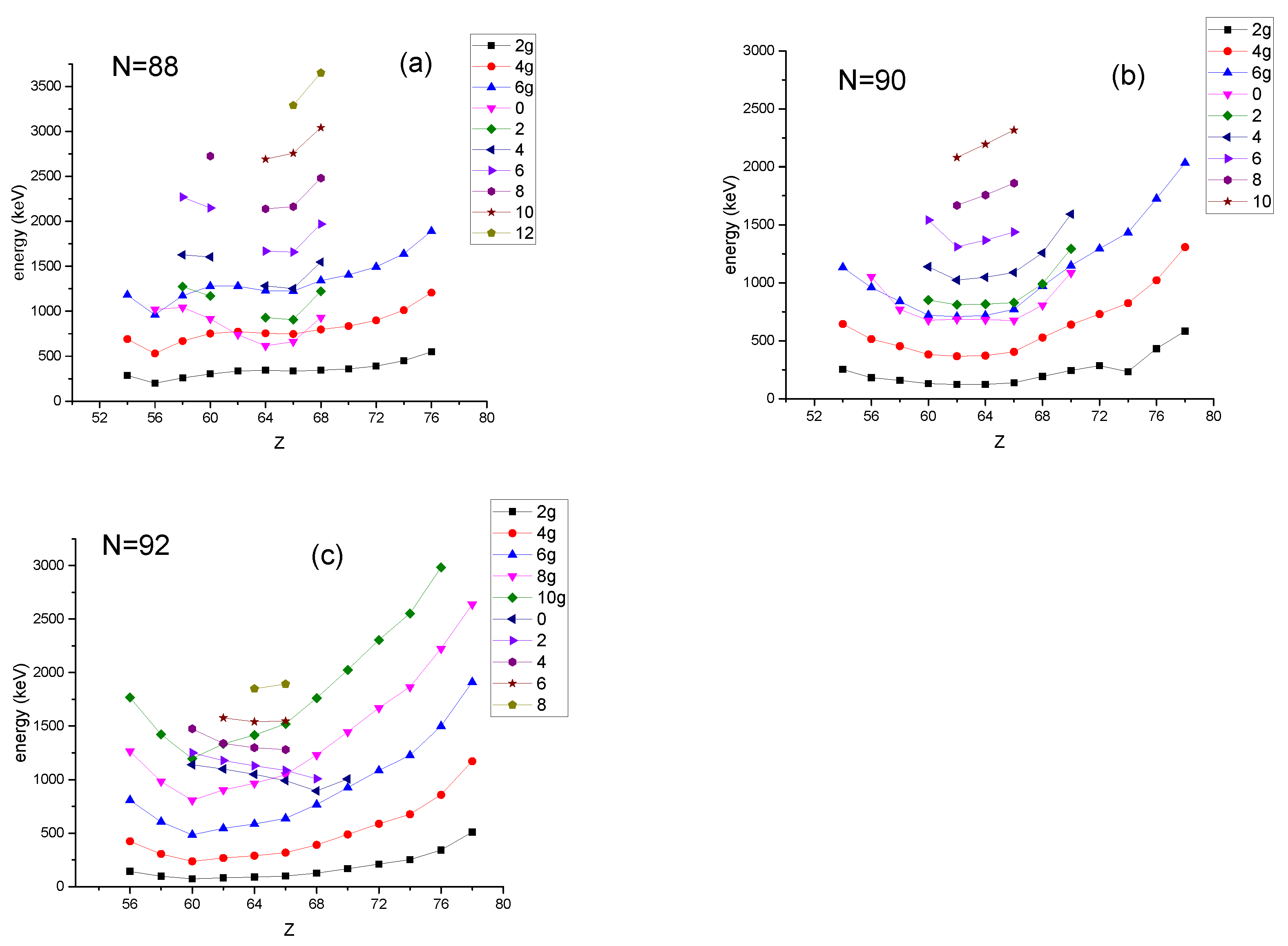
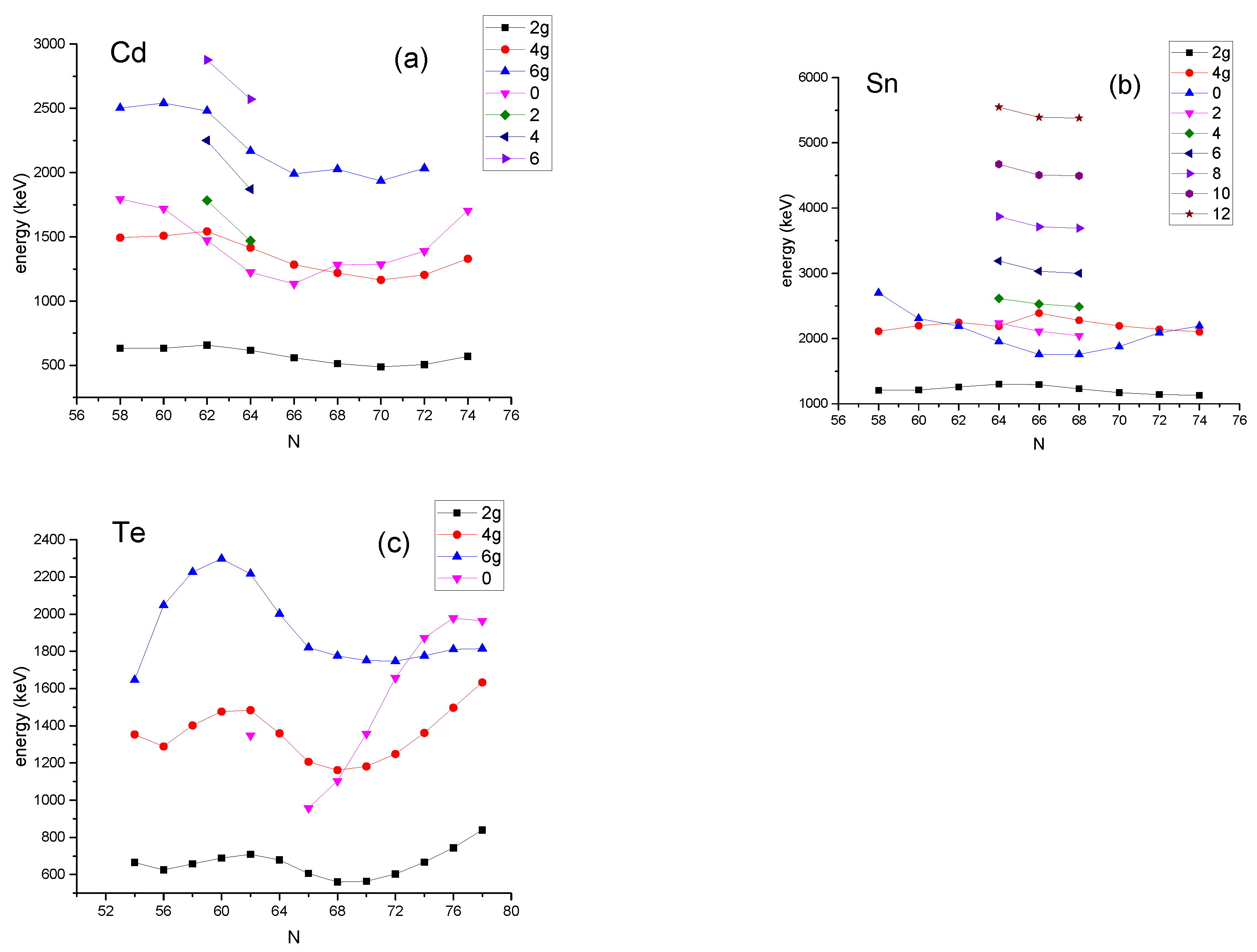
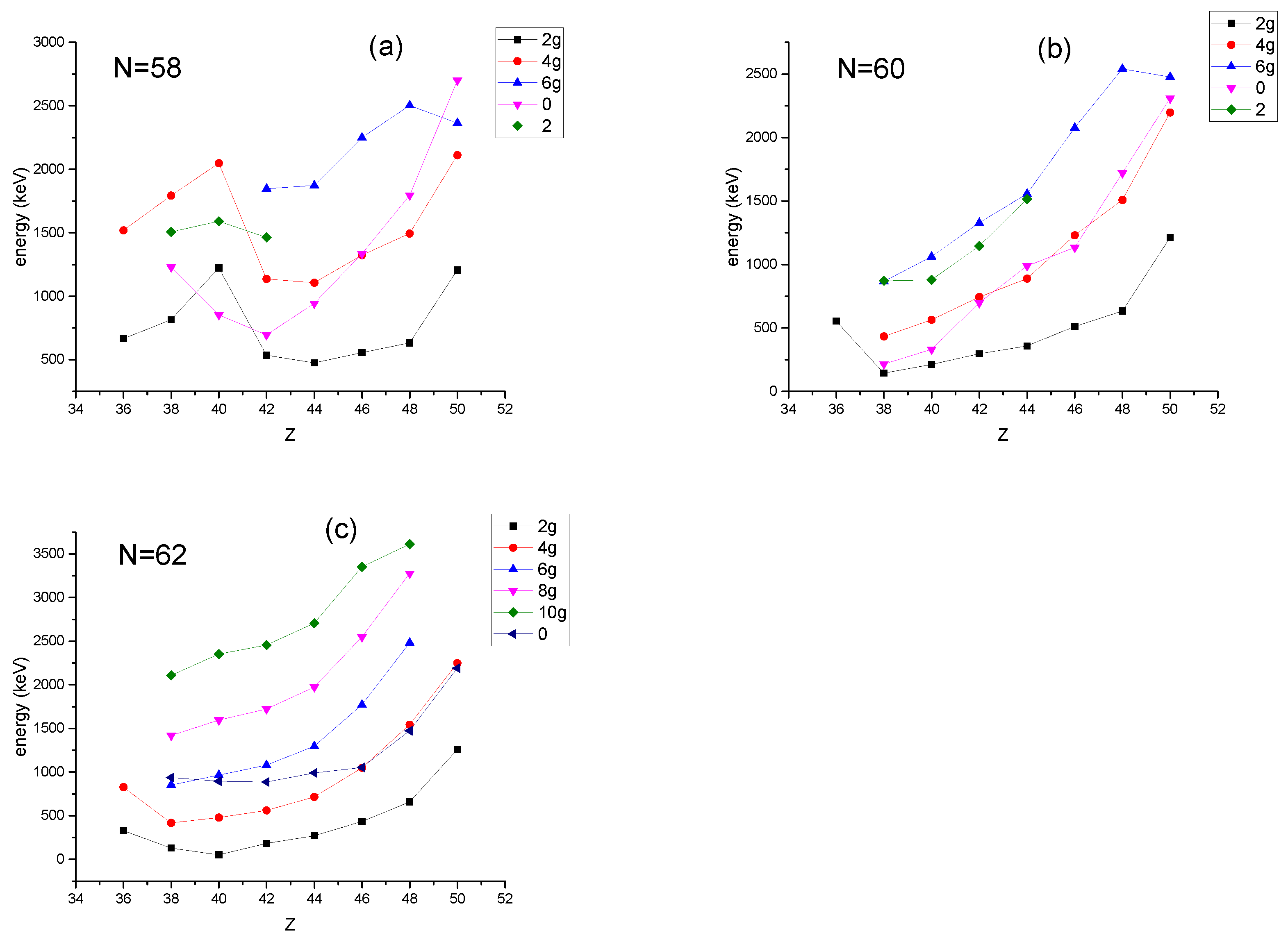
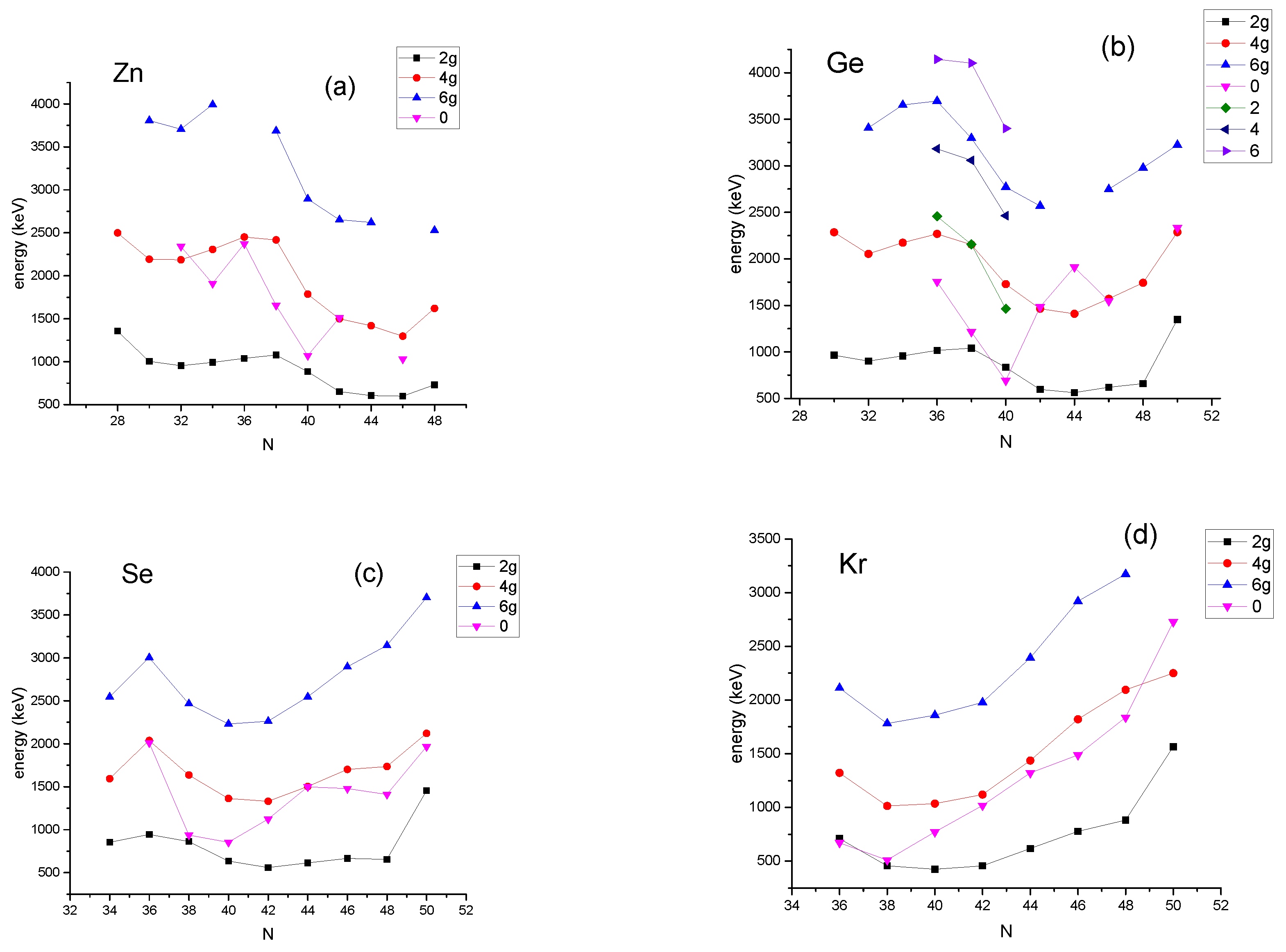
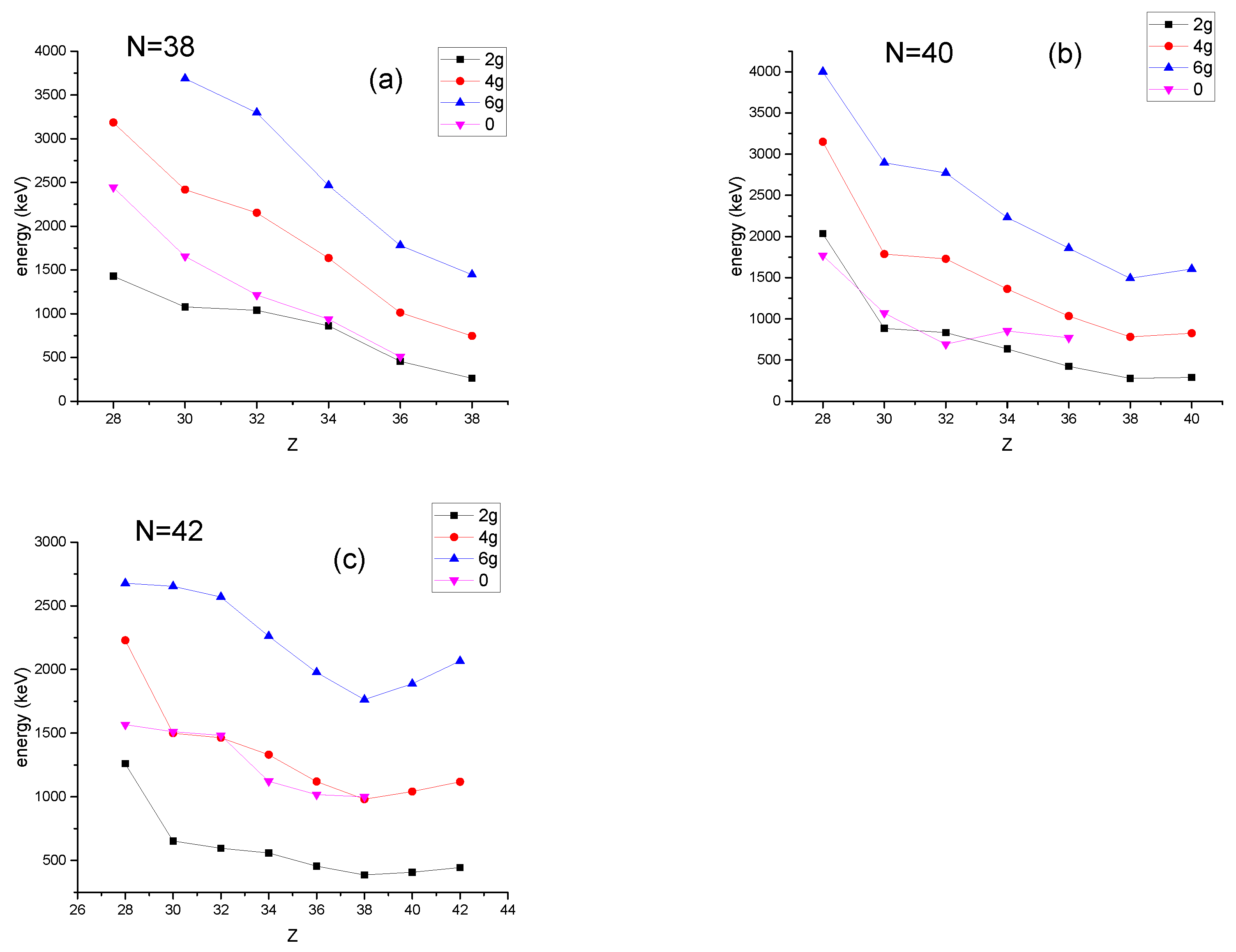
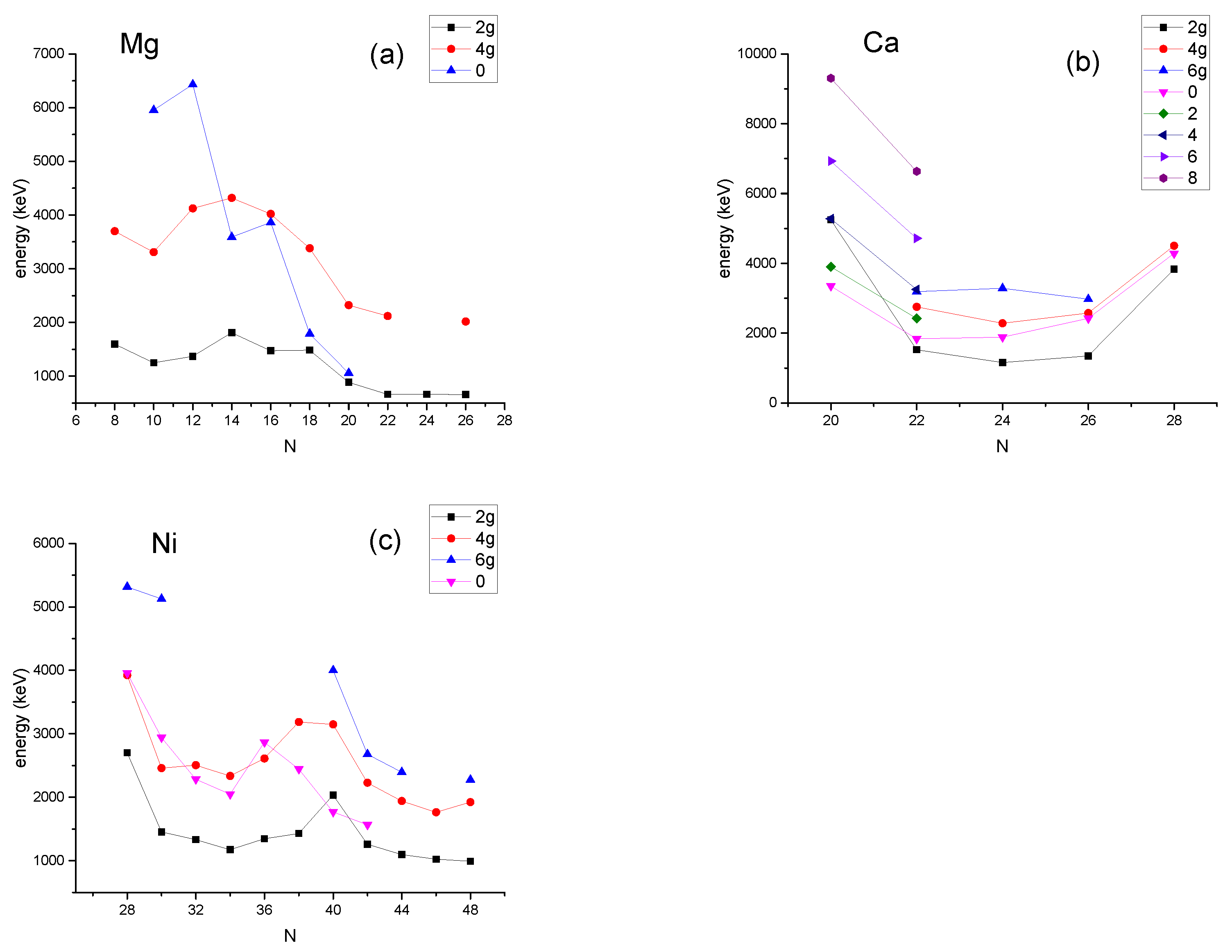

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonatsos, D.; Martinou, A.; Peroulis, S.K.; Mertzimekis, T.J.; Minkov, N. Shape Coexistence in Even–Even Nuclei: A Theoretical Overview. Atoms 2023, 11, 117. https://doi.org/10.3390/atoms11090117
Bonatsos D, Martinou A, Peroulis SK, Mertzimekis TJ, Minkov N. Shape Coexistence in Even–Even Nuclei: A Theoretical Overview. Atoms. 2023; 11(9):117. https://doi.org/10.3390/atoms11090117
Chicago/Turabian StyleBonatsos, Dennis, Andriana Martinou, Spyridon K. Peroulis, Theodoros J. Mertzimekis, and Nikolay Minkov. 2023. "Shape Coexistence in Even–Even Nuclei: A Theoretical Overview" Atoms 11, no. 9: 117. https://doi.org/10.3390/atoms11090117
APA StyleBonatsos, D., Martinou, A., Peroulis, S. K., Mertzimekis, T. J., & Minkov, N. (2023). Shape Coexistence in Even–Even Nuclei: A Theoretical Overview. Atoms, 11(9), 117. https://doi.org/10.3390/atoms11090117







