Modeling Femtosecond Reduction of Atomic Scattering Factors in X-ray-Excited Silicon with Boltzmann Kinetic Equations

Abstract

In this communication, we describe the application of Boltzmann kinetic equations for modeling massive electronic excitation in a silicon nanocrystal film after its irradiation with intense femtosecond hard X-ray pulses. This analysis was inspired by an experiment recently performed at the X-ray free-electron laser facility SACLA, which measured a significant reduction in atomic scattering factors triggered by an X-ray pulse of the intensity ∼${10}^{19}$ W/cm${}^2$, occurring on a timescale comparable with the X-ray pulse duration (6 fs full width at half maximum). We show that a Boltzmann kinetic equation solver can accurately follow the details of the electronic excitation in silicon atoms caused by such a hard X-ray pulse, yielding predictions in very good agreement with the experimental data.

1. Introduction

X-ray free-electron lasers (XFELs) [1,2,3,4,5,6,7], which produce intense X-ray pulses with femtosecond pulse durations, have stimulated the development of unique atomic-scale structure determination methods, such as protein crystallography beyond the conventional radiation dose limit [8] and visualization of ultrafast electronic and structural changes in photoinduced phase transitions [9]. In such experiments, X-rays may also act as a pump, inducing the strong excitation of electronic subsystems occurring on femtosecond timescales. Such excitation brings the matter rapidly into a strongly nonequilibrium regime (see, e.g., [10,11,12]), followed by a subpicosecond relaxation.

For the analysis of experimental results on X-ray-excited solid samples, in particular with application to diffraction and scattering experiments, the development of dedicated theoretical tools, capable of describing the evolution of irradiated solid materials under strongly nonequilibrium conditions, is needed. In [13], we gave a review on a robust and computationally efficient plasma simulation tool, the Boltzmann model. It is based on solving a set of Boltzmann kinetic equations for free-electron and charge-state densities present in the sample using atomistic approximation (i.e., under the assumption that the simulated sample can be initially represented as consisting of unbound atoms). Consistently, for all physical processes occurring during a sample evolution, atomic cross sections and rates are applied. This modeling approach works most accurately for the simulation of solid samples, irradiated with high-intensity X-rays. In such a case, interatomic bonds break early in the exposure, and chemical dynamics can be neglected. The Boltzmann model can also accurately describe nonequilibrium evolution stages of an irradiated sample. This includes the treatment of atomic excitation and relaxation pathways, which can be very complicated, especially in heavy elements.

In this communication, we show that the computationally efficient Boltzmann kinetic equation code can describe the development of a massive electronic excitation in a silicon film caused by an 11.5 keV X-ray pulse with a 6 fs full-width-at-half-maximum (FWHM) duration. Its predictions on the measured diffraction signal are in very good agreement with the experimental data [1]. This confirms the strong application potential of the Boltzmann model in the hard X-ray regime due to the efficient “predominant excitation and relaxation path” (PERP) approach applied [13,14], without the need to involve a superconfiguration approach.

2. Results

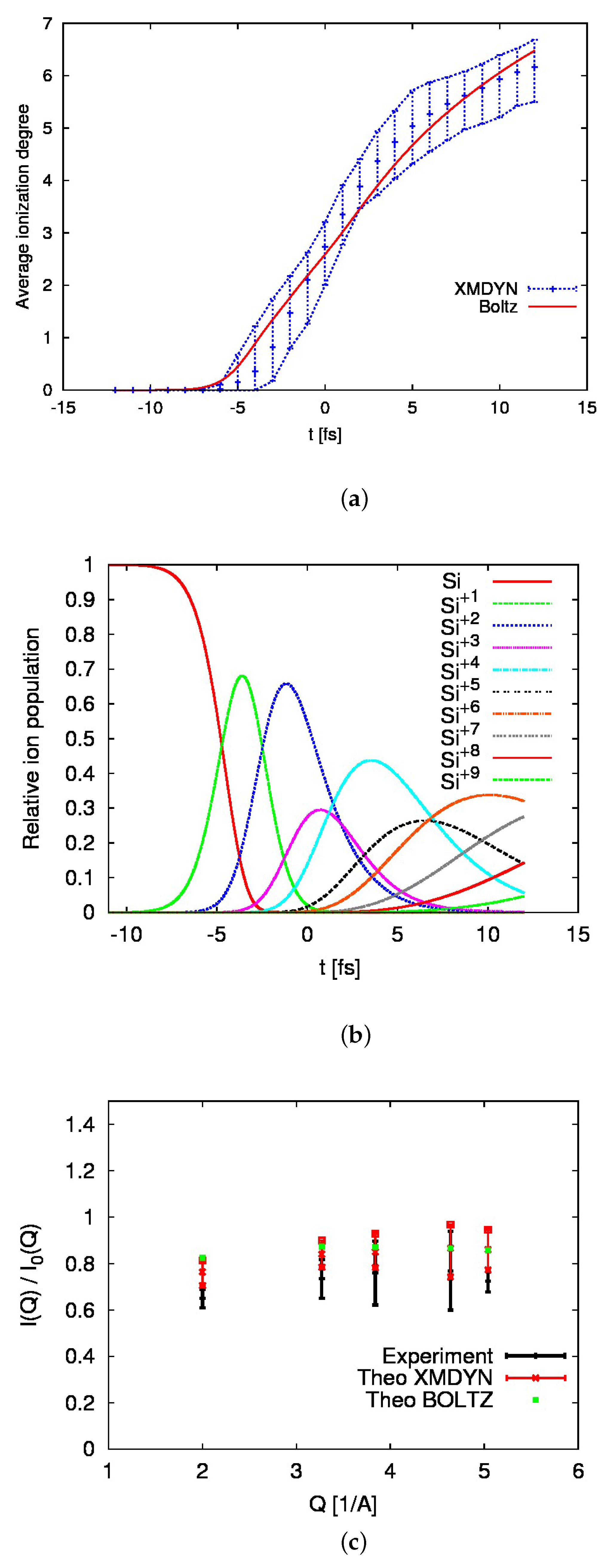
2.1. Experimental Findings

Figure 2 in Ref. [1] shows X-ray diffraction intensity profiles of silicon obtained at three high X-ray peak intensities, ∼$2.8\times {10}^{17}$ W/cm${}^2$, $3.5\times {10}^{18}$ W/cm${}^2$, and $4.9\times {10}^{19}$ W/cm${}^2$, compared with the corresponding diffraction intensity profiles at a low X-ray peak intensity, ∼$2.1\times {10}^{16}$ W/cm${}^2$. One can clearly see that the diffraction intensity profiles are similar for all X-ray intensities considered except for the peak intensity, $4.9\times {10}^{19}$ W/cm${}^2$. In this case, the diffraction intensity profiles obtained after the high-intensity irradiation are lower than those obtained with the reference intensity. From the diffraction intensity profiles, the diffraction efficiency can be defined as the ratio of the X-ray diffraction intensity of silicon (normalized by incident pulse energy) at a high peak intensity to that at a low peak intensity (also normalized by incident pulse energy). One can check (not shown) that for intensities of ∼$2.8\times {10}^{17}$ W/cm${}^2$ and $3.5\times {10}^{18}$ W/cm${}^2$, the diffraction efficiency practically does not change. On the contrary, for the highest intensity of $4.9\times {10}^{19}$ W/cm${}^2$, one observes a reduction of up to 40% of the diffraction efficiency. This surprising finding was analyzed in [1] with molecular dynamics calculations, using the code XMDYN [15,16,17].

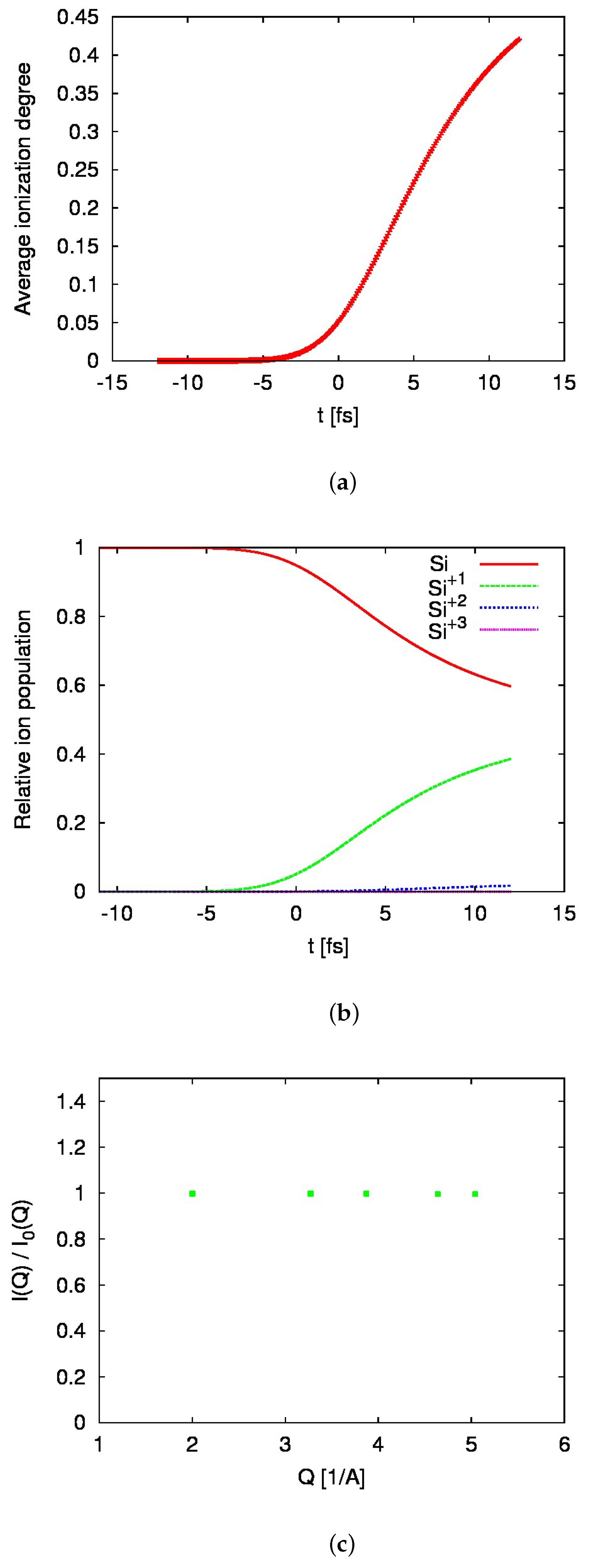
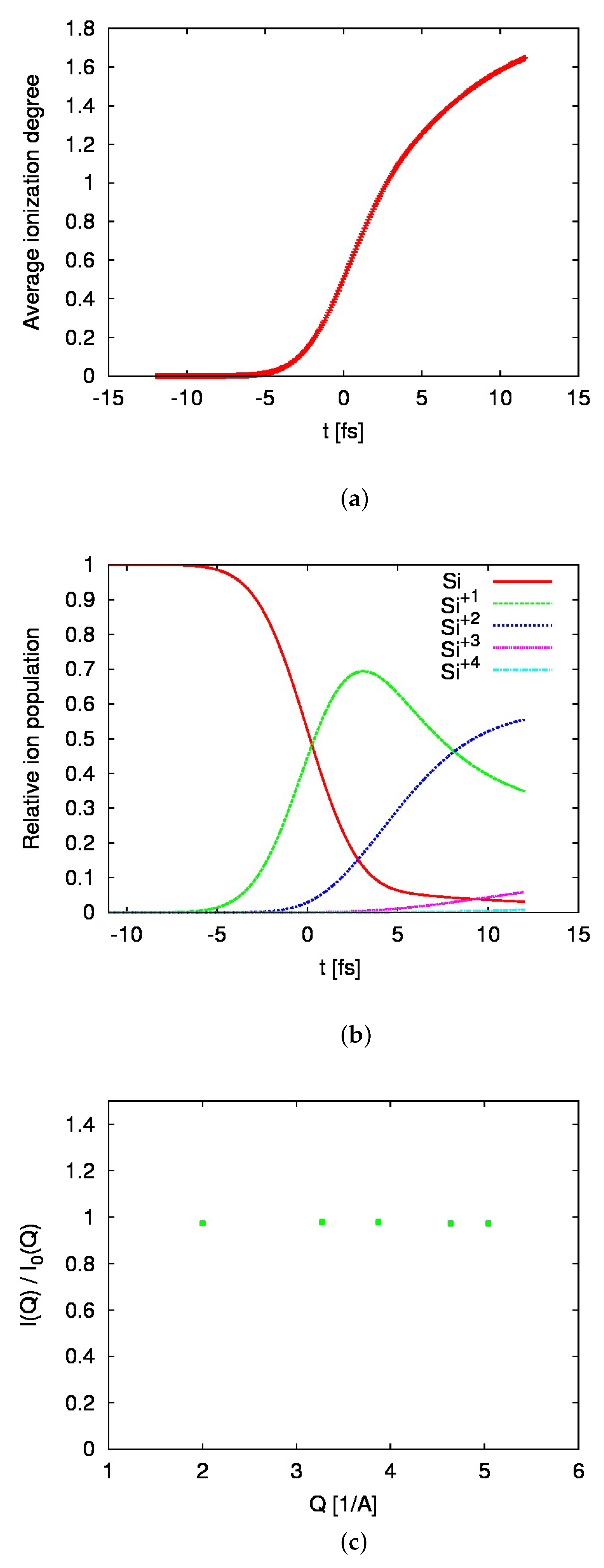
2.2. Boltzmann Code Simulations

The XMDYN code predictions shown in Figure 3b of Ref. [1] confirmed that atomic displacements even in cases with the highest X-ray peak intensity tested are negligible. The simulation predicted massive ionization (depicted in Figure 3c of Ref. [1]) and implied a femtosecond decrease in atomic form factors, resulting in a significant decrease in diffraction efficiency. XMDYN is a molecular dynamics code connected to the atomic structure calculation package XATOM [15,16]. Therefore, it can follow the evolution of all atomic configurations in the sample, calling XATOM on the fly for necessary cross sections and rates, when a specific atomic configuration appears.

The simulation scheme is different in the Boltzmann model. Here, kinetic equations are solved for a predefined set of atomic configurations, selected using the PERP approach [13,14]. For the actual case of silicon (Z = 14) irradiated with 11.5 keV X-ray photons, the total number of active configurations included was 282. Charge states of up to +14 were followed. The question is how accurately such a selected set of configurations can describe the massive electron excitation going on in the sample. Figure 1, Figure 2 and Figure 3 show the results predicted for the intensities $2.8\times {10}^{17}$ W/cm${}^2$, $3.5\times {10}^{18}$ W/cm${}^2$, and $1.0\times {10}^{20}$ W/cm${}^2$.

For each X-ray peak intensity, (i) the average ionization degree of silicon as a function of time, (ii) relative charge-state populations as a function of time, and (iii) diffraction efficiency, i.e., the actual diffraction intensity, $I\left(Q\right)$, divided by the intensity, $I_0\left(Q\right)$, obtained after the irradiation of silicon with the X-ray pulse of the reference peak intensity, $2.1\times {10}^{16}$ W/cm${}^2$, are shown. Both scattering intensities were normalized with the incident pulse energy. Note that in the simulations, we used a Gaussian temporal profile for the X-ray pulse, neglecting the spiky nature of a self-amplified spontaneous emission (SASE) XFEL pulse [18]. This problem was considered in detail in a recent publication by F. Rosmej et al. [19]. In our case, the experimental results on Bragg peak intensities presented in [1] and in Figure 3c of our manuscript are obtained after averaging the peak intensities obtained from 500 different XFEL shots [1]. The effect of the spiky pulse structure then averages out. As a shot-averaged XFEL pulse has a Gaussian temporal profile (see, e.g., Figure 1 in [18]), using the Gaussian pulse for modeling the shot-averaged data on Bragg peak intensities is justified.

In the case of two lower X-ray Bragg peak intensities, no significant change of diffraction signal is observed, in agreement with the similar diffraction intensity profiles observed in Figure 2 in Ref. [1]. The Boltzmann-model-predicted change of diffraction efficiency for the highest intensity case is in perfect agreement with the one predicted by the XMDYN code and in agreement with the experimental data. Predictions on the average charge and relative ion populations associate the change of diffraction intensity with the presence of highly charged states (up to +9) in the ionized sample. In particular, the presence of core hole states that strongly modify the diffraction properties of the sample is crucial [20]. The obtained predictions on average charge-state and transient charge-state contributions are also in very good agreement with the respective XMDYN predictions for the highest X-ray peak intensity case. This confirms the high accuracy of the Boltzmann model and its reliable applicability in the hard X-ray regime.

3. Materials and Methods

3.1. Experimental Scheme

The experiment described in Ref. [1] was performed at the XFEL facility SACLA [21,22] using a 10 $\mathsf{\mu }$m thick silicon nanocrystal film attached to a polyimide film. The 11.5 keV X-ray pulses with a duration of 6 fs FWHM were focused with a Kirkpatrick–Baez focusing system [23] on an FWHM beam size of 180 nm (horizontal) × 150 nm (vertical). The sample was placed at the beam focus, and five diffraction peaks (corresponding to 111, 220, 311, 400, 331 reflections) in the vertical plane were measured with a multiport charge-coupled device (MPCCD) detector [24]. The pulse energy at the sample position was monitored by a calibrated inline intensity monitor at the experimental hutch [25]. The average fluence for each pulse was determined by dividing the pulse energy by the product of horizontal and vertical beam sizes. From the average fluence, the peak intensity was derived. The diffraction intensity averaged over multiple pulses was measured for four different peak intensities: (i) ∼$2.1\times {10}^{16}$ W/cm${}^2$ (below damage threshold, used as reference data), (ii) ∼$2.8\times {10}^{17}$ W/cm${}^2$, (iii) ∼$3.5\times {10}^{18}$ W/cm${}^2$, and (iv) ∼$4.9\times {10}^{19}$ W/cm${}^2$.

3.2. Modeling Tool

Below, we briefly discuss the main components of the Boltzmann model. For further details on the code, please see the recent review paper [13] and the references therein. As mentioned above, in the Boltzmann model, the initially unexcited sample is represented as an assembly of unbound atoms. After X-ray irradiation, free electrons and various charge states appear in the sample. The continuum approach [26,27,28] is a computationally efficient modeling technique, well applicable in such a case. It follows ionization dynamics by solving the evolution equations for density distributions of electrons and charge states on a phase-space grid. The resulting reduction in computational costs—which now depend only on the grid size and do not scale quadratically with the number of particles, $O\left(N^2\right)$ (as typical for particle approaches, e.g., classical molecular dynamics)—is then significant.

The accurate description of the evolution of the irradiated sample also requires modeling its nonequilibrium stage, which is only possible by solving the full kinetic equations. They deliver information on the transient-electron and charge-state distributions, including various atomic configurations active during the excitation and relaxation stages in the irradiated sample.

Another modeling challenge is that highly energetic X-ray photons can release not only valence but also inner-shell electrons. They leave behind vacancies in core shells of atoms, which typically relax along very complex pathways. The relaxation occurs with the contribution of collisional processes and creates many atomic configurations. In heavier elements, a very large number of active atomic configurations involved can make the kinetic equation approach practically insolvable due to a very high computational cost, rapidly increasing with the atomic number Z. For example, in [14], we analyzed the case of carbon (Z = 6) irradiated by X-rays. The total number of atomic configurations was in that case equal to 27. The corresponding set of evolution equations could then be easily solved. Similarly, respective sets of kinetic equations can be formulated and solved for other light elements. However, for heavier elements, there is a strong increase in the total number of possible atomic configurations. For example, for argon (Z = 18), it already amounts to 1323. In order not to restrict the kinetic equation approach only to low Z elements, superconfiguration approaches were introduced (see, e.g., [29,30,31,32,33,34]). They used sets of ”average” configurations [35,36] or, for spectroscopic applications, a virtual contour shape kinetic method [37], instead of treating the individual atomic configurations.

For the Boltzmann model, we proposed and tested in [14] an alternative approach to reduce the number of active atomic configurations involved in the excitation and relaxation of X-ray-irradiated materials. It is called the “predominant excitation and relaxation path” (PERP) approach, and follows the sample excitation and relaxation only along the most probable relaxation paths (including predominant photoinduced and collisional processes). This scheme, indeed, significantly restricts the number of active atomic configurations during a simulation with the Boltzmann model. In this way, computationally efficient simulations of atomic excitation and relaxation in heavier materials, such as gold [38] and copper [39], have become feasible.

Here, we applied the PERP scheme to calculate the response of a silicon sample to the impact of 11.5 keV photons, i.e., in the regime of very high photon energies, which was never tested before.

4. Discussion

We have described the implementation of the Boltzmann kinetic equations model to simulate femtosecond electron excitation in a silicon crystal during its irradiation with a 11.5 keV X-ray pulse with an FWHM duration of 6 fs. The predictions on the measured diffraction signal are in very good agreement with the experimental data and with the predictions of the MD code, XMDYN. However, both theoretical predictions systematically overestimate the experimental scattering efficiency. In order to understand the reason for that, we carefully analyzed experimental errors of X-ray pulse parameters and background subtraction. We have already included a measure of these errors in our simulations. This has improved the agreement between the simulations and the data. Still, some discrepancy has remained. The reason for this can be that the regime of very high X-ray intensities, so far poorly investigated, can bring many challenges to theoretical modeling, to mention only a possible effect of nonlinear absorption, which can manifest at such high intensities, and possible changes of atomic ionization potentials and cross sections induced by a strongly ionized and rapidly changing plasma environment. Considering all these theoretical “unknowns”, the achieved agreement between the predictions by the “low-X-ray-intensity” theory model and the experimental data can be considered very good. Of course, the development of more accurate models dedicated to a high-intensity regime is very important. The data from Ref. [1] can then be used to benchmark such models.

The simulation involved 282 active configurations, out of a total of 567 possible configurations. Charge states of up to +14 were allowed. Depending on the X-ray peak intensity used in the simulations, the calculations took a maximum of several hours on a single CPU. This shows a strong application potential of the Boltzmann model in the hard X-ray regime, without the need to involve any superconfiguration approach.

Let us discuss the scaling of computational costs in XMDYN and the Boltzmann model in more detail. The XMDYN model is a particle approach; i.e., its computational cost increases with the squared number of particles used in the simulation. In the case of X-ray irradiation, the XMDYN simulation box should contain a sufficient number of atoms to ensure that at least several photoionization events occur in the box. For the XMDYN simulation presented in [1], when a very high X-ray fluence was applied (corresponding to X-ray peak intensities of ${10}^{19}$–${10}^{20}$ W/cm${}^2$), the simulation box with 64 atoms was sufficiently large. The simulation then took ∼2 minutes on a single CPU. However, for lower X-ray fluences, the number of atoms needed for a reliable XMDYN simulation would have to be correspondingly higher. This significantly increases the computational costs when reducing the pulse fluence by a few orders of magnitude. For example, for a fluence corresponding to 10% of the above (nominal) fluence, we would need approximately 10 times as many atoms (640). The XMDYN simulation time could then be roughly estimated to ≤3 h. With a fluence corresponding to ∼1% of the nominal fluence, we would need ∼6400 atoms. This would increase the XMDYN simulation time to ≤14 days.

The Boltzmann code is based on the so-called continuum approach (see, e.g., [13]). In the case of bulk simulations, it does not scale with the number of atoms. Therefore, both low- and high-fluence simulation cases can be performed at a similar computational cost with the Boltzmann model, taking several hours on a single CPU for each fluence case.

Further foreseen developments, which include an improved treatment of electron–ion interaction and ionization potential lowering and implementation of Fermi–Dirac statistics for electrons [13], should remove the existing limitations of the actual Boltzmann model and transform it into a comprehensive, versatile tool for simulations of X-ray-irradiated bulk solids. The computational efficiency of the improved modeling tool is expected to be much higher than that of typical molecular dynamics approaches. The respective extensions of the Boltzmann model are already underway. Experiments necessary to validate the predictions of the extended model are being planned.