Next Article in Journal
Quantum Imprints on CMBR
Previous Article in Journal
Evolved Pulsar Wind Nebulae
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Universe
Volume 9
Issue 9
10.3390/universe9090403
universe-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Influence of the Surface Temperature Evolution over Organic and Inorganic Compounds on Iapetus

by
Katherine Villavicencio-Valero
1,
Emilio Ramírez-Juidias
2,*,
Antonio Madueño-Luna
3,
José Miguel Madueño-Luna
2 and
Miguel Calixto López-Gordillo
2
1
Department of Geology and Engineering, University of Chieti-Pescara, 65127 Pescara, Italy
2
Graphic Engineering Department, University of Seville, 41092 Seville, Spain
3
Department of Aerospace Engineering and Fluid Mechanics, University of Seville, 41092 Seville, Spain
*
Author to whom correspondence should be addressed.
Universe 2023, 9(9), 403; https://doi.org/10.3390/universe9090403
Submission received: 30 June 2023 / Revised: 22 August 2023 / Accepted: 1 September 2023 / Published: 4 September 2023
(This article belongs to the Section Planetary Sciences)
Browse Figures
Review Reports Versions Notes

Abstract

:
In this manuscript, there were performed simulations of the evolution of the surface temperature for each of the two hemispheres of Iapetus. This icy moon of Saturn shows the most differentiated albedo dichotomy of the Solar System. The dark leading side has a lower albedo than the bright trailing side. Spectral data on the visible light reveal the existence of two types of materials on the surface. The darkening in the leading side is thought to be due to the presence of organic material and carbonaceous compounds on the surface, while the trailing side is covered by water ice due to migration processes from the dark side. On airless bodies like Iapetus, the surface escape speed is greater than the speed of water molecules, resulting in the retention of a H2O atmosphere that allows some species to diffuse through it. Results showed a slow yet steady increment of temperatures for both sides, with a steeper slope for the dark hemisphere. It was also simulated how much energy can be accumulated on both sides and the consequences of that. Finally, we calculated the diffusion coefficients for ammonia, methane, and water ice. The results allowed us to infer how these compounds could evolve over time.

1. Introduction

Iapetus has two different types of terrain on its surface. One is the dark material, concentrated on the leading side, possibly composed of carbonaceous elements and organic materials that are thought to come from Phoebe, Titan, or Hyperion [1,2]. The other one is the bright material on the trailing side, which shows the spectral signature of water ice, which could have originated from the migration of water as a result of temperature variations in both hemispheres [3]. The leading hemisphere presents a lower albedo than the trailing side, a fact that might have two possible explanations: the first one being endogenic processes like flooding of magma, evidence of which is the existence of in-filled craters; and the second one being the accretion of exogenous particles, where previous studies reveal the existence of dark material [1,4,5]. These divergences in the hemispheres make Iapetus the celestial body with the most notable albedo dichotomy of the Solar System. The dark hemisphere, called Cassini Regio, has a low albedo of 0.04, and the bright one an albedo of 0.39 [6]. The dark side is warmer than the bright side, facilitating the sublimation and volatile migration of compounds that could form and retain a fast exosphere [7]. Regarding the concept of a “fast exosphere”, it is important to highlight that numerous airless bodies within the Solar System which are typically considered to lack an atmosphere actually have extremely thin surface-bound exospheres. These exospheres, which might exist only temporarily, play a role in facilitating the movement of volatile substances across the surfaces and environments of these bodies. The creation of these exospheres occurs relatively quickly.
Spectral data taken by the Visible and Infrared Mapping Spectrometer (VIMS) on board the Cassini mission detected a prominent presence of CO2 on the dark side [8]. On the other hand, ref. [2] reported the concentration of some polycyclic aromatic hydrocarbon (PAH) molecules in a region of low albedo and an association of CH2 aliphatic hydrocarbons. There were also found concentrations of water ice located in the dark regions far away from the apex, which are consistent with the thermal segregation of water ice at the darkest and warmest latitudes [9,10]. This might be a hint of an emplacement of dark material from an exogenous source. On the other hand, ref. [1] proposed a thermodynamic internal origin for the organic and carbonaceous material on the surface. Volatile compounds like ammonia have been also detected in the trailing hemisphere [7].
Dynamical dust models, like the one proposed by [11], suggest that deposition regions are either formed from Phoebe’s dust ring, or this material could have been interplanetary dust transported onto the moon [12]. Volatile frosts tend to create high albedos and prolong residence times; the sublimation of such volatile compounds and water molecules acts as a powerful coolant in the process of producing transient exospheres located at the impact zones, where the pressure decreases symmetrically with the distance to the impact zone. During the formation of the fast exosphere, and according to [7], around 23% of created water molecules escape to space. Moreover, in the bright hemisphere, the sublimation of ice molecules is only possible during the diurnal period [7].
Exospheres could act as a limit between the surface and the adjacent environment. The composition exospheres is based on a combination of gases released from the surface through various processes like thermal release or vaporization [13]. Those molecules emitted from the surface are ejected through trajectories until they make collisions again with the surface, altering the chemistry of the material present on the surface and modifying the optical surface properties [14,15]. Here, we assume that the sublimation of volatiles like ammonia, water ice, and methane contributes to the formation of an H2O exosphere on airless bodies like Iapetus [7,13], and the sublimation of water ice is two orders of magnitude higher on the dark side than on the bright one [16]. We also assume that the bright hemisphere is fully covered by pure water ice due to its migration from the dark side [3].
Studying the evolution of the surface temperature of Iapetus, and the influence of the energy, is crucial because it could help us to improve our understanding of the evolution over time of certain organic and inorganic compounds when they are present on airless bodies. Here, we consider a time window (1 Gyr) that is wide enough to observe a variation in the temperature. Then we simulate how much energy can be accumulated on each hemisphere, considering different albedos [6], during the same time window. This has the purpose of figuring out whether this contribution could assist with the dispersion of species into the atmosphere of the moon [7,17]. Then, we calculate the diffusion coefficients for ammonia, methane, and water ice, based on the increment of the temperature obtained by the simulation. The aim of this study is to understand how these organic and inorganic compounds evolve in extreme environments, like the surface of Iapetus.

2. Materials and Methods

In this study, we use the Navier–Stokes equations [18,19] to simulate the evolution of the surface temperature in a two-dimensional Cartesian geometry for 1 Gyr of model time. As is known, according to [19], the system of flows between the atmosphere, the soil, and the ice is highly interactive, and introduces positive feedback. For example, if the ice on the bright side of Iapetus starts to melt, the ground it leaves bare absorbs solar radiation, so it becomes hotter and more ice melts, which warms the atmosphere, which acts on the ice again.
The equations for the conservation of mass, momentum, and energy are solved on a staggered grid for a compressible fluid with an infinitive Prandtl number (a full description of these equations can be found, e.g., in [20]). In order to fix an initial surface temperature for the dark side and bright side of Iapetus, and according to [7], it is important to note that, to form an exosphere from surface volatiles, the illuminated surface of an object must be sufficiently warm such that volatiles are likely to sublimate from the surface into the gas phase. This process is described by the residence time of the volatile, which specifies the expected time that a molecule will remain adsorbed/condensed on the surface before desorbing/subliming as a function of temperature. The residence time is highly sensitive to temperature, with sufficiently cold surfaces on the night sides and high latitudes of bodies leading to residence times many orders of magnitude longer than that body’s diurnal period. This temperature depends on the specific species: around 130 K for H2O (on the bright side because volatile frosts tend to create high albedos and prolong residence times) and 90 K for CO2 (on the dark side as a consequence of the prominent presence of this gas on this side, along with the higher sublimation rate of water ice on the dark side). Therefore, these temperatures were taken as initial temperatures to carry out the simulations. Different albedos were also considered for each hemisphere: 0.04 and 0.39, respectively [6,11,21]. In this context, when selecting the initial temperatures on opposite sides of Iapetus, it should be emphasized that the interplay among the atmosphere, surface, and ice creates a strongly interconnected system of flows that involves a positive feedback loop. Consequently, on the bright side, as the ice begins to melt, the exposed ground absorbs solar energy, leading to increased warmth and further ice melting. This, in turn, raises the atmospheric temperature, causing a temperature increase on the bright side and influencing the ice once again. However, on the dark side, this does not occur.
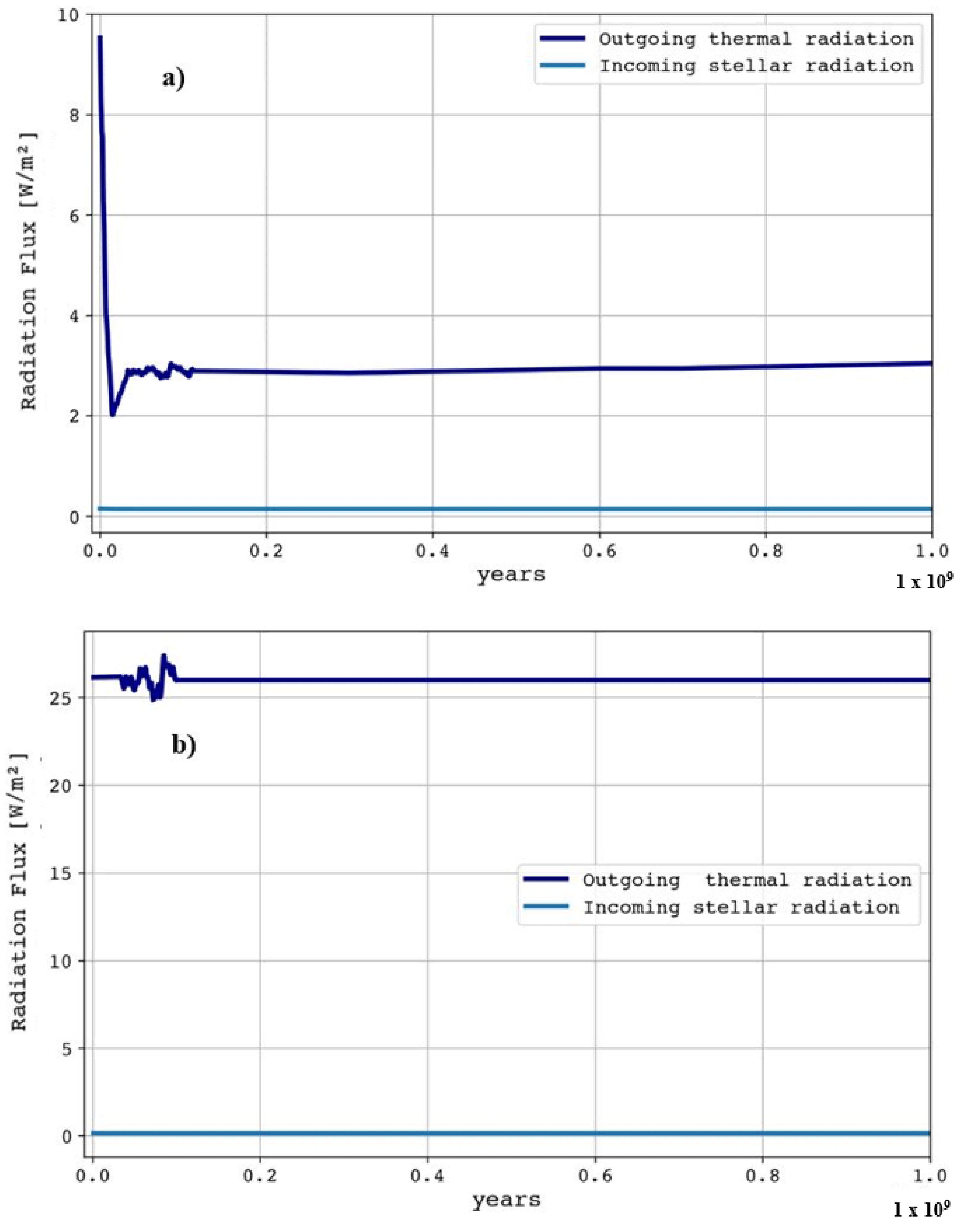
For the energy, we considered the effect of the eccentricity of the orbit of Iapetus around the Sun, the influence of emissivity and heat capacity of Saturn, the contribution of radiation from Saturn, and the internal heating from Iapetus. This study also takes into account the diurnal cycles in both hemispheres. For albedos, we selected the values described above [6]. In order to obtain the energy, we computed the net radiation “Rn” (this is all net wave radiation), the ground heat flux “G”, the sensible heat flux “H” (this is the heat flux due to convection and is responsible for temperature change), and the latent heat flux “L” (this is the flow of energy carried by the water vapor and is responsible for the change of state).
R n = H + L + G
In terms of the surface radiation, the net radiation denotes the equilibrium between the incoming radiation received from the atmosphere and the outgoing radiation emitted from the surface of Iapetus. The total net radiation, encompassing both shortwave net radiation (SW) and longwave net radiation (LW), can be formulated as follows:
R n = S W ↓ − S W ↑ + L W ↓ − L W ↑ = 1 − a l b e d o · S W ↓ + ε · L W ↓ − σ · ε · T s 4
where the albedo (shortwave radiation reflected from the surface) is “SW ↑ ”, “SW ↓ ” is shortwave downward fluxes incident on the surface, “LW ↓ ” and “LW ↑ ” are longwave downward and upward radiation, “ε” is the surface longwave broadband emissivity, “Ts” is the surface temperature, and “σ” is Stefan–Boltzmann’s constant. Regarding the emissivity (0  ≤  ε  ≤  1), it should be noted that a theoretical blackbody has ε = 1, while the emissivity of real objects such as soil and regolith is typically in the range 0.95 ≤ ε ≤ 0.99 for far infrared wavelengths. In this study, ε = 0.95 as a consequence of the surface characteristics of Iapetus. To infer this average emissivity value, it was decided to take into account the geometric characteristics of the surface of both sides of the icy moon, which is why the Digital Elevation Models (DEMs) of each side of Iapetus were obtained. To create each DEM through the free software ImageJ (https://imagej.nih.gov/ij/index.html (accessed on 22 February 2023)), a total of 100 images (with a resolution around of 800 m per pixel) were downloaded from the Planetary Image Locator Tool (PILOT) (https://pilot.wr.usgs.gov/ (accessed on 15 January 2023)), 50 for each side of Iapetus. Subsequently, the composition of each side was carried out with Global Mapper v.24 (https://www.bluemarblegeo.com/global-mapper-download/ (accessed on 25 February 2023)). After this operation, each composition was exported to ImageJ, where a calibration was carried out, to later extract the topographic characteristics of each side of Iapetus from each composition through the “compute topography” plugin. It must be borne in mind that, for the entire process to be correct, it was necessary that the image composition be in grayscale.
On the other hand, since, in sensitive heat flux, “H” the driving potential is a difference in temperature, “H” is proportional to the increase in temperature “ΔT”, and therefore it can be written:
H = ρ · C p · ∆ T r = ρ · C p · T s − T a r
where “ ρ ” is the density, “Cp” is the heat capacity (we used a volumetric heat capacity of 438.1 kJm−3K−1 for fine-grained ice with an assumed porosity of 0.33 at low temperatures), “Ta” is the air temperature, and “r” is the aerodynamic resistance (the aerodynamic resistance for sensible heat is 45 sm−1, while that for latent heat is 4·102 sm−1).
In a similar way to the sensible heat flux, in the latent heat flux “L”, the driving potential is a difference in water vapor pressure, and for this reason, “L” is proportional to the increase in vapor pressure “Δe”, and as consequence it can be written:
L = ρ · C p γ · ∆ e r = ρ · C p γ · ( e s a t · T s ) − e a r
where “ γ = 0.066 kPaC−1” is the psychrometric constant, “esat” is the saturation vapor pressure (note that esat·Ts = es, where “es” is the vapor pressure in surface) and “ea” is the vapor pressure of the air.
Regarding the ground heat flux “G”, it is important to note that its storage is negligible over land (G ~ 0), being inversely proportional to the increase in depth “Δz”. Its equation is presented below:
G = k · ( T s − T g ) ∆ z
where “ k = 0.005 Wm−1K−1” is the thermal conductivity (this value is for fine-grained ice with an assumed porosity of 0.33 at low temperatures) and “Tg” is the ground temperature at certain depth.
Substituting Equations (2)–(5) in Equation (1) and operating the energy model used in this work, the following is obtained:
d Q d t = − 1 − a l b e d o S W ↓ − L W ↓ + ε σ T s 4 + k T s − T g ∆ z − ρ C p T a − T s r − ρ C p γ e a + ( e s a t T s ) r
In another vein, the diffusion coefficient can be estimated from the empirical relation of diffusion of species (H2O vapor, NH3, and CH4) in air proposed by [22], where they simplified the two theoretical equations of the kinetic theory of gases, derived by Stefan and Maxwell [23]. In our calculation, we modified the original empirical relation as:
D a = 2 · 10 − 12 ∗ T 1 + m o l a r   f r a c t i o n
where 2·10−12 is a coefficient that we calculated assuming a column of homogeneous dark material overlaying ice of 1 cm [24], the collision diameter of the species in angstroms, the turbulence effect, the average atmospheric temperature at 110 K, and the collision integral for diffusion (this is a rate of change of the distribution function or, in other words, the change of the electron number per unit time in the phase space volume due to scattering). We used a data mining process, through the application of modified genetic algorithms [25] to calculate the concentration (g/kg) of each species present in the atmosphere. It is necessary to highlight that data mining techniques use multidimensional rotation, translation, reflection, and transformation along with random tuple (ordered immutable set of elements (“atmospheric species”) of the same or different types) shuffling and randomized expansion.
It is important to highlight that data mining is a process of identifying relevant information extracted from large volumes of data, with the aim of discovering patterns and trends, structuring the information obtained in an understandable way for later use by modified genetic algorithms in this work. Basically, the modified genetic algorithms used [25] consist in a parallel procedure that works as follows. The big data set that needs to be categorized is stored within a central storage unit. When the execution begins, individual sections are handled by separate mapping tasks. Each mapping task initially accesses the training dataset and proceeds to train the classifier. Subsequently, the trained classification model is employed to categorize the extensive dataset. The repeated training process for each mapping task should have minimal impact on computational performance since the training dataset is relatively small in comparison to the significant dataset, which is responsible for the majority of the processing time.
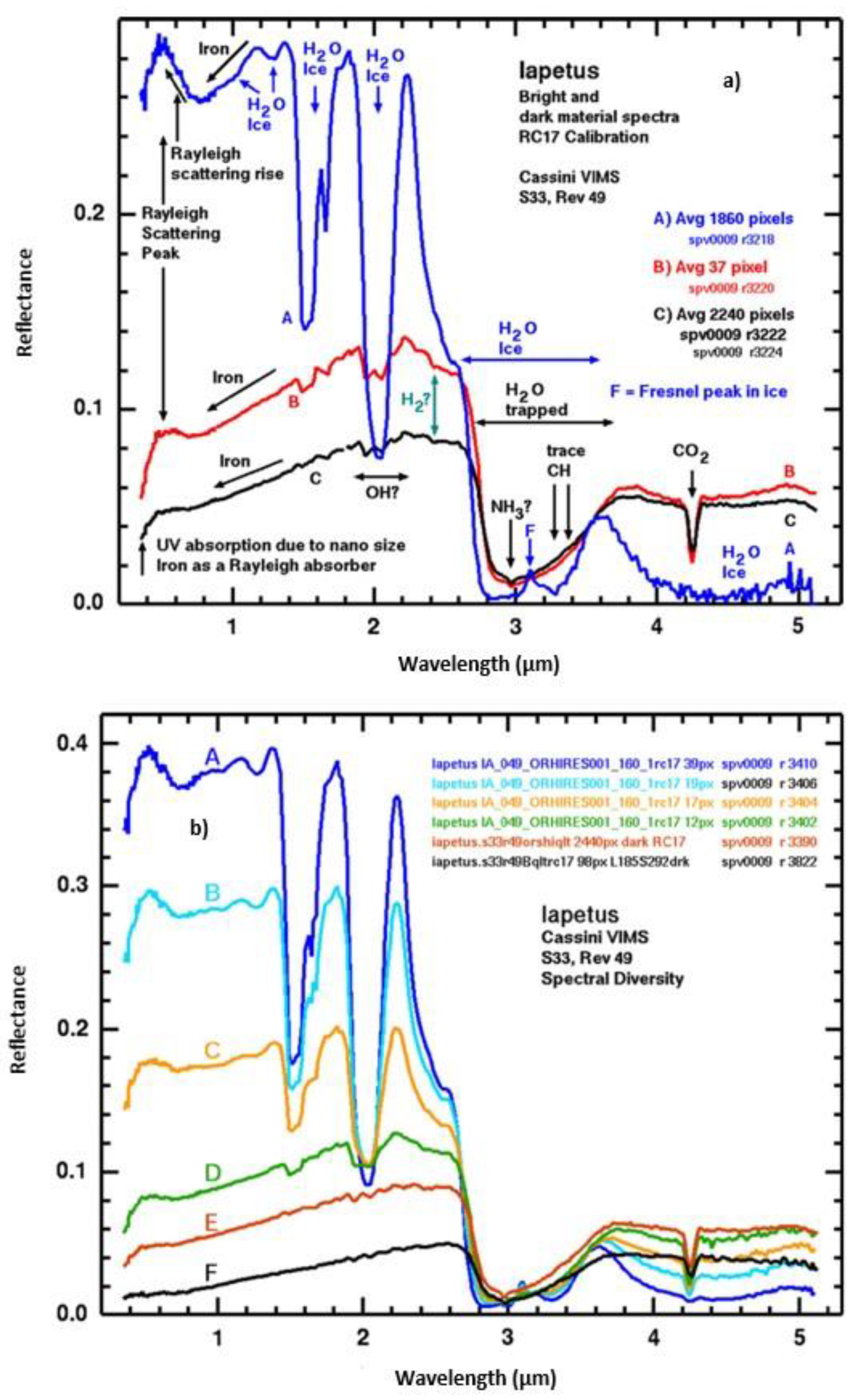
To calculate the concentration (g/kg) of each species present in the atmosphere, we identified the spectral signatures detected in the bands between 0.35 μm to 1.07 μm from the data taken by the VIMS instrument on board of the Cassini mission [26] (Figure 1). Then, we calculate the total number of moles per mole of air for each compound and multiply it by their molecular weight. In this way, we obtain the mass in grams for each species. Equation (7) considers the molar fraction, which is calculated by dividing the number of moles by the total number of moles of all species present in the air. In our case, we measured the sum of the moles of water ice, ammonia, carbon dioxide, and methane. For Iapetus, we found a total weight of one mol of air of around 17.48 g/mol. For this reason, the atmosphere thickness model (which describes how the gas properties of an atmosphere change) was assumed to play a dominant role both in heat distribution and the climate of Iapetus. We also included the concentrations of moles in one mole per air of some compounds detected on the surface of Iapetus, such as CO2, CH, and NH [26], in order to obtain the total molecular weight of these species in the air. The results of these calculations are displayed in Table 1.
In order to construct the atmospheric structure of Iapetus, as well as carry out the simulation of both the surface temperature evolution and the energy, NetLogo (https://ccl.northwestern.edu/netlogo/ (accessed on 1 March 2023)), a programming language and integrated development environment for the realization of agent-based models, was used. Model parameters and constants were: Iapetus’ rotation period (79.33 days), orbital period around Sun (29.4577 days), Iapetus’ inclination (14.7°), Saturn’s semi-major axis (9.54 AU), Saturn’s eccentricity (0.056), emissivity (0.95 mean value for the icy moon), Solar constant at 1 AU (1371 Wm−2), surface thermal diffusivity (6.61·10−9 m2s−1), heliocentric longitude at perihelion (281), finite element thickness (0.4 cm), and temporal scale (1 Gyr).

3. Results

We first describe, in Section 3.1, the procedure carried out to obtain the DEMs of both sides of Iapetus. In Section 3.2, we describe the evolution of the surface temperature. In this model, the evolution of the temperature is treated as an energy transfer model. In Section 3.3, we describe the outgoing thermal radiation and the incoming stellar radiation of the energy for both hemispheres. In this model, we consider both contributions, the one with the fluxes that can be retained on the surface and the ground heat flux that tends to escape into space. Finally, in Section 3.4, we describe the diffusion coefficients found for water ice, ammonia, and methane.

3.1. Obtaining the DEMs

Figure 2 shows the DEMs of both sides of Iapetus.
Topography is one of the most important factors when carrying out simulations aimed at obtaining both the evolution of temperatures and the energy. This is due to the great spatial variability of the topographic features existing on both sides of Iapetus [26].
After obtaining the DEMs, a complex topography is observed on both sides, in which the slope varies between 0 and 30%. This fact is of enormous importance, since, among other things, and according to [26], it affects the amount of radiation received on the surface, and therefore, its emissivity. It is important to note that emissivity is a very important parameter both for calculating the evolution of surface temperature and for obtaining the energy. This is a consequence of the fact that both the slope and the terrain orientation on the surface have fundamental effects on the entry of radiation and on the temperature conditions.

3.2. Surface Temperature Evolution

Figure 3 illustrates the changes in surface temperature for the bright and dark hemispheres of Iapetus, considering that both the atmosphere and surface are in a state of chemical and phase equilibrium., although influenced by their mutual interaction (surface vs atmosphere). The simulation shows that, for both sides of the moon, the temperature slightly and steadily increases from the onset up to the end of the model time (1 Gyr). We initiated the temperature in the dark hemisphere at 90 K. The maximum temperature reached in this hemisphere is 128 K, which is marginally above the seasonal maximum temperature of 130 K conditioned by the apparent surface thermal inertia, as reported by [24], where the effects of the maximum temperature were negligible. Volatile compounds resulting from the segregation of ammonia on the surface, and the fast vaporization of water ice due to the migration to the bright side, could influence the increment of this temperature, as specified by [27,28]. Moreover, the increase in the temperature in our model is enough to represent a significant change in the surface thermal inertia on the dark side of Iapetus [21,29,30,31]. The dark hemisphere absorbs approximately 58% more solar radiation than the bright one [24,27]. Because of this excess absorption existing in the dark hemisphere, it is possible to infer that the thermal segregation of some organic and inorganic compounds on this side could play an important role in the surface alteration process [24]. Hence, on the bright side, as the ice commences melting, the exposed surface absorbs solar energy, leading to heightened warmth and further ice melting. This sequence of events subsequently elevates the atmospheric temperature, inducing a temperature surge on the bright side (with an albedo value of 0.39), thereby affecting the ice once more. Conversely, on the dark side, the contrary occurs: the prevalence of organic materials composed of carbon and nitrogen compounds, resulting in reddish and brownish hues, contributes to an extremely low albedo (value of 0.04). This phenomenon has given rise to thermal separation, which, in conjunction with Iapetus’ slow rotation (approximately 79 days), has led to a global-scale process wherein water ice on the dark side increasingly evaporates towards the bright side. This ongoing process has led to the dark side growing darker and the bright side becoming brighter over time.
For the bright side, the initial temperature was set at 130 K. Figure 3 shows the growth of this temperature up to 147 K, at the end of the simulation. Here, the temperature increases with a lower slope compared to that of the dark side. This could be a consequence of the high albedo of 0.39, which makes its surface reflect more light [29,30,31] or, in other words, absorb less energy from light. The condensed water is highly reflective [32], and it is present on the bright side due to the migration from the dark hemisphere [3]. On the bright side, which is less emissive than the dark one, the diffuse scattering by water ice particles takes place [31]. Analysis of polarization in the bright side performed by [33] shows that this effect is much more pronounced on the surface, making it more sensitive to a diversity of scattering parameters like particle size, shape, surface texture, and reflectance of objects. However, it is still possible to infer the diffusion of methane ice and water ice, since what happened on the surface of Trans Neptunian Objects can be taken as a reference, mainly because both compounds are very abundant in them [34].

3.3. Energy Evolution over Time

Figure 4a shows the outgoing thermal radiation and incoming stellar radiation on the dark hemisphere of Iapetus, which has an albedo of 0.04 [6], over a time window of 1 Gyr. At the very beginning of the simulation, due to changes in frost on the surface, the outgoing thermal radiation drops from roughly 10 W m−2 to 2 W m−2; then it bounces back to 2.8 W m−2 and, after some fluctuations between 2.7 W m−2 and 3.1 W m−2, it stabilizes to this value. On the other hand, Figure 4b displays the outgoing thermal radiation and incoming stellar radiation for the bright side, with an albedo of 0.39 [6]. Here, there were obtained values between 25 W m−2 and 29 W m−2 for the first million years, then it tends to be stable at 26 W m−2 of model time. For both hemispheres, the incoming stellar radiation is around 0.2 W m−2 (although slightly higher in the dark hemisphere), and it does not change over time. There is a notable difference in outgoing thermal radiation between the two hemispheres. The bright side is covered by water ice that, being reflective, is an obstacle for absorbing energy.
Previous analysis of the energy balance on Iapetus [24] shows that the thermal inertia for the dark terrain ranges between 11 J m−2 K−1 s−1/2 and 14.8 J m−2 K−1 s−1/2, while for the bright terrains, it ranges between 15 J m−2 K−1 s−1/2 and 25 J m−2 K−1 s−1/2. These values allow some species, like water ice and carbon dioxide, which are assumed to be present on both sides, to have a slow diffusion rate, through both intermolecular and pore interactions. Our models show, in fact, that an airless surface with a low temperature cannot retain too much energy on surface; nonetheless, the small accumulation observed in the simulations (between 0.2 W m−2 and 2.8 W m−2) could provoke the volatilization of ammonia and methane, allowing for the diffusion in the atmosphere [7,24].

3.4. Diffusion Coefficients of Ammonia, Methane, and Water Ice

All the diffusion coefficients obtained in this work, for organic and inorganic compounds that grow at atmospheric temperatures ranging from 90 K to 130 K, are displayed in Figure 3. In these simulations, ammonia, methane, and water ice are assumed not to be homogeneously distributed on the surface.
The diffusion coefficients obtained for methane vary between 2.7·10−8 cm2 s−1 at 90 K and 5.6·10−8 cm2 s−1 at 130 K. Hence, for the temperatures considered, they are always bigger than the coefficients for the other two compounds. This can be explained due to the increment of temperature found in the dark hemisphere, and possibly because of the high concentration of organic material on the surface [1,35]. In this sense, [36] reports diffusion coefficients for methane of 2.5·10−13 cm2 s−1 at 50 K, values which differ from the ones obtained in this study since those experiments were performed in a range between 30 K and 50 K. We could expect a high diffusion of methane if the atmosphere of Iapetus were similar to the one of Pluto, where the interaction between methane and cosmic rays produces C2H2. This interaction also warms the atmosphere, bringing the methane to high altitudes and generating a greenhouse effect, leading to the generation of a circulatory current [37,38].
We found diffusion coefficients for water ice varying between 9.4·10−10 cm2 s−1 at 90 K and 1.9·10−9 cm2 s−1 at 130 K, values that are lower than the ones for methane. These low diffusion coefficients can be explained by taking into account the transportation of water isotopes through atom diffusion in dry ice in a matrix of interconnected porosity [23]. Experimental studies show that some species can be diffused through water ice backgrounds, like water vapor with coefficients of 0.2·10−5 cm2 s−1 [39], or amorphous ices with coefficients of 4.2·10−4 cm2 s−1 at 130 K [40]. On Iapetus, it could be expected that species like ammonia or methane can be diffused with small coefficients due to the low temperatures on the surface [23,41].
The diffusion coefficients found for ammonia ice vary between 1.8·10−9 cm2 s−1 at 90 K and 3.9·10−9 cm2 s−1 at 130 K. Previous experiments on diffusion of ammonia in hemihydrate environments reveal a diffusion coefficient of 4.3·10−10 cm2 s−1 at 140 K [42]. Other experiments show ammonia adsorption bands in combination with ice particles at 120 K [43]. In this way, ref. [44] also reports peaks of ammonia adsorption in ice at 120 K. On Iapetus, the emergence of regions where ammonia can diffuse, after reaching 113 K, could contribute to the sublimation and volatilization of elements along the surface [7,24].

4. Discussion

From the results obtained, it is evident that our model could offer initial understanding regarding the anticipated arrangement of cloud layers in the atmosphere of Iapetus. This arrangement depends on factors such as surface temperature, surface pressure, and crust composition. These cloud condensation sequences in equilibrium serve as a foundation for future exploration in kinetic models that study cloud formation. However, our paper does not encompass models that consider boundary fluxes at the atmospheric boundaries, atmospheric exhaust rates, or non-equilibrium processes like photochemistry. These aspects extend beyond the scope of our current study.
On the other hand, from the study of the DEMs, it can be inferred that Iapetus’ surface is dominated by impact-related topography. Craters are ubiquitous on Iapetus, including large impact basins. The highest areas have a height of up to 20 km (this value is on the bright side; on the dark side, the highest areas are up to 14 km), while the lowest can reach around −11 km below the surface (on both sides). These height differences are of great importance, since the intensity of incoming solar radiation in the higher areas gives rise to a higher surface temperature. In general, the dark area of Iapetus (South Pole) presents a steeper slope (around 20%) than the bright area (around 15%), the latter being where the highest altitudes are reached (up to 20 km).
There is no doubt that the inclusion of both DEMs in our model has given rise to a more realistic result when it comes to obtaining the simulation of both the evolution of temperatures and the energy over time.
In another vein, the use of modified genetic algorithms [25] has allowed for obtaining the evolution of the different chemical species considered in this work, over time within our model, thus offering a realistic basis to make the simulation of both the evolution of temperatures and the energy over time much more reliable.
Basically, the process to obtain the chemical species evolution over time consisted of calculating a connection matrix, in which each element measures the concentration difference between two species, weighting it by the distance in the solution space that exists between them, such that said concentration difference is more important the closer they are. If the sum of all the elements of the connection matrix in which a species intervenes is positive (positive survival coefficient), that species survives and increases and expands through space. Otherwise, it is extinguished. If it survives, it stays as it is in the next generation, which affects its diffusion. If it becomes extinct, it is replaced by a species (called colonizer) that can be randomly generated or can be derived from the extinct species and any other that survives.
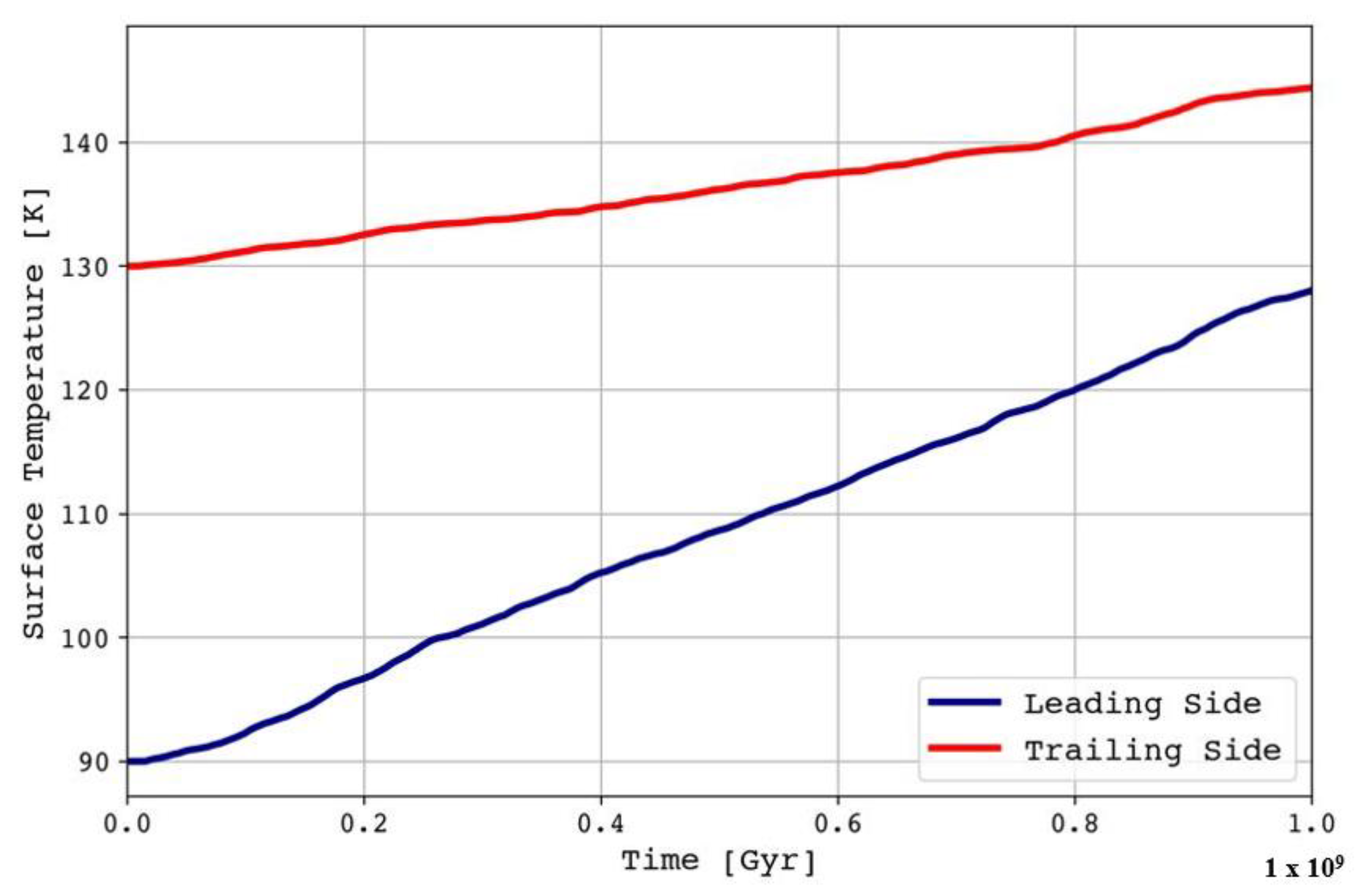
As a result, our study of the diffusion of organic and inorganic material detected in the bright and dark hemispheres of Iapetus relies on understanding how they could evolve in airless bodies, starting with initial surface temperatures of 90 K and 130 K. On a slow rotator like Iapetus, maximum temperatures are dependent on Sun-Saturn distance, albedo, and the available solar heat flux [21,24]. The simulations performed for this work show a steady increase from the initial temperatures, reaching at the end the maximum temperatures for the dark and the bright hemispheres of 130 K and 147 K, respectively. During the 1 Gyr of model time, the increment in these temperatures was not enough to provoke significant changes on the surface, but the growth for the dark hemisphere was bigger, due to its composition, low albedo, and high flux absorption [21,35,45]. Organic compounds in the dark hemisphere are spread all over it, across a layer that probably was formed by internal thermochemistry between methane and HCN compounds, which transformed them into organic material [1]. There had been experiments conducted by [46] that show how methane is thought to be transformed into organic material due to ion bombardment on Phoebe; the same process, mutatis mutandis, could happen on Iapetus.
In that study, it is suggested that the constant ion bombardment on Phoebe converts methane into yellow material, then into brown material, and finally into black material, causing the darkening of the surface [47,48]. The time scale required to do this conversion is 107 years [46]. On the other hand, [2] proposed that the growth of organic material on Iapetus is a uniform process, with an accretion rate of 9·10−10 g cm−2 year−1, where the time required to achieve the carbonization is 2·106 years, lower than the carbonization time of 107 years for Phoebe. One could potentially deduce that the methane diffusion coefficients may lead to a continuous transformation of organic matter into carbonaceous compounds on Iapetus, resulting in a relatively low accretion rate over a period of 1 Gyr.
Generally, low temperatures represent a barrier in the diffusion of species through the atmosphere [23]. Water TDS curves have demonstrated that the presence of ammonia molecules changes the water desorption behavior [44]. At an atomic level, the interaction between ammonia molecules and icy surfaces generates reactions of conversion from ice into ammonia [44]. The occurrence of this phenomenon is due to the replacement of surface-bonded water molecules with ammonia molecules when subjected to heating at 113 K. This explanation may account for the nearly identical ranges of diffusion coefficients observed for both ammonia and water ice.
Experimental results of ammonia diffusion in amorphous ice for temperatures ranging between 35 K to 140 K [40] show diffusion coefficients of 1.1·10−11 cm2 s−1 and 1.9·10−11 cm2 s−1 at 120 K, which are similar to the ones obtained in our simulations. The diffusion timescale in that analysis corresponds to 102 s to 106 s. If on Iapetus we would like to observe how ammonia and water ice could evolve through time, we should expect billions of years for the sublimation of water ice and one billion years for its evaporation at 110 K [49,50].
As ammonia and methane are the predominant non-aqueous volatile substances in the outer Solar System, it is reasonable to anticipate their gradual accumulation over time, likely facilitated by internal geodynamic processes. These substances, along with water ice, could contribute to an increase in their abundance on the surface as they approach the melting point. However, it is important to note that this particular analysis falls outside the scope of the current study. Another possible way to extend this work is through an investigation of the effects of a possible global warming caused by an increment of methane and the concentration of carbon dioxide [51] on the surface of Iapetus.

5. Conclusions

In this manuscript, we have presented the results of our research on the evolution of the surface temperature and the energy of Iapetus over time, with the goal to understand the link between the surface temperature evolution and the distribution of organic and inorganic compounds on the surfaces of airless bodies. We assumed a solid planetary surface that is in a state of chemical and phase equilibrium with the nearby atmospheric layer close to the crust. This equilibrium ensures that the deposition and outgassing rates of all the considered species are in balance. The model employs a step-by-step approach, starting from the bottom layer, to identify the condensates that become thermally stable in each subsequent layer. We then gradually eliminate the elements present in these condensates until chemical and phase equilibrium is once again achieved.
As has been specified, the temperature and the energy are clearly influenced by the land topography, in addition to the concentration of species over time taken into account by our model. For this reason, the use of complex simulation models, such as the one used in this work, are very useful to obtain real results on other moons of the Solar System.
From the results obtained, it can be concluded that the model used in this manuscript has the capability to provide initial insights into the expected configuration of cloud layers in Iapetus’ atmosphere. This configuration is influenced by various factors, including surface temperature, surface pressure, and crust composition. The equilibrium cloud condensation sequences established by our model can serve as a fundamental basis for future investigations in kinetic models aimed at studying cloud formation.
Despite the fact that, in this work, images with a resolution of approximately 800 m have been used, it is evident that the use of much better resolution images will result in a much better simulation of temperatures, as well as other variables of the slopes of the terrain topography, such as emissivity. That is why future missions, either from NASA or from ESA, aimed at obtaining data from the icy moons, must, as a challenge, improve the devices with which the images are taken.

Author Contributions

Conceptualization, K.V.-V., E.R.-J., A.M.-L., J.M.M.-L. and M.C.L.-G.; methodology, K.V.-V., E.R.-J., A.M.-L., J.M.M.-L. and M.C.L.-G.; formal analysis, K.V.-V., E.R.-J., A.M.-L., J.M.M.-L. and M.C.L.-G.; investigation, K.V.-V., E.R.-J., A.M.-L., J.M.M.-L. and M.C.L.-G.; resources, K.V.-V., E.R.-J., A.M.-L., J.M.M.-L. and M.C.L.-G.; writing—original draft preparation, K.V.-V., E.R.-J., A.M.-L., J.M.M.-L. and M.C.L.-G.; writing—review and editing, K.V.-V., E.R.-J., A.M.-L., J.M.M.-L. and M.C.L.-G.; supervision, K.V.-V., E.R.-J., A.M.-L., J.M.M.-L. and M.C.L.-G. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data used to support the findings of this study can be made available by the corresponding author upon request. The images in Figure 3 have been used with permission from the publisher, as shown in the following link: https://s100.copyright.com/CustomerAdmin/PrintableOrder.jsp?appSource=cccAdmin&orderID=501824388.

Acknowledgments

Authors are grateful for the disinterested collaboration of the Knowledge-Based Company RSV3 Remote Sensing S.L. Authors appreciate the contributions of the reviewers aimed at improving this paper.

Conflicts of Interest

The authors declare no conflict of interests.

References

  1. Wilson, P.D.; Sagan, C. Spectrophotometry and Organic Matter on Iapetus. Icarus 1996, 122, 92–106. [Google Scholar] [CrossRef]
  2. Cruikshank, D.P.; Wegryn, E.; Dalle Ore, C.M.; Brown, R.H.; Bibring, J.-P.; Buratti, B.J.; Clark, R.N.; McCord, T.B.; Nicholson, P.D.; Pendleton, Y.J.; et al. Hydrocarbons on Saturn’s Satellites Iapetus and Phoebe. Icarus 2008, 193, 334–343. [Google Scholar] [CrossRef]
  3. Tosi, F.; Turrini, D.; Coradini, A.; Filacchione, G. Probing the Origin of the Dark Material on Iapetus. Mon. Not. R. Astron. Soc. 2010, 403, 1113–1130. [Google Scholar] [CrossRef]
  4. Smith, B.A.; Soderblom, L.; Beebe, R.; Boyce, J.; Briggs, G.; Bunker, A.; Collins, S.A.; Hansen, C.J.; Johnson, T.V.; Mitchell, J.L.; et al. Encounter with Saturn: Voyager 1 Imaging Science Results. Science 1981, 212, 163–191. [Google Scholar] [CrossRef]
  5. Matthews, R.A.J. The Darkening of Iapetus and the Origin of Hyperion. Q. J. R. Astron. Soc. 1992, 33, 253–258. [Google Scholar]
  6. Spencer, J.R.; Denk, T. Formation of Iapetus’ Extreme Albedo Dichotomy by Exogenically Triggered Thermal Ice Migration. Science 2010, 327, 432–435. [Google Scholar] [CrossRef]
  7. Steckloff, J.K.; Goldstein, D.; Trafton, L.; Varghese, P.; Prem, P. Exosphere-Mediated Migration of Volatile Species on Airless Bodies across the Solar System. Icarus 2022, 384, 115092. [Google Scholar] [CrossRef]
  8. Buratti, B.J.; Cruikshank, D.P.; Brown, R.H.; Clark, R.N.; Bauer, J.M.; Jaumann, R.; McCord, T.B.; Simonelli, D.P.; Hibbitts, C.A.; Hansen, G.B.; et al. Cassini Visual and Infrared Mapping Spectrometer Observations of Iapetus: Detection of CO2. Astrophys. J. 2005, 622, L149–L152. [Google Scholar] [CrossRef]
  9. Hendrix, A.R.; Hansen, C.J. Ultraviolet Observations of Phoebe from the Cassini UVIS. Icarus 2008, 193, 323–333. [Google Scholar] [CrossRef]
  10. Hendrix, A.R.; Hansen, C.J. The Albedo Dichotomy of Iapetus Measured at UV Wavelengths. Icarus 2008, 193, 344–351. [Google Scholar] [CrossRef]
  11. Tamayo, D.; Burns, J.A.; Hamilton, D.P.; Hedman, M.M. Finding the Trigger to Iapetus’ Odd Global Albedo Pattern: Dynamics of Dust from Saturn’s Irregular Satellites. Icarus 2011, 215, 260–278. [Google Scholar] [CrossRef]
  12. Mendis, D.A.; Axford, W.I. Revisiting Iapetus Following Recent Cassini Observations. J. Geophys. Res. Space Phys. 2008, 113, 13532. [Google Scholar] [CrossRef]
  13. Lammer, H.; Scherf, M.; Ito, Y.; Mura, A.; Vorburger, A.; Guenther, E.; Wurz, P.; Erkaev, N.V.; Odert, P. The Exosphere as a Boundary: Origin and Evolution of Airless Bodies in the Inner Solar System and Beyond Including Planets with Silicate Atmospheres. Space Sci. Rev. 2022, 218, 15. [Google Scholar] [CrossRef]
  14. Zurbuchen, T.H.; Raines, J.M.; Gloeckler, G.; Krimigis, S.M.; Slavin, J.A.; Koehn, P.L.; Killen, R.M.; Sprague, A.L.; McNutt, R.L.; Solomon, S.C. MESSENGER Observations of the Composition of Mercury’s Ionized Exosphere and Plasma Environment. Science 2008, 321, 90–92. [Google Scholar] [CrossRef]
  15. Mansfield, M.; Kite, E.S.; Hu, R.; Koll, D.D.B.; Malik, M.; Bean, J.L.; Kempton, E.M.-R. Identifying Atmospheres on Rocky Exoplanets through Inferred High Albedo. Astrophys. J. 2019, 886, 141. [Google Scholar] [CrossRef]
  16. Howett, C.J.A.; Spencer, J.R.; Pearl, J.; Segura, M. Thermal Inertia and Bolometric Bond Albedo Values for Mimas, Enceladus, Tethys, Dione, Rhea and Iapetus as Derived from Cassini/CIRS Measurements. Icarus 2010, 206, 573–593. [Google Scholar] [CrossRef]
  17. Squyres, S.W.; Reynolds, R.T.; Summers, A.L.; Shung, F. Accretional Heating of the Satellites of Saturn and Uranus. J. Geophys. Res. 1988, 93, 8779. [Google Scholar] [CrossRef]
  18. Manabe, S.; Möller, F. On the Radiative Equilibrium and Heat Balance of the Atmosphere. Mon. Weather Rev. 1961, 89, 503–532. [Google Scholar] [CrossRef]
  19. Acevedo, P.; Amrouche, C.; Conca, C.; Ghosh, A. Stokes and Navier–Stokes Equations with Navier Boundary Condition. C. R. Math. 2019, 357, 115–119. [Google Scholar] [CrossRef]
  20. Bayat, E.; Egan, R.; Bochkov, D.; Sauret, A.; Gibou, F. A Sharp Numerical Method for the Simulation of Stefan Problems with Convective Effects. J. Comput. Phys. 2022, 471, 111627. [Google Scholar] [CrossRef]
  21. Castillo-Rogez, J.C.; Matson, D.L.; Sotin, C.; Johnson, T.V.; Lunine, J.I.; Thomas, P.C. Iapetus’ Geophysics: Rotation Rate, Shape, and Equatorial Ridge. Icarus 2007, 190, 179–202. [Google Scholar] [CrossRef]
  22. Geiger, G.H.; Poirier, D.R. Transport Phenomena in Metallurgy; Addision-Weley Publishing Company: Reading, MS, USA, 1973; Volume 115, p. 88. [Google Scholar]
  23. Jean-Baptiste, P.; Jouzel, J.; Stievenard, M.; Ciais, P. Experimental Determination of the Diffusion Rate of Deuterated Water Vapor in Ice and Application to the Stable Isotopes Smoothing of Ice Cores. Earth Planet Sci. Lett. 1998, 158, 81–90. [Google Scholar] [CrossRef]
  24. Rivera-Valentin, E.G.; Blackburn, D.G.; Ulrich, R. Revisiting the Thermal Inertia of Iapetus: Clues to the Thickness of the Dark Material. Icarus 2011, 216, 347–358. [Google Scholar] [CrossRef]
  25. Ramírez-Juidías, E.; Pozo-Morales, L.; Galán-Ortiz, L. Procedimiento Para La Obtención de Una Imagen Teledetectada a Partir de Fotografía ES-2537783-B2 (PCT/ES2014/000097), 2015.
  26. Clark, R.N.; Cruikshank, D.P.; Jaumann, R.; Brown, R.H.; Stephan, K.; Dalle Ore, C.M.; Eric Livo, K.; Pearson, N.; Curchin, J.M.; Hoefen, T.M.; et al. The Surface Composition of Iapetus: Mapping Results from Cassini VIMS. Icarus 2012, 218, 831–860. [Google Scholar] [CrossRef]
  27. Blackburn, D.G.; Buratti, B.J.; Ulrich, R. A Bolometric Bond Albedo Map of Iapetus: Observations from Cassini VIMS and ISS and Voyager ISS. Icarus 2011, 212, 329–338. [Google Scholar] [CrossRef]
  28. Jewitt, D.C.; Luu, J. Crystalline Water Ice on the Kuiper Belt Object (50000) Quaoar. Nature 2004, 432, 731–733. [Google Scholar] [CrossRef] [PubMed]
  29. Bonnefoy, L.E.; Le Gall, A.; Lellouch, E.; Leyrat, C.; Janssen, M.; Sultana, R. Rhea’s Subsurface Probed by the Cassini Radiometer: Insights into Its Thermal, Structural, and Compositional Properties. Icarus 2020, 352, 113947. [Google Scholar] [CrossRef]
  30. Bonnefoy, L.E.; Le Gall, A.; Azevedo, M.; Lellouch, E.; Leyrat, C.; Janssen, M.A. Dione’s Leading/Trailing Dichotomy at 2.2 Cm. In Proceedings of the Europlanet Science Congress, Online, 21 September–9 October 2020. EPSC2020-329. [Google Scholar]
  31. Bonnefoy, L.E.; Lestrade, J.-F.; Lellouch, E.; Le Gall, A.; Leyrat, C.; Ponthieu, N.; Ladjelate, B. Probing the Subsurface of the Two Faces of Iapetus. EPJ Web Conf. 2020, 228, 00006. [Google Scholar] [CrossRef]
  32. Zheng, W.; Jewitt, D.; Kaiser, R.I. On the State of Water Ice on Saturn’s Moon Titan and Implications to Icy Bodies in the Outer Solar System. J. Phys. Chem. A 2009, 113, 11174–11181. [Google Scholar] [CrossRef]
  33. Ejeta, C.; Boehnhardt, H.; Bagnulo, S.; Tozzi, G.P. Spectro-Polarimetry of the Bright Side of Saturn’s Moon Iapetus. Astron. Astrophys. 2012, 537, A23. [Google Scholar] [CrossRef]
  34. Alvarez-Candal, A.; Fornasier, S.; Barucci, M.A.; de Bergh, C.; Merlin, F. Visible Spectroscopy of the New ESO Large Program on Trans-Neptunian Objects and Centaurs. Astron. Astrophys. 2008, 487, 741–748. [Google Scholar] [CrossRef]
  35. Hamilton, D.P. Iapetus: 4.5 Billion Years of Contamination by Phoebe Dust. In Proceedings of the AAS/Division for Planetary Sciences Meeting Abstracts# 29; AAS: Washington, DC, USA, 1997. [Google Scholar]
  36. Maté, B.; Cazaux, S.; Satorre, M.Á.; Molpeceres, G.; Ortigoso, J.; Millán, C.; Santonja, C. Diffusion of CH4 in Amorphous Solid Water. Astron. Astrophys. 2020, 643, A163. [Google Scholar] [CrossRef]
  37. Gladstone, G.R.; Young, L.A. New Horizons Observations of the Atmosphere of Pluto. Annu. Rev. Earth Planet Sci. 2019, 47, 119–140. [Google Scholar] [CrossRef]
  38. Elliot, J.L.; Dunham, E.W.; Bosh, A.S.; Slivan, S.M.; Young, L.A.; Wasserman, L.H.; Millis, R.L. Pluto’s Atmosphere. Icarus 1989, 77, 148–170. [Google Scholar] [CrossRef]
  39. Calonne, N.; Geindreau, C.; Flin, F. Macroscopic Modeling for Heat and Water Vapor Transfer in Dry Snow by Homogenization. J. Phys. Chem. B 2014, 118, 13393–13403. [Google Scholar] [CrossRef]
  40. Mispelaer, F.; Theulé, P.; Aouididi, H.; Noble, J.; Duvernay, F.; Danger, G.; Roubin, P.; Morata, O.; Hasegawa, T.; Chiavassa, T. Diffusion Measurements of CO, HNCO, H2CO, and NH3 in Amorphous Water Ice. Astron. Astrophys. 2013, 555, A13. [Google Scholar] [CrossRef]
  41. McQuaid, S.A.; Johnson, B.K.; Gambaro, D.; Falster, R.; Ashwin, M.J.; Tucker, J.H. The Conversion of Isolated Oxygen Atoms to a Fast Diffusing Species in Czochralski Silicon at Low Temperatures. J. Appl. Phys. 1999, 86, 1878–1887. [Google Scholar] [CrossRef]
  42. Livingston, F.E.; Smith, J.A.; George, S.M. General Trends for Bulk Diffusion in Ice and Surface Diffusion on Ice. J. Phys. Chem. A 2002, 106, 6309–6318. [Google Scholar] [CrossRef]
  43. Uras, N.; Buch, V.; Devlin, J.P. Hydrogen Bond Surface Chemistry: Interaction of NH3 with an Ice Particle. J. Phys. Chem. B 2000, 104, 9203–9209. [Google Scholar] [CrossRef]
  44. Takaoka, T.; Inamura, M.; Yanagimachi, S.; Kusunoki, I.; Komeda, T. Ammonia Adsorption on and Diffusion into Thin Ice Films Grown on Pt(111). J. Chem. Phys. 2004, 121, 4331–4338. [Google Scholar] [CrossRef]
  45. Squyres, S.W.; Sagan, C. Albedo Asymmetry of Iapetus. Nature 1983, 303, 782–785. [Google Scholar] [CrossRef]
  46. Strazzulla, G. Organic Material from Phoebe to Iapetus. Icarus 1986, 66, 397–400. [Google Scholar] [CrossRef]
  47. Foti, G.; Calcagno, L.; Sheng, K.L.; Strazzulla, G. Micrometre-Sized Polymer Layers Synthesized by MeV Ions Impinging on Frozen Methane. Nature 1984, 310, 126–128. [Google Scholar] [CrossRef]
  48. Greenberg, J.M. What Are Comets Made of? A Model Based on Interstellar Dust. In Comets; Wilkening, L.L., Ed.; University of Arizona Press: Tucson, AZ, USA, 1982; pp. 131–163. [Google Scholar]
  49. Vasavada, A. Near-Surface Temperatures on Mercury and the Moon and the Stability of Polar Ice Deposits. Icarus 1999, 141, 179–193. [Google Scholar] [CrossRef]
  50. Killen, R.; Benkhoff, J.; Morgan, T. Mercury’s Polar Caps and the Generation of an OH Exosphere☆. Icarus 1997, 125, 195–211. [Google Scholar] [CrossRef]
  51. Palmer, E.E.; Brown, R.H. Production and Detection of Carbon Dioxide on Iapetus. Icarus 2011, 212, 807–818. [Google Scholar] [CrossRef]
Universe 09 00403 g001
Figure 1. The first image (a) displays the spectra of Iapetus, indicating absorption bands that have been identified according to [26]. In contrast, the second image (b) presents a range of representative spectral variations observed in the VIMS data during the Rev 49 fly-by. It is worth noting that the position of the blue peak around 0.5 µm varies depending on the reflectance level and the amount of dark material present. Although the phase angle for the ORSHIRES001 sequence changed from approximately 127 at 13:30 to 12.6 at 14:42 and then to 30 at 17:11, the average phase angle for these spectra is around 20, except for the bottom spectrum. The bottom spectrum was obtained earlier and has been scaled by a factor of 2.0× to compensate for the higher solar incidence and phase angle, allowing for comparison with the spectra at a lower phase angle (https://s100.copyright.com/CustomerAdmin/PrintableOrder.jsp?appSource=cccAdmin&orderID=501824388).
Figure 1. The first image (a) displays the spectra of Iapetus, indicating absorption bands that have been identified according to [26]. In contrast, the second image (b) presents a range of representative spectral variations observed in the VIMS data during the Rev 49 fly-by. It is worth noting that the position of the blue peak around 0.5 µm varies depending on the reflectance level and the amount of dark material present. Although the phase angle for the ORSHIRES001 sequence changed from approximately 127 at 13:30 to 12.6 at 14:42 and then to 30 at 17:11, the average phase angle for these spectra is around 20, except for the bottom spectrum. The bottom spectrum was obtained earlier and has been scaled by a factor of 2.0× to compensate for the higher solar incidence and phase angle, allowing for comparison with the spectra at a lower phase angle (https://s100.copyright.com/CustomerAdmin/PrintableOrder.jsp?appSource=cccAdmin&orderID=501824388).
Universe 09 00403 g001
Universe 09 00403 g002
Figure 2. DEM of both bright and dark sides of Iapetus obtained using ImageJ.
Figure 2. DEM of both bright and dark sides of Iapetus obtained using ImageJ.
Universe 09 00403 g002
Universe 09 00403 g003
Figure 3. Surface temperature evolution for the dark and bright hemispheres of Iapetus. The temperature for the leading side, represented with a blue line, starts at 90 K and evolves until almost 130 K during the model time. The trailing side, depicted with a red line, starts at 130 K and grows to 147 K. There is a substantial increment in temperature for both sides, but the increment in the leading side is greater, possibly due to the low albedo of 0.04 and its composition.
Figure 3. Surface temperature evolution for the dark and bright hemispheres of Iapetus. The temperature for the leading side, represented with a blue line, starts at 90 K and evolves until almost 130 K during the model time. The trailing side, depicted with a red line, starts at 130 K and grows to 147 K. There is a substantial increment in temperature for both sides, but the increment in the leading side is greater, possibly due to the low albedo of 0.04 and its composition.
Universe 09 00403 g003
Universe 09 00403 g004
Figure 4. The outgoing thermal radiation and the incoming stellar radiation are displayed for the dark and bright hemispheres in (a,b) respectively. In the leading hemisphere, the outgoing radiation is constant at 2.8 W m−2, while in the trailing side it remains constant at 26 W m−2. This discrepancy could be a consequence of the different values of their albedos. Low temperatures and high albedo on the bright side do not allow for the retaining of flux radiation in the atmosphere; that is why the outgoing thermal radiation is higher. On both sides, the incoming radiation is weak, with a rough value of 0.2 W m−2.
Figure 4. The outgoing thermal radiation and the incoming stellar radiation are displayed for the dark and bright hemispheres in (a,b) respectively. In the leading hemisphere, the outgoing radiation is constant at 2.8 W m−2, while in the trailing side it remains constant at 26 W m−2. This discrepancy could be a consequence of the different values of their albedos. Low temperatures and high albedo on the bright side do not allow for the retaining of flux radiation in the atmosphere; that is why the outgoing thermal radiation is higher. On both sides, the incoming radiation is weak, with a rough value of 0.2 W m−2.
Universe 09 00403 g004
Table 1. Concentration of species present in the atmosphere of Iapetus. Previous studies assume that the exosphere on Iapetus is mainly composed of H2O [7]. In this study, there were included other species detected in the bands between 0.35 μm and 1.07 μm by the VIMS instrument on board of the Cassini mission. The concentration of species was calculated by applying genetic algorithms [25]. Water ice and ammonia are the main compounds present in the atmosphere.
Table 1. Concentration of species present in the atmosphere of Iapetus. Previous studies assume that the exosphere on Iapetus is mainly composed of H2O [7]. In this study, there were included other species detected in the bands between 0.35 μm and 1.07 μm by the VIMS instrument on board of the Cassini mission. The concentration of species was calculated by applying genetic algorithms [25]. Water ice and ammonia are the main compounds present in the atmosphere.
Atmospheric CompositionConcentration (g/kg)Presence among Other Species (%)Presence in the Air (%)Mass (g)Molar Fraction (mol/g)
Air 100
H2O8.8250.49498.820.49
NH38.3347.68498.330.49
CH40.331.8320.320.02
Total17.4710010017.471
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Villavicencio-Valero, K.; Ramírez-Juidias, E.; Madueño-Luna, A.; Madueño-Luna, J.M.; López-Gordillo, M.C. Influence of the Surface Temperature Evolution over Organic and Inorganic Compounds on Iapetus. Universe 2023, 9, 403. https://doi.org/10.3390/universe9090403

AMA Style

Villavicencio-Valero K, Ramírez-Juidias E, Madueño-Luna A, Madueño-Luna JM, López-Gordillo MC. Influence of the Surface Temperature Evolution over Organic and Inorganic Compounds on Iapetus. Universe. 2023; 9(9):403. https://doi.org/10.3390/universe9090403

Chicago/Turabian Style

Villavicencio-Valero, Katherine, Emilio Ramírez-Juidias, Antonio Madueño-Luna, José Miguel Madueño-Luna, and Miguel Calixto López-Gordillo. 2023. "Influence of the Surface Temperature Evolution over Organic and Inorganic Compounds on Iapetus" Universe 9, no. 9: 403. https://doi.org/10.3390/universe9090403

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop