Synthesis of Elements in Compact Stars in Pycnonuclear Reactions with Carbon Isotopes: Quasibound States vs. States of Zero-Points Vibrations
Abstract
:1. Introduction
2. Method of Quantum Mechanics for Nucleus–Nucleus Scattering with Fusion
3. Analysis
3.1. Potential of Interaction for Nuclei in Lattice Sites
3.2. Space Location of Nuclei in Lattice Sites
3.3. Energy Spectra of Zero-Point Vibrations of Nuclei in Lattice Sites
3.4. Probabilities of Formation of Compound Nuclei in Pycnonuclear Reactions
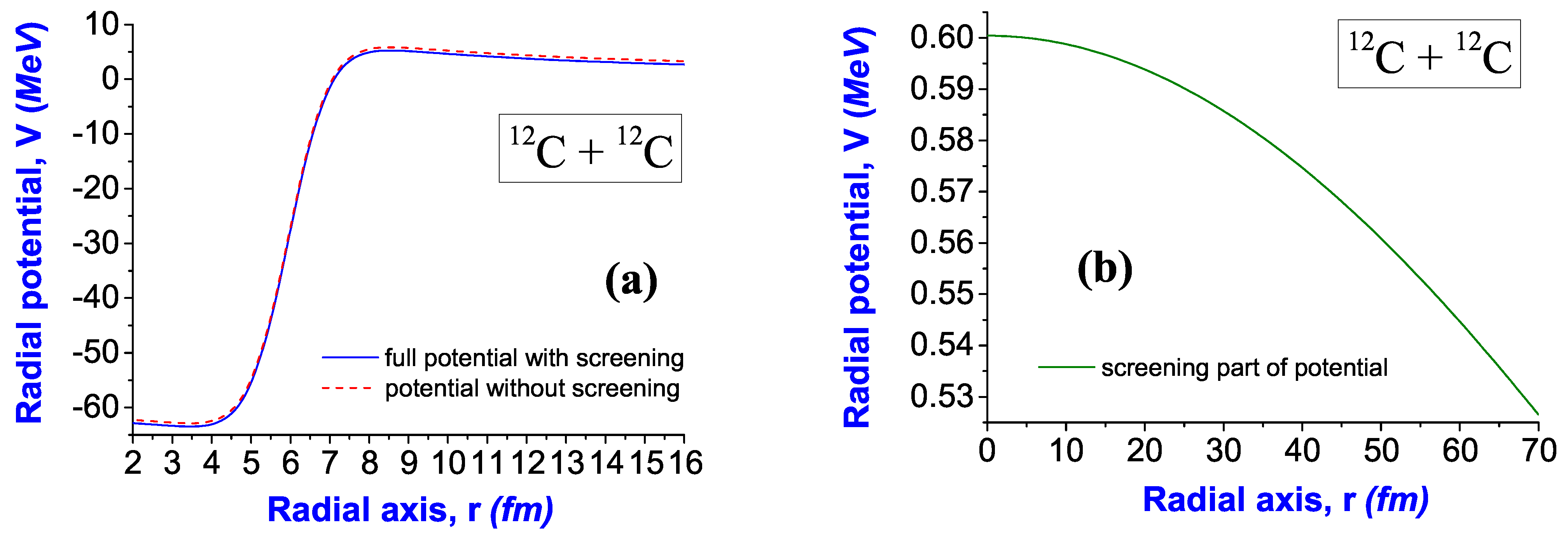
4. Plasma Screening in Nuclear Reactions
5. Influence of Vibration of External Nuclei on Calculation of Quasibound States
6. Conclusions and Perspectives
- In this research, pycnonuclear processes are studied, taking the nuclear part of the potential of interactions between nuclei into account. The requirement of continuity of quantum flux (describing pycnonuclear reactions on the basis of quantum mechanics) gives new states in which the compound nuclear system of 2XMg is formed with the highest probability (see Figure 2). Following the logic in Refs. [13,14,17], we call such states quasibound states in pycnonuclear reactions. Note that these states have not been studied yet by other researchers in the study of the synthesis of elements in stars.
- As shown in Figure 2, the probability of formation of a compound nuclear system in quasibound states is essentially higher than the probability of formation of this system in states of zero-point vibrations studied by Zel’dovich [5] and followers of that idea. The synthesis of more heavy nuclei of Magnesium from isotopes of Carbon is essentially more probable in quasibound states than in states of zero-point vibrations. This leads to the revision (reconsideration) of pictures of the formation of heavy elements in compact stars to use quasibound states as the basis for synthesis. Note the perspective to study in more detail the method in this paper on the basis of experimental measurements in Ref. [25].
- Only the first quasibound energies for 10C + 10C, 12C + 12C, and 24C + 24C (see Table 4) are smaller than the barrier maximums for these nuclear systems (see Table 1). Therefore, at such energies, the compound nuclear systems have barriers that prevent their decays from going through the tunneling phenomenon. At such energies, the compound nuclear systems are the most probable and the most long lived. These systems are transformed into new synthesized isotopes of Magnesium 20Mg, 24Mg, and 48Mg with large probabilities. There is a simple way to estimate the half-lives of these obtained more heavy nuclei using Gamow’s approach or the method of multiple internal reflections for higher precision. Note that other approaches cannot estimate the quasibound energies needed for the prediction of the synthesis of more stable nuclear systems by such a way described above. At the same time, the method of multiple internal reflections calculates such energies with high precision, also providing tests to check calculations. However, the analysis of binding energies for the obtained isotopes of Magnesium shows that only 24Mg will be stable after synthesis.
- For the first time, the influence of plasma screening on quasibound states and states of zero-point vibrations in pycnonuclear processes has been studied. It is found that the energy spectrum of zero-point vibrations is essentially modified after taking plasma screening into account (see Table 5 for the reaction 12C + 12C).
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Salpeter, E.E.; Horn, H.M.V. Nuclear reaction rates at high densities. Astrophys. J. 1969, 155, 183. [Google Scholar]
- Schramm, S.; Koonin, S.E. Pycnonuclear Fusion Rates. Astrophys. J. 1990, 365, 296, Erratum in Astrophys. J. 1991, 377, 343. [Google Scholar] [CrossRef]
- Haensel, P.; Zdunik, J.L. Equation of state and structure of the crust of an accreting neutron star. Astron. Astrophys. 1990, 229, 117, Erratum in Astron. Astrophys. 2003, 404, L33. [Google Scholar]
- Cameron, A.G.W. Pycnonuclear reactions and nova explosions. Astrophys. J. 1959, 130, 916. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B.; Guseynov, O.H. Collapsed stars in binaries. Astrophys. J. 1965, 144, 840. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects; Wiley: Weinheim, Germany, 2004; 645p. [Google Scholar]
- Yakovlev, D.G.; Gasques, L.R.; Beard, M.; Wiescher, M.; Afanasjev, A.V. Fusion reactions in multicomponent dense matter. Phys. Rev. C 2006, 74, 035803. [Google Scholar]
- Beard, M.; Afanasjev, A.V.; Chamon, L.C.; Gasques, L.R.; Wiescher, M.; Yakovlev, D.G. Astrophysical S factors for fusion reactions involving C, O, Ne, and Mg isotopes. At. Data Nucl. Data Tables 2010, 96, 541–566. [Google Scholar]
- Afanasjev, A.V.; Beard, M.; Chugunov, A.I.; Wiescher, M.; Yakovlev, D.G. Large collection of astrophysical S-factors and its compact representation. Phys. Rev. C 2012, 85, 054615. [Google Scholar]
- Kravchuk, P.A.; Yakovlev, D.G. Strong plasma screening in thermonuclear reactions: Electron drop model. Phys. Rev. C 2014, 89, 015802. [Google Scholar]
- Gasques, L.R.; Afanasjev, A.V.; Aguilera, E.F.; Beard, M.; Chamon, L.C.; Ring, P.; Wiescher, M.; Yakovlev, D.G. Nuclear fusion in dense matter: Reaction rate and carbon burning. Phys. Rev. C 2005, 72, 025806. [Google Scholar]
- Maydanyuk, S.P.; Belchikov, S.V. Calculations of penetrability of barriers in the proton decay problem: The fully quantum approach and initial condition of decay. J. Phys. Stud. 2011, 14, 40. [Google Scholar]
- Maydanyuk, S.P.; Zhang, P.-M.; Belchikov, S.V. Quantum design using a multiple internal reflections method in a study of fusion processes in the capture of alpha-particles by nuclei. Nucl. Phys. A 2015, 940, 89–118. [Google Scholar]
- Maydanyuk, S.P.; Zhang, P.-M.; Zou, L.-P. New quasibound states of the compound nucleus in α-particle capture by the nucleus. Phys. Rev. C 2017, 96, 014602. [Google Scholar]
- Eberhard, K.A.; Appel, C.; Bangert, R.; Cleemann, L.; Eberth, J.; Zobel, V. Fusion cross sections for α + 40,44Ca and the problem of anomalous large-angle scattering. Phys. Rev. Lett. 1979, 43, 107–110. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Kvantovaya Mehanika, Kurs Teoreticheskoi Fiziki (Quantum Mechanics, Course of Theoretical Physics); Nauka Publishing: Moscow, Russia, 1989; Pergamon: Oxford, UK, 1982; Volume 3, p. 768. (In Russian) [Google Scholar]
- Maydanyuk, S.P.; Shaulskyi, K.A. Quantum design in study of pycnonuclear reactions in compact stars: Nuclear fusion, new quasibound states and spectroscopy. Eur. Phys. J. 2022, A58, 220. [Google Scholar]
- Chien, L.H.; Khou, D.T.; Cuong, D.C.; Phuc, N.H. Consistent mean-field description of the 12C + 12C optical potential at low energies and the astrophysical S factor. Phys. Rev. C 2018, 98, 064604. [Google Scholar]
- Olkhovsky, V.S.; Maydanyuk, S.P. Method of multiple internal reflections in description of tunneling evolution through barriers. Ukr. Phys. J. 2000, 45, 1262–1269. [Google Scholar]
- Maydanyuk, S.P.; Olkhovsky, V.S.; Zaichenko, A.K. The method of multiple internal reflections in description of tunneling evolution of nonrelativistic particles and photons. J. Phys. Stud. 2002, 6, 1–16. [Google Scholar]
- Hamada, T.; Salpeter, E.E. Models for zero-temperature stars. Astrophys. J. 1961, 134, 683. [Google Scholar]
- Maydanyuk, S.P.; Olkhovsky, V.S.; Mandaglio, G.; Manganaro, M.; Fazio, G.; Giardina, G. Bremsstrahlung emission of high energy accompanying spontaneous of 252Cf. Phys. Rev. C 2010, 82, 014602. [Google Scholar]
- Salpeter, E.E. Electron screening and thermonuclear reactions. Aust. J. Phys. 1954, 7, 373. [Google Scholar] [CrossRef]
- Rosenfeld, Y.; Chabrier, G. Onsager molecules for the Yukawa potentials: Screening potentials and the Jancovici coefficient in strongly coupled electron-screened plasmas. J. Stat. Phys. 1997, 89, 283. [Google Scholar]
- Fang, X.; Tan, W.P.; Beard, M.; deBoer, R.J.; Gilardy, G.; Jung, H.; Liu, Q.; Lyons, S.; Robertson, D.; Setoodehnia, K.; et al. Experimental measurement of 12C + 16O fusion at stellar energies. Phys. Rev. C 2017, 96, 045804. [Google Scholar]
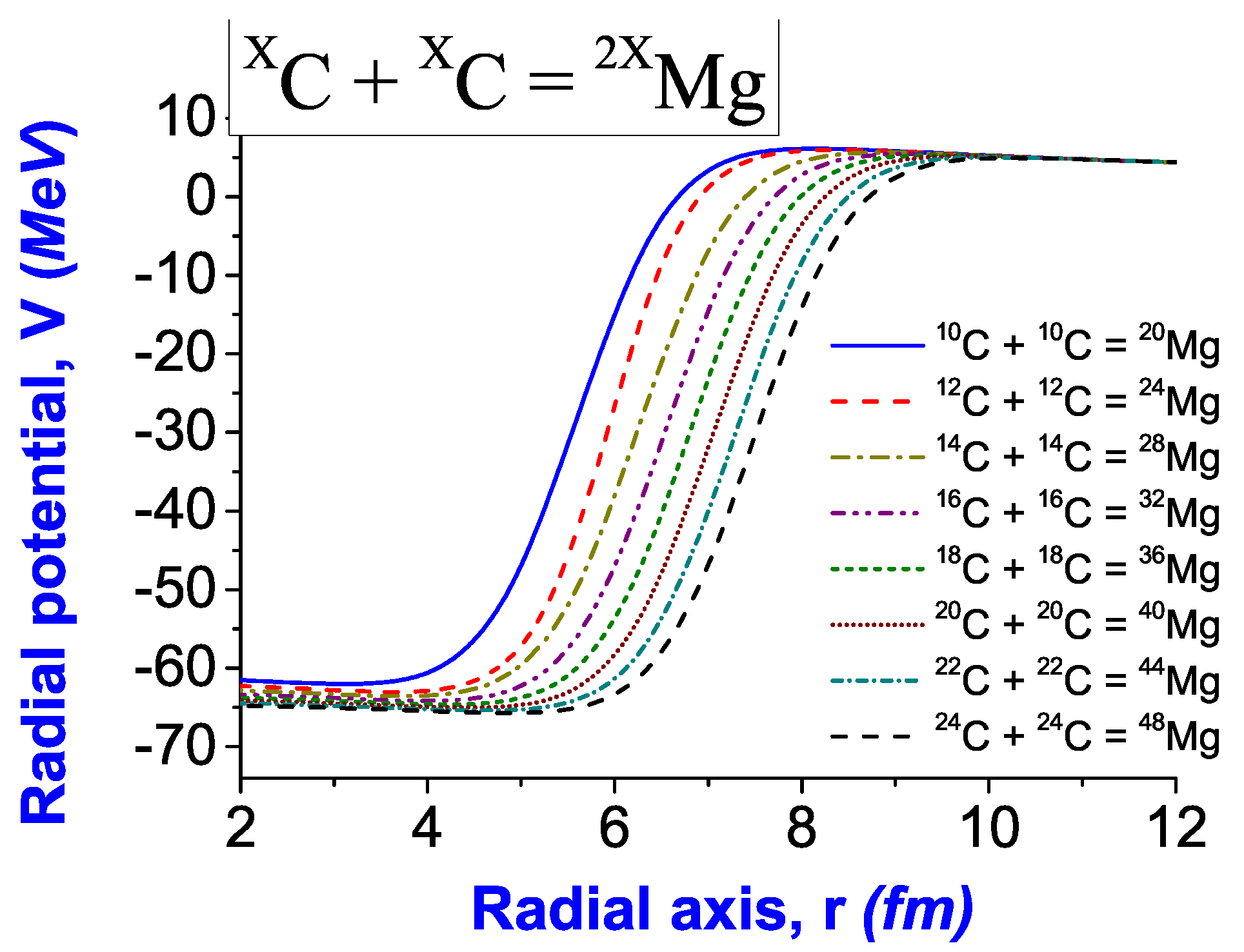

| Reaction XC + XC | , fm | , MeV | , fm | , MeV | , fm | , |
|---|---|---|---|---|---|---|
| 10C + 10C | 3.36 | 7.98 | 87.06 | 3.61702731 | ||
| 12C + 12C | 3.64 | 8.33 | 92.52 | 3.01418941 | ||
| 14C + 14C | 3.92 | 8.68 | 97.40 | 2.58359092 | ||
| 16C + 16C | 4.20 | 8.96 | 101.83 | 2.26064206 | ||
| 18C + 18C | 4.48 | 9.24 | 105.91 | 2.00945961 | ||
| 20C + 20C | 4.62 | 9.52 | 109.69 | 1.80851365 | ||
| 22C + 22C | 4.90 | 9.80 | 113.23 | 1.64410331 | ||
| 24C + 24C | 5.04 | 10.08 | 116.57 | 1.50709470 |
| No. | Energy, , MeV | Energy, , MeV |
|---|---|---|
| 1 | 0.021808061833736 | 0.589680437522993 |
| 2 | 0.065424185501208 | 0.633296561190465 |
| 3 | 0.109040309168680 | 0.676912684857937 |
| 4 | 0.152656432836153 | 0.720528808525410 |
| 5 | 0.196272556503626 | 0.764144932192882 |
| 6 | 0.239888680171098 | 0.807761055860354 |
| 7 | 0.283504803838570 | 0.851377179527827 |
| 8 | 0.327120927506043 | 0.894993303195299 |
| 9 | 0.370737051173515 | 0.938609426862772 |
| 10 | 0.414353174840987 | 0.982225550530244 |
| No. | 10C + 10C | 12C + 12C | 14C + 14C | 16C + 16C |
|---|---|---|---|---|
| 1 | 0.517434869739479 | 0.517434869739479 | 0.517434869739479 | 0.527054108216433 |
| 2 | 0.536673346693387 | 0.536673346693387 | 0.536673346693387 | 0.536072144288577 |
| 3 | 0.546292585170341 | 0.546292585170341 | 0.546292585170341 | 0.545090180360721 |
| 4 | 0.565531062124249 | 0.555911823647295 | 0.555911823647295 | 0.554108216432866 |
| 5 | 0.584769539078156 | 0.575150300601202 | 0.565531062124249 | 0.572144288577154 |
| 6 | 0.613627254509018 | 0.594388777555110 | 0.575150300601202 | 0.581162324649299 |
| 7 | 0.642484969939880 | 0.613627254509018 | 0.594388777555110 | 0.599198396793587 |
| 8 | 0.680961923847695 | 0.642484969939880 | 0.623246492985972 | 0.626252505010020 |
| 9 | 0.738677354709419 | 0.680961923847695 | 0.652104208416834 | 0.653306613226453 |
| 10 | 0.815631262525050 | 0.729058116232465 | 0.690581162324649 | 0.689378757515030 |
| 11 | 0.950300601202405 | 0.806012024048096 | 0.729058116232465 | 0.734468937875752 |
| 12 | 1.27735470941884 | 0.911823647294589 | 0.796392785571142 | 0.797595190380762 |
| 13 | 2.23927855711423 | 1.11382765531062 | 0.892585170340681 | 0.878757515030060 |
| 14 | 3.69178356713427 | 2.76833667334669 | 1.04649298597194 | 1.02304609218437 |
| 15 | — | 4.08617234468938 | 1.64288577154309 | 1.39278557114228 |
| 16 | — | — | 3.04729458917836 | 1.99699398797595 |
| 17 | — | — | 4.28817635270541 | 3.20541082164329 |
| 18 | — | — | — | 4.37775551102204 |
| No. | 18C + 18C | 20C + 20C | 22C + 22C | 24C + 24C |
| 1 | 0.517434869739479 | 0.527054108216433 | 0.536673346693387 | 0.517434869739479 |
| 2 | 0.527054108216433 | 0.546292585170341 | 0.546292585170341 | 0.527054108216433 |
| 3 | 0.536673346693387 | 0.555911823647295 | 0.555911823647295 | 0.536673346693387 |
| 4 | 0.546292585170341 | 0.565531062124249 | 0.565531062124249 | 0.584769539078156 |
| 5 | 0.555911823647295 | 0.584769539078156 | 0.575150300601202 | 0.594388777555110 |
| 6 | 0.565531062124249 | 0.604008016032064 | 0.594388777555110 | 0.613627254509018 |
| 7 | 0.575150300601202 | 0.623246492985972 | 0.604008016032064 | 0.632865731462926 |
| 8 | 0.584769539078156 | 0.642484969939880 | 0.623246492985972 | 0.661723446893788 |
| 10 | 0.613627254509018 | 0.709819639278557 | 0.680961923847695 | 0.729058116232465 |
| 11 | 0.632865731462926 | 0.748296593186373 | 0.719438877755511 | 0.767535070140281 |
| 12 | 0.661723446893788 | 0.806012024048096 | 0.757915831663327 | 0.825250501002004 |
| 13 | 0.738677354709419 | 0.882965931863727 | 0.815631262525050 | 0.911823647294589 |
| 14 | 0.796392785571142 | 1.00801603206413 | 0.892585170340681 | 1.02725450901804 |
| 15 | 0.882965931863727 | 1.27735470941884 | 1.01763527054108 | 1.29659318637275 |
| 16 | 1.00801603206413 | 2.24889779559118 | 1.27735470941884 | 2.20080160320641 |
| 17 | 1.30621242484970 | 3.26853707414830 | 2.24889779559118 | 3.14348697394790 |
| 18 | 2.18156312625251 | 4.29779559118237 | 3.22044088176353 | 4.08617234468938 |
| 19 | 3.26853707414830 | — | 4.21122244488978 | — |
| No. | 10C + 10C | 12C + 12C | 14C + 14C | 16C + 16C | 18C + 18C | 20C + 20C | 22C + 22C | 24C + 24C |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.63471 | 4.88176 | 9.06212 | 7.27054 | 6.37475 | 5.47896 | 5.18036 | 4.58317 |
| 2 | 15.33267 | 11.45090 | 16.52705 | 13.83968 | 11.74950 | 10.55511 | 9.06212 | 8.46493 |
| 3 | 26.38076 | 20.40882 | 25.78357 | 21.90180 | 18.31864 | 16.52705 | 14.43687 | 13.24248 |
| 4 | 40.11623 | 31.45691 | 36.23447 | 30.85972 | 26.38076 | 23.69339 | 20.70741 | 19.21443 |
| 5 | 55.04609 | 43.69940 | 47.58116 | 40.71343 | 34.74148 | 31.15832 | 27.57515 | 25.48497 |
| 6 | 71.76754 | 57.13627 | 59.82365 | 51.46293 | 43.99800 | 39.51904 | 35.04008 | 32.35271 |
| 7 | 89.68337 | 71.76754 | 72.96192 | 62.80962 | 53.85170 | 48.47695 | 42.80361 | 39.81764 |
| 8 | 109.39078 | 87.29459 | 86.99599 | 74.75351 | 64.30261 | 57.73347 | 51.16433 | 47.58116 |
| 9 | 130.29259 | 104.01603 | 101.62725 | 87.59319 | 75.35070 | 67.88577 | 60.12224 | 55.64329 |
| 10 | – | 121.93186 | 117.45291 | 101.03006 | 86.99599 | 78.03808 | 69.37000 | 64.30261 |
| 11 | – | – | 134.17435 | 115.36273 | 98.93988 | 89.08617 | 79.23246 | 72.96192 |
| 12 | – | – | – | 130.29259 | 112.07816 | 100.43287 | 89.08617 | 82.51703 |
| 13 | – | – | – | 146.11824 | 125.21643 | 112.37675 | 99.83567 | 92.07214 |
| 14 | – | – | – | – | 139.25050 | 124.91784 | 110.88377 | 102.22445 |
| 15 | – | – | – | – | – | 137.75752 | 122.23046 | 112.67535 |
| 16 | – | – | – | – | – | – | 134.17435 | 123.42485 |
| 17 | – | – | – | – | – | – | 146.11824 | 134.77154 |
| 18 | – | – | – | – | – | – | – | 146.11824 |
| No. | 12C + 12C with Screening | 12C + 12C without Screening |
|---|---|---|
| 1 | 0.209619238476954 | 0.517434869739479 |
| 2 | 0.267334669338677 | 0.536673346693387 |
| 3 | 0.344288577154309 | 0.546292585170341 |
| 4 | 0.478957915831663 | 0.555911823647295 |
| 5 | 0.786773547094188 | 0.575150300601202 |
| 6 | 2.21042084168337 | 0.594388777555110 |
| 7 | 3.83607214428858 | 0.613627254509018 |
| 8 | 0.642484969939880 | |
| 9 | 0.680961923847695 | |
| 10 | 0.729058116232465 | |
| 11 | 0.806012024048096 | |
| 12 | 0.911823647294589 | |
| 13 | 1.11382765531062 | |
| 14 | 2.76833667334669 | |
| 15 | — | 4.08617234468938 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maydanyuk, S.P.; Wolf, G.; Shaulsky, K.A. Synthesis of Elements in Compact Stars in Pycnonuclear Reactions with Carbon Isotopes: Quasibound States vs. States of Zero-Points Vibrations. Universe 2023, 9, 354. https://doi.org/10.3390/universe9080354
Maydanyuk SP, Wolf G, Shaulsky KA. Synthesis of Elements in Compact Stars in Pycnonuclear Reactions with Carbon Isotopes: Quasibound States vs. States of Zero-Points Vibrations. Universe. 2023; 9(8):354. https://doi.org/10.3390/universe9080354
Chicago/Turabian StyleMaydanyuk, Sergei P., Gyorgy Wolf, and Kostiantyn A. Shaulsky. 2023. "Synthesis of Elements in Compact Stars in Pycnonuclear Reactions with Carbon Isotopes: Quasibound States vs. States of Zero-Points Vibrations" Universe 9, no. 8: 354. https://doi.org/10.3390/universe9080354
APA StyleMaydanyuk, S. P., Wolf, G., & Shaulsky, K. A. (2023). Synthesis of Elements in Compact Stars in Pycnonuclear Reactions with Carbon Isotopes: Quasibound States vs. States of Zero-Points Vibrations. Universe, 9(8), 354. https://doi.org/10.3390/universe9080354









