Charged Particle Pseudorapidity Distributions Measured with the STAR EPD
Abstract
1. Introduction
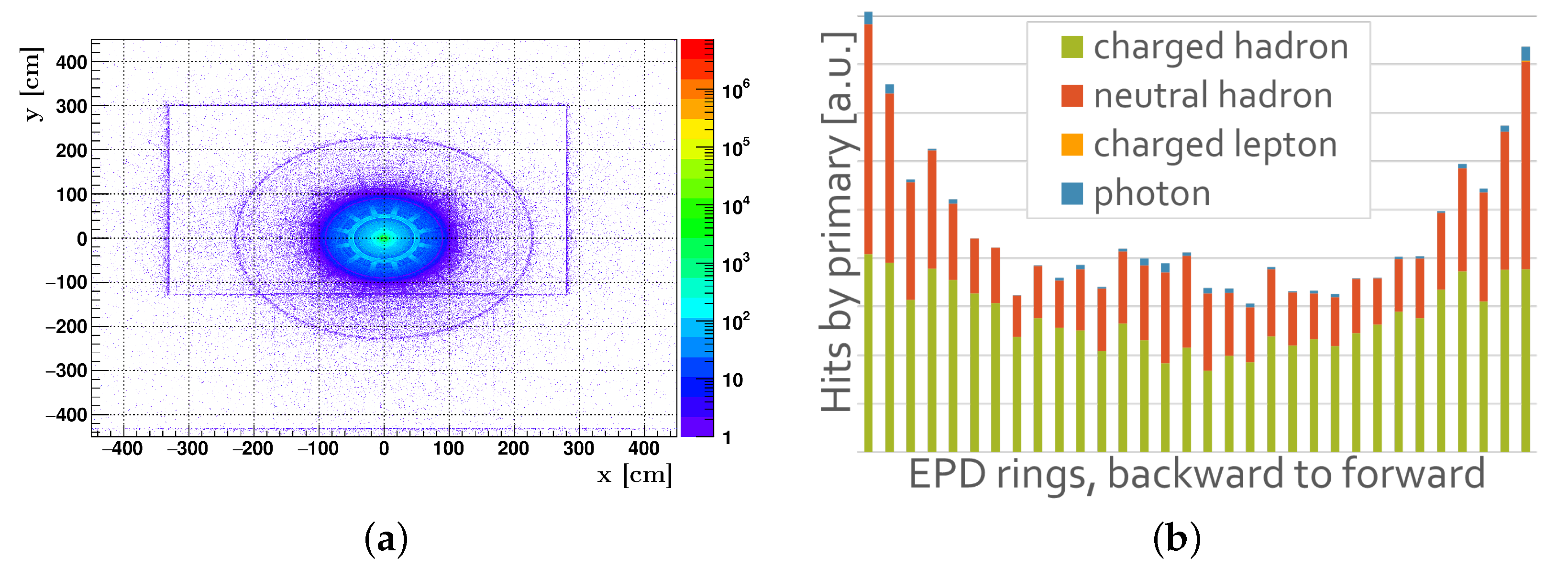
1.1. The EPD
2. Methodology
2.1. Charged Particle Pseudorapidity Measurement with the EPD
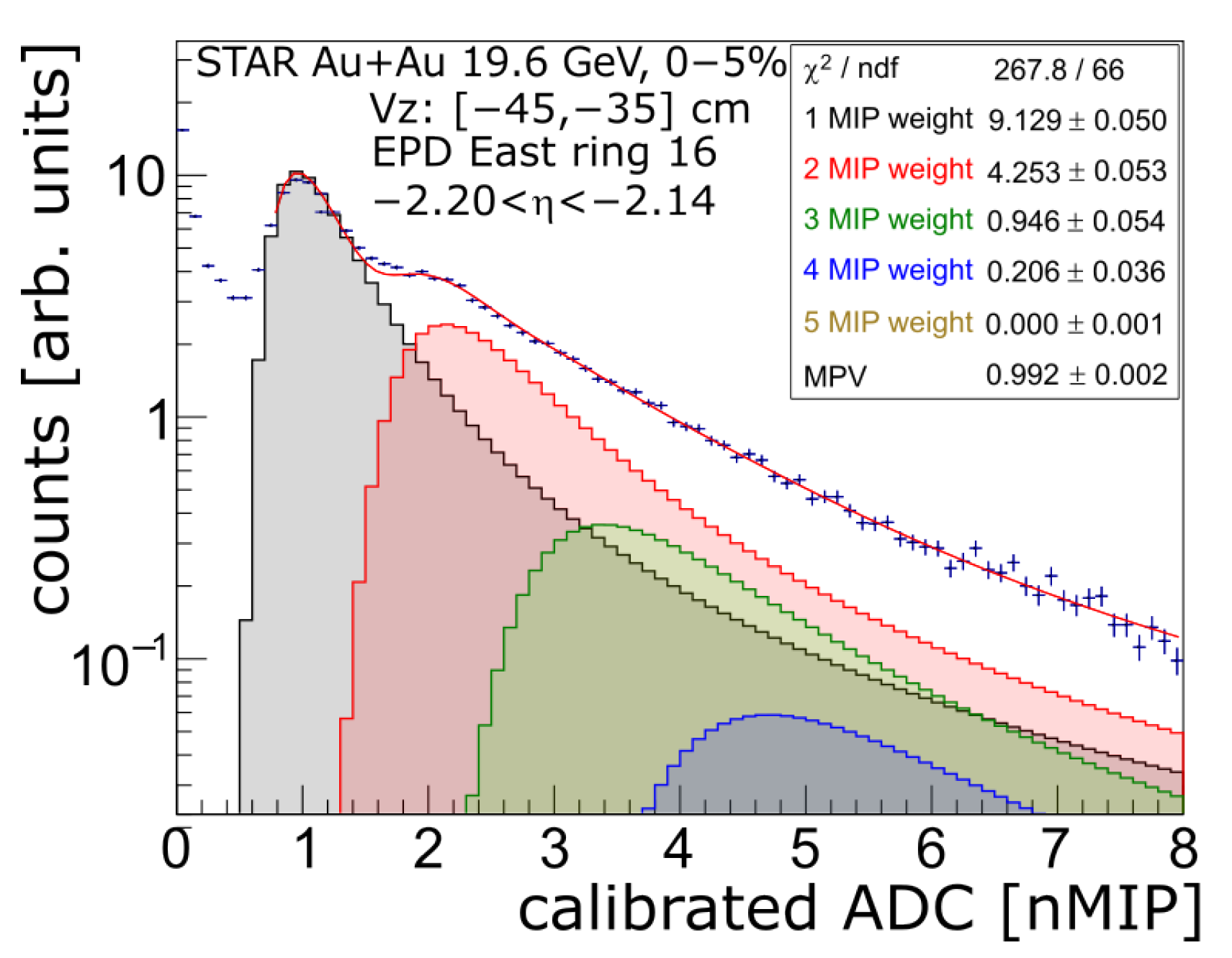
2.2. From Raw EPD Data to Pseudorapidity Distribution []
2.3. Extracting Charged Particle Pseudorapidity Distribution
- Bin-by-bin correction of the already unfolded using the charged particle fraction from MC data;
- Bin-by-bin correction of the raw EPD data via from MC data; then unfolding of the EPD charged particle distribution.7
- Mark neutral particles as background and fill the response matrix as in the second method, except that the hits from neutral primaries are considered as “fake”.
2.4. Consistency Check of the Unfolding Methods
3. Systematic Checks
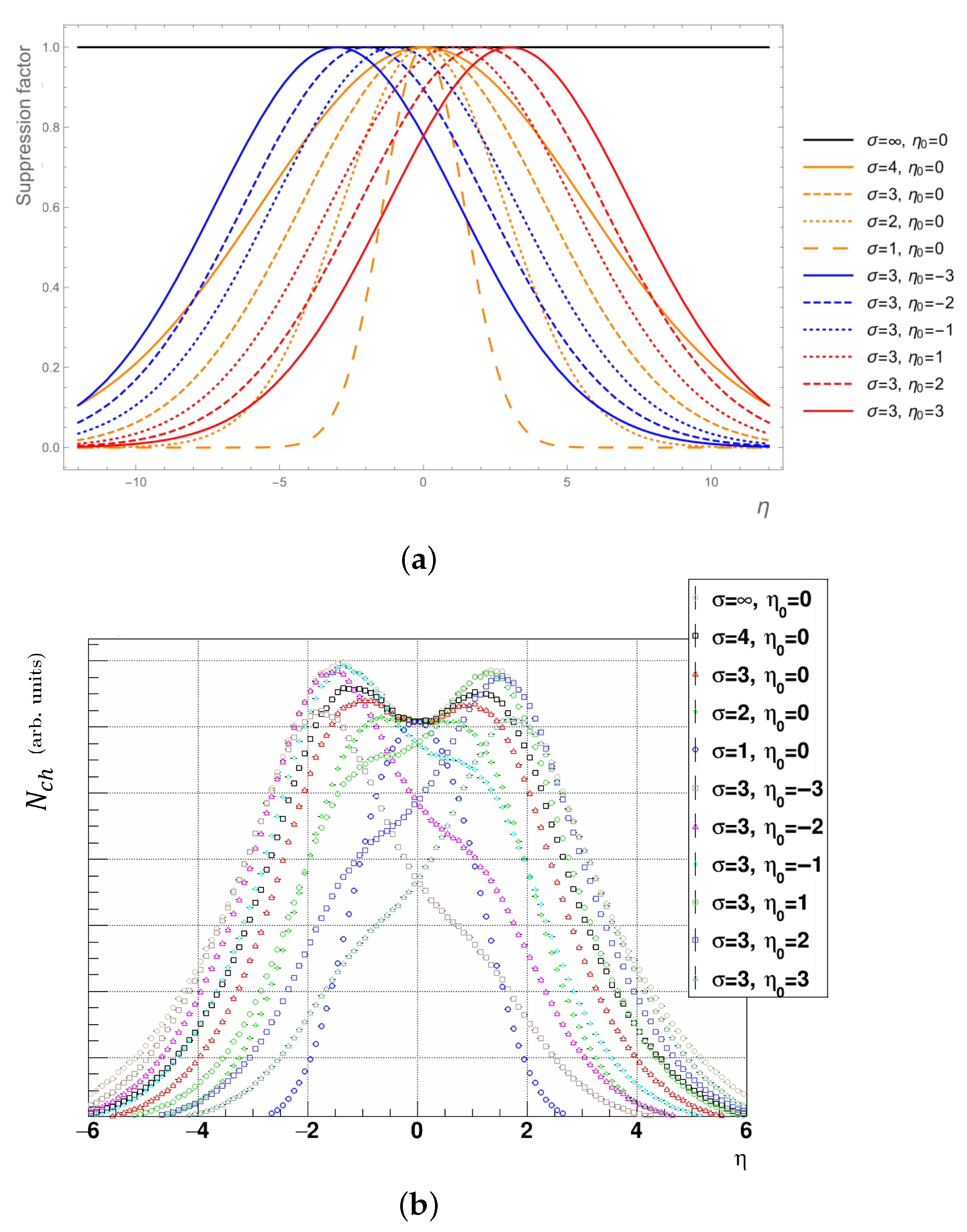
3.1. Dependence on Input MC Distribution
3.1.1. Tightening and Shifting the Input MC
3.1.2. Broadening the Input MC
3.2. Changing the Charged Fraction in the MC Training Dataset
3.3. Changing the Slope of the MC Training Dataset
3.4. Centrality and z-Vertex Selection
3.5. z-Vertex Choice
3.6. Unfolding Method Choice
3.7. EPD Related Uncertainties
4. Results
Comparison with the PHOBOS Results
5. Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| QGP | quark–gluon plasma |
| RHIC | Relativistic Heavy-Ion Collider |
| STAR | Solenoidal Tracker |
| EPD | Event Plane Detector |
| BES | Beam Energy Scan |
| MIP | minimum ionizing particle |
| ADC | analog-to-digital converter |
| MC | Monte Carlo (simulation) |
| QCD | quantum chromodynamics |
| 1 | The EPD is more sensitive to charged particles, as detailed subsequently. |
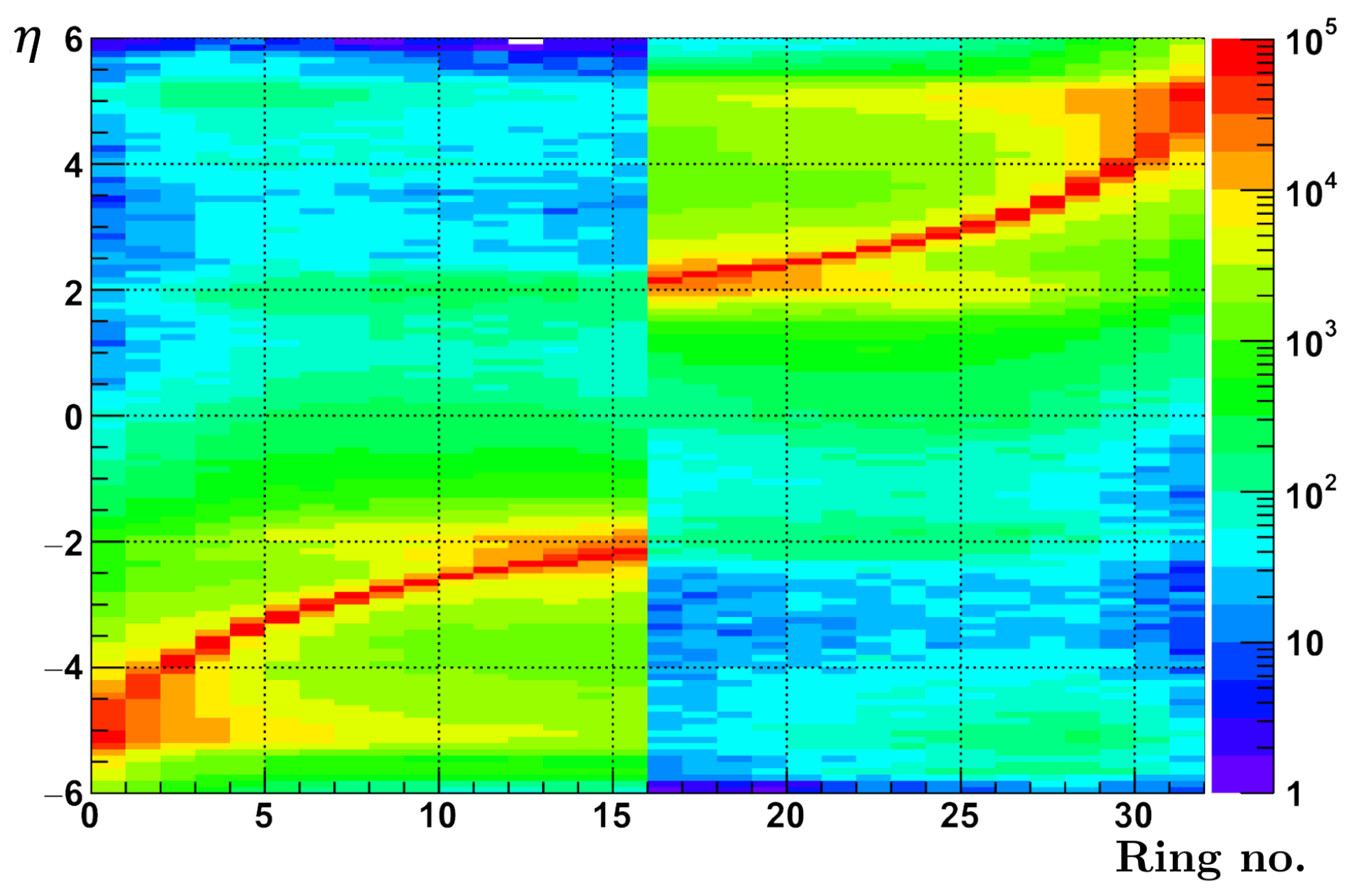
| 2 | The rings are numbered from 1 to 32 in the following manner: the innermost East EPD ring is the #1 which follows outward until #16; then, the #17 continues on the West EPD side’s outermost ring until #32 being the innermost one. |
| 3 | In the ultrarelativistic limit, it approaches to rapidity (in unit system, c being the speed of light): , with E being the energy of the particle. |
| 4 | Fill(, ); naturally, “measured” and “truth” here stand for the training datasets obtained from MC (simulation). |
| 5 | Miss() and Fake(). |
| 6 | Caused by both primary and secondary particles. |
| 7 | In this case, another type of response matrix has to be used that was filled only with the charged particles’ data. |
| 8 | Note that the mentioned unfolding procedure was at this stage still done on the MC EPD ring distribution and thus on the training sample. |
References
- Ackermann, K.; Adams, N.; Adler, C.; Ahammed, Z.; Ahmad, S.; Allgower, C.; Amonett, J.; Amsbaugh, J.; Anderson, B.; Anderson, M.; et al. STAR detector overview. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2003, 499, 624–632, The Relativistic Heavy Ion Collider Project: RHIC and its Detectors. [Google Scholar] [CrossRef]
- Adams, J.; Ewigleben, A.; Garrett, S.; He, W.; Huang, T.; Jacobs, P.; Ju, X.; Lisa, M.; Lomnitz, M.; Pak, R.; et al. The STAR event plane detector. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2020, 968, 163970. [Google Scholar] [CrossRef]
- Tlusty, D. The RHIC beam energy scan phase II: Physics and upgrades. arXiv 2018, arXiv:1810.04767. [Google Scholar]
- Whitten, C.A., Jr. et al. [STAR Collaboration]. The Beam-Beam Counter: A Local Polarimeter at STAR. AIP Conf. Proc. 2008, 980, 390–396. [Google Scholar] [CrossRef]
- Wong, C.-Y. et al. [Oak Ridge National Laboratory]. Introduction to High-Energy Heavy-Ion Collisions; World Scientific: Singapore, 1994; p. 24. [Google Scholar] [CrossRef]
- Wang, X.N.; Gyulassy, M. HIJING 1.0: A Monte Carlo Program for Parton and Particle Production in High Energy Hadronic and Nuclear Collisions. Comp. Phys. Comm. 1995, 83, 307–331. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. Geant4—A simulation toolkit. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2003, 506, 250–303. [Google Scholar] [CrossRef]
- D’Agostini, G. A multidimensional unfolding method based on Bayes’ theorem. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1995, 362, 487–498. [Google Scholar] [CrossRef]
- Alver, B. et al. [PHOBOS Collaboration]. Participant and spectator scaling of spectator fragments in Au + Au and Cu + Cu collisions at = 19.6 and 22.4 GeV. Phys. Rev. C 2016, 94, 024903. [Google Scholar] [CrossRef]
- Adye, T. Unfolding algorithms and tests using RooUnfold. arXiv 2011, arXiv:1105.1160. [Google Scholar] [CrossRef]
- Antcheva, I.; Ballintijn, M.; Bellenot, B.; Biskup, M.; Brun, R.; Buncic, N.; Canal, P.; Casadei, D.; Couet, O.; Fine, V.; et al. ROOT—A C++ framework for petabyte data storage, statistical analysis and visualization. Comput. Phys. Commun. 2011, 182, 1384–1385. [Google Scholar] [CrossRef]
- Back, B.; Baker, M.; Ballintijn, M.; Barton, D.; Becker, B.; Betts, R.; Bickley, A.; Bindel, R.; Budzanowski, A.; Busza, W.; et al. The PHOBOS perspective on discoveries at RHIC. Nucl. Phys. A 2005, 757, 28–101. [Google Scholar]
- Alver, B.; Back, B.B.; Baker, M.D.; Ballintijn, M.; Barton, D.S.; Betts, R.R.; Bickley, A.A.; Bindel, R.; Budzanowski, A.; Busza, W.; et al. Charged-particle multiplicity and pseudorapidity distributions measured with the PHOBOS detector in Au + Au, Cu + Cu, d + Au, and p + p collisions at ultrarelativistic energies. Phys. Rev. C 2011, 83, 024913. [Google Scholar] [CrossRef]
- Odyniec, G. RHIC beam energy scan program—Experimental approach to the QCD phase diagram. J. Phys. G Nucl. Part. Phys. 2010, 37, 094028. [Google Scholar] [CrossRef]
- Csanád, M.; Csörgo, T.; Jiang, Z.F.; Yang, C.B. Initial energy density of = 7 and 8 TeV p + p collisions at the LHC. Universe 2017, 3, 9. [Google Scholar] [CrossRef]
- Ze-Fang, J.; Chun-Bin, Y.; Csanad, M.; Csorgo, T. Accelerating hydrodynamic description of pseudorapidity density and the initial energy density in p + p, Cu + Cu, Au + Au, and Pb + Pb collisions at energies available at the BNL Relativistic Heavy Ion Collider and the CERN Large Hadron Collider. Phys. Rev. C 2018, 97, 064906. [Google Scholar] [CrossRef]
- Adare, A. et al. [PHENIX Collaboration]. Cold-Nuclear-Matter Effects on Heavy-Quark Production at Forward and Backward Rapidity in d + Au Collisions at = 200 GeV. Phys. Rev. Lett. 2014, 112, 252301. [Google Scholar] [CrossRef] [PubMed]

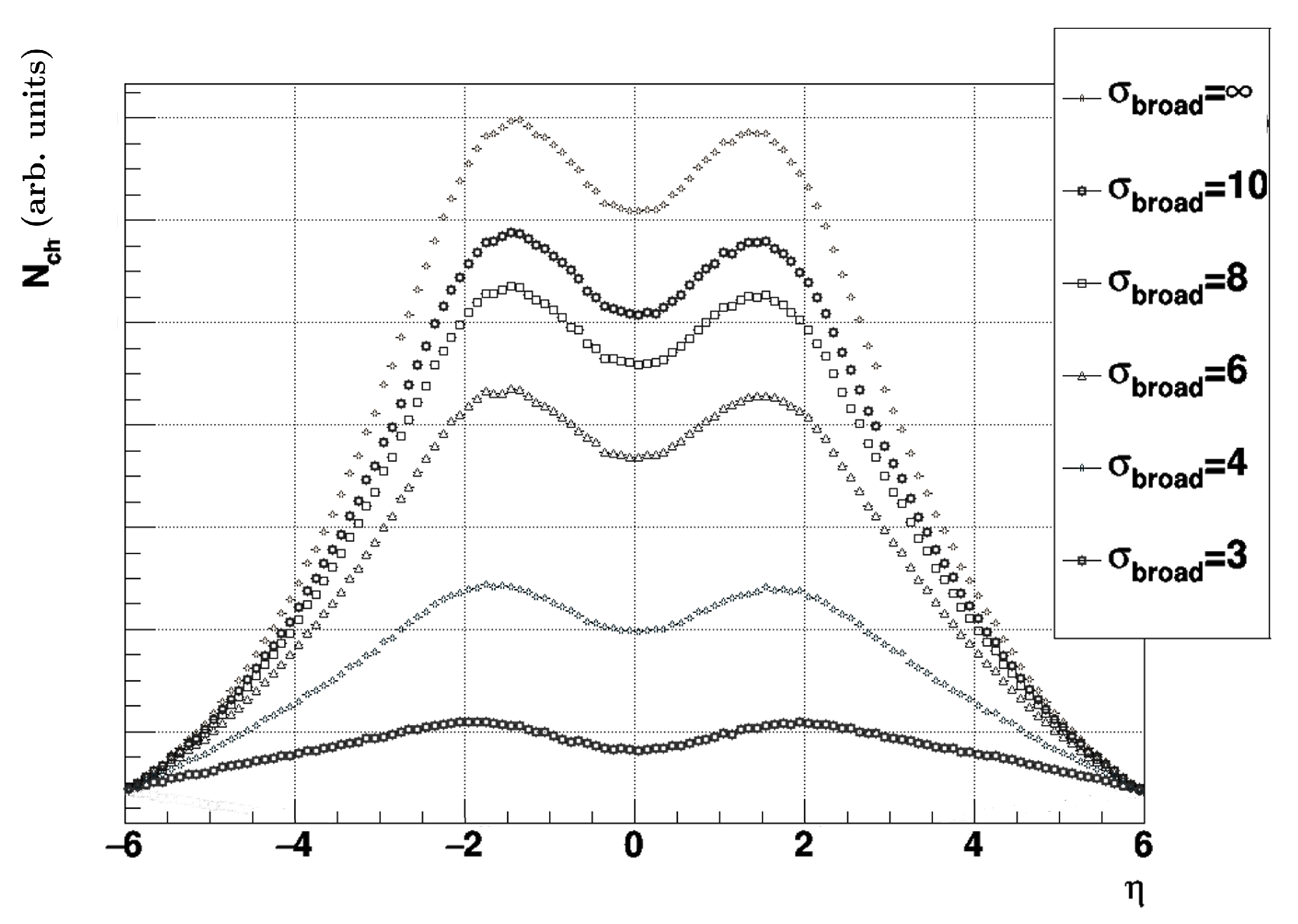

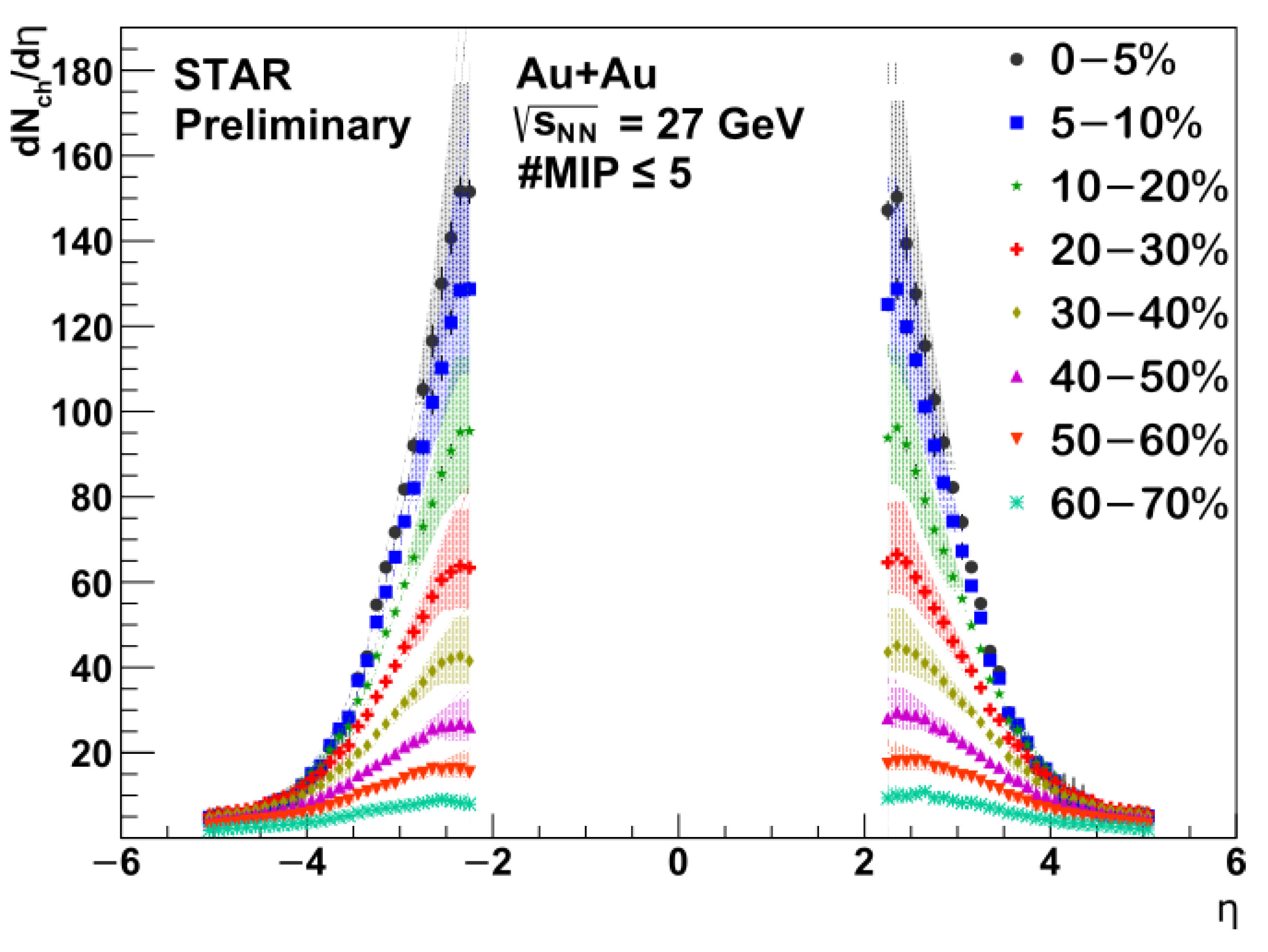

| Source | Systematic Uncertainty |
|---|---|
| MC input tightening, shifting | 6% |
| MC input broadening | 4% |
| Charged fraction in MC | 6% |
| slope change in MC | 1% |
| Centrality selection | 2% |
| z-vertex selection | negligible |
| z-vertex choice | 1% |
| Unfolding method choice | 8% |
| EPD related uncertainties, electronics, efficiency | negligible |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Molnár, M., for the STAR Collaboration. Charged Particle Pseudorapidity Distributions Measured with the STAR EPD. Universe 2023, 9, 335. https://doi.org/10.3390/universe9070335
Molnár M for the STAR Collaboration. Charged Particle Pseudorapidity Distributions Measured with the STAR EPD. Universe. 2023; 9(7):335. https://doi.org/10.3390/universe9070335
Chicago/Turabian StyleMolnár, Mátyás for the STAR Collaboration. 2023. "Charged Particle Pseudorapidity Distributions Measured with the STAR EPD" Universe 9, no. 7: 335. https://doi.org/10.3390/universe9070335
APA StyleMolnár, M., for the STAR Collaboration. (2023). Charged Particle Pseudorapidity Distributions Measured with the STAR EPD. Universe, 9(7), 335. https://doi.org/10.3390/universe9070335






