Dark Matter in Fractional Gravity II: Tests in Galaxy Clusters
Abstract
1. Introduction
2. Theoretical Background and Data Analysis
2.1. DM in Fractional Gravity
2.2. Forward Modeling of the ICM Thermodynamics
2.3. Bayesian Data Analysis
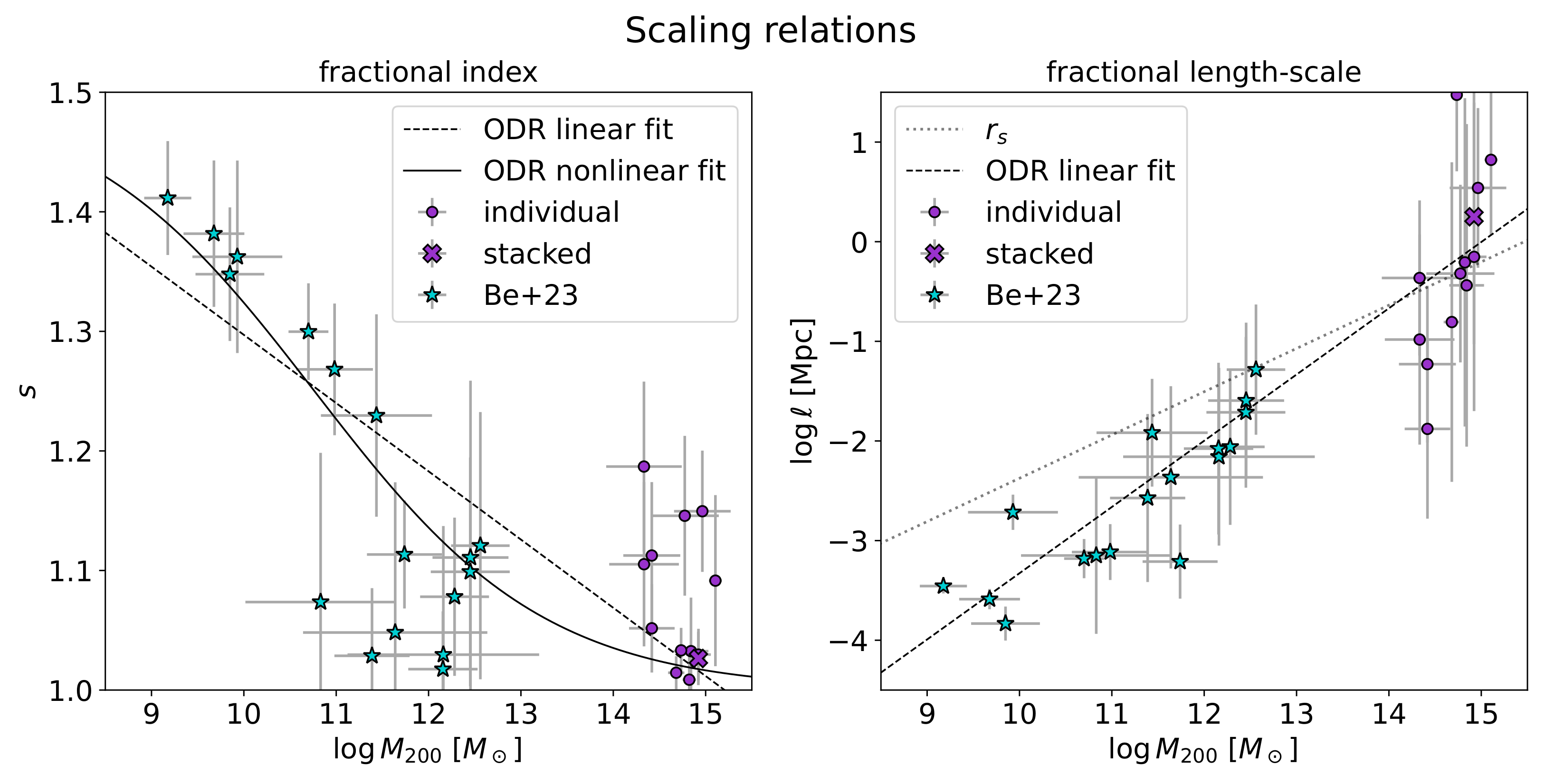
3. Results
4. Summary and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
| 1 | Hereafter, indicates the radius where the average DM density is times the critical density at the redshift z of the cluster. |
| 2 | See https://dominiqueeckert.wixsite.com/xcop/about-x-cop (accessed on 30 May 2023). |
| 3 | Note that in computing the overall gravitational potential , we have neglected the stellar contribution , mainly originated by the brightest central galaxy; this would add a term to the integrand on the right-hand side of Equation (11). For the X-COP cluster sample exploited in this work (stellar profiles were available for 5 out of 12 clusters), the related contribution has been shown by [38] to become relevant only for kpc and as such can barely influence the innermost available data point of the pressure profile; as a consequence, our results were negligibly affected, as we also checked numerically. |
| 4 | Actually, in principle, fractional gravity can also alter somewhat the total depth of the gravitational potential, thus biasing the overall WL mass estimates; however, given that the fractional gravity masses estimated without WL prior and the Newtonian ones are consistent with each other within (see fifth and last column in Table 1), we ignored such a small bias and used the Newtonian WL masses as prior, with their uncertainties, in the fractional gravity analysis. |
References
- Aghanim, M. et al. [Planck Collaboration]. Planck 2018 results. I. Overview and the cosmological legacy of Planck. Astron. Astrophys. 2020, 641, 1. [Google Scholar]
- Sarazin, C.L. X-ray Emission from Clusters of Galaxies; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Cavaliere, A.; Lapi, A. The astrophysics of the Intracluster Plasma. Phys. Rep. 1988, 533, 69–94. [Google Scholar] [CrossRef]
- Sunyaev, R.A.; Zeldovich, I.B. Microwave background radiation as a probe of the contemporary structure and history of the universe. Annu. Rev. Astron. Astrophys. 1980, 18, 537–560. [Google Scholar] [CrossRef]
- Rephaeli, Y. Comptonization of the Cosmic Microwave Background: The Sunyaev-Zeldovich Effect. Annu. Rev. Astron. Astrophys. 1995, 33, 541–580. [Google Scholar] [CrossRef]
- Terukina, A.; Lombriser, L.; Yamamoto, K.; Bacon, D.; Koyama, K.; Nichol, R.C. Testing chameleon gravity with the Coma cluster. J. Cosmol. Astropart. Phys. 2014, 4, 13. [Google Scholar] [CrossRef]
- Wilcox, H.; Bacon, D.; Nichol, R.C.; Rooney, P.J.; Terukina, A.; Romer, A.K.; Koyama, K.; Zhao, G.-B.; Hood, R.; Mann, R.G.; et al. The XMM Cluster Survey: Testing chameleon gravity using the profiles of clusters. Mon. Not. R. Astron. Soc. 2015, 452, 1171–1183. [Google Scholar] [CrossRef]
- Sakstein, J.; Wilcox, H.; Bacon, D.; Koyama, K.; Nichol, R.C. Testing gravity using galaxy clusters: New constraints on beyond Horndeski theories. J. Cosmol. Astropart. Phys. 2016, 7, 19. [Google Scholar] [CrossRef]
- Haridasu, B.S.; Karmakar, P.; De Petris, M.; Cardone, V.F.; Maoli, R. Testing generalized scalar-tensor theories of gravity with clusters of galaxies. Phys. Rev. D 2023, 107, 124059. [Google Scholar] [CrossRef]
- Harikumar, S.; Biesiada, M. Moffat’s modified gravity tested on X-COP galaxy clusters. Eur. Phys. J. C 2022, 82, 241. [Google Scholar] [CrossRef]
- Boumechta, Y.; Haridasu, B.S.; Pizzuti, L.; Butt, M.A.; Baccigalupi, C.; Lapi, A. Constraining Chameleon screening using galaxy cluster dynamics. arXiv 2023, arXiv:2303.02074. [Google Scholar]
- Gandolfi, G.; Haridasu, B.S.; Liberati, S.; Lapi, A. Looking for Traces of Non-minimally Coupled Dark Matter in the X-COP Galaxy Clusters Sample. Astrophys. J. 2023, in press. [Google Scholar]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified gravity and cosmology. Phys. Rep. 2012, 513, 1–189. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified gravity theories on a nutshell: Inflation, bounce and late-time evolution. Phys. Rep. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Saridakis, E.N.; Lazkoz, R.; Salzano, V.; Moniz, P.V.; Capozziello, S.; Beltran, J.J.; De Laurentis, M.; Olmo, G.J. Modified Gravity and Cosmology: An Update by the CANTATA Network. arXiv 2021, arXiv:2105.12582. [Google Scholar]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 2017, 270, 365–370. [Google Scholar] [CrossRef]
- Famaey, B.; McGaugh, S.S. Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions. Living Rev. Relat. 2012, 15, 10. [Google Scholar] [CrossRef]
- Verlinde, E.P. Emergent Gravity and the Dark Universe. Sci. Post. Phys. 2017, 2, 16. [Google Scholar] [CrossRef]
- Yoon, Y.; Park, J.-C.; Hwang, H.S. Understanding galaxy rotation curves with Verlinde’s emergent gravity. Class. Quant. Gravity 2023, 40, 02LT01. [Google Scholar] [CrossRef]
- Gandolfi, G.; Lapi, A.; Liberati, S. Self-gravitating Equilibria of Non-minimally Coupled Dark Matter Halos. Astrophys. J. 2021, 910, 76. [Google Scholar] [CrossRef]
- Gandolfi, G.; Lapi, A.; Liberati, S. Empirical Evidence of Nonminimally Coupled Dark Matter in the Dynamics of Local Spiral Galaxies? Astrophys. J. 2022, 929, 48. [Google Scholar] [CrossRef]
- de Blok, W.J.G.; McGaugh, S.S. Testing Modified Newtonian Dynamics with Low Surface Brightness Galaxies: Rotation Curve FITS. Astrophys. J. 1998, 508, 132. [Google Scholar] [CrossRef]
- Sanders, R.H.; McGaugh, S.S. Modified Newtonian Dynamics as an Alternative to Dark Matter. Annu. Rev. Astron. Astrophys. 2002, 40, 263–317. [Google Scholar] [CrossRef]
- Clowe, D.; Bradac, M.; Gonzalez, A.H.; Markevitch, M.; Randall, S.W.; Jones, C.; Zaritsky, D. A Direct Empirical Proof of the Existence of Dark Matter. Astrophys. J. 1996, 648, L109. [Google Scholar] [CrossRef]
- Angus, G.W.; Famaey, B.; Zhao, H.S. Can MOND take a bullet? Analytical comparisons of three versions of MOND beyond spherical symmetry. Mon. Not. R. Astron. Soc. 2006, 371, 138–146. [Google Scholar] [CrossRef]
- Calcagni, G.; Varieschi, G.U. Gravitational potential and galaxy rotation curves in multi-fractional spacetimes. J. High Energy Phys. 2022, 8, 24. [Google Scholar] [CrossRef]
- Calcagni, G. Multi-scale gravity and cosmology. J. Cosmol. Astropart. Phys. 2013, 12, 41. [Google Scholar] [CrossRef]
- Varieschi, G.U. Newtonian Fractional-Dimension Gravity and MOND. Found. Phys. 2020, 50, 1608–1644. [Google Scholar] [CrossRef]
- Varieschi, G.U. Newtonian fractional-dimension gravity and rotationally supported galaxies. Mon. Not. R. Astron. Soc. 2021, 503, 1915–1931. [Google Scholar] [CrossRef]
- Giusti, A. MOND-like fractional Laplacian theory. Phys. Rev. D 2020, 101, 124029. [Google Scholar] [CrossRef]
- Giusti, A.; Garrappa, R.; Vachon, G. On the Kuzmin model in fractional Newtonian gravity. Eur. Phys. J. Plus 2020, 135, 798. [Google Scholar] [CrossRef]
- Garcia-Aspeitia, M.A.; Fernandez-Anaya, G.; Hernandez-Almada, A.; Leon, G.; Magana, J. Cosmology under the fractional calculus approach. Mon. Not. R. Astron. Soc. 2022, 517, 4813–4826. [Google Scholar] [CrossRef]
- Borjon-Espejel, S.; Escalante-Martinez, J.E.; Padilla-Longoria, P. Newtonian gravity and MOND: A fractional Fourier approach. Indian J. Phys. 2022, 96, 3405–3411. [Google Scholar] [CrossRef]
- Benetti, F.; Lapi, A.; Gandolfi, G.; Salucci, P.; Danese, L. Dark Matter in Fractional Gravity I: Astrophysical Tests on Galactic Scales. arXiv 2023, arXiv:2303.15767. [Google Scholar]
- Eckert, D.; Ettori, S.; Pointecouteau, E.; Molendi, S.; Paltani, S.; Tchernin, C. The XMM cluster outskirts project (X-COP). Astron. Nachr. 2017, 338, 293–298. [Google Scholar] [CrossRef]
- Ettori, S.; Ghirardini, V.; Eckert, D.; Pointecouteau, E.; Gastaldello, F.; Sereno, M.; Gaspari, M.; Ghizzardi, S.; Roncarelli, M.; Rossetti, M. Hydrostatic mass profiles in X-COP galaxy clusters. Astron. Astrophys. 2019, 621, 39. [Google Scholar] [CrossRef]
- Ghirardini, V.; Eckert, D.; Ettori, S.; Pointecouteau, E.; Molendi, S.; Gaspari, M.; Rossetti, M.; De Grandi, S.; Roncarelli, M.; Bourdin, H.; et al. Universal thermodynamic properties of the intracluster medium over two decades in radius in the X-COP sample. Astron. Astrophys. 2022, 621, 41. [Google Scholar] [CrossRef]
- Eckert, D.; Ettori, S.; Pointecouteau, E.; van der Burg, R.F.J.; Loubser, S.I. The gravitational field of X-COP galaxy clusters. Astron. Astrophys. 2022, 662, 123. [Google Scholar] [CrossRef]
- Aghanim, M. et al. [Planck Collaboration]. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A Universal Density Profile from Hierarchical Clustering. Astrophys. J. 1997, 490, 493. [Google Scholar] [CrossRef]
- Vikhlinin, A.; Kravtsov, A.; Forman, W.; Jones, C.; Markevitch, M.; Murray, S.S.; Van Speybroeck, L. Chandra Sample of Nearby Relaxed Galaxy Clusters: Mass, Gas Fraction, and Mass-Temperature Relation. Astrophys. J. 2006, 640, 691. [Google Scholar] [CrossRef]
- Biffi, V.; Borgani, S.; Murante, G.; Rasia, E.; Planelles, S.; Granato, G.L.; Ragone-Figueroa, C.; Beck, A.M.; Gaspari, M.; Dolag, K. On the Nature of Hydrostatic Equilibrium in Galaxy Clusters. Astrophys. J. 2016, 827, 112. [Google Scholar] [CrossRef]
- Ansarifard, S.; Rasia, E.; Biffi, V.; Borgani, S.; Cui, W.; De Petris, M.; Dolag, K.; Ettori, S.; Movahed, S.M.S.; Murante, G.; et al. The Three Hundred Project: Correcting for the hydrostatic-equilibrium mass bias in X-ray and SZ surveys. Astron. Astrophys. 2020, 634, 113. [Google Scholar] [CrossRef]
- Pizzuti, L.; Sartoris, B.; Borgani, S.; Biviano, A. Calibration of systematics in constraining modified gravity models with galaxy cluster mass profiles. J. Cosmol. Astropart. Phys. 2020, 4, 24. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 2013, 125, 306. [Google Scholar] [CrossRef]
- Herbonnet, R.; Sifon, C.; Hoekstra, H.; Bahe, Y.; van der Burg, R.F.J.; Melin, J.-B.; von der Linden, A.; Sand, D.; Kay, S.; Barnes, D. CCCP and MENeaCS: (Updated) weak-lensing masses for 100 galaxy clusters. Mon. Not. R. Astron. Soc. 2020, 497, 4684–4703. [Google Scholar] [CrossRef]
- Dutton, A.A.; Maccio, A.V. Cold dark matter haloes in the Planck era: Evolution of structural parameters for Einasto and NFW profiles. Mon. Not. R. Astron. Soc. 2014, 441, 3359–3374. [Google Scholar] [CrossRef]
- Eckert, D.; Ghirardini, V.; Ettori, S.; Rasia, E.; Biffi, V.; Pointecouteau, E.; Rossetti, M.; Molendi, S.; Vazza, F.; Gastaldello, F.; et al. Non-thermal pressure support in X-COP galaxy clusters. Astron. Astrophys. 2019, 621, 40. [Google Scholar] [CrossRef]


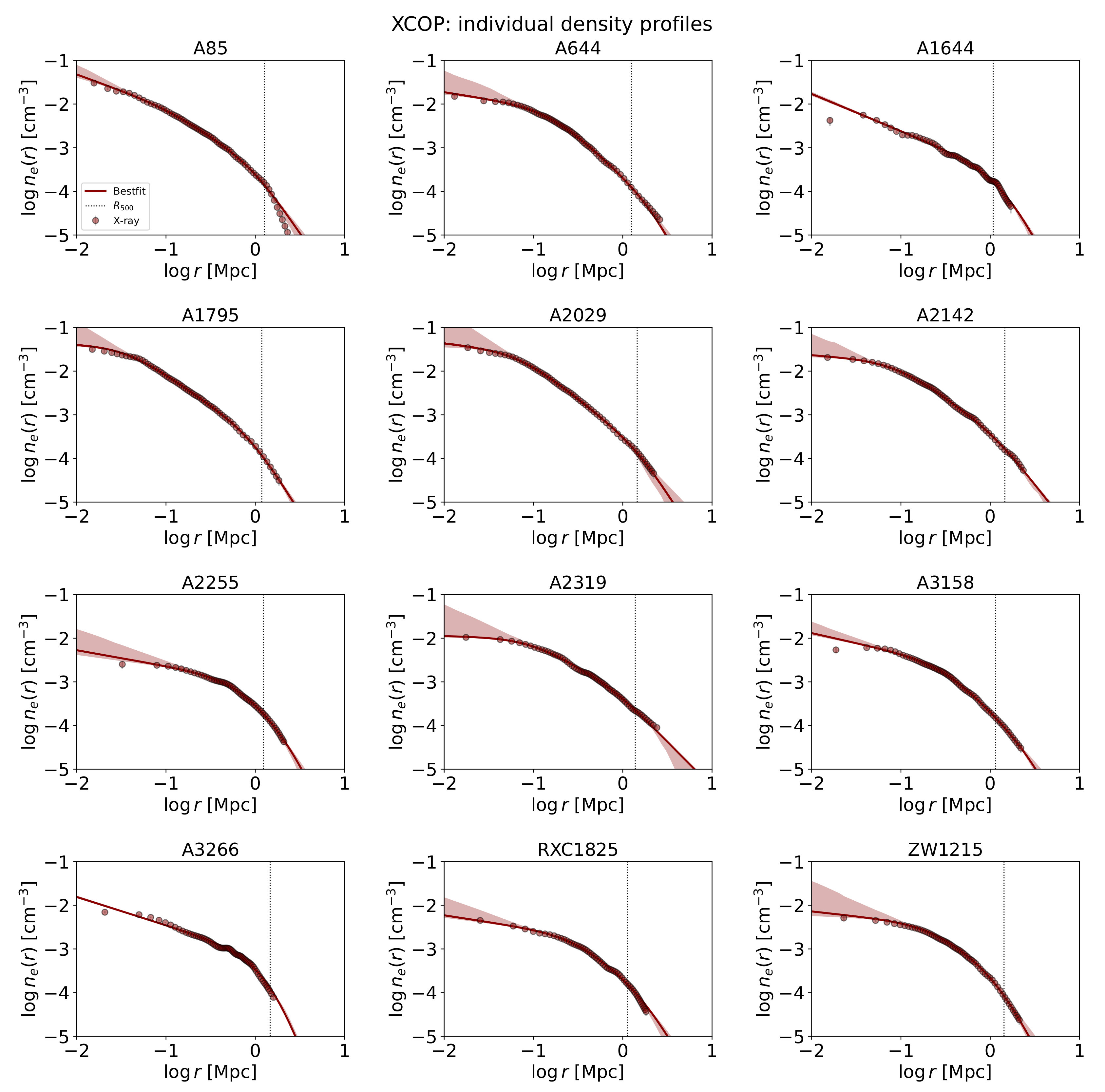
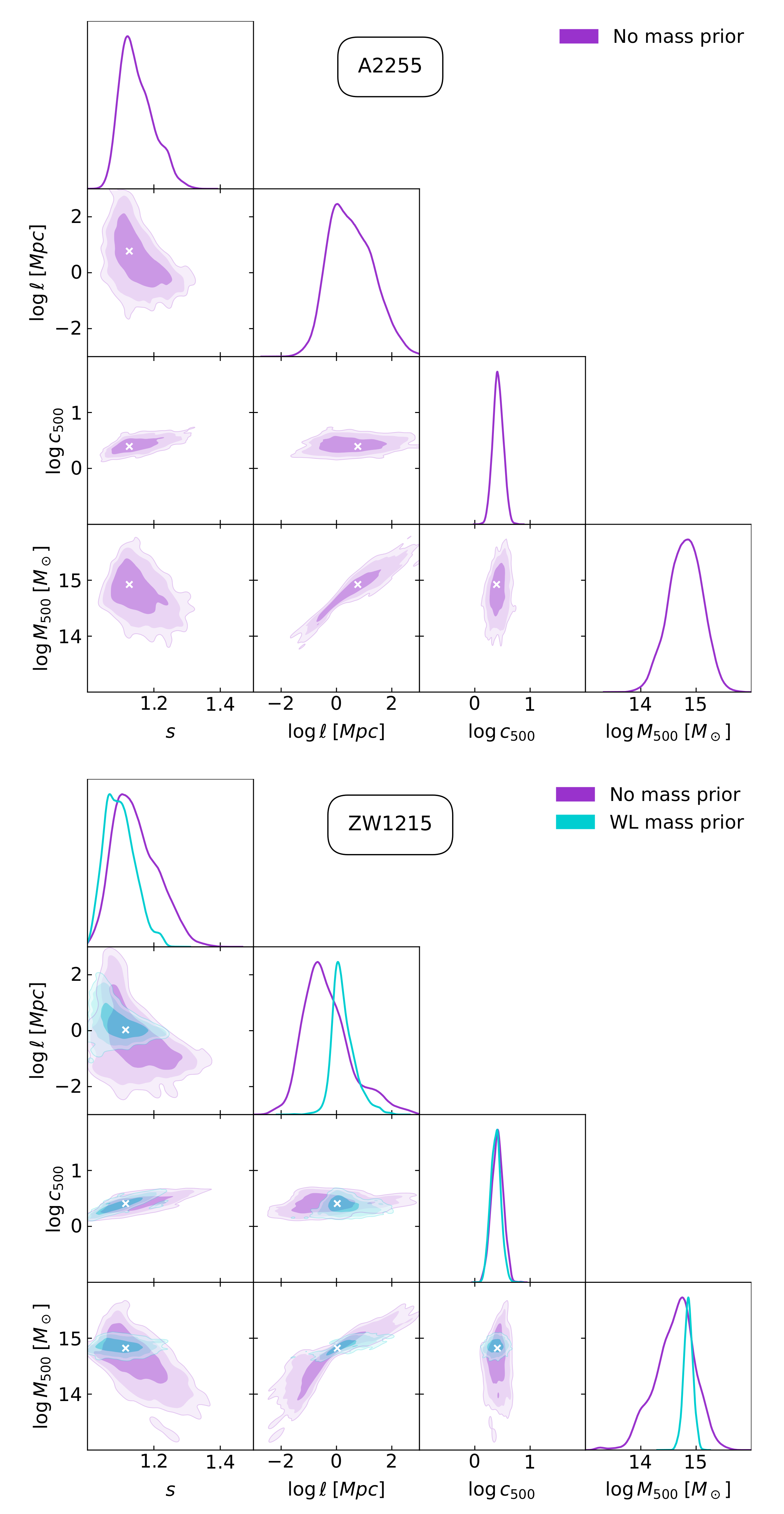
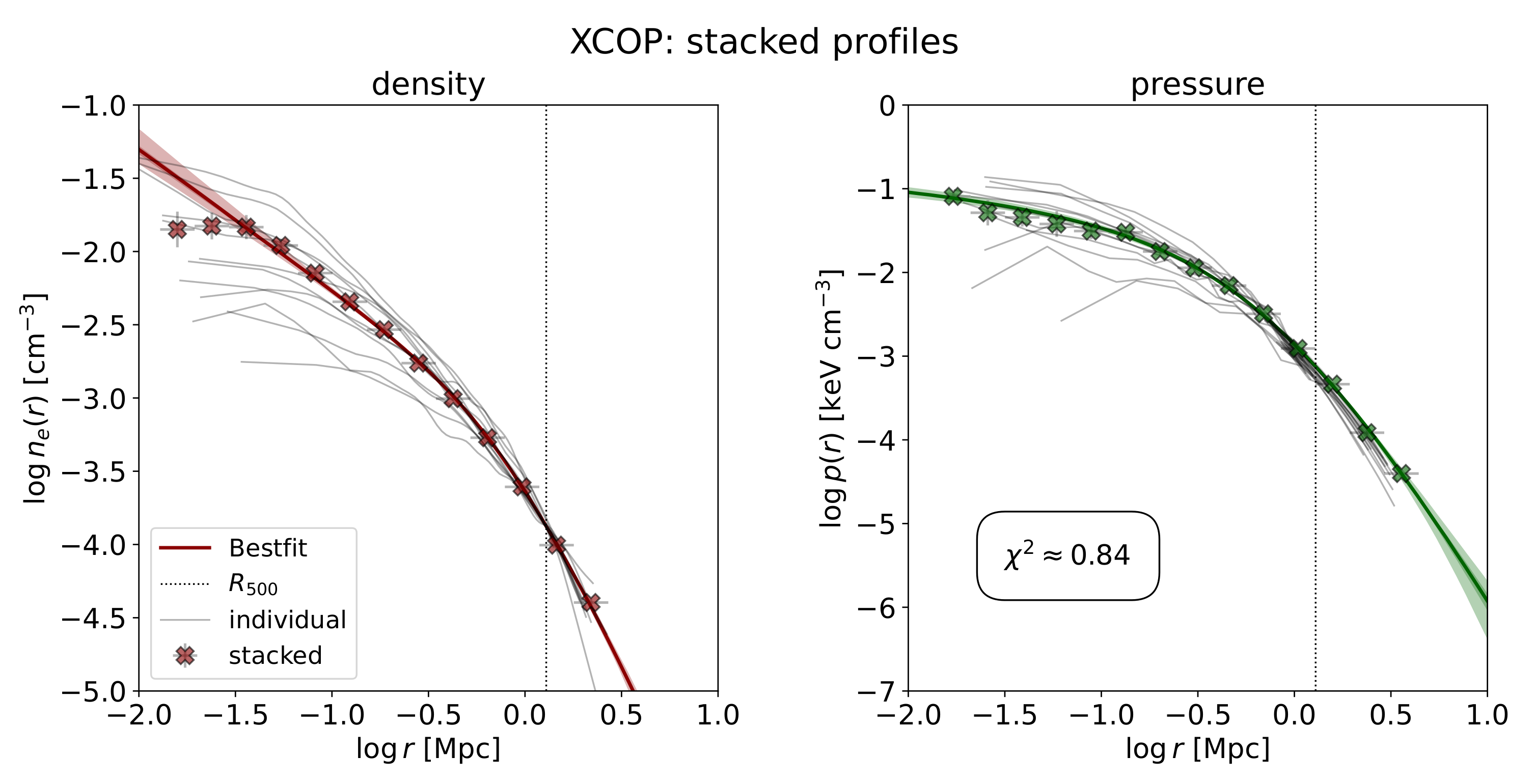

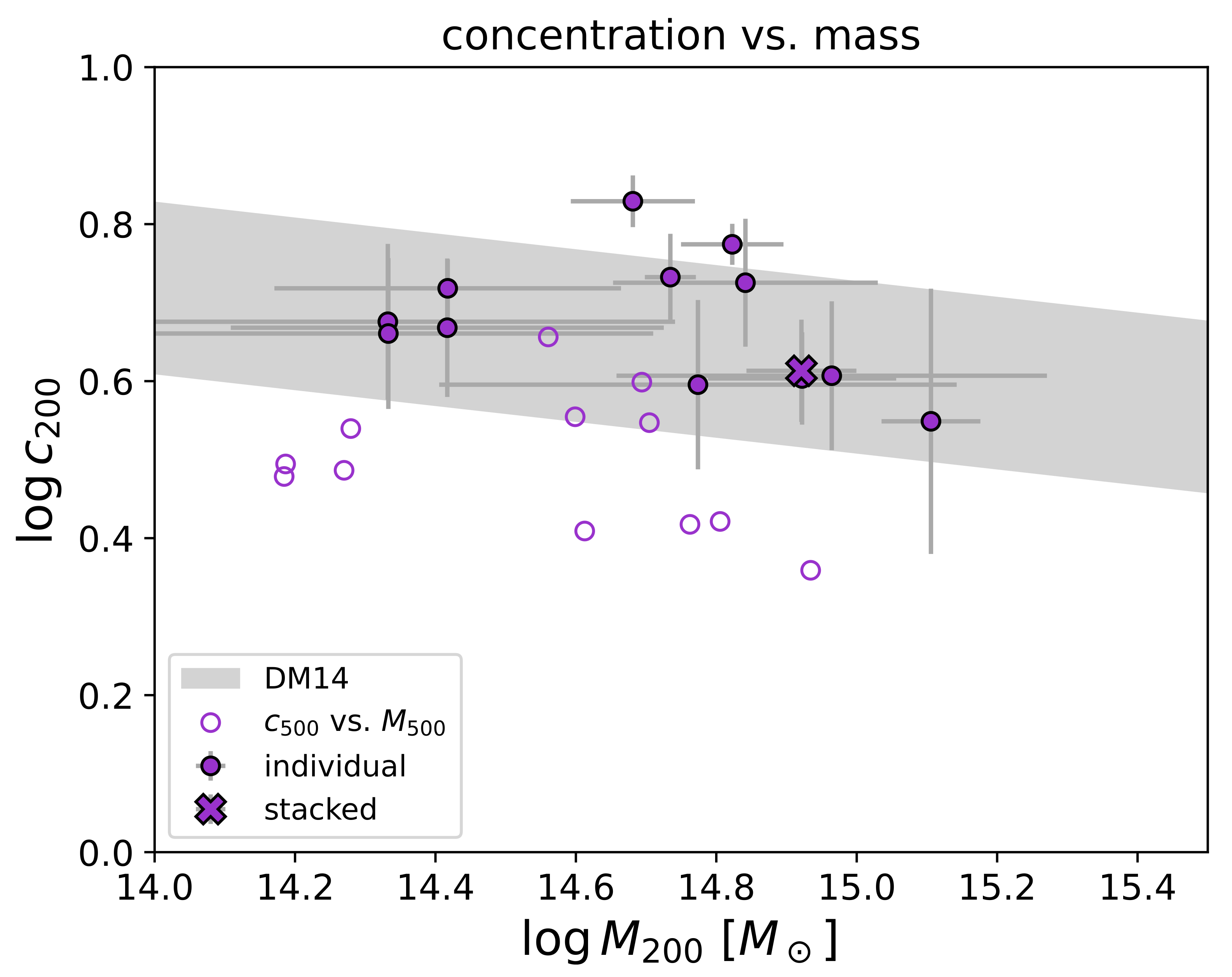
| Cluster | s | (Mpc) | ||||
|---|---|---|---|---|---|---|
| A85 | ||||||
| A644 | ||||||
| A1644 | ||||||
| A1795 | ||||||
| A2029 | ||||||
| A2142 | ||||||
| A2255 | ||||||
| A2319 | ||||||
| A3158 | ||||||
| A3266 | ||||||
| RXC1825 | ||||||
| ZW1215 | ||||||
| A85 +WL | ||||||
| A1795 +WL | ||||||
| A2029 +WL | ||||||
| A2142 +WL | ||||||
| ZW1215 +WL | ||||||
| Stacked |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benetti, F.; Lapi, A.; Gandolfi, G.; Haridasu, B.S.; Danese, L. Dark Matter in Fractional Gravity II: Tests in Galaxy Clusters. Universe 2023, 9, 329. https://doi.org/10.3390/universe9070329
Benetti F, Lapi A, Gandolfi G, Haridasu BS, Danese L. Dark Matter in Fractional Gravity II: Tests in Galaxy Clusters. Universe. 2023; 9(7):329. https://doi.org/10.3390/universe9070329
Chicago/Turabian StyleBenetti, Francesco, Andrea Lapi, Giovanni Gandolfi, Balakrishna Sandeep Haridasu, and Luigi Danese. 2023. "Dark Matter in Fractional Gravity II: Tests in Galaxy Clusters" Universe 9, no. 7: 329. https://doi.org/10.3390/universe9070329
APA StyleBenetti, F., Lapi, A., Gandolfi, G., Haridasu, B. S., & Danese, L. (2023). Dark Matter in Fractional Gravity II: Tests in Galaxy Clusters. Universe, 9(7), 329. https://doi.org/10.3390/universe9070329







