Double Beta Decay Experiments: Recent Achievements and Future Prospects
Abstract
1. Introduction
2. Results of Recent Experiments
2.1. Results for Decay
| Nucleus (, kev) | M, kg·yr | FWHM, keV | BI, c/kev·kg·yr | BI·FWHM, c/kg·yr | , yr (90% C.L.) | , meV | Experiment, Detector |
|---|---|---|---|---|---|---|---|
| Ge (2039.0) | 127.2 (110.7) | 2.6–4.9 | ∼ | > | <79–180 | GERDA [27], HPGe | |
| 73.3 (64.5) | 2.52 | > | <113–269 | Majorana [25], HPGe | |||
| Xe (2457.8) | ∼34,000 (970) | ∼247 | ∼ (∼) | ∼ (∼) | > | <36–156 | KamLAND-Zen [24], Xe in liquid scintillator |
| 290.4 (234.1) | 66.4 | 0.12 | > | <93–286 | EXO-200 [28], liquid Xe TPC | ||
| Te (2527.5) | 1038.4 (288.8) | 7.8 | 0.12 | > | <90–305 | CUORE [29], LTB TeO | |
| Te (866.7) | 309.33 (78.56) | 4.3 | 1.4 | 6.0 | > | - | CUORE [30], LTB TeO |
| Se (2997.9) | 9.94 (5.29) | 20 | > | <263–545 | CUPID-0 [31], LTB ZnSe | ||
| 5.90 (4.90) | ∼250 | ∼ | ∼1 | > | <1200–3000 | NEMO-3 [26], tracking detector | |
| Mo (3 034.4) | 2.71 (1.47) | 7.4 | > | <280–490 | CUPID-Mo [32], LTB LiMoO | ||
| Cd (2813.5) | 4.68 (1.22) | 170 | 0.15 | 25 | > | <1000–1700 | AURORA [37], CdWO scintillator |
| Ca (4268.0) | ∼108 (∼0.12) | 241 | 0.24 | > | <2900–16,000 | CANDLES-III [23], CaF scintillation crystals |
2.2. Results for Decay
| Nucleus (, keV) | N | , yr | S/B | Experiment Ref., Year |
|---|---|---|---|---|
| Se (2997.9) | 3472 | 4 | NEMO-3 [26], 2018 | |
| ∼200,000 | 10 | CUPID-0 [41], 2019 | ||
| Zr (3356.1) | Geochemical measurement | - | [54], 2018 | |
| Mo (3034.4) | 500,000 | 80 | NEMO-3 [44], 2019 | |
| 35,638 | 10 | CUPID-Mo [42], 2020 | ||
| Cd (2813.5) | 93,000 | ∼1.5 | AURORA [37], 2018 | |
| Te (2527.5) | ∼200,000 | > 1 | CUORE [43], 2021 | |
| Xe (2457.8) | ∼90,000 | ∼30 | KamLAND-Zen [55], 2019 | |
| ∼17,468 | > 1 | PandaX-4T [56], 2022 | ||
| 291 | ∼1 | NEXT [57], 2022 | ||
| Xe (2857) | −(2KK) | > (90% C.L.) | - | XMASS-I [51], 2018 |
| 126 (2KK) | ∼0.2 | XENON1T [52], 2019 | ||
| 262 (2ECEC) | ∼0.2 | XENON1T [53], 2022 |
2.3. Search Results for Processes with the Emission of Majoron and Majoron-like Particles
| Nucleus | , keV | , yr (90% C.L.) | (90% C.L.) | Experiment Ref., Year |
|---|---|---|---|---|
| Ge | 2039.0 | > | <(1.8–4.4) | GERDA [77] 2022 |
| Se | 2997.9 | > | <(3.2–8.0) | NEMO-3 [26] 2018 |
| > | <(1.8–4.4) | CUPID-0 [78] 2023 | ||
| Cd | 2813.5 | > | <(6.1–9.3) | AURORA [37] 2018 |
| Xe | 2457.8 | > | <(0.4–0.9) | EXO-200 [75] 2021 |
| Spectral Index | Ge [77] | Se [78] | Mo [44] | Cd [37] | Xe [75] |
|---|---|---|---|---|---|
| n = 2 | > | > | > | > | > |
| n = 3 | > | > | > | > | > |
| n = 7 | > | > | > | > | > |
2.4. Results for Transitions to Excited States of Daughter Nuclei
| Nucleus, Ref. | E, keV | , yr (90% C.L.) | |
|---|---|---|---|
| 2 | 0 | ||
| Ge [83] | 1479.9 | > | > |
| Se [31] | 2221.4 | - | > |
| Mo [79] | 2494.9 | > | > |
| Cd [37] | 1519.9 | > | > |
| Nd [80] | 3037.4 | > | > |
| Nucleus, Ref. | E, keV | , yr (90% C.L.) | |
|---|---|---|---|
| 2 | 0 | ||
| Ge [83] | 916.7 | > | > |
| Se [84] | 1510.3 | > | > |
| Se [31] | - | > | |
| Mo [79] | 1904.1 | > | |
| Cd [37] | 1056.6 | > | > |
| Te [85] | 734.0 | > | > |
| Xe [86] | 878.8 | > | - |
| Nd [81] | 2630.9 | - | |
| Nd [80] | > | ||
3. Prospects for New Experiments
| Experiment | Nucleus | M, kg | Sensitivity , yr (90% C.L.) | Sensitivity , meV (90% C.L.) | Status |
|---|---|---|---|---|---|
| LEGEND [94] | Ge | 200 | ∼ | ∼34–80 | Current |
| 1000 | 8.5–19.4 | R&D | |||
| CUPID [95,96,97] | Mo | 250 | 10–17 | R&D | |
| 1000 | 4.1–6.8 | R&D | |||
| nEXO [98] | Xe | 5000 | 4.7–20.3 | R&D | |
| KamLAND2-Zen [99] | Xe | 1000 | ∼ | ∼12–52 | R&D |
| AMoRE [100] | Mo | 100 | ∼ | ∼13–28 | R&D |
| SNO+ [101,102] | Te | ∼1300 | 37–89 | In progress | |
| ∼8000 | ∼ | ∼20–40 | R&D |
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fukugita, M.; Yanagida, T. Baryogenesis without Grand Unification. Phys. Lett. B 1986, 174, 45–47. [Google Scholar] [CrossRef]
- Majorana, E. Teoria simmetrica dell’elettrone e del positrone. Nuovo Cim. 1937, 14, 171–184. [Google Scholar] [CrossRef]
- Pascoli, S.; Petcov, S.T.; Schwetz, T. The absolute neutrino mass scale, neutrino mass spectrum, Majorana CP-violation and neutrinoless double-beta decay. Nucl. Phys. B 2006, 734, 24–49. [Google Scholar] [CrossRef]
- Bilenky, S.M.; Giunti, G. Neutrinoless double-beta decay: A probe of physics beyond the Standard Model. Int. J. Mod. Phys. A 2015, 30, 1530001. [Google Scholar] [CrossRef]
- Vergados, J.D.; Ejiri, H.; Simkovic, F. Neutrinoless double beta decay and neutrino mass. Int. J. Mod. Phys. E 2016, 25, 1630007. [Google Scholar] [CrossRef]
- Girardi, I.; Petcov, S.T.; Titov, A.V. Predictions for the Majorana CP violation phases in the neutrino mixing matrix and neutrinoless double beta decay. Nucl. Phys. B 2016, 911, 754–804. [Google Scholar] [CrossRef]
- Barabash, A.S.; Dolgov, A.D.; Dvornicky, R.; Simkovic, F.; Smirnov, A.Y. Statistics of neutrinos and the double beta decay. Nucl. Phys. B 2007, 783, 90–111. [Google Scholar] [CrossRef]
- Nitescu, O.; Ghinescu, S.; Stoica, S. Lorentz violation effects in 2νββ decay. J. Phys. G 2020, 47, 055112. [Google Scholar] [CrossRef]
- Ghinescu, S.; Nitescu, O.; Stoica, S. Investigation of the Lorentz invariance violation in two-neutrino double-beta decay. Phys. Rev. D 2022, 105, 05532. [Google Scholar] [CrossRef]
- Deppisch, F.F.; Graf, L.; Rodejohann, W.; Xu, X.-J. Neutrino self-interactions and double beta decay. Phys. Rev. D 2020, 102, 051701. [Google Scholar] [CrossRef]
- Bolton, P.D.; Deppisch, F.F.; Graf, L.; Simkovic, F. Two-neutrino double beta decay with sterile neutrinos. Phys. Rev. D 2021, 103, 055019. [Google Scholar] [CrossRef]
- Deppisch, F.F.; Graf, L.; Simkovic, F. Searching for New Physics in two-neutrino double beta decay. Phys. Rev. Lett. 2020, 125, 171801. [Google Scholar] [CrossRef]
- Barabash, A.S. Precise half-life values for two-neutrino double-β decay: 2020 review. Universe 2020, 6, 159. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Incicchitti, A.; Merlo, V. Double beta decay to excited states of daughter nuclei. Universe 2020, 6, 239. [Google Scholar] [CrossRef]
- Dolinski, M.J.; Poon, A.W.P.; Rodejohann, W. Neutrinoless double-beta decay: Status and prospects. Ann. Rev. Part. Sci. 2019, 69, 219–251. [Google Scholar] [CrossRef]
- Barabash, A.S. Main features of detectors and isotopes to investigate double beta decay with increased sensitivity. Int. J. Mod. Phys. A 2018, 33, 1843001. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Caracciolo, V. Status and Perspectives of 2e, eβ+ and 2β+ Decays. Particles 2021, 4, 241–274. [Google Scholar] [CrossRef]
- Agostini, M.; Benato, G.; Detwiler, J.A.; Menendez, J.; Vissani, F. Toward the discovery of matter creation with neutrinoless double-beta decay. arXiv 2022, arXiv:2202.01787. [Google Scholar]
- Simkovic, F. Neutrino masses and interactions and neutrino experiments in the laboratory. Physics-Uspekhi 2021, 64, 1238–1260. [Google Scholar] [CrossRef]
- Engel, J.; Menendez, J. Status and future of nuclear matrix elements for neutrinoless double-beta decay: A review. Rep. Prog. Phys. 2017, 80, 046301. [Google Scholar] [CrossRef]
- Kotila, J.; Iachello, F. Phase-space factors for double-β decay. Phys. Rev. C 2012, 85, 034316. [Google Scholar] [CrossRef]
- Mirea, M.; Pahomi, T.; Stoica, S. Values of the phase space factor involved in double beta decay. Rom. Rep. Phys. 2015, 67, 872–889. [Google Scholar]
- Ajimura, S.; Chan, W.M.; Ichimura, K.; Ishikawa, T.; Kanagawa, K.; Khai, B.T.; Kishimoto, T.; Kino, H.; Maeda, T.; Matsuoka, K. Low background measurement in CANDLES-III for studying the neutrinoless double beta decay of 48Ca. Phys. Rev. D 2021, 103, 092008. [Google Scholar] [CrossRef]
- Abe, S.; Asami, S.; Eizuka, M.; Futagi, S.; Gando, A.; Gando, Y.; Gima, T.; Goto, A.; Hachiya, T.; Hata, K.; et al. Search for the Majorana nature of neutrinos in the inverted mass ordering region with KamLAND-Zen. Phys. Rev. Lett. 2023, 130, 051801. [Google Scholar] [CrossRef] [PubMed]
- Arnquist, I.J.; Avignone, F.T., III; Barabash, A.S.; Barton, C.J.; Barton, P.J.; Bhimani, K.H.; Blalock, E.; Bos, B.; Busch, M.; Buuck, M.; et al. Final result of the Majorana Demonstrator’s search for neutrinoless double-β decay in 76Ge. Phys. Rev. Lett. 2023, 130, 062501. [Google Scholar] [CrossRef]
- Arnold, R.; Augier, C.; Barabash, A.S.; Basharina-Freshville, A.; Blondel, S.; Blot, S.; Bongrand, M.; Boursette, D.; Brudanin, V.; Busto, J.; et al. Final results on 82Se double beta decay to the ground state of 82Kr from the NEMO-3 experiment. Eur. Phys. J. C 2018, 78, 821. [Google Scholar] [CrossRef]
- Agostini, M.; Araujo, G.R.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Baudis, L.; Bauer, C.; Bellotti, E.; Belogurov, S.; Bettini, A.; et al. Final results of GERDA on the search for neutrinoless double-β decay. Phys. Rev. Lett. 2020, 125, 252502. [Google Scholar] [CrossRef]
- Anton, G.; Badhrees, I.; Barbeau, P.S.; Beck, D.; Belov, V.; Bhatta, T.; Breidenbach, M.; Brunner, T.; Cao, G.F.; Cen, W.R.; et al. Search for neutrinoless double-β decay with the complete EXO-200 dataset. Phys. Rev. Lett. 2019, 123, 161802. [Google Scholar] [CrossRef]
- Adams, D.Q.; Alduino, C.; Alfonso, K.; Avignone, F.T., III; Azzolini, O.; Bari, G.; Bellini, F.; Benato, G.; Beretta, M.; Biassoni, M.; et al. Search for Majorana neutrinos exploiting millikelvin cryogenics with CUORE. Nature 2022, 604, 53–66. [Google Scholar]
- Adams, D.Q.; Alduino, C.; Alfonso, K.; Avignone, F.T., III; Azzolini, O.; Bari, G.; Bellini, F.; Benato, G.; Beretta, M.; Biassoni, M.; et al. New direct limit on neutrinoless double beta decay half-life of 128Te with CUORE. Phys. Rev. Lett. 2022, 129, 222501. [Google Scholar] [CrossRef]
- Azzolini, O.; Beeman, J.W.; Bellini, F.; Beretta, M.; Biassoni, M.; Brofferio, C.; Bucci, C.; Capelli, S.; Caracciolo, V.; Cardani, L.; et al. Final result on the neutrinoless double beta decay of 82Se with CUPID-0. Phys. Rev. Lett. 2022, 129, 111801. [Google Scholar] [CrossRef] [PubMed]
- Augier, C.; Barabash, A.S.; Bellini, F.; Benato, G.; Beretta, M.; Bergé, L.; Billard, J.; Borovlev, Y.A.; Cardani, L.; Casali, N.; et al. Final results on the 0νββ decay half-life limit of 100Mo from the CUPID-Mo experiment. Eur. Phys. J. C 2022, 82, 1033. [Google Scholar] [CrossRef]
- Coraggio, L.; Itaco, N.; De Gregorio, G.; Gargano, A.; Mancino, R.; Pastore, S. Present status of nuclear shell-model calculations of 0νββ decay matrix elements. Universe 2020, 6, 233. [Google Scholar] [CrossRef]
- Brase, C.; Menéndez, J.; Coello Pérez, E.A.; Schwenk, A. Neutrinoless double-β decay from an effective field theory for heavy nuclei. Phyc. Rev. C 2022, 106, 034309. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Capozzi, F.; Di Valentino, E.; Lisi, E.; Marrone, A.; Melchiorri, A.; Palazzo, A. Global constraints on absolute neutrino masses and their ordering. Phys. Rev. D 2017, 95, 096014. [Google Scholar] [CrossRef]
- Barabash, A.S.; Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; Danevich, F.A.; d’Angelo, S.; Incicchitti, A.; et al. Final results of the Aurora experiment to study 2β decay of 116Cd with enriched 116CdWO4 crystal scintillators. Phys. Rev. D 2018, 98, 092007. [Google Scholar] [CrossRef]
- Suhonen, J. Impact of the quenching of gA on the sensitivity of 0νββ experiments. Phys. Rev. C 2017, 96, 055501. [Google Scholar] [CrossRef]
- Suhonen, J.; Kostensalo, J. Double β decay and the axial strength. Front. Phys. 2019, 7, 00029. [Google Scholar] [CrossRef]
- Gysbers, P.; Hagen, G.; Holt, J.D.; Jansen, G.R.; Morris, T.D.; Navrátil, P.; Papenbrock, T.; Quaglioni, S.; Schwenk, A.; Stroberg, S.R.; et al. Discrepancy between experimental and theoretical β-decay rates resolved from first principles. Nat. Phys. 2019, 15, 428–431. [Google Scholar] [CrossRef]
- Azzolini, O.; Beeman, J.W.; Bellini, F.; Beretta, M.; Biassoni, M.; Brofferio, C.; Bucci, C.; Capelli, S.; Cardani, L.; Carniti, P.; et al. Evidence of single state dominance in the two-neutrino double-β decay of 82Se with CUPID-0. Phys. Rev. Lett. 2019, 123, 262501. [Google Scholar] [CrossRef]
- Armengaud, E.; Augier, C.; Barabash, A.S.; Bellini, F.; Benato, G.; Benoît, A.; Beretta, M.; Berge, L.; Billard, J.; Borovlev, Y.A.; et al. Precise measurement of 2νββ decay of 100Mo with the CUPID-Mo detection technology. Eur. Phys. J. C 2020, 80, 674. [Google Scholar] [CrossRef]
- Adams, D.Q.; Alduino, C.; Alfonso, K.; Avignone, F.T., III; Azzolini, O.; Bari, G.; Bellini, F.; Benato, G.; Biassoni, M.; Branca, A.; et al. Measurement of the 2νββ decay half-life of 130Te with CUORE. Phys. Rev. Lett. 2021, 126, 171801. [Google Scholar] [CrossRef]
- Arnold, R.; Augier, C.; Barabash, A.S.; Basharina-Freshville, A.; Blondel, S.; Blot, S.; Bongrand, M.; Boursette, D.; Brudanin, V.; Busto, J.; et al. Detailed studies of 100Mo two-neutrino double beta decay in NEMO-3. Eur. Phys. J. C 2019, 79, 440. [Google Scholar] [CrossRef]
- Domin, P.; Kovalenko, S.; Šimkovic, F.; Semenov, S.V. Neutrino accompanied β±β±, β+/EC and EC/EC processes within single state dominance hypothesis. Nucl. Phys. A 2005, 753, 337–363. [Google Scholar] [CrossRef]
- Kawashima, A.; Takahashi, K.; Masuda, A. Geochemical estimation of the half-life for the double beta decay of 96Zr. Phys. Rev. C 1993, 47, R2452–R2456. [Google Scholar] [CrossRef]
- Wieser, M.E.; De Laeter, J.R. Evidence of the double β decay of zirconium-96 measured in 1.8×109 year-old zircons. Phys. Rev. C 2001, 64, 024308. [Google Scholar] [CrossRef]
- Azzolini, O.; Beeman, J.W.; Bellini, F.; Beretta, M.; Biassoni, M.; Brofferio, C.; Bucci, C.; Capelli, S.; Cardani, L.; Carniti, P.; et al. First search for Lorentz violation in double beta decay with scintillating calorimeters. Phys. Rev. D 2019, 100, 092002. [Google Scholar] [CrossRef]
- Bossio, E.; Agostini, M. Probing beyond the standard model physics with double-beta decays. arXiv 2023, arXiv:2304.07198. [Google Scholar]
- Doi, M.; Kotani, T.; Takasugi, E. Double beta decay and Majorana neutrino. Prog. Theor. Phys. Suppl. 1985, 83, 1–175. [Google Scholar] [CrossRef]
- Abe, K.; Hiraide, K.; Ichimura, K.; Kishimoto, Y.; Kobayashi, K.; Kobayashi, M.; Moriyama, S.; Nakahata, M.; Norita, T.; Ogawa, H.; et al. Improved search for two-neutrino double electron capture on 124Xe and 126Xe using particle identification in XMASS-I. Prog. Theor. Exp. Phys. 2018, 2018, 053D03. [Google Scholar]
- Aprile, E.; Aalbers, J.; Agostini, F.; Alfonsi, M.; Althueser, L.; Amaro, F.D.; Anthony, M.; Antochi, V.C.; Arneodo, F.; Baudis, L.; et al. Observation of two-neutrino double electron capture in 124Xe with XENON1T. Nature 2019, 568, 532–535. [Google Scholar]
- Aprile, E.; Abe, K.; Agostini, F.; Ahmed Maouloud, S.; Alfonsi, M.; Althueser, L.; Andrieu, B.; Angelino, E.; Angevaare, J.R.; Antochi, V.C.; et al. Double-weak decays of 124Xe and 136Xe in the XENON1T and XENONnT experiments. Phys. Rev. C 2022, 106, 024328. [Google Scholar] [CrossRef]
- Mayer, A.J.; Wieser, M.; Alanssari, M.; Frekers, D.; Matthews, W.; Dilling, J.; Thompson, R.I. Isotope abundance measurement of the half-life of the ββ-decaying nucleus 96Zr from a 2.68 Gyr zircon sample. Phys. Rev. C 2018, 98, 024617. [Google Scholar] [CrossRef]
- Gando, A.; Gando, Y.; Hachiya, T.; Ha Minh, M.; Hayashida, S.; Honda, Y.; Hosokawa, K.; Ikeda, H.; Inoue, K.; Ishidoshiro, K.; et al. Precision analysis of the 136Xe two-neutrino ββ spectrum in KamLAND-Zen and its impact on the quenching of nuclear matrix elements. Phys. Rev. Lett. 2019, 122, 192501. [Google Scholar] [CrossRef]
- Si, L.; Cheng, Z.; Abdukerim, A.; Bo, Z.; Chen, W.; Chen, X.; Chen, Y.; Cheng, C.; Cheng, Y.; Cui, X.; et al. Determination of double beta decay half-life of 136Xe with the PandaX-4T natural xenon detector. Research 2022, 2022, 9798721. [Google Scholar] [CrossRef]
- Novella, P.; Sorel, M.; Usón, A.; Adams, C.; Almazán, H.; Álvarez, V.; Aparicio, B.; Aranburu, A.I.; Arazi, L.; Arnquist, I.J.; et al. Measurement of the 136Xe two-neutrino double beta decay half-life via direct background subtraction in NEXT. Phys. Rev. C 2022, 105, 055501. [Google Scholar] [CrossRef]
- Kotila, J.; Barea, J.; Iachello, F. Phase-space factors and half-life predictions for majoron-emitting β-β- decay. Phys. Rev. C 2015, 91, 064310, Erratum in Phys. Rev. C 2015, 92, 029903. [Google Scholar] [CrossRef]
- Chikashige, Y.; Mohapatra, R.N.; Peccei, R.D. Spontaneously broken lepton number and cosmological constraints on the neutrino mass spectrum. Phys. Rev. Lett. 1980, 45, 1926–1929. [Google Scholar] [CrossRef]
- Chikashige, Y.; Mohapatra, R.N.; Peccei, R.D. Are there real goldstone bosons associated with broken lepton number? Phys. Lett. B 1981, 98, 265–268. [Google Scholar] [CrossRef]
- Aulakh, C.; Mohapatra, R. Neutrino as the supersymmetric partner of the majoron. Phys. Lett. B 1982, 119, 136–140. [Google Scholar] [CrossRef]
- Gelmini, G.; Roncadelli, M. Left-handed neutrino mass scale and spontaneously broken lepton number. Phys. Lett. B 1981, 99, 411–415. [Google Scholar] [CrossRef]
- Caso, C.; Conforto, G.; Gurtu, A.; Aguilar-Benitez, M.; Amsler, C.; Barnett, R.M.; Burchat, P.R.; Carone, C.D.; Dahl, O.; Doser, M.; et al. The review of particle physics. Eur. Phys. J. C 1998, 3, 1. [Google Scholar]
- Berezhiani, Z.G.; Smirnov, A.Y.; Valle, J.W.F. Observable majoron emission in neutrinoless double beta decay. Phys. Lett. B 1992, 291, 99–105. [Google Scholar] [CrossRef][Green Version]
- Mohapatra, R.N.; Takasugi, E. Neutrinoless double beta decay with double majoron emission. Phys. Lett. B 1988, 211, 192–196. [Google Scholar] [CrossRef]
- Burgess, C.P.; Cline, J.M. Majorons without Majorana masses and neutrinoless double beta decay. Phys. Lett. B 1993, 298, 141–148. [Google Scholar] [CrossRef]
- Burgess, C.P.; Cline, J.M. A New class of majoron emitting double beta decays. Phys. Rev. D 1994, 49, 5925–5944. [Google Scholar] [CrossRef]
- Bamert, P.; Burgess, C.P.; Mohapatra, R.N. Multi-majoron modes for neutrinoless double beta decay. Nucl. Phys. B 1995, 449, 25–48. [Google Scholar] [CrossRef]
- Berezinsky, V.; Valle, J.W.F. The keV majoron as a dark matter particle. Phys. Lett. B 1993, 318, 360–366. [Google Scholar] [CrossRef]
- Garcia-Cely, C.; Heeck, J. Neutrino lines from majoron dark matter. J. High Energy Phys. 2017, 05, 102. [Google Scholar] [CrossRef]
- Brune, T.; Päs, H. Massive majorons and constraints on the majoron-neutrino coupling. Phys. Rev. D 2019, 99, 096005. [Google Scholar] [CrossRef]
- Cepedello, R.; Deppisch, F.F.; González, L.; Hati, C.; Hirsch, M. Neutrinoless double-β decay with nonstandard majoron emission. Phys. Rev. Lett. 2019, 122, 181801. [Google Scholar] [CrossRef] [PubMed]
- Carone, C.D. Double beta decay with vector majorons. Phys. Lett. B 1993, 308, 85–88. [Google Scholar] [CrossRef]
- Gunther, M.; Hellmig, J.; Heusser, G.; Hirsch, M.; Klapdor-Kleingrothaus, H.V.; Maier, B.; Päs, H.; Petry, F.; Ramachers, Y.; Strecker, H. Bounds on new majoron models from the Heidelberg-Moscow experiment. Phys. Rev. D 1996, 54, 3641–3644. [Google Scholar] [CrossRef]
- Al Kharusi, S.; Anton, G.; Badhrees, I.; Barbeau, P.S.; Beck, D.; Belov, V.; Bhatta, T.; Breidenbach, M.; Brunner, T.; Cao, G.F.; et al. Search for majoron-emitting modes of 136Xe double beta decay with the complete EXO-200 dataset. Phys. Rev. D 2021, 104, 112002. [Google Scholar] [CrossRef]
- Arnold, R.; Augier, C.; Baker, J.D.; Barabash, A.S.; Basharina-Freshville, A.; Blondel, S.; Blot, S.; Bongrand, M.; Boursette, D.; Brudanin, V.; et al. Measurement of the 2νββ decay half-life and search for the 0νββ decay of 116Cd with the NEMO-3 detector. Phys. Rev. D 2017, 95, 012007. [Google Scholar] [CrossRef]
- Agostini, M.; Alexander, A.; Araujo, G.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Baudis, L.; Bauer, C.; Belogurov, S.; Bettini, A.; et al. Search for exotic physics in double-β decays with GERDA Phase II. J. Cosm. Astrop. Phys. 2022, 12, 012. [Google Scholar] [CrossRef]
- Azzolini, O.; Beeman, J.W.; Bellini, F.; Beretta, M.; Biassoni, M.; Brofferio, C.; Bucci, C.; Capelli, S.; Caracciolo, V.; Cardani, L.; et al. Search for majoron-like particles with CUPID-0. Phys. Rev. D 2023, 107, 032006. [Google Scholar] [CrossRef]
- Augier, C.; Barabash, A.S.; Bellini, F.; Benato, G.; Beretta, M.; Bergé, L.; Billard, J.; Borovlev, Y.A.; Cardani, L.; Casali, N.; et al. New measurement of double beta decays of 100Mo to excited states of 100Ru with the CUPID-Mo experiment. Phys. Rev. C 2023, 107, 025503. [Google Scholar] [CrossRef]
- Arnold, R.; Augier, C.; Barabash, A.S.; Basharina-Freshville, A.; Blondel, S.; Blot, S.; Bongrand, M.; Boursette, D.; Breier, R.; Brudanin, V.; et al. Measurement of double beta decay of 150Nd to the state of 150Sm in NEMO-3. arXiv 2022, arXiv:2203.03356. [Google Scholar]
- Polischuk, O.G.; Barabash, A.S.; Belli, P.; Bernabei, R.; Boiko, R.S.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Di Marco, A.; et al. Double beta decay of 150Nd to the first 0+ excited level of 150Sm. Phys. Scr. 2021, 96, 085302. [Google Scholar] [CrossRef]
- Piepke, A.; Beck, M.; Bockholt, J.; Glatting, D.; Heusser, G.; Klapdor-Kleingrothaus, H.V.; Maier, B.; Perty, F.; Schmidt-Rohr, U.; Strecker, H.; et al. Investigation of the ββ decay of 116Cd into excited states of 116Sn. Nucl. Phys. A 1994, 577, 493–510. [Google Scholar] [CrossRef]
- Arnquist, I.J.; Avignone, F.T., III; Barabash, A.S.; Barton, C.J.; Bertrand, F.E.; Blalock, E.; Bos, B.; Busch, M.; Buuck, M.; Caldwell, T.S.; et al. Search for double-β decay of 76Ge to excited states of 76Se with the Majorana Demonstrator. Phys. Rev. C 2021, 103, 015501. [Google Scholar] [CrossRef]
- Arnold, R.; Augier, C.; Barabash, A.S.; Basharina-Freshville, A.; Blondel, S.; Blot, S.; Bongrand, M.; Boursette, D.; Breier, R.; Brudanin, V.; et al. Search for the double-beta decay of 82Se to the excited states of 82Kr with NEMO-3. Nucl. Phys. A 2020, 996, 121701. [Google Scholar] [CrossRef]
- Adams, D.Q.; Alduino, C.; Alfonso, K.; Avignone, F.T., III; Azzolini, O.; Bari, G.; Bellini, F.; Benato, G.; Biassoni, M.; Branca, A.; et al. Search for double-beta decay of 130Te to the 0+ states of 130Xe with CUORE. Eur. Phys. J. C 2021, 81, 567. [Google Scholar] [CrossRef]
- Al Kharusi, S.; Anton, G.; Badhrees, I.; Barbeau, P.S.; Beck, D.; Belov, V.; Bhatta, T.; Breidenbach, M.; Brunner, T.; Cao, G.F.; et al. Search for two-neutrino double-beta decay of 136Xe to the excited state of 136Ba with the complete EXO-200 dataset. arXiv 2023, arXiv:2303.01103. [Google Scholar]
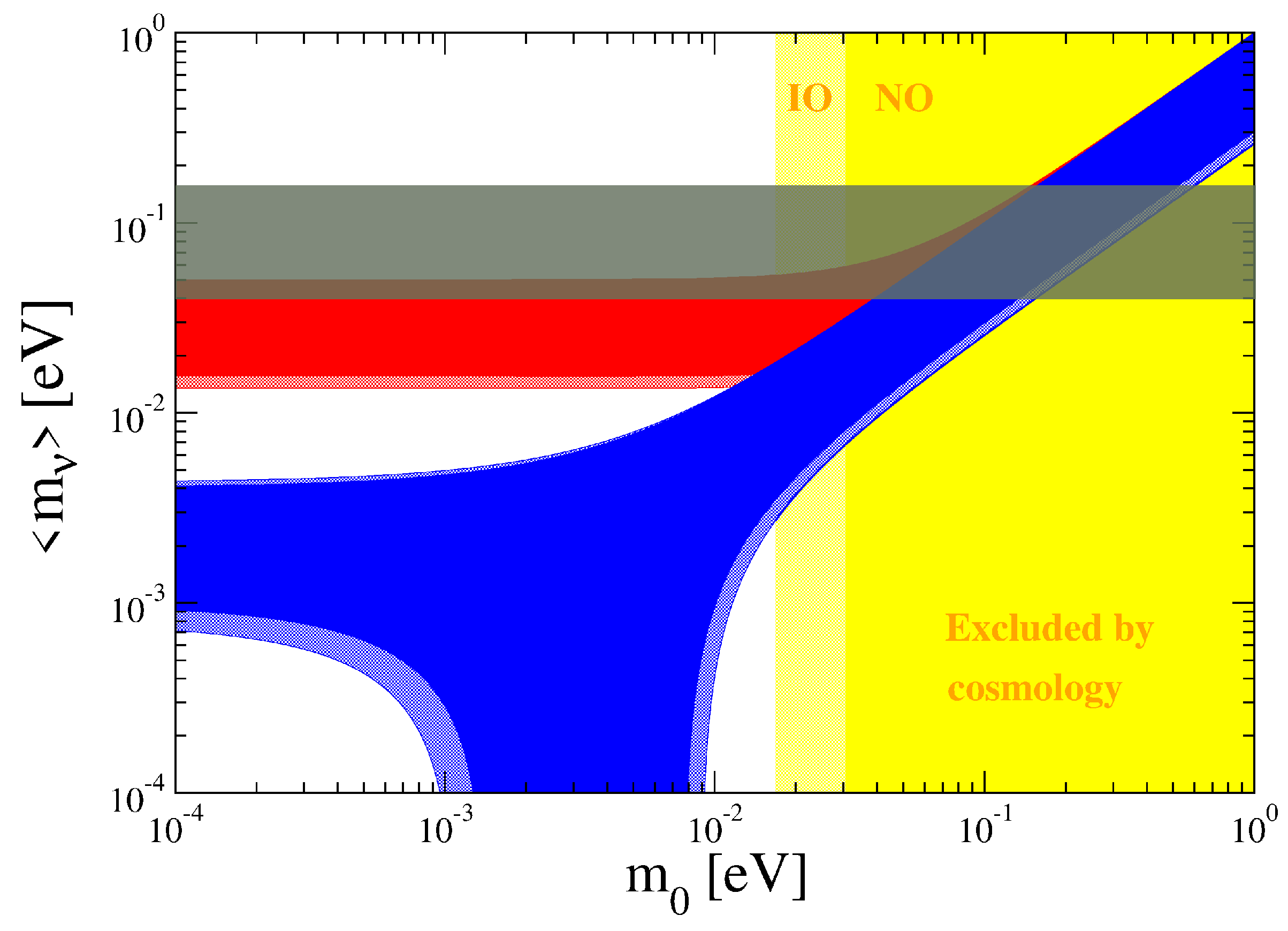
- Barabash, A.S. Possibilities of future double beta decay experiments to investigate inverted and normal ordering region of neutrino mass. Front. Phys. 2019, 6, 00160. [Google Scholar] [CrossRef]
- Adams, C.; Alfonso, K.; Andreoiu, C.; Angelico, E.; Arnquist, I.J.; Asaadi, J.A.A.; Avignone, F.T.; Axani, S.N.; Barabash, A.S.; Barbeau, P.S.; et al. Neutrinoless double beta decay. arXiv 2022, arXiv:2212.11099. [Google Scholar]
- Shimizu, I.; Chen, M. Double beta decay experiments with loaded liquid scintillator. Front. Phys. 2019, 7, 00033. [Google Scholar] [CrossRef]
- Gomez-Cadenas, J.J.; Capilla, F.M.; Ferrario, P. High pressure gas xenon TPCs for double beta decay searches. Front. Phys. 2019, 7, 00051. [Google Scholar] [CrossRef]
- Biassoni, M.; Cremonesi, O. Search for neutrinoless double beta decay with thermal detectors. Prog. Part. Nucl. Phys. 2020, 114, 103803. [Google Scholar] [CrossRef]
- D’Andrea, V.; Di Marco, N.; Junker, M.B.; Laubenstein, M.; Macolino, C.; Morella, M.; Salamida, F.; Vignoli, C. Neutrinoless double beta decay with germanium detectors: 1026 yr and Beyond. Universe 2021, 7, 341. [Google Scholar] [CrossRef]
- Poda, D. Scintillation in low-temperature particle detectors. Physics 2021, 3, 473–535. [Google Scholar] [CrossRef]
- Abgral, N.; Abt, I.; Agostini, M.; Alexander, A.; Andreoiu, C.; Araujo, G.R.; Avignone, F.T., III; Bae, W.; Bakalyarov, A.; Balata, M.; et al. The large enriched germanium experiment for neutrinoless ββ decay, LEGEND-1000 preconceptual design report. arXiv 2021, arXiv:2107.11462. [Google Scholar]
- Armstrong, W.R.; Chang, C.; Hafidi, K.; Lisovenko, M.; Novosad, V.; Pearson, J.; Polakovic, T.; Wang, G.; Yefremenko, V.; Zhang, J.; et al. CUPID pre-CDR. arXiv 2019, arXiv:1907.09376. [Google Scholar]
- Alfonso, K.; Armatol, A.; Augier, C.; Avignone, F.T., III; Azzolini, O.; Balata, M.; Barabash, A.S.; Bari, G.; Barresi, A.; Baudin, D.; et al. CUPID: The next-generation neutrinoless double beta decay experiment. J. Low Temp. Phys. 2023. [Google Scholar] [CrossRef]
- Armatol, A.; Augier, C.; Avignone, F.T., III; Azzolini, O.; Balata, M.; Ballen, K.; Barabash, A.S.; Bari, G.; Barresi, A.; Baudin, D.; et al. Toward CUPID-1T. arXiv 2022, arXiv:2203.08386. [Google Scholar]
- Adhikari, G.; Al Kharusi, S.; Angelico, E.; Anton, G.; Arnquist, I.J.; Badhrees, I.; Bane, J.; Belov, V.; Bernard, E.P.; Bhatta, T.; et al. nEXO: Neutrinoless double beta decay search beyond 1028 year half-life sensitivity. J. Phys. G. 2022, 49, 015104. [Google Scholar] [CrossRef]
- Ishimizu, I. Search for Majorana neutrinos. arXiv 2023, arXiv:2303.05127. [Google Scholar]
- Oh, Y. Status of AMoRE. J. Phys. Con. Ser. 2022, 2156, 012146. [Google Scholar] [CrossRef]
- Albanese, V.; Alves, R.; Anderson, M.R.; Andringa, S.; Anselmo, L.; Arushanova, E.; Asahi, S.; Askins, M.; Auty, D.J.; Back, A.R.; et al. The SNO+ experiment. JINST 2021, 16, P08059. [Google Scholar] [CrossRef]
- Inacio, A.S. Status and prospects of the SNO+ experiment. PoS 2022, PANIC2021, 274. [Google Scholar]
- Barabash, A.S. The new generation of double beta decay experiments: Are there any limitations? J. Phys. G 2012, 39, 085103. [Google Scholar] [CrossRef][Green Version]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barabash, A. Double Beta Decay Experiments: Recent Achievements and Future Prospects. Universe 2023, 9, 290. https://doi.org/10.3390/universe9060290
Barabash A. Double Beta Decay Experiments: Recent Achievements and Future Prospects. Universe. 2023; 9(6):290. https://doi.org/10.3390/universe9060290
Chicago/Turabian StyleBarabash, Alexander. 2023. "Double Beta Decay Experiments: Recent Achievements and Future Prospects" Universe 9, no. 6: 290. https://doi.org/10.3390/universe9060290
APA StyleBarabash, A. (2023). Double Beta Decay Experiments: Recent Achievements and Future Prospects. Universe, 9(6), 290. https://doi.org/10.3390/universe9060290






