Deep Learning of Quasar Lightcurves in the LSST Era
Abstract
1. Introduction
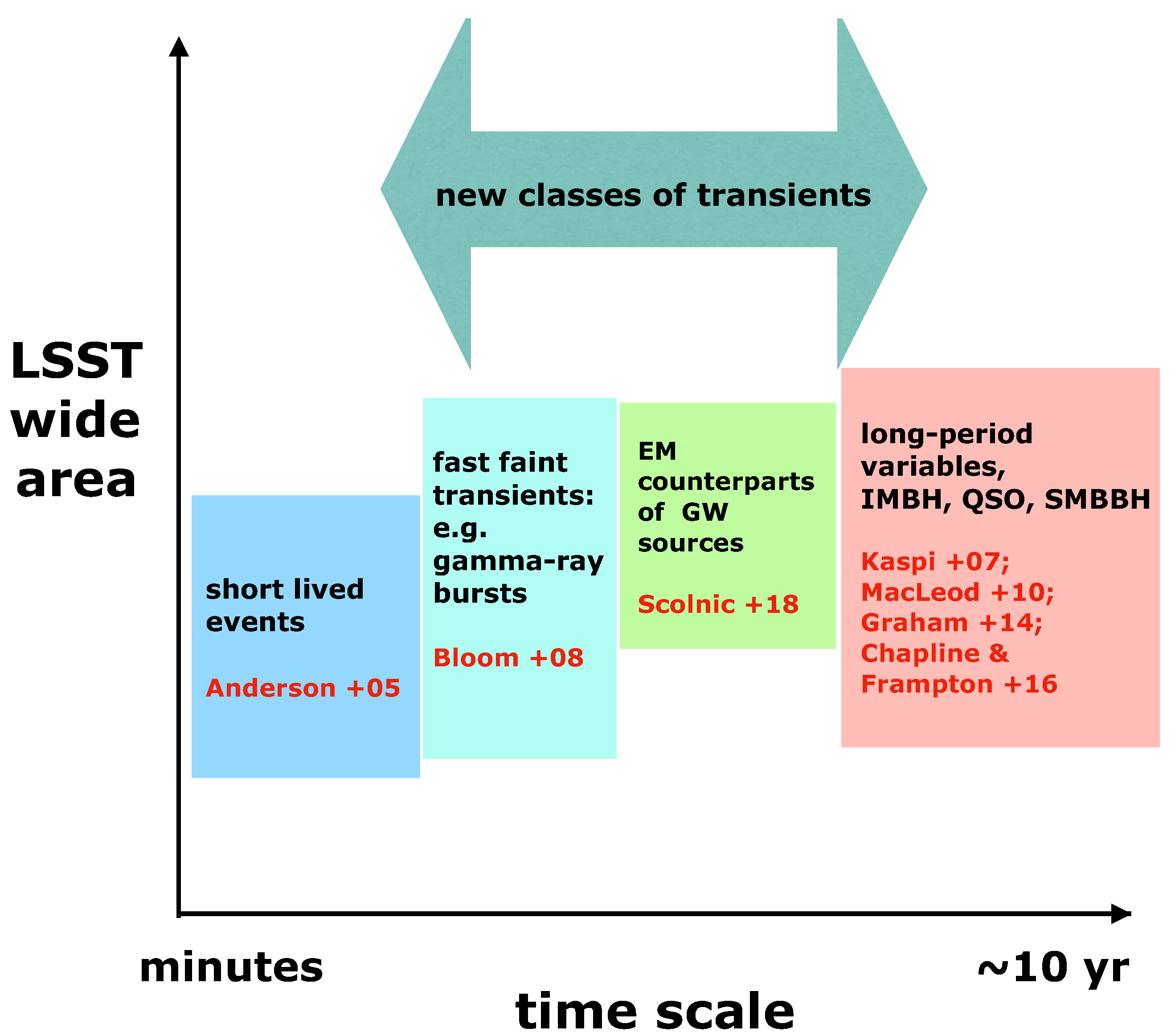
2. Materials
2.1. Description of Quasar Data in LSST_AGN_DC
2.2. Sample Selection
3. Methods
3.1. Motivation
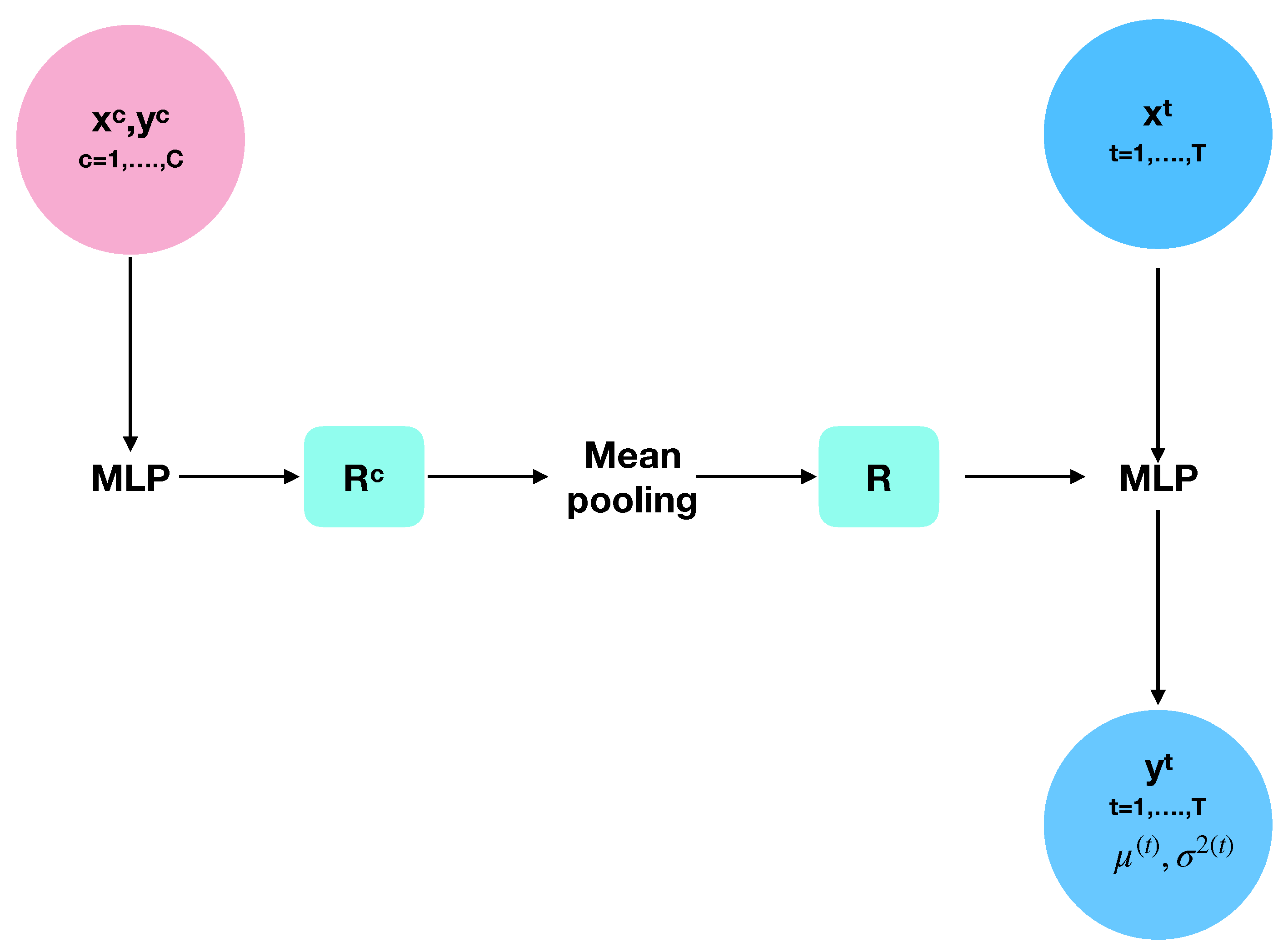
3.2. Conditional Neural Process
- Model architecture;
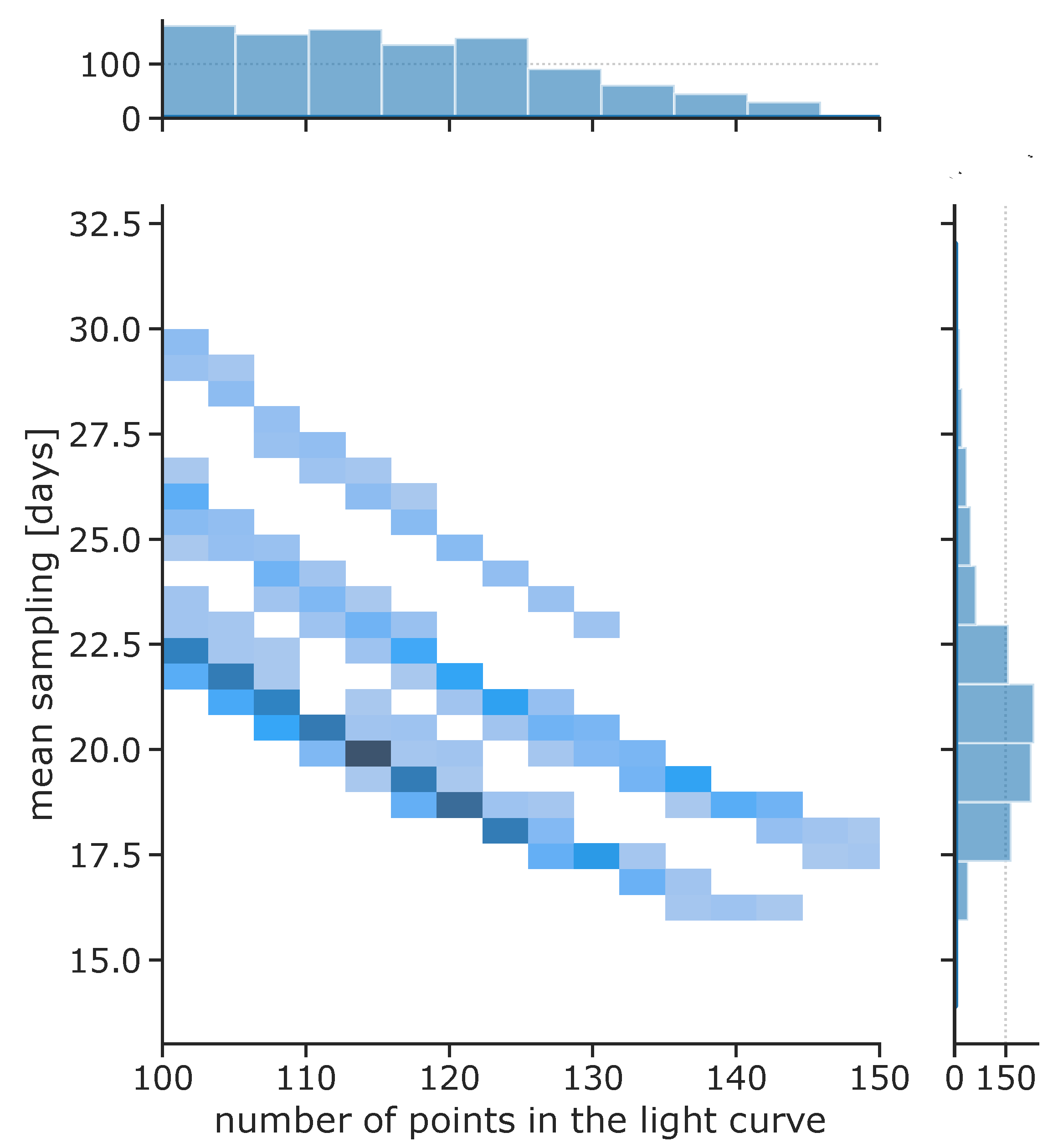
- Definition of dataset class and collate function;
- Metrics (loss and mean squared error—MSE);
- Training and calculation of training and validation metrics (loss and MSE);
- Saving model in predefined repository;
- Upload of the trained model so that prediction can be performed anytime.
4. Results and Discussion
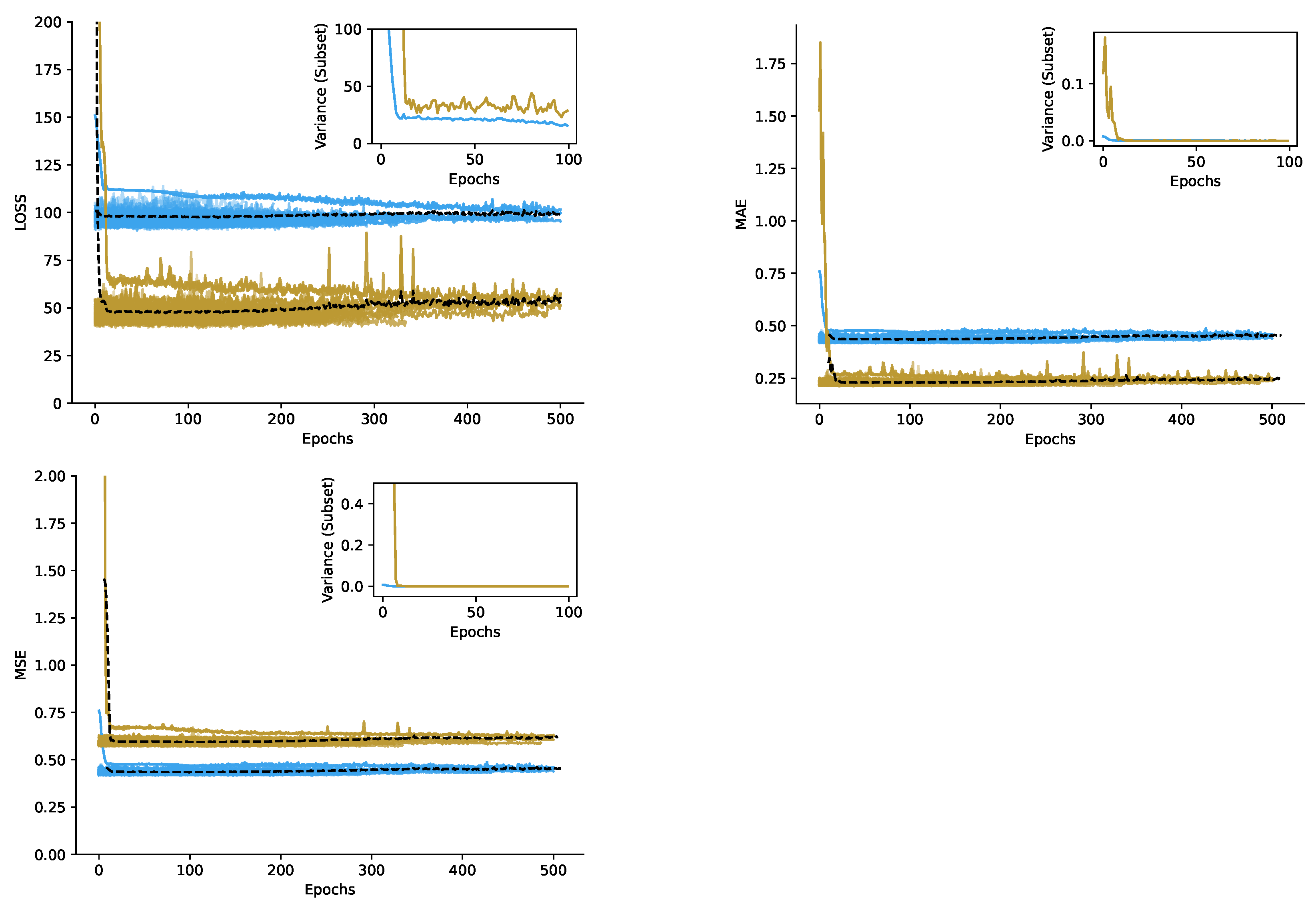
4.1. Training of CNP
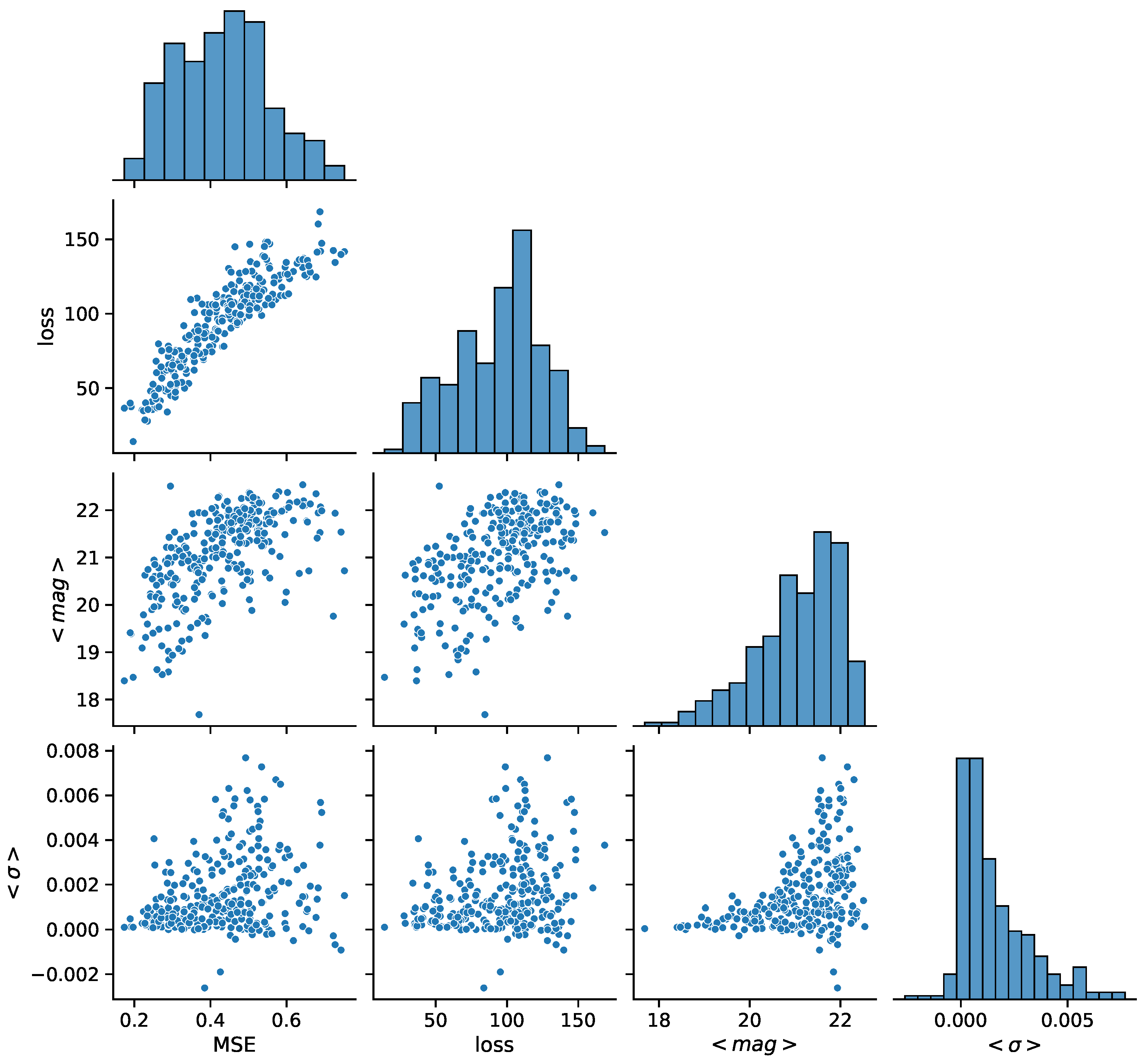
4.2. CNP Modeling of Quasar Variability
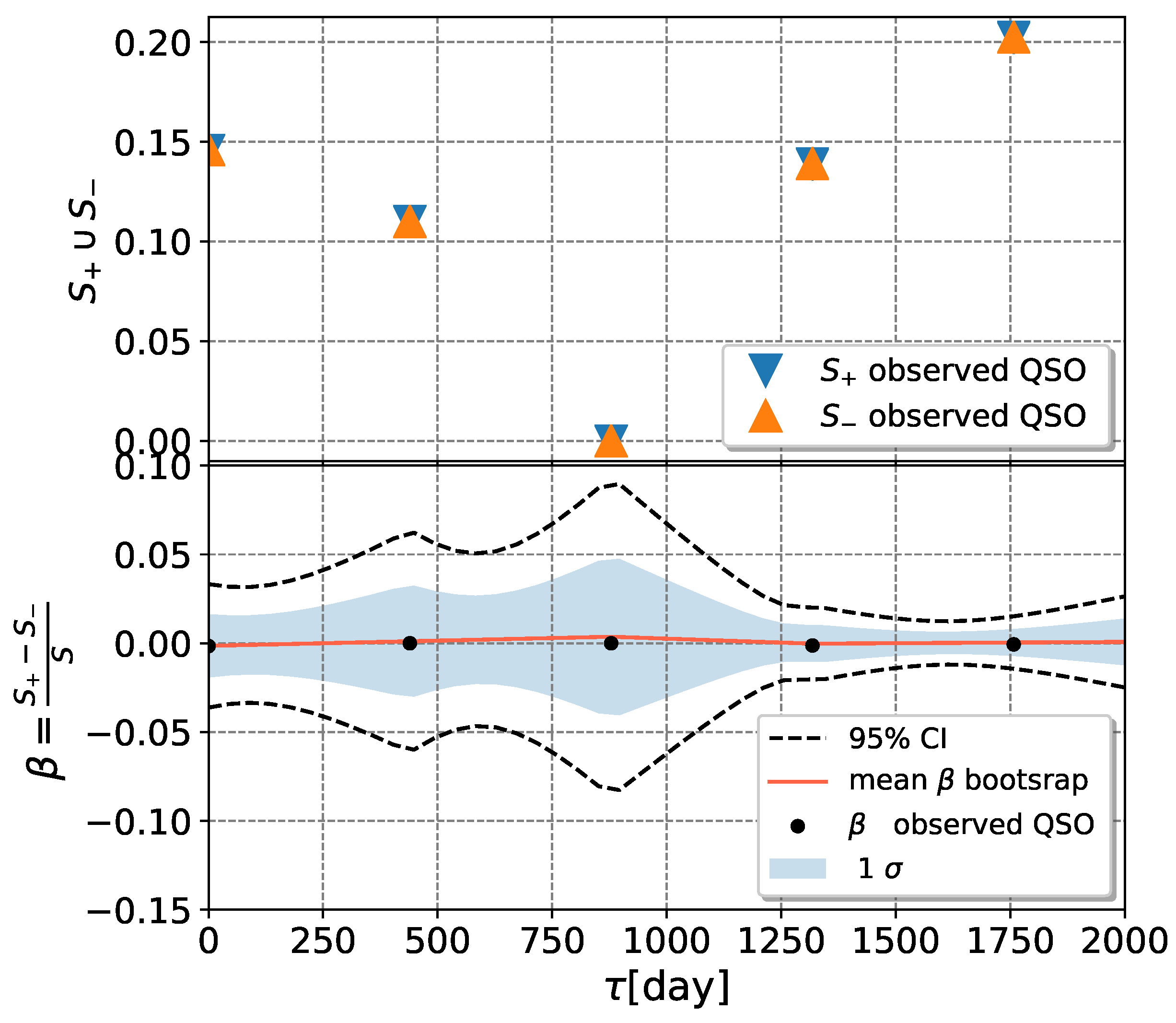
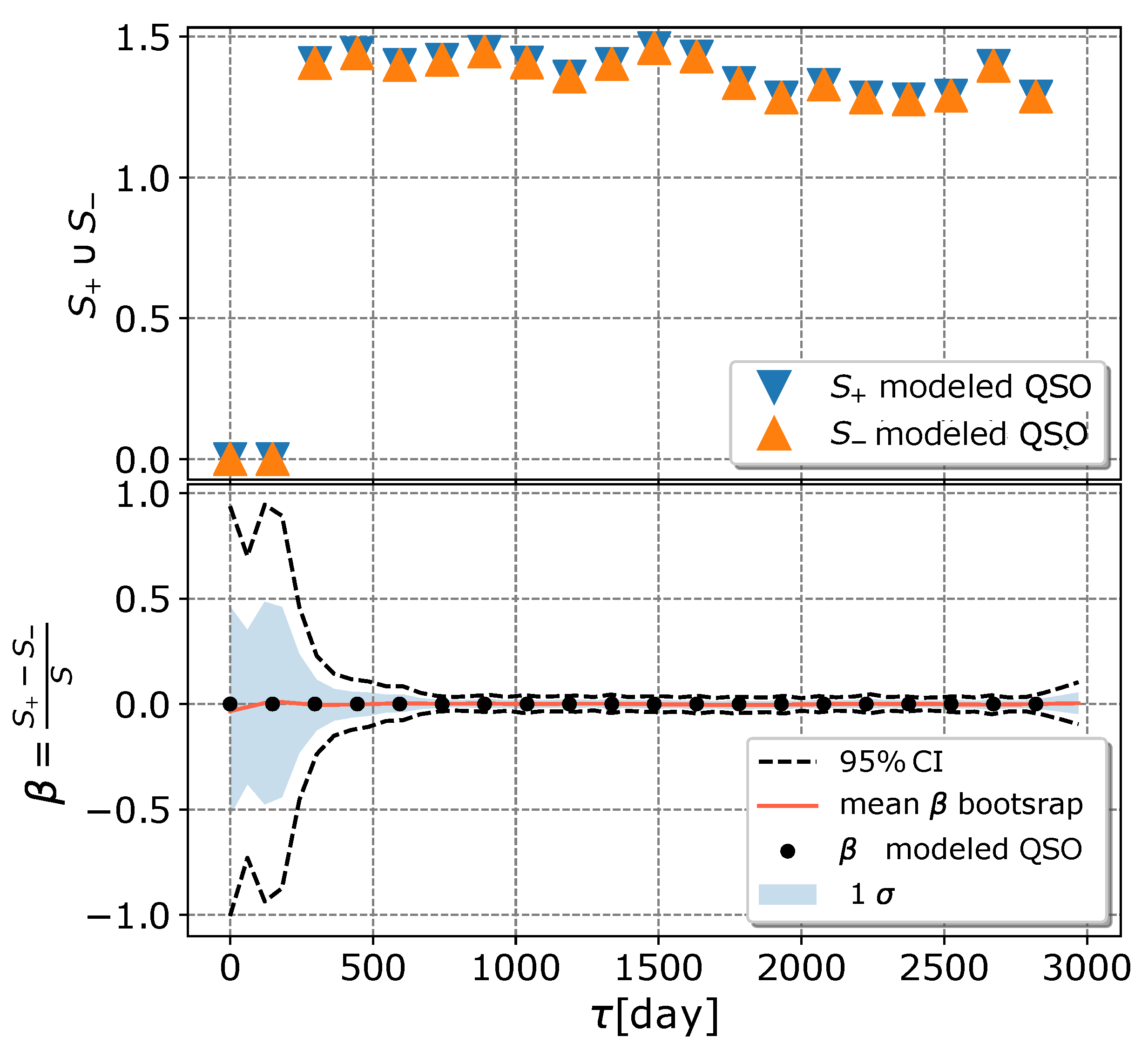
4.3. Modified Structure–Function Analysis of Observed and Modeled Light Curves
5. Conclusions
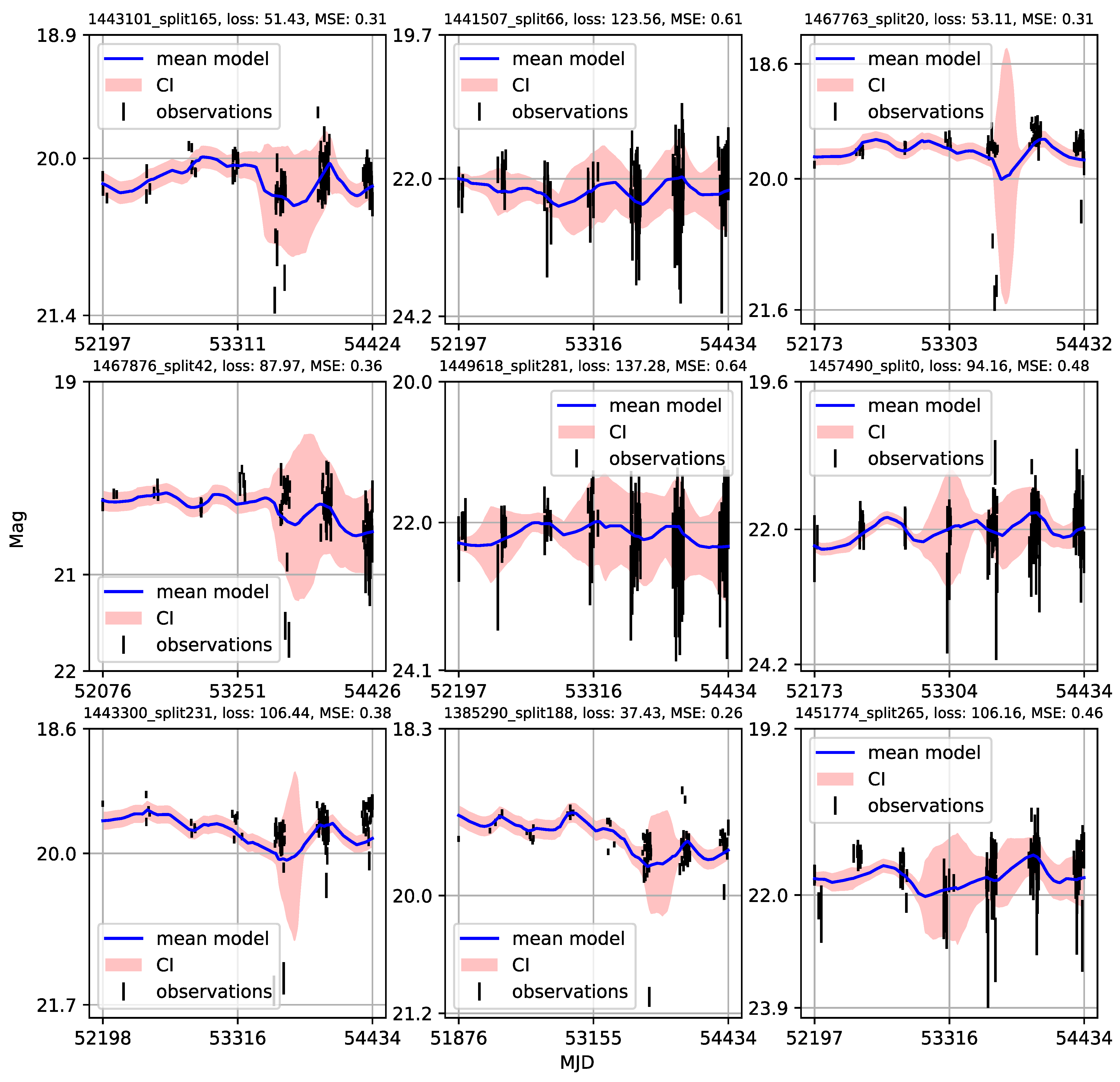
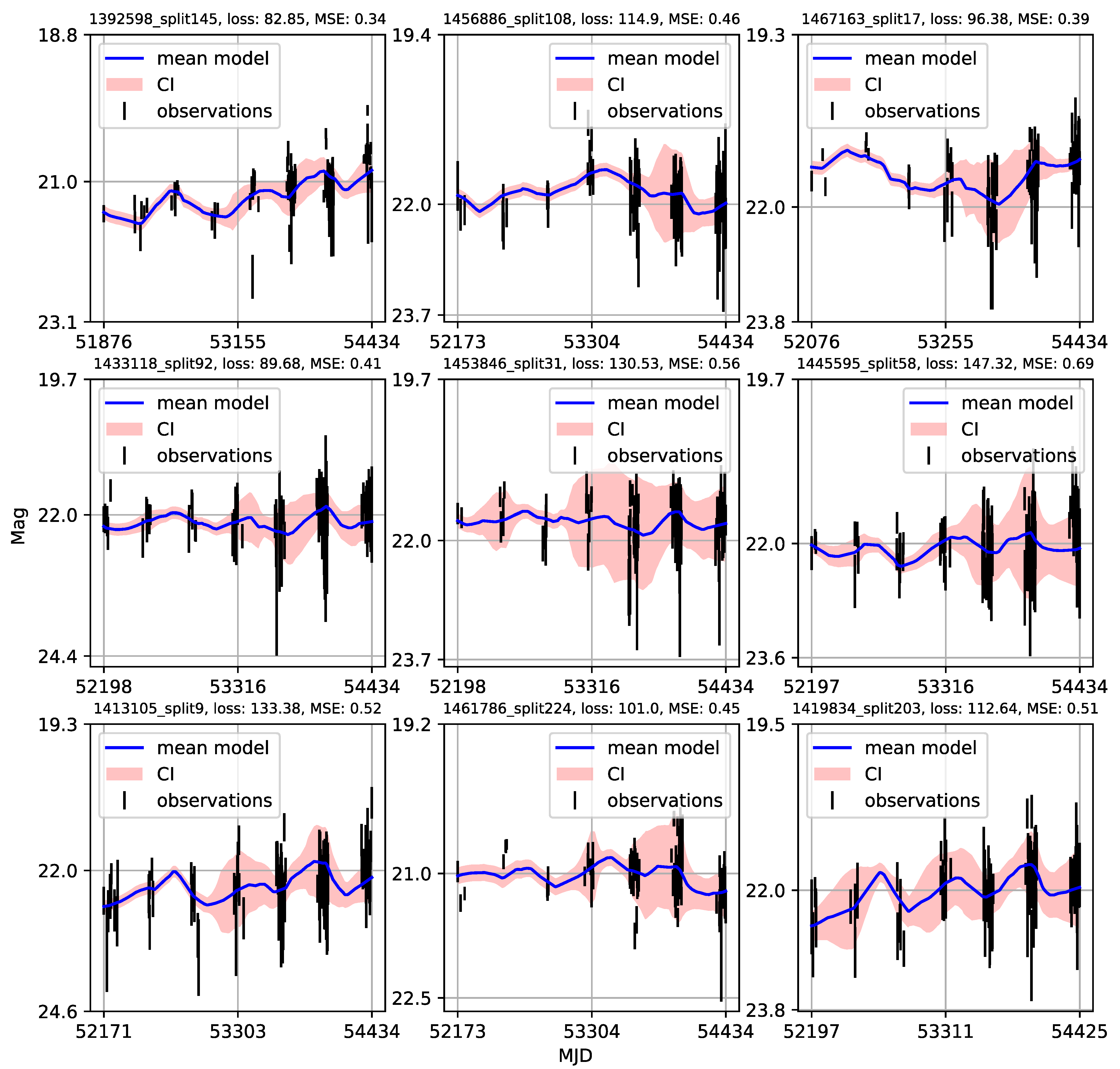
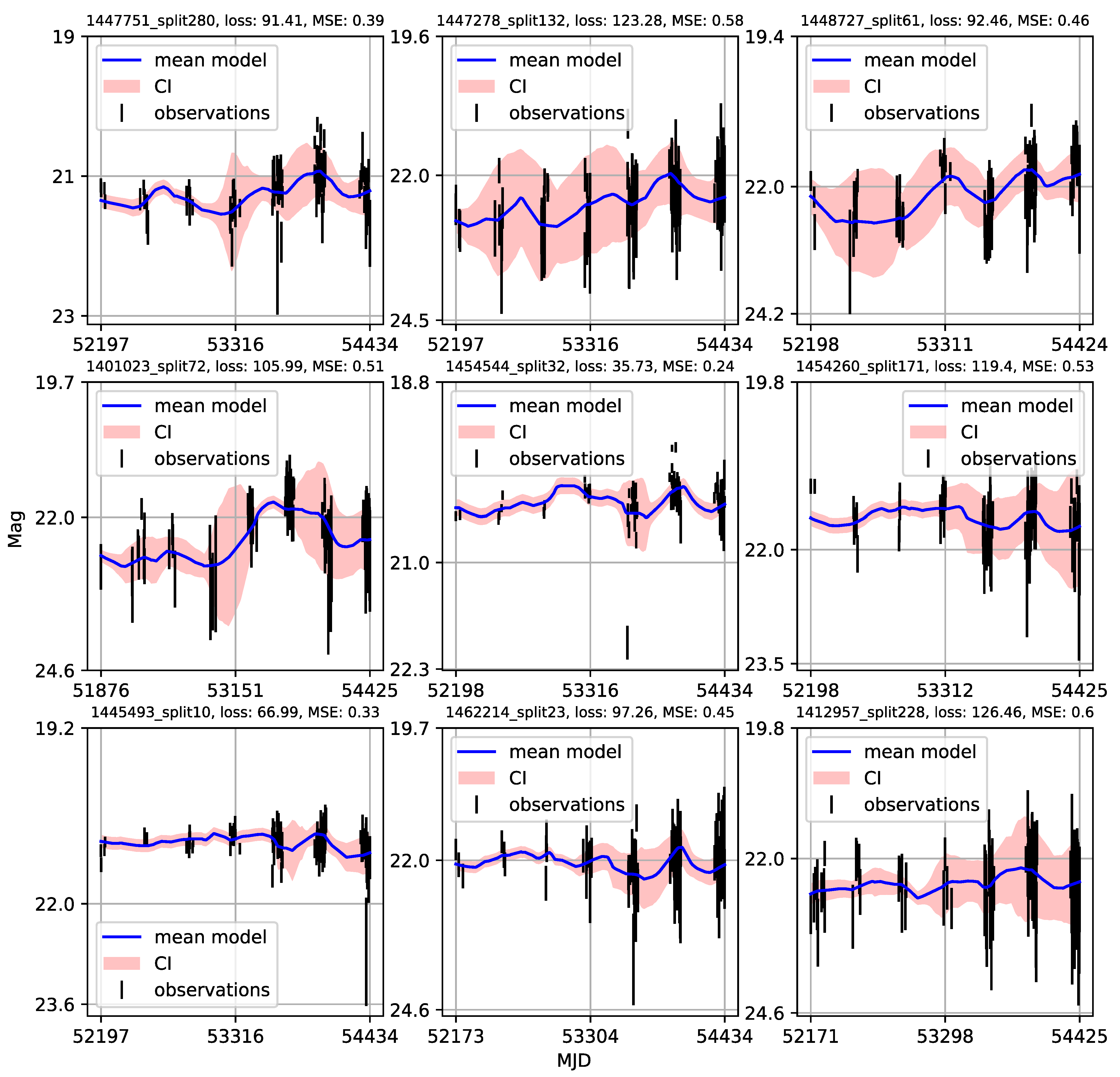
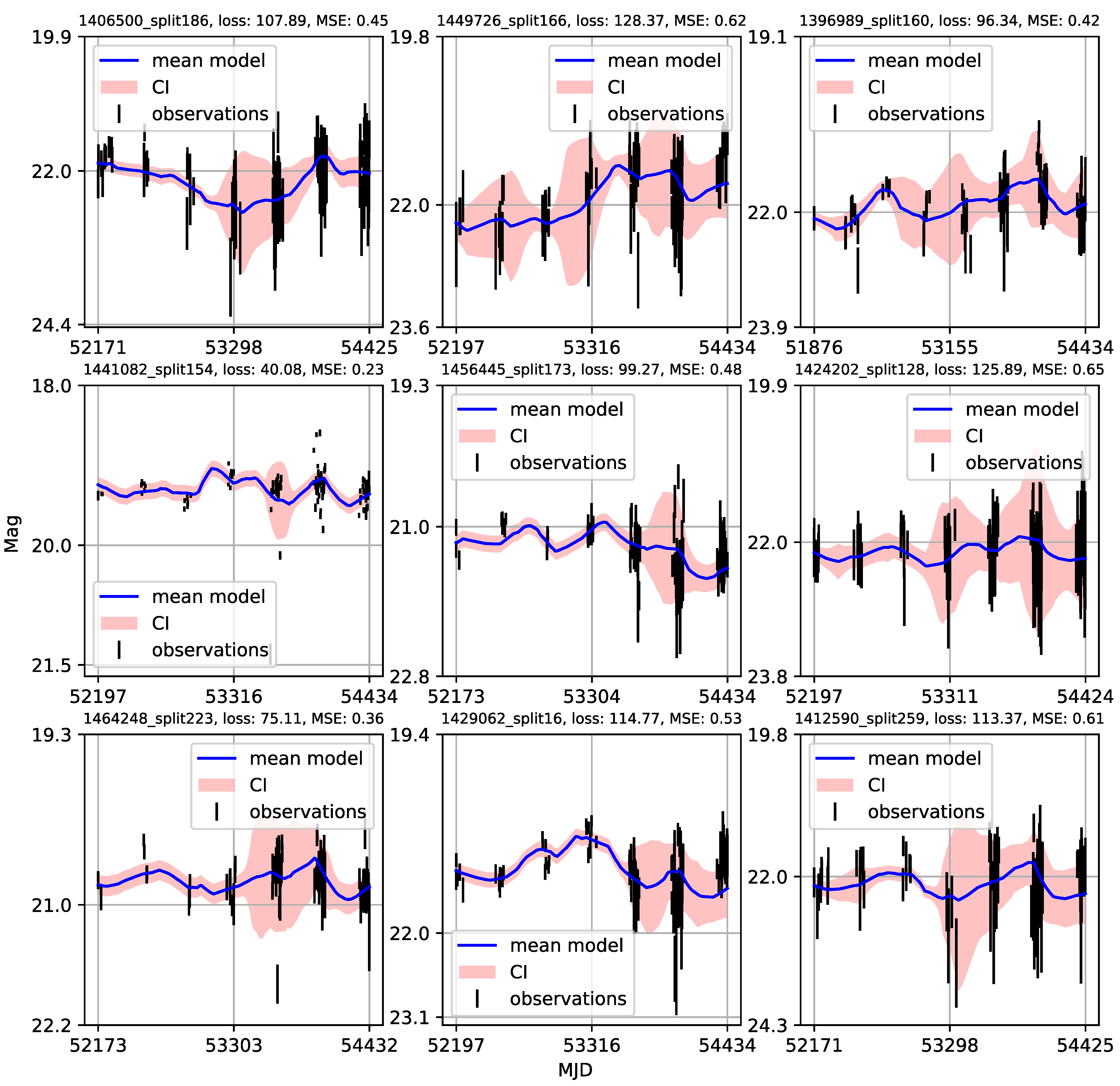
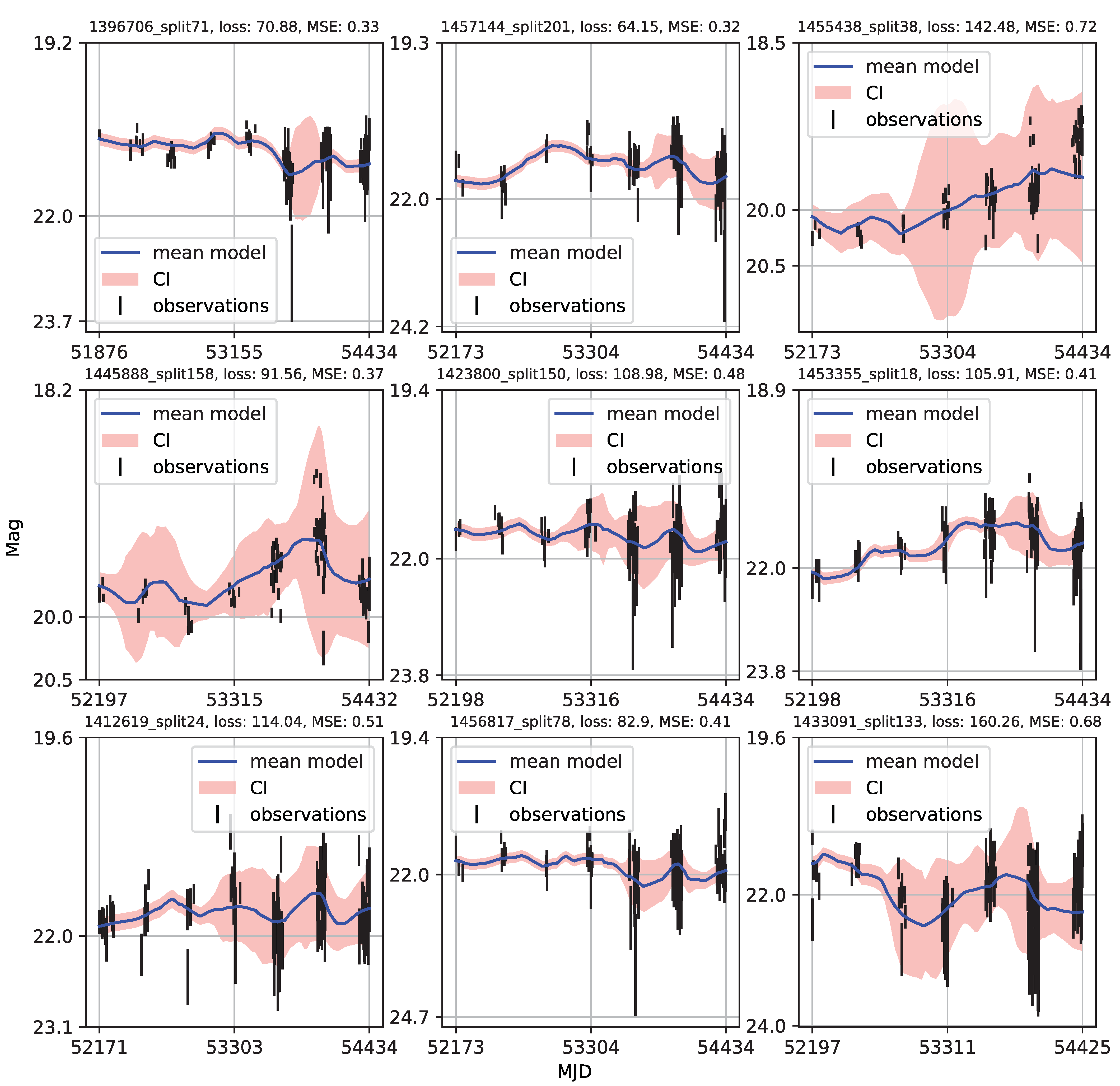
- Individual light curves of 1006 quasars having more than 100 epochs in LSST Active Galactic Nuclei Scientific Collaboration data challenge database exhibit a variety of behaviors, which can be generally stratified via the neural network into 36 clusters.
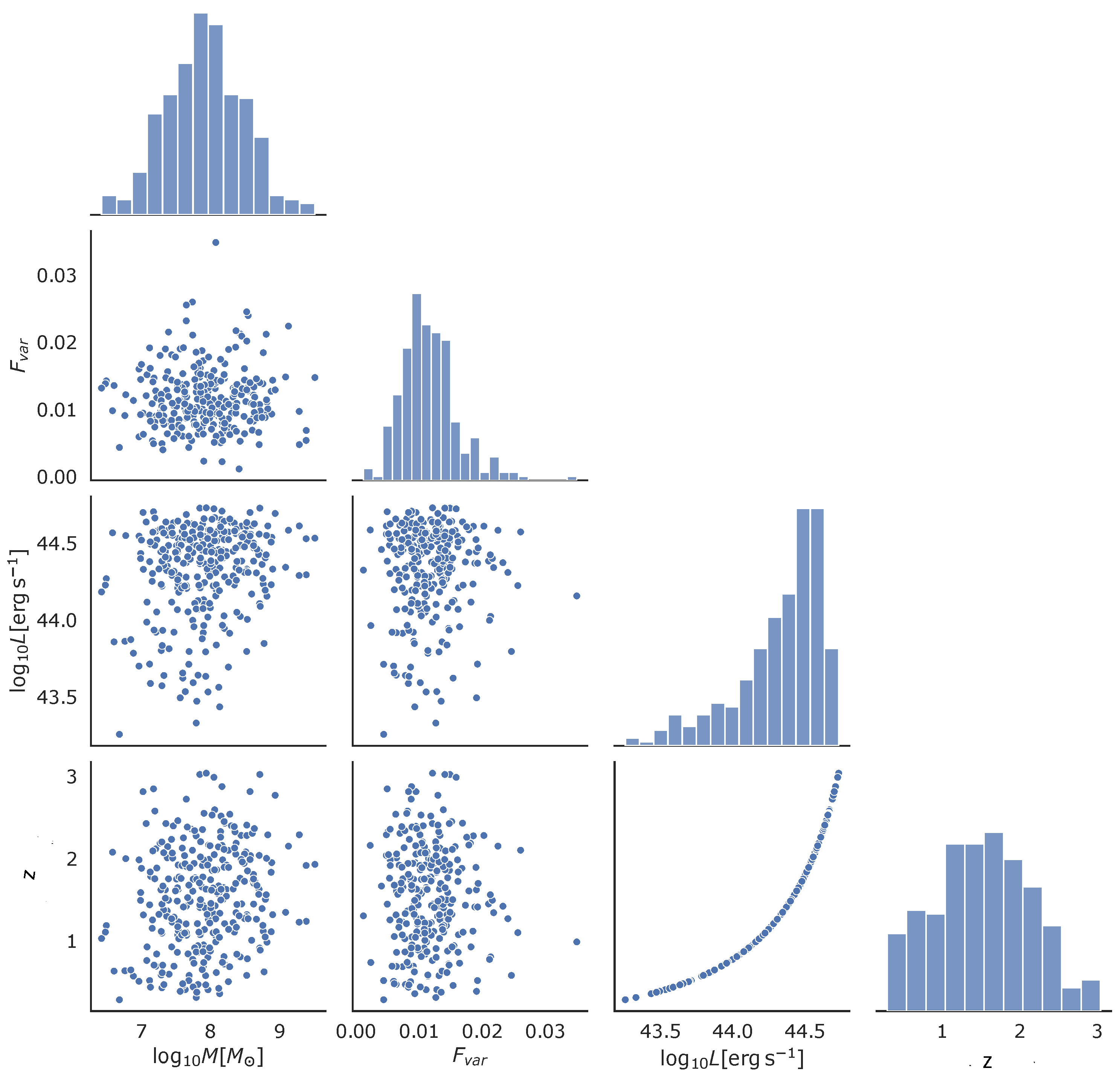
- A case study of one of the stratified sets of u-band light curves for 283 quasars with very low variability 0.03 is presented here. The CNP model has an average mean square error of ∼5% (0.5 mag) on this stratum. Interestingly, all of the light curves in this stratum show features resembling the flares. An initial modified structure-function analysis suggests that these features may be linked to microlensing events that occur over longer time scales of five to ten years.
- As many of the light curves in the LSST AGN data challenge database could be modeled with CNP, there are still enough objects having interesting features in the light curves (as our case study suggests) to urge a more extensive investigation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AGN | active galactic nuclei |
| LSST | Legacy Survey of Space and Time |
| LSST_AGN_DC | LSST AGN data challenge database |
| SMBH | Supermassive black hole |
Appendix A. Catalogue of CNP Models of u-Band Light Curves
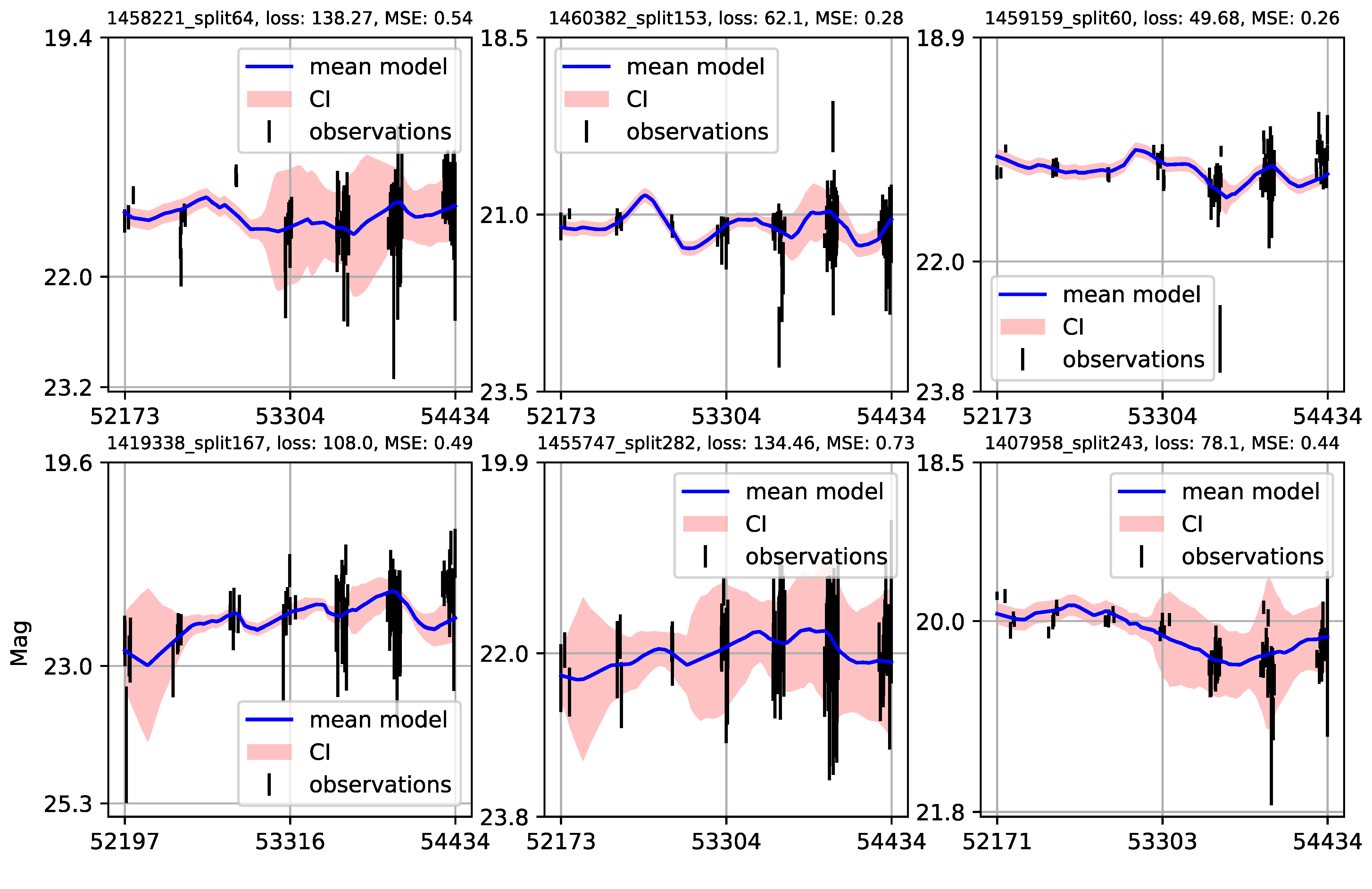
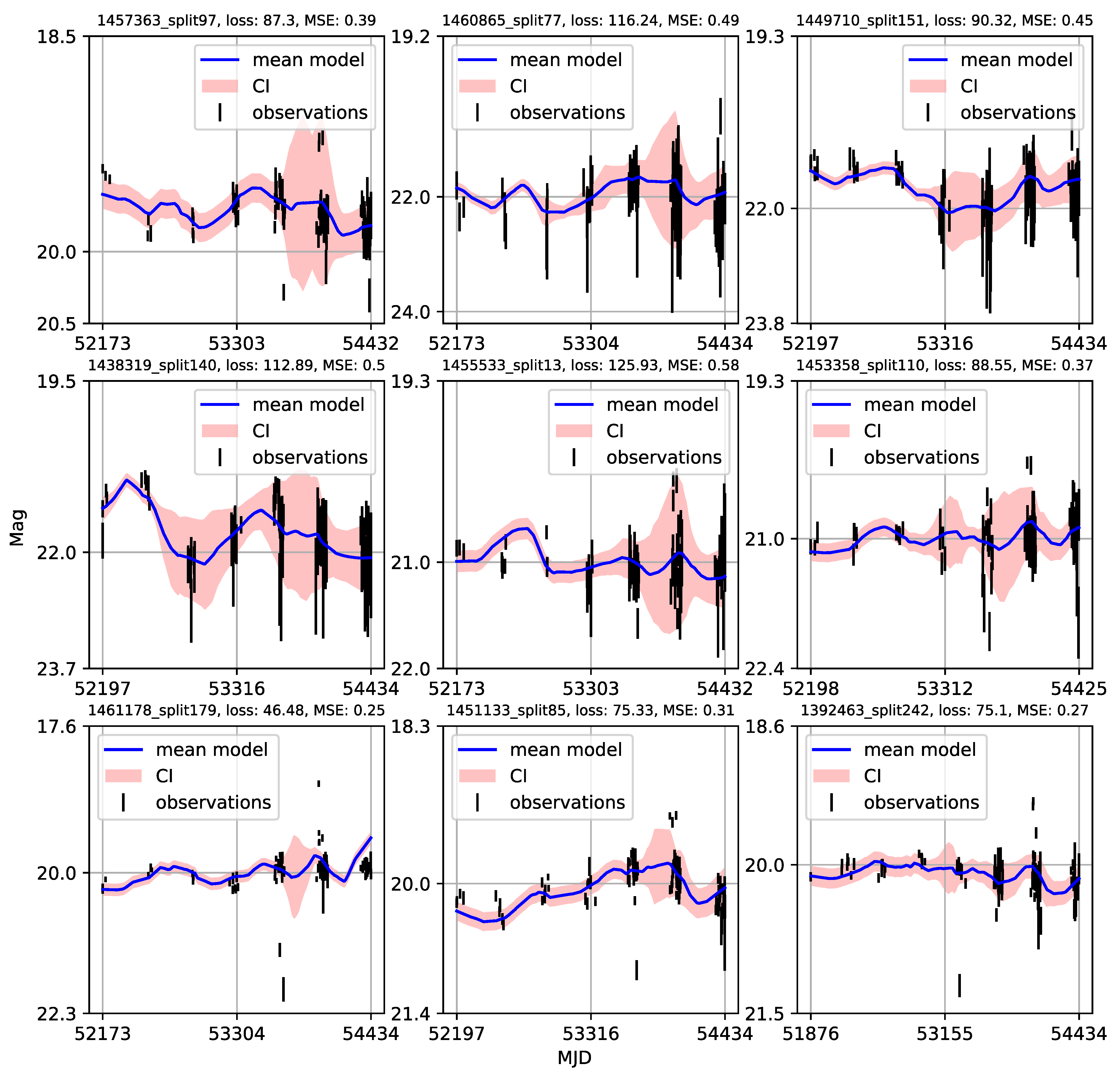
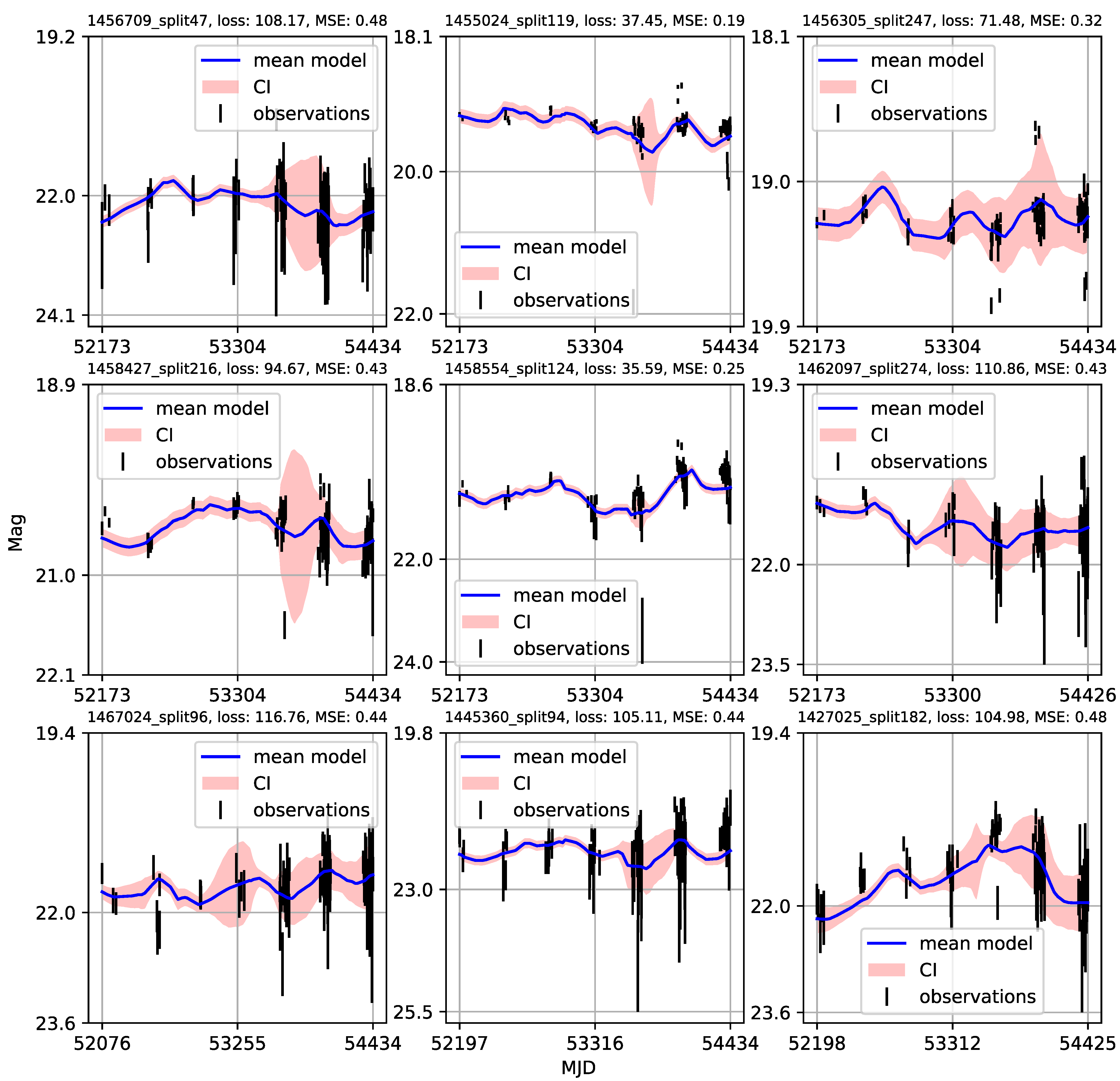
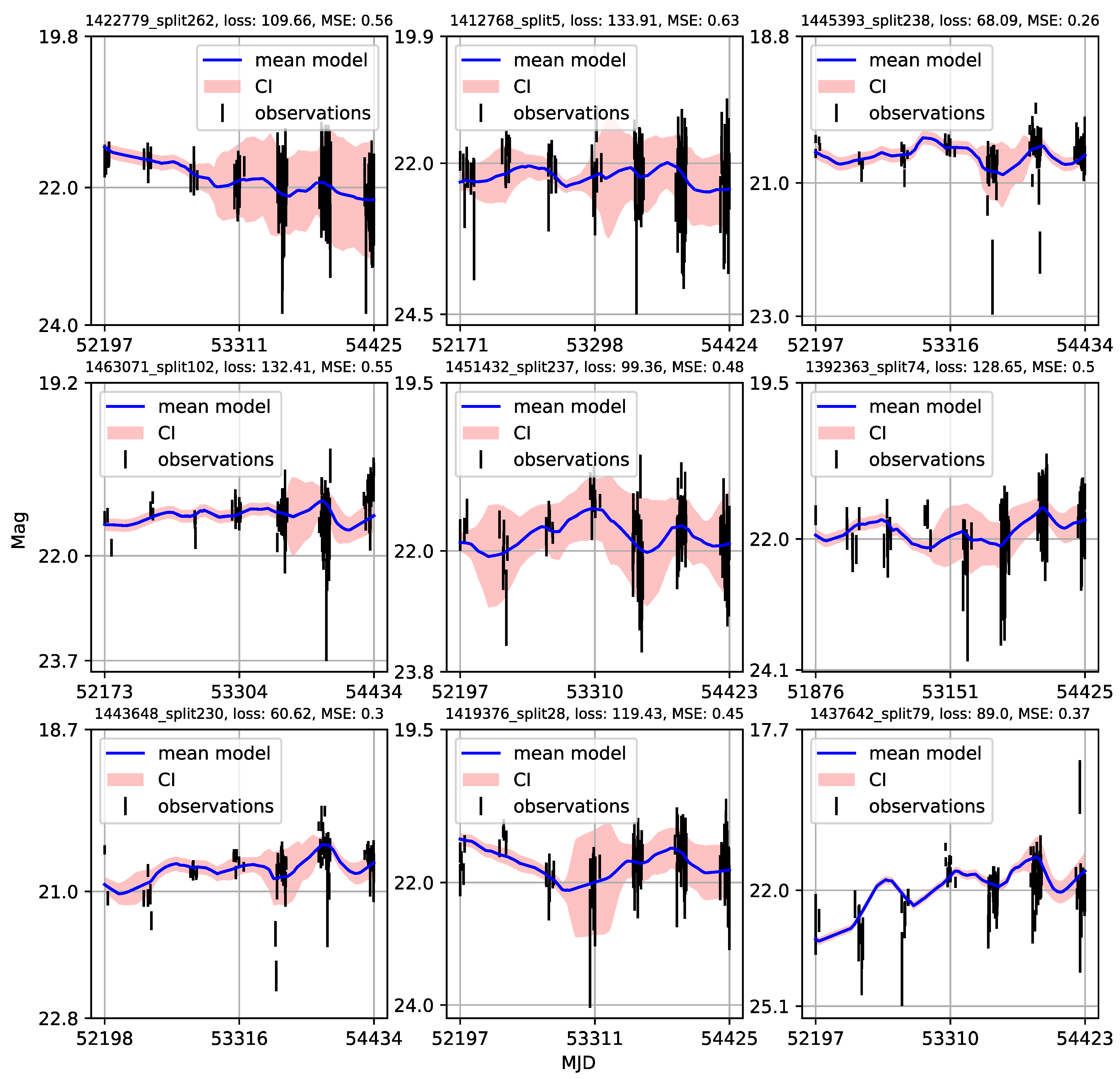
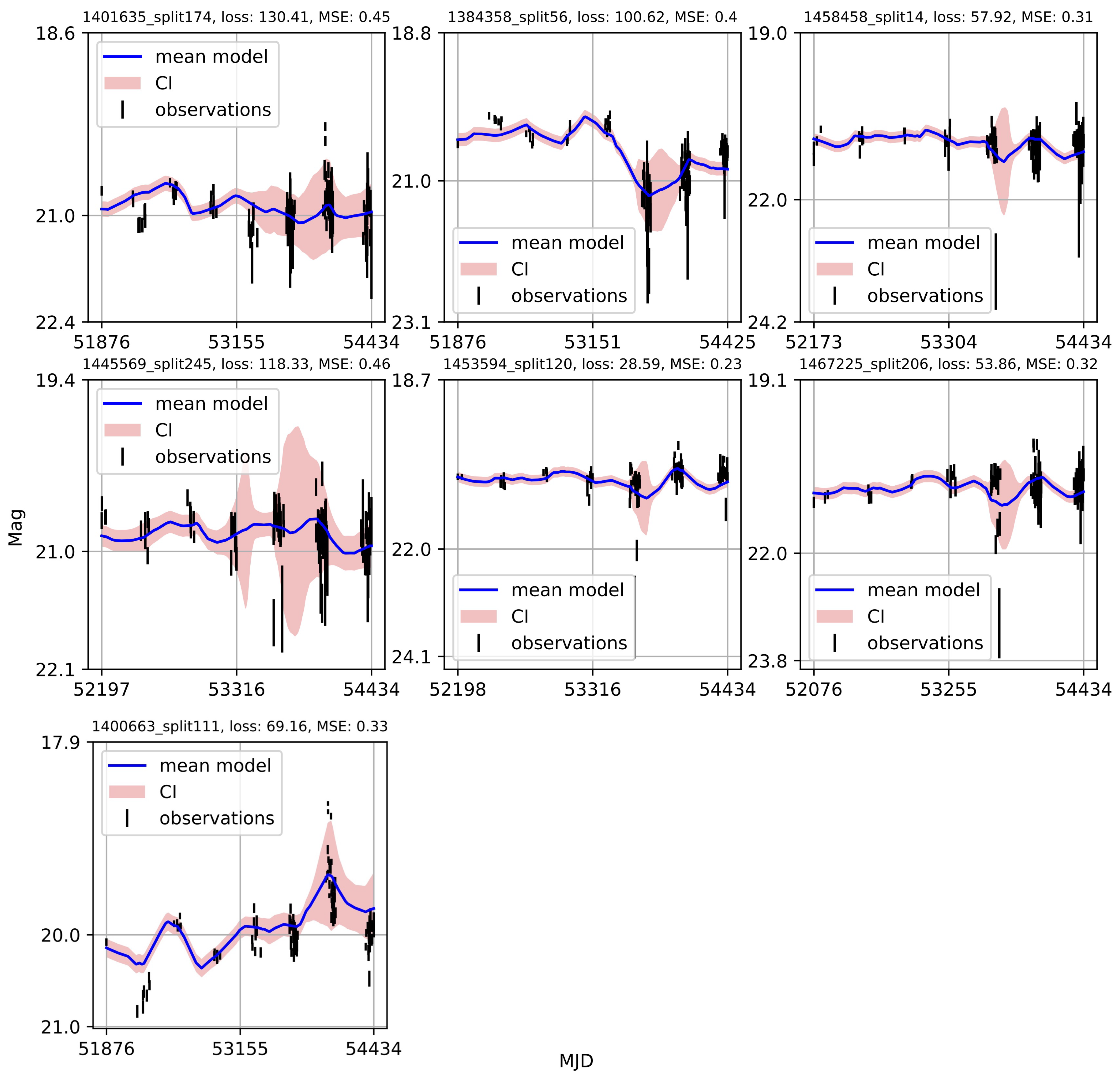
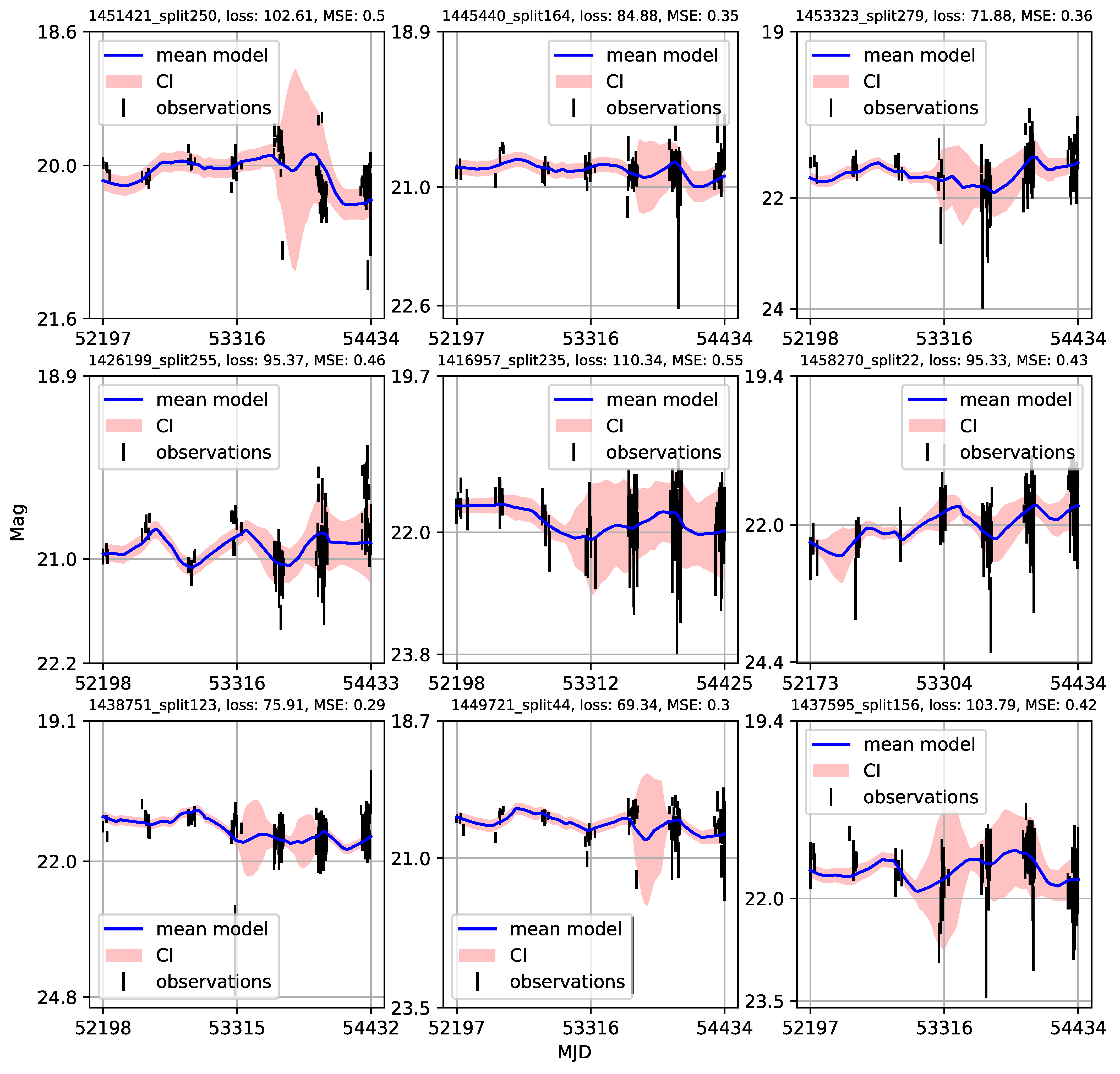
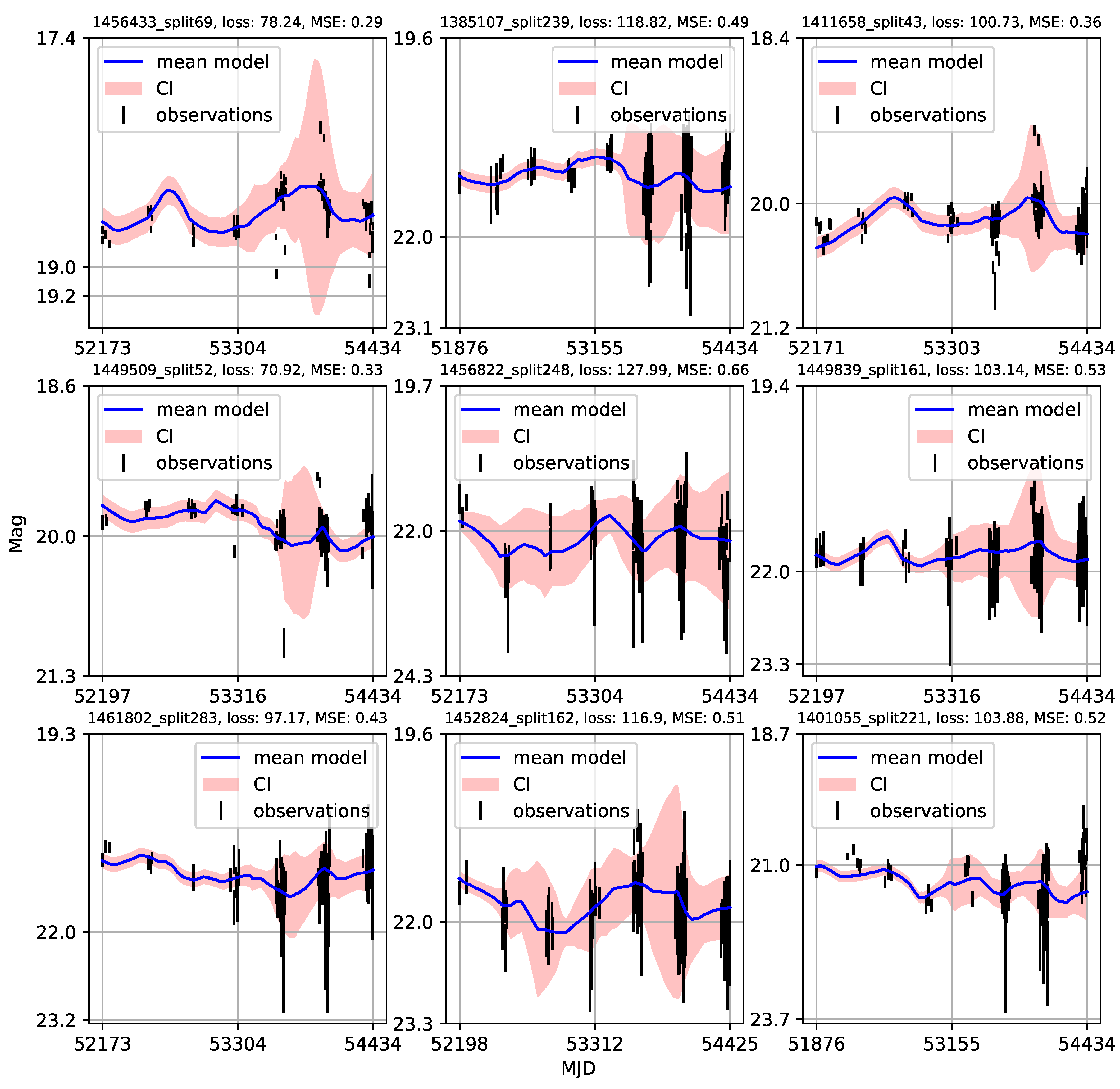


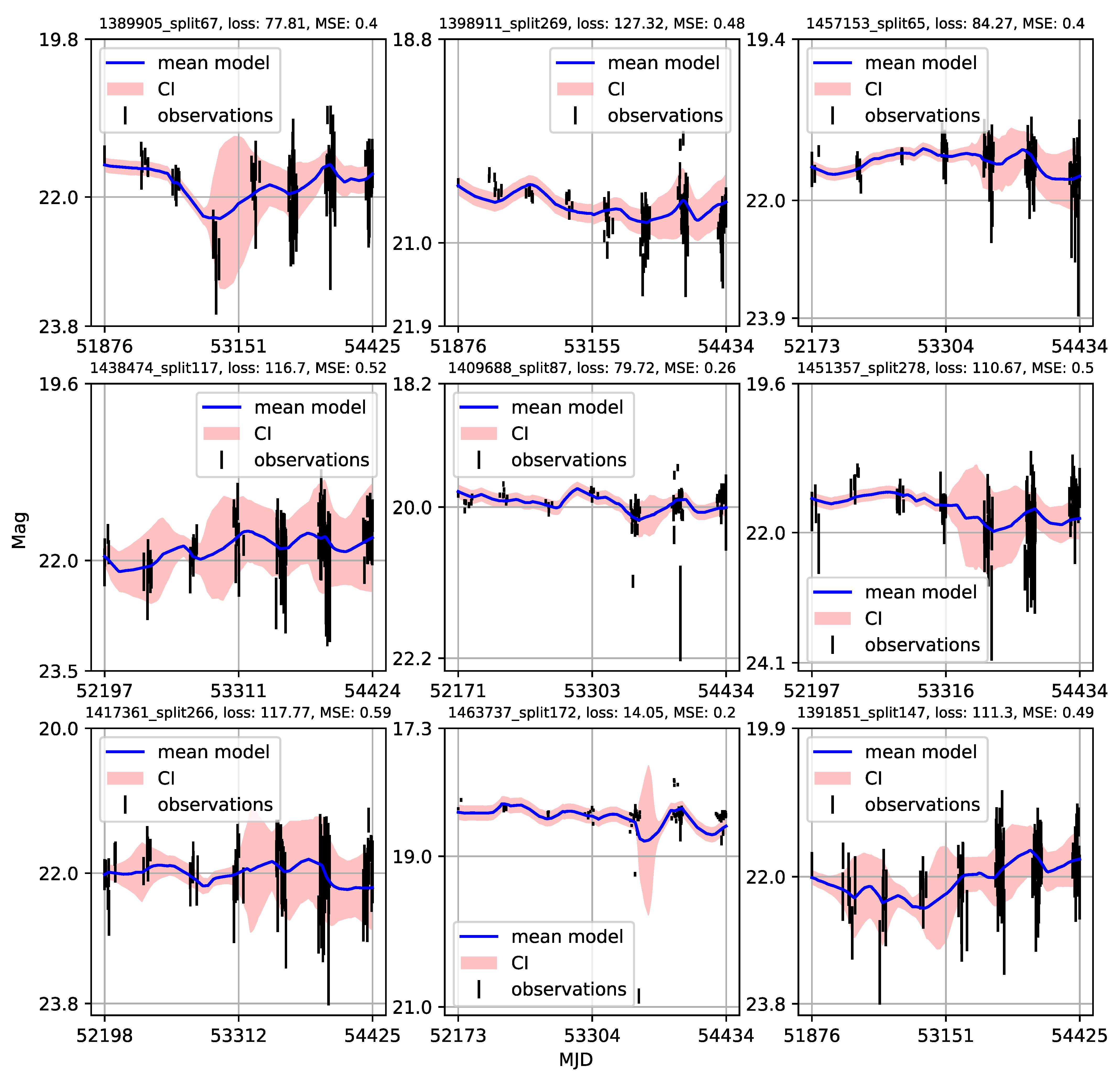
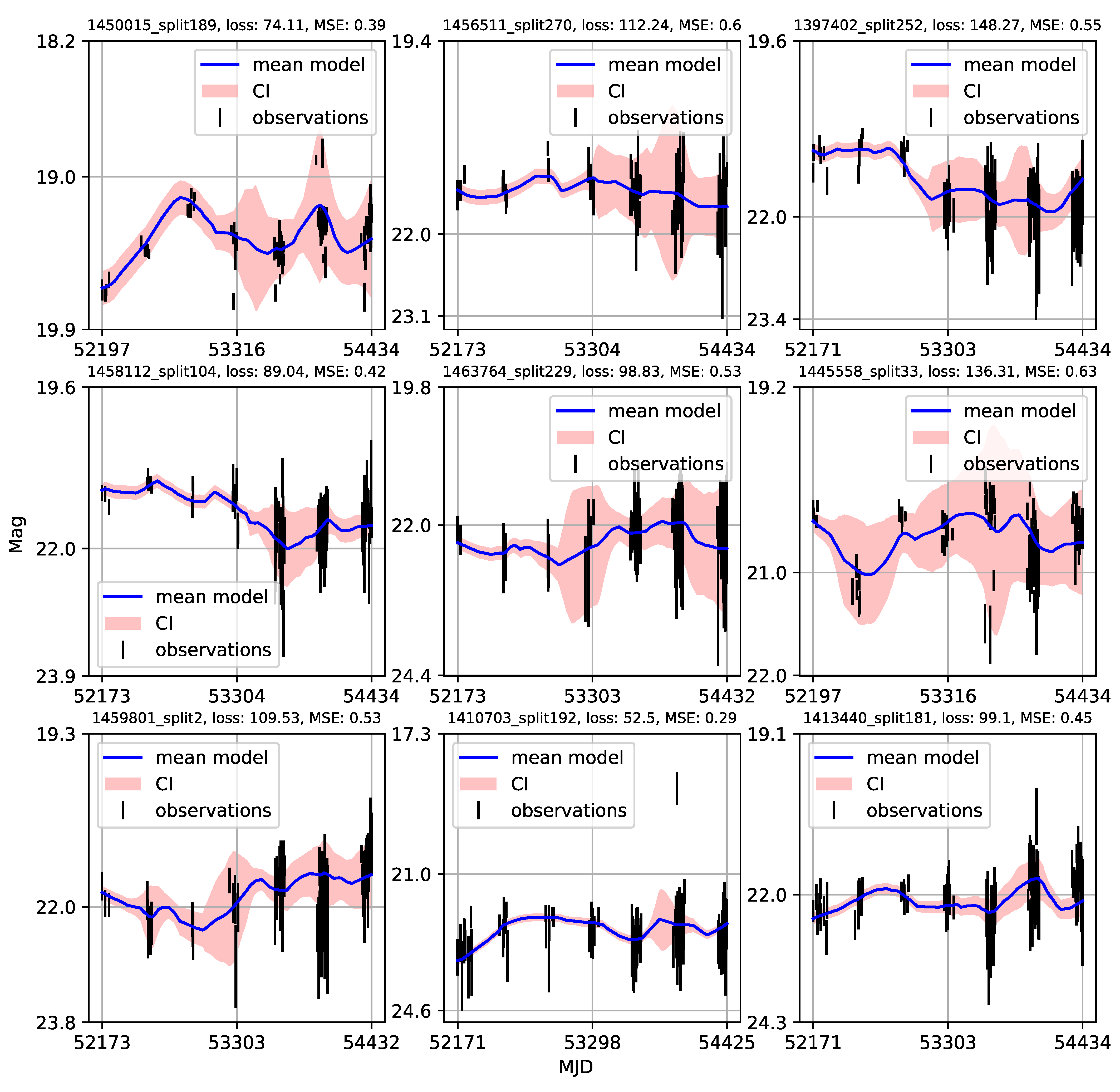
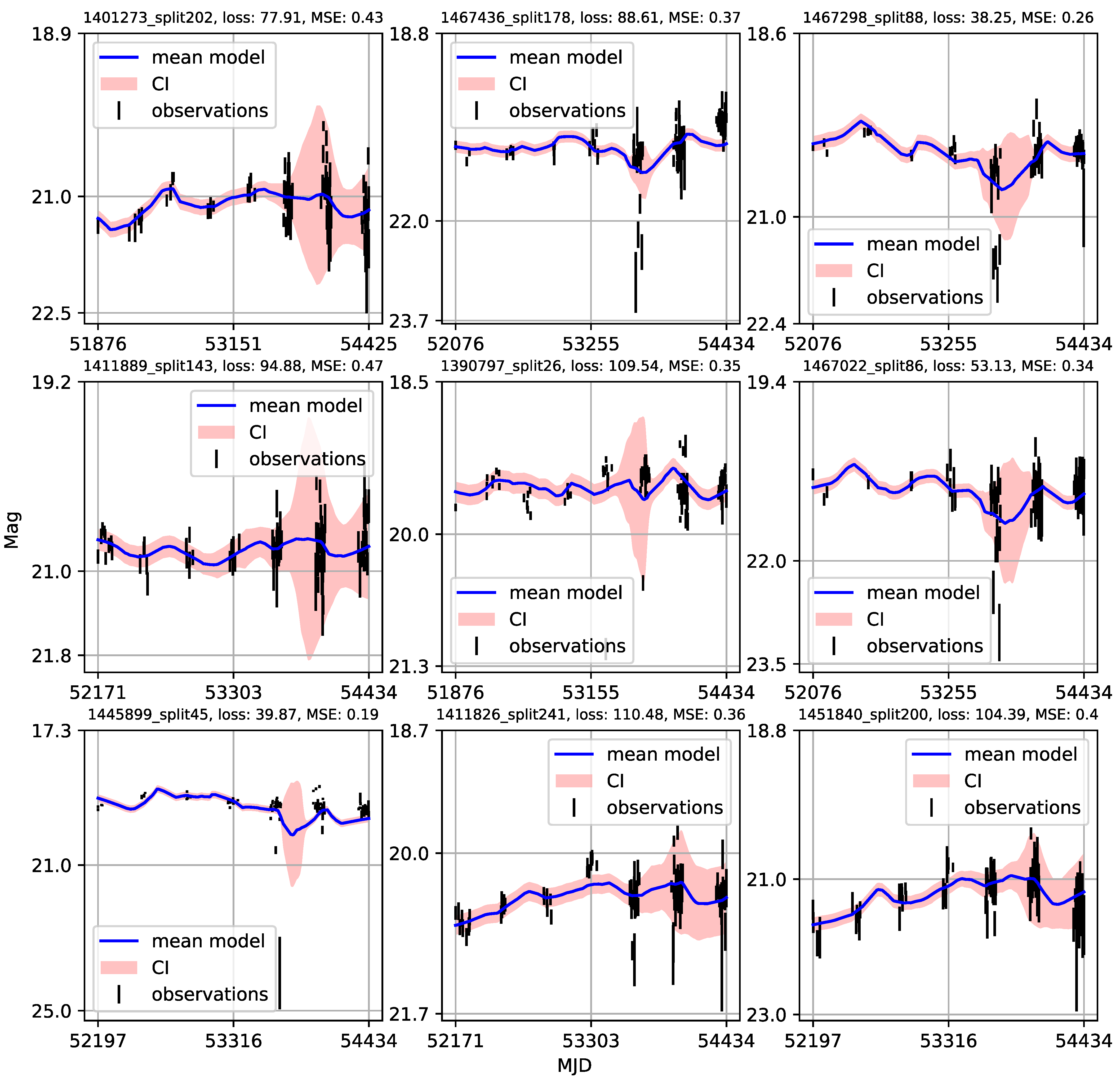

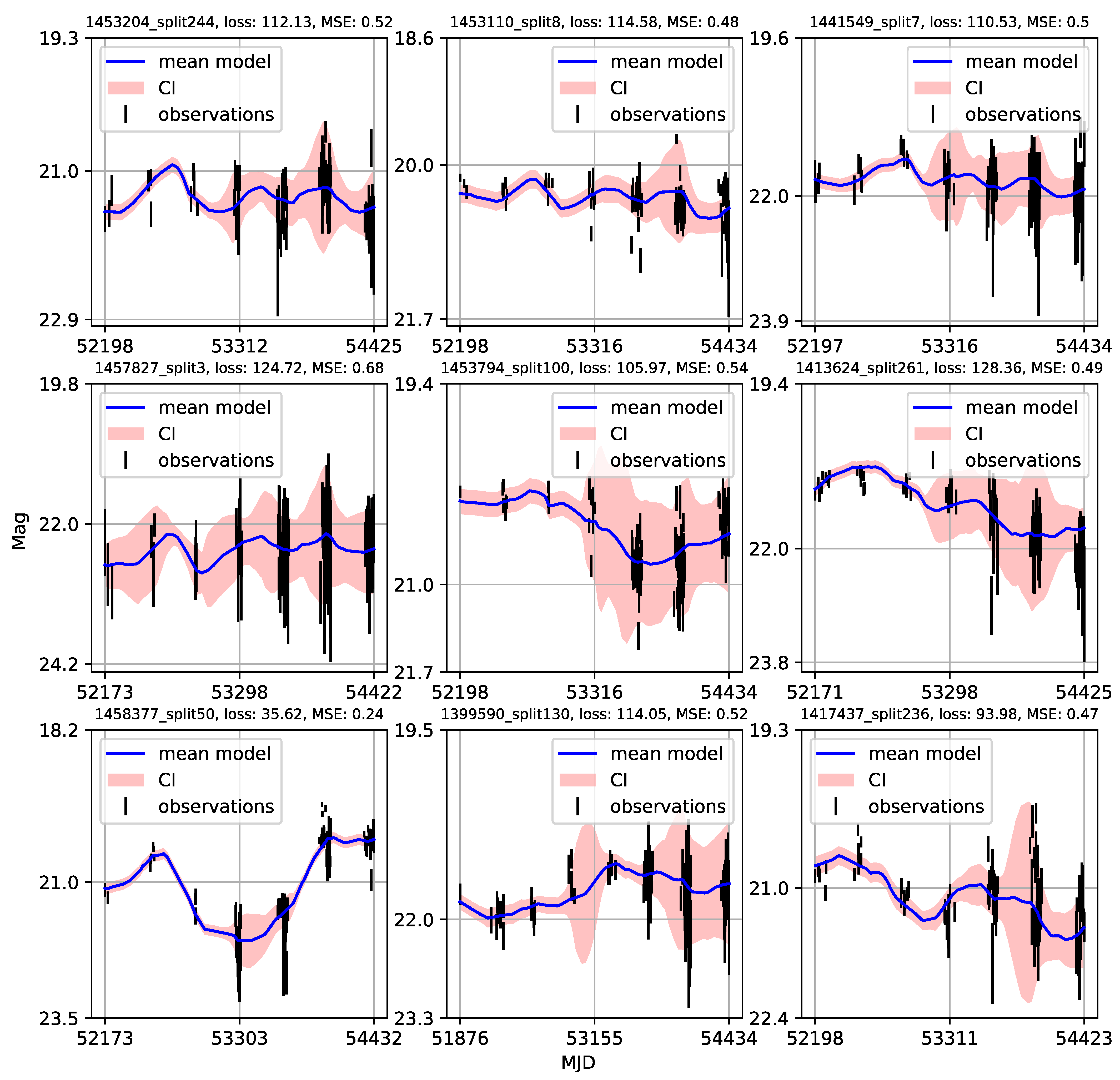
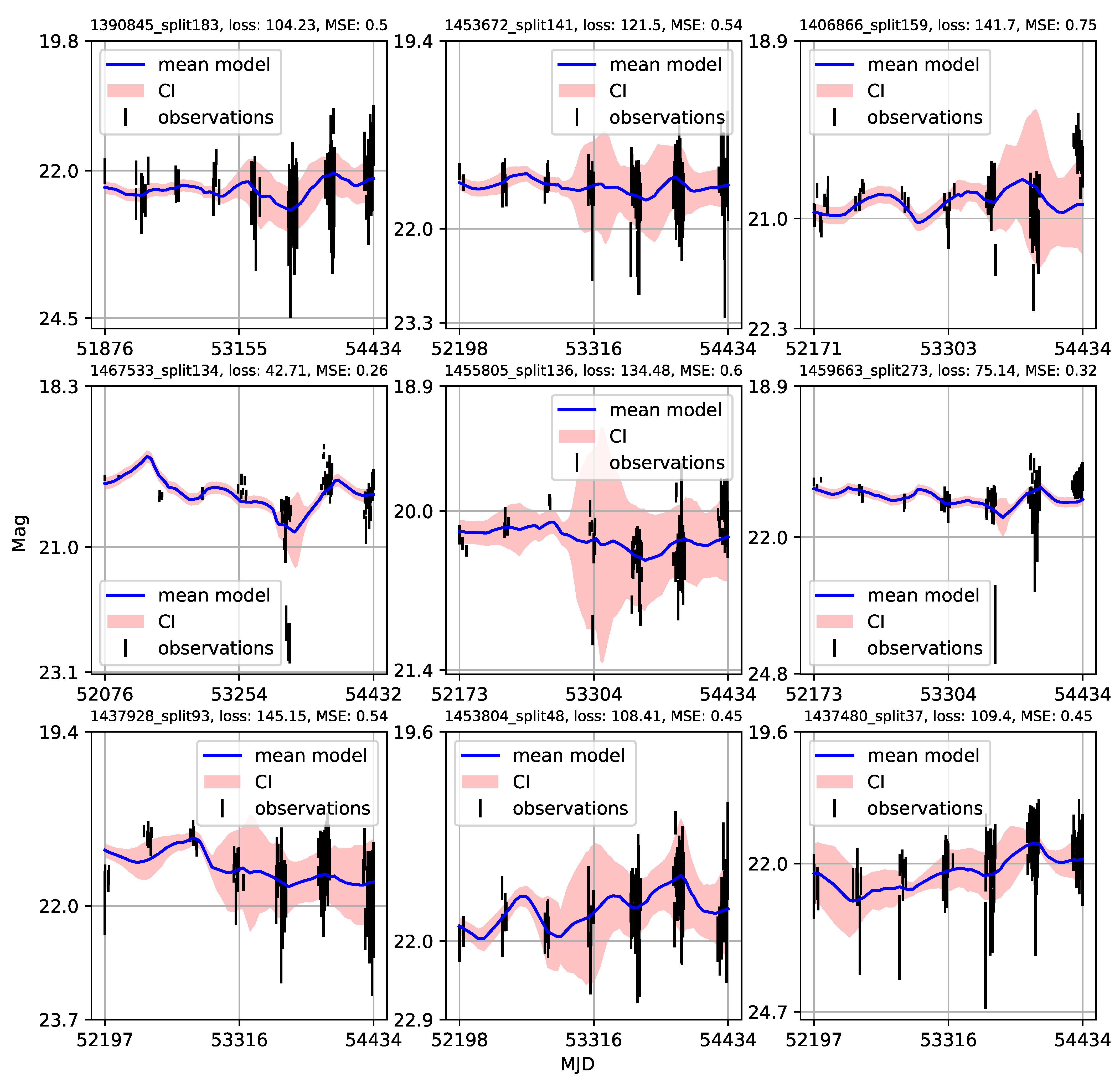
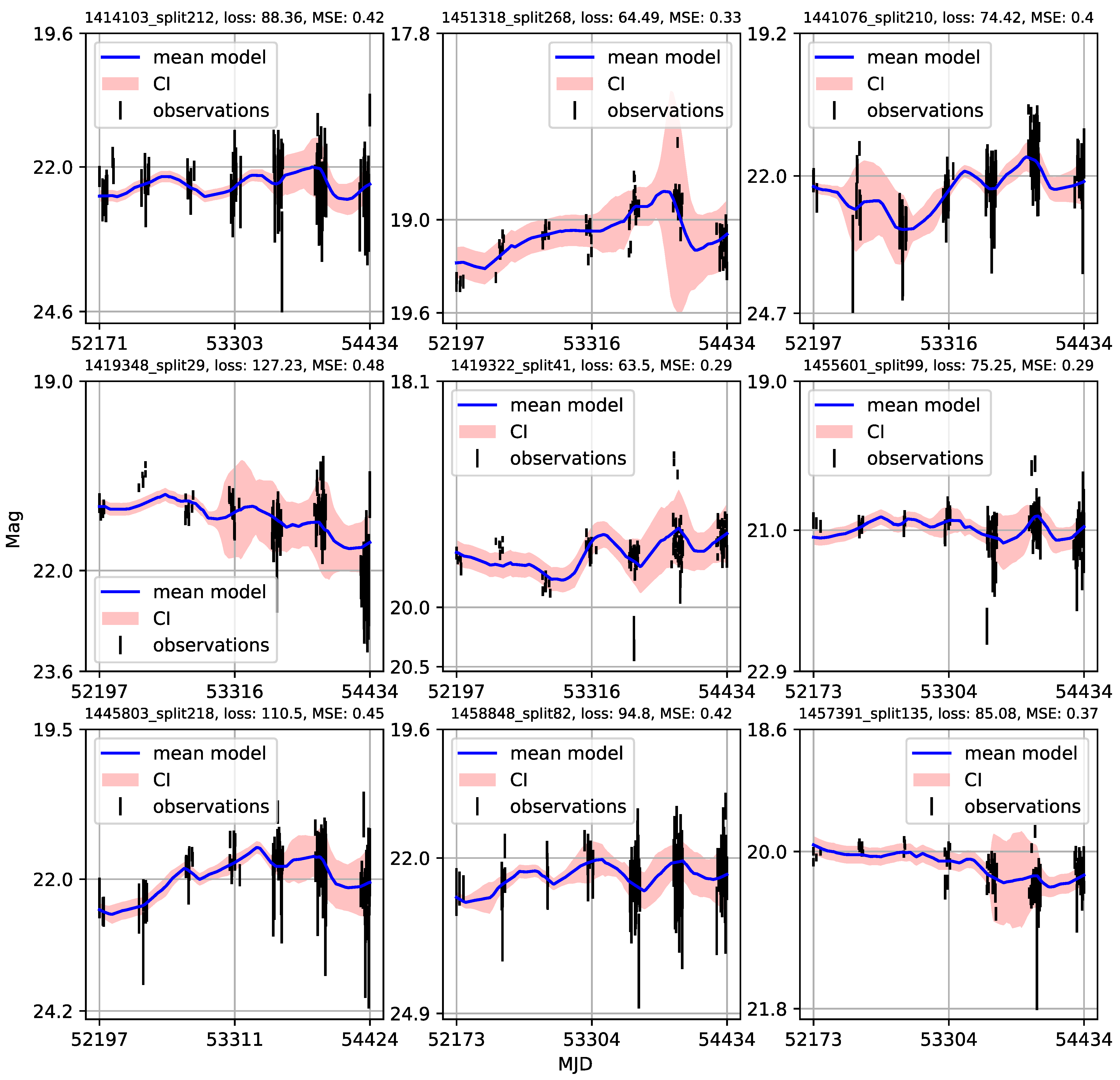
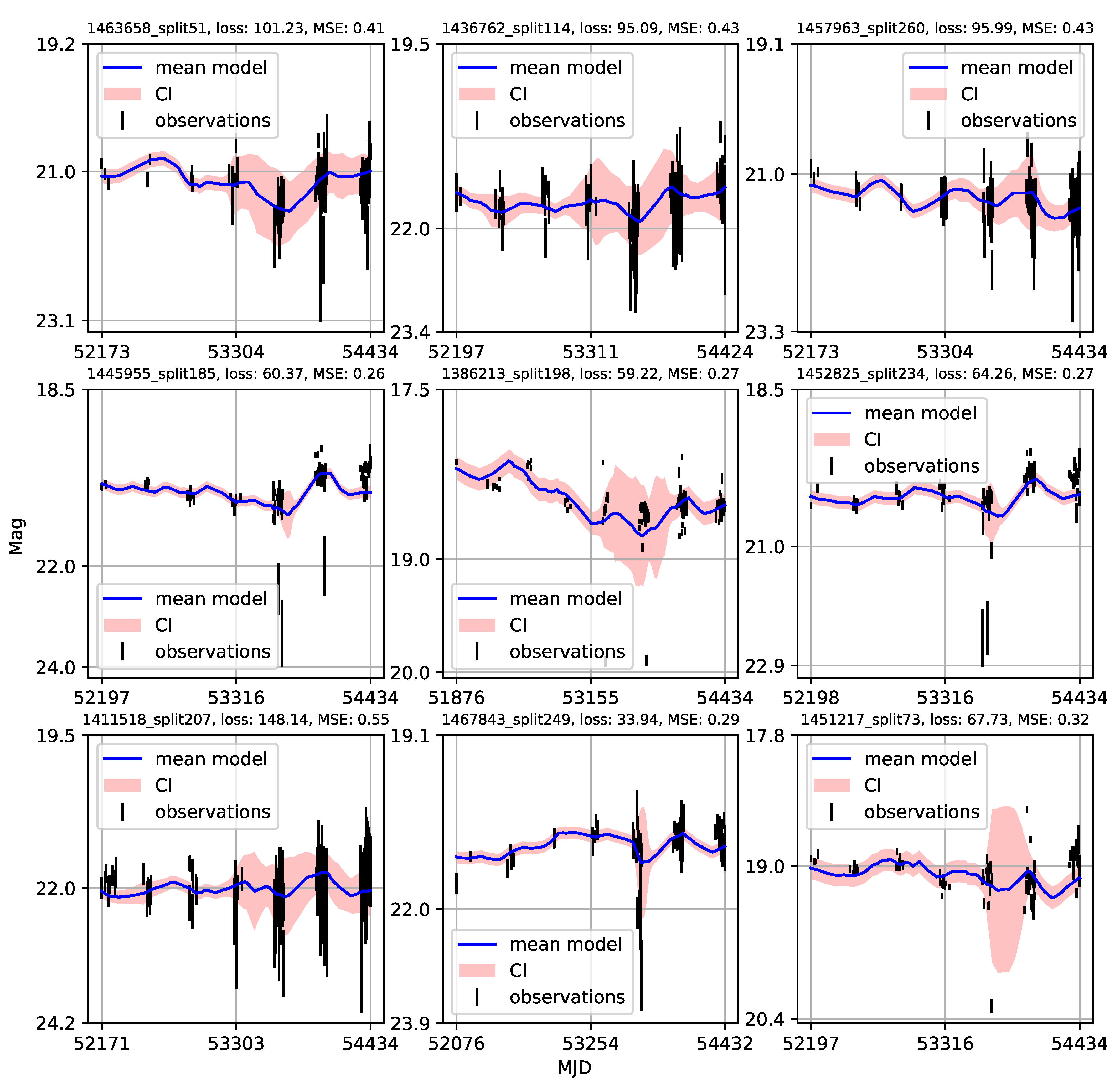
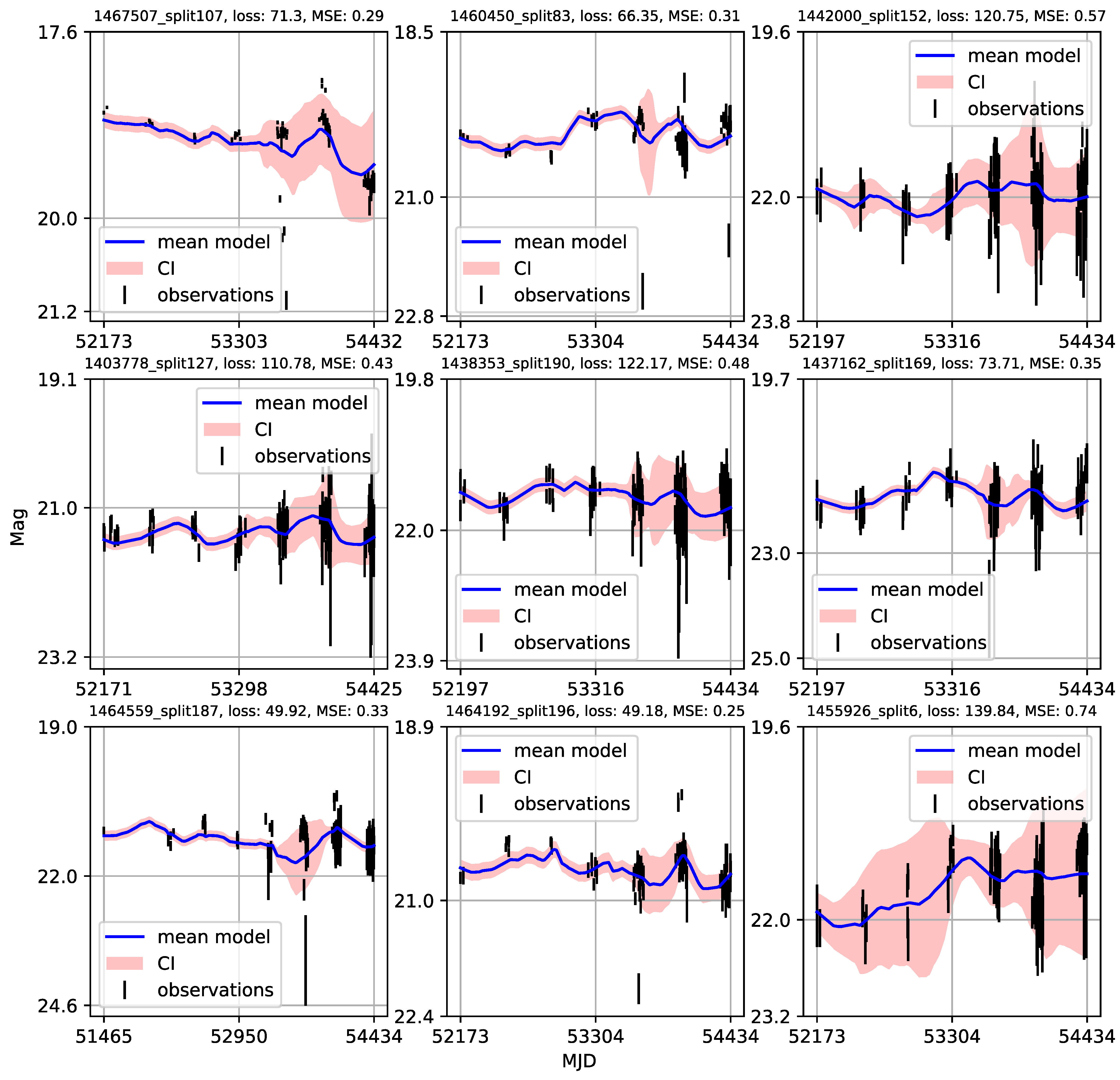

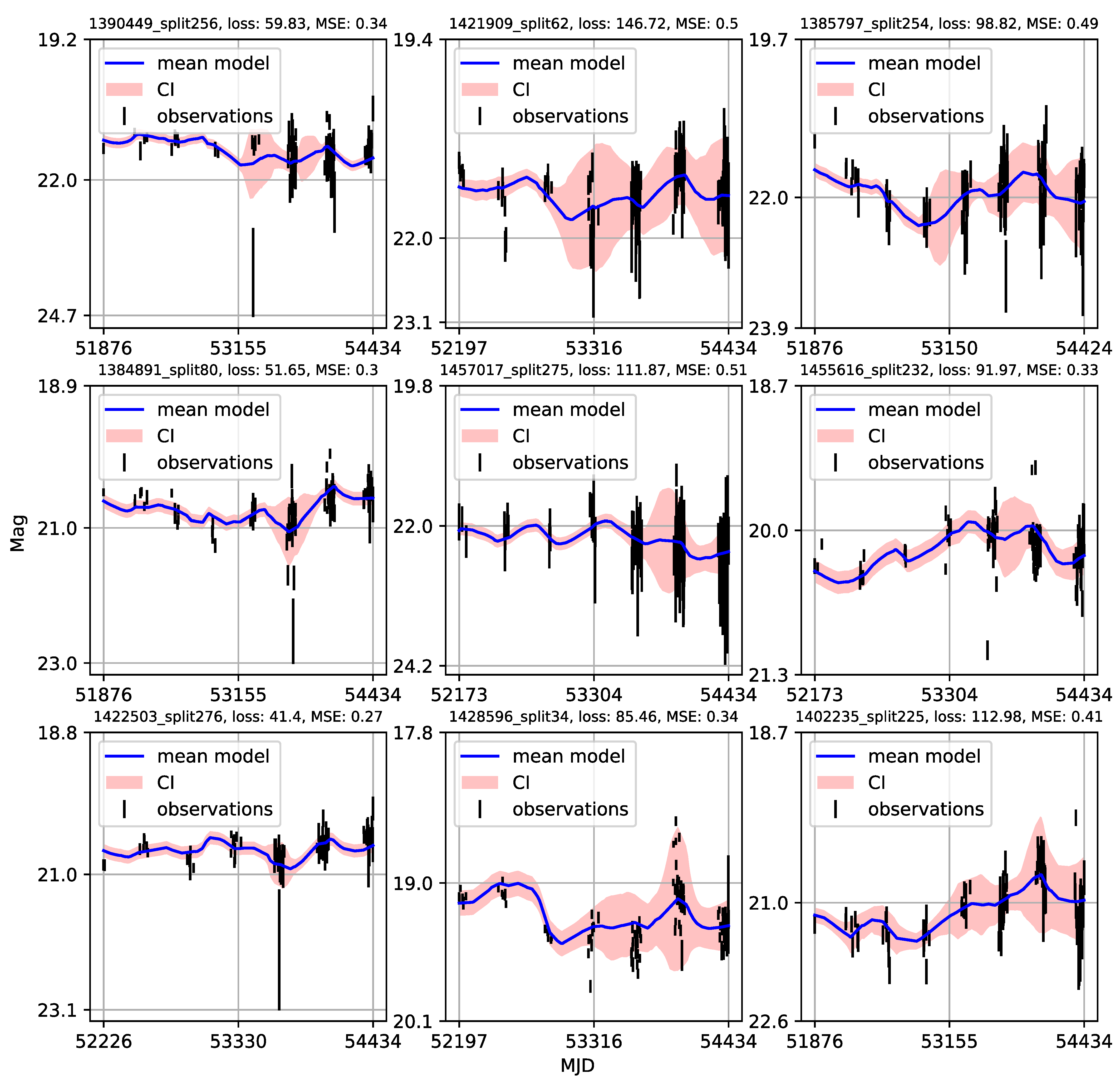
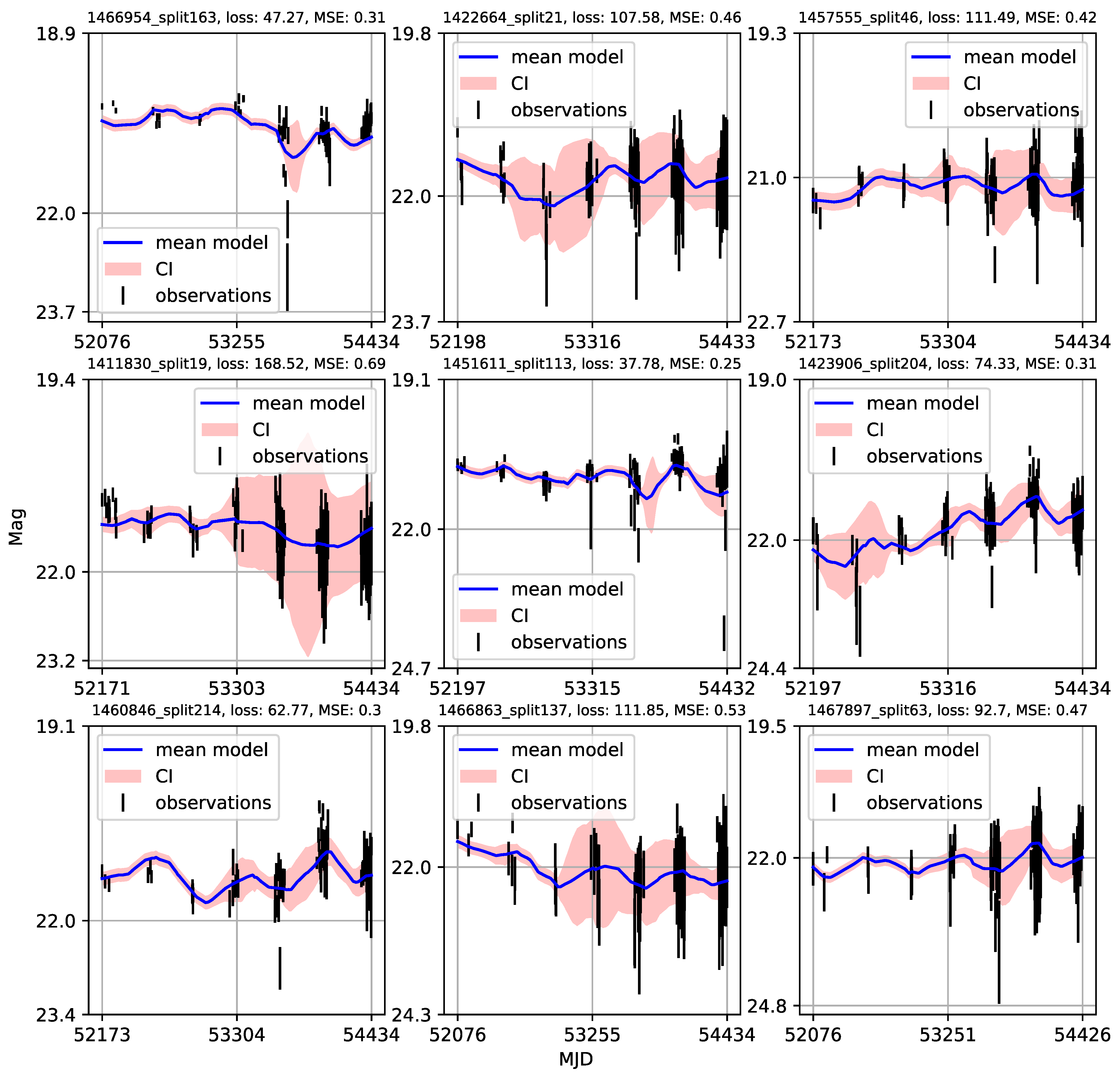
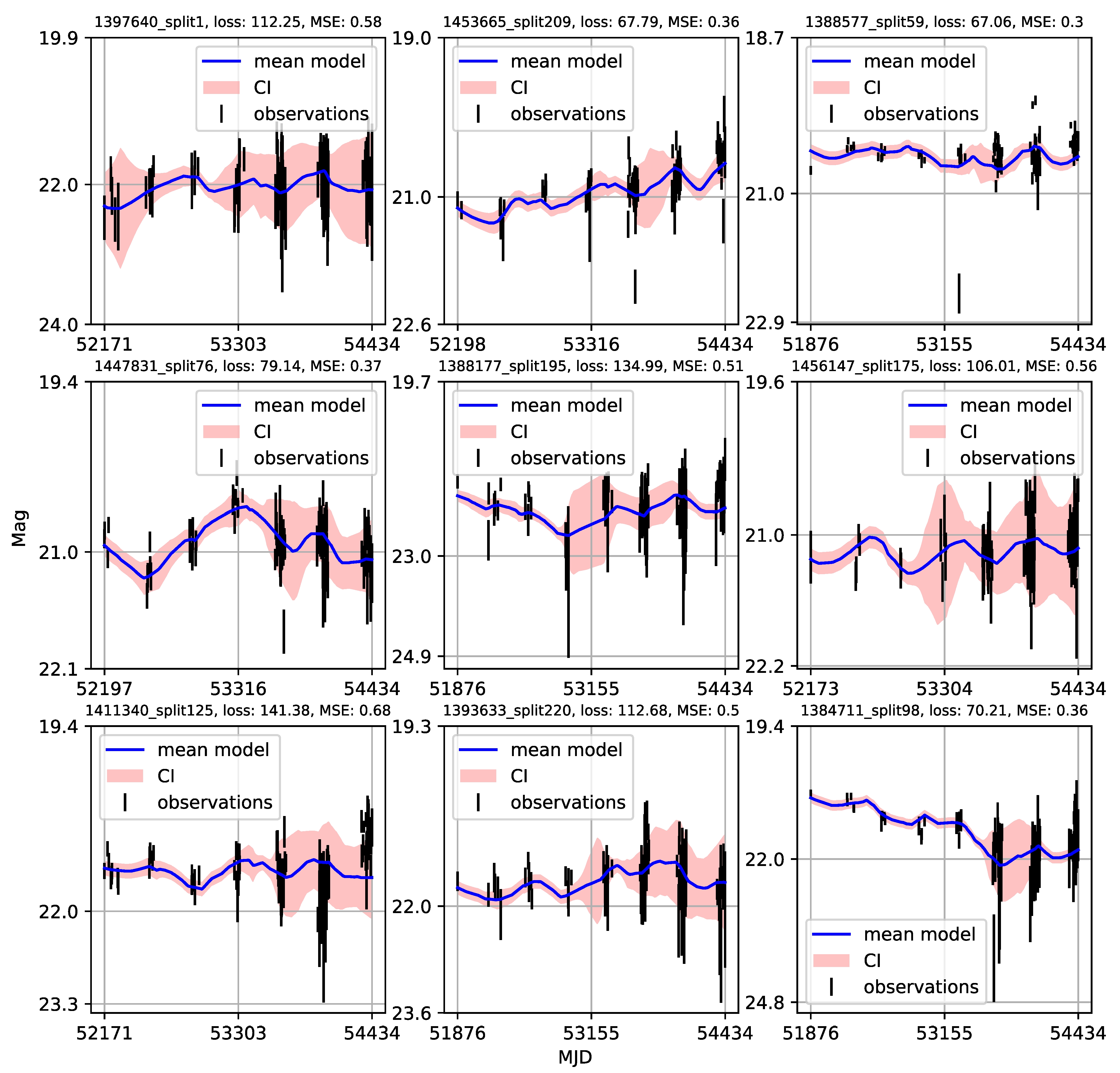
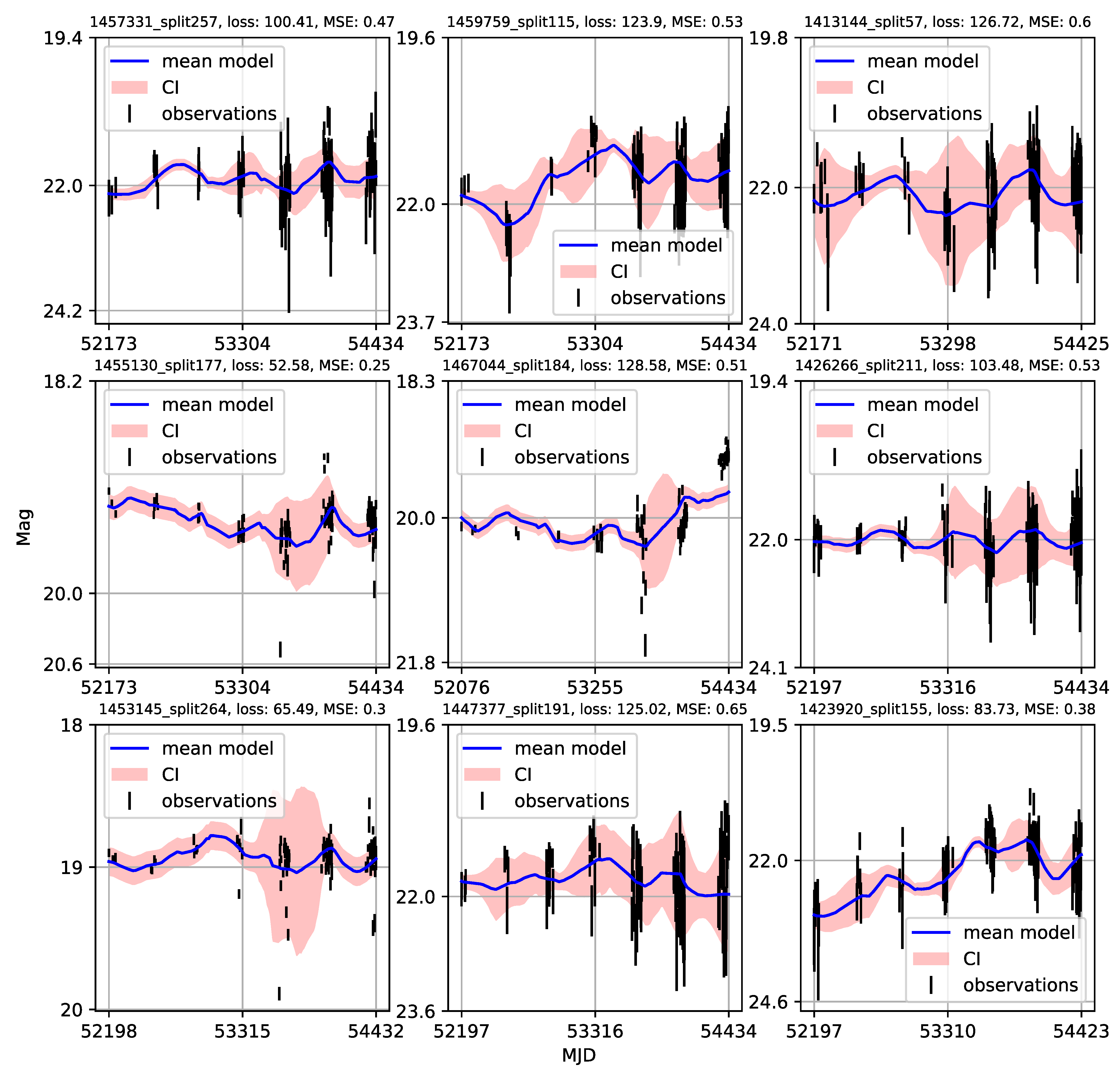


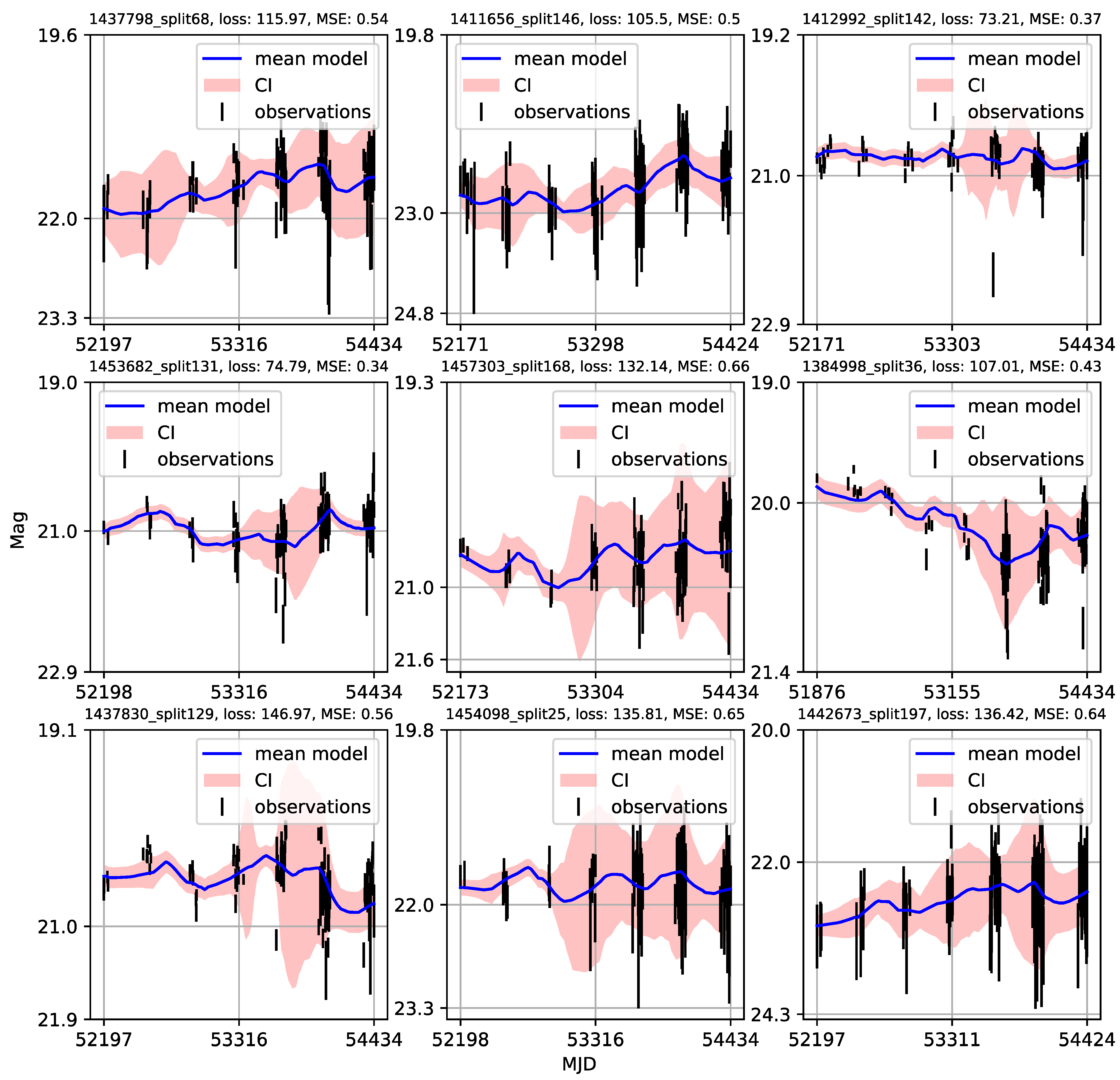

| 1 | Gaining knowledge from large astronomical databases is a complex procedure, including various deep learning algorithms and procedures so we will use ’deep learning’ in that wide context. |
| 2 | SER-SAG is Serbian team that contributes to AGN investigation and participates in the LSST AGN Scientific Collaboration |
| 3 | behaves as normalized variance so it is more robust to outliers, flares |
| 4 | We underline the distinction between NPs and both classic neural networks and GPs previously applied to quasars’ light curves. Classical neural network fit a single model across points based on learning from a large data collection, whereas GP fits a distribution of curves to a single set of observations (i.e., one light curve). NP combines both approaches, taking use of neural network ability to train on a large collection and GP’s ability to fit the distribution of curves because it is a metalearner. |
| 5 | In neural processes, the predicted distribution over functions is typically a Gaussian distribution, parameterized by a mean and variance. |
| 6 | We will use a subscript to denote all the parameters of the neural network such as number of layers, learning rate, size of batches, etc. |
| 7 | An assumption on is that all finite sets of function evaluations of f are jointly Gaussian distributed. This class of random functions are known as Gaussian Processes (GPs). |
| 8 | We note that the our loss function works quite similarly to the Cross-Entropy. In the PyTorch ecosystem, Cross-Entropy Loss is obtained by combining a log-softmax layer and loss. |
| 9 | Data were transformed using min-max scaler adapted to the range where and stands for the input data (time instances, magnitudes, magnitudes errors), is the maximum of the , and is the minimum of the . This linear transformation (or more precisely affine) preserves the original distribution of data, does not reduce the importance of outliers, and preserves the covariance structure of the data. We used the range of for enabling direct comparisons with [33] original testing data, ensuring consistency in our analysis. |
| 10 | The N is the maximum number of points in the light curves in the given batch; missing values are zeropadded for shorter light curves. We emphasize that our sample of light curves is well balanced as a result of SOM clustering (see for an counter example [58]), so that the number of points per light curve covers a fairly limited range [103, 127] points, requiring negligible padding. |
References
- Ivezić, Ž.; Kahn, S.M.; Tyson, J.A.; Abel, B.; Acosta, E.; Allsman, R.; Alonso, D.; AlSayyad, Y.; Anderson, S.F.; Andrew, J.; et al. LSST: From Science Drivers to Reference Design and Anticipated Data Products. Astrophys. J. 2019, 873, 111. [Google Scholar] [CrossRef]
- Anderson, S.F.; Haggard, D.; Homer, L.; Joshi, N.R.; Margon, B.; Silvestri, N.M.; Szkody, P.; Wolfe, M.A.; Agol, E.; Becker, A.C.; et al. Ultracompact AM Canum Venaticorum Binaries from the Sloan Digital Sky Survey: Three Candidates Plus the First Confirmed Eclipsing System. Astron. J. 2005, 130, 2230–2236. [Google Scholar] [CrossRef]
- Bloom, J.S.; Starr, D.L.; Butler, N.R.; Nugent, P.; Rischard, M.; Eads, D.; Poznanski, D. Towards a real-time transient classification engine. Astron. Nachr. 2008, 329, 284. [Google Scholar] [CrossRef]
- Scolnic, D.; Kessler, R.; Brout, D.; Cowperthwaite, P.S.; Soares-Santos, M.; Annis, J.; Herner, K.; Chen, H.Y.; Sako, M.; Doctor, Z.; et al. How Many Kilonovae Can Be Found in Past, Present, and Future Survey Data Sets? Astrophys. J. Lett. 2018, 852, L3. [Google Scholar] [CrossRef]
- Nuttall, L.K.; Berry, C.P.L. Electromagnetic counterparts of gravitational-wave signals. Astron. Geophys. 2021, 62, 4.15–4.21. [Google Scholar] [CrossRef]
- Kaspi, S.; Brandt, W.N.; Maoz, D.; Netzer, H.; Schneider, D.P.; Shemmer, O. Reverberation Mapping of High-Luminosity Quasars: First Results. Astrophys. J. 2007, 659, 997–1007. [Google Scholar] [CrossRef]
- MacLeod, C.L.; Ivezić, Ž.; Kochanek, C.S.; Kozłowski, S.; Kelly, B.; Bullock, E.; Kimball, A.; Sesar, B.; Westman, D.; Brooks, K.; et al. Modeling the Time Variability of SDSS Stripe 82 Quasars as a Damped Random Walk. Astrophys. J. 2010, 721, 1014–1033. [Google Scholar] [CrossRef]
- Graham, M.J.; Djorgovski, S.G.; Drake, A.J.; Mahabal, A.A.; Chang, M.; Stern, D.; Donalek, C.; Glikman, E. A novel variability-based method for quasar selection: Evidence for a rest-frame ∼54 d characteristic time-scale. Mon. Not. R. Astron. Soc. 2014, 439, 703–718. [Google Scholar] [CrossRef]
- Chapline, G.F.; Frampton, P.H. A new direction for dark matter research: Intermediate-mass compact halo objects. J. Cosmol. Astropart. Phys. 2016, 2016, 042. [Google Scholar] [CrossRef]
- Burke, C.J.; Shen, Y.; Blaes, O.; Gammie, C.F.; Horne, K.; Jiang, Y.F.; Liu, X.; McHardy, I.M.; Morgan, C.W.; Scaringi, S.; et al. A characteristic optical variability time scale in astrophysical accretion disks. Science 2021, 373, 789–792. [Google Scholar] [CrossRef]
- Risaliti, G.; Lusso, E. A Hubble Diagram for Quasars. Astrophys. J. 2015, 815, 33. [Google Scholar] [CrossRef]
- Marziani, P.; Dultzin, D.; del Olmo, A.; D’Onofrio, M.; de Diego, J.A.; Stirpe, G.M.; Bon, E.; Bon, N.; Czerny, B.; Perea, J.; et al. The quasar main sequence and its potential for cosmology. Proc. Nucl. Act. Galaxies Cosm. Time 2021, 356, 66–71. [Google Scholar] [CrossRef]
- Tachibana, Y.; Graham, M.J.; Kawai, N.; Djorgovski, S.G.; Drake, A.J.; Mahabal, A.A.; Stern, D. Deep Modeling of Quasar Variability. Astrophys. J. 2020, 903, 54. [Google Scholar] [CrossRef]
- Kawaguchi, T.; Mineshige, S.; Umemura, M.; Turner, E.L. Optical Variability in Active Galactic Nuclei: Starbursts or Disk Instabilities? Astrophys. J. 1998, 504, 671–679. [Google Scholar] [CrossRef]
- Hawkins, M.R.S. Timescale of variation and the size of the accretion disc in active galactic nuclei. Astron. Astrophys. 2007, 462, 581–589. [Google Scholar] [CrossRef]
- Zakharov, F.; Popović, L.Č.; Jovanović, P. On the contribution of microlensing to X-ray variability of high-redshifted QSOs. Astron. Astrophys. 2004, 420, 881–888. [Google Scholar] [CrossRef]
- Kelly, B.C.; Bechtold, J.; Siemiginowska, A. Are the variations in quasar optical flux driven by thermal fluctuations? Astrophys. J. 2009, 698, 895. [Google Scholar] [CrossRef]
- Sesar, B.; Ivezić, Ž.; Lupton, R.H.; Jurić, M.; Gunn, J.E.; Knapp, G.R.; DeLee, N.; Smith, J.A.; Miknaitis, G.; Lin, H.; et al. Exploring the Variable Sky with the Sloan Digital Sky Survey. Astron. J. 2007, 134, 2236–2251. [Google Scholar] [CrossRef]
- MacLeod, C.L.; Ivezić, Ž.; Sesar, B.; de Vries, W.; Kochanek, C.S.; Kelly, B.C.; Becker, A.C.; Lupton, R.H.; Hall, P.B.; Richards, G.T.; et al. A description of quasar variability measured using repeated sdss and poss imaging. Astrophys. J. 2012, 753, 106. [Google Scholar] [CrossRef]
- Kozłowski, S. Limitations on the recovery of the true AGN variability parameters using damped random walk modeling. Astron. Astrophys. 2017, 597, A128. [Google Scholar] [CrossRef]
- Kelly, B.C.; Becker, A.C.; Sobolewska, M.; Siemiginowska, A.; Uttley, P. Flexible and scalable methods for quantifying stochastic variability in the era of massive time-domain astronomical data sets. Astrophys. J. 2014, 788, 33. [Google Scholar] [CrossRef]
- Graham, M.J.; Djorgovski, S.G.; Drake, A.J.; Stern, D.; Mahabal, A.A.; Glikman, E.; Larson, S.; Christensen, E. Understanding extreme quasar optical variability with CRTS—I. Major AGN flares. Mon. Not. R. Astron. Soc. 2017, 470, 4112–4132. [Google Scholar] [CrossRef]
- Xin, C.; Haiman, Z. Ultra-short-period massive black hole binary candidates in LSST as LISA ‘verification binaries’. MNRAS 2021, 506, 2408–2417. [Google Scholar] [CrossRef]
- Amaro-Seoane, P.; Audley, H.; Babak, S.; Baker, J.; Barausse, E.; Bender, P.; Berti, E.; Binetruy, P.; Born, M.; Bortoluzzi, D.; et al. Laser Interferometer Space Antenna. arXiv 2017, arXiv:1702.00786. [Google Scholar] [CrossRef]
- Haiman, Z.; Kocsis, B.; Menou, K. The Population of Viscosity- and Gravitational Wave-Driven Supermassive Black Hole Binaries among Luminous Active Galactic Nuclei. Astrophys. J. 2009, 700, 1952. [Google Scholar] [CrossRef]
- Emmanoulopoulos, D.; McHardy, I.M.; Papadakis, I.E. Generating artificial light curves: Revisited and updated. Mon. Not. R. Astron. Soc. 2013, 433, 907–927. [Google Scholar] [CrossRef]
- Kelly, B.C.; Treu, T.; Malkan, M.; Pancoast, A.; Woo, J.H. Active Galactic Nucleus Black Hole Mass Estimates in the Era of Time Domain Astronomy. Astrophys. J. 2013, 779, 187. [Google Scholar] [CrossRef]
- Mushotzky, R.F.; Edelson, R.; Baumgartner, W.; Gandhi, P. Kepler Observations of Rapid Optical Variability in Active Galactic Nuclei. Astrophys. J. Lett. 2011, 743, L12. [Google Scholar] [CrossRef]
- Smith, K.L.; Mushotzky, R.F.; Boyd, P.T.; Malkan, M.; Howell, S.B.; Gelino, D.M. The Kepler Light Curves of AGN: A Detailed Analysis. Astrophys. J. 2018, 857, 141. [Google Scholar] [CrossRef]
- Yu, W.; Richards, G.T.; Vogeley, M.S.; Moreno, J.; Graham, M.J. Examining AGN UV/Optical Variability beyond the Simple Damped Random Walk. Astrophys. J. 2022, 936, 132. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Wang, F.; Fan, F.L. Neural Network Gaussian Processes by Increasing Depth. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Danilov, E.; Ćiprijanović, A.; Nord, B. Neural Inference of Gaussian Processes for Time Series Data of Quasars. arXiv 2022, arXiv:2211.10305. [Google Scholar] [CrossRef]
- Garnelo, M.; Schwarz, J.; Rosenbaum, D.; Viola, F.; Rezende, D.; Eslami, S.; Teh, Y. Neural Processes. In Proceedings of the Theoretical Foundations and Applications of Deep Generative Models Workshop, International Conference on Machine Learning (ICML), Stockholm, Sweden, 14–15 July 2018; pp. 1704, 1713. [Google Scholar]
- Yu, W.; Richards, G.; Buat, V.; Brandt, W.N.; Banerji, M.; Ni, Q.; Shirley, R.; Temple, M.; Wang, F.; Yang, J. LSSTC AGN Data Challenge 2021; Zenodo: Geneve, Switzerland, 2022. [Google Scholar] [CrossRef]
- Čvorović-Hajdinjak, I.; Kovačević, A.B.; Ilić, D.; Popović, L.Č.; Dai, X.; Jankov, I.; Radović, V.; Sánchez-Sáez, P.; Nikutta, R. Conditional Neural Process for nonparametric modeling of active galactic nuclei light curves. Astron. Nachr. 2022, 343, e210103. [Google Scholar] [CrossRef]
- Oguri, M.; Marshall, P.J. Gravitationally lensed quasars and supernovae in future wide-field optical imaging surveys. Mon. Not. R. Astron. Soc. 2010, 405, 2579–2593. [Google Scholar] [CrossRef]
- Neira, F.; Anguita, T.; Vernardos, G. A quasar microlensing light-curve generator for LSST. Mon. Not. R. Astron. Soc. 2020, 495, 544–553. [Google Scholar] [CrossRef]
- Savić, D.V.; Jankov, I.; Yu, W.; Petrecca, V.; Temple, M.; Ni, Q.; Shirley, R.; Kovačević, A.; Nikolić, M.; Ilić, D.; et al. The LSST AGN Data Challenge: Selection methods. Astrophys. J. 2022. submitted. [Google Scholar]
- Richards, J.W.; Starr, D.L.; Butler, N.R.; Bloom, J.S.; Brewer, J.M.; Crellin-Quick, A.; Higgins, J.; Kennedy, R.; Rischard, M. On Machine-learned Classification of Variable Stars with Sparse and Noisy Time-series Data. Astrophys. J. 2011, 733, 10. [Google Scholar] [CrossRef]
- Kovacevic, A.; Ilic, D.; Jankov, I.; Popovic, L.C.; Yoon, I.; Radovic, V.; Caplar, N.; Cvorovic-Hajdinjak, I. LSST AGN SC Cadence Note: Two metrics on AGN variability observable. arXiv 2021, arXiv:2105.12420. [Google Scholar] [CrossRef]
- Kovačević, A.B.; Radović, V.; Ilić, D.; Popović, L.Č.; Assef, R.J.; Sánchez-Sáez, P.; Nikutta, R.; Raiteri, C.M.; Yoon, I.; Homayouni, Y.; et al. The LSST Era of Supermassive Black Hole Accretion Disk Reverberation Mapping. Astrophys. J. Suppl. 2022, 262, 49. [Google Scholar] [CrossRef]
- Kasliwal, V.P.; Vogeley, M.S.; Richards, G.T. Are the variability properties of the Kepler AGN light curves consistent with a damped random walk? Mon. Not. R. Astron. Soc. 2015, 451, 4328–4345. [Google Scholar] [CrossRef]
- Vettigli, G. MiniSom: Minimalistic and NumPy-Based Implementation of the Self Organizing Map. 2018. Available online: https://github.com/JustGlowing/minisom (accessed on 8 June 2023).
- Edelson, R.A.; Krolik, J.H.; Pike, G.F. Broad-Band Properties of the CfA Seyfert Galaxies. III. Ultraviolet Variability. Astrophys. J. 1990, 359, 86. [Google Scholar] [CrossRef]
- Vaughan, S.; Edelson, R.; Warwick, R.S.; Uttley, P. On characterizing the variability properties of X-ray light curves from active galaxies. Mon. Not. R. Astron. Soc. 2003, 345, 1271–1284. [Google Scholar] [CrossRef]
- Solomon, R.; Stojkovic, D. Variability in quasar light curves: Using quasars as standard candles. J. Cosmol. Astropart. Phys. 2022, 2022, 060. [Google Scholar] [CrossRef]
- Condon, J.J.; Matthews, A.M. ΛCDM Cosmology for Astronomers. Publ. Astron. Soc. Pac. 2018, 130, 073001. [Google Scholar] [CrossRef]
- Planck Collaboration; Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck 2018 results—VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Rodrigo, C.; Solano, E.; Bayo, A. SVO Filter Profile Service, Version 1.0; IVOA Working Draft: València, Spain, 15 October 2012. [Google Scholar] [CrossRef]
- Rodrigo, C.; Solano, E. The SVO Filter Profile Service. In Proceedings of the XIV. 0 Scientific Meeting (Virtual) of the Spanish Astronomical Society, Virtual, 5–9 September 2020. [Google Scholar]
- Dexter, J.; Agol, E. Quasar Accretion Disks are Strongly Inhomogeneous. Astrophys. J. Lett. 2011, 727, L24. [Google Scholar] [CrossRef]
- Zu, Y.; Kochanek, C.S.; Kozłowski, S.; Udalski, A. Is Quasar Optical Variability a Damped Random Walk? Astrophys. J. 2013, 765, 106. [Google Scholar] [CrossRef]
- Caplar, N.; Lilly, S.J.; Trakhtenbrot, B. Optical Variability of AGNs in the PTF/iPTF Survey. Astrophys. J. 2017, 834, 111. [Google Scholar] [CrossRef]
- Ruan, J.J.; Anderson, S.F.; MacLeod, C.L.; Becker, A.C.; Burnett, T.H.; Davenport, J.R.A.; Ivezić, Ž.; Kochanek, C.S.; Plotkin, R.M.; Sesar, B.; et al. Characterizing the Optical Variability of Bright Blazars: Variability-based Selection of Fermi Active Galactic Nuclei. Astrophys. J. 2012, 760, 51. [Google Scholar] [CrossRef]
- Foong, A.; Bruinsma, W.; Gordon, J.; Dubois, Y.; Requeima, J.; Turner, R. Meta-learning stationary stochastic process prediction with convolutional neural processes. Adv. Neural Inf. Process. Syst. 2020, 33, 8284–8295. [Google Scholar]
- Tak, H.; Mandel, K.; Van Dyk, D.A.; Kashyap, V.L.; Meng, X.L.; Siemiginowska, A. Bayesian estimates of astronomical time delays between gravitationally lensed stochastic light curves. Ann. Appl. Stat. 2017, 13, 1309–1348. [Google Scholar] [CrossRef]
- Breivik, K.; Connolly, A.J.; Ford, K.E.S.; Jurić, M.; Mandelbaum, R.; Miller, A.A.; Norman, D.; Olsen, K.; O’Mullane, W.; Price-Whelan, A.; et al. From Data to Software to Science with the Rubin Observatory LSST. arXiv 2022, arXiv:2208.02781. [Google Scholar] [CrossRef]
- Sánchez-Sáez, P.; Lira, H.; Martí, L.; Sánchez-Pi, N.; Arredondo, J.; Bauer, F.E.; Bayo, A.; Cabrera-Vives, G.; Donoso-Oliva, C.; Estévez, P.A.; et al. Searching for Changing-state AGNs in Massive Data Sets. I. Applying Deep Learning and Anomaly-detection Techniques to Find AGNs with Anomalous Variability Behaviors. Astron. J. 2021, 162, 206. [Google Scholar] [CrossRef]
- Holmstrom, L.; Koistinen, P. Using additive noise in back-propagation training. IEEE Trans. Neural Netw. 1992, 3, 24–38. [Google Scholar] [CrossRef] [PubMed]
- Matsuoka, K. Noise injection into inputs in back-propagation learning. IEEE Trans. Syst. Man Cybern. 1992, 22, 436–440. [Google Scholar] [CrossRef]
- Bishop, C. Training with noise is equivalent to Tikhonov regularization. Neural Comput. 1995, 7, 108–116. [Google Scholar] [CrossRef]
- Wang, C.; Principe, J. Training neural networks with additive noise in the desired signal. IEEE Trans. Neural Netw. 1999, 10, 1511–1517. [Google Scholar] [CrossRef]
- Zur, R.M.; Jiang, Y.; Pesce, L.L.; Drukker, K. Noise injection for training artificial neural networks: A comparison with weight decay and early stopping. Med. Phys. 2009, 36, 4810–4818. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Adaptive computation and machine learning. In Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Zhang, X.; Yang, F.; Guo, Y.; Yu, H.; Wang, Z.; Zhang, Q. Adaptive Differential Privacy Mechanism Based on Entropy Theory for Preserving Deep Neural Networks. Mathematics 2023, 11, 330. [Google Scholar] [CrossRef]
- Reed, R.D.; Marks, R.J. Neural Smithing: Supervised Learning in Feedforward Artificial Neural Networks; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Naul, B.; Bloom, J.S.; Pérez, F.; van der Walt, S. A recurrent neural network for classification of unevenly sampled variable stars. Nat. Astron. 2018, 2, 151–155. [Google Scholar] [CrossRef]
- Kasliwal, V.P.; Vogeley, M.S.; Richards, G.T.; Williams, J.; Carini, M.T. Do the Kepler AGN light curves need reprocessing? Mon. Not. R. Astron. Soc. 2015, 453, 2075–2081. [Google Scholar] [CrossRef]
- De Cicco, D.; Bauer, F.E.; Paolillo, M.; Sánchez-Sáez, P.; Brandt, W.N.; Vagnetti, F.; Pignata, G.; Radovich, M.; Vaccari, M. A structure function analysis of VST-COSMOS AGN. Astron. Astrophys. 2022, 664, A117. [Google Scholar] [CrossRef]
- Hawkins, M. Variability in active galactic nuclei: Confrontation of models with observations. Mon. Not. R. Astron. Soc. 2002, 329, 76–86. [Google Scholar] [CrossRef]
- Lewis, G.F.; Miralda-Escude, J.; Richardson, D.C.; Wambsganss, J. Microlensing light curves: A new and efficient numerical method. Mon. Not. R. Astron. Soc. 1993, 261, 647–656. [Google Scholar] [CrossRef]
- Hopkins, P.F.; Richards, G.T.; Hernquist, L. An Observational Determination of the Bolometric Quasar Luminosity Function. Astrophys. J. 2007, 654, 731. [Google Scholar] [CrossRef]
- Shen, X.; Hopkins, P.F.; Faucher-Giguère, C.A.; Alexander, D.M.; Richards, G.T.; Ross, N.P.; Hickox, R.C. The bolometric quasar luminosity function at z = 0–7. Mon. Not. R. Astron. Soc. 2020, 495, 3252–3275. [Google Scholar] [CrossRef]
- De Paolis, F.; Nucita, A.A.; Strafella, F.; Licchelli, D.; Ingrosso, G. A quasar microlensing event towards J1249+3449? Mon. Not. R. Astron. Soc. 2020, 499, L87–L90. [Google Scholar] [CrossRef]
- Graham, M.J.; McKernan, B.; Ford, K.E.S.; Stern, D.; Djorgovski, S.G.; Coughlin, M.; Burdge, K.B.; Bellm, E.C.; Helou, G.; Mahabal, A.A.; et al. A Light in the Dark: Searching for Electromagnetic Counterparts to Black Hole-Black Hole Mergers in LIGO/Virgo O3 with the Zwicky Transient Facility. Astrophys. J. 2023, 942, 99. [Google Scholar] [CrossRef]
- Jovanović, P.; Zakharov, A.F.; Popović, L.Č.; Petrović, T. Microlensing of the X-ray, UV and optical emission regions of quasars: Simulations of the time-scales and amplitude variations of microlensing events. Mon. Not. R. Astron. Soc. 2008, 386, 397–406. [Google Scholar] [CrossRef]
- Wang, J.; Smith, M.C. Using microlensed quasars to probe the structure of the Milky Way. Mon. Not. R. Astron. Soc. 2010, 410, 1135–1144. [Google Scholar] [CrossRef]
- Wambsganss, J. Microlensing of Quasars. Publ. Astron. Soc. Aust. 2001, 18, 207–210. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovačević, A.B.; Ilić, D.; Popović, L.Č.; Andrić Mitrović, N.; Nikolić, M.; Pavlović, M.S.; Čvorović-Hajdinjak, I.; Knežević, M.; Savić, D.V. Deep Learning of Quasar Lightcurves in the LSST Era. Universe 2023, 9, 287. https://doi.org/10.3390/universe9060287
Kovačević AB, Ilić D, Popović LČ, Andrić Mitrović N, Nikolić M, Pavlović MS, Čvorović-Hajdinjak I, Knežević M, Savić DV. Deep Learning of Quasar Lightcurves in the LSST Era. Universe. 2023; 9(6):287. https://doi.org/10.3390/universe9060287
Chicago/Turabian StyleKovačević, Andjelka B., Dragana Ilić, Luka Č. Popović, Nikola Andrić Mitrović, Mladen Nikolić, Marina S. Pavlović, Iva Čvorović-Hajdinjak, Miljan Knežević, and Djordje V. Savić. 2023. "Deep Learning of Quasar Lightcurves in the LSST Era" Universe 9, no. 6: 287. https://doi.org/10.3390/universe9060287
APA StyleKovačević, A. B., Ilić, D., Popović, L. Č., Andrić Mitrović, N., Nikolić, M., Pavlović, M. S., Čvorović-Hajdinjak, I., Knežević, M., & Savić, D. V. (2023). Deep Learning of Quasar Lightcurves in the LSST Era. Universe, 9(6), 287. https://doi.org/10.3390/universe9060287







