Regular Polygon Central Configuration of the Restricted 1 + N-Body Problem
Abstract
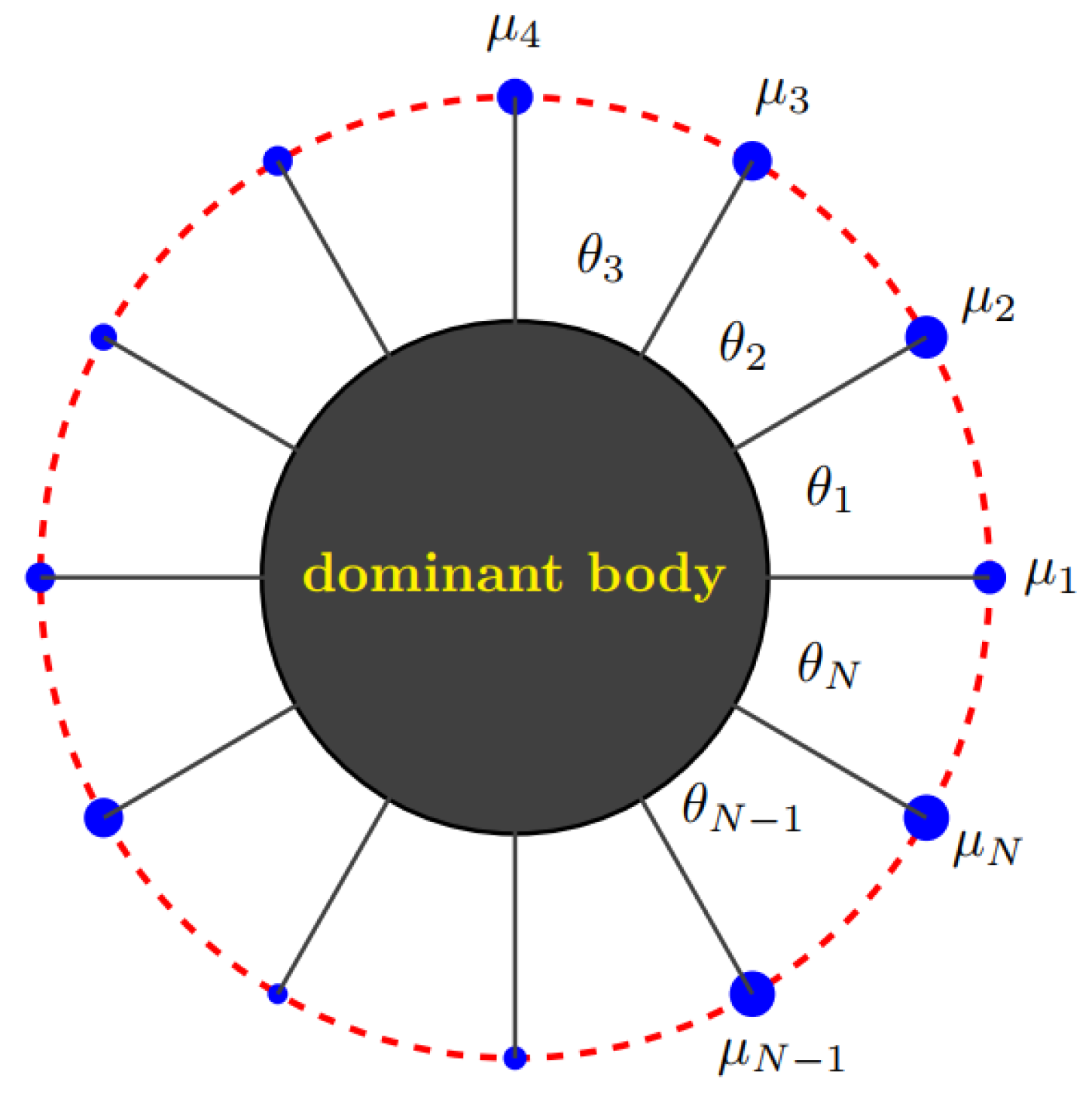
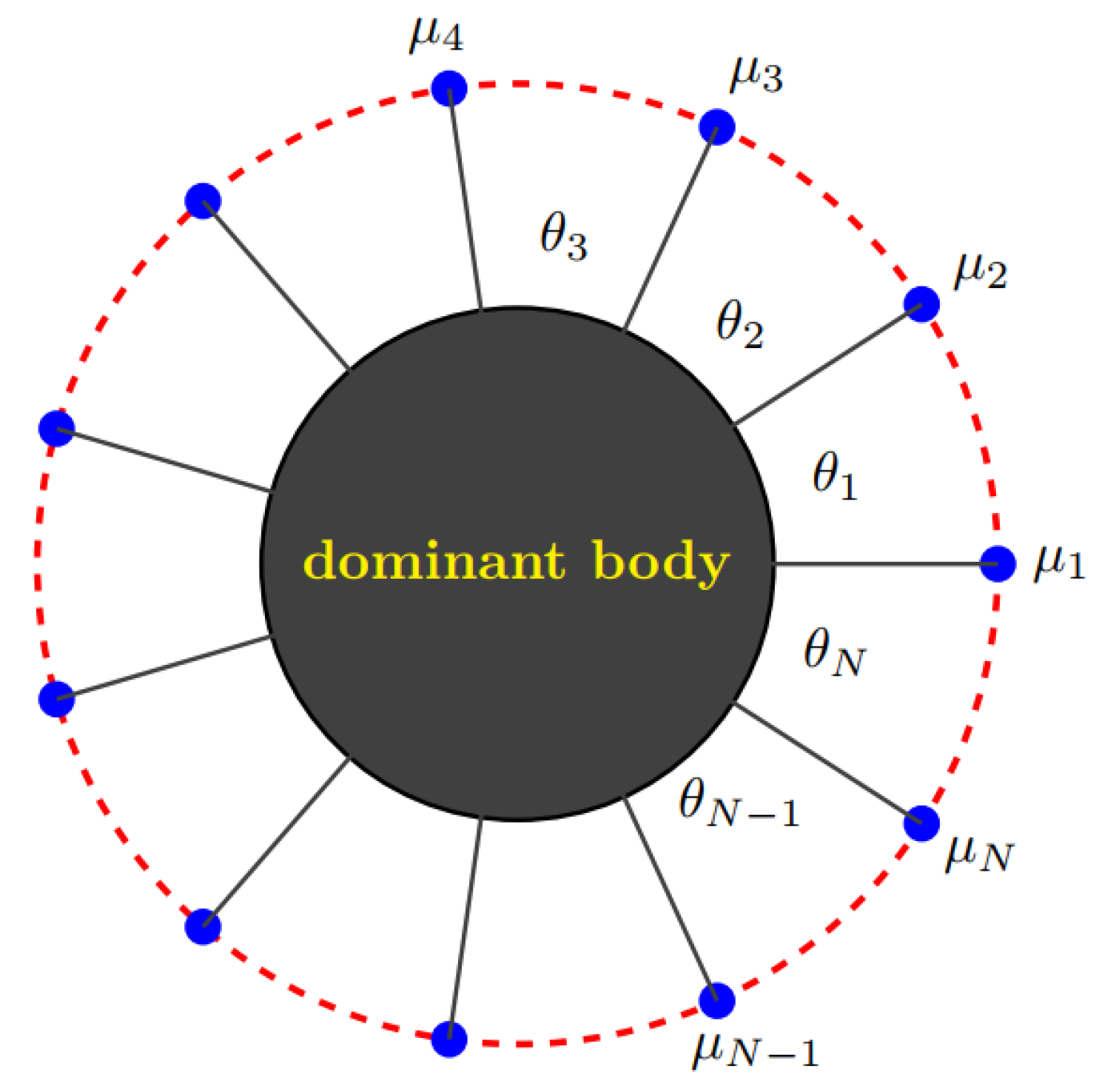
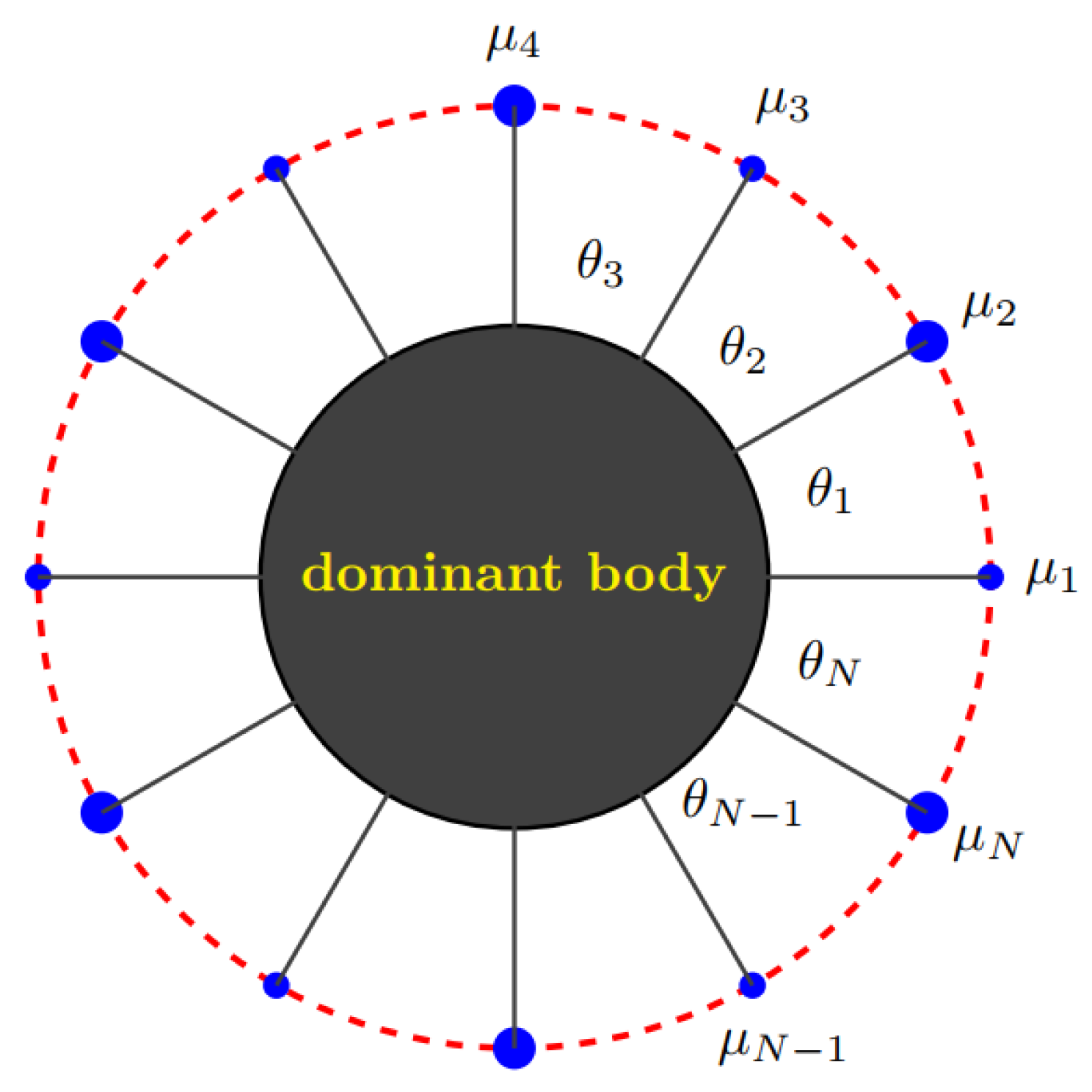
1. Introduction
- (i)
- When N is odd, the mass parameters of all the infinitesimal bodies must be equal, i.e., ;
- (ii)
- When N is even, the mass parameters of the alternate infinitesimal bodies are equal, i.e., and .
2. Propositions and Corollaries
3. Preliminary
4. Theorems and Proofs
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saari, D.G. Collisions, Rings and Other Newtonian N-Body Problems; AMS: Providence, RI, USA, 2005; pp. 32–34. [Google Scholar]
- Saari, D.G. On the role and the properties of n body central configurations. Celest. Mech. Dyn. Astron. 1980, 21, 9–20. [Google Scholar] [CrossRef]
- Maxwell, J.C. Stability of the motion of Saturn’s rings. In Maxwell on Saturn’s Rings; Brush, S., Everitt, C.W.F., Garber, E., Eds.; MIT Press: Cambridge, UK, 1983; pp. 1–71. [Google Scholar]
- Casasayas, J.; Llibre, J.; Nunes, A. Central configurations of the planar 1+n body problem. Celest. Mech. Dyn. Astron. 1994, 60, 273–288. [Google Scholar] [CrossRef]
- Moeckel, R. Linear stability of relative equilibria with a dominant mass. J. Dyn. Differ. Equ. 1994, 6, 37–51. [Google Scholar] [CrossRef]
- Renner, S.; Sicardy, B. Stationary configurations for coorbital satellites with small arbitrary masses. Celest. Mech. Dyn. Astron. 2004, 88, 397–414. [Google Scholar] [CrossRef]
- Cors, J.; Llibre, J.; Ollé, M. Central configurations of the planar coorbital satellite problem. Celest. Mech. Dyn. Astron. 2004, 89, 319–342. [Google Scholar] [CrossRef]
- Albouy, A.; Fu, Y. Relative equilibria of four identical satellites. Proc. R. Soc. A 2009, 465, 2633–2645. [Google Scholar] [CrossRef]
- Corbera, M.; Cors, J.; Llibre, J. On the central configurations of the planar 1+3 body problem. Celest. Mech. Dyn. Astron. 2011, 109, 27–43. [Google Scholar] [CrossRef]
- Oliveira, A. Symmetry, bifurcation and stacking of the central configurations of the planar 1+4 body problem. Celest. Mech. Dyn. Astron. 2013, 116, 11–20. [Google Scholar] [CrossRef]
- Xu, X. Linear Stability of the n-gon Relative Equilibria of the 1+n-Body Problem. Qual. Theory Dyn. Syst. 2013, 12, 255–271. [Google Scholar] [CrossRef]
- Deng, C.; Li, F.; Zhang, S. On the symmetric central configurations for the planar 1+4 body problem. Complexity 2019, 2019, 4680716. [Google Scholar] [CrossRef]
- Chen, J.; Yang, M. Central Configurations of the 5-Body Problem with Four Infinitesimal Particles. Few-Body Syst. 2020, 61, 26. [Google Scholar] [CrossRef]
- Su, X.; Deng, C. On the symmetric central configurations for the planar 1+5-body problem with small arbitrary masses. Celest. Mech. Dyn. Astron. 2022, 138, 28. [Google Scholar] [CrossRef]
- Marcus, M.; Minc, H. A Survey of Matrix Theory and Matrix Inequalities; Allyn and Bacon, Inc: Boston, MA, USA, 1964; pp. 1–81. [Google Scholar]
- Roberts, G.E. Linear Stability in the 1+N-Gon Relative Equilibrium. In Hamiltonian Systems and Celestial Mechanics(HAMSYS-98); Delgado, J., Lacomba, E.A., Pérez-Chavela, E., Llibre, J., Eds.; Proceedings of the III International Symposium; World Scientific: Pàtzcuaro, Mexico, 2000; pp. 303–330. [Google Scholar]
- Chen, J.; Luo, J. Solutions of regular polygon with an inner particle for Newtonian N+1-body problem. J. Differ. Equ. 2018, 265, 1248–1258. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Bi, P.; Yang, M. Regular Polygon Central Configuration of the Restricted 1 + N-Body Problem. Universe 2023, 9, 254. https://doi.org/10.3390/universe9060254
Chen J, Bi P, Yang M. Regular Polygon Central Configuration of the Restricted 1 + N-Body Problem. Universe. 2023; 9(6):254. https://doi.org/10.3390/universe9060254
Chicago/Turabian StyleChen, Jian, Peng Bi, and Mingfang Yang. 2023. "Regular Polygon Central Configuration of the Restricted 1 + N-Body Problem" Universe 9, no. 6: 254. https://doi.org/10.3390/universe9060254
APA StyleChen, J., Bi, P., & Yang, M. (2023). Regular Polygon Central Configuration of the Restricted 1 + N-Body Problem. Universe, 9(6), 254. https://doi.org/10.3390/universe9060254





