Abstract
The theory of equatorward moving east-west elongated auroral arcs associated with field line resonance (FLR) has been proposed for decades. However, confirming this theory requires in-situ observations of FLR within the magnetosphere and simultaneous all-sky imager observations of equatorward moving auroral arcs near satellite footpoints. In this study, we present the first observations of multiple equatorward moving auroral arcs related to impulse-excited FLR, using datasets from the WIND, Geotail satellites, and an all-sky imager at China’s Zhongshan Station (ZHS) in Antarctica. In the presented event, the ultra-low-frequency waves associated with solar wind dynamic pressure pulse was mainly toroidal mode, which is consistent with the theory that the toroidal mode waves usually related with external source. The all-sky imager located in Zhongshan station recorded several equatorward moving auroral arcs, followed by reverse propagating ones. The latitudinal width of the equatorward moving auroral arcs was on the order of 25 km and had an average equatorward propagation of ~0.37 km/s, which is very similar to the value from previous work. To better illustrate the observed evolution of auroral arcs related with the FLRs we proposed a simple model to evaluate the FACs induced by the FLRs in different latitudes. The latitudinal distribution evolution of FACs agrees well with the ground-based optical observations.
1. Introduction
The phenomenon of equatorward moving aurora arcs (EMAAs) observed in the high latitude area has caught considerable attention [1,2,3]. The EMAAs are usually elongated in the east-west direction as observed by all-sky imager and exhibit a quasi-periodic appearance with propagation speeds of several km/s [3]. In the past twenty years, the generation mechanism and propagation characteristics of EMAAs have been attributed to field line resonances (FLR) [1,2,3,4,5].
Field line resonance has been studied through observational and theoretical methods, which can be deduced by two different driving mechanisms: fast magnetosonic mode waves induced by external source could drive toroidal modes FLR [6,7], and wave-particle interactions inside magnetosphere would produce poloidal modes FLR [8,9]. The first type of FLR induced by fast mode waves are thought to be associated with cavity/waveguide modes related with solar wind dynamic pulses [5,10,11] and Kelvin-Helmholtz instabilities along the magnetopause [6,7,12]. In the magnetotail area, the process of magnetic field reconfiguration induced by substorm is believed to be an internal generation mechanism for fast mode compressional waves [13]. On a geomagnetic field line, a fast mode compressional wave would convert to be a Shear Alfven mode wave via mode conversion in a matching eigenfrequency. The wave energy would lose at ionospheric latitude via joule heating or some kind of collisionless dissipation mechanisms near the footpoints of field lines [14]. The second type of FLR is poloidal mode standing waves, which are believed to be generated inside magnetosphere via the process of injecting energetic particles into the magnetosphere from the magnetotail region. After that process, ions and electrons would propagate at the direction of westward and eastward, respectively. Then, the propagation direction of waves would determine by the interacting driving particle population [15,16,17], resulting in their azimuthal scale sizes are smaller than toroidal mode waves related with external source [18].
Magnetospheric FLRs are often related to periodic auroral phenomena [19,20] and associated with modulating existing auroral arcs [21] or shown to be capable of increasing the intensity of auroral arcs [22,23]. FLRs can be observed on the nightside closed field lines, and some works have indicated that FLRs can be excited even in stretched and nonaxisymmetric magnetosphere configurations [1,24,25]. The characteristic of poleward phase propagation associated with FLRs usually existed in closed field lines [26,27,28], but equatorward phase propagation can also occur when the magnetic field lines are stretched [29]. References [24,28] proposed that the area between the plasma boundary layer (PSBL) and central plasma sheet (CPS) can act as a waveguide, generating fast mode compressional waves inside that propagate earthward to excite Alfven waves with earthward propagation. Equatorward phase propagation also can exist when the Alfven frequency raises as the L shell increases. Besides, ref. [1] found that equatorward phase propagation could be induced when phase lags from fast magnetosonic waves are larger than the typical poleward phase propagation of FLRs.
In contrast to poleward moving auroral arcs associated with FLR, there have been limited studies on EMAAs [1,3]. The aforementioned scenario has not been firmly established due to a lack of conjugate observations. In this paper, we present the first observations of EMAAs induced by impulse-excited FLRs, providing direct evidence to support the formation mechanism of EMAAs.
2. Data Presentation
In this paper, the solar wind and interplanetary magnetic field (IMF) parameters are derived from the WIND satellite [30,31] and OMNI database. The magnetospheric measurements are obtained from Geotail spacecraft, which provide the magnetic field data from a fluxgate magnetometer and plasma parameters from an electric field detector. The aurora data presented in this paper are obtained from the all-sky imager at ZHS station located at the geographic coordinates (69.37° S, 76.38° E) and geomagnetic coordinates (−74.66° MLAT, 96.80° MLON), which is one of Chinese Science and Research Stations in Antarctica [32,33]. The all-sky imager has high detection accuracy from N2+ 427.8 nm to O1 557.7 nm, which has a 10° latitudes field of view at 100 km altitude and time resolution is 2 s.
3. Observations
On 27 May 1997, a positive solar wind dynamic pressure pulse (from 2 to 2.5 nPa) induced by an elevation in solar wind density was observed by WIND satellite at 1151 universal time (UT), as shown in Figure 1a–c, indicated by the arrows. The satellite was positioned within the solar wind at GSM coordinates (147.1, 18.0, 6.5) Re, and concurrently observed the three Interplanetary Magnetic Field (IMF) components given in Figure 1d. The IMF exhibited distinct alterations correlated with the solar wind discontinuity accompanying the positive dynamic pressure pulse. The near-Earth solar wind dynamic pressure and SYM-H index from the OMNI data show similar impulses with the WIND observations at 1240 UT as presented in Figure 1e,f, which indicated the arrival of the positive solar wind dynamic pressure pulse at the magnetosphere. It is worth noting that there is a time delay between the solar wind dynamic pressure in the OMNI data and the SYM-H index. As the OMNI data only shift solar wind data to the bow shock nose, the signals still require some time to propagate to the magnetosphere.
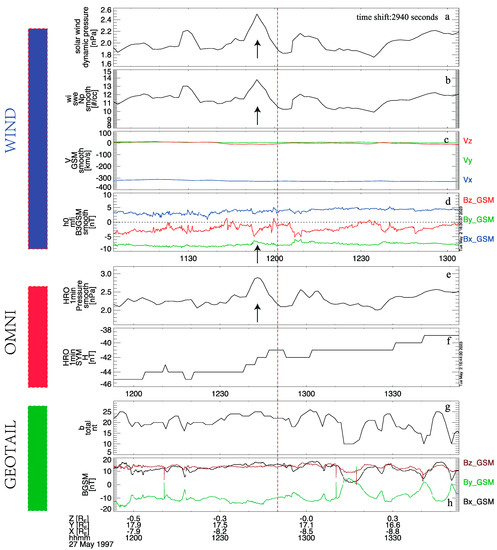
Figure 1.
Solar wind dynamic pressure (a), density (b), velocity in three components (c) and interplanetary magnetic (IMF) in three components (d) from WIND spacecraft. Solar wind dynamic pressure (e) and SYM-H index (f) derived from OMNI data. Geotail observations of the total magnetic field (g) and three components of magnetic field (h) variations in the GSM coordinates.
A few minutes after the positive solar wind dynamic pressure pulse arrived at dayside magnetopause, the GEOTAIL satellite located at duskside magnetosphere with GSM coordinates [−8.5, 17.1, 0] Re detected noticeable magnetic field perturbations, as shown in Figure 1g,h. To show the wave properties clearer, the magnetic field data were converted from GSM coordinates to field-aligned coordinates using a 15-min window for the background magnetic field, in which the p direction is parallel to the background magnetic, the azimuthal (a) is at the direction of east and perpendicular to the background magnetic, and the radial (r) is completes the triad. It is reasonable that the wave signatures observed by GEOTAIL could be related to the impulse in WIND and OMNI data, as the impulse would require several minutes to propagate from the dayside magnetopause to the GEOTAIL position. In Figure 2, all three components of magnetic fields exhibit quasi-sinusoidal perturbations, while the perturbations in azimuthal component being more significant than those in the radial component. Figure 2 also presents wavelet power spectra for the three components of magnetic fields in FAC coordinates, with wave power peaking at 1.7 mHz, 1.4 mHz, and 1.7 mHz for Br, Ba, and Bp, respectively.
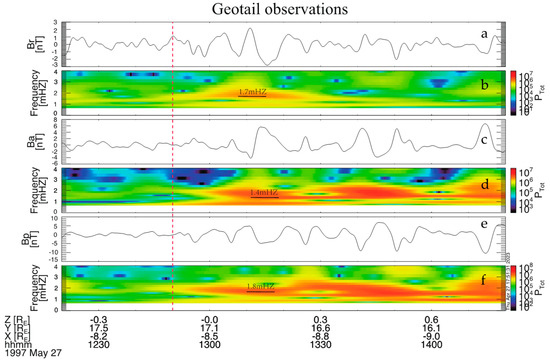
Figure 2.
Geotail observations measured the three components of magnetic field variations in field-aligned coordinates, utilizing a non-stationary filtering technique. Radial component of the magnetic field is correspondent to poloidal mode waves, and azimuthal component of the magnetic field is related to toroidal mode waves. Wavelet power spectra of three components of magnetic field in field-aligned coordinate are presented in (b,d,f) column, in which the solid black lines are the frequencies with maximum power (a,c,e).
In order to establish a connection with ground observations, the magnetic foot point of GEOTAIL was derived by tracing magnetic field line from the satellite position to the southern hemisphere based on T96 model with realistic solar wind and IMF parameters [34], as shown in Figure 3. The foot point of GEOTAIL was located at 17MLT in AACGM (altitude-adjusted corrected geomagnetic) coordinates and in proximity to the field of view of the Zhongshan all-sky imager (the solid red circle), which was located at 14–16 MLT. Figure 4 and Figure 5 present the auroral images obtained from the all-sky imager at the Zhongshan station, selected at a certain time interval between 1301 UT and 1350 UT, with magnetic north and west corresponding to the bottom and left sides, respectively. In addition, Figure 6 presents the vector magnetic field measured by a fluxgate magnetometer at Zhongshan station (ZHS), at −74.5° in magnetic latitude (MLAT). As Figure 6 illustrates, prior to the arrival of the solar wind dynamic pressure pulse, geomagnetic perturbations were weak. However, following the arrival of the solar wind dynamic pressure at the magnetosphere, enhanced ULF waves were observed in the Bx component at ZHS. Figure 6 also includes wavelet power spectra for the components of the magnetic field at ZHS, which shows that wave power peaked at 1.3 mHz for Bx. Notably, the frequency derived from the ground magnetometer closely matched the frequency of waves observed by the Geotail satellite, further supporting the scenario that ULF waves are generated by solar wind dynamic pressure.
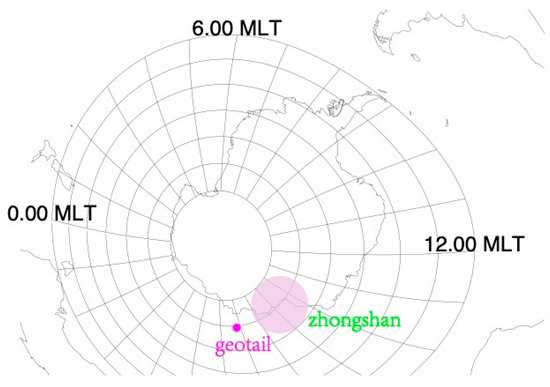
Figure 3.
The magnetic foot point of Geotail spacecraft in the southern hemisphere. The magenta solid circle represents the field view of the ZHS all sky imager.
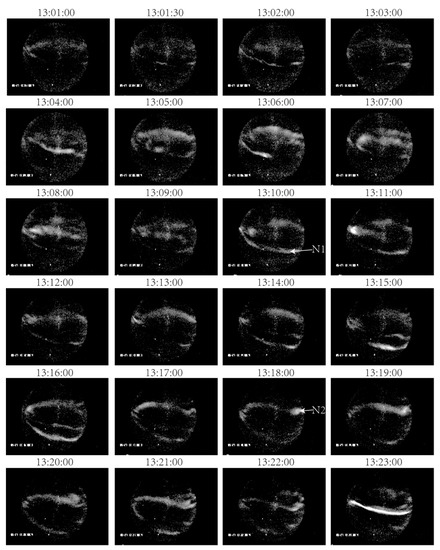
Figure 4.
Auroral images obtained from all-sky imager in Zhongshan station, in which the magnetic north and west are on the bottom and left, respectively.
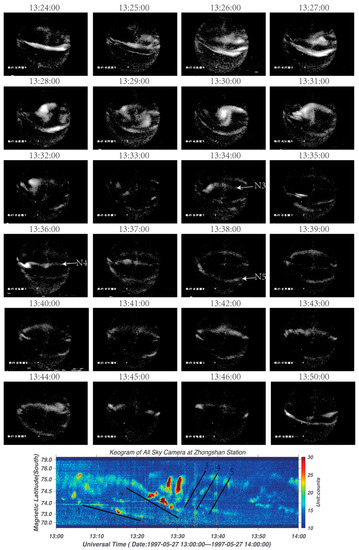
Figure 5.
Auroral observations obtained from all-sky imager in Zhongshan station, the upper images indicate the time sequence of the auroral images same as Figure 4. The bottom row represents the keogram of auroral arcs as a function of time and latitude between 1300 UT and 1400 UT.
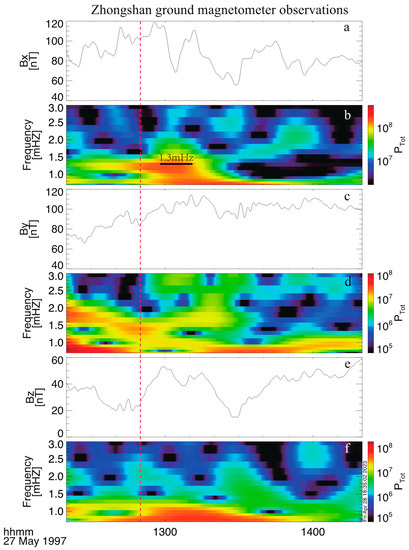
Figure 6.
Three components of geomagnetic field observed at Zhongshan magnetometer, utilizing a non-stationary filtering technique (a,c,e). Wavelet power spectra of three components of magnetic field are presented in (b,d,f) column, in which the solid black line is the frequency with maximum power.
The auroral images in Figure 4 and Figure 5 show remarkable and captivating evolutions. Between ~1304 UT and ~1322 UT, the first equatorward moving auroral arc (N1) began to form in the lower-latitude area and moved equatorward with increasing luminosity. At ~1318 UT, another auroral arc (N2) started moving equatorward and arrived at equatorward boundary at ~1331 UT. Meanwhile, an area of significant luminosity enhancement was observed at high latitudes between ~1325 UT and ~1332 UT. After the disappearance of arc N2, several poleward moving auroral arcs were detected. At ~1333 UT, an east-west elongated auroral arc (N3) began to form at low latitudes and moved poleward. At ~1335 UT, the second east-west elongated poleward moving auroral arc (N4) began to form and coexisted with the former auroral arc before both arcs fade out around 1340 UT. At ~1336 UT, another auroral arc (N5) appeared at low latitudes, although its luminosity was lower than the former arc.
The keogram of the auroral activities is also showed at the bottom of Figure 5 as a function of magnetic latitude and time. An auroral keogram is a type of graph that displays the intensity and location of auroral emissions over time, created by stacking together images taken by an all-sky camera over a period of several hours or more. The resulting keogram shows the evolution of the aurora over time, with time on the horizontal axis and magnetic latitude on the vertical axis. The keogram clearly demonstrates that discrete auroral arcs first exhibit earthward phase propagation before transitioning to poleward phase propagation, with phase shifts across latitudes increasing over time. It is worth noting that during ~1327 UT and ~1332 UT, vertical stripes can be observed between the equatorward and poleward moving auroral arcs at latitudes 74.5–75 degrees in the keogram, corresponding to the area of significant luminosity enhancement at high latitudes visible in the auroral images. Based on the keogram, the average speed of equatorward moving auroral arc N2 is calculated to be 0.37 km/s. Ref. [3] has calculated the average equatorward propagation speed is on the order of ~0.46 km/s, which is roughly equal to the value in our event. The latitudinal width of the equatorward moving auroral arcs N2 is on the order of 25 km, which is also consistent with the findings of [3,11]. Notably, the equatorward moving auroral arcs spatially coincide with the toroidal-mode ULF waves, bearing a striking resemblance to the observations presented by [11].
4. Discussion
In this paper, we have presented multi-point observations of equatorward moving east-west elongated auroral arcs related with toroidal mode ultra-low-frequency (ULF) waves after positive solar wind dynamic pressure pulse in the dusk magnetosphere. In this specific case, the WIND satellite observed clear solar wind dynamic pressure pulses, followed by a sudden impulse recorded in ground-based data approximately 2940 s later. The GEOTAIL satellite, located in the dusk-side magnetosphere, observed strong toroidal mode ULF waves shortly thereafter. Near the magnetic footpoint of the GEOTAIL satellite, the all-sky imager located in Zhongshan station recorded equatorward moving auroral arcs, followed by reverse propagating ones. The average speed of the equatorward moving auroral arcs is 0.37 km/s.
Discrete auroral arcs associated with ULF waves usually exhibit poleward phase propagation when observed in meridian scanning photometer (MSP) and all-sky imager. Under dipolar magnetic field configuration, the standing Alfven wave eigenfrequency generally decreases with increasing latitude except near the plasmapause. Thus, poleward phase propagation would be expected to present in wave-related fields, FACs and possibly auroral signatures. However, refs. [24,28] proposed that in open field lines equatorward moving auroral arcs could be induced. In their theory, fast mode waves originating from nightside plasma sheet would propagate earthward in the waveguide between central plasma sheet and plasma sheet boundary layer (PSBL) at a low group velocity. These fast mode waves would drive Alfven waves, which then propagate earthward along open field lines at a velocity larger than the earthward group velocity of the fast mode waves. Thus, the driven Alfven waves in the open field lines that map to higher latitudes at the ionosphere will reach the Earth first, followed by waves on lower latitude field lines, possibly leading to the equatorward phase propagation of auroral arcs. This hypothesis may explain the equatorward phase propagation of auroral arcs mapping to open field lines in the magnetotail, but not those associated with closed magnetic field lines. Further, ref. [1] presented a similar concept, suggesting that equatorward propagating auroral arcs could also occur on stretched closed field lines. When field lines are stretched out of meridional planes and into the magnetotail, the distance between the equatorial crossing points of the two field lines would increases, meanwhile, the group velocity of fast mode wave would be low. Thus, the configuration of stretched closed field lines becomes like that of open field lines. Sunward propagating fast mode waves in this configuration can overcome the standard poleward phase propagation of typical field line resonances, producing equatorward propagating discrete auroral arcs on closed field lines.
By comparing with the theoretical work [11,35,36], the moving auroral arcs associated with FLRs are corresponding to the field-aligned currents (FACs) accelerated by a parallel electric field due to the kinetic effects of the thermal electron interaction with FLRs [23]. To better illustrate the equatorward moving auroral arcs related with the FLRs under the circumstance of geomagnetic perturbations, Greenwald and Walker et al. 1980 proposed a model to evaluate the FACs induced by the FLRs in different latitudes. Following the theoretical framework by [11], we use the same method to estimate the latitudinal distribution of FACs associated with FLRs. The magnetic field perturbations at the height of ionosphere are observed in the azimuthal direction, and the toroidal wave field profile can be represented as
in which the x represents poleward direction, the azimuthal y directs westward direction, and the z points vertically upward direction. (x) represents the local field line eigenfrequency which varies with latitude, G(t,x) controls the spatial and temporal extents of the waves, and controls the phases of the waves. By setting G(t,x) and as proper functions, we could control the propagation direction and velocity of the fast mode driver. We would like to emphasize that, as discussed in [11], when (x) is set as a constant, as in the standard FLR theory, the phase shift across latitudes remains unchanged over time, resulting in constant propagation speeds for auroral arcs. However, a solar wind pressure pulse can trigger earthward compressional pulsations, typically characterized by a broad spectrum, and globally excite narrow-band FLRs at different frequencies that match the local field line eigenfrequency [37,38]. In the present case, we adopt the second assumption, as the propagation speed of auroral arcs varies with time. The FACs induced by FLR can be obtained through Ampere’s law:
By using this simplistic calculation, We could illustrate the wave-associated FACs following the configuration of stretched field lines in [1].
Figure 7 shows an example of the magnetic field (as solid lines) and FACs disturbance (as color patches) associated with standing hydromagnetic waves as functions of time and latitude, using the same method as [11]. In contrast to [11], the standing hydromagnetic waves in Figure 7 are assumed to be excited first at high latitudes (large L shell) and then propagate to low latitudes (small L shell) with a low velocity, which is in accord with the situation proposed by [1]. In Figure 7, the magnetic field perturbations first arise at high latitudes and then spread to low latitudes, corresponding to the earthward propagating fast mode driver. The first upward FAC (corresponding to positive ) stripe appear during the ascending stage of the magnetic field perturbations, presenting equatorward phase propagation. After the excitation of standing hydromagnetic waves, the phase shift across latitudes increases with time, because standing wave eigenfrequency decreases with increasing latitude as mentioned earlier. The propagation direction of second upward FAC is still equatorward, but with a greater propagation velocity. It is striking that a Y-shape downward FAC structure within an embedded upward FAC region is presented following the second earthward propagating FAC stripe in Figure 7. The embedded upward FAC region closely resembles the vertical stripes depicted in the keogram in Figure 5, serving as the transition region between the equatorward and poleward propagating arcs. After that, upward FACs start to exhibit poleward phase propagation with velocity decreasing over time, as shown in [11]. Thus, one can find that the calculated evolution of FACs is very similar to the observed auroral arcs as presented in Figure 4 and Figure 5.
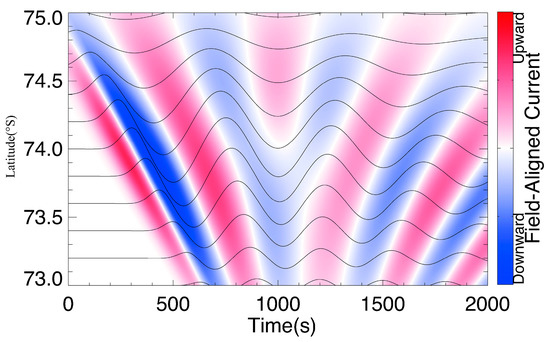
Figure 7.
Schematic diagram of the evolution along latitude of field-aligned currents associated with toroidal ULF waves. The azimuthal component of magnetic is represented by black lines in different latitudes, and the red and blue stripes are upward and downward field-aligned currents deduced from azimuthal component magnetic field oscillations, respectively.
5. Conclusions
In conclusion, we establish a scenario in which equatorward moving auroral arcs are induced by impulse-excited FLR, combining solar wind, magnetospheric and ionospheric observations. We present the first observations of equatorward moving auroral arcs related to FLR after positive solar wind dynamic pressure pulse, which seem to be a direct evidence to clarify the formation and evolution of equatorward moving auroral arcs.
Author Contributions
Conceptualization, H.Z., H.Y., Q.Z. and Y.L.; methodology, H.Z., H.Y., Z.H. and Y.L.; software, H.Z., H.Y. and Y.L.; validation, H.Z., H.Y. and Y.L.; formal analysis, H.Z., H.Y. and Y.L.; investigation, H.Z., H.Y. and Y.L.; resources, H.Z., H.Y., Y.L., J.S., Y.W., Z.H., X.Z. and B.L.; data curation, H.Z., H.Y. and Y.L.; writing—original draft preparation, H.Z., H.Y. and Y.L.; writing—review and editing, H.Z., H.Y. and Y.L.; visualization, H.Z., H.Y. and Y.L.; supervision, H.Z., H.Y. and Y.L.; project administration, H.Z., H.Y. and Y.L.; funding acquisition, H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (grant numbers 41831072, 42074199, 42204169) and Shanghai Pujiang Program (No. 21PJD078).
Data Availability Statement
We acknowledge the use of Geotail data obtained from Data ARchives and Transmission System (DARTS), provided by the Center for Science-satellite Operation and Data Archive (C-SODA) at ISAS/JAXA (http://www.darts.isas.jaxa.jp/stp/geotail/) (accessed on 31 March 2023). The all-sky imager observations from Zhongshan Station. The OMNI data is obtained from https://spdf.gsfc.nasa.gov/pub/data/omni/ (accessed on 31 March 2023) and the WIND data is accessible at https://spdf.gsfc.nasa.gov/pub/data/wind/ (accessed on 31 March 2023).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mathews, J.T.; Mann, I.R.; Rae, I.J.; Moen, J. Multi-instrument observations of ULF wave-driven discrete auroral arcs propagating sunward and equatorward from the poleward boundary of the duskside auroral oval. Phys. Plasmas 2004, 11, 1250–1259. [Google Scholar] [CrossRef]
- Rae, I.J.; Murphy, K.R.; Watt, C.E.J.; Rostoker, G.; Rankin, R.; Mann, I.R.; Hodgson, C.R.; Frey, H.U.; Degeling, A.W.; Forsyth, C. Field line resonances as a trigger and a tracer for substorm onset. J. Geophys. Res. Space Phys. 2014, 119, 5343–5363. [Google Scholar] [CrossRef]
- Baddeley, L.J.; Lorentzen, D.; Partamies, N.; Denig, M.; Pilipenko, V.; Oksavik, K.; Chen, X.; Zhang, Y. Equatorward propagating auroral arcs driven by ULF wave activity: Multipoint ground- and space-based observations in the dusk sector auroral oval. J. Geophys. Res. Space Phys. 2017, 122, 5591–5605. [Google Scholar] [CrossRef]
- Mann, I.R.; Wright, A.N. Diagnosing the Excitation Mechanisms of Pc5 Magnetospheric Flank Waveguide Modes and FLRs. Geophys. Res. Lett. 1999, 26, 16. [Google Scholar] [CrossRef]
- Wright, A.N. Dispersion and wave coupling in inhomogeneous MHD waveguides. J. Geophys. Res. 1994, 99, 159–167. [Google Scholar] [CrossRef]
- Southwood, D.J. Some features of field line resonances in the magnetosphere. Planet. Space Sci. 1974, 22, 483–491. [Google Scholar] [CrossRef]
- Chen, L.; Hasegawa, A. A theory of long-period magnetic pulsations: 2. Impulse excitation of surface eigenmode. J. Geophys. Res. 1974, 79, 1033–1037. [Google Scholar] [CrossRef]
- Southwood, D.J.; Dungey, J.W.; Etherington, R.J. Bounce resonant interaction between pulsations and trapped particles. Planet. Space Sci. 1969, 17, 349–361. [Google Scholar] [CrossRef]
- Hughes, W.; McPherron, R.; Barfield, J. Geomagnetic pulsations observed simultaneously on three geostationary satellites. J. Geophys. Res. 1978, 83, 1109–1116. [Google Scholar] [CrossRef]
- Allan, W.; Poulter, E.M.; Glassmeier, K.-H.; Junginger, H. Spatial and temporal structure of a high-latitude transient ULF pulsation. Planet. Space Sci. 1985, 33, 159–173. [Google Scholar] [CrossRef]
- Zhao, H.Y.; Zhou, X.-Z.; Liu, Y.; Zong, Q.-G.; Rankin, R.; Wang, Y.F.; Shi, Q.Q.; Shen, X.-C.; Ren, J.; Liu, H.; et al. Poleward-moving recurrent auroral arcs associated with impulse-excited standing hydromagnetic waves. Earth Planet. Phys. 2019, 3, 305–313. [Google Scholar] [CrossRef]
- Mann, I.R.; Voronkov, I.; Dunlop, M.; Donovan, E.; Yeoman, T.K.; Milling, D.K.; Wild, J.; Kauristie, K.; Amm, O.; Bale, S.D.; et al. Co-ordinated ground-based and cluster observations of large amplitude global magnetospheric oscillations during a fast solar wind speed interval. Ann. Geophys. 2002, 20, 405. [Google Scholar] [CrossRef]
- Zheng, Y.; Lui, A.T.Y.; Mann, I.R.; Takahashi, K.; Watermann, J.; Chen, S.H.; Rae, I.J.; Mukai, T.; Russell, C.T.; Balogh, A. Coordinated observation of field line rsonance in the mid-tail. Ann. Geophys. 2006, 24, 707–723. [Google Scholar] [CrossRef]
- Newton, R.S.; Southwood, D.J.; Hughes, W.J. Damping of geomagnetic pulsations by the ionosphere. Planet. Space Sci. 1978, 26, 201–209. [Google Scholar] [CrossRef]
- Southwood, D.J.; Hughes, W.J. Theory of hydromagnetic waves in the magnetosphere. Space Sci. Rev. 1983, 35, 301. [Google Scholar] [CrossRef]
- Chen, L.; Hasegawa, A. Kinetic theory of geomagnetic pulsations, 1, Internal excitations by energetic particles. J. Geophys. Res. 1991, 96, 1503–1512. [Google Scholar] [CrossRef]
- Mager, P.N.; Klimushkin, D.Y. Alfvén ship waves: High-m ULF pulsations in the magnetosphere generated by a moving plasma inhomogeneity. Ann. Geophys. 2008, 26, 1653–1663. [Google Scholar] [CrossRef]
- Chisham, G.; Mann, I.R.; Orr, D. A statistical study of giant pulsation latitudinal polarization and amplitude variation. J. Geophys. Res. Atmos. 1997, 102, 9619–9629. [Google Scholar] [CrossRef]
- Rae, I.; Watt, C.; Fenrich, F.R.; Mann, I.R.; Ozeke, L.G.; Kale, A. Energy deposition in the ionosphere through a global field line resonance. Ann. Geophys. 2007, 25, 2529–2539. [Google Scholar] [CrossRef]
- Roldugin, V.C.; Roldugin, A.V. Pc5 pulsations on the ground, in the magnetosphere, and in the electron precipitation: Event of 19 January 2005. J. Geophys. Res. Atmos. 2008, 113, A04222. [Google Scholar] [CrossRef]
- Lotko, W.; Streltsov, A.V.; Carlson, C.W. Discrete auroral arc, electrostatic shock and suprathermal electrons powered by dispersive, anomalously resistive field line resonance. Geophys. Res. Lett. 1998, 25, 4449–4452. [Google Scholar] [CrossRef]
- Rankin, R.; Kabin, K.; Marchand, R. Alfvénic field line resonances in arbitrary magnetic field topology. Adv. Space Res. 2006, 38, 1720–1729. [Google Scholar] [CrossRef]
- Rankin, R.; Watt, C.E.J.; Samson, J.C. Self-consistent wave-particle interactions in dispersive scale long-period field-line-resonances. Geophys. Res. Lett. 2007, 34, L23103. [Google Scholar] [CrossRef]
- Wright, A.N.; Mills, K.J.; Ruderman, M.S.; Brevdo, L. The absolute and convective instability of the magnetospheric flanks. J. Geophys. Res. Atmos. 2000, 105, 385–393. [Google Scholar] [CrossRef]
- Russell, A.J.B.; Wright, A.N. Resonant absorption with 2D variation of field line eigenfrequencies. Astron. Astrophys. 2010, 511, A17. [Google Scholar] [CrossRef]
- Fenrich, F.R.; Samson, J.C.; Sofko, G.; Greenwald, R.A. ULF high- and low-mfield line resonances observed with the Super Dual Auroral Radar Network. J. Geophys. Res. Atmos. 1995, 100, 21535–21547. [Google Scholar] [CrossRef]
- Wright, A.N.; Allan, W. Structure, phase motion, and heating within Alfvén resonances. J. Geophys. Res. Atmos. 1996, 101, 17399–17408. [Google Scholar] [CrossRef]
- Wright, A.N.; Elphinstone, R.D.; Cogger, L.L.; Allan, W. Phase mixing and phase motion of Alfvén waves on tail-like and dipole-like magnetic field lines. J. Geophys. Res. Atmos. 1999, 104, 10159–10175. [Google Scholar] [CrossRef]
- Samson, J.C.; Harrold, B.G.; Ruohoniemi, J.M.; Greenwald, R.A.; Walker, A.D.M. Field line resonances associated with MHD waveguides in the magnetosphere. Geophys. Res. Lett. 1992, 19, 441–444. [Google Scholar] [CrossRef]
- Farrell, W.; Thompson, R.; Lepping, R.; Byrnes, J. A method of calibrating magnetometers on a spinning spacecraft. IEEE Trans. Magn. 1995, 31, 966–972. [Google Scholar] [CrossRef]
- Gloeckler, G.; Balsiger, H.; Bochsler, P.; Fisk, L.A.; Galvin, A.B.; Geiss, J.; Gliem, F.; Hamilton, D.C.; Holzer, T.E.; Hovestadt, D.; et al. The solar WIND and suprathermal ion composition investigation on the WIND spacecraft. Space Sci. Rev. 1995, 71, 79–124. [Google Scholar] [CrossRef]
- Yang, H.; Sato, N.; Makita, K.; Kikuchi, M.; Kadokura, A.; Ayukawa, M.; Hu, H.; Liu, R.; Häggström, I. Synoptic observations of auroras along the postnoon oval: A survey with all-sky TV observations at Zhongshan, Antarctica. J. Atmos. Solar-Terr. Phys. 2000, 62, 787–797. [Google Scholar] [CrossRef]
- Liu, R.-Y.; Liu, Y.-H.; Xu, Z.-H.; Hu, H.-Q.; Yang, H.-G.; Zhang, B.-C.; Xu, W.-Y.; Chen, G.-X.; Wu, J.; Zhen, W.-M.; et al. The Chinese ground-based instrumentation in support of the combined Cluster/Double Star satellite measurements. Ann. Geophys. 2005, 23, 2943–2951. [Google Scholar] [CrossRef]
- Tsyganenko, N.; Stern, D.P. Modeling the global magnetic field of the large-scale Birkeland current systems. J. Geophys. Res. Atmos. 1996, 101, 27187–27198. [Google Scholar] [CrossRef]
- Greenwald, R.A.; Walker, A.D.M. Energetics of long period resonant hydromagnetic waves. Geophys. Res. Lett. 1980, 7, 745–748. [Google Scholar] [CrossRef]
- Milan, S.E.; Sato, N.; Ejiri, M.; Moen, J. Auroral forms and the field-aligned current structure associated with field line resonances. J. Geophys. Res. Atmos. 2001, 106, 25825–25833. [Google Scholar] [CrossRef]
- Sarris, T.E.; Liu, W.; Kabin, K.; Li, X.; Elkington, S.R.; Ergun, R.; Rankin, R.; Angelopoulos, V.; Bonnell, J.; Glassmeier, K.H.; et al. Characterization of ULF pulsations by THEMIS. Geophys. Res. Lett. 2009, 36, L04104. [Google Scholar] [CrossRef]
- Sarris, T.E.; Liu, W.; Li, X.; Kabin, K.; Talaat, E.R.; Rankin, R.; Angelopoulos, V.; Bonnell, J.; Glassmeier, K.-H. THEMIS observations of the spatial extent and pressure-pulse excitation of field line resonances. Geophys. Res. Lett. 2010, 37, L15104. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).