Abstract
High-energy lepton scattering constitutes the focus of this study. Developments are provided to motivate the basic choices of kinematic variables for the particular case of semi-inclusive electron scattering where these variables are devised to match well with the underlying dynamics to be expected for the general “nuclear landscape”. Various nuclear structure issues and other issues related to the nature of the electroweak currents at high energies are then discussed, as are some of the issues related to the different conditions occurring for electron scattering versus what is typically the case for charge-changing neutrino reactions.
1. Introduction
The present discussions center around high-energy lepton scattering, in particular, inclusive scattering where only the scattered lepton is assumed to be detected and semi-inclusive reactions where additionally some particle “x” (typically a hadron and frequently a proton) is assumed to be detected in coincidence with the scattered lepton. The goal for studies of this type is to address the reaction dynamics for electroweak processes, both electromagnetic (specifically electron scattering) and weak interaction (specifically charge-changing neutrino reactions) at GeV-energy scales. Material from previous studies form the basis for these discussions and, in particular, the reader is directed to very recent work on semi-inclusive electron scattering of polarized electrons from polarized spin-1/2 targets [1]. Both electron scattering and neutrino reactions may be treated in closely related ways although in the present work only the former will be discussed in detail (see also [2]).
Before discussing the implications for nuclear structure studies it is important to understand the relevant variables for the reactions of interest. Hence, in Section 2 the kinematics for semi-inclusive electron scattering are treated in some detail. The basic concepts of missing energy and missing momentum together with the energy and momentum transfers employed in treatments of electron scattering are discussed in depth in that section (subsection Section 2.1). Importantly, these developments show in complete generality where the physical region lies and what constitutes the boundaries of that region; moreover, one can see how a scaling variable can be introduced as the lowest point in the missing-momentum, missing-energy plane (see Section 2.2).
As will be clear in Section 3 where nuclear structure issues are discussed, although there are alternative choices for the variables introduced in Section 2, it should be clear that the ones made here match the dynamics of the nuclear response in an important way. This section begins with a subsection, Section 3.1, where the basic landscape of the nuclear response is discussed, largely without reference to details of nuclear modeling; there the problem is cast in terms of the (asymptotic) physical states that define the open channels to be found for various choices of the kinematic variables introduced in Section 2. Following this, in subsection Section 3.2 the constraints from inclusive scattering are briefly summarized, and then in subsection Section 3.3 further comments are collected, including on various nuclear structure issues including the potential importance of meson-exchange currents (MEC), on the difficulties of dealing with the low missing-energy region lying above the two-particle emission threshold, and on the interplay between semi-inclusive electron scattering and semi-inclusive neutrino reactions at relatively high energies.
Finally, in Section 4 some observations and a summary are presented.
2. Kinematics for Semi-Inclusive Scattering
2.1. Basic Variables for Semi-Inclusive Electron Scattering
We begin with some discussion of the kinematics for semi-inclusive electron scattering1. We assume that the incident electron with mass has 4-momentum , namely, with 3-momentum and energy . The scattered electron is assumed to have 4-momentum where , and we assume that the scattering takes place with scattering angle . The 4-momentum transferred is then where and , and one has that
It is usually a good approximation to invoke the extreme relativistic limit where and , in which case
For the target (of mass M) following [1] we start by assuming that it is moving with general 4-momentum , with 3-momentum and energy ; later we will specialize to the target rest frame, although, for the present, we shall keep the developments completely general. Conservation of 4-momentum requires that the final hadronic state has 4-momentum
and has invariant mass
So far, these developments do not specify the nature of the reaction. One may have inclusive scattering where no further information about the final state is assumed, or semi-inclusive scattering where the final state is assumed to be divided into two pieces (see Figure 1), one a specific particle “x” that is assumed to be detected, having 4-momentum , where , together with the undetected (“missing”) parts of the final state having 4-momentum with missing energy , missing momentum , and invariant mass . Note: for the total missing energy we use , since we reserve the notation to denote a different, but related quantity (see below). Of course even more complicated reactions having more than two particles detected can be studied; however, for the present discussions we shall restrict our attention to inclusive and semi-inclusive reactions. Moreover, note that particle x has been left unspecified: often for nuclear physics this is a nucleon and for semi-inclusive scattering we mean reactions of the sort or . However, other cases are also of interest such as (see [4]) or .
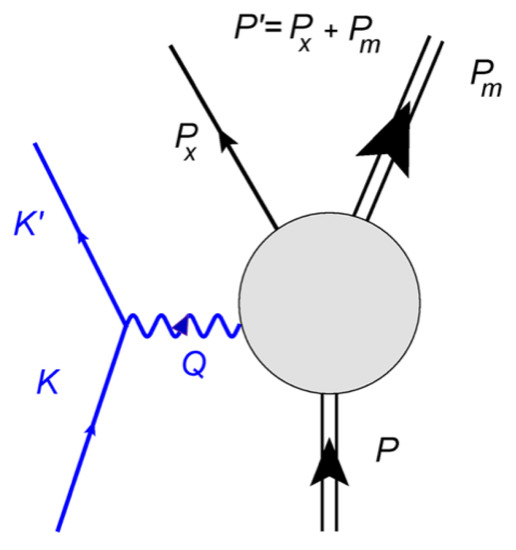
Figure 1.
Feynman diagram for semi-inclusive electron scattering; figure from [1]. The 4-momenta here are discussed in the text. In particular, particle x is assumed to be detected in coincidence with the scattered electron and thus is assumed to be known. Since the total final-state momentum is known (see text) this implies that the missing 4-momentum is also known via the relationship .
Conservation of 4-momentum requires that
and thus
From above we have that
and therefore that
Following the procedures adopted in studies of scaling, ref. [5] let us employ as independent kinematic variables the missing momentum and, rather than the missing energy , the following energy
where the threshold value of the invariant mass of the missing momentum is denoted . This quantity has the merit of taking on the value at threshold. When used in the context of nuclear physics the missing 3-momentum is typically much smaller than the invariant masses of either the daughter threshold value (the daughter ground-state mass) or any higher-energy daughter state and thus Equation (14) may be written
Typically, but not always, we can assume that
and thus setting to zero is often an excellent approximation; this correction involves only the difference between the kinetic energy of recoil when the daughter system is at threshold and when it is in some excited state. However, it is not necessary ever to make these approximations and the exact expressions can always be employed.
In studies of nuclear physics it is common to define a different quantity, , (confusingly also called the missing energy) where kinetic energies are employed. Defining the kinetic energies
one has
where the so-called separation energy
has been introduced and the approximation in Equation (23) corresponds to neglecting the correction involving discussed above.
2.2. Physical Region and Scaling Variables
Using the energy conservation condition in Equation (11), we have
where is the angle between and and . By setting to zero and solving the above equation for under the limiting conditions where it is straightforward to show that the above equation at has two solutions
where, following the notation of [5] we have introduced the quantity
The quantity y in Equation (27) has been used as a scaling variable for reasons that will be discussed in the following section. Note that the quantity in the square root may be written
and, since the argument of the square root must be non-negative, that
Upon setting one finds that
Given these relationships, it is then straightforward to determine the physically allowed regions in the – plane: for corresponding to one has
whereas for corresponding to one has
where
namely, the value of when . These regions are shown in Figure 2 and Figure 3. The region in Figure 3 is seen to be bounded from below by the curve which occurs when and above by the curve which occurs when for , whereas the other regions are all bounded by zero from below and by the curve from above. When one has from Equation (25) that
which determines for this boundary.
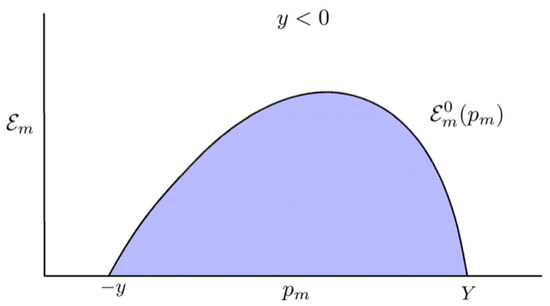
Figure 2.
Physically allowed region for the situation where . The upper boundary labelled has . (The variables employed here are discussed in the text; figure from [1]).
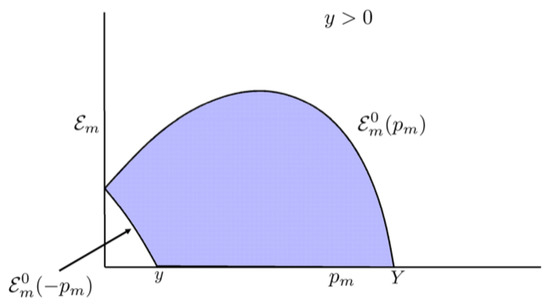
Figure 3.
Physically allowed region for the situation where . The upper boundary labeled has whereas that labeled has . (The variables employed here are discussed in the text; figure from [1]).
Thus we have the allowed regions of kinematics in the – plane for given values of q and or, equivalently, of q and y, where is given above; note that in Figure 2 is the lowest-, lowest- point allowed and as such is often used as a scaling variable to replace in scaling analyses (see below and also [5]). In turn, these impose limits on the allowed values of the energy, 3-momentum, and polar angle for the detected particle x: first, taking the scalar and cross product of with yields
and thus
By evaluating these expressions on the above boundaries, one can then determine the physically allowed regions for . The above equations define the kinematic boundaries within which all values of are allowed and outside of which no physically allowed values exist.
The developments to this point have been kept general in that the target has been assumed to have a general 4-momentum . Various specific choices of frame are typically made, depending on the experimental situation or based on special aspects of the theory. In particular, for many experiments in nuclear physics the target rest frame is the relevant one (see below), although in the future one anticipates experiments being performed at a collider—say involving colliding beams of electrons with He nuclei—in collider kinematics where then . Moreover, it is well known that for some reactions where exclusive final states are reached the virtual-photon/target center-of-momentum frame plays a special role; see, for instance, studies of pion electroproduction for kinematics where simply a pion and a nucleon define the final state. Or, finally, sometimes the Breit frame is advantageous to use.
Using the developments presented in [1] the kinematics and dynamics of semi-inclusive electron scattering including polarization degrees of freedom can be handled in any frame of reference, and results in different frames can be inter-related via their representations in terms of invariant response functions. This full discussion goes beyond the scope of the present paper and so we shall not expand on the issues of dynamics in different frames, but only employ the above results for the kinematics, since they are essential for understanding which variables are most useful for treatments of nuclear physics, together with some discussion of dynamics specifically in the rest frame for the nuclear case. In that case, where and thus from Equation (18) , one has the following replacements: the energy E and the 3-momentum are replaced by M and , respectively, and becomes the angle between and ; W and are Lorentz invariants and so do not change. The results obtained are then the ones that are familiar from analyses of scaling [5].
Before turning to nuclear structure issues, let us make a few comments. First, although the above developments are for electron scattering it is straightforward to extend the discussion to include neutrino reactions both for inclusive and semi-inclusive scattering. The essential changes there are to allow for different lepton masses and to understand that potentially different final states are reached for the weak interaction cases. Second, although the following discussions are oriented to nuclear physics, it should be noted that all of these developments are completely general and therefore also valid for studies of particle physics at any energy scale.
3. Nuclear Physics Issues
Having discussed the general kinematic variables involved in treating semi-inclusive electron scattering reactions, namely , we now turn to some general remarks about the underlying dynamics involved in studies of nuclear physics. We have seen that for given values of q and y two characteristic situations occur, namely, those with (see Figure 2) where the upper boundary that defines the physical region has whereas the lower boundary has , and those with (see Figure 3) where again the upper boundary that defines the physical region has whereas the lower boundary is split into two regions, one when where the boundary occurs at and the other for where . At given nothing can occur outside of these boundaries. The next question is what do we expect for the nuclear dynamics in typical nuclei for the semi-inclusive and hence inclusive responses across this “nuclear landscape”.
3.1. General Shape of the “Nuclear Landscape”
Clearly, the nuclear response is limited to the space where and , the latter by construction—in fact, this is a reason to employ rather than the missing energy since its lower limit is simply defined. The line corresponds to threshold. So, for example, if one were studying the semi-inclusive reaction CB the threshold value would be attained when the reaction proceeded to the ground state of B. In typical nuclei there are discrete excited states, i.e., there are very narrow excitations which lie below the thresholds for emission of protons or neutrons and have finite widths only because they decay via gamma de-excitation. Such decays are much slower than typical hadronic processes where the strong interaction enters, the latter having a characteristic timescale which is on the order of s (see Section 3.3). Accordingly, when the focus is on hadronic processes, as it is here, it is an excellent approximation to take the discrete states as being stationary, namely, treat them as -functions. This means that in typical nuclei one should expect lines in the – plane that follow Equation (14) or, upon making the approximation of Equation (17), are essentially straight lines (independent of ) at
For very light nuclei there are only a few such lines; for light- to medium-weight nuclei such as C, O or sd-shell nuclei there are typically 10s of lines of this type; for heavy nuclei there are many. For each line (each value of ) in high-resolution semi-inclusive electron scattering, usually studies, the experimental results (see, for instance, [6,7]) show very sharp features with particular -dependencies yielding what are called the momentum distributions of the individual excitations—this interpretation supposes a simplified reaction mechanism where the detected proton may be treated approximately, typically in the plane-wave impulse approximation (PWIA) or distorted-wave impulse approximation (DWIA) (see for instance chapter 16 of [7] or the detailed studies in [8]), although the actual dynamics of the process can be much more complicated.
Of course, typical modeling of the discrete-state region for high-energy lepton scattering is not performed at such a microscopic level. Usually some relatively crude approximation is made where the detailed structure discussed above is approximated by a few contributions that reflect the basic missing-momentum dependence of the shells expected to be most relevant (for instance, 1p momentum distributions for light to medium-weight nuclei such as C or O) and these are assigned widths (spreads in ) to account for the fact that the actual discrete-state response involves many excitations. As discussed in the following subsection, this may be adequate for treatments of charge-changing neutrino reactions where line integrals in the – plane are usually required.
As the focus shifts to higher excitation energies, i.e., larger values of , a threshold is reached where the daughter nucleus breaks up, which typically leads to the emission of a second nucleon. Namely, for missing energies larger than this threshold one has two nucleons in the final state, the high-energy one that is presumed to be detected plus a second one. Note this is not optional: there are no states above the nucleon emission threshold where only the high-energy nucleon is present. Moreover, note that there is no requirement that two-body meson-exchange currents are required for these two-nucleon excitations to occur—they occur naturally via one-body currents and only when extreme approximations are made for the excitations (for instance, the extreme independent-particle model) is the situation more restricted. In contrast to the discrete-state region discussed above where typically the excitations contain large contributions from promotion of nucleons in the valence region, this slightly higher missing-energy region is potentially much more difficult to model. In the latter case (at least in typical modeling) one expects promotion of a nucleon from deep-lying shells such as the -shell in C or O to occur together with the two-nucleon configurations; this situation will be discussed more later.
Clearly, as is increased more and more complicated multi-particle excitations are encountered as successively one passes higher missing-energy thresholds. Eventually, one reaches a large enough value of that the threshold for pion production is attained, whereas for lower missing energies this is forbidden (see also below for some discussion of the role that “virtual pion production” may play at these lower missing energies).
3.2. Constraints from Inclusive Scattering
One constraint on the semi-inclusive electron scattering cross section is the inclusive cross section which is more extensively known than the former. The latter is a total cross section and, as such, is less dependent on the details that are inevitable when one attempts to model the semi-inclusive reactions. For instance, what is called the quasielastic (QE) cross section arises from the sum of the integrals over the allowed regions in the – plane (see Figure 2 and Figure 3) of the and cross-sections corrected for double-counting. For this part of the cross section one expects various sum rules to be reasonably satisfied and, as long as relativistic kinematics are enforced in the modeling, the peak of the QE cross section occurs reasonably close to where it is found experimentally. Accordingly, since each model typically has some scale that may come from other modeling or may be adjusted phenomenologically as in the relativistic Fermi gas (RFG) model, one finds that most models of this part of the inclusive electron scattering cross section agree reasonably well with what is found experimentally. At high excitation energies (larger values of than the peak value) the problem becomes less clear, since there pion production and eventually other inelastic processes become important. Additionally, although the QE cross section is typically modeled using one-body current operators, clearly two-body meson-exchange currents also play a role. Studies of scaling (see, for example, [9] and references therein) show that a reasonably clear picture emerges for the various contributions to the inclusive cross section, and, accordingly, one should expect the underlying semi-inclusive cross sections to integrate properly to reproduce the inclusive (total hadronic) cross section.
That said, it should also be obvious that obtaining a reasonably good description for the inclusive cross section, although necessary, is not sufficient to have confidence in the modeling of the semi-inclusive processes. For example, the RFG model is not too bad for treatments of the inclusive QE response, but is not at all good for the semi-inclusive and cross sections [8]. Said another way: knowing the integral of some function does not mean one knows the integrand that underlies that integral. This is typically seen in modeling nuclei such as C and O when one dissects the contributions (say for ) using better models than the RFG—see [8] for discussions of the limitations of the RFG for semi-inclusive reactions and for comparisons with models that employ more realistic spectral functions than that of the RFG. Such better models have the ability to represent the various regions in the – plane discussed above, and when q and y lie in the vicinity of the QE peak one finds that the integrals required to yield the inclusive cross section amount to the following: the discrete-state region yields ∼50–60% of the total; the region lying at moderate missing energy, but lying above the threshold to two-nucleon emission yields perhaps 20% of the total; and the high missing-energy region amounts to ∼20–25% of the total (these percentages are not exact and depend on the chosen kinematics).
As noted above, these estimates are borne out in studies of scaling, and so let us see why that type of behavior is to be expected, at least roughly, given our understanding of where the strength lies in the – plane. When (the so-called “scaling region”) and in the extreme circumstance that all of that strength were to lie at one can see from Figure 2 that the integrals over the – plane would now entail an integral over the missing momentum spanning the interval . To the extent that the strength is also concentrated at relatively modest values of , this implies that the most important region determining the integrals that constitute the inclusive cross section should be expected to arise from the vicinity of the point, and this, together with the assumption that factorization is reasonably good, motivates the choice of y as a scaling variable (see [5] for more discussion). So, for example, these rough arguments lead one to expect the quasielastic peak to occur near , which is found to be reasonably the case. Of course, as we have seen, the strength is not quite so simply concentrated and so deviations should be expected from such a zero-order view of scaling—indeed, although scaling is reasonably good it is not found to be perfect. Moreover, note that these arguments are only approximately valid in the scaling region and one knows that effects from two-body MEC, potentially from the high-, high- region and from pion electroproduction can play significant or dominant roles when .
3.3. Further Comments
However, even the statements above should be taken only as rough indications of the dynamical content in the problem. They are based on observations of the scaling behavior of the inclusive cross section together with model assumptions. Moreover, it should be clear that one must make severe assumptions for said modeling, since the kinematic regions of greatest interest in the field lie at high energies and momenta where relativistic modeling is essential. Two approaches are commonly pursued: (1) One frequently assumes that the high-energy interaction of the virtual photon in electron scattering or the W boson in charge-changing neutrino reactions with a nucleon in the nucleus, producing a high-energy final-state outgoing nucleon, factorizes from the low-energy knowledge of the energy-momentum distribution of that struck nucleon, namely, the so-called spectral function traditionally used in PWIA or DWIA studies; or (2) one invokes relativistic mean field theory where the nucleons in the nucleus (whether bound or scattering states) are taken to be solutions of the Dirac equation with appropriate potentials. In some cases one can glean some insights into the importance of having relativistic modeling, and clearly for the GeV energy region it is essential to have such modeling. Both approaches are of course approximations and at present one cannot be fully confident that the nuclear structure content is under control. Nevertheless, one does have varying degrees of confidence in what can be learned from existing modeling.
Some of the contributions are likely to be more robustly understood than others: for instance, the discrete-state region is relatively well understood from PWIA/DWIA analyses, whereas the low-, two-nucleon emission region is likely not, as discussed below. The high- region is often attributed to short-range correlations; however, these are representation-dependent contributions and not observables. In the absence of a complete, consistent, relativistic model of the reaction one should take any statement concerning what dynamical ingredients cause what to be observed experimentally with some caution. For instance, largely lacking in modeling of the entire – plane is a consistent treatment of two-body MEC contributions despite the fact that there is reason to expect these effects to constitute typically ∼15–20% of the inclusive response under typical conditions. One can have both one- and two-nucleon ejection via one-body currents or via two-body MEC and, as with assumptions about the role played by short-range correlations, these are representation dependent: only when a consistent, relativistic model becomes available will one be able to state what roles should be expected for the various contributions (and then only within the context of a specific, chosen representation). Note that two-body MEC contributions are not optional; they are required by gauge invariance and in typical non-relativistic nuclear modeling the Heisenberg equation of motion for the current manifestly leads to two-body current operators.
With regard to the interplay of potential short-range correlations with MEC let us note that studies of inclusive electron scaling in the high-q, low-y region were initially attributed to the former, whereas studies of the latter [10] indicated that they are expected to play a very important, perhaps dominant role in this region.
Above it is stated that the low-, two-nucleon emission region is harder to model successfully than is the discrete-state region. Let us expand on this a bit. Suppose we assume that we are modeling C and detect a proton with 3-momentum MeV/c. The usual relativistic variables are then and . Using the familiar formula for the radius of a nucleus, one finds that fm and thus that the detected nucleon takes roughly 3 × s to exit the nucleus. The same small calculation for a proton with GeV/c yields an exit time of roughly 1 × s. For comparison, from semi-inclusive electron scattering in this region one finds a “bump” (frequently called the -shell peak) which is 5–10 MeV wide. This can serve as a measure of the complicated processes at play, specifically the interplay of the configuration where a proton has been removed from the lowest shell with that where two nucleons have been ejected from the valence shell. Using the uncertainty principle one finds experimentally that the relaxation timescale is somewhat larger than 7 × s and, since these two time scales are on the same decade, i.e., are very similar, this provides a clear indication that this is a complicated coupled-channel problem. Even in the case of electrodisintegration of He this is a very difficult issue involving the continuum three-body problem, and for heavier nuclei is expected to be a severe challenge, especially with relativistic modeling.
Another statement made earlier is that in semi-inclusive reactions below the missing energy at which pion electroproduction is physically allowed, viz, where a pion is produced and “escapes to infinity”, one has only “virtual pion production”. This is really a matter of semantics: the latter process occurs when the virtual photon interacts with the nucleons in the nucleus, produces a pion ( i.e., introduces a pion propagator which is off-shell), and where that pion is absorbed typically on another nucleon ( i.e., where the pion propagator terminates on another nucleon). That is what others call a meson-exchange current. Modeling such effects as the MEC community does is not a trivial task, since it is essential that the pion be treated as a propagator. If one were to attempt to use pion electroproduction and pion absorption cross sections to model these effects one would find that the answers would be quite different, and quite wrong. What is important is to connect real pion electroproduction and pionic MEC via a common Lagrangian; and this is typically performed by the MEC community.
Above it was stated that neutrino reactions can be treated in much the same way as electron scattering, that is, both for charge-changing neutrino and anti-neutrino reactions. Certainly this has been the approach taken in scaling analyses for inclusive reactions [9], and it may be possible to extend these scaling ideas to semi-inclusive reactions as well. Although an in-depth analysis of this more extended electroweak problem is beyond the scope of the present paper, a few comments are called for here. We have seen that inclusive scattering involves and may be dominated by a total cross section formed from the integrals over the open channels of the various underlying semi-inclusive reaction, of course, paying attention to potential issues of double-counting. Semi-inclusive electron scattering determines the response at given values of and the inclusive cross section involves the appropriate integrals over the missing energy and missing momentum. Or, alternatively, one can assume the incident electron energy , the final scattered electron energy , and the scattering angle to be given, which will determine q and y. And as well one can assume that an outgoing nucleon is detected which determines , and , the last being the azimuthal angle of that nucleon (see [1]), and which then fixes and . As we have discussed above, this allows one to probe the nuclear response in all four dimensions. In contrast, most neutrino beams are not monoenergetic, but rather are broadly spread in energy, and accordingly the situation is different from electron scattering where the incident electron’s energy is typically very well known. If one assumes that the scattered lepton’s energy and scattering angle are measured (a scattered electron in the electron scattering case; a final-state lepton, say a muon, in the charge-changing neutrino reaction case) and that a final-state nucleon is also detected (energy and angles) then for each incident lepton energy a point for the nuclear response in the – plane is given. For electron scattering that is the end of the story, whereas for neutrino reactions for each incident neutrino energy one has such a point and therefore for the entire spread of neutrino energies a curve in the – plane, in other words, a “trajectory” [8]. The neutrino cross section will then involve an integral along this trajectory weighted by the distribution of neutrino energies in the incident beam—of course, with finite energy and angle resolutions this line integral will actually be an integral over a “band”. To be useful as new information beyond the inclusive cross section discussed above this region of integration should be relatively limited (see below).
There are several important observations to make about this situation. Depending on the specific values of the kinematic variables that are measured the trajectories may follow quite different paths. For instance, on the one hand if one focuses on the family of trajectories that pass through the peak of the discrete-state region (i.e., in shell-model language, the region dominated by emission of nucleons from the valence region) then, relatively speaking, a large cross section is found. On the other hand, if this is not the case, then relatively speaking a much smaller cross section is obtained. Moreover, for some choices of kinematics the trajectories curve to smaller values of for increasing values of and may therefore encounter the low- region discussed earlier, but then, being at low at increasing do not encounter the region where short-range correlations are thought to play a role. Alternatively, other kinematical situations produce the opposite and the high-, high- region can be emphasized. Such selectivity—even when integrals over the trajectories are involved—can be very important in disentangling the inevitable uncertainties of the nuclear modeling [8,11,12]. Moreover, what is clearly very important here is to realize that understanding gained from inclusive and semi-inclusive electron scattering underlies our hope to be able to represent the closely related charge-changing neutrino reactions (both for inclusive and semi-inclusive reactions) for similar kinematics—if modeling cannot account for the electron scattering reactions one should have no confidence that it will be useful for the neutrino reaction cases.
Another comment is in order: when comparing the weighting of the discrete-state region with the effects from higher values of and comparing inclusive scattering to semi-inclusive scattering rather different pictures emerge. Inclusive scattering involves broad integrals over the response in the – plane and there one finds the typical breakdown from the discrete-state region, the low-, low- region and the region where both and are large discussed above. In contrast, semi-inclusive scattering typically obtains contributions from the first two regions (with relative weighting depending on the kinematics, as mentioned above), whereas the high-, high- region typically is much less important for semi-inclusive scattering than for inclusive scattering as it is expected to be rather broadly spread over the – plane and thus de-emphasized when line integrals are involved rather than inclusive cross section integrals over a large part of the region.
All of this focus on semi-inclusive scattering for neutrino reaction studies is important because of the wish to determine the most relevant range of neutrino energies involved—namely, those where the underlying nuclear structure leads to peaking of the trajectory integrals—as this is critical for reasonable-resolution measurements of neutrino oscillations. Moreover, as emphasized in this work, the choice of the variables is dictated by this wish.
4. Summary
This study has focused on high-energy lepton scattering and various issues that relate to the underlying nuclear structure. The emphasis has been placed on semi-inclusive electron scattering, particularly on kinematics where and/or reactions are dominant. As in typical analyses of electron scattering whatever the actual open channel of interest, the energy transfer and 3-momentum transfer q enter naturally given the electron scattering kinematics; of course, the 4-momentum transfer squared may replace, say q, and some choice of scaling variable such as Bjorken x or the y-scaling variable that is well-suited to treatments of nuclear physics may replace, say, . These are familiar concepts. For semi-inclusive scattering one needs two more independent variables and the present discussions revolve around the choices of missing momentum and of missing energy, actually of a variable that is closely related to the total missing energy . The “nuclear landscape” is appropriately represented through its dependence on these last two kinematic variables. Here some general discussions have been presented to explain, without detailed treatments of specific nuclear modeling, why much of the strength in typical semi-inclusive electron scattering is rather localized as functions of , especially coming from the discrete-state region and somewhat less so from the low- two-nucleon knockout region, with less strength arising from the high-, high- region.
Inclusive scattering involves integrating over the open channels involved in semi-inclusive scattering, avoiding double counting, and, when the focus is on where the inclusive cross section is large (this is always practically the case for neutrino reactions since the cross sections are so small), accordingly tends to magnify the effects coming from the high-, high- region, since these effects are believed to be spread rather broadly over the nuclear landscape. In other words, for inclusive scattering one has an integral that picks up what lies in this broad region, whereas semi-inclusive electron scattering can focus on specific regions in the – plane. Even charge-changing semi-inclusive neutrino reactions, which as discussed in the text involve limited line-integrals over “trajectories” in the – plane and therefore typically are much less sensitive to contributions from the high-, high- region.
In all cases there are important issues of nuclear structure and nuclear currents that are not fully resolved at present. In particular, two-body meson-exchange currents are likely to play a non-trivial role and, although some high-energy modeling has been performed for inclusive scattering, much more remains to be considered for semi-inclusive scattering. Moreover, of course, the emphasis in this work has been placed on high-energy lepton scattering where relativistic effects are important and many aspects of nuclear modeling can only be undertaken in specific relativistic models that, despite the importance of employing such models, do not have all of the desired ingredients one might like to have.
[custom]
Funding
This work was supported in part by the Office of Nuclear Physics of the U.S. Department of Energy under Grant Contract DE-FG02-94ER40818.
Acknowledgments
The author thanks Sabine Jeschonnek for her helpful comments on this work.
Conflicts of Interest
The author declares no conflict of interest.
Note
| 1 | We use the conventions of [3] in this work. We also employ the conventions previously used by us and others in many previous studies. Namely, we denote 4-vectors by capital letters and 3-vectors by lower case letters, , , etc. The scalar product of two 4-vectors is then and, therefore, the scalar product of a 4-vector with itself is where . One potential point of confusion can occur with these conventions, viz. for the momentum transfer 4-vector we have which for electron scattering is space-like, and accordingly . One should be careful not to confuse our sign convention for this quantity with the so-called SLAC convention which has the opposite sign |
References
- Donnelly, T.W.; Jeschonnek, S.; Van Orden, J.W. General tensor structure for electron scattering in terms of invariant responses. Ann. Phys. 2023, 448, 169174. [Google Scholar] [CrossRef]
- Moreno, O.; Donnelly, T.W.; Van Orden, J.W.; Ford, W.P. Semi-inclusive charged-current neutrino-nucleus reactions. Phys. Rev. D 2014, 90, 013014. [Google Scholar] [CrossRef]
- Bjorken, J.D.; Drell, S.D. Relativistic Quantum Mechanics. In International Series in Pure and Applied Physics; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Friscic, I.; Donnelly, T.W.; Milner, R.G. New approach to determining radiative capture reaction rates at astrophysical energies. Phys. Rev. C 2019, 100, 025804. [Google Scholar] [CrossRef]
- Day, D.; McCarthy, J.; Donnelly, T.; Sick, I. Scaling in inclusive electron-nucleus scattering. Ann. Rev. Nucl. Part. Sci. 1990, 40, 357. [Google Scholar] [CrossRef]
- Bobeldijk, I.; Bouwhuis, M.; Ireland, D.G.; de Jager, C.W.; Jans, E.; de Jonge, N.; Kasdorp, W.J.; Konijn, J.; Lapikás, L.; van Leeuwe, J.J.; et al. High-Momentum Protons in Pb 208. Phys. Rev. Lett. 1994, 73, 2684. [Google Scholar] [CrossRef] [PubMed]
- Donnelly, T.W.; Formaggio, J.A.; Holstein, B.R.; Milner, R.G.; Surrow, B. Foundations of Nuclear and Particle Physics; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Van Orden, J.W.; Donnelly, T.W. Nuclear theory and event generators for charge-changing neutrino reactions. Phys. Rev. C 2019, 100, 044620. [Google Scholar] [CrossRef]
- Megias, G.D.; Amaro, J.E.; Barbaro, M.B.; Caballero, J.A.; Donnelly, T.W. Inclusive electron scattering within the SuSAv2 meson-exchange current approach. Phys. Rev. D 2016, 94, 013012. [Google Scholar] [CrossRef]
- De Pace, A.; Nardi, M.; Alberico, W.M.; Donnelly, T.W.; Molinari, A. Role of 2p–2h MEC excitations in superscaling. Nucl. Phys. A 2004, 741, 249. [Google Scholar] [CrossRef]
- Amaro, J.E.; Barbaro, M.B.; Caballero, J.A.; Donnelly, T.W.; Gonzalez-Jimenez, R.; Megias, G.D.; Simo, I.R. Neutrino-nucleus scattering in the SuSA model. Eur. Phys. J. Spec. Top. 2021, 230, 4321–4338. [Google Scholar] [CrossRef]
- Gonzalez-Jimenez, R.; Barbaro, M.B.; Caballero, J.A.; Donnelly, T.W.; Jachowicz, N.; Megias, G.D.; Niewczas, K.; Nikolakopoulos, A.; Van Orden, J.W.; Udias, J.M. Neutrino energy reconstruction from semi-inclusive samples. Phys. Rev. C 2022, 105, 025502. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).