Evolution of Cosmological Parameters and Fundamental Constants in a Flat Quintessence Cosmology: A Dynamical Alternative to ΛCDM

Abstract

The primary purpose of this work is the provision of accurate, analytic, evolutionary templates for cosmological parameters and fundamental constants in a dynamical cosmology. A flat quintessence cosmology with a dark energy potential that has the mathematical form of the Higgs potential is the specific cosmology and potential addressed in this work. These templates, based on the physics of the cosmology and potential, are intended to replace those parameterizations currently used to determine the likelihoods of dynamical cosmologies. Acknowledging that, unlike $\Lambda$CDM, the evolutions are dependent on both the specific cosmology and the dark energy potential, the templates are referred to as specific cosmology and potential (SCP) templates. The requirements set for the SCP templates are that they must be accurate, analytic functions of an observable, such as the scale factor or redshift. This is achieved through the utilization of a modified beta function formalism that is based on a physically motivated dark energy potential to calculate the beta function. The methodology developed here is designed to be adaptable to other cosmologies and dark energy potentials. The SCP templates are essential tools in determining the relative likelihoods of a range of dynamical cosmologies and potentials. The ultimate purpose is the determination of whether dark energy is dynamical or static in a quantitative manner. It is suggested that the SCP templates calculated in this work can serve as fiducial dynamical templates in the same manner as $\Lambda$CDM serves for static dark energy.

1. Introduction

This manuscript examines the evolutions in the late time, matter, and dark energy dominated epoch between the scale factors of 0.1 and 1.0 for a flat quintessence cosmology. This epoch is the primary focus of the upcoming Rubin and Roman observatories observations. This study does not consider radiation but only matter and dark energy and is therefore only relevant to late epochs not under the influence of radiation. The farthest look back time considered here is at a scale factor of 0.1, where radiation has no measurable effect.

Some preliminary aspects of areas covered in this publication are discussed in [1]. This work, however, expands the study and is intended for both experts in the field and those who wish an introduction to calculations of the evolution of cosmological parameters and fundamental constants. The methodology presented here is particular to the specific cosmology, quintessence, and the evolutionary templates it calculates are for a specific dark energy potential. The templates from the methodology are therefore referred to as specific cosmology and potential (SCP) templates.

The nature of dark energy has been declared one of the “grand challenges in both physics and astronomy” by the Decadal Survey of Astronomy and Astrophysics 2022 [2]. A major part of that challenge is the question of whether dark energy is static or dynamic. An important aspect of the question is whether a dynamical cosmology can fit the current and future observational data as well or better than $\Lambda$CDM. This work explores a flat quintessence cosmology with current parameter boundary conditions close but not equal to $\Lambda$CDM to provide accurate predictions of parameter and fundamental constant evolutions for comparison with data. The calculation of the evolutions is described in detail, particularly the use of a modified beta function formalism that produces accurate, analytic functions of the parameters and constants as a function of the observable scale factor. The dark energy potential has a natural origin, having the same mathematical polynomial form as the Higgs potential. It is, however, not the Higgs field and has none of the rich physics of the Higgs. It is simply a rolling scalar field with quintessence physics that is coupled to gravity. Since the potential has the same mathematical form as the Higgs potential, it is referred to as the Higgs inspired or HI potential.

The development of the SCP templates for a flat, minimally coupled quintessence cosmology takes advantage of the property of minimally coupled systems, that the dark energy and matter density evolutions are independent of each other. Each can be calculated separately, as is traditionally done for quintessence [3,4,5,6], and then combined when necessary for the calculation of the cosmological parameters such as the Hubble parameter. As an example, the evolution of matter density is simply $\frac{{\rho }_{m_0}}{a^3}$ where ${\rho }_{m_0}$ is the current matter density and a is the scale factor. The evolution of the scalar and other dark energy functions are calculated in Section 3, Section 4, Section 5, Section 6, Section 7, Section 8, Section 9 and Section 10 without reference to the matter density, except in the introduction of the Friedmann constraints. The matter density is incorporated in Section 11, where the Hubble parameter is calculated using the first Friedmann constraint. An approximation is made in Equation (16), where the $\frac{{\beta }^2}{6}$ term is set to zero to achieve Equation (17), which is only a function of the dark energy potential and scalar. The approximation is valid for all of the dark energy EoS values in this study but could lose accuracy for high deviations of w from −1.

Beyond demonstrating the methodology for producing SCP templates for cosmological parameter evolution, this work also examines the role of fundamental constants in setting constraints on both static and dynamical cosmologies. Without invoking special symmetries, it is difficult to prevent a scalar field that couples with gravity from also coupling with other sectors such as the weak, electromagnetic, and strong forces [7]. The values of the fundamental constants such as the fine structure constant $\alpha$ and the proton to electron mass ratio $\mu$ are determined by the quantum chromodynamic scale ${\Lambda }_{QCD}$, the Higgs vacuum expectation value $\nu$, and the Yukawa couplings h [8]. It is assumed here that the HI scalar responsible for dark energy also interacts with these sectors. The temporal evolution of the constants produced by the interactions is examined in Section 17 along with the connection to the dark energy equation of state (EoS) w.

The study utilizes natural units with ℏ, c, and $8\pi G$ set to 1, where G is the Newton gravitational constant. The mass units are reduced Planck masses $m_p$. The constant $\kappa$ is the inverse reduced Planck mass $1/m_p$. In the mass units of this study $\kappa =1$, but it is retained in equations to display the proper mass units.

2. The Need for SCP Templates

The SCP templates generated in this study are candidates for a fiducial set of templates to compare with the observations in the same way that the well-known static $\Lambda$CDM templates are currently used. Although accurate analytic templates for the static $\Lambda$CDM cosmology exist, similar templates for dynamical cosmologies are exceedingly rare. Currently, the primary tools for analyzing dynamical cosmologies are parameterizations such as the Chevallier, Polarski, and Linder (CPL) [9,10] linear parameterization of the dark energy equation of state (EoS) $w\left(a\right)=w_o+(1-a)w_a$. Such parameterizations do not contain any of the physics of the dynamical cosmology and its dark energy potential. 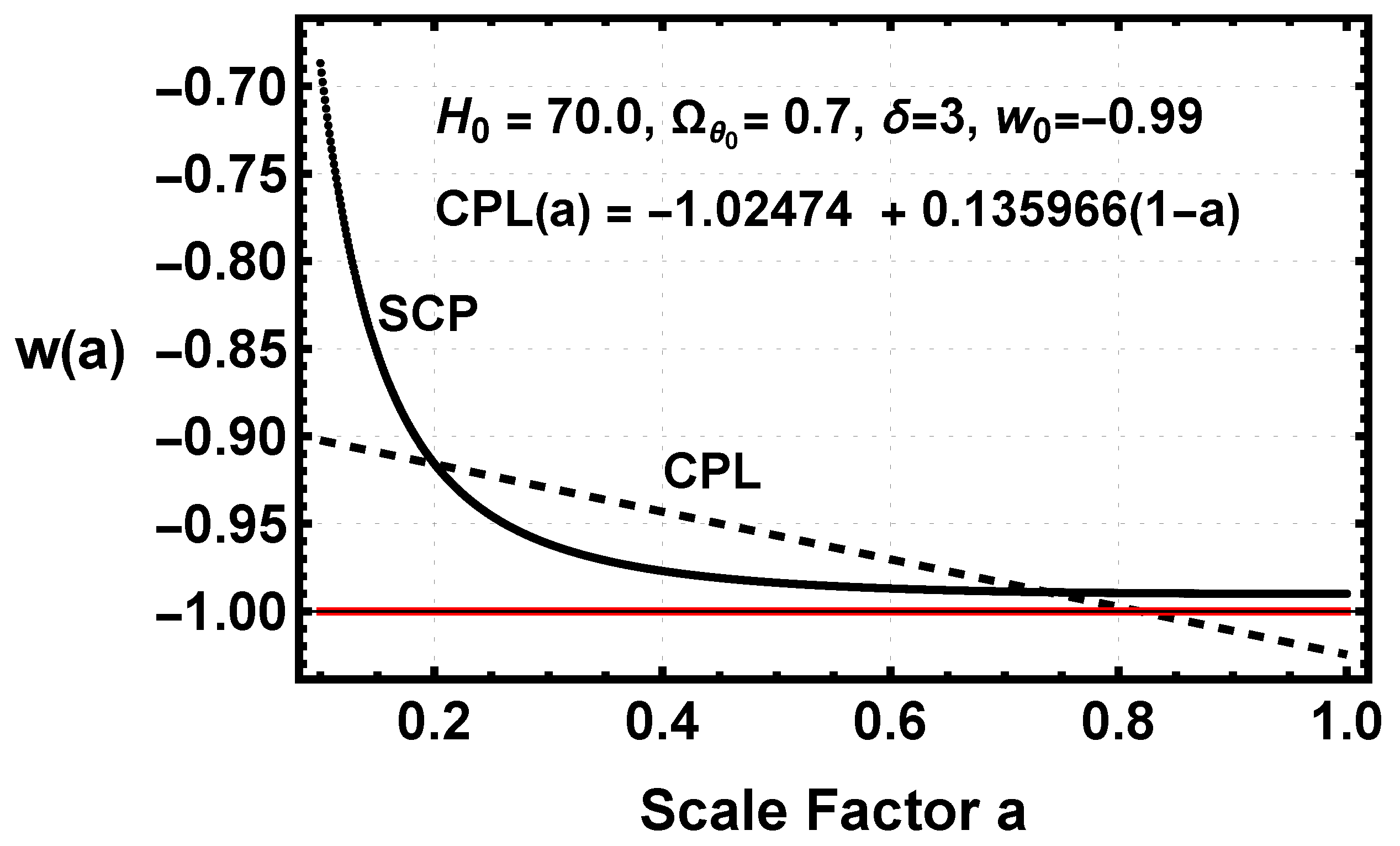Figure 1 shows the CPL fit to a quintessence cosmology w with the dark energy potential described in Section 5.

The linear CPL, dashed line, is a poor fit to the true evolution, solid line, and is not an accurate measure of its likelihood. Beyond producing an erroneous likelihood, the CPL fit also produces erroneous conclusions. At scale factors greater than 0.8, the CPL fit is in the phantom region, $w<-1$, even though the true evolution has no phantom values. It is well known that it is quite difficult for quintessence to cross the phantom boundary [11]. Three recent analyses of observational data [12,13,14] using a MCMC analysis with a CPL dark energy template find phantom values of w at low redshift. The presence of phantom values of w can be interpreted as strong evidence against quintessence; however, Figure 1 clearly shows that for a quintessence cosmology with no phantom values, a CPL fit erroneously produces phantom values due to fitting a nonlinear evolution with a linear parameterization. The methodology described here produces templates based on the action of the quintessence cosmology and a specific dark energy potential for comparison with the observational data. SCP templates are essential for properly comparing accurate predictions with the observational data in establishing the true likelihood of the cosmology and potential.

3. Quintessence

As one of the simplest dynamical cosmologies, flat quintessence provides a straightforward example of a methodology for producing SCP templates. Quintessence is a well-studied [4] and well-known cosmology, but for easy reference some important aspects of its physics are given here.

The quintessence cosmology is defined by its action $S_q$.

$$S_q=\int d^{4}x\sqrt{-g}\left[m_p^2\frac{R}{2}-\frac{1}{2}{g}^{\mu \nu }{\partial }_{\mu }\varphi {\partial }_{\nu }\varphi -V\left(\varphi \right)\right],S_m=\frac{{\rho }_{m_0}}{a^3}$$

(1)

where $S_q$ is the dark energy action and $S_m$ is the matter (dust) action. R is the Ricci scalar, g is the determinant of the metric $g^{\mu \nu }$, $\varphi$ is the scalar, and $V\left(\varphi \right)$ is the dark energy potential. The scalar $\varphi$ is the true scalar with a value on the order of ${10}^{-32}{m}_p$. A second scalar $\theta$ is introduced in Section 5 for the Ratra–Peebles form of the dark energy potential. This scalar is, therefore, referred to as the Ratra–Peebles, or RP scalar, and has a value on the order of unity in units of $m_p$. In the matter action, ${\rho }_{m_0}$ is the current matter density and a is the scale factor. The matter component of the total action $S_m$ is separate from the quintessence dark energy component $S_q$ resulting in a total action of $S_{tot}=S_q+S_m$ as in Equation (3.1) of [5]. The matter component is introduced via the first Friedmann constraint in Section 11 in the calculation of the Hubble parameter. In the following, only dark energy is considered in the derivation of the scalar, since its evolution is not affected by matter. Matter is then introduced in Section 11 to derive the proper Hubble parameter that includes both dark energy and matter.

The kinetic component of $S_q$ is

$$X=-\frac{1}{2}{g}^{\mu \nu }{\partial }_{\mu }\varphi {\partial }_{\nu }\varphi =-\frac{{\dot{\varphi }}^2}{2}.$$

(2)

The common kinetic symbol X for $-\frac{{\dot{\varphi }}^2}{2}$ is used throughout the manuscript. X is a function of only time, since the universe is assumed to be spatially homogeneous.

The quintessence dark energy density and pressure are set by the action as

$${\rho }_{\varphi }\equiv -X+V\left(\varphi \right),p_{\varphi }\equiv -X-V\left(\varphi \right)$$

(3)

In natural units both the density and the pressure have units of $m_p^4$ and the time derivative of the scalar $\dot{\varphi }$ has units of $m_p^2$. The dark energy EoS $w\left(\varphi \right)$ is

$$w\left(\varphi \right)=\frac{P_{\varphi }}{{\rho }_{\varphi }}=\frac{-X-V\left(\varphi \right)}{-X+V\left(\varphi \right)},$$

(4)

which is a pure number. Combining Equations (3) gives

$$P_{\varphi }+{\rho }_{\varphi }=-2X.$$

(5)

It follows that

$$\frac{P_{\varphi }+{\rho }_{\varphi }}{{\rho }_{\varphi }}=w+1=\frac{-2X}{{\rho }_{\varphi }},$$

(6)

giving $\dot{\varphi }$ a relationship to the dark energy EoS and the dark energy density.

$$-2X={\rho }_{\varphi }(w+1)$$

(7)

4. General Cosmological Constraints

Independent of the particular cosmology, there are general constraints on the evolution of the cosmological parameters. The first are the Friedmann constraints.

4.1. The Friedmann Constraints

The two Friedmann constraints play an important role in calculating the SCP templates. The forms of the first and second Friedman constraints used here are

$$3{\left(\frac{H\left(a\right)}{\kappa }\right)}^2={\rho }_{\varphi }\left(a\right)+{\rho }_m\left(a\right),3\left(\frac{\dot{H}\left(a\right)}{{\kappa }^2}+{\left(\frac{H\left(a\right)}{\kappa }\right)}^2\right)=-\frac{\rho \left(a\right)+3P\left(a\right)}{2}$$

(8)

where ${\rho }_{\varphi }\left(a\right)$ is the dark energy density, ${\rho }_m\left(a\right)$ is the matter density, $\rho \left(a\right)$ is the sum of the matter and dark energy densities, and $P\left(a\right)$ is the dark energy pressure. In a universe with only dark energy, the Friedmann constraints are

$$3{\left(\frac{H_{\varphi }\left(a\right)}{\kappa }\right)}^2=3{\left(\frac{\sqrt{{\mathsf{\Omega }}_{\varphi }}H\left(a\right)}{\kappa }\right)}^2={\rho }_{\varphi }\left(a\right),3\left(\frac{{\dot{H}}_{\varphi }\left(a\right)}{{\kappa }^2}+{\left(\frac{H_{\varphi }\left(a\right)}{\kappa }\right)}^2\right)=-\frac{{\rho }_{\varphi }\left(a\right)+3P\left(a\right)}{2}$$

(9)

where $H_{\varphi }$ denotes the dark energy only Hubble parameter. The critical density is $3H^2$ and the ratios of the dark energy density and matter density to the critical density are ${\mathsf{\Omega }}_{\varphi }$ and ${\mathsf{\Omega }}_m$ that add to one in a flat universe. The dark energy only Hubble parameter is then $\sqrt{{\mathsf{\Omega }}_{\varphi }}H$.

4.2. The Boundary Conditions

Since we are looking for solutions of differential equations, the second set of constraints is imposed by the boundary conditions, the current values of certain cosmological parameters.

Table 1. Boundary conditions and parameter values in this work. $H_0$ is the current value of the Hubble parameter in units of $\frac{km/sec}{Mpc}$. ${\mathsf{\Omega }}_{m_0}$ and ${\mathsf{\Omega }}_{{\varphi }_0}$ are the current ratios of the matter and dark energy densities to the critical density. $w_0$ are the current values of the dark energy equation of state.

${\mathit{H}}_0$	${\mathbf{\Omega }}_{{\mathit{m}}_0}$	${\mathbf{\Omega }}_{{\mathit{\varphi }}_0}$		${\mathit{w}}_0$		Scale Factor a
73	0.3	0.7	−0.99	−0.995	−0.999	0.1–1.0

displays the cosmological boundary conditions chosen for this study. The range of the scale factor is slightly arbitrary but is set to include the range covered by the Rubin and Roman observations. The range of $w_0$ is set close to −1 to be near, but not exactly, −1. The $H_0$ value is set to 73 consistent with the current late time expectations [15]. ${\mathsf{\Omega }}_{m_0}$ and ${\mathsf{\Omega }}_{{\varphi }_0}$ are the current concordance values. All of the boundary conditions appear in the evolutionary functions of the SCP templates and are therefore easily changed.

5. The Higgs Inspired Potential

The dark energy potential has the mathematical form of the Higgs potential $V\left(\varphi \right)\propto {({\varphi }^2-{\gamma }^2)}^2$, a quartic polynomial with a constant $\gamma$. It is chosen for two reasons. The first is that the mathematical form is identical to the Higgs potential, which gives rise to a scalar field that is known to exist and is therefore physically motivated, hence the name Higgs inspired or HI potential. A second reason is that by varying the constant term $\gamma$, it produces dark energy equations of state that are freezing, thawing, and transitioning between freezing and thawing. This makes it a good choice for a fiducial potential that covers a wide range of evolutions.

The most convenient form for the potential is a modified Ratra–Peebles format [16,17] with a scalar field denoted by $\theta$, the RP scalar introduced in Section 3 that has units of mass in $m_p$. The potential is then

$$V\left(\kappa \theta \right)=M^4{({\left(\kappa \theta \right)}^2-{\left(\kappa \delta \right)}^2)}^2=M^4({\left(\kappa \theta \right)}^4-2{\left(\kappa \delta \right)}^2{\left(\kappa \delta \right)}^2+{\left(\kappa \delta \right)}^4),$$

(10)

where the true scalar is $\varphi =M\kappa \theta$. M and $\delta$ are constants with units of mass, and both $\left(\kappa \theta \right)$ and $\left(\kappa \delta \right)$ are dimensionless; therefore, all of the dimensionality is in the $M^4$ leading term. Since both arguments are dimensionless, there is no need for the n in the usual $M^{4-n}{\varphi }^n$ Ratra–Peebles format. The terms $\theta$ and $\delta$ replace the scalar $\varphi$ and $\gamma$ terms to differentiate them from the true scalar $\varphi$ and constant $\gamma$, which have values on the order of ${10}^{-31}{m}_p$. The values of $\theta$ and $\delta$ are of the order unity, and the value of $\delta$ is chosen to be greater than the current scalar ${\theta }_0$ to place the equilibrium point $\theta =\delta$ in the future. This makes the constant ${\left(\kappa \delta \right)}^4$ the dominant term, followed by the two dynamical terms $-2{\left(\kappa \theta \right)}^2{\left(\kappa \delta \right)}^2$ and ${\left(\kappa \theta \right)}^4$ in descending order.

6. The Quintessence Methodology

The methodology developed here is for the specific quintessence cosmology and only applies to a cosmology whose action is given by Equation (1). Among the current plethora of dynamical cosmologies, there are some with quite different names that have the same action as quintessence where this methodology will apply but not for cosmologies such as k-essence, which has a different action. The methodology is demonstrated with the modified Ratra–Peebles HI potential of Equation (10).

6.1. The Modified Beta Function Formalism

The key to producing SCP templates that are accurate analytic functions of the scale factor is beta function formalism [5,18,19,20]. The beta function is a differential equation relating the scalar $\kappa \theta$ to the scale factor a, allowing the calculation of an analytic form of $\kappa \theta \left(a\right)$. The analytic form of the scalar is achieved via the approximation of a dominant potential component of the dark energy density that allows exclusion of the kinetic component to calculate the beta function given in Equation (17). This, in turn, enables calculation of the analytic function of the scalar. The cosmological parameters are analytic functions of the scalar that are quite accurate but not exact. The cosmological parameter templates do not contain any numerical calculations.

The primary beta function formalism papers relative to this work are [5,18]. The work by [18] considers a quintessence dark energy only universe, while the work of [5] considers a quintessence universe with both matter and dark energy, which is the universe considered in this work. Both [5,18] consider the general physics of the beta function formalism rather than the explicit evolution of cosmological parameters. Their approach is therefore modified in this work to provide analytic evolutionary templates for cosmological parameters. These modifications are noted in the following discussion.

The generalized beta function [19] is defined as

$$\beta \left(\kappa \theta \right)\equiv {\left(-\frac{\partial p}{\partial X}\right)}^{\frac{1}{2}}\frac{d\kappa \theta }{dln\left(a\right)}$$

(11)

From Equation (3) for the quintessence dark energy pressure, it is evident that ${(-\frac{\partial p}{\partial X})}^{\frac{1}{2}}$ is 1, giving a quintessence beta function of

$$\beta \left(\kappa \theta \right)\equiv \frac{d\kappa \theta }{dln\left(a\right)}=\frac{d\kappa \theta }{da}a.$$

(12)

From Equation (12) and the definition of the quintessence beta function and the Hubble parameter

$$\frac{d\kappa \theta }{da}=\frac{\beta }{a},\kappa \dot{\theta }=\beta H_{\theta }.$$

(13)

The dark energy only Hubble parameter $H_{\varphi }$ is used in Equation (13) to be consistent with the dark energy only derivation of the scalar; however, when the matter density is introduced in Section 11, the Hubble parameter for both dark energy and matter should be used since it sets the time evolution of the scale factor $\frac{da}{dt}$. Equations (7) and (13) provide the useful relation

$$\beta \left(\kappa \theta \right)=\sqrt{3{\mathsf{\Omega }}_{\theta }(w+1)}.$$

(14)

Since the beta function formalism is developed for dark energy, the first Friedmann constraint in Equation (9) applies, and

$$3H_{\theta }^2={\rho }_{\theta }=-X+V\left(\theta \right)=\frac{{\left(\beta H_{\theta }\right)}^2}{2}+V\left(\theta \right)$$

(15)

where the subscript $\theta$ now designates the dark energy density.

In [5,18], the beta function is defined as the negative of the logarithmic derivative of the dark energy density. To achieve the desired analytic SCP templates, Equation (15) is rearranged to a slightly modified density

$$3H_{\theta }^2\left(1-\frac{{\beta }^2}{6}\right)=V\left(\theta \right)$$

(16)

noting that $\frac{{\beta }^2}{6}\ll 1$ for all of the cases considered here. Using the modified density, the beta function is then the negative of the logarithmic derivative of the analytic HI potential.

$$\beta \left(\kappa \theta \right)=-\frac{\frac{\partial V\left(\kappa \theta \right)}{\partial \left(\kappa \theta \right)}}{V\left(\kappa \theta \right)}=\frac{\partial \left(\kappa \theta \right)}{\partial lna}$$

(17)

The leading constant, $M^4$, in the dark energy potential does not appear in the logarithmic derivative defining the beta function, leaving it as an adjustable parameter to satisfy the Friedmann constraints. Note that the approximation that $\frac{{\beta }^2}{6}\ll 1$ is equivalent to the statement that the kinetic term $X=-\frac{{\left(\beta H_{\theta }\right)}^2}{2}$ is small compared with the dark energy potential. This is roughly equivalent to the slow roll condition often used in evaluating dynamical cosmologies. In fact, Equation (17) is the negative of the first slow roll condition. The first slow roll condition is often set to a small constant, e.g., [3], which is only valid for an exponential potential. Here, the approximation of a small value of X is only used to calculate the analytic form of the scalar, and the nonconstant time derivative of the scalar is used in all parameter calculations. The approximation that $\beta H_{\theta }$ is set to 0 in determining the beta function also means that the Hubble parameter is not used in the derivation of the scalar and that its value of either $H_{\theta }$ or H is not a factor.

Although the beta density $3H^2(1-\frac{{\beta }^2}{6})$ is slightly different than the real density, application of the boundary conditions and the Friedmann constraints produces evolutionary SCP templates of high accuracy as illustrated in Section 15.

The Beta Function for the HI Potential

Using the HI potential in Equation (10), the negative of the logarithmic derivative is

$$\beta \left(\kappa \theta \right)=\frac{-4\kappa \theta }{{\left(\kappa \theta \right)}^2-{\left(\kappa \delta \right)}^2}=\sqrt{3{\mathsf{\Omega }}_{\theta }(w+1)}$$

(18)

where the last term is from Equation (14). Solving the equation formed by the last two terms for the current time yields the current value ${\theta }_0$ for the scalar which is an important boundary condition.

$$\kappa {\theta }_0=-\frac{4-\sqrt{16+12{\mathsf{\Omega }}_{{\theta }_0}(w_0+1){\left(\kappa \delta \right)}^2}}{2\sqrt{3{\mathsf{\Omega }}_{{\theta }_0}(w_0+1)}}$$

(19)

Since the argument of the square root in the numerator is greater than 16, Equation (19) is the positive solution of the quadratic equation.

6.2. The Scalar as a Function of the Scale Factor

An essential step in achieving SCP templates as analytic functions of the scale factor a is finding the scalar $\kappa \theta$ as a function of a. From the definition of the beta function in Equation (17), the differential equation for the scalar as a function of the scale factor is

$$\frac{\partial \left(\kappa \theta \right)}{\partial lna}=\frac{-4\kappa \theta }{{\left(\kappa \theta \right)}^2-{\left(\kappa \delta \right)}^2}.$$

(20)

Separating the scale factor and scalar terms gives

$$4d(ln\left(a\right))=-\frac{{\left(\kappa \theta \right)}^2-{\left(\kappa \delta \right)}^2}{\kappa \theta }d\left(\kappa \theta \right).$$

(21)

An integral of both sides of Equation (21) from 1 to a for the left side and from ${\theta }_0$ to $\theta$ on the right side gives

$$8ln\left(a\right)=2{\left(\kappa \delta \right)}^{2}ln\left(\kappa \theta \right)-{\left(\kappa \theta \right)}^2-\left(2{\left(\kappa \delta \right)}^{2}ln\left(\kappa {\theta }_0\right)-{\left(\kappa {\theta }_0\right)}^2\right).$$

(22)

Equation (19) provides the value of $\kappa {\theta }_0$. The following manipulations from [1] provide a solution for $\kappa \theta \left(a\right)$ involving the Lambert W function in terms of a constant $c=2{\left(\kappa \delta \right)}^{2}ln\left(\kappa {\theta }_0\right)-{\left(\kappa {\theta }_0\right)}^2$ and the scale factor. Dividing both sides of Equation (22) by ${\left(\kappa \delta \right)}^2$ gives

$$\frac{8}{{\left(\kappa \delta \right)}^2}ln\left(a\right)+\frac{c}{{\left(\kappa \delta \right)}^2}=2ln\left(\kappa \theta \right)-{\left(\frac{\theta }{\delta }\right)}^2.$$

(23)

Taking the exponential of both sides of Equation (23) and dividing again by ${\left(\kappa \delta \right)}^2$ yields

$$-\frac{a^{\frac{8}{{\left(\kappa \delta \right)}^2}}}{{\left(\kappa \delta \right)}^2}{e}^{\frac{c}{{\left(\kappa \delta \right)}^2}}=-{\left(\frac{\theta }{\delta }\right)}^2{e}^{-{\left(\frac{\theta }{\delta }\right)}^2}.$$

(24)

Equation (24) has the mathematical form of the Lambert W function that is the solution to

$$\chi =W\left(\chi \right)e^{W\left(\chi \right)}$$

(25)

where

$$\chi \left(a\right)=-\frac{a^{\frac{8}{{\left(\kappa \delta \right)}^2}}}{{\left(\kappa \delta \right)}^2}{e}^{\frac{c}{{\left(\kappa \delta \right)}^2}}W\left(\chi \right)=-{\left(\frac{\theta }{\delta }\right)}^2.$$

(26)

Equations (25) and (26) provide an analytic solution for $\kappa \theta \left(a\right)$

$$\kappa \theta \left(a\right)=\kappa \delta \sqrt{-W\left(-\frac{a^{\frac{8}{{\left(\kappa \delta \right)}^2}}}{{\left(\kappa \delta \right)}^2}{e}^{\frac{c}{{\left(\kappa \delta \right)}^2}}\right)}$$

(27)

that is the positive solution for the square root, which is real since $W\left(x\right)$ is negative. The following variable changes produce a concise form for $\kappa \theta \left(a\right)$.

$$q=-\frac{e^{\frac{c}{{\left(\kappa \delta \right)}^2}}}{{\left(\kappa \delta \right)}^2},p=\frac{8}{{\left(\kappa \delta \right)}^2},\chi \left(a\right)=q{a}^p,$$

(28)

which yields

$$\kappa \theta \left(a\right)=\kappa \delta \sqrt{-W\left(\chi \right(a\left)\right)}.$$

(29)

Equation (29) provides the key to transforming evolutions that are a function of the scalar into functions of the observable scale factor to produce the SCP templates.

The term ${\left(\kappa \theta \right)}^2-{\left(\kappa \delta \right)}^2$ appears often in this manuscript. In terms of the Lambert W function $W\left(\chi \right(a\left)\right)$, it is

$${\left(\kappa \theta \right)}^2-{\left(\kappa \delta \right)}^2=-{\left(\kappa \delta \right)}^2(W\left(\chi \left(a\right)\right)+1).$$

(30)

The form of the HI potential is then

$$V\left(a\right)={\left(M\kappa \delta \right)}^4{(W\left(\chi \left(a\right)\right)+1)}^2.$$

(31)

The beta function also has a compact form in the W function format

$$\beta \left(\kappa \theta \right)=\frac{-4\kappa \theta }{{\left(\kappa \theta \right)}^2-{\left(\kappa \delta \right)}^2}=\frac{4\sqrt{-W\left(\chi \right(a\left)\right)}}{\kappa \delta \left(W\right(\chi \left(a\right))+1)}.$$

(32)

6.3. Summary of the Methodology

Although the methodology may appear to be complex, the separate steps of the quintessence beta function formalism are relatively simple. The quintessence beta function is given in Equation (12), which connects the scalar $\kappa \theta$ to the scale factor a. As stated in the text, the beta function is defined as the negative of the logarithmic derivative of the dark energy density, but here it is noted that the kinetic term in the density is small compared with the potential term, and a legitimate approximation is to ignore it and set the beta function to the negative of the logarithmic derivative of the potential as given in Equation (17). This is the only place in the methodology that $\frac{{\beta }^2}{6}$ is set to 0. The kinetic term $-X$, as shown in Equation (15), is used in all subsequent calculations of the templates. Equation (18) shows the beta function calculated from Equation (17) and is shown in differential form in Equations (20) and (21). The solution for $\kappa \theta \left(a\right)$ is achieved through mathematical manipulation to the simple form in Equation (29). This provides a solution for a cosmological parameter as a function of the scale factor if the solution as a function of the scalar is known.

Since the matter (dust) action is separate from the dark energy action, the evolution dark energy scalar is calculated from the dark energy action as described above. The matter is included in Section 11 that derives the Hubble parameter, which is a function of the dark energy and matter. It is added to the total density in Equation (38) for the first Friedmann constraint and is present in the Hubble parameter template in Equation (40). This is the Hubble parameter that is used in the calculation of the time derivative of the scalar $\dot{\theta }=\beta H$. Adherence to the Friedmann constraints and inclusion of the matter density in the Hubble parameter that calculates $\dot{\theta }$ produces accurate SCP templates that are functions of both the matter and the dark energy densities and conforms to both Friedmann constraints.

7. The Cosmology of $\mathit{W}\left(\mathit{\chi }\right)$

Before moving on to consider the evolution of $\kappa \theta \left(a\right)$, $\beta \left(a\right)$ and other parameters, it is worthwhile to examine the cosmology embedded in the evolution of $W\left(\chi \right)$. A thorough discussion of the mathematical properties of the Lambert W function is in [21]. There, it is shown that W has negative values if its argument is between $-\frac{1}{e}$ and 0, which is true for all cases considered here. This makes the argument of the square root in Equation (29) positive, producing a real value of the scalar $\kappa \theta$. 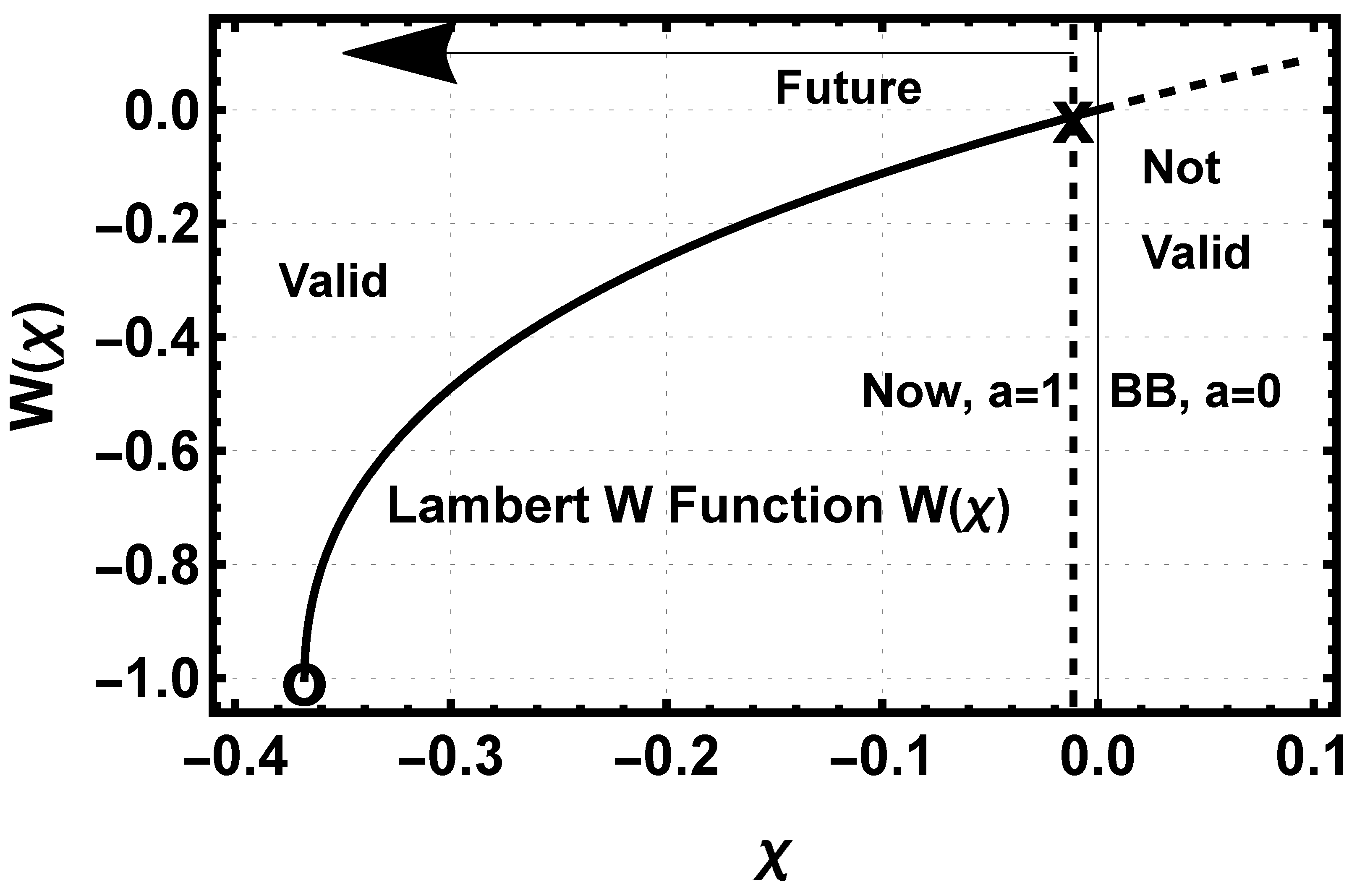Figure 2 shows the evolution of the principal branch of $W\left(\chi \right)$. The formal designation of the principal branch is $W_0\left(\chi \right)$, but the subscript is dropped in the following since only the principal branch is used in this work.

Figure 2 shows the evolution of $W(\chi$) as a solid line for negative $\chi$ and a dashed line for positive $\chi$. The negative portion of the Lambert W function terminates at $\chi =-\frac{1}{e}$, while the positive portion continues indefinitely. Only the negative portion has real solutions for the scalar. Equation (26) shows that $\chi$ is negative for all positive values of the scale factor a. Evolution in Figure 2 proceeds from right to left as the top arrow indicates. The variable $\chi$ is zero when $a=0$; therefore, the Big Bang is at $\chi =0$ as shown by the vertical thin line. The dashed vertical line just to the left of the Big Bang shows the maximum excursion of the greatest evolution case, $\delta =3$ and $w_0=-0.99$. All of the cases considered here have $-W\left(\chi \right)$ values much less than 1, which means that $\theta \ll \delta$.

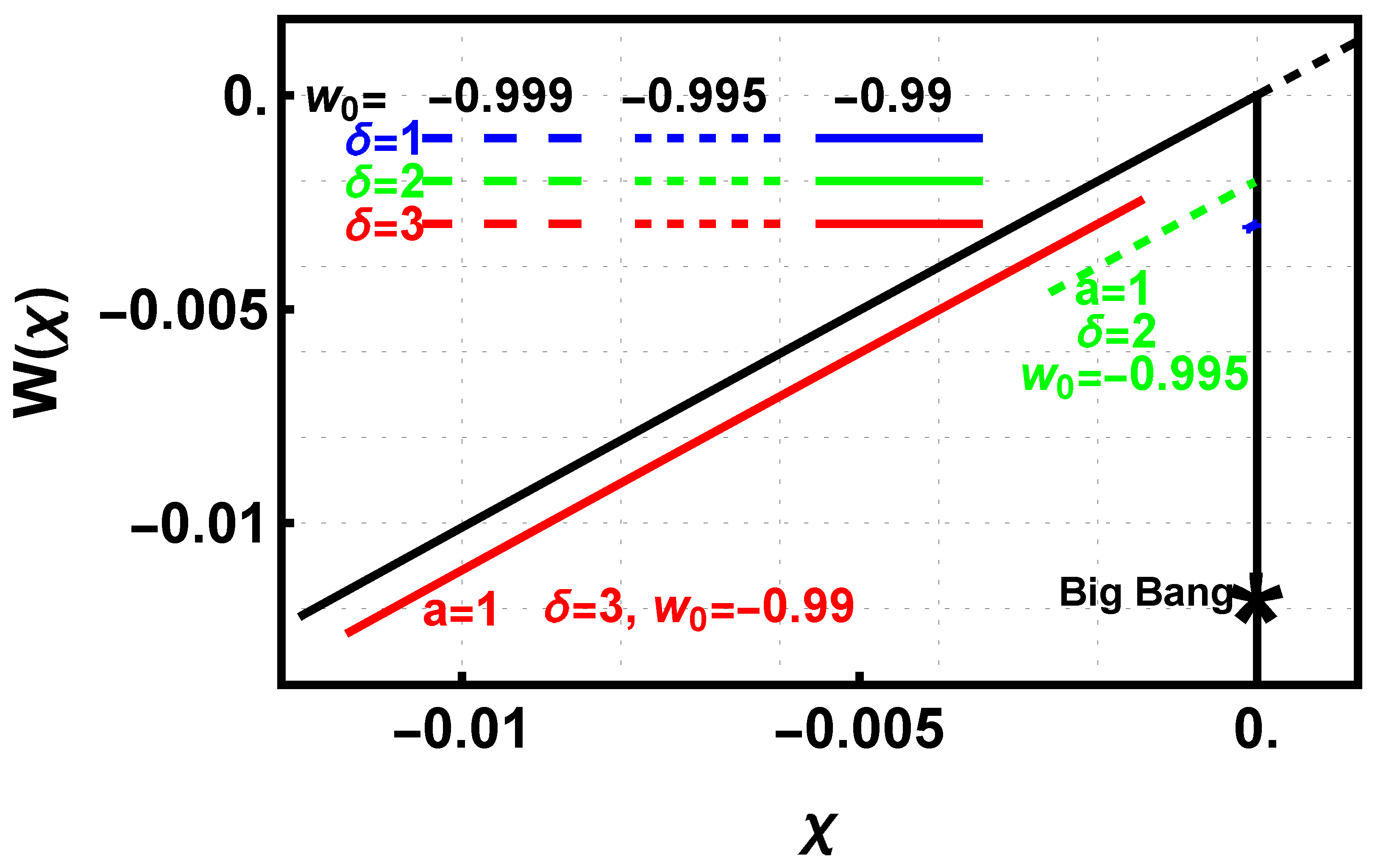
Figure 3 shows the detail of the evolution region of Figure 2. The black solid and dashed lines are the same as in Figure 2 but only for the evolution region between the thick dashed and thin solid vertical lines. The first case, $\delta =3$ $w_0=-0.99$ in red, with the highest $\delta$ and largest deviation of $w_0$ from −1 has the most extensive evolution with the right end of the evolution, $a=0.1$, significantly after the Big Bang. Note the evolutions that actually overlap the black lines have been shifted downward for visibility. The third case with the lowest value of $\delta$ and the least deviation of $w_0$ from −1 has the least evolution with its $a=0.1$ start $\chi$ at $-1.312\times {10}^{-12}$ and its maximum $\chi$ of $1.3119\times {10}^{-4}$ barely visible on the diagram. The middle excursion with $\delta$ = 2 and $w_0$ = −0.995 starts with $\chi$ = $2.604\times {10}^{-5}$ and a current $\chi$ of $2.6404\times {10}^{-3}$. The similar numbers are due to the end scale factor being ten times the beginning scale factor. Recall that $\chi$ is not time so that a small value of $\chi$ does not mean that the scale factor of 0.1 is very near the Big Bang. As hinted at in Figure 2 the evolution region’s small extent make the evolutionary tracks in $\chi$ appear linear. Figure 3 is an indication, verified later on, that the value of $\delta$ has a strong influence on the SCP templates. The upper left of the figure shows the color code of the $\delta$ values and the line styles of the $w_0$ values are maintained throughout the manuscript.

The black sloped solid and dashed line is the same as in Figure 2 for the small expanded region. The red solid and green dashed line are the evolutions of the $\delta =3$, $w_0=-0.99$, and the $\delta =2$, $w_0=0.995$ cases. The long dashed blue evolution for the $\delta =1$ $w_0=-0.999$ is so short that it appears only as a small dot near $\chi =0$ below the $\delta =3$ and 2 evolutions. The evolutions are offset downward from the black track for visibility.

To aid comprehension of Figure 3,

Table 2. The values of $\chi$ for all values of $\delta$ and $w_0$ for scale factors of 0.1, 0.5, and 1.0. The barely visible Figure 3 blue $\delta =1$ and $w_0=-0.999$ $\chi$ values are given by the last row of the $\delta =1$ $\chi$ values in the table. The equilibrium values of the scale factor $a_{eq}$, discussed in Section 7.2, are in the last column.

		The Values of $\mathit{\chi }$
		Scale Factor $\mathit{a}$
$\mathbf{\delta }$	${\mathit{w}}_{\mathbf{0}}$	0.1	0.5	1.0	${\mathit{a}}_{\mathit{eq}}$
1.	−0.99	$-1.307\times {10}^{-11}$	$-5.107\times {10}^{-6}$	$-0.00131$	2.024
1.	−0.995	$-6.550\times {10}^{-12}$	$-2.558\times {10}^{-6}$	$-0.000655$	2.206
1.	−0.999	$-1.312\times {10}^{-12}$	$-5.125\times {10}^{-7}$	$-0.000131$	2.698
2.	−0.99	$-0.0000517$	$-0.00129$	$-0.00517$	8.437
2.	−0.995	$-0.0000260$	$-0.000651$	$-0.00260$	11.885
2.	−0.999	$-5.243\times {10}^{-6}$	$-0.000131$	$-0.000524$	26.492
3.	−0.99	$-0.00147$	$-0.00616$	$-0.0114$	49.776
3.	−0.995	$-0.000750$	$-0.00313$	$-0.00580$	106.479
3.	−0.999	$-0.000152$	$-0.000636$	$-0.00118$	640.859

gives the value of $\chi$ at scale factors of 0.1, 0.5, and 1.0 for all values of $\delta$ and $w_0$. All values of $\chi$ are negative The magnitude of $\chi$ increases with increasing values of $\delta$ and higher deviations of $w_0$ from −1. The time evolution of the tracks in Figure 3 is from right to left, the same as in Figure 2. The time extents for all tracks are the same, $a=0.1$ to 1.0, but the evolution of $\chi$ has a large variation.

7.1. Past Evolution

The main content of this manuscript is the past evolution from the present to a past scale factor of 0.1, which is a redshift of 9. This encompasses a large fraction of the history of the universe in the matter and dark energy dominant epochs. An important question is how far back can the SCP templates be utilized. A hard limit is the onset of the radiation-dominated epoch, since the radiation density is not included in the present work. A reasonable limit is when the radiation density is $1\%$ of the matter density. The present matter density for $H_0=73$ and $\mathsf{\Omega }{m}_0$ of 0.3 is $3.68\times {10}^{-121}$ $m_p^4$ and a present radiation density of $6.17\times {10}^{-125}$ $m_p^4$. The radiation density is $1\%$ of the matter density at a scale factor of 0.0168 or a redshift of 58.5. This is strictly a physics limit on the validity of the templates. Figure 2 and Figure 3 plus Table 2 indicate that the template for the scalar $\theta$ is valid back to this limit, but the templates have not been tested for mathematical stability at scale factors smaller than 0.1. Inclusion of the radiation density is beyond the scope of this work, but it can probably be included in the same manner as the matter density.

7.2. Future Evolution

A perhaps even more intriguing question is how far in the future can the templates be extended. The solution of $\theta$ is analytic at scale factors greater than 1, which is all of the region to the left of the dashed vertical line in Figure 2. There is a limit, however, to the principal branch of the Lambert W function at $\chi =-\frac{1}{e}$. Figure 2 marks this location with a O at $W\left(\chi \right)=-1$. Equation (29) shows that at $W\left(\chi \right)=-1$ $\theta =\delta$, which is an equilibrium point where the dark energy potential is zero. The scale factor, $a_{eq}$, where this occurs is given by

$$a_{eq}={\left(\frac{-1}{qe}\right)}^{\frac{1}{p}}.$$

(33)

where p and q are the same as in Equation (28). The values of $a_{eq}$ are listed in the last column of Table 2. It is beyond the scope of this manuscript to determine whether this is a stable equilibrium point. If it is a stable equilibrium, with $\dot{\theta }$ also zero, then it would be the end of dark energy acceleration. The universe would return to a matter-dominated evolution, with $3H^2=\frac{{\rho }_{m_0}}{a^3}$ making a graceful exit from acceleration. The speed of expansion would be

$$\dot{a}=aH=\sqrt{\frac{{\rho }_{m_0}}{a}}.$$

(34)

The universe would then evolve in a classical manner, slowing down to zero expansion at infinity. Given the past history of the universe it is reasonable that the lowering level of total density might reveal a new source of accelerated expansion whose density is below that of the current density.

8. The Evolution of the Scalar and the Beta Function

The scalar $\kappa \theta \left(a\right)$ and the beta function $\beta \left(a\right)$ influence the evolution of all of the cosmological parameters in this study. The sections below document their evolution.

8.1. The Evolution of $\kappa \theta \left(a\right)$

Figure 4 shows the evolution of the scalar $\kappa \theta$ over the scale factors considered in this work. The colors and line styles are consistent with the previous figure.

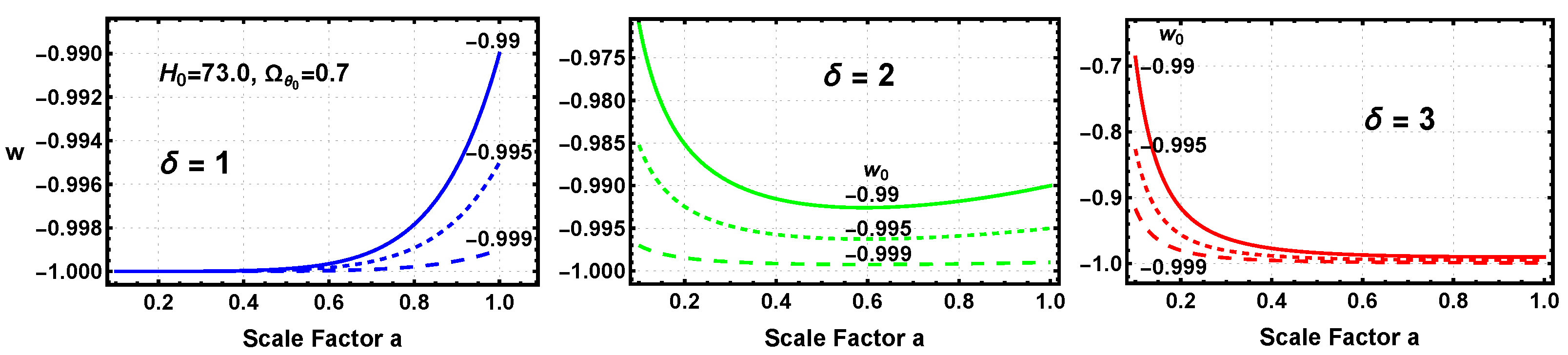
The $w_0$ values for the $\delta =3$ case are labeled on the plot. The order and line styles are the same for the other two $\delta$ values. The evolution is relatively small consistent with a slow roll. As expected the scalar values are monotonically increasing. The most striking feature is that the second derivative of the evolution changes from positive for $\delta =1$ to almost zero for $\delta =2$ to negative for $\delta =3$. The three, seemingly arbitrary, delta values were chosen to illustrate this transition. The transition has a large effect on some parameters, such as the dark energy EoS, w, but relatively little effect on the Hubble parameter as is shown later in Figure 7.

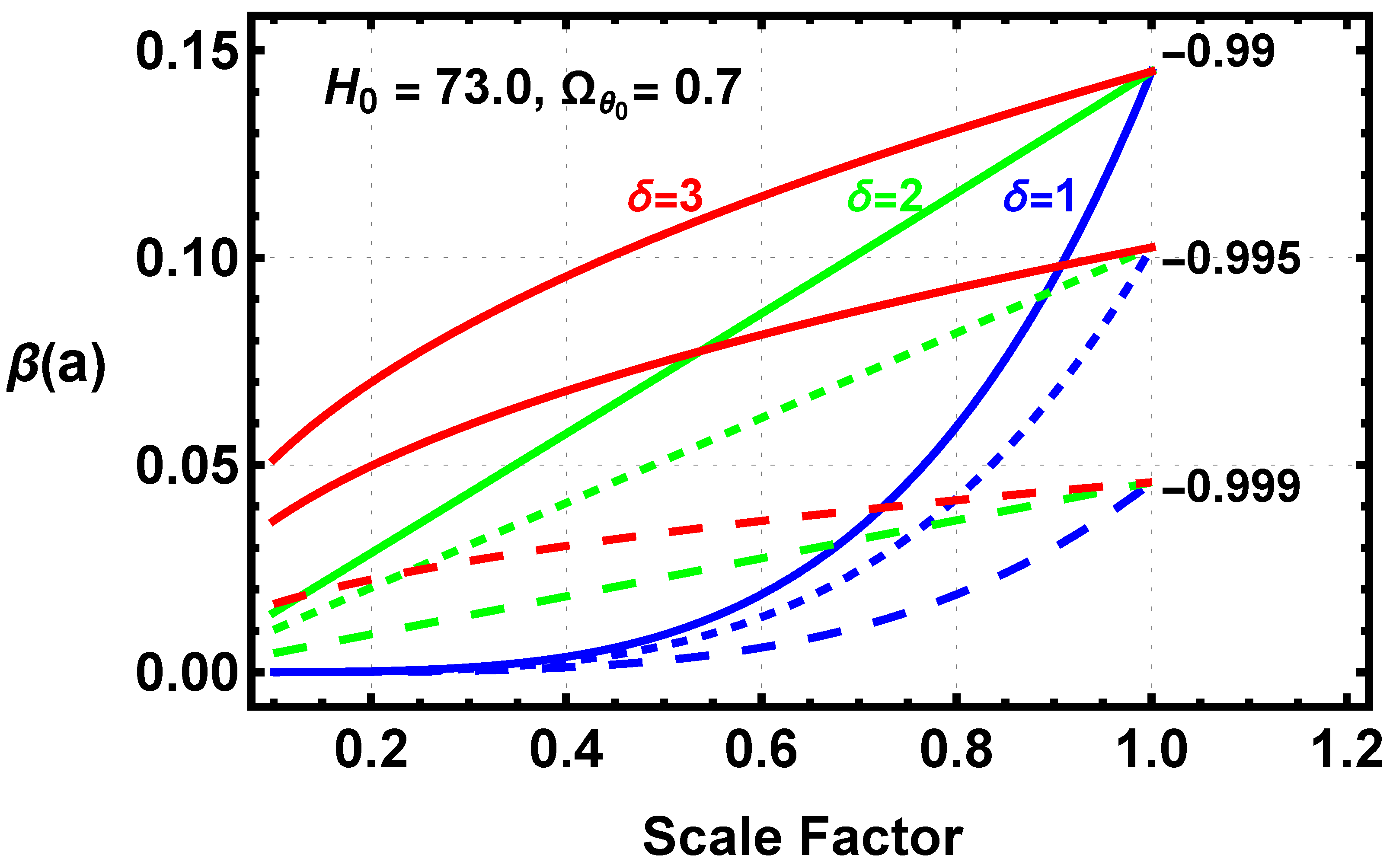
8.2. The Evolution of $\beta \left(a\right)$

The beta function evolution is shown in Figure 5.

Although the general nature of the evolution of the beta function is different from the scalar, it shows the same change in the second derivative of the evolution, positive for $\delta =1$, almost zero for $\delta =2$, and negative for $\delta =3$. The absolute value of $\beta$ is small and decreases as $w_0$ approaches −1. The current value of beta, ${\beta }_0$, is identical for a given value of $w_0$ due to Equation (14), which sets ${\beta }_0$ at $\sqrt{3{\mathsf{\Omega }}_{{\theta }_0}(w_0+1)}$, where the subscript 0 indicates the current values. The beta function appears in many cosmological parameters due to Equation (13) that links $\kappa \dot{\theta }$ and the Hubble parameter.

9. The Value of $\mathit{M}$ in the Dark Energy Potential

At this point, the value of M in Equation (10) has not been calculated. The Friedmann constraints and Equation (3) provide the means of calculating M. The dark energy density is

$${\rho }_{\theta }=\frac{{(\kappa \dot{\theta })}^2}{2}+M^4{({\left(\kappa \theta \right)}^2-{\left(\kappa \delta \right)}^2)}^2=3{\mathsf{\Omega }}_{\theta }{H}^2.$$

(35)

Using $\kappa \dot{\theta }=\beta H$

$$3{\mathsf{\Omega }}_{\theta }{H}^2=\frac{{\left(\beta H\right)}^2}{2}+M^4{({\left(\kappa \theta \right)}^2-{\left(\kappa \delta \right)}^2)}^2.$$

(36)

Since M is a constant it can be set using the current boundary conditions which insures adherence to the first Friedmann constraint at a scale factor of 1. This eliminates any constant offsets due to the approximation in Equation (17) further improving the accuracy of the templates.

Rearranging Equation (36) and using the current values of the parameters gives

$$3H_0^2({\mathsf{\Omega }}_{{\theta }_0}-\frac{{\beta }_0^2}{6})-M^4{({\left(\kappa {\theta }_0\right)}^2-{\left(\kappa \delta \right)}^2)}^2,M=\sqrt[4]{\frac{3H_0^2}{{({\left(\kappa {\theta }_0\right)}^2-{\left(\kappa \delta \right)}^2)}^2}\left({\mathsf{\Omega }}_{{\theta }_0}-\frac{{\beta }_0^2}{6}\right)}.$$

(37)

10. The Evolution of the HI Dark Energy Potential

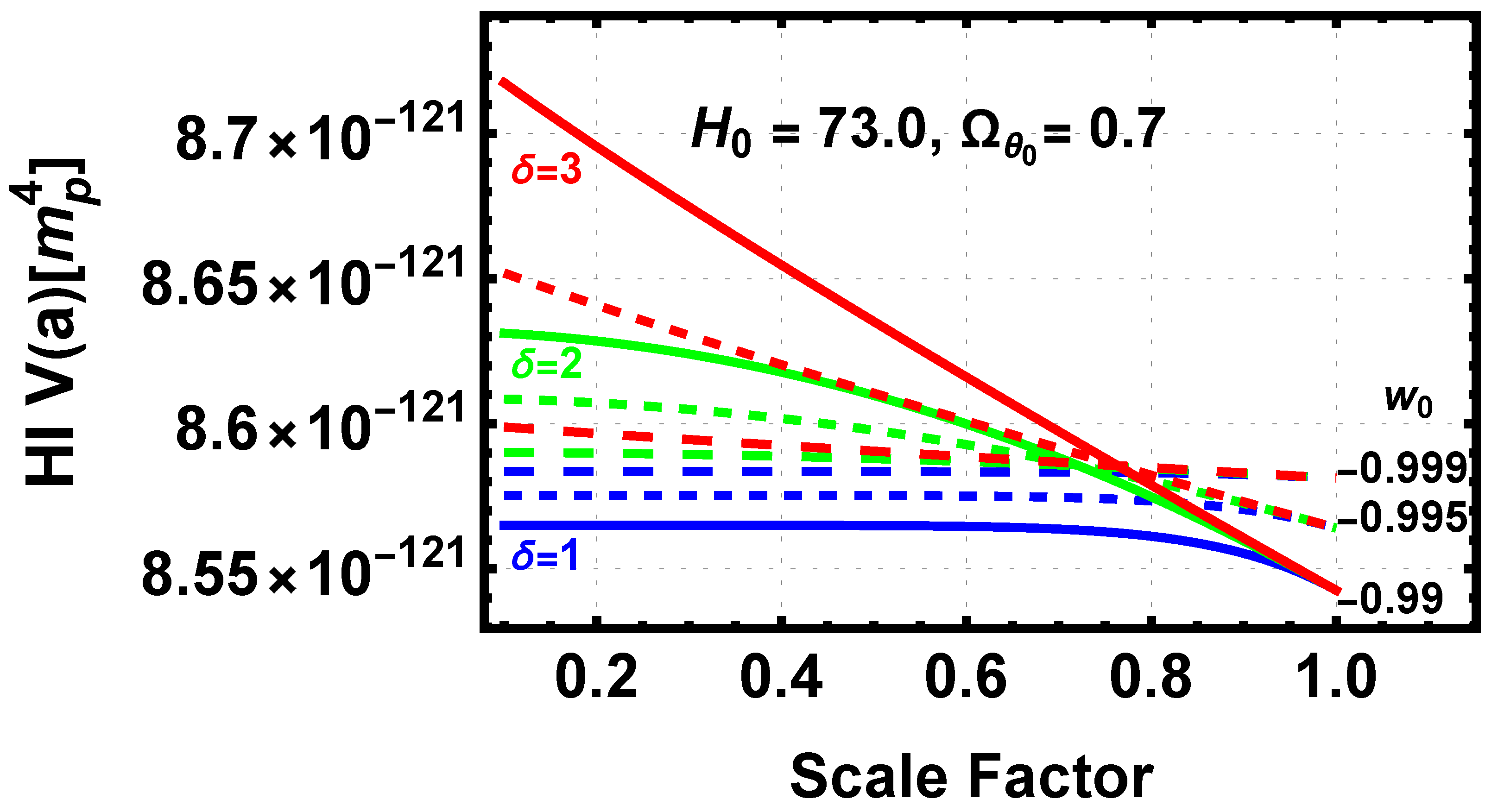
The evolution of the dark energy potential can now be calculated. Figure 6 shows the evolution of the HI dark energy potential for all of the cases.

Figure 6 shows that there is only a small evolution of the potential between scale factors of 0.1 and 1.0, again consistent with a slow roll. The maximum evolution is $1.7\%$ for the $\delta =3$ $w_0=-0.99$ case. The $\delta =1$ evolutions are essentially constant, mimicking $\Lambda$CDM, until a scale factor of ≈0.7, and then decrease slightly to the $a=1.0$ value for $w_0=-0.99$ and −0.995. The $\delta =2$ cases deviate from constant evolution earlier than the $\delta =1$ cases, and the $\delta =3$ cases have almost linear evolution and have the highest values, particularly at small scale factors. All of the $w_0=-0.999$ cases have a very flat evolution. For a given value of $w_0$, the current value of the potential is the same for all $\delta$ values. From Equations (10) and (37) the potential at a scale factor of one is $3H_0({\mathsf{\Omega }}_{{\theta }_0}-\frac{{\beta }_0^2}{6})$. Equation (14) shows that the value of the beta function at a scale factor of 1 is $\sqrt{3{\mathsf{\Omega }}_{{\theta }_0}(w_0+1)}$, making $V_0$ the same for a given $w_0$.

11. The Hubble Parameter

The calculation of the Hubble parameter for the real universe requires the inclusion of both dark energy and matter. In [5], matter is introduced via a differential equation involving the Hubble parameter and the beta function. Here, the Friedmann constraints are the primary tools for deriving the Hubble parameter in a universe with both matter and dark energy. The first Friedmann constraint gives

$$3H^2\left(a\right)={\rho }_{\theta }+{\rho }_m=\frac{{(\kappa \dot{\theta })}^2}{2}+M^4{({\left(\kappa \theta \right)}^2-{\left(\kappa \delta \right)}^2)}^2+\frac{{\rho }_{m_0}}{a^3}.$$

(38)

Here, ${\rho }_{m_0}$ is the current matter density and $\frac{{\rho }_{m_0}}{a^3}$ is the mass density as a function of the scale factor. Using Equation (13), $\beta H$ is substituted for $\kappa \dot{\theta }$ in Equation (38) to obtain

$$3H^2\left(a\right)(1-\frac{\beta {\left(a\right)}^2}{6})=M^4{({\left(\kappa \theta \right)}^2-{\left(\kappa \delta \right)}^2)}^2+\frac{{\rho }_{m_0}}{a^3}.$$

(39)

The Hubble parameter is therefore

$$H\left(a\right)=\sqrt{\frac{M^4{({\left(\kappa \theta \right)}^2-{\left(\kappa \delta \right)}^2)}^2+\frac{{\rho }_{m_0}}{a^3}}{3(1-\frac{\beta {\left(a\right)}^2}{6})}}.$$

(40)

11.1. The Time Derivative of the Hubble Parameter

The second Friedmann constraint in Equation (9) provides the method for calculating $\dot{H}$.

$$\dot{H}=-\left(\frac{{\rho }_{\theta }\left(a\right)+{\rho }_m\left(a\right)+3P\left(a\right)}{6}+H^2\right)=-\frac{1}{2}\left({\left(M\kappa \right)}^4{\dot{\theta }}^2+\frac{{\rho }_{m_0}}{a^3}\right)$$

(41)

where $\dot{\varphi }=M^2{\kappa }^2\dot{\theta }$ in units of the reduced Planck mass.

11.2. The Evolution of the Hubble Parameter

Figure 7 shows the evolution of the Hubble parameter for all values of $\delta$ and $w_0$ plus $\Lambda$CDM. At the resolution of the figure, all of the tracks overlap each other to the thickness of the line.

The dashed line on Figure 7 shows the time derivative of the scale factor $\dot{a}$ to show the transition to acceleration of the expansion of the universe. It occurs at a scale factor of ≈0.6 consistent with current observations, e.g., [22]. The $\dot{a}$ track has been multiplied by 10 to remove its overlap with the H parameter track. The following section shows the percentage deviation of the HI Hubble parameters from $\Lambda$CDM for all of the cases.

11.3. The Percentage Deviation from $\Lambda$CDM

The fractional deviation of the HI Hubble parameters from $\Lambda$CDM is given by

$$dev=\frac{H_{HI}-H_{\Lambda CDM}}{H_{\Lambda CDM}}$$

(42)

Figure 8 shows the percentage deviation of the HI H parameters from the $\Lambda$CDM H parameter.

The figure readily shows that the percentage deviation of the HI Hubble parameter from $\Lambda$CDM is exceedingly small. The highest deviation is $0.17\%$ for the $\delta =3$, $w_0=-0.99$ and the smallest deviation is $0.005\%$ for the $\delta =1$, $w_0=-0.999$ case. All of the $\delta =1$ cases have a negative deviation, indicating that the HI Hubble parameter is slightly less than $\Lambda$CDM, while the other $\delta$ values have positive deviations with the HI Hubble parameter slightly higher than $\Lambda$CDM. The maximum deviations occur at scale factors between 0.6 for $\delta =3$ and 0.8 for $\delta =1$, where dark energy begins to dominate. The overall shape of the deviations are reasonable. The deviation is zero at $a=1$, since it is set by the $H_0$ boundary condition. After the peak, the deviation drops again as the density becomes matter-dominated. Currently, the deviations of the $w_0=-0.999$ cases are impossible to detect observationally, and the highest deviation is below the detection limit of the proposed near-future facilities. Further discussion of the implications of the HI quintessence cosmology appears in Section 16.

12. The Scale Factor and Time Derivatives of the Scalar

The scale factor and time derivatives of the scalar are not observables but are essential for the calculation of the SCP templates. The starting point is the derivative of the Lambert W function in Equation (43).

$$\frac{dW\left(x\right)}{dx}=\frac{W\left(x\right)}{x(1+W(x\left)\right)}$$

(43)

From this base, the derivative of the scalar $\left(\kappa \theta \right)$ with respect to the scale factor a is

$$\frac{d\kappa \theta }{da}=\frac{d\left(\kappa \delta \sqrt{-W\left(q{a}^p\right)}\right)}{da}=\kappa \delta \frac{p\sqrt{-W\left(q{a}^p\right)}}{2a(1+W\left(q{a}^p\right))}.$$

(44)

The derivative of the scalar with respect to time is then

$$\frac{d\kappa \theta }{dt}=\frac{d\kappa \theta }{da}\frac{da}{dt}=\frac{d\kappa \theta }{da}Ha=\kappa \delta \frac{p\sqrt{-W\left(q{a}^p\right)}}{2(1+W\left(q{a}^p\right))}H.$$

(45)

Equation (45) gives the same answer as Equation (13).

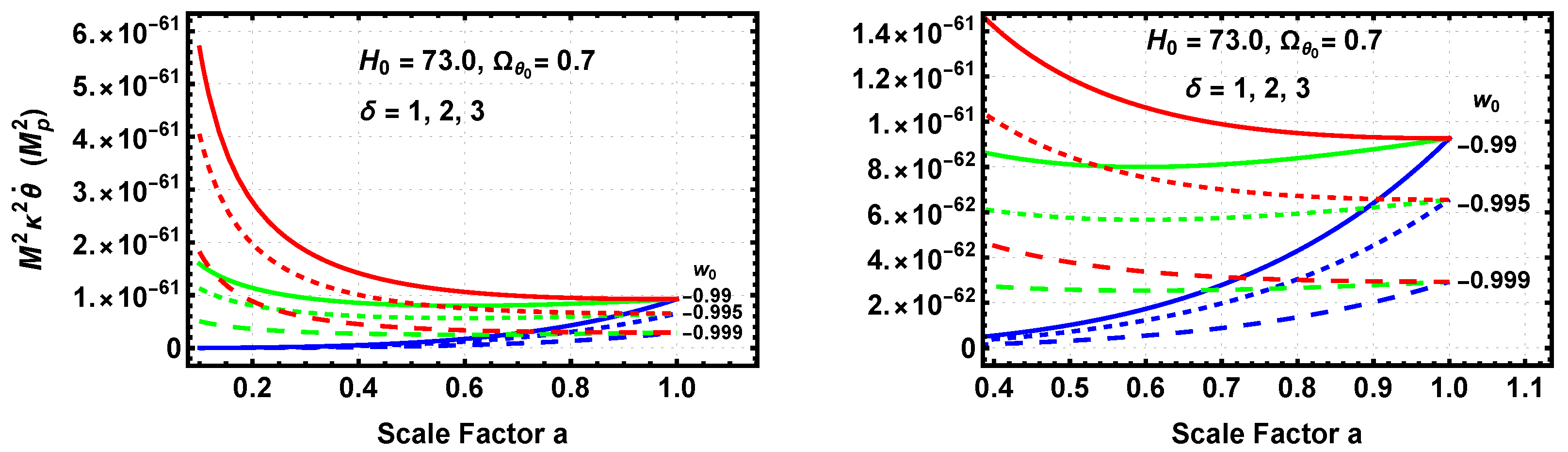
Figure 9 shows the evolution of $\dot{\varphi }=M^2{\kappa }^2\dot{\theta }$ in units of $m_p^2$ for all of the cases along with a more detailed plot of the region between a scale factor of 0.4 and 1.0.

The units of $\dot{\theta }$ are $m_p^2$, since $\theta$ has the units of mass and time has units of inverse mass. In Figure 9, ${\kappa }^2\dot{\theta }$ is multiplied by $M^2$ to show the value of the time derivative of the true scalar $\dot{\varphi }$. In the left panel, the full evolution of $\dot{\theta }$ is shown for the scale factors between 0.1 and 1.0. Unlike the scalar, the magnitude of $\dot{\theta }$ is decreasing for $\delta =3$ but increasing for $\delta =1$ with corresponding differences in the second derivative. The right hand panel shows the evolution between scale factors of 0.4 and 1.0 in more detail. Close inspection of the $\delta =2$ and $w_0=-0.99$ track show that it was initially decreasing but is currently increasing. This nonmonotonic evolution is also present in the dark energy EoS described later.

13. The Dark Energy Density and Pressure

Several cosmological parameters depend on the evolution of the dark energy density and pressure. Equation (3) gives the functions for them in terms of the kinetic term X and the dark energy potential. Figure 10 shows the evolution of the dark energy density for all of the cases.

As usual, the $\delta =1$ evolutions have a different character from the other two. The density evolution for $w_0=-0.999$ is essentially flat, and the highest evolution case, $w_0=-0.99$, only changes by $0.3\%$. For all values of $w_0$, the $\delta =1$ density has a slight rise near a scale factor of 1. For scale factors less than 0.6, the densities are essentially constant acting like a cosmological constant in the matter-dominated epoch. For $\delta =2$ and 3, the density is monotonically decreasing with increasing scale factor. The second derivative of the decrease of density for the $\delta =2$ case changes from negative to positive with increasing scale factor similar to the scalar. The decrease in density for the $\delta =3$ case is larger than for the other two cases but is still only on the order of $20\%$ for the maximum case. Unlike the $\delta =2$ case, the second derivative of the evolution is negative at all scale factors.

Figure 11 shows the evolution of the dark energy pressure.

The dark energy pressures have their characteristic negative values and, although more than the density, the absolute evolution is relatively small. The $\delta =1$ and 3 evolutions are monotonically positive and negative, respectively, but the $\delta =2$ pressure evolutions have stronger transitions from negative to positive than the density. As in the dark energy density, the $w_0=-0.999$ evolution is quite flat, as would be expected for a $w_0$ value so close to −1.

14. The Dark Energy Equation of State

By definition, the dark energy EoS is the ratio of the dark energy pressure to the dark energy density. Figure 12 shows the evolution of $w=\frac{p_{\theta }}{{\rho }_{\theta }}$.

The $\delta =1$w evolution is the classic thawing evolution, where w is initially near −1 and then thaws to the less negative values of $w_0$. The $\delta =3$ case is the classic freezing case, where w starts at values less negative than −1 and then freezes toward −1. The $\delta =2$ evolution, however, is nonmonotonic, starting as a freezing solution and then transitioning to a thawing evolution. These evolutions mirror the evolution of the dark energy pressure in Figure 11, since the magnitude of the pressure evolution is greater than the evolution of the density. The author does not know of any similar case in the literature but suggests that it may be called the freeze and thaw evolution. Figure 12 demonstrates the motivation for the simple choices of 1, 2, and 3 for the $\delta$ values. The $\delta =3$ cases have late time evolutions very similar to $\Lambda$CDM but significant and observable deviations at early times. The $\delta =1$ evolutions of w are indistinguishable from $\Lambda$CDM at early times and only slightly deviant from $\Lambda$CDM at late times due to the purposely chosen $w_0$ values very near −1. The $w_0=-0.999$ evolution of w would not be distinguishable from $\Lambda$CDM using the current analysis techniques. These aspects are discussed more thoroughly in Section 16, where the HI quintessence is considered as a candidate for a fiducial dynamical cosmology in the same way that $\Lambda$CDM is a fiducial static cosmology.

15. The Accuracy of the Cosmology and Dark Energy Potential

At this point, the SCP evolutionary templates of all of the cosmological parameters considered in this work are calculated. It is appropriate then to consider the accuracy of the cosmology and HI potential as a whole. The metric for the accuracy utilized here is the accuracy of the two Friedmann constraints that contain the Hubble parameter and its time derivative, the dark energy density, and pressure plus the matter density and HI potential. Other parameters, such as the dark energy equation of state, are functions of the parameters in the Friedmann constraints. The first and second Friedmann constraints are given in Equation (8). The two constraints are considered separately below.

15.1. The Accuracy of the First Friedmann Constraint

The left and right sides of the first Friedmann constraint should be equal; therefore, the accuracy, $fracerr$, is determined by

$$fracerr=\frac{3H^2-({\rho }_{\theta }+{\rho }_m)}{3H^2}.$$

(46)

The results for all of the cases are similar in the overall magnitude but of course dissimilar in detail. The results for $w_0=-0.995$ and the three values of $\delta$ are shown in Figure 13.

It is obvious that the first Friedmann constraint is satisfied to better than one part in ${10}^{16}$. This is on the order of the digital accuracy of the Mathematica code used in the calculation.

15.2. The Accuracy of the Second Friedmann Constraint

The second Friedmann constraint explicitly covers more parameters including the time derivative of the Hubble parameter. The fractional error for the second Friedmann constraint is given by

$$fracerr=\frac{3(\dot{H}+H^2)+\frac{({\rho }_{\theta }+{\rho }_m+3P)}{2}}{3(\dot{H}+H^2)}.$$

(47)

Unlike the first Friedmann constraint, where all of the terms are positive, the second Friedmann constraint has a mixture of positive and negative terms. Both the left and right hand term in the numerator of the constraint transition between positive and negative values. The left hand term is the denominator in Equation (47), which means that it goes through zero, making the fractional error infinite. The transition occurs at a scale factor of approximately 0.6. Since the calculations in Mathematica are digital, true zero rarely occurs, but the fractional error does spike at the transition point. Figure 14 shows the fractional error for the same cases considered in the first Friedmann constraint.

The regions away from the spike have similar fractional errors as for the first Friedmann constraint but build slightly before the spike. Even including the spike, the second Friedmann constraint is satisfied to a high accuracy, indicating that the SCP evolutionary templates also have a high degree of accuracy, exceeding the accuracy of the observations by a high degree.

16. The HI Quintessence as a Fiducial Dynamical Cosmology

In most likelihood, examinations of cosmological data $\Lambda$CDM are considered the fiducial static cosmology. A fiducial dynamical cosmology, however, has not been identified. This may be due in part to the multitude of dynamical cosmologies and the number of possible dark energy potentials. This leads to the use of parameterizations and their incumbent pitfalls as discussed in Section 2. HI quintessence may be a good candidate for a fiducial dynamical cosmology for comparison with $\Lambda$CDM. This confronts the question of whether dark energy is static or dynamic, with the canonical scientific method of comparing physics-based predictions with the data to measure the likelihood of the predictions.

There are compelling reasons for picking HI quintessence as one of perhaps several fiducial dynamical cosmologies. A particularly compelling reason is that the HI potential has a natural physical basis, since its mathematical form is the same as the only confirmed isotropic and homogeneous field, the Higgs field. It should be emphasized again here that the HI scalar is not the Higgs field. It is just a quintessence scalar field with the mathematical form of the Higgs potential. Another compelling reason is that, unlike monomial potentials, the HI potential covers a wide range of possible evolutions by simply varying the value of $\delta$ in the potential. Section 14 showed that both freezing and thawing evolutions of the dark energy EoS, w, are easily obtained as well as evolutions that transition between freezing and thawing. The SCP templates for all of these evolutions are physics-based and test real predictions for discriminating between static and dynamic dark energy plus determining the nature of a dynamical dark energy.

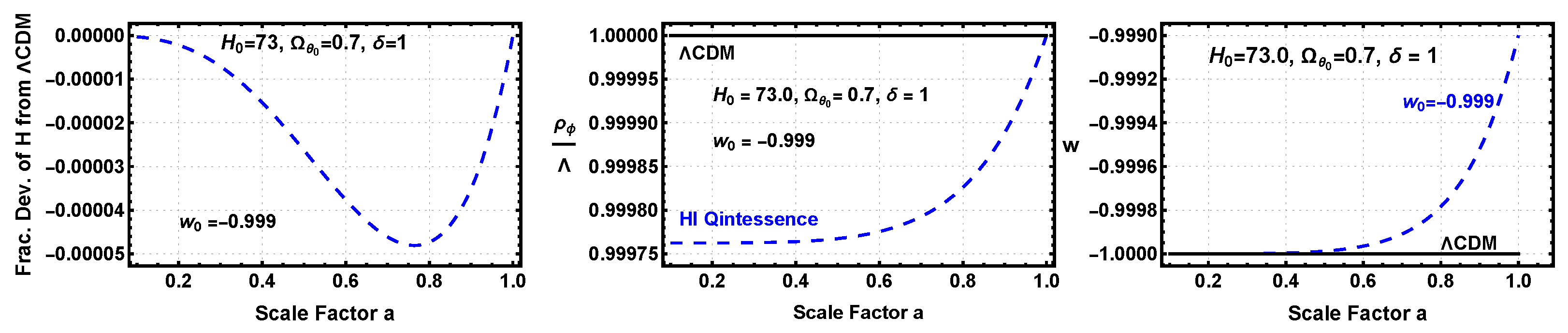
An additional reason for utilizing HI quintessence as a fiducial cosmology is that it comes arbitrarily close to $\Lambda$CDM by varying the constant in the HI potential and adjusting the boundary conditions, such as $w_0$, without invoking a cosmological constant. The best example of a $\Lambda$CDM type of evolution in this work is the $\delta =1$ and $w_0=-0.999$ case, examined more closely in the next section.

A $\Lambda$CDM-like Dynamical Cosmology

Due to the many successes of the $\Lambda$CDM cosmology in matching the observational data, the dark energy EoS $w_0$ values were purposely set close to but not equal to −1. The $\delta =1$ and $w_0=-0.999$ case is the closest one to $\Lambda$CDM. All of the $\delta =1$ cases are thawing, which means that the maximum value of w is $w_0$, and the early time values of w are very close to −1. It is this dynamical case, of all studied in this work, that has the best chance of having a likelihood close to that of $\Lambda$CDM. In earlier plots that show evolutions for all cases, the evolution of this case is often hard to discern, since it is much smaller than the maximum evolution case in the plots. 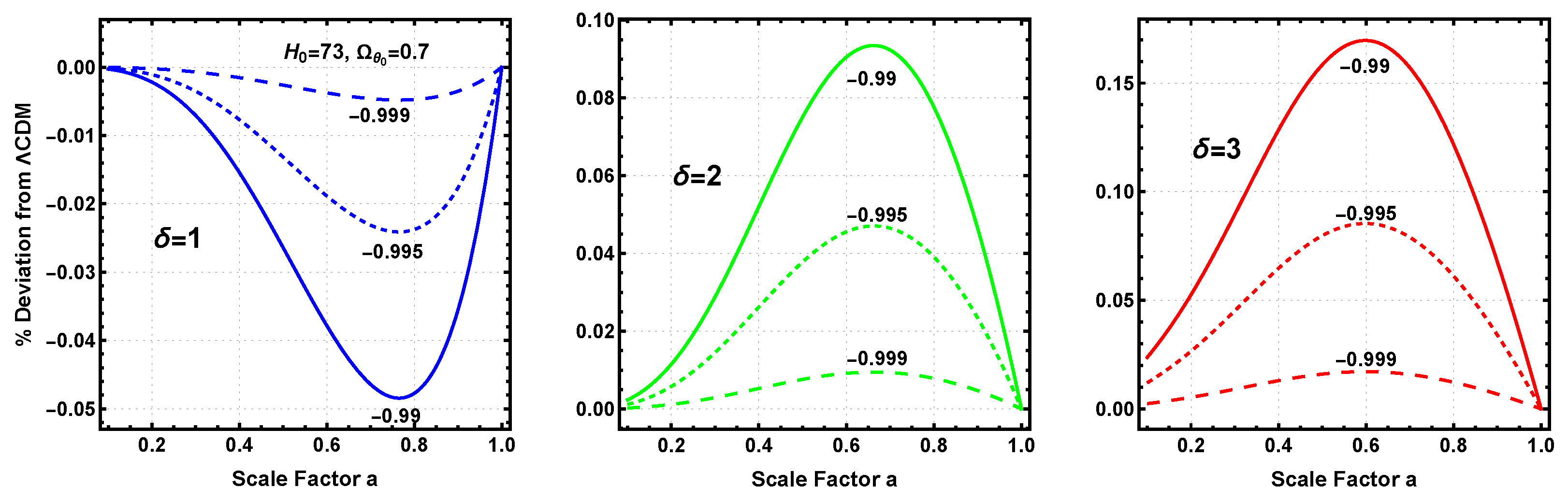To better illustrate the $\delta =1$, $w_0=-0.999$ evolutions, Figure 15 plots the fractional deviations from $\Lambda$CDM of this case only for the Hubble parameter, the dark energy density, and the dark energy EoS.

The left panel shows the fractional, not percentage as in Figure 8, deviation of the HI Hubble parameter from $\Lambda$CDM. The maximal fractional deviation is only −0.00005, which is below any current or expected near-term detectable limit. The center panel shows the ratio of the dark energy density to the cosmological constant, black line at 1.0, with a maximum deviation of 0.00025 at small scale factors. The boundary conditions set the deviation at $a=1$ to zero. The first panel of Figure 10 indicates that the deviation for scale factors smaller than 0.6 is constant at the $a=0.1$ value. It is unlikely that the small deviation produces any detectable effects. The right hand panel shows the dark energy EoS w which has a maximum deviation from −1 of 0.001. This also is below current or expected near-term detection limits. It is clear that any constraint on the deviation of w can be met by moving $w_0$ closer to −1, which also lowers the deviations of the other two parameters. This indicates that it is very difficult to falsify a dynamical cosmology or to confirm $\Lambda$CDM. On the other hand, a confirmed deviation from the $\Lambda$CDM predictions can falsify it but not necessarily confirm a dynamical cosmology. It would, however, produce a higher likelihood for a dynamical cosmology than for $\Lambda$CDM.

17. Temporal Evolution of Fundamental Constants

Constraints on the temporal and spatial variance of fundamental constants are excellent, but seldom used, discriminators between static and dynamic dark energy. They are also sensitive tests of the validity of the standard model of physics. Fundamental constants are dimensionless numbers whose values determine the laws of physics. Primary examples are the fine structure constant $\alpha$ and the proton to electron mass ratio $\mu$ that are cosmological observables. Both are measured by spectroscopic observation of atomic and molecular transitions, respectively. As discussed briefly in the introduction, the same scalar that produces the late time inflation by interacting with gravity most likely interacts with other sectors producing changes in the values of the fundamental constants. Since the same scalar is determining the value of the dark energy EoS and the values of the constants, there is a relationship that makes the fundamental constants w meters in the universe. The summation of the interactions of the scalar with the quantum chromodynamic scale ${\Lambda }_{QCD}$, the Higgs vacuum expectation value $\nu$, and the Yukawa couplings h produce a net coupling constant ${\zeta }_x$, where x can be either $\mu$ or $\alpha$. In the absence of any knowledge of the coupling, it is assumed to be linear as in Equation (48), which can be thought of as the first term of a Taylor series of the real coupling.

$$\frac{\Delta x}{x}={\zeta }_x(\kappa \theta -\kappa {\theta }_0)$$

(48)

Current limits on the temporal variation of the constants are $\Delta \alpha /\alpha =-(1.3\pm 1.3_{stat}\pm 0.4_{sys})\times {10}^{-6}$, $1\sigma$ [23] at $z=1.15$, and $\Delta \mu /\mu \le \pm 1.1\times {10}^{-7}$ $2\sigma$ [24,25] at $z=0.89$. The redshifts for both of these measurements are look back times greater than half the age of the universe. The $\alpha$ constraints are from optical spectroscopy of multiple atomic fine structure lines, and the $\mu$ constraints are from radio observations of methanol absorption lines in cold molecular clouds along the line of sight to a quasar. In the following, the tighter constraint on the temporal variation of $\mu$ is used as an example.

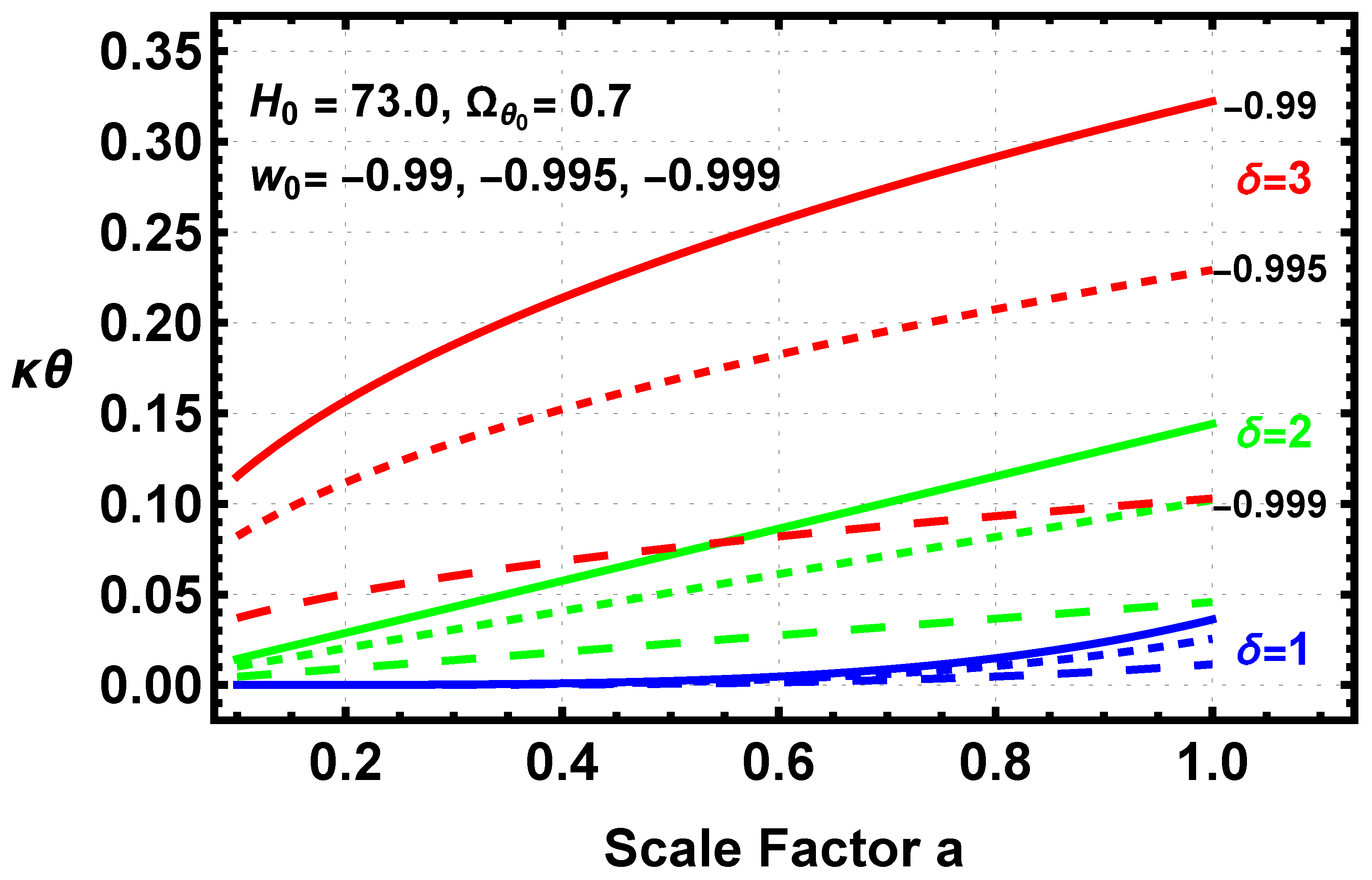
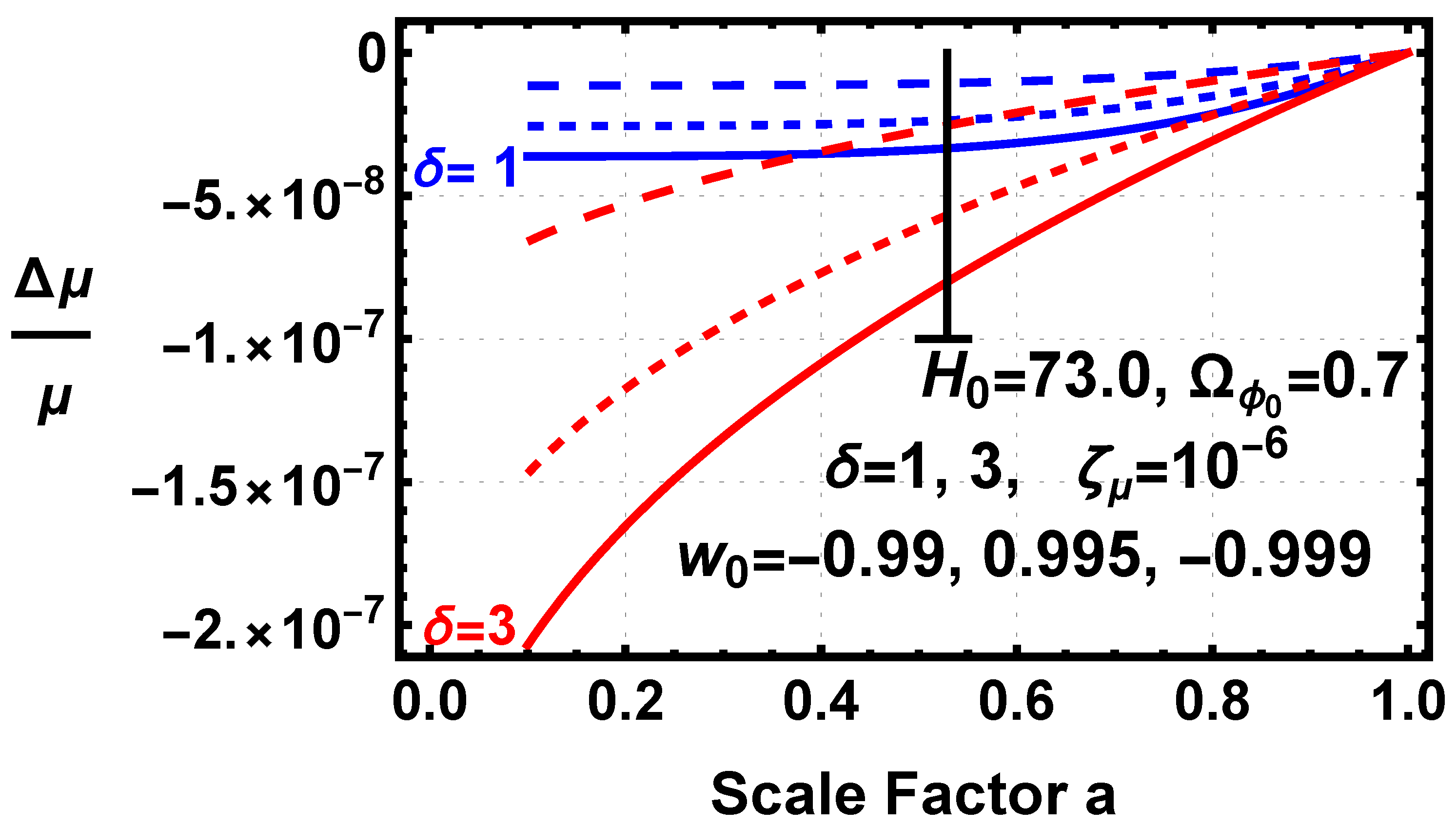
Figure 16 shows the evolution of $\frac{\Delta \mu }{\mu }$ for $\delta =1$ and 3 for all three $w_0$ values and ${\zeta }_{\mu }={10}^{-6}$.

The $\delta =1$ cases represent the least evolution, and the $\delta =3$ cases represent the most evolution with the $\delta =2$ lying between the two. All of the cases satisfy the constraint, mainly because of the small deviations of $w_0$ from −1. Only a small tightening of the constraint would start to eliminate some of the $\delta =3$ cases. The proposed fiducial case of $\delta =1$ and $w_0=-0.999$ is well within the observational constraint. Additionally restrictive observational constraints can always be cosmologically accommodated by making $w_0$ closer to −1 or by lowering the value of the particle physics parameter ${\zeta }_{\mu }$.

The last sentence in the above paragraph indicates that a constraint on the temporal variance of either $\mu$ or $\alpha$ is a constraint on a cosmology–particle physics plane defined by w and ${\zeta }_{\mu }$. An earlier analysis [26] determined the relationship between ${\zeta }_{\mu }$ and w as

$${\zeta }_{\mu }=\frac{\pm \frac{\Delta \mu }{\mu }}{\kappa \theta (a_{ob},w_0,{\mathsf{\Omega }}_{{\theta }_0})-\kappa {\theta }_o(1,w_0,{\mathsf{\Omega }}_{{\theta }_0})}$$

(49)

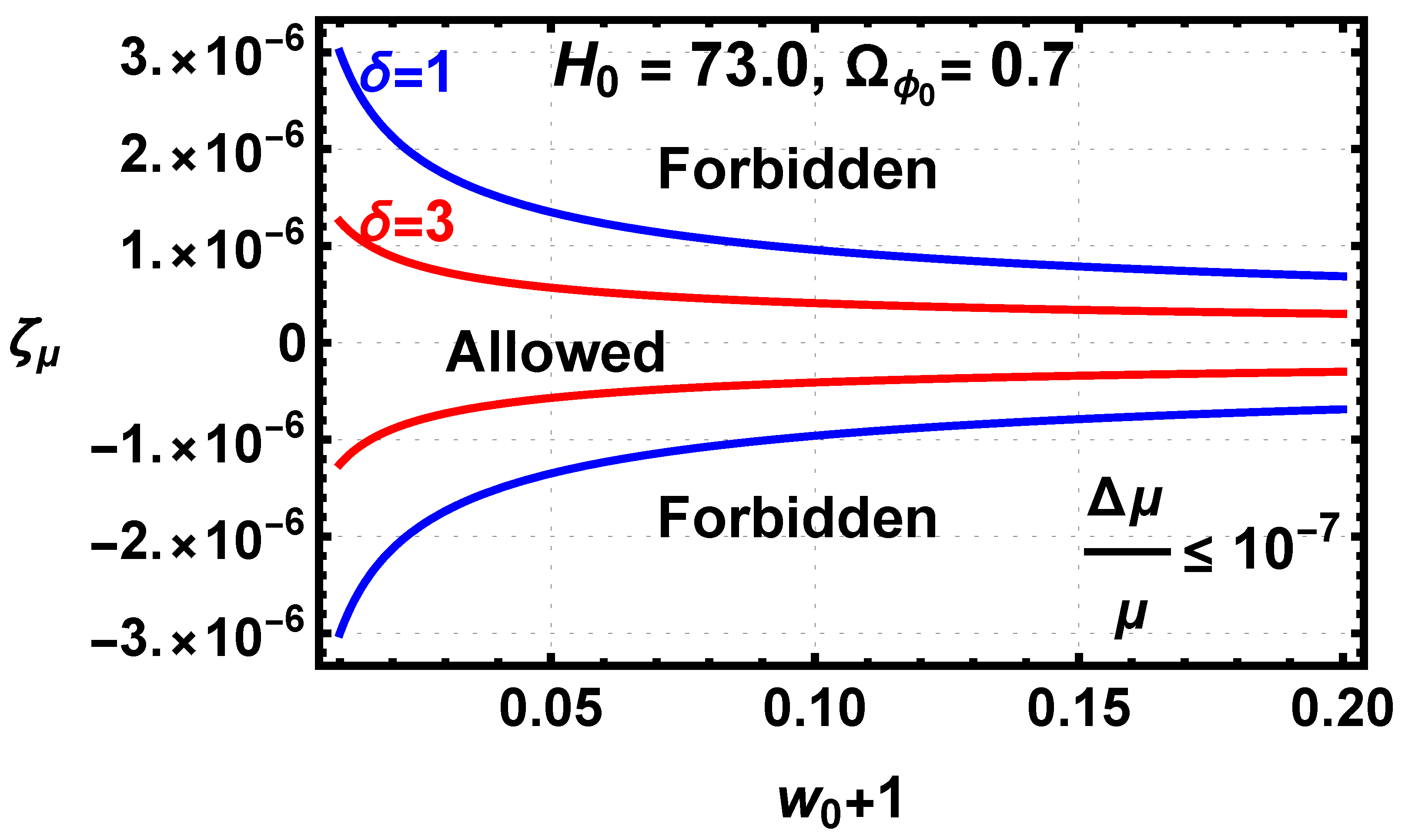
where $a_{ob}$ is the scale factor of the observation. Equation (19) for ${\theta }_0$ is the source of the ${\mathsf{\Omega }}_{{\theta }_0}$ term in Equation (49). Equation (49) defines regions in the ${\zeta }_{\mu }-(w_0+1)$ plane that satisfy the observational constraint and those that do not. Figure 17 shows the allowed and forbidden area for the $\frac{\Delta \mu }{\mu }$ constraint.

The positive and negative tracks for each $\delta$ case are due to the positive and negative values for ${\zeta }_{\mu }$ in Equation (49). The $\delta =3$ more restricted allowed area is due to the greater evolution of $\frac{\Delta \mu }{\mu }$ as shown in Figure 16, which requires a smaller ${\zeta }_{\mu }$ to meet the constraint than the $\delta =1$ case. The $\Lambda$CDM point in the figure is the 0, 0, origin where ${\zeta }_{\mu }=0$ and $(w_0+1)=0$. A confirmed observation of $(w_0+1)\ne 0$ with no detected variance of $\mu$ would place a hard limit on the particle physics parameter ${\zeta }_{\mu }$ but would also require new physics to account for the deviation of w from −1.

18. Conclusions

This study addresses the question of whether dark energy is static or dynamic by first pointing out that the use of parameterizations to represent dynamical cosmologies results in not only erroneous likelihoods but also in erroneous conclusions about the validity of dynamical cosmologies such as quintessence. The study then presents a methodology for creating accurate analytic templates of the evolution of cosmological parameters and fundamental constants for the flat quintessence dynamical cosmology. The methodology utilizes a modified beta function formalism to determine the evolution of the quintessence scalar as a function of the observable scale factor. Solutions for the evolution of parameters and constants that were previously only functions of the unobservable scalar are then translated to templates that are functions of the scale factor for direct comparison with the current and expected cosmological observations. Recognizing that dynamical cosmologies can have a multitude of dark energy potentials the study introduced the concept of specific cosmology and potential (SCP) templates to replace the parameterizations with SCP evolutionary templates based on the physics of the cosmology and dark energy potential. For this reason, the study is concentrated on the methodology to produce SCP templates that can embrace a broad range of analytic physics based potentials.

To demonstrate the formalism in the study, the SCP templates of several observable and some necessary but not observable parameters, such as the time derivative of the scalar that appear in the functions of many observable parameters, were then calculated. An important aspect of the study is the example quartic polynomial dark energy HI potential. The modified beta function formalism applied to flat quintessence with the HI potential resulted in a scalar that is a simple function of the Lambert W function. This step provides the means to produce accurate analytic SCP templates as a function of the scale factor.

Given the many observational successes of the $\Lambda$CDM static cosmology, boundary conditions close to $\Lambda$CDM were chosen in the study. In particular, $w_0$ values close but not equal to −1 were adopted. This choice produced a simplification of the beta function formalism, where the beta function for quintessence is the negative of the logarithmic derivative of a slightly modified dark energy density. The beta function was then accurately approximated by the logarithmic derivative of the potential. Care should be taken in using the formalism for w values significantly different than −1. Equation (7) shows that the kinetic term X is directly proportional to $(w+1)$. If $(w+1)$ becomes too large, the approximation can break down, and other means must be employed. The SCP templates are calculated by imposing the Friedmann constraints on the parameters. Since the studied epoch included only the matter-dominated and dark energy-dominated epochs, radiation is not included in the calculations. This precludes utilization of the templates for scale factors smaller than 0.016, such as the CMB-dominated epoch, that have significant radiation densities.

The polynomial HI potential provided a significantly larger range of evolutions than the often used monomial potentials. In particular, small changes of the constant term $\delta$ in the potential produced dark energy EoS evolution that were both freezing and thawing plus evolutions that transitioned from freezing to thawing. Given the naturalness of the HI potential and the large range of evolutions, the study suggests that the HI SCP templates become a fiducial dynamical cosmology in the same way as $\Lambda$CDM is for static cosmologies. Several of the studied cases are indistinguishable from $\Lambda$CDM with the accuracy of the present and near-future observations, even though their dark energy density arises from a dynamical scalar field rather than a cosmological constant. Given this and the relative rigidity of the predicted evolutions, it appears that $\Lambda$CDM is easy to falsify but hard to confirm and that flat HI quintessence is hard to falsify but easy to confirm if new observations confirm predictions such as a dynamical dark energy EoS (Appendix A).

The study concluded with an examination of the role of fundamental constants in the discrimination between static and dynamical cosmologies. The scalar in a dynamical dark energy that interacts with gravity will most likely interact with other sectors, which produces temporal variations in the fundamental constants. To date, no confirmed variations of either $\alpha$ or $\mu$ have been found at the one part in ${10}^7$ level. For all of the cases in this study, the predicted variations are less than the current limits. Future observations may, however, lower the limit, which would make it difficult to meet the constraints or find a variation that is consistent with the dynamical predictions.