Abstract
We investigate the dynamics of test particles endowed with both electric charge and a magnetic dipole moment around a Schwarzschild black hole (BH) immersed in an externally asymptotically uniform magnetic field. We further analyse the effective potential and specific angular momentum and energy of the particles. Furthermore, we show that the upper limit for magnetic interaction parameter increases with increasing cyclotron frequency , while the radius of the innermost stable circular orbit (ISCO) for charged test particles decreases for the upper value of . Furthermore, we show that the energy efficiency released from the BH increases up to about 90% due to the presence of the magnetic dipole moment of the test particle. We explore a degeneracy between the spin parameter of rotating Kerr BH and the magnetic parameter for the values of the ISCO radius and energy efficiency. We study in detail the centre of mass energy for collisions of charged and magnetized particles in the environment surrounding the Schwarzchild BH. Finally, as an astrophysical application, we explore the magnetized parameter and cyclotron frequency numerically for a rotating magnetized neutron star. Interestingly, we show that the corresponding values of the above-mentioned parameters for the magnetar PSR J1745-2900 that orbits around the supermassive black hole (SMBH) that exists at the centre of the Milky Way galaxy are and , respectively, for the magnetic field is about 10 G.
PACS:
04.50.-h; 04.40.Dg; 97.60.Gb
1. Introduction
The presence of black holes is a generic property of Einstein’s general theory of gravity. However, they had been so far considered as candidates since the discovery of gravitational waves via LIGO-VIRGO detection was announced as a result of two stellar black holes merging [1,2] as well as the first supermassive M87 black hole image under collaboration of the Event Horizon Telescope (EHT) [3,4]. These observations give new prosperity in understanding unexplored problems of black holes and the universe. It is well known that particles and even photons are affected drastically due to the strong gravitational fields of black holes. However, it is essential to explore other existing forces acting on particles moving around the black hole. These alternative forces are connected to the forces caused by the magnetic field and other sources surrounding the black hole; however, these forces, that are negligible or weak compared with the gravitational field, are effective for astrophysical processes occurring around the black hole [5,6,7,8,9,10,11,12]. Of them, the magnetic field can exert its powerful influence on particles near the black hole, although it is weak. Knowing this, we investigate charged and magnetized particle motion around a static and spherically symmetrical black hole placed in an external magnetic field, thus allowing us to test the general theory of relativity in a strong gravitational field regime.
Recent modern astronomical investigations of the output (≈–) from active galactic nuclei (AGN) in various forms, such as winds and jets, have been detected by X-ray, very long baseline interferometer (VLBI), and -ray telescopes. High-energy production near a black hole horizon by means of two colliding particles was first theoretically addressed by Banados, Silk, and West (BSW) [13] to model such a high-energy phenomenon. Following [13] there has been a huge amount of work in the different frameworks of standard general relativity in recent years [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. Furthermore, theoretical investigation of high-energy phenomena associated with the well-known Penrose process was addressed by authors of [31]. Recently, the relations of the collisional Penrose process with spinning particles have been considered [32].
The magnetic field becomes very important not only in developing accurate theoretical investigations of astrophysical processes but also as a powerful tool in the investigation of the output from active galactic nuclei for the transition from high energy to jets [33]. However, black holes are not endowed with their own magnetic fields [34] because of gravitational collapse decaying with ; instead, they invoke external magnetic fields induced by nearby magnetars or neutron stars [35,36] and the accretion disc around rotating black holes [5]. Hence, in an astrophysical scenario, the magnetic field can be regarded as a test field, thereby not modifying the spacetime geometry [37,38,39,40,41,42,43,44,45]. An extensive analysis was addressed for the magnetic field strength [46] and at the horizon radius [47,48]. Observational studies of the binary black hole system V404 Cygni in the infrared, optical, X-ray, and radio wave regions reported that the strength of the magnetic field can be around G (see, for example [49]). However, its strength was estimated to be between 200 G and G [50]. A lot of work has been conducted [51,52,53,54,55,56,57,58,59] addressing the charged particle motion around black holes placed in the electromagnetic field in a variety of gravity models. There are also investigations that address an extensive analysis on periodic motions in various gravity models [60,61,62,63]. In previous papers, we have widely discussed the dynamics of magnetized and spinning particles in the environment surrounding magnetized and magnetically charged black holes in various theories of gravity (see, for example [64,65,66,67,68,69,70,71,72,73,74,75,76,77,78]).
Testing gravity theories using observational data from black holes is one of the most important issues in relativistic astrophysics. In this sense, the GR is a well-tested theory. In real astrophysical cases, it is impossible to “feel” the gravity theories dominating spacetime around black holes. However, these can be mimicked by electromagnetic interactions between charged and magnetized particles with external magnetic fields around the black hole in general relativity (GR). In fact, there are neutron stars and white dwarfs that have not yet been observed in the vicinity of Sgr A* by the GRAVITY collaboration. One may consider that the problem is connected to electromagnetic interactions. On the other hand, the objects may have a high magnetic moment and fast rotation which may create an induced electric field (charge); thus, it is important to compare the charge and magnetic moment electromagnetic interactions between external magnetic fields. In this paper, we plan to study the dynamics and collisions of test magnetized particles with electric charge around a Schwarzschild black hole immersed in an external asymptotically uniform magnetic field, taking into account electromagnetic interactions between the external magnetic field with both electric charge and a magnetic dipole moment.
The paper is organized as follows: In Section 2, we explore the motion of particles possessing electric charge and a magnetic dipole in the spherically symmetrical black hole placed in an external magnetic field. In Section 4, we focus on particle collisions that occur very close to the black hole for specific collision scenarios. Section 5 is devoted to discussing the relevance of the analysis for astrophysical applications. We end up with the concluding remarks of the obtained results in Section 6. We use a system of units in which throughout the paper.
2. Particles with Electric Charge and a Magnetic Dipole
In this section, we will propose a formalism to model the motion of particles endowed with electric charge e and a magnetic dipole moment orbiting around a black hole immersed in an external uniform magnetic field. The spacetime metric describing the spherically symmetrical black hole is given by
where has the form as
with M referred to as the black hole mass.
Using the Wald method [5] the electromagnetic four-potential can be derived, corresponding to the magnetic field around the BH in the following form,
where is the asymptotic value of the external uniform magnetic field. One may immediately calculate the non-zero components of the electromagnetic tensor using the definition in the form
The magnetic fields around the Schwarzschild BH, measured in the proper observer frame of reference,
where, the four-velocity of the proper observer is, ; and is the pseudo-tensorial form of the Levi–Civita symbol, with the following relations:
Here, g is the spacetime metric (1) . is the Levi–Civita symbol with even permutations, and for odd permutations, it is . Consequently, we have,
2.1. Equation of Motion
For a charged test particle with a magnetic dipole, we exploit the Hamilton–Jacobi equation to describe its equation of motion as follows:
where is regarded as scalar as the product of polarization and electromagnetic field tensors and describes the interaction between the magnetic field and dipole moment of the particle. The tensor and magnetic dipole of the particle are related by the expression [35]:
where and refer to the four-dipole moment vector and four-velocity of the particle measured by a proper observer, respectively. The relationship between the electromagnetic field tensor and electric and magnetic fields is given by
Taking into account the condition given in Equation (10) the product of polarization and electromagnetic tensors for the proper observer is defined by
For further analysis, we shall assume that the direction of the magnetic dipole moment with components is parallel with the magnetic field (i.e., perpendicular to the equatorial plane). Thus, particle dynamics around a magnetized black hole at the equatorial plane (i.e., and ) can be described by the following action
With this in view, one can write the variables in a separate form in the Hamilton–Jacobi equation. The radial motion of the particle can be then defined by
where for the radial motion takes the form
where is the specific angular momentum of the particle and is the magnetic coupling parameter that describes the interaction between the dipole moment and the magnetic field. Here, is a dimensionless parameter and refers to the “effective” cyclotron frequency (or the magnetic parameter).
In Figure 1, we demonstrate the radial profiles of the effective potential for the radial motion of magnetized and charged test particles. In the figure, we show how positively and negatively charged particles with a magnetic dipole as well as neutral particles affect the effective potential of the radial motion. As can be seen from Figure 1 that positive values of both the magnetic-coupling parameter and cyclotron frequency give rise to a decrease in the strength of the potential, while for negatively charged particles its maximum is higher in contrast to neutral particles. Alternatively, the magnetic field decreases (increases) the height of the potential for positive (negative) magnetic parameter accordingly.
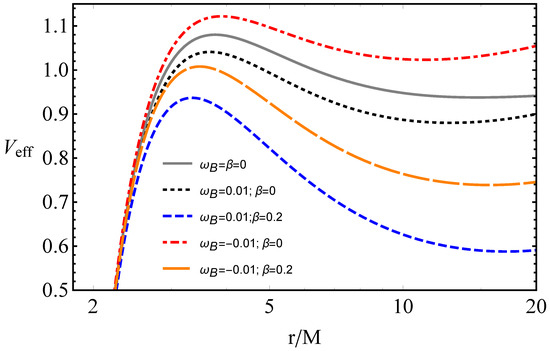
Figure 1.
The radial dependence of the effective potential for magnetized and charged test particles.
Now we focus on stable circular orbits around the black hole. For circular orbits, the following conditions for the effective potential and its first derivative must hold:
The above equations solve to give the specific angular momentum and the energy of particles moving at the circular orbits, respectively:
where
It is easy to see from Equation (17) that there are the following symmetries in the solutions of angular momentum:
In further analysis, we will study the solution .
The radial dependence of the corresponding specific energy and angular momentum at the circular orbits is shown in Figure 2 for different values of the interaction parameters and . It is certain that the corresponding values of the specific energy and angular momentum increase with increasing , while they decrease as a consequence of the increase in the magnetic interaction parameter .
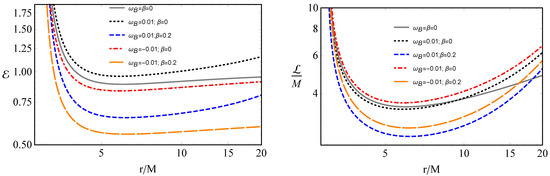
Figure 2.
Radial profiles of the specific energy (left panel) and angular momentum (right panel) for magnetized and charged particles at the circular orbits.
For the innermost stable circular orbits (ISCOs), one needs to solve the following equation
For magnetized and charged particles around the black hole in the magnetic field, the above equation implicitly gives the ISCO radius from the condition:
In Figure 3, we show the ISCO radius as a function of parameters (left panel) and (right panel) for different values of and , respectively. It is clearly seen that the ISCO radius decreases with increasing cyclotron frequency . We notice that the decreasing rate for the ISCO radius is slightly stronger for negatively charged particles in comparison with positively charged particles.
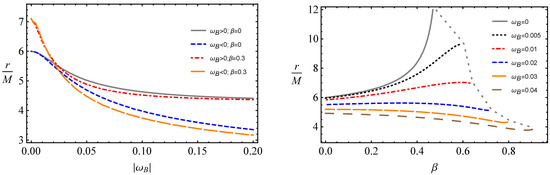
Figure 3.
The dependence of the ISCO radius on the parameters (left panel) and (right panel).
Moreover, it is seen from the figure that there is an upper value of the parameter of the particles with positive electric charge , while the upper value for electrically neutral magnetized particles is , and in that value of the ISCO lies at infinity. This means that the particles with 3 cannot be in stable orbits around magnetized black holes. The upper value of parameter increases as increases. However, the ISCO radius is limited in the case of 0, and it decreases as the parameters increase. Therefore, we are now interested in which relationships of parameters and the ISCO radius takes the value M; the same as ISCO radius of electrically neutral particles around the Schwarzschild black hole. We provide relations between the parameters and for a constant ISCO radius in Figure 4.
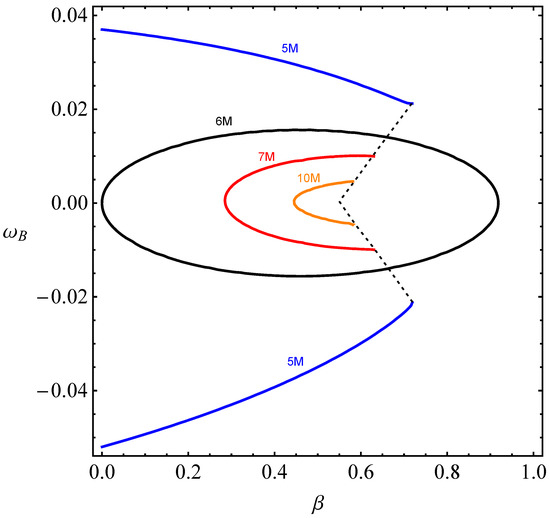
Figure 4.
Possible values of parameters and for a ISCO radius between 5 and 10 M.
One can see from the figure that there is no symmetry in that relationship with respect to . The line at M is closed, but for the cases when M one can see cutting the values of the parameters limited by the dashed lines.
2.2. Energy Efficiency
The Keplerian accretion around astrophysical black holes can be used to model the geometrically thin disk governed by properties of circular geodesics in spacetime [79]. The energy efficiency of the accretion disk refers to the maximum energy extracted as radiation as that of falling matter into the black hole from the disk.
Energy efficiency can be obtained by taking the following expression
where is the particle energy at the ISCO radius, characterized by the ratio of the binding energy (BH-particle system).
In Figure 5, we show the dependence of the energy efficiency on the magnetic-coupling parameter for different values of the cyclotron frequency.
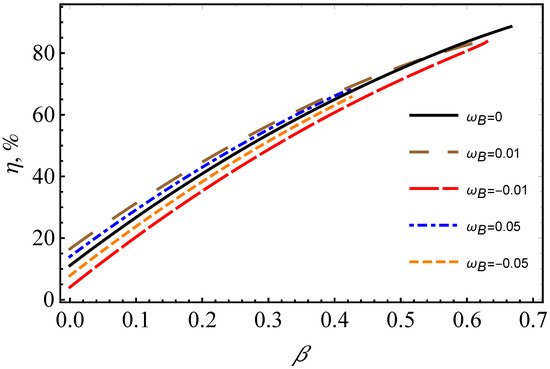
Figure 5.
Dependence of the energy efficiency on the magnetic-coupling parameter for different values of the parameter .
As shown in Figure 5 the energy efficiency linearly grows when increasing the parameter , while it slightly increases as a consequence of the positive values of . In contrast, for positive values, it is observed that the energy efficiency decreases similar to negatively charged particles. For simplicity, we show the numerical calculations to understand in depth the behaviour of energy efficiency. The efficiency reaches 88.6% in the case of particles with zero electric charges (i.e., ), while its highest values reaches ∼84% for and up to ∼70% for 0.05 for the corresponding upper values of parameter . These numerical results imply that the model considered here may be helpful to explain in depth the source of highly energetically charged and magnetized (elementary) particles in cosmic rays.
3. Spin of Kerr BH versus Magnetic Interactions
Relying on astrophysical observations with so-called accretion disk luminosity, quasiperiodic oscillation (QPO) analysis (i.e., the QPOs possessing the X-ray power observed in microquasars as a primary source of low-mass X-ray binary systems including neutron stars or black holes) and observations related to the ISCO measurements around black holes, it is believed that black holes can be regarded as rotating Kerr black holes. However, in theoretical studies of direct/indirect measurements in the context of alternative theories of gravity, another gravity parameter can be obtained, thus being an alternative to the spin of a rotating Kerr black hole. Here the challenging question is how to distinguish the black holes with the help of these above-mentioned measurements.
To settle this question, one can analyse mimicking cases for several gravity parameters, and so one is able to distinguish these parameters from the spin parameter of the Kerr black hole (see, for example [76]).
3.1. In the Same ISCO Radius
With the above motivation, one can compare the ISCO radius around the Schwarzschild black hole embedded in the magnetic field with the one around the Kerr black hole.
In Figure 6, we show the degeneracy for the ISCO radius value between the parameter and the spin parameter in the case of different values of parameter . As can be seen from Figure 6, in the case of 0.417129 it can mimic the spin of an extreme rotating Kerr black hole (i.e., ) for electrically neutral particles. Moreover, based on the numerical calculations, we show that can mimic the spin parameter a up to 0.551657 () for the fixed 0.05 (0.05), while up to with its upper value .
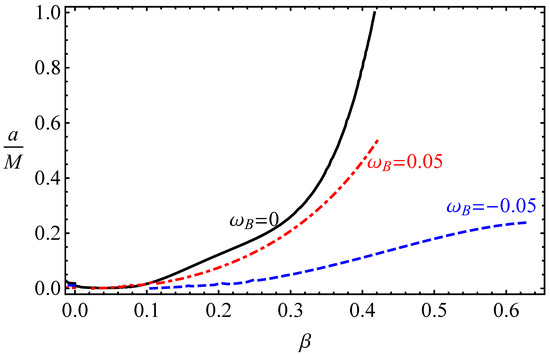
Figure 6.
Degeneracy between parameter and a, i.e., for a given value of there exists a Kerr geometry with a given value of spin parameter that has the same ISCO radius for various combinations of parameter . The point to be noted here is that represents a black hole rotation (spin) parameter.
3.2. In the Same Accretion Disk Luminosity
In this subsection, we analyse the energy efficiency, which is relevant to the total bolometric luminosity of the accretion disk around a black hole. Note that the bolometric luminosity is proportional to the efficiency of the energy release from the black hole, i.e., with being the rate of accretion matter falling into the black hole [73,80]. Thus, it is of primary importance in astrophysical observations.
Figure 7 shows the same behaviour as Figure 6 for the same energy efficiency. Here, the parameter mimics the spin parameter up to (0.752–1) for its corresponding values (0–0.1786), while for particles with () it mimics up to (0.4617–1) and ( (0.8724–1)), respectively.
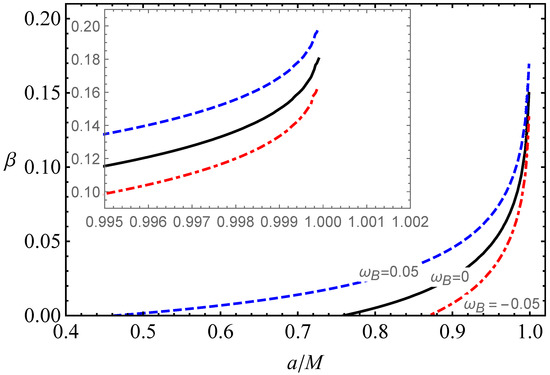
Figure 7.
Degeneracy between the parameter and the spin parameter of Kerr BH, providing the same energy efficiency for different values of parameter .
4. Particle Collisions
It is still of primary importance to estimate the total amount of energy released by various relativistic astrophysical processes occurring around compact gravitational objects. It is well known that the luminosity of AGN is of order and powered by supermassive black holes.
There are several models proposed to extract energy from rotating black holes. Penrose first proposed a mechanism for energy extraction from black holes [81]. Later, this mechanism was developed by a number of authors [31,55,82]. According to the Penrose mechanism, when a falling particle enters the so-called ergosphere restricted by an event horizon at one end and by the static radius at the other, it can be decayed into two particles, i.e., one falls into the black hole and the other escapes to infinity with energy greater than initial one. This is precisely what has been shown with explicit calculation by the Penrose mechanism. Note that energy efficiency with this process is relevant to how large the ergoregion is, i.e., the energy released becomes larger if the ergoregion is large.
Another interesting process was theoretically studied by Banados–Silk–West (BSW) [13,22] considering the high-energy collisions of particles in the vicinity of the black hole horizon. In this context, a large amount of work has since been developed in various situations [16,17,18,19,20,21,22,23,24,26,27,28,29,70,83,84,85,86]). It has been shown that the energy efficiency extracted from the central black hole is more effective in the cases of head-on collisions.
Here, we wish to address the study of high-energy collisions between neutral particles and electrically charged particles with a magnetic dipole in the background of a Schwarzschild BH immersed in an external asymptotically uniform magnetic field. Here, we assume that particles come from infinity with and . Following [13] we use the following general expression for the centre-of-mass energy extracted by collisions of two particles.
with and being the four-velocities and being rest masses of the particles. By proposing the normalization condition, , we obtain the expression for as
Hereafter, for simplicity we consider the equal masses . In doing so, we study the high-energy collisions of particles.
4.1. Critical Angular Momentum
In this sub-subsection, we study the critical value of the angular momentum of colliding particles. The centre-of-mass energy of colliding particles reaches its maximum near the horizon, for this reason the particles must come close to the BH. To move towards the BH, the radial velocity of the particles should meet the condition. is the function of the angular momentum of the particles as well as the other parameters. An increase in angular momentum decreases radial velocity near the BH, and if the angular momentum is higher than its critical value then becomes negative or, in other words, there are turning points before reaching the BH’s horizon. We can find critical values of the angular momentum by solving two equations: , and . Furthermore, we have a non-linear system of equations which can be solved numerically.
In Figure 8, the dependence of the critical values of the angular momentum on the magnetic-coupling parameter is illustrated by varying the magnetic parameter from positive (left panel) to negative (right panel). It can be seen that larger values of the magnetic-coupling parameter and magnetic parameter correspond to larger values of the angular momentum;
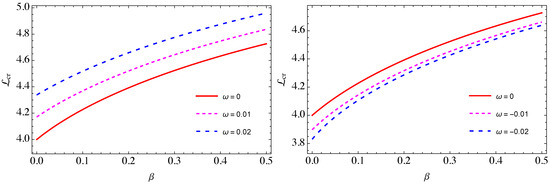
Figure 8.
The dependence of critical angular momentum on parameter with the different values of .
4.2. Collisions of Neutral and Electrically Charged Particles
In this subsection, to compare the collision scenarios between charged particles with a magnetic dipole, we shall first consider collisions between neutral and positively (negatively) charged particles as stated by Equation (23). Let us write the equations of motion for neutral particles as follows:
and for charged particles
Substituting Equations (24) and (25) into Equation (23), we are able to define the centre-of-mass energy as
Here, let us then analyse the behaviour of extracted by the collision between positively charged and electrically neutral particles for different values of .
In Figure 9, we show the radial dependence of for colliding electrically charged and neutral particles for different values of including the particle charge. The left panel shows the impact of on the radial profile of extracted by the collision between positively charged and neutral particles, while the right panel shows the impact of for the collision between test particles and negatively charged particles. As shown in Figure 9, one can observe that energy increases with increasing very near to the horizon as a consequence of the interaction between charged particles and the magnetic field. From Figure 9, one can easily notice that all coloured curves match with the black one, provided that the external magnetic field is switched off. Note that all curves intersect at the horizon, taking the same values for due to the dominant effect of the gravitational field. Furthermore, one can observe that the curves are cut at a critical distance from the BH. This happens because the Lorentz force arising from the external magnetic field dominates over the rest of the forces, thus drastically affecting the charged particle geodesics. energy for collisions of neutral–neutral particles reaches , while it continues to increase with the increase in for charged particles.
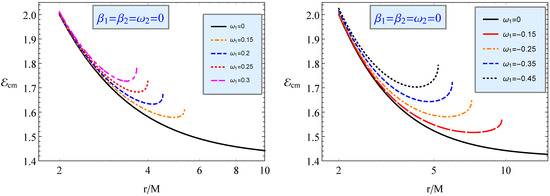
Figure 9.
Figure shows the radial dependence of of the collisions of two positively and negatively charged particles with electrically neutral particles on the different values of the charge.
4.3. Collisions of Electrically Neutral and Magnetized Particles
In this subsection, we study energy extracted by the collision between magnetized and neutral particles. Similarly, the equations of motion for particles with a magnetic dipole moment are defined by
In Figure 10, we show the radial dependence of on the collision of neutral and magnetized particles without charge for different values of the magnetic parameter. The left panel shows the impact of the magnetic parameter on the radial profile of energy extracted by the collision between positively magnetized particles and neutral particles, while the right panel shows the impact of on the collision between test particles and negatively magnetized particles.
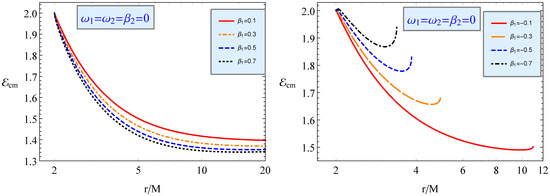
Figure 10.
The same as Figure 9 but for collisions of neutral-magnetized particles with positive magnetic dipole particles.
As seen in Figure 10, one can infer that energy decreases with the increase in the value of magnetized particles very near to the horizon, similar to the interaction between magnetized particles and the magnetic field surrounding the black hole.
4.4. Charged-Magnetized
The expression for the centre-of-mass energy of charged and magnetized particle collisions can be described by the following expression:
where i and j can be taken as 1 and 2, and they cannot be equal to each other.
4.4.1. Positively Charged Particle–Magnetized Particle with Positive
In Figure 11, we show the radial dependence of for two colliding charged and magnetized particles.
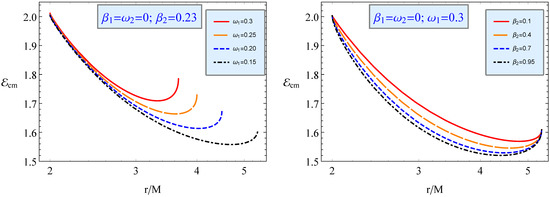
Figure 11.
The same as Figure 9 but for collisions of positively charged particles with no magnetic dipole-positive magnetized particles with no charge.
We now focus on a collision scenario in which the collision between charged particles without a magnetic dipole and magnetized particles without electric charge is taken into account.
The left panel of Figure 11 shows the impact of the parameter including different values of charge on the radial profile of for fixed , the right panel shows the impact of including different values of the magnetic dipole for fixed .
From Figure 11, interestingly, one can deduce that energy grows up as the parameter increases. Note here that an increase in the value of gives rise to the increase of the particle charge accordingly. Moreover, one can see from the right panel that the extracted energy is similar behaviour for all values of the magnetic coupling parameter at the distance around the horizon, while in the case of far away from the horizon, we observe that an increase in the value of the coupling parameter leads to the decrease of energy. This happens because, at a far distance from the horizon, the gravitational force starts dominating over the force arising from the external magnetic field affecting the particle’s geodesics. This continues up a critical distance and beyond which energy grows again.
4.4.2. Negatively Charged Particle–Magnetized Particle with Positive
In Figure 12, we show the radial dependence of for two colliding negatively charged particles and magnetized particles with .
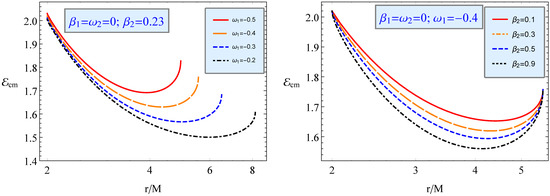
Figure 12.
The same as Figure 9 but for the collisions of negatively charged particles with non-dipole-positive magnetized particles with no charge.
Note that here the magnetized particle and charged particle parameters are given by and , respectively.
The left panel of Figure 12 shows the impact of parameter including different negative charges on the radial profile of for fixed values of magnetized particle , while the right panel shows the impact of for fixed for negatively charged particle. This clearly shows that energy increases with the increase in charged particles near to the horizon, similar to the interaction between the particle’s electric charge and external magnetic field.
From Figure 12, the curves merge at the horizon; however, the initial energy takes a larger value as one increases the magnetic field while keeping the value of the negative charge fixed. As was mentioned above, curves are cut at a particular distance from the black hole. This happens because of the dominance of the Lorentz force drastically affecting the particle geodesics, thereby leading to the absence of particle collisions at that distance (left panel). However, the opposite is observed for the below one. For this, curves start at the same point and end at 2 M, thus indicating that the magnetic-coupling parameter has little effect on energy (right panel).
4.4.3. Positively Charged Particle–Magnetized Particle with Negative
In Figure 13, we show the radial dependence of energy extracted by the collision of two particles endowed with charge and a magnetic dipole. In the left panel, the different charge values are used to fix the magnetic dipole, while both the values of charge and the magnetic dipole are used in the right panel. In contrast, in the left panel, as a consequence of the increase in the particle charge value, the collision between particles occurs at a distance close to the horizon with larger energy (Figure 13 (right panel)).
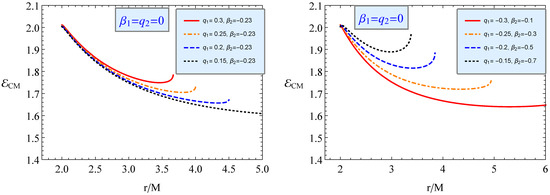
Figure 13.
The same as Figure 9 but for collisions of positively charged particles with non-dipole-negative magnetized particles with no charge.
4.5. Particles Collision Having Electric Charge and a Magnetic Dipole
In Figure 14, we show the radial profile of energy for two colliding electrically charged particles for the different particle charge values. The left panel shows the combined effects of positively charged particles having the magnetic dipole on the radial profile of energy for different values of the magnetic-coupling parameter , while the right one reflects the combined effects of positively charged particles for different values of parameter in the case of fixed . As seen in Figure 14, the collision occurs at a particular distance close to the black hole with larger energy. Regardless of this fact, the curves in both panels approach energy at 2 M.
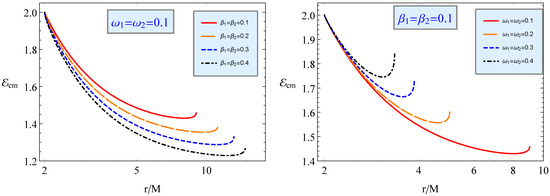
Figure 14.
The same as Figure 9 but for the collisions of two positively charged particles with a magnetic dipole for different values of (left panel) and (right panel).
5. Particles with Electric Charge and a Magnetic Dipole Moment in Astrophysics
It is worth noting that current astronomical observations associated with very long baseline interferometers (VLBI) [1,2], black hole cameras, and EHT [3,4] have been regarded as viable sources to provide very useful tests to precisely measure the parameters related to astrophysical black holes. Furthermore, Sgr A* existing at the centre of the Milky Way galaxy has currently been considered the leading astrophysical laboratory to understand in depth the nature of the black hole accretion disk, jet formation, and magnetic field structure in the surrounding black hole environment [87,88,89,90]. In this context, in a realistic astrophysical scenario, it is particularly important to take into account the motion of neutron stars orbiting around supermassive black holes, such as Sgr A*, as well as the motion of elementary particles (i.e., protons) that exist in an accretion disk around the stellar black hole. With this in view, we further wish to make an approximate numerical analysis to estimate the values of and for neutron stars and elementary particles.
5.1. Neutron Stars and White Dwarfs as Test Particles with a Magnetic Dipole Moment and Electric Charge
It is worth noting that the magnetic field configuration for astrophysical neutron stars and white dwarfs behaves as a dipolar structure. This happens because an induced electric field generates high magnetic fields due to rapid rotation.
Let us now focus on the magnetic interaction parameter and cyclotron frequency corresponding to the interaction between the external magnetic field and charged particles. Here, we can consider a magnetized neutron star for the test particle, having a magnetic dipole and electric charge. As is known, neutron stars refer to the rapid rotation of stars and thus have a tremendous surface magnetic field.
Of them, neutron stars appear with a slightly different nature, according to which the magnetic field lines are not aligned with the rotational axis due to the fact that, at the surface of the star, an induced electric field is created due to the rapid rotation, i.e., with being the angular momentum of the neutron star. In other words, the induced electric charge plays an important role in generating the induced electric field. Therefore, the particles with an electric charge considered here may have interesting consequences in the magnetized neutron star applications. With this motivation, we then further estimate the values of the dimensionless parameters and using a geometrized system tabulated in Table A1.
Here, we can assume that a neutron star is a magnetized particle with and orbits around a supermassive black hole in the case of an external magnetic field with different configurations. Thus, the magnetic-coupling parameter can be easily estimated with the help of the observational parameters of the neutron star and the approximate value of the external magnetic field for a supermassive black hole.
Let us now evaluate and for neutron stars and white dwarfs orbiting a supermassive black hole in the case of an external asymptotically uniform magnetic field.
With this in view, we separate the parameters of NS/WD and BH from the external magnetic field using the dimensionless parameter , responsible for the object’s parameters.
From the above equation, we can easily calculate for the NS and SMBH systems,
where and are the dimensionless surface magnetic fields of the NS and WD normalized to and , respectively; and are the normalized radii of the NS and WD to 10 km and , respectively; and the mass of the star, WD and SMBH is also given in the normalized form as , and , respectively.
Thus, the parameter can be estimated using Equations (32) and (33), and thus we have
where we have defined .
A neutron star or white dwarf, owing to its rotation, creates an induced electric field that is proportional to the surface magnetic field , and the induced electric charge is defined as
Now, we evaluate the value of the total induced charge for typical NSs and WDs.
and the charge-to-mass relation
Using the above assumptions, one can estimate the magnetic parameter for NSs and WDs.
where and are the period of the NS and WD measured in seconds and , respectively.
Now, we can obtain the relationships between the parameters and for NSs and WDs in the following form:
As is seen from Equation (38), the charge interaction is larger than the magnetic dipole in NSs, while in WDs the magnetic dipole interaction dominates.
One may apply the calculation to estimate the value of the magnetic-coupling parameter for a realistic case of the magnetar SGR (PSR) J1745–2900 orbiting around Sagittarius A* (Sgr A*). Through the estimation of the coupling parameter, we considered the magnetic field around Sgr A* to be in the order of 10 G, the magnetic dipole moment of the magnetar G and its mass [91]. Consequently, the value of for the system is 0.67, 5, where the magnetic field is 10 G and its induced charge is about ∼ C. These estimated high values of the parameters and can explain the further position of the magnetar from Sgr A* and implies that due to the huge magnetic interactions, up to now, only NS has been observed.
5.2. Electron and Protons as Candidates for Particles with Electric Charge and a Magnetic Dipole Moment
Moreover, our calculations, using Table A1 and Table A2, show that the parameter for electrons in the magnetic field B normalized to is about , while for protons and neutrons . While, for electrons and for protons. It can be seen from these values of that the dipole moment interaction is almost negligible for elementary particles. This means that electrons and protons can only be considered charged particles in the presence of external magnetic fields. However, in the absence of external magnetic fields, the dynamics of the particles are the same as neutral particles.
6. Conclusions
In this paper we studied the dynamics of electrically charged particles with a magnetic dipole moment using a “hybrid” form of the Hamilton–Jacobi equation. We derived a general form for the effective potential for radial motion. We further analysed the effective potential. As a consequence of ISCO analysis we showed that particles can be stable in circular orbits if, and only if, they have a magnetic moment with an magnetic parameter upper limit of . We showed that the upper limit increases as a consequence of the increase in parameter , while the ISCO radius decreases for .
Furthermore, we studied the energy efficiency released from a BH as a result of charged particles possessing a magnetic dipole and electric charge and orbiting around the accretion disk as stated by the Novikov–Thorn model. We showed that the energy efficiency increases by up to ∼93% as a consequence of the presence of a magnetic dipole. Interestingly, we realized that increasing the particle charge leads to a decrease in energy efficiency.
It is particularly important to understand possible black hole mimickers. In this regard, we studied whether the effect of the magnetic interaction could mimic the spin of Kerr BHs, thus providing the same ISCO and energy efficiency. We showed that the spin parameter can mimic the magnetic-coupling parameter up to nearly 0.15 with a possible range of for electrically neutral particles. For positively (negatively) charged particles, the above range expands (shrinks) to (). The process becomes quite different in the case of the same energy efficiency such that the spin parameter can mimic the magnetic-coupling parameter up to for the neutral particles, while can mimic the spin parameter up to within the range for positively charged particles with and only up to within the range for the negative particles.
For the collision between charged and magnetized particles, we showed that the collision of electrically charged particles limits the collision area, i.e., the area shrinks (expands) when increasing particle charge (magnetic dipole moment).
We have interpreted neutron stars and elementary particles such as electrons, protons, and neutrons, estimating their magnetic interaction parameter and cyclotron frequencies where the magnetic field is about 100 G. We have shown that the magnetic interaction of elementary particles is almost negligible.
In the next project, we plan to consider possible comparisons with the event GW170817 neutron star–neutron star collision energy. It would be of primary importance to understand the dynamics of magnetized objects carrying electric charges.
Author Contributions
Conceptualization, J.R. and S.S.; methodology, J.R. and S.S.; software, F.A. and S.A.; validation, S.S. and D.B.; formal analysis, J.R. and F.A.; investigation, J.R. and S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Table A1 displays the details used to convert into unit.

Table A1.
Units and conversions in Gaussian and geometrized systems.
Table A1.
Units and conversions in Gaussian and geometrized systems.
| 1 s | cm | c | |
| Mass | 1 g | cm | |
| Electric charge | 1 | cm | |
| Magnetic field | 1 | 1/cm |

Table A2.
The realtion between elctron, proton and neutron.
Table A2.
The realtion between elctron, proton and neutron.
| 1 | − | ||
| 1 | 1836 | ||
| 0 | 1839 |
References
- Abbott, B.P. et al. [Virgo and LIGO Scientific Collaborations] Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [Virgo and LIGO Scientific Collaborations] Properties of the Binary Black Hole Merger GW150914. Phys. Rev. Lett. 2016, 116, 241102. [Google Scholar] [CrossRef]
- Akiyama, K. et al. [Event Horizon Telescope Collaboration] First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. 2019, 875, L1. [Google Scholar] [CrossRef]
- Akiyama, K. et al. [Event Horizon Telescope Collaboration] First M87 Event Horizon Telescope Results. VI. The Shadow and Mass of the Central Black Hole. Astrophys. J. 2019, 875, L6. [Google Scholar] [CrossRef]
- Wald, R.M. Black hole in a uniform magnetic field. Phys. Rev. D 1974, 10, 1680–1685. [Google Scholar] [CrossRef]
- Herrera, L.; Paiva, F.M.; Santos, N.O.; Ferrari, V. Geodesics in the γ Spacetime. Int. J. Mod. Phys. D 2000, 9, 649–659. [Google Scholar] [CrossRef]
- Herrera, L.; Magli, G.; Malafarina, D. Non-spherical sources of static gravitational fields: Investigating the boundaries of the no-hair theorem. Gen. Relativ. Gravit. 2005, 37, 1371–1383. [Google Scholar] [CrossRef]
- Dey, D.; Joshi, P.S. Gravitational Collapse of Baryonic and Dark matter. arXiv 2019, arXiv:1907.12738. [Google Scholar] [CrossRef]
- Benavides-Gallego, C.A.; Abdujabbarov, A.; Malafarina, D.; Ahmedov, B.; Bambi, C. Charged particle motion and electromagnetic field in γ spacetime. Phys. Rev. D 2019, 99, 044012. [Google Scholar] [CrossRef]
- Boshkayev, K.; Malafarina, D. A model for a dark matter core at the Galactic Centre. Mon. Not. R. Astron. Soc. 2019, 484, 3325–3333. [Google Scholar] [CrossRef]
- Shaymatov, S.; Ahmedov, B.; Jamil, M. Testing the weak cosmic censorship conjecture for a Reissner-Nordström-de Sitter black hole surrounded by perfect fluid dark matter. Eur. Phys. J. C 2021, 81, 588. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Shaymatov, S.; Jamil, M. Dynamics and epicyclic motions of particles around the Schwarzschild-de Sitter black hole in perfect fluid dark matter. Eur. Phys. J. C 2021, 81, 699. [Google Scholar] [CrossRef]
- Bañados, M.; Silk, J.; West, S.M. Kerr Black Holes as Particle Accelerators to Arbitrarily High Energy. Phys. Rev. Lett. 2009, 103, 111102. [Google Scholar] [CrossRef] [PubMed]
- Grib, A.A.; Pavlov, Y.V. On particle collisions near rotating black holes. Gravit. Cosmol. 2011, 17, 42–46. [Google Scholar] [CrossRef]
- Jacobson, T.; Sotiriou, T.P. Spinning Black Holes as Particle Accelerators. Phys. Rev. Lett. 2010, 104, 021101. [Google Scholar] [CrossRef] [PubMed]
- Harada, T.; Kimura, M. Collision of an innermost stable circular orbit particle around a Kerr black hole. Phys. Rev. D 2011, 83, 024002. [Google Scholar] [CrossRef]
- Wei, S.W.; Liu, Y.X.; Guo, H.; Fu, C.E. Charged spinning black holes as particle accelerators. Phys. Rev. D 2010, 82, 103005. [Google Scholar] [CrossRef]
- Zaslavskii, O.B. Acceleration of particles as a universal property of rotating black holes. Phys. Rev. D 2010, 82, 083004. [Google Scholar] [CrossRef]
- Zaslavskii, O.B. Acceleration of particles by nonrotating charged black holes? Sov. J. Exp. Theor. Phys. Lett. 2011, 92, 571–574. [Google Scholar] [CrossRef]
- Zaslavskii, O.B. Acceleration of particles by black holes—A general explanation. Class. Quantum Grav. 2011, 28, 105010. [Google Scholar] [CrossRef]
- Kimura, M.; Nakao, K.I.; Tagoshi, H. Acceleration of colliding shells around a black hole: Validity of the test particle approximation in the Banados-Silk-West process. Phys. Rev. D 2011, 83, 044013. [Google Scholar] [CrossRef]
- Bañados, M.; Hassanain, B.; Silk, J.; West, S.M. Emergent flux from particle collisions near a Kerr black hole. Phys. Rev. D 2011, 83, 023004. [Google Scholar] [CrossRef]
- Igata, T.; Harada, T.; Kimura, M. Effect of a weak electromagnetic field on particle acceleration by a rotating black hole. Phys. Rev. D 2012, 85, 104028. [Google Scholar] [CrossRef]
- Frolov, V.P. Weakly magnetized black holes as particle accelerators. Phys. Rev. D 2012, 85, 024020. [Google Scholar] [CrossRef]
- Patil, M.; Joshi, P. Kerr naked singularities as particle accelerators. Class. Quantum Grav. 2011, 28, 235012. [Google Scholar] [CrossRef]
- Atamurotov, F.; Ahmedov, B.; Shaymatov, S. Formation of black holes through BSW effect and black hole-black hole collisions. Astrophys. Space Sci. 2013, 347, 277–281. [Google Scholar] [CrossRef]
- Liu, C.; Chen, S.; Ding, C.; Jing, J. Particle acceleration on the background of the Kerr-Taub-NUT spacetime. Phys. Lett. B 2011, 701, 285–290. [Google Scholar] [CrossRef]
- Shaymatov, S.R.; Ahmedov, B.J.; Abdujabbarov, A.A. Particle acceleration near a rotating black hole in a Randall-Sundrum brane with a cosmological constant. Phys. Rev. D 2013, 88, 024016. [Google Scholar] [CrossRef]
- Shaymatov, S.; Ahmedov, B.; Stuchlík, Z.; Abdujabbarov, A. Effect of an external magnetic field on particle acceleration by a rotating black hole surrounded with quintessential energy. Int. J. Mod. Phys. D 2018, 27, 1850088. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Rayimbaev, J.; Turimov, B.; Atamurotov, F. Dynamics of magnetized particles around 4-D Einstein Gauss–Bonnet black hole. Phys. Dark Universe 2020, 30, 100715. [Google Scholar] [CrossRef]
- Abdujabbarov, A.A.; Ahmedov, B.J.; Shaymatov, S.R.; Rakhmatov, A.S. Penrose process in Kerr-Taub-NUT spacetime. Astrophys. Space Sci. 2011, 334, 237–241. [Google Scholar] [CrossRef]
- Okabayashi, K.; Maeda, K.I. Maximal efficiency of the collisional Penrose process with a spinning particle. II. Collision with a particle on the innermost stable circular orbit. Prog. Theor. Exp. Phys. 2020, 2020, 013E01. [Google Scholar] [CrossRef]
- McKinney, J.C.; Narayan, R. Disc-jet coupling in black hole accretion systems—II. Force-free electrodynamical models. Mon. Not. R. Astron. Soc. 2007, 375, 531–547. [Google Scholar] [CrossRef]
- Anderson, J.L.; Cohen, J.M. Gravitational Collapse of Magnetic Neutron Stars. Astrophys. Space Sci. 1970, 9, 146–152. [Google Scholar] [CrossRef]
- de Felice, F.; Sorge, F. Magnetized orbits around a Schwarzschild black hole. Class. Quantum Grav. 2003, 20, 469–481. [Google Scholar] [CrossRef]
- de Felice, F.; Sorge, F.; Zilio, S. Magnetized orbits around a Kerr black hole. Class. Quantum Grav. 2004, 21, 961–973. [Google Scholar] [CrossRef]
- Frolov, V.P.; Shoom, A.A. Motion of charged particles near a weakly magnetized Schwarzschild black hole. Phys. Rev. D 2010, 82, 084034. [Google Scholar] [CrossRef]
- Aliev, A.N.; Özdemir, N. Motion of charged particles around a rotating black hole in a magnetic field. Mon. Not. R. Astron. Soc. 2002, 336, 241–248. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Ahmedov, B. Test particle motion around a black hole in a braneworld. Phys. Rev. D 2010, 81, 044022. [Google Scholar] [CrossRef]
- Shaymatov, S.; Atamurotov, F.; Ahmedov, B. Isofrequency pairing of circular orbits in Schwarzschild spacetime in the presence of magnetic field. Astrophys. Space Sci. 2014, 350, 413–419. [Google Scholar] [CrossRef]
- Shaymatov, S.; Dadhich, N.; Ahmedov, B.; Jamil, M. Five-dimensional charged rotating minimally gauged supergravity black hole cannot be over-spun and/or over-charged in non-linear accretion. Eur. Phys. J. C 2020, 80, 481. [Google Scholar] [CrossRef]
- Shaymatov, S.; Malafarina, D.; Ahmedov, B. Effect of perfect fluid dark matter on particle motion around a static black hole immersed in an external magnetic field. Phys. Dark Universe 2021, 34, 100891. [Google Scholar] [CrossRef]
- Shaymatov, S.; Vrba, J.; Malafarina, D.; Ahmedov, B.; Stuchlík, Z. Charged particle and epicyclic motions around 4 D Einstein–Gauss–Bonnet black hole immersed in an external magnetic field. Phys. Dark Universe 2020, 30, 100648. [Google Scholar] [CrossRef]
- Shaymatov, S.; Dadhich, N. On overspinning of black holes in higher dimensions. Phys. Dark Universe 2021, 31, 100758. [Google Scholar] [CrossRef]
- Shaymatov, S.; Atamurotov, F. Geodesic Circular Orbits Sharing the Same Orbital Frequencies in the Black String Spacetime. Galaxies 2021, 9, 40. [Google Scholar] [CrossRef]
- Piotrovich, M.Y.; Silant’ev, N.A.; Gnedin, Y.N.; Natsvlishvili, T.M. Magnetic Fields of Black Holes and the Variability Plane. arXiv 2010, arXiv:1002.4948. [Google Scholar]
- Eatough, R.P.; Falcke, H.; Karuppusamy, R.; Lee, K.J.; Champion, D.J.; Keane, E.F.; Desvignes, G.; Schnitzeler, D.H.F.M.; Spitler, L.G.; Kramer, M.; et al. A strong magnetic field around the supermassive black hole at the centre of the Galaxy. Nature 2013, 501, 391–394. [Google Scholar] [CrossRef]
- Shannon, R.M.; Johnston, S. Radio properties of the magnetar near Sagittarius A* from observations with the Australia Telescope Compact Array. Mon. Not. R. Astron. Soc. 2013, 435, L29–L32. [Google Scholar] [CrossRef]
- Dallilar, Y.; Eikenberry, S.S.; Garner, A.; Stelter, R.D.; Gottlieb, A.; Gandhi, P.; Casella, P.; Dhillon, V.S.; Marsh, T.R.; Littlefair, S.P.; et al. A precise measurement of the magnetic field in the corona of the black hole binary V404 Cygni. Science 2017, 358, 1299–1302. [Google Scholar] [CrossRef]
- Baczko, A.K.; Schulz, R.; Kadler, M.; Ros, E.; Perucho, M.; Krichbaum, T.P.; Böck, M.; Bremer, M.; Grossberger, C.; Lindqvist, M.; et al. A highly magnetized twin-jet base pinpoints a supermassive black hole. Astron. Astrophys. 2016, 593, A47. [Google Scholar] [CrossRef]
- Prasanna, A.R. General-relativistic analysis of charged-particle motion in electromagnetic fields surrounding black holes. Nuovo C. Riv. Ser. 1980, 3, 1–53. [Google Scholar] [CrossRef]
- Kovář, J.; Stuchlík, Z.; Karas, V. Off-equatorial orbits in strong gravitational fields near compact objects. Class. Quantum Grav. 2008, 25, 095011. [Google Scholar] [CrossRef]
- Kovář, J.; Kopáček, O.; Karas, V.; Stuchlík, Z. Off-equatorial orbits in strong gravitational fields near compact objects II: Halo motion around magnetic compact stars and magnetized black holes. Class. Quantum Grav. 2010, 27, 135006. [Google Scholar] [CrossRef]
- Shaymatov, S.; Patil, M.; Ahmedov, B.; Joshi, P.S. Destroying a near-extremal Kerr black hole with a charged particle: Can a test magnetic field serve as a cosmic censor? Phys. Rev. D 2015, 91, 064025. [Google Scholar] [CrossRef]
- Dadhich, N.; Tursunov, A.; Ahmedov, B.; Stuchlík, Z. The distinguishing signature of magnetic Penrose process. Mon. Not. R. Astron. Soc. 2018, 478, L89–L94. [Google Scholar] [CrossRef]
- Pavlović, P.; Saveliev, A.; Sossich, M. Influence of the vacuum polarization effect on the motion of charged particles in the magnetic field around a Schwarzschild black hole. Phys. Rev. D 2019, 100, 084033. [Google Scholar] [CrossRef]
- Shaymatov, S. Magnetized Reissner–Nordström black hole restores cosmic censorship conjecture. Int. J. Mod. Phys. Conf. Ser. 2019, 49, 1960020. [Google Scholar] [CrossRef]
- Shaymatov, S.; Jamil, M.; Jusufi, K.; Bamba, K. Constraints on the magnetized Ernst black hole spacetime through quasiperiodic oscillations. Eur. Phys. J. C 2022, 82, 636. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, Y. Probing a black-bounce-Reissner-Nordström spacetime with precessing and periodic motion. Eur. Phys. J. C 2022, 82, 854. [Google Scholar] [CrossRef]
- Zhou, T.Y.; Xie, Y. Precessing and periodic motions around a black-bounce/traversable wormhole. Eur. Phys. J. C 2020, 80, 1070. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, Y. Probing a self-complete and Generalized-Uncertainty-Principle black hole with precessing and periodic motion. Astrophys. Space Sci. 2022, 367, 17. [Google Scholar] [CrossRef]
- Deng, X.M. Geodesics and periodic orbits around quantum-corrected black holes. Phys. Dark Universe 2020, 30, 100629. [Google Scholar] [CrossRef]
- Lin, H.Y.; Deng, X.M. Rational orbits around 4 D Einstein–Lovelock black holes. Phys. Dark Universe 2021, 31, 100745. [Google Scholar] [CrossRef]
- Rayimbaev, J.R. Magnetized particle motion around non-Schwarzschild black hole immersed in an external uniform magnetic field. Astrophys. Space Sci. 2016, 361, 288. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Turimov, B.; Palvanov, S. Plasma magnetosphere of slowly rotating magnetized neutron star in branewold. Int. J. Mod. Phys. Conf. Ser. 2019, 49, 1960019. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Figueroa, M.; Stuchlík, Z.; Juraev, B. Test particle orbits around regular black holes in general relativity combined with nonlinear electrodynamics. Phys. Rev. D 2020, 101, 104045. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Bardiev, D.; Abdulxamidov, F.; Abdujabbarov, A.; Ahmedov, B. Magnetized and Magnetically Charged Particles Motion around Regular Bardeen Black Hole in 4D Einstein Gauss–Bonnet Gravity. Universe 2022, 8, 549. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Abdujabbarov, A.; Jamil, M.; Ahmedov, B.; Han, W.B. Dynamics of test particles around renormalization group improved Schwarzschild black holes. Phys. Rev. D 2020, 102, 084016. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Abdujabbarov, A.; Jamil, M.; Han, W.B. Dynamics of magnetized particles around Einstein-Æther black hole with uniform magnetic field. Nuclear Phys. B 2021, 966, 115364. [Google Scholar] [CrossRef]
- Juraeva, N.; Rayimbaev, J.; Abdujabbarov, A.; Ahmedov, B.; Palvanov, S. Distinguishing magnetically and electrically charged Reissner–Nordström black holes by magnetized particle motion. Eur. Phys. J. C 2021, 81, 124078. [Google Scholar] [CrossRef]
- Shaymatov, S.; Narzilloev, B.; Abdujabbarov, A.; Bambi, C. Charged particle motion around a magnetized Reissner-Nordström black hole. Phys. Rev. D 2021, 103, 124066. [Google Scholar] [CrossRef]
- Abdulxamidov, F.; Benavides-Gallego, C.A.; Han, W.B.; Rayimbaev, J.; Abdujabbarov, A. Spinning test particle motion around a rotating wormhole. Phys. Rev. D 2022, 106, 024012. [Google Scholar] [CrossRef]
- Bokhari, A.H.; Rayimbaev, J.; Ahmedov, B. Test particles dynamics around deformed Reissner-Nordström black hole. Phys. Rev. D 2020, 102, 124078. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Rayimbaev, J.; Atamurotov, F.; Ahmedov, B. Magnetized Particle Motion in γ-Spacetime in a Magnetic Field. Galaxies 2020, 8, 76. [Google Scholar] [CrossRef]
- Narzilloev, B.; Rayimbaev, J.; Abdujabbarov, A.; Bambi, C. Charged particle motion around non-singular black holes in conformal gravity in the presence of external magnetic field. arXiv 2020, arXiv:2005.04752. [Google Scholar] [CrossRef]
- Narzilloev, B.; Rayimbaev, J.; Shaymatov, S.; Abdujabbarov, A.; Ahmedov, B.; Bambi, C. Can the dynamics of test particles around charged stringy black holes mimic the spin of Kerr black holes? Phys. Rev. D 2020, 102, 044013. [Google Scholar] [CrossRef]
- Shaymatov, S.; Ahmedov, B. Overcharging process around a magnetized black hole: Can the backreaction effect of magnetic field restore cosmic censorship conjecture? Gen. Relativ. Gravit. 2023, 55, 36. [Google Scholar] [CrossRef]
- Vrba, J.; Abdujabbarov, A.; Kološ, M.; Ahmedov, B.; Stuchlík, Z.; Rayimbaev, J. Charged and magnetized particles motion in the field of generic singular black holes governed by general relativity coupled to nonlinear electrodynamics. Phys. Rev. D 2020, 101, 124039. [Google Scholar] [CrossRef]
- Novikov, I.D.; Thorne, K.S. Astrophysics of black holes. In Black Holes (Les Astres Occlus); Gordon & Breach: New York, NY, USA, 1973; pp. 343–450. [Google Scholar]
- Bian, W.H.; Zhao, Y.H. Accretion Rates and the Accretion Efficiency in AGNs. Publ. Astron. Soc. Jpn. 2003, 55, 599–603. [Google Scholar] [CrossRef]
- Penrose, R. Gravitational Collapse: The Role of General Relativity. Nuovo C. Riv. Ser. 1969, 1, 252. [Google Scholar]
- Wagh, S.M.; Dhurandhar, S.V.; Dadhich, N. Revival of the Penrose process for astrophysical applications. Astrophys. J. 1985, 290, 12–14. [Google Scholar] [CrossRef]
- Tursunov, A.; Kološ, M.; Abdujabbarov, A.; Ahmedov, B.; Stuchlík, Z. Acceleration of particles in spacetimes of black string. Phys. Rev. D 2013, 88, 124001. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Hledík, S.; Truparová, K. Evolution of Kerr superspinars due to accretion counterrotating thin discs. Class. Quantum Grav. 2011, 28, 155017. [Google Scholar] [CrossRef]
- Abdujabbarov, A.A.; Tursunov, A.A.; Ahmedov, B.J.; Kuvatov, A. Acceleration of particles by black hole with gravitomagnetic charge immersed in magnetic field. Astrophys. Space Sci. 2013, 343, 173–179. [Google Scholar] [CrossRef]
- Atamurotov, F.; Shaymatov, S.; Sheoran, P.; Siwach, S. Charged black hole in 4D Einstein–Gauss–Bonnet gravity: Particle motion, plasma effect on weak gravitational lensing and centre-of-mass energy. J. Cosmol. Astropart. Phys. 2021, 2021, 045. [Google Scholar] [CrossRef]
- Lacroix, T. Dynamical constraints on a dark matter spike at the Galactic centre from stellar orbits. Astron. Astrophys. 2018, 619, A46. [Google Scholar] [CrossRef]
- Nucita, A.A.; De Paolis, F.; Ingrosso, G.; Qadir, A.; Zakharov, A.F. Sgr A*: A Laboratory to Measure the Central Black Hole and Stellar Cluster Parameters. Publ. Astron. Soc. Pac. 2007, 119, 349–359. [Google Scholar] [CrossRef]
- Ghez, A.M.; Salim, S.; Hornstein, S.D.; Tanner, A.; Lu, J.R.; Morris, M.; Becklin, E.E.; Duchêne, G. Stellar Orbits around the Galactic Center Black Hole. Astrophys. J. 2005, 620, 744–757. [Google Scholar] [CrossRef]
- Ghez, A.M.; Morris, M.; Becklin, E.E.; Tanner, A.; Kremenek, T. The accelerations of stars orbiting the Milky Way’s central black hole. Nature 2000, 407, 349–351. [Google Scholar] [CrossRef]
- Mori, K.; Gotthelf, E.V.; Zhang, S.; An, H.; Baganoff, F.K.; Barrière, N.M.; Beloborodov, A.M.; Boggs, S.E.; Christensen, F.E.; Craig, W.W.; et al. NuSTAR Discovery of a 3.76 s Transient Magnetar Near Sagittarius A*. Astron. J. Lett. 2013, 770, L23. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).