Theoretical Arguments and Experimental Signals for a Second Resonance of the Higgs Field

Abstract

Theoretical arguments and lattice simulations suggest that, beside the known resonance of mass $m_h=$ 125 GeV, the Higgs field could exhibit a second mass scale ${\left(M_H\right)}^{\mathrm{theor}}=690\pm 10\left(\mathrm{stat}\right)\pm 20\left(\mathrm{sys}\right)\mathrm{GeV}$. In spite of its large mass, the heavier state would couple to longitudinal Ws with the same typical strength as the low-mass state at 125 GeV and thus represent a relatively narrow resonance mainly produced at LHC by gluon–gluon fusion. After summarizing these general aspects, we review a recent analysis of LHC data which support the idea of a new resonance in the predicted mass range. Since the correlation among these measurements is very small and since, with a definite theoretical prediction in some mass region, local excesses should not be downgraded by the look-elsewhere effect, we emphasize the present substantial statistical evidence which could become an important discovery by simply adding two, still missing, key analyses of the full RUN2 statistics.

1. Introduction

Spontaneous Symmetry Breaking (SSB) through the Higgs field is an essential component of present particle physics. The idea is so simple and familiar that, after the discovery of the resonance with mass $m_h=$ 125 GeV, one might conclude that modifications of this general picture, if any, can only come from new physics, e.g., supersymmetry. Though, in spite of the present phenomenological consistency, this conclusion is not so obvious due to the persistent uncertainty on the physical mechanisms at the base of SSB.

To illustrate this point, let us consider the present view as summarized in the review of the Particle Data Group [1] by a scalar potential of the form

$$V_{\mathrm{PDG}}\left(\phi \right)=-\frac{1}{2}{m}_{\mathrm{PDG}}^2{\phi }^2+\frac{1}{4}{\lambda }_{\mathrm{PDG}}{\phi }^4$$

(1)

By fixing $m_{\mathrm{PDG}}\sim$ 88.8 GeV and ${\lambda }_{\mathrm{PDG}}\sim 0.13$, this has a minimum at $\left|\phi \right|=\langle \Phi \rangle \sim$ 246 GeV and a second derivative $V_{\mathrm{PDG}}^{″}\left(\langle \Phi \rangle \right)\equiv m_h^2=$ (125 GeV)${}^2$ (one is adopting here the identification $m_h^2=V_{\mathrm{PDG}}^{″}\left(\langle \Phi \rangle \right)=\left|G^{-1}(p=0)\right|$ in terms of the inverse, zero-momentum propagator).

Now, the form of Equation (1) depends on assuming a renormalizable interaction among the fluctuations around the minimum of the potential. However, there is also a tacit assumption behind it: regardless of the physical mechanisms inducing SSB, the phenomenology of the Higgs field is only determined by the two parameters $\langle \Phi \rangle$ and $m_h$.

To see why this second assumption may be incorrect, we first observe that, by disposing only of Equation (1), one is driven to identify the physical mechanism for SSB in the condition $V_{\mathrm{PDG}}^{″}(\phi =0)=-m_{\mathrm{PDG}}^2<0$. This condition characterizes SSB as a second-order phase transition and mimics the Ginzburg–Landau picture of superconductivity. However, this conventional idea of a “tachyonic” mass term has no obvious interpretation in ordinary quantum field theory 1. Therefore, one could re-consider the idea of a second-order phase transition by observing, for instance, that in the presence of gauge bosons, SSB is actually a (weak) first-order phase transition. This is because, as an effect of radiative corrections, the ground state of the classically scale-invariant theory defined by $V_{\mathrm{eff}}^{″}(\phi =0)=0$ corresponds to the broken-symmetry phase [4]. As such, SSB occurs earlier when the physical, renormalized mass $m_R^2\equiv V_{\mathrm{eff}}^{″}(\phi =0)$ of the quanta in the symmetric phase is extremely small but still in the physical region $m_R^2>0$.

However, even in a pure ${\Phi }^4$ theory, things are not so simple. The underlying rationale for a “tachyonic” mass term derives from assuming ${\Phi }^4$ as an interaction which is always repulsive. In this case, with a repulsive interaction, any state made out of physical massive particles would necessarily have an energy density which is higher than the trivial empty vacuum. However, as discussed in [5], the ${\Phi }^4$ interaction is not always repulsive. The inter-particle potential between the basic quanta of the symmetric phase, beside the +$\lambda {\delta }^3\left(\mathbf{r}\right)$ tree-level repulsion, contains a $-{\lambda }^2\frac{e^{-2r{m}_R}}{r^3}$ attraction which originates from the ultraviolet-finite part of the one-loop diagrams and whose range becomes longer and longer in the $m_R\to 0$ limit 2.

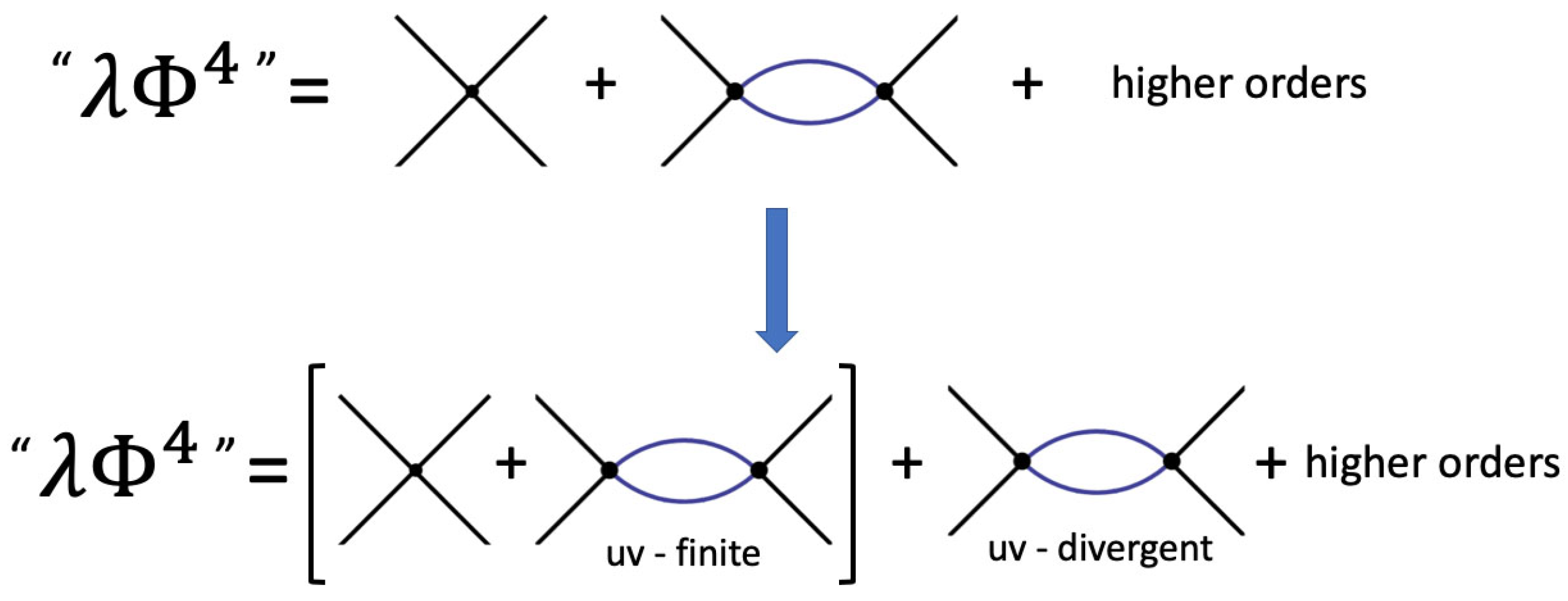
Due to the qualitative difference of the two effects, to consistently include higher-order effects, one should re-arrange the perturbative expansion by renormalizing symmetrically both the tree-level contact repulsion and the long-range attraction as discussed by Stevenson [8], see Figure 1. In this way, by taking into account both effects, a calculation of the energy density in the dilute-gas limit [5] (i.e., when more than two-body interactions are negligible) indicates that, for positive and small enough $m_R$, the attractive tail dominates. Then, the lowest-energy state is not the trivial, empty vacuum but a state with a non-zero density of scalar quanta which are Bose-condensed in the zero-momentum mode. The instability corresponds to spontaneous symmetry breaking and happens when the mass $m_R$ is extremely small but still in the physical region 3.

Notably, one can establish an analogy, between the dilute-gas approximation of [5] and the standard 1-loop effective potential, where the attractive interaction among the basic quanta of the symmetric phase can also be read as zero-point energy of the excitations of the broken-symmetry vacuum. This zero-point mass is not $m_h$, as defined by the quadratic shape of the effective potential at the minimum, but a much larger mass scale $M_H$. Therefore, trying to improve on the traditional “tachyonic-mass” picture is not a waste of time. Instead, one arrives to envisage new phenomena such as the existence of a second resonance of the Higgs field with a mass $M_H\gg m_h$. Since vacuum stability would depend on the large $M_H$, and not on $m_h$, SSB could then originate within the pure scalar sector regardless of the other parameters of the theory, e.g., the vector boson and top-quark mass.

As this review will mostly be focused on the phenomenological implications, we briefly review in Section 2 the theoretical motivations at the base of the two-mass picture while referring to [10,11,12] for all formal derivations. Then, after resuming in Section 3 the expected phenomenology, we report in Section 4, Section 5 and Section 6 the results of [13] about various experimental signals from LHC which support the existence of the second resonance. Section 7 finally contains a summary and our conclusions.

2. Physical Picture of SSB and the Second Resonance

Let us start from scratch by considering SSB at the classical level. Here, one needs only look at the potential

$$V_{\mathrm{cl}}\left(\phi \right)=\frac{1}{2}{m}^2{\phi }^2+\frac{1}{4!}\lambda {\phi }^4$$

(2)

to see that the phase transition, as one varies the $m^2$ parameter, is second order and occurs at $m^2=$ 0. However, in the quantum theory, i.e., when we consider the full effective potential, the question is not so simple because then, through quantum loops, the ultraviolet cutoff also enters and the difference between a second-order and a weak first-order transition can become very delicate. Clearly, the symmetric vacuum is locally stable if its excitations have a physical mass $m^2>0$. However, is a locally stable symmetric vacuum necessarily globally stable? Here, the standard approximation methods to the quantum effective potential $V_{\mathrm{eff}}\left(\phi \right)$ give contradictory results.

To get an intuitive insight, let us first consider the following toy model

$$V_{\mathrm{toy}}\left(\phi \right)=\frac{1}{2}{m}^2{\phi }^2+\frac{1}{4!}\lambda {\phi }^4\left(1+ϵln{\phi }^2/{\mu }^2\right)$$

(3)

where $\mu$ is some mass scale and $ϵ$ is a small parameter (the case in the quantum theory is with $ϵ\sim \lambda$ but in this toy model, we treat $ϵ$ as a separate parameter). For $ϵ=0$, as one varies the $m^2$ parameter, one has a second-order phase transition, occurring at $m^2=$ 0. However, for any $ϵ>0$, no matter how small, one has a first-order transition, occurring at a positive $m^2$. The size of the critical $m_c^2$ is exponentially small ${\mu }^{2}exp(-1/ϵ)$, as well as the difference between $V_{\mathrm{toy}}$ and $V_{\mathrm{cl}}$ in the relevant region. This means that an infinitesimally weak, first-order phase transition can become indistinguishable from a second-order transition if one does not look on a fine enough scale.

Let us then analyze various approximation schemes starting from the straightforward 1-loop Coleman–Weinberg (CW) potential [4]. This predicts a (weak) first-order transition because the massless limit, defined by $V_{\mathrm{eff}}^{″}(\phi =0)=0$, lies already within the broken phase. On the other hand, the Renormalization-Group-improved result, obtained by resumming the leading-logarithmic terms [4], predicts a second-order transition 4. The conventional view is that the latter result is trustworthy while the former is not because the 1-loop minimum occurs where the 1-loop term is as large as the tree-level term. However, also the RG-improved result is questionable because in the relevant region of $\phi$, one is re-summing a series of leading logs that is actually a divergent series [14].

To better understand, a crucial observation is that the same 1-loop potential admits two different readings. The perspective we have considered amounts to regard the genuine 1-loop contribution as simply renormalizing the coupling $\lambda$ in the classical potential

$$\frac{\lambda }{4!}{\phi }^4\to \frac{\lambda }{4!}{\phi }^4(1-\frac{3\lambda }{32{\pi }^2}ln(2{\Lambda }_s^2\sqrt{e}/\lambda {\phi }^2+\dots )$$

(4)

Therefore, re-summing the higher-order leading logarithmic terms, i.e., by replacing

$$1-x\to 1-x+x^2-x^3\dots =1/(1+x)$$

(5)

the 1-loop minimum disappears. However, there is a second perspective, recently emphasized in [10,11,12] and anticipated in the Introduction, in which the same 1-loop potential can be read as the sum of the classical potential + the zero-point energy of a particle with mass $M^2\left(\phi \right)\equiv \frac{1}{2}\lambda {\phi }^2$

$$V_{1-\mathrm{loop}}\left(\phi \right)=\frac{\lambda {\phi }^4}{4!}-\frac{M^4\left(\phi \right)}{64{\pi }^2}ln\frac{{\Lambda }_s^2\sqrt{e}}{M^2\left(\phi \right)}$$

(6)

Once interpreted in this way, the 1-loop potential acquires a non-perturbative meaning as the prototype of an infinite number of approximations which correspond to very different resummations of graphs but effectively reproduce the same result. This is illustrated by the Gaussian approximation [15] which produces a result in agreement with the one-loop effective potential. This is not because it contains no non-vanishing corrections beyond the 1-loop; it does, but those higher-order terms [5] do not alter the functional form of the result.

The agreement between the two approximations (1-loop and Gaussian effective potential) has to be emphasized because it gives physical insight into the true meaning of the “triviality” of ${\Phi }^4$ in 4D. This basic property implies that, in the continuum limit of the theory (i.e., for an ultraviolet cutoff ${\Lambda }_s\to \infty$), all bare interactions have to be reabsorbed into the first two moments of a Gaussian distribution. This does not forbid a $\langle \Phi \rangle \ne 0$ but dictates trivially free fluctuations. Therefore, consistency with “triviality” would naturally require an effective potential which is physically equivalent to the 1-loop result, namely a $V_{\mathrm{eff}}\left(\phi \right)$ given again by some classical background + zero-point energy of a free fluctuation field with some $\phi$-dependent mass $M\left(\phi \right)$.

Notice that we are saying “physically equivalent to…” not “equal to…”; it is not that multi-loop graphs produce no contributions but that those contributions affect both the classical background and $M\left(\phi \right)$ in a way that preserves the functional form of the 1-loop result, up to terms that vanish in the continuum limit. This physical equivalence 5 is embodied in the following replacements

$$\lambda \to {\lambda }_G=\frac{\lambda }{1+\frac{\lambda }{16{\pi }^2}ln\frac{{\Lambda }_s}{M_G\left(\phi \right)}}$$

(7)

$$M^2\left(\phi \right)\to M_G^2\left(\phi \right)=\frac{{\lambda }_G{\phi }^2}{2}$$

(8)

$$V_{1-\mathrm{loop}}\left(\phi \right)\to V_G\left(\phi \right)=\frac{{\lambda }_G{\phi }^4}{4!}-\frac{M_G^4\left(\phi \right)}{64{\pi }^2}ln\frac{{\Lambda }_s^2\sqrt{e}}{M_G^2\left(\phi \right)}$$

(9)

We emphasize that the above picture of SSB as a (weak) first-order phase transition in ${\Phi }^4$ theory is also in agreement with lattice simulations. To this end, one can compare with [18,19,20] which indeed support this conclusion. As an example, one can look at Figure 7 of [20] where the data for the magnetization as function of the temperature show the characteristic first-order jump and not the expected, smooth second-order trend 6.

Now, let us consider the phenomenological implications of exploring the effective potential $V_{\mathrm{eff}}\left(\phi \right)$ in the 1-loop and Gaussian approximations. By defining $m_h^2=V_{\mathrm{eff}}^{″}\left(\phi \right)$ at the minimum, $M_H$ as the value of $M\left(\phi \right)$ (or of $M_G\left(\phi \right)$) at the minimum, and introducing $L=ln({\Lambda }_s/M_H)$, one finds [10,11,12] the same pattern of scales

$$\lambda \sim L^{-1}{m}_h^2\sim {\langle \Phi \rangle }^2·L^{-1}{M}_H^2\sim L·m_h^2=K^2{\langle \Phi \rangle }^2$$

(10)

K being a cutoff-independent constant. Furthermore, the relation $V_{\mathrm{eff}}\left(\langle \Phi \rangle \right)\sim -M_H^4$ supports the cutoff independence of $M_H$, and therefore of $\langle \Phi \rangle$, because the ground state energy is a Renormalization Group-invariant quantity, see [10,11,12].

To explore the meaning of the $m_h-M_H$ difference, we first observe that the quadratic shape and depth of the potential are different quantities. At a more formal level, we recall that the derivatives of the effective potential produce (minus) the n-point functions at zero external momentum. Hence, by defining the inverse propagator $G^{-1}\left(p\right)=(p^2-\Pi \left(p\right))$, the mass parameter $m_h^2$, which is $V_{\mathrm{eff}}^{″}\left(\phi \right)$ at the minimum, is directly the 2-point function $|\Pi (p=0)|=|G^{-1}(p=0)|$. On the other hand, the zero-point energy is (one-half of) the trace of the logarithm of the inverse propagator. Therefore, after subtracting constant terms and quadratic divergences, matching the 1-loop zero-point energy(“$zpe$”) gives the relation

$$zpe\sim -\frac{1}{4}{\int }_{p_{\min }}^{p_{\max }}\frac{d^{4}p}{{\left(2\pi \right)}^4}\frac{{\Pi }^2\left(p\right)}{p^4}\sim -\frac{\langle {\Pi }^2\left(p\right)\rangle }{64{\pi }^2}ln\frac{p_{\max }^2}{p_{\min }^2}\sim -\frac{M_H^4}{64{\pi }^2}ln\frac{{\Lambda }_s^2}{M_H^2}$$

(11)

Thus, $M_H^2$ effectively includes the contribution of the higher momenta and thus reflects a typical average value $|\langle \Pi (p)\rangle |$ at larger $p^2$. A non-trivial momentum dependence of $\Pi \left(p\right)$ would then indicate the coexistence in the broken-symmetry phase of two kinds of “quasi-particles”, with masses $m_h$ and $M_H$, and thus closely resemble the two branches (phonons and rotons) in the energy spectrum of superfluid He-4 which is usually considered the non-relativistic analog of the broken phase 7.

With these premises, this two-mass structure was checked with lattice simulations of the propagator [10]. While in the symmetric phase, no momentum dependence of the mass parameter was observed, in the broken-symmetry phase, the situation was different. By computing $m_h^2$ from the $p\to 0$ limit of $G\left(p\right)$ and $M_H^2$ from its behavior at higher $p^2$, the lattice data are consistent with a transition between two regimes and with the scaling trend $M_H^2\sim L{m}_h^2$. As such, in the full momentum region, the propagator could be described by a model form [12]

$$G\left(p\right)\sim \frac{1-I\left(p\right)}{2}\frac{1}{p^2+m_h^2}+\frac{1+I\left(p\right)}{2}\frac{1}{p^2+M_H^2}$$

(12)

with an interpolating function $I\left(p\right)$ which depends on an intermediate momentum scale $p_0$ and tends to $+1$ for large $p^2\gg p_0^2$ and to $-1$ when $p^2\to 0$. Therefore, the lattice data support the idea that, beside the known resonance with mass $m_h=$ 125 GeV, the Higgs field might exhibit a second resonance with a much larger mass. At the same time, by extrapolating from various lattice sizes, the cutoff-independent constant was found $K=2.80\pm 0.04\left(\mathrm{stat}\right)\pm 0.08\left(\mathrm{sys}\right)$ giving the prediction [10,11,12]

$${\left(M_H\right)}^{\mathrm{Theor}}=690\pm 10\left(\mathrm{stat}\right)\pm 20\left(\mathrm{sys}\right)\mathrm{GeV}$$

(13)

This numerical estimate is a definite prediction to be checked by experiments. However, it also helps to get in touch with the standard picture where there is only $m_h$. To this end, we observe that, from the third relation in (10), one finds $m_h\ll M_H$ for large ${\Lambda }_s$. However, since $M_H$ is ${\Lambda }_s$-independent, it means that by decreasing ${\Lambda }_s$ also $m_h$ increases and approaches its maximum value ${\left(m_h\right)}^{\max }\sim M_H$ for $L\sim 1$, i.e., when ${\Lambda }_s$ is a few times $M_H$. Therefore, this maximum value corresponds to

$${\left(m_h\right)}^{\max }\sim {\left(M_H\right)}^{\mathrm{Theor}}=690\pm 10\left(\mathrm{stat}\right)\pm 20\left(\mathrm{sys}\right)\mathrm{GeV}$$

(14)

in good agreement with the upper bound derived from the conventional first two relations in Equation (10) ${\left(m_h\right)}^{\max }=$ 670(80) GeV, see Lang’s complete review [23]. Equivalently, we could have avoided to perform our own lattice simulations of the scalar propagator and just predict ${\left(M_H\right)}^{\mathrm{Theor}}=$ 670(80) GeV by combining the ${\Lambda }_s$-independence of $M_H$, the third relation in (10) and Lang’s estimate of ${\left(m_h\right)}^{\max }$. In conclusion, for ${\Lambda }_s\to \infty$, the two masses decouple from each other while for ${\Lambda }_s=O\left(1\right)$ TeV, they tend to coincide. However, in the real world, $m_h=$ 125 GeV. Therefore, if $M_H$ exists, ${\Lambda }_s$ has to be very large. At the same time, since vacuum stability only depends on the large $M_H$, and not on $m_h$, SSB could well originate from the pure scalar sector regardless of the other physical parameters of the theory, e.g., the vector boson and top quark mass 8.

3. Basic Phenomenology of the Second Resonance

The two masses $m_h$ and $M_H$ are very different but represent excitations of the same Higgs field. Therefore, the observable interactions of this field, with itself, and with the other fluctuations about the minimum of the potential, as the Goldstone bosons, are governed by the same coupling: the mass parameter $m_h^2$ which fixes the scalar coupling $\lambda =3m_h^2/{\langle \Phi \rangle }^2$ at the Fermi scale. This means that, in spite of its large mass, the heavy H-resonance would couple to longitudinal Ws and Zs with the same typical strength as the low-mass state 9 at 125 GeV and represent a relatively narrow resonance. This can be taken into account by replacing the conventional large width ${\Gamma }^{\mathrm{conv}}(H\to WW+ZZ)\sim G_F{M}_H^3$ with the corresponding relation $\Gamma (H\to WW+ZZ)\sim M_H\left(G_F{m}_h^2\right)$ which retains the same phase-space factor $M_H$ but has a coupling re-scaled by the factor $m_h^2/M_H^2\sim$ 0.032. Numerically, for $M_H\sim$ 700 GeV, we find from [26]

$$\Gamma (H\to ZZ)\sim \frac{M_H}{700\mathrm{GeV}}·\frac{m_h^2}{{\left(700\mathrm{GeV}\right)}^2}50.1\mathrm{GeV}\sim \frac{M_H}{700\mathrm{GeV}}·1.6\mathrm{GeV}$$

(15)

$$\Gamma (H\to WW)\sim \frac{M_H}{700\mathrm{GeV}}·\frac{m_h^2}{{\left(700\mathrm{GeV}\right)}^2}102.6\mathrm{GeV}\sim \frac{M_H}{700\mathrm{GeV}}·3.3\mathrm{GeV}$$

(16)

At the same time, the other decays which are proportional to the gauge and Yukawa couplings (such as the decays into fermions, gluons, photons, etc.) will remain unchanged and can be taken from [26] with the result

$$\Gamma (H\to \mathrm{fermions}+\mathrm{gluons}+\mathrm{photons}\dots )\sim \frac{M_H}{700\mathrm{GeV}}·26.2\mathrm{GeV}$$

(17)

Therefore, one might expect a total width ${\Gamma }_H\equiv \Gamma (H\to all)\sim 30÷31\mathrm{GeV}$. This estimate, however, does not include the new decays of the heavier resonance into the 125 GeV resonance such as $H\to hh$, the three-body processes $H\to hhh$, $H\to hZZ$, $H\to h{W}^{+}{W}^{-}$, and the higher-multiplicity final states allowed by phase space. For this reason, the value ${\Gamma }_H\sim 30÷31\mathrm{GeV}$ should just be considered a lower bound.

The new contributions to the total width are not so easy to estimate because the $h-H$ overlapping makes this a non-perturbative problem. Perhaps, methods such as the RSE approach [27], which are used in analogous problems with meson resonances could be useful. For this reason, in [28], it was only considered a test in the charged 4-lepton final state which does not require to know the total width and just relies on two assumptions:

(a)

A resonant 4-lepton production through the chain $H\to ZZ\to 4l$;

(b)

The value of $\Gamma (H\to ZZ)$ in Equation (15).

Therefore, in terms of ${\gamma }_H={\Gamma }_H/M_H$, we find a fraction

$$B(H\to ZZ)=\frac{\Gamma (H\to ZZ)}{{\Gamma }_H}\sim \frac{1}{{\gamma }_H}·\frac{50.1}{700}·\frac{m_h^2}{{\left(700\mathrm{GeV}\right)}^2}$$

(18)

that can be inserted in the cross section approximated by on-shell branching ratios

$${\sigma }_R(pp\to H\to 4l)\sim \sigma (pp\to H)·B(H\to ZZ)·4B^2(Z\to l^{+}{l}^{-})$$

(19)

In this approximation, which should work for a relatively narrow resonance, one thus predicts the relation

$${\gamma }_H·{\sigma }_R(pp\to H\to 4l)\sim \sigma (pp\to H)·\frac{50.1}{700}·\frac{m_h^2}{{\left(700\mathrm{GeV}\right)}^2}·4B^2(Z\to l^{+}{l}^{-})$$

(20)

With the value $4B^2(Z\to l^{+}{l}^{-})\sim 0.0045$, the only missing piece is then the production cross section $\sigma (pp\to H)$. As discussed in [12], this will mainly proceed through the gluon–gluon Fusion (ggF) process because production through Vector-Boson Fusion (VBF) plays no role once the large coupling to longitudinal Ws and Zs is suppressed by the small factor $m_h^2/M_H^2\sim$ 0.032. Therefore, the sizeable VBF cross section ${\sigma }^{\mathrm{VBF}}(pp\to H)\sim$ 300 fb is reduced to about 10 fb and can be neglected with respect to the ggF contributions $O\left({10}^3\right)$ fb. In fact, for 13 TeV pp collisions, and with a typical $\pm 15\%$ uncertainty (due to the parton distributions, to the choice of $\mu$ in ${\alpha }_s\left(\mu \right)$ and to other effects), we find the typical value [26] ${\sigma }^{\mathrm{ggF}}(pp\to H)=$ 1090(170) fb which, in our case, would also account for the mass range $M_H=660÷700$ GeV. In conclusion, for $m_h=$ 125 GeV, we obtain [28] a prediction which, for not too large ${\gamma }_H$ where Equation (19) looses validity, is formally insensitive to the value of ${\Gamma }_H$

$${[{\gamma }_H·{\sigma }_R(pp\to H\to 4l)]}^{\mathrm{theor}}\sim (0.011\pm 0.002)\mathrm{fb}$$

(21)

and can be compared with precise LHC data.

4. The ATLAS ggF-like 4-Lepton Events

Looking for a possible new resonance around 700 GeV, we started from the charged 4-lepton channel by considering the ATLAS sample [29] of events that, for their characteristic topology, can be interpreted as being produced through the ggF mechanism. For these 4-lepton data, the ATLAS experiment has performed a sophisticated analysis where the ggF events, depending on the degree of contamination with the background, are divided into four mutually exclusive categories: ggF-high-4$\mu$, ggF-high- 2e2$\mu$, ggF-high-4e, ggF-low.

In view of the modest weight of the very pure ggF-high samples, in [28], the event numbers for the 4 categories were summed up and the total number of events was considered to compare with the phenomenological picture of Section 3, in spite of the fact that the selection criteria for each ggF-like category are not exactly the same. That analysis was also restricted to a relatively small region of invariant mass $M_{4l}=E=620÷740$ GeV ($l=e,\mu$) extending about ±60 GeV around our central mass value $M_H=$ 690 GeV. Then, within the general model of a resonating amplitude $A^R\left(s\right)\sim 1/(s-M_R^2)$ which interferes with a smooth background $A^B\left(s\right)$, given the limited size of the energy region, the background was approximated as a linear slope and fitted from the same data.

Since one may object to this procedure, in [13], it was argued differently. First, the analysis was restricted to the ggF-low category, the only sample of events which is homogeneous from the point of view of the selection and has a sufficient statistics. Furthermore, the background was assumed the same as estimated by ATLAS. Finally, the region of invariant mass was extended to about $\pm 150$ GeV around our central mass value of 690 GeV.

With these premises, we report in

Table 1. For luminosity 139 fb${}^{-1}$, we report the observed ATLAS ggF-low events and the corresponding estimated background [29] in the range of invariant mass $M_{4l}=E=530÷830$ GeV. To avoid spurious fluctuations, due to migration of events between neighboring bins, we have followed the same criterion as in Figure 5 of [30] by grouping the data into larger bins of 60 GeV, centered at 560, 620, 680, 740, and 800 GeV. These were obtained by combining the corresponding 10 bins of 30 GeV, centered, respectively, at the neighboring pairs: 545(15) ÷ 575(15) GeV, 605(15) ÷ 635(15) GeV, 665(15) ÷ 695(15), 725(15) ÷ 755(15) GeV, and 785(15) ÷ 815(15) GeV as reported in [29]. In this energy range, the errors in the background are below $5\%$ and will be neglected.

$\mathbf{E}$ [GeV]	${\mathbf{N}}_{\mathbf{EXP}}\left(\mathbf{E}\right)$	${\mathbf{N}}_{\mathbf{B}}\left(\mathbf{E}\right)$	${\mathbf{N}}_{\mathbf{EXP}}\left(\mathbf{E}\right)-{\mathbf{N}}_{\mathbf{B}}\left(\mathbf{E}\right)$
560(30)	38 $\pm 6.16$	32.0	$6.00\pm 6.16$
620(30)	25 $\pm 5.00$	20.0	$5.00\pm 5.00$
680(30)	26 $\pm 5.10$	13.04	$12.96\pm 5.10$
740(30)	3 $\pm 1.73$	8.71	$-5.71\pm 1.73$
800(30)	7 $\pm 2.64$	5.97	$1.03\pm 2.64$

the observed ATLAS 4-lepton events within the ggF-low category and the estimated background as taken from [29]. To avoid spurious fluctuations which may be due to migration of events between neighboring bins, we have followed the same criterion adopted in Figure 5 of the other ATLAS paper [30], where events were grouped in larger bins of 60 or even 80 GeV.

From this Table 1, one gets the same impression as from Figure 5 of [30] in the same energy region. Namely, there is a 2.5-sigma excess over the background, in the bin centered around 680 GeV, which is followed by a 3-sigma defect in the bin centered around 740 GeV. The simplest explanation for these two simultaneous features would be the existence of a resonance of mass $M_H\sim$ 700 GeV which, beside the Breit–Wigner peak, produces the characteristic interference pattern proportional to $(M_H^2-s)$.

To describe the data in Table 1, in [13], the model cross section of [12,28] was adopted

$${\sigma }_T={\sigma }_B+\frac{2(M_H^2-s){\Gamma }_H{M}_H}{{(s-M_H^2)}^2+{\left({\Gamma }_H{M}_H\right)}^2}\sqrt{{\sigma }_B{\sigma }_R}+\frac{{\left({\Gamma }_H{M}_H\right)}^2}{{(s-M_H^2)}^2+{\left({\Gamma }_H{M}_H\right)}^2}{\sigma }_R$$

(22)

where, together with the mass $M_H$ and total width ${\Gamma }_H$ of the resonance, one introduces a background cross section ${\sigma }_B={\sigma }_B\left(E\right)$ and the resonating peak cross section ${\sigma }_R$. Of course, due to the very large size of the bins, ours should only be considered a first, rough approximation. Nevertheless, a good consistency was found with the phenomenological picture of Section 3.

As a first ingredient, we searched for an accurate description of the ATLAS background in terms of a power law $N_B\left(E\right)\sim A·{(710\mathrm{GeV}/E)}^{\nu }$ with $A\sim 10.55$ and $\nu \sim 4.72$. Then, by simple redefinitions, the theoretical number of events was expressed as

$$N_{TH}\left(E\right)=N_B\left(E\right)+\frac{P^2+2P·x\left(E\right)·\sqrt{N_B\left(E\right)}}{{\gamma }_H^2+x^2\left(E\right)}$$

(23)

where $x\left(E\right)=(M_H^2-E^2)/M_H^2$, $N_R={\sigma }_R·\mathcal{A}·139$ fb${}^{-1}$ denotes the extra events at the resonance peak for an acceptance $\mathcal{A}$ and finally $P\equiv {\gamma }_H\sqrt{N_R}$.

Without specific information on the ggF-low category, in [13], a value of $\mathcal{A}\sim 0.38$ was adopted by averaging the two extremes, 0.30 and 0.46, for all ggF-like events [29]. As a consequence, the resonance parameters will be affected by a corresponding uncertainty. Nevertheless, to have a first check of our picture, we fitted with Equation (23) the experimental number of events in Table 1. 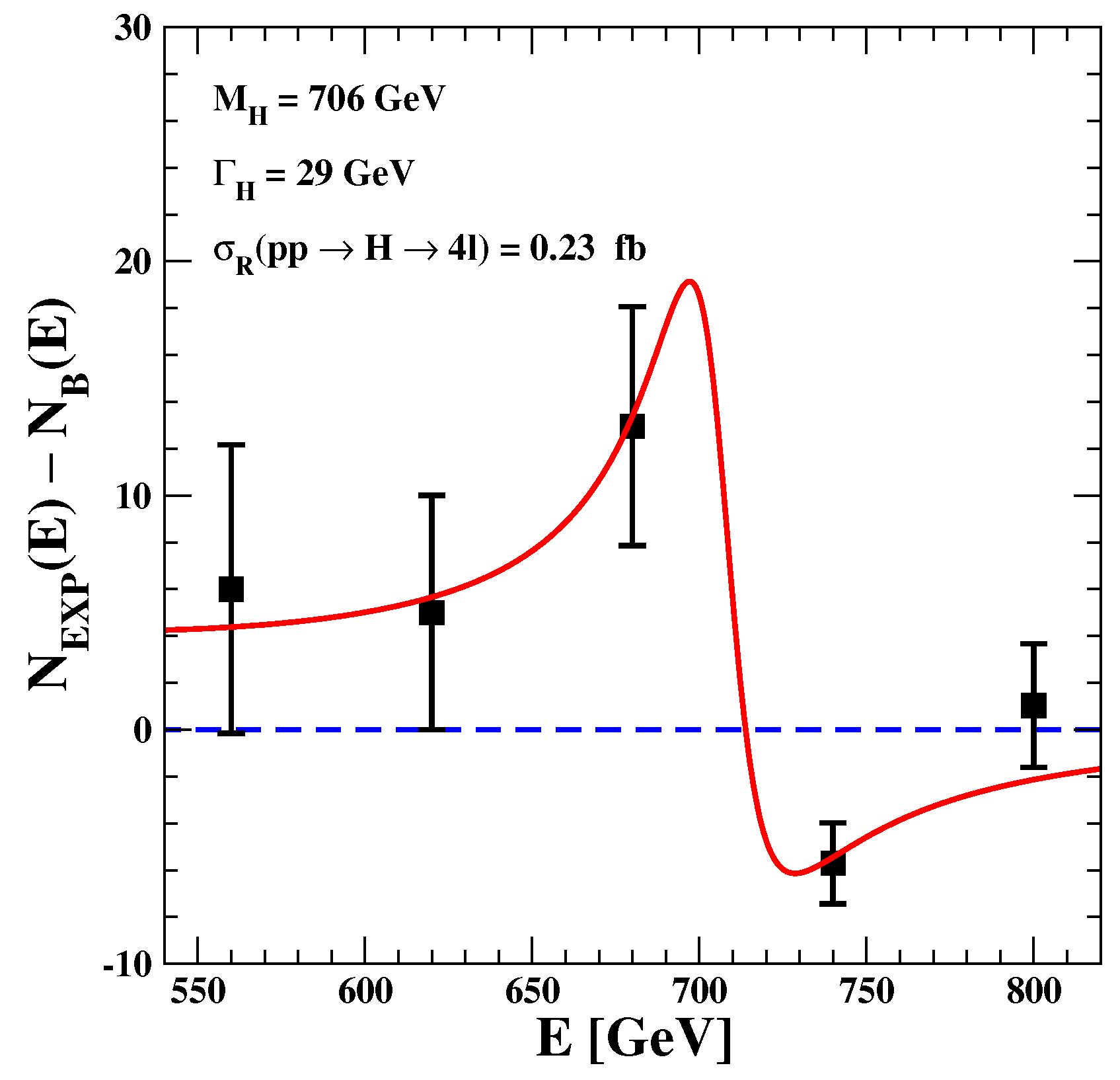The results were: $M_H=$ 706(25) GeV, ${\gamma }_H=0.041\pm 0.029$ (corresponding to a total width ${\Gamma }_H=29\pm 20$ GeV) and $p=0.14\pm 0.07$. From these, we obtain central values $N_R\sim$ 12, and ${\sigma }_R\sim$ 0.23 fb with very large errors. Our theoretical values are shown in

Table 2. We report the observed ATLAS ggF-low events and our theoretical prediction Equation (23) for $M_H=$ 706 GeV, ${\gamma }_H=$ 0.041, P = 0.14.

$\mathbf{E}$ [GeV]	${\mathbf{N}}_{\mathbf{EXP}}\left(\mathbf{E}\right)$	${\mathbf{N}}_{\mathbf{TH}}\left(\mathbf{E}\right)$	${\mathit{\chi }}^2$
560(30)	38 $\pm 6.16$	36.72	0.04
620(30)	25 $\pm 5.00$	25.66	0.02
680(30)	26 $\pm 5.10$	26.32	0.00
740(30)	3 $\pm 1.73$	3.23	0.02
800(30)	7 $\pm 2.64$	3.87	1.40

and a graphical comparison in Figure 2.

The quality of the fit is good but, with the exception of the mass, errors are very large so that a test of our picture is not so stringent. Still, with the partial width of Section 3, $\Gamma (H\to ZZ)\sim$ 1.6 GeV, and fixing ${\Gamma }_H$ to its central value of 29 GeV, we find a branching ratio $B(H\to ZZ)\sim$ 0.055 which, for the central value ${\sigma }^{\mathrm{ggF}}(pp\to H)\sim$ 923 fb of [26] at $M_H=$ 700 GeV, would imply a theoretical peak cross section ${\left({\sigma }_R\right)}^{\mathrm{theor}}=923·0.055·0.0045\sim$ 0.23 fb which coincides with the central value from our fit. In addition, from the central values $\langle {\sigma }_R\rangle =$ 0.23 fb and $\langle {\gamma }_H\rangle =$ 0.041, we find $\langle {\sigma }_R\rangle ·\langle {\gamma }_H\rangle \sim$ 0.0093 fb, consistent with Equation (21).

In conclusion, as shown in [13], the ATLAS ggF-low category of 4-lepton events indicate the existence of a new resonance whose mass and basic parameters are consistent with our picture.

5. The ATLAS High-Mass $\gamma \gamma$ Events

Searching for further signals, in [13], we considered the invariant mass distribution of the inclusive diphoton production as measured by ATLAS [31] in the rather wide range of invariant mass $600÷770$ GeV which extends about $\pm 90$ GeV around our central mass value. The relevant entries in

Table 3. The ATLAS number of $N=N\left(\gamma \gamma \right)$ events, in bins of 16 GeV and for luminosity 139 fb${}^{-1}$, for the range of invariant mass $\mu =\mu \left(\gamma \gamma \right)=600÷770$ GeV. These values were extracted from Figure 3 of [31] because the relevant numbers are not reported in the companion HEPData file.

$\mu$	604	620	636	652	668	684	700	716	732	748	764
N	349(19)	300(17)	267(16)	224(15)	218(15)	235(15)	157(13)	146(12)	137(12)	108(10)	120(11)

were extracted from Figure 3 of [31] because the numerical values are not reported in the companion HEPData file.

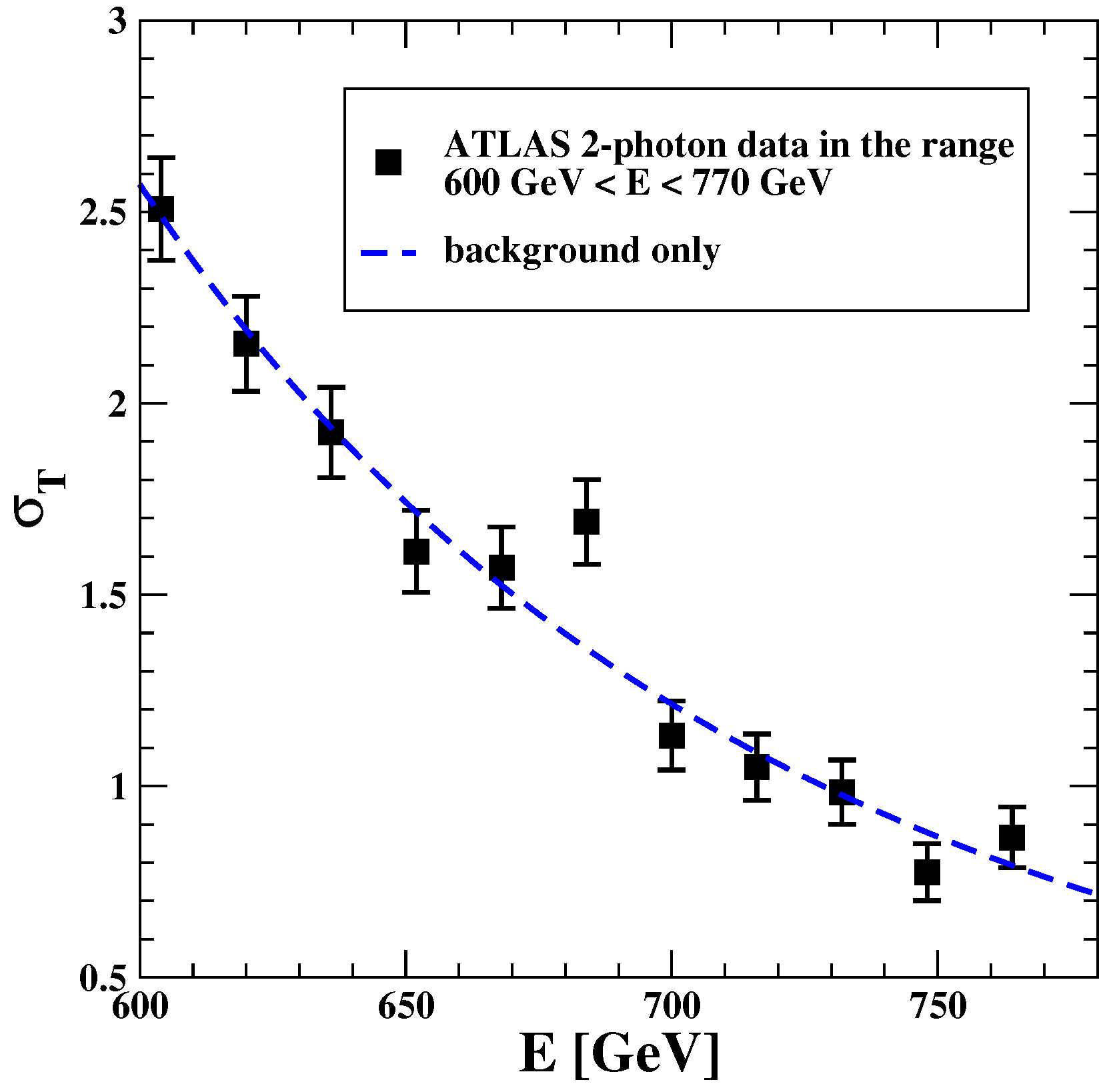
By parameterizing the background with a power-law form ${\sigma }_B\left(E\right)\sim A·{(685\mathrm{GeV}/E)}^{\nu }$, we performed various fits to the data in Table 3. This gives a good description of all data points, except the sizeable excess at 684 GeV (estimated by ATLAS to have a local significance of about 3.3-sigma). Just to give an idea, by fixing ${\sigma }_R=0$ in Equation (22), a pure background fit in the considered mass range gives $A=1.35\left(3\right)$ fb, $\nu =4.87\left(38\right)$, and total ${\chi }^2=14$, where 10 of which are due to the single point at 684 GeV, see Figure 3.

This illustrates that a (hypothetical) new resonance might well remain hidden behind the large background almost everywhere, the main signal being just the interference effect. However, this interference effect itself is much smaller than the background in the resonance region (${\sigma }_B\sim$ 1.3 fb); therefore, the resonance parameters will be determined very poorly.

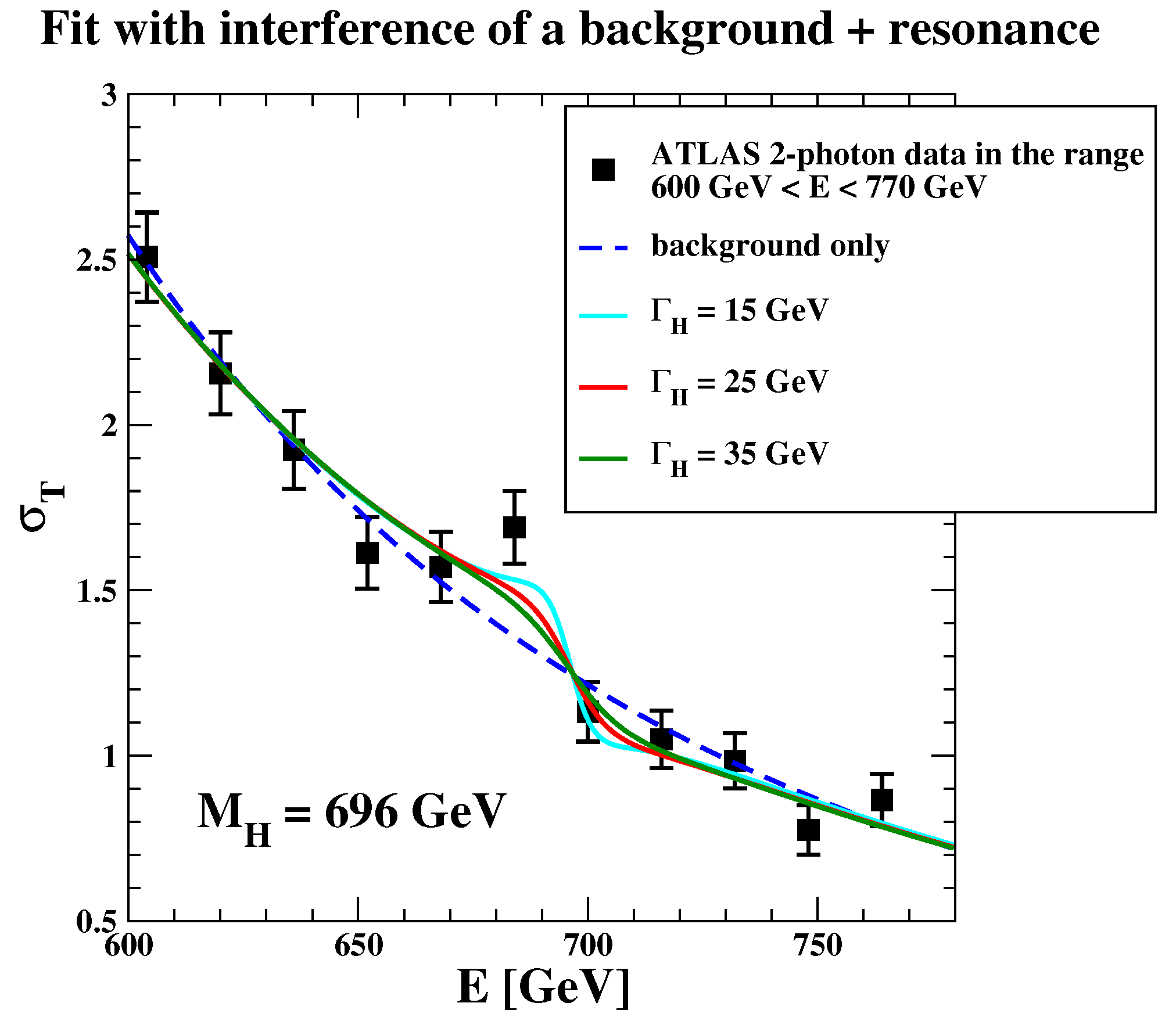
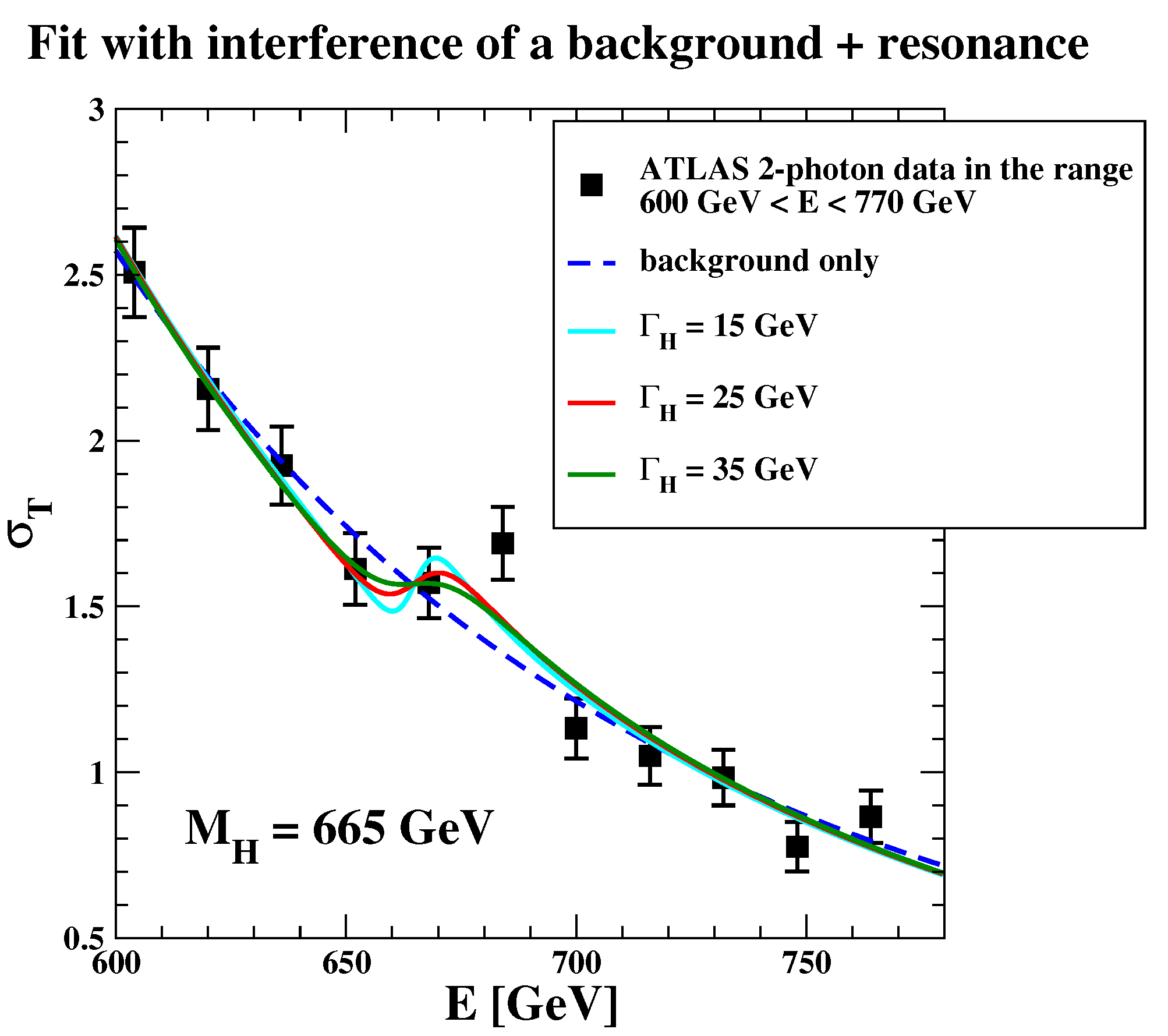
By constraining the background parameters A and $\nu$ in ${\sigma }_B$ within the previous range obtained for ${\sigma }_R=0$, we considered the full Equation (22). Three fits are shown in Figure 4 for $M_H=$ 696 GeV and for the values ${\Gamma }_H=$ 15, 25, and 35 GeV.

Due to the dominant role of the interference, in this $\gamma \gamma$ case, we also performed another series of fits by reversing the sign of the interference term (from positive-to-negative below peak) which is not known a priori. For the same values of the width reported in Figure 4, the corresponding fits are shown in Figure 5. Note that, in this second case, there is a shift of about −30 GeV, in the central value of the mass, from $M_H=$ 696(13) GeV down to $M_H=$ 665(13) GeV.

Thus, in principle, the localized 3.3-sigma excess at 684 GeV admits two different interpretations:

(a)

A statistical fluctuation above a pure background, see Figure 3;

(b)

The signal of a new heavy resonance, see Figure 4 and Figure 5.

As for the total width, the $\gamma \gamma$ data tend to place an upper limit ${\left({\Gamma }_H\right)}^{\exp }<50$ GeV in agreement with the rather loose determination ${\left({\Gamma }_H\right)}^{\exp }=$ 29(20) GeV from the 4-lepton data. The analogous combined determination for the mass could be summarized as ${\left(M_H\right)}^{\exp }=$ 680(15) GeV which includes the results obtained with the two possible signs of the interference term in Equation (22).

About the peak cross section ${\sigma }_R={\sigma }_R(pp\to H\to \gamma \gamma )$, for the first type of fits, the central values lie in the range $0.007÷0.012$ fb but with minus errors which, at the 70% CL, extend very close to ${\sigma }_R=0$ (where ${\chi }^2=14$). Namely, ${\left({\sigma }_R\right)}_{\mathrm{low}}=$ 0.0015 fb for ${\Gamma }_H=$ 15 GeV and ${\left({\sigma }_R\right)}_{\mathrm{low}}=$0.0002 fb for ${\Gamma }_H=$ 35 GeV.

Therefore, it is appropriate to comment on the theoretical prediction for this quantity which depends on the partial width $\Gamma (H\to \gamma \gamma )$. For $M_H\sim 700$ GeV, the value reported in [26] is $\Gamma (H\to \gamma \gamma )\sim$ 29 keV so that, for ${\left({\Gamma }_H\right)}^{\mathrm{Exp}}\sim 35$ GeV, we might expect a fraction $B(H\to \gamma \gamma )\sim 8·{10}^{-7}$ with a peak value ${\sigma }_R(pp\to H\to \gamma \gamma )\sim \sigma (pp\to H)·B(H\to \gamma \gamma )\sim 0.0008$ fb which lies within the 70% confidence area of our fit. However, this estimate of $\Gamma (H\to \gamma \gamma )$ contains the non-decoupling, the so-called “$-2$” term proportional to $M_H^3$ whose presence (or not) in the WW contribution was much discussed in the literature. At present, except the unitary-gauge calculations of Gastmans, Wu and Wu [32,33,34] and the dispersion-relation approach of Christova and Todorov [35], the general consensus is that this non-decoupling term should be there. However, in the context of a second Higgs resonance, which does not couple to longitudinal Ws proportionally to its mass but with the same typical strength as the low-mass state at 125 GeV, the whole issue could probably be re-considered. The point is that for a mass around $M_H=$ 700 GeV, there is a cancellation between the WW and $t\overline{t}$ contributions. As we have checked, excluding the non-decoupling term would increase the lowest-order value (i.e., without QCD corrections in the top-quark loop) by an order of magnitude. For this reason, a somewhat larger partial decay width, say $\Gamma (H\to \gamma \gamma )\lesssim$ 100 keV, cannot be excluded. This would increase the theoretical branching ratio and, therefore, the theoretical peak cross section toward the larger central values is favored by our fit to the $\gamma \gamma$ data.

Of course, more precise data are needed for a significant test. Meanwhile, one could also search for additional checks in other channels. For instance, in the $\gamma \gamma$ events which are observed in connection with $pp$ double-diffractive scattering, i.e., in the process

$$p+p\to p+X+p$$

(24)

when both final protons are tagged and have large Feynman $x_F$. For $X=H$, which is the “diffractive excitation of the vacuum” considered by Albrow [36], one could then look for an excess of $\gamma \gamma$ events in the region of invariant mass $\mu \left(\gamma \gamma \right)\sim M_H$. Since, here, the background is different, a corresponding excess could have a larger statistical significance. Remarkably, as we will briefly discuss in the following section, such an excess is indeed present in the CMS data.

6. Experimental Signals from CMS: A Short Review

Right now, CMS analyses of charged 4-lepton and fully inclusive diphoton events, with the whole statistics collected during RUN2, are not yet available. Nevertheless, some excesses of events over the background in the relevant mass region are present in smaller statistical samples.

For example, the charged 4-lepton invariant mass distribution measured by CMS with an integrated luminosity of 35.9 fb${}^{-1}$ shows a clean excess at 660 GeV (see Figure 3, left panel of [37]), consistently with the corresponding ATLAS excess at 680 GeV observed with the full RUN2 statistics. The corresponding $\gamma \gamma$ sample, for the same statistics of 35.9 fb${}^{-1}$, also shows a modest 1-sigma excess for the EBEB selection mode, see Figure 2, left panel of [38]. There, the data were presented in bins of 20 GeV and the relevant region extends from 620(10) to 660(10) GeV. The corresponding EBEE plot has also a very slight excess at 660 GeV but this is really too small. For a scalar resonance, and for a value ${\gamma }_H=$ 0.056 which is the closest to our model, the 1-sigma excess in the EBEB case at 640(30) GeV, is also visible in panel 5 of Figure 4 of [38]. Notice that, as in the ATLAS 4-lepton case, the excess is immediately followed by a defect of events which could again indicate a negative-interference effect proportional to $(M_H^2-s)$. The corresponding graph in panel 6 for the EBEE mode shows only a defect of events.

CMS 4-lepton events with the larger 77.4 fb${}^{-1}$ integrated luminosity were also reported in [39] but it is very hard to deduce anything from the very compressed scale adopted for the figures (see, however, Cea’s claim [40] of substantial excess around 700 GeV). From this point of view, these CMS measurements based on partial statistics certainly do not contradict our present analysis.

However, a second resonance of the Higgs field, if there, should also be visible in other decay channels as well. For this reason, we briefly discuss some results presented by CMS at the ICHEP 2022 Conference. A first analysis [41] concerns the search for high mass resonances decaying into W-pairs which then decay into neutrinos and the charged leptonic final state ($e\mu$, $\mu \mu$, $ee$). Excesses with non-negligible local significance ranging from 2.6 to 3.8 sigmas, depending on the different mechanisms for the resonance production mode (ggF and/or VBF), are observed in the region of invariant mass $600÷1200$ GeV (Figure 4). The maximal significance for the various scenarios ranges from 650 to 950 GeV (Table 3) but, due to the presence of neutrinos in the final states, the excess for each scenario spreads over a quite broad range of invariant mass. For our prediction, the most relevant scenario is the $f_{\mathrm{VBF}}$ = 0, whose maximal significance is observed for an invariant mass of 950 GeV, but one can see that the significance starts deviating about 1-sigma from the expected value already at 600 GeV, reaches the 2-sigmas at about 700 GeV, and remains always close to 2 sigmas up to about 1100 GeV.

The other CMS analysis considered in [13] was concerning the search for new resonances decaying, through two intermediate scalars, into the peculiar final state made by a $b\overline{b}$ quark pair and a $\gamma \gamma$ pair. In particular, in [42], one has been considering the cross section for the full process

$$\sigma \left(\mathrm{full}\right)=\sigma (pp\to H\to hh\to b\overline{b}+\gamma \gamma )$$

(25)

(in the CMS paper, the new heavy resonance is called X and the 125 GeV resonance is called H while, here, we denote $X\equiv H$ and define $h=h\left(125\right)$). For a spin-zero resonance, the 95% upper limit $\sigma \left(\mathrm{full}\right)<0.16$ fb, for invariant mass of 600 GeV, was found to increase by about a factor of two, up to $\sigma \left(\mathrm{full}\right)<0.30$ fb in a plateau $650÷700$ GeV, and then to decrease for larger energies. The local statistical significance is modest, about 1.6-sigma, but the relevant mass region 675(25) GeV is precise and agrees well with our analysis of the ATLAS data. Interestingly, if the cross section is approximated as

$$\sigma \left(\mathrm{full}\right)\sim \sigma (gg\to H)·B(H\to hh)·2·B(h\to b\overline{b})B(h\to \gamma \gamma )$$

(26)

after replacing our reference value $\sigma (gg\to H)=1090\left(170\right)$ fb, $B(h\to b\overline{b})\sim$0.57 and $B(h\to \gamma \gamma )\sim$ 0.002, the CMS 95% upper bound $\sigma \left(\mathrm{full}\right)<0.30$ fb gives a rather precise upper bound $B(H\to hh)<$ 0.12. In view of the mentioned non-perturbative nature of the decay process $H\to hh$, this represents a precious indication.

Finally, as anticipated, CMS has been searching for high-mass photon pairs exclusively produced in $pp$ double-diffractive scattering, i.e., when both final protons have large $x_F$. For our scopes, the relevant information is contained in Figure 5, fourth panel (second row, right) of [43] that shows the measured diphoton invariant mass in highly double-diffractive events, without requiring the very stringent condition of exclusive production. In practice, one is analyzing the vacuum excitation decaying to all allowed final states containing 2 photons. In the range of invariant mass 650(40) GeV, and for a statistics of 102.7 fb${}^{-1}$, the observed number of $\gamma \gamma$ events was $N_{\mathrm{obs}}\sim$ 76(9) to be compared with an estimated background $N_{\mathrm{BKG}}\sim$ 40(6) that is quoted to be the best estimate by the experiment, with a relatively small uncertainty. In the most conservative case, this is a local excess of 3.3-sigma significance. Summarizing, at present, the excesses found in the previous CMS analyses point to a new resonance of mass ${\left(M_H\right)}^{\mathrm{Exp}}\sim$ 670(20) GeV.

7. Summary and Conclusions

In [10,11,12], it was argued that, beside the known resonance with mass $m_h=$ 125 GeV, the Higgs field could exhibit a second resonance with a much larger mass $M_H$. This new state, however, would couple to longitudinal Ws with the same typical strength as the low-mass state at 125 GeV and thus represent a relatively narrow resonance mainly produced at LHC by gluon–gluon fusion (ggF). From theoretical arguments and lattice simulations, its mass can be estimated to have a value ${\left(M_H\right)}^{\mathrm{Theor}}=690\pm 10\left(\mathrm{stat}\right)\pm 20\left(\mathrm{sys}\right)$ GeV.

Looking for some experimental signal, in [13], we considered various samples of LHC data. Namely, in the ATLAS search for a new resonance in the charged 4-lepton channel, we have reviewed in Section 4 the indications from the ggF-low category of events. This sample, which forms a homogeneous sample and has sufficient statistics, shows a 2.5-sigma excess around 680(30) GeV followed by a 3-sigma defect at 740(30) GeV. This feature is also confirmed by Figure 5 of [30]. As we have argued, the simplest explanation would be the existence of a new resonance with mass $M_H\sim$ 700 GeV which, besides the Breit–Wigner peak, produces the characteristic $(M_H^2-s)$ interference effect. As shown in Table 2 and in Figure 2, this interpretation is consistent with the data for the range of parameters suggested by the phenomenological picture of Section 3.

After this first indication, we have considered in Section 5 the ATLAS $\gamma \gamma$ events in the high-mass region $600÷770$ GeV. As we have shown, see Figure 3, Figure 4 and Figure 5, the sizeable 3.3-sigma (local) excess at 684 GeV in the $\gamma \gamma$ distribution can also be interpreted as the interference signal, with a dominant background, of a new heavy resonance whose mass ${\left(M_H\right)}^{\exp }\sim$ 680(15) GeV is again in the expected mass range. As for the total width, the $\gamma \gamma$ data tend to place an upper limit ${\left({\Gamma }_H\right)}^{\exp }<$ 50 GeV, consistent with the loose indication ${\left({\Gamma }_H\right)}^{\exp }=$ 29(20) GeV from the 4-lepton sample.

Since the analogous CMS full distributions for the high-mass 4-lepton and inclusive $\gamma \gamma$ events are still missing, we first considered in Section 6 previous CMS small-sized samples for these two channels. These are consistent with the existence of a new resonance in the relevant mass region and certainly do not disfavor our hypothesis, but do not add much to the present discussion due to their modest significance.

We thus considered two more recent CMS analyses which indicate a modest 1.6-sigma (local) excess at 675(25) GeV in the $b\overline{b}+\gamma \gamma$ final state and a sizeable 3.3-sigma (local) excess at 650(40) GeV in the invariant mass of $\gamma \gamma$ pairs produced in $pp$ double-diffractive scattering. Altogether, by themselves, these two CMS results point toward a new resonance with a mass of about 670(20) GeV.

In view of the good agreement with the indications extracted from the ATLAS data, it is natural to wonder about the present, overall statistical significance. To this end, one should first take into account that, when comparing with a theoretical prediction which refers to a definite mass region, as in the case of Equation (13), local excesses should maintain intact their statistical significance intact and not be downgraded by the look-elsewhere effect.

For this reason, since the correlation among the above measurements is presumably very small and all effects are concentrated in the same mass region (the 2.5-sigma excess at at 680(30) GeV followed by a 3-sigma defect at 740(30) GeV in the ATLAS 4-lepton channel, the 3.3-sigma excess at 684(8) GeV in the ATLAS $\gamma \gamma$ channel, the 1.6-sigma excess at 675(25) GeV in the CMS $b\overline{b}+\gamma \gamma$ final state and the 3.3-sigma excess at 650(40) GeV in the CMS diphoton events produced in $pp$ double-diffractive scattering), one may observe that the cumulated statistical significance is close to (or even above) the traditional 5-sigma discovery threshold. Though, announcing a discovery would be too premature for, at least, two reasons.

First, we have only taken into account the typical $\sqrt{N}$ statistical errors and neglected the systematic uncertainties which are needed to claim that something new has been discovered. In the end, with a more careful re-evaluation of the backgrounds and by increasing the statistics, the cumulated significance could be considerably weakened with respect to the present sizeable level. Second, there are other final states which, at present, show no appreciable difference from the estimated background. This represents a general warning but is not a good reason to ignore the indications we have brought to the attention of the reader. Actually, it is just the opposite because, given the present energy and luminosity of LHC, the hypothetical second resonance is too heavy to be immediately seen in all possible final states. Instead, the existence of deviations, in some channel and in a particular energy range, should give motivation to sharpen the analysis in the other sectors.

Of course, the idea that, beside the known 125 GeV Higgs resonance, there might be additional heavier scalars is not peculiar of our approach but, within the conventional description of SSB, is also found in other contexts, e.g., in supersymmetric extensions of the Standard Model where one expects two Higgs doublets and not just one. In these models, the neutral scalars are two CP-even states (the h(125) resonance and a new heavier H) and a heavier CP-odd scalar A. In principle, such heavier scalar states could also decay into a pair of Z-bosons (and then into 4 leptons) as well as in a photon-pair. For instance, in [44], the heavier CP-odd state was proposed as a plausible explanation for the sizeable excess in the 2-photon spectrum at 750 GeV, observed in 2016 by both ATLAS and CMS. Additional singlet or doublet scalars may also produce entirely new final states, such as long-lived particles, see, e.g., [45], which are quite unlike those expected in our case from the direct Higgs coupling to Standard Model particles.

Thus, in principle, there are many possible scenarios. The present attitude is that before announcing the discovery of a new Higgs resonance, one has to control so many nuisance parameters that, most likely, everything has to be postponed to the future High-Luminosity phase of LHC [46]. We are not so pessimistic because two crucial pieces of information are still missing, namely the high-mass distributions for the charged 4-lepton channel and for the inclusive $\gamma \gamma$ final state of the CMS Collaboration with full RUN2 statistics. If these long-awaited sets of data will further confirm our analysis, the existence of the new resonance could definitely be decided now, even before the end of RUN3.