Abstract
The temperature dependence of the QCD string-breaking distance is evaluated in terms of the string tension and the rate of production of light mesons in the chromo-electric field of a flux tube. As a function of the meson mass, the mentioned rate can be falling off either as a Gaussian, as suggested by the Schwinger formula, or as an exponential, which is the case in the London limit of the dual superconductor. We find an excellent agreement of the so-evaluated temperature dependence of the string-breaking distance with the respective lattice data, for the case of the meson-production rate corresponding to the London limit.
Keywords:
string breaking in QCD; static quark-antiquark potential; QCD flux tubes; pair production in the chromo-electric field; dual-superconductor scenario of quark confinement; London limit; deconfinement phase transition; finite-temperature effects in quantum field theory; confining Yang–Mills vacuum 1. Introduction
In QCD, due to the presence of dynamical quarks, string breaking is expected to occur with the increase of the distance between a heavy quark and an antiquark. At zero temperature, the static potential accounting for the phenomenon of string breaking has been measured on the lattice in and QCD, in Refs. [1] and [2], respectively. In the present note, we will perform an analytic evaluation of the QCD string-breaking distance at finite temperature. The purpose of this study is the description of a decrease of the string-breaking distance with the temperature approaching the deconfinement critical temperature , found on the lattice [3].
Let us start with the pure Yang–Mills theory and consider there an adjoint string interconnecting two static adjoint sources separated from each other by a spatial distance R. There, the string breaking occurs through the creation of a glueball, which instantaneously—through a recombination process—leads to the formation of two imaginary bound states of a gluon in the field of a static adjoint source, called one-gluon gluelumps [4]. Minimizing the difference of the actions of the initial and the final states as , we obtain . Here, M is the mass of the one-gluon gluelump, is the adjoint string tension, and is the time of observation. (Note that the same expression for follows just from the equation , in the limit of of interest. This equation stems from the comparison of exponentials in the expression for the adjoint Wilson loop [5,6], .) Now, since [4], we obtain the following critical behavior of at (where T henceforth stands for temperature, and the critical exponent is rigorously defined only in the SU(2)-case, where the so-called Svetitsky–Yaffe conjecture [7] suggests for it the 3D-Ising value [8]):
where . That is, increases at . (In full QCD, the counterparts of the one-gluon gluelump would be D-mesons, which are formed, e.g., by breaking the -string. Recent studies [9] suggest, however, that the masses of D-mesons stay almost constant at . Therefore, with a decrease of the string tension at , would be increasing in full QCD as well.) On general grounds, however, is expected to decrease at since the string at such temperatures experiences strong thermal fluctuations, which eventually – at – lead to the string breaking even without the creation of glueballs. The results of lattice measurements, presented, e.g., in Figure 8b of Ref. [3], indeed yield a decrease of at . These results are well described by a phenomenological model of the Debye screening of the string, developed in Ref. [10]. Within that model, the string breaking thus occurs at the Debye screening length, which decreases at . Nevertheless, the physical mechanism of string screening remains unclear since there are neither free gluons nor free quarks in vacuum at . Hence, it would be promising to have an alternative method of evaluation of the string-breaking distance, based on the initial pair-creation process.
Such an evaluation, provided in the next Section, will be based on the model of the quark–antiquark string as a flux tube in the dual-superconductor scenario of confinement [11,12] (for a review, see [13]). Within that scenario, the confining dynamics of the Yang–Mills vacuum is modeled by the magnetically charged dual Higgs field. The condensation of that field is described within the dual Abelian Higgs model, which represents a 4D relativistic generalization of the Landau–Ginzburg theory of dual superconductivity. Once two opposite electric charges are inserted into such a magnetically charged medium, a dual Abrikosov–Nielsen–Olesen string [14,15], representing a tube of the electric flux in case of static charges, gets formed between those charges. Such a flux tube is characterized by two typical transverse distances to its center line, which are given by the inverse masses of the dual Higgs field and the dual vector boson. As long as the transverse distance to the center line is smaller than the so-called coherence length, given by the inverse mass of the dual Higgs field, i.e., in the region inside the core of the dual string, the dual-Higgs condensate is partially destroyed by the field of the two external electric charges. At the same time, at transverse distances equal to the London penetration depth, given by the inverse mass of the dual vector boson, the electric field of the two external charges falls off exponentially. The type-II dual superconductor, which realizes stable flux tubes, corresponds to the situation where the coherence length is smaller than the London penetration depth, i.e., the dual Higgs boson is heavier than the dual vector boson.
Dedicated lattice simulations in the Yang–Mills theory [16,17,18,19] indicate that the transverse-distance dependence of the chromo-electric field in the flux tube, which is formed between an external static quark and an antiquark, is indeed very similar to the one described above. Still, the open question is whether the type-II dual-superconductor vacuum is closer to the so-called London limit, where the coherence length is much smaller than the London penetration depth, or to the so-called Bogomolny limit [20], which is the border regime between the type-II and type-I dual superconductors, where the coherence length is equal to the London penetration depth. It turns out that, due to the specific logarithmic increase of the chromo-electric field towards the center line of the flux tube in the London limit, the standard Schwinger formula, describing the pair-production rate in a constant electric field, gets changed [21]. By evaluating the temperature dependence of the string-breaking distance with the use of the standard and the modified Schwinger formulae, we will demonstrate in the next Section that the respective lattice data in QCD can be well described by the modified Schwinger formula, while the standard Schwinger formula fails to describe them. This finding indicates that, at least at temperatures relatively close to , the confining Yang–Mills vacuum resembles the London limit of the dual superconductor much stronger than the Bogomolny limit.
2. Evaluating the String-Breaking Distance and Its Temperature Dependence
Let us now see how the rate of pair production in the field of a flux tube can be used for a derivation of the static potential, , with the account for the phenomenon of string breaking in full QCD with light quarks. Such a potential can be obtained by diagonalizing the matrix, whose diagonal entries represent eigenenergies of the initial and the final states of the system, while the off-diagonal entries represent the matrix element of some phenomenological Hamiltonian, which describes the transitions between those initial and final states. That is, one has to solve the secular equation [22] corresponding to the following matrix [23]:
Henceforth, stands for the fundamental string tension, and M stands for the mass of one of the two heavy-light mesons that constitute the final state of the system. These mesons emerge by way of the hadronization process, i.e., through the recombination of light quarks, q and , which form the initially produced light meson, with the heavy quarks Q and . Furthermore, the parameter V stands for the aforementioned phenomenological matrix element. By solving the secular equation corresponding to matrix (1), one obtains the following potential:
At asymptotically large Q- separations of interest, namely, at , it goes over to
In order to express the matrix element V through the rate w of production of light mesons in the flux-tube field, we use Fermi’s golden rule [22]:
Here, m is the mass of a light meson, and the factor of 4 represents the number of spin states of two spin − quarks. In order to integrate both sides of Equation (3), we introduce the function , for which we have
so that
Thus, Equation (3) yields , which results in the following expression:
Substituting it into Equation (2), we obtain:
By using further for w, in Equation (4), an expression that one has away from the London limit of the dual superconductor,
or in the London limit [21],
we estimate the temperature dependence of the string-breaking distance at . To this end, we notice that, in the absence of string breaking, the thickness of the flux tube in the dual superconductor is . For the potential accounting for the effect of string breaking, one can introduce an effective string tension as
Accordingly, in this case can be formally defined as a quantity proportional to . Therefore, due to the R-independence of w, grows at large R’s as , which explicitly demonstrates that the string gets broken since its thickness gets parametrically larger than its length. With the decrease of R, one eventually reaches some critical distance for which becomes equal to R. Such a distance can, therefore, be identified with and defined through the relation (In macroscopic physics, an analogous situation, leading to the appearance of a certain critical distance, takes place in the problem of the gravitational instability of large bodies. In that case, the Schwarzschild radius of a body is proportional to its mass, i.e., to , for a body of a constant energy density. Accordingly, as soon as the equality is reached with the increase of R, the gravitational instability occurs.) , which yields
We will now use Equations (5) and (6) to confront this estimate for against the lattice data for . To this end, we assume that m is the pion mass, and we make use of the known critical behavior, and , as well as of the critical index corresponding to the O(4) RG fixed point [24,25], . Here, O(4) ≃ SU(2)×SU(2) corresponds to the chiral-symmetry group of QCD with two massless flavors. The respective critical exponent of the O(4)-invariant -theory in reads [26] . We note that it coincides remarkably well with the mentioned value of in the 3D Ising model, which describes the second-order phase transition at finite temperature and magnetic field, with the counterpart of the magnetic field for the second-order phase transition in QCD at and being the (approximately one and the same) mass of light u- and d-quarks. Hence, we adopt the approximate value of . On the other hand, lattice values for can be extracted from the mentioned Figure 8b of Ref. [3]. Defining as a distance at which each of the curves depicted in that figure deviates from the linear potential more than by the corresponding error bars, one gets the following naked-eye values of : 2.4 for , 2.30 for , 2.13 for , 2.0 for , and 1.7 for , where is the zero-temperature string tension. The ratio vanishes at , so that Equation (5) yields an increase, , instead of the decrease, thereby ruling out the applicability of Equation (5) at such temperatures. Rather, Equation (6) yields
Fitting the cited values of by the function , we obtain an excellent agreement with this prediction, corresponding to and , as shown in Figure 1.
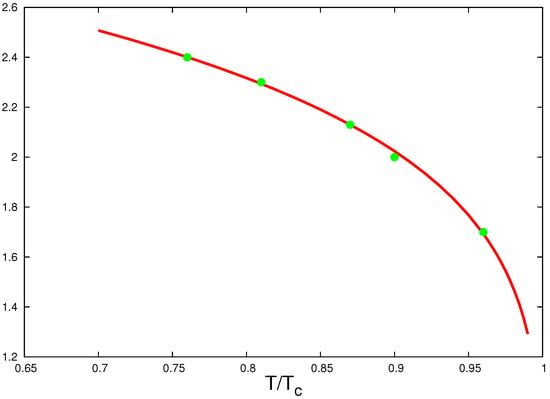
Figure 1.
Plotted are the cited values for vs. the fitting function .
3. Summary
In this note, we evaluated the QCD string-breaking distance in terms of the string tension and the rate of production of light mesons in the field of a flux tube. That rate is given by Equations (5) and (6), away from the London limit and in the London limit of the dual superconductor, respectively. The major difference between Equations (5) and (6) is that, due to the logarithmic increase of the chromo-electric field towards the center line of the flux tube in the London limit, Schwinger’s Gaussian dependence—of the production rate on the meson mass—gets changed to the exponential dependence. Additionally, the pre-exponential factor in Equation (6) differs from that in Equation (5). It turns out that, due to this difference, at temperatures close to the critical one, Equation (6) reproduces the respective lattice data for the temperature dependence of the string-breaking distance remarkably well, while Equation (5) yields the wrong prediction for that dependence. This finding indicates that, at least at temperatures deviating from the critical one by less than 25%, i.e., corresponding to , the Yang–Mills vacuum is likely to be much closer, in its confining properties, to the London limit of the dual superconductor than to the opposite, Bogomolny, limit.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Bali, S.; Neff, H.; Duessel, T.; Lippert, T.; Schilling, K.; [SESAM Collaboration]. Observation of string breaking in QCD. Phys. Rev. D 2005, 71, 114513. [Google Scholar] [CrossRef]
- Bulava, J.; Hörz, B.; Knechtli, F.; Koch, V.; Moir, G.; Morningstar, C.; Peardon, M. String breaking by light and strange quarks in QCD. Phys. Lett. B 2019, 793, 493–498. [Google Scholar] [CrossRef]
- Satz, H. Charm and beauty in a hot environment. arXiv 2006, arXiv:hep-ph/0602245. [Google Scholar]
- Antonov, D. World-line formalism: Non-perturbative applications. Universe 2016, 2, 28. [Google Scholar] [CrossRef]
- Khokhlachev, S.B.; Makeenko, Y.M. Phase transition over the gauge group center and quark confinement in QCD. Phys. Lett. B 1981, 101, 403–406. [Google Scholar] [CrossRef]
- Greensite, J.; Halpern, M.B. Suppression of color screening at large N. Phys. Rev. D 1983, 27, 2545–2547. [Google Scholar] [CrossRef]
- Svetitsky, B.; Yaffe, L.G. Critical behavior at finite-temperature confinement transitions. Nucl. Phys. B 1982, 210, 423–447. [Google Scholar] [CrossRef]
- Antonov, D. Monopole-based scenarios of confinement and deconfinement in 3D and 4D. Universe 2017, 3, 50. [Google Scholar] [CrossRef]
- Montaña, G.; Ramos, À.; Tolos, L.; Torres-Rincon, J.M. Pseudoscalar and vector open-charm mesons at finite temperature. Phys. Rev. D 2020, 102, 096020. [Google Scholar] [CrossRef]
- Digal, S.; Kaczmarek, O.; Karsch, F.; Satz, H. Heavy-quark interactions in finite-temperature QCD. Eur. Phys. J. C 2005, 43, 71–75. [Google Scholar] [CrossRef]
- Mandelstam, S. Vortices and quark confinement in non-Abelian gauge theories. Phys. Lett. B 1975, 53, 476–478. [Google Scholar] [CrossRef]
- ’t Hooft, G. Topology of the gauge condition and new confinement phases in non-Abelian gauge theories. Nucl. Phys. B 1981, 190, 455–478. [Google Scholar] [CrossRef]
- Ripka, G. Dual Superconductor Models of Color Confinement; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Abrikosov, A.A. On the magnetic properties of superconductors of the second group. J. Exp. Theor. Phys. 1957, 5, 1174–1182. [Google Scholar]
- Nielsen, H.B.; Olesen, P. Vortex-line models for dual strings. Nucl. Phys. B 1973, 61, 45–61. [Google Scholar] [CrossRef]
- Di Giacomo, A.; Maggiore, M.; Olejnik, S. Evidence for flux tubes from cooled QCD configurations. Phys. Lett. B 1990, 236, 199–202. [Google Scholar] [CrossRef]
- Di Giacomo, A.; Maggiore, M.; Olejnik, S. Confinement and chromoelectric flux tubes in lattice QCD. Nucl. Phys. B 1990, 347, 441–460. [Google Scholar] [CrossRef]
- Cea, P.; Cosmai, L.; Papa, A. Chromoelectric flux tubes and coherence length in QCD. Phys. Rev. D 2012, 86, 054501. [Google Scholar] [CrossRef]
- Cea, P.; Cosmai, L.; Cuteri, F.; Papa, A. Flux tubes in the SU(3) vacuum: London penetration depth and coherence length. Phys. Rev. D 2014, 89, 094505. [Google Scholar] [CrossRef]
- Bogomolny, E.B. The stability of classical solutions. Sov. J. Nucl. Phys. 1976, 24, 449–454. [Google Scholar]
- Antonov, D. Calculating non-perturbative quantities through the world-line formalism. J. Phys. Conf. Ser. 2019, 1208, 012005. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics: Non-Relativistic Theory, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 1981. [Google Scholar]
- Drummond, I.T.; Horgan, R.R. Lattice string breaking and heavy-meson decays. Phys. Lett. B 1999, 447, 298–307. [Google Scholar] [CrossRef]
- Pisarski, R.D.; Wilczek, F. Remarks on the chiral phase transition in chromodynamics. Phys. Rev. D 1984, 29, 338–341. [Google Scholar] [CrossRef]
- Rajagopal, K.; Wilczek, F. Static and dynamic critical phenomena at a second-order QCD phase transition. Nucl. Phys. B 1993, 399, 395–425. [Google Scholar] [CrossRef]
- Yagi, K.; Hatsuda, T.; Miake, Y. Quark-Gluon Plasma; Cambridge Univ. Press: Cambridge, UK, 2005; Chapter 6. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).