Tidal Resonance: A Factor Worth Considering in the Orbital Evolution of Heartbeat Stars
Abstract
1. Introduction
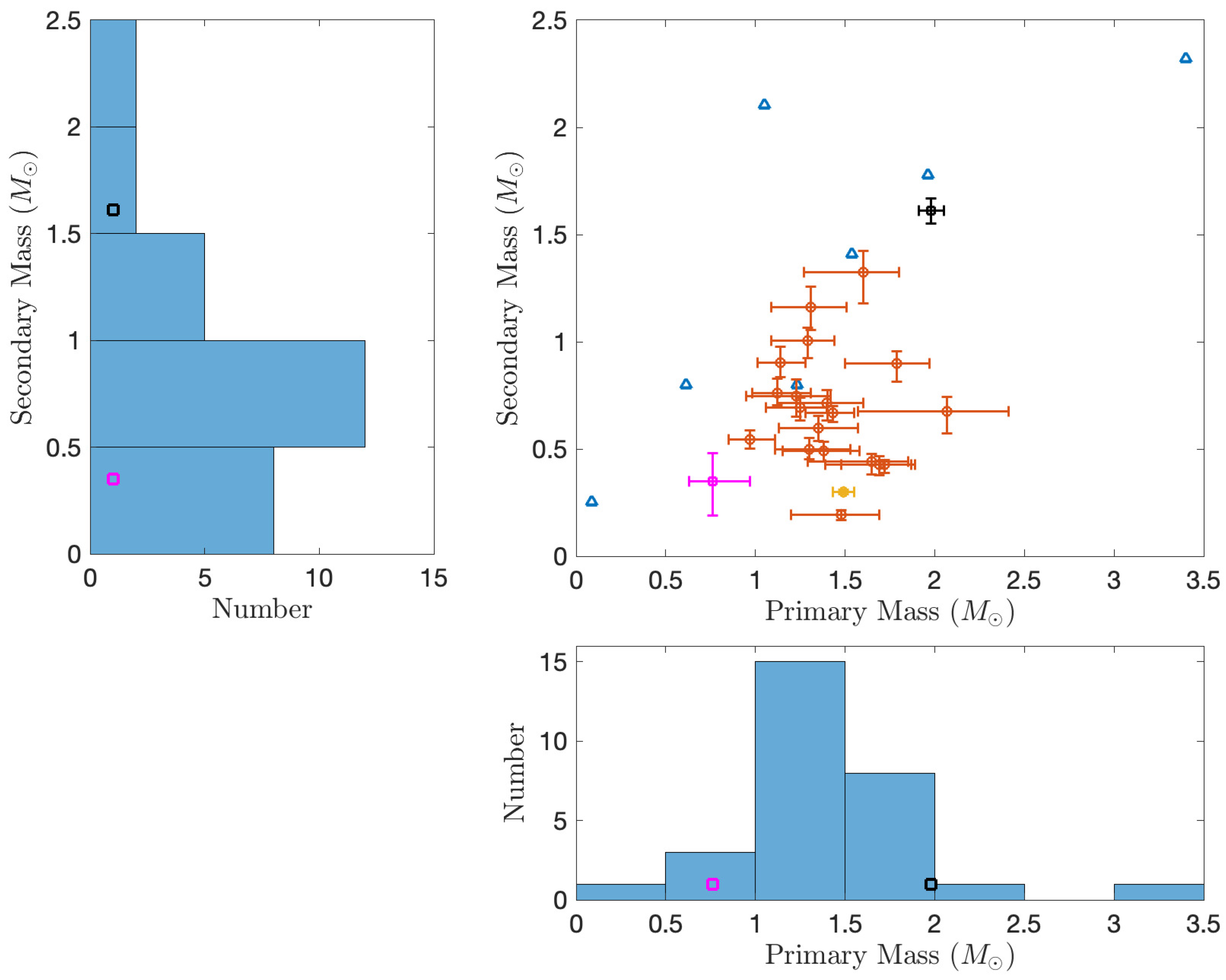
2. Samples of HB Stars
3. Kepler Data and Their Analysis
3.1. Photometric Data and Data Preprocessing
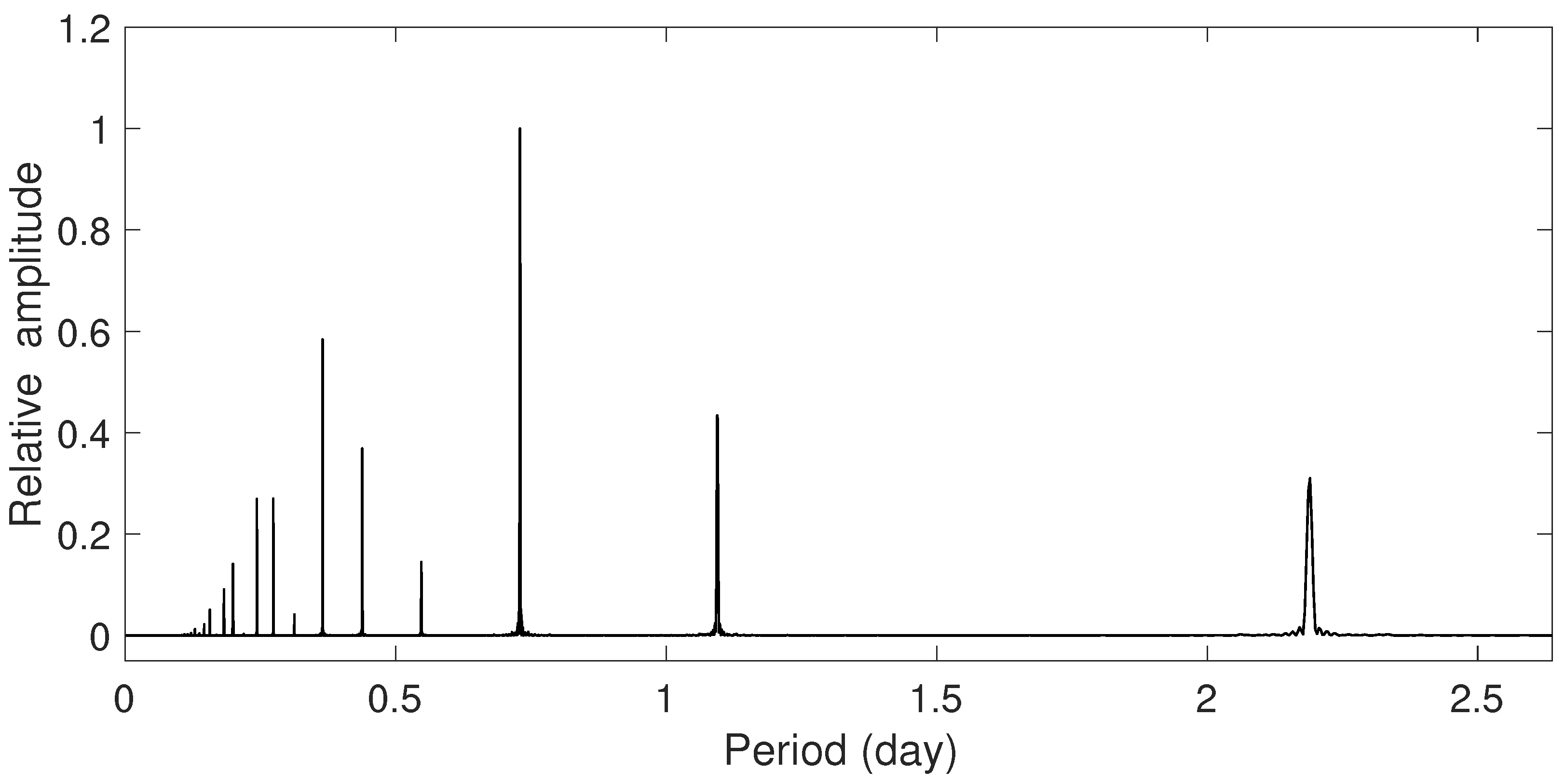
3.2. Binary Model and Frequency Extraction
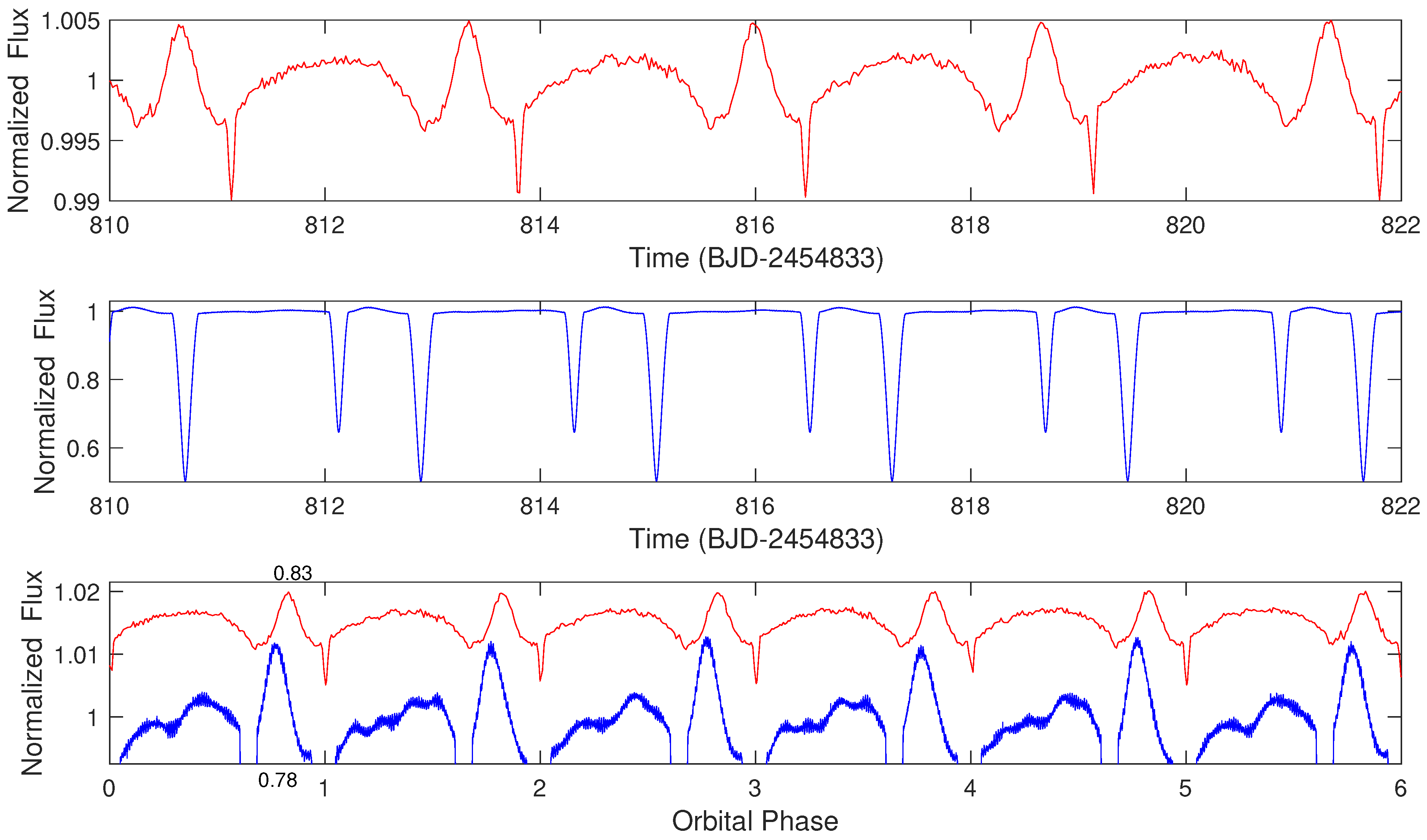
4. Observation of the Tidal Resonance State
4.1. KIC 4544587 with Pulsation–Orbital Resonance
4.2. KIC 3766353 without Pulsation–Orbital Resonance
5. Two Different Orbital Dynamics
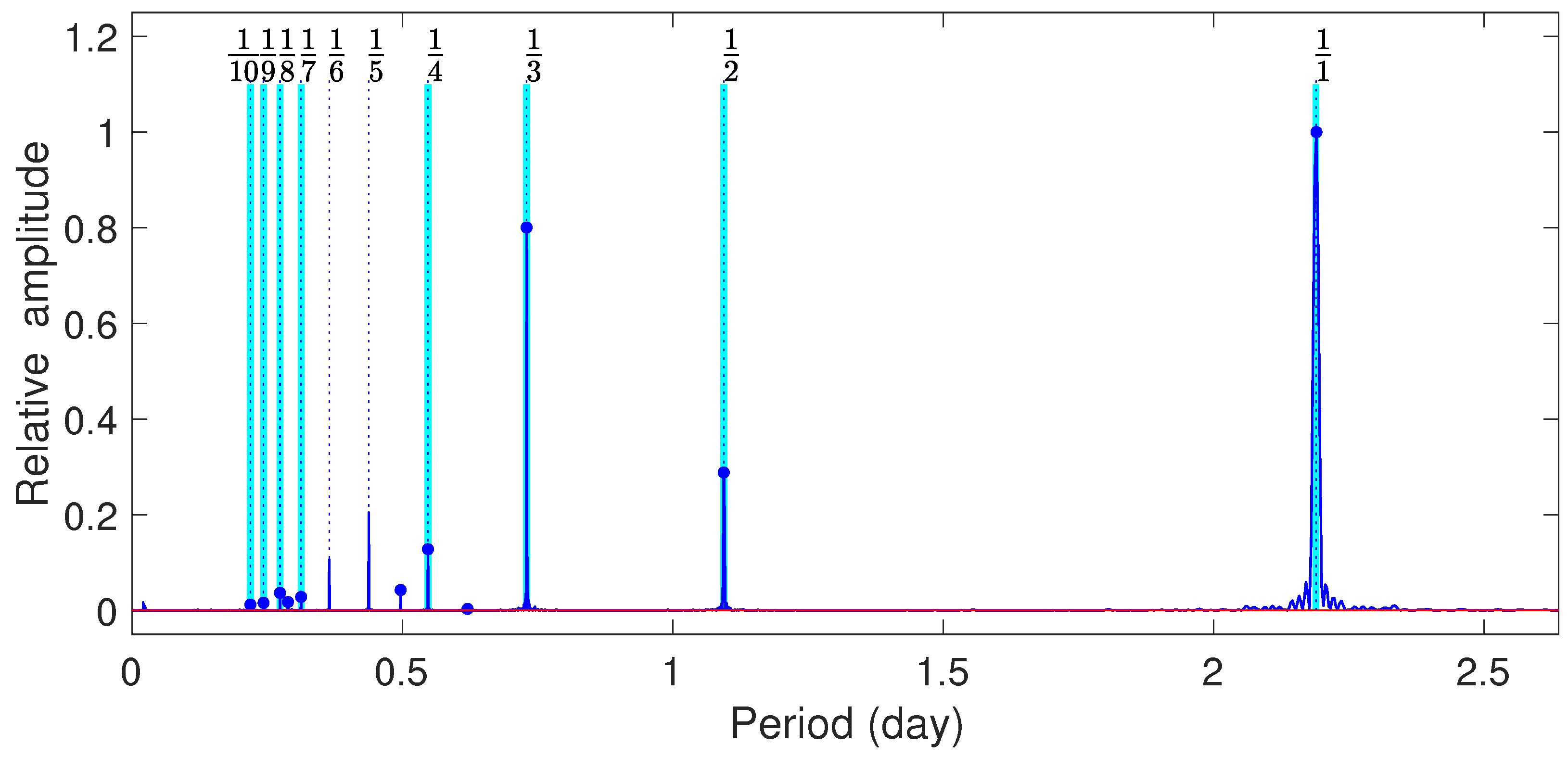
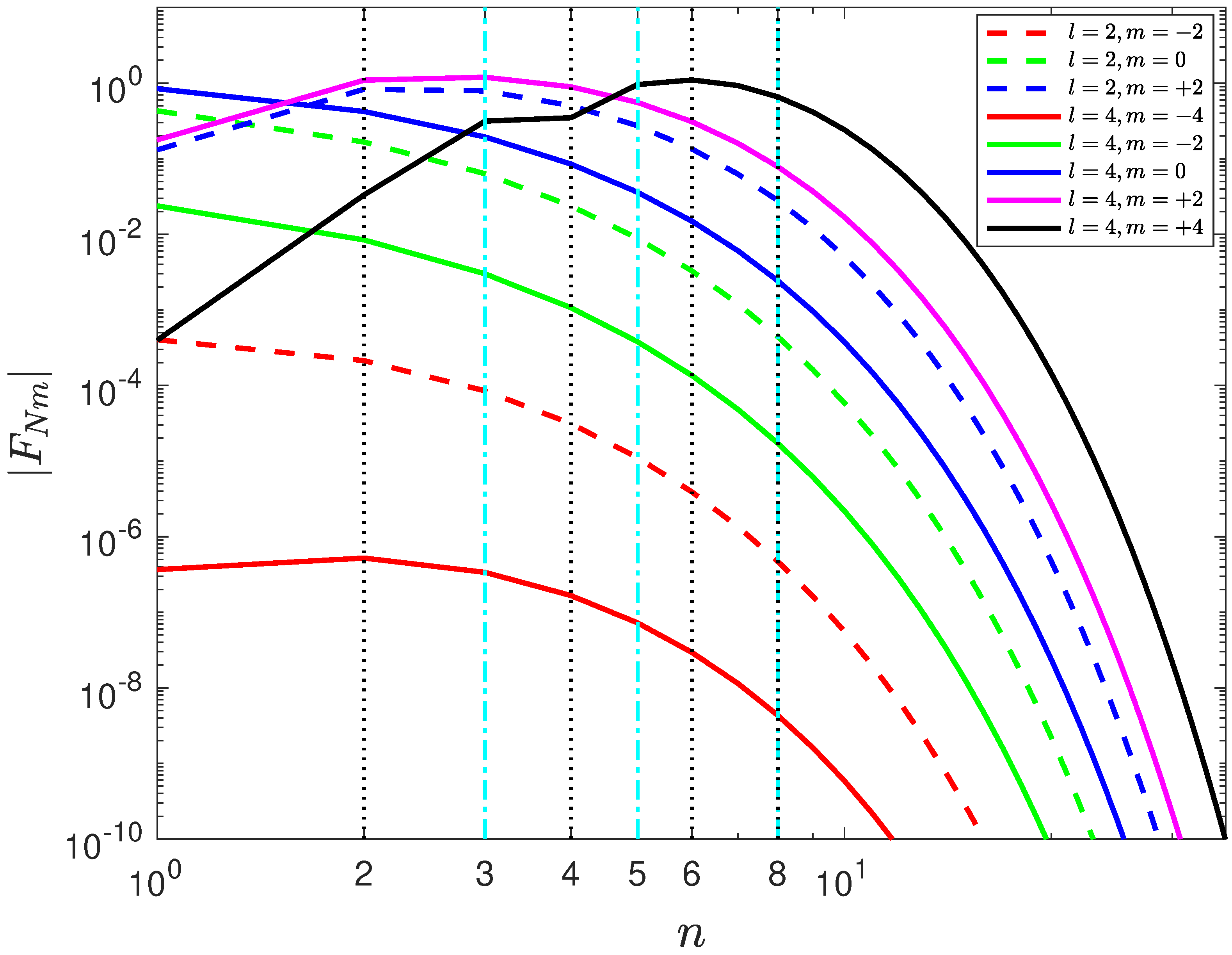
5.1. A Potential Simple Relationship between Pulsation and the Orbital Period
5.2. Resonance Criterion of KIC 4544587 and KIC 3766353
6. Evolutions from Orbital Decay to Apsidal Precession
7. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 |
References
- Thompson, S.E.; Everett, M.; Mullally, F.; Barclay, T.; Howell, S.B.; Still, M.; Rowe, J.; Christiansen, J.L.; Kurtz, D.W.; Hambleton, K.; et al. A Class of Eccentric Binaries with Dynamic Tidal Distortions Discovered with Kepler. Astrophys. J. 2012, 753, 86. [Google Scholar] [CrossRef]
- Shporer, A.; Fuller, J.; Isaacson, H.; Hambleton, K.; Thompson, S.E.; Prsa, A.; Kurtz, D.W.; Howard, A.W.; O’Leary, R.M. Radial Velocity Monitoring of Kepler Heartbeat Stars. Astrophys. J. 2016, 829, 34. [Google Scholar] [CrossRef]
- Fuller, J. Heartbeat stars, tidally excited oscillations and resonance locking. Mon. Not. R. Astron. Soc. 2017, 472, 1538. [Google Scholar] [CrossRef]
- Guo, Z. Asteroseismology of Close Binary Stars: Tides and Mass Transfer. Front. Astron. Space Sci. 2021, 8, 67. [Google Scholar] [CrossRef]
- Welsh, W.F.; Orosz, J.A.; Aerts, C.; Brown, T.M.; Brugamyer, E.; Cochran, W.D.; Gillil, R.L.; Guzik, J.A.; Kurtz, D.W.; Latham, D.W.; et al. KOI-54: The Kepler Discovery of Tidally Excited Pulsations and Brightenings in a Highly Eccentric Binary. Astrophys. J. Suppl. Ser. 2011, 197, 4. [Google Scholar] [CrossRef][Green Version]
- Burkart, J.; Quataert, E.; Arras, P.; Weinberg, N.N. Tidal asteroseismology: Kepler’s KOI-54. Mon. Not. R. Astron. Soc. 2012, 421, 983. [Google Scholar] [CrossRef]
- Fuller, J.; Lai, D. Dynamical tides in eccentric binaries and tidally excited stellar pulsations in Kepler KOI-54. Mon. Not. R. Astron. Soc. 2012, 420, 3126. [Google Scholar] [CrossRef]
- Guo, Z.; Ogilvie, G.I.; Li, G.; Townsend, R.H.D.; Sun, M. A new window to tidal asteroseismology: Non-linearly excited stellar eigenmodes and the period spacing pattern in KOI-54. Mon. Not. R. Astron. Soc. 2022, 517, 437. [Google Scholar] [CrossRef]
- Beck, P.G.; Hambleton, K.; Vos, J.; Kallinger, T.; Bloemen, S.; Tkachenko, A.; García, R.A.; Østensen, R.H.; Aerts, C.; Kurtz, D.W.; et al. Pulsating red giant stars in eccentric binary systems discovered from Kepler space-based photometry. A sample study and the analysis of KIC 5006817. Astron. Astrophys. 2014, 564, A36. [Google Scholar] [CrossRef]
- Dimitrov, D.P.; Kjurkchieva, D.P.; Iliev, I.K. Simultaneous solutions of Kepler light curves and radial velocity curves of seven heartbeat variables. Mon. Not. R. Astron. Soc. 2017, 469, 2089. [Google Scholar] [CrossRef]
- Kuszlewicz, J.S.; North, T.S.H.; Chaplin, W.J.; Bieryla, A.; Latham, D.W.; Miglio, A.; Bell, K.J.; Davies, G.R.; Hekker, S.; Campante, T.L.; et al. KOI-3890: A high-mass-ratio asteroseismic red giant+M-dwarf eclipsing binary undergoing heartbeat tidal interactions. Mon. Not. R. Astron. Soc. 2019, 487, 14. [Google Scholar] [CrossRef]
- Cheng, S.J.; Fuller, J.; Guo, Z.; Lehman, H.; Hambleton, K. Detailed Characterization of Heartbeat Stars and Their Tidally Excited Oscillations. Astrophys. J. 2020, 903, 122. [Google Scholar] [CrossRef]
- Wrona, M.; Kołaczek-Szymański, P.A.; Ratajczak, M.; Kozłowski, S. Photometric Analysis of the OGLE Heartbeat Stars. Astrophys. J. 2022, 928, 135. [Google Scholar] [CrossRef]
- Barker, A.J. Tidal Dissipation Due to Inertial Waves Can Explain the Circularization Periods of Solar-type Binaries. Astrophys. J. Lett. 2022, 927, L36. [Google Scholar] [CrossRef]
- Su, Y.; Lai, D. Dynamics of Colombo’s top: Tidal dissipation and resonance capture, with applications to oblique super-Earths, ultra-short-period planets and inspiraling hot Jupiters. Mon. Not. R. Astron. Soc. 2022, 509, 3301. [Google Scholar] [CrossRef]
- Murray, C.D.; Dermott, S.F. Solar System Dynamics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Sterne, T.E. Apsidal motion in binary stars. Mon. Not. R. Astron. Soc. 1939, 99, 451. [Google Scholar] [CrossRef]
- Claret, A. New grids of stellar models including tidal-evolution constants up to carbon burning. I. From 0.8 to 125 M⊙ at Z = 0.02. Astron. Astrophys. 2004, 424, 919. [Google Scholar] [CrossRef]
- Hut, P. Stability of tidal equilibrium. Astron. Astrophys. 1980, 92, 167. [Google Scholar]
- Hambleton, K.M.; Kurtz, D.W.; Prša, A.; Guzik, J.A.; Pavlovski, K.; Bloemen, S.; Southworth, J.; Conroy, K.; Littlefair, S.P.; Fuller, J. KIC 4544587: An eccentric, short-period binary system with δ Sct pulsations and tidally excited modes. Mon. Not. R. Astron. Soc. 2013, 434, 925. [Google Scholar] [CrossRef]
- Ou, J.W.; Yu, C.; Jiang, C.; Yang, M.; Niu, H. Searching for orbital decay in a heartbeat star system KIC 3766353. Mon. Not. R. Astron. Soc. 2021, 508, 3967. [Google Scholar] [CrossRef]
- Ou, J.W.; Yu, C.; Yang, M.; Jiang, C.; Ma, B.; Liu, G.; Liu, S.F.; Luo, J.J. The Measurement of Dynamic Tidal Contribution to Apsidal Motion in Heartbeat Star KIC 4544587. Astrophys. J. 2021, 922, 37. [Google Scholar] [CrossRef]
- Hambleton, K.; Kurtz, D.W.; Prša, A.; Quinn, S.N.; Fuller, J.; Murphy, S.J.; Thompson, S.E.; Latham, D.W.; Shporer, A. KIC 3749404: A heartbeat star with rapid apsidal advance indicative of a tertiary component. Mon. Not. R. Astron. Soc. 2016, 463, 1199. [Google Scholar] [CrossRef]
- Claret, A.; Willems, B. New results on the apsidal-motion test to stellar structure and evolution including the effects of dynamic tides. Astron. Astrophys. 2002, 388, 518. [Google Scholar] [CrossRef]
- Giménez, A. The Apsidal Motion Test in Eclipsing Binaries. Proc. Int. Astron. Union 2007, 240, 290. [Google Scholar] [CrossRef]
- Claret, A. Updating the theoretical tidal evolution constants: Apsidal motion and the moment of inertia. Astron. Astrophys. 2019, 628, A29. [Google Scholar] [CrossRef]
- Liang, Y.; Winn, J.N.; Albrecht, S.H. DI Herculis Revisited: Starspots, Gravity Darkening, and 3D Obliquities. Astrophys. J. 2022, 927, 114. [Google Scholar] [CrossRef]
- Prša, A.; Conroy, K.E.; Horvat, M.; Pablo, H.; Kochoska, A.; Bloemen, S.; Giammarco, J.; Hambleton, K.M.; Degroote, P. Physics Of Eclipsing Binaries. II. Toward the Increased Model Fidelity. Astrophys. J. Suppl. Ser. 2016, 227, 29. [Google Scholar] [CrossRef]
- Conroy, K.E.; Kochoska, A.; Hey, D.; Pablo, H.; Hambleton, K.M.; Jones, D.; Giammarco, J.; Abdul-Masih, M.; Prša, A. Physics of Eclipsing Binaries. V. General Framework for Solving the Inverse Problem. Astrophys. J. Suppl. Ser. 2020, 250, 34. [Google Scholar] [CrossRef]
- Lomb, N.R. Least-Squares Frequency Analysis of Unequally Spaced Data. Astrophys. Space Sci. 1976, 39, 447. [Google Scholar] [CrossRef]
- Scargle, J.D. Studies in astronomical time series analysis. II. Statistical aspects of spectral analysis of unevenly spaced data. Astrophys. J. 1982, 263, 835. [Google Scholar] [CrossRef]
- Yang, M.; Zhang, H.; Wang, S.; Zhou, J.L.; Zhou, X.; Wang, L.; Wang, L.; Wittenmyer, R.A.; Liu, H.G.; Meng, Z.; et al. Eclipsing Binaries From the CSTAR Project at Dome A, Antarctica. Astrophys. J. 2015, 217, 28. [Google Scholar] [CrossRef]
- Kallinger, T.; Reegen, P.; Weiss, W.W. A heuristic derivation of the uncertainty for frequency determination in time series data. Astron. Astrophys. 2008, 481, 571. [Google Scholar] [CrossRef]
- Donati, J.F.; Semel, M.; Carter, B.D.; Rees, D.E.; Cameron, A.C. Spectropolarimetric observations of active stars. Mon. Not. R. Astron. Soc. 1997, 291, 658. [Google Scholar] [CrossRef]
- Witte, M.G.; Savonije, G.J. Orbital evolution by dynamical tides in solar type stars. Application to binary stars and planetary orbits. Astron. Astrophys. 2002, 386, 222. [Google Scholar] [CrossRef]
- Lanza, A.F. Tidal excitation of auto-resonant oscillations in stars with close-by planets. Astron. Astrophys. 2022, 665, A47. [Google Scholar] [CrossRef]
- Zanazzi, J.J.; Wu, Y. Tidal Circularization of Binaries by Resonance Locking. I. The Importance of the Pre-main Sequence. Astron. J. 2021, 161, 263. [Google Scholar] [CrossRef]
- Zanazzi, J.J. A Tale of Two Circularization Periods. Astrophys. J. Lett. 2022, 929, L27. [Google Scholar] [CrossRef]
- Lurie, J.C.; Vyhmeister, K.; Hawley, S.L.; Adilia, J.; Chen, A.; Davenport, J.R.A.; Jurić, M.; Puig-Holzman, M.; Weisenburger, K.L. Tidal Synchronization and Differential Rotation of Kepler Eclipsing Binaries. Astron. J. 2017, 154, 250. [Google Scholar] [CrossRef]
- MacLeod, M.; Vick, M.; Lai, D.; Stone, J.M. Polygram Stars: Resonant Tidal Excitation of Fundamental Oscillation Modes in Asynchronous Stellar Coalescence. Astrophys. J. 2019, 877, 28. [Google Scholar] [CrossRef]
- Lai, D. Tidal dissipation in planet-hosting stars: Damping of spin-orbit misalignment and survival of hot Jupiters. Mon. Not. R. Astron. Soc. 2012, 423, 486. [Google Scholar] [CrossRef]
- Barker, A.J. On turbulence driven by axial precession and tidal evolution of the spin-orbit angle of close-in giant planets. Mon. Not. R. Astron. Soc. 2016, 460, 2339. [Google Scholar] [CrossRef]
- Damiani, C.; Mathis, S. Influence of stellar structure, evolution, and rotation on the tidal damping of exoplanetary spin-orbit angles. Astron. Astrophys. 2018, 618, A90. [Google Scholar] [CrossRef]
- Anderson, K.R.; Winn, J.N.; Penev, K. On a Possible Solution to the Tidal Realignment Problem for Hot Jupiters. Astrophys. J. 2021, 914, 56. [Google Scholar] [CrossRef]
- Fuller, J.; Lai, D. Dynamical tides in compact white dwarf binaries: Tidal synchronization and dissipation. Mon. Not. R. Astron. Soc. 2012, 421, 426. [Google Scholar] [CrossRef][Green Version]
- Lee, U. Tidal oscillations of rotating hot Jupiters. Mon. Not. R. Astron. Soc. 2020, 494, 3141. [Google Scholar] [CrossRef]
- Ma, L.; Fuller, J. Orbital Decay of Short-period Exoplanets via Tidal Resonance Locking. Astrophys. J. 2021, 918, 16. [Google Scholar] [CrossRef]
- Shapley, H. On the Nature and Cause of Cepheid Variation. Astrophys. J. 1914, 40, 448. [Google Scholar] [CrossRef]
- Christensen-Dalsgaard, J. Lecture Notes on Stellar Oscillations, 5th ed.; Aarhus Universitet Press: Aarhus, Denmark, 2003. [Google Scholar]
- de Mink, S.E.; Langer, N.; Izzard, R.G.; Sana, H.; de Koter, A. The Rotation Rates of Massive Stars: The Role of Binary Interaction through Tides, Mass Transfer, and Mergers. Astrophys. J. 2013, 764, 166. [Google Scholar] [CrossRef]
- Barker, A.J. Tidal dissipation in evolving low-mass and solar-type stars with predictions for planetary orbital decay. Mon. Not. R. Astron. Soc. 2020, 498, 2270. [Google Scholar] [CrossRef]
- Fuller, J.; Hambleton, K.; Shporer, A.; Isaacson, H.; Thompson, S. Accelerated tidal circularization via resonance locking in KIC 8164262. Mon. Not. R. Astron. Soc. 2017, 472, L25. [Google Scholar] [CrossRef]
- Guo, Z.; Fuller, J.; Shporer, A.; Li, G.; Hambleton, K.; Manuel, J.; Murphy, S.; Isaacson, H. KIC 4142768: An Evolved Gamma Doradus/Delta Scuti Hybrid Pulsating Eclipsing Binary with Tidally Excited Oscillations. Astrophys. J. 2019, 885, 46. [Google Scholar] [CrossRef]
- Yu, H.; Fuller, J.; Burdge, K.B. Tidally excited oscillations in hot white dwarfs. Mon. Not. R. Astron. Soc. 2021, 501, 1836. [Google Scholar] [CrossRef]
- Kołaczek-Szymański, P.A.; Pigulski, A.; Wrona, M.; Ratajczak, M.; Udalski, A. Tidally excited oscillations in MACHO 80.7443.1718: Changing amplitudes and frequencies, high-frequency tidally excited mode, and a decrease in the orbital period. Astron. Astrophys. 2022, 659, A47. [Google Scholar] [CrossRef]
- Marcussen, M.L.; Albrecht, S.H. The BANANA Project. VI. Close Double Stars are Well Aligned with Noticeable Exceptions; Results from an Ensemble Study Using Apsidal Motion and Rossiter-McLaughlin Measurements. Astrophys. J. 2022, 933, 227. [Google Scholar] [CrossRef]
- Jayasinghe, T.; Kochanek, C.S.; Strader, J.; Stanek, K.Z.; Vallely, P.J.; Thompson, T.A.; Hinkle, J.T.; Shappee, B.J.; Dupree, A.K.; Auchettl, K.; et al. The loudest stellar heartbeat: Characterizing the most extreme amplitude heartbeat star system. Mon. Not. R. Astron. Soc. 2021, 506, 4083. [Google Scholar] [CrossRef]
| Orbital Parameters | KIC 4544587 | KIC 3766353 | ||
|---|---|---|---|---|
| Dynamic type: | apsidal precession (mrad yr): | orbital decay (ms yr): | ||
| Orbital period (d): | ||||
| Semi-major axis (): a | ||||
| Orbital eccentricity: e | ||||
| Argument of periastron (): | ||||
| Orbital inclination (): i | ||||
| Stellar parameters | Primary | Secondary | Primary | Secondary |
| Mass () | ||||
| Radius () | ||||
| (K) | ||||
| log g (cgs) | ||||
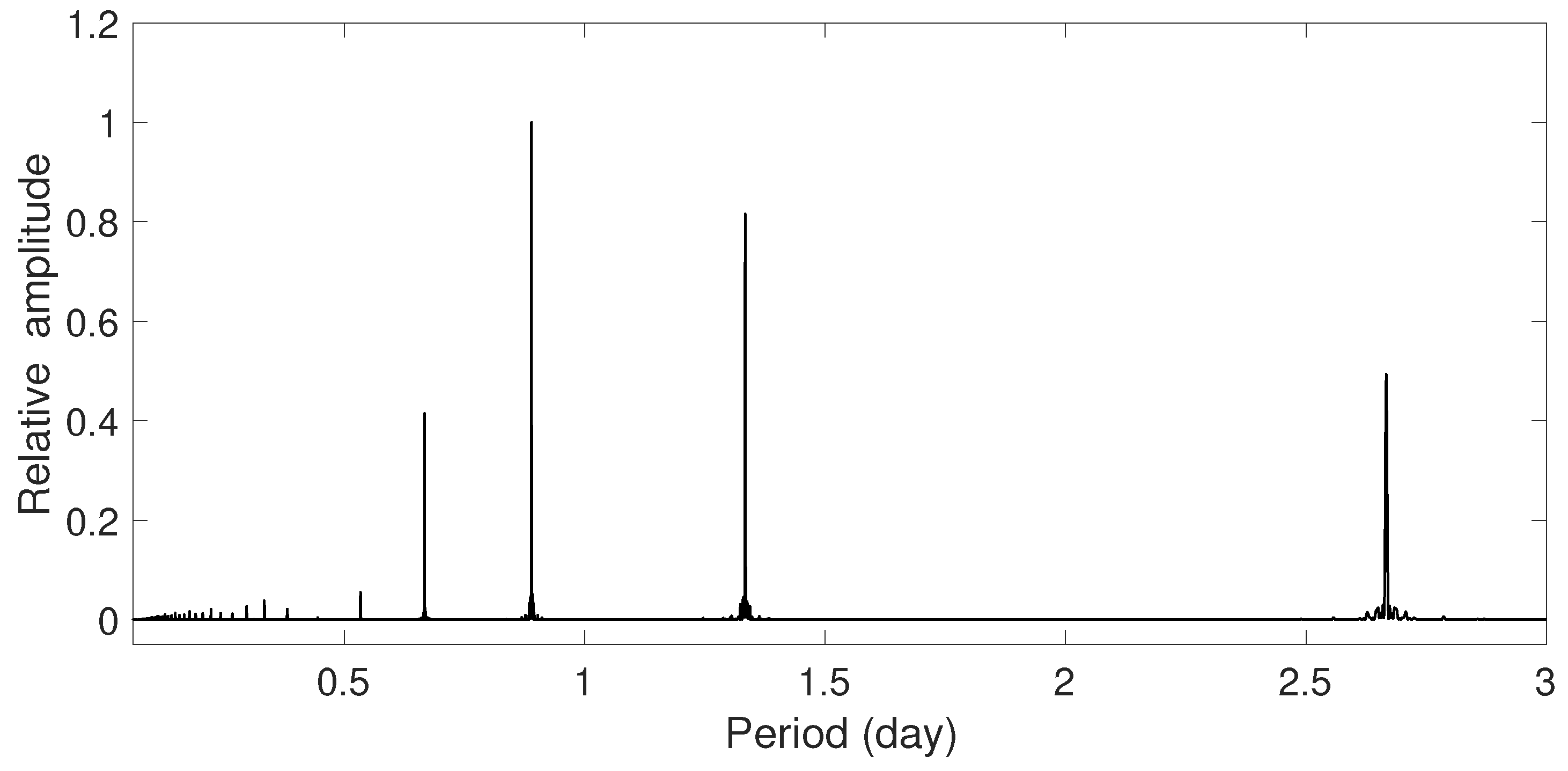
| Frequency (d−1) | Amplitude (Relative) | Comment (Porb = 2.189 d) |
|---|---|---|
| 0.45663 (1) | 1.000 (1) | |
| 0.91393 (2) | 0.288 (2) | |
| 1.37055 (1) | 0.800 (2) | |
| 1.61170 (10) | 0.003 (1) | |
| 1.82718 (2) | 0.128 (2) | |
| 2.01293 (2) | 0.043 (1) | |
| 3.19773 (3) | 0.028 (1) | |
| 3.46860 (5) | 0.017 (1) | |
| 3.65435 (3) | 0.037 (1) | |
| 4.11098 (5) | 0.016 (2) | |
| 4.56828 (6) | 0.012 (2) |
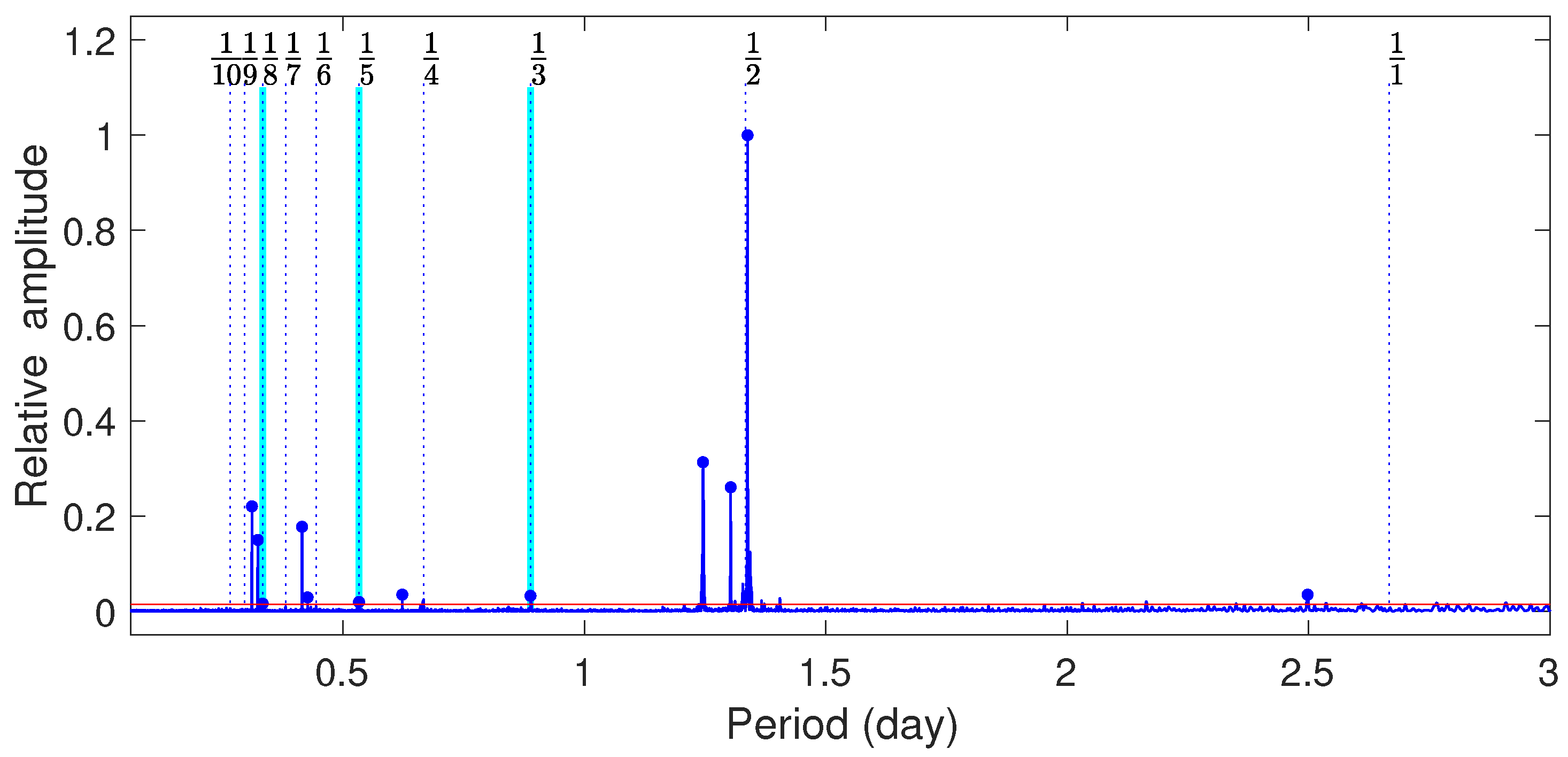
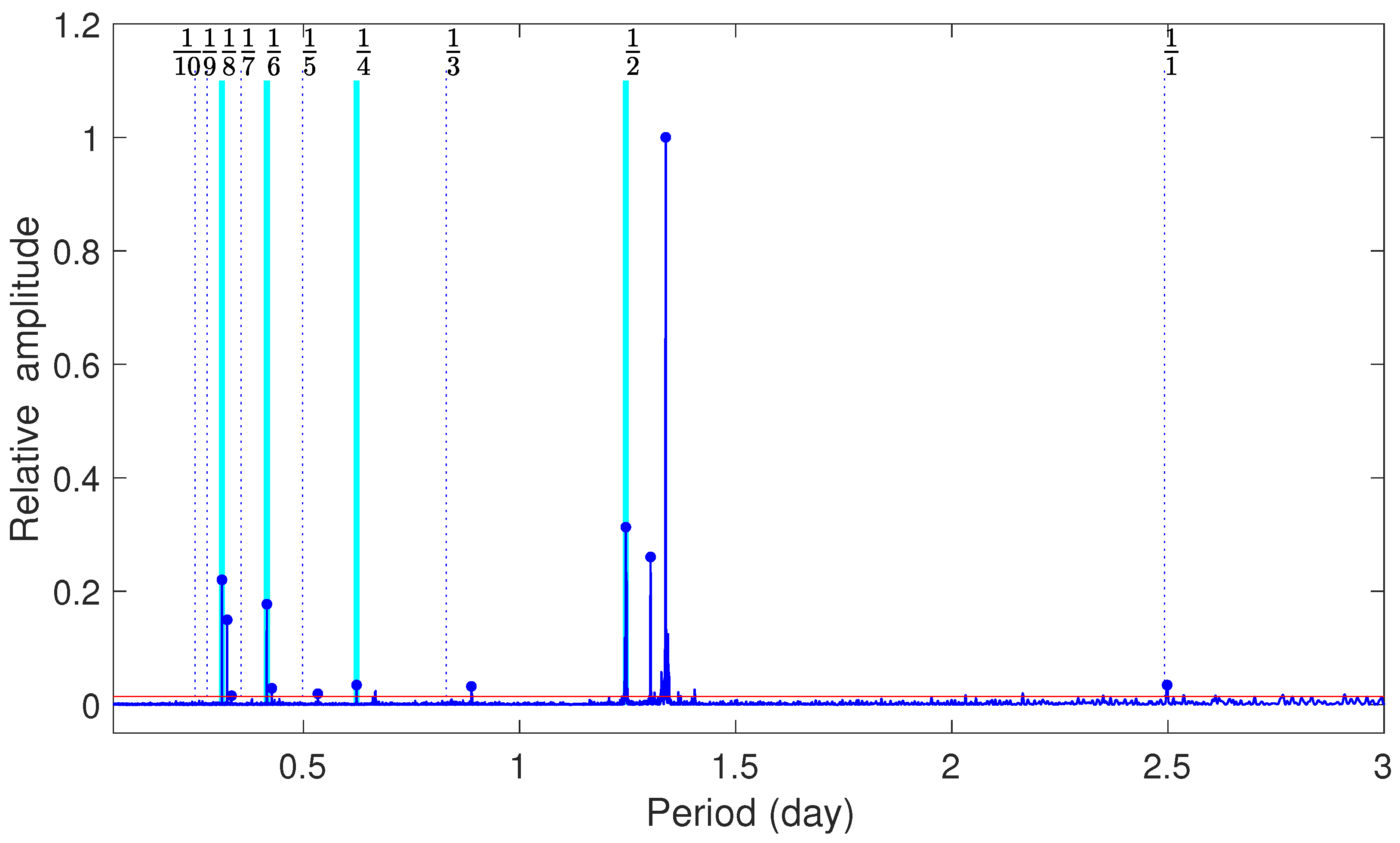
| Frequency (d−1) | Amplitude (Relative) | Comment (Porb = 2.666 d) † | Comment ( = 2.492 d) § |
|---|---|---|---|
| 0.40031 (5) | 0.035 (4) | ||
| 0.74735 (1) | 1.000 (2) | ||
| 0.76739 (1) | 0.260 (2) | ||
| 0.80268 (1) | 0.313 (2) | ||
| 1.12557 (3) | 0.032 (3) | ||
| 1.60536 (3) | 0.035 (2) | ||
| 1.87531 (5) | 0.020 (2) | ||
| 2.34329 (4) | 0.029 (2) | ||
| 2.40786 (1) | 0.177 (2) | ||
| 2.99711 (7) | 0.016 (4) | ||
| 3.09081 (1) | 0.150 (2) | ||
| 3.21054 (1) | 0.220 (2) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, J.-W.; Jiang, C.; Yang, M.; Yu, C.; Gao, D.-Y.; Long, G. Tidal Resonance: A Factor Worth Considering in the Orbital Evolution of Heartbeat Stars. Universe 2023, 9, 514. https://doi.org/10.3390/universe9120514
Ou J-W, Jiang C, Yang M, Yu C, Gao D-Y, Long G. Tidal Resonance: A Factor Worth Considering in the Orbital Evolution of Heartbeat Stars. Universe. 2023; 9(12):514. https://doi.org/10.3390/universe9120514
Chicago/Turabian StyleOu, Jian-Wen, Chen Jiang, Ming Yang, Cong Yu, Dong-Yang Gao, and Guangbo Long. 2023. "Tidal Resonance: A Factor Worth Considering in the Orbital Evolution of Heartbeat Stars" Universe 9, no. 12: 514. https://doi.org/10.3390/universe9120514
APA StyleOu, J.-W., Jiang, C., Yang, M., Yu, C., Gao, D.-Y., & Long, G. (2023). Tidal Resonance: A Factor Worth Considering in the Orbital Evolution of Heartbeat Stars. Universe, 9(12), 514. https://doi.org/10.3390/universe9120514






