Ionospheric Response on Solar Flares through Machine Learning Modeling

Abstract

Following solar flares (SF), the abrupt increase in X-radiation and EUV emission generates additional ionization and higher absorption of, e.g., electromagnetic waves in the sunlit hemisphere of the Earth’s ionosphere. The modeling of the ionosphere under solar flares are motivated by new observations with spacecrafts, satellites, and ground-based measurements. The estimation of modeling parameters for the ionospheric D-region during SF events poses a significant challenge, typically requiring a trial-and-error approach. This research presents a machine learning (ML) methodology for modeling the sharpness (β) and reflection height (H′) during SF events occurred from 2008 to 2017. The research methodology was divided into two separate approaches: an instance-based approach, which involved obtaining SF parameters during the peak SF, and a time-series approach, which involved analyzing time-series data during SFs. The findings of the study revealed that the model for the instance-based approach exhibited mean absolute percentage error (MAPE) values of 9.1% for the β parameter and 2.45% for the H′ parameter. The findings from the time-series approach indicated that the model exhibited lower error rates compared to the instance-based approach. However, it was observed that the model demonstrated an increase in β residuals as the predicted β increased, whereas the opposite trend was observed for the H′ parameter. The main goal of the research is to develop an easy-to-use method that provides ionospheric parameters utilizing ML, which can be refined with additional and novel data as well as other techniques for data pre-processing and other algorithms. The proposed method and the utilized workflow and datasets are available at GitHub.

1. Introduction

The low ionosphere, located between approx. 50 and 90 km above the Earth’s surface [1], varies in ionization with the solar flow [2] and displays the effects of solar flares (SF) [3,4,5]. Crucial for its modeling, the ionosphere parameters are directly/indirectly measured with sounding rockets, which offer a single measuring point [6] and are associated with high operational costs [7,8,9]. Consequently, the utilization of the very low frequency (VLF) approach is commonly employed [10,11]. Usually, both the VLF signal’s amplitude and phase display the impacts of SF occurrences that follow X-ray flux, in most cases often seen as increased values during such events, but with patterns highly influenced with VLF trace geometry [11,12,13,14]. The D-region of the ionosphere is defined by two parameters: sharpness (β) in km⁻¹ and reflection height (H′) in km [15], also known as Wait’s parameters or waveguide ionospheric parameters. The electron density (ED) may be computed for both undisturbed and disturbed ionospheric conditions using an equation displayed by Wait and Spies [16]. Typically, the estimation of the ionospheric parameters is performed by the utilization of the Long Wavelength Propagation Capability (LWPC) software LWPC. Computer Programs for Assessment of Long-Wavelength Radio Communications, V2.1. Available online: https://github.com/space-physics/LWPC (accessed on 2 February 2023). [17], which is a challenging task due to the complex nature of ionospheric modeling during disturbances, especially related to SF events of extreme intensity [18]. Figure 1 gives an example of one such energetic event, i.e., X17.2 SF that occurred on 28 October 2003 with peak soft X-ray Irradiance at 11:10UT, third in strength within the entire 23rd solar cycle. The response of the mid-latitude lower ionosphere over the Balkan region to this energetic SF, as recorded by BEL VLF station in Belgrade (Serbia), is given in Figure 2, together with the modeling results of the obtained electron density estimated by the use of a numerical procedure developed by Srećković et al. [19], relying on approximate equations for obtaining ionospheric parameters directly from measured X-ray data. In many cases of intense SFs, obtaining lower ionospheric response based on VLF signal technology indirectly from amplitude and phase perturbations of monitored VLF signals through classical approach using LWPC software can be problematic due to many factors, in first line including model limitations/restrictions and factors related to the geometry of Great Circle Paths of VLF signals. So, developing new approaches for retrieving necessary data for estimation of electron density profiles during such extreme events is of great importance.

Previous research has examined the estimation of ionospheric parameters by employing artificial neural networks (ANNs) and utilizing synthetic data created using the LWPC software [21]. Furthermore, Alpatov et al. [22] demonstrated that the inherent characteristics of the ionosphere necessitate the utilization of statistical and probabilistic approaches for effective ionospheric modeling. Gross and Cohen [21] developed an ANN target function that was designed to accept a single time-step of VLF amplitude and phase as the input and generate the waveguide parameters as the output. Subsequent research revealed that the model underwent expansion to encompass nighttime conditions [23]. In relation to the use of ANNs, the tuning of several hyperparameters, such as the number of epochs, learning rate, number of hidden layers, and number of nodes per hidden layer, presents challenges in the process of fine-tuning and renders them more vulnerable to overfitting. In this study, the primary focus will not be on ANNs. Instead, attention will be directed on comparatively simpler yet still-efficient ML models.

The research objectives have been divided into two distinct components. The initial step involves assessing the feasibility of deploying an ML model for the accurate prediction of β and H′ parameters. The primary objective can be categorized into two distinct methods: the instance-based approach and the time-series approach. In the instance-based approach, a specific set of features, such as X-ray irradiance, SF class, amplitude changes (ΔA), and phase shifts (ΔP), are utilized to effectively provide input to a ML regression model to determine the peak SF effect on waveguide parameters. On the other hand, the time-series approach involves training the model using a limited number of days’ worth of X-ray irradiance and statistical data derived from X-ray irradiance. Afterwards, the model is tested on subsequent days to forecast waveguide parameters, i.e., to continuously determine waveguide parameters as a time-series. The secondary aim of this study is to determine the need for utilizing oversampling techniques with a post hoc analysis of oversampling. The advantages of employing an ML technique for the estimation of ionospheric parameters are evident in the (computationally) time consuming process involved in the LWPC modeling of those parameters. Four frequently employed ML algorithms are employed, namely, Random Forest (RF), Decision Tree (DT), K-nearest neighbors (KNN), and XGBoost (XGB). The datasets used in this study, along with certain components of the workflow, are available for access on GitHub (see Supplementary Material).

As ionospheric research focuses on radio signal propagation and influences on the great diversity of space-borne and ground-based technological systems [24,25,26,27], the overall aim of this study is to provide an alternative approach allowing the wider scientific community to obtain crucial ionospheric parameters being affected by SFs, promptly and efficiently. As existing and standard methods to determine ionospheric parameters are based on a trial-and-error process, e.g., the method presented in [17], there is a need to develop other methods to determine the β and H′ like easyFit [19] and FlareED [20]. Our aim is to develop a user-friendly method that can be refined with new data, other pre-processing techniques, and algorithms, etc. In future research, if the ML method provides satisfactory accuracy and stability, we can compare the ML method with the aforementioned methods (e.g., under different SF classes, etc.).

2. Materials and Methods

The research methodology was divided into two parts. The first part involved an instance-based approach, where instances of SF peaks and their associated features (such as ΔP, ΔA, X-ray irradiance, etc.) were provided. Based on these features, waveguide parameters were to be determined using ML techniques. The second methodology employed in this study involved the utilization of a time-series approach. Specifically, a time-series dataset of X-ray irradiance was provided, and various statistical features were computed based on the X-ray irradiance values. The determination of waveguide parameters was conducted using an ML model, based on the aforementioned features.

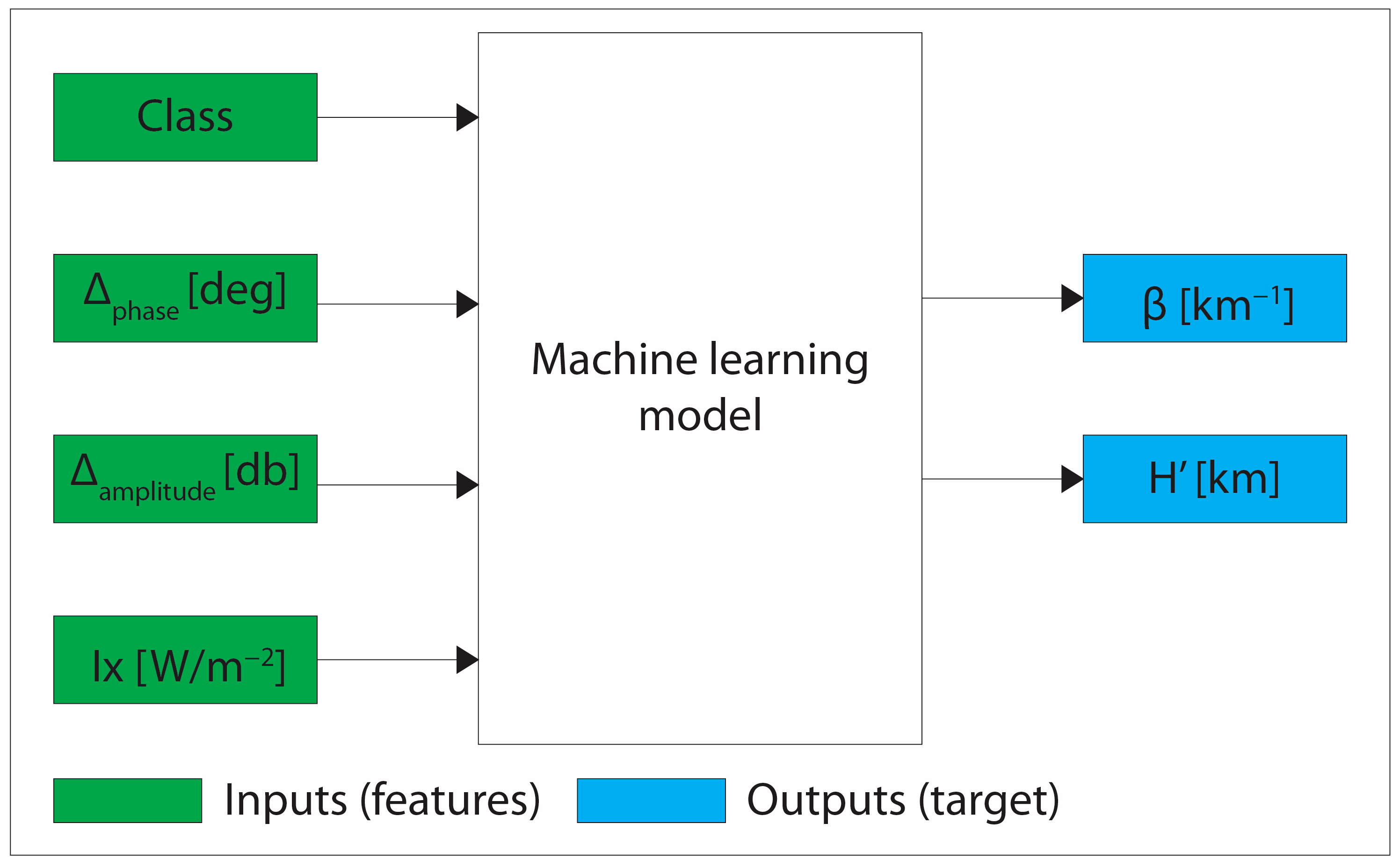
2.1. Instance-Based Approach

The data analysis initiated with the utilization of the original dataset, which contained 212 unique observations conducted throughout the course of various SF’s. The initial dataset was utilized to generate synthetic data points in subsequent stages of the workflow. However, the validation data, consisting of an extra 45 data points, was excluded from the original dataset prior to the pre-processing phase (Figure 3). The initial dataset included observations pertaining to the X-ray irradiance, the difference between the amplitude and phase of the VLF signal, and the ionospheric parameters namely. The initial data cleaning process involved randomizing the data to obtain a representative sample and transforming the X-ray irradiance to assure accurate Kernel Density Estimation (KDE) without any errors, and subsequent de-transformation was performed before the ML modeling.

The KDE serves as the initial stage in the synthetic data preparation procedure, aiming to generate a more extensive collection of samples (in this case, 5000) to facilitate the training of the ML model. The KDE method is utilized to estimate the underlying distribution of the original data. Subsequently, multiple samples are generated from this estimated distribution, therefore producing an increased number of samples. In order to verify the accuracy of the KDE’s estimation and sampling from the original data distribution, it is necessary to incorporate two more stages. This involves employing the Kolmogorov–Smirnov test (KST), a non-parametric statistical test used to assess whether two datasets follow the same distributions [28]. The interpretation of the findings of the KST involves the evaluation of the p-value. If the p-value exceeds the predetermined significance level of 0.05, it is not possible to reject the null hypothesis, i.e., the two datasets originate from the same distribution, and vice versa [29]. The second stage validating the KDE involves doing a visual and statistical examination. This entails visualizing the distributions of both the original and synthetic data for all features and target variables, as well as calculating and comparing various statistical metrics such as the mean, median, mode, skewness, and kurtosis, etc.

If the results of the preceding statistical analysis are deemed to be valid, then the initial stage in data preparation for ML involves feature extraction. Feature extraction, also known as feature discovery, is a procedure in ML that involves adding to a dataset additional feature(s). This is performed with the objective of increasing the number of features available, hence potentially enhancing the performance of the ML model. In this particular instance, the sole addition made was the inclusion of the SF class, wherein solely the alphabetical component of the SF class (B, C, M, or X) was retained and afterwards converted into a numerical representation (e.g., 1, 2, 3, or 4).

The synthetic data for training and the original data for testing were used as inputs to the ML modeling process. Four distinct algorithms were employed in this study, namely, Random Forest (RF) [30], Decision Tree (DT) [31], K-nearest neighbors (KNN) [32,33], and XGBoost (XGB) [34]. With the exception of the DT algorithm, each of the algorithms applied in this study required the tuning of at least one hyperparameter (RF and KNN) or two hyperparameters (XGB). The hyperparameter that determines the performance of the RF model is the number of trees. Additionally, the number of trees is also a hyperparameter for the XGB algorithm. On the other hand, for the KNN algorithm, the hyperparameter is the value of K, i.e., the number of nearest neighbors. The XGB method has an extra hyperparameter known as the learning rate (LR). The hyperparameter values used for the algorithms employed are presented in Figure 3.

The outputs generated by all models were employed in order to choose the most optimal model, as determined by the mean and maximum percentage errors computed on the testing dataset. Following the selection of the optimal model based on the in-distribution training and testing, model validation was performed using the validation data, and, subsequently, an error analysis was carried out.

One noteworthy aspect of this study is the inclusion of an extra target variable. Unlike conventional regression or classification models that include n features and a single target variable, this research incorporates two output variables, namely, ionospheric parameters (β and H′), as seen in Figure 4. The utilized methods incorporate SF class, ΔP, ΔA, and X-ray irradiance as their respective features, whereas the output parameters are waveguide parameters.

The evaluation metrics employed in this study to distinguish between models, specifically to determine which model performs better, are the mean absolute percentage error (MAPE) and the maximum absolute percentage error observed over all occurrences of the testing or validation datasets. Furthermore, the model’s outputs may be further analyzed by displaying absolute errors, visual representations of predicted and true observations, etc.

2.2. Time-Series Approach

The time-series based approach necessitated minimal data pre-processing, specifically in terms of data cleaning and feature extraction, with the utilization of statistical features. The time-series based approach employed a methodology that closely resembled the instance-based approach. In this approach, the modeling process utilized the best model and (hyper)parameters determined from the instance-based approach. The dissemination of results exhibited similarities to the instance-based approach.

3. Results and Discussion

3.1. Instance-Based Approach

3.1.1. Data Pre-Processing

The original dataset comprises 212 data points representing SF events from 2008 to 2017. Each data point includes the recorded time of measurement, transmitter information, X-ray irradiance, ΔA and ΔP, ionospheric parameters, and the corresponding computed electron density. The validation dataset, initially removed from the original dataset and subsequently excluded from any subsequent analysis, was exclusively employed for model validation. It comprises 45 data points collected between 2004 and 2017, with a notable concentration of data points occurring during the periods of 2004–2006 and 2014–2017.

The comparison of SF intensities between the initial dataset used for ML model testing and the validation dataset reveals the distribution of each class of SF as a percentage. In the initial dataset, a small proportion of SFs belong to the X-class, specifically accounting for 1.89% (four occurrences). Conversely, in the validation dataset, this number significantly increases to 20% (nine instances). Similar observations can be made about the M-class SFs in the datasets. Approximately 18% (38 occurrences) of the original dataset consist of M-class SFs, but the validation dataset exhibits an almost doubled percentage of 35.56% (16 instances). The proportion of C-class SFs is larger in the original dataset (79%, 169 instances) compared to the validation dataset (42%, 19 instances). Ultimately, the B-class SFs in both datasets exhibit a similar level of outcomes, with a prevalence of 0.47% in the original dataset and 2.22% in the validation dataset. It is worth noting that both datasets contain only a single occurrence of B-class SFs.

The allocation of classes within the original dataset, specifically the testing and validation subsets, was conducted in a deliberate manner to ensure that the model undergoes initial testing with a distribution that is known and expected to yield higher performance. This approach allows for the selection of the most optimal model based on the original testing dataset. The aforementioned best model will then undergo further testing, using an unfamiliar distribution, i.e., the validation dataset. As a result, the evaluation metrics obtained from the validation dataset will accurately reflect the model’s predictive performance.

The output of the KDE is a synthetic dataset that is drawn from the identical distribution as the original dataset, however, with an increased number of data points, namely, 5000 in this instance. The verification of the KDE was conducted using the KST. The results of the KST test demonstrated that the original dataset and the synthetic dataset exhibited similar distributions for all five parameters, namely, X-ray irradiance, ΔA, ΔP, β, and H′. Further examination was conducted by visually inspecting and comparing the two distributions (Figure 5).

Based on the analysis of Figure 5, it is apparent that all synthetic distributions exhibit a high degree of resemblance to the original distributions. The X-ray irradiance distribution in the original dataset had a pronounced skewness, with a tail extending towards positive values. As a result, the synthetic data also display a similar characteristic, with a severely skewed distribution towards positive values. This can also be expressed by using the skewness and kurtosis parameters. In the case of the original data, these parameters assume values of 6.178 and 42.932, respectively. Conversely, for the synthetic data distribution, the corresponding values are 6.22 and 42.622. These values, along with the KST, the visualization of the distribution, further confirm the efficacy of the KDE and the validity of the generated samples. A parallel analysis may be conducted on the target variables, such as the β parameter. In the original distribution, the mean value is 0.401, which is consistent with the value seen in the synthetic distribution. The median values for the original and synthetic distributions exhibit a little disparity, namely, 0.383 and 0.386, respectively. The H′ parameter exhibits comparable mean and median values between the original and synthetic distributions, which highlights that the synthetic data have been generated correctly.

Following the successful application of data oversampling techniques, the training dataset, i.e., the oversampled dataset, was prepared. Additionally, the testing dataset, which consists of the original, non-oversampled, measured data, and the validation dataset, comprising out-of-sample, measured data that was not utilized in the data pre-processing phase, were also finalized. These datasets were then employed for the purpose of ML modeling.

3.1.2. Initial Phase of Machine Learning Modeling

The first iteration of ML modeling involved the utilization of four distinct algorithms (RF, DT, KNN, and XGB). In all, a set of 16 models were created and evaluated. The evaluation metrics (MAPE) for both target variables is presented in Figure 6, with the upper panel representing the β parameter, and the lower panel representing the H′ parameter. Based on Figure 6, it is apparent that the algorithms DT and KNN, throughout all iterations, may be disregarded since they exhibit greater MAPE values compared to RF and XGB. On the other hand, both RF models and XGB models exhibit relatively comparable MAPE values. The RF models have constant MAPE values for both target variables. Consequently, additional analysis may be conducted to identify the most optimal RF model for exclusion. The model with 250 trees was selected as the optimal RF model across all iterations, based on the maximal percentage error observed for both target variables (11.5% for β and 1.1% for H′). In the initial round of modeling, the XGB model with 150 trees was identified as the most optimal choice. This particular model exhibited MAPE values of about 0.8 and 0.029% for the respective target variables. It is important to emphasize that the MAPE values should be interpreted cautiously due to the fact that the model was evaluated using the original dataset (in-sample model evaluation). When applying the model to new data (out-of-sample validation data), it is likely that the MAPE values will be higher. However, the purpose of this modeling is to identify the best overall model.

The XGB method was employed for the second stage of modeling because of the inclusion of an extra hyperparameter, specifically the LR. The XGB additional modeling was conducted using a predetermined number of trees (150) and a varying LR value ranging from 0.1 to 0.5, with increments of 0.1. A comparison was conducted between the optimal XGB model obtained in the initial phase of modeling, characterized by a learning rate of 0.3, and the model derived from the additional phase of XGB modeling, featuring a learning rate of 0.2. The MAPE values indicate that both models exhibit comparable error rates. Specifically, the LR = 0.3 model has MAPE values of 0.8 and 0.029 for β and H′, whereas the LR = 0.2 model shows MAPE values of 0.71 and 0.033 for β and H′, respectively. In contrast, there is a disparity in the maximal percentage error values between the LR = 0.3 model, which exhibits a maximal percentage value of 4.6% for the β parameter, and the LR = 0.2 model, which demonstrates a maximal percentage value of 3.29% for the same parameter. The XGB model with 150 trees and a LR value of 0.2 was selected as the optimal model, both within the XGB models and in comparison to the other models. A comparison was conducted between the optimal XGB model and the optimal RF model, revealing disparities in both the MAPE and the maximal percentage error. Specifically, the RF model exhibited maximal percentage errors of 11% for the β value, whereas the XGB model demonstrated values of 3%. This distinction was crucial in finding the most optimal model overall.

3.1.3. Model Validation

The process of model validation involved the utilization of an out-of-sample dataset that was initially omitted from the original dataset at the beginning of the analysis. MAPE values for both β and H′ exhibit greater values compared to the training dataset, as anticipated, with values of 9.1% and 2.45%, respectively. The maximum percentage error values for both parameters are around 38.8% and 12.2%, respectively. Figure 7 presents the error distribution for the parameters, denoted as Figure 7a,b, as well as the error distribution for the averaged error (Figure 7c), which is calculated as the average of both percentage errors.

It is worth mentioning that the distributions for β and H′ exhibit a pronounced skew towards higher values, indicating that a majority of the values correspond to lower error rates. Approximately 66% of the data points pertaining to the β parameter exhibit a percentage error below 10%, whereas approximately 55% of the data points exhibit a percentage error below 5%. In contrast, it can be observed that around 97% of the data points exhibit an error rate of less than 10% for the H′ parameter, whereas 82% of the data points have error rates below 5%. This suggests that the MAPE is significantly impacted by a small number of high percentage errors. This observation is supported by the fact that there are nine occurrences where the percentage error values for β exceed 20%, and three cases where they exceed 30%. In contrast, the H′ parameter exhibits a single outlier, namely, the outlier characterized by a percentage inaccuracy of over 12%. This indicates that the model can produce relatively satisfactory β and H′ values, with the exception of a few significantly exaggerated errors, especially in the β parameter case. It is important to acknowledge the absolute range of errors generated by this method (MAE). The MAE for the β value is around 0.039 km⁻¹, whereas, for the H′ value, the MAE is around 1.64 km.

Further model validation may be conducted by visually analyzing the predicted and real data for both parameters, as seen in Figure 8. Linear fit line was used to construct a line of best fit across the predicted and observed data. The coefficient of determination (CD) for the β parameter was about 0.67, whereas, for the H′ parameter, the fit was greater at 0.8. The CD had values that were reasonably satisfactory. Significant outlier data points are evident in both cases. For instance, a notable outlier for the β parameter is observed (upper panel on Figure 8, green rectangle), where the predicted value was about 0.38 km⁻¹, whereas the real value was approximately 0.53 km⁻¹, resulting in an error rate of almost 28%. The observed data point can be associated with a C4.8 SF event, characterized by a very modest ΔA of around 0.06 dB, whereas the ΔP measured around 26 degrees. In the given case, the H′ parameter exhibited a minimal percentage error of 0.82%, with a true value of 70 km and a predicted value of 70.6 km. Another noteworthy example is observed in the lower section of Figure 8 (green rectangle), where a C9.6 SF yielded a ΔA measurement of 5.13 dB and a ΔP measurement of 50.04 degrees. The predicted value was 61.4 km, whereas the actual value was 70 km. In a prior case, there was an incorrect prediction of the β parameter, but the H′ parameter was predicted with a significantly low error rate. In the current circumstance, we observe a similar scenario where the β parameter was predicted with a minimal error rate of 1.2% (0.57 km⁻¹ reality against 0.563 km⁻¹ predicted).

The inclusion of a residuals plot in conjunction with the predicted β and H′ values provide valuable insights into the predictive performance of the model (Figure 9). Specifically, the upper panel of Figure 9 which represents the residuals plot of the β parameter, does not exhibit any noticeable pattern, as well as the residual distribution is a normal distribution. Most of the residuals are concentrated within the range of −0.05 to 0.05 km⁻¹, with the largest outlier being the previously mentioned discrepancy of 0.14 km⁻¹, which is associated with a C4.8 SF. In contrast, the residuals plot for the H′ parameter exhibits a discernible pattern that aligns with a decrease in residuals as the predicted H′ parameter increases. The lower panel of Figure 9 reveals that the predicted value of 62 km and beyond exhibit residuals within the range of −2 to 2 km. However, before these values, the residuals are greater, ranging from −4 to 6 km. This suggests that the model’s predictions of the H′ parameter over 62 km (with the exception of two cases) are associated with reduced error rates compared to its predictions of H′ values below 62 km. This observation is further substantiated by examining the average percentage error rates for predictions made below 62 km and those made beyond 62 km. The MAPE for predictions above 62 km is around 1.23%, but predictions below 62 km exhibit a greater MAPE value at 5.15%.

The XGB model exhibited a minor bias in its predictions of H′ parameters above a certain threshold value of 62 km. It is important to acknowledge, for future studies employing a similar methodology, that there exists a possible association between the SF class and the predicted H′ parameter. Specifically, among all the predictions in the validation dataset that are below 62 km, 8 out of 9 X-class solar flares are shown to have predictive values of H′ below 62 km. The observation can be understood as the model exhibiting elevated error rates when predicting ionospheric parameters on X-class SFs. This observation is supported by the fact that the validation dataset contains a significantly higher proportion of X-class SFs (20%) compared to the testing dataset (1.89%). The primary objective of the validation dataset was to serve as an out-of-sample test for the model, in which the original distribution of the SF classes is not present. In this regard, the validation dataset proved to be effective in achieving its intended purpose. The possible bias shown in this research might be mitigated by increasing the number of original samples and refraining from employing an oversampling approach.

A potential alternative approach, while hardly employed, is the balanced distribution of SF class features, ensuring an equal representation of X-, M-, and C-class SFs. The utilization of class balancing approaches in ML regression is not commonly employed, as these techniques are often utilized in ML classification tasks and are applied to the target variable. However, it may be worthwhile to investigate this approach further in future research, as the outcomes have the potential to alleviate potential model bias.

3.1.4. Post Hoc Analysis of the Sample Size

In ML tasks, the determination of the optimal number of samples is a challenging problem that often requires the researcher to engage in iterative experimentation. When granted permission, the collection of additional samples becomes advantageous until a specific threshold is reached, beyond which enlarging the sample size does not result in a reduction in the associated model error rate. In this study, we choose to augment the original dataset by oversampling through the utilization of KDE. This approach allows us to preserve the original data distribution while simultaneously expanding the sample size. The efficacy of the KDE approach was confirmed, and the oversampling technique yielded positive results. However, it would be advantageous for future research to conduct a concise assessment of the necessity for oversampling.

The test was conducted using both the original dataset and a synthetic dataset that shared the same distribution as the original. The datasets located between the original dataset and the synthetic dataset were acquired using the Random Undersampling (RUS) technique [35]. Afterwards, the KST was conducted to assess if these datasets exhibited the same distribution as the original dataset. The intermediate datasets were generated to represent various proportions of the synthetic dataset (e.g., 10%, 20%, etc.). The XGB method was employed for the modeling process, employing 150 trees and a LR value of 0.2. This LR value and the number of trees was previously established to be the optimal choice for the modeling process. The findings of the post hoc examination of the sample size are presented in

Table 1. Post hoc analysis results for the sample size; MAPE—Mean absolute percentage error; PE—Percentage error; KST—Kolmogorov–Smirnov test; RUS—Random undersampling; T—True (passed the KST); NA—Not applicable.

Percentage of Synthetic Data	β (km−1)		H′ (km)		Note	KST
	MAPE (%)	Max PE (%)	MAPE (%)	Max PE (%)
4.24	8.46	39.58	2.28	9.70	Original dataset	NA
10	9.24	36.45	2.36	11.38	RUS	T
20	9.61	38.57	2.45	11.52	RUS	T
30	9.94	46.13	2.52	12.17	RUS	T
40	10.39	49.20	2.44	12.31	RUS	T
50	9.13	35.78	2.48	11.91	RUS	T
60	10.07	49.05	2.54	12.01	RUS	T
70	9.28	40.48	2.31	11.82	RUS	T
80	9.04	47.01	2.64	12.61	RUS	T
90	9.47	43.95	2.35	11.08	RUS	T
100	9.08	38.83	2.46	12.25	Full synthetic data	T
Minimum	8.46	35.78	2.28	9.70
Maximum	10.39	49.20	2.64	12.61
Range	1.94	13.42	0.36	2.91

.

The post hoc examination of the sample size reveals that all intermediate samples, which constitute a portion of the synthetic sample, successfully passed the KST, thus they maintained the same distribution as the original and synthetic datasets. Both the β and H′ exhibit a MAPE range that is less than 2%, namely, 1.94% for β and 0.36% for H′. This suggests that expanding the sample size with the KDE did not result in any improvements for the model in terms of reducing the error rate. However, it is important to note that the highest percentage error for the β parameter does not exhibit the same trend, as it spans a range of 13.42%. Furthermore, the correlation analysis revealed that there was no significant association seen between the rise in the dataset and the decrease in the evaluation metric for both parameters. The observed maximum correlation coefficient was 0.49, indicating the relationship between the percentage of synthetic data and the maximal percentage error of the H′ parameter. However, this correlation coefficient does not reach a significant level, i.e., suggesting a lack of strong correlation intensity. Therefore, it may be inferred that the augmentation of the sample size, while preserving the initial distribution, did not confer any notable benefits for the ML model.

The examination of sample size in a post hoc analysis is a crucial aspect for future research, particularly when considering the utilization of oversampling techniques on smaller datasets, such as this one. This specific example demonstrates that even with a sample size of 212 data points from the original dataset, it is possible to attain error rates comparable to those observed with synthetic, oversampled data.

3.2. Time-Series Approach

3.2.1. Data Pre-Processing

The training data consisted of observations from 6 September 2017 to 9 September 2017, whereas the model testing was conducted using data from 10 September measured on a 1 min interval. The utilization of statistical attributes as features for modeling time-series ionospheric VLF data have been demonstrated in the study conducted by Arnaut et al. [36]. Similar statistical features were developed for the present research. Specifically, the characteristics encompassed rolling mean, median, and standard deviation statistics for different window sizes (5, 20, and 60 min). Additionally, it includes the first and second differential of the data and the percentage change between adjacent data points as well as lagged values in 1–5 min intervals. The identical model, specifically XGBoost with 150 trees and a LR of 0.2, was employed in a manner consistent with the instance-based approach.

3.2.2. Machine Learning Modeling for the Time-Series Approach

Figure 10 illustrates the training and testing datasets. Specifically, the training dataset showcases a prominent SF of X9.4 class that transpired on 6 September 2017. The training dataset contains a variety of smaller SF, which contributes to its suitability for training the model. In contrast, the testing dataset also exhibits a prominent SF of X8.2 class, which transpired on 10 September 2017. The objective of time-series-based modeling for β and H′ can be described as the determination of waveguide parameters during an extreme SF event, given the availability of a training dataset containing waveguide parameters for training the model. Further support for the utilization of such modeling can be derived from the observed correlation between X-ray irradiance data and both β and H′. Specifically, by employing the Spearman correlation coefficient, the correlations between X-ray irradiance and both β and H′ are found to be 0.804 and −0.876, respectively. The observed values of the correlation coefficient indicate a significant association between the waveguide parameters and X-ray irradiance, thereby suggesting their appropriateness for utilization in ML modeling.

The outcomes of the modeling demonstrated significantly better results compared to those achieved through the instance-based approach. The MAPE value for the β parameter was 0.1%. Additionally, the maximum percentage error observed was 2.1%, corresponding to a maximum absolute error of 0.01 km⁻¹. In contrast, the findings pertaining to the H′ parameter reveal a MAPE of 0.04% and a maximum percentage error of 1.2%. The aforementioned values exhibit a correlation with MAE values of 0.02 km and 0.74 km, respectively. Additional analysis was conducted in the time-series based approach, similar to the instance-based approach, to validate the predicted values against the actual values (Figure 11). The evaluation metrics were validated by comparing the predicted and actual values, with both variables yielding an R² score close to 1 (i.e., 100%), which signified a highly accurate regression model. In a similar vein, the linear regression analysis conducted on the data substantiated the alignment with the 45-degree line, thereby providing additional evidence of a highly accurate correspondence between the predicted and observed waveguide parameters.

Akin to the previous example involving the instance-based approach, an analysis of residuals was conducted for the time-series approach, as depicted in Figure 12. In contrast to the previous instance of residual analysis, the residuals observed in the time-series approach exhibited pronounced patterns. Specifically, in the upper panel of Figure 12, it is evident that the residuals increases as the predicted β also increase. Additionally, there is a negative relationship between the predicted H′ and the corresponding residuals, indicating that as the predicted H′ increases, the residuals decrease. The β predictions at a rate of 0.45 km⁻¹ exhibit a notable increase in residual values compared to the previous range of +0.005 to −0.005 km⁻¹. Similarly, for H′ values exceeding the predicted threshold of 66 km, the residuals fall within the range of +0.25 to −0.25 km.

The analysis of feature importance involved the ranking of features based on their informedness. Consistent with expectations, the X-ray irradiance feature exhibited the highest importance, accounting for approximately 89% of the overall feature importance. Following this, the rolling median statistic with a 5 min window demonstrated a significance of 8.38%. The collective contribution of additional features amounts to approximately 2.76% of the informedness for the model, suggesting that these features can be readily modified or eliminated to align with the researcher’s requirements. One potential challenge faced by researchers is the exclusion of the initial 60 data points from the analysis due to the implementation of a rolling window statistic with a duration of 60 min. However, it is worth noting that from the information given by the feature importance analysis, these features can be disregarded without compromising the model’s effectiveness, thus enabling the development of an equally proficient model.

4. Conclusions

The employment of ML regression techniques on the provided SF data yielded significant insights into the feasibility of modeling ionospheric parameters without relying on the complicated and difficult to use software, e.g., LWPC software. One possible advantage of this approach, provided that the models are optimized, and the error rates are minimized, is the possibility of automatically determining ionospheric parameters in real-time or, at the very least, near-real time. Also, another potential benefit of such a model is the determination of the ED from the ionospheric parameters. The primary findings of this research can be summarized as:

• The utilization of synthetic data estimated using the KDE technique yielded datasets that were deemed adequate for ML modeling, as they closely adhered to the distribution of the original dataset. Further investigation is required to validate the outcomes of this study. Subsequent research should involve a more extensive dataset and, if feasible, refrain from relying on synthetic data, instead opting for a greater number of original samples. In relation to the present study, the utilization of synthetic data proved to be adequate, as the primary aim of this research was to determine the feasibility of employing ML regression techniques for the estimation of ionospheric parameters.
• The RF and XGB algorithms demonstrated adequate performance; however, the KNN and DT algorithms exhibited greater error rates compared to the aforementioned techniques. Subsequent investigations ought to integrate and prioritize the utilization of ANNs due to their benefits; however, they do necessitate careful hyperparameter tuning in order not overfit the model. Regarding XGB, it is worth noting that it possesses an additional hyperparameter compared to RF. This additional hyperparameter allows for finer adjustments to the model, perhaps leading to improved predictions. Nevertheless, both RF and XGB are highly recommended as primary methodologies for investigating concepts that have not been completely explored.
• The residual analysis conducted in this study revealed that the final model had a possible minor bias towards predicting H′ values greater than 62 km, with a reduced error rate compared to predictions below 62 km.
• The results obtained from the time-series based approach exhibited a higher level of favorability compared to the instance-based approach, as indicated by the lower error rates. The model exhibited a potential bias in both the β and H′ parameters. Specifically, the β parameter demonstrated an increasing error rate as the predicted value increased, whereas the H′ parameter showed a decreasing error rate as the predicted value increased. Future research should consider placing more emphasis on a time-series based approach. This approach has shown the ability to efficiently present precise values of waveguide parameters over an extended period of time. Additionally, it has been observed that the features of this approach can be customized to meet the specific requirements of the researcher. Notably, it has been found that only two features contribute significantly to the informativeness of the model.
• Standard methods for determining ionospheric parameters are tedious and time-consuming, necessitating the development of other methods for determining such parameters. As to our knowledge, the literature and freely available methods for providing ionospheric parameters utilizing ML are not widely realized. Future comparison of the displayed ML method can be performed with methods such as easyFit and FlareED, where all the techniques can be tested and mutually compared under different SF classes and ionospheric perturbations.

The primary objective of this study is to employ an alternative approach for estimating low ionospheric parameters under the influence of SF events that enable easy modeling of this medium. An advantage of this method is the potential ability to streamline the process and obtain results in real-time or near-real time, as well as the potential to obtain parameters for the calculation of ED. However, further investigation is required to refine the methodology, investigate alternative algorithms, and explore additional pre-processing techniques. The wider statistical determination of the capabilities of the model for all SF classes can be enabled with additional data. As expected, the majority of the data fell within the C or M class, and future research is needed with more B- (barely detectable except in conditions of solar minimum) and X-class SFs. The research demonstrates the promise of the approach; nonetheless, additional comprehensive research is required to ensure its readiness for production.